数值分析实验报告--最小二乘拟合
最小二乘法数值分析实验报告

最小二乘法数值分析实验报告最小二乘法数值分析实验报告篇一:数值分析+最小二乘法实验报告数学与信息工程学院实课程名称:实验室:实验台号:班级:姓名:实验日期:验报告数值分析 201X年 4 月 13日篇二:数值分析上机实验最小二乘法数值分析实验报告五最小二乘法一、题目设有如下数据用三次多项式拟合这组数据,并绘出图形。
二、方法最小二乘法三、程序M文件:sy ms x f; xx=input( 请输入插值节点 as [x1,x2...]\n ff=i nput( 请输入插值节点处对应的函数值 as [f1,f 2...]\n m=input(请输入要求的插值次数m= n=leng th(xx); fr i=1:(m+1) syms faix; fai=x^(i-1); fr j=1:n x=xx(j);H(i,j)=eval(fai); end endA=ff*(H) *inv(H*(H) syms x; f=0; fr i=1:(m+1) f=f+A(i)*x^(i-1); end f plt(xx,ff, * ) hldnezplt(f,[xx(1),xx(n)])四、结果 sav e and run之后:请输入插值节点 as [x1,x2...] [-3 -2-1 0 1 2 3] 请输入插值节点处对应的函数值 as[f1,f2...] [-1.76 0.42 1.21.341.432.254.38]请输入要求的插值次数m=3 f =133/100+121469856021/35184372088832*x-8042142191733/450359 9627370496*x^2+1020815915537309/9007199254740992*x^3五、拓展:最小二乘法计算方法比较简单,是实际中常用的一种方法,但是必须经计算机来实现,如果要保证精度则需要对大量数据进行拟合,计算量很大。
最小二乘法的实验报告

最小二乘法的实验报告最小二乘法的实验报告引言:最小二乘法是一种常用的数学方法,用于拟合数据和求解最优解。
它适用于各种领域,如统计学、经济学、工程学等。
本实验旨在通过实际案例,探讨最小二乘法在实际问题中的应用和效果。
一、实验目的本实验旨在通过最小二乘法,对一组实际数据进行拟合,得出最佳拟合曲线,并分析拟合结果的合理性和可靠性。
二、实验材料与方法1. 实验材料:- 一组实际数据:包含自变量和因变量的数据对。
- 计算机软件:如MATLAB、Python等,用于进行最小二乘法计算和绘制拟合曲线。
2. 实验方法:- 数据处理:对实际数据进行预处理,包括数据清洗、异常值处理等。
- 模型选择:根据实际问题和数据特点,选择适当的拟合模型。
- 参数估计:利用最小二乘法,求解模型参数的最优估计值。
- 拟合效果评估:通过计算残差平方和、确定系数等指标,评估拟合效果的好坏。
三、实验过程与结果1. 数据处理:在本实验中,我们选择了一组汽车销量与广告投入的数据。
首先,我们对数据进行了清洗,排除了异常值和缺失值。
2. 模型选择:根据实际问题和数据特点,我们选择了线性模型进行拟合。
即假设广告投入与汽车销量之间存在线性关系。
3. 参数估计:利用最小二乘法,我们求解了线性模型的参数估计值。
具体计算过程如下: - 建立线性模型:y = β0 + β1x,其中y表示汽车销量,x表示广告投入。
- 最小化残差平方和:min Σ(yi - (β0 + β1xi))^2,其中yi为实际销量,xi为实际广告投入。
- 对β0和β1求偏导,并令偏导数为0,得到最优解的估计值。
4. 拟合效果评估:通过计算残差平方和和确定系数等指标,我们评估了拟合效果的好坏。
结果显示,残差平方和较小,确定系数较接近1,表明拟合效果较好。
四、实验讨论1. 拟合效果的合理性:通过对拟合效果的评估,我们认为拟合结果较为合理。
然而,我们也要注意到,拟合结果仅仅是对观测数据的一个估计,并不能完全代表真实情况。
最小二乘拟合实验报告

实验名称: 最小二乘拟合1 引言在科学实验和生产实践中,经常要从一组实验数据(,)(1,2,,)i i x y i m =出发,寻求函数y=f (x )的一个近似表达式y=φ(x),称为经验公式,从几何上来看,这就是一个曲线拟合的问题。
多项式的插值虽然在一定程度上解决了由函数表求函数近似表达式的问题,但用它来解决这里的问题,是有明显的缺陷的。
首先,由实验提供的数据往往有测试误差。
如果要求近似曲线y=φ(x)严格地通过所给的每个数据点(,)i i x y ,就会使曲线保留原来的测试误差,因此当个别数据的误差较大的时候,插值的效果是不理想的。
其次,当实验数据较多时,用插值法得到的近似表达式,明显缺乏实用价值。
在实验中,我们常常用最小二乘法来解决这类问题。
定义()i i i x y δϕ=-为拟合函数在i x 处的残差。
为了是近似曲线能尽量反映所给数据点的变化趋势,我们要求||i δ尽可能小。
在最小二乘法中,我们选取()x ϕ,使得偏差平方和最小,即2211[()]min mmi i i iix y δϕ===-=∑∑,这就是最小二乘法的原理。
2 实验目的和要求运用matlab 编写.m 文件,要求用最小二乘法确定参数。
以下一组数据中x 与y 之间存在着bx y ae =的关系,利用最小二乘法确定式中的参数a 和b ,并计算相应的军方误差与最大偏差。
数据如下:3 算法原理与流程图(1) 原理最小二乘是要求对于给定数据列(,)(1,2,,)i i x y i m =,要求存在某个函数类01{(),(),()}()n x x x n m ϕϕϕΦ=<中寻求一个函数:****0011()()()()n n x a x a x a x ϕϕϕϕ=+++,使得*()x ϕ满足*22()11[()]min[()]nni i i i x iix y x y ϕϕϕ∈Φ==-=-∑∑。
根据以上条件可知,点***01(,,,)n a a a 是多元函数2011(,,,)[()]m nn k k i i i kS a a a a x y ϕ===-∑∑ 的极小点,从而***01,,,na a a 满足方程组 0(0,1,,)kSk n a ∂==∂即00111111()()()()()()()mmmmk i i k i i n k i n i k i i i i i ia x x a x x a x x x y ϕϕϕϕϕϕϕ====+++=∑∑∑∑, 记1(,)()()mi i ih g h x g x ==∑,则上述方程组可表示成0011(,)(,)(,)(,)k k n k n k a a a f ϕϕϕϕϕϕϕ+++=,(k=0,1,…,n)写成矩阵形式为0001000101111101(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)n n n n n n n n a f a f a f ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,这个方程组成为法方程组,可以证明,当01(),(),()n x x x ϕϕϕ线性无关时,它有唯一解。
数值分析论文--曲线拟合的最小二乘法

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 数值分析论文--曲线拟合的最小二乘法曲线拟合的最小二乘法姓名:徐志超学号:2019730059 专业:材料工程学院:材料科学与工程学院科目:数值分析曲线拟合的最小二乘法一、目的和意义在物理实验中经常要观测两个有函数关系的物理量。
根据两个量的许多组观测数据来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。
这类问题通常有两种情况:一种是两个观测量 x 与 y 之间的函数形式已知,但一些参数未知,需要确定未知参数的最佳估计值;另一种是 x 与 y 之间的函数形式还不知道,需要找出它们之间的经验公式。
后一种情况常假设 x 与 y 之间的关系是一个待定的多项式,多项式系数就是待定的未知参数,从而可采用类似于前一种情况的处理方法。
在两个观测量中,往往总有一个量精度比另一个高得多,为简单起见把精度较高的观测量看作没有误差,并把这个观测量选作x,而把所有的误差只认为是y 的误差。
设 x 和 y 的函数关系由理论公式 y=f(x; c1, c2, cm)1 / 13(0-0-1)给出,其中 c1, c2, cm 是 m 个要通过实验确定的参数。
对于每组观测数据(xi, yi) i=1, 2,, N。
都对应于 xy 平面上一个点。
若不存在测量误差,则这些数据点都准确落在理论曲线上。
只要选取m 组测量值代入式(0-0-1),便得到方程组yi=f (x;c1,c2,cm)(0-0-2)式中 i=1,2,, m.求 m 个方程的联立解即得 m 个参数的数值。
显然Nm 时,参数不能确定。
在 Nm 的情况下,式(0-0-2)成为矛盾方程组,不能直接用解方程的方法求得 m 个参数值,只能用曲线拟合的方法来处理。
工程数值分析实验龙格库塔,最小二乘法

工程数值分析实验报告指导老师班级 学号 姓名实验一:最小二乘法拟合曲线实验一、实验名称:最小二乘法拟合曲线实验实验时间: 2015-5-14 实验地点: 主楼机房 实验器材: 计算机matlab二、实验目的:学会用最小二乘法求拟合数据的多项式,并应用算法于实际问题。
三、实验要求:(1)根据最小二乘法和加权最小二乘法的基本理论,编写程序构造拟合曲线的法方程,要求可以方便的调整拟合多项式的次数;(2)采用列主元法解(1)中构造的法方程,给出所拟合的多项式表达式; (3)编写程序计算所拟合多项式的均方误差,并作出离散函数 和拟合函数的图形; (4) 用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差,并用MATLAB 的内部函数plot 作出其图形,并与(1)的结果进行比较。
四、算法描述(实验原理与基础理论)基本原理:从整体上考虑近似函数 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)( (i=0,1,…,m) i i i y x p r -=)( (i=0,1,…,m)绝对值的最大值imi r ≤≤0max ,即误差 向量Tm r r r r ),,(10 = 的∞—范数;二是误差绝对值的和∑=mi ir,即误差向量r 的1—范数;三是误差平方和∑=mi ir2的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=mi ir2来 度量误差 i r (i=0,1,…,m)的五、实验内容:共有两组给定数据,把给定的数据拟合成多项式。
第一组给定数据点如表1所示如下:表1 数据表表2 数据表六、程序流程图七、实验结果ans =27-May-2015ans =7.3611e+05ans =1.0e+03 *2.0150 0.0050 0.0270 0.0140 0.0010 0.0213 >>八、实验结果分析实验程序 quxiannihe.m clear alldate,now,clockx0=[0.0 0.5 0.6 0.7 0.8 0.9 1.0]; y0=[1 1.75 1.96 2.19 2.44 2.71 3.00]; w=ones(size(x0)); x=0:0.01:1; %进行五次曲线拟合 N=5;for i=1:Na1=LSF(x0,y0,w,i) ; y=polyval(a1,x); figure(i)plot(x0,y0,'ok',x,y,'r') title('最小二乘法'); legend('y0','y'); xlabel('x'); ylabel('y'); end实验二:4阶经典龙格库塔法解常微分方程一、实验名称: 4阶经典龙格库塔法解常微分方程实验时间: 2015-5-14 实验地点: 主楼机房 实验器材: 计算机matlab二、实验目的:学习掌握4阶经典R-K 方法,体会参数和步长对问题的影响。
数值分析+最小二乘法实验报告

数学与信息工程学院
实验报告
课程名称:数值分析
实验室:
实验台号:
班级:
姓名:
实验日期:2012 年 4 月13 日
实验名称最小二乘法求多项式拟合
实验目的和要求(1)了解最小二乘法求多项式拟合原理和方法;
(2)通过实例掌握用MATLAB求拟合函数及拟合图像;(3)编程实现用最小二乘法求多项式拟合。
实验内容和步骤:
实验内容:
根据matlab编写算法,用最小二乘法求多项式拟合。
实验步骤:
(1)开启软件平台——MATLAB,编程;
在command window 编写程序,求出拟合函数
x=[-2,-1,0,1,2];
y=[-0.1,0.1,0.4,0.9,1.6];
>> p=polyfit(x,y,3);
>> pa=poly2str(p,'x')
pa =
0.0083333 x^3 + 0.085714 x^2 + 0.39167 x + 0.40857(2)根据数值解法步骤编写M文件;
x=[-2 -1 0 1 2];
y=[-0.1 0.1 0.4 0.9 1.6];
p1=polyfit(x,y,3)
x1=-3:0.01:3;
y1=polyval(p1,x1);
plot(x,y,'b^',x1,y1,'r-')
(3)观察运行结果。
实验数据记录:
实验结果分析:
1.画图中点与函数要用不同的表现法,否则图片就是五点的连接。
2.3次拟合比2次拟合更准确。
3.在写M文件时,注意数据点乘的运用。
成绩评定
签字:年月日。
数值分析实验之最小二乘拟合含有噪声扰动(python实现)

数值分析实验之最⼩⼆乘拟合含有噪声扰动(python实现)⼀、实验⽬的掌握最⼩⼆乘法拟合离散数据,多项式函数形式拟合曲线以及可以其他可以通过变量变换转化为多项式的拟合曲线⽬前待实现功能:1. 最⼩⼆乘法的基本实现。
2. ⽤不同数据量,不同参数,不同的多项式阶数,⽐较实验效果。
3. 语⾔python。
⼆、实验原理最⼩⼆乘法(⼜称最⼩平⽅法)是⼀种数学优化技术。
它通过最⼩化误差的平⽅和寻找数据的最佳函数匹配。
利⽤最⼩⼆乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平⽅和为最⼩。
最⼩⼆乘法还可⽤于曲线拟合。
其他⼀些优化问题也可通过最⼩化能量或最⼤化熵⽤最⼩⼆乘法来表达。
三、实验内容求y=f(x)=sin(x)+h(x)在区间[0,10]上按101等距节点确定的离散数据点组(x i,y i)的直线拟合以及曲线拟合,其中是服从h(x)标准正态分布的噪声扰动四、程序实现• ⼀次拟合:1import numpy as np2import matplotlib.pyplot as plt3import math4#定义x、y散点坐标5 x = np.arange(0.0, 10.0,0.1)6 x = np.array(x)7print('x is :\n',x)8 num = np.sin(x)+np.random.randn(100)9 y = np.array(num)10print('y is :\n',y)11 f1 = np.polyfit(x, y, 1)#⽤1次多项式拟合,若要多次拟合,相应的改变这个常数即可12print('f1 is :\n',f1)1314 p1 = np.poly1d(f1)15print('p1 is :\n',p1)1617#也可使⽤yvals=np.polyval(f1, x)18 yvals = p1(x) #拟合y值19print('yvals is :\n',yvals)20#绘图21 plot1 = plt.plot(x, y, 's',label='original values',color="blue")22 plot2 = plt.plot(x, yvals, 'r',label='polyfit values',color="red")23 plt.xlabel('x')24 plt.ylabel('y')25 plt.legend(loc=4) #指定legend的位置右下⾓26 plt.title('polyfitting')27 plt.show()运⾏结果:所得图形:• 曲线拟合(⽤a*sin(x)+b拟合):1import numpy as np2import matplotlib.pyplot as plt3import math4from scipy.optimize import curve_fit56#⾃定义函数7def func(x, a, b):8return a*np.sin(x)+b910#定义x、y散点坐标11 x = np.arange(0.0, 10.0,0.1)12 x = np.array(x)13 num = np.sin(x)+np.random.randn(100)14 y = np.array(num)1516#⾮线性最⼩⼆乘法拟合17 popt, pcov = curve_fit(func, x, y)18#获取popt⾥⾯是拟合系数19print(popt)20 a = popt[0]21 b = popt[1]22#c = popt[2]23#d = popt[3]24#e = popt[4]25 yvals = func(x,a,b) #拟合y值26print('popt:', popt)27print('系数a:', a)28print('系数b:', b)29#print('系数c:', c)30#print('系数d:', d)31#print('系数e:', e)32print('系数pcov:', pcov)#⽅差33print('系数yvals:', yvals)#x代⼊拟合出的函数得到的函数值34#绘图35 plot1 = plt.plot(x, y, 's',label='original values',color="purple")36 x_test = np.arange(0.0, 10.0, 0.01)37 y_test = func(x_test,a,b)38 plot2 = plt.plot(x_test, y_test, 'r',label='polyfit values',color="red")39 plt.xlabel('x')40 plt.ylabel('y')41 plt.legend(loc=4) #指定legend的位置右下⾓42 plt.title('curve_fit')43 plt.show()运⾏结果所得图形:•曲线拟合(⽤a*np.sin(b*x+c)+d拟合):1import numpy as np2import matplotlib.pyplot as plt3import math4from scipy.optimize import curve_fit56#⾃定义函数7def func(x, a, b, c, d):8return a*np.sin(b*x+c)+d910#定义x、y散点坐标11 x = np.arange(0.0, 10.0,0.1)12 x = np.array(x)13 num = np.sin(x)+np.random.randn(100)14 y = np.array(num)1516#⾮线性最⼩⼆乘法拟合17 popt, pcov = curve_fit(func, x, y)18#获取popt⾥⾯是拟合系数19print(popt)20 a = popt[0]21 b = popt[1]22 c = popt[2]23 d = popt[3]24 yvals = func(x,a,b,c,d) #拟合y值25print('popt:', popt)26print('系数a:', a)27print('系数b:', b)28print('系数c:', c)29print('系数d:', d)30print('系数pcov:', pcov)#⽅差31print('系数yvals:', yvals)#x代⼊拟合出的函数得到的函数值32#绘图33 plot1 = plt.plot(x, y, 's',label='original values',color='orange')34 x_test = np.arange(0.0, 10.0, 0.01)35 y_test = func(x_test,a,b,c,d)36 plot2 = plt.plot(x_test, y_test, 'r',label='polyfit values',color='brown')37 plt.xlabel('x')38 plt.ylabel('y')39 plt.legend(loc=4) #指定legend的位置右下⾓40 plt.title('curve_fit')41 plt.show()运⾏结果:所得图形:•⾃定义函数实现:1import numpy as np2import matplotlib.pyplot as plt3import math4from scipy.optimize import curve_fit56#⾃定义函数7def func(x, a0,a1,a2,a3,a4,a5,a6,a7,a8,b1,b2,b3,b4,b5,b6,b7,b8,w):8return a0 + a1*np.cos(x*w) + b1*np.sin(x*w) + \9 a2*np.cos(2*x*w) + b2*np.sin(2*x*w) + a3*np.cos(3*x*w) + b3*np.sin(3*x*w) + \10 a4*np.cos(4*x*w) + b4*np.sin(4*x*w) + a5*np.cos(5*x*w) + b5*np.sin(5*x*w) + \11 a6*np.cos(6*x*w) + b6*np.sin(6*x*w) + a7*np.cos(7*x*w) + b7*np.sin(7*x*w) + \12 a8*np.cos(8*x*w) + b8*np.sin(8*x*w)1314#定义x、y散点坐标15 x = np.arange(0.0, 10.0,0.1)16 x = np.array(x)17 num = np.sin(x)+np.random.randn(100)18 y = np.array(num)1920#⾮线性最⼩⼆乘法拟合21 popt, pcov = curve_fit(func, x, y)22#获取popt⾥⾯是拟合系数23print(popt)24 a0 = popt[0]25 a1 = popt[1]26 a2 = popt[2]27 a3 = popt[3]28 a4 = popt[4]29 a5 = popt[5]30 a6 = popt[6]31 a7 = popt[7]32 a8 = popt[8]33 b1 = popt[9]34 b2 = popt[10]35 b3 = popt[11]36 b4 = popt[12]37 b5 = popt[13]38 b6 = popt[14]39 b7 = popt[15]40 b8 = popt[16]41 w = popt[17]42 yvals = func(x,a0,a1,a2,a3,a4,a5,a6,a7,a8,b1,b2,b3,b4,b5,b6,b7,b8,w) #拟合y值43print('popt:', popt)44print('系数a0:', a0)45print('系数a1:', a1)46print('系数a2:', a2)47print('系数a3:', a3)48print('系数a4:', a4)49print('系数a5:', a5)50print('系数a6:', a6)51print('系数a7:', a7)52print('系数a8:', a8)53print('系数b1:', b1)54print('系数b2:', b2)55print('系数b3:', b3)56print('系数b4:', b4)57print('系数b5:', b5)58print('系数b6:', b6)59print('系数b7:', b7)60print('系数b8:', b8)61print('系数w:', w)62print('系数pcov:', pcov)#⽅差63print('系数yvals:', yvals)#x代⼊拟合出的函数得到的函数值64#绘图65 plot1 = plt.plot(x, y, 's',label='original values',color='yellow')66 x_test = np.arange(0.0, 10.0, 0.01)67 y_test = func(x_test,a0,a1,a2,a3,a4,a5,a6,a7,a8,b1,b2,b3,b4,b5,b6,b7,b8,w)68 plot2 = plt.plot(x_test, y_test, 'r',label='polyfit values',color='blue')69 plt.xlabel('x')70 plt.ylabel('y')71 plt.legend(loc=4) #指定legend的位置右下⾓72 plt.title('curve_fit')73 plt.show()所得图形:⼼得体会通过本次实验,我对MATLAB的操作更加熟悉,也对本学期正在学习的Python有了更深层次的认识,对着两种编程软件更加熟悉。
实验4 最小二乘拟合法
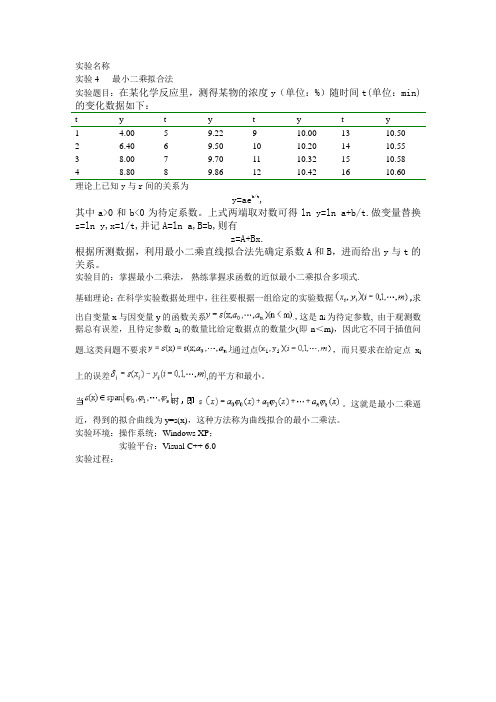
实验名称实验4 最小二乘拟合法实验题目:在某化学反应里,测得某物的浓度y(单位:%)随时间t(单位:min)的变化数据如下:t y t y t y t y1 4.00 5 9.22 9 10.00 13 10.502 6.40 6 9.50 10 10.20 14 10.553 8.00 7 9.70 11 10.32 15 10.584 8.80 8 9.86 12 10.42 16 10.60理论上已知y与r间的关系为y=ae b/t,其中a>0和b<0为待定系数。
上式两端取对数可得ln y=ln a+b/t.做变量替换z=ln y,x=1/t,并记A=ln a,B=b,则有z=A+Bx.根据所测数据,利用最小二乘直线拟合法先确定系数A和B,进而给出y与t的关系。
实验目的:掌握最小二乘法,熟练掌握求函数的近似最小二乘拟合多项式.基础理论:在科学实验数据处理中,往往要根据一组给定的实验数据求出自变量x与因变量y的函数关系,这是a i为待定参数, 由于观测数据总有误差,且待定参数a i的数量比给定数据点的数量少(即n<m),因此它不同于插值问题.这类问题不要求通过点,而只要求在给定点x i 上的误差,的平方和最小。
这就是最小二乘逼近,得到的拟合曲线为y=s(x),这种方法称为曲线拟合的最小二乘法。
实验环境:操作系统:Windows XP;实验平台:Visual C++ 6.0实验过程:附录:#include<stdio.h>int main(){double a0,a1,sumTi=0,sumTi2=0,sumRi=0,TiRi=0;double T[100],R[100];int n,m,i,j;printf("输入数据的个数n:");scanf("%d",&n);printf("输入各组数据T[i]与R[i]:\n");m=n;i=0;j=0;while(n--)scanf("%lf%lf",&T[i],&R[i++]);printf("%d\n",i);for(j=0;j<i;j++){sumTi+=T[j];sumRi+=R[j];sumTi2+=T[j]*T[j];TiRi+=T[j]*R[j];}a0=-(sumTi*TiRi-sumTi2*sumRi)/(m*sumTi2-sumTi*sumTi);a1=(m*TiRi-sumTi*sumRi)/(m*sumTi2-sumTi*sumTi);printf("a0=%.3lf a1=%.3lf\n",a0,a1);printf("最小二乘拟合曲线为:R=%.3lf+%.3lfT\n",a0,a1);return 0;}。
最小二乘法实验报告

最小二乘法实验报告最小二乘法实验报告引言最小二乘法是一种常用的数学方法,用于拟合数据和估计模型参数。
它通过最小化观测值与理论值之间的误差平方和,寻找最优解。
本实验旨在通过实际数据拟合的方式,探索最小二乘法的原理和应用。
实验步骤1. 数据采集在实验开始前,我们选择了一个简单的线性回归模型进行拟合。
为了收集数据,我们在实验室里设置了一个简单的装置,用于测量物体的运动距离和所需时间。
通过多次重复实验,我们得到了一组数据,包括物体运动距离和所需时间的测量值。
2. 数据处理在进行最小二乘法拟合之前,我们需要对数据进行处理。
首先,我们计算每次实验的平均速度,通过将运动距离除以所需时间得到。
然后,我们将平均速度作为自变量,所需时间作为因变量,得到一组有序的数据点。
3. 拟合模型接下来,我们使用最小二乘法来拟合线性回归模型。
线性回归模型可以表示为:y = a + bx,其中y是因变量(所需时间),x是自变量(平均速度),a和b是待估计的模型参数。
通过最小化残差平方和,我们可以得到最优的a和b的估计值。
4. 拟合结果分析通过最小二乘法拟合得到的模型参数估计值,我们可以进一步分析拟合结果的准确性和可靠性。
首先,我们计算拟合优度,即拟合值与观测值之间的相关系数。
较高的拟合优度表明模型拟合效果较好。
此外,我们还可以计算参数估计的标准误差,用于评估参数估计值的可靠性。
结果与讨论在本实验中,我们使用最小二乘法对一组实际测量数据进行了线性回归拟合。
通过计算拟合优度,我们发现拟合效果较好,相关系数接近1。
这表明我们选择的线性回归模型较为合适,并且可以用于预测因变量(所需时间)。
此外,我们还计算了参数估计的标准误差。
标准误差是对参数估计值的精度进行评估的指标。
较小的标准误差表示参数估计值较可靠。
通过计算,我们发现参数估计值的标准误差较小,说明我们得到的模型参数估计值较为准确。
结论通过本实验,我们深入了解了最小二乘法的原理和应用。
《数学实验》实验报告——最小二乘法
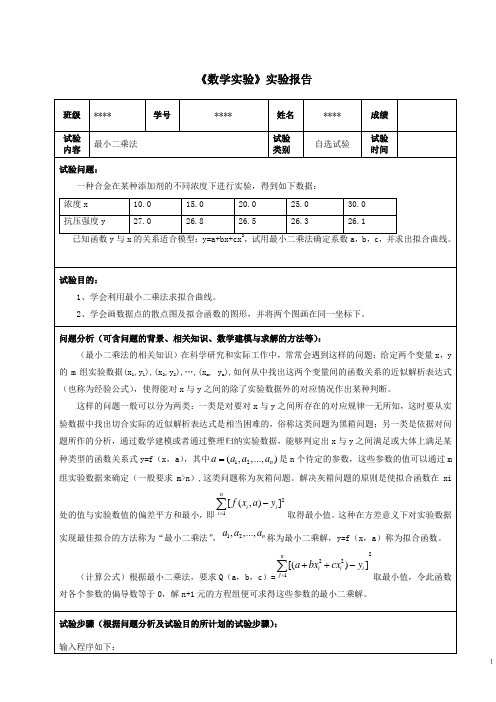
《数学实验》实验报告1x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02]];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25}];Show[t1,t2]首先得到a,b,c三个值: {{a->27.56,b->-0.0574286,c->0.000285714}}然后得到同一坐标系下的数据点散点图及拟合函数的图形:试验过程(含详细试验步骤、程序清单及异常情况记录等)输入以下mathematica语句求解参数a,b,c:运行后可得解:2为求得数据点的散点图及拟合函数的图形,输入以下语句,并将两个图画在同一坐标下:运行得:3在最开始时,我输入的程序是这样的:x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02],DisplayFunction->Identity];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25},DisplayFunction->Identity];Show[t1,t2, DisplayFunction->$ DisplayFunction]然而得到的结果没有图形(如下):我比照了老师的讲义,改动了“DisplayFunction->Identity”,可是,结果还是一样,没有图形。
数值分析(22)离散数据的最小二乘拟合

xi
m i0
(
m
n)上至多只有n个不同零点,则称0
(
x
),
1
(
x),
...,
n
(
x
)在点集
xi
m i0
上满足Haar条件。
可以证明,如果0
(
x
),
1
(
x),
...,
n
(
x
)在
xi
m i0
上满足
Haar条件,则法方程的系数矩阵非奇异。
数值分析
数值分析
法方程的另一种形式
记 A (0 , 1 , ..., n ), 由矩阵乘法可知 G ATWA,F ATWY
则
1
A
1
x0 x1
x02 x12
x0n x1n
1
xm
xm2
xmn
m
实际计算中要计算x0n,x1n,...,xmn , xik ,(k 0,1, ..., 2n)
i 1
当数据点数值很大时,可能会在计算中溢出,可采用
P240的方法处理。
数值分析
数值分析
三、法方程的求解
求解法方程AT AC ATY或GC F (取W I )
1.确定n+1个线性无关函数
j( x)
n 的具体形式
j=0
常用的代数多项式拟合是取
j( x)=x j (j 0,1, , n) 最佳平方逼近函数的形式是
s( x)=c0 c1 x c2 x2 cn xn
G
(1
工程数值分析实验龙格库塔最小二乘法

工程数值分析实验报告指导老师班级学号姓名实验一:最小二乘法拟合曲线实验一、实验名称:最小二乘法拟合曲线实验实验时间: 2015-5-14实验地点:主楼机房实验器材:计算机matlab二、实验目的:学会用最小二乘法求拟合数据的多项式,并应用算法于实际问题。
三、实验要求:(1)根据最小二乘法和加权最小二乘法的基本理论,编写程序构造拟合曲线的法方程,要求可以方便的调整拟合多项式的次数;(2)采用列主元法解(1)中构造的法方程,给出所拟合的多项式表达式;(3)编写程序计算所拟合多项式的均方误差,并作出离散函数和拟合函数的图形;(4) 用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差,并用MATLAB 的内部函数plot 作出其图形,并与(1)的结果进行比较。
四、算法描述(实验原理与基础理论)基本原理:从整体上考虑近似函数 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)( (i=0,1,…,m)的大小,常用的方法有以下三种:一是误差i i i y x p r -=)( (i=0,1,…,m)绝对值的最大值i m i r ≤≤0max ,即误差 向量T m r r r r ),,(10 = 的∞—范数;二是误差绝对值的和∑=m i i r 0,即误差向量r 的1—范数;三是误差平方和∑=m i i r02 的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=m i i r 02 来 度量误差 i r (i=0,1,…,m)的整体大小。
五、实验内容:共有两组给定数据,把给定的数据拟合成多项式。
第一组给定数据点如表1所示如下:表1 数据表0.5 0.6 0.7 0.8 0.9 1.01 1.75 1.96 2.19 2.44 2.71 3.00表2 数据表六、程序流程图七、实验结果>> zuixiaoerchenfa ans =27-May-2015ans =+05ans =+03 *>>八、实验结果分析实验程序clear alldate,now,clockx0=[ ];y0=[1 ];w=ones(size(x0));x=0::1;%进行五次曲线拟合N=5;for i=1:Na1=LSF(x0,y0,w,i) ;y=polyval(a1,x);figure(i)plot(x0,y0,'ok',x,y,'r') title('最小二乘法'); legend('y0','y');xlabel('x');ylabel('y');end实验二:4阶经典龙格库塔法解常微分方程一、实验名称: 4阶经典龙格库塔法解常微分方程实验时间: 2015-5-14实验地点:主楼机房实验器材:计算机matlab二、实验目的:学习掌握4阶经典R-K方法,体会参数和步长对问题的影响。
最小二乘法实验报告

最小二乘法实验报告1. 引言最小二乘法是一种常用的参数估计方法,用于求解线性回归问题。
本实验旨在通过使用最小二乘法,从一组给定的数据点中拟合出一条最优的直线。
本报告将详细介绍实验的步骤和思路。
2. 实验步骤2.1 数据收集首先,我们需要收集一组数据点作为实验的输入。
可以通过实地调查、采集历史数据或利用模拟工具生成数据集。
为了简化实验过程,我们假设已经收集到了一组包含 x 和 y 坐标的数据点,分别表示自变量和因变量。
2.2 数据可视化在进行最小二乘法拟合之前,我们先对数据进行可视化分析。
使用数据可视化工具(如Matplotlib),绘制出数据点的散点图。
这有助于我们直观地观察数据的分布特征,并初步判断是否适用线性回归模型。
2.3 参数计算最小二乘法的目标是找到一条直线,使得所有数据点到该直线的距离之和最小。
为了实现这个目标,我们需要计算直线的参数。
设直线的方程为 y = ax + b,其中 a 和 b 是待求的参数。
为了求解这两个参数,我们需要利用数据集中的 x 和 y 坐标。
首先,我们计算x 的均值(记作 x_mean)和 y 的均值(记作 y_mean)。
然后,计算 x 与 x_mean的差值(记作 dx)和 y 与 y_mean 的差值(记作 dy)。
接下来,我们计算直线的斜率 a,使用以下公式:a = sum(dx * dy) / sum(dx^2)最后,计算直线的截距 b,使用以下公式:b = y_mean - a * x_mean2.4 拟合直线通过上述步骤,我们得到了直线的斜率 a 和截距 b 的值。
现在,我们将利用这些参数将直线绘制在散点图上,以观察拟合效果。
使用绘图工具,绘制出散点图和拟合的直线。
直线应当通过散点的中心,并尽可能贴近这些点。
通过观察可视化结果,我们可以初步评估拟合的效果。
2.5 评估拟合效果为了定量评估拟合的效果,我们需要引入误差指标。
最常用的误差指标是均方误差(Mean Squared Error,简称MSE),定义如下:MSE = sum((y - (ax + b))^2) / n其中,y 是实际的因变量值,(ax + b) 是拟合直线给出的因变量值,n 是数据点的数量。
数值分析最小二乘拟合法实验报告
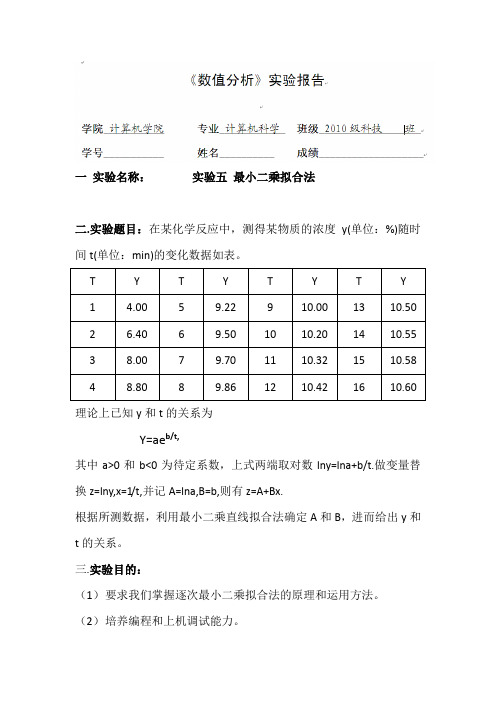
一实验名称:实验五最小二乘拟合法二.实验题目:在某化学反应中,测得某物质的浓度y(单位:%)随时间t(单位:min)的变化数据如表。
理论上已知y和t的关系为Y=ae b/t,其中a>0和b<0为待定系数,上式两端取对数lny=lna+b/t.做变量替换z=lny,x=1/t,并记A=lna,B=b,则有z=A+Bx.根据所测数据,利用最小二乘直线拟合法确定A和B,进而给出y和t的关系。
三.实验目的:(1)要求我们掌握逐次最小二乘拟合法的原理和运用方法。
(2)培养编程和上机调试能力。
四.基础理论:要求会熟练运用C语言中的基本数学函数和逐次超松弛迭代法的具体操作思路。
五.实验环境:必须要有一台PC机,并且装有winXP,win7及以上版本的操作系统,还必须有Visual C++6.0或其他编程软件。
六实验过程:理解题意,然后试着在草稿纸上写出伪代码,接着再用C语言编译,接着要在编程环境中调试。
在实验过程中,经常遇到一些棘手的问题,需要通过百度才能够解决,最后还是很艰难的把代码都做好,最后写成实验报告。
七.实验完整代码:#include<stdio.h>#include<math.h>void main(){int i,n;doubletx,ty,x[16],y[16],sum_x=0,sum_y=0,sum_x2=0,sum_xy=0,D,a,b, A,B;for(i=0;i<16;i++){scanf("f%f",&tx,&ty);x[i]=1/tx,y[i]=log(ty);}for(i=0;i<15;i++){sum_x=sum_x+x[i];sum_x2=sum_x2+x[i]*x[i];sum_y=sum_y+y[i];sum_xy=sum_xy+x[i]*y[i];}D=sum_x2*15-sum_x*sum_x;a=(n*sum_xy-sum_x*sum_y)/D;b=(sum_x2*sum_y-sum_x*sum_xy)/D;A=log(a);B=b;printf("A=%.6f B= %.6f\n");}八实验结果:y=11.343e-1.057/t.。
最小二乘法曲线拟合实验报告

竭诚为您提供优质文档/双击可除最小二乘法曲线拟合实验报告篇一:实验3曲线拟合的最小二乘法实验三曲线拟合的最小二乘法1、实验目的:在科学研究与工程技术中,常常需要从一组测量数据出发,寻找变量的函数关系的近似表达式,使得逼近函数从总体上与已知函数的偏差按某种方法度量能达到最小而又不一定过全部的点。
这是工程中引入最小二曲线拟合法的出发点。
充分掌握:1.最小二乘法的基本原理;2.用多项式作最小二乘曲线拟合原理的基础上,通过编程实现一组实验数据的最小二乘拟合曲线。
2、实验要求:1)认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法;2)编写上机实验程序,作好上机前的准备工作;3)上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果);4)分析和解释计算结果;5)按照要求书写实验报告;3、实验内容:1)给定数据如下:x:0.15,0.4,0.6,1.01,1.5,2.2,2.4,2.7,2.9,3.5,3.8,4.4,4.6,5.1,6.6,7.6;y:4.4964,5.1284,5.6931,6.2884,7.0989,7.5507,7.5106,8.0756,7.8708,8.2403,8.5303,8.7394,8.9981,9.1450,9.5070,9.9115;试作出幂函数拟合数据。
2)已知一组数据:x:0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1y:-0.447,1.978,3.28,6.16,7.08,7.34,7.66,9.56,9.48,9.30,11.2;试用最小二乘法求多项式函数,使与此组数据相拟合。
4、题目:曲线拟合的最小二乘法5、原理:从整体上考虑近似函数同所给数据点(i=0,1,…,m)误差(i=0,1,…,m)的大小,常用的方法有以下三种:一是误差(i=0,1,…,m)绝对值的最大值,即误差向量的∞—范数;二是误差绝对值的和,即误差向量r的1—范数;三是误差平方和的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2—范数的平方,因此在曲线拟常采用误差平方和来度量误差(i=0,1,…,m)的整体大小.。
数值分析最小二乘法

y
t
F (1 )(t)
8.6 06 t 1 2.6 11 822
y = F(t) 是指数形式 yabe /t (b0)
为了确定a 与b,对上式两边取对数得
lnylnab
令
yˆlny,Aln ta,x1
t
于是由 (ti , yi ) 计算出 (xi, yˆi) ,拟合数 据 (xi, yˆi) 的曲线仍设为
根据这些条件,可设想两种形式的函数关系:
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
y = F(t) 是指数形式 yaeb/t
b<0
y = F(t) 是双曲线型
1ab,即 y t
yt
(a t b)
为了确定a、b,令
y 1, x1
y
t
于是可用 x 的线性函数 S1(x)abx拟合 数据 (x i,y i) (i 1 ,.1 .)。.6 (,xi, yi) 可由原始 数据 (ti , yi ) 计算出来。
解 根据所给数据,在坐标纸上标出,得以下 图y
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就根本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反响未开始,浓 度为0。概括起来为
(1)y是t的增函数 ; (2)当t 0时,y 0; (3)t 时,y趋于一个定值
二、求解方法
求S*(x)
求如下多元函数的最小值
m
n
I(a 0,a 1,.a .n .) , (xi)[aj j(xi)f(xi)2 ]
i 0
j 0
由多元函数 求极值的必 要条件
I 0, (k0,1,,n) 即 ak
数值分析曲线拟合的最小二乘法实验报告

数值分析曲线拟合的最小二乘法实验报告数值分析曲线拟合的最小二乘法实验报告篇一:数值分析设计曲线拟合的最小二乘法曲线拟合的最小二乘法一、目的和意义在科学实验的统计方法研究中,往往要从一组实验数据?xi,yi??i?0,1,2,?,m?中,寻找自变量x与因变量y之间的函数关系y?F?x?。
由于观测数据往往不准确,因此不要求y?F?x?经过所有点?xi,yi?,而只要求在给定点xi上误差而只要求所在所有给定点xi上的误差?i?F(xi)?yi ?i?0,1,2,?,m?按某种标准最小。
若记????0,?1,?2,?,?m?,就是要求向量?的范数如果用最大范数,计算上困难较大,通常采用欧式范数?最小。
2T 作为误差度量的标准。
F?x?的函数类型往往与实验的物理背景以及数据的实际分布有关,它一般含有某些待定参数。
如果F?x?是所有待定参数的线性函数,那么相应的问题称为线性最小二乘问题,否则称为非线性最小二乘问题。
最小二乘法还是实验数据参数估计的重要工具。
这是因为这种方法比其他方法更容易理解,即使在其他方法失效的情况下,用最小二乘法还能提供解答,而且从统计学的观点分析,用该方法求得各项估计具有最优统计特征,因此这一方法也是系统识别的重要基础。
线性最小二乘问题可以借助多元微分学知识通过求解法方程组得到解答。
用最小二乘法求拟合曲线时,首先要确定S?x?的形式。
这不单纯是数学问题,还与所研究问题的运动规律以及所得观测数据?xi,yi?有关;通常要从问题的运动规律以及给定数据描图,确定S?x?的形式,并通过实际计算选出较好的结果。
为了使问题的提法更有一般性,通常把最小二乘法中的? 22 都考虑为加权平方和22 ? ????xi???S?xi??f?xi??? i?0 m 2 这里??xi??0是?a,b?上的加权函数,它表示不同点?xi,f?xi?处的数据比重不同。
?二、计算方法在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量y与时间t的拟合曲线。
数值分析拟合实验报告(3篇)

第1篇一、实验目的本次实验旨在通过数值分析方法对一组已知数据点进行拟合,掌握线性插值、多项式插值、样条插值等方法的基本原理和实现过程,并学会使用MATLAB进行数值拟合。
二、实验内容1. 线性插值线性插值是一种简单的插值方法,适用于数据点分布较为均匀的情况。
其基本原理是通过两个相邻的数据点,利用线性关系拟合出一条直线,然后通过该直线来估算未知的值。
2. 多项式插值多项式插值是一种较为精确的插值方法,通过构造一个多项式函数来逼近已知数据点。
其基本原理是利用最小二乘法求解多项式的系数,使得多项式在已知数据点上的误差最小。
3. 样条插值样条插值是一种更灵活的插值方法,通过构造一系列样条曲线来逼近已知数据点。
其基本原理是利用最小二乘法求解样条曲线的系数,使得样条曲线在已知数据点上的误差最小。
三、实验步骤1. 线性插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`linspace`生成插值点:xi = linspace(1, 5, 100);(3)使用MATLAB内置函数`interp1`进行线性插值:yi = interp1(x, y, xi, 'linear');(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');2. 多项式插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`polyfit`求解多项式系数:p = polyfit(x, y, 3);(3)使用MATLAB内置函数`polyval`进行多项式插值:yi = polyval(p, xi);(4)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');3. 样条插值(1)在MATLAB中输入已知数据点,如:x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];(2)使用MATLAB内置函数`spline`进行样条插值:yi = spline(x, y, xi);(3)绘制插值曲线:plot(xi, yi, 'b-', x, y, 'ro');四、实验结果与分析1. 线性插值线性插值方法简单易行,但精度较低,适用于数据点分布较为均匀的情况。
数值分析大作业曲线拟合的最小二乘法

数值分析上机作业实验报告专业:建筑与土木工程姓名:学号:联系电话:课题四 曲线拟合的最小二乘法一、问题提出从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。
在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量 y 与时间t 的拟合曲线。
二、要求1 、用最小二乘法进行曲线拟合;2 、近似解析表达式为()t ϕ=a 1t+a 2t 2+a 3t 33 、打印出拟合函数()t ϕ,并打印出()tj ϕ与()y tj 的误差,j=1,2...,12:4 、另外选取一个近似表达式,尝试拟合效果的比较;5 、* 绘制出曲线拟合图﹡。
三、目的和意义1 、掌握曲线拟合的最小二乘法;2 、最小二乘法亦可用于解超定线代数方程组;3 、探索拟合函数的选择与拟合精度间的关系。
四、实验结果:1.用最小二乘法做出的曲线拟合为三次多项式a1= -0.0052 ,a2= 0.2634 ,a3= 0.0178。
()tϕ= (-0.0052) t+ (0.2634) t2 + (0.0178) t3三次多项式的误差平方和=0.2583。
图形为:图形上红线表示拟合曲线,*表示实验所给的点。
源代码为:x=[0,5,10,15,20,25,30,35,40,45,50,55];y=[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.02,4.64]; a1=polyfit(x,y,3) %三次多项式拟合%b1= polyval(a1,x)r1= sum((y-b1).^2) %三次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%(说明本程序调用了MATLAB中的函数polyfit、polyval、plot)2.另外选取几个近似表达式:主要选取6次、9次和12次的拟合表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验过程:
一、根据所给数据作出温度随时间变化的散点图。
>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>>stem(x,y,'k*')
点的标记是黑色的*.
这是温度随时间变化的散点图。
二、输入数据,拟合出各类函数的各个系数。
(用polyfit
命令来求拟合系数)
(1)>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>> b2=polyfit(x,y,2)
b2 =
-0.0936 2.5943 8.4157
---这是拟合出的二次多项式的各项系数。
(2)>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>> b3=polyfit(x,y,3)
>>b3 =
-0.0080 0.1931 -0.1022 13.2513
---这是拟合出的三次多项式的各项系数。
(3)>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>> b4=polyfit(x,y,4)
>>b4 =
0.0009 -0.0521 0.8658 -3.5257 16.6041
---这是拟合出的四次多项式的各项系数。
(4)
function y=f1(x)
for i=1:25
y(i)=log(x(i));
end
>> y1=f1( x);
>> b5=polyfit(x,y1,2)
b5 =
-0.0045 0.1253 2.3866
>> y_=f1(y);
>> b6=polyfit(x,y4,2)
>> b6=polyfit(x,y_,2)
b6 =
-0.0045 0.1253 2.3866
>> exp(0.0045*13.9222* 13.9222+2.3866)
ans =
26.0189
---这是拟合出来的指数函数的各系数。
三、计算误差平方和
1.二次函数的误差平方和
function y=f2(x)
x=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
y2=-0.0936*x.^2+2.5943*x+8.4157;
s2=y2-y;
s21=0;
for i=1:25
s21=s21+s2(i)^2;
end
s21
s21 =
241.2445
2.三次函数的误差平方和
function y3=f3(x)
>> x=0:24;
y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
y3=-0.0080*x.^3+0.1931*x.^2-0.1022.*x+13.2513;
s3=y3-y;
s31=0;
for i=1:25
s31=s31+s3(i)^2;
end
s31
s31 =
107.0314
3.四次函数的误差平方和
function y=f4(x)
>> x=0:24;
>>y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>>y4=0.0009*x.^4-0.0521*x.^3+0.8658*x.^2-3.5257.*x+16.6041;
>>s4=y4-y;
s41=0;
for i=1:25
s41=s41+s4(i)^2;
end
>>s41
s41 =
157.9107
4.指数函数2
)()(c x b ae x y --=的误差平方和
function y=f5(x) >> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>> y5=26.0189*exp(-0.0045*((x-13.9222).^2));
s5=y5-y;
s51=0;
for i=1:25
s51=s51+s5(i)^2;
end
s51
s51 =
184.3426
四、下面列程序作出图形。
(最后一张为所有图形的比较)
>> function y2=f2(x)
>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18
17 16];
>>y2=-0.0936*x.^2+2.5943*x+8.4157;
>>plot(x,y2,'-m',x,y,'d')
这是拟合出来的二次函数的图像与散点图的对比
>>function y3=f3(x)
>>y3=-0.0080*x.^3+0.1931*x.^2-0.1022.*x+13.2513;
>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24
22 20 18 17 16];
>>plot(x,y3,'g',x,y,'d')
这是拟合出来的三次函数的图像与散点图的对比
>>function y4=f4(x)
>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22
20 18 17 16];
>>y4=0.0009*x.^4-0.0521*x.^3+0.8658*x.^2-3.5257.*x+16.604 1;
>>plot(x,y4,'r',x,y,'d')
这是拟合出来的四次函数的图像与散点图的对比
>>function y5=f5(x)
>> x=0:24;
>> y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22
20 18 17 16];
>>y5=26.0189*exp(-0.0045*x-13.9222).^2);
>>plot(x,y5,'k',x,y,'d')
这是拟合出来的指数函数的图像与散点图的对比。
将以上图形置于同一张图中
(二次、三次、四次、指数函数的图象分别为梅红色、绿色、红色、黑色)
实验总结:。
