最小二乘法 多项式拟合 实验报告
最小二乘法的实验报告

最小二乘法的实验报告最小二乘法的实验报告引言:最小二乘法是一种常用的数学方法,用于拟合数据和求解最优解。
它适用于各种领域,如统计学、经济学、工程学等。
本实验旨在通过实际案例,探讨最小二乘法在实际问题中的应用和效果。
一、实验目的本实验旨在通过最小二乘法,对一组实际数据进行拟合,得出最佳拟合曲线,并分析拟合结果的合理性和可靠性。
二、实验材料与方法1. 实验材料:- 一组实际数据:包含自变量和因变量的数据对。
- 计算机软件:如MATLAB、Python等,用于进行最小二乘法计算和绘制拟合曲线。
2. 实验方法:- 数据处理:对实际数据进行预处理,包括数据清洗、异常值处理等。
- 模型选择:根据实际问题和数据特点,选择适当的拟合模型。
- 参数估计:利用最小二乘法,求解模型参数的最优估计值。
- 拟合效果评估:通过计算残差平方和、确定系数等指标,评估拟合效果的好坏。
三、实验过程与结果1. 数据处理:在本实验中,我们选择了一组汽车销量与广告投入的数据。
首先,我们对数据进行了清洗,排除了异常值和缺失值。
2. 模型选择:根据实际问题和数据特点,我们选择了线性模型进行拟合。
即假设广告投入与汽车销量之间存在线性关系。
3. 参数估计:利用最小二乘法,我们求解了线性模型的参数估计值。
具体计算过程如下: - 建立线性模型:y = β0 + β1x,其中y表示汽车销量,x表示广告投入。
- 最小化残差平方和:min Σ(yi - (β0 + β1xi))^2,其中yi为实际销量,xi为实际广告投入。
- 对β0和β1求偏导,并令偏导数为0,得到最优解的估计值。
4. 拟合效果评估:通过计算残差平方和和确定系数等指标,我们评估了拟合效果的好坏。
结果显示,残差平方和较小,确定系数较接近1,表明拟合效果较好。
四、实验讨论1. 拟合效果的合理性:通过对拟合效果的评估,我们认为拟合结果较为合理。
然而,我们也要注意到,拟合结果仅仅是对观测数据的一个估计,并不能完全代表真实情况。
通过最小2乘法和多项式拟合求解线性方程。

《Matlab实验报告》实验序号:01 日期:2011年10月2日问题背景描述:有一组测试数据如下表,数据具有Y=x2的变化趋势,用最小二乘法求解Y。
X 1 1.5 2 2.5 3 3.5 4 4.5 5Y —1.4 2.7 3 5.9 8.4 12.2 16.6 18.8 26.2实验目的:1.学会用MA TLAB软件求解线性代数问题。
2. 通过实例学习多项式拟合和使用最小2乘法的超定系统。
实验原理与数学模型:多项式拟合,最小2乘法,实验所用软件及版本:Matlab6.1主要内容(要点):通过最小2乘法和多项式拟合求解线性方程。
实验过程记录(含基本步骤、主要程序清单及异常情况记录等):方法一:最小2乘法程序如下:x=[1 1.5 2 2.5 3 3.5 4 4.5 5]'y=[-1.4 2.7 3 5.9 8.4 12.2 16.6 18.8 26.2]'e=[ones(size(x)) x.^2]c=e\y;x1=[1:0.1:5]';y1=[ones(size(x1)),x1.^2]*c;plot(x,y,'ro',x1,y1,'k')实验结果:由图可知拟合效果很好,故:y=x2方法二:多项式拟合程序如下:x=[1 1.5 2 2.5 3 3.5 4 4.5 5]'y=[-1.4 2.7 3 5.9 8.4 12.2 16.6 18.8 26.2]'e=[ones(size(x)) x.^2];c=lsqlin(e,y);x1=[1:0.1:5]'y1=[ones(size(x1)),x1.^2]*c;plot(x,y,'w0',x1,y1,'k')实验结果:由图可知拟合效果较好,故:y=x2思考与深入:。
最小二乘法多项式拟合实验报告.docx

连续系统仿真实验报告实验数据拟合建模姓名:专业:学号:时间:2013年5月1日实验单元二实验数据拟合建模一、实验目的1、 用C 语言实现最小二乘的多项式拟合和LU 分解法;2、 熟练掌握最小二乘拟合和LU 分解法的基本原理。
3、 体会用计算机编程解决计算问题的方法。
二、需求说明(一) 、需求阐述本次实验是要求根据己知的自变量和函数值,通过多项式拟合來分别计 算2、3、4阶拟合多项式,并根据拟合结果分別计算出待求点的函数值。
其中解 拟合系数方程组时采用LU 分解的方法计算拟合多项式的系数。
(二) 、实验公式m 次拟合函数公式为:(p (x )=ao 七1対~・・・可点"计算系数4的方程组为:Sg a 0 +S] a 】 +...4-s ni a ni =t 0 < S]a ()+s?a]+...+s mF ]a m =t]k Sm a 0 +S mH a i +• •丹加^冃 其中 》= 士疋E ,i-0所以,在编程计算时,先计算出方程组①,再用LU 分解法计算求出耳的 值,即可得到拟合多项式。
LU 分解法的公式为:其中L 矩阵和U 矩阵的计算公式如下: 第一步,当k 二1,有:「1 0 0・・・01〔21 1 0-0^31 彳32 1 ••::::0 厶L ……1-i=0n-l最后求 u nn : U nn =a nn -^l m u m r=l三、设计说明(一) 、数据结构程序采用一维数组的形式来读取文件中给出的己知点处的值和要计算的未 知点处的H 变量值,最终的拟合计算结果也是采用一维数组的形式输出到文件中。
拟合多项式的系数a 和拟合系数方程组的参数t 都是采用一维数组來存储的,而 拟合系数方程组中的参数s 和L 、U 矩阵都是用二维数组來表示的。
由于要分别 计算2、3、4阶拟合结果,所以数组的规模取为5,矩阵的规模取为5*5.(二) 、算法设计及效率分析在进行LU 分解函数中,在计算L 矩阵和U 矩阵时,因为当k=2,3.-,n-l 时, 计算丈M 和土皿的循环条件不允许k=l 时进入,而正好k=l 时,计算1“和i 町不 x-1 r-1k-1 k ・l需要工1丿匕和工1以崎,因而对k=l 和k=2,3,-,n-l,就可以和在一起计算,这样就减少了 r=lr=l程序的长度。
数值分析+最小二乘法实验报告

数学与信息工程学院
实验报告
课程名称:数值分析
实验室:
实验台号:
班级:
姓名:
实验日期:2012 年 4 月13 日
实验名称最小二乘法求多项式拟合
实验目的和要求(1)了解最小二乘法求多项式拟合原理和方法;
(2)通过实例掌握用MATLAB求拟合函数及拟合图像;(3)编程实现用最小二乘法求多项式拟合。
实验内容和步骤:
实验内容:
根据matlab编写算法,用最小二乘法求多项式拟合。
实验步骤:
(1)开启软件平台——MATLAB,编程;
在command window 编写程序,求出拟合函数
x=[-2,-1,0,1,2];
y=[-0.1,0.1,0.4,0.9,1.6];
>> p=polyfit(x,y,3);
>> pa=poly2str(p,'x')
pa =
0.0083333 x^3 + 0.085714 x^2 + 0.39167 x + 0.40857(2)根据数值解法步骤编写M文件;
x=[-2 -1 0 1 2];
y=[-0.1 0.1 0.4 0.9 1.6];
p1=polyfit(x,y,3)
x1=-3:0.01:3;
y1=polyval(p1,x1);
plot(x,y,'b^',x1,y1,'r-')
(3)观察运行结果。
实验数据记录:
实验结果分析:
1.画图中点与函数要用不同的表现法,否则图片就是五点的连接。
2.3次拟合比2次拟合更准确。
3.在写M文件时,注意数据点乘的运用。
成绩评定
签字:年月日。
矩阵理论作业3:最小二乘法拟合

用最小二乘法确定m 次拟合多项式()m y P x =摘 要在实际问题中测得的实验数据有时需要较简单的函数逼近来解 , 最小二乘法拟合在解决这类问题的数据处理和误差分析中应用非常广泛 ,已成为这类问题数据处理的重要且可靠的技术手段。
本文针对最小二乘法的多项式拟合,进行了拟合曲线系数矩阵的理论公式推导,并由matlab 工具实现了拟合函数的编程。
然后在实际数据上进行了应用,并通过对结果的比较分析得出了结论,旨在提升对这种在工程中应用广泛的方法的理解和应用能力。
关键字:最小二乘法 多项式 拟合引言最小二乘拟合是一种数学上的近似和优化,利用某种方法由已知的数据得出一条直线或者曲线,使之在坐标系上与已知数据之间距离的平方和达到最小。
最小二乘拟合在工程中具有普遍应用,是数据分析的重要方法。
最小二乘法拟合的模型有很多种,其中多项式拟合模型应用比较广泛。
()m P x 表示次数不高于m 次的多项式。
本文结合线性代数中有关矩阵的运算等知识[2],在最小二乘法多项式拟合基本公式的推导[1][3]基础上,应用matlab 工具进行编程实现[3],并对实际的例子进行一次、二次及多次拟合,做出拟合曲线。
实验发现,程序运行良好,基本可以很好地进行数据拟合分析。
最小二乘法基本原理对于一组给定数据点1122(,),(,),,(,)N N x y x y x y ,求一个次数不高于m 次的多项式2012()m m m y a a x a x a x P x =++++= (1)使得拟合出的近似曲线尽可能反映所给数据点的变化趋势(一般来说m N )。
那么,就要求()m P x 在所有数据点i x 上的偏差()i m i i P x y δ=-,(=12i N ,,,) (2)都较小。
为达到这个目标,令偏差的平方和最小,即2211()[()]min N Nimiii i P x y δ===-=∑∑ (3)称这种方法为最小二乘法,利用这一原则确定拟合多项式()m P x 的方法即为最小二乘法多项式拟合。
最小二乘法实验报告

最小二乘法实验报告最小二乘法实验报告引言最小二乘法是一种常用的数学方法,用于拟合数据和估计模型参数。
它通过最小化观测值与理论值之间的误差平方和,寻找最优解。
本实验旨在通过实际数据拟合的方式,探索最小二乘法的原理和应用。
实验步骤1. 数据采集在实验开始前,我们选择了一个简单的线性回归模型进行拟合。
为了收集数据,我们在实验室里设置了一个简单的装置,用于测量物体的运动距离和所需时间。
通过多次重复实验,我们得到了一组数据,包括物体运动距离和所需时间的测量值。
2. 数据处理在进行最小二乘法拟合之前,我们需要对数据进行处理。
首先,我们计算每次实验的平均速度,通过将运动距离除以所需时间得到。
然后,我们将平均速度作为自变量,所需时间作为因变量,得到一组有序的数据点。
3. 拟合模型接下来,我们使用最小二乘法来拟合线性回归模型。
线性回归模型可以表示为:y = a + bx,其中y是因变量(所需时间),x是自变量(平均速度),a和b是待估计的模型参数。
通过最小化残差平方和,我们可以得到最优的a和b的估计值。
4. 拟合结果分析通过最小二乘法拟合得到的模型参数估计值,我们可以进一步分析拟合结果的准确性和可靠性。
首先,我们计算拟合优度,即拟合值与观测值之间的相关系数。
较高的拟合优度表明模型拟合效果较好。
此外,我们还可以计算参数估计的标准误差,用于评估参数估计值的可靠性。
结果与讨论在本实验中,我们使用最小二乘法对一组实际测量数据进行了线性回归拟合。
通过计算拟合优度,我们发现拟合效果较好,相关系数接近1。
这表明我们选择的线性回归模型较为合适,并且可以用于预测因变量(所需时间)。
此外,我们还计算了参数估计的标准误差。
标准误差是对参数估计值的精度进行评估的指标。
较小的标准误差表示参数估计值较可靠。
通过计算,我们发现参数估计值的标准误差较小,说明我们得到的模型参数估计值较为准确。
结论通过本实验,我们深入了解了最小二乘法的原理和应用。
拟合多项式的最小二乘法

数值计算理论报告题目:有一只对温度敏感的电阻,已经测得了一组温度T 和电阻R 的数据如下,问当温度为60o C时,电阻有多大?多项式拟合:已知变量x ,y 之间的函数关系为: n n-112n n+1y=a x +a x ++a x+a通过实验获得一组{i x ,i y | i =1,2,3,···,m}测量数据,确定出系数12n+1a a a (,,,)。
当n=1时,函数为线性关系若函数为线性关系,其形式为:y=ax+b (1)式中a, b 为要用实验数据确定的常数。
由实验测得的数据是总是存在着误差,所以,把各组数据代入(1)式中,两边并不相等。
相应的作图时,数据点也并不能准确地落在公式对应的直线上,误差的的平方和为:为了使拟合出的近似曲线能尽量反映所给数据的变化趋势,要求在所有数据点上的残差|)(|||i i i y x f -=δ都较小。
为达到上述目标,可以令上述偏差的平方和最小,即min ])([)(2121=-=∑∑==ii N i i N i y x f δ称这种方法为最小二乘原则,利用这一原则确定拟合多项式)(x f 的方法即为最小二乘法多项式拟合。
按最小二乘法,当a, b 选择适当,能使为最小时y=ax+b 才是最佳曲线。
用偏导数的方法求出此式的最小值。
以上是线性拟合的基本原理。
程序:x0=[20.5, 32.7, 51.0, 73.0, 95.7]; %t 的行向量y0=[765, 826, 873, 942, 1032]; %r 的列向量%plot(x0,y0,'r'); %画连续的图形,颜色设置为红()2112∑∑=--==∂n i bx a y n i v i i in=1;P=polyfit(x0,y0,n) %生成拟合多项式xx=0:1:100;z=polyval(P,xx); %计算z的值plot(xx,z,'-b',x0,y0,'.r') %绘图legend('拟合曲线','原始数据','Location','SouthEast') %注标题xlabel('x')zz=polyval(P,60); %计算60时拟合多项式的值display(zz)当n=1时,即线性拟合。
实验报告-使用多项式模型拟合数据

实验题目: 使用多项式模型进行数据拟合 1 实验目的数据拟合在实际的生产和生活中有着广泛应用。
本实验使用多项式模型对数据进行拟合,目的在于掌握数据拟合基本的基本原理,并且掌握最小二乘法的计算方法,同时学会使用数学的方法来判定数据拟合的情况。
2 实验步骤2.1 算法原理(1)最佳均方逼近多项式设n H 是次数不超过n 次的全体多项式集合。
若存在*()nn P x H ∈,使得**22()||()()||||()()||min n nn n P x H f x P x f x P x ∈-=-则称*()n P x 是()f x 在[a ,b]上的最佳均方逼近多项式。
设()nkn k k P x a x ==∑,则求最佳均方逼近多项式*()n P x ,就是求一组系数(0,1,...,)k a k n =使得22*00()[()][()]min n nnnbbkk k k aak k P x H f x a x dx f x a x dx==∈-=-∑∑⎰⎰由于积分2[()]nbkk ak f x a x dx=-∑⎰是待定系数k a 的多元函数,记做01(,,...,)n I a a a 。
由函数极值条件得到方程组,解方程组,可得到唯一确定的*k a ,从而得到*()n P x 为最小均方逼近多项式。
(2)最小二乘法在最小均方逼近多项式的讨论中,f(x)已知。
但在多数情况下,我们不能确切的指导f(x),只能知道一组数据{,}i i x y ,将最小均方误差的思想用于点集上,便得到曲线拟合的最小二乘法。
设给定一组m 个数量的数据{,}i i x y ,01{,,...}n ϕϕϕϕ=是i x 所在区间的连续函数集合,对于多项式:011,,...nn x x ϕϕϕ===。
取权值函数()1W x =,在公式中未写出。
若存在*()()nk k k S x a x ϕ==∑,使得误差平方和最小,即*22()1[()]min [()]mmiii i s x i i S x y S x y ϕ∈==-=-∑∑,则*()S x 是最小二乘逼近多项式。
计算方法实验报告 拟合

南京信息工程大学实验(实习)报告
一、实验目的:
用最小二乘法将给定的十个点拟合成三次多项式。
二、实验步骤:
用matlab编制以函数为基的多项式最小二乘拟合程序,并用于对下列数据作三次多项式最小二乘拟合(取权函数wi=1)
给定直线方程为:y=1/4*x3+1/2*x2+x+1
三、实验结论:
最小二乘法:通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
一般地。
当测量数据的散布图无明显的规律时,习惯上取n次代数多项式。
程序运行结果为:
a =
0.9731
1.1023
0.4862
0.2238
即拟合的三次方程为:y=0.9731+1.1023x+0.4862*x2+0.2238*x3
x 轴
y 轴
拟合图
结论:
一般情况下,拟合函数使得所有的残差为零是不可能的。
由图形可以看出最小二乘解决了残差的正负相互抵消的问题,使得拟合函数更加密合实验数据。
优点:曲线拟合是使拟合函数和一系列的离散点与观测值的偏差平方和达到最小。
缺点:由于计算方法简单,若要保证数据的精确度,需要大量的数据代入计算。
最小二乘法实验报告
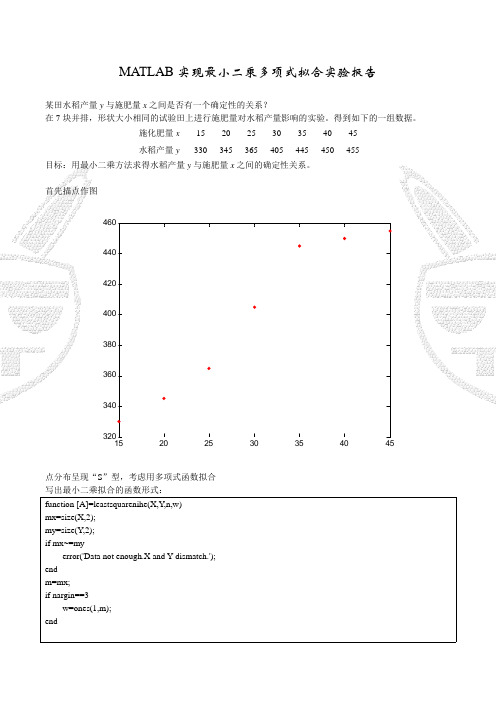
MA ATLAB 实现最小 实 小二乘多项式拟合 合实验报 报告某田水稻产量 量 y 与施肥量 量 x 之间是否 否有一个确定 定性的关系? 在 7 块并排,形状大小相 相同的试验田 田上进行施肥 肥量对水稻产 产量影响的实 实验。
得到如 如下的一组数 数据。
施化肥量 x 水稻产量 y 15 330 2 20 345 25 365 30 405 35 445 40 450 45 455 5目标:用最小 小二乘方法求 求得水稻产量 量 y 与施肥量 量 x 之间的确 确定性关系。
首先描点作图460440420400380360340320 15202530354045点分布呈现“S”型,考 考虑用多项式 式函数拟合 写出最小二乘 乘拟合的函数 数形式: function [A]= =leastsquaren nihe(X,Y,n,w) mx=size(X,2 2); my=size(Y,2) ); if mx~=my error('D Data not enoug gh.X and Y dismatch.'); d end m=mx; if nargin==3 w=ones(1,m); end Q=zeros(n+1 1,1); P=zeros(n+1,n+1); f=@(x,p,y,q,w,t)(x(t)^p)*(y(t)^q)*w(t) ); for i=1:n+1 for j=1:n n+1 sum m=0; for r t=1:m sum=sum+ +f(X,i-1,X,j-1 1,w,t); end d P(i i,j)=sum; end sum=0; for t=1:m m sum m=sum+f(X,i i-1,Y,1,w,t); end Q(i,1)=s sum; end A=P\Q; xx=min(X):0 0.01:max(X); yy=zeros(1,s size(xx,2)); for i=1:size(x xx,2) for j=1:n n+1 yy( (i)=yy(i)+A(j j)*xx(i)^(j-1) ); end end plot(X,Y,'r.'); ; hold on; plot(xx,yy); title('最小二乘法多项式拟 拟合'); xlabel('x'),yla abel('y'); X=[15 20 25 30 35 40 45] ] Y=[330 345 365 405 445 450 455] 运行结果如下 下: 4 次多项式拟 拟合的结果:系数阵 A= 1.0e+002 * 6.084523 3809758176 -0.423712121248494 0.020787 7878789875 -0.000351515151561 0.000001 1818181819 即对应的函数 数关系式为: :y=608.4523 38-42.37121x+2.07879x2-0.03515 x3+0 0.00018x4最小二乘法多项式拟合460440420400 y 380 360 340 320 15202530 x3540455 次多项式拟 拟合的结果:系数阵 A= 1.0e+003 * -1.756547676480133 0.416562 2132318929 -0.032046212944121 0.001184 4015180810 -0.000020818182321 0.000000 0140000003 即函数关系式 式为 y=-1756.54768+416.5621 13x-32.04621x2+1.18402x3+0.02082x4+0.00014 + x5 最小二乘法多项式拟合460440420400 y 380 360 340 320 15202530 x354045。
最小二乘法实验报告

最小二乘法实验报告【实验目的】:观察最小二乘多项式的数值不稳定现象【实验内容】:1 在[-1,1]区间上取n=20个等距节点,计算出以相应节点上x e 的值做为数据样本,以21,,,,l x x x 为基函数作出3,5,7,9,11,13,15l =次的最小二乘多项式,画出2ln(())cond A ~l 之间的曲线,其中A 是确定最小二乘多项式的系数矩阵。
计算出不同阶最小二乘多项式给出的最小误差21()(())niii l y x y σ==-∑2 在[-1,1]区间上取n=20个等距节点,计算出以相应节点上x e 的值做为数据样本,以121,(),(),()l p x p x p x 为基函数作出3,5,7,9,11,13,15l =次的最小二乘多项式,其中,()i p x 是勒让德多项式。
画出2ln(())cond A ~l 之间的曲线,其中A 是确定最小二乘多项式的系数矩阵。
计算出不同阶最小二乘多项式给出的最小误差21()(())niii l y x y σ==-∑,把结果与1比较【实验步骤及结果】:在[-1,1]区间上取n=20个等距节点,步长h=2/19,计算出以相应节点上xe 的值做为数据样本,数据如表格1。
表格 1 数据样本值(1)以21,,,,lx x x 为基函数拟合x e在matlab 中编写函数lsmex (x, y, l ),生成最小二乘法的系数矩阵A 、右端向量d ,求出系数a =[a 0,a 1,a 2,…,a l ]T =A −1d ,得不同阶数下的最小二乘多项式y l x = a i x ll i =0=a T X ,其中,X =[1,x ,x 2,…,x l ]T 。
计算系数a 的结果如下:①l=3,a=0.9955489867169420.9975790016896890.5403514958744690.176998749075551②l=5,a=1.0000385524900931.0000200232735780.4992468083082510.1664971114258690.0437538102273870.008681888224899③l=7,a=0.9999998328590330.9999999168306320.5000057659443580.1666678539174880.0416364317252140.0083288507266840.0014385132646550.000204569079642④l=9,a=1.0000000004096801.0000000001936090.4999999775598710.1666666623932540.0416668593915860.0083333592774580.0013883192520920.0001983493275470.0000254781225020.000002822438546⑤l=11,a=1.0000000000087061.0000000000027290.5000000000509660.1666666666715170.0416666660046380.0083333331858740.0013888917549870.0001984115224330.0000247953487620.0000027562491600.0000002815437980.000000025378540 ⑥ l=13,a = 0.999999999770700 0.999999998584826 0.500000000002793 0.166666666744277 0.041666666993633 0.008333334699273 0.001388894421398 0.000198394060135 0.000024799884896 0.000002682209015 0.000000272755242 0.000000014901161 0.000000003426662 0 ⑦ l=15,a = 1.000000006592917 1.000000012805685 0.500000000015796 0.166666664183140 0.041666662936834 0.008333325386047 0.0013888428039190.0001977682113650.000025072928111 0.000001430511475 0.000000863215519 0.000001907348633 0.000000217004981 -0.000002384185791 0.0000000115726380.000000238418579计算出不同阶最小二乘多项式的误差并比较得到最小误差,最后计算cond (A )2,绘出2ln(())cond A ~l 之间的曲线如图1,拟合误差与阶数的关系曲线如图2。
实验三 曲线拟合最小二乘法

实验三曲线拟合最小二乘法一、实验目的(1)掌握最小二乘法,(2)熟练掌握求函数的近似最小二乘拟合多项式(3)掌握数据拟合的思想,清楚数据拟合与插值法的区别及最小二乘法原理在数据拟合中的重要作用及最小二乘法解的求法。
二、实验(或算法)原理最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法拟合:对给定数据点{(Xi,Yi)}(i=0,1,…,m),在取定的函数类Φ中,求p(x)∈Φ ,使误差的平方和E^2最小,E^2=∑[p(Xi)-Yi]^2。
从几何意义上讲,就是寻求与给定点 {(XiYi)}(i=0,1,…,m)的距离平方和为最小的曲线y=p(x)。
函数p(x)称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为曲线拟合的最小二乘法。
三、实验步骤(1)根据算法事先写出相应程序。
(2)启动PC机,进入vc集成环境,输入代码。
(3)编译调试。
(4)调试通过,计算出正确结果。
四、代码#include<stdio.h>#include<math.h>#include<conio.h>float cf(int i,float f){float g=1.0;while(i--)g*=f;return g;}void ColPivot(float a[99][99], int n, float b[99][1],float x[99]){float max,m,temp;int k,q=0,i,j,I;for(k=0;k<n && q==0;k++){max=a[k][k];for(i=k+1;i<n;i++)if(fabs(max)<fabs(a[i][k])){max=a[i][k];I=i;}if(max==0)q=1;else{if(I!=k){temp=b[I][0]; b[I][0]=b[k][0];b[k][0]=temp;for(j=k;j<n;j++){temp=a[I][j]; a[I][j]=a[k][j];a[k][j]=temp;}}for(i=k+1;i<n;i++){m=a[i][k]/a[k][k];b[i][0]=b[i][0]-b[k][0]*m;for(j=0;j<n;j++)a[i][j]=a[i][j]-a[k][j]*m;}}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--)b[i][0]=b[i][0]-a[i][j]*x[j];x[i]=b[i][0]/a[i][i];}}void main(){float x[99],y[99],z[99],s[99][99],t[99][1]; int n,m,i,j,k;printf("n=");scanf("%d",&n);printf("m=");scanf("%d",&m);printf("y[%]=",n);for(i=0;i<n;i++)scanf("%f",&y[i]);printf("z[%d]=",n);for(i=0;i<n;i++)scanf("%f",&z[i]);for(i=0;i<=m;i++){for(j=0;j<=m;j++){s[i][j]=0.0;for(k=0;k<=n-1;k++)s[i][j]+=cf(i+j,y[k]);}t[i][0]=0.0;for(j=0;j<=n-1;j++)t[i][0]+=z[j]*cf(i,y[j]);}for(i=0;i<=m;i++)s[i][m+1]=t[i][0];for(i=0;i<=m;i++){for(j=0;j<=m+1;j++) printf("%f\t",s[i][j]);printf("\n");}ColPivot(s,m+1,t,x);printf("\n\n");for(i=0;i<=m;i++)printf("\na[%d]=%f",i,x[i]); printf("\n\n");}四、实验结果、实验体会通过实验的验证,可以更深刻地理解曲线拟合最小二乘法在数值计算的重要性,同时了解了其基本原理在计算机数值拟合的应用,更深刻地理解了曲线拟合最小二乘法的计算原理。
最小二乘拟合实验报告

工程学院《计算方法》实验报告课 程 名 称 计算方法 系 院 理 学 院 专 业 信息与计算科学 班 级 12级一班 学 生 姓 名 志辉 学 号 2012101316《最小二乘求解》1 引言在科学实验和生产实践中,经常要从一组实验数据(,)(1,2,,)i i x y i m 出发,寻求函数y=f (x )的一个近似表达式y=φ(x),称为经验公式,从几何上来看,这就是一个曲线拟合的问题。
多项式的插值虽然在一定程度上解决了由函数表求函数近似表达式的问题,但用它来解决这里的问题,是有明显的缺陷的。
首先,由实验提供的数据往往有测试误差。
如果要求近似曲线y=φ(x)严格地通过所给的每个数据点(,)i i x y ,就会使曲线保留原来的测试误差,因此当个别数据的误差较大的时候,插值的效果是不理想的。
其次,当实验数据较多时,用插值法得到的近似表达式,明显缺乏实用价值。
在实验中,我们常常用最小二乘法来解决这类问题。
定义()i i i x y δϕ=-为拟合函数在i x 处的残差。
为了是近似曲线能尽量反映所给数据点的变化趋势,我们要求||i δ尽可能小。
在最小二乘法中,我们选取()x ϕ,使得偏差平方和最小,即 2211[()]min mmi i i i ix y δϕ===-=∑∑,这就是最小二乘法的原理。
2 实验目的和要求运用matlab 编写.m 文件,要求用最小二乘法确定参数。
以下一组数据中x 与y 之间存在着bx y ae =的关系,利用最小二乘法确定式中的参数a 和b ,并计算相应的军方误差与最大偏差。
数据如下:3 算法原理与流程图(1) 原理最小二乘是要求对于给定数据列(,)(1,2,,)i i x y i m =,要求存在某个函数类01{(),(),()}()n x x x n m ϕϕϕΦ=<中寻求一个函数:****0011()()()()n n x a x a x a x ϕϕϕϕ=+++,使得*()x ϕ满足*22()11[()]min[()]nni i i i x iix y x y ϕϕϕ∈Φ==-=-∑∑。
最小二乘法数值计算实验报告

数学与计算科学学院实验报告实验项目名称最小二乘多项式拟合所属课程名称数值计算实验类型验证型实验日期 5.8.2012班级隧道1002班学号************姓名李彬彬成绩一、实验概述:【实验目的】通过上机计算,对曲线的最小二乘法的拟合有进一步的掌握,并且能够熟练的运用这种方法。
【实验原理】在科学实验数据处理中,往往要根据一组给定的实验数据,求出自变量x与因变量y的函数关系,这是为待定参数,由于观测数据总有误差,且待定参数ai的数量比给定数据点的数量少(即n<m),因此它不同于插值问题.这类问题不要求通过点,而只要求在给定点上的误差的平方和最小.当时,即(4.4.1)这里是线性无关的函数族,假定在上给出一组数据,以及对应的一组权,这里为权系数,要求使最小,其中这就是最小二乘逼近,得到的拟合曲线为y=s(x),这种方法称为曲线拟合的最小二乘法.(4.4.2)中实际上是关于的多元函数,求I的最小值就是求多元函数I的极值,由极值必要条件,可得(4.4.3)根据内积定义(见第三章)引入相应带权内积记号(4.4.4)则(4.4.3)可改写为这是关于参数的线性方程组,用矩阵表示为(4.4.5) (4.4.5)称为法方程.当线性无关,且在点集上至多只有n个不同零点,则称在X上满足Haar条件,此时(4.4.5)的解存在唯一(证明见[3]).记(4.4.5)的解为从而得到最小二乘拟合曲线(4.4.6)可以证明对,有故(4.4.6)得到的即为所求的最小二乘解.它的平方误差为(4.4.7)均方误差为在最小二乘逼近中,若取,则,表示为(4.4.8)【实验环境】Microsoft visual c++二、实验内容:【实验方案】测得铜导线在温度Ti(℃)时的电阻Ri(Ω)如表,求电阻R与温度T的近似函数关系。
i 0 1 2 3 4 5 6Ti(℃)19.1 25.0 30.1 36.0 40.0 45.1 50.0Ri(Ω)76.30 77.80 79.25 80.80 82.35 83.90 85.10用计算机程序进行多项式拟合上述T与R的近似函数关系。
最小二乘法拟合多项式程序实现

计算方法实验报告2【课题名称】最小二乘法拟合多项式程序实现【目的和意义】在一般情况下,不能要求近似曲线y =p (x )严格地通过所有数据点(x i ,y i ),亦即不能要求拟合函数在x i 处的残差(亦称偏差)都严格地等于零。
但是,为了使近似曲线能尽量反映所给数据点的变化趋势,要求残差的绝对值都较小还是需要的。
达到这一目标的途径很多,如使残差平方和最小来选取拟合曲线y=p (x )的最小二乘法。
【计算公式】设拟合函数的形式为 为已知的线性无关函数,求系数 最小,则称相应的为最小二乘拟合函数,特别地,若,则称P(x)为m 次最小二乘拟合多项式。
此时即取 1)(0=x ϕ,x x =)(1ϕ,…,()mm x x ϕ=,则由1(,)()()njjj u x v x ==∑u v 知11(,) (,0,1,,)nnik i k i k j jjj j x x xi k m ϕϕ+=====∑∑ ,1(,) (0,1,,)nk k j j j y x y k m ϕ===∑故相应的法方程组为11102111111121111nnnm jj j j j j n n n n m j j j j j j j j j n n n nn mm m m j j j j j j j j j n xx y a x x x x y a a x x x x y ===+====+====⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦∑∑∑∑∑∑∑∑∑∑∑解出此时的法方程即得多项式的系数。
【列主元高斯消去法程序流程图】0011()()()() (4.62)m m P x a x a x a x ϕϕϕ=+++ ()(0,,)k x k m ϕ= 其中01,,,,m a a a 使得2201110(,,,)()()(4.63)n n m m j j k k j j j j k a a a P x y a x y ϕϕ===⎡⎤⎡⎤=-=-⎢⎥⎣⎦⎣⎦∑∑∑***0011()()()()m m P x a x a x a x ϕϕϕ=+++ ***2*012()mm P x a a x a x a x =+++【列主元高斯消去法Matlab主程序】function f=zxec(x,y,z) %定义最小二乘法函数,其中x是自变量,y是因变量,为输入方便,x与y均定义为行向量,z为最小二乘法拟合多项式的最高次n=length(x); %读取地区数据个数c=ones(n,z+1);for i=2:z+1 %构造中间矩阵Cfor j=1:nc(j,i)=x(j)^(i-1);endendA=c'*c; %做出系数矩阵Ab=c'*y'; %做出矩阵ba=inv(A)*b; %计算求adet=0;max=0;for i=1:nsum=a(1);for j=2:z+1sum=sum+ a(j)*(x(i)^(j-1));endtemp1=abs(y(i)-sum);if temp1>maxmax=temp1; %比较记录最大偏差enddet=det+temp1^2; %累加求均方误差endm=length(a); %将a矩阵倒过来写,以配合函数输出函数poly2str for k=1:floor(m/2)temp2=a(k);a(k)=a(m-k+1);a(m-k+1)=temp2;endpoly2str(a,'x') %以函数形式输出表达式disp(['最大偏差=',num2str(max)]); %输出均方误差和最大偏差det=sqrt(det);disp(['均方误=',num2str(det)]);【调用函数解题】【编程疑难】本次的最小二乘法的算法实现较为简单,过程比较清晰,只在调用poly2str函数直接输出表达式时碰到困难。
基于最小二乘法的多项式拟合

基于最小二乘法的多项式拟合一 最小二乘法的基本原理设已知某物理过程)(x f y =的一组观测数据))(,(i i x f x ,m i ,,2,1 =. (1)要求在某特定函数类)(x φ寻求一个函数)(x ϕ作为)(x f y =的近似函数,使得二者在i x 上的残差)()(i i i x f x -=ϕδ, m i ,,2,1 = (2)按某种度量标准为最小,这就是拟合问题.要求残差i δ按某种度量标准为最小,即要求由残差i δ构成的残差向量T m ],,,[10δδδδ =的某种范数δ为最小,要求1δ,或∞δ即∑∑==-==mi mi i i i x f x 01)()(ϕδδ)()(max max i i ii ix f x -==∞ϕδδ为最小,这本来都是很自然的,可是计算不太方便.通常要求:∑∑==-==mi i i mi ix f x 02122122})]()([{)(ϕδδ或者∑∑==-==m i mi i i i x f x 02222)]()([ϕδδ(3)为最小.这种要求误差平方和最小的拟合称为曲线拟合的最小二乘法.就是说,最小二乘法提供了一种数学方法,利用这种方法可以对实验数据实现在最小平方误差意义下的最好拟合.在曲线拟合中,函数类Φ可有不同的选取方法.下面就常用的多项式拟合做介绍。
二 多项式拟合假设给定数据点),(i i y x (i=0,1,…,m),Φ为所有次数不超过)(m n n ≤的多项式构成的函数类,现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min)(00202=⎪⎭⎫ ⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (4)当拟合函数为多项式时,称为多项式拟合,满足式(4)的)(x p n称为最小二乘拟合多项式。
特别地,当n=1时,称为线性拟合或直线拟合。
显然∑∑==-=mi nk i k i k y x a I 02)(为n aa a ,,10的多元函数,因此上述问题即为求),,(10n a a a I I =的极值 问题。
最小二乘法多项式拟合

最小二乘法多项式拟合对于给定的数据点N i y x i i ≤≤1),,(,可用下面的n 阶多项式进行拟合,即∑==+++=nk k k x a x a x a a x f 02210)(为了使拟合出的近似曲线能尽量反映所给数据的变化趋势,要求在所有数据点上的残差|)(|||i i i y x f -=δ都较小。
为达到上述目标,可以令上述偏差的平方和最小,即min ])([)(2121=-=∑∑==iiNi iN i y x f δ称这种方法为最小二乘原则,利用这一原则确定拟合多项式)(x f 的方法即为最小二乘法多项式拟合。
确定上述多项式的过程也就是确定)(x f 中的系数n k a k ≤≤0,的过程,根据最小二乘原则,则偏差平方和应该是这些系数的函数,即min ])([)(),,,(212110=-==∑∑==i i Ni i N i n y x f a a a S δ为使上式取值最小,则其关于n k a k ≤≤0,的一阶导数应该为零,即有∑∑∑∑=====⇒=-⇒=-=∂∂Ni i N i i i i N i i i N i y x f y x f y x f a S11110)(0])([0])([2 ∑∑∑∑=====⇒=-⇒=-=∂∂N i i i N i i i i i N i i i i N i i y x x f x y x f x y x f x a S11111)(0])([0])([2∑∑∑∑=====⇒=-⇒=-=∂∂N i i k i N i i ki i i N i k i i i N i k i k y x x f x y x f x y x f kx a S 1111)(0])([0])([2∑∑∑∑=====⇒=-⇒=-=∂∂N i i n i N i i ni i i N i n i i i N i n i n y x x f x y x f x y x f nx a S 1111)(0])([0])([2 将上面各等式写成方程组的形式可有∑∑∑∑∑∑=======++++⇒=Ni i N i n in N i iN i i Ni iN i iy x a x a x a N a yx f 1112211011)(∑∑∑∑∑∑==+=====++++⇒=Ni i i Ni n in Ni iNi ii Ni iiNi iiy x xa x a x a x a yx x f x 111132121011)(∑∑∑∑∑∑==+=+=+===++++⇒=Ni i k i Ni k n in Ni k iNi k ik iNi i k i Ni i k iy x xa xa xa x a y x x f x11122111011)(∑∑∑∑∑∑===+=+===++++⇒=Ni i n i Ni n in Ni n iNi n in iNi i n i Ni i n iy x xa xa xa x a y x x f x112122111011)(写成矩阵形式有⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⋅⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑======+=+==+==+===+=====N i i n i Ni ik i N i i i N i i n k N i ni Ni k n iNi n iNi ni N i k n i N i ki N i k i N i kiN i n i Ni k iNi i N i i Ni niNi k iNi iy x y x y x y a a a a x xxx x x x x x xxx x x x N 111110121111112111111121111上述方程组可以通过克莱姆法则来计算,从而解出各系数n k a k ≤≤0,得到拟合方程。
最小二乘拟合实验报告

实验名称: 最小二乘拟合1 引言在科学实验和生产实践中,经常要从一组实验数据(,)(1,2,,)i i x y i m =出发,寻求函数y=f (x )的一个近似表达式y=φ(x),称为经验公式,从几何上来看,这就是一个曲线拟合的问题。
多项式的插值虽然在一定程度上解决了由函数表求函数近似表达式的问题,但用它来解决这里的问题,是有明显的缺陷的。
首先,由实验提供的数据往往有测试误差。
如果要求近似曲线y=φ(x)严格地通过所给的每个数据点(,)i i x y ,就会使曲线保留原来的测试误差,因此当个别数据的误差较大的时候,插值的效果是不理想的。
其次,当实验数据较多时,用插值法得到的近似表达式,明显缺乏实用价值。
在实验中,我们常常用最小二乘法来解决这类问题。
定义()i i i x y δϕ=-为拟合函数在i x 处的残差。
为了是近似曲线能尽量反映所给数据点的变化趋势,我们要求||i δ尽可能小。
在最小二乘法中,我们选取()x ϕ,使得偏差平方和最小,即2211[()]min mmi i i iix y δϕ===-=∑∑,这就是最小二乘法的原理。
2 实验目的和要求运用matlab 编写.m 文件,要求用最小二乘法确定参数。
以下一组数据中x 与y 之间存在着bx y ae =的关系,利用最小二乘法确定式中的参数a 和b ,并计算相应的军方误差与最大偏差。
数据如下:3 算法原理与流程图(1) 原理最小二乘是要求对于给定数据列(,)(1,2,,)i i x y i m =,要求存在某个函数类01{(),(),()}()n x x x n m ϕϕϕΦ=<中寻求一个函数:****0011()()()()n n x a x a x a x ϕϕϕϕ=+++,使得*()x ϕ满足*22()11[()]min[()]nni i i i x iix y x y ϕϕϕ∈Φ==-=-∑∑。
根据以上条件可知,点***01(,,,)n a a a 是多元函数2011(,,,)[()]m nn k k i i i kS a a a a x y ϕ===-∑∑ 的极小点,从而***01,,,na a a 满足方程组 0(0,1,,)kSk n a ∂==∂即00111111()()()()()()()mmmmk i i k i i n k i n i k i i i i i ia x x a x x a x x x y ϕϕϕϕϕϕϕ====+++=∑∑∑∑, 记1(,)()()mi i ih g h x g x ==∑,则上述方程组可表示成0011(,)(,)(,)(,)k k n k n k a a a f ϕϕϕϕϕϕϕ+++=,(k=0,1,…,n)写成矩阵形式为0001000101111101(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)n n n n n n n n a f a f a f ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,这个方程组成为法方程组,可以证明,当01(),(),()n x x x ϕϕϕ线性无关时,它有唯一解。
用多项式模型进行数据拟合实验报告(附代码)

实验题目: 用多项式模型进行数据拟合实验 1 实验目的本实验使用多项式模型对数据进行拟合,目的在于:(1)掌握数据拟合的基本原理,学会使用数学的方法来判定数据拟合的情况; (2)掌握最小二乘法的基本原理及计算方法; (3)熟悉使用matlab 进行算法的实现。
2 实验步骤2.1 算法原理所谓拟合是指寻找一条平滑的曲线,最不失真地去表现测量数据。
反过来说,对测量 的实验数据,要对其进行公式化处理,用计算方法构造函数来近似表达数据的函数关系。
由于函数构造方法的不同,有许多的逼近方法,工程中常用最小平方逼近(最小二乘法理论)来实现曲线的拟合。
最小二乘拟合利用已知的数据得出一条直线或曲线,使之在坐标系上与已知数据之间的距离的平方和最小。
模型主要有:1.直线型2.多项式型3.分数函数型4.指数函数型5.对数线性型6.高斯函数型等,根据应用情况,选用不同的拟合模型。
其中多项式型拟合模型应用比较广泛。
给定一组测量数据()i i y x ,,其中m i ,,3,2,1,0 =,共m+1个数据点,取多项式P (x ),使得min )]([0202=-=∑∑==mi i im i i y xp r ,则称函数P (x )为拟合函数或最小二乘解,此时,令∑==nk kk n x a x p 0)(,使得min ])([02002=⎪⎪⎭⎫ ⎝⎛-=-=∑∑∑===mi n k i ki k mi i i n y x a y x p I ,其中n a a a a ,,,,210 为待求的未知数,n 为多项式的最高次幂,由此该问题化为求),,,(210n a a a a I I =的极值问题。
由多元函数求极值的必要条件:0)(200=-=∂∂∑∑==m i j i nk i k i k i x y x a a I,其中n j ,,2,1,0 = 得到:∑∑∑===+=n k mi i j i k mi kj iy x a x)(,其中n j ,,2,1,0 =,这是一个关于n a a a a ,,,,210 的线性方程组,用矩阵表示如下所示:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+∑∑∑∑∑∑∑∑∑∑∑=====+==+====m i i n i m i i i m i i n mi n imi n imi n i mi n i mi im i imi n imi iy x y x y a a a x xx x xxx x m 000100201001020001因此,只要给出数据()i i y x ,,数据点个数m ,所要拟合的参数n ,就可求出未知数据阵),,,,(210n a a a a2.2 实验步骤(1)根据已知数据(ch3 huaxuefy.m ),绘制出数据的散点图,如图1所示: 注:x 从1开始取值,值与值间隔为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续系统仿真实验报告实验数据拟合建模姓名:专业:学号:时间:2013年5月1日实验单元二 实验数据拟合建模一、实验目的1、用C 语言实现最小二乘的多项式拟合和LU 分解法;2、熟练掌握最小二乘拟合和LU 分解法的基本原理。
3、体会用计算机编程解决计算问题的方法。
二、需求说明(一)、需求阐述本次实验是要求根据已知的自变量和函数值,通过多项式拟合来分别计算2、3、4阶拟合多项式,并根据拟合结果分别计算出待求点的函数值。
其中解拟合系数方程组时采用LU 分解的方法计算拟合多项式的系数。
(二)、实验公式m 次拟合函数公式为:01x =++m m a a x a x ϕ()⋯计算系数i a 的方程组为:{0011++...+=m m s a s a s a t1021+11++...+=m m s a s a s a t ⋮0+112++...+=m m m m s a s a s a t○1其中 ++=0=nk jj k ii s x ∑, =0=nj i i i t y x ∑所以,在编程计算时,先计算出方程组○1,再用LU 分解法计算求出i a 的值,即可得到拟合多项式。
LU 分解法的公式为:[ 1l 21l 31 ⋮l n101l 32⋮l n2001⋮⋯⋯⋯⋱⋱⋯0 0⋮01] [u 110000 u 12 u 22000 u 13 u 23u 33⋱⋯⋯⋯⋱⋱0 u 1nu 2n ⋮ u n−1n u nn ] =[ a 11a 21a 31⋮a n1a 12a 22a 32⋮a n2a 13a 23a 33⋮a n3⋯⋯⋯⋱⋯a 1n a 2n a 3n ⋮a nn ]其中L 矩阵和U 矩阵的计算公式如下: 第一步,当k=1,有:{11= (=2,3,,n)j j u a j 1111111== (=2,3,,n)i i i a al i u a第二步,当k=2,3,⋯,n-1时,有:{-1=1=- (j=+1,+2,)k kjkj kr rj r u a l u k k n ∑-1(k)=1(k)-=(j=,+1,)k ikir rkr ik kka l u l k k n u∑最后求 u nn :-1=1=-n nn nn nr rn r u a l u ∑三、设计说明(一)、数据结构程序采用一维数组的形式来读取文件中给出的已知点处的值和要计算的未知点处的自变量值,最终的拟合计算结果也是采用一维数组的形式输出到文件中。
拟合多项式的系数a 和拟合系数方程组的参数t 都是采用一维数组来存储的,而拟合系数方程组中的参数s 和L 、U 矩阵都是用二维数组来表示的。
由于要分别计算2、3、4阶拟合结果,所以数组的规模取为5,矩阵的规模取为5*5. (二)、算法设计及效率分析 在进行LU 分解函数中,在计算L 矩阵和U 矩阵时,因为当k=2,3,⋯,n-1时,计算-1=1k ir rk r l u ∑和-1=1k kr rj r l u ∑的循环条件不允许k=1时进入,而正好k=1时,计算1i l 和1j u 不需要-1=1k irrk r lu ∑和-1=1k kr rj r l u ∑,因而对k=1和k=2,3,⋯,n-1,就可以和在一起计算,这样就减少了程序的长度。
而在分别计算2、3、4阶拟合系数方程组的参数时,没有很好的利用前一阶计算的,而每次都要重新计算;而且矩阵是一个堆成矩阵,没有好好利用对称矩阵的特性,导致了重复计算,增加了计算量,降低了程序的效率。
而造成这一结果的原因是自己为了编程的简单而忽视了计算量,在以后的编程时要注意改变这一习惯。
(三)、程序结构程序主要步骤的流程图如下:以上流程图对应的源程序中的函数分别如下://计算拟合系数方程组中的参数svoid computers(double s[p][p],double x1[],int m) //计算拟合系数方程组中的参数tvoid computert(double t[],double x1[],double y1[],int m) //对拟合系数方程组中的参数s 组成的矩阵进行LU 分解 void LV(double L[p][p],double V[p][p],double s[p][p],int m) //计算拟合多项式的系数void computera(double L[p][p],double V[p][p],double t[],double x[],int m) //由得到的的拟合多项式计算待求点处的函数值 void computerty2(double a[],double x2[],double y2[],int m) //保存得到的拟合多项式和计算处的参数void save(double a[],int m,double y2[])四、编码实现#include <iostream> #include <fstream> #include <string> #include <math.h>#define p 5 //拟合方程的阶次+1#define q 5 //已知点的数目,也是带计算点的数目 using namespace std;ofstream outDatay("G:\\连续系统仿真\\拟合实验\\outy.txt"); //用于保存计算结果 int main() {void computers(double s[p][p],double x1[],int m); //计算拟合方程组的系数svoid computert(double t[],double x1[],double y1[],int m); //计算拟计算出拟合系数方程组中的参数S 计算出拟合系数方程组中的参数t 对列出的拟合方程组阵进行LU 分解根据分解的结果计算拟合多项式的系数,即拟合方程组的解根据得到的拟合多项式计算待求点出函数值保存得到的拟合多项式系数和计算出的函数值合方程组的系数tvoid LV(double L[p][p],double V[p][p],double s[p][p],int m); //LU分解void computera(double L[p][p],double V[p][p],double t[],double x[],int m); //计算拟合多项式的系数void computerty2(double a[],double x2[],double y2[],int m);void save(double a[],int m,double y2[]);ifstream inDatax,outDatax,inDatay;int i;double x1[q],x2[q],y1[q],y2[q],s[p][p]={0},t[p]={0},a[p],L[p][p],V[p][p]; inDatax.open("G:\\连续系统仿真\\拟合实验\\inx.txt"); //已知点的自变量x值i=0;while(!inDatax.eof())inDatax>>x1[i++];inDatax.close();i=0;outDatax.open("G:\\连续系统仿真\\拟合实验\\outx.txt"); //要求的插值点的x值while(!outDatax.eof())outDatax>>x2[i++];outDatax.close();i=0;inDatay.open("G:\\连续系统仿真\\拟合实验\\iny.txt"); //已知点的因变量y值while(!inDatay.eof())inDatay>>y1[i++];inDatay.close();computers(s,x1,2);computert(t,x1,y1,2);LV(L,V,s,2);computera(L,V,t,a,2);computerty2(a,x2,y2,2);save(a,2,y2);computers(s,x1,3);computert(t,x1,y1,3);LV(L,V,s,3);computera(L,V,t,a,3);computerty2(a,x2,y2,3);save(a,3,y2);computers(s,x1,4);computert(t,x1,y1,4);LV(L,V,s,4);computera(L,V,t,a,4);computerty2(a,x2,y2,4);save(a,4,y2);return 0;}void computers(double s[p][p],double x1[],int m){int i,j;for (i=0;i<=m;i++){ for(j=0;j<=m;j++)s[i][j]=0;}for ( i=0;i<=m;i++)for (j=0;j<=m;j++){for(int k=0;k<q;k++){s[i][j]+=pow(x1[k],i+j);}}}void computert(double t[],double x1[],double y1[],int m) {int i;for (i=0;i<=m;i++){t[i]=0;}for (i=0;i<=m;i++)for (int j=0;j<q;j++){t[i]+=y1[j]*pow(x1[j],i);}}void LV(double L[p][p],double V[p][p],double s[p][p],int m) {double sum;for (int i=0;i<=m;i++)for(int j=0;j<=m;j++ ){L[i][j]=0;V[i][j]=0;}for(i=0;i<=m;i++){L[i][i]=1;}for (i=0;i<=m;i++){//计算U矩阵的第i行for (int j=0;j<=m;j++){ sum=0;for (int k=0;k<=i-1;k++){sum+=L[i][k]*V[k][j];}V[i][j]=s[i][j]-sum;}if(i<m){//计算L矩阵的第i列for (j=1;j<=m;j++){sum=0;for (int k=0;k<=i-1;k++){sum+=L[j][k]*V[k][i];}L[j][i]=(s[j][i]-sum)/V[i][i];}}}}void computera(double L[p][p],double V[p][p],double t[],double x[],int m) //计算拟合多项式的系数{double y[p],sum;for (int i=0;i<=m;i++){sum=0;for (int j=0;j<i;j++){sum+=L[i][j]*y[j];}y[i]=t[i]-sum;}for (i=m;i>=0;i--){sum=0;for (int j=m;j>i;j--){sum+=V[i][j]*x[j];}x[i]=(y[i]-sum)/V[i][i];}}void computerty2(double a[],double x2[],double y2[],int m)//由得到的的拟合多项式计算待求点处的函数值{double sum;for (int i=0;i<q;i++){sum=0;for (int j=0;j<=m;j++){sum=sum+a[j]*pow(x2[i],j);}y2[i]=sum;}}void save(double a[],int m,double y2[]) //保存得到的拟合多项式和计算处的参数{outDatay<<m<<"阶拟合模型的系数为:"<<endl;for (int i=0;i<=m;i++){outDatay<<a[i]<<" ";}outDatay<<endl;outDatay<<"在待求点处的计算结果为:"<<endl;for (i=0;i<q;i++){outDatay<<y2[i]<<" ";}outDatay<<endl;outDatay<<"---------------------------------------"<<endl;}四、实验及分析(一)实验情况2阶拟合模型的系数为:-0.0196404 1.14058 -0.278175在待求点处的计算结果为:0.091636 0.297498 0.481106 0.642461 0.781561---------------------------------------3阶拟合模型的系数为:-0.0013368 1.01202 -0.0330375 -0.136187在待求点处的计算结果为:0.0993986 0.295619 0.47939 0.644177 0.78344---------------------------------------4阶拟合模型的系数为:0.000276 0.99682 0.0132292 -0.192187 0.0233333在待求点处的计算结果为:0.0999004 0.295513 0.479428 0.644214 0.783334---------------------------------------而在上一个插值实验中计算出待求点的值分别为:0.0999004 0.295513 0.479428 0.644214 0.783334从以上计算结果中,我们可以看出4阶拟合模型的计算结果最接近原函数的真实值。
