洛伦兹力
洛伦兹力的微观解释

洛伦兹力的微观解释摘要:1.洛伦兹力的概念2.洛伦兹力的微观解释a.带电粒子在磁场中的运动b.运动电荷受到的磁场力c.洛伦兹力的公式表示3.洛伦兹力在实际应用中的例子a.电子在电磁场中的运动b.磁流体动力学c.地球磁场的产生4.洛伦兹力对科技进步的贡献a.电磁制动系统b.磁悬浮列车c.核磁共振成像正文:洛伦兹力是指运动电荷在磁场中受到的一种力。
这个概念最早由爱因斯坦和洛伦兹在20世纪初提出,为电磁学的发展奠定了基础。
在微观层面上,洛伦兹力可以通过以下方式解释。
假设有一个带电粒子在磁场中运动,磁场会对带电粒子施加一个力。
这个力的大小和方向由粒子的电荷、速度和磁场的方向共同决定。
根据左手定则,当左手的食指指向粒子的运动方向,中指指向磁场方向时,拇指所指的方向就是洛伦兹力的方向。
洛伦兹力的公式表示为:F = q(v × B),其中F是洛伦兹力,q是粒子的电荷,v是粒子的速度,B是磁场的磁感应强度。
根据这个公式,我们可以计算出洛伦兹力的大小。
洛伦兹力在许多实际应用中都有重要作用。
例如,在电子学领域,电子在电磁场中运动时会受到洛伦兹力,这个力会影响电子的运动轨迹和电磁场的分布。
在磁流体动力学中,洛伦兹力是磁流体运动的主要驱动力,可以用来控制磁流体的流动。
此外,地球磁场的产生也与洛伦兹力有关。
洛伦兹力对科技进步做出了巨大贡献。
电磁制动系统利用洛伦兹力来控制运动的物体,使其减速或停止。
磁悬浮列车利用洛伦兹力使列车悬浮在轨道上,减小了运行阻力,提高了运行速度。
核磁共振成像利用洛伦兹力来探测人体内部结构,为医学诊断提供了重要手段。
总之,洛伦兹力是电磁学中的一个重要概念,它在微观层面上的解释有助于我们理解电磁现象。
高中物理-洛伦兹力

洛伦兹力洛伦兹力是带电粒子在磁场中运动时受到的磁场力。
洛伦兹力f的大小等于Bvq,其最大的特点就是与速度的大小相关,这是高中物理中少有的一个与速度相关的力。
我们从力的大小、方向、与安培力关系这三个方面来研究洛伦兹力。
洛伦兹力的大小⒈当电荷速度方向与磁场方向垂直时,洛伦兹力的大小f=Bvq;高中物理网建议同学们用小写的f来表示洛伦兹力,以便于和安培力区分。
⒉磁场对静止的电荷无作用力,磁场只对运动电荷有作用力,这与电场对其中的静止电荷或运动电荷总有电场力的作用是不同的。
⒊当时电荷沿着(或逆着)磁感线方向运行时,洛伦兹力为零。
⒋当电荷运动方向与磁场方向夹角为θ时,洛伦兹力的大小f=Bvqsinθ;洛伦兹力的方向⒈用左手定则来判断:让磁感线穿过手心,四指指向正电荷运动的方向(或负电荷运动方向的反方向),大拇指指向就是洛伦兹力的方向。
⒉无论v与B是否垂直,洛伦兹力总是同时垂直于电荷运动方向与磁场方向。
洛伦兹力的特点洛伦兹力的方向总与粒子运动的方向垂直,洛伦兹力只改变速度的方向,不改变速度的大小,故洛伦兹力永远不会对v有积分,即洛伦兹力永不做功。
安培力和洛伦兹力的关系洛伦兹力是磁场对运动电荷的作用力,安培力是磁场对通电导线的作用力,两者的研究对象是不同的。
安培力是洛伦兹力的宏观表现,洛伦兹力是安培力的微观实质。
两者之间的推导请阅读《安培力与洛伦兹力》对洛伦兹力和安培力的联系与区别,可从以下几个方面理解:1.安培力大小为F=ILB,洛伦兹力大小为F=qvB。
安培力和洛伦兹力表达式虽然不同,但可互相推导,相互印证。
2.洛伦兹力是微观形式,安培力是宏观表现。
洛伦兹力是单个运动电荷在磁场中受到的力,而安培力是导体中所有定向移动的自由电荷受的洛伦兹力的宏观表现。
3.尽管安培力是导体中所有定向移动的自由电荷受的洛伦兹力的宏观表现,但也不能认为定培力就简单地等于所有定向移动电荷所受洛伦兹力的和,一般只有当导体静止时才能这样认为。
物理洛伦兹力-概述说明以及解释

物理洛伦兹力-概述说明以及解释1.引言1.1 概述在物理学中,洛伦兹力是一种与带电粒子在电场和磁场中的相互作用有关的力。
这种力是由19世纪的荷兰物理学家洛伦茨提出的,他发现当带电粒子移动时,会受到电场和磁场的双重影响,从而产生一种受力。
洛伦茨力的存在和性质对于解释许多物理现象和现代科学的发展都至关重要。
本文将会对洛伦兹力的概念、公式以及其在物理学中的应用进行深入探讨,同时也将探讨洛伦兹力在现代科学中的作用以及展望其未来的发展。
通过本文的阐述,读者将能更全面地了解洛伦兹力对于物理学和科学发展的重要性。
1.2文章结构1.2 文章结构本文将分为以下几个部分来详细介绍物理洛伦兹力的相关概念、公式和应用。
首先,在引言部分将对物理洛伦兹力进行简要概述,介绍文章的结构和目的。
接下来,在正文部分将详细解释洛伦兹力的概念,介绍洛伦兹力的公式以及讨论洛伦兹力在实际应用中的重要性。
最后,在结论部分将总结洛伦兹力在物理学中的重要性,并探讨其在现代科学中的作用,展望未来洛伦兹力的发展方向。
通过以上分析和讨论,读者将能够更深入地了解物理洛伦兹力的相关知识,为其在科学研究和实践中的应用提供更多参考和启发。
1.3 目的本文的主要目的是探讨物理学中的洛伦兹力,并深入了解其在电磁学和磁场中的重要性。
通过对洛伦兹力的概念、公式和应用进行全面的分析和讨论,我们希望读者能够更加深入地理解洛伦兹力在物理学领域中的作用和意义。
此外,本文也将探讨洛伦兹力在现代科学研究中的应用以及未来的发展趋势,以便读者能够更好地认识和理解这一重要力学概念的前沿研究和应用领域。
通过阐述洛伦兹力的重要性和影响,本文旨在引发读者对物理学领域的兴趣和思考,促进科学研究和相关学科的发展。
2.正文2.1 洛伦兹力的概念洛伦兹力是指在电磁场中,带电粒子受到的力。
这个力是由荷电粒子在电场和磁场中相互作用而产生的。
洛伦兹力的大小和方向取决于带电粒子的电荷量、速度以及电场和磁场的强度。
洛伦兹力

洛伦兹力
从阴极发射出来的电子束,在
阴极和阳极间的高电压作用下,轰
击到长条形的荧光屏上激发出荧
光,可以在示波器上显示出电子束
运动的径迹.实验表明,在没有外
磁场时,电子束是沿直线前的.如
果把射线管放在蹄形磁铁的两极洛伦兹力演示仪间,荧光屏上显示的电子束运动的径迹就发生了弯曲.这表明,运动电荷确实受到了磁场的作用力,荷兰物理学家洛伦兹首先提出了运动电荷产生磁场和电场对运动电荷有作用力的观点,为纪念他,人们称这种
力为洛伦兹力。
安培力是洛伦兹力的宏观表现,洛伦兹力是安
培力的微观体现。
洛仑兹力---重点

洛仑兹力[P1]洛仑兹力:运动电荷受到的磁场的作用力,叫做洛仑兹力.(1)洛仑兹力大小: f = q v B sin θ f = B q V (当B ⊥V 时), 当电荷静止或运动电荷的速度方向跟磁感强度的方向平行时,电荷都不受洛仑兹力。
(2)洛仑兹力的方向——由左手定则判断。
注意:①洛仑兹力一定垂直于B 和V 所决定的平面.②四指的指向是正电荷的运动方向或负电荷运动的反方向;(3)特性:洛仑兹力对电荷不做功,它只改变运动电荷的速度方向,不改变速度的大小。
(4)洛伦兹力和安培力的关系:洛伦兹力是安培力的微观表现。
[P2]洛伦兹力计算公式的推导:如图所示,整个导线受到的磁场力(安培力)为F 安=BIL ;其中I=nesv ;设导线中共有N 个自由电子N=nsL ;每个电子受的磁场力为F ,则F 安=NF 。
由以上四式得F=qvB 。
条件是v 与B 垂直。
当v 与B 成θ角时,F=qvB sin θ。
[P3]带电粒子在磁场中的圆周运动:若带电粒子速度方向与磁场方向平行(相同或相反),带电粒子以不变的速度做匀速直线运动.当带电粒子速度方向与磁场垂直时,带电粒子在垂直于磁感应线的平面内做匀速圆周运动.带电粒子在匀强磁场中仅受洛伦兹力而做匀速圆周运动时,洛仑兹力充当向心力:rmv qvB 2=, 由此可以推导出该圆周运动的半径公式和周期公式:Bqm T ,Bq mv r π2== m )qBR (mv E k 22122==动能[P4]2007年上海卷)在磁感应强度B 的匀强磁场中,垂直于磁场放入一段通电导线。
若任意时刻该导线中有N 个以速度v 做定向移动的电荷,每个电荷的电量为q 。
则每个电荷所受的洛伦兹力f = q v B __,该段导线所受的安培力为F = N q v B ___。
[P5]2007高考理综北京卷)图1是电子射线管示意图.接通电源后,电子射线由阴极沿x 轴方向射出,在荧光屏上会看到一条亮线.要使荧光屏上的亮线向下(z 轴负方向)偏转,在下列措施中可采用的是____B______。
洛伦兹力

洛伦兹力
1.洛伦兹力
运动电荷在磁场中受到的力叫做洛伦兹力.
2.洛伦兹力的方向
(1)判定方法
左手定则:掌心——磁感线垂直穿入掌心;
四指——指向正电荷运动的方向或负电荷运动的反方向;
拇指——指向洛伦兹力的方向.
(2)方向特点:F⊥B,F⊥v,即F垂直于B和v决定的平面(注意:洛伦兹力不做功).3.洛伦兹力的大小
(1)v∥B时,洛伦兹力F=0.(θ=0°或180°)
(2)v⊥B时,洛伦兹力F=q v B.(θ=90°)
(3)v=0时,洛伦兹力F=0.
[深度思考]为什么带电粒子在电场力、重力和洛伦兹力共同作用下的直线运动只能是匀速直线运动?
答案如果是变速,则洛伦兹力会变化,而洛伦兹力总是和速度方向垂直的,所以就不可能是直线运动.
第1页共1页。
细谈洛伦兹力

法拉第电磁感应定律应用
01
法拉第电磁感应定律内容
当一个回路中的磁通量发生变化时,就会在回路中产生感应电动势。感
应电动势的大小与磁通量的变化率成正比,即$e=-Nfrac{dPhi}{dt}$,
其中$N$为回路匝数,$Phi$为磁通量。
02
洛伦兹力与感应电动势关系
在电磁感应现象中,洛伦兹力作用于运动电荷上,使得电荷在磁场中发
电荷运动方向与磁场方向成任意角度
03
此时θ为v与B的夹角,洛伦兹力F=qvBsinθ,其大小随θ的变化
而变化。
03
洛伦兹力与电场关系
电场对运动电荷作用
电场力
电场对电荷的作用力,与电荷的电量和 电场强度成正比,方向沿电场线切线方 向。
VS
运动电荷在电场中的轨迹
运动电荷在电场中受到电场力的作用,其 运动轨迹与电场线的形状和电荷的初速度 有关。
粒子加速器还应用于材料科学 、化学、生物学等领域。例如 ,利用粒子加速器可以模拟太 空环境,研究材料在太空中的 性能变化;还可以用于研究化 学反应的动力学过程等。
06
总结与展望
洛伦兹力研究意义和价值
揭示电磁相互作用机制
洛伦兹力是电磁学中的基本力,研究 它有助于深入理解电磁相互作用的本 质和机制。
多场耦合效应的复杂性
在实际应用中,洛伦兹力往往与其他物理场(如电场、热场等)相互耦合,使得问题变 得更为复杂,难以精确求解。
高性能计算资源的需求
对洛伦兹力的精确模拟和计算需要高性能的计算资源,如何有效利用和优化计算资源是 当前面临的挑战之一。
未来发展趋势及前景预测
01
深入研究极端条件下 的洛伦兹力
洛伦兹
洛伦兹力的方向由左手定则判定。
洛伦兹力

带电粒子是以 B的正方向(负电荷)或负方 向(正电荷)为转轴作圆周运动的,角频率的 大小也与带电粒子的运动速度无关。
洛伦兹力演示仪
亥姆霍兹线圈
电 加速电压 选择挡
子
枪
磁场强弱选择挡
c. v0 与 B斜交成 θ 角
把 0 分解成两个分矢量:平行于B的分矢量v// v0 cos 和垂直于B的分矢量 v v0 sin .由于磁场作用,带电 粒子在垂直于磁场的平面内以 v作匀速圆周运动 .但 由于同时有平行于B的速度分矢量v//不受磁场影响, 所以带电粒子合运动的轨迹是一螺旋线,螺旋线的半 径是 m v m v0 sin
t 2 qB
因此为了粒子和交变电场的频率仍能保持同步,必须使交变电场的角频率ω 同步降低
交变电场角频率应保持满足ωm=qB
qB 即其频率满足 f 2m
根据这个原理设计的回旋加速器,叫做同步回旋加速器。
北 京 正 负 粒 子 对 撞 机
实物图
高大上的比如这个(*´・ω・)ノ
蠢一点的比如这个(*´_⊃`)ノ
mv 随着粒子一次次被加速,粒子在盒中绕行的半径 R qB
也不断增大,最后以很高的速度由致偏电极引出,这样 就获得了高能粒子束。 若设粒子最后一次在D形盒内的绕行半径 为 qBR D 则粒子的出射速度: v max
RD
m
然而当粒子被加速到接近光速的时候,必须考虑相 对论效应,粒子的质量将随速度的增大而增加。由 T m 粒子在半盒内的运动时间也增加。 于
磁聚焦的应用:电真空器件中对电子束的聚焦 利用示波管和磁聚焦法可以测定电子的 荷质比
2.回旋加速器
回旋加速器是原子核物理、高能物理等实验中获得 高能粒子的一种基本设备。
洛伦兹力

洛伦兹力导言:磁场对放入其中的电流有力的作用,而电流是电荷的定向运动形成的,故,磁场对电流的作用力的本质原因是磁场对运动电荷有作用力,我们把磁场对运动电荷的作用力称为洛伦兹力。
安培力应是洛伦兹力宏观的表现。
一、洛伦兹力的大小推导:取静止通电导线分析洛安Nf F =BIL F =安 qvIL q It N == qvB qvILBIL f ==洛 对于运动的通电导线,安培力是洛伦兹力与导线垂直方向的分力的合力二、洛伦兹力的方向判断左手定则:伸出左手,大拇指跟四指垂直且与掌心在同一平面内;让磁感线垂直穿入手心,并使四指指向正电荷的运动方向(负电荷运动的反方向),则大拇指所指方向为该电荷所受洛伦兹力的方向。
洛伦兹力的方向垂直于速度方向和磁场方向确定的平面。
即洛伦兹力总是和速度方向垂直,永不做功。
类比:安培力左手定则:伸出左手,大拇指跟四指垂直且与掌心在同一平面内;让磁感线垂直穿入手心,并使四指指向电流方向,则大拇指所指方向为电流所受安培力的方向。
安培力的方向垂直于电流和磁场确定的平面。
☆问题1:结合上节课所学安培力的知识,判断电荷在磁场中一定受到洛伦兹力吗?哪些情况不受到洛伦兹力?☆问题2:运动电荷在磁场强的位置一定比在磁场弱的位置受洛仑兹力大吗?☆问题3:运动电荷不受洛仑兹力,所在处的磁感应强度为零对吗?☆问题4:左手定则判断洛仑兹力方向时,四指指向电荷运动的方向吗?☆问题5:安培力可以对电流做功,故洛伦兹力也可以对带电粒子做功对吗?例1、关于带电粒子所受洛仑兹力F 、磁感应强度B 和粒子速度v 三者方向之间的关系,下列说法正确的是( )A. F 、B 、v 三者必定均保持垂直B. F 必定垂直与B 、v ,但B 不一定垂直与vC. B 必定垂直与F 、v ,但F 不一定垂直与vD . v 必定垂直与B 、F ,但v 不一定垂直与B练一练、B表示磁感应强度,v表示负电荷运动方向,F表示洛仑兹力方向。
洛伦兹力的微观解释

洛伦兹力的微观解释(原创版)目录一、洛伦兹力的概念及公式二、洛伦兹力的微观解释1.电荷在电场中的受力2.电荷在磁场中的受力3.洛伦兹力的微观本质正文一、洛伦兹力的概念及公式洛伦兹力,又称为洛伦兹磁力,是由荷兰物理学家洛伦兹(Hendrik Antoon Lorentz)在 19 世纪末 20 世纪初提出的一种力。
洛伦兹力是描述电荷在电磁场中受到的力的公式,该公式为:F = q(E + v x B)。
其中,F 表示洛伦兹力,q 表示电荷量,E 表示电场强度,v 表示电荷的速度,B 表示磁场强度,x 表示叉乘符号。
二、洛伦兹力的微观解释1.电荷在电场中的受力当电荷处在电场中时,它会受到电场力。
根据库仑定律,电场力 F_E = qE,其中 q 为电荷量,E 为电场强度。
电荷在电场中的受力与电荷的电量和电场强度成正比。
2.电荷在磁场中的受力当电荷处在磁场中时,它会受到磁场力。
根据安培环路定律,磁场力F_B = qvB,其中 q 为电荷量,v 为电荷的速度,B 为磁场强度。
电荷在磁场中的受力与电荷的电量、速度和磁场强度成正比。
3.洛伦兹力的微观本质洛伦兹力实际上是电荷在电场和磁场共同作用下所受到的力。
从微观角度来看,洛伦兹力可以解释为电荷在磁场中受到的力是由于磁场对电荷的运动产生了影响,使得电荷的运动轨迹发生了偏转。
这种偏转现象在电子显微镜中尤为明显,电子在磁场中受到洛伦兹力作用,从而在磁场中形成特定的轨迹。
综上所述,洛伦兹力是一种描述电荷在电磁场中受到的力的公式。
电荷在电场中的受力与电荷的电量和电场强度成正比,电荷在磁场中的受力与电荷的电量、速度和磁场强度成正比。
洛伦兹力
2. 洛伦兹力大小 若 B⊥v, f = Bqv
若 B∥v,
f =0
f = Bqvsin θ
若 B与v间的夹角为θ,
例:带电量为+q的粒子在匀强磁场中运动,下列说法中 正确的是: A.只要速度大小相同,粒子所受的洛伦兹力大小就相同 B. 粒子由+ q 换成- q,速度反向,大小不变, 粒子所受洛伦兹 力大小方向一定不变 C.洛伦兹力的方向一定与速度方向垂直,磁场方向一定与 运动方向垂直 D.粒子只受洛伦兹力作用, 其动能不变.
3.正方形容器处在匀强磁场中,一束电子从孔a 垂直于磁 场沿a b射入容器中,其中一部分从c孔沿b c射出,一部 分从d孔沿c d射出,容器处在真空中. 试求: (1)从两孔射出的电子速度之比vc:vd (2)从两孔射出的电子在磁场中的运动时间之比tc:td a b
d
c
例1.(2001年全国,18)如图所示,在y<0的区域内存在匀 强磁场,磁场方向垂直于xy平面并指向纸面外,磁感应强 度为B.一带正电的粒子以速度V0从O点射入磁场,入射 方向在xy平面内,与x轴正方向的夹角为θ,若粒子射出磁 场的位置与O点的距离为L,求该粒子的电荷量和质量之 比q/m.
作业:
• 1.教材P97 练习与评价1,2; • 2.三维P80 例1,跟1,例2,跟2.
思考与讨论:带电粒子在磁场中运动时,洛伦兹力对带电 粒子是否做功? • 洛伦兹力只改变速度方向不改变速度大小,洛伦兹力对 电荷永不做功。
作业:
• 1.教材P97 练习与评价1,2; • 2.三维P80 例1,跟1,例2,跟2.
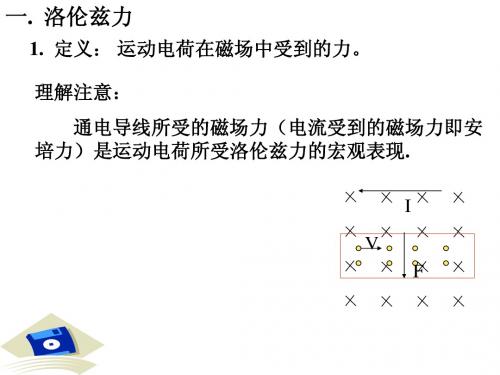
一. 洛伦兹力
1. 定义: 运动电荷在磁场中受到的力。 理解注意: 通电导线所受的磁场力(电流受到的磁场力即安 培力)是运动电荷所受洛伦兹力的宏观表现. I V
4.3-洛伦兹力

4.3 洛伦兹力
基础物理学 18
3. 霍耳(E.C.Hall)效应
在一个通有电流的导体板上,垂直于板面施加 一磁场,则平行磁场的两面出现一个电势差,这一 现象是1879年美国物理学家霍耳发现的,称为霍耳 效应。该电势差称为霍耳电势差 。
d
l
主讲:张国才
qb
– – – –
E
v
I
E
+ + ++
注意:螺距仅与平行于磁场方向的初速度有关
主讲:张国才
差不磁大聚的焦带电在粒4.均子3 匀, 洛它磁伦们场兹的中力v某0点与AB发之射间一基的束础夹初物角速理相学 5
不尽相同 , 但都较小, 这些粒子沿半径不同的螺旋 线运动, 因螺距近似相等, 都相交于屏上同一点, 此 现象称之为磁聚焦 .
显象管中电子的磁聚焦装置示意图 B
轨道 半径
R mv 0
R
qB
T 2R 2m
v0 qB
角频率
主讲:张国才
周期
2 qB
Tm
4.3 洛伦兹力
基础物理学 4
(3)如果v0 与 B斜交成角
粒子作螺旋运动,半径 Rmv m0vsin
qB
qB
周期
v v0
B
T 2m
qB
v //
R
螺距
h
hv//Tv//
2m2mv0cos
qB qB
v
B
q
I
a
+ + ++
N 型半导体 载流子为电子
ub ua RH 0
主讲:张国才
q
I
a –– – –
P 型半导体 载流子为空穴
洛伦兹力

V
例.质子和α粒子在同一匀强 磁场中做半径相同的圆周运动, 由此可知:质子和α粒子的动 能之比为 1:1 .周期之 比为 1:2 .
例、光滑斜面,倾角为θ,匀强磁
场的磁感应强度为B,一质量为M, 带电量q的小球在斜面上自静止释放, 求小球在斜面上运动的时间和最大 速度(设斜面足够长)
例.如图a、b分别为氘核和氚核射 入一正方形的匀强磁场区域的轨 迹,则它们的速率之比为 3:4 .及 在该区域的飞行时间为 4:3 .
关于电场力与洛伦兹力,以下说法正确的是 ( D). A.电荷只要处在电场中,就会受到电场 力,而电荷静止在磁场中,也可能受到洛伦 兹力 B.电场力对在电场中的电荷一定会做功, 而洛伦兹力对在磁场中的电荷却不会做功 C.电场力与洛伦兹力一样,受力方向都在 电场线和磁感线上 D.只有运动的电荷在磁场中才可能会受到 洛伦兹力的作用
磁感线B线垂直穿过手心,四指 指向+q的速度V方向,-q的速度V反 方向,大拇指F洛方向
③F洛⊥B 且 F洛⊥V。
一、洛伦兹力 4、洛伦磁力作用
偏转
①只改变运动电荷的速度方向, 不改变速度大小; ②对运动电荷不做功。
例1.下列各图中带电粒子刚刚进入磁 场,试判断这时粒子所受格伦兹力 的方向 × × × V V V
+× × × +
× × ×
+
+
V V
× × ×
+× × ×
× × ×
+
V
V
V
求洛伦兹力的大小
例2.如图:磁场方向,正电荷的运 动方向,电荷所受洛伦兹力的方向 两两垂直,则正确的是( D )
F V B V
+
B
洛伦兹力

带电粒子在磁场一、运动电荷在磁场中的运动 运动电荷在磁场中的运动规律只有磁场时,若带电粒子进入磁场的初速度与磁场平行,则不受洛伦兹力作用,带电粒子仍做匀速直线运动;只有当带电粒子的速度方向与磁场方向垂直时,粒子在洛伦兹力作用下才做匀速圆周运动。
安培力是洛伦兹力的宏观表现,因而洛伦兹力的方向仍由左手定则判定,只是注意:四指的指向为正电荷运动方向或负电荷运动的反方向。
由于洛伦兹力与带电粒子的运动方向垂直,故洛伦兹力不做功。
当带电粒子的运动方向与磁场方向垂直时,洛伦兹力为带电粒子做匀速圆周运动提供向心力,即r v m qvB f 2==。
由此得出粒子的回旋半径:qBm v r =;回旋周期:qBmT π2=。
注意:从半径公式可以看出,同一带电粒子在同一磁场中运动,速度越大,轨道半径越大;从周期公式可知,同一带电粒子在同一磁场中运动,不论速度多大,周期都一样。
确定带电粒子在磁场中做匀速圆周运动的圆心、半径和运动时间的方法解决在洛伦兹力作用下带电粒子在磁场中的匀速圆周运动问题时,要注意以下三点: ①圆心的确定。
因为v f ⊥,只要画出轨迹中的任意两点(一般是射入与射出有界磁场的两点)的洛伦兹力的方向,其延长线的交点即为圆心;②半径的计算。
一般是利用几何知识解直角三角形求出;③带电粒子在磁场中运动时间的确定。
利用圆心角与弦切角的关系或四边形内角和等于360°计算圆心角θ,再由公式T t ︒=360θ求运动时间。
1.质子(p)和α粒子以相同的速率在同一匀强磁场中作匀速圆周运动,轨道半径分别为RP 和Rα,周期分别为TP 和Tα,则下列选项正确的是 A 、p α:1:2R R =,p α:1:2T T =B 、p α:1:1R R =,p α:1:1T T =C 、p α:1:1R R =,p α:1:2T T = D 、p α:1:2R R =,p α:1:1T T =2.如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过此区域的时间为t ,若加上磁感应强度为B 水平向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出时偏离原方向60°,利用以上数据可求出下列物理量中的哪几个A 、带电粒子的比荷B 、带电粒子在磁场中运动的周期C 、带电粒子的初速度D 、带电粒子在磁场中运动的半径1.如图所示,竖直向下的匀强磁场穿过光滑的绝缘水平面,平面上一个钉子O 固定一根细线,细线的另一端系一带电小球,小球在光滑水平面内绕O 做匀速圆周运动.在某时刻细线断开,小球仍然在匀强磁场中做匀速圆周运动,下列说法一定错误的是A.速率变小,半径变小,周期不变B.速率不变,半径不变,周期不变C.速率不变,半径变大,周期变大D.速率不变,半径变小,周期变小 2.如图所示,x 轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O 点射入磁场中,射入方向与x 轴均夹θ角.则正、负离子在磁场中A.运动时间相同B.运动轨道半径相同C.重新回到x 轴时速度大小和方向均相同D.重新回到x 轴时距O 点的距离相同3. 如图直线MN 上方有磁感应强度为B 的匀强磁场。
第五节 洛仑兹力

《讲与练》: P86-88 (1)例题与应用 (2)课后自主检测 (3)《红对勾》课时作业24
推导:
v2 粒子做匀速圆周运动所需的向心力 F m r
是由
粒子所受的洛伦兹力提供的,所以 mv v2 r qvB m qB r 2r 2m T T v qB 说明:
1、轨道半径和粒子的运动速率成正比。
2.如图,在阴极射线管正上方水平放置一通 有强电流的长直导线,则阴极射线将: A.向纸内偏转; B.向纸外偏转; C.向下偏转; D.向上偏转;
(D)
阴极射线:高速电子流.(带负电)
3. 一个电子穿过某一空间而未发生偏转,则: A.此空间一定不存在磁场 ( B、D ) B.此空间可能有磁场,方向与电子速度平行
2.回旋加速器原理图
劳伦斯制造的世界 第一台回旋加速器
带电粒子在回旋加速器中的周期和最大动能
2.周期 粒子每经过一次加速,其轨道半径就大一些, 不变 但粒子绕圆周运动的周期_____ 2m 交变电场的周期与粒子的旋转周期相同 T qB 3.最大动能
v 由: qvB m r 2 2 2 q Br 得: E K 2m
F v B A F B v F B v B
F
C
v D
B
判断下列各运动电荷所受洛仑兹力的方向:
F垂直纸面向里 F垂直纸面向外 F竖直向上 F竖直向上 F竖直向上
F斜向右下
1.当一带正电q的粒子以速度v沿螺线管中轴 线进入该通电螺线管,若不计重力,则 : A.带电粒子速度大小改变; (C.D) B.带电粒子速度方向改变; C.带电粒子速度大小不变; D.带电粒子速度方向不变。
电荷在磁场中受洛仑 兹力的作用发生偏转 电阻R上电流方向从 下向上
洛仑兹力

三、洛伦兹力大小
F洛=qVB ( V⊥B)
F洛= 0 ( V∥B) F洛=qVBsinθ (当V与B成一角度θ时)
V2 V1
四、洛伦兹力的特点:
1、洛伦兹力的方向总是既垂直于速度,又垂直 于磁场, 即垂直于V和B所组成的平面. 总是:F⊥V F⊥B F⊥SVB
2、洛伦兹力只改变速度的方向, 不改变速度的大小. 3、洛伦兹力对电荷总是不做功.
5.如图所示,空间有磁感应强度为B,方向竖直向上的匀强磁场,一束电子 流以初速v从水平方向射入,为了使电子流经过磁场时不偏转(不计重力), 则在磁场区域内必须同时存在一个匀强电场,这个电场的场强大小与方向 应是 ( ) A.B/v,方向竖直向上 B.B/v,方向水平向左 C.Bv,垂直纸面向里 D.Bv,垂直纸面向外第5题第6题
1、定义:磁场对运动电荷的作用力 安培力是洛伦兹力的宏观表现 2、方向:左手定则 F⊥V F⊥B 3、大小: F洛=qVBsinθ V⊥B F洛=qVB V∥B F洛= 0
4、特点:洛伦兹力只改变速度的方向; 洛伦兹力对运动电荷不做功.
五、电视显像管的工作原理
1、构造:
电子枪(阴极) 偏转线圈
荧光屏等
电荷量为+q的粒子在匀强磁场中运 动,下列说法正确的是( B )
A.只要速度大小相同,所受洛伦兹力就 相同 B.如果把+q改为-q,且速度反向,大 小不变,则洛伦兹力的大小方向不变 C.洛伦兹力方向一定与电荷速度方向垂 直,磁场方向一定与电荷运动方向垂直 D.粒子的速度一定变化
在太阳创造的诸如光和热等形式的能量中, 有一种能量被称为“太阳风”。这是一束可以 覆盖地球的强大的带电亚原子颗粒流,该太阳 风在地球上空环绕地球流动,以大约每秒400 公里的速度撞击地球磁场,磁场使该颗粒流偏 向地磁极下落,它们与氧和氮的原子碰撞,击 走电子,使之成为激发态的离子,这些离子发 射不同波长的辐射,产生出红、绿或蓝等色的 极光特征色彩,形成极光。在南极地区形成的 叫南极光。在北极地区同样可看到这一现象, 称之为北极光。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4磁场对运动电荷的作用——洛伦兹力
★教学目标
(一)知识与技能
1、知道什么是洛伦兹力。
2、理解安培力和洛伦兹力的关系,掌握洛伦兹力大小的推理过程。
3、知道洛伦兹力产生条件,会用左手定则判定洛伦兹力的方向。
4、了解洛伦兹力的特点,会推导电荷在磁场中运动的半径和周期。
(二)过程与方法
通过洛伦兹力大小的推导过程进一步培养学生的分析推理能力。
(三)情感、态度与价值观
让学生认真体会科学研究思维方法。
★教学重点
1、掌握洛伦兹力大小的推导过程。
2、会推导电荷在磁场中运动的半径和周期。
★教学难点
1、理解洛伦兹力对运动电荷不做功。
2、洛伦兹力方向的判断。
★教学过程
(一)引入新课:同学们,我们首先来观看一下神奇而有美丽的极光。
播放极光的图片。
师:同学们知道极光是怎样形成的吗?
生:来自太阳的高能粒子进入大气后,在地磁场作用下与大气发生作用而产生的。
师:你们知道极光一般出现在什么地方吗?
生:两极等高纬度地区。
师:为什么极光不能在赤道等低纬度地区出现呢?
生:学生好奇。
师:我们通过这一节课的学习就知道这是为什么了。
今天我们一起来学习第三章第四节
磁场对运动电荷的作用——洛伦兹力(板书标题)
一.洛伦兹力
我们先来做一个实验。
这是一个蹄形磁铁,它周围存在磁场。
这是阴极射线管,它能产生运动电荷。
介绍:阴极射线管的玻璃管内已经抽成真空,当左右两个电极按标签上的极性接上高压电源时,阴极会发射电子。
在电场的加速下飞向阳极,电子束掠射到荧光板上,显示出电子束的轨迹。
演示:
1.没有磁场时电子束是一条直线。
2.用一个蹄形磁铁在电子束的路径上加磁场,尝试不同方向的磁场对电子束径迹的不同影响,并填下表。
磁场方向竖直向下竖直向上垂直于纸面向里垂直于纸面向外电子束偏转方向向外偏转向里偏转向下偏转向上偏转通过这个实验我们可以得到什么结论?
结论:磁场对运动电荷有作用力,我们把这一个作用力称为洛伦兹力。
(板书)运动电荷在磁场中受到的作用力叫做洛伦兹力。
二:洛仑兹力的大小(板书)
师:我们之前学习了磁场对通电导线的作用力,也就是安培力。
那么安培力的公式是什么?
生:F=BIL.
师:那当导线中没有电流时,安培力是多大呢?
生:安培力为零。
师:磁场对通电的导线才有作用力,那么这个作用就与电流有关,那么电流是如何形成的呢?
生:电荷的定向移动形成的。
师:之前的实验我们已经证明了磁场对运动电荷也有作用力,也就是洛伦兹力。
那洛伦兹力和安培力有关系吗?
生:有。
电流是电荷的定向移动形成的,那么,静止的通电导体在磁场中受到的安培力,在数值上等于大量定向运动电荷受到的洛伦兹力的总和。
建模
师:这就需要我们建立一个模型。
而模型的建立,我们总是选择简单的,所以:
磁场:匀强磁场
电流:通以恒定电流的直导线,并与磁场垂直
设有一段长为L,横截面积为S的直导线,单位体
积内的自由电荷数为n ,每个自由电荷的电荷量为q ,自由电荷定向移动的速率为v 。
这段通电导线垂直磁场方向放入磁感应强度为B 的匀强磁场中,求
(1)通电导线中的电流
(2)通电导线所受的安培力
(3)这段导线内的自由电荷数
(4)每个电荷所受的洛伦兹力
同学们自己计算一下,一会找同学回答。
最后总结:(板书) 通电导线中的电流nqSv t
Q I ==
通电导线所受的安培力BnqSvL BIL F ==安 这段导线内的自由电荷数nSL N =
每个电荷所受的洛伦兹力qvB F =
师:我们刚刚推导出的公式qvB F =的适用条件是什么?
生:当电荷q 以速度v 垂直进入磁感应强度为B 的磁场中,它所受的洛仑兹力qvB F = 师:当运动电荷的方向与磁场的方向夹角为θ时,电荷所受的洛伦兹力怎么求? θsin qvB F =
当运动电荷的方向和磁场方向水平时,洛仑兹力为零。
此时洛伦兹力最小。
当运动方向和磁场方向垂直时,洛伦兹力为qvB F =,此时洛伦兹力最大。
当v=0,既电荷与磁场没有相对运动时,F=0.这也就是说,磁场只对相对于磁场运动的电荷有力的作用,而对相对于磁场静止的电荷没有作用力。
三:洛仑兹力的方向(板书)
师:作为一种力,洛伦兹力是有方向的,那么,我们怎样来确定它的方向呢?
引导学生:既然安培力是洛伦兹力的宏观表现,那么洛伦兹力的方向是不是可以根据安培力的方向判断方法来判断呢?
生:用左手定则判断
师:那我找同学来说一下左手定则的内容。
左手定则:伸开左手,使拇指与其余四个手指垂直,并且都与手掌在同一个平面内;让磁感线从掌心进入,并使四指指向正电荷运动的方向,这时拇指所指的方向就是运动的正电荷在磁场中所受洛伦兹力的方向。
(正电荷运动的方向与电流的方向相同,负电荷运动的方向与电流的方向相反。
)
负电荷受力的方向与正电荷受力的方向相反。
我们是不是也可以从开始做的实验中证明洛伦兹力的方向是通过左手定则来判断的。
我们回过头看一下。
让同学们用左手定则判断一下是否符合。
四:洛伦兹力的特点:
1.洛伦兹力的方向既垂直于磁场,又垂直于速度,即垂直于v 和B 所组成的平面.
2.洛伦兹力对电荷不做功,只改变速度的方向,不改变速度的大小.
五.带电粒子在磁场中的应用
一个带正电荷q 的带电粒子,在磁感应强度为B 的匀强磁场中,以垂直于磁场的方向运动,粒子所受的洛伦兹力恒为qvB F ,方向总跟速度方向垂直。
在力学的学习中我们已经知道,如果一个物体只受一个垂直于运动方向且大小不变的的力的作用,并且这个力始终在同一个平面内,则这个物体将做匀速圆周运动。
那这个正电荷在匀强磁场中必定做匀速圆周运动。
圆周运动的轨道平面与磁场方向垂直,向心力来自洛伦兹力。
那我们来看一下,带电粒子在匀强磁场中做圆周运动的轨道半径R 和周期T 。
1. 运动半径:洛伦兹力充当向心力q v B =m v 2R
,得出半径公式: R =m v qB
. 2.运动周期:根据T =
2πR v
得出周期公式: T =2πm qB
. 由公式我们可以看出带电粒子做圆周运动的周期与运动速度·半径无关。
现在我们再来看在课最开始我们提出的问题:为什么极光不能在赤道等低纬度地区出现呢?
极光现象
问题:极光是来自太阳的高能粒子进入大气后,与大气发生作用而产生的。
为什么在赤道却从来没有它的身影呢?
在两极,高能粒子的运动方向与磁场平行,没受到洛伦兹力作用,高能粒子就长驱
直入了。
而在纬度较低的地区,高能粒子在地磁场的作用下发生了偏转,故看不到极光现象。
也正因为这个原因,使我们人类的生产生活免遭宇宙高能粒子的伤害。
师:现在,我们明白了上课开始时那个美丽有神秘的极光现象吗?
板书设计:
磁场对运动电荷的作用—洛仑兹力
一洛仑兹力
1.定义:运动电荷在磁场中受到的作用力叫做洛伦兹力.
2.大小
(1) 当v⊥B时,F=qvB.
(2)当v∥B时,F=0.
(3)当磁感应强度B的方向与电流I的方向夹角为θ时,
(4)当v=0, F=0.
3.方向:左手定则
4.特点
(1).洛伦兹力的方向既垂直于磁场,又垂直于速度,即垂直于v和B所组成的平面.
(2).洛伦兹力对电荷不做功,只改变速度的方向,不改变速度的大小.
二.带电粒子在磁场中的运动
R=m v qB
T=2πm qB。
