(相似三角形)证明题

合集下载

完整版)相似三角形题型归纳

完整版)相似三角形题型归纳1、在平行四边形ABCD中，点E为对角线AC上的一点，且AE∶EC=1∶3.将BE延长至与CD的延长线交于点G，与AD交于点F。

证明BF∶FG=1∶2.2、在直角三角形ABC中，∠BAC=90°，AB=AC，D为BC的中点，E为AC上的一点。

点G在BE上，连接DG并延长至交AE于点F，且∠FGE=45°。

证明：（1）BD·BC=BG·BE；（2）AG⊥BE；（3）若E为AC的中点，则EF∶FD=1∶2.3、在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上的一点，连接BO交AD于点F，OE⊥OB交BC边于点E。

证明：（1）△ABF∽△COE；（2）当O为AC的中点时，求△ABC的面积；（3）当O为AC边中点时，求△ABC的面积。

4、在平行四边形ABCD和平行四边形ACED中，点R为DE的中点，BR分别交AC、CD于点P、Q。

写出各对相似三角形（相似比为1除外），并求出BP∶PQ∶QR的值。

5、在△ABC中，AD平分∠BAC，EM为AD的中垂线，交BC延长线于点E。

证明DE=BE·CE。

6、过△ABC的顶点C任作一直线，与边AB及中线AD分别交于点F和E。

证明AE∶ED=2AF∶FB。

7、在Rt△ABC中，CD为斜边AB上的高，点M在CD 上，DH⊥BM且与AC的延长线交于点E。

证明：（1）△AED∽△CBM；（2）DE=DM。

8、在△ABC中，BD、CE分别是两边上的高，过D作DG⊥BC于点G，分别交CE及BA的延长线于点F、H。

证明：（1）DG＝BG·CG；（2）BG·CG＝GF·GH。

9、在平行四边形ABCD中，点P为对角线AC上的一点。

过P的直线与AD、BC、CD的延长线、AB的延长线分别相交于点E、F、G、H。

证明：AG∶GB=CP∶PD。

1、求证：如图，已知平行四边形ABCD中，点P在AC上，点Q在BC上，且AP=CQ。

相似三角形的判定(证明题)

相似三角形的判定1 •如图，锐角A4BC的髙CD和BE相交于点0,图中与△OD3相似的三角形有(A4个 B3个 C2个 D1个3•已知：AACB为等腰直角三角形，ZACB=90°延长BA至E,延长AB至F, ZECF二135°求证:CBF5・、如图，点C、D在线段AB上，且APCD是等边三角形.(1)当AC, CD, DB满足怎样的关系时，AACP S APDB：⑵当A PDBs A ACP时，试求ZAPB的度数.6•如图，Z1 = Z3, ZB = Z£>, AB = DE = 5, EC = 4(1)AABC- AADE吗？说明理由。

(2)求AD的长。

7.已知：如图,CE是RtAABC的斜边AB上的髙,BG丄AP・求证:CE:=ED €P.9 •如图，D为A ABC内一点，E为AABC外一点，且Z1=Z2, Z3：⑴AABD与4CBE相似吗？请说明理由.(2) A ABC与ADBE相似吗?请说明理由.AA EACs AB C判断题:⑴两个顶角相等的等浸三角形是相似的三角形。

((2)两个等腰直角三角形是相似三角形。

((3)底角相等的两个等艮三角形是相似三角形，((4)两个直角三角形一定是相似三角形。

((5)—个钝角三角形和一个锐角三角形有可能相似n ((6)有一个角相等的两个宜角三角形是相似三角形n ((7)有一个锐角相等的两个直角三角形是相似三角形。

( (3)三角形的三条中位线围成的三角形与原三角形相似.((9)所有的正三角形都相似n ( )(10)两个等艮三角形只要有一个角对应相等就相似. ( ) 2・如圍,AD/J BC, AE平分ZDAB, BE平分ZABC・ EF丄AB•证明：AAEF^AABE.3 •如尿，AABC是等边三角形，点D、E分别在BC、AC上，且BD^CE, AD与BE相交于点F・<1)试说明△ ABD坐ZkBCEj<2)AEAF与相似吗？说说你的理也.4.如釦在AABC中’ ZBAC=90\ D为BC的中点，AE丄AD, AE交CB的延长纟壬于点E・(1)求证：AEAB^AECA.:(2)4ABE和AADC是否一定相似？妇果相似，加以说明5如杲不相似，那么增加一个怎徉的条件，A.4BE和4ADC-定相似.5・如囲在AABC中,ZC=905, D. E衽BC上,BD=DE=EC=AC,指出團中哪两个三角形棉似,并证明你的结论.A6・如團，ZkABC 申，ZBAC=90% AB=AC, D 在BC 匕 E 在AC 匕且上ADETS 廈 (1) 求证：△ABD S /XDCE ・ (2) 台D 莊什么位贵时，AABD^ADCE ・7. 如图，在AABC 中，AB ・8cm, BC-16c 叫点P 从点A 开始沿AB 向B 以2cE 啲速度移动‘点 Q 从点B 幵弟沿BC 向C 点^4cm,s 的速虔移动.加果P, Q 分别从、B 同时出拓经过几秒绅ZkPB Q与△ ABC 相似？8. 如囹，已知AABC 中CE 丄AB 干E, BF 丄AC 于F,求证；△AEF S ^ACB.9 •如图、UAABC 中，ZACB=PO% AC=4, BO3,点P 在线段AB 上臥每秽1个单位的速度从点B 问点A 运动，同时点Q 曲圭段A C 上以同样的速虎从点A 向点C 运动，运动的时间用1 (单位：秒)表示.(1)求线股AB 的长；<2)求当t 为何值时，AAPQ 与AABC 相似？10・如虱在MBCD 中’ E 豹BC 边上一点'连接AE 、DE, F 为线段DE 上一点，且ZAFE=ZB .试说明△ADF S ADEC ・11 ・如釦已知MBC 中’ AB=2& AC=4js, BC=6? AMN 与AABC 相似，求MN 的长.3A312・如團，点E 是匹边形ABCD 的对角线BD 上一点，SZBAC-Z3DC-ZDAE ・求证：AABE^AAC D.14.已知，如團：在AABC 中，AD=CD, /ADE=ZDCB, 求还；△ABCsACDE.16・已知：D 、ElAABC^j±AB^ AC±^].^, AB=9, AD=4, AC=7.2, AE=5,求证：AABCooAAE D ・18 ・已知：如园.在△ ABC 和△ ADE 中,ZBAC=ZDAE, ZABC=ZADE. 求证：AABIX^AACE・D17 ・ 4±AABC 中，ZBAC=90c , E,求证：AABIX O ADCE ・19・如园.在正万形网格上有6个斜三角形：①②△CDB,③ADEB, @AFBG, ©AHGF,⑥△ERF 请在三角形②〜⑥中，找出与①相佩的三鱼形的序号是_〈把前序号埴上〉并证明你的结论.20.如冒所示，在A ABC 中，AB=8cm ? BC=16cm ?点P 从点A 开始沿边AB 向点B 以lens 的速庶移动，点Q 从点B 幵始沿边BC 向点C 以2cm/啲速庚移动，如果点.P 、Q 同时出紀经过多长时间后，厶PB ABC 相似?试说明理由■21・将两个全等的等腰宜角三角形摆成如團所示的祥子（團中所有的点、线都在同一平面内〉・ CD 请在图中找出两対相似而不全手的三角形〉话从其中一对说明埋宙.C2）你还能再找一对相似而不全等的三角形吗？请说明遅由.22・如园：己知△ABgZkADE 的边BC 、AD 相交于点0,旦Z1=Z2-Z3.求证：AABCsAADE.23.如园，APQR 罡尊边三角形，ZAPBJ20J I 乩每两个三角形沏一组写出园中所有的相似三角形，并迭择耳中的一爼加以证明.2S.如图’已知:厶ABC 中〉ZABC-90% AB-BC,延长BC 到E,使得CE-2BC,馭CE 的中点D,连接AE 、 AD ・求iib AACD<7>AECA ・26.如阂.D 是Z\ABC 的边BC 上的一点,AB=2, BD=1, DC=3,求证：AABD^ACBA.5 I D327・已知：AABC为手瑕直角三角形，ZACB=90%延长BA至E,延长AB至F, ZECF=135S求证：AEAC^ACBF.28・如因所示'R仏ABC中’已^DZBAC=O0\ AB=AC=2,点D在BC上运动(不能到达点B, C),过点D作ZADE=45% DE交AC于点E.(1)求证：△AEIX^XDCE;(2)当AADE是等腰三角形时，求AE的长.29・如團已知AB丄BD, CD丄BD・若・4B=9, CD=4, BD-10,话问在BD上是否存在P点，使以P、4、B三点为页点的三角形与以P、C、D三点为顶点的三角形相似・?若存在，求BP的长：若不存在'请说明理由.30・如臥AABCx ADEPf两个全竽的等腰直毎三角形，ZBAC=ZPDE=90\(1)若将ADEP的顶点.P放在BC上(如图1) , PD、PE分别与AC、AB相交于点F. G.求证：△PBGs^FCP;(2)肴使ADEP的顶点P与顶点A重台〔如图2) , PD-. PE与BC相交干点几G・试问APBG与AFCP还相似吗勺为什么？1・如国,在4ABC和ADEF中ZA=ZD=90\ AB=DE=3, AC=2DF=4 ・(1)判断这两个三角形杲否殆似并说明为什么？(2)能否分别过A, D在这两个三角形中各作一条湘助纵使△ ABC分黑成的两个三角形与ADEFB-割成的两个三角形分别对应相似？证明惋的结论.2 •如團，在A ABC中，AB=AC,若4 ABC^ADEF,且点A往DE上，点E在BC上，EF与AC交于点M・求证：AABE^AECM・5.己知：如图'AABC中'AD=DB, Zl=/2.求证：AABCxoAEAD.S・如图'在厶ABC中,AB=AC, ZADB=90°, ZCBE=ZCAD；求证：△BECsAADC ・10・?0g.. ZABC=ZBCD,且BC^=AB・CD・ ^15： AABC^ABCD.O11・已务Ih如图，AD是△ ABC的高,BE丄AB, AE交BC于点、F> AB・AC-AD・AE・求证:ABEFcoAACF ・13.妇團所不‘在铁角AABC中，高CD： BE相交于点、F・ <1)拷出图中所有的相似三角形，并证明一对三角形柜似3 (2)连结DE,试说明：AADEccAACB.4・如凰，集一时別一根2米长的竹竿EF嶷长GE为I球'此时，小红测得一棵被凤吹斜的杨树与地面成30。

(相似三角形)证明题

1、如图，△ABC中，三条内角平分线交于D，过D作AD垂线，分别交AB、AC于M、N，请写出图中相似的三角形，并说明其中两对相似的正确性。

2、如图，AD为△ABC的高，DE⊥AB，DF⊥AC，垂足分别为E、F，试判断∠ADF与∠AEF的大小，并说明明理由，…3、如图，在△ABC中，点D、E分别在BC、AB上，且∠CAD=∠ADE=∠B，AC：BC=1：2，设△EBD、△ADC、△ABC的周长分别为m1 、m2、m3，求的值，*4、如图，已知△ABC中，D为BC中点，AD=AC，DE⊥BC，DE与AB交于E，EC与AD相交于点F，（1）△ABC与△FCD相似吗请说明理由；（2）若S =5，BD=10，求DE的长。

：5、AD是△ABC的高，E是BC的中点，EF⊥BC交AC于F，若BD＝15，DC=27，AC=45.求AF的长。

\6、已知:如图，在△PAB中,∠APB=120O,M、N是AB上两点，且△PMN是等边三角形。

求证: BM·PA=PN·BP7、已知：如图，D是△ABC的边AC上一点，且CD=2AD，AE⊥BC于E, 若BC=13, △BDC的面积是39, 求AE的长。

?????*8、已知：如图，在△ABC中，AB=15，AC=12，AD是∠BAC的外角平分线且AD交BC的延长线于点D，DE ∥AB交AC的延长线于点E。

《9、已知: 如图，四边形ABCD中，CB⊥BA于B，DA⊥BA于A，BC=2AD，DE⊥CD交AB于E，连结CE，求证：DE2=AE?CE】10、如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.(1)ΔABE与ΔADF相似吗请说明理由.(2)若AB=6，AD=12，BE=8，求DF的长./11、如图：三角形ABC是一快锐角三角形余料，边BC＝120mm,高AD ＝80mm,要把它加工成正方形零件，是正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少ANP12、已知：如图：FGHI 为矩形，AD ⊥BC 于D ，95GH FG ，BC ＝36cm,AD ＝12cm 。

相似三角形性质与判定专项练习30题(有答案)

相似三角形性质与判定专项练习30题(有答案)1.在三角形ABC中，点D在边BC上，且∠BAC=∠DAG，∠XXX∠BAD。

证明：=。

当GC⊥BC时，证明：∠BAC=90°。

2.在三角形ABC中，∠ACB=90°，点D在边BC上，CE⊥AB，CF⊥AD，E、F分别是垂足。

证明：AC^2=AF•AD。

联结EF，证明：AE•DB=AD•EF。

3.在三角形ABC中，PC平分∠ACB，PB=PC。

证明：△APC∽△ACB。

若AP=2，PC=6，求AC的长。

4.在平行四边形ABCD中，过B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠XXX∠C。

证明：△ABF∽△EAD。

若AB=4，∠BAE=30°，求AE的长。

5.在三角形ABC中，∠ABC=2∠C，BD平分∠ABC。

证明：AB•BC=AC•CD。

6.在直角三角形ABC中，AC=BC，点E、F在AB上，∠ECF=45°，设△ABC的面积为S。

说明AF•BE=2S的理由。

7.在等边三角形ABC中，边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P。

若AE=CF，证明：AF=BE，并求∠APB的度数。

若AE=2，试求AP•AF的值。

若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长。

8.在钝角三角形ABC中，AD，BE是边BC上的高。

证明。

9.在三角形ABC中，AB=AC，DE∥BC，点F在边AC 上，DF与BE相交于点G，且∠XXX∠ABE。

证明：（1）△DEF∽△BDE；（2）DG•DF=DB•EF。

10.在等边三角形ABC、△DEF中，点D为AB的中点，E在BC上运动，DF和EF分别交AC于G、H两点，BC=2.问E在何处时CH的长度最大？11.在AB和CD交于点O的图形中，当∠A=∠C时，证明：OA•OB=OC•OD。

12.在等边三角形△AEC中，以AC为对角线做正方形ABCD（点B在△AEC内，点D在△AEC外）。

全等(相似)三角形证明经典50题及相似三角形-精品.pdf

2016专题：《全等三角形证明》1.已知：D 是AB 中点，∠ACB=90°，求证：12CD AB2.已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23.已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE4. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

AB C DEF 21 DABC5.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C6.已知：AB=CD ，∠A=∠D ，求证：∠B=∠C7.如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．8.如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBADC BA FE A B CD9.已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：10.如图：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

11.如图：在△ABC 中，BA=BC ，D 是AC 的中点。

求证：BD ⊥AC 。

12.AB=AC ，DB=DC ，F 是AD 的延长线上的一点。

求证：BF=CF13.如图：AB=CD ，AE=DF ，CE=FB 。

求证：AF=DE 。

O E DCB AF E D CBA DCB AF DCB AFEDC BAD CBAE14.已知：点A 、F 、E 、C 在同一条直线上， AF ＝CE ，BE ∥DF ，BE ＝DF ．求证：△ABE ≌△CDF ．15.已知：如图所示，AB ＝AD ，BC ＝DC ，E 、F 分别是DC 、BC 的中点，求证： AE ＝AF 。

相似三角形推理证明复习题(含答案)

相似三角形推理证明1．（顺义18期末19）如图，E 是□ABCD 的边BC 延长线上一点，AE 交CD 于点F ，FG ∥AD 交AB 于点G ．（1）填空：图中与△CEF 相似的三角形有；（写出图中与△CEF 相似的所有三角形）（2）从（1）中选出一个三角形，并证明它与△CEF 相似．19．（1）△ADF ，△EBA ，△FGA ；………………………….3分（每个一分）（2）证明：△ADF ∽△ECF∵四边形ABCD 为平行四边形∴BE ∥AD …………………………………………………….4分 ∴∠1=∠E ，∠2=∠D∴△ADF ∽△ECF …………………………………………….5分（其它证明过程酌情给分）2．（大兴18期末19）已知：如图，在△ABC 中，D ，E 分别为AB 、 AC 边上的点，且AE AD 53=，连接DE . 若AC ＝4，AB ＝5. 求证：△ADE ∽△ACB.19．证明：∵ AC =3，AB =5，35AD AE =，∴AC ABAD AE=．……………………………… 3分 ∵ ∠A =∠A ，……………………………… 4分 ∴ △ADE ∽△ACB ．……………………… 5分3．（丰台18期末18）如图，△ABC 中，DE ∥BC ，如果AD = 2，DB = 3，AE = 4，求AC 的长.18. 解：∵DE ∥BC ， ∴AD AE DBEC=.……2分即243EC=． ∴EC ＝6．……4分∴AC ＝AE + EC ＝10． ……5分其他证法相应给分.4．（怀柔18期末18）如图，在△ABC 中，D 为AC 边上一点，BC ＝4，AC ＝8，CD=2．求证：△BCD ∽△ACB .18.证明：∵BC ＝4，AC ＝8，CD =2.…………………………1分∴………………………………………3分又∵∠C =∠C …………………………………………………………………………4分 ∴ △BCD ∽△ACB ……………………………………………………………………5分DB5．（西城18期末18）如图，AB ∥CD ，AC 与BD 的交点为E ，∠ABE=∠ACB ．（1）求证：△ABE ∽△ACB ；（2）如果AB=6，AE=4，求AC ，CD 的长．6．（密云18期末19）如图，BO 是ABC ∆的角平分线，延长BO 至D 使得BC=CD.（1）求证：AOB COD ∆∆∽.（2）若AB=2，BC=4，OA=1，求OC 长.19.（1）证明：BO 是ABC ∆的角平分线∴ ABO OBC ∠=∠…………………………………………………………………………..1分 BC=CD∴ OBC ODC ∠=∠∴ABO ODC ∠=∠…………………………………………………………………………..2分又AOB COD ∠=∠∴AOB ∆∽COD ∆…………………………………………………………………………….3分（2）解：AOB∆∽COD∆∴AB OACD OC=…………………………………………………………………………..4分又AB=2，BC=4，OA=1，BC=CD∴OC=2 …………………………………………………………………………….5分7．（东城18期末19）如图，在四边形ABCD中，AD∥BC，AB⊥BC，点E在AB上，∠DEC=90°.（1）求证：△ADE∽△BEC.（2）若AD=1，BC=3，AE=2, 求AB的长.8．（海淀18期末21）如图，在△ABC中，∠B=90°，AB=4，BC=2，以AC为边作△ACE，∠ACE=90°，AC=CE，延长BC至点D，使CD=5，连接DE．求证：△ABC∽△CED．21．证明：∵ ∠B =90°，AB =4，BC =2，∴ AC == ∵ CE =AC ，∴ CE = ∵ CD =5， ∴AB ACCE CD=. ………………3分 ∵ ∠B =90°，∠ACE =90°，∴ ∠BAC +∠BCA =90°，∠BCA +∠DCE =90°.∴ ∠BAC =∠DCE .∴ △ABC ∽△CED . ………………5分9．（朝阳18期末23）如图，正方形ABCD 的边长为2，E 是CD 中点，点P 在射线AB上，过点P 作线段AE 的垂线段，垂足为F . （1）求证：△P AF ∽△AED ；（2）连接PE ，若存在点P 使△PEF 与△AED 相似，直接写出P A 的长10．（石景山18期末23）如图，四边形ABCD 是平行四边形，CE ⊥AD 于点E ，DF ⊥BA 交BA 的延长线于点F ．（1）求证：△ADF ∽△DCE ；（2）当AF =2，AD =6，且点E 恰为AD 中点时，求AB 的长．23．（本小题满分5分）（1）证明：∵四边形ABCD 是平行四边形，∴AB ∥DC ，∴∠D A F =∠C D E ， ……………………………………………… 1分 ∵ DF ⊥BA ，CE ⊥AD ，∴∠F =∠C E D =90°，……………………………………………… 2分 ∴△A D F ∽△D C E ； ………………………………………………3分（2）解：∵△ADF ∽△DCE ，∴DE AFDC AD = ∴326=DC ， ∴DC =9．∵四边形ABCD 是平行四边形， ∴AB =DC∴A B =9．…………………………………………………………5分11．（平谷18期末19）如图，∠ABC =∠BCD =90°，∠A =45°，∠D =30°，BC =1，AC ，BD 交于点O ．求BODO的值．19．解：∵∠ABC =∠BCD =90°，∴AB ∥CD ． .................................................................................................................. 1 ∴∠A =∠ACD ． ............................................................................................................ 2 ∴△ABO ∽△CDO ． .. (3)∴BO ABCO CD=． ··········································································································· 4 在Rt △ABC 中，∠ABC =90°，∠A =45°，BC =1， ∴AB =1．在Rt △BCD 中，∠BCD =90°，∠D =30°，BC =1，∴CD∴BO CO ==． (5)12．（顺义18期末22）已知：如图，在△ABC的中，AD是角平分线，E是AD上一点，且AB：AC = AE ：AD．求证：BE=BD．22．证明：∵AD是角平分线，∴∠1=∠2，……………………………………….1分又∵AB AD = AE AC，……………………….2分∴△ABE∽△ACD，………………………………………..…….3分∴∠3=∠4，……………………………………………………….4分∴∠BED=∠BDE，∴BE=BD．………………………………………………………..5分13．（门头沟18期末18）如图，在△ABC 中，AB =AC ，BD =CD ，CE ⊥AB 于E ．求证：△ABD ∽△CBE .18．（本小题满分5分）证明：∵ AB =AC ，BD =CD∴ AD BC ⊥, ……………………………………2分∵ CE ⊥AB∴90ADB BEC ∠=∠=︒……………………………………4分∵B B ∠=∠ABD CBE ∴△∽△ ……………………………………5分14．（平谷18期末23）如图，在□ABCD 中，对角线AC ，BD 交于点O ，过点O 作EO ⊥BD ，交BA 延长线于点E ，交AD 于点F ，若EF=OF ，∠CBD =30°，BD =63AF 的长．23．解：方法一：∵□ABCD ，∴AD ∥BC ，OD =12BD =33 ··················································································· 1 ∵∠CBD =30°， ∴∠ADB =30°． ∵EO ⊥BD 于O ， ∴∠DOF =90°．在Rt △ODF 中，tan30°=OF OD =， ∴OF=3． (2)∴FD =6．过O 作OG ∥AB ，交AD 于点G ． ∴△AEF ∽△GOF ． ∴AF EFGF OF=． ∵EF=OF ， ∴AF=GF ．∵O 是BD 中点， ∴G 是AD 中点． ········································································································· 3 设AF=GF=x ，则AD =6+x ． ∴AG =62xx x ++=． ................................................................................................ 4 解得x =2． ∴AF =2． (5)方法二：延长EF 交BC 于H ．由△ODF ≌△OHB 可知， OH =OF ． ············································3 ∵AD ∥BC ，∴△EAF ∽△EBH ．∴EF AFEH BH=． ∵EF=OF ， ∴13AF BH =． ··············································································································· 4 由方法一的方法，可求BH =6． ∴AF =2．15．（怀柔18期末23）数学课上老师提出了下面的问题：在正方形ABCD 对角线BD 上取一点F ，使15DF BD =. 小明的做法如下：如图①应用尺规作图作出边AD 的中点M ; ②应用尺规作图作出MD 的中点E ; ③连接EC ，交BD 于点F . 所以F 点就是所求作的点.请你判断小明的做法是否正确，并说明理由.23.解：正确. ………………………………………………………………………………………1分理由如下：由做法可知M 为AD 的中点，E 为MD 的中点， ∴AD DE =41. …………………………………………………………2分 ∵四边形ABCD 是正方形，∴AD=BC ，ED ∥BC . ………………………………………………3分 ∴△DEF ∽△BFC ∴BC DE =BFDF ………………………………………………………..4分 ∵AD =BC∴BF DF =BC DE =41∴BD DF =51………………………………………………………………………………………5分。

相似三角形判定专项练习30题(有答案)

相似三角形判定专项练习30题（有答案）1．如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且CF=3FD，△ABE与△DEF相似吗？为什么？2．如图，△BAC、△AGF为等腰直角三角形，且△BAC≌△AGF，∠BAC=∠AGF=90°．若△BAC固定不动，△AFG绕点A旋转，AF、AG与边BC的交点分别为D、E．请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明．3．如图，在正三角形ABC中，D，E分别在AC，AB上，且，AE=EB．求证：△AED∽△CBD．4．如图，已知∠1=∠2，且AB•ED=AD•BC，则△ABC与△ADE相似吗？是说明理由．5．已知：如图，在△ABC中，∠C=90°，点D、E分别AB、CB延长线上的点，CE=9，AD=15，连接DE．若BC=6，AC=8，求证：△ABC∽△DBE．6．如图，点D在等边△ABC的BC边上，△ADE为等边三角形，DE与AC交于点F．（1）证明：△ABD∽△DCF；（2）除了△ABD∽△DCF外，请写出图中其他所有的相似三角形．7．如图，CD、BE分别是锐角△ABC中AB、AC边上的高线，垂足为D、E．（1）证明：△ADC∽△AEB；（2）连接DE，则△AED与△ABC能相似吗？说说你的理由．8．如图，在△ABC，AC⊥BC，D是BC延长线上的一点，E是AC上的一点，连接ED，∠A=∠D．求证：△ABC∽△DEC．9．在任意△ABC中，作CD⊥AB，垂足为D，BE⊥AC，垂足为E，F为BC上的中点，连接DE，EF，DF．（1）求证：DF=EF；（2）直接写出除直角三角形以外的所有相似三角形；（3）在（2）中的相似三角形中选择一对进行证明．10．如图，△ABC是等边三角形，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F．（1）试说明△ABD≌△BCE；（2）△EAF与△EBA相似吗？说说你的理由．11．如图，在△ABC中，D是BC边上的中点，且AD=AC，DE⊥BC，交BA于点E，EC与AD相交于点F．求证：△ABC∽△FCD．12．已知：在Rt△ABC中∠C=90°，CD为AB边上的高．求证：Rt△ADC∽Rt△CDB．13．如图，D为△ABC内一点，E为△ABC外一点，且∠1=∠2，∠3=∠4，找出图中的两对相似三角形并说明理由．14．如图，∠DEC=∠DAE=∠B，试说明：（1）△DAE∽△EBA；（2）找出两个与△ABC相似的三角形（第2小题不要求写出证明过程）．15．如图，锐角三角形ABC中，CD，BE分别是AB，AC边上的高，垂足为D，E．（1）证明：△ACD∽△ABE．（2）若将D，E连接起来，则△AED与△ABC能相似吗？说说你的理由．16．如图，在△ABC中，∠BAC=90°，D为BC的中点，AE⊥AD，AE交CB的延长线于点E．（1）求证：△EAB∽△ECA；（2）△ABE和△ADC是否一定相似？如果相似，加以说明；如果不相似，那么增加一个怎样的条件，△ABE和△ADC 一定相似．（1）求证：△ADE∽△ABC；（2）△ABD与△ACE相似吗？为什么？（3）图中还有哪些三角形相似？请直接写出来．18．如图，已知：△ABC为等腰直角三角形，∠ACB=90°，延长BA至E，延长AB至F，∠ECF=135°，求证：△EAC∽△CBF．19．如图所示，Rt△ABC中，已知∠BAC=90°，AB=AC=2，点D在BC上运动（不能到达点B，C），过点D作∠ADE=45°，DE交AC于点E．（1）求证：△ABD∽△DCE；（2）当△ADE是等腰三角形时，求AE的长．20．如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE．求证：△ABE∽△ACD．21．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s 的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的22．如图，矩形ABCD中，AB=6，BC=8，动点P从B点出发沿着BC向C移动，速度为每秒2个单位，动点Q 从点C出发沿CD向D出发，速度为每秒1个单位，几秒后由C、P、Q三点组成的三角形与△ABC相似？这时线段PQ与AC的位置关系如何？请说明理由．23．已知，如图，，点B，D，F，E在同一条直线上，请找出图中的相似三角形，并说明理由．24．已知线段AC上有一动点B，分别以AB、BC为边向线段的同一侧作等边三角形△ABD和△BCE．连接AE、CD （如图），若MN分别为AE、CD的中点，（1）求证：AM=CN；（2）求∠MBN的大小；（3）若连接MN，请你尽可能多的说出图中相似三角形和全等三角形．25．如图，已知△ABC和△MBN都是等腰直角三角形，∠BAC=∠MBN=90°，BD⊥AN．请找出与△ABD相似的三角形并给出证明，直接写出∠ANC的度数．26．如图，在△ABC中，AB=6，BC=8．点D以每秒1个单位长度的速度由B向A运动，同时点E以每秒2个单位长度的速度由C向B运动，当点E停止运动时，点D也随之停止．设运动时间为t秒，当以B，D，E为顶点的三角形与△ABC相似时，求t的值．27．如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF=CD，证明：△ABE∽△AEF．28．如图，在四边形ABCD中，AB⊥BC，AD⊥DC，连接BD，AC，且DE⊥AC于E，交AB于F，求证：△AFD∽△ADB．29．已知，如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B、A、D在一条直线上，连接BE、CD．（2）若M、N分别是BE和CD的中点，将△ADE绕点A按顺时针旋转，如图②所示，试证明在旋转过程中，△AMN 是等腰三角形；（3）试证明△AMN与△ABC和△ADE都相似．30．如图，在△ABC中，AB=AC，BD=CD，CE⊥AB于E．求证：△ABD∽△CBE．相似三角形判定专项练习30题参考答案：1．解：△ABE 与△DEF 相似．理由如下： ∵四边形ABCD 为正方形， ∴∠A=∠D=90°，AB=AD=CD ，设AB=AD=CD=4a ， ∵E 为边AD 的中点，CF=3FD ， ∴AE=DE=2a ，DF=a ，∴==2，==2，∴=，而∠A=∠D ， ∴△ABE ∽△DEF ． 2．解：△EAD ∽△EBA ，△DAE ∽△DCA ．对△ABE ∽△DAE 进行证明： ∵△BAC 、△AGF 为等腰直角三角形， ∴∠B=45°，∠GAF=45°， ∴∠EAD=∠EBA ，而∠AED=∠BEA ， ∴△EAD ∽△EBA ． 3．证明：∵△ABC 为正三角形， ∴∠A=∠C=60°，BC=AB ， ∵AE=BE ， ∴CB=2AE ， ∵，∴CD=2AD ，∴==，而∠A=∠C ， ∴△AED ∽△CBD ． 4．解：△ABC ∽△ADE ，理由为：证明：∵AB •ED=AD •BC ，∴=，∵∠1=∠2， ∴∠1+∠ABE=∠2+∠ABE ，即∠BAC=∠DAE ， ∴△ABC ∽△ADE ．5．证明：∵在RT △ABC 中，∠C=90°，BC=6，AC=8， ∴AB==10，∴DB=AD ﹣AB=15﹣10=5 ∴DB ：AB=1：2，又∵EB=CE ﹣BC=9﹣6=3， ∴EB ：BC=1：2，又∵∠DBE=∠ABC，∴△ABC∽△DBE．6．（1）证明：∵△ABC，△ADE为等边三角形，∴∠B=∠C=∠3=60°，∴∠1+∠2=∠DFC+∠2，∴∠1=∠DFC，∴△ABD∽△DCF；（2）解：∵∠C=∠E，∠AFE=∠DFC，∴△AEF∽△DCF，∴△ABD∽△AEF，故除了△ABD∽△DCF外，图中相似三角形还有：△AEF∽△DCF，△ABD∽△AEF，△ABC∽△ADE，△ADF∽△ACD．7．（1）证明：∵如图，CD、BE分别是锐角△ABC中AB、AC边上的高线，∴∠ADC=∠AEB=90°．又∵∠A=∠A，∴△ADC∽△AEB；（2）由（1）知，△ADC∽△AEB，则AD：AE=AC：AB．又∵∠A=∠A，∴△AED∽△ABC．8．证明：∵AC⊥BC，∴∠ACB=∠DCE=90°，又∵∠A=∠D，∴△ABC∽△DEC．9．（1）证明：∵CD⊥AB，BE⊥AC，∴∠BEC=∠BDC=90°，而F为BC上的中点，∴EF=BC，DF=BC，∴DF=EF；（2）解：△ADE∽△ACB；△PDE∽△PCB；△PDB∽△PEC；（3）△ADE∽△ACB．理由如下：证明：∵∠ADC=∠AEB=90°，而∠BAE=∠CAD，∴△ABE∽△ACD，∴=，∵∠DAE=∠CAB，∴△ADE∽△ACB．10．（1）证明：∵△ABC是等边三角形，∴AB=BC，∠ABD=∠BCE=∠BAC，又∵BD=CE，∴△ABD≌△BCE；（2）答：相似；理由如下：∵△ABD≌△BCE，∴∠BAD=∠CBE，∴∠BAC﹣∠BAD=∠CBA﹣∠CBE，∴∠EAF=∠EBA，又∵∠AEF=∠BEA，∴△EAF∽△EBA．11．证明：∵AD=AC，∴∠ADC=∠ACD，∵D为BC中点，且DE⊥BC，∴EB=EC．∴∠B=∠DCF．∴△ABC∽△FCD．12．证明：∵CD为AB边上的高，∴∠ADC=∠CDB=90°，∵∠ACB=90°，∴∠A+∠ACD=90°，∠ACD+∠BCD=90°，∴∠A=∠BCD，∵∠ADC=∠CDB=90°，∴Rt△ADC∽Rt△CDB．13．解：△ABD∽△CBE，△ABC∽△DBE．∵∠1=∠2，∠3=∠4，∴△ABD∽△CBE，∴∵∠1=∠2，∴∠ABC=∠DBE，∴△ABC∽△DBE14．解：（1）∵∠DEC=∠B，∴DE∥AB，∴∠DEA=∠EAB，又∵∠DAE=∠B，∴△DAE∽△EBA；（2）△CDE∽△ABC，△EAC∽△ABC．15．证明：（1）∵CD，BE分别是AB，AC边上的高，∴∠ADC=∠AEB=90°．∵∠A=∠A，∴△ACD∽△ABE．（2）∵△ACD∽△ABE，∴AD：AE=AC：AB．∵∠A=∠A，∴△AED∽△ABC．16．证明：（1）∵△ABC中，∠BAC=90°，D为BC的中点，∴BD=CD，AD=CD，∴∠C=∠DAC，又∵AE⊥AD，∴∠EAB+∠BAD=90°，∠BAD+∠DAC=90°，∴∠EAB=∠C，∴△EAB∽△ECA；（2）由（1）得，∠EAB=∠CAD，∴当∠ABE=∠ADC或AB=BE或∠E=∠C或=时，△ABE和△ADC一定相似．17．解：（1）证明∵∠A=∠A，∠ADE=∠ABC，∴△ADE∽△ABC；（2）相似．证明：∵△ADE∽△ABC；∴，∵∠A=∠A，∴△ABD∽△ACE；（3）△DOE∽△COB；△EOB∽△DOC．18．证明：∵△ABC为等腰直角三角形，∠ACB=90°，∴∠CAB=∠CBA=45°，∴∠E+∠ECA=45°（三角形外角定理）．又∠ECF=135°，∴∠ECA+∠BCF=∠ECF﹣∠ACB=45°，∴∠E=∠BCF；同理，∠ECA=∠F，∴△EAC∽△CBF．19．（1）证明：Rt△ABC中，∠BAC=90°，AB=AC=2，∴∠B=∠C=45°．∵∠ADC=∠B+∠BAD，∠ADC=∠ADE+∠EDC，∴∠ADE+∠EDC=∠B+∠BAD．又∵∠ADE=45°，∴45°+∠EDC=45°+∠BAD．∴∠EDC=∠BAD．∴△ABD∽△DCE．（2）解：讨论：①若AD=AE时，∠DAE=90°，此时D点与点B重合，不合题意．②若AD=DE时，△ABD与△DCE的相似比为1，此时△ABD≌△DCE，于是AB=AC=2，BC=2，AE=AC﹣EC=2﹣BD=2﹣（2﹣2）=4﹣2③若AE=DE，此时∠DAE=∠ADE=45°，如下图所示易知AD⊥BC，DE⊥AC，且AD=DC．由等腰三角形的三线合一可知：AE=CE=AC=1．20．解：∵∠BAC=∠BDC，∠AOB=∠DOC，∴∠ABE=∠ACD又∵∠BAC=∠DAE∴∠BAC+∠EAC=∠DAE+∠EAC∴∠DAC=∠EAB∴△ABE∽△ACD．21．解：设经x秒后，△PBQ∽△BCD，由于∠PBQ=∠BCD=90°，（1）当∠1=∠2时，有：，即；（2）当∠1=∠3时，有：，即，∴经过秒或2秒，△PBQ∽△BCD．22．解：要使两个三角形相似，由∠B=∠PCQ ∴只要或者∵AB=6，BC=8∴只要设时间为t则PC=8﹣2t，CQ=t∴t=或者t=；①当t=时，△ABC∽△PCQ，PQ⊥AC理由：△ABC∽△PCQ∴∠BAC=∠CPQ∵∠BAC+∠ECP=90°，∴∠EPC+∠ECP=90°即PQ⊥AC；②当t=，△ABC∽△QCP，AC平分PQ理由：△ABC∽△QCP∴∠BAC=∠CQP，∠ACB=∠QPC∴∠QCE=∠EQC，∠ACB=∠QPC∴PE=EQ=CE即AC平分PQ23．解：△ABC∽△ADE，△BAD∽△CAE．理由：∵，∴△ABC∽△ADE，∴∠BAC=∠DAE，∴∠BAD=∠CAE，∵，∴，∴△BAD∽△CAE，∵∠ACB=∠AED，∠AFE=∠BFC，∴△AFE∽△BFC．24．（1）证明：∵△ABD和△BCE是等边三角形，∴AB=BD，BC=BE，∠EBC=∠ABC=60°，∴∠ABE=∠DBC，在△ABE和△DBC中∴△ABE≌△DBC（SAS）∴AE=DC，∵M、N分别为AE、CD的中点，∴AM=AE，CN=DC∴AM=CN；（2）解：∵△ABE≌△DBC，∴∠EAB=∠CDB，在△AMB和△DNB中∴△AMB≌△DNB（SAS），∴∠ABM=∠DBN，∵∠ABC=∠ABM+∠MBD=60°，∴∠DBN+∠MBD=60°，即∠MBN=60°；（3）解：图中的全等三角形有：△ABM≌△DBN，△BME≌△BCN，△ABE≌△DBC；相似三角形有：△ABD∽△BCE，△ABD∽△BMN，△BMN∽△BCE．25．解：△ABD∽△CBN，理由：∵△ABC和△MBN都是等腰直角三角形，BD⊥AN，∴∠MBD=∠NBD=∠BNM=∠ABC=45°，∴==，∵∠MBA+∠ABD=45°，∠ABD+∠CBN=45°，∴∠ABD=∠CBN，∴△ABD∽△CBN，∴∠BNC=∠ADB=90°，∵∠BNA=45°，∴∠ANC=45°．26．解：∵点D以每秒1个单位长度的速度由B向A运动，同时点E以每秒2个单位长度的速度由C向B运动，∴BD=t，BE=8﹣2t，∴△BDE∽△BAC时，=，即=，解得t=2.4（秒）；当△BED∽△BAC时，=，即=，解得t=（秒）．综上所述，t的值为2.4秒或秒．27．证明：∵在正方形ABCD中，E是BC的中点，F是CD上一点，且CF=CD，∴∠B=∠C=90°，AB：EC=BE：CF=2：1．∴△ABE∽△ECF．∴AB：EC=AE：EF，∠AEB=∠EFC．∵BE=CE，∠FEC+∠EFC=90°，∴AB：AE=BE：EF，∠AEB+∠FEC=90°．∴∠AEF=∠B=90°．∴△ABE∽△AEF．28．证明：∵∠AEF=∠ABC=90°，∠EAF=∠BAC．∴△EAF∽△BAC，=，即AE•AC=AF•AB．同理可得，△AED∽△ADC，=，即AE•AC=AD2，∴AD2=AF•AB，即=，又∵∠DAF=∠BAD，∴△AFD∽△ADB．29．证明：（1）∵∠BAC=∠DAE，∴∠BAC+∠CAE=∠DAE+∠CAE，即∠BAE=∠CAD．在△ABE与△ACD中，，∴△ABE≌△ACD，∴BE=CD；（2）由（1）得△ABE≌△ACD，∴∠ABE=∠ACD，BE=CD．∵M，N分别是BE，CD的中点，∴BM=CN．在△ABM与△ACN中，，∴△ABM≌△ACN，∴AM=AN，∴△AMN为等腰三角形；（3）由（2）得△ABM≌△ACN，∴∠BAM=∠CAN，∴∠BAM+∠BAN=∠CAN+∠BAN，即∠MAN=∠BAC，又∵AM=AN，AB=AC，∴AM：AB=AN：AC，∴△AMN∽△ABC；∵AB=AC，AD=AE，∴AB：AD=AC：AE，又∵∠BAC=∠DAE，∴△ABC∽△ADE；∴△AMN∽△ABC∽△ADE．30．证明：在△ABC中，AB=AC，BD=CD，∴AD⊥BC，∵CE⊥AB，∴∠ADB=∠CEB=90°，又∵∠B=∠B，∴△ABD∽△CBE．。

相似三角形证明题精选题

E1、已知:如图,DE ∥BC,AF ∶FB=AG ∶GE 。

求证:ΔAFG ∽ΔAED 。

2、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC.求证:ΔAEF ∽ΔACB.3、如图,∠ADC=∠ACB=900,∠1=∠B,AC=5,AB=6,求AD 的长4、已知，如图，在正方形ABCD 中，P 是BC 上的点，且BP=3PC ，Q 是CD 的中点，△ADQ 与△QCP 是否相似？为什么？5、如图，CD 是Rt △ABC 的斜边AB 上的高，∠BAC 的平分线分别交BC 、CD 于点E 、F ，AC ·AE=AF ·AB 吗？说明理由。

6、如图，AD 是Rt △ABC 斜边BC 上的高，DE ⊥DF ，且DE 和DF 分别交AB 、7、如图，在⊿ABC （AB>AC ）的边AB 上取一点，在边AC 上取一点E ，使AD=AE ，直线DE 和BC 的延长线交于点P ，求证：BP ：CP=BD ：CE8、已知：如图，在△ABC 中，AB ＝AC ，AD ⊥AB ，AD 交BC 于点E ，DC ⊥BC ，与AD 交于点D ．求证：AC 2＝AE ·AD ．9、已知：如图，在△ABC 中，∠CAB ＝90°，AD ⊥BC 于点D ，点E 是AC 边的中点，ED 的延长线与AB 的延长线交于点F ．求证：△AFD ∽△DFB ．10、已知：如图，矩形ABCD 的对角线AC 、BD 相交于O ，OF ⊥AC 于点O ，交AB 于点E ，交CB的延长线于点F ，求证：AO 2＝OE · OF．11、己知:如图,AB ∥CD,AF=FB,CE=EB. 求证:GC 2=GF ·GD.12、已知:如图,ΔABC 中,∠ACB=900,F 为AB 的中点,EF ⊥AB.求证:ΔCDF ∽ΔECF.13、已知:如图,DE ∥BC,AD 2=AF ·AB 。

(完整word版)相似三角形精选好题-证明题25题

相似三角形精选好题解答题学校:___________姓名：___________班级：___________考号：___________一、解答题（本大题共25小题，共200.0分）1.如图,在中，，点P从A点出发，沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发，沿着CA以每秒3cm的速度向A点运动，设运动时间为x秒．为何值时,；是否存在某一时刻，使∽？若存在，求出此时AP的长；若不存在,请说明理由；当时,求的值．2.如图，中，于是BC中点，连接AD与BE交于点F，求证:∽．3.如图，已知四边形ABCD中，的延长线与AD的延长线交于点E．若，求BC的长；若,求AD的长．注意：本题中的计算过程和结果均保留根号4.如图，在中，点D在BC边上，点E在AD边上，．求证：∽；若，求AE的长．5.如图,在四边形ABCD中，,交BC于点F，连接AF．求CF的长；若,求AB的长．6.如图,在锐角三角形ABC中，点分别在边上，于点于点．求证:∽；若,求的值．7.如图，在中，，点D是BC边的中点,．求AD和AB的长;求的值．8.从三角形不是等腰三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．如图1,在中，CD为角平分线，，求证：CD为的完美分割线．在中，是的完美分割线,且为等腰三角形,求的度数．如图中，是的完美分割线,且是以CD为底边的等腰三角形，求完美分割线CD的长．9.如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为,测得大楼顶端A的仰角为点在同一水平直线上,已知，求障碍物两点间的距离结果精确到参考数据：10.如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图已知长方体货厢的高度BC为米，，现把图中的货物继续往前平移，当货物顶点D与C重合时，仍可把货物放平装进货厢，求BD 的长结果保留根号11.如图,某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为沿坡面AB向上走到B处测得广告牌顶部C的仰角为，已知山坡AB的坡度:米,米：是指坡面的铅直高度BH与水平宽度AH的比求点B距水平面AE的高度BH；求广告牌CD的高度．测角器的高度忽略不计，结果精确到米参考数据：12.如图，在中,，动点P从点C出发，沿CA方向运动;动点Q同时从点B出发，沿BC方向运动，如果点P的运动速度为点的运动速度为，那么运动几秒时,和相似?13.如图所示，，点P从点B出发,沿BC向点C以的速度移动,点Q从点C出发沿CA向点A以的速度移动，如果P、Q分别从B、C同时出发，过多少时，以C、P、Q为顶点的三角形恰与相似？14.如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为，顶部的仰角为,已知教学楼和实验楼在同一平面上，观测点距地面的垂直高度AB为15m，求实验楼的垂直高度即CD长精确到参考值：．15.如图，某校数学兴趣小组为测量校园主教学楼AB的高度，由于教学楼底部不能直接到达，故兴趣小组在平地上选择一点C，用测角器测得主教学楼顶端A的仰角为，再向主教学楼的方向前进24米，到达点E处三点在同一直线上，又测得主教学楼顶端A的仰角为，已知测角器CD的高度为米，请计算主教学楼AB的高度,结果精确到米16.已知：如图，是等边三角形，点D、E分别在边BC、AC上，．求证：∽；如果,求DC的长．17.如图,CD是一高为4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角，从平台底部向树的方向水平前进3米到达点E，在点E处测得树顶A点的仰角，求树高结果保留根号18.钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测一日,中国一艘海监船从A点沿正北方向巡航，其航线距钓鱼岛设N、M为该岛的东西两端点最近距离为15海里即海里，在A点测得岛屿的西端点M在点A的东北方向，航行4海里后到达B点，测得岛屿的东端点N在点B的北偏东方向其中N、M、C在同一条直线上,求钓鱼岛东西两端点MN之间的距离精确到海里参考数据：．19.探究证明：如图1，矩形ABCD中，点M、N分别在边上,，求证：．如图2，矩形ABCD中，点M在边BC上,分别交于点E、点F，试猜想与有什么数量关系？并证明你的猜想．拓展应用：综合、的结论解决以下问题：如图3,四边形ABCD中,，点分别在边上,求的值．20.如图，在某次数学活动课中，小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角的度数为，测得旗杆顶端A的仰角的度数为，旗杆底部B处与教学楼底部C处的水平距离BC为9m，求旗杆的高度结果精确到．【参考数据：】21.已知,如图，在四边形ABCD中,,延长AD、BC相交于点求证：∽；．22.如图,在中，点D为BC边的任意一点，以点D为顶点的的两边分别与边交于点E、F，且与互补．如图1，若为BC的中点时,则线段DE与DF有何数量关系？请直接写出结论；如图2，若为BC的中点时，那么中的结论是否还成立？若成立，请给出证明；若不成立，请写出DE与DF的关系并说明理由;如图3,若，且，直接写出______ ．23.放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝如图，他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处，此时风筝AD与水平线的夹角为，为了便于观察，小明迅速向前边移动，收线到达了离A处10米的B处，此时风筝线BD与水平线的夹角为已知点在同一条水平直线上，请你求出小明此时所收回的风筝线的长度是多少米？风筝线均为线段，，最后结果精确到1米．24.禁渔期间,我渔政船在A处发现正北方向B处有一艘可以船只,测得A、B两处距离为200海里,可疑船只正沿南偏东方向航行，我渔政船迅速沿北偏东方向前去拦截，经历4小时刚好在C处将可疑船只拦截求该可疑船只航行的平均速度结果保留根号．25.某市开展一项自行车旅游活动，线路需经A、B、C、D四地,如图，其中A、B、C三地在同一直线上,D地在A地北偏东方向，在C地北偏西方向，C地在A 地北偏东方向且，问沿上述线路从A地到D地的路程大约是多少？最后结果保留整数,参考数据：答案和解析【答案】1。

相似三角形证明专题练习

相似的判定证明题1、如图所示，在⊙O 中，CD 过圆心O ，且CD ⊥AB 于D ，弦CF 交AB 于E ．求证：CB 2＝CF ·CE ．2、如图，已知⊙O 的弦CD 垂直于直径AB ，点E 在CD 上，且EC = EB .（1）求证：△CEB ∽△CBD ；（2）求证：CB 2=CE ·CD（3）若CE = 3，CB=5 ，求DE 的长.3、（绥化）如图，点A ，B ，C ，D 为⊙O 上的四个点，AC 平分∠BAD ，AC 交BD 于点E ，CE=4，CD=6，（1）求证：CD 2=CE •CA （2）求：AE 的长为多少？4．已知：如图19，在Rt △ABC 中，∠ABC ＝90°，以AB 上的点O 为圆心，OB 的长为半径的圆与AB 交于点E ，与AC 切于点D ．（1）求证：BC ＝CD ；（2）求证：∠ADE ＝∠ABD ；（3）设AD ＝2，AE ＝1，求⊙O 直径的长．5．已知：如图，AB 是半圆O 的直径，CD ⊥AB 于D 点。

（1）求证：CD 2=AD •BD（2）求证：CB 2=BD •BA6、（黔东南州）如图，⊙O 是△ABC 的外接圆，圆心O 在AB 上，过点B 作⊙O 的切线交AC 的延长线于点D ．（1）求证：CB 2=AC •CD（2）若AC=8，BC=6，求△BDC 的面积．7. （四川雅安）如图，在△ABC 中，AB=AC ，以AB 为直径作⊙O ，交BC 于点D ，过点D 作DE ⊥AC ，垂足为E ．（1）求证：DE 是⊙O 的切线；（2）求证：CD 2=CE •CA8．（2016•呼和浩特）如图，已知AD 是△ABC 的外角∠EAC 的平分线，交BC 的延长线于点D ，延长DA 交△ABC 的外接圆于点F ，连接FB ，FC ．（1）求证：∠FBC=∠FCB ；（2）求证：FB 2=FA ·FD（3）若AB 是△ABC 外接圆的直径，FA=2，AD=4，求CD 的长．•ABC DEO。

相似三角形证明题

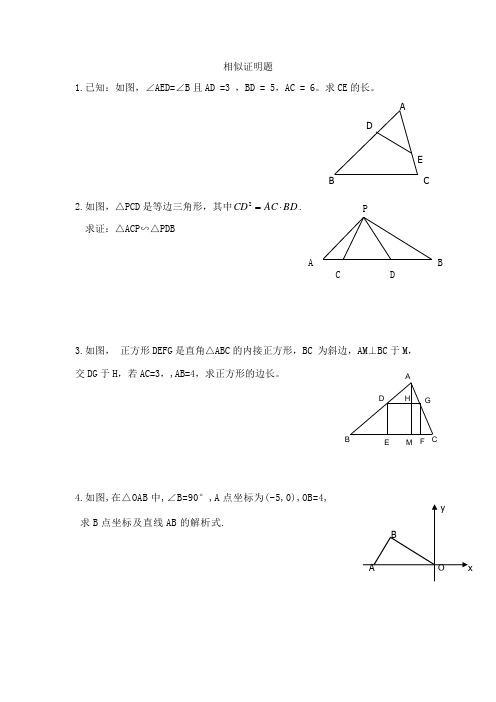
相似证明题1.已知：如图，∠AED=∠B 且AD =3 ，BD = 5，AC = 6。

求CE 的长。

2.如图，△PCD 是等边三角形，其中BD AC CD ⋅=2求证：△ACP∽△PDB3.如图，正方形DEFG 是直角△ABC 的内接正方形，BC 为斜边，AM ⊥BC 于M ，交DG 于H ，若AC=3，,AB=4，求正方形的边长。

4.如图,在△OAB 中,∠B=90°,A 点坐标为(-5,0),OB=4, 求B 点坐标及直线AB 的解析式.A CF EBDGHMD CBAABCD 5.如图，梯形ABCD 中，AB ∥CD,F 是DC 的中点,BF 的延长线交射线AD 于点G,BG 交AC 于点E.求证： FE GB BE GF ⋅=⋅6．已知：AB⊥DB 于B 点，CD⊥DB 于D 点，AB=6，CD ＝4，BD ＝14，则在DB 上是否存在P 点，使以C 、D 、P 为顶点的三角形与以P 、B 、A 为顶点的三角形相似?如果存在，请你求DP 的长；如果不存在，请你说明理由．7．梯形ABCD 中，AD ∥BC ，∠A ＝90°，∠ADC ＝150°，对角线BD ⊥DC ，若AD ＝8，求BC 的长。

8.已知，如图△ABC 中，AB=7，AD=4，∠B=∠ACD ，求AC 的长。

GEF BCDACEAB D CF9.已知：ΔACB 为等腰直角三角形，∠ACB=900 延长BA 至E ，延长AB 至F ，∠ECF=1350求证：ΔEAC ∽ΔCBF10、如图:在大小为4×4的正方形方格中， △ABC 的顶点A 、B 、C 在单位正方形的顶点上，请在图中画一个△A 1B 1C 1 ，使△A 1B 1C 1∽△ABC （相似比不为1），且点A 1 、B 1 、C 1 都在单位正方形的顶点上。

11、已知：如图，平行四边形ABCD 中，E 是CB 延长线上一点，DE 交AB 于F 。

相似三角形证明题

相似三角形证明题1．如图：⊿ABC 中，D 是AB 上一点，AD =AC ，BC 边上的中线AE 交CD 于F ，求证：DF CF AC AB ::=2．四边形ABCD 中，AC 为AB 、AD 的比例中项，且AC 平分∠DAB ，求证：22CD BC DE BE =3．如图，已知菱形ABCD 中，在AD 上任取一点E ，连结CE 并延长与BA 的延长线交于点F ，过E 作EG ∥FB 交FD 于G ，求证：GF =AECA BB4．在Rt ⊿ABC 中，∠ACB =Rt ∠，AD 平分∠CAB ，CE ⊥AB 于E ，交AD 于F ，过F 作FG ∥AB 交CB 于G ，求证：CD =GB5．矩形ABCD 中，a AB =，b BC =，M 是BC 的中点，DE ⊥AM ，E 是垂足，求证：2242b a ab DE +=C6．如图，过平行四边形ABCD 的顶点A 的直线交BD 于P ，交CD 于Q ，并交BC 的延长线于R ，求证：22PB PD PR PQ 7．已知，如图，在平行四边形ABCD 中，E 为AC 三分之一处，即AE =31AC ，DE 的延长线交AB 于F ，求证：AF =FB8．如图所示，在平行四边形ABCD 中，过点B 作BE ⊥CD ，垂足为E ，连结AE ，F 为AE 上一点，且∠BFE ＝∠C(1)求证：△ABF ∽△EAD ;(2)若AB ＝4，∠BAE ＝30°，求AE 的长；(3)在(1)(2)的条件下，若AD ＝3，求BF 长.(计算结果含根号).R9．如图，P 在线段MN 上，如果PM 2=PM ·PN ，，那么，P 是线段MN 的一个黄金分割点。

现有一等腰ΔABC （如图），AB=AC ，∠ABC=2∠A ，BD 是角平分线。

（1）求证：D 是AC 的黄金分割点。

（2）若AC=1，求AD 的长。

选择题；1．如图是一个正方体包装盒的表面展开图，若在其中的三个正方形A 、B 、C 内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在A 、B 、C 内的三个数依次是（）（A ）0，－2，1（B ）0，1，－2（C ）1，0，－2（D ）－2，0，12．如图是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（A ）25（B ）66（C ）91（D ）1203．如图:在一块长为a ,宽为b 的长方形的草地上,修两条宽度为h 的小路,则下列结论中成立的是:()A.修路后,留下草地的面积是：bhah ab --B.))((2h b h a h ha hb ab --=+--C.))((2h b h a h ha hb ab --=---D.))((2h b h a h ha hb ab -+=---(1)(2)(3)a bh h。