敏感性参数下的期权策略
投资决策实物期权方法的敏感性分析

投资决策实物期权方法的敏感性分析投资决策新方法——实物期权一定的资金,可能会有很多的投资机会,这就要进行投资决策。
由于未来情况总是不确定的,传统的决策分析方法是刚性的(即立即接受或放弃),不能根据环境的变化对投资项目进行拓展或放弃,以此带来收益或减少损失。
借鉴金融思想的实物期权方法能弥补传统方法的不足,很好地适应不确定环境下的动态且灵活的投资策略。
实物期权是以期权概念定义的现实选择权,它是指公司进行长期投资在决策时能根据在决策时不确定的因素改变行为的权利。
假设一项项目投资赋予决策者在未来采取一定投资决策的权利而不是义务,那么这项投资就会有实物期权。
企业投资项目中或多或少都包含一个或多个实物期权,这些实物期权的价值评估大多可通过运用金融期权定价的布莱克-舒尔斯模型得出。
分析投资项目所包含的实物期权的敏感性即是对该模型的影响因素进行分析,使管理者在决策及管理过程中利用实物期权各影响因素的敏感性水平来主动地调整项目投资的具体方案和投资战略,控制项目的风险水平,提高投资项目收益。
实物期权的敏感性分析实物期权与金融期权相关因素的比较金融期权定价的布莱克-舒尔斯模型的影响因素包括市场价格、约定价格、无风险利率、波动率及到期时间等,而利用实物期权方法评价投资项目的前提就是找出投资项目与这几个因素的对应特征。
首先,与投资项目中所能得到的全部现金流量的现值相对应的是市场价格。
其次,金融期权中的执行价格在实物期权中的等值含义就是投资项目有效期内的全部固定成本的现值,它与投资项目的水平、生产经营规模以及与原有生产经营技术的关联程度有关。
再次,到期时间在实物期权中的对应含义是失去投资机会的时间,而并不是指投资项目的有效时间。
当到期时间越短,如产品的生命周期越短,期权的价值就越低,决策者会加速投资。
第四,波动率是一个不可预见性的指标。
在数值上是相关现金流入价值增长率的标准差。
在实物期权中,投资项目的未来现金流与其技术及市场等影响因素的不确定性有关,这种不确定性就相当于波动率,可用项目收益的标准差来描述。
期权敏感性分析
伽玛Г
维嘉ν 看涨 西塔 θ 看跌 看涨 柔ρ 看跌 随着标的资产价 格单调递增
S/K影响更大, 与期权价格成正比 波动率作用被弱 化 非平价期权的西 塔先变小后变 通常为负值 大,接近到期收 敛于0 均为负值 越是虚值期权, 利率变化对期权 价值的影响越小
S/K(标的资产价格/执行价格) 1(平价或其附近) ↑,变大并趋于1,↓,趋于0 ↓,趋于0,↑,变大并趋于-1 最大 较小 1.5或更大
变量 敏感性指标 德尔塔Δ
期权分类 看涨 看跌 S/K=0 S/K=1 S/K=1.5
标的资产价格
取值范围
S/K(标的资产价格/执行价格) 0 ↑,变大并趋于1,↓,趋于0 ↓,趋于0,↑,变大并趋于-1 较小
对标的资产价格 Δ ∈(0,1) 变动的敏感性 Δ ∈(-1,0) 对标的资产价格 变动的敏感性 正值
度量期权价格对到期日变动的
随时间到期, 单调收敛于零
时间(距离到期时间) 0.5 1
利率
则收敛于1,平收敛于0.5,虚收敛于0
则收敛于-1,平收敛于-0.5,虚收敛于0
先增大,然后变小,接近到期收敛于0
先增大,然后变小,接近到期收敛于0
度量期权价格对到期日变动的敏感度
度量期权价 格对利率变 动敏感性
波动率
时间(距离到期时间) 0
实则收敛于1,平收敛于0.5,虚
实则收敛于-1,平收敛于-0.5,
1、波动率和伽玛的最大值呈现反比 虚,先增大,然后变小,接近到期 平,趋于无穷 2、↑,行权价格附近的伽玛减少 大 虚,先增大,然后变小,接近到期 3、↑,远离行权价的伽玛增加 此时对期权价 格影响变小
S/K影响更大, 波动率作用被弱 期权价格对波动率的敏感性 化 非平价期权的西 此处附近绝对值最大, 平价,单调递增至无穷 塔先变小后变 大,接近到期收 大 敛于0 最敏感 越是实值期权,利率变 越是虚值期权, 化对期权价值的影响越 利率变化对期权 大 价值的影响越小
外汇期权敏感性分析_陈荣达

第28卷 第2期2006年2月武 汉 理 工 大 学 学 报J OURNAL OF WUHAN UNIVERSITY OF TECHNOLOGY Vol .28 No .2 Feb .2006外汇期权敏感性分析陈荣达1,肖德云2(1.浙江财经学院金融学院,杭州310018;2.武汉理工大学经济学院,武汉430074)摘 要: 由于对外汇期权套期保值,需要了解各种因素对外汇期权价格的影响程度,为此对外汇期权的3个参数(Delta 、G amma 、T heta )进行了深入的分析,并用这些金融参数从不同角度来描述外汇期权和含期权的投资组合的风险特征,同时给出相应的经济意义以及如何利用这3个敏感性金融参数进行套期保值。
关键词: 外汇期权; 套期保值; 敏感性分析中图分类号: F 830文献标志码: A 文章编号:1671-4431(2006)02-0134-03Sensibility Analysis About Foreign Exchange OptionCHEN Rong -da 1,X IAO De -yun 2(1.School of Finance ,Zhejiang University of Finance and Eco nomics ,Hang zhou 310018,China ;2.School o f Eco nomics ,Wuhan University of Technology ,W uhan 430074,China )Abstract : A ll Factors w hich affected the prices of foreign exchange options should be understood in the course of hedge of the options .The paper analy zed three parameters ,Delta ,Gamma and T he ta ,and described the risk features of the options and its portfolio by using the financial parameters from the different angles .Mo reover ,it gave the eco nomic implication of the three financial parameters and carried out hedg e of the o ptions ho w to use them .Key words : foreig n exchange optio n ; hedge ; sensibility analy sis 收稿日期:2005-09-21.作者简介:陈荣达(1971-),男,博士.E -mail :applecnqk @在外汇期权交易中,尤其是在外汇期权的套期保值交易中,不仅要知道各种因素对期权价格的影响方向,而且还必须知道各种因素对外汇期权价格的影响程度[1~3]。
期权定价的敏感度分析

期权定价的敏感度分析期权定价有六种基本敏感性度量,主要是衡量影响期权价格的因素,包括:德尔塔(delta )、 伽马(gamma )、 希塔(theta )、拉姆达lambda 、罗(rho )和维加(vega )(一)德尔塔(∆)在任何确定的时间内,衍生证券的价值是标的资产价格的函数。
这个函数对标的资产价格变化的敏感度用希腊字母德尔塔(Delta ,∆)来描述。
德尔塔是Black-Scholes 期权定价模型的一个重要衍生概念,在证券组合中对投资者具有重要意义。
其公式表达为:S f∂∂=∆其中S f ∂∂/是期权价值对股票价格的一阶偏导数。
在Black-Scholes 期权定价模型中,德尔塔特性如下:(1)看涨期权的Delta 为正,看跌期权的Delta 一定为负值。
这正负号表示期权价格和标的资产价格之间的变动关系。
(2)Delta 数值的范围介于-1和+1之间。
当时,期权的价格收敛于,期权的价格与的变化基本上是同步变化,于是;当时的推理类似。
(3)平价期权的Delta 数值约为0.5。
(二) 伽马(gamma )Gammar 是衡量标的物价格变化所引起的Delta 值的变化,即Delta 对标的资产价格S 的一阶偏导数(或期权价值对资产价格S 的二阶偏导数),方程表达方式为:tT S d N S C S c -'=∂∂=∂∆∂=Γσ)(122这一指标反映了保值比率变动的幅度和频度。
参数既可以用来作为对市场变化的反应,也可以用来说明更敏感和更深入分析的对冲。
在此,由于的变化所引起的的变化进行展开,得到:为了使股票价格变化之后,期权价格变化与执行匹配,我们必须“增加一些”。
当且到期时间很短时,达到最大。
因此,当我们买入的是快要到期且处于平值状态的看涨期t S X >T S X -C t S 1C S ∂∆=≈∂t S X <0c p Γ=Γ>Γ∆S C 21()2dC dS dS ≈∆+ΓΓS X ≈Γ权时,我们进行的对冲成本将很低。
金融期权价格的敏感性指标

绝对值较大时,该组合的Delta对于标的资产价格相当敏感,此时
在任何时间段内,若对一个Delta中性的有价证券不作调整有很大
的风险。
注
2C
(当资产组合为看涨期权时)
S 2
(实际操作者有时称为期权的 为曲度)
三、Lambda( )
定义为有价证券组合的价值变化与标的资产波动率变化的比率,
的绝对值越大,证券组合的价值对于波动率的微小变化很敏感,
自价格变动的幅度来确定,大体做到数量相当。
做市商(market maker) 是指在证券市场上,由具备一定实力和信
誉的证券经营法人作为特许交易商,不断地向公众投资者报出某些特 定证券的买卖价格(即双向报价),并在该价位上接受公众投资者的 买卖要求,以其自有资金和证券与投资者进行证券交易。做市商通过 这种不断买卖来维持市场的流动性,满足公众投资者的投资需求。
例5-10 在相关的期货市场价格为19.00美元时,某交易商卖出 10份平值状态19.00看涨期权合约,平值状态的Delta的值为 0.50 ,问所需的等价的期货仓盘为多少?当期货价格上涨到 19.50美元,该看涨期权的协定价格,仍为19.00美元,Delta 变化为0.60,所需的等价期货合约为多少?
解 Delta的值为0.50 时等价的期货仓盘为
10 x 0.5=5 份期货合约
若期货价格上涨到19.50美元,该看涨期权的协定价格,仍 为19.00美元,Delta变化为0.60,则所需的等价期货合约为
10 x 0.60= 6份期货合约
3、中性期权对冲
例5-11 Delta 风险管理: 某交易商卖出10份平值状态19.00点 看涨期权合约,每份合约的交易单位为1000,该期权费为 0.80美元,Delta值为0.50 所以期权费为 0 .8 1 0 1 00 8 00 (0 美0 元)0
期权定价以及隐含波动率敏感度的研究

期权交易策略利用Vega对冲波动率风险

期权交易策略利用Vega对冲波动率风险期权交易是金融市场中一种重要的衍生品交易方式,它允许投资者在未来某个特定时间以约定价格购买或出售一定数量的资产。
然而,期权交易也会面临波动率风险。
波动率是指资产价格的波动程度,对期权交易尤为重要。
Vega是期权的一个风险指标,用于衡量波动率变动对期权价格的影响。
在期权交易中,利用Vega对冲波动率风险是一种常见的策略。
一、了解波动率和Vega在进行期权交易前,投资者首先需要了解波动率和Vega的概念。
波动率是资产价格变动的标准差,反映了市场对资产价格未来波动的预期。
高波动率代表市场对价格的不确定性较高,低波动率则表示市场对价格的不确定性较低。
Vega是期权价格对波动率变动的敏感度。
当波动率上升时,期权价格往往上升;当波动率下降时,期权价格往往下降。
Vega越高,表明期权价格对波动率的敏感度越大。
二、利用Vega对冲波动率风险的策略1. Vega为正的期权策略当投资者持有的期权具有正的Vega时,意味着该期权价格对波动率的敏感度为正。
此时,应该采取对冲策略以减轻波动率上升对期权价格的负面影响。
一种常见的对冲策略是持有相应数量的期权合约的反向头寸。
比如,如果持有Vega为正的认购期权,可以同时卖出相应数量的认沽期权,从而抵消波动率上升对期权价格的影响。
2. Vega为负的期权策略当投资者持有的期权具有负的Vega时,意味着该期权价格对波动率的敏感度为负。
此时,应该采取对冲策略以减轻波动率下降对期权价格的负面影响。
一种常见的对冲策略是持有相应数量的股票或期货合约的头寸。
通过持有相应的正向头寸,当波动率下降时,合约价格的上涨可以抵消期权价格下降的影响。
3. Vega对冲的实施在实施Vega对冲策略时,投资者需要根据期权的Vega值和风险承受能力确定对冲比例。
当波动率变化时,投资者需要及时调整对冲头寸,以保持对冲效果。
为了实施Vega对冲,投资者还需要及时获取波动率数据。
期权风险及策略案例分析

02 期权风险分析
CHAPTER
内在风险
价格波动风险
期权价格受标的资产价格、剩余到期时间、波动率等 因素影响,存在较大的波动性。
时间衰减风险
期权价值随时间流逝而逐渐减少,尤其是深度实值或 虚值期权,其时间价值衰减更快。
流动性风险
某些期权可能交易不活跃,导致难以买卖或交易成本 过高。
市场风险
利率风险
操作失误风险
在期权交易过程中,可能 因操作失误导致交易错误 或损失。
流动性风险
买卖价差风险
在期权交易中,买方和卖 方可能面临较大的买卖价 差,影响交易成本和效率。
难以平仓风险
在某些情况下,可能难以 找到对手方进行平仓,导 致无法及时止损或获利。
冲击成本风险
在大量交易时,市场冲击 成本可能导致实际交易成 本高于预期。
合理配置资金
分散投资
01
将资金分散投资于多个期权品种和策略,以降低单一投资的风
险。
控制杠杆
02
合理控制杠杆比例,避免过度使用杠杆带来的风险。
设定止损点
03
为每个期权头寸设定止损点,一旦触及止损点,及时止损以控
制风险。
关注市场动态
密切关注市场走势
及时了解市场动态,分析影响期权价格的因素,以便做出正确的 投资决策。
03 期权策略案例
CHAPTER
买入看涨期权策略
总结词
通过购买看涨期权,获得赚取收 益的权利,但需承担高风险。
详细描述
当预期某资产价格上涨时,买入 看涨期权可获得赚取收益的权利 ,但需支付较高的期权费,且不 具有赚取收益的确定性。
卖出看跌期权策略
总结词
通过卖出看跌期权,获得赚取收益的 权利,但需承担高风险。
期权的交易策略、期权价格的敏感性、期权的套期保值

-15 20
X 40 60 短期权到期时的股价
80
期限短的期权盈亏
期限长的期权盈亏
组合的总盈亏
协议价格
图5.14 看涨期权的正向差期组合
第三节 期权交易策略
差期组合
15
盈亏
0
-15 20
期限短的期权盈亏
X 40 60 短期权到期时的股价
期限长的期权盈亏 组合的总盈亏
80
协议价格
图5.15
看跌期权的正向差期组合
蝶式差价组合(Butterfly Spreads)
如图 为什么叫做蝶式差价组合? 为什么要构建蝶式差价组合? – 预期价格会在一定的区间内波动 如何构建蝶式差价组合? – 由四份具有相同期限、不同协议价格的同种期权头寸组成。 – 若X1 < X2 < X3,且X2=(X1+X3)/2,则蝶式差价组合有如下四种:
期权到期时的股价
15 0 -15 -30 0 20 40
X1
X2
盈亏
60
80
100
组合的总盈亏
低协议价格的期权盈亏 低协议价格
高协议价格的期权盈亏 高协议价格
图5.9看跌期权的牛市差价组合
熊市差价(Bear Spreads)组合
如图 为什么叫做熊市差价组合? 怎样的情况下熊市差价组合有利?(为什么要构建?) – 预期价格下跌 – 预期价格下跌幅度不大,降低初始成本 – 在用看涨期权构造看跌预期投机时,进行保险 怎样构建熊市差价组合?(买高卖低) – 一份看涨期权多头和一份相同期限、协议价格较低的看涨期权空头组 成 – 一份看跌期权多头和一份相同期限、协议价格较低的看跌期权空头组 成 熊市差价组合看涨期权的熊市差价组合和看跌期权的熊市差价组
期权价格的敏感性和期权的套期保值

7
14.1.2 期权Delta值的性质和特征分析
无收益资产看涨期权和欧式看跌期权 值与到期期限之间的关系
8
14.1.2 期权Delta值的性质和特征分析
无收益资产看涨期权和欧式看跌期权Delta值与r之间的关系
9
14.1.3 证券组合的Delta值
从概率分布的性质可知,0N(d1)1,因此无 收益资产看涨期权的值总在0与1之间;而无 收益资产欧式看跌期权的 值则总是在-1到0之 间。反过来,无收益资产欧式看涨期权空头 值就总在-1和0之间;而无收益资产欧式看跌期 权空头的 值则总在0与1之间。
6
14.1.2 期权Delta值的性质和特征分析
这意味着要使组合Delta中性,在出售该看涨期权的同时,
需要借入美元购买52200股股票,借入的美元数量为:
5220 40 9$2557800
第一周内发生的相应利息费用为(以千美元为单位并保留
小数点后一位数字,则为2.5千美元)
2557 (e0.0 8 5 1/5 02 0 1)$2461
若到第一周末,股票价格下降到了 48 1
11
案例 14.1 期权的Delta中性保值
某金融机构在OTC市场出售了基于100000股不支 付红利股票的欧式看涨期权,收入$300000。该股票的 市场价格为49美元,执行价格为50美元,无风险利率 为连续复利年利率5%,股票价格年波动率为20%,距 离到期时间为20周。由于该金融机构无法在市场上找 到相应的看涨期权多头对冲,请问如何运用标的资产 (股票)进行Delta套期保值操作?
当证券组合中含有标的资产、该标的资产的各 种期权和其他衍生证券的不同头寸时,该证券组合 的 值就等于组合中单个资产 值的总和(注意这 里的标的资产都应该是相同的):
期权定价的敏感性分析

同理可求得看跌期权 的 G m a a m 值为 :
( ÷ b .
从上式可看 出, 看涨期权和看跌期权 的 G m a—
d::
迎
√T
:
’
。
对 于有连续股利支付率 的看涨期权 , b卜q 即 = 时 , Dea=e l t ~N(1 d):
看跌期权
~ Ⅳ
对于欧式外汇看涨期权 , b r 时 , 即 =一
( [ 一
ⅣI/ r J ((盯cT [ S (2' 一 Xb/ ̄ n )+2 + ) ,
S未来现金流 的现值 ( " - 美元 )x:t ; g 行成本 ( 美
元) ;
.
.
一 "(+ 击‘ lX 去‘1 e N1 - 二 _-二 d &r _ e 7 ) ", U r o 赤  ̄ 赤 ~
.
d r r
r无风险利率( ; : , - %)T 到期时间( ; 年) 盯 波动率( ; : : %)N 标准正态分布的累积函数 ;
} t e a
D el L t
X
1
O —
X
S
一 1
( 一
e
一 1
1
看 涨期 权
图1
上式表明未来现金流 的现值 上升 I 美分 , 看 涨期权费上升e - N(. 美 分 。看 涨 期 权 的 r " d) D l 值在( , ) ea t 0 1之间。 △>O 说 明期 权价格 的 .
的变化 ,即期权价格关 于它 的参数的变化率的分 b c—co s l k s l 模型求关于 s a he 的偏导数。 析。这些过程 的计算都隐含一个假定 : 即影响期权 Det l a =eb) (r - +S (rr eb) - 一 价格的其他 因素都保持不变。
期权价格的敏感性和期权的套期保值(PPT 49页)

29
14.3.3 证券组合的Gamma值
标的资产及远期和期货合约的 值均为0。 这意味着只有期权有值。因此,当证券组合 中含有标的资产和该标的资产的各种期权和其 他衍生产品时,该证券组合的 值就等于组合 内各种期权 值与其数量乘积的总和:
9
14.1.3 证券组合的Delta值
当证券组合中含有标的资产、该标的资产的各 种期权和其他衍生证券的不同头寸时,该证券组合 的 值就等于组合中单个资产 值的总和(注意这 里的标的资产都应该是相同的):
n
wii i 1
其中,wi表示第i种证券的数量, i 表示第i种证券值。
6
14.1.2 期权Delta值的性质和特征分析
无收益资产看涨期权和看跌期权 值与标的资产价格的关系
7
14.1.2 期权Delta值的性质和特征分析
无收益资产看涨期权和欧式看跌期权 值与到期期限之间的关系
8
14.1.2 期权Delta值的性质和特征分析
无收益资产看涨期权和欧式看跌期权Delta值与r之间的关系
15
案例14.1 期权的Delta中性保值
可以通过标的资产的买卖实现对期权的Δ中性套期 保值,在不考虑交易费用(指买入卖出的佣金等费用, 利息费用则是需要考虑的)并假设波动率为常数的情况 下,运用标的资产进行Δ中性套期保值的成本和效果就和 买入了一个看涨期权多头一样。
在实际操作中,Δ中性保值方法更常见的是利用同 种标的资产的期货头寸而非现货头寸来进行保值,可以 获得杠杆作用。
期权定价的敏感性分析

龙源期刊网
期权定价的敏感性分析
作者:李仕群
来源:《沿海企业与科技》2009年第01期
[摘要]文章针对广义black-scholes模型,研究看涨期权的6个参数(Delta、Gamma、Rho、Then、Vega、Xi)以及详细的推导,并用这些金融参数从不同角度描述期权和含期权的投资组合的风险特征,同时给出相应的经济意义以及如何利用这6个敏感性金融参数进行套期保值
[关键词]期权定价;广义black-scholes模型;套期保值;敏感性分析
[作者简介]李仕群,广州大学数学与信息科学学院概率论与数理统计专业统计精算与金融数学研究生,广东广州,510006。
期权价值敏感性——希腊字母

第三章 期权敏感性(希腊字母)顾名思义,期权敏感性是指期权价格受某些定价参数的变动而变动的敏感程度,本章主要介绍期权价格对其四个参数(标的资产市场价格、到期时间、波动率和无风险利率)的敏感性指标,这些敏感性指标也称作希腊值(Greeks )。
每一个希腊值刻画了某个特定风险,如果期权价格对某一参数的敏感性为零,可以想见,该参数变化时给期权带来的价格风险就为零。
实际上,当我们运用期权给其标的资产或其它期权进行套期保值时,一种较常用的方法就是分别算出保值工具与保值对象两者的价值对一些共同的变量(如标的资产价格、时间、标的资产价格的波动率、无风险利率等)的敏感性,然后建立适当数量的证券头寸,组成套期保值组合,使组合中的保值工具与保值对象的价格变动能相互抵消,也就是说让套期保值组合对该参数变化的敏感性变为零,这样就能起到消除相应风险的套期保值的目的。
本章将主要介绍Delta 、Gamma 、Vega 、Theta 、Rho 五个常用希腊字母。
符号风险因素 量化公式Gamma Γ 标的证券价格变化 Delta 变化/标的证券价格变化 Vega ν 波动率变化 权利金变化/波动率变化 Theta Θ到期时间变化 权利金变化/到期时间变化本章符号释义:T 为期权到期时间S 为标的证券价格,0S 为标的证券现价,T S 为标的证券行权时价格K 为期权行权价格 r 为无风险利率σ 为标的证券波动率 t π 为资产组合在t 时刻的价值()N 为标准正态分布的累积密度函数,可以查表或用计算机(如 Excel)求得'()N 为标准正态分布的密度函数,22'()x N -=第一节 Delta (德尔塔,∆)1.1 定义Delta 衡量的是标的证券价格变化对权利金的影响,即标的证券价格变化一个单位,权利金相应产生的变化。
新权利金=原权利金+Delta ×标的证券价格变化1.2 公式从理论上,Delta 准确的定义为期权价值对于标的证券价格的一阶偏导。
财务中的敏感性分析技巧和应对策略

财务中的敏感性分析技巧和应对策略财务分析对于任何企业来说都是至关重要的,它可以帮助企业了解自身的财务状况以及未来的发展趋势。
然而,在进行财务分析时,面临的一个重要问题就是敏感性分析。
敏感性分析可以帮助企业更好地预测和应对不同情境下的财务变化,并采取相应的应对策略来降低风险。
本文将介绍财务中的敏感性分析技巧和应对策略。
一、敏感性分析的概念和方法敏感性分析是通过改变某个因素,观察其对企业财务指标的影响程度,以评估财务指标对该因素的敏感性。
它帮助企业了解不同因素对财务状况的影响程度,从而为决策提供有力的依据。
在进行敏感性分析时,我们可以采用以下几种方法:1. 变化一个变量:这种方法是最常见的敏感性分析方法,通过逐一改变某个变量的值,观察其对财务指标的影响。
2. 变化多个变量:在现实情况中,多个因素常常同时发生变化,因此,变化多个变量的敏感性分析方法更符合实际情况。
它可以帮助企业了解多个因素对财务指标的综合影响。
3. 制定敏感性分析模型:通过建立数学模型,模拟不同因素对财务指标的影响。
这种方法可以帮助企业更准确地评估财务指标的敏感性。
二、敏感性分析的应用场景敏感性分析广泛应用于企业的财务决策中。
下面列举几个常见的应用场景:1. 投资决策:在进行投资决策时,敏感性分析可以帮助企业评估投资方案在不同市场环境下的可行性和风险程度。
通过分析不同情境下的财务指标变化,企业可以更好地制定投资策略。
2. 融资决策:企业的融资决策需要考虑多个因素,如利率、偿还期限等。
敏感性分析可以帮助企业预测不同融资方式对财务指标的影响,并为融资决策提供科学依据。
3. 成本控制:敏感性分析可以帮助企业评估成本结构对利润的影响。
企业可以通过分析成本敏感性,找出成本控制的关键点,并采取相应的措施降低成本。
三、敏感性分析的应对策略当企业进行敏感性分析后,可以采取以下几种应对策略来降低财务风险:1. 多方案比较:在不同情境下,企业可以制定多种方案,并通过敏感性分析来比较不同方案的风险和收益。
股票期权估值敏感性分析

STUDY AND EXPLORE研究与探索·综合(中)2009年第10期表1估值模型参数取值表股票现行价格S 股票预计波动率σ无风险利率r 剩余时间t 期权行权价格L10.00元40%3% 2.5年 6.80元现代企业会计常涉及到股票期权的公允价值计量。
由于大多数股票期权无法直接取得公允价值,企业往往采用估值技术进行估算。
为此,证监会公告〔2008〕48号中要求上市公司做好同公允价值计量相关的会计和信息披露工作,并在附注中详细披露估值模型、重要参数的选取依据和估值过程,以及必要的敏感性分析。
本文试图以实例说明如何对股票期权公允价值估值进行敏感性分析,以供实务界参考。
T 公司为一家上市公司,2007年7月1日获股东大会批准向公司高管定向发行1000万份本公司股票期权作为股权激励。
该股票期权有效期3年,自发行日起满三年后的下一交易日一次行权。
2007年12月31日,T 公司按照《企业会计准则第11号———股份支付》有关规定,以2007年7月1日该股票期权的公允价值对股份支付进行计量。
假设在等待期内可行权的公司高管人数保持不变。
T 公司运用B-S 估值模型估算股票期权公允价值。
在不考虑预计股息率的条件下,B-S 估值模型计算公式为:C=S ·N (d 1)-L ·e -rt N (d 2)d 1=ln (S/L )+(r+σ2/2)·t σn 姨,d 2=d 1-σt 姨(1)其中参数C 为期权价值;S 为期权对应的标的资产现行市场价格;L 为执行价格或履约价格;e 为自然对数底数;r 为无风险利率,以连续复利计息;t 为期权有效期;σ为期权预计价格波动率;N (d 1)、N (d 2)分别为标准正态分布变量小于等于d 1、小于等于d 2时的概率。
T 公司选取的主要参数值如表1所示。
上述参数为依据有关规定而得,据此计算得到2007年资产负债表日T 公司1000万份股票期权的公允价值为4356万元(每份股票期权公允价值4.3560×1000万份)。
股指期权敏感性分析课件

Delta(△)
• 看涨期权Delta= 看跌期权Delta+1
• Delta 并非一成不变的, 其数值大小, 会随着期 权市价与执行价的距离, 及距离到期的远近不同 而有变化.
Gamma
• Gamma= △Delta/ △S
• 用于测量Delta的稳定性
• 看涨期权的Gamma=看跌期权的Gamma • 期权多头: + Gamma • 期权空头: -Gamma • 其定义是标的价格变动一个单位时,Delta值会改变的数量,好
主要内容
• 一、期权B-S定价公式及影响因素 • 二、期权的价格曲线 • 三、期权价格的敏感性分析
期权的定价模型—BSM公式
• 在风险中性的条件下,欧式看涨期权到期时(T时刻 )的期望值为:
• • 根据风险中性定价定理,欧式看涨期权的价格C等于
此期望值按无风险利率进行贴现后的现值,即
• • 积分后,结果为:
比 说标的价格上涨 一 元 , 而 Delta 值 由 0.5 提 高 至 0.505 , 则 Gamma 值 便 是 0.005 , 所 以 说Gamma 值 是 用 来衡量Delta 值 的 稳定 程 度 , Gamma 值 越 高 表 示 Delta 值 越 不 稳定 , 越 低 表 示 Delta值越稳定
• 尤其是越接近到期日时,这样的效果越明显(Vega除外)。 所以期权就是在平值附近到期时,最能淋漓尽致的呈现其 期权的特性。
希腊字母之间的关系与符号
• 组合价值
Gamma
• 越接近到期日时,且越接近执行价时,Gamma值会快 速跳动,这表示此时的Delta值最不稳定。
• Delta的变动越大,对期权的买方来说是件好事,因为Delta的快速变 动,可以带来高度的杠杆效应,获利机会高于风险,所以对期权的 买方而言Gamma都是正数。
期权价格的敏感性和期权的套期保值

期权价格的敏感性和期权的套期保值【学习目标】本章是期权部分的重点内容之一。
本章的重要内容之一,就是介绍了期权价格对其四个参数(标的资产市场价格、到期时间、波动率和无风险利率)的敏感性指标,并以此为基础讨论了相关的动态套期保值问题。
学习完本章,读者应能掌握与期权价格敏感性有关的五个希腊字母及其相应的套期保值技术。
在前面几章中,我们已经分析了决定和影响期权价格的各个重要因素,以及这些因素对期权价格的影响方向。
进一步来看,根据Black-Scholes 期权定价公式()()(2)(1d N Xe d SN c t T r ---=),我们还可以更深入地了解各种因素对期权价格的影响程度,或者称之为期权价格对这些因素的敏感性。
具体地说,所谓期权价格的敏感性,是指当这些因素发生一定的变化时,会引起期权价格怎样的变化。
本章的重要内容之一,就是对期权价格的敏感性作具体的、量化的分析,介绍期权价格对其四个参数(标的资产市场价格、到期时间、波动率和无风险利率)的敏感性指标。
如果我们从另一个角度来考虑期权价格的敏感性,我们可以把它看作当某一个参数发生变动时,期权价格可能产生的变化,也就是可能产生的风险。
显然,如果期权价格对某一参数的敏感性为零,可以想见,该参数变化时给期权带来的价格风险就为零。
实际上,当我们运用衍生证券(如期权)为标的资产或其它衍生证券进行套期保值时,一种较常用的方法就是分别算出保值工具与保值对象两者的价值对一些共同的变量(如标的资产价格、时间、标的资产价格的波动率、无风险利率等)的敏感性,然后建立适当数量的证券头寸,组成套期保值组合,使组合中的保值工具与保值对象的价格变动能相互抵消,也就是说让套期保值组合对该参数变化的敏感性变为零,这样就能起到消除相应风险的套期保值的目的。
这就是我们在本章将要介绍的“动态套期保值”技术。
第一节 Delta 与期权的套期保值期权的Delta 用于衡量期权价格对标的资产市场价格变动的敏感度,它等于期权价格变化与标的资产价格变化的比率。
Chapter9期权价格的敏感性和期权的套期保值

• 假定股票价钱为100美元,期权价钱为10美元。并假定金融机构 的买卖员卖出了20份该股票上的看涨期权〔期权持有者有权置办 2000份股票〕。买卖员的头寸可以经过(jīngguò)置办 份股票来对冲。
• 期权头寸的盈利〔盈余〕可由股票头寸上的盈余〔盈利〕来抵消
。例如0,.6假定20股0票0 价 1钱2下00跌1美元〔买入的股票会升值1200美元
Chapter9期权价格(jiàgé) 的敏感性和期权的套期保
值
2021/11/10
第一页,共48页。
期权头寸难以(nányǐ)对冲的缘由
• 假定一个金融机构在OTC市场卖出一个期权头寸,而在买 卖所又找不到与其婚配的对冲头寸;
• 期权价钱随着(suízhe)时间和市场状况的变化,关于标的 资产价钱变化较为敏感,意味着保值头寸也会变化。
〕,期权价钱将下跌
美元〔卖出期权会带来损失1200
美元〕;假定股票价钱下跌1美元〔买入股票会损失1200美元〕
,期权价钱下跌0.6美元〔卖出期权会带来收0.益6 112000美.6元〕。
4
第四页,共48页。
令f表示期权的价钱,S表示标的资产(zīchǎn)的 价钱, 表示期权的Delta,那么:
f S
无收益(shōuyì)资产看涨期权 Theta值与S的关系
无收益资产看涨期权Theta值 与有效期之间的关系
第二十页,共48页。
20
对Theta的了解(liǎojiě)
• 事前间是以年为单位时某期权头寸的Theta为-0.2,这 句话的含义是什么?假定买卖员以为(yǐwéi)股票价钱 与坚定率均不会发作变化,什么样的期权头寸比拟适 宜?
假定到第一周末25,57股80票0价 (钱e0下.05降1/到52 了1) 1$。24这6使1 得期权Δ值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
敏感性参数下的期权策略
敏感性参数是期权衍生品特有的属性,它从定量角度解释了各个定价因素对期权价格
的影响程度,在期权交易中发挥着重要作用。
本文在介绍敏感性参数的前提下,解释了如
何从敏感性参数角度理解期权交易策略,并讨论了如何利用敏感性参数构建组合策略。
敏感性参数的作用
由期权定价理论可知,标的资产价格、执行价格、距离到期时间、波动率和无风险利
率是影响期权价格的五个影响因素。
这几个因素到底在多大程度上影响期权价格呢?这需
要借助敏感性参数来分析,每一个定价因素都有相对应的敏感性参数。
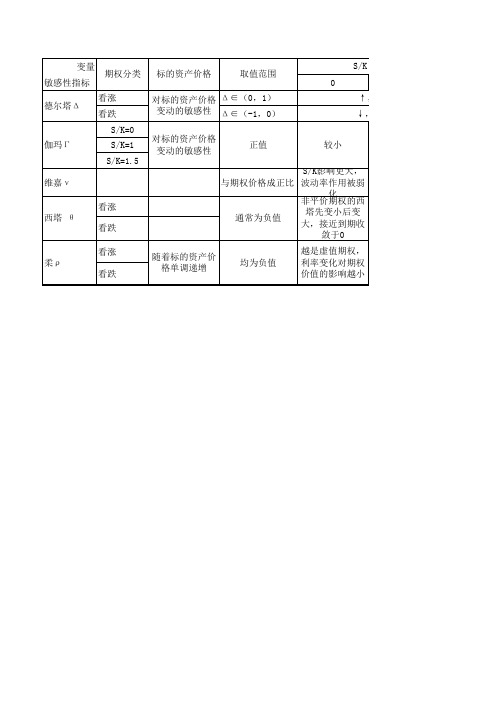
表为期权
敏感性参数
通俗讲,敏感性参数告诉我们,定价因素每变动一个单位,期权价格会变动几个单位。
以Delta为例,若Delta=0.4,这表示标的资产价格每变动1个单位,期权价格将变动0.4
个单位。
可以说,敏感性参数可以精确地告诉我们期权价格的变动规律。
需要注意的是,敏感性参数并非一成不变,它们会随着市场状况的变化而不断变化。
换言之,定价因素在不同的市场状况下,对期权价格的影响程度不同,这是定量分析与定性分析的核心区别。
定量理解期权交易
当交易者面对复杂期权投资组合时,往往很难厘清策略盈亏状况,此时通过计算总体
敏感性参数,可以了解各种市场变化下的策略表现。
例如,某投资组合的Delta=1.5、Theta=-0.3、Vega=4.2,这表明由Delta=1.5可知,该投资组合的价值与标的资产价格波动成正比。
当标的资产价格上涨(下跌)1个单位时,投资组合价值上涨(下跌)1.5个单
位价值,这种特性被称为Long Delta,反之为Short Delta。
由Theta=-0.3可知,该投资组合的价值与距离到期时间成反比。
每经过一天,投资组合价值即减少0.3个单位价值,这种特性被称为Short Theta,反之为Long Theta。
由Vega=4.2可知,该投资组合的价值与波动率成正比。
当波动率上涨(下跌)1个单位时,投资组合价值上涨(下跌)4.2个单位价值,这种特性被称为Long Vega,反之为Short Vega。
值得注意的是,有一种特殊的敏感性参数交易特征,即组合参数为零的情况,称为Neutral(中性)状态。
以Delta=0为例,即Delta Neutral状态,这表明组合价值不受标的资产价格波动的影响,此时组合价值只会因为波动率和时间的变化而改变,免去了投资者研判行情的苦恼。
然而,Theta=0表明组合价值不受时间流逝的影响,这使得投资者不必因为时间价值衰减而造成心理压力。
由此可见,Neutral状态使投资者免受某一定价因素的影响,降低了投资难度。
表为不同状态下的敏感性参数交易特征
很显然,我们只要知道各个敏感性参数的大小,便可以了解策略组合在市场变化时的价值表现。
对敏感性参数运用最为频繁的便是期权做市商,做市商每天主动或被动地建立大量头寸,而通过敏感性参数了解价值变化成为做市商每天最重要的工作。
构建策略的优势
利用敏感性参数构建交易策略的优势在于,可使交易策略的盈利来源更精确。
举个例子,投资者观察到当前市场波动率很低,未来波动率会大概率走高,那么此时适宜构建Long Vega策略。
相反,当预期未来波动率走低时,建立Short Vega策略更合理。
表为基本策略的敏感性参数交易特征
如果一个投资者既想赚取波动率下降的收益,又不想受标的资产价格波动的影响,那么需要投资者构建Short Vega策略的同时,再构建一个Delta Neutral策略。
Short Vega
方面,可通过卖出期权实现,但卖出期权带来了负值Delta(卖出看涨期权)或正值Delta
(卖出看跌期权),所以若想Delta Neutral,可以通过交易标的资产完成。
总之,为同时达到Short Vega和Short Theta的目的,需要构建包括标的资产和期权空头的组合策略,并随时调整标的资产数量,才能使组合一直保持Delta Neutral状态,这就是期权交易领域很有名的Delta中性交易法。
综合来看,任何复杂的交易策略都是由单一头寸组合而成的,对于打算构建敏感性参数特征组合交易的投资者来说,了解单一头寸策略的敏感性参数特征大有裨益。
