(整理)7用Mathematica求偏导数与多元函数的极值.
第三节 利用Mathematica计算极限

利用Mathematica计算极限 利用Mathematica计算极限 Mathematica
第二章
在计算极限时,常常需要应用一些运算技巧对 函数 f (x)进行初等变换 . 如果利用Mathematica 计
算极限可以比较迅速地得到计算结果。 可以简化计算过程,节约大量时间。
机动
目录
上页
Байду номын сангаас下页
作 业
P33
1,2
机动
目录
上页
下页
返回
结束
ex 1 (1) lim x→0 x
x+2 3 (2) lim x→ 1 x 1
1 x
(3) lim(1 2x) x→0
x→ 0
1 cos x lim (4) x→0 xsin x
lim x4 ln x (5)
(6)lim x→∞
ln(1+ ex ) 1+ x2
x
x +5 (7)lim x→∞ x 6
(2)1 cos x与 x 解:
2
(3)tan x sin x 与
x
2
机动
目录
上页
下页
返回
结束
因此, 因此, x + tan2x 是比 1cosx 低阶的无穷小;
1 cosx 与
x2 是同阶的无穷小; x2 高阶的无穷小。
tan x sin x 是比
机动
目录
上页
下页
返回
结束
内容小结
1. 掌握 六种计算极限的语句,从而熟练 利用Mathematica 计算极限。 2. 利用Mathematica 计算极限,比较无穷 小的阶
x→ 1
高数项目-微积分(Mathematica)

附录Ⅰ 大学数学实验指导书(仅供交流学习)项目三 多元函数微积分实验1 多元函数微分学(基础实验)实验目的 掌握利用Mathematica 计算多元函数偏导数和全微分的方法, 掌握计算二元 函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元 函数的性质、方向导数、梯度和等高线的概念.基本命令1.求偏导数的命令D命令D 既可以用于求一元函数的导数, 也可以用于求多元函数的偏导数. 例如: 求),,(z y x f 对x 的偏导数, 则输入D[f[x,y,z],x] 求),,(z y x f 对y 的偏导数, 则输入D[f[x,y,z],y]求),,(z y x f 对x 的二阶偏导数, 则输入D[f[x,y,z],{x,2}] 求),,(z y x f 对y x ,的混合偏导数, 则输入D[f[x,y,z],x,y] …………2.求全微分的命令Dt该命令只用于求二元函数),(y x f 的全微分时, 其基本格式为Dt[f[x,y]]其输出的表达式中含有Dt[x],Dt[y], 它们分别表示自变量的微分d x ,d y . 若函数),(y x f 的表 达式中还含有其它用字符表示的常数, 例如a, 则Dt[f[x,y]]的输出中还会有Dt[a], 若采用选 项Constants->{a}, 就可以得到正确结果, 即只要输入Dt[f[x,y],Constants->{a}]3.在Oxy 平面上作二元函数),(y x f 的等高线的命令ContourPlot 命令的基本格式为ContourPlot[f[x,y],{x,x1,x2},{y,y1,y2}]例如,输入ContourPlot[x^2-y^2,{x,-2,2},{y,-2,2}]则输出函数22y x z -=的等高线图(图1.1). 该命令的选项比较多(详细的内容参见光盘中的实验案例库). 如选项Contours->15表示作15条等高线, 选项Contours->{0}表示只作函数值为0的等高线.实验举例求多元函数的偏导数与全微分例1.1 (教材 例1.1) 设),(cos )sin(2xy xy z +=求.,,,222yx z x z y z x z ∂∂∂∂∂∂∂∂∂ 输入Clear[z];z=Sin[x*y]+Cos[x*y]^2; D[z,x] D[z,y] D[z,{x,2}] D[z,x,y]则输出所求结果.例1.2 设,)1(y xy z +=求yzx z ∂∂∂∂,和全微分dz. 输入Clear[z];z=(1+x*y)^y; D[z,x] D[z,y]则有输出⎪⎪⎭⎫ ⎝⎛++++++-]1[1)1()1(12xy Log xy xy xy xy y y y再输入Dt[z]则得到输出⎪⎪⎭⎫⎝⎛+++++]1[][1])[][()1(xy Log y Dt xy y xDt x yDt y xy y 例1.3 (教材 例1.2) 设,)(y xy a z +=其中a 是常数, 求dz.输入Clear[z,a];z=(a+x*y)^y;wf=Dt[z,Constants->{a}]//Simplify则输出结果:(a+xy)-1+y (y 2Dt[x,Constants->{a}]+Dt[y,Constants->{a}](xy+(a+xy)Log[a+xy]))其中Dt[x,Constants->{a}]就是d x , Dt[y,Constants->{a}]就是d y . 可以用代换命令“/.”把它们 换掉. 输入wf/.{Dt[x,Constants->{a}]->dx,Dt[y,Constants->{a}]->dy}输出为(a+xy)-1+y (dxy 2+dy(xy+(a+xy)Log[a+xy]))例1.4 (教材 例1.3) 设v u e y v u e x u u cos ,sin -=+=,求.,,,yv x v y u x u ∂∂∂∂∂∂∂∂ 输入eq1=D[x==E^u+u*Sin[v],x,NonConstants->{u,v}](*第一个方程两边对x 求导数, 把u,v 看成x,y 的函数*) eq2=D[y==E^u-u*Cos[v],x,NonConstants->{u,v}](*第二个方程两边对x 求导数, 把u,v 看成x,y 的函数*) Solve[{eq1,eq2},{D[u,x,NonConstants->{u,v}],D[v,x,NonConstants->{u,v}]}]//Simplify(*解求导以后由eq1,eq2组成的方程组*)则输出}}][][1(][}],{tan ,,[,][][1][}],{tan ,,[{{v Sin E v Cos E u v Cos E v u ts NonCons x v D v Sin E v Cos E v Sin v u ts NonCons x u D u u u u u -+-->->-+->->-其中D[u,x,NonConstants->{u,v}]表示u 对x 的偏导数, 而D[v,x,NonCosnstants->{u,v}]表示v 对x 的偏导数. 类似地可求得u ,v 对y 的偏导数.微分学的几何应用例1.5 求出曲面222y x z +=在点(1,1)处的切平面、法线方程, 并画出图形. 解(1) 画出曲面的图形. 曲面的参数方程为⎪⎩⎪⎨⎧=∈∈==2]2,0[],2,0[,cos 2/sin rz r u u r y u f x π 输入命令Clear[f];f[x_,y_]=2x^2+y^2;p1=Plot3D[f[x,y],{x,-2,2},{y,-2,2}];g1=ParametricPlot3D[{r*Sin[u]/Sqrt[2.],r*Cos[u],r^2}, {u,0,2*Pi},{r,0,2}] 则输出相应图形(图1.2).(2) 画出切平面的图形. 输入命令a=D[f[x,y],x]/.{x->1,y->1}; b=D[f[x,y],y]/.{x->1,y->1}; p[x_,y_]=f[1,1]+a(x-1)+b(y-1);g2=Plot3D[p[x,y],{x,-2,2},{y,-2,2}];则输出切平面方程为,012=-+y x 及相应图形(图1.3).(3) 画出法线的图形. 输入命令ly[x_]=1+b(x-1)/a;lz[x_]=f[1,1]-(x-1)/a;g3=ParametricPlot3D[{x,ly[x],lz[x]},{x,-2,2}]; Show[p1,g2,g3,AspectRatio->Automatic,ViewPoint->{-2.530,-1.025,2.000}];则输出相应图形(图1.4).图1.4例1.6 (教材 例1.4) 求曲面14),(22++=y x y x k 在点⎪⎭⎫⎝⎛2164,21,41处的切平面方程, 并把曲面和它的切平面作在同一图形里.输入Clear[k,z];k[x_,y_]=4/(x^2+y^2+1); (*定义函数k(x,y)*)kx=D[k[x,y],x]/.{x->1/4,y->1/2};(*求函数k(x,y)对x 的偏导数, 并代入在指定点的值*) ky=D[k[x,y],y]/.{x->1/4,y->1/2};(*求函数k(x,y)对y 的偏导数, 并代入在指定的值*) z=kx*(x-1/4)+ky*(y-1/2)+k[1/4,1/2]; (*定义在指定点的切平面函数*)再输入qm=Plot3D[k[x,y],{x,-2,2},{y,-2,2},PlotRange->{0,4}, BoxRatios->{1,1,1},PlotPoints->30, DisplayFunction->Identity]; qpm=Plot3D[z,{x,-2,2},{y,-2,2}, DisplayFunction->Identity];Show[qm,qpm,DisplayFunction->$DisplayFunction]多元函数的极值例1.7 (教材 例1.5) 求x y x y x y x f 933),(2233-++-=的极值. 输入Clear[f];f[x_,y_]=x^3-y^3+3x^2+3y^2-9x; fx=D[f[x,y],x] fy=D[f[x,y],y]critpts=Solve[{fx==0,fy==0}]则分别输出所求偏导数和驻点:2236369y y x x -++-{{x->-3,y->0},{x->-3,y->2},{x->1,y->0},{x->1,y->2}}再输入求二阶偏导数和定义判别式的命令fxx=D[f[x,y],{x,2}]; fyy=D[f[x,y],{y,2}]; fxy=D[f[x,y],x,y]; disc=fxx*fyy-fxy^2输出为判别式函数2xy yy xx f f f -的形式:(6+6x)(6-6y)再输入data={x,y,fxx,disc,f[x,y]}/.critpts;TableForm[data,TableHeadings->{None,{ "x ", "y ", "fxx ", "disc ", "f "}}]最后我们得到了四个驻点处的判别式与xx f 的值并以表格形式列出.X y fxx disc f -3 0 -12 -72 27 -3 2 -12 72 31 1 0 12 72 -5 1 2 12 -72 -1易见,当2,3=-=y x 时,12-=xx f 判别式disc=72, 函数有极大值31;当0,1==y x 时,12=xx f 判别式disc=72, 函数有极小值-5;当0,3=-=y x 和2,1==y x 时, 判别式disc=-72, 函数在这些点没有极值. 最后,把函数的等高线和四个极值点用图形表示出来,输入d2={x,y}/.critpts;g4=ListPlot[d2,PlotStyle->PointSize[0.02],DisplayFunction->Identity]; g5=ContourPlot[f[x,y],{x,-5,3},{y,-3,5},Contours->40,PlotPoints->60,ContourShading->False,Frame->False,Axes->Automatic,AxesOrigin->{0,0},DisplayFunction->Identity];Show[g4,g5,DisplayFunction->$DisplayFunction]则输出图1.6.从上图可见, 在两个极值点附近, 函数的等高线为封闭的. 在非极值点附近, 等高线不 封闭. 这也是从图形上判断极值点的方法.注:在项目一的实验4中,我们曾用命令FindMinimum 来求一元函数的极值, 实际上,也可 以用它求多元函数的极值, 不过输入的初值要在极值点的附近. 对本例,可以输入以下命令FindMinimum[f[x,y],{x,-1},{y,1}]则输出{-5.,{x->1.,y->-2.36603×10-8}}从中看到在0,1==y x 的附近函数),(y x f 有极小值-5, 但y 的精度不够好.例1.8 求函数22y x z +=在条件0122=-+++y x y x 下的极值. 输入Clear[f,g,la]; f[x_,y_]=x^2+y^2;g[x_,y_]=x^2+y^2+x+y-1; la[x_,y_,r_]=f[x,y]+r*g[x,y]; extpts=Solve[{D[la[x,y,r],x]==0,D[la[x,y,r],y]==0,D[la[x,y,r],r]==0}]得到输出⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+->-+->-+->-⎩⎨⎧⎭⎬⎫⎩⎨⎧-->--->--->-)31(21),31(21),33(31,)31(21),31(21),33(31y x r y x r再输入f[x,y]/.extpts//Simplify得到两个可能是条件极值的函数值}.32,32{-+但是否真的取到条件极值呢? 可利用等高线作图来判断.输入dian={x,y}/.Table[extpts[[s,j]],{s,1,2},{j,2,3}] g1=ListPlot[dian,PlotStyle->PointSize[0.03],DisplayFunction->Identity]cp1=ContourPlot[f[x,y],{x,-2,2},{y,-2,2},Contours->20,PlotPoints->60,ContourShading->False,Frame->False,Axes-> Automatic,AxesOrigin->{0,0},DisplayFunction->Identity]; cp2=ContourPlot[g[x,y],{x,-2,2},{y,-2,2},PlotPoints->60,Contours->{0},ContourShading-> False,Frame->False,Axes->Automatic,ContourStyle->Dashing[{0.01}],AxesOrigin->{0,0},DisplayFunction->Identity]; Show[g1,cp1,cp2,AspectRatio->1,DisplayFunction->$DisplayFunction]输出为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+-+-⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----)31(21,2321,)31(21,2321及图1.7. 从图可见,在极值可疑点,2321,2321⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛+-+-2321,2321 处, 函数),(y x f z =的等高线与曲线0),(=y x g (虚线)相切. 函数),(y x f z =的等高线是一系列同心圆, 由里向外, 函数值在增大, 在)31(21),31(21--=--=y x 的附近观察, 可以得出),(y x f z =取条件极大的结论. 在),31(21+-=x)31(21+-=y 的附近观察, 可以得出),(y x f z =取条件极小的结论.梯度场例1.9 画出函数222),,(y x z z y x f --=的梯度向量. 解 输入命令<<Graphics`ContourPlot3D` <<Graphics`PlotField3D` <<Calculus`VectorAnalysis`SetCoordinates[Cartesian[x,y,z]];f=z^2-x^2-y^2;cp3d=ContourPlot3D[f,{x,-1.1,1.1},{y,-1.1,1.1},{z,-2,2},Contours->{1.0},Axes->True,AxesLabel->{"x","y","z"}];vecplot3d=PlotGradientField3D[f,{x,-1.1,1.1},{y,-1.1,1.1},{z,-2,2},PlotPoints->3,VectorHeads->True];Show[vecplot3d, cp3d];则输出相应图形(图1.8)例1.10 在同一坐标面上作出⎪⎪⎭⎫⎝⎛++=2211),(y x x y x u 和 ,11),(22⎪⎪⎭⎫⎝⎛+-=y x y y x v 的等高线图(0>x ), 并给出它们之间的关系.解 输入命令<<Calculus`VectorAnalysis` <<Graphics`PlotField`SetCoordinates[Cartesian[x,y,z]];check[u_,v_]:={Grad[u][[1]]-Grad[v][[2]],Grad[v][[1]]+Grad[u][[2]]} u=x(1+1/(x^2+y^2));v=y(1-1/(x^2+y^2)); check[u,v]//Simplifyugradplot=PlotGradientField[u,{x,-2,2},{y,-2,2},DisplayFunction->Identity];uplot=ContourPlot[u,{x,-2,2},{y,-2,2},ContourStyle->GrayLevel[0],ContourShading->False,DisplayFunction->Identity,Contours->40,PlotPoints->40]; g1=Show[uplot,ugradplot,DisplayFunction->$DisplayFunction];vgradplot=PlotGradientField[v,{x,-2,2},{y,-2,2},DisplayFunction->Identity];vplot=ContourPlot[v,{x,-2,2},{y,-2,2},ContourStyle->GrayLevel[0.7],ContourShading->False,DisplayFunction->Identity,Contours->40,PlotPoints->40]; g2=Show[vplot,vgradplot,DisplayFunction->$DisplayFunction]; g3=Show[uplot,vplot,DisplayFunction->$DisplayFunction];g4=Show[ugradplot,vgradplot,DisplayFunction->$DisplayFunction];则输出相应图形(图1.9),其中(a) ),(y x u 的梯度与等高线图;(b) ),(y x v 的梯度与等高线图; (c) ),(y x u 与),(y x v 的等高线图; (d) ),(y x u 与),(y x v 的梯度图.图1.9从上述图中可以看出它们的等高线为一族正交曲线. 事实上, 有,,2222x v y x x y u y v y x x x u ∂∂-=+=∂∂∂∂=+=∂∂ 且,0=∇⋅∇v u 它们满足拉普拉斯方程022222222=∂∂+∂∂=∂∂+∂∂y vx v y u x u 例1.11 (教材 例1.6) 设,),()(22y x xe y x f +-=作出),(y x f 的图形和等高线, 再作出它的梯度向量gradf 的图形. 把上述等高线和梯度向量的图形叠加在一起, 观察它们之间的关系.输入调用作向量场图形的软件包命令<<Graphics\PlotField.m再输入Clear[f];f[x_,y_]=x*Exp[-x^2-y^2];dgx=ContourPlot[f[x,y],{x,-2,2},{y,-2,2},PlotPoints->60, Contours->25,ContourShading->False,Frame->False,Axes->Automatic,AxesOrigin->{0,0}] td=PlotGradientField[f[x,y],{x,-2,2},{y,-2,2},Frame->False] Show[dgx,td]输出为图1.10. 从图可以看到Oxy 平面上过每一点的等高线和梯度向量是垂直的, 且梯度的 方向是指向函数值增大的方向.图1.10例1.12 求出函数244),(y xy x y x f +-=的极值, 并画出函数),(y x f 的等高线、驻点以及),(y x f -的梯度向量的图形.输入命令<<Graphics`PlotField`f=x^4-4*x*y+y^2;FindMinimum[f,{x,1},{y,1}]conplot=ContourPlot[f,{x,-2,2},{y,-3,3},ContourShading->False,PlotPoints->100,Cont ours->{-4,-2,0,2,4,10,20}];fieldplot=PlotGradientField[-f,{x,-2,2},{y,-3,3},ScaleFunction->(Tanh[#/5]&)];critptplot=ListPlot[{{-Sqrt[2],-2*Sqrt[2]},{0,0},{Sqrt[2],2*Sqrt[2]}},PlotStyle->{Point Size[0.03]}];Show[conplot,fieldplot,critptplot];则得到),(y x f 的最小值.4)82843.2,41421.1(-=f 以及函数的图形(图1.11).实验习题 1.设,xy e z =求.dz2.设),,(y xy f z =求.,,22222y x zy z x z ∂∂∂∂∂∂∂3.设),sin (cos ),(228/)(22y x e y x g y x +=+-求.,,2yx z y z x z ∂∂∂∂∂∂∂4.试用例1.5的方法求265433051830120),(xy x x x x y x f +++--=的极值.5.求324y x z +=在01422=-+y x 条件下的极值.6.作出函数42210/)2(),(y x e y x f +-=的等高线和梯度线的图形, 并观察梯度线与等高线的 关系.实验2 多元函数积分学(基础实验)实验目的掌握用Mathematica 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的 概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.基本命令1. 计算重积分的命令lntegrate 和NIntegrate 例如,计算dydx xy x ⎰⎰1002, 输入Integrate[x*y^2,{x,0,1},{y,0,x}]则输出 151又如,计算dydx xy )sin(1102⎰⎰的近似值, 输入NIntegrate[Sin[x*y^2],{x,0,1},{y,0,1}] 则输出 0.160839注: Integrate 命令先对后边的变量积分.计算三重积分时,命令Integrate 的使用格式与计算二重积分时类似. 由此可见, 利用 Mathematica 计算重积分, 关键是确定各个积分变量的积分限. 2. 柱坐标系中作三维图形的命令CylindricalPlot3D使用命令Cylindricalplot3D, 首先要调出作图软件包. 输入 <<Graphics`ParametricPlot3D` 执行成功后便可继续下面的工作.使用命令Cylindricalplot3D 时,一定要把z 表示成r ,θ的函数. 例如,在直角坐标系中方 程22y x z +=是一旋转抛物面, 在柱坐标系中它的方程为2r z =. 因此,输入 CylindricalPlot3D[r^2,{r,0,2},{t,0,2Pi}] 则在柱坐标系中作出了该旋转抛物面的图形.3. 球面坐标系中作三维图形命令SphericalPlot3D使用命令SphericalPlot3D, 首先要调出作图软件包. 输入 <<Graphics`ParametricPlot3D` 执行成功后便可继续下面的工作.命令SphericalPlot3D 的基本格式为SphericalPlot3D[r[],θϕ, {}],,{},,,2121θθθϕϕϕ其中r[],θϕ是曲面的球面坐标方程, 使用时一定要把球面坐标中的r 表示成ϕ、θ的函数. 例如,在球面坐标系中作出球面,22222=++z y x 输入Sphericalplot3D[2,{u,0,pi},|v,0,2,pi|,plotpoints->40]则在球面坐标系中作出了该球面的图形.4. 向量的内积用“.”表示两个向量的内积. 例如,输入 vecl={al,bl,cl} vec2={a2,b2,c2} 则定义了两个三维向量, 再输入 vec1. vec2 则得到它们的内积a1a2+b1b2+c1c2实验举例计算重积分 例2.1 (教材 例2.1) 计算,2dxdy xyD⎰⎰ 其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.先作出区域D 的草图, 易直接确定积分限,且应先对x 积分, 因此, 输入 Integrate[x*y^2,{y,1,2},{x,2-y,Sqrt[y]}] 则输出所求二重积分的计算结果.120193例2.2 (教材 例2.2) 计算,)(22dxdy e Dy x⎰⎰+- 其中D 为.122≤+y x如果用直角坐标计算, 输入Clear[f,r];f[x,y]=Exp [-(x^2+y^2)];Integrate[f[x,y],{x,-1,1},{y,-Sqrt[1-x^2],Sqrt[1-x^2]}]则输出为dx x 1Erf e 211x 2⎥⎦⎤⎢⎣⎡-π⎰--其中Erf 是误差函数. 显然积分遇到了困难.如果改用极坐标来计算, 也可用手工确定积分限. 输入Integrate[(f[x,y]/.{x->r*Cos[t],y->r*Sin[t]})*r,{t,0,2 Pi},{r,0,1}] 则输出所求二重积分的计算结果eπ-π 如果输入NIntegrate[(f[x,y]/.{x->r*Cos[t],y->r*Sin[t]})*r,{t,0,2 Pi},{r,0,1}] 则输出积分的近似值1.98587例2.3 (教材 例2.3) 计算dxdydz z y x)(22++⎰⎰⎰Ω, 其中Ω由曲面222y x z --=与22y x z +=围成.先作出区域Ω的图形. 输入g1=ParametricPlot3D[{Sqrt[2]*Sin[fi]*Cos[th],Sqrt[2]*Sin[fi]*Sin[th], Sqrt[2]*Cos[fi]},{fi,0,Pi/4},{th,0,2Pi}] g2=ParametricPlot3D[{z*Cos[t],z*Sin[t],z},{z,0,1},{t,0,2Pi}] Show[g1,g2,ViewPoint->{1.3,-2.4,1.0}]则分别输出三个图形(图2.1(a), (b), (c)).考察上述图形, 可用手工确定积分限. 如果用直角坐标计算, 输入 g[x_,y_,z_]=x^2+y^2+z;Integrate[g[x,y,z],{x,-1,1},{y,-Sqrt[1-x^2], Sqrt[1-x^2]},{z,Sqrt[x^2+y^2],Sqrt[2-x^2-y^2]}] 执行后计算时间很长, 且未得到明确结果.现在改用柱面坐标和球面坐标来计算. 如果用柱坐标计算,输入Integrate[(g[x,y,z]/.{x->r*Cos[s],y->r*Sin[s]})*r,{r,0,1},{s,0,2Pi},{z,r,Sqrt[2-r^2]}]则输出π⎪⎪⎭⎫⎝⎛+-15281252 如果用球面坐标计算,输入Integrate[(g[x,y,z]/.{x->r*Sin[fi]*Cos[t],y->r*Sin[fi]*Sin[t],z->r*Cos[fi]})*r^2*Sin[fi],{s,0,2Pi},{fi,0,Pi/4},{r,0,Sqrt[2]}]则输出π⎪⎪⎭⎫ ⎝⎛+-321662551这与柱面坐标的结果相同.重积分的应用例2.4 求由曲面()y x y x f --=1,与()222,y x y x g --=所围成的空间区域Ω的体积.输入Clear[f,g];f[x_,y_]=1-x -y;g[x_,y_]=2-x^2-y^2;Plot3D[f[x,y],{x,-1,2},{y,-1,2}] Plot3D[g[x,y],{x,-1,2},{y,-1,2}] Show[%,%%]一共输出三个图形, 最后一个图形是图2.1.首先观察到Ω的形状. 为了确定积分限, 要把两曲面的交线投影到Oxy 平面上输入 jx=Solve[f[x,y]==g[x,y],y] 得到输出 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛-++→⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛-+-→22445121,445121x x y x x y为了取出这两条曲线方程, 输入 y1=jx[[1,1,2]] y2=jx[[2,1,2]] 输出为⎪⎭⎫ ⎝⎛-+-2445121x x⎪⎭⎫ ⎝⎛-++2445121x x再输入tu1=Plot[y1,{x,-2,3},PlotStyle->{Dashing[{0.02}]},DisplayFunction->Identity];tu2=Plot[y2,{x,-2,3},DisplayFunction->Identity]; Show[tu1,tu2,AspectRatio->1, DisplayFunction-> $DisplayFunction]输出为图2.2, 由此可见,1y 是下半圆(虚线),2y 是上半圆,因此投影区域是一个圆.设21y y =的解为1x 与2x ,则21,x x 为x 的积分限. 输入 xvals=Solve[y1==y2,x]输出为 ()()⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+→⎭⎬⎫⎩⎨⎧-→6121,6121x x 为了取出21,x x , 输入x1=xvals[[1,1,2]]x2=xvals[[2,1,2]]输出为()6121- ()6121+ 这时可以作最后的计算了. 输入V olume=Integrate[g[x,y]-f[x,y],{x,x1,x2},{y,y1,y2}]//Simplify 输出结果为 89π例2.5 (教材 例2.4) 求旋转抛物面224y x z --=在Oxy 平面上部的面积.S 先调用软件包, 输入<<Graphics`ParametricPlot3D` 再输入CylindricalPlot3D[4-r^2,{r,0,2},{t,0,2 Pi}] 则输出图2.3.利用计算曲面面积的公式⎰⎰++=xyD y z dxdy z z S 221, 输入Clear[z,z1];z=4-x^2-y^2;z=Sqrt[D[z,x]^2+D[z,y]^2+1]输出为22441y x ++, 因此,利用极坐标计算. 再输入z1=Simplify[z/.{x->r*Cos[t],y->r*Sin[t]}]; Integrate[z1*r,{t,0,2 Pi},{r,0,2}]//Simplify则输出所求曲面的面积()π1717161+-例2.6 在Oxz 平面内有一个半径为2的圆, 它与z 轴在原点O 相切, 求它绕z 轴旋转一周所得旋转体体积.先作出这个旋转体的图形. 因为圆的方程是,422x z x =+它绕z 轴旋转所得的圆环面的方程为)(16)(222222y x z y x +=++,所以圆环面的球坐标方程是.sin 4φ=r 输入SphericalPlot3D[4 Sin[t],{t,0,Pi},{s,0,2 Pi},PlotPoints->30,ViewPoint->{4.0,0.54,2.0}]输出为图2.4.图2.4这是一个环面, 它的体积可以用三重积分计算(用球坐标). 输入 Integrate[r^2*Sin[t],{s,0,2 Pi},{t,0,Pi},{r,0,4 Sin[t]}] 得到这个旋转体的体积为216π计算曲线积分例2.7 (教材 例2.5) 求⎰Lds z y x f ),,(, 其中(),10301,,2y x z y x f ++=积分路径为L :,3,,22t z t y t x ===.20≤≤y注意到,弧长微元dt z y x ds t t t 222++=, 将曲线积分化为定积分,输入 Clear[x,y,z];luj={t,t^2,3t^2}; D[luj,t]则输出z y x ,,对t 的导数 }6,2,1{t t再输入ds=Sqrt[D[luj,t].D[luj,t]];Integrate[(Sqrt[1+30 x^2+10y]/.{x->t, y->t^2,z->3t^2})*ds,{t,0,2}]则输出所求曲线积分的结果:326/3.例2.8 (教材 例2.6) 求dr F L.⎰, 其中.20,sin cos 2)(,)2(356π≤≤+=++=t tj ti t r j xy x i xy F输入vecf={x*y^6,3x*(x*y^5+2)};vecr={2*Cos[t],Sin[t]};Integrate[(vecf.D[vecr,t])/.{x->2Cos[t],y->Sin[t]}, {t,0,2 Pi}]则输出所求积分的结果12π例2.9 求锥面0,222≥=+z z y x 与柱面x y x =+22的交线的长度.先画出锥面和柱面的交线的图形. 输入g1=ParametricPlot3D[{Sin[u]*Cos[v], Sin[u]*Sin[v], Sin[u]}, {u,0,Pi},{v,0,2Pi},DisplayFunction->Identity]; g2=ParametricPlot3D[{Cos[t]^2,Cos[t]*Sin[t],z}, {t,0,2Pi},{z,0,1.2}, DisplayFunction->Identity]; Show[g1,g2,ViewPoint->{1,-1,2},DisplayFunction->$DisplayFunction]输出为图2.5.输入直接作曲线的命令ParametricPlot3D[{Cos[t]^2,Cos[t]*Sin[t],Cos[t]},{t,-Pi/2,Pi/2}, ViewPoint->{1,-1,2},Ticks->False]输出为图2.6.为了用线积分计算曲线的弧长, 必须把曲线用参数方程表示出来. 因为空间曲线的投影曲线的方程为x y x =+22, 它可以化成t x 2cos =,,sin cos t t y =再代入锥面方程222z y x =+, 得[]().2/,2/cos ππ=∈=t t z因为空间曲线的弧长的计算公式是()()()⎰'+'+'=21222t t dt t z t y t x s ,因此输入Clear[x,y,z]; x=Cos[t]^2; y=Cos[t]*Sin[t]; z=Cos[t]; qx={x,y,z};95Integrate[Sqrt[D[qx,t]. D[qx,t]]//Simplify, {t,-Pi/2,Pi/2}]输出为 2Elliptice[-1]这是椭圆积分函数. 换算成近似值. 输入 %//N 输出为3.8202计算曲面积分例2.10 (教材 例2.7) 计算曲面积分⎰⎰∑++dS zx yz xy )(, 其中∑为锥面22y x z +=被柱面x y x 222=+所截得的有限部分.注意到,面积微元dxdy z z dS y x 221++=, 投影曲线x y x 222=+的极坐标方程为,22,cos 2ππ≤≤-=t t r将曲面积分化作二重积分,并采用极坐标计算重积分.输入Clear[f,g,r,t];f[x_,y_,z_]=x*y+y*z+z*x; g[x_,y_]=Sqrt[x^2+y^2];mj=Sqrt[1+D[g[x,y],x]^2+D[g[x,y],y]^2]//Simplify; Integrate[(f[x,y,g[x,y]]*mj/.{x->r*Cos[t],y->r* Sin[t]})*r,{t,-Pi/2,Pi/2},{r,0,2Cos[t]}]则输出所求曲面积分的计算结果15264例2.11 计算曲面积分,333dxdy z dzdx y dydz x ++⎰⎰∑其中∑为球面2222a x y x =++的外侧.可以利用两类曲面积分的关系, 化作对曲面面积的曲面积分⎰⎰∑nds A .. 这里{}{}a z y x n z y x A /,,,,,333==. 因为球坐标的体积元素,sin 2θϕϕd drd r dv =注意到在球面∑上a r =, 取1=dr 后得到面积元素的表示式:().20,0sin 2πθπϕθϕθ≤≤≤≤=d d a ds把对面积的曲面即直接化作对θϕ,的二重积分. 输入Clear[A,fa,ds]; A={x^3,y^3,z^3}; fa={x,y,z}/a; ds=a^2*Sin[u];Integrate[(A.fa/.{x->a*Sin[u]*Cos[v],y->a*Sin[u]*Sin[v], z->a*Cos[u]})*ds//Simplify,{u,0,Pi}, {v,0,2Pi}]输出为96 5122πa如果用高斯公式计算, 则化为三重积分()d v z y x ⎰⎰⎰Ω++2223, 其中Ω为2222a z y x ≤++.采用球坐标计算, 输入<<Calculus`VectorAnalysis` 执行后再输入SetCoordinates[Cartesian[x,y,z]]; (*设定坐标系*) diva=Div[A]; (*求向量场的散度*)Integrate[(diva/.{x->r*Sin[u]*Cos[v],y->r*Sin [u]*Sin[v],z->r*Cos[u]})*r^2Sin[u],{v,0,2Pi}, {u,0,Pi},{r,0,a}]输出结果相同.实验习题 1. 计算⎰⎰-6/02/0.sin sin ππydydx x x y2. 计算下列积分的近似值: (1)();cos 022dydx y x ⎰⎰-ππ(2)().sin 1010dydx e xy ⎰⎰3. 计算下列积分 (1)();23012dydzdx z y e x x z xz x -⎰⎰⎰+- (2)⎰⎰1010.)arctan(dydx xy4. 交换积分次序并计算下列积分 (1)()d ydx y x x⎰⎰30922cos . (2) .20422dxdy e yx ⎰⎰5. 用极坐标计算下列积分: (1) ;10122dydx y x yx ⎰⎰+ (2) .13/3/22dxdy yx y y y ⎰⎰-+6. 用适当方法计算下列积分:(1)(),2/3222dv zy x z⎰⎰⎰Ω++ 其中Ω是由22y x z +=与1=z 围成;(2),)(224dv z y x++⎰⎰⎰Ω其中Ω是.1222≤++z y x7. 求()ds z y x f L⎰,,的近似值. 其中(),51,,33y x z y x f ++=,路径L :3/,2t y t x ==,.20,≤≤=t t z8. 求⎰L dr F ., 其中().0,sin cos ,121322π≤≤+=+++=t tj ti t r j y i x F 9. 用柱面坐标作图命令作出xy z =被柱面122=+y x 所围部分的图形,并求出其面积.9710. 求曲面积分,22zdxdy y x⎰⎰∑其中∑为球面2222a z y x =++的下半部分的下侧.11. 求曲面积分⎰⎰∑++zdS y x ,其中∑为球面2222a z y x=++上)0(a h z <<≥的部分.实验3 最小二乘拟合(基础实验)实验目的 了解曲线拟合问题与最小二乘拟合原理. 学会观察给定数表的散点图, 选择 恰当的曲线拟合该数表.最小二乘拟合原理 给定平面上的一组点,,,2,1),,(n k y x k k = 寻求一条曲线),(x f y =使它较好的近似这组数据, 这就是曲线拟合. 最小二乘法是进行曲线拟合的常用方法.最小二乘拟合的原理是, 求),(x f 使∑=-=nk k kyx f 12])([δ达到最小. 拟合时, 选取适当的拟合函数形式),()()()(1100x c x c x c x f m m ϕϕϕ+++=其中)(,),(),(10x x x m ϕϕϕ 称为拟合函数的基底函数.为使δ取到极小值, 将)(x f 的表达式 代入, 对变量i c 求函数δ的偏导数, 令其等于零, 就得到由1+m 个方程组成的方程组, 从中 可解出).,,2,1,0(m i c i =基本命令1.求数据的拟合函数的命令Fit 拟合函数Fit[ ]的基本格式为Fit[data,funs,vars],其中,data 是数据, vars 为变量(可以是多个变量), funs 为1+m 个以vars 为变量的基底函数. 其 输出结果是以基底函数(funs)的线性组合形式为拟合函数的最佳拟合函数(最小二乘估计的 结果). Fit 命令既可以作曲线拟合, 也可以作曲面拟合. 这里只讨论曲线拟合问题.曲线拟合时的数据格式为}}.,{,},,{},,{{2211n n y x y x y x下面是作曲线拟合时常用的几种拟合函数的形式Fit[data,{1,x},x] 用线性函数bx a +拟合数据data.Fit[data,{1,x,x^2},x] 用二次函数2cx bx a ++拟合数据data.Fit[data,Table[x^i,Table[x^i,{i,0,n}],x] 用x 的n 次多项式拟合数据data. 2.多项式拟合函数PolynomialFitMathematica 在程序包NumericalMath 中提供了多项式拟合函数PolynomialFit, 其基本格 式为PolynomialFit[data,n]它按最小二乘法构造n 次多项式函数拟合数据data. 例如,输入<<NumericalMath`PolynomialFit`98 p=PolynomialFit[{1,4,9,16,25,36,49},3]则输出FittingPolynomial[< >, 3]这里虽然没有给出拟合多项式的解析表达式, 但在计算机中已经存在. 因此可以用来计算函 数的近似值. 输入p[10] (*计算)10(f 的近似值*) 就得到函数的近似值100. 如果要拟合多项式的解析表达式, 输入Expand[p[x]]则输出321515x .0x .1x 1077636.11010543.7++⨯+⨯---3.去掉矩阵中非数值列的命令DropNonNumericColumn 如果矩阵M 中有非数值的列, 可先输入调用软件包命令<<Statistics\DataManipulation.m执行以后, 再输入DropNonNumericColumn[M]则在输出的矩阵中已经把含有非数值的列去掉.4.在Mathematica 中作曲线拟合的一般步骤在Mathematica 中作曲线拟合, 可按以下步骤进行:(1)用ListPlot[数据]作散点图, 观察曲线的分布形状, 确定基底函数; (2)用Fit[ ]命令求拟合函数; (3)用Plot[ ]命令作拟合曲线图;(4)最后用Show[ ]命令把散点图与拟合曲线图放在同一坐标系内, 观察拟合效果.实验举例曲线拟合 例 3.1 (教材 例 3.1) 为研究某一化学反应过程中温度)(C x 对产品得率(%)y 的影响, 测得数据如下:x 100 110 120 130 140 150 160 170 180 190 y 45 51 54 61 66 70 74 78 85 89试求其拟合曲线.输入点的坐标, 作散点图, 即输入b2={{100,45},{110,51},{120,54},{130,61},{140,66},{150,70},{160,74},{170,78},{180,85},{190,89}};fp=ListPlot[b2]99通过观察发现散点基本位于一条直线附近, 可用直线拟合. 输入Fit[b2,{1,x},x] (*用Fit 作拟合, 这里是线性拟合*)则输出拟合直线-2.73939+0.48303x作图观察拟合效果. 输入gp=Plot[%,{x,100,190},PlotStyle->{RGBColor[1,0,0]},DisplayFunction->Identity]; (*作拟合曲线的图形*)Show[fp,gp,DisplayFunction->$DisplayFunction](*显示数据点与拟合曲线*)例3.2 (教材 例3.2) 给定平面上点的坐标如下表:3627.100253.99493.70978.74337.69378.55687.53057.51234.59.08.07.06.05.04.03.02.01.0y x 试求其拟合曲线.输入data={{0.1,5.1234},{0.2,5.3057},{0.3,5.5687},{0.4, 5.9378},{0.5,6.4337},{0.6,7.0978},{0.7,7.9493},{0.8,9.0253},{0.9,10.3627}};pd=ListPlot[data];观察发现这些点位于一条抛物线附近. 用抛物线拟合, 即取基底函数.,,12x x 输入f=Fit[data,{1,x,x^2},x]则输出100 5.30661-1.83196x+8.17149x 2再输入fd=Plot[f,{x,0,1},DisplayFunction->Identity]; Show[pd,fd,DisplayFunction->$DisplayFunction]则输出平面上的点与拟合抛物线的图形(图3.2).下面的例子说明Fit 的第二个参数中可以使用复杂的函数, 而不限于2,,1x x 等. 例3.3 (教材 例3.3) 使用初等函数的组合进行拟合的例子. 先计算一个数表. 输入ft=Table[N[1+2Exp[-x/3]],{x,10}]则输出{2.43306,2.02683,1.73576,1.52719,1.37775,1.27067,1.19394,1.13897,1.09957,1.07135}然后用基函数)exp(),3/exp(,sin ,1x x x --来做曲线拟合. 输入Fit[ft,{1,Sin[x],Exp[-x/3],Exp[-x]},x]则输出拟合函数][1022045.2.21044089.4.1163/15x Sin e e x x ----⨯++⨯-其中有些基函数的系数非常小, 可将它们删除. 输入Chop[%]则输出3/.2.1x e -+实际上,我们正是用这个函数做的数表.注:命令Chop 的基本格式为Chop[expr,δ]其含义是去掉表达式expr 的系数中绝对值小于δ的项,δ的默认值为1010-.实验4 水箱的流量问题(综合实验)实验目的 掌握应用最小二乘拟合原理分析和解决实际问题的思想和方法,能通过观察测试数据的散点图,建立恰当的数学模型,并用所学知识分析和解决所给问题.问题 (1991年美国大学生数学建模竞赛的A 题. 问题中使用的长度单位为E(英尺, 1 E=30.24cm), 容积单位是G(加仑, 1 G=3.785L)).101某些州的用水管理机构需估计公众的用水速度(单位:G/h)和每天的总用水量. 许多供水单位由于没有测量流入或流出量的设备, 而只能测量水箱中的水位(误差不超过5%). 当水箱水位低于水位L 时, 水泵开始工作将水灌入水箱, 直至水位达到最高水位H 为止. 但是依然无法测量水泵灌水流量, 因此, 在水泵工作时无法立即将水箱中的水位和水量联系起来. 水泵一天灌水1~2次, 每次约2h. 试估计在任一时刻(包括水泵灌水期间) t 流出水箱的流量),(t f 并估计一天的总用水量.表1给出了某镇某一天的真实用水数据. 水箱是直径为57E, 高为40E 的正圆柱体. 当水位落到27E 以下, 水泵自动启动把水灌入水箱; 当水位回升至35.5E 时, 水泵停止工作.模型假设(1) 影响水箱流量的唯一因素是该区公众对水的普通需求. 所给数据反映该镇在通常情况下一天的用水量, 不包括任何非常情况, 如水泵故障、水管破裂、自然灾害等. 并且认为水位高度、大气情况、温度变化等物理因素对水的流速均无直接影响;(2) 水泵的灌水速度为常数;(3) 从水箱中流出水的最大流速小于水泵的灌水速度. 为了满足公众的用水需求不让水箱中的水用尽, 这是显然的要求;(4) 因为公众对水的消耗量是以全天的活动(诸如洗澡、做饭、洗衣服等)为基础的, 所以,可以认为每天的用水量分布都是相似的;(5) 水箱的水流量速度可用光滑曲线来近似.问题分析与模型建立为方便起见,记V 表示水的容积;i V 表示时刻i t (单位:h)水的容积;)(t f 表示流出水箱的水的流速(单位;G/h),它是时间的函数;p 表示水泵的灌水速度(G/h).先将表1中数据作变换, 时间单位用小时(h), 水位高转换成水的体积(,2h r V π=单位:G 481.7E 1,G 1033= ). 输入tt={0,3316,6635,10619,13937,17921,21240,25223, 28543,32284,35932, 39332,39435,43318,46636,49953,53936,57254,60574,64554,68535, 71854,75021,79254,82649,85968,89953,93270}/3600//Nvv=Pi*(57/2)^2*{3175,3110,3054,2994,2947,2892, 2850,2795,2752,2697, no_data,no_data,3550,3445,3350,3260,3167,3087,3012,2927,2842,2767,2697,no_data,no_data,3475,3397,3340}*10^(-2)*7.481/10^3//N则输出下表.由于要求的是水箱流量与时间的关系, 因此须由表2的数据计算出相邻时间区间的中点及在时间区间内水箱中流出的水的平均速度.平均流速=(区间左端点的水量-区间右端点的水量)/时间区间长度输入tt1=Table[(tt[[i+1]]+tt[[i]])/2,{i,27}]vv1=Table[(vv[[i]]-vv[[i+1]])/(tt[[i+1]]-tt[[i]]),{i,27}]则输出下表模型求解为了作出时间tt1与平均水流量vv1之间的散点图, 先输入调用统计软件包的命令<<Statistics\DataManipulation.m执行以后再输入102103Clear[L];L=Transpose[DropNonNumericColumn[{tt1,vv1*10^3}]](*命令中vv1*10^3,使平均水流量vv1的单位变为G/h*) g1=ListPlot[L]则输出图4.1图中空白区域为泵水时间. 从中可以看出数据分布不均匀. 我们采用8阶多项式进行拟合. 输入ft=Fit[L,Table[t^i,{i,0,8}],t]则输出8765432t 00024547.0t 0248438.0t 01085.1t 1138.21t 101.240t 79.1468t 62.4690t 96.78394.16281+-+-+-+-这就是流出水箱的水的流速关于时间t 的函数)(t f . 为作出其拟合曲线图, 输入fg=Plot[ft,{t,0,26},DisplayFunction->Identity]; Show[g1,fg,DisplayFunction->$DisplayFunction]则输出图4.2.求解结果将460556.0=t h 和460556.24=t h 代入到水的流速拟合函数),(t f 我们得到这两时刻的流速分别近似为13532.5G/h 和13196.1G/h,相差仅2.48587%, 从而可以认为)(t f 能近似表达一天的用水流量.于是, 一天里的用水总量近似地等于函数)(t f 在24小时周期内的积分.输入Integrate[ft,{t,0.46,24.46}]104 则输出 336013.G若按常规每1000人的用水量为105000G/d, 因此估计出这个地区大约有3200人.模型评价该模型数学概念简单, 并且容易实现, 任意时刻从水箱中流出水的速度都可通过该模型计算出来, 可以推测速度. 但数据太少, 只能参照一天的数据. 另外, 如果知道水泵的灌水速度, 就能更准确地估算水泵灌水期间水的流速.实验报告某装饰材料商店欲以每瓶2元的成本价购进一批彩漆. 一般来说, 随着彩漆售价的提高,预期销售量将减少, 对此进行了估算, 见下表.202225282932343841/00.650.500.550.400.450.300.350.200.2/万瓶预期销售量元售价为了尽快收回资金并获得较多的赢利, 装饰材料商店打算做广告. 投入一定的广告费后,销售量将有一个增长, 可由销售增长因子来表示. 例如, 投入4万元的广告费, 销售增长因子为1.95. 即销售量将是预期销售量的1.95倍. 根据经验, 广告费与销售增长因子的关系见下表.8.195.100.295.185.170.140.100.1706050403020100)(销售增长因子元广告费用试确定装饰材料商店的最佳营销策略, 即确定彩漆售价和广告费投入使得预期的利润最大?实验5 线性规划问题(综合实验)实验目的 通过建立投资收益和风险问题的线性规划模型, 掌握利用线性规划理论建立实际问题的数学模型的思想和方法. 掌握用Mathematica 求解线性规划问题的基本方法.基本命令1.约束最大与约束最小命令求解线性规划问题的命令为ConstrainedMax 与ConstrainedMin. 其的基本格式是:ConstrainedMax[f,{inequalities},{x,y,…}]在不等式或等式{inequalities}确定的可行区域上求线性目标函数f 的最大值, 约定变量{x ,y ,…}都大于或等于0;ConstrainedMin{f,{inequalities},{x,y,…}}在不等式或等式{inequalities}确定的可行区域上求线性目标函数f 的最小值, 约定变量{x ,y ,…}都大于或等于0.注:上面两个命令都有一个可选参数:Tolerance 允许误差 (默认值是610-).例如, 输入ConstrainedMin[1.5 x+2.5 y,{x+3 y>=3,x+y>=2},{x,y}]则输出{3.5,{x->1.5,y->0.5}}即当5.0y ,5.1x ==时, 函数取得最小值3.5. 在约束条件中可以使用等号, 但要用“= =”表105示. 例如,输入ConstrainedMax[5 x+3 y+2 z+4 t,{3 x+y+2 z+8 t==10,2 x+4 y+2 z+t==10},{x,y,z,t}]则输出{18,{x->3,y->1,z->0,t->0}}有时, 输出结果可能有些问题. 输入ConstrainedMax[3x+2y-1,{x<1,y<2},{x,y}]则输出{6,{x->1,y->2}}即当2,1==y x 时, 函数取最大值6.注: 约束条件使用严格不等号, 结果仍旧取在边界上. 输入ConstrainedMax[x+y,{x+y<=15},{x,y}]则输出{15,{x->15,y->10}}这个问题有无穷多最优解, 这里只给出其中之一, 而且没有给出任何提示信息.前面的例题总是给出一个最优解, 属于正常情况.下面的例子是非正常的情况. 例如, 输入ConstrainedMax[x+y,{x-y>=0,3x-y<=-3},{x,y}]则在输入行的下面给出提示ConstrainedMax::nsat:The specified constraints cannot be satisfied.并输出ConstrainedMax[x+y,{x-y>=0,3x-y<=-3},{x,y}]其含义是: 没有可行解, 因此没有最优解. 然后返回投资的收益和风险问题.输入ConstrainedMax[2x+y,{x-y>=-1,-0.5x+y<=2},{x,y}]在输入行的下面给出提示ConstrainedMax::nbddt:Specified domain appearsunbounded,with tolerance1.’*^-6.并输出{∞,{x->Indeterminate,y->Indeterminate}}其含义是: 可行区域无界, 问题没有最大值, 或说最大值是无穷大. 然后返回投资的收益和风险问题.2.线性规划命令LinearProgramming当自变量和约束不等式较多时, 用ConstrainedMax 或ConstrainedMin 求解就比较麻烦. 此时, 可将目标函数和约束条件用向量或矩阵表示, 然后使用LinearProgramming. 其基本格式为LinearProgramming[c,m,b]其中c 是行向量, b 是列向量, m 是矩阵, 自变量用x 表示, 使用该命令, 则在满足不等式b mx ≥且0≥x 的可行区域中, 求出函数cx 的最小值点x .注: 实际输入时, b 仍以行向量表示. 此外, 这个命令也有可选参数Tolerance, 其含义与前面的说明相同.例如, 用约束最小命令计算, 输入ConstrainedMin[2x-3y,{x+y<10,x-y>2,x>1},{x,y}]则输出{0,{x->6,y->4}}改为用线性规划命令计算, 输入LinearProgramming[{2,-3},{{-1,-1},{1,-1},{1,0}},{-10,2,1}]。
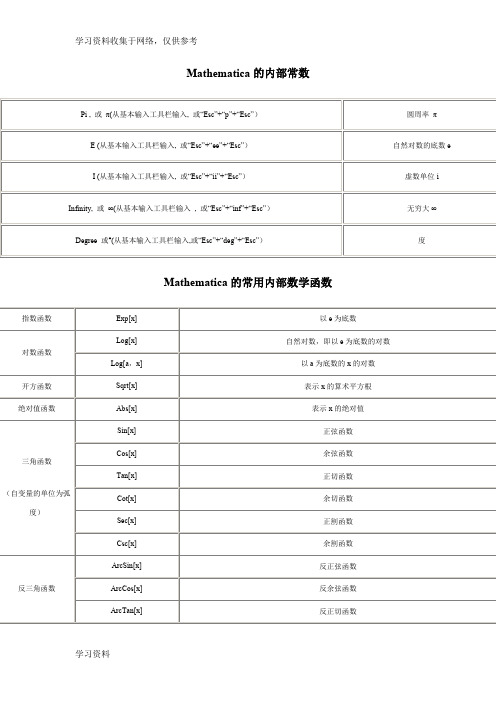
Mathematica的命令大全

Mathematica的命令大全Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数,即以e为底数的对数Log[a,x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数(自变量的单位为弧度)Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...]最大公约数函数LCM[a,b,c,...]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m,n]求商函数(表示m除以n的商)Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解,即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为FalseRandom[Integer,{m,n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)N[num,n]把精确数num化成具有n个有效数字的浮点数NumberForm[num,n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float,dx]将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...]求最大数Min[a,b,c,...]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为:“Ctrl ”+ “/ ”) 除法a^b (输入方法为:“Ctrl ”+ “^ ”)乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注:上面的关系运算符也可从基本输入工具栏输入。
用Mathematica进行求导运算

y ln ln x
In[2] : D Log[Log[x]],x
Out[2]
1
xLog[x ]
例:求下列函数的二阶导数
y x8
In[3] : D x 8,x,2
Out[3] 56x 6
y 1 x2 arctan x
In[4] :
f (x)
f (x0 )
f (x0 )(x x0 )
f
( x0 2
)
(x
x0
)2
L
f
(n) (x0 n!
)
(x
x0
)n
Rn
(x)
麦克劳林公式:
f (x)
f (0)
f (0)x
f (0) x2 L 2
f
(n) (0) n!
xn
Rn
(x)
用Mathematica进行级数运算
Out[1]
x
x2
2
x3
6
x4
12
O(x 5 )
练习7
将函数 y ex 在x=1处展开到x的4次幂 将函数 y sin x和y cos x 在x= 0处展开到x的y 5ex次幂
将函数 y ln(x 1) 在x=1处展开到x的3次幂 x
用Mathematica进行求导运算
在Mathematica 中,求函数的导数或偏导数的格式为:
D[ f , x]
表示f对x求一阶导数
D[ f ,{x, n}] 表示f对x求n阶导数
例:求下列函数的一阶导数
y x3 cos x
In[1] : D x 3 * Cos[x ],x
Mathematical常用功能大全-精简版

Mathematica for Windows 常用用法一、Mathematica 的主要功能Mathematica 是美国Wolfram 公司开发的一个功能强大的计算机数学系统,提供了范围广泛的数学计算功能,主要包括三个方面:符号演算、数值计算、图形。
例如:多项式的四则运算、展开、因式分解,有理式的各种计算,有理方程、超越方程的解,向量和矩阵的各种计算,求极限、导数、极值、不定积分、定积分、幂级数展开式,求解微分方程,作一元、二元函数的图形等等。
二、Mathematica 的基本知识 1.输入表达式:直接输入一个表达式(包括算式和命令,长表达式用“Enter ”换行)后,按“Shift+Enter ”执行,执行后以“Out[命令序号]= ……”形式输出执行结果,输出的结果可在后续的表达式中使用。
若命令后有分号,则不输出执行结果(图形输出与Print 命令除外)。
“%”表示上一个输出,“%%”表示倒数第2个输出,“%i”表示第i个命令的输出。
2.运算符:+、-、*、/、^ ,“*”可用空格代替,“^”表示乘方。
如:In[1]:=2^10,输出为“Out[1]= 1024”,其中“In[1]:=”不需要输入。
In[2]:=3+5,Out[2]= 8;In[3]:=%-2,Out[3]= 6;In[4]:=%2+4,Out[4]= 12;In[5]:=1/3-1/4,Out[5]=121;In[6]:=N[%],Out[6]= 0.0833333; In[7]:=N[%5+12,10],Out[7]= 12.08333333(注意字母的大小写) 3.变量赋值:变量=表达式,“x=.”或Clear[x] 表示清除对x 的赋值。
表达式/.t ->c ,将表达式中的t 全替换成c 。
?x ,查x 信息。
4.常用的数学常数:Pi (π)、E(e)、Infinity (∞)、I (1-)5.常用的数学函数:Abs, Sin, Cos, Tan, Cot, ArcSin, Log (自然对数), Sqrt, Exp 如:In[1]:=Sqrt[2]+1;In[2]:=Sin[2]+ArcSin[1];In[3]:=Exp[2]+% (自变量用[ ]括,区分大小写,首字母大写) 三、常用运算 1.多项式运算:In[1]:= (2+4*x^2)*(1-x)^3 或 In[1]:= t = (2+4*x^2)*(1-x)^3 (将右端表达式赋值给t ); In[2]:=a=t/.x->4 (计算表达式t 当x=4时的值,并赋值给变量a ) In[3]:=a=. (清除变量a ) In[3]:=Expand[t](展开);In[4]:=Factor[%](把上一个结果因式分解) 2.解方程:In[1]:=Solve[x^2+3*x = = 2];In[2]:=N[%]; In[3]:=Solve[a*x-b= = 0, x]; In[4]:=NSolve[{x-2*y= =0,x^2-y= =1},{x,y}](解方程组并得到数值解) 3.自定义函数:In[1]:= f [x_ ]:=x^2+2*x ; In[2]:=f[5]+7; In[3]:=f[a+b] 4.求极限:In[1]:=Limit[Sin[x]/x, x ->0]; In[2]:=Limit[(1+1/n)^n, n->Infinity],Out[2]=E 5.求(偏)导数:In[1]:=D[a*x^2+3, x];In[2]:=D[x^2+y^3-Sin[2*y], y](对y 的偏导数); In[3]:=D[Log[x], {x,2}] (求对x 的二阶导数); In[4]:=D[Sin[x+y]*Exp[z*y^2],x,y] (求对x 、y 的二阶混合偏导数); In[5]:=Simplify[%] (对前一结果化简); In[6]:=D[Sin[x+y]*Exp[z*y^2],{x,2},{y,3}] 6.求不定积分:In[1]:=Integrate[x^2,x];In[2]:=Integrate[1/(x^2+a^2),x] 7.定积分:In[1]:=Integrate[x^2, {x,0,1}];In[2]:=Integrate[x^2,{x,a,b}]; In[3]:=Integrate[x^2+y^2, {x,0,a},{y,0,b}];(求矩形域上的二重积分) In[4]:=Integrate[1, {x,-1,1},{y,-Sqrt[1-x^2],Sqrt[1-x^2]}];Out[4]=Pi (圆面积) 8.幂级数展开:In[1]:=Series[Exp[x],{x,0,4}](在x=0处展开到x 的四次幂) 9.矩阵的输入和输出:In[1]:= a ={{1,2},{3,4}}(定义一个2x2的矩阵a ,按行写);In[2]:=MatrixForm[a](输出为矩阵形式);In[3]:=Transpose[a](a 的转置); In[4]:=a[[2]](a 的第2行);In[5]:=Tanspose[a][[2]](a 的第2列); In[6]:=Inverse[a](求a 的逆矩阵);In[7]:=Det[a](矩阵的行列式); In[8]:=Eigenvalues[a](求特征值);In[9]:=Eigenvectors[a](求特征向量); In[10]:=RowReduce[a](把a 化为阶梯形,可用于求矩阵的秩、判断线性相关性); In[11]:= b ={{5,6,7},{8,9,10}};In[12]:= a .b (矩阵a 与b 的乘积) 10.解线性方程组:In[1]:= a ={{3,4,5,6},{6,8,10,12},{4,5,6,7},{5,6,7,8}};(a 的秩为2) In[2]:= b ={1,2,3,5}(列向量);(增广矩阵的秩也为2) In[3]:=LinearSolve[a,b](求线性方程组ax=b 的一个特解); In[4]:=NullSpace[a](求线性方程组ax=0的一个基础解系);In[5]:= x =k1%4[[1]]+k2%4[[2]]+%3(ax=b 的全部解,k1、k2为任意常数)11.求和:In[1]:=NSum[Sin[n]/n^3,{n,1,Infinity}](求级数∑∞=13sin n nn 的和)12.求极小值:In[1]:=FindMinimum[Sin[x]*Cos[x],{x,0.5}](求函数在0.5附近的极小值);In[2]:=FindMinimum[Sin[x*y]*Exp[x^2],{x,0.2}, {y,0.3}](求多元函数极小值) 13.求解线性规划问题:Min cx ,mx ≥b ,x ≥0,求向量x 。
利用Mathematica求函数极值

4
x 2 3 y 2 9x (2)求函数 f ( x, y) x 3 y 3 3的最值 解 自定义函数 f[x_,y_]:=x^3-y^3+3*x^2+3*y^2-9*x; 求驻点 Solve[{D[f[x,y],x]==0,D[f[x,y],y]==0}] \输出结果为{{x->-3,y->0},{x->-3,y->2},{x>1,y->0},{x->1,y->2}} 比较各点函数值 f[x,y]/.% \输出结果为 {27,31, -5,-1} 可求得最值为31
边学边做: (一)用命令FindMinimum求极小值: FindMinimum[f[x],{x,x0}] FindMinimum[f[x,y],{x,x0},{y,y0}] (1)先作图,观察之后求函数 f ( x) x 4 在 2 x 2 [-3,3] 内的极值 3x 2 y 3 (2)作图之后求函数 f ( x, y) x 2 y 2 xy 的极值 (二)用求驻点的方法求函数极值 (1)求函数 的极值 4( x 1)
处 有极值,求此极值,并说明是极大值还是极小 值. 3 2 f ( x ) ax bx cx d 在x=-1处有极大 (2)若函数 值为8,在x=2处有极小值为-19,求a,b,c,d. (3)把一根直径为d的圆木锯成截面为矩形的梁, 问矩形截面高h与宽b如何选择时,才能使梁 1 2 W bh 达到最大? 的抗弯截面系数 6 (4)求表面积为a2且体积最大的长方体体积.
f ( x)
(2)求函数
x2 1
f ( x, y) x 3 y 3 3x 2 3 y 2 9x
的最值
用Mathematica求偏导数与多元函数的极值练习参考解答

用Mathematica求偏导数与多元函数的极值练习参考解答§10 用Mathematica 求偏导数与多元函数的极值练习参考解答1 求下列函数的偏导数。
(1) 221y x z +=(2) xy e z = (3) zx x z x y u -+= (4) z xy u )(= 2 求下列函数的偏导数或导数。
(1) 设x e y xy arctg z ==),(,求dxdz 。
(2) 设),ln(xy x z =求y x z 23??,23xyz ?? (3) 设,23,,ln 2v u y v u x y x z -===求u z ??,vz ??。
(4) 设),(z y y x f u =,求z u ??,yu ??,x u ??。
(5) 设),,(yx xy y x f z +=,求xy xx x z z z ,,。
3 求下列方程所确定的隐函数的导数。
(1) 043322=-+y x y x ,求dx dy 。
(2) 02=+--z xy e z e ,求x z ??,yz ??。
(3) ),,(xyz z y x f z ++=求x z ??,y x ??,yz ??。
(4) ax y x a z y x =+=++222222,,求dx dy ,dx dz 。
4 求函数61065),(22++-+=y x y x y x f 的极值。
5 求函数22y x z -=,在}4|),{(22≤+y x y x 范围内的最大最小值。
练习参考解答1 求下列函数的偏导数。
(1) 221y x z += (2) xy e z = (3) zx x z x y u -+= (4) z xy u )(= 解 (1) In[1]:= D[1/Sqrt[x^2+y^2,x] In[2]:= D[1/Sqrt[x^2+y^2,y] Out[1]= 2/322)(y x x +- Out[2]= 2/322)(y x y +- (2) In[3]:= D[E^(x*y),x]In[4]:= D[E^(x*y),x]Out[3]= y e xyOut[4]= x e xy(3) In[5]:= D[y/x+z/x-x/z,x]In[6]:= D[y/x+z/x-x/z,y]In[7]:= D[y/x+z/x-x/z,z] Out[5]= 221z z z x y ---Out[6]= x1 Out[7]= 21zx x + (4) In[8]:= D[(x*y)^z,x]In[9]:= D[(x*y)^z,x]In[10]:= D[(x*y)^z,z]Out[8]= z xy y z +-1)(Out[9]= z xy x z +-1)(Out[10]= ][)(xy Log xy z2 求下列函数的偏导数或导数。
Mathematica数学实验——极限和导数

Mathematica数学实验——极限和导数教师指导实验4实验名称:极限和导数的运算⼀、问题:求⼀元函数的极限和导数。
⼆、实验⽬的:学会使⽤Mathematica 求数列和⼀元函数的极限(包括左极限、右极限),会求⼀元函数的导数,及利⽤导函数求原函数的单调区间和极值。
三、预备知识:本实验所⽤的Mathematica 命令提⽰1、Limit[f,x →x 0] 求函数f(x) 在x →x 0时的极限;2、Limit[f,x →x 0,Direction →-1] 求函数f(x) 在x →x 0时的右极限;Limit[f,x →x 0,Direction →1] 求函数f(x) 在x →x 0时的左极限; 3、D[f, var] 求函数f(x) 对⾃变量var 的导数;SetAttributes[k,Constant] 设定k 为常数;4、FindMinimum[f, {x, x 0}] 从x 0出发求函数f(x)的⼀个极⼩值点和极⼩值。
四、实验的内容和要求:1、求数列的极限1lim 1nn n →∞??+ 、11lim (1)nn i i i →∞=+∑;2、求函数的极限0sin lim x xx →、/2lim tan x x π→+;1lim (1)x x x e →∞-3、求下列函数的导数;sin cos n x nx ?、2cos ln x x ?、2(sin )(cos2)f x f x +4、求函数2()2ln f x x x =-的导数,求其单调区间和极值。
五、操作提⽰1、求数列的极限1lim 1nn n →∞+ 、11lim (1)nn i i i →∞=+∑;In[1]:= Limit[?n11+n ,n->Infinity]Out[1]= e In[2]:= Limit[∑ni=11i(i+1),n->∞] Out[2]= 12、求函数的极限0sin lim x xx→、/2lim tan x x π→+;1lim (1)x x x e →∞-In[3]:= Limit[Sin[x]x,x->0]Out[3]= 1In[4]:= Limit[Tan[x],x->Pi/2,Direction->-1] Out[4]= -∞ In[5]:= Limit[x(E^1 x-1),x->Infinity] Out[5]= 13、求下列函数的导数;sin cos nx nx ?、2cos ln x x ?、2(sin )(cos2)f x f x +In[6]:= D[Sin[x]^n Cos[nx],x] Out[6]= nCos[nx]Cos[x]Sin[x]-1+nIn[7]:= ?x (Cos[x]^2 Log[x])(注:?x 可以在基本输⼊输出模板中输⼊)Out[7]=2Cos[x]-x2Cos[x]Log[x]Sin[x] In[8]:= D[f[Sin[x]^2]+f[Cos[2x]]]Out[8]= -2Sin[2x]f ’[Cos[2x]]+2Cos[x]Sin[x]f ’[Sin[x]2]4、求函数2()2ln f x x x =-的导数,求其单调区间和极值。
整理mathematica数学常用命令大全
Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注:上面的关系运算符也可从基本输入工具栏输入。
如何用mathematica求多项式的最大公因式和最小公倍式如何用mathematica求整数的最大公约数和最小公倍数如何用mathematica进行整数的质因数分解如何用mathematica求整数的正约数如何用mathematica判断一个整数是否为质数n个质数如何用mathematica求第如何用mathematica配方Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。
如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同,格式如下:下列命令可以生成特殊的集合:如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注:方程的等号必须用:= =如何在Mathematica中解方程组Solve[{方程组},{变元组}]注:方程的等号必须用:= =如何在Mathematica中解不等式先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve` 然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效,但对自定义的函数不起任何作用,也许是方法不对。
mathematical用法大全实用版

M a t h e m a t i c a l用法大全实用版(总1页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--Mathematica for Windows 用法一、Mathematica的主要功能Mathematica是美国Wolfram公司开发的一个功能强大的计算机数学系统,提供了范围广泛的数学计算功能,主要包括三个方面:符号演算、数值计算、图形。
例如:多项式的四则运算、展开、因式分解,有理式的各种计算,有理方程、超越方程的解,向量和矩阵的各种计算,求极限、导数、极值、不定积分、定积分、幂级数展开式,求解微分方程,作一元、二元函数的图形等等。
二、Mathematica的基本知识1.输入表达式:直接输入一个表达式(包括算式和命令,长表达式用“Enter”换行)后,按“Shift+Enter”执行,执行后以“Out[命令序号]= ……”形式输出执行结果,输出的结果可在后续的表达式中使用。
若命令后有分号,则不输出执行结果(图形输出与Print命令除外)。
“%”表示上一个输出,“%%”表示倒数第2个输出,“%i”表示第i个命令的输出。
2.运算符:+、-、*、/、^ ,“*”可用空格代替,“^”表示乘方。
如:In[1]:=2^10,输出为“Out[1]= 1024”,其中“In[1]:=”不需要输入。
In[2]:=3+5,Out[2]= 8;In[3]:=%-2,Out[3]= 6;In[4]:=%2+4,Out[4]= 12;In[5]:=1/3-1/4,Out[5]=121;In[6]:=N[%],Out[6]= ; In[7]:=N[%5+12,10],Out[7]= (注意字母的大小写)3.变量赋值:变量=表达式,“x=.”或Clear[x] 表示清除对x 的赋值。
表达式/.t ->c ,将表达式中的t全替换成c。
x,查x信息。
4.常用的数学常数:Pi (π)、E(e)、Infinity (∞)、I (1-) 5.常用的数学函数:Abs, Sin, Cos, Tan, Cot, ArcSin, Log (自然对数), Sqrt, Exp如:In[1]:=Sqrt[2]+1;In[2]:=Sin[2]+ArcSin[1];In[3]:=Exp[2]+%(自变量用[]括,区分大小写,首字母大写)三、常用运算1.多项式运算:In[1]:= (2+4*x^2)*(1-x)^3或 In[1]:= t = (2+4*x^2)*(1-x)^3 (将右端表达式赋值给t);In[2]:=a=t/.x->4 (计算表达式t当x=4时的值,并赋值给变量a )In[3]:=a=. (清除变量a )In[3]:=Expand[t](展开);In[4]:=Factor[%](把上一个结果因式分解)2.解方程:In[1]:=Solve[x^2+3*x = = 2];In[2]:=N[%];In[3]:=Solve[a*x-b= = 0, x];In[4]:=NSolve[{x-2*y= =0,x^2-y= =1},{x,y}](解方程组并得到数值解) 3.自定义函数:In[1]:= f [x_ ]:=x^2+2*x ;In[2]:=f[5]+7; In[3]:=f[a+b]4.求极限:In[1]:=Limit[Sin[x]/x, x ->0];In[2]:=Limit[(1+1/n)^n, n->Infinity],Out[2]=E5.求(偏)导数:In[1]:=D[a*x^2+3, x];In[2]:=D[x^2+y^3-Sin[2*y], y](对y的偏导数); In[3]:=D[Log[x], {x,2}](求对x的二阶导数);In[4]:=D[Sin[x+y]*Exp[z*y^2],x,y] (求对x、y的二阶混合偏导数);In[5]:=Simplify[%] (对前一结果化简);In[6]:=D[Sin[x+y]*Exp[z*y^2],{x,2},{y,3}]6.求不定积分:In[1]:=Integrate[x^2,x];In[2]:=Integrate[1/(x^2+a^2),x]7.定积分:In[1]:=Integrate[x^2, {x,0,1}];In[2]:=Integrate[x^2,{x,a,b}];In[3]:=Integrate[x^2+y^2, {x,0,a},{y,0,b}];(求矩形域上的二重积分)In[4]:=Integrate[1, {x,-1,1},{y,-Sqrt[1-x^2],Sqrt[1-x^2]}];Out[4]=Pi(圆面积)8.幂级数展开:In[1]:=Series[Exp[x],{x,0,4}](在x=0处展开到x的四次幂)9.矩阵的输入和输出:In[1]:= a ={{1,2},{3,4}}(定义一个2x2的矩阵a ,按行写);In[2]:=MatrixForm[a](输出为矩阵形式);In[3]:=Transpose[a](a的转置);In[4]:=a[[2]](a的第2行);In[5]:=Tanspose[a][[2]](a的第2列);In[6]:=Inverse[a](求a的逆矩阵);In[7]:=Det[a](矩阵的行列式);In[8]:=Eigenvalues[a](求特征值);In[9]:=Eigenvectors[a](求特征向量);In[10]:=RowReduce[a](把a化为阶梯形,可用于求矩阵的秩、判断线性相关性); In[11]:= b ={{5,6,7},{8,9,10}};In[12]:= (矩阵a与b的乘积)10.解线性方程组:In[1]:= a={{3,4,5,6},{6,8,10,12},{4,5,6,7},{5,6,7,8}};(a的秩为2)In[2]:= b ={1,2,3,5}(列向量);(增广矩阵的秩也为2)In[3]:=LinearSolve[a,b](求线性方程组ax=b的一个特解);In[4]:=NullSpace[a](求线性方程组ax=0的一个基础解系);In[5]:= x =k1%4[[1]]+k2%4[[2]]+%3(ax=b的全部解,k1、k2为任意常数)11.求和:In[1]:=NSum[Sin[n]/n^3,{n,1,Infinity}](求级数∑∞=13sinnnn的和)12.求极小值:In[1]:=FindMinimum[Sin[x]*Cos[x],{x,}](求函数在附近的极小值);In[2]:=FindMinimum[Sin[x*y]*Exp[x^2],{x,}, {y,}](求多元函数极小值)13.求解线性规划问题:Min cx,mx≥b,x≥0,求向量x 。
§7用Mathematica求偏导数与多元函数的极值演习参考解答.doc

§10用Mathematica 求偏导数与多元函数的极值练习参考解答求下列函数的偏导数。
、八 rz^du du du、 x设 2 = /(兀+)“儿一),求y求下列方程所确定的隐函数的导数。
心+ 3*八4 = 0,求另。
e-—2+=0,求埶 |z = /(x + y + syz),求牛,字 dx dy x1+ b +八=a 2,x 2 + y 2=ax,求函数/(x.y) = x 2 +5)“ -6x + 10y+ 6 的极值。
求函数z = X 2 -y 2,在{(x,y)\x 2 + y 2 W 4}范围内的最大最小值。
练习参考解答 1求下列函数的偏导数。
(1) z(2) z=e■V丁 丄 z * (3) u = —I ---------X X z求下列函数的偏导数或导数。
⑷ u = (xy)(I)设 z = arct^{xy\ y = e x设z =兀ln(xy),求上-〜dx zy , 刁Qodx, 设"臼"求鲁,&dvdz ~d x(1)/ (2) 2 =严(3) «=2 + --- (4) u = (xy)z&Sy? X X Z解⑴ In[l]:= D[l/Sqrt[x A2+y A2,x]In[2]:= D[l/Sqrt[x A2+y A2,y]Out[2]=- (宀)计Out[ 11=-⑵ In[3]:= D[E A(x*y),x]In[4]:= D[E A(x*y),x]Out[3J= KyOut[4]=严兀(3)Inf5]:= D[y/x+z/x-x/z,x] In ⑹:二D[y/x+z/x-x/z,y] In[7]:=D[y/x+z/x-x/z,z]Out[5]= -鸟-丄-二X z zOut[6]=-XC 「F 1 XOut[7]= —+ —x 百(4)In[8]:= D[(x*y)A z,x]In[9]:= D[(x*y)A z,x]In[10]:= D[(x*y)A z,z]Out[8]= y(xyy i+z zOut[9]= x(x)^y[+z zOut[10]= (xy)z Log[xy]2求下列函数的偏导数或导数。
Mathematica软件在多元函数微分学中的应用

Mathematica软件在多元函数微分学中的应用
辛春元
【期刊名称】《山东农业工程学院学报》
【年(卷),期】2013(000)006
【摘要】本文主要介绍Mathematica软件的计算功在求多元函数偏导数、全微分、二元函数极值中的应用,以及作图功能在做曲面的切平面、方向导数、梯度和等高线中的应用.以此激发学生的学习兴趣,提高教学质量.
【总页数】2页(P)
【作者】辛春元
【作者单位】辽宁对外经贸学院,辽宁大连,116052
【正文语种】中文
【中图分类】TP31
【相关文献】
1.Mathematica软件在多元函数微分学中的应用
2.转化思想在多元函数微分学教学中的应用
3.多元函数微分学于经济分析中的应用探究
4.连续归纳法在多元函数微分学中的应用
5.类比法在多元函数微分学构造反例教学中的应用
因版权原因,仅展示原文概要,查看原文内容请购买。
Mathematica求函数的极值线性规划(精品)

第七章求极值及解线性规划问题命令与例题在一些实际问题中, 经常遇到需要知道某个已知函数(带有条件约束或不带条件约束)在哪些点取得极大值或极小值的问题,所考虑的已知函数常称为目标函数,Mathematica 提供了求目标函数的局部极小值命令和线性规划(即带有线性条件约束的线性目标函数在约束范围内的极小和极大值)命令。
7.1求函数的局部极值Mathematica只给出了求局部极小值的命令,如果要求局部极大值只要把命令中的目标函数加上负号即可,即把“目标函数”变为“-目标函数”就可以求局部极大值了。
Mathematica求函数局部极小值的一般形式为:FindMinimum [目标函数, {自变量名1,初始值1}, {自变量名2,初始值2},…]具体的拟合命令有:命令形式1:FindMinimum [f[x], {x, x0}]功能:以x0为初值, 求一元函数f(x)在x0附近的局部极小值。
命令形式2:FindMinimum [f[x], {x, { x0 , x1}}]功能:以x0和x1为初值,求一元函数f(x)在它们附近的局部极小值。
命令形式3:FindMinimum [f[x], {x, x0 , xmin,xmax }]功能:以x0为初值, 求一元函数f(x)在x0附近的局部极小值, 如果中途计算超出自变量范围[xmin,xmax], 则终止计算。
命令形式4:FindMinimum [f[x,y,...], {x, x0},{y, y0},…]功能:以点(x0, y0,…)为初值, 求多元函数f(x,y,…)在(x0, y0,…)附近的局部极小值。
注意:1)所有命令结果显示形式为:{极小值, {自变量-> 极小值点}}2)把上面命令中的目标函数f[…]写为–f[…],对应的命令就可以用来求局部极大值了,但要注意的是此时求出的结果是–f[…]的局部极小值,因此,还要把所求出的极小值前面加上负号才是所要的局部极大值。
用Matlab软件求多元函数的偏导数和极值

数学实验五 用Matlab 软件求多元函数的偏导数和极值一、多元函数的偏导数1.调用格式一:diff('多元函数','自变量',n)其中,n 为所求偏导数的阶数.例1 已知y x z 2cos 2=,求x z ∂∂、x y z ∂∂∂2和22y z ∂∂. 解 打开M文件编辑窗口,在其中输入下面命令集:pzpx=diff('x^2*cos(2*y)','x')p2zpypx=diff(pzpx,'y')p2zpy2=diff('x^2*cos(2*y)','y',2)取名为exa9保存,再在命令窗口中输入命令exa9,程序运行结果如下:pzpx =2*x*cos(2*y)p2zpypx =-4*x*sin(2*y)p2zpy2 =-4*x^2*cos(2*y)即y x x z 2cos 2=∂∂,y x x y z 2sin 42−=∂∂∂,y x yz 2cos 4222−=∂∂. 2.调用格式二:syms x y z …diff(f,自变量,n)例2 已知)5sin(32z y x u +−=,求x u ∂∂、x y z u ∂∂∂∂3和33z u ∂∂. 解 在命令行中依次输入:syms x y zu=sin(x^2-y^3+5*z);ux=diff(u,x);uxy=diff(ux,y);uxyz=diff(uxy,z);uz3=diff(u,z,3);ux,uxyz,uz3运行结果如下:ux =2*cos(x^2-y^3+5*z)*xuxyz =30*cos(x^2-y^3+5*z)*y^2*xuz3 =-125*cos(x^2-y^3+5*z)即)5cos(232z y x x xu +−=∂∂,)5cos(303223z y x xy x y z u +−=∂∂∂∂, )5cos(1253233z y x zu +−−=∂∂. 二、隐函数的导数在Matlab 中没有直接求隐函数导数的命令,但可调用Maple 中求隐函数导数的命令,调用格式如下:maple('implicitdiff(f(u,x,y,z,…,)=0,u,x)')例3 求由多元方程xyz z y x =++222所确定的隐函数dxz ∂. 解 在命令行中输入:pzpx=maple('implicitdiff(x^2+y^2+z^2-x*y*z=0,z,x)')运行结果是:pzpx =(2*x-y*z)/(-2*z+x*y)即 zxy yz x x z 22−−=∂∂. 三、多元函数的极(或最)值在Matlab 中同样有求多元函数的极(或最)小值的函数,但由于多元函数的形式比较复杂,不同情况用到不同的Matlab 函数.若要求多元函数u 在某一区域的极(或最)大值,可转化为求u −在该区域内的极(或最)小值.1.非线性无约束情形求极(或最)小值点或极(或最)小值的调用格式是:[x,fval]=fminsearch(‘f ’,x0)f 是被最小化的目标函数名,x0是求解的初始值向量.例4 求二元函数2331042),(y xy xy x y x f +−+=的最值点和最值.解 打开M文件编辑窗口,在其中输入下面命令集:%必须对自变量进行转化x=x(1),y=x(2)[Xmin,fmin]=fminsearch('2*x(1)^3+4*x(1)*x(2)^3-10*x(1)*x(2)+x(2)^2',[0,0]);[Xmax,Fmin]=fminsearch('-2*x(1)^3-4*x(1)*x(2)^3+10*x(1)*x(2)-x(2)^2',[0,0]);fmax=-Fmin;Xmin,fminXmax,fmax取名为exa10保存,再在命令窗口中输入命令exa10,程序运行结果如下:Xmin =1.0016 0.8335fmin =-3.3241Xmax =-1.0000 1.0000fmax =2.非线性有约束情形非线性有约束优化问题的数学模型如下:式中,x,b,beq,lb 和ub 是向量,A 和Aeq 是矩阵,c(x)和ceq(x)为函数,返回标量.f(x),c(x)和ceq(x)可以是非线性函数.求极(或最)小值点或极(或最)小值的调用格式如下:[x,fval]=fmincon('fun',x0,A,b,Aeq,beq,lb,ub,nonlcon)nonlcon 参数计算非线性不等式约束c(x)<=0和非线性等式约束ceq(x)=0.例5 求表面积为6m 2的体积最大的长方体体积.解 设长方体的长、宽、高分别为x1、x2、x3,则f(x)=-x(1)*x(2)*x(3),S.t x(1)*x(2)+x(2)*x(3)+x(3)*x(1)-3=0,x(i)>0,i=1,2,3.⑴ 建立函数文件fun1打开M文件编辑窗口,在其中输入下面命令集:function F=fun1(x) %函数文件必须是function 开头F=-x(1)*x(2)*x(3);单击“保存”按钮,自动取名为fun1,再击保存.⑵ 建立非线性约束函数文件yceqfunction [c,ceq]=yceq(x)c=x(1)*x(2)+x(2)*x(3)+x(3)*x(1)-3;ceq=[];保存方法同上,自动取名为yceq ,再击保存.⑶ 编制主程序:打开M文件编辑窗口,在其中输入下面命令集:x0=[3;3;3]; %给长宽高一个初值A=[];b=[];Aeq=[];beq=[];lb=[0,0,0];ub=[];[xmax,fmin]=fmincon('fun1',x0,A,b,Aeq,beq,lb,ub,'yceq'); %函数要加单引号Vmax=-fmin;xmax,Vmax取名为exa11保存,再在命令窗口中输入命令exa11,程序运行结果如下:xmax =1.00001.00001.0000Vmax =ubx lb beqx Aeq bx A x ceq x c x f Min ≤≤≤⋅≤⋅=≤0)(0)()(四、上机实验1.用help命令查看函数diff,fminsearch和fmincon等的用法.2.上机验证上面各例.3.作相关小节练习中多元函数的偏导数,极(或最)值.。
用Mathematica求偏导数与多元函数的极值.docx
§10用Mathematica求偏导数与多元函数的极值10. 1用Mathematica作三维函数图在多元函数微积分小,作图可以使得问题更为直观,易于理解。
这里首先给大家介绍"用Mathematica作三维函数图”。
1常用的三维绘图函数Plot3D[f[x,y], {x,a,b}, {y,c,d},可选项]:作 /(兀,刃的图形。
ParametricPlot3D [ {x[u, v] ,y [u, v] ,z[u,v]}, {u,a,b} {v,c,d}]: 作三维参数方程的图形。
Show[fl,f2,f3,・・・]:将多个图形组合重新显示。
2常用的可选项Plot3D函数有许多可选项可以用来修饰三维图形的外观。
可以借助于可选项改变图形的外观,以便于观察。
表10・1常用的可选项选择合适的观测点在也有助于观察图形,下面是典型的Viewpoint值: 表10・2典型的VicwPoint值例10.1画出函数Z = sin7x2 + y2图形,并使图形表面不上色。
解In[l]:= Plot3D[Sin[Sqrt[xA2+yTH,{x,0,2Pi},{y,0,2Pi}]Out[l]= -SurfaceGraphics-In[2]:= Show[%,Shading->False]60?226Out[2]= -SurfaceGraphics-例10・2 |Hii岀函数Z二sinxcosy图形,并使调整图形观测点观察图形是否对称。
解In[l]:=Plot3D[Sin[x*y],{x,0,2Pi},{y,0,2Pi},AxesLabel->{“x”,”y”,”z”}]Out[l]= -SurfaceGraphics-In[2]:= Show|%,ViewPoint->{-1,-1,2}]0 0Out[2]= -SurfaceGraphics-例10.3画一单位双曲面。
解首先,写出单位双曲面的参数方程厂x=Cosh[u]*Cos[v]y y=Cosh[u]*Sin[v]< z=uIn[l]:=ParametricPlot3D[{Cosh[uFCo§[v],Cosh[uFSin[v],u},{iiQPi},{v,・Pi,Pi},AxesLabel・>{“x”,”y”,”z”}]Out| 1 ]= -Graphics3D-2 2 2例MU画出函数py話“图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§10 用Mathematica求偏导数与多元函数的极值10.1 用Mathematica 作三维函数图在多元函数微积分中,作图可以使得问题更为直观,易于理解。
这里首先给大家介绍“用Mathematica作三维函数图”。
1 常用的三维绘图函数Plot3D[f[x,y],{x,a,b},{y,c,d},可选项]: 作)f的图形。
x(y,ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},{u,a,b}{v,c,d}]: 作三维参数方程的图形。
Show[f1,f2,f3,…]: 将多个图形组合重新显示。
2 常用的可选项Plot3D函数有许多可选项可以用来修饰三维图形的外观。
可以借助于可选项改变图形的外观,以便于观察。
表10-1 常用的可选项选择合适的观测点在也有助于观察图形,下面是典型的ViewPoint 值:表10-2 典型的ViewPoint 值例10.1 画出函数22sin y x z +=图形,并使图形表面不上色。
解 In[1]:= Plot3D[Sin[Sqrt[x^2+y^2]],{x,0,2Pi},{y,0,2Pi}]Out[1]= -SurfaceGraphics- In[2]:= Show[%,Shading->False]Out[2]= -SurfaceGraphics-例10.2 画出函数y图形,并使调整图形观测点观察图形是否对称。
sinxz cos解In[1]:= Plot3D[Sin[x*y],{x,0,2Pi},{y,0,2Pi},AxesLabel->{“x”, “y”, “z”}]Out[1]= -SurfaceGraphics-In[2]:= Show[%,ViewPoint->{-1,-1,2}]Out[2]= -SurfaceGraphics-例10.3 画一单位双曲面。
解 首先,写出单位双曲面的参数方程x=Cosh[u]*Cos[v] y=Cosh[u]*Sin[v] z=uIn[1]:=ParametricPlot3D[{Cosh[u]*Cos[v],Cosh[u]*Sin[v],u},{u,0,Pi},{v,-Pi,Pi},AxesLabel->{“x ”, “y ”, “z ”}]Out[1]= -Graphics3D-例10.4 画出函数11634222=++z y x 图形。
解 In[1]:=ParametricPlot3D[{2Sin[u]*Cos[v],3Sin[u]*Sin[v],4Cos[u]},{u,0,Pi},{v,-Pi,Pi},AxesLabel->{x, y, z}]Out[1]= -Graphics3D-In[2]=: Show[%,ViewVertical->{1,0,0}]Out[2]=-Graphics3D-例10.5 画出由02=+y x 与1)1(22=+-y x 所围的立体图形。
解 In[1]:= a1=Plot3D[x+2y,{x,0,2},{y,0,2},DisplayFunction->Identity]; a2=ParametricPlot3D[{1+Cos[u],Sin[u],v},{u,0,2Pi},{v,0,3.5},DisplayFunction->Identity];a3=Plot3D[0,{x,-1,2},{y,-1,2},DisplayFunction->Identity]; Show[a1,a2,a3,AxesLabel->{x, y},AspectRatio->Automatic,PlotRange->{0,4},DisplayFunction->$DisplayFunction]Out[1]= -Graphics3D-9.2 用Mathematica 求偏导数与多元函数的极值函数[]x n x Dt ,^实际上给出了偏导数,在这个表达式中,假设n 个不是x 的函数,在Mathematica 中,它有一个函数Dt ,它代表的是全微分,在这个函数中,所以的变量都有联系。
在Mathematica 的说明中,[]x f D ,代表了x f ∂∂,而[]x f Dt ,则代表了dxdf 。
可以认为Dt 表示了“全微分”。
例如:1. 下面给出了一个全微分,其中n 是x 的函数,[]x f Dt ,则代表了dxdf。
])log[],[(]1[],^[:]1[x x n Dt xnx Out x n x Dt In n+== 2. 下面是一个全微分。
其中[]x f Dt ,代表了dx 。
])log[][][(]2[]^[:]2[x n Dt xx nDt x Out n x Dt In n +== 注:在Mathematica 中,还是有些微分函数用于直接计算的,如下表所示: 表10-3 部分的微分函数例10.6 求下列函数对x 的偏导数1. ()22ln y x x u ++=; 2. xyyx arctgu -+=1; 3. xyeu s i n = ; 4. u=zy x ⎪⎪⎭⎫⎝⎛。
解In[1]:= D[Log[x+Sqrt[x^2+y^2] ],x];Simplify[%] (*通常Mathematica 不自动化简微分结果,要借助于Simplify 函数*)Out[1]=221yx +In[2]: = D[ArcTanh[(x+y)/(1-x*y)],x];Simplify[%]Out[2]= )22221(411y x y xy y +-+--+ In[3]: = D[E^Sin[y/x],x]; Simplify[%]Out[3]= 2x x y yCos ex y Sin ⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡ In[4]: = D[(x/y)^z,x]; Simplify[%]Out[4]= xzy x z⎪⎪⎭⎫ ⎝⎛例10.7 设x y y x z sin sin 33+=,求y z ∂∂,1,1==∂∂y x yz, 22x z ∂∂,336yx z∂∂。
解 In[1]:= Clear[z,x,y];z[x,y]:=x^3*Sin[y]+y^3Sin[x]; /*定义二元函数.*/ D[z[x,y],y]Out[1]= ][3][23x Sin y y Cos x +In[2]:= D[z[x,y],y]/.{x->1,y->1} /*给函数的变量赋值.*/ Out[2]= ]1[3]1[Sin Cos + In[3]:= D[z[x,y],{x,2}] Out[3]= ][6][3y xSin x Sin y +- In[4]:= D[z[x,y],{x,3},{y,3}] Out[4]= ][6][6y Cos x Cos +-例10.8 设v u y y u x y x z 23,,ln 2-===,求u z ∂∂,v z∂∂,22vz ∂∂。
解 In[1]:= x[u_,v_]:=u/v;y[u_,v_]:=3u-2v;z[x_,y_]:=x[u,v]^2*Log[y[u,v]]; D[z[x,y],u]; Simplify[%]Out[1]=2])23[2233(v v u Log v u uu -+- In[2]:= D[z[x,y],v];Simplify[%]Out[2]=3])23[23(22v v u Log v u vu ---In[3]:= D[z[x,y],{v,2}];Simplify[%]Out[3]= 4222)23(])23[)23(3)56(2vv u v u Log v u v v u u ---+- 例10.9 设),()2(xy x g y x f z +-=,其中函数()f t 二阶可导,(,)g u v 具有二阶连续的偏导数,求x z∂∂,22x z ∂∂,yx z ∂∂∂2。
解 In[1]:= D[f[2x-y]+g[x,x*y],x]Out[1]= ],[],[]2['2)1,0()1,0(xy x g xy x yg y x f ++- In[2]:= D[f[2x-y]+g[x,x*y],{x,2}] Out[2]=],[]),[],[(],[]2[''4)0,2()1,1()2,0()1,1(xy x g xy x g xy x yg y xy x yg y x f ++++-In[3]:= D[f[2x-y]+g[x,x*y],x,y]Out[3]= ]),[],[],[]2[''2)1,1()2,0()1,0(xy x xg xy x xyg xy x g y x f +++--其中u g v u g ∂∂为],[)0,1(,v g v u g ∂∂为],[)1,0(,v u g v u g ∂∂∂为],[)1,1(,2)0,2(],[ug v u g ∂∂为,2)2,0(],[vg v u g ∂∂为。
例10.10 已知函数)(xyxF xy z +=,证明xy z y z yx z x +=∂∂+∂∂。
解 In[1]:= z=x*y+x*F[y/x];D[z,x]*x+y*D[z,y]-z-x*y; Simplify[%] Out[1]= 0例10.11 求由下列方程所确定的隐函数和导数或偏导数: 1.xyarctgy x =+22ln , 求dy dx 。
2.u v u y u v u x sin ,cos ==,求x u ∂∂,y u ∂∂,xv∂∂,y v ∂∂。
解 In[1]:= eq1=Log[Sqrt[x^2+y[x]^2]= = ArcTanh[y[x]/x];D[eq1,x]; Solve[%,y′ [x]]; Simplify[%]Out[1]= ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧++-+-+→32233223][][][][][][]['x y x xy x y x x x y x xy x y x x x y In[2]:= D[{x==u[x]*Cos[v[x]/u[x]],y==u[x]*Sin[v[x]/u[x]]},x]; Simplify[Solve[%,{u′ [x],v ′[x]}]]Out[2]= ⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧+-→→][][]][][[]][][[]['],][][[]['x u x v x u x v Cos x u x v Sin x v x u x v Cos x uIn[3]:= D[{x==u[y]*Cos[v[y]/u[y]],y==u[y]*Sin[v[y]/u[y]]},y]; Simplify[Solve[%,{u′ [y],v ′[y]}]]Out[3]= ⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧+→→][][]][][[]][][[]['],][][[]['y u y v y u y v Sin y u y v Cos y v x u x v Sin y u例10.12 求下列极值问题:1.函数y x xy x y x f 12153),(3--+=.2.求函数y y x y x f 1612),(22+-+=,在2522≤+y x 上的最大最小值. 解 1. In[1]:= Clear[x,y,z,a,b,c,d,t];f[x_,y_]:=x^3+3*x*y^2-15x-12y;a=D[f[x,y],{x,2}];b=D[f[x,y],x,y];c=D[f[x,y],{y,2}];d=a*c-b^2;t=Slove[{D[f[x,y]= =0,x],D[f[x,y]= =0,y]},{x,y}];l=Length[t]lFor[i=1,i<=1,i++,Print[t[[i]];d1=d/.t[[i]];a1=a/.t[[i]];z=f[x,y]/.t[[i]];Which[d1>0&&a1<0,Print[“fmax=”,z],d1>0&&a1>0,Print[“fmin=”,z],d1= =0,Print[“No Sure”,z],d1= =0,Print[No]]]Out[1]= {x->-2,y->-1}fmax=28{x->-1,y->-2}No{x->1,y->2}No{x->-2,y->-1}fmin=-282. 先求(,)f x y 在圆域内2522<+y x 的最大最小值:In[2]:= f[x_,y_]:=x^2+y^2-12x+16y;t=Solve[{D[f[x,y]= =0,x],D[f[x,y]= =0,y]},{x,y}]Out[2]={{x->6,y->-8}} (*驻点*) In[3]:= x^2+y^2-25/.t[[1]]Out[3]=75该驻点在圆外,圆内无驻点,故不取极值。
