电磁场数值计算作业报告
武大电气工程电磁场实验报告(90分精品)

工程电磁场实验报告电气工程学院XXX2014302540XXX平行输电线电场计算1.问题描述:导线半径0.01m,导线对地高度为10m,导线间距为5m,每根导线对地电压为6V,6根导线平行放置,建立模型并求解电场分布。
2.创建项目,选择求解类型(1)启动并建立项目文件(2)重命名并保存(3)选择分析类型和求解器新建工程文件,单击菜单命令Project/Insert Maxwell 2D Design,或者单击工具栏上的图标。
执行菜单命令Maxwell 2D/Solution Type,在弹出的对话框中选择求解类型Electrostatic,如图2-1所示:图2-1 选择求解器类型3.绘制几何模型(1)设置绘图单位执行菜单命令Modeler/Units,根据需要进行单位设置。
本例中单位为m。
(2)绘制模型(a)绘制导线绘制导线1:点击快捷键(或者执行命令Draw/Circle),绘图区下方坐标状态栏输入(-2.5,10,0)后回车,此时坐标(X,Y,Z)变为(dX,dY,dZ),在其中输入(0,0.01,0),如图3-1所示,回车则会出现面圆Circle1。
图3-1 第一根导线坐标示意图同理,绘制导线2-6,导线2的圆心坐标为(-7.5,10,0),半径为(0,0.01,0);导线3的圆心坐标为(-12.5,10,0),半径为(0,0.01,0);导线4的圆心坐标为(2.5,10,0),半径为(0,0.01,0);导线5的圆心坐标为(7.5,10,0),半径为(0,0.01,0);导线6的圆心坐标为(12.5,10,0),半径为(0,0.01,0);(b)绘制求解区域执行菜单命令Draw/Circle或单击工具栏上的,输入坐标(0,0,0)回车,输入(0,62.5,0)回车确认,得到cricle7。
只选择上半区域进行求解,选中circle7,执行菜单命令Modeler/Boolean/Split或单击工具栏上的,选择XZ平面,点击确定,如图3-2所示。
电磁场实验报告

电磁场实验报告电磁场实验报告一、实验题目:用有限差分法求解金属槽内电位分布一足够长(忽略边缘效应)的方形金属槽,边宽1m ,除顶盖电位为100sin x πV外,其他三方的电位均为零,求槽内电位分布二、数学原理有限差分法(Finite Differential Method )是基于差分原理的一种数值计算法。
有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点; 把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似; 把原方程和定解条件中的微商用差商来近似, 积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组, 解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
对于简单迭代法有如下公式φ( i , j) = (φ( i- 1 , j) +φ( i+1 , j) +φ( i , j - 1) +φ( i , j+1) )*1/4 三、编程计算=?= 100sin x π=?0=?实验代码如下:u=zeros(21,21); %定义数组w=0; %赋初值for j=1:21;u(1,j)=100*sin((j-1)*pi/20);w=w+u(1,j);endfor i=2:20for j=2:20u(i,j)=w./20;endendu %打印数组un=1000; %简单迭代1000次for w=1:n;for i=2:20;for j=2:20;a=u(i+1,j);b=u(i,j+1);c=u(i-1,j);d=u(i,j-1);u(i,j)=0.25.*(a+b+c+d); %简单迭代法endendendu %打印数组u(11,11) %打印点(0.5,0.5)x=1:-0.05:0; y=1:-0.05:0;[x,y]=meshgrid(x,y); %画图mesh(x,y,u) hold offgrid onxlabel('0<x<1')< p="">ylabel('0<y<1')< p="">zlabel('0<u<100')< p="">四、计算结果: u的值如下ans =19.9858 说明u (11,11)=19.98580<1<="" p="">0<y<1< p="">0<100<="" p="">五、实验分析由图像知u关于x=0.5对称且y=1时u关于x的表达式变为100sin xπ,与该图像相符,因此结果是正确的六、实验心得与思考通过设计程序并进行完善调试,我对有限差分法有了进一步的认识,这次的代码是针对于特定题目编出的程序,如果边值条件有所改变那么代码也得改变,显得不是很方便。
电磁场数值计算上机题报告

电磁场数值计算上机题报告第一题计算长直接地金属槽中的电场分布。
金属槽横截面如图1所示,其侧壁与底面电位均为零,顶盖电位相对值为10。
槽内电位函数满足拉普拉斯方程。
计算槽内电位分布。
要求:(1)先用正方形网格粗分,每边取4个网格计算,取不同的松弛因子,比较其收敛速度。
取计算精度为千分之一。
(2)划分网格加倍,计算电位分布,并与上面计算结果比较。
(一)建立问题的数学物理模型首先列出方程及其边界条件 槽内的电位满足二维的拉普拉斯方程:222220x y ϕϕϕ∂∂∇=+=∂∂其中,x y 的范围是:0,0x a y a <<<<边界条件是:0000;10x x ay y aϕϕϕϕ========图1 (二)算法设计及其实现在本题中,因为区域为正方形区域,网格采用正方形网格,每边四个网格,因此,每边要有5个结点, 网格数m=n=4,比较少,不能用课本中的公式计算收敛因子,取收敛因子为 1.4α=,计算的程序的流程为:①选取计算的场域,并划分网格,网格划分如右图2所示:右图表示网格的划分,共16个网格,一共划分了25个结点,每个节点用相应的下标(i,j )来表示,对应的电位为(,)u i j 。
根据题意,边界条件的 处理如下: 图 2(1,)(,1)(,1)0(,)10(21)u j u i u n u k j k n ===⎧⎨=≤≤-⎩其中n 为一行对应的节点数,根据题意,这里n=5② 用(,)u i j 表示节点的电位,设经过第n 次迭代之后的结点电位用(),n i j u 来表示,则超松弛迭代法的差分格式(记,(,)i j u u i j =)为:(1)()()()(1)(1)(),,1,,11,,1,(4)4n n n n n n n i j i j i j i j i j i j i j u u u u u u u α+++++--=++++- 边界条件前面已经给出 ③给各个节点赋初值,对于非边界上的点(对于边界点的值前面已经赋过初值),如下10(,)(1)1u i j j n =--④迭代计算,直到已经满足精度条件为止,这里精度为0.0001,最后输出计算的结果,输出结果见生成的数据文件shuju.txt 中 ⑤计算框图如图3所示图 3 计算框图⑥用fortran90语言编写计算机程序,计算各点的电位,程序清单如下:(三)计算结果及数据分析当网格数目为4(节点数目为5),加速收敛因子为1.4,计算精度为0.0001时,计算出各结点电位如下所示(对不同的收敛因子的比较后面进行)不可能完全对称,只能是近似对称的),这点不难从理论上进行分析得到。
电磁场实验报告

大连理工大学本科实验报告实验名称:均匀无耗介质介电参数的测量
课程名称:电磁场与电磁波实验
学院(系):电子信息与电气工程学部
专业:电子信息工程
班级:
学号:
学生姓名:
2013年月日
六、实验结果分析
1.完成参数测量,整理并计算出被测样品的rε值,媒质中的电磁波参量β、λ和V。
2.对实验中现象分析讨论,并对实验误差产生的原因进行分析。
七、问题与建议、体会
1.除了上述的运用相干波节点位移法,测试均匀无耗介质的参量rε,你还能设计出其它的方案实现均匀无耗介质参量rε的测试吗?如果可以,请说明测试原理。
2.本测量设定1=
μ进行均匀无耗介质参量rε的测试,可否测量1≠rμ的r
磁介质?请说明原因。
3.对实验的建议与体会。
大连理工大学本科实验报告实验名称:电磁波参量的测量
课程名称:电磁场与电磁波实验
学院(系):电子信息与电气工程学部
专业:电子信息工程
班级:
学号:
学生姓名:
2013年月日
六、实验结果分析
1.完成数据运算及整理,计算出电磁波波长;
2.对实验中的现象分析讨论,并对实验误差产生的原因进行分析。
七、问题与建议、体会
1.思考题:用相干波测电磁波波长时,图1-1中的介质板Pr4放置位置若转90度,将出现什么现象?这时能否测准 值?为什么?
2.对实验的建议与体会。
电磁场数值方法仿真实验报告

电磁场数值方法仿真实验实验项目:FDTD方法模拟电磁波传播班级:姓名:学号:指导教师:实验日期:一、实验目的要求1、了解数值方法的基本原理,熟悉时域有限差分方法(FDTD)的计算思路。
2、学习Matlab语言,学习编程的基本技巧和编程思路。
3、加强对电磁波理论的了解。
4、形象展示电磁波的传播过程。
二、实验内容利用FDTD(时域有限差分法)方法模拟电磁波传播过程三、实验结果四、原程序五、附录(matlab程序)%FDTD_1.1.m. 1D FDTD simulation in free space clear allmax_time = 400;max_space=200;E=zeros(max_space,1); %Initialize Electric arrayH=E; %Initialize Magnetic arraycenter_problem_space=max_space/2; % center of the problem spacet0=40; % center of the incident pulsespread=12; % width of the incident pulsefor n=1:max_time%Inner loop E-Increments electric wave in spacefor k=2:max_spaceE(k)=E(k)+eta *( H(k-1)-H(k) );end%Hardsource-imposes a value on the gridpulse=exp((-0.5)*( (t0-n)/spread )^2);E(center_problem_space )=pulse +E(center_problem_space );for j=1:(max_space-1)H(j)=H(j)+eta*(E(j)-E(j+1));%plot progreesion of the electric wavefigure(1);plot(E);%axis([1 max_space -1.1 1.1]);title('FDTD Simulation of and electric pulse in Free Space');xlabel('problem space');ylabel('E_x');pause(0.00001);end%Plots electric and magnetic fields at max_time figure(2);subplot(2,1,2);plot(E,'r');title('Simulation of Electric Pulse');ylabel('E_x');axis([0 max_space -1.1 1.1]);subplot(2,1,1);plot(H,'g');ylabel('H_y');title('Simulation of Magnetic Pulse');axis([0 max_space -1.1 1.1]);六、心得体会通过这次实验,加深了我对C语言以及MATLAB的理解以及运用,锻炼了我的程序编写能力,同时初步了解了电磁工程仿真与设计的相关知识。
南京理工大学工程电磁场实验报告

MATlAB 绘制等电位线视图如下:
三维图像:
100 80 60 40 20 0 4 3 2 1 1 3 2 4
8
二维图像:
4
3.5 3
2.5
2
1.5
1
0.5 0.5 1 1.5 2 2.5 3 3.5 4
五、实验总结:
通过本次实验,我们在很大程度上把书本上的知识应用于实践中去, 例如 VC++的应用, 是我们第一次把其应用到工程实验上去, 超越了以 往只限于基础原理的学习。另一方面,在画图方面对于 MATlAB 的应 用,让我们初步认识到这款软件功能的强大,也让我们意识到掌握这 门软件的重要性,其在可视化,仿真方面发挥了很大的作用,大大地 帮助我们更深刻地理解和把握工程电磁场这门课程的相关知识。
三、程序设计及其运行情况:
#include<stdio.h> #include<math.h> #include<windows.h> fun(float u[][41],float p) /*此函数即为差分求解的方 法过程*/ {long int i,j,flag=1,num=0;float t,e=p/4; /*定义变量,在此 p 为收敛 因子*/ while(flag) {flag=0; for(i=1;i<40;i++) {for(j=1;j<20;j++) { t=u[i][j]; u[i][j]=u[i][j]+e*(u[i][j-1]+u[i-1][j]+u[i][j+1]+u[i+1][j]4*u[i][j]); if(fabs(u[i][j]-t)>=1e-5) flag=1; /*该判断语句用于判断 u[i][j]前后两次计算之差绝对值是否符合实验误 差要求*/ }u[i][20]=u[i][19]; }num++; } return num; } int main(void) { long int i,j,num=0,min=100000;float q,p,t,eps=1,e=p/4,u[41][41]; for(i=0;i<41;i++) {u[0][i]=100;u[40][i]=0;} /*定义初值*/ for(i=1;i<40;i++) {u[i][0]=u[i][40]=0;} for(i=1;i<40;i++) for(j=1;j<21;j++) u[i][j]=2.5*(j-1); printf("左半边初始值如下:\n"); for(i=0;i<41;i++) {printf("\n"); for(j=0;j<21;j++) { printf("%-11.5f",u[i][j]);
ansoft实验报告

电磁场ansoft软件应用作业姓名学号班级静电场范例:一、题目单心电缆有两层绝缘体,分界面为同轴圆柱面。
已知,R1=10mm,R2=20mm,R3=30mm,R4=31mm,内导体为copper,外导体为lead,中间的介质ε1=5ε0, ε2=3ε0, ,内导体U=100V,外导体为0V求1用解析法计算电位,电场强度,电位移随半径的变化,计算单位长度电容和电场能量。
2用ansfot软件计算上述物理量随半径的变化曲线,并画出电压分布图,计算出单位长度电容,和电场能量二、解答1、解析法:在介质中取任意点P ,设它到电缆中心距离为r 。
过P 点作同轴圆柱面,高为l 。
该面加上上下两底面作为高斯面S 。
Drl S d D S)2(π=⋅⎰ε11DE = ε22DE =⎰⎰+=RR drR R dr U E E 322121将方程联立,代入数据解得:m V r E /05.731≈,m V r E /75.1212≈所以 12921158.8573.05 3.23/1010D C r r mE ε--⨯⨯⨯=⋅==电位rR RR dr dr l d E r rE E ln 05.7341.236232211--=⋅+⋅=⋅=⎰⎰⎰∞ϕ VrR dr l d E rrE ln 75.12192.426322--=⋅=⋅=⎰⎰∞ϕ V电场能量97211 3.23 1.181173.05221010e D r r E rω--⨯⨯=⋅=⋅⋅= 3J m97222 3.23 1.9711121.75221010e D r r E rω--⨯⨯=⋅=⋅⋅= 3J m单位长度电场能量2312776321212222(1.18ln 1.97ln ) 1.02101010e e e R R rdr rdr J m R R R R W R R πππωω---=+=⋅⨯⋅+⨯⋅=⨯⎰⎰单位长度电容6102222 1.0210 2.0410100e W C F m U --⨯⨯===⨯2、ansoft 仿真根据题目的要求,利用Maxwell—2D仿真建立相应的模型。
工程电磁场实验报告上交版

实验报告——叠片钢涡流损耗分析实验目的:1)认识钢的涡流效应的损耗, 以及减少涡流的方法;2)学习涡流损耗的计算方法;3)学习用MAXWELL SV计算叠片钢的涡流。
实验内容:作用在磁钢表面的外磁场Hz=397.77A/m, 即Bz=1T, 要求理论分析与计算机仿真:叠片钢的模型为四片钢片叠加而成, 每一片界面的长和宽分别是12.7mm和0.356mm, 两片之间的距离为8.12um, 叠片钢的电导率为2.08e6S/m, 相对磁导率为2000, 建立相应几何模型, 并指定材料属性, 制定边界条件。
分析不同频率下的涡流损耗。
实验简介:在交流变压器和驱动器中, 叠片钢的功率损耗很重要。
大多数扼流圈和电机通常使用叠片, 以减少涡流损耗, 但是这种损耗仍然很大, 特别是在高频的情况下, 交变设备中由脉宽调制波形所产生的涡流损耗不仅降低了设备的整体性能, 也产生了热。
设计工程师通常采用两种方法预测叠片钢的损耗:使用叠片钢厂商提供的铁耗随频率的变化曲线, 但是往往很难得到这样的曲线;使用简单的计算公式, 公式中的涡流损耗是叠片厚度的函数, 但是这样的公式往往仅在频率为60Hz或更低的频率情况下才是正确的。
而大多数交变电磁设备, 所使用的频率可达千赫兹或兆赫兹, 因此需要用其它的方法预测涡流损耗。
在非常高的频率下, 涡流损耗远大于磁滞损耗, 铁损几乎完全是由涡流引起的。
涡流损耗可以使用有限元法通过数值计算获得。
本实验就采用轴向磁场涡流求解器来计算不同频率下的涡流损耗。
实验步骤:根据实验内容分析建立实验模型, 由于四片叠片钢关于XY轴具有对称性, 故可以只计算第一象限。
定义模型的长宽及两片之间距离, 电导率, 相对磁导率以及外磁场场强之后就可以进行仿真。
通过生成几何模型, 制定材料属性, 指定边界条件和源, 设定求解参数选项极乐进行数据的统计了。
数值计算结果:图一Hz=1Hz时叠片钢的磁场分布图二Hz=60Hz时叠片钢的磁场分布图三Hz=360Hz时叠片钢的磁场分布图四Hz=1kHz时叠片钢的磁场分布图五Hz=2kHz时叠片钢的磁场分布图六Hz=5kHz时叠片钢的磁场分布图七Hz=10kHz时叠片钢的磁场分布1.数值结果与低频损耗计算公式的比较低频涡流损耗的计算公式为P=t2ω2B2σ2/24 V式中, V为叠片体积;t为叠片厚度;B为峰值磁通密度;δ为叠片电导率;ω为外加磁场角频率。
工程电磁场实验报告

一、实验目的a)认识钢的涡流效应的损耗,以及减少涡流的方法;b)学习涡流损耗的计算方法;c)学习用MAXWELL 2D计算叠片钢的涡流。
二、软件环境的使用简介及实验步骤以螺线管电磁阀静磁场分析为例,练习在MAXWELL 2D环境下建立磁场模型,并求解分析磁场分布以及磁场力等数据。
a) 建立项目:其中包括生成项目录,生成螺线管项目,打开新项目与运行MAXWELL 2D。
b) 生成螺线管模型:使用MAXWELL 2D求解电磁场问题首先应该选择求解器类型,静磁场的求解选择Magnetostatic,然后在打开的新项目中定义画图平面,建立要求尺寸的螺线管几何模型,螺线管的组成包括Core、Bonnet、Coil、Plugnut、Yoke。
c) 指定材料属性:访问材料管理器,指定各个螺线管元件的材料,其中部分元件的材料需要自己生成,根据给定的BH曲线进行定义。
d) 建立边界条件和激励源:给背景指定为气球边界条件,给线圈Coil施加电流源。
e) 设定求解参数:本实验中除了计算磁场,还需要确定作用在螺线管铁心上的作用力,在求解参数中要注意进行设定。
f) 设定求解选项:建立几何模型并设定其材料后,进一步设定求解项,在对话框Setup Solution Options进入求解选项设定对话框,进行设置三、实验的结果及理论分析1.不同频率时的最低的磁通密度B和涡流损耗下图是Hz=1Hz和Hz=1kHZ时叠片钢的磁场分布。
图1 Hz=1Hz时叠片钢的磁场分布图1 Hz=1KHz时叠片钢的磁场分布由MAXWELL 2D软件通过有限元分析得出的不同频率出最低的磁通密度B和涡流损耗,见下表。
表不同频率下的B(T)和PF(Hz)Bmin(T)P(W)1 0.999 1.92947e-660 0.999 6.95679e-3360 0.989 2.44296e-11K 0.915 1.648422K 0.732 4.577485K 0.408 9.5638210K 0.096 1.244e1由表格可以知道:频率越大,B的大小越小,磁集肤现象越明显,涡流损耗p会迅速增大。
电磁场理论实验报告

CENTRAL SOUTH UNIVERSITY题目利用Matlab模拟点电荷电场的分布姓名学号班级任课老师实验日期一.实验目的:1.熟悉单个点电荷及一对点电荷的电场分布情况; 2.学会使用Matlab 进行数值计算,并绘出相应的图形;二.实验原理:根据库伦定律:在真空中,两个静止点电荷之间的作用力与这两个电荷的电量乘积成正比,与它们之间距离的平方成反比,作用力的方向在两个电荷的连线上,两电荷同号为斥力,异号为吸力,它们之间的力F 满足: R R Q Q k F ˆ212= (式1) 由电场强度E 的定义可知:R R kQ E ˆ2=(式2) 对于点电荷,根据场论基础中的定义,有势场E 的势函数为 RkQU =(式3) 而 U E -∇= (式4) 在Matlab 中,由以上公式算出各点的电势U ,电场强度E 后,可以用Matlab 自带的库函数绘出相应电荷的电场分布情况。
三.实验内容:(1) 单个正电荷的平面电场线与等势线: 代码如下:a=0.12; k=9*10^9;q=10^(-9);r=0.1; theta=linspace(0,2*pi,13); [x,y]=pol2cart(theta,a) x=[x;0.05*x];y=[y;0.05*y]; plot(x,y);hold onquiver(0.4*x,0.4*y,x,y); hold on u=k*q/r;u1=linspace(1,3,7)*u;x=linspace(-0.1,0.1,100); [X,Y]=meshgrid(x); r1=sqrt(X.^2+Y.^2); U=k.*q./r1;contour(X,Y,U,u1)图一、单个正电荷的等势线和电场线平面图(2)两个等量正电荷的平面电场线与等势线:代码如下:[x,y]=meshgrid(-2:0.2:2,-2:0.2:2); %建立数据网格z=1./sqrt((x-1).^2+y.^2+0.01)+1./sqrt((x+1).^2+y.^2+0.01) ;%k*q1=k*q2=1[dx,dy]=gradient(-z);D= sqrt(dx.^2+dy.^2);dx=dx./D ;dy=dy./D;%进行归一化contour(x,y,z,[-2,-1.8,-1.6,-1.4,-1.2,-1,-0.8,-0.5,-0.1,0.1,0.5,0.8,1,1.2,1.4,1.6,1.8 ,2]);%画等势线hold onquiver(x,y,dx,dy,'r');%画电场线大小和方向xx=[linspace(-2,2,10),2*linspace(1,1,10),linspace(-2,2,10 ),-2*linspace(1,1,10)];yy=[2*linspace(1,1,10),linspace(-2,2,10),-2*linspace(1,1, 10),linspace(-2,2,10)];streamline(x,y,-dx,-dy,xx,yy)图二、两个等量正电荷的等势线和电场线平面图(3)两个不等量正电荷的平面电场线与等势线:[x,y]=meshgrid(-2:0.2:2,-2:0.2:2); %建立数据网格z=1./sqrt((x-1).^2+y.^2+0.01)+1.5./sqrt((x+1).^2+y.^2+0.0 1);%k*q1=k*q2=1[dx,dy]=gradient(-z);D= sqrt(dx.^2+dy.^2);dx=dx./D ;dy=dy./D;%进行归一化contour(x,y,z,[-2,-1.8,-1.6,-1.4,-1.2,-1,-0.8,-0.5,-0.1,0.1,0.5,0.8,1,1.2,1.4,1.6,1.8 ,2]);%画等势线hold onquiver(x,y,dx,dy,'r');%画电场线大小和方向xx=[linspace(-2,2,10),2*linspace(1,1,10),linspace(-2,2,10 ),-2*linspace(1,1,10)];yy=[2*linspace(1,1,10),linspace(-2,2,10),-2*linspace(1,1, 10),linspace(-2,2,10)];streamline(x,y,-dx,-dy,xx,yy)图四、两个不等量正电荷的等势线和电场线平面图(4)电场分布的三维图形。
电磁仿真中的数值计算方法研究与实践

电磁仿真中的数值计算方法研究与实践电磁场仿真在电磁学和电子工程领域发挥着重要作用,可以帮助工程师和研究人员分析、设计和优化电磁设备和系统。
数值计算方法是电磁场仿真中常用的方法之一,本文将对电磁仿真中的数值计算方法进行研究与实践,探讨其原理、特点和应用。
在电磁仿真中,数值计算方法主要包括有限差分法(Finite Difference method,简称FDM)、有限元法(Finite Element Method,简称FEM)和时域积分方程方法(Time Domain Integral Equation method,简称TDIE)。
这些方法都是基于数值离散的原理,通过将连续的电磁场问题离散化为离散网格上的有限点问题,采用数值计算方法求解得到电磁场分布。
首先,我们来研究有限差分法。
有限差分法是一种常用的数值计算方法,其基本原理是对电磁场的微分方程进行近似,将微分算子替换为差分算子,通过离散网格上的节点上的估计值来求解。
有限差分法简单易懂,计算效率高,尤其适用于规则结构网格的情况。
然而,有限差分法需要网格分辨率较高才能得到精确的结果,对于存在复杂几何形状的问题,可能出现数值误差较大的情况。
接下来,我们研究有限元法。
有限元法是一种广泛应用于工程问题的数值计算方法,其基本思想是将求解域划分为多个小区域(有限元),通过在每个小区域上建立局部近似函数,将原始的微分方程转化为多个局部方程组,通过求解这些局部方程组,最终得到整个求解域上的电磁场分布。
有限元法适用于各种复杂几何形状的问题,并且具有良好的数值稳定性和精度。
然而,有限元法的计算量较大,需要较长的计算时间,并且对于非线性和时变问题的处理稍有复杂。
最后,我们来研究时域积分方程方法。
时域积分方程方法是一种基于时域的电磁场求解方法,它将电磁场问题转化为时域的积分方程,并通过在时域上进行数值积分求解得到电磁场分布。
相比于频域方法,时域积分方程方法具有较好的时域分辨率,可以更好地处理信号的时域演化。
北理工电磁场实验报告

北理工电磁场实验报告北理工第四次实验报告、实验四实验报告实验名称:一条指令的执行过程学号姓名班级:实验时间:年月日实验报告表4-1 一条指令执行过程记录表12篇二:电磁场实验报告CENTRAL SOUTH UNIVERSITY题目利用Matlab模拟点电荷电场的分布姓名刘畅学号0917110121 班级电气试验1101班任课老师李志勇实验日期2013年11月10日一、实验目的:1、熟悉单个点电荷及一对点电荷的电场分布情况;2、学会使用Matlab进行数值计算,并绘出相应的图形;二、实验原理:根据库伦定律:在真空中,两个静止点电荷之间的作用力与这两个电荷的电量乘积成正比,与它们之间距离的平方成反比,作用力的方向在两个电荷的连线上,两电荷同号为斥力,异号为吸力,它们之间的力F满足:F?kQ1Q2?R2R(式1)由电场强度E的定义可知:E?kQ?RR2 (式2)对于点电荷,根据场论基础中的定义,有势场E的势函数为U?kQR(式3)而EU(式4) 在Matlab中,由以上公式算出各点的电势U,电场强度E后,可以用Matlab自带的库函数绘出相应电荷的电场分布情况。
三、实验内容:1.根据库伦定律,利用Matlab强大的绘图功能画出单个点电荷的电场分布情况,包括电力线和等势面。
实验代码:r0=0.12; %取射线半径th=linspace(0,2*pi,13); %电力线的角度[x,y]=pol2cart(th,r0); %将极坐标转化为直角坐标x=[x;0.1*x]; %插入X的起始坐标y=[y;0.1*y]; %插入Y的起始坐标plot(x,y,'b') %用蓝色画出所有电力线grid on %加网格Hold on %保持图像plot(0,0,'o','MarkerSize',12) %画电荷xlabel('x','fontsize',16) %用16号字体标出X 轴ylabel('y','fontsize',16) %用16号字体标出Y轴k=9e9; %设定K值q=1e-9; %设定电荷电量r1=0.1; %设定最大等势线的半径u0=k*q/r1; %算出最小的电势u=linspace(1,3,7)*u0; %求出各条等势线的电势大小x=linspace(-r0,r0,100); %将X坐标分成100等份[X,Y]=meshgrid(x); %在直角坐标中形成网格坐标r=sqrt(X.+Y.); %各个网格点到电荷点的距离U=k*q./r; %各点的电势contour(X,Y,U,u); 画出点电荷的点失眠title('单个正点电荷的电场线与等电势','fontsize',20); %显示标题截图:2.根据库伦定律,利用Matlab强大的绘图功能画出一对点电荷的电场分布情况,包括电力线的分布和等势面。
【工程】南京理工大学工程电磁场实验报告

P(W)
1
0.9997
1.9605e-006
60
0.9993
7.0578e-003
360
0.9881
2.5408e-001
1k
0.9192
1.9605e+000
2k
0.7585
7.8420e+000
5k
0.4124
4.9012e+001
10k
0.1996
1.9605e+002
经过对比发现在2kHz以下频率,数值结果与低频涡流损耗公式的计算结果吻合的非常好。
}
五、求解结果
六、实验总结
通过工程电磁场这门课的学习,掌握了二维静电场边值问题的分析,但是对有限差分法的掌握还不够深入,所以这次实验还是有点难度的。本次实验,编写C++程序即可,源程序的编写是在参照了许多资料完成的。通过本次实验。对有线差分法和超松弛迭代法有了进一步的了解。
实验二螺线管电磁阀静磁场分析
六、磁通等势线
七、Plugnut的BH曲线
八、实验总结
本次实验练习了在MAXWELL 2D环境下建立磁场模型,并求解分析磁场的分布,深入地认识螺线管静磁场的分布。通过建立磁场模型,熟悉了MAXWELL 2D的使用,整个实验过程比较顺利、完成了实验任务要求的内容,对课程的学习有了很大的帮助作用。
实验三叠片钢涡流损耗分析
2、实验要求
做不同频率下的叠片钢磁场分布图,计算不同频率下的最低磁通密度和涡流
损耗,与理论计算结果进行比较。
二、不同频率下的叠片钢磁场分布图
f=1hz:
f=60hz:
f=360hz:
f=1khz:
2018电磁场数值计算实验

二维场域的有限差分法
差分运算的基本概念
拉普拉斯方程的有限差分形式
简单迭代法 超松弛法
差分运算的基本概念
一阶差分
f ( x) f ( x h) f ( x)
f ( x ) f ( x h ) f ( x ) x h
一阶差商
二阶差分
2
2 f ( x) f ( x h) f ( x)
二维场域的有限差分法
差分运算的基本概念
拉普拉斯方程的有限差分形式
简单迭代法 超松弛法
超松弛法
n 1 i, j n 1 i, j
1 n (i , j 1 in, j 1 in1, j in1, j ) 4 1 n 1 n 1 n (i , j 1 in, j 1 i 1, j i 1, j ) 4
计算电磁学的重要性
现代科学研究手段 科学实验
理论分析
计算电磁学
高性能计算
电磁学研究领域的重要分支之一
主要内容
1. 计算电磁学的重要性 2. 电磁场计算方法分类 3.二维场域的有限差分法 4.二维场域的有限单元法
电磁场计算方法分类
镜像法 解析法 分离变量法 保角映射法 …… 有限差分法
数值法
有限元法 ……
计算电磁学的重要性
计算电磁场
相互联系
相互依赖
电磁场工程 电磁场理论
计算电磁场解决实际电磁场工程中越来越复 杂的建模与仿真、优化设计等问题; 电磁场工程为计算电磁场提供实验结果,以 验证其计算结果的正确性。
计算电磁学的重要性
计算电磁场
相互联系 相互依赖
电磁场工程 电磁场理论
计算电磁场为电磁场理论提供研究提供复杂 的数值及解析运算的方法、手段和计算结果; 电磁场理论为计算电磁场问题提供了电磁规 律、数学方程,进而验证其计算结果。
工程电磁场实验报告

工程电磁场实验报告电磁场实验报告姓名:咳咳学号:201230254咳咳咳咳班级:电气工程学院2012级1班问题:有一极长的方形金属槽,边宽为1米,除顶盖电位为100V外,其他三面的电位均为零,试用差分法求槽内的电位分布。
有限差分法(Finite Differential Method,FDM)是基于差分原理的一种数值计算法。
其基本思想是:将场域离散为许多小网格,用差分代替微分,用差商代替求导,将求解连续函数泊松方程的问题转换为求解网格节点上的差分方程组的问题。
用所求网格的数值解代替整个场域的真实解。
因而数值解即是所求场域的离散点的解。
虽然数值解是一种近似解法,但当划分的网格或单元愈密时,离散点的数目也愈多,近似解(数值解)也就愈逼近于真实解。
设求解二维静电场边值问题:①网格划分将场域划分为小的网格。
设为正方形网格,边长h。
② 方程离散 将节点上的电位值作为求解变量,把微分方程化为关于的线性代数方程组。
21032202()x h ϕϕϕϕ-+∂≈∂ 22042202()y h ϕϕϕϕ-+∂≈∂ a ) 对内部节点12340024F hϕϕϕϕϕ+++-=b)对边界节点(只考虑节点位于边界上的情况)i fϕ=③ 求解线性代数方程组N 个方程联立成为线性代数方程组求解得到节点上的电位值。
当内点数较少时,可直接用代元消去法或列式法,张弛法等少算;当内点较多时,即内点不是几个,十几个而是成百个,上千个时,手算几乎不可能,这就必须借助计算机进行计算。
求解高阶方程有赛德尔迭代法等方法。
解:对于本例而言,用差分法可直接求得场域中离散点上电位的近似值。
首先对场域进行等距剖分,此处取步长h=0.1米,对于正方形场域则可使用网络格线自边界处起始, 边界节点的电位值(i=0,10;j=0,10)由边界条件给出,其内部节点的电位值(i=1,2,...9;j=1,2,...9)则待求。
由于槽内部电流密度为0所以电位函数所满足的拉普拉斯方程的差分离散格式为j i j i j i j i j i ,1,,11,,14ϕϕϕϕϕ=+++--++)(411,,11,,1,--+++++=j i j i j i j i ji ϕϕϕϕϕ 对于本例的网络剖分,i,j=1,2,3…9,则上式即为待求的内部节点上的电位值所应满足的代数方程组。
武汉大学研究生工程电磁场报告

工程电磁场分析课程报告架空输电线路磁场计算尾号为2,架空输电线路磁场计算。
选取典型的交流500kV架空输电线路进行计算。
考虑分裂导线,给出导线电感矩阵(或者图)、导线截面电流密度分布以及导线下方1.5米处路径上的磁场分布,考虑导线的趋肤效应。
目录1.计算原理 (3)2.计算模型 (4)2.1合理简化 (4)2.2导线模型 (4)3.计算结果 (6)3.1电感矩阵 (6)3.2截面电流密度 (10)4.源代码 (12)5.参考文献 (12)1.计算原理当输电线路中有交流电流流过时,其周围会产生磁场,磁场大小仅和电流有关而与其电压无关,对于三相交流电来说,一般研究认为,在远离导线的地方,其磁场相互抵消,但是对于高电压等级线路而言,导线的分裂间距和相间距离较大,三相电流产生的磁场便不能再忽略了。
利用安倍环路定理分别计算线路每根导线上的电流所产生的的磁场,然后将计算结果进行叠加,即可得出线路周围的磁场强度。
由安倍定律可得:H dl i •=⎰r r Ñ 对于载有一定电流值的一根导线来讲,假定在与导线垂直的平面上有一个圆,圆心也在导线中心,半径比导线半径大,所以磁场强度H 可以表示为:2I H rπ= 磁感应强度B 为:2IB rμπ= 其中,μ为磁导率,I 为导线电流值,r 为半径。
若考虑导线的镜像,其镜像导线深度d 的计算公式为:d =其中,为电阻率,f 为到线上流过电流的频率,取50Hz ,d 的单位为m 。
地球的电阻率一般在几千左右,因此d 的计算值较大,所以在满足工程需要的前提下一般忽略镜像导线的影响,在本报告中也仅考虑架空输电线的作用。
第n 相导线在空间一点产生的磁感应强度的大小为:2nni I B r μπ==其中n=1,2,3,…;In 为第n 相导线的电流,μ=74*10π- 。
考虑磁感应强度的方向,上式改为:02n ni I B r rμπ=r r所以在x ,y 方向上的磁感应强度分别为:()222n n i n nxi x I y y I B r r r μμππ-===r r()2 22n n i nnji yI x xIB rr rμμππ-=== r r由叠加原理可知,N相导线在该点产生的x,y方向上的磁感应强度为:1Nxi nijnB B==∑1Nyi nyinB B==∑合成磁感应强度为:iB=2.计算模型2.1合理简化为了便于计算架空输电线路的模型,在此做如下合理简化:(1)视工频交变磁场为准静态磁场;(2)把实际线路的三维磁场简化为二维磁场;(3)视导线为标准的长圆柱体;(4)不考虑线路舞动等现象,认为三相分裂导线为多平行圆柱体;(5)由于500KV架空输电线路的输电电流较大,趋肤效应和邻近效应较为显著,导线内部流过的电流较小,磁场可以视为0,将导线表面视为等磁面;(6)磁导率均取真空磁导率。
变压器绕组电磁场的数值计算

变压器绕组电磁场的数值计算变压器是电力系统中常用的电力传输设备,它的核心组成部分是绕组。
绕组是电磁场的产生和传输中不可缺少的部分,其特性对于变压器的性能有着至关重要的影响。
因此,对于变压器绕组电磁场的数值计算及其相关问题进行研究,有着重要的理论意义和实际应用价值。
一、绕组的电磁场特性分析绕组是变压器电磁场产生的关键部分,其中电流是影响电磁场强度的主要因素。
根据安培定理,绕组中的电流会在空间中产生一个相应的磁场,该磁场与电流方向相垂直,大小与电流强度成正比。
在变压器中,绕组内的电磁场不仅取决于绕组电流,还受到铁心的影响。
铁心在绕组附近会产生磁场,从而影响绕组中的电磁场分布和强度。
二、基于磁电场耦合的数值计算模型通过数值计算,可以准确地计算绕组中的电磁场特性,包括电场、磁场和电磁场强度等。
在计算中,需要利用磁电场耦合的数值计算模型。
该模型基于有限元方法,将绕组和铁心划分成许多小的区域,对每个区域进行耦合计算,得到全局的电磁场分布和强度。
三、计算模型的实际应用利用计算模型,可以对变压器绕组电磁场的各项特性进行实际应用研究。
比如,可以对绕组中的电流分布和强度进行优化,以减少损耗和提高效率。
同时,可以对绕组的设计和材料进行改进,从而更好地满足实际应用需求。
此外,通过计算模型,还可以研究变压器的故障诊断和预测,为电力系统的安全运行提供技术支持。
四、面临的挑战和未来展望虽然变压器绕组电磁场的数值计算已经取得了一定的进展,但是仍然面临着很多挑战。
比如,目前的数值计算方法还不能完全解决非线性和非均匀磁场分布等问题。
同时,计算模型的建立和计算精度的提高需要大量的计算资源和专业知识。
未来,我们需要进一步改进计算模型和方法,加强多领域协作,提高计算效率和准确性。
这些努力将促进变压器技术的发展,为电力系统的可靠性和稳定性做出积极贡献。
五、结语变压器是电力系统的核心设备之一,其绕组电磁场特性对于其性能有着至关重要的影响。
通过数值计算,可以准确地分析绕组电磁场的各项特性,为变压器设计和运行提供技术支持。
电磁场数值分析实验报告
电器数值分析实验报告
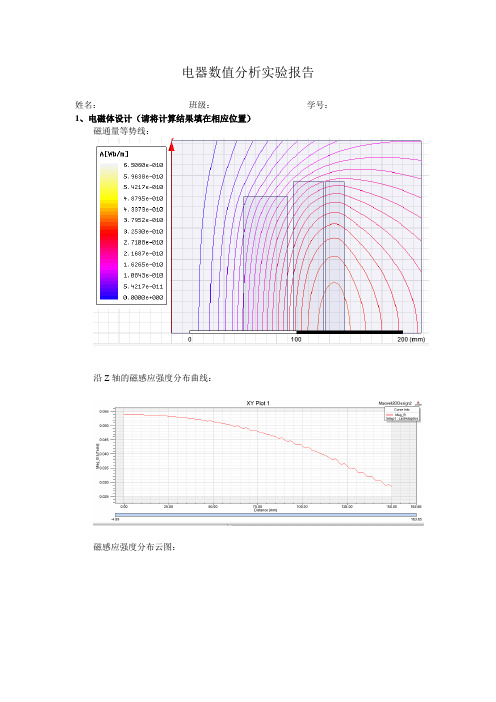
姓名:班级:学号:1、电磁体设计(请将计算结果填在相应位置)
磁通量等势线:
沿Z轴的磁感应强度分布曲线:
磁感应强度分布云图:
2、同轴线电感分析(请将计算结果填在相应位置)
电感值:0.00026485
画出相应的场量云图:
等势线图:
电场强度幅度云图:
4、基于Ansoft软件的电磁场分析基本步骤
1.建模
2.材料属性
3.载荷及边界条件
4.网格剖分
5.计算机解算
6.后处理
5、列举一到两个实验中遇到的问题及解决的方法
问题:在实验中,做好了磁通量等势线图,磁感应强度分布云图后,不知道怎么得到沿Z轴的磁感应强度分布曲线。
解决方案:自己在百度上查找相关资料,然后又找班里学的比较好的的同学问问,知道可以在第一步建立模型时,在Z轴上画一条线段,继而再次对工程进行求解,然后通过在field对话框中选择line1得到沿Z轴的磁密B的分布曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《电磁场数值计算》—有限元法报告第一题(一)问题描述及数学物理模型的建立有一矩形场区,尺寸为6×9,如图1所示,在区域内部J=0,的左边界A=0,右边界A=100,上下边界满足:0An∂=∂,媒质均为的磁导率为μ,利用有限元法求A 的分布首先,2222000(0,0)0;1000x x a y y b A Ax a y b x y A A A A yy ====⎧∂∂+=<<<<⎪∂∂⎪⎪==⎨⎪∂∂⎪==⎪∂∂⎩图1 求解场域及网格划分如果利用有限元来求解,那么对应的泛函为(注:24,l l 分别为上边界和下边界):2422221()221min(0;0)2S l l S A A AF A JA dxdy dl x y n A A A dxdy J x y n μ+⎡⎤⎛⎫∂∂∂⎛⎫=+--⎢⎥ ⎪ ⎪∂∂∂⎝⎭⎢⎥⎝⎭⎣⎦⎡⎤⎛⎫∂∂∂⎛⎫=+===⎢⎥⎪ ⎪∂∂∂⎝⎭⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰⎰第一类边界条件为: 00;100x x aAA====(二)场域的离散化及单元节点的编号处理网格的划分如图1所示,先求出每个单元的刚度矩阵,然后再进行整体合成,得到系数矩阵,具体的做法可参考教材,注意,这里左边界和右边界属于第一类边界,因此,利用下式进行计算:11I 112II=-⎧⎨=⎩K A R K dA d 这里,因为J=0,所以1R =0,11I 12=-K A K d节点编号如图1所示,这里,由于网格的划分和节点的编号都不是很规则,但节点数目和网格数目不是很多,所以,在程序中,通过穷举的办法,找到相应单元的(i ,j ,m )的值,以及相应的节点坐标。
各单元的(i,j,m)(按逆时针方向)如下:1(3,7,1) 2(3,8,7) 3(9,8,3) 4(5,9,3) 5(6,5,3) 6(6,3,4) 7(4,3,1) 8(4,1,2) 9(4,2,10) 10(11,4,10) 11(12,4,11) 12(12,6,4) 节点i的坐标为:if i=1,3,5 then x(i)=3, y(i)=1.5(i-1)if i=2,4,6 then x(i)=6, y(i)=1.5iif i=7,8,9 then x(i)=0, y(i)=3(i-7)if i=10,11,12 then x(i)=9, y(i)=3(i-10)边界节点及其位函数的值为:7(0) 8(0) 9(0)10(100) 11(100) 12(100)然后建立有限元方程组,进行求解,方程组的建立过程参考教材(三)利用数值模拟计算按照有限元法计算的相关步骤,用FORTRAN 90语言编写的程序清单如下:程序运行结果如下:理论结果与实际结果的比较本题对应的偏微分方程及相应的定界问题为:2222000(0,0)0;1000x x a y y b A Ax a y b x y A A A A yy ====⎧∂∂+=<<<<⎪∂∂⎪⎪==⎨⎪∂∂⎪==⎪∂∂⎩数学上不难求出下面偏微分方程的解为:100(,)A x y x a=可以看出,理论结果与数值计算的结果几乎是相同,这是因为数值计算的方法给予有限元的离散,而每个单元都是用线性插值函数来近似的,因为这里A 与坐标x,y 本来就是线性的关系,因此,用线性插值函数来近似真实函数可以得到0误差,这时,误差的主要来源是解方程组的迭代误差。
上述程序中迭代误差取为0.0000000001(1010-)因此,本题得到的精确度极高。
但是,一般的问题A 与坐标x,y 是线性的关系的情况很少,这种情况下,由于线性插值函数近似代替真实函数的截断误差便不可被忽略了,而且一般来说,在两个单元形状类似的情况下,单元面积越小,截断误差也越小。
下面的几个例子将会说明这一点。
第二题2.1(一)问题描述及数学物理模型的建立 如图2,矩形场域ABCD 内的电荷密度为0,AB=CD=a;AC=BD=0.6a;在边界AC,CD,BD 上,电位为0,在顶端BD 上电位分布为f(x)。
分别求出()100f x =(本题的情形) 以及()100sinxfx aπ=时对应的电位分布。
网格可以用边长为1的正方形网格,对于 本题,将计算结果与有限差分法进行对比图2此问题对应的偏微分方程及相应的定解问题为:22220,00.60,00.5,00.50.5,00((0,),(0,0.6))0()0x y a y x a y a x a x a y ax a y a x y f x x ϕϕϕϕϕϕ=<<=<<=<<=<<∂∂⎧+=∈∈⎪∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩这里:()100f x =对应于本题的情况,而()100sin xf x aπ=则对应于下题的情况。
此题对应的泛函及等价的变分问题为:()()()22/20,00.500.5,000.5,0.6()d d min(0;0)20;100D x y a x a y x a y a F x y x y n εϕϕϕϕρϕϕϕ=≤≤<≤=<≤=⎧⎡⎤⎛⎫∂∂∂⎛⎫⎪=+===⎢⎥ ⎪ ⎪⎪∂∂∂⎝⎭⎢⎥⎝⎭⎨⎣⎦⎪===⎪⎩⎰⎰ 由于题目没有给我们划分网格,也没有给我们定好节点,这时,要自己划分网格,为了容易编写程序,减少用户输入网格和节点的信息这一步,采用网格自动剖分的办法,网格划分如图3所示(网格单元及节点的编号规则下面介绍):图3 网格的划分(注:上题未给出标号的节点及单元可按照图中的规律仿照进行编号。
)这里,先讲一下节点和单元的编号规则: ①首先,有三条边上的节点属于第一类边界条件的节点,因此,这些点的编号要靠后,先对电位未知的节点进行编号,然后再对电位已知的节点编号。
②对于内部电位未知的节点,单元和节点的编号采用与课本相同的处理办法,按照一定的顺序和规律进行编号。
设长和宽方向每行分别有y ,x N N 个结点。
对于内部的及节点,节点编号h (i,j )与(i ,j )的关系为:()y y y y (2)(2)12;21(1)(2)(1)(,)(1)(2)1(1;1)(1)(2)1(1;)x y xx x xx y i N j i N j N N N i j h i j N N N j j i N N N j i j N ⎧--+-≤≤≤≤-⎪--+=⎪=⎨--++->=⎪⎪--++->=⎩ 先确定各个节点的编号信息,设∆x 与∆y 分别是x 轴和y 轴方向直角三角形的直角边长。
则节点(i ,j )的坐标为:(,)(1)(,)(1)x i j i xy i j j y=-∆⎧⎨=-∆⎩ 再确定节点的统一编号。
这里,做一个约定,用tp 代表网格的类型,tp=0代表a 类三角形单元,tp=1代表了b 类三角形单元。
如图4所示:图4 两类三角形单元因此,如果网格位于第i 行,j 列,那么三个节点相应的位置就应该为: 对于a 类三角形单元:I(i+1,j+1) J(i,j+1) M(i,j) 对于b 类三角形单元:I(i,j) J(i+1,j) M(i+1,j+1) 统一起来,可以写为:I(i+1-tp,j+1-tp) J(i+tp,j+1-tp) M(i+tp,j+tp)因此,对于任一个三角形单元,如果已知单元的编号,只要知道该三角形单元位于哪一行哪一列,三角形单元是什么样的(a 类还是b 类),就可以知道该三角形单元三个节点I,J,M 的统一编号。
下面讨论如何根据三角形单元的编号,确定该单元所在的行列和三角形单元的类型的信息。
对于编号规则的三角形单元(这部分三角形单元的三个顶点的节点电位都是未知的),编号E 与单元最左下方的节点所在行列(i,j)的关系为: 对于a 类三角形单元:JMI J(,)2(2)(3)1(2,31;2,32)y x y E i j i N j i N j N =--+-=-=-对于b 类三角形单元:(,)(23)(3)1(2,31;2,32)y x y E i j i N j i N j N =--+-=-=-对于这些三角形单元,编号的最大值为: 0max 2(2)(3)x y E N N =--(一)当0max E E ≤时,根据上面计算E(i,j)的公式可知:a 类三角形单元与b 类三角形单元的区别在于3y N -前面是奇数还是偶数,因为2y j N ≤-,因此,24y j N -≤-,而2(2)(3)2(,)1(23)(3)2y y i N j E i j i N j --+-⎧⎪-=⎨--+-⎪⎩可知,①当(,)13y E i j N --的整数部分为偶数时,单元为a 类三角形单元,即tp=0,反之,则为b 类三角形单元,tp=1.②2j -为((,)1)(3)y E i j N --的余数,用[x]表示对x 进行取整运算,mod(a,b)表示整数a 除以整数b 的余数。
那么tp 与j 的计算如下:(,)1mod ,23mod((,)1,3)2y y E i j tp N j E i j N ⎧⎛⎫⎡⎤-⎪= ⎪⎢⎥⎪ ⎪-⎨⎢⎥⎣⎦⎝⎭⎪=--+⎪⎩ 知道了这两个数之后,i 也不难计算,i 的计算公式如下:1(,)1423y E i j i tp N ⎧⎫⎡⎤-⎪⎪=+-⎢⎥⎨⎬-⎢⎥⎪⎪⎣⎦⎩⎭上面讨论的是当 0max E E ≤的情形(二)当0max E E >时,处理起来比较简单,只是相应的情形比较多,例如,按照上面的标号规则,如果0max 0max 2(1)x E E E N <≤+-,在上图中相当于:(32<E ≤42)那么j=1,此时,E 与i 的关系为:0max 0max(0)(11)1(1)x x E iif tp E i N E N i if tp +=⎧=≤≤-⎨+-+=⎩采用与上面类似的办法,可以求出i 和tp 的表达式,下面仅给出E 取值不同情况下(i,j,tp)的计算公式:①0max 0max 2(1)x E E E N <≤+-时[]()()0max 0max mod 11,2mod 1,111x x tp E E N i E E N j ⎧=---⎪⎪=---+⎨⎪=⎪⎩②0max 0max 2(1)2(1)2(2)x x y E N E E N N +-<≤+-+-时:()()0max 0max mod 212,21mod 1,12x y y tp E E N N i j E E N ⎧⎡⎤=--+-⎣⎦⎪⎪=⎨⎪=---+⎪⎩③当0max 0max 2(1)2(2)2(1)2(2)2(2)x y x y x E N N E E N N N +-+-<≤+-+-+- 时,即0max 2(1)2(2)2(1)(1)x y x y E N N E N N +-+-<≤--时:()()0max 0max mod 2252,2mod 225,221x y x x y x y tp E E N N N i E E N N N j N ⎧⎡⎤=---+-⎣⎦⎪⎪=---+-+⎨⎪=-⎪⎩以上给出了如何根据网格的编号计算三个顶点的位置,并给出三角形单元的类型,知道了这些就可以计算三角形单元三个节点的整体编号,进一步计算系数矩阵,求解有限元方程组。
