直线定向、坐标正反算
全面坐标正反算分解

一、坐标正算与坐标反算1、坐标正算已知点的坐标、边的方位角、两点间的水平距离,计算待定点的坐标,称为坐标正算. 如图6-6 所示,点的坐标可由下式计算:式中、为两导线点坐标之差,称为坐标增量,即:[例题6-1]已知点A坐标,=1000、=1000、方位角=35°17'36.5",两点水平距离=200.416,计算点的坐标?35o17'36.5"=1163.58035o17'36.5"=1115.7932、坐标反算已知两点的坐标,计算两点的水平距离与坐标方位角,称为坐标反算.如图6-6可知,由下式计算水平距离与坐标方位角. 〔6-3〕〔6-4〕式中反正切函数的值域是-90°~+90°,而坐标方位角为0°~360°,因此坐标方位角的值,可根据、的正负号所在象限,将反正切角值换算为坐标方位角. [例题6-2]=3712232.528、=523620.436、=3712227.860、=523611.598,计算坐标方位角计算坐标方位角、水平距离.=62°09'29.4"+180°=242°09'29.4" 注意:一直线有两个方向,存在两个方位角,式中:、的计算是过A点坐标纵轴至直线的坐标方位角,若所求坐标方位角为,则应是A 点坐标减点坐标. 坐标正算与反算,可以利用普通科学电子计算器的极坐标和直角坐标相互转换功能计算,普通科学电子计算器的类型比较多,操作方法不相同,下面介绍一种方法. [例题6-3]坐标反算,已知=2365.16、=1181.77、=1771.03、=1719.24,试计算坐标方位角、水平距离. 键入1771.03-2365.16按等号键[=]等于纵坐标增量,按储存键[], 键入1719.24-1181.77按等号键[=]等于横坐标增量,按[]键输入,按[]显示横坐标增量,按[]键输入,按第二功能键[2ndF ],再按[]键,屏显为距离,再按[]键,屏显为方位角. [例题6-4]坐标正算,已知坐标方位角=294°42'51",=200.40,试计算纵坐标增量横坐标增量. 键入294.4251,转换为以度为单位按[DEG ],按[]键输入,键入200.40,按[]键输入,按第二功能键[2ndF ],按[]屏显,按[]屏显. 计算坐标与坐标方位角的基本公式控制测量的主要目的是通过测量和计算求出控制点的坐标,控制点的坐标是根据边长与方位角计算出来的.下面介绍计算坐标与坐标方位角的基本公式,这些公式是矿山测量工中最基本最常用的公式.一、坐标正算和坐标反算公式1.坐标正算根据已知点的坐标和已知点到待定点的坐标方位角、边长计算待定点的坐标,这种计算在测量中称为坐标正算.如图5—5所示,已知A 点的坐标为A x 、A y ,A 到B 的边长和坐标方位角分别为AB S 和AB ,则待定点B 的坐标为AB A B ABA B y y y x x x ∆+=∆+= } 〔5—1〕式中 AB x ∆ 、AB y ∆——坐标增量.由图5—5可知AB AB AB ABAB AB S y S x ααsin cos =∆=∆ } 〔5—2〕式中 AB S ——水平边长;AB α——坐标方位角.将式〔5-2〕代入式〔5-1〕,则有AB AB A B ABAB A B S y y S x x ααsin cos +=+= } 〔5—3〕当A 点的坐标A x 、A y 和边长AB S 与其坐标方位角AB α为已知时,就可以用上述公式计算出待定点B 的坐标.式〔5—2〕是计算坐标增量的基本公式,式〔5—3〕是计算坐标的基本公式,称为坐标正算公式.从图5—5可以看出AB x ∆是边长AB S 在x 轴上的投影长度,AB y ∆是边长AB S 在y 轴上的投影长度,边长是有向线段,是在实地由A 量到B 得到的正值.而公式中的坐标方位角可以从0°到360°变化,根据三角函数定义,坐标方位角的正弦值和余弦值就有正负两种情况,其正负符号取决于坐标方位角所在的象限,如图5—6所示.从式〔5—2〕知,由于三角函数值的正负决定了坐标增量的正负,其符号归纳成表5—3.图5—5 坐标计算 图5—6 坐标增量符号表5—3 坐标增量符号表例1 已知A 点坐标A x =100.00m,A y =300.10m ;边长AB s =100m,方位角AB α=330°.求B 点的坐标B x 、B y .解:根据公式〔5—3〕有2、坐标反算由两个已知点的坐标计算出这两个点连线的坐标方位角和边长,这种计算称为坐标反算.由式〔5—1〕有A B AB AB AB y y y x x x -=∆-=∆ } 〔5—4〕该式说明坐标增量就是两点的坐标之差.在图5—5中AB x ∆ 表示由A 点到达B 点的纵坐标之差称纵坐标增量; AB y ∆表示由A 点到B 点的横坐标之差称横坐标增量.坐标增量也有正负两种情况,它们决定于起点和终点坐标值的大小.在图5—5中如果A 点到B 点的坐标已知,需要计算AB 边的坐标方位角AB α和边长时AB S ,则有ABAB AB AB AB y x S ααsin cos ∆=∆= } <5—5> 或 ()()22AB AB AB y x S ∆+∆=公式〔5—5〕称为坐标反算公式.应当指出,使用公式〔5—5〕中第一式计算的角是象限角R,应根据⊿x 、⊿y 的正负号,确定所在象限,再将象限角换算为方位角.因此公式〔5—5〕中的第一式还可表示为:例2.已知A x =300m, A y =500m,B x =500m,B y =300m,求A 、B 二点连线的坐标方位角AB α和边长AB S .解:由公式〔5-5〕有因为AB x ∆为正 、AB y ∆为负,直线AB 位于第四象限.所以︒=45NW R AB根据第四象限的坐标方位角与象限角的关系得:AB 边长为:坐标正算公式和坐标反算公式都是矿山测量中最基本的公式,应用十分广泛.在测量计算时,由于公式中各元素的数字较多,测量规范对数字取位与计算成果作了规定.例如图根控制点要求边长计算取至毫米;角度计算取至秒;坐标计算取至厘米.二、坐标方位角的推算公式由公式〔5-2〕知,计算坐标增量需要边长和该边的坐标方位角两个要素,其中边长是 在野外直接测量或通过三角学的公式计算得到的,坐标方位角则是根据已知坐标方位角和水平角推算出来的.下面介绍坐标方位角的推算公式.如图5-7所示,箭头所指的方向为"前进"方向,位于前进方向左侧的观测角称为左观测角,简称左角;位于前进方向右侧的角称为右观测角,简称右角.1.观测左角时的坐标方位角计算公式在图5—7与5—8中,已知AB 边的方位角为AB α,左β为左观测角,需要求得BC 边的方位角BC α.左β是外业观测得到的水平角,从图上可以看出已知方位角AB α与左观测角左β之和有两种情况:即大于180°或小于180°.图5—7中为大于180°的情况,图5—8中为小于180°的情况.《建筑工程测量》试题库一、填空题1、测量工作的基准线是.2、测量工作的基准面是.3、测量计算的基准面是.4、真误差为减.5、水准仪的操作步骤为、、、.6、相邻等高线之间的水平距离称为.7、标准北方向的种类有、、.8、用测回法对某一角度观测4测回,第3测回零方向的水平度盘读数应配置为左右.9、三等水准测量中丝读数法的观测顺序为、、、、.10、四等水准测量中丝读数法的观测顺序为后、后、前、前、.11、设在测站点的东南西北分别有A 、B 、C 、D 四个标志,用方向观测法观测水平角,以B 为零方向,则盘左的观测顺序为.12、在高斯平面直角坐标系中,中央子午线的投影为坐标轴.13、权等于1的观测量称.14、已知A 点高程为14.305m,欲测设高程为15.000m 的B 点,水准仪安置在A,B 两点中间,在A 尺读数为2.314m,则在B 尺读数应为m,才能使B 尺零点的高程为设计值.15、水准仪主要由、、组成.16、经纬仪主要由、、组成.17、用测回法对某一角度观测6测回,则第4测回零方向的水平度盘应配置为左右.18、等高线的种类有、、、.19、设观测一个角度的中误差为±8″,则三角形内角和的中误差应为.20、用钢尺丈量某段距离,往测为112.314m,返测为112.329m,则相对误差为.21、水准仪上圆水准器的作用是使,管水准器的作用是使.22、望远镜产生视差的原因是.23、通过海水面的水准面称为大地水准面.24、地球的平均曲率半径为km.25、水准仪、经纬仪或全站仪的圆水准器轴与管水准器轴的几何关系为.26、直线定向的标准北方向有真北方向、磁北方向和方向.27、经纬仪十字丝分划板上丝和下丝的作用是测量.28、水准路线按布设形式分为、、.29、某站水准测量时,由A 点向B 点进行测量,测得AB 两点之间的高差为0.506m,且B 点水准尺的读数为2.376m,则A 点水准尺的读数为m.30、三等水准测量采用"后—前—前—后"的观测顺序可以削弱的影响.31、用钢尺在平坦地面上丈量AB 、CD 两段距离,AB 往测为476.4m,返测为476.3m ;CD 往测为126.33m,返测为126.3m,则AB 比CD 丈量精度要 高 .32、测绘地形图时,碎部点的高程注记在点的右侧、字头应.33、测绘地形图时,对地物应选择角点立尺、对地貌应选择立尺.34、汇水面积的边界线是由一系列连接而成. 35、已知A 、B 两点的坐标值分别为=A x 5773.633m,=A y 4244.098m,=B x 6190.496m,=B y 4193.614m,则坐标方位角=AB α、水平距离=AB D m.36、在1∶2000地形图上,量得某直线的图上距离为18.17cm,则实地长度为m.37、地面某点的经度为131°58′,该点所在统一6°带的中央子午线经度是.38、水准测量测站检核可以采用或测量两次高差.39、已知路线交点JD 桩号为K2+215.14,圆曲线切线长为61.75m,圆曲线起点桩号为.40、地形图应用的基本内容包括量取、、、.41、象限角是由标准方向的北端或南端量至直线的,取值范围为.42、经纬仪的主要轴线有、、、、.43、等高线应与山脊线与山谷线.44、水准面是处处与铅垂线的连续封闭曲面.45、绘制地形图时,地物符号分、和.46、为了使高斯平面直角坐标系的y 坐标恒大于零,将x 轴自中央子午线西移km.47、水准仪的圆水准器轴应与竖轴.48、钢尺量距时,如定线不准,则所量结果总是偏.49、经纬仪的视准轴应垂直于.50、衡量测量精度的指标有、、.51、由于照准部旋转中心与不重合之差称为照准部偏心差.52、天文经纬度的基准是,大地经纬度的基准是.53、权与中误差的平方成.54、正反坐标方位角相差.55、测图比例尺越大,表示地表现状越详细.56、试写出下列地物符号的名称:,,,,,,,,,,,,,,,,,,,,,,,,,.57、用经纬仪盘左、盘右两个盘位观测水平角,取其观测结果的平均值,可以消除、、对水平角的影响.58、距离测量方法有、、、.59、测量误差产生的原因有、、.60、典型地貌有、、、.61、某直线的方位角为123°20′,其反方位角为.62、圆曲线的主点有、、.63、测设路线曲线的方法有、、.64、路线加桩分为、、和.65、建筑变形包括和.66、建筑物的位移观测包括、、、挠度观测、日照变形观测、风振观测和场地滑坡观测.67、建筑物主体倾斜观测方法有、、、、.68、路线勘测设计测量一般分为和两个阶段.69、里程桩分和加桩.70、加桩分为、、和.二、判断题<下列各题,你认为正确的,请在题后的括号内打"√",错的打"×".>1、大地水准面所包围的地球形体,称为地球椭圆体.…………………………………………<>2、天文地理坐标的基准面是参考椭球面.………………………………………………………<>3、大地地理坐标的基准面是大地水准面.………………………………………………………<>4、视准轴是目镜光心与物镜光心的连线.………………………………………………………<>5、方位角的取值范围为0°~±180°.………………………………………………………<>6、象限角的取值范围为0°~±90°.………………………………………………………<>7、双盘位观测某个方向的竖直角可以消除竖盘指标差的影响°.……………………………<>8、系统误差影响观测值的准确度,偶然误差影响观测值的精密度.…………………………<>9、经纬仪整平的目的是使视线水平.……………………………………………………………<>10、用一般方法测设水平角时,应采用盘左盘右取中的方法.………………………………<>11、高程测量时,测区位于半径为10km的范围内时,可以用水平面代替水准面.…………<>三、选择题1、我国使用高程系的标准名称是<>.A.1956黄海高程系B.1956年黄海高程系C.1985年国家高程基准D.1985国家高程基准2、我国使用的平面坐标系的标准名称是<>.A.1954坐标系B. 1954年坐标系C.1980西安坐标系D. 1980年西安坐标系3、在三角高程测量中,采用对向观测可以消除<>的影响.A.视差B.视准轴误差C.地球曲率差和大气折光差D.水平度盘分划误差4、设对某角观测一测回的观测中误差为±3″,现要使该角的观测结果精度达到±1.4″,需观测<>个测回.5、下列四种比例尺地形图,比例尺最大的是<>.A.1∶5000B.1∶2000C.1∶1000D.1∶5006、钢尺的尺长误差对距离测量产生的影响属于<>.A.偶然误差B.系统误差C.偶然误差也可能是系统误差D.既不是偶然误差也不是系统误差7、在地形图上有高程分别为26m、27m、28m、29m、30m、31m、32m的等高线,则需加粗的等高线为<>m.8、高差与水平距离之<>为坡度.A.和B.差C.比D.积9、设AB距离为200.23m,方位角为121°23′36″,则AB的x坐标增量为<>m..19192210、在高斯平面直角坐标系中,纵轴为< >.A.x 轴,向东为正B.y 轴,向东为正C.x 轴,向北为正D.y 轴,向北为正11、在以< >km 为半径的范围内,可以用水平面代替水准面进行距离测量.12、水准测量中,设后尺A 的读数a=2.713m,前尺B 的读数为b=1.401m,已知A 点高程为15.000m,则视线高程为< >m.13、在水准测量中,若后视点A 的读数大,前视点B 的读数小,则有< >.A.A 点比B 点低B.A 点比B 点高C.A 点与B 点可能同高D.A 、B 点的高低取决于仪器高度14、电磁波测距的基本公式D ct D 221=,式中D t 2为< >. A.温度B.光从仪器到目标传播的时间C.光速D.光从仪器到目标往返传播的时间15、导线测量角度闭合差的调整方法是< >.A.反号按角度个数平均分配B.反号按角度大小比例分配C.反号按边数平均分配D.反号按边长比例分配16、丈量一正方形的4条边长,其观测中误差均为±2cm,则该正方形周长的中误差为±< >cm.17、在地形图上,量得A 点高程为21.17m,B 点高程为16.84m,AB 距离为279.50m,则直线AB 的坡度为< >.A.6.8%B.1.5%C.-1.5%D.-6.8%18、自动安平水准仪,< >.A.既没有圆水准器也没有管水准器B.没有圆水准器C. 既有圆水准器也有管水准器D.没有管水准器19、A 点的高斯坐标为=A x 112240m,=A y 19343800m,则A 点所在6°带的带号与中央子午线的经度分别为<>A 11带,66B 11带,63C 19带,117D 19带,11120、进行水准仪i 角检验时,A,B 两点相距80m,将水准仪安置在A,B 两点中间,测得高差=AB h 0.125m,将水准仪安置在距离B 点2~3m 的地方,测得的高差为='AB h =0.186m,则水准仪的i 角为<>A 157″B -157″C 0.00076″D –0.00076″21、用光学经纬仪测量水平角与竖直角时,度盘与读数指标的关系是<>A 水平盘转动,读数指标不动;竖盘不动,读数指标转动;B 水平盘转动,读数指标不动;竖盘转动,读数指标不动;C 水平盘不动,读数指标随照准部转动;竖盘随望远镜转动,读数指标不动;D 水平盘不动,读数指标随照准部转动;竖盘不动,读数指标转动.22、衡量导线测量精度的一个重要指标是<>A 坐标增量闭合差B 导线全长闭合差C 导线全长相对闭合差23、用陀螺经纬仪测得PQ 的真北方位角为=PQ A 62°11′08″,计算得P 点的子午线收敛角=P γ-0°48′14″,则PQ 的坐标方位角=PQ α<>A 62°59′22″B 61°22′54″C 61°06′16″24、地形图的比例尺用分子为1的分数形式表示时,<>A 分母大,比例尺大,表示地形详细B 分母小,比例尺小,表示地形概略C 分母大,比例尺小,表示地形详细D 分母小,比例尺大,表示地形详细25、测量使用的高斯平面直角坐标系与数学使用的笛卡儿坐标系的区别是< >.A x 与y 轴互换,第一象限相同,象限逆时针编号B x 与y 轴互换,第一象限相同,象限顺时针编号C x 与y 轴不变,第一象限相同,象限顺时针编号D x 与y 轴互换,第一象限不同,象限顺时针编号26、坐标方位角的取值范围为< >.A 0°~270°B -90°~90°C 0°~360°D -180°~180°27、某段距离丈量的平均值为100m,其往返较差为+4mm,其相对误差为< >.A.1/25000B 1/25C 1/2500D 1/25028、直线方位角与该直线的反方位角相差< >.A 180°B 360°C 90°D 270°29、转动目镜对光螺旋的目的是使< >十分清晰.A 物像B 十字丝分划板C 物像与十字丝分划板30、地面上有A 、B 、C 三点,已知AB 边的坐标方位角AB α=35°23′,测得左夹角∠ABC=89°34′,则CB 边的坐标方位角CB α=< >.A 124°57′B 304°57′C -54°11′D 305°49′31、测量仪器望远镜视准轴的定义是< >的连线.A 物镜光心与目镜光心B 目镜光心与十字丝分划板中心C 物镜光心与十字丝分划板中心32、已知A 点高程A H =62.118m,水准仪观测A 点标尺的读数a =1.345m,则仪器视线高程为< >.A 60.773B 63.463C 62.11833、对地面点A,任取一个水准面,则A 点至该水准面的垂直距离为<>.A.绝对高程B.海拔C.高差D.相对高程34、1:2000地形图的比例尺精度是<>35、观测水平角时,照准不同方向的目标,应如何旋转照准部?<>A.盘左顺时针,盘右逆时针方向B.盘左逆时针,盘右顺时针方向C.总是顺时针方向D.总是逆时针方向36、展绘控制点时,应在图上标明控制点的<>A.点号与坐标B.点号与高程C.坐标与高程D.高程与方向37、在1:1000地形图上,设等高距为1m,现量得某相邻两条等高线上A 、B 两点间的图上距离为0.01m,则A 、B 两点的地面坡度为<>A.1%B.5%C.10%D.20%38、道路纵断面图的高程比例尺通常比水平距离比例尺<>A.小一倍B.小10倍C.大一倍D.大10倍39、高斯投影属于<>.A 等面积投影B 等距离投影C 等角投影D 等长度投影40、产生视差的原因是<>.A 观测时眼睛位置不正B 物像与十字丝分划板平面不重合C 前后视距不相等D 目镜调焦不正确41、地面某点的经度为东经85°32′,该点应在三度带的第几带?<>A28B29C27D3042、测定点的平面坐标的主要工作是<>.A 测量水平距离B 测量水平角C 测量水平距离和水平角D 测量竖直角43、经纬仪对中误差所引起的角度偏差与测站点到目标点的距离<>.A 成反比B 成正比C 没有关系D 有关系,但影响很小44、坐标反算是根据直线的起、终点平面坐标,计算直线的<>.A 斜距、水平角B 水平距离、方位角C 斜距、方位角D 水平距离、水平角45、山脊线也称<>.A 示坡线B 集水线C 山谷线D 分水线46、设=A H 15.032m,=B H 14.729m,=AB h <>m.A -47、在高斯平面直角坐标系中,x 轴方向为<>方向.A.东西B.左右C.南北D.前后48、高斯平面直角坐标系中直线的方位角是按以下哪种方式量取的?<>A 纵坐标北端起逆时针B 横坐标东端起逆时针C 纵坐标北端起顺时针D 横坐标东端起顺时针49、地理坐标分为<>.A 天文坐标和大地坐标B 天文坐标和参考坐标C 参考坐标和大地坐标D 三维坐标和二维坐标50、某导线全长620m,算得=x f 0.123m,=y f -0.162m,导线全长相对闭合差=K <>.A.1/2200B.1/3100C.1/4500D.1/304851、已知AB 两点的边长为188.43m,方位角为146°07′06″,则AB 的x 坐标增量为<>.A-156.433mB105.176mC105.046mD -156.345m52、竖直角<>.A 只能为正B 只能为负C 可为正,也可为负D 不能为零53、对某边观测4测回,观测中误差为±2cm,则算术平均值的中误差为<>.A ±0.5cmB ±1cmC ±4cmD ±2cm54、普通水准测量,应在水准尺上读取<>位数.A5B3C2D455、水准尺向前或向后方向倾斜对水准测量读数造成的误差是<>.A 偶然误差B 系统误差C 可能是偶然误差也可能是系统误差D 既不是偶然误差也不是系统误差56、下列比例尺地形图中,比例尺最小的是<>.A1:2000B1:500C1:10000D1:500057、对高程测量,用水平面代替水准面的限度是<>.A 在以10km 为半径的范围内可以代替B 在以20km 为半径的范围内可以代替C 不论多大距离都可代替D 不能代替58、水准器的分划值越大,说明<>.A 内圆弧的半径大B 其灵敏度低C 气泡整平困难D 整平精度高59、某直线的坐标方位角为121°23′36″,则反坐标方位角为<>.A238°36′24″B301°23′36″C58°36′24″D -58°36′24″60、普通水准尺的最小分划为1cm,估读水准尺mm 位的误差属于<>.A 偶然误差B 系统误差C 可能是偶然误差也可能是系统误差D 既不是偶然误差也不是系统误差61、水准仪的<>应平行于仪器竖轴.A 视准轴B 圆水准器轴C 十字丝横丝D 管水准器轴62、竖直角的最大值为<>.A90°B.180°C.270°D.360°63、各测回间改变零方向的度盘位置是为了削弱<>误差影响.A 视准轴B 横轴C 指标差D 度盘分划64、DS1水准仪的观测精度要<>DS3水准仪.A 高于B 接近于C 低于D 等于65、观测某目标的竖直角,盘左读数为101°23′36″,盘右读数为258°36′00″,则指标差为<>.A24″B -12″C -24″D12″66、水准测量中,同一测站,当后尺读数大于前尺读数时说明后尺点< >.A 高于前尺点B 低于前尺点C 高于测站点A 等于前尺点67、水准测量时,尺垫应放置在< >.A 水准点B 转点C 土质松软的水准点上D 需要立尺的所有点68、转动目镜对光螺旋的目的是< >.A 看清十字丝B看清物像C消除视差四、名词解释1、圆水准器轴——2、管水准器轴——3、水平角——4、垂直角——5、视差——6、真北方向——7、等高距——8、水准面——9、直线定向—— 10、直线定线—— 11、竖盘指标差—— 12、坐标正算—— 13、坐标反算——14、直线的坐标方位角—— 15、地物—— 16、地貌—— 17、地形—— 18、测定—— 19、测设——20、误差传播定律——五、简答题1、测量工作的基本原则是什么?2、比例尺精度是如何定义的?有何作用?3、微倾式水准仪有哪些轴线?4、用公式ABABAB x y R ∆∆=arctan计算出的象限角AB R ,如何将其换算为坐标方位角AB α? 5、等高线有哪些特性?6、用中丝读数法进行四等水准测量时,每站观测顺序是什么?7、导线坐标计算的一般步骤是什么?8、水准测量时为什么要求前后视距相等?9、视差是如何产生的?消除视差的步骤?六、计算题1、设A 点高程为15.023m,欲测设设计高程为16.000m 的B 点,水准仪安置在A 、B 两点之间,读得A 尺读数a=2.340m,B 尺读数b 为多少时,才能使尺底高程为B 点高程.2、在1∶2000地形图上,量得一段距离d =23.2cm,其测量中误差=d m ±0.1cm,求该段距离的实地长度D 与中误差D m .3、已知图中AB 的坐标方位角,观测了图中四个水平角,试计算边长B →1,1→2,2→3,3→4的坐标方位角. 4、在同一观测条件下,对某水平角观测了五测回,观测值分别为:39°40′30″,39°40′48″,39°40′54″,39°40′42″,39°40′36″,试计算:①该角的算术平均值?; ②一测回水平角观测中误差? ③五测回算术平均值的中误差? 5、在一个直角三角形中,独立丈量了两条直角边a ,b ,其中误差均为m ,试推导由a ,b 边计算所得斜边c 的中误差c m 的公式?6、已知=AB α89°12′01″,=B x 3065.347m,=B y 2135.265m,坐标推算路线为B →1→2,测得坐标推算路线的右角分别为=B β32°30′12″,=1β261°06′16″,水平距离分别为=1B D 123.704m,=12D 98.506m,试计算1,2点的平面坐标.789、用式为L L -=090α.<水平距离和高差计算取位至0.01m,需要写出计算公式和计算过程>10、已知1、2点的平面坐标列于下表,试用计算器计算坐标方位角,计算取位到1″.11、2.56m,视距间隔为=l 0.586m,竖盘读数L =93°28′,求水平距离D 与高差h . 1213、如图所示,已知水准点A BM 的高程为33.012m,1、2、3点为待定高程点,水准测量观测的各段高差与路线长度标注在图中,试计算各点高程.要求在下列表格中计算.图 推算支导线的坐标方位角计算题1315、为了求得E点的高程,分别从已知水准点A,B,C出发进行水准测量,计算得到E点的高程值与各段的路线长列于下表中,试求⑴E点高程的加权平均值<取位至mm>;78.321m⑵单位权中误差;⑶E16、已知1、2、3、4、5五个控制点的平面坐标列于下表,试计算出方位角31,32,34α与35α31α=?,32=?34=?,35=?17、在相同的观测条件下,对某段距离丈量了5次,各次丈量的长度分别为:139.413、139.435、139.420、139.428m 、139.444.试求:<1> 距离的算术平均值; <2> 观测值的中误差; <3> 算术平均值的中误差<4> 算术平均值的相对中误差.。
直线定向、坐标正反算
教师备课教案首页
教研室主任签字:年月日任课教师:沈杰
举例分析说明课程任务。
解释注意互动问答
教学难点
注意举例加以区分
讨论法
提出问题,学生思考回答。
发现法
注意教学互动(二)象限角
1、象限角的定义:由标准方向北端或南端起,顺时针或逆时针方向量到某直线所夹的水平锐角,称为该直线的象限角,并注记象限,通常用R 表示,角值从0度~~~90度恒为正值。
2、说明:在一般测量工作中,通常都是采用坐标方位角来表示直线方向的,只有在坐标计算中才可能用到象限角。
象限角也有真象限角、磁象限角和坐标象限角之分。
四、正、反坐标方位角
1、直线定向的定义
2、正反方位角的确定
3、正、反方向的确定
4、正、反坐标方位角之间的关系式的计算:
180
αα
=±
正
反
说明:当
180
α〈
正时,上式用加180度,
当
180
α〉
正时,上式用减180度。
五、坐标方位角的推算:(难点)
讲解例题4-1和4-2。
说明:用文字表达为:前一边BC的坐标方位角,等于后一边AB边的坐标方位角加180度,再加左夹角或减右夹角。
计算的结果大于360度应减去360度,为负值时应加360度。
六、坐标正算公式
由 A 、 B 两点边长 D AB和坐标方位角αAB计算坐标增量。
其中:ΔX AB =X B -X A;ΔY AB =Y B -Y A。
坐标正反算定义及公式

坐标正反算定义及公式一、坐标正算(地理坐标转平面坐标)坐标正算是将地球上的地理坐标(经纬度)转换为平面坐标(笛卡尔坐标或者极坐标)。
坐标正算是地图制图的一项基本工作。
1.大地参考椭球体模型在进行坐标正算之前,需要先定义一个大地参考椭球体模型,用于近似地球的形状。
常用的大地参考椭球体模型有WGS84、北京54等。
这些模型定义了地球的椭球体参数,如长半轴、扁率等。
2.经度、纬度的度分秒表示法地理坐标通常使用度分秒表示法来表示经度和纬度。
经度是以东西方向为正负,以本初子午线(通常是格林威治子午线)为基准;纬度是以南北方向为正负,以赤道为基准。
3.大地坐标系和平面坐标系大地坐标系是地球表面的经纬度坐标系,平面坐标系是一个笛卡尔坐标系或者极坐标系,用于表示地球表面的平面位置。
4.坐标正算公式坐标正算的公式根据大地参考椭球体模型的不同而有所不同,这里以WGS84椭球体模型为例。
假设待转换的地理坐标是经度λ、纬度φ,转换后的平面坐标是X、Y。
首先,计算出椭球体的参数e:e=√(a^2-b^2)/a其中,a是椭球体的长半轴,b是椭球体的短半轴。
然后,计算出曲率半径N:N = a / √(1 - e^2 * sin^2(φ))接着,计算出当前点的平面坐标:X = (N + h) * cos(φ) * cos(λ)Y = (N + h) * cos(φ) * sin(λ)其中,h是当前点的海拔高度。
以上就是坐标正算的基本公式,可以将地理坐标转换为平面坐标。
二、坐标反算(平面坐标转地理坐标)坐标反算是将平面坐标(笛卡尔坐标或者极坐标)转换为地理坐标(经纬度)。
坐标反算是地图制图或者位置定位的一项重要工作。
1.平面坐标的原点和单位平面坐标通常以其中一点为原点,单位长度为米或者其他距离单位。
原点可以在任意位置,但是通常选择区域的中心或者其中一突出地物为原点。
2.坐标反算的过程坐标反算的过程是根据平面坐标和大地参考椭球体模型,计算出对应的地理坐标。
工程测量:坐标正反算

=+Δ=1376.00−57.69=1318.31
=+Δ=748.00+52.86=800.86
坐标反算
02
二、坐标反算
坐标反算,就是根据直线两个端点的已知坐标,计算直线的水平距离D和坐
标方位角α。
X
◎
X
B
X
◎
A
B
Δ = −
= + Δ
= + Δ
思考
坐标正算和坐标反算的适用情形?
谢谢观看
T
H
A
N
K
Y
O
U
已知直线AB的水平距离为78.25m,坐标方位角为137°30′00″,其中一个端点A的坐标
为(1376.00,748.00),求直线另一个端点B的坐标(、)。
解:先求出直线AB的坐标增量
Δ=·cos=78.25×cos137°30′00″= −57.69
Δ=·sin=78.25×sin137°30′00″=52.86
《工程测量》
坐标正反算
目录
01
02
坐标正算
坐标反算
坐标正算
01
一、坐标正算
坐标正算,就是根据直线的起点坐标、水平距离和坐标方位角,计算直线
另一个端点的坐标。
X
◎
X
B
X
◎
A
B
A
Y
Y
A
B
Y
一、坐标正算
(一)坐标正算原理
如图所示,已知直线AB的一个端点A的坐标为(、),水平距离、坐标方位
A
Y
Y
(整理)第七章 定向测量1

第七章定向测量第一节直线定向在数学上,两点确定一条直线,而在测量学中,还要研究直线定向,所谓直线定向,就是确定一条直线与标准方向之间的角度关系。
“北”被视为基准方向或基本方向,在测量学中所说的“北”通常是指三北方向,即:真北、磁北和坐标北。
一、三北方向1.真北方向真子午线是经过地面某点的真子午面与地球表面的交线,真子午线北端所指的方向就是真北方向,或者说真子午线的切线北方向为真北方向。
由于所有的真子午线的北端指的是共同的点(北极),所以,地面各点的真北方向是互不平行的。
真北方向的确定,一般用天文测量方法或陀螺经纬仪测量方法测定。
2.磁北方向罗盘的磁针静止时所指的方向称为磁子午线方向,其中指向北极的方向为磁北方向。
磁北的方向一般用罗盘来确定。
3.坐标北方向我国采用的是高斯平面直角坐标系,用3°带或6°带的中央子午线作为坐标纵轴,因此在该带内的直线定向,可以用该带的坐标纵轴方向作为基准方向,坐标纵线北端所指的方向为坐标北方向。
与真北方向不同的是,地面各点的坐标北方向是互相平行的。
二、三北的关系我国位于北半球,三北虽然都指向北方,可实际上他们之间是有差异的。
1.磁偏角罗盘磁针静止时指向北极的方向是磁北方向,该方向是地球磁场的南极方向,这个方向与北极方向并不一致,就是说,同一点的磁北与真北并不吻合,磁北方向和真北方向之间的夹角称为磁偏角。
用δ表示,磁北在真北以东称为东偏,δ取正值,反之称为西偏,δ取负值(图7-1)。
图7-1 三北关系2.子午线收敛角地球上各点的真子午线互不平行,中央子午线经高斯投影后成为坐标的纵轴,其他的子午线投影后成为曲线。
同一点的坐标北方向和真北方向之间的夹角称为子午线收敛角,用γ表示。
坐标北在真北以东为东偏,γ取正值,反之为西偏,γ取负值。
子午线收敛角如图7-1所示。
3.磁坐偏角同一点的磁北方向偏离坐标北方向的夹角称为磁坐偏角,以坐标纵轴为准,磁北在坐标北以东取正值,反之取负值。
简述坐标正算和坐标反算的原理

坐标正算和坐标反算的原理及应用一、坐标正算坐标正算是指根据给定的点坐标和直线之间的水平距离 DAB 与坐标方位角 AB,推算出另一条直线的坐标方位角 AB 和水平距离DAB 的方法。
坐标正算的计算公式为:XB = XA + DAB·cos(AB)YB = YA + DAB·sin(AB)其中,XB 和 YB 分别称为 A~B 的纵、横坐标增量,XA、YA 分别是直线 AB 的起点和终点的坐标,DAB 是直线 AB 的水平距离。
需要注意,XB 和 YB 均有正、负号,其符号取决于直线 AB 的坐标方位角所在的象限。
二、坐标反算坐标反算是指根据给定的两个点坐标和直线之间的水平距离DAB,推算出直线 AB 的坐标方位角 AB 和水平距离 DAB 的方法。
坐标反算的计算公式为:AB = (YB - YA) / (XB - XA) - 90°其中,AB 是直线 AB 的坐标方位角,XB、YA 分别是直线 AB 的起点和终点的坐标,YB 和 XA 分别是 A~B 和 B~A 的横纵坐标增量。
需要注意,坐标反算得到的方位角是一个锐角,必须先根据 YB-YA 与 XB-XA 的正负号,确定直线 AB 所在的象限,再将象限角换算为坐标方位角。
三、坐标正算和坐标反算的应用坐标正算和坐标反算在实际应用中有着广泛的应用,下面列举几个典型的应用:1. 航空航天领域:在航空航天领域中,坐标正算和坐标反算被用来确定飞行器的位置和方向,从而确保飞行器的安全和准确性。
2. 机械设计领域:在机械设计中,坐标正算和坐标反算被用来计算机械零部件的位置和方向,从而确保机械设计的精确性和合理性。
3. 地理信息系统:在地理信息系统中,坐标正算和坐标反算被用来确定地图中各个点的位置和方向,从而支持地图数据的采集、管理和分析。
4. 机器人领域:在机器人领域中,坐标正算和坐标反算被用来确定机器人的位置和方向,从而确保机器人的准确移动和作业。
建筑施工测量课件子单元4-4 直线定向与坐标计算

αA 1 = αAB - β1
αA 2 = αAB + β2
在当观测角在已知方向的左边 时,已知方向逆时针旋转才到达观 测边,使方位角减小,因此用减号。
在当观测角在已知方向的右边 时,已知方向顺时针旋转才到达观 测边,使方位角增大,因此用加号。
子单元4 直线定向 与坐标计算
一、标准方向
二、方位角
单元4 距离测量与坐标测量
确定地面两点在平面上的相对位置,除 了测定两点之间的距离外,还应确定两点所连 直线的方向。一条直线的方向,是根据某一标 准方向来确定的。
确定直线与标准方向之间的关系,称为直 线定向,一般用方位角来表示。通过方位角和 水平距离,可以计算得到点的坐标。
陀螺仪
电子 经纬仪
单元4 距离测量与坐标测量 子单元4 直线定向与坐标计算
2.磁北方向
包含地球磁北南极Nm、 Sm的平面与地球表面的交线 称为磁子午线。过地面点A的 磁子午线切线方向,指向北方 的一端,称为该点的磁北方向 。
磁北方向用指南针或罗盘仪 测定。
地球 磁北极
地球 磁南极
指南针
单元4 距离测量与坐标测测量与坐标测量 子单元4 直线定向与坐标计算
单元4 距离测量与坐标测量 子单元4 直线定向与坐标计算
陀螺经纬仪
右图为由一台陀螺仪(上)和一台 电子经纬仪(下)组成的陀螺经纬仪 。在陀螺仪中自由悬挂的转子在陀 螺马达带动的高速旋转(约215O0 转/分)下,因受地球自转的影响 而产生一个重力矩,使转子的轴指 向通过测站的子午线方向,即真北 方向。
平面直角坐标系中,通过某 点且平行于坐标纵轴(X轴) 的方向,指向北方的一端称为 坐标北方向。
角度计算和坐标计算

基本计算1直线定向和坐标推算一、直线定向1、正、反方位角换算对直线AB而言,过始点A的坐标纵轴平行线指北端顺时针至直线的夹角αAB是AB的正方位角,而过端点B的坐标纵轴平行线指北端顺时针至自线的夹角αBA的反方位角,同一条直线的正、反方位角相派180°.,即同一自线的下反方位角αAB=αBA+180°上式右端,若αBA<180°,用“+”号,若αBA>180°,用“—”号。
2、象限角与方位角的换算一条直线的方向有时一也可用象限角表示,所谓象限角是揣从坐标纵轴的指北端或指南端起始,至直线的锐角,用R表示,取值范围为0°~90°。
为了说明肖线所在的象限,在R前应加注直线所在象限的名称。
四个象限的名称分别为北东〔NE?、南东(5E ) ,南酉(sw)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
3、坐标方位角的推算测量工作中一般不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地而有相邻的A、B、C三点,连成折线(图1-17),已知AB边的方位角αAB。
,又测定了AB和BC之间的水平角β,求BC边的方位角气αBC,即是相邻边坐标方位角的推算。
水平角β又有左、右之分,前进方向左侧的水平角为β左,前进方向右侧的水平角β右。
设三点相关位置如图1-I7(c)所示,应有αBC=αAB+β左+180°(1一14)设三点相关位置如图1-I7沪)所不,应有αBC=αAB+β左+180°=αAB+β-180°(1一15)若按折线前进方向将AB视为后边,BC边视为前边,综合上二式即得相邻边坐标方位角推算的通式:α前=α后+β左±180°(1一16)显然,如果测定的是AB和BC方向之间的前进方向右侧水平角β右,因为有β左=360°-β右。
代入上式即得通式:α前=α后-β右±180°上二式右端,若前两项计算结果<180°,180°前而用“十”号,否则180°前而用“一”号。
坐标正算反算计算公式

坐标正算反算计算公式--------------------------------------------------------------------------------本文介绍基本的坐标计算公式1.坐标正算根据直线起点的坐标、直线长度及其坐标方位角计算直线终点的坐标,称为坐标正算。
如图6-10所示,已知直线AB起点A的坐标为(xA,yA),AB边的边长及坐标方位角分别为DAB和αAB,需计算直线终点B的坐标。
附:导线的载流量对照表。
直线两端点A、B的坐标值之差,称为坐标增量,用ΔxAB、ΔyAB表示。
由图6-10可看出坐标增量的计算公式为:坐标增量计算公式根据式(6-1)计算坐标增量时,sin和cos函数值随着α角所在象限而有正负之分,因此算得的坐标增量同样具有正、负号。
坐标增量正、负号的规律如表6-5所示。
表6-5 坐标增量正、负号的规律则B点坐标的计算公式为:2.坐标反算根据直线起点和终点的坐标,计算直线的边长和坐标方位角,称为坐标反算。
如图6-10所示,已知直线AB两端点的坐标分别为(xA,yA)和(xB,yB),则直线边长DAB和坐标方位角αAB的计算公式为:坐标正算计算公式应该注意的是坐标方位角的角值范围在0˚~360˚间,而arctan函数的角值范围在-90˚~+90˚间,两者是不一致的。
按式(6-4)计算坐标方位角时,计算出的是象限角,因此,应根据坐标增量Δx、Δy的正、负号,按表6-5决定其所在象限,再把象限角换算成相应的坐标方位角。
例6-2 已知A、B两点的坐标分别为直线边长DAB和坐标方位角αAB计算公式:试计算AB的边长及坐标方位角。
解计算A、B两点的坐标增量。
坐标反算正算计算公式

坐标反算正算计算公式一、坐标正算 根据A点的坐标X A、Y A和直线AB的水平距离D AB与坐标方位角αAB,推算B点的坐标X B、Y B,为坐标正算,其计算公式为: X B=X A + ΔX AB Y B=X A + ΔY AB (1-18)二式中,ΔX AB与ΔY AB分别称为A~B的纵、横坐标增量,其计算公式为: ΔX AB=X B-X A=D AB · cosαAB ΔY AB=Y B-Y A=D AB · sinαAB (1-19) 注意,ΔX AB和ΔY AB均有正、负,其符号取决于直线AB的坐标方位角所在的象限。
二、坐标反算 根据A、B两点的坐标X A、Y A和X B、Y B,推算直线AB的水平距离D AB与坐标方位角αAB,为坐标反算。
其计算公式为: (1-20) (1-21)注意,由(1-20)式计算αAB时往往得到的是象限角的数值,必须先根据ΔX AB、ΔY AB的正、负号,确定直线AB所在的象限,再将象限角换算为坐标方位角。
三角函数内容规律 三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
而掌握三角函数的内部规律及本质也是学好三角函数的关键所在. 1、三角函数本质: 三角函数的本质来源于定义,如右图: 根据右图,有 sinθ=y/ R; cosθ=x/R; tanθ=y/x; cotθ=x/y。
深刻理解了这一点,下面所有的三角公式都可以从这里出发推导出来,比如以推导 sin(A+B) = sinAcosB+cosAsinB 为例: 推导: 首先画单位圆交X轴于C,D,在单位圆上有任意A,B点。
角AOD为α,BO D为β,旋转AOB使OB与OD重合,形成新A'OD。
A(cosα,sinα),B(cosβ,sinβ),A'(cos(α-β),sin(α-β)) OA'=OA=OB=OD=1,D(1,0) ∴[cos(α-β)-1]^2+[sin(α-β)]^2=(cosα-cosβ)^2+(sinα-sinβ)^2 和差化积及积化和差用还原法结合上面公式可推出(换(a+b)/2与(a-b)/2)[1] 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)[编辑本段]倍角公式 Sin2A=2SinA•CosA Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=2tanA/(1-tanA^2) (注:SinA^2 是sinA的平方sin2(A))[编辑本段]三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a)[编辑本段]三倍角公式推导 sin3a =sin(2a+a) =sin2acosa+cos2asina =2sina(1-sin²a)+(1-2sin²a)sina =3sina-4sin³a cos3a =cos(2a+a) =cos2acosa-sin2asina =(2cos²a-1)cosa-2(1-sin²a)cosa =4cos³a-3cosa sin3a=3sina-4sin³a =4sina(3/4-sin²a) =4sina[(√3/2)²-sin²a] =4sina(sin²60°-sin²a) =4sina(sin60°+sina)(sin60°-sina) =4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a) cos3a=4cos³a-3cosa =4cosa(cos²a-3/4) =4cosa[cos²a-(√3/2)²] =4cosa(cos²a-cos²30°) =4cosa(cosa+cos30°)(cosa-cos30°) =4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°) =-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)] =-4cosacos(60°-a)[-cos(60°+a)] =4cosacos(60°-a)cos(60°+a) 上述两式相比可得 tan3a=tanatan(60°-a)tan(60°+a)[编辑本段]半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.[编辑本段]和差化积 sinθ+sinφ= 2sin[(θ+φ)/2]cos[(θ-φ)/2] sinθ-sinφ= 2cos[(θ+φ)/2]sin[(θ-φ)/2] cosθ+cosφ= 2cos[(θ+φ)/2]cos[(θ-φ)/2] cosθ-cosφ= -2sin[(θ+φ)/2]sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) [编辑本段]积化和差 sinαsinβ= -1/2*[cos(α+β)-cos(α-β)] cosαcosβ= 1/2*[cos(α+β)+cos(α-β)] sinαcosβ= 1/2*[sin(α+β)+sin(α-β)] cosαsinβ= 1/2*[sin(α+β)-sin(α-β)][编辑本段]诱导公式 sin(-α) = -sinα cos(-α) = cosα sin(π/2-α) = -cosα cos(π/2-α) = sinα sin(π/2+α) = cosα cos(π/2+α) = -sinα sin(π-α) = sinα cos(π-α) = -cosα sin(π+α) = -sinα cos(π+α) = -cosα tanA= sinA/cosA tan(π/2+α)=-cotα tan(π/2-α)=cotα tan(π-α)=-tanα tan(π+α)=tanα[编辑本段]万能公式[编辑本段]其它公式(sinα)^2+(cosα)^2=1 1+(tanα)^2=(secα)^2 1+(cotα)^2=(cscα)^2 证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可 对于任意非直角三角形,总有 tanA+tanB+tanC=tanAtanBtanC 证: A+B=π-C tan(A+B)=tan(π-C) (tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC) 整理可得 tanA+tanB+tanC=tanAtanBtanC 得证 同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立[编辑本段]其他非重点三角函数 csc(a) = 1/sin(a) sec(a) = 1/cos(a)[编辑本段]双曲函数 sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tg h(a) = sin h(a)/cos h(a) 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)= sinα cos(2kπ+α)= cosα cot(kπ+α)= cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)= -sinα cos(π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三: 任意角α与-α的三角函数值之间的关系: sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot(-α)= -cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)= sinα cos(π-α)= -cosα tan(π-α)= -tanα cot(π-α)= -cotα 公式五: 利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)= cosα cos(π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan(π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) 这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A^2 +B^2 +2ABcos(θ-φ)} • sin{ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容。
距离测量与直线定向坐标正反算(工程测量)

αAB— 正坐标方位角;
x
αBA— 反坐标方位角。
x
= − 180∘
αAB
直线 B-A:
= + 180∘
所以一条直线的正、反坐标方位角互差180º
反 = 正 ±
180∘
B
αBA
A
o
注意:若此式计算出的反方位角αBA大于360°,则将此值减去360°作为αBA 的最后结果。
总结:
前 = 后 + 180∘ ± 左
右
如果α前>360˚,应自动减去360°;
如果α前<0˚ ,则自动加上360˚。
1
2
21
x
34
3
32
一、坐标方位角计算
5
解:
前进方向
x
2
46° 125°10´
1
α23 =α12+180°-β2 = 46°+180°-125°10´ = 100°50´
136°30´
3
4
247°20´
α34 =α23+180°+β3 = 100°50´+180°+136°30´
= 417°20´
57°20´
>360°
(417°20´-360°)
α45=α34+180°-β4 = 57°20´+180°-247°20´
=
350°
=-10°
<0°
(- 10°+360°)
测各接点处两条直线之间的转折角,若
已知第一条直线的坐标方位角,便可根
据上述两种算法依次推算出其它各条直
线的坐标方位角。
一、坐标方位角计算
x
12
1
测量学 附录:坐标计算原理
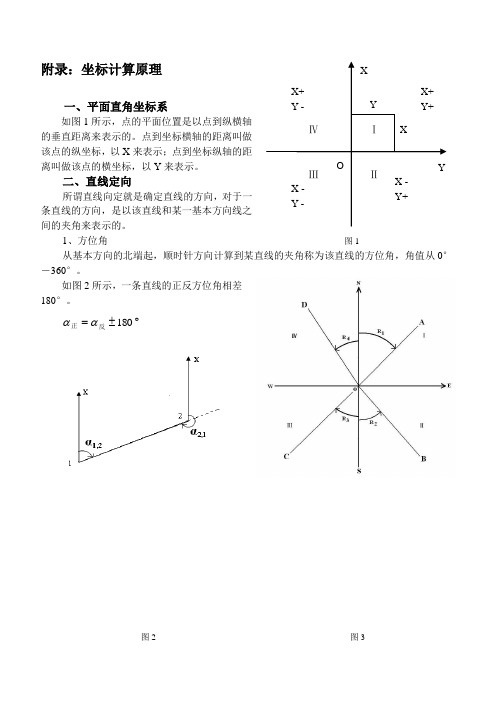
附录:坐标计算原理一、平面直角坐标系如图1所示,点的平面位置是以点到纵横轴的垂直距离来表示的。
点到坐标横轴的距离叫做该点的纵坐标,以X 来表示;点到坐标纵轴的距离叫做该点的横坐标,以Y 来表示。
二、直线定向所谓直线向定就是确定直线的方向,对于一条直线的方向,是以该直线和某一基本方向线之间的夹角来表示的。
1、方位角 图1从基本方向的北端起,顺时针方向计算到某直线的夹角称为该直线的方位角,角值从0° ―360°。
如图2所示,一条直线的正反方位角相差180°。
︒±=180反正αα图2 图32、象限角从基本方向的北端或南端起,顺时针或逆时针计算到某直线的夹角称为象限角,角值从0°—90°,参见图3。
方位角与象限角的换算关系见表1。
两点的坐标之差称为坐标增量,用△X 、△Y 表示。
A 至B 点的坐标增量为:起点终点起点终点Y Y Y -Y Y X A B AB -==∆-=-=∆X X X X A B AB反之B 至A 点的坐标增量为:BA BA Y -Y Y =∆-=∆B A BA X X XA 至B 和B 至A 的坐标增量绝对值相等,符号相反,可见一直线坐标增量的正负决定于直线的方向。
在测量工作中,应用△X 、△Y 解决两类问题。
1、正算:依直线起点的坐标和线段长度、方位角求直线终点的坐标; 图42、反算:依直线起点和终点的坐标、计算直线的水平距离和方位角。
四、坐标正算如图4所示,1点至2点的坐标增量为:2,12,12,12,12,12,1sin cos αα⨯=∆⨯=∆D Y D X则2点坐标为:2,12,112,1122,12,112,112sin cos αα⨯+=∆+=⨯+=∆+=D Y Y Y Y D X X X X 坐标增量的正负决定于直线的方位角的大小和它所在的象限,图5表示了在四个象限中坐标增量的正负情况。
五、坐标反算 图5如图6所示,按三角原理有:122,1122,1Y Y Y X X X -=∆-=∆2,12,12,12,12,12,12,1121212,12,112,1cos sin αααX Y Y X D X X Y Y tg X Y tg ∆=∆=∆+∆=--=∆∆=--例1,已知:X 1=1234.57m ,Y 1=7654.32m ,α1,2=221°16′,D 1,2=246.28m ,求X 2,Y 2。
直线方位测量

8.6 坐标计算原理
一、坐标正反算的定义
地面上两点之间的平面位置与两点之间的水平距离 和坐标方位角有密切关系。
1.坐标正算
根据直线起点的坐标、直线的水平距离以及坐标 方位角来计算终点坐标,称为坐标正算。
2. 坐标反算
三、方位角与象限角之间的关系
象限 第一象限 第二象限
关系 α=R
α=180-R
象限 第三象限 第四象限
关系 α=R+180
α=360-R
8.2 直线定向的表示方法 四、几种方位角之间的关系
磁偏角δ—真北方向与磁北方向之间的夹角;
子午线收敛角γ—真北方向与坐标北方向之间的夹角。
真方位角与坐标方位角关系:
《地形测量》学习情境三—图根平面控制测量
子 情 境 8:直线方位测量
内容提要: 1.直线定向 2.方位角及象限角 3.用罗盘仪测量磁方位角
知识目标: 1.掌握直线定向的方法 2.了解几种方位角之间的关系 3.掌握方位角与象限角之间的关系 4.掌握罗盘仪测定磁方位角的方法
能力目标: 1.会方位角与象限角之间换算 2.会测量磁方位角
8.1 直线定向
一、直线定向
确定一条直线与标准方向之间所夹的水平角的工 作称为直线定线。 二、标准方向(基准方向或者起始方向)
我国通用的标准方向:
真子午线方向
标
准
磁子午线方向
方
向
坐标纵轴方向
•真子午线方向——真子午线的切线方向。 天文测量确定。
•磁子午线方向——磁针北端确定的方向。 罗盘仪测定。
终=始 n 180
8.5 坐标方位角的推算
直线定向和坐标推算

建筑测量基本计算1直线定向和坐标推算一、直线定向1、正、反方位角换算对直线AB 而言,过始点A 的坐标纵轴平行线指北端顺时针至直线的夹角AB α是AB 的正方位角,而过端点B 的坐标纵轴平行线指北端顺时针至直线的夹角BA α则是AB 的反方位角,同一条直线的正、反方位角相差180,即 图 1-15 同一直线的正反方位角AB α=BA α± 180 (1-13)上式右端,若BA α<0180,用“+”号,若≥BA α0180,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用R 表示,取值范围为90~0。
为了说明直线所在的象限,在R 前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE )、南东(SE )、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
图 1-16 象限角表1-4 象限角与方位角关系表象 限象限角R 与方位角a 换算公式第一象限 (NE ) a =R 第二象限 (SE ) a = 180-R 第三象限 (SW ) a = 180+R 第四象限 (NW )a = 360-R3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的A 、B 、C 三点,连成折线(图1-17),已知AB 边的方位角AB α,又测定了AB 和BC 之间的水平角β,求BC 边的方位角BC α,即是相邻边坐标方位角的推算。
水平角β又有左、右之分,前进方向左侧的水平角为左β,前进方向右侧的水平角右β。
图1-17 相邻边坐标方位角的推算设三点相关位置如图1-17(a )所示,应有BC α=AB α+左β+180 (1-14)设三点相关位置如图1-17(b )所示,应有BC α=AB α+左β+ 180- 360=AB α+左β-180 (1-15)若按折线前进方向将AB 视为后边,BC 视为前边,综合上二式即得相邻边坐标方位角推算的通式:前α=后α+左β±180 (1-16)显然,如果测定的是AB 和BC 之间的前进方向右侧水平角右β,因为有左β=0360-右β,代入上式即得通式前α=后α-右β±180 (1-17)上二式右端,若前两项计算结果<180,180前面用“+”号,否则180前面用“-”号。
工程测量计算之-1坐标正反算详解

工程测量计算之-----(一)坐标正反算详解一、方位角、坐标方位角测量工作中、常用方位角来表示直线的方向。
方位角是由标准方向的北端起,顺时针方向度量到某直线的夹角,取值范围为0°-360°,如下图所示。
若标准方向为真子午线方向,则其方位角称为真方位角,用A表示真方位角;若标准方向为磁子午线方向,则其方位角称为磁方位角,用Am表示磁方位角。
若标准方向为坐标纵轴,则称其为坐标方位角,用α表示。
(在高斯直角坐标系中,由坐标纵轴方向的北端起,顺时针度量到直线间的夹角,称为该直线的坐标方位角,常简称方位角,用α表示。
)所以,我们测量中常说的方位角其实是坐标方位角,也就是X轴顺时针旋转至所在直线的角度。
二、象限角以基本方向北端或南端起算,顺时针或逆时针方向量至直线的水平角,称为象限角,用R表示。
象限角不但要表示角度大小,而且还要注明该直线所在的象限。
从坐标纵轴的北端或南端顺时针或逆时针起算至直线的锐角称为坐标象限角。
其角值变化从0°~90°,为了表示直线的方向,应分别注明北偏东、北偏西或南偏东、南偏西。
如北东85°,南西47°等。
显然,如果知道了直线的方位角,就可以换算出它的象限角,反之,知道了象限也就可以推算出方位角。
三、坐标正反算公式详解坐标正算根据直线的坐标方位角、边长和一个已知端点的坐标计算直线上另一端点坐标的过程。
或若两点间的平面位置关系由极坐标化为直角坐标,称为坐标正算。
1、坐标计算条件①起算点(定位点)的平面坐标(X0,Y0),②起算点至待求点的坐标方位角α,③起算点至待求点的平面距离D。
2、坐标计算过程坐标反算根据两已知点的平面坐标,计算该直线的方位角及两点间平面距离的过程。
或若两点间的平面位置关系由直角坐标化为极坐标,称为坐标反算。
α=arctan(△y / △x)D=√(△x*△x + △y*△y)其中,用计算器计算出的α称为象限角,之后还要根据△x、△y的正负号转换为坐标方位角。
建筑测量基本计算1直线定向和坐标推算名师精编资料汇编
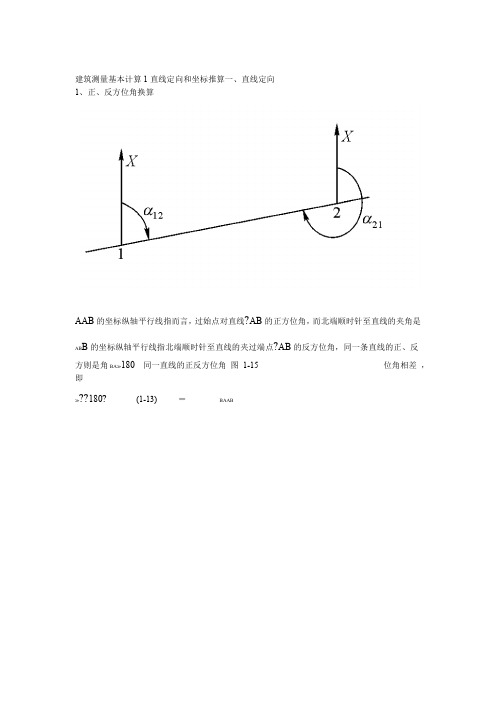
建筑测量基本计算1直线定向和坐标推算一、直线定向1、正、反方位角换算AAB的坐标纵轴平行线指而言,过始点对直线?AB的正方位角,而北端顺时针至直线的夹角是?AB的反方位角,同一条直线的正、反AB B的坐标纵轴平行线指北端顺时针至直线的夹过端点方则是角BA 180同一直线的正反方位角图1-15 位角相差,即??180?(1-13) =BAAB00???180180,,用<“+”号,若上式右端,若BABA用“-”号。
2、象限角与方位角的换算所谓象限角一条直线的方向有时也可用象限角表示。
是指从坐标纵轴的指北端或指南端起始,至直线的锐角, 900~R为了说明直线所在的象表示,取值范围为。
用R四个象限的名称在前应加注直线所在象限的名称。
限,。
SE)、南西(SW)、北西(NW)分别为北东(NE)、南东(1-4。
象限角和坐标方位角之间的换算公式列于表象限角图1-16象限角与方位角关系1-a R限象与方位角象限角换算公式a R NE)第一象限(= a R180)第二象限(SE-= a180R SW 第三象限()=+ a360R NW第四象限()=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
?ABBAC,又,已知、边的方位角三点,连成折线(图1-17设地面有相邻的)、AB??BCBCAB,即是相邻边坐标方位角的推算。
和之间的水平角,求边的方位角测定了BC???前进方向右侧的水平角前进方向左侧的水平角为水平角又有左、右之分,,。
右左.图1-17 相邻边坐标方位角的推算a)所示,应有1-17( 设三点相关位置如图 ???180=++(1-14)?????180180360++-=+-(1-15) ABBC左b)所示,应有设三点相关位置如图1-17(=ABABBC左左ABBC视为前边,综合上二式即得相邻边坐标视为后边,若按折线前进方向将方位角推算的通式:????180=+(1-16)左后前??BCAB=之间的前进方向右侧水平角显然,如果测定的是,因为有和左右0?360,代入上式即得通式-右 ????180-=(1-17)右后前 180180180前面用上二式右端,若前两项计算结果<前面用“+”号,否则,“-”号。
直线定向和坐标推算

直线定向和坐标推算3.1 直线定向方位角直线定向就是确定一条直线的方向,直线方向一般用方位角表示。
所谓方位角就是自某标准方向起始,顺时针至一条直线的水平角,取值范围为0o~360o(图1-11)。
由于标准方向的不同,方位角可分为:真方位角―以过直线起点和地球南、北极的真子午线指北端为标准方向的方位角,以A 表示。
磁方位角―以过直线起点和地球磁场南、北极的磁子午线指北端为标准方向的方位角,以A m表示。
坐标方位角―以过直线起点的平面坐标纵轴平行线指北端为标准方向的方位角,以a表示。
测量中坐标方位角往往简称为方位角。
二、正、反方位角对直线AB而言,αAB是AB的正方位角,而αBA则是AB的反方位角,同一条直线的正、反方位角相差180o(图1-14),即αAB= αBA ± 180o上式右端,若αBA<180o,用“+”号,若αBA≥180o,用“-”号。
三、象限角象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用R表示,取值范围为0o~90o。
在R前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)(图1-15)。
同一条直线的象限角和坐标方位角之间可用公式进行换算。
坐标方位角的推算,设地面有相邻的A、B、C三点(图1-16),已知AB边的方位角αAB,又测定了AB和BC之间的水平角β,求BC边的方位角αBC,即是相邻边坐标方位角的推算。
水平角β有左、右之分,前进方向左侧的水平角为β左,前进方向右侧的水平角β右。
若按折线前进方向将AB视为后边,BC视为前边,相邻边坐标方位角推算的通式为:1.3.2 坐标推算一、坐标正算根据A点的坐标X A、Y A和直线AB的水平距离D AB与坐标方位角αAB,推算B点的坐标X B、Y B,为坐标正算,其计算公式为:X B= X A + ΔX ABY B= X A+ ΔY AB (1-18)二式中,ΔX AB与ΔY AB分别称为A~B的纵、横坐标增量,其计算公式为:ΔX AB= X B- X A= D AB· cosαABΔY AB= Y B- Y A= D AB· sinαAB(1-19)注意,ΔX AB和ΔY AB均有正、负,其符号取决于直线AB的坐标方位角所在的象限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教师备课教案首页
教研室主任签字:年月日任
课教师:沈杰
说明:用文字表达为:前一边BC的坐标方位角,等于后一边AB边的坐标方位角加180度,再加左夹角或减右夹角。
计算的结果大于360度应减去360度,为负值时应加360度。
六、坐标正算公式
由 A 、 B 两点边长 D AB和坐标方位角αAB计算坐标增量。
其中:ΔX AB =X B -X A;ΔY AB =Y B -Y A
七、坐标反算
与坐标正算相反,根据两上已知点的坐标求算出两点间的边长及其方位角,称为坐标反算。
在施工放样前,经常需要利用坐标反算求得放样数据。
如图设A、B为两已知点,其坐标分别为(Xa,Ya)
和(Xb、Yb),欲求AB间水平距离D及坐标方位角。
根据三角形原理可得公式:
(1)水平距离
(2)计算中注意
(3)坐标方位角
小结:
1、直线定向概念
2、标准方向
3、表示直线方向的方法
(学习的目的是增长知识,提高能力,相信一分耕耘一分收获,努力就一定可以获得应有的回报)。
