数字电子技术课后习题答案(全部)
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
数字电子技术课后习题答案

❖ 3.21 用8选1数据选择器74151设计一个组合 逻辑电路。该电路有3三个输入逻辑变量A、B、 C和一个工作状态控制变量M。当M=0时电路 实现“意见一致”功能( A、B、C状态一致 时输出为1,否则输出为0),而M=1时电路 实现“多数表决”功能,即输出与A、B、C中 多数的状态一致。
数字电子技术作业
第一章数字逻辑基础 第二章逻辑门电路 第三章组合逻辑电路 第四章触发器 第五章时序逻辑电路 第六章脉冲波形的产生与整形 第七章半导体存储器 第八章可编程逻辑器件 第九章数/模和模/数转换器
1.12 写出下图所示各逻辑图的输出函数表达式,列 出它们的真值表。
F1 F4
F2
F3
解: F1 AB F2 A B F3 BC
ABACBC
BC
A
00 01 11 10
00
1
0
1
11
0
1
0
Y ABC
❖ 3.13某医院有一、二、三、四号病室4间,每室设有 呼叫按钮,同时在护士值班室内对应的装有一号、 二号、三号、四号4个指示灯。
❖ 现要求当一号病室的按钮按下时,无论其它病室的 按钮是否按下,只有一号灯亮。当一号病室的按钮 没有按下而二号病室的按钮按下时,无论三、四号 病室的按钮是否按下,只有二号灯亮。当一、二号 病室的按钮都未按下而三号病室的按钮按下时,无 论四号病室的按钮是否按下,只有三号灯亮。只有 在一、二、三号病室的按钮均未按下四号病室的按 钮时,四号灯才亮。试用优先编码器74148和门电路 设计满足上述控制要求的逻辑电路,给出控制四个 指示灯状态的高、低电平信号。
Y CBA CB CA CBACB CA
数字电子技术基础. 第四版. 课后习题答案详解

(1)Y=A+B
(2)YABCABC
解:BCABCCABC(A+A=)
(5)Y=0
(2)(1101101)2=(6D)16=(109)10
(4)(11.001)2=(3.2)16=(3.125)10
(2)(127)10=(1111111)2=(7F)16
(4) (25.7)10(11001.1011 0011)2(19.B3)16
1.12
将下列各函数式化为最大项之积的形式
(1)Y(ABC)(ABC)(ABC)
(3)YM0⋅M3⋅M4⋅M6⋅M7
(5)YM0⋅M3⋅M5
(2)Y(ABC)(ABC)(ABC)
(4)YM0⋅M4⋅M6⋅M9⋅M12⋅M13
1.13
用卡诺图化简法将下列函数化为最简与或形式:
(3)Y(AB)(AC)ACBC
(2)Y
ACD
解:(AB)(AC)ACBC[(AB)(AC)AC]⋅BC
(ABACBCAC)(BC)BC
(5)YADACBCDC
解:Y(AD)(AC)(BCD)CAC(AD)(BCD)
ACD(BCD)ABCD
(4)YABC
(6)Y0
1.11
将函数化简为最小项之和的形式
(3)Y=1
(4)YAB CDABDAC D
解:YAD(B CBC)AD(BCC)AD
(7)Y=A+CD
(6)YAC(C DA B)BC(BADCE)
解:YBC(B⋅ADCE)BC(BAD)⋅CEABCD(CE)ABCDE
(8)YA(BC)(ABC)(ABC)
解:YA(B⋅C)(ABC)(ABC)A(AB CB C)(ABC)
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
解:(1)(1110.01)2(2)(1010.11)2(3)(1001.0101)2【题1-6】将下列十进制数转换为二进制数。
解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
(1)01101100;(2)11001100;(3)11101110;(4)11110001解:(1)01101100是正数,所以其反码、补码与原码相同,为01101100 (2)11001100反码为10110011,补码为10110100(3)11101110反码为10010001,补码为10010010(4)11110001反码为10001110,补码为10001111【题1-8】将下列自然二进制码转换成格雷码。
《数字电子技术(第二版)》课后习题参考答案
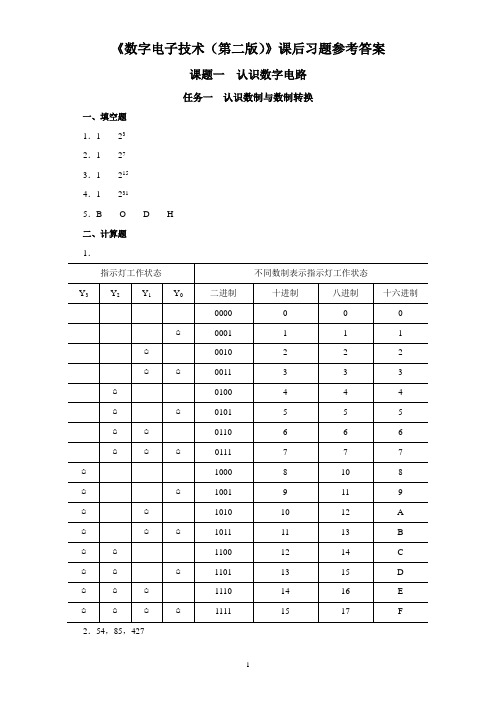
《数字电子技术(第二版)》课后习题参考答案课题一认识数字电路任务一认识数制与数制转换一、填空题1.1 232.1 273.1 2154.1 2315.B O D H二、计算题1.2.54,85,4273.0101,1100,1 1000,11 01114.17O,37O,66 O5.110B,010 111B,001 101 110B6.0FH,36H,0AE63H7.0001 0110B,0010 1010B,1111 1100 0000B任务二学习二进制数算术运算一、计算题(给出的二进制均是无符号数)1.(1)1 0000 (2)1 0000 10012.(1)10 1010 (2)1010 11113.(1)1 0100 (2)110 00004.(1)101 (2)11二、写出下列带符号位二进制数(原码)所表示的十进制数(1)+110 (2)-15 (3)-42 (4)+127 (5)+111(6)-63 (7)+0 (8)+32 767 (9)-32 768三、问答题1.(1)答:左移,移动3位,应作乘以8运算。
(2)答:左移,移动4位,应作乘以16运算。
(3)答:右移,移动7位,应作除以128运算。
(4)答:右移,移动3位,应作除以8运算。
2.答:4位二进制无符号数的最大值是15。
3.答:8位二进制无符号数、有符号数的最大值分别是255和+127。
4.答:16位二进制有符号数的最大值是+32 767。
任务三学习二进制代码一、填空题1.二进制数2.43.8,4,2,1二、判断题1.×2.× 3.√ 4.× 5.× 6.×三、计算题1.36,55,892.[0011 0010]8421,[0101 0010 0111]8421,[0001 0011 0110 1001]8421任务四认识基本逻辑关系并测试逻辑门一、填空题1.与或非2.13.04.1 05.Y=AB6.Y=A+B7.Y=A8.Y=AB9.Y=A+B10.Y=A B=AB+AB二、选择题1.D 2.A 3.B,C 4.A,D三、判断题1.× 2.× 3.× 4.√四、问答题1.答:Y1=ABCD2.答:Y2=A+B+C+D五绘图题1.2.3.4.任务五测试TTL集成门电路1.答:TTL集成门电路电源电压范围为4.75~5.25V之间,额定电压为5V。
数字电子技术课后习题及答案

第二章2.2 证明下列异或运算公式(1)A0A证明:左侧A0 A 0A得证(2)A1A证明:左侧 A 1 A 1A得证(3)A A0证明:左侧 A A A A得证(4)AA A证明:左侧 A A A AA得证(5)ABAB证明:右侧A B A BA B A BA B得证(6)(A B) C A (B C)证明:等式右侧 A (B C) A (BC BC)A(BC BC) A (BC BC)A(BC BC) A BC A BCA (B C)( B C)ABC A BCA (BB BC BC CC)ABC ABCABC ABC ABC ABC(A B AB)C (AB A B)C(A B)C (A B)C(将看成一个整体 (A B) ,用M来表示MC MCM C再替换 M ,则)(A B)C得证2.3 用逻辑代数法将下列逻辑函数式化简为最简与或表达式(1) L=AB(BC+A)解: L=AB(BC+A)=ABC+AB=AB(C+1)=AB(2)L=AB AB B解:L= AB AB B= AB (A1)B=AB B=AB B+A=A+B(3)L A ABC ABC BC BC解: L A ABC ABC BC BCA(1 BC ABC) C(B B)A C(4)L A B BD DCE AD解: L AB (A B)D DCEA B A BD DCEA B D DCEA B D (1CE)A B D(5)L( A B)AB A B AB解: L( A B)( A B)AB(A B)ABA B AB ABA B AB AB ABA (B B)B(A A )A B(6)L (A B C) (D E)(A B C DE )解: L(A B C) (D E)(A B C DE)(( A B C)(D E))(ABC DE )(A BC DE)(ABC DE )(0 DE( ABC ) ABCDE DE )DE2.4 已知函数L(A ,B,C)ABC ABC ABC 。
《数字电子技术基础》课后习题及参考答案

【题
(
(2) ;
(3) ;
(
【题
(
(2) =
(3) =
【题
(
(2) =
(3) =
第3章习题与参考答案
【题3-1】试画出74HC与74LS系列逻辑门电路的输出逻辑电平与输入逻辑电平示意图。
解:74HC系列(5V):74LS系列:
【题3-2】某逻辑门的输入低电平信号范围为3~12V,输入高电平范围为3~12V。若该逻辑门的输入电压值为5V、8V、+5V、+8V,对于正逻辑约定,这些电压值各代表什么逻辑值?若是采用负逻辑约定,这些电压值各代表什么逻辑值?
【题
解:
【题
解:若使上拉高电平与74LS输出高电平VOHmin相同,则有
Rmax=(Vcc-VOHmin)/(15×IIHmax)=(5-2.7)/(15×20μA)=7.66kΩ
选为7.5kΩ。
对于所选7.5kΩ电阻,有上拉高电平=5-(7.5kΩ×(15×20μA))=2.75V,因此有噪声容限为0.75V。
(
(
(
【题
000;001;010;011;100;101;110;111
解:格雷码:000、001、011、010、110、111、101、100
【题
(1)
解:(1)25=(0010 0101)BCD
(
(
(
【题
解:4位数格雷码;
0000、0001、0011、0010、0110、0111、0101、0100、1100、1101、1111、1010、1011、1001、1000、
1
1
1
1
0
1
1
1
1
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
数字电子技术课后习题答案

ABACBC
BC
A
00 01 11 10
00
1
0
1
11
0
1
0
Y ABC
❖ 3.13某医院有一、二、三、四号病室4间,每室设有 呼叫按钮,同时在护士值班室内对应的装有一号、 二号、三号、四号4个指示灯。
❖ 现要求当一号病室的按钮按下时,无论其它病室的 按钮是否按下,只有一号灯亮。当一号病室的按钮 没有按下而二号病室的按钮按下时,无论三、四号 病室的按钮是否按下,只有二号灯亮。当一、二号 病室的按钮都未按下而三号病室的按钮按下时,无 论四号病室的按钮是否按下,只有三号灯亮。只有 在一、二、三号病室的按钮均未按下四号病室的按 钮时,四号灯才亮。试用优先编码器74148和门电路 设计满足上述控制要求的逻辑电路,给出控制四个 指示灯状态的高、低电平信号。
HP RI/BIN
I0
0/ Z1 0 10 ≥1
I1
1/ Z1 1 11
I2
2/ Z1 2 12 18
YS
I3
3/ Z1 3 13
I4
4/ Z1 4 14
YEX
I5
5/ Z1 5 15
I6
6/ Z1 6 16
I7
7/ Z1 7 17
Y0
V18
Y1
ST
E N
Y2
(b)
74148
(a)引脚图;(b)逻辑符号
A
00 01 11 10
00
0
0
1
11
1
0
1
Y AB BC AC
由于存在AC 项,不存在相切的圈,故无冒险。
❖ 4.1在用或非门组成的基本RS触发器中,已知 输入SD 、RD的波形图如下,试画出输出Q, Q
数字电子技术基础(数电)课后习题解答

解: ① (0011101)2 =1×24+ 1×23+ 1×22+ 1×20=(29)10
(0011101)2 =(0 011 101)2= (35)8 (0011101)2 =(0001 1101)2= (1D)16 同理:② (27.75)10,(33.6)8,(1B.C)16; ③ (439)10,(667)8,(1B7)16;
(1) Y=AB+BC+A'C'
=B+A'C'
BC
A
00 01 11 10
0
1
11
1
11
(2) Y=AB'C'+A'B'+A'D+C+BD =B’+C+D (或用圈0法)
CD 00 01 11 10
AB
00 1
1
1
1
01
1
1
1
11
1
1
1
10 1
1
1
1
(3) Y=A' (B'C+B(CD'+D))+ABC'D
1
010
1
011
1
100
1
101
1
110
1
111
0
题1.9 在举重比赛中,有甲、乙、丙三名裁判,其中甲为主裁判,乙、丙为副裁判,当主裁判 和一名以上(包括一名)副裁判认为运动员上举合格后,才可发出合格信号。列出该函数的 真值表。
数字电子技术习题附答案

数字电子技术习题附答案(共20页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、填空题。
1.基本的逻辑门电路有 与 , 或 , 非 。
2.基本逻辑运算有_与_、或、非3种。
3.描述逻辑函数各个变量取值组合与函数值对应关系的表格叫 真值表 。
4.十进制数72用二进制数表示为 1001000 ,用8421BCD 码表示为 01110010 。
二进制数111101用十进制数表示为 615.数制转换: (8F)16 = ( 143 )10= ( )2 = ( 217 )8;(3EC)H = ( 1004 )D ; (2003) D = ()B = ( 3723)O 。
6.有一数码,作为自然二进制数时,它相当于十进制数 147 ,作为8421BCD 码时,它相当于十进制数 93 。
7.10=( )2 = ( )8421BCD 。
8.在8421BCD 码中,用 4 位二进制数表示一位十进制数。
9.在逻辑运算中,1+1= 1 ;十进制运算中1+1= 2 ;二进制运算中1+1= 10 。
10、表示逻辑函数功能的常用方法有逻辑表达式、逻辑真值表、卡诺图等。
11.将2004个“1”异或得到的结果是( 0 )。
12.TTL 门电路中,输出端能并联使用的有__OC 门__和三态门。
13. 在TTL 与非门电路的一个输入端与地之间接一个10K 电阻,则相当于在该输入端输入 高 电平。
14.TTL 与非门多余输入端的处理方法通常有 接至正电源 , 接至固定高电平 , 接至使用端 。
逻辑门是 单 极型门电路,而TTL 逻辑门是 双 极型门电路。
16.与TTL 电路相比,COM 电路具有功耗 低 、抗干扰能力 强 、便于大规模集成等优点。
门电路的电源电压一般为 5 V , CMOS 电路的电源电压为 3—18 V 。
门的输出端可并联使用,实现线与功能;三态门可用来实现数据的双向传递、总线结构等。
数字电子技术基础课后习题及答案

第1章习题与参考答案【题1-1】将以下十进制数转换为二进制数、八进制数、十六进制数。
〔1〕25;〔2〕43;〔3〕56;〔4〕78解:〔1〕25=〔11001〕2=〔31〕8=〔19〕16〔2〕43=〔101011〕2=〔53〕8=〔2B〕16〔3〕56=〔111000〕2=〔70〕8=〔38〕16〔4〕〔1001110〕2、〔116〕8、〔4E〕16【题1-2】将以下二进制数转换为十进制数。
〔1〕10110001;〔2〕10101010;〔3〕11110001;〔4〕10001000解:〔1〕10110001=177〔2〕10101010=170〔3〕11110001=241〔4〕10001000=136【题1-3】将以下十六进制数转换为十进制数。
〔1〕FF;〔2〕3FF;〔3〕AB;〔4〕13FF解:〔1〕〔FF〕16=255〔2〕〔3FF〕16=1023〔3〕〔AB〕16=171〔4〕〔13FF〕16=5119【题1-4】将以下十六进制数转换为二进制数。
〔1〕11;〔2〕9C;〔3〕B1;〔4〕AF解:〔1〕〔11〕16=〔00010001〕2〔2〕〔9C〕16=〔10011100〕2〔3〕〔B1〕16=〔1011 0001〕2〔4〕〔AF〕16=〔10101111〕2【题1-5】将以下二进制数转换为十进制数。
〔1〕1110.01;〔2〕1010.11;〔3〕1100.101;〔4〕1001.0101解:〔1〕〔1110.01〕2=14.25〔2〕〔1010.11〕2=10.75〔3〕〔1001.0101〕2=9.3125【题1-6】将以下十进制数转换为二进制数。
〔1〕20.7;〔2〕10.2;〔3〕5.8;〔4〕101.71解:〔1〕20.7=〔10100.1011〕2〔2〕10.2=〔1010.0011〕2〔3〕5.8=〔101.1100〕2〔4〕101.71=〔1100101.1011〕2【题1-7】写出以下二进制数的反码与补码〔最高位为符号位〕。
数字电子技术基础课后答案全解

【 3-5】用卡诺图化简下列带有约束条件的逻辑函数
(1) P1 A, B, C, D
m(3,6,8,9,11,12)
(0,1,2,13,14,15) AC BD BCD (或ACD)
d
(2) P2(A,B,C,D)= m(0,2,3,4,5,6,11,12)
(8,9,10,13,14,15) BC BC D
有” 1”
4、摩根定理表示为: A B = A B ; A B = A B 。
5、函数表达式 Y= AB C D ,则其对偶式为 Y = ( A B)C D 。
6、根据反演规则,若 Y= AB C D C ,则 Y ( AB C D) C 。
7、指出下列各式中哪些是四变量 A B C D 的最小项和最大项。在最小项后的(
(1) F1 = ABC AB 1
(2) F2 = ABCD ABD ACD AD
(3) F3 AC ABC ACD CD A CD
(4) F4 A B C ( A B C ) ( A B C ) A BC
【 3-3】 用卡诺图化简下列各式
(1) F1 BC AB ABC AB C
(3) F3 AC AC BC BC AB AC BC
第 3 页 /共 46 页
CMOS
A F1
10k
(a)
TTL
A
B
F2
100
(b)
CMOS
A
B
F3
51
(c)
TTL
A
B
F4
100k
CMOS
A
B
F5
10k
(d)
解: (a) F1 A (b)
(e) 图 4.4
《数字电子技术基础》课后习题及参考标准答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16(【题1-2】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)=177(2)=170(3)=241(4)=136【题1-3】将下列十六进制数转换为十进制数。
%(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF*解:(1)(11)16=(00010001)2(2)(9C)16=()2(3)(B1)16=(1011 0001)2(4)(AF)16=()2【题1-5】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)()2=?(2)()2=(3)()2=【题1-6】将下列十进制数转换为二进制数。
(1);(2);(3);(4)解:(1)=()2(2)=()2(3)=()2、(4)=()2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
(1)01101100;(2);(3);(4)解:(1)01101100是正数,所以其反码、补码与原码相同,为01101100(2)反码为,补码为(3)反码为,补码为(4)反码为,补码为>【题1-8】将下列自然二进制码转换成格雷码。
000;001;010;011;100;101;110;111解:格雷码:000、001、011、010、110、111、101、100【题1-9】将下列十进制数转换成BCD码。
电子课件-《数字电子技术(第二版)》-B02-8756 《数字电子技术(第二版)》课后习题参考答案
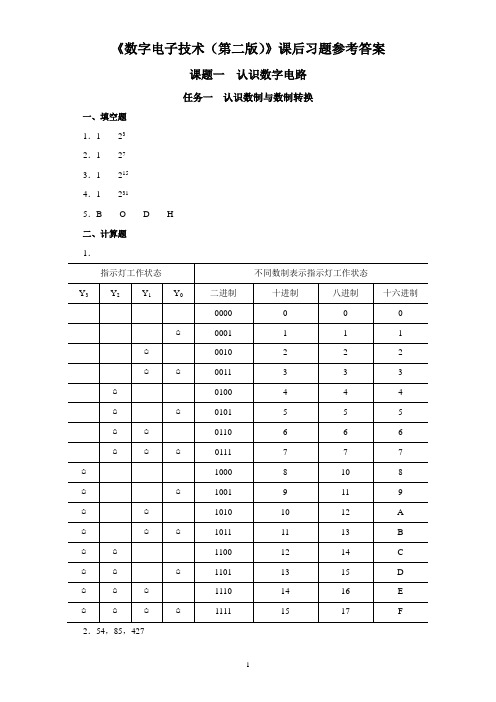
《数字电子技术(第二版)》课后习题参考答案课题一认识数字电路任务一认识数制与数制转换一、填空题1.1 232.1 273.1 2154.1 2315.B O D H二、计算题1.2.54,85,4273.0101,1100,1 1000,11 01114.17O,37O,66 O5.110B,010 111B,001 101 110B6.0FH,36H,0AE63H7.0001 0110B,0010 1010B,1111 1100 0000B任务二学习二进制数算术运算一、计算题(给出的二进制均是无符号数)1.(1)1 0000 (2)1 0000 10012.(1)10 1010 (2)1010 11113.(1)1 0100 (2)110 00004.(1)101 (2)11二、写出下列带符号位二进制数(原码)所表示的十进制数(1)+110 (2)-15 (3)-42 (4)+127 (5)+111(6)-63 (7)+0 (8)+32 767 (9)-32 768三、问答题1.(1)答:左移,移动3位,应作乘以8运算。
(2)答:左移,移动4位,应作乘以16运算。
(3)答:右移,移动7位,应作除以128运算。
(4)答:右移,移动3位,应作除以8运算。
2.答:4位二进制无符号数的最大值是15。
3.答:8位二进制无符号数、有符号数的最大值分别是255和+127。
4.答:16位二进制有符号数的最大值是+32 767。
任务三学习二进制代码一、填空题1.二进制数2.43.8,4,2,1二、判断题1.×2.× 3.√ 4.× 5.× 6.×三、计算题1.36,55,892.[0011 0010]8421,[0101 0010 0111]8421,[0001 0011 0110 1001]8421任务四认识基本逻辑关系并测试逻辑门一、填空题1.与或非2.13.04.1 05.Y=AB6.Y=A+B7.Y=A8.Y=AB9.Y=A+B10.Y=A B=AB+AB二、选择题1.D 2.A 3.B,C 4.A,D三、判断题1.× 2.× 3.× 4.√四、问答题1.答:Y1=ABCD2.答:Y2=A+B+C+D五绘图题1.2.3.4.任务五测试TTL集成门电路1.答:TTL集成门电路电源电压范围为4.75~5.25V之间,额定电压为5V。
《数字电子技术》课后习题答案

第1单元能力训练检测题(共100分,120分钟)一、填空题:(每空0.5分,共20分)1、由二值变量所构成的因果关系称为逻辑关系。
能够反映和处理逻辑关系的数学工具称为逻辑代数。
2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。
3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称为逻辑电路。
在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。
4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的权不同。
十进制计数各位的基数是10,位权是10的幂。
5、8421 BCD码和2421码是有权码;余3码和格雷码是无权码。
6、进位计数制是表示数值大小的各种方法的统称。
一般都是按照进位方式来实现计数的,简称为数制。
任意进制数转换为十进制数时,均采用按位权展开求和的方法。
7、十进制整数转换成二进制时采用除2取余法;十进制小数转换成二进制时采用乘2取整法。
8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换的二进数,按照三个数码一组转换成八进制;按四个数码一组转换成十六进制。
9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。
10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。
13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。
14、在化简的过程中,约束项可以根据需要看作1或0。
二、判断正误题(每小题1分,共10分)1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。
(对)2、异或函数与同或函数在逻辑上互为反函数。
(对)3、8421BCD码、2421BCD码和余3码都属于有权码。
(错)4、二进制计数中各位的基是2,不同数位的权是2的幂。
(对)3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。
(对)4、因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章数制与编码1.1自测练习1.1.1、模拟量数字量1.1.2、(b)1.1.3、(c)1.1.4、(a)是数字量,(b)(c)(d)是模拟量1.2 自测练习1.2.1. 21.2.2.比特bit1.2.3.101.2.4.二进制1.2.5.十进制1.2.6.(a)1.2.7.(b)1.2.8.(c)1.2.9.(b)1.2.10.(b)1.2.11.(b)1.2.12.(a)1.2.13.(c)1.2.14.(c)1.2.15.(c)1.2.16.1.2.17.111.2.18.1.2.19.11011.2.20.8进制1.2.21.(a)1.2.22.0,1,2,3,4,5,6,71.2.23.十六进制1.2.24.0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1.2.25.(b)1.3自测练习1.3.1.1221.3.2.675.521.3.3..011.3.4.521.3.5.1BD.A81.3.6..11101.3.7.38551.3.8.28.3751.3.9..111.3.10.135.6251.3.11.570.11.3.12.120.51.3.13.2659.A1.4自测练习1.4.1.BCD Binary coded decimal 二—十进制码1.4.2.(a)1.4.3.(b)1.4.4.8421BCD码,4221BCD码,5421BCD1.4.5.(a)1.4.6. 1.10001.4.7.1.4.8.1.4.9.1.4.10.61.051.4.11..1.4.12.余3码1.4.13.XS31.4.14.XS31.4.15.1000.10111.4.16. 11.4.17.521.4.18.110101.4.19.1.4.20.(b)1.4.21.ASCII1.4.22.(a)1.4.23.ASCII American Standard Code for Information Interchange美国信息交换标准码EBCDIC Extended Binary Coded Decimal Interchange Code 扩展二-十进制交换吗1.4.24.1.4.25.ASCII1.4.26.(b)1.4.27.(b)1.4.28.1.4.29.-1131.4.30.+231.4.31.-231.4.32.-861.5 自测练习 1.5.1 略 1.5.2 1.5.31.5.4 补码形式 1.5.51.5.6 补码形式 1.5.7 补码形式 习题1.1 (a )(d )是数字量,(b )(c )是模拟量,用数字表时(e )是数字量,用模拟表时(e )是模拟量1.2 (a )7, (b )31, (c )127, (d )511, (e )40951.3 (a )22104108⨯+⨯+, (b )26108108⨯+⨯+,(c )321102105100⨯+⨯+⨯+(d )322104109105⨯+⨯+⨯+1.4 (a )212121⨯+⨯+, (b )4311212121⨯+⨯+⨯+, (c )64212+12+12+12+1⨯⨯⨯⨯(d )9843212+12+12+12+12⨯⨯⨯⨯⨯ 1.5 2201210327.15310210710110510--=⨯+⨯+⨯+⨯+⨯,3210-1-221011.0112+02+12+12+02+12=⨯⨯⨯⨯⨯⨯, 210-18437.448+38+78+48=⨯⨯⨯⨯, 10-1-2163A.1C 316+A 16+116+C 16=⨯⨯⨯⨯1.6 (a )11110, (b ),(c ), (d )1011 1.7 (a )00, (b )1.8 = 2610, 1011.0112 = 11.37510, 57.6438 = 71., 76.EB 16 = 118. 1.9 12 = 65118 = D4916,0. = 0.468 = 0.9816,. = 137.328 = 5F.6816 1.10 168 = 1410,1728 = 12210,61.538 = 49., 126.748 = 86.1.11 2A 16 = 4210 = = 528, B2F 16 = = 12 = 54578, D3.E 16 = 211.87510 = .11102 =323.78, 1C3.F916 = 451. = . = 703.7628 1.12 (a )E, (b )2E, (c )1B3, (d )349 1.13 (a )22, (b )110, (c )1053, (d )2063 1.14 (a )4094, (b )1386, (c )49282 1.15 (a )23, (b )440, (c )27771.16 = 2 = BCD , 67.31110 = . = .18421BCD , 1. = 1. = 0001.BCD , 0. = 0. =0000.BCD1.17 1310 = 1BCD = XS3 = 1011Gray , 6.2510 = 0110.1BCD = 1001. XS3 = 0101.01Gray ,0.12510 = 0000.18421BCD = 0011.0XS3 = 0.001 Gray 1.18 = 11101 Gray , = Gray1.19 = 18421BCD , 45610 = 08421BCD , 1748 =08421BCD , 2DA 16 = 08421BCD , 1BCD=,XS3 = 1BCD1BCD1.20 0.0000原= 0.0000反= 0.0000补,0.1001原= 0.1001反= 0.1001补,11001原= 10110反= 10111补1.21 原= 补,原= 补,原= 补,原= 补1.22 1310 = 补,11010 = 补,-2510 = 补,-90 = 补1.23 补= 11210,补= 3110,补= -3910,补= -56101.241.251.26 BEN SMITH1.271.28第二章逻辑门1.1 自测练习2.1.1. (b)2.1.2. 162.1.3. 32, 62.1.4. 与2.1.5. (b)2.1.6. 162.1.7. 32, 62.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习2.2.1. F A B=⋅2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16,52.2.6. 12.2.7. 串联2.2.8. (b)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC,上拉电阻2.3.2. 0,1,高阻2.3.3. (b)2.3.4. (c)2.3.5. F A B=⋅, 高阻2.3.6. 不能2.4 自测练习1.29 TTL,CMOS1.30 Transisitor Transistor Logic1.31 Complementary Metal Oxide Semicoductor1.32 高级肖特基TTL,低功耗和高级低功耗肖特基TTL1.33 高,强,小1.34 (c)1.35 (b)1.36 (c)1.37 大1.38 强1.39 (a)1.40 (a)1.41 (b)1.42 高级肖特基TTL1.43 (c)习题2.1 与,或,与2.2 与门,或门,与门2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD 2.4 (a)0 (b)1 (c)0 (d)02.5 (a)0 (b)0 (c)1 (d)02.6 (a)1 (b)1 (c)1 (d)12.7 (a)4 (b)8 (c)16 (d)322.8 (a)3 (b)4 (c)5 (d)6A B C F0 0 0 00 0 1 10 1 0 10 1 1 01 0 0 12.9 (a )(b ) A B C D F 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 11112.10 Y AB AC =+2.11A B C Y 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 11111 0 1 0 1 1 0 0 11 1 12.122.13F1 = A(B+C), F2=A+BCA B C F1F20 0 0 0 00 0 1 0 00 1 0 0 00 1 1 0 11 0 1 1 11 0 0 0 11 1 0 1 11 1 1 1 12.142.15 (a)0 (b)1 (c)1 (d)02.16 (a)1 (b)0 (c)0 (d)12.17 (a)0 (b)02.182.19 Y AB BC DE F=⋅⋅⋅2.20 Y AB CD EF=⋅⋅2.21 102.22 402.23 当TTL反相器的输出为3V,输出是高电平,红灯亮。
当TTL反相器的输出为0.2V时,输出是低电平,绿灯亮。
2.24 当TTL反相器输出高电平时三极管会导通,LED灯会点亮;当TTL反相器输出低电平时三极管不会导通,LED灯不会点亮。
3.1自测练习答案1. 逻辑函数2. 逻辑表达式、真值表、逻辑电路图、卡诺图和波形图3.F=真值表表3-1ABCA B CABCF=0 0 0 10 0 1 10 1 0 10 1 1 11 0 0 11 0 1 11 1 0 11 1 1 04.5. (略)3.2自测练习答案1. 与、或、非2. 代入规则 、 反演规则、 对偶规则3. a 和 c4. a d5. a6. D C B A +、D C AB +7. )(E D C B A ++、)(E D C B A ++ 8. *F F =3.3自测练习答案1. A2. AD3. AC D +4. B AC +5. BC C A +6. B A +7. C AB +8. C A AB +9. C A AB +3.4自测练习答案1. 标准与或表达式、 标准或与表达式2. 1、12-n3. n24. 最大项5. 4,5,6,7,12,13,14,156. )5,4,3,1(M ∏7. )4,2,0(M ∏8. )7,5,4,1,0(m ∑9.A B C F 0 0 010. D BC A D C B A +11. ))((D C B A D C B A ++++++ 12. C3.5自测练习答案1. 12. n2 3. 格雷码4.C B A 、C B A ++5. m 66. M 17.8.9.0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 1 0 110.)7,6,5(d ∑第三章练习答案3.1、C AB C B A BC A F ++= 3.2、(a)1,0,0 (b)1,1,1 (c)0,1,03.3.略3.4.(a)))()((D C A C B B A F +++= (b))]))([(G F E D C B A F ++++= 3.5(a)))((*C B C A F ++= (b)D E D C B A F )]([*++=3.6 提示: 列出真值表可知: (1)不正确, (2)不正确, (3 正确, (4) 正确 3.7(a )B A F = (b )ABD ABC + (c )C B BC A F ++=(d )0=F (e )C B F += (f )C B D B AB ++ (g )BC F = (h )0=F(i)C B A F +=(j)C A C B AB F ++=3.8 ()()∏=∑=6,5,4,2,0)7,3,1(,,M m C B A F 3.9 (a) ())7,6,5,4,1(,,m C B A F ∑=(b) (),,,(4,5,6,7,9,12,14)F A B C D m =∑ 3.10 函数Y 和函数Z 互补, 即:Y Z Z Y ==, 3.11、0 0 0 0 0 0 0 0 ABCD11 0000 0111 10 01 103.12D C A CD A D B BC B A D C A CD A D B BC B A F ∙∙∙∙=++++=3.13 D C B A F +=3.14 CD B A D C A F +=1 C B B A D F ++=2 D C B B A D C A A C D F +++=3 3.15 ACD C A B A F ++= 3.163.17习题4.1写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
