实验四 Lagrange函数插值方法(新)
计算方法 插值法Lagrange插值

的n次插值基函数
以n+1个n次基本插值多项式lk(x)(k 0,1, … , n) 为基础,可直接写出满足插值条件
P(xi ) f(x i ) (i 0,1,2, … , n)
的n次代数插值多项式:
P(x) l0(x)y 0 l1(x)y1 … ln(x)yn
B(x1, f(x1))
x0
x1
由解析几何知道,这条直线用点斜式表示为
改写为
p(x)
y0
y1 x1
y0 x0
(x
x0)
p(x)
x x1 x0 x1
y0
x x0 x1 x0
y1
为了便于推广,记
推导
l0(x)
x x1 , x0 x1
l1(x )
x x0 x1 x0
线性插值 基函数
或者写成:
(i 0,1,2)
其几何意义是用经过3个点
(x0, y0 ), (x1, y1), (x2, y2 )
的抛物线 y P(x) 用以近似计算 y f(x)
y=f(x)
y
y = L 2 (x)
y0
y1
x0
x1
y2 x
x2
P(x)的系数 a0 , a1, a2 直接由插值条件决定,即
a0 , a1, a2 满足代数方程组:
(x 0 x1)(x 0 x2 )
从而导出 l0(x)
(x (x 0
x1)(x x2 ) x1)(x 0 x2 )
类似地可以构造出插值多项式 l1(x )和l2 (x )
于是确定了3个抛物插值的基函数:
l0(x)
(x (x 0
x1)(x x1)(x
实验四 插值法

实验四、插值法插值法是函数逼近的一种重要方法,它是数值积分、微分方程数值解等数值计算的基础与工具,其中多项式插值是最常用和最基本的方法。
拉格朗日插值多项式的优点是表达式简单明确,形式对称,便于记忆,它的缺点是如果想要增加插值节点,公式必须整个改变,这就增加了计算工作量。
而牛顿插值多项式对此做了改进,当增加一个节点时只需在原牛顿插值多项式基础上增加一项,此时原有的项无需改变,从而达到节省计算次数、节约存储单元、应用较少节点达到应有精度的目的。
一、实验目的1、理解插值的基本概念,掌握各种插值方法,包括拉格朗日插值和牛顿插值等,注意其不同特点;2、通过实验进一步理解并掌握各种插值的基本算法。
二、Matlab 命令和程序命令 poly :创建一个向量,其分量为一个多项式的系数,该多项式具有给定的根。
命令polyval:求多项式的值,命令 conv : 创建一个向量,其分量为一个多项式的系数,该多项式是另外两个多项式的积polyval(C,2)>> P=poly(2)P=1 -2Q=poly(3)Q=1 -3>> conv(P,Q)ans=1 -5 6>> polyval(P,2)ans=1、拉格朗日插值( 基于N+1个点 ,计算0(()()nn k k k L x f x l x ==∑)拉格朗日多项式)function [C,L]=lagran(X,Y)%input --X is a vector that contains a list of abscissas% Y is a vector that contains a list of ordinates%output--C is a matrix that contains the coefficient of the lagrane % interplatory polynomial% -- L is a matrix that contains the Lagrange coefficent polynomials w=length(X);n=w-1;L=zeros(w,w);%Form the Lagrange coefficient polynomialsfor k=1:n+1V=1;for j=1:n+1if k~=jV=conv(V,poly(X(j)))/(X(k)-X(j));endendL(k,:)=V;end%Determine the coefficiants of the Lagrange interpolating polynomial C=Y*L;2、牛顿插值function [C,D,Newton]=newpoly(X,Y,p)%Input -X is a vector that contains a list of abscissas% -Y is a vector that contains a list of ordinates% -p is the%Output -C is a vector that contains the coefficents of% the Newton interpolatory polynomia% -D is the divided-difference table% -Newton is the value of Newton interplatory polynomia in pn=length(X);D=zeros(n,n);D(:,1)=Y';%Use formula to form the divided-difference tablefor j=2:nfor k=j:nD(k,j)=(D(k,j-1)-D(k-1,j-1))/(X(k)-X(k-j+1));endend%Determine the coefficient fo the newton interpolating polynomialC=D(n,n);for k=(n-1):-1:1C=conv(C,poly(X(k)));m=length(C);C(m)=C(m)+D(k,k);End%Determine the value of the newton interpolating polynomial at pNewton=D(n,n);for k=(n-1):-1:1Newton=Newton*(p-X(k))+D(k,k);End三、实验任务1、已知函数表x 0.56160 0.56280 0.56401 0.56521iy 0.82741 0.82659 0.82577 0.82495i用二次拉格朗日插值多项式求5635x时的函数近似值。
Lagrange 插值
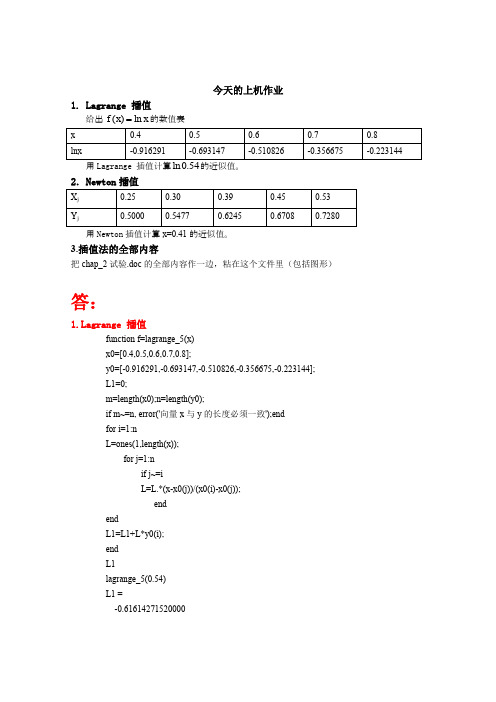
今天的上机作业1. Lagrange 插值给出()ln f x x 的数值表用Lagrange 插值计算ln 0.54的近似值。
2.Newton 插值用Newton 插值计算x=0.41的近似值。
3.插值法的全部内容把chap_2试验.doc 的全部内容作一边,粘在这个文件里(包括图形)答:grange 插值function f=lagrange_5(x) x0=[0.4,0.5,0.6,0.7,0.8];y0=[-0.916291,-0.693147,-0.510826,-0.356675,-0.223144]; L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x 与y 的长度必须一致');end for i=1:nL=ones(1,length(x)); for j=1:n if j~=iL=L.*(x-x0(j))/(x0(i)-x0(j)); end endL1=L1+L*y0(i); end L1lagrange_5(0.54) L1 =-0.616142715200002.Newton插值function f=newton_li5(x) %x0为入的节点值,y0相应节点的函数值x0=[0.25 0.30 0.39 0.45 0.53];y0=[0.5000 0.5477 0.6245 0.6708 0.7280];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)Hxnewton(0.41)n =5hx =0.64030542443064ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.948930296755483.插值法的全部内容把chap_2试验.doc的全部内容作一边,粘在这个文件里(包括图形)P28 例22点插值function f=lagrange_2(x)x0=[0.32,0.34];y0=[0.314567,0.333487];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_2(0.3367)L1 =0.330365200000003点插值function f=lagrange_3(x)x0=[0.32,0.34,0.36];y0=[0.314567,0.333487,0.352274];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_3(0.3367)L1 =0.33037436203750Lagrange插值法%eg1_lagr.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=lagr1(x1,y1,xx); %2次插值chazhi_y45_2=lagr1(x1,y1,4.5);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=lagr1(x2,y2,xx); %4次插值chazhi_y45_4=lagr1(x2,y2,4.5);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=lagr1(x3,y3,xx); %8次插值chazhi_y45_8=lagr1(x3,y3,4.5);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on计算函数值function f=newton_li4(x) %x0为入的节点值,y0相应节点的函数值x0=[0.40,0.55,0.65,0.80,0.90,1.05];y0=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)hxnewton(0.596)n =5hx =0.77193768707246ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.94893029675548Newton插值法%eg1_newton.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=newton1(x1,y1,xx,2); %2次插值chazhi_y45_2=newton1(x1,y1,4.5,2);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=newton1(x2,y2,xx,4); %4次插值chazhi_y45_4=newton1(x2,y2,4.5,4);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=newton1(x3,y3,xx,8); %8次插值chazhi_y45_8=newton1(x3,y3,4.5,8);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on。
Lagrange插值法

{double yy,t;
int j,k;
yy=0.0;
for(j=0;j<N;j++)
{t=1.0;
for(k=0;k<N;k++)
if(k!=j)
t=t*(xx-x[k])/(x[j]-x[k]);
1.根据算法事先写出相应程序。
2.启动PC机,进入vc集成环境,输入代码。
3.编译调试。
4.调试通过,计算出正确结果。
实验内容(包括实验具体内容、算法分析、源代码等等):
1.算法设计。
↓
↓
↓
↓
2.编写相应的程序上机调试。
#include<stdio.h>
#include<math.h>
#define N
实 验 报 告
实验课程名称数值计算方法
实验项目名称Lagrange插值法
年 级
专 业
学生姓名
学 号
理 学 院
实验时间:2012 年 10月 8日
学生所在学院: 专业: 班级:
姓 名
学 号
实称
Lagrange插值法
实验目的及要求:
实验(或算法)原理
一、若给定两个插值点 其中 ,在公式中取 ,则 插值多项式为:
yy=yy+t*y[j];
}
return yy;
}
void main()
{double xx,yy;
double x[N]={};
double y[N]={};
xx=;
yy=lagrange(x,y,xx);
拉格朗日插值法ppt课件

在节点xi处的函数值必然相等 但在节点 P(x外 )的值可能就会 f(x偏 ) 离 因此 P(x)近似代f(替 x)必然存在着误差 8
整体误差的大小反映了插值函数的好坏 为了使插值函数更方便在计算机上运算,一般插值函 数都使用代数多项式和有理函数
本章讨论的就是代数插值多项式
二、代数插值多项式的存在唯一性
n1(x) n1(xj )(xxj )
j0,1,2,,n -------(7')
显l然 0(x)l,1(x)l,2(x) , ,ln(x)线性(无 请同学关 们思考)
且
l j ( xi )
1 0
i j i j
i,j0,1,2,,n -------(8)
16
如果 l0(x)l用 1 ,(x)l2 ,(x) ,,ln(x)作 yf(x)的插值 而Pn(x) 为f(x)的插值多 ,则 项式
6
问题
• 是否存在唯一 • 如何构造 • 误差估计
如函 ys数 ixn ,若给 [0,]上 定 5个等分点
其插值函数的图象如图
7
yy
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 0
0.522
22..55
33
xxx
33..55
对于被插 f(x)和 函插 数值P(函 x) 数
一、插值余项
从上,节 yf可 (x)的 L 知 ag插 ran 值 ge
满足
n
Ln(x) yjlj(x) j0
L n(x i)f(x i) i 0 ,1 , ,n
但 x[a,b]
Ln(x)f(x) 不会完全成立
因此,插值多项式存在着截断误差,那么我们怎样估 计这个截断误差呢?
拉格朗日(Lagrange)插值算法

拉格朗⽇(Lagrange)插值算法拉格朗⽇插值(Lagrange interpolation)是⼀种多项式插值⽅法,指插值条件中不出现被插函数导数值,过n+1个样点,满⾜如下图的插值条件的多项式。
也叫做拉格朗⽇公式。
这⾥以拉格朗⽇3次插值为例,利⽤C++进⾏实现:1//利⽤lagrange插值公式2 #include<iostream>3using namespace std;45double Lx(int i,double x,double* Arr)6 {7double fenzi=1,fenmu=1;8for (int k=0;k<4;k++)9 {10if (k==i)11continue;12 fenzi*=x-Arr[k];13 fenmu*=Arr[i]-Arr[k];14 }15return fenzi/fenmu;16 }1718int main()19 {20double xArr[4]={};21double yArr[4]={};22//输⼊4个节点坐标23 cout<<"请依次输⼊4个节点的坐标:"<<endl;24for (int i=0;i<4;i++)25 cin>>xArr[i]>>yArr[i];2627//输⼊要求解的节点的横坐标28 cout<<"请输⼊要求解的节点的横坐标:";29double x;30 cin>>x;31double y=0;32for (int i=0;i<4;i++)33 y+=Lx(i,x,xArr)*yArr[i];34 printf("x=%lf时,y=%lf\n",x,y);3536//分界,下⾯为已知y求x37 cout<<"请输⼊要求解的节点的纵坐标:";38 cin>>y;39 x=0;40for (int i=0;i<4;i++)41 x+=Lx(i,y,yArr)*xArr[i];42 printf("y=%lf时,x=%lf\n",y,x);4344 system("pause");45return0;46 }作者:耑新新,发布于转载请注明出处,欢迎邮件交流:zhuanxinxin@。
数值计算方法实验之Lagrange多项式插值(Python代码)

数值计算⽅法实验之Lagrange多项式插值(Python代码)⼀、实验⽬的在已知f(x),x∈[a,b]的表达式,但函数值不便计算,或不知f(x),x∈[a,b]⽽⼜需要给出其在[a,b]上的值时,按插值原则f(x i)= y i(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点x i,处成⽴P(x i)=y i(i=0,1,……,n),⽽在[a,b]上的其它点处成⽴f(x)≈P(x).⼆、实验原理三、实验内容求之f(x)=x4在[0,2]上按5个等距节点确定的Lagrange插值多项式.四、实验程序1import matplotlib.pyplot as plt2from pylab import mpl34#计算插值多项式的系数。
5 x = [0, 0.5, 1, 1.5, 2]6 y = [0, 0.0625, 1, 5.0625, 16]78def ParametersOfLagrangeInterpolation(data_x,data_y,size):9 parameters=[]1011 i=0;#i⽤来控制参数的个数12while i < size:13 j = 0;#j⽤来控制循环的变量做累乘14 temp = 1;15while j < size:16if(i != j):17 temp*=data_x[i]-data_x[j]18 j+=1;19 parameters.append(data_y[i]/temp)20 i += 1;21return parameters2223#计算拉格朗⽇插值公式的值。
2425def CalculateTheValueOfLarangeInterpolation(data_x,parameters,x):26 returnValue=027 i = 0;28while i < len(parameters):29 temp = 130 j = 0;31while j< len(parameters):32if(i!=j):33 temp *=x-data_x[j]34 j+=135 returnValue += temp * parameters[i]36 i += 137return returnValue3839#将函数绘制成图像40def Draw(data_x,data_y,new_data_x,new_data_y):41 plt.plot(new_data_x, new_data_y, label="拟合曲线", color="red")42 plt.scatter(data_x,data_y, label="离散数据",color="yellow")43 plt.scatter(1.75, 9.37890625, label="真实数据", color="orange")44 plt.scatter(1.25, 2.44140625, color="green")45 mpl.rcParams['font.sans-serif'] = ['SimHei']46 mpl.rcParams['axes.unicode_minus'] = False47 plt.title("Lagrange插值拟合数据")48 plt.legend(loc="upper left")49 plt.show()5051 parameters=ParametersOfLagrangeInterpolation(x,y,5)52 datax=[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2]53 datay=[]54for temp in datax:55 datay.append(CalculateTheValueOfLarangeInterpolation(x,parameters,temp))56 x.append(1.75)57 y.append(CalculateTheValueOfLarangeInterpolation(x,parameters,1.75))58 Draw(x,y,datax,datay)59print("得到的四次Lagrange插值多项式为:L(x) = %f(x-0)(x-1)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1.5)(x-2) + %f(x-0)(x-0.5)(x-1)(x-2) + %f(x-0)(x-0.5)(x-1)(x-1.5)"%(parameters[1],parameters[2],parameters[3],parameters[4]))五、运算结果(1)图像得到的四次Lagrange插值多项式为:L(x) = -0.166667(x-0)(x-1)(x-1.5)(x-2) + 4.000000(x-0)(x-0.5)(x-1.5)(x-2) + -13.500000(x-0)(x-0.5)(x-1)(x-2) + 10.666667(x-0)(x-0.5)(x-1)(x-1.5)。
四个点拉格朗日插值多项式的导数

四个点拉格朗日插值多项式的导数拉格朗日插值多项式是一种常用的插值方法,用于通过已知的数据点来构建一个近似于这些数据点的函数。
它的原理是假设函数通过已知数据点的连线,并且在每个数据点上具有相同的函数值和导数。
设已知的n个数据点为(x0, y0), (x1, y1), ..., (xn, yn),其中xi表示自变量的取值,yi表示相应的函数值。
拉格朗日插值多项式的一般形式为:P(x) = L0(x)y0 + L1(x)y1 + ... + Ln(x)yn其中Lk(x)表示Lagrange插值基函数,定义如下:Lk(x) = (x - x0)(x - x1)...(x - xk-1)(x - xk+1)...(x - xn) / (xk - x0)(xk - x1)...(xk - xk-1)(xk - xk+1)...(xk - xn) 我们需要求的是这个拉格朗日插值多项式的导数,即P'(x)。
根据导数的定义,我们可以对P(x)进行求导,得到其导数的表达式。
由于拉格朗日插值多项式的形式较为复杂,为了简化计算,我们可以采用数值计算的方法。
以下将分别讨论四个点拉格朗日插值多项式的导数的计算方法。
一、二点拉格朗日插值多项式的导数当已知两个数据点(x0, y0)和(x1, y1)时,拉格朗日插值多项式为:P(x) = (x - x1)y0 / (x0 - x1) + (x - x0)y1 / (x1 - x0)对其进行求导,得到导函数P'(x)为:P'(x) = y0 / (x0 - x1) + y1 / (x1 - x0)二、三点拉格朗日插值多项式的导数当已知三个数据点(x0, y0),(x1, y1)和(x2, y2)时,拉格朗日插值多项式为:P(x) = (x - x1)(x - x2)y0 / (x0 - x1)(x0 - x2) + (x -x0)(x - x2)y1 / (x1 - x0)(x1 - x2) + (x - x0)(x - x1)y2 / (x2 - x0)(x2 - x1)对其进行求导,得到导函数P'(x)为:P'(x) = [(x - x1)(2x - x2 - x1)y0 / (x0 - x1)(x0 - x2) + (x - x0)(2x - x2 - x0)y1 / (x1 - x0)(x1 - x2) + (x - x0)(2x - x1 - x0)y2 / (x2 - x0)(x2 - x1)]三、四点拉格朗日插值多项式的导数当已知四个数据点(x0, y0),(x1, y1),(x2, y2)和(x3, y3)时,拉格朗日插值多项式为:P(x) = (x - x1)(x - x2)(x - x3)y0 / (x0 - x1)(x0 - x2)(x0 - x3) + (x - x0)(x - x2)(x - x3)y1 / (x1 - x0)(x1 - x2)(x1 -x3) + (x - x0)(x - x1)(x - x3)y2 / (x2 - x0)(x2 - x1)(x2 - x3) + (x - x0)(x - x1)(x - x2)y3 / (x3 - x0)(x3 - x1)(x3 - x2) 对其进行求导,得到导函数P'(x)为:P'(x) = [(x - x1)(x - x2)(3x - x3 - x2 - x1)y0 / (x0 -x1)(x0 - x2)(x0 - x3) + (x - x0)(x - x2)(3x - x3 - x2 - x0)y1 / (x1 - x0)(x1 - x2)(x1 - x3) + (x - x0)(x - x1)(3x - x3 - x2 - x0)y2 / (x2 - x0)(x2 - x1)(x2 - x3) + (x - x0)(x - x1)(x -x2)y3 / (x3 - x0)(x3 - x1)(x3 - x2)]通过以上的计算方法,我们可以得到四个点拉格朗日插值多项式的导函数的表达式。
拉格朗日(Lagrange)插值

18
x1 x2 利用 x0 = π , x1 = π L1 ( x ) = x π / 4 × 1 + x π / 6 × 1 6 4 π / 6 π / 4 2 π / 4 π / 6 2 π sin 50 0 ≈ L1 ( 5 ) ≈ 0.77614 这里 f ( x) = sin x , f (2) (ξ x ) = sinξ x , ξ x ∈(π , π ) 内插通常优于外插。 ) 18 内插通常优于外插。2选择 6 3 ( f (ξ x ) 而 1要计算的3x 所在的区间的x π )( x π ) , R1 ( x) = ( < sinξ x < 2 2 2! 6 4 端点,插值效果较好。 端点,插值效果较好。 sin 50° = 0.7660444… 0.01319 < R1 ( 5π ) < 0.00762 18
+1)
( n + 1) ! Nhomakorabeax
Rn ( x) =
(n + 1) !
∏( x x )
i i =0
注:
M n +1 n 作为误差估计上限。 将 ( n + 1)! ∏ | x x i | 作为误差估计上限。 i =0
通常不能确定 ξx , 而是估计
f ( n + 1 ) ( x ) ≤ M n + 1, x∈(a,b) ∈
这样求Lagrange插值多项式计算量大,不便于实际应用。 Lagrange插值多项式计算量大 注: 这样求Lagrange插值多项式计算量大,不便于实际应用。 过两点直线。 一次多项式插值 --- 过两点直线。 过三点抛物线。 二次多项式插值 --- 过三点抛物线。 则插值多项式不唯一 不唯一。 若不将多项式次数限制为 n ,则插值多项式不唯一。
数值分析实验报告Lagrange插值法

2) 选取插值节点为 x1 0.50,x 2 0.70, x 3 0.80 作抛物线插值
运行结果和总结 运行结果 例一: 设 y ln x 且给出函数表 x lnx 0.40 -0.916291 0.50 -0.693147 0.70 -0.356675 0.80 -0.223144
试计算 f(0.6)=ln0.6 近似值。 1)选取插值节点为 x1 0.50,x 2 0.70 作线性插值
>> X=[0.50 0.70 0.80;-0.693147 -0.356675 -0.223144]; >> x=0.60; >> format long >> f=Lagrange(X,x) f= -0.513342666666667
总结 ( 1 )线性插值与抛物线插值都是 Lagrange 插值的特殊形式,两者可以用 Lagrange 插值算法进行计算; (2)并不是给出的插值节点越多越精确,要看步长的大小。 指导教师意见
山东师范大学数学科学学院实验报告
实验课程: 数值分析引论 实验项目: 拉格朗日插值多项式
姓名: XXX 学号: 2015XXXXXX2 班级: XXX 班 专业: 数学与应用数学 指导教师: 实验目的 1、Lagrange 插值法的 matlab 实现; 2、用 Lagrange 插值程序进行插值计算。 实验内容: 问题分析和算法设计 Lagrange 插值 已知 y f(x )函数表(xi ,y i ) ,(a x 0 xi x n b ),给定 xx [a,b ] 及 表示选取 x i , ,x i n 作为插值节点作 n0 次插值多项式 Ln (xx ), 计算 f(xx )近 i0、n0 ,
第4章 Lagrange插值

x xi i 0 x j xi
i j
⑤
l j (x j ) 1 l j ( xi ) 0 i j
显然 l j ( x ) 满足{
Lagrange插值函数Ln(x)
定理 4.2 在[a、b]上有
2 n
span 1, x, x , , x span l0 ( x), l1 ( x), l2 ( x), , ln ( x)
这只是一张函数表;有的函数虽然有解析表达式,但由于计 算复杂,使用不方便,通常也构造一个函数表。如三角函数表、 对数表、平方根表、立方根表等等。
引言
科学实验得到数据: i , yi ) (x yi f ( xi ) (i 0,1,2,..., n), 它反映客观存在的函数y f ( x)在这些点的情况: (i 0,1,..., n) (i 0,1,2,..., n)。 但f ( x)时未知的。因此就想寻找函数 ( x ) f ( x ) 且保持 ( xi ) f ( xi ) yi 的插值函数。 称xi为节点, ( x)为f ( x)关于节点xi (i 0,1,2,..., n)
o i 0 i j n
2o v v l j y j ; 4) 输出 : u, v。
4.3 误差估计
定理 4.3 设函数 f ( x) C n [a, b] , f ( n1) ( x) 在开区间 (a,b)内存在,则 Lagrange 插值多项式 Ln( x) 的余式有如下估 计式
第4章 函数逼近的插值法 与曲线拟和法
引言
许多实际问题都用函数y f (x)来表示某种内在规律的数量
关系,其中相当一部分函数是通过实验或观测得到的.虽然 f (x)
在某个区间[a,b]上是存在的,有的还是连续的,但却只能 给出[a,b]上一系列点 xi的函数值yi f ( xi )
数值分析实验四(Lagrange插值)

《数值分析》实验报告实验编号:实验四课题名称:Lagrange插值一、算法介绍对Lagrange型的n次插值多项式,先构造n+1个插值节点x[0],x[1],…,x[n]上的n次插值基函数对任一点xi所对应的插值基函数l[i](x)=[(x-x[0])…(x-x[i-1])(x-x[i+1])…(x-x[n])]/[(x[i]-x[0])…(x[i]-x[i-1])(x[i]-x[i+1 ])…(x[i]-x[n])],其中i=0,1,2,…,n。
有了这n+1个n次插值基函数,n次Lagrange 型插值多项式就容易写出来了,表达式为:f(x)=y[1]*l[1](x)+y[2]*l[2](x)+…+y[n]*l[n](x)。
此程序中n=10。
二、程序代码// testView.cpp : implementation of the CTestView class//#include "stdafx.h"#include "test.h"#include "testDoc.h"#include "testView.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CTestViewIMPLEMENT_DYNCREATE(CTestView, CView)BEGIN_MESSAGE_MAP(CTestView, CView)//{{AFX_MSG_MAP(CTestView)// NOTE - the ClassWizard will add and remove mapping macros here.// DO NOT EDIT what you see in these blocks of generated code!//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview)END_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CTestView construction/destructionCTestView::CTestView(){// TODO: add construction code here}CTestView::~CTestView(){}BOOL CTestView::PreCreateWindow(CREATESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying // the CREATESTRUCT csreturn CView::PreCreateWindow(cs);}/////////////////////////////////////////////////////////////////////////////// CTestView drawingvoid CTestView::OnDraw(CDC* pDC){CTestDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data hereint i,j,k;double x,y,p_x,p_y,l,xx[100],f[100],F[100],sum,p_sum;CPen MyPen,*OldPen;pDC->SetViewportOrg(400,400); //定义坐标原点for(i=-500;i<500;i++){pDC->SetPixel(0,i,RGB(0,0,0));pDC->SetPixel(i,0,RGB(0,0,0)); //画出坐标}pDC->TextOut(-210,5,"-1");pDC->TextOut(196,5,"1");//原函数MyPen.CreatePen(PS_SOLID,1,RGB(255,0,0));//定义画笔颜色OldPen=pDC->SelectObject(&MyPen);x=-1.0,y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->MoveTo(p_x,p_y);for (x=-1.0;x<=1.0;x+=0.0001){y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->LineTo(p_x,p_y);}pDC->SelectObject(OldPen);MyPen.DeleteObject();//Lagrange插值x=-1.0;MyPen.CreatePen(PS_SOLID,1,RGB(0,255,0));OldPen=pDC->SelectObject(&MyPen);for(i=0;i<=10;i++){f[i]=1/(1+25*x*x);xx[i]=x;x+=0.2;}x=-1.0;y=1/(1+25*x*x);p_x=x*200,p_y=-y*200; //将x和y坐标各放大200倍pDC->MoveTo(p_x,p_y);for(k=0;k<=1000;k++){sum=0;for(i=0;i<=10;i++){l=1;for(j=0;j<=10;j++){if(i!=j)l=l*(x-xx[j])/(xx[i]-xx[j]);}sum+=f[i]*l;}p_x=x*200;p_y=-sum*200;pDC->LineTo(p_x,p_y);x+=0.002;}pDC->SelectObject(OldPen);MyPen.DeleteObject();}/////////////////////////////////////////////////////////////////////////////// CTestView printingBOOL CTestView::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CTestView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add extra initialization before printing}void CTestView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add cleanup after printing}/////////////////////////////////////////////////////////////////////////////// CTestView diagnostics#ifdef _DEBUGvoid CTestView::AssertValid() const{CView::AssertValid();}void CTestView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CTestDoc* CTestView::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CTestDoc)));return (CTestDoc*)m_pDocument;}#endif //_DEBUG/////////////////////////////////////////////////////////////////////////////// CTestView message handlers三、运算结果截屏红色的曲线为原函数图像,绿色曲线为Lagerange插值多项式函数对应的图像四、算法分析上述图像中绿色的曲线为Lagrange插值多项式所对应的图像,通过观察可见函数图像在靠近区间端点的地方出现了Runge现象。
Lagrange插值

二、插值余项 /* Remainder */
定理1 若 f (n1) ( x) 在[a , b]内存在, 则在[a , b]上
的n+1个互异的点,对 f(x)所作的n次Lagrange插
值多项式Ln (x) 有误差估计
Rn (x)
f (x) Ln (x)
f (n1) ( )
(n 1) !
cos x
3!
(x
6
)( x
4
)( x
3
);
1 2
cos x
3 2
0.00044
R2
5
18
0.00077
sin 50 = 0.7660444…
2次插值的实际误差 0.00061
关于Langrange插值的几点说明
(1) Ln (x) 仅与已知数据 (xi , yi ) (i 0,1,,n) 有关, 与 f (x) 的原来形式无关,但余式与 f (x)密切
L1
(
x)
x /
/ 6
4 /
4
1 2
x /
/ 4
6 /6
1 2
sin 500
5
L1( 18
)
0.77614
R1(x)
f
(2) (x )
2!
(x
6
)( x
4
),
1 2
sin x
3 2
0.01319
lagrange插值函数 C语言算法

//mathanaly.c//一元n次Lagrange插值,无需手动数值#include"stdio.h"#include"stdlib.h"double newton(const unsigned int N,const double x[],const double y[],const double t) //插值函数{unsigned int i,j;double sum=0.0,muly=1.0;for(i=0;i<=N-1;i++) //连加循环{for(j=0;j<=N-1;j++){if(j!=i)muly=muly*(t-*(x+j))/(*(x+i)-*(x+j));continue;}sum+=muly*(*(y+i));muly=1.0;}return sum;}int main(){char j; //"char j"用于显示结果,若visual无显示问题,可以删去unsigned int NUM=6;double *a=NULL,*b=NULL,t=0.668,clu;a=(double *)malloc(NUM*sizeof(double));*(a+0)=0.4;*(a+1)=0.5;*(a+2)=0.6;*(a+3)=0.7;*(a+4)=0.8;*(a+5)=0.9;b=(double *)malloc(NUM*sizeof(double));*(b+0)=0.38942;*(b+1)=0.47943;*(b+2)=0.56464;*(b+3)=0.64422;*(b+4)=0.71736;* (b+5)=0.23781;clu=newton(NUM,a,b,t); //调用函数计算结果printf("the conclusion is %lf\n",clu);getchar(); //用来显示结果,若visual无显示问题,可以删去 j=getchar();return 0;}//mathanaly.c//一元n次Lagrange插值,手动输入#include"stdio.h"#include"stdlib.h"double newton(const unsigned int N,const double x[],const double y[],const double t) //插值函数{unsigned int i,j;double sum=0.0,muly=1.0;for(i=0;i<=N-1;i++) //连加循环{for(j=0;j<=N-1;j++){if(j!=i)muly=muly*(t-*(x+j))/(*(x+i)-*(x+j));continue;}sum+=muly*(*(y+i));muly=1.0;}return sum;}int main(){int i; char j; //"char j"用于显示结果,若visual无显示问题,可以删去unsigned int NUM;double *a=NULL,*b=NULL,t,clu;printf("How many nodes is the function?\n");//输入节点个数scanf("%d",&NUM);a=(double *)malloc(NUM*sizeof(double));for(i=0;i<NUM;i++){printf("enter No.%d value of x ",i); //输入节点自变量值scanf("%lf",(a+i));}b=(double *)malloc(NUM*sizeof(double));for(i=0;i<NUM;i++){printf("enter No.%d value of y ",i); //节点函数值scanf("%lf",(b+i));}printf("what's the value of t?\n"); //任给自变量tscanf("%lf",&t);clu=newton(NUM,a,b,t); //调用函数计算结果printf("the conclusion is %lf\n",clu);getchar(); //用来显示结果,若visual无显示问题,可以删去 j=getchar();return 0;}//mathanaly.c//一元n次Lagrange插值,用数组实现#include"stdio.h"#define NUM 6 //NUM=N,是数组长度(常量),结点个数,插值多项式的次数是N-1//不能用const int NUM=6;double newton(const unsigned int N,const double x[],const double y[],const double t) //插值函数{unsigned int i,j;double sum=0.0,muly=1.0;for(i=0;i<=N-1;i++) //连加循环{for(j=0;j<=N-1;j++){if(j!=i)muly=muly*(t-x[j])/(x[i]-x[j]);continue;}sum+=muly*y[i];muly=1.0;}return sum;}int main(){int i; char j; //"char j"用于显示结果,若visual版本无显示问题,可以删去unsigned int n;double a[NUM],b[NUM],t,clu;printf("How many nodes is the function?\n");//输入节点个数scanf("%d",&n);for(i=0;i<NUM;i++){printf("enter No.%d value of x ",i); //输入节点自变量值scanf("%lf",&a[i]);}for(i=0;i<NUM;i++){printf("enter No.%d value of y ",i); //节点函数值scanf("%lf",&b[i]);}printf("what's the value of t?\n"); //任给自变量tscanf("%lf",&t);clu=newton(n,a,b,t); //调用函数计算结果printf("the conclusion is %lf\n",clu);getchar(); //用来显示结果,若visual版本无显示问题,可以删去j=getchar();return 0;}。
lagrange插值法

lagrange 插值法实验基本原理: lagrange 插值法是用来解决离散点的插值问题。
若给定两个插值点),(),,(1100y x y x 其10x x ≠,在公式中取1=n ,则La g r a n g e 插值多项式为:)()()()()()(001010010110101x x x x y y y x x x x y x x x x y x p ---+=--+--=是经过),(),,(1100y x y x 的一条直线,故此法称为线性插值法。
2、若函数给定三个插值点 2,1,0),,(=i y x i i ,,其中i x 互不相等,在公式中取1=n ,则Lagrange 插值多项式为: ))(())(())(())(())(())(()(1202102210120120102102x x x x x x x x y x x x x x x x x y x x x x x x x x y x p ----+----+----=是一个二次函数,若2,1,0),,(=i y x i i 三点不在一条直线上,则该曲线是一条抛物线,这种插值法称为二次插值或抛物插值。
为了解决这个问题,我们为此构造了这个矩阵⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----+---.........))(())(()())((12010212010212010x x x x x x x x x x x x x x x x 就可以找到相应系数。
实验结果分析:在应用拉格朗日插值法时应注意以下几个问题:1、在能获得原始资料时应尽量获取原始资料, 不能盲目地用组数据代入公式来估计未知数据。
2、在利用拉格朗日多项式进行插值估计时, 要求所研究范围的值的变化不受特殊或偶照因素的影响, 即的值是在正常条件下的。
3、如果有两组值(i x ,iy ),(j x ,j y ) 的i x =j x ;则这两组值只能取一组代入多项式计算, 否则便会出现 i y 与j y 的项分母为零的情况这种情况对于这种情况, 用哪组值代入多项式估计更好, 往往不易确定。
拉格朗日插值法

Lagrange polynomial 维基百科,自由的百科全书
定义
对某个多项式函数,已知有给定的 个取值点:
其中 对应着自变量的位置,而 对应着函数在这个位置(每一个y值都不等于0)的取 值。 假设任意两个不同的 都互不相同,那么应用拉格朗日插值公式所得到的拉格朗 日插值多项式为:
其中每个
几何性质
拉格朗日插值法中用到的拉格朗日基本多项式 (由某一组 确定)可以看做是由次数不超过 n 的多项式所组成的线性空 间: 的一组基底。首先,如果存在一组系数: 使得, , 那么,一方面多项式P是满足 的拉格 朗日插值多项式,另一方面P是零多项式,所以取值永远是0。所以 。 这证明了 是线性无关的。同时它一共包含 个多项式,恰好等于 的维数。所以 构成了 的一组基底。 拉格朗日基本多项式作为基底的好处是所有的多项式都是齐次的(都是 n 次多项 式)。
重心拉格朗日插值法
重心拉格朗日插值法是拉格朗日插值法的一种改进。在拉格朗日插值法中,运用 多项式 可以将拉格朗日基本多项式重新写为:
定义重心权
上面的表达式可以简化为:
于是拉格朗日插值多项式变为:
即所谓的重心拉格朗日插值公式(第一型)或改进拉格朗日插值公式。它的优点 是当插值点的个数增加一个时,将每个 都除以 ,就可以得到新的重 心权 ,计算复杂度为 ,比重新计算每个基本多项式所需要的复杂度 降了一个量级。 将以上的拉格朗日插值多项式用来对函数 插值,可以得到:
优点与缺点
拉格朗日插值法的公式结构整齐紧凑,在理论分析中十分方便,然而在计算中, 当插值点增加或减少一个时,所对应的基本多项式就需要全部重新计算,于是整 个公式都会变化,非常繁琐。这时可以用重心拉格朗日插值法或牛顿插值法来代 替。此外,当插值点比较多的时候,拉格朗日插值多项式的次数可能会很高,因 此具有数值不稳定的特点,也就是说尽管在已知的几个点取到给定的数值,但在 附近却会和“实际上”的值之间有很大的偏差(如右下图)。这类现象也被称为龙 格现象,解决的办法是分段用较低次数的插值多项式。
《Lagrange插值》课件

( j k 1, k 1);
( j k 1, k).
Lagrange插值多项式的构造
例如 : 求lk1( x),
因它
有
两个零
点xk
及xk
,故可表
1
示
为
lk1 ( x) A( x xk )( x xk1 ), 其中A为待定系数,可由条件lk1( xk1 ) 1
定出
A
( xk1
xk
若在 a,b上用Ln( x)近似 f ( x),则其截断误差 R(n x) f(x)Ln x,
被称为插值多项式的余项 关于插值余项估计有以下定理。
Lagrange插值余项与误差估计
定理2 设f (n)( x)在a, b上连续,f (n1)( x)在(a, b)内存在,
Ln( x)是满足条件Ln( x j )
从而 (t) 在[a,b]区间上有n 2个零点,由罗尔定理知:
'(t) 在(a,b)内至少有n 1个零点
''(t) 在(a,b)内至少有n个零点
(n1)(t) 在(a, b)内至少有1个零点
记 该零点为 (a,b),则有 (n1) ( ) f (n1) ( ) (n 1)! K( x) 0
L1( xk ) yk , L1( xk1) yk1.
yk
xk
y f (x)
y L1 ( x)
yk1
xk1
Lagrange插值多项式的构造
L1( x)
yk
yk 1 xk 1
yk xk
(x
xk )
( 点斜式),
L1( x)
x xk1 xk xk1
yk
x xk xk1 xk
yk1
Lagrange插值法.ppt

第1列是病人编号,第2列是4种疗法的代码:
1 = 600mg zidovudine(齐多夫定) 与400mg
didanosine(去羟肌苷)按月轮换使用;
2 = 600mg zidovudine 加2.25mg zalcitabine(双脱
氧胞苷 );
3 = 600mg zidovudine 加400mg didanosine;
4 = 600mg zidovudine 加400mg didanosine 加
400mg nevirapine(奈韦拉平 )。
第3列是病人年龄,第4列是测试CD4的时刻(周),第5列是
测得的CD4,取值log(CD4+1).
ID 疗法 年龄
时间 Log(CD4 count+1)
1 2 36.4271 0
第四章 插值与拟合
1/46
引例及问题综述
在生产和实验中,函数f (x)无表达式, 只知道f(x) 在一些给定点的函数值(或其导数值) ,或者其表达式 复杂不便于计算,此时我们希望建立一个简单而又便 于计算的函数(x),使其近似的代替f(x).
求近似函数(x)的方法一般分为两类: 一类是插值, 另一类是拟合.
CD40 0
第一组
20
40
时刻(周)
第二组
CD4(/mm3)
400 300 200 100
0 0
20
40
时刻(周)
计算方法四①
CD4浓度(/mm3)
60
400 300 200 100
0 0
60
8/46
第三组
20
40
60
时刻(周)
CD4/HIV
CD4/HIV
实验四 Lagrange函数插值方法(新)
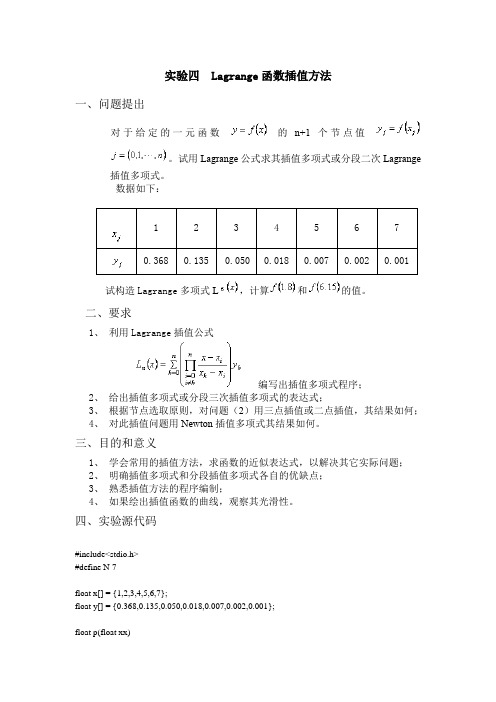
实验四 Lagrange函数插值方法一、问题提出对于给定的一元函数的n+1个节点值。
试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。
数据如下:试构造Lagrange多项式L,计算和的值。
二、要求1、利用Lagrange插值公式编写出插值多项式程序;2、给出插值多项式或分段三次插值多项式的表达式;3、根据节点选取原则,对问题(2)用三点插值或二点插值,其结果如何;4、对此插值问题用Newton插值多项式其结果如何。
三、目的和意义1、学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;2、明确插值多项式和分段插值多项式各自的优缺点;3、熟悉插值方法的程序编制;4、如果绘出插值函数的曲线,观察其光滑性。
四、实验源代码#include<stdio.h>#define N 7float x[] = {1,2,3,4,5,6,7};float y[] = {0.368,0.135,0.050,0.018,0.007,0.002,0.001};float p(float xx){int i,k;_______________for( i=0; i<N; i++ ){m1 = 1; m2 = 1;_______________if( k != i ) {________________ ________________________________ }return pp;}main(){printf( "f(1.8)=%lf\n", p(1.8) ); ____________________}五、实验结果六、实验心得与体会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 Lagrange函数插值方法
一、问题提出
对于给定的一元函数的n+1个节点值。
试用Lagrange公式求其插值多项式或分段二次Lagrange
插值多项式。
数据如下:
试构造Lagrange多项式L,计算和的值。
二、要求
1、利用Lagrange插值公式
编写出插值多项式程序;
2、给出插值多项式或分段三次插值多项式的表达式;
3、根据节点选取原则,对问题(2)用三点插值或二点插值,其结果如何;
4、对此插值问题用Newton插值多项式其结果如何。
三、目的和意义
1、学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;
2、明确插值多项式和分段插值多项式各自的优缺点;
3、熟悉插值方法的程序编制;
4、如果绘出插值函数的曲线,观察其光滑性。
四、实验源代码
#include<stdio.h>
#define N 7
float x[] = {1,2,3,4,5,6,7};
float y[] = {0.368,0.135,0.050,0.018,0.007,0.002,0.001};
float p(float xx)
{
int i,k;
_______________
for( i=0; i<N; i++ )
{
m1 = 1; m2 = 1;
_______________
if( k != i ) {
________________ ________________
________________ }
return pp;
}
main()
{
printf( "f(1.8)=%lf\n", p(1.8) ); ____________________
}
五、实验结果
六、实验心得与体会。
