Astar算法与深度优先算法解决走迷宫问题

合集下载

迷宫问题算法

迷宫问题算法一、引言迷宫问题是一个经典的算法问题，对于寻找路径的算法有着广泛的应用。

迷宫是一个由通路和墙壁组成的结构，从起点出发，要找到通往终点的路径。

迷宫问题算法主要解决的是如何找到一条从起点到终点的最短路径。

二、DFS（深度优先搜索）算法深度优先搜索算法是迷宫问题求解中最常用的算法之一。

其基本思想是从起点开始，沿着一个方向不断向前走，当走到无法继续前进的位置时，回退到上一个位置，选择另一个方向继续前进，直到找到终点或者无路可走为止。

1. 算法步骤1.初始化一个空栈，并将起点入栈。

2.当栈不为空时，取出栈顶元素作为当前位置。

3.如果当前位置是终点，则返回找到的路径。

4.如果当前位置是墙壁或者已经访问过的位置，则回退到上一个位置。

5.如果当前位置是通路且未访问过，则将其加入路径中，并将其邻居位置入栈。

6.重复步骤2-5，直到找到终点或者栈为空。

2. 算法实现伪代码以下为DFS算法的实现伪代码：procedure DFS(maze, start, end):stack := empty stackpath := empty listvisited := empty setstack.push(start)while stack is not empty docurrent := stack.pop()if current == end thenreturn pathif current is wall or visited.contains(current) thencontinuepath.append(current)visited.add(current)for each neighbor in getNeighbors(current) dostack.push(neighbor)return "No path found"三、BFS（广度优先搜索）算法广度优先搜索算法也是解决迷宫问题的常用算法之一。

迷宫问题_上机实验报告

一、实验目的1. 熟悉迷宫问题的基本概念和解决方法。

2. 掌握一种或多种迷宫求解算法。

3. 通过编程实践，提高算法设计和编程能力。

二、实验环境1. 操作系统：Windows 102. 编程语言：Python3.73. 开发工具：PyCharm三、实验内容迷宫问题是指在一个二维网格中，给定起点和终点，求解从起点到终点的路径。

本实验采用深度优先搜索（DFS）和广度优先搜索（BFS）两种算法进行迷宫求解。

1. 深度优先搜索（DFS）（1）算法原理：DFS算法是一种非确定性算法，其基本思想是沿着一个分支一直走到底，直到无法继续为止，然后回溯到上一个节点，再选择另一个分支继续走。

（2）算法步骤：a. 初始化迷宫，将起点设置为当前节点，将终点设置为目标节点。

b. 创建一个栈，将起点入栈。

c. 当栈不为空时，执行以下操作：a. 弹出栈顶元素，将其标记为已访问。

b. 判断是否为终点，如果是，则输出路径并结束算法。

c. 获取当前节点的上下左右邻居节点，如果邻居节点未被访问，则将其入栈。

d. 当栈为空时，算法结束。

（3）代码实现：```pythondef dfs(maze, start, end):stack = [start]visited = set()path = []while stack:node = stack.pop()if node == end:return path + [node]visited.add(node)for neighbor in get_neighbors(maze, node): if neighbor not in visited:stack.append(neighbor)path.append(node)return Nonedef get_neighbors(maze, node):x, y = nodeneighbors = []if x > 0 and maze[x-1][y] == 0:neighbors.append((x-1, y))if y > 0 and maze[x][y-1] == 0:neighbors.append((x, y-1))if x < len(maze)-1 and maze[x+1][y] == 0:neighbors.append((x+1, y))if y < len(maze[0])-1 and maze[x][y+1] == 0:neighbors.append((x, y+1))return neighbors```2. 广度优先搜索（BFS）（1）算法原理：BFS算法是一种确定性算法，其基本思想是从起点开始，按照一定顺序遍历所有节点，直到找到终点。

迷宫问题程序设计课设

迷宫问题程序设计课设迷宫问题是一个经典的程序设计课设题目。

下面我将从多个角度全面完整地回答这个问题。

首先，我们需要明确迷宫问题的具体要求。

通常来说，迷宫由一个矩形网格组成，其中包含起点和终点。

我们的任务是设计一个程序，能够找到从起点到终点的路径，并将其输出。

在程序设计的过程中，我们可以采用不同的算法来解决迷宫问题。

下面是一些常用的算法：1. 深度优先搜索（DFS），这是一种经典的算法，通过递归的方式搜索迷宫中的路径。

它会沿着一个方向一直前进，直到无法继续为止，然后回溯到上一个节点，继续搜索其他方向。

这个算法的优点是简单易懂，但可能会陷入无限循环。

2. 广度优先搜索（BFS），这是另一种常用的算法，通过队列的方式搜索迷宫中的路径。

它会先搜索距离起点最近的节点，然后逐层扩展搜索，直到找到终点或者搜索完所有可能的路径。

这个算法的优点是能够找到最短路径，但可能会消耗更多的内存。

3. A算法，这是一种启发式搜索算法，通过估计距离终点的代价来指导搜索。

它综合了深度优先搜索和广度优先搜索的优点，能够在保证找到最短路径的情况下，减少搜索的时间和空间复杂度。

在实现迷宫问题的程序时，我们需要考虑以下几个方面：1. 迷宫的表示，我们可以使用二维数组或者图的数据结构来表示迷宫。

二维数组中的每个元素可以表示一个网格，其中不同的值代表不同的状态（如墙壁、通道、起点、终点等）。

2. 路径搜索，根据选择的算法，我们需要实现相应的搜索函数。

搜索函数的输入参数通常包括迷宫的表示、起点和终点的坐标等。

输出可以是找到的路径或者一个布尔值（表示是否存在路径）。

3. 路径输出，一旦找到路径，我们需要将其输出。

可以使用递归或者栈等数据结构来保存路径，并按照一定的格式输出。

4. 可视化展示，为了更好地理解算法的执行过程，我们可以考虑将迷宫和路径进行可视化展示。

可以使用图形库或者终端输出等方式实现。

最后，我们还需要进行测试和优化。

对于测试，我们可以设计一些具有不同特点的迷宫，并验证程序的正确性和效率。

数据结构程序设计(迷宫问题)

数据结构程序设计(迷宫问题)数据结构程序设计(迷宫问题)一、引言迷宫问题是计算机科学中常见的问题之一，它涉及到了数据结构的设计和算法的实现。

本文将介绍迷宫问题的定义、常见的解决算法和程序设计思路。

二、问题定义迷宫问题可以描述为：给定一个迷宫，迷宫由若干个连通的格子组成，其中有些格子是墙壁，有些格子是路径。

任务是找到一条从迷宫的起点（通常是左上角）到终点（通常是右下角）的路径。

三、基本数据结构1.迷宫表示：迷宫可以使用二维数组来表示，数组中的每个元素代表一个格子，可以用0表示路径，用1表示墙壁。

2.坐标表示：可以使用二维坐标表示迷宫中的每一个格子，使用(x, y)的形式表示。

四、算法设计1.深度优先搜索算法：深度优先搜索算法可以用来解决迷宫问题。

算法从起点开始，尝试向四个方向中的一个方向前进，如果可以移动则继续向前，直到到达终点或无法继续移动。

如果无法继续移动，则回溯到上一个节点，选择另一个方向继续搜索，直到找到一条路径或者所有路径都已经探索完毕。

2.广度优先搜索算法：广度优先搜索算法也可以用来解决迷宫问题。

算法从起点开始，先将起点加入队列，然后不断从队列中取出节点，并尝试向四个方向中的一个方向移动，将新的节点加入队列。

直到找到终点或者队列为空，如果队列为空则表示无法找到路径。

五、程序设计思路1.深度优先搜索算法实现思路：a) 使用递归函数来实现深度优先搜索算法，参数为当前节点的坐标和迷宫数据结构。

b) 判断当前节点是否为终点，如果是则返回成功。

c) 判断当前节点是否为墙壁或已访问过的节点，如果是则返回失败。

d) 将当前节点标记为已访问。

e) 递归调用四个方向，如果存在一条路径则返回成功。

f) 如果四个方向都无法找到路径，则将当前节点重新标记为未访问，并返回失败。

2.广度优先搜索算法实现思路：a) 使用队列保存待访问的节点。

b) 将起点加入队列，并标记为已访问。

c) 不断从队列中取出节点，尝试向四个方向移动，如果新的节点未被访问过且不是墙壁，则将新的节点加入队列，并标记为已访问。

迷宫问题求解算法设计实验报告

迷宫问题求解算法设计实验报告一、引言迷宫问题一直是计算机科学中的一个经典问题，其解决方法也一直是研究者们探讨的重点之一。

本实验旨在通过设计不同的算法，对迷宫问题进行求解，并对比不同算法的效率和优缺点。

二、算法设计1. 暴力搜索算法暴力搜索算法是最简单直接的求解迷宫问题的方法。

其基本思路是从起点开始，按照某种规则依次尝试所有可能的路径，直到找到终点或所有路径都被尝试过为止。

2. 广度优先搜索算法广度优先搜索算法也称为BFS（Breadth First Search），其基本思路是从起点开始，按照层次依次遍历每个节点，并将其相邻节点加入队列中。

当找到终点时，即可得到最短路径。

3. 深度优先搜索算法深度优先搜索算法也称为DFS（Depth First Search），其基本思路是从起点开始，沿着某一个方向走到底，再回溯到上一个节点继续向其他方向探索。

当找到终点时，即可得到一条路径。

4. A* 算法A* 算法是一种启发式搜索算法，其基本思路是综合考虑节点到起点的距离和节点到终点的距离，选择最优的路径。

具体实现中，可以使用估价函数来计算每个节点到终点的距离，并将其加入优先队列中。

三、实验过程本实验使用 Python 语言编写程序，在不同算法下对迷宫问题进行求解。

1. 数据准备首先需要准备迷宫数据，可以手动输入或从文件中读取。

本实验使用二维数组表示迷宫，其中 0 表示墙壁，1 表示路径。

起点和终点分别用 S 和 E 表示。

2. 暴力搜索算法暴力搜索算法比较简单直接，只需要按照某种规则遍历所有可能的路径即可。

具体实现中，可以使用递归函数来实现深度遍历。

3. 广度优先搜索算法广度优先搜索算法需要使用队列来存储待遍历的节点。

具体实现中，每次从队列中取出一个节点，并将其相邻节点加入队列中。

4. 深度优先搜索算法深度优先搜索算法也需要使用递归函数来实现深度遍历。

具体实现中，在回溯时需要将已经访问过的节点标记为已访问，防止重复访问。

迷宫求解实验报告

迷宫求解实验报告迷宫求解实验报告引言：迷宫作为一种经典的智力游戏，一直以来都备受人们的喜爱。

在这个实验中，我们尝试使用计算机算法来解决迷宫问题。

通过设计并实现一个迷宫求解程序，我们将探索不同的算法和策略，以找到最佳路径解决迷宫。

实验设计：我们首先定义了迷宫的基本结构。

迷宫由一个二维矩阵表示，其中0代表通路，1代表墙壁。

我们使用了一个常见的5x5迷宫作为实验样本，其中包括了起点和终点。

接下来，我们尝试了两种不同的算法来解决迷宫问题。

算法一：深度优先搜索（DFS）深度优先搜索是一种常见的图搜索算法，在解决迷宫问题中也有广泛的应用。

该算法从起点开始，沿着一个路径一直向前探索，直到遇到死路或者到达终点。

如果遇到死路，则回溯到上一个节点，继续探索其他路径，直到找到一条通往终点的路径。

我们实现了一个递归函数来实现深度优先搜索算法。

通过不断调用该函数，我们可以找到一条从起点到终点的路径。

然而，由于深度优先搜索的特性，它并不能保证找到最短路径。

在我们的实验中，深度优先搜索找到的路径长度为8步。

算法二：广度优先搜索（BFS）广度优先搜索是另一种常见的图搜索算法，与深度优先搜索不同的是，它优先探索所有的相邻节点，再逐层向外扩展。

在解决迷宫问题时，广度优先搜索可以保证找到最短路径。

我们使用了一个队列数据结构来实现广度优先搜索算法。

通过不断将相邻节点加入队列，并记录每个节点的前驱节点，我们可以在找到终点后，追溯回起点，从而找到最短路径。

在我们的实验中，广度优先搜索找到的路径长度为6步。

实验结果：通过对比深度优先搜索和广度优先搜索的结果，我们可以看出广度优先搜索算法在解决迷宫问题时更加高效。

虽然深度优先搜索算法可以找到一条路径，但它并不能保证是最短路径。

而广度优先搜索算法通过逐层扩展的方式，可以保证找到的路径是最短的。

讨论与总结：通过这个实验，我们不仅学习了迷宫求解的基本算法，还深入了解了深度优先搜索和广度优先搜索的原理和应用。

迷宫最短路径算法

迷宫最短路径算法一、引言迷宫最短路径算法是指在迷宫中找到从起点到终点的最短路径的算法。

在实际应用中，迷宫最短路径算法可以用于机器人导航、游戏设计等领域。

本文将介绍几种常见的迷宫最短路径算法，包括深度优先搜索、广度优先搜索、Dijkstra 算法和 A* 算法。

二、深度优先搜索深度优先搜索是一种基于栈的搜索算法，其主要思想是从起点开始，沿着某个方向一直走到底，直到无路可走时回溯到上一个节点。

具体实现时，可以使用递归或手动维护栈来实现。

三、广度优先搜索广度优先搜索是一种基于队列的搜索算法，其主要思想是从起点开始，依次将与当前节点相邻且未被访问过的节点加入队列，并标记为已访问。

然后从队列头部取出下一个节点作为当前节点，并重复以上操作直到找到终点或队列为空。

四、Dijkstra 算法Dijkstra 算法是一种贪心算法，在图中寻找从起点到终点的最短路径。

具体实现时，首先将起点标记为已访问，并将其与所有相邻节点的距离加入一个优先队列中。

然后从队列中取出距离最小的节点作为当前节点，并更新其相邻节点到起点的距离。

重复以上操作直到找到终点或队列为空。

五、A* 算法A* 算法是一种启发式搜索算法，其主要思想是在广度优先搜索的基础上引入启发函数，用于评估每个节点到终点的估计距离。

具体实现时，将起点加入开放列表，并计算其到终点的估价函数值。

然后从开放列表中取出估价函数值最小的节点作为当前节点，并将其相邻未访问节点加入开放列表中。

重复以上操作直到找到终点或开放列表为空。

六、总结以上介绍了几种常见的迷宫最短路径算法，包括深度优先搜索、广度优先搜索、Dijkstra 算法和 A* 算法。

不同算法适用于不同场景，需要根据实际情况选择合适的算法。

在实际应用中，还可以结合多种算法进行优化，以提高寻路效率和精确度。

深度优先搜索实验报告

深度优先搜索实验报告引言深度优先搜索（Depth First Search，DFS）是图论中的一种重要算法，主要用于遍历和搜索图的节点。

在实际应用中，DFS被广泛用于解决迷宫问题、图的连通性问题等，具有较高的实用性和性能。

本实验旨在通过实际编程实现深度优先搜索算法，并通过实际案例验证其正确性和效率。

实验中我们将以迷宫问题为例，使用深度优先搜索算法寻找从入口到出口的路径。

实验过程实验准备在开始实验之前，我们需要准备一些必要的工具和数据。

1. 编程环境：我们选择使用Python语言进行编程实验，因其语法简洁而强大的数据处理能力。

2. 迷宫地图：我们需要设计一个迷宫地图，包含迷宫的入口和出口，以及迷宫的各个路径和墙壁。

实验步骤1. 首先，我们需要将迷宫地图转化为计算机可处理的数据结构。

我们选择使用二维数组表示迷宫地图，其中0表示墙壁，1表示路径。

2. 接着，我们将编写深度优先搜索算法的实现。

在DFS函数中，我们将使用递归的方式遍历迷宫地图的所有路径，直到找到出口或者遇到墙壁。

3. 在每次遍历时，我们将记录已经访问过的路径，以防止重复访问。

4. 当找到出口时，我们将输出找到的路径，并计算路径的长度。

实验结果经过实验，我们成功地实现了深度优先搜索算法，并在迷宫地图上进行了测试。

以下是我们的实验结果：迷宫地图：1 1 1 1 11 0 0 0 11 1 1 0 11 0 0 0 11 1 1 1 1最短路径及长度：(1, 1) -> (1, 2) -> (1, 3) -> (1, 4) -> (2, 4) -> (3, 4) -> (4, 4) -> (5, 4)路径长度：7从实验结果可以看出，深度优先搜索算法能够准确地找到从入口到出口的最短路径，并输出了路径的长度。

实验分析我们通过本实验验证了深度优先搜索算法的正确性和有效性。

然而，深度优先搜索算法也存在一些缺点：1. 只能找到路径的一种解，不能确定是否为最优解。

深度优先搜索（深搜）——DeepFirstSearch【例题：迷宫】

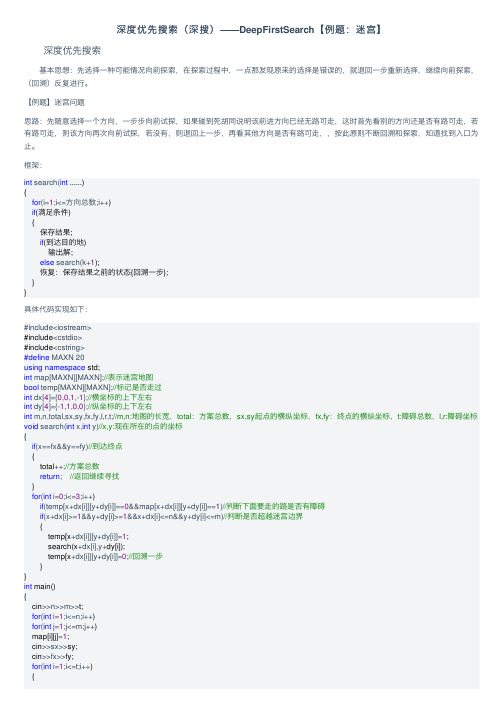
深度优先搜索（深搜）——DeepFirstSearch【例题：迷宫】深度优先搜索基本思想：先选择⼀种可能情况向前探索，在探索过程中，⼀点那发现原来的选择是错误的，就退回⼀步重新选择，继续向前探索，（回溯）反复进⾏。

【例题】迷宫问题思路：先随意选择⼀个⽅向，⼀步步向前试探，如果碰到死胡同说明该前进⽅向已经⽆路可⾛，这时⾸先看别的⽅向还是否有路可⾛，若有路可⾛，则该⽅向再次向前试探，若没有，则退回上⼀步，再看其他⽅向是否有路可⾛，，按此原则不断回溯和探索，知道找到⼊⼝为⽌。

框架：int search(int ......){for(i=1;i<=⽅向总数;i++)if(满⾜条件){保存结果;if(到达⽬的地)输出解;else search(k+1);恢复：保存结果之前的状态{回溯⼀步};}}具体代码实现如下：#include<iostream>#include<cstdio>#include<cstring>#define MAXN 20using namespace std;int map[MAXN][MAXN];//表⽰迷宫地图bool temp[MAXN][MAXN];//标记是否⾛过int dx[4]={0,0,1,-1};//横坐标的上下左右int dy[4]={-1,1,0,0};//纵坐标的上下左右int m,n,total,sx,sy,fx,fy,l,r,t;//m,n:地图的长宽，total：⽅案总数，sx,sy起点的横纵坐标，fx,fy：终点的横纵坐标，t:障碍总数，l,r:障碍坐标void search(int x,int y)//x,y:现在所在的点的坐标{if(x==fx&&y==fy)//到达终点{total++;//⽅案总数return; //返回继续寻找}for(int i=0;i<=3;i++)if(temp[x+dx[i]][y+dy[i]]==0&&map[x+dx[i]][y+dy[i]]==1)//判断下⾯要⾛的路是否有障碍if(x+dx[i]>=1&&y+dy[i]>=1&&x+dx[i]<=n&&y+dy[i]<=m)//判断是否超越迷宫边界{temp[x+dx[i]][y+dy[i]]=1;search(x+dx[i],y+dy[i]);temp[x+dx[i]][y+dy[i]]=0;//回溯⼀步}}int main(){cin>>n>>m>>t;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)map[i][j]=1;cin>>sx>>sy;cin>>fx>>fy;for(int i=1;i<=t;i++){cin>>l>>r;map[l][r]=0;}map[sx][sy]=0; search(sx,sy); printf("%d",total); return0;}。

栈和队列的应用——迷宫问题（深度、广度优先搜索）

栈和队列的应⽤——迷宫问题（深度、⼴度优先搜索）⼀、迷宫问题给⼀个⼆维列表，表⽰迷宫（0表⽰通道，1表⽰围墙）。

给出算法，求⼀条⾛出迷宫的路径。

maze = [[1,1,1,1,1,1,1,1,1,1],[1,0,0,1,0,0,0,1,0,1],[1,0,0,1,0,0,0,1,0,1],[1,0,0,0,0,1,1,0,0,1],[1,0,1,1,1,0,0,0,0,1],[1,0,0,0,1,0,0,0,0,1],[1,0,1,0,0,0,1,0,0,1],[1,0,1,1,1,0,1,1,0,1],[1,1,0,0,0,0,0,0,0,1],[1,1,1,1,1,1,1,1,1,1]] 1代表墙，0代表路，图⽰如下：⼆、栈——深度优先搜索应⽤栈解决迷宫问题，叫做深度优先搜索（⼀条路⾛到⿊），也叫做回溯法。

1、⽤栈解决的思路思路：从上⼀个节点开始，任意找下⼀个能⾛的点，当找不到能⾛的点时，退回上⼀个点寻找是否有其他⽅向的点。

使⽤栈存储当前路径。

后进先出，⽅便回退到上⼀个点。

2、⽤栈代码实现maze = [[1,1,1,1,1,1,1,1,1,1],[1,0,0,1,0,0,0,1,0,1],[1,0,0,1,0,0,0,1,0,1],[1,0,0,0,0,1,1,0,0,1],[1,0,1,1,1,0,0,0,0,1],[1,0,0,0,1,0,0,0,0,1],[1,0,1,0,0,0,1,0,0,1],[1,0,1,1,1,0,1,1,0,1],[1,1,0,0,0,0,0,0,0,1],[1,1,1,1,1,1,1,1,1,1]]# 四个移动⽅向dirs = [lambda x,y: (x+1, y), # 下lambda x,y: (x-1, y), # 上lambda x,y: (x, y-1), # 左lambda x,y: (x, y+1) # 右]def maze_path(x1, y1, x2, y2): # (x1,y1)代表起点；(x2,y2)代表终点stack = []stack.append((x1, y1))while(len(stack)>0):curNode = stack[-1] # 当前的节点(栈顶)if curNode[0] ==x2 and curNode[1] == y2: # 判断是否⾛到终点# ⾛到终点，遍历栈输出路线for p in stack:print(p)return True"""搜索四个⽅向"""for dir in dirs:nextNode = dir(curNode[0], curNode[1])# 如果下⼀个阶段能⾛if maze[nextNode[0]][nextNode[1]] == 0:stack.append(nextNode) # 将节点加⼊栈maze[nextNode[0]][nextNode[1]] = 2 # 将⾛过的这个节点标记为2表⽰已经⾛过了break # 找到⼀个能⾛的点就不再遍历四个⽅向else:# ⼀个都找不到，将该位置标记并该回退maze[nextNode[0]][nextNode[1]] = 2stack.pop()else:print("没有路")return Falsemaze_path(1,1,8,8)"""(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (5, 2) (5, 3) (6, 3) (6, 4)(6, 5) (7, 5) (8, 5) (8, 6) (8, 7) (8, 8)""" 总结算法就是：创建⼀个空栈，⾸先将⼊⼝位置进栈。

如何使用深度优先搜索算法求解迷宫问题

如何使用深度优先搜索算法求解迷宫问题深度优先搜索算法是一种在解决迷宫问题时非常重要的算法。

迷宫问题是指一个由墙壁和路径组成的迷宫，其中寻找通往出口的路径是一个有趣和富有挑战性的问题。

深度优先搜索算法可以从起点开始搜索所有可能的路径，直到找到通向出口的路径为止。

本文将介绍如何使用深度优先搜索算法来解决迷宫问题。

1. 确定问题的规模和范围在开始解决迷宫问题前，我们需要确定迷宫的规模和范围。

迷宫的规模通常由迷宫的行数和列数表示。

例如，一个5行7列的迷宫由35个方格组成。

确定迷宫的范围还包括确定哪些方格是起点和终点，以及哪些方格是墙壁和路径。

2. 确定深度优先搜索算法的基本原理和步骤深度优先搜索算法是一种无向图算法，其基本原理是从起点开始搜索，沿着路径向前探索下去，每当遇到岔路口的时候就随机选择一条路径继续前进，直到走到终点或遇到死路为止。

搜索的顺序是从最深处开始向外扩展。

在搜索过程中，需要维护一个栈来存储当前路径。

深度优先搜索算法的步骤如下：（1）初始化：将起点加入栈中。

（2）循环：从栈中取出一个节点进行扩展。

（3）判断是否到达终点：如果当前节点是终点，则搜索结束。

（4）扩展节点：将当前节点的所有相邻节点加入栈中。

（5）递归深度优先搜索：从栈中取出下一个节点进行搜索。

（6）回溯：如果当前节点没有可扩展的节点，则从栈中取出上一个节点进行搜索。

3. 编写深度优先搜索算法的伪代码在深度优先搜索算法的基础上，我们需要编写具体的伪代码来实现解决迷宫问题。

算法输入：一个迷宫。

算法输出：通向终点的路径。

1. 初始化：将起点加入栈中。

记录起点的位置为（x1，y1）。

将起点标记为已访问。

2. 循环：如果栈不为空，则：取出栈顶节点进行扩展。

记录扩展节点的位置为（x，y）。

标记扩展节点为已访问。

如果当前节点是终点，则搜索结束。

如果当前节点不是终点，则：遍历当前节点的所有相邻节点：如果相邻节点未访问且不是墙壁，则：将相邻节点加入栈中。

数学迷宫用数学思维解决迷题寻找正确答案的路径

数学迷宫用数学思维解决迷题寻找正确答案的路径数学迷宫：用数学思维解决迷题寻找正确答案的路径迷宫一直以来都是个令人神往的地方，充满未知和挑战。

而当我们以数学的眼光看待迷宫时，它可能不再那么神秘。

数学思维可以帮助我们解决迷题，寻找迷宫中的正确答案路径。

本文将探讨如何运用数学思维解决数学迷宫问题。

一、迷宫的数学模型在寻找路径的过程中，我们首先需要将迷宫抽象成一个数学模型。

通常，我们可以使用二维坐标系来表示迷宫的布局。

将每个迷宫单元格看作一个节点，而每个节点之间的路径看作连线。

这样，我们就可以将迷宫转化为一个图论问题。

二、图论的应用图论是数学中研究节点和节点之间关系的一个分支。

在求解迷宫问题时，我们可以将迷宫表示为一个图。

每个节点代表一个迷宫单元格，而每条边代表两个相邻节点之间的路径。

通过分析这个图，我们可以找到解决迷宫问题的方法。

三、深度优先搜索算法深度优先搜索算法是一种常用的图搜索算法，可用于求解迷宫问题。

算法的基本思想是从起点开始，沿着一条路径一直向前，直到无法继续为止。

然后，回退到上一个节点，选择另一条路径继续前进，直到找到终点为止。

在应用深度优先搜索算法解决迷宫问题时，我们需要使用一个栈来保存访问过的节点。

当到达一个节点后，将其加入栈中，并标记为已访问。

然后，选择一个相邻节点，继续前进。

如果到达终点，则成功找到了路径；如果无法继续前进，则回退到上一个节点，选择另一条路径。

不断重复这个过程，直到找到路径或者遍历完所有可能的路径。

四、最短路径算法除了深度优先搜索算法外，最短路径算法也是解决迷宫问题的一种常见方法。

最短路径算法可以找到从起点到终点的最短路径，并给出这条路径的长度。

其中，迪杰斯特拉算法是一种常用的最短路径算法之一。

该算法通过不断更新起点到其他节点的最短距离来求解最短路径。

具体而言，算法首先将起点到所有其他节点的距离初始化为无穷大，然后逐步迭代，更新起点到每个节点的最短距离。

最后，根据这些最短距离构造出最短路径。

深度优先搜索算法利用深度优先搜索解决迷宫问题

深度优先搜索算法利用深度优先搜索解决迷宫问题深度优先搜索算法（Depth-First Search, DFS）是一种常用的图遍历算法，它通过优先遍历图中的深层节点来搜索目标节点。

在解决迷宫问题时，深度优先搜索算法可以帮助我们找到从起点到终点的路径。

一、深度优先搜索算法的实现原理深度优先搜索算法的实现原理相当简单直观。

它遵循以下步骤：1. 选择一个起始节点，并标记为已访问。

2. 递归地访问其相邻节点，若相邻节点未被访问，则标记为已访问，并继续访问其相邻节点。

3. 重复步骤2直到无法继续递归访问，则返回上一级节点，查找其他未被访问的相邻节点。

4. 重复步骤2和3，直到找到目标节点或者已经遍历所有节点。

二、利用深度优先搜索算法解决迷宫问题迷宫问题是一个经典的寻找路径问题，在一个二维的迷宫中，我们需要找到从起点到终点的路径。

利用深度优先搜索算法可以很好地解决这个问题。

以下是一种可能的解决方案：```1. 定义一个二维数组作为迷宫地图，其中0代表通路，1代表墙壁。

2. 定义一个和迷宫地图大小相同的二维数组visited，用于记录节点是否已经被访问过。

3. 定义一个存储路径的栈path，用于记录从起点到终点的路径。

4. 定义一个递归函数dfs，参数为当前节点的坐标(x, y)。

5. 在dfs函数中，首先判断当前节点是否为终点，如果是则返回True，表示找到了一条路径。

6. 然后判断当前节点是否越界或者已经访问过，如果是则返回False，表示该路径不可行。

7. 否则，将当前节点标记为已访问，并将其坐标添加到path路径中。

8. 依次递归访问当前节点的上、下、左、右四个相邻节点，如果其中任意一个节点返回True，则返回True。

9. 如果所有相邻节点都返回False，则将当前节点从path路径中删除，并返回False。

10. 最后，在主函数中调用dfs函数，并判断是否找到了一条路径。

```三、示例代码```pythondef dfs(x, y):if maze[x][y] == 1 or visited[x][y] == 1:return Falseif (x, y) == (end_x, end_y):return Truevisited[x][y] = 1path.append((x, y))if dfs(x+1, y) or dfs(x-1, y) or dfs(x, y+1) or dfs(x, y-1): return Truepath.pop()return Falseif __name__ == '__main__':maze = [[0, 1, 1, 0, 0],[0, 0, 0, 1, 0],[1, 1, 0, 0, 0],[1, 1, 1, 1, 0],[0, 0, 0, 1, 0]]visited = [[0] * 5 for _ in range(5)]path = []start_x, start_y = 0, 0end_x, end_y = 4, 4if dfs(start_x, start_y):print("Found path:")for x, y in path:print(f"({x}, {y}) ", end="")print(f"\nStart: ({start_x}, {start_y}), End: ({end_x}, {end_y})") else:print("No path found.")```四、总结深度优先搜索算法是一种有效解决迷宫问题的算法。

A星算法解决迷宫问题说明文档

A*算法解决迷宫问题算法思想：迷宫问题可以表述为：一个二维的网格，0表示点可走，1表示点不可以走，点用（x，y）表示，寻找从某一个给定的起始单元格出发，经由行相邻或列相邻的单元格(可以通过的)，最终可以到达目标单元格的、所走过的单元格序列。

在任一个单元格中，都只能看到与它邻近的4个单元格(如果位于底边，则只有3个；位于4个角上，则只有2个是否能通过)。

A*算法是人工智能中的一种搜索算法，是一种启发式搜索算法，它不需遍历所有节点，只是利用包含问题启发式信息的评价函数对节点进行排序，使搜索方向朝着最有可能找到目标并产生最优解的方向。

它的独特之处是检查最短路径中每个可能的节点时引入了全局信息，对当前节点距终点的距离做出估计，并作为评价节点处于最短路线上的可能性的度量。

A*算法中引入了评估函数，评估函数为：f（n）=g（n）+h（n）其中：n是搜索中遇到的任意状态。

g(n)是从起始状态到n的代价。

h(n)是对n到目标状态代价的启发式估计。

即评估函数f ( n) 是从初始节点到达节点n 处已经付出的代价与节点n 到达目标节点的接近程度估价值的总和。

这里我们定义n点到目标点的最小实际距离为h（n）*，A*算法要满足的条件为：h（n）<=h（n）*迷宫走的时候只能往上下左右走，每走一步，代价为1，这里我们采用的估价函数为当前节点到目标节点的曼哈顿距离，即：h（n）=|end.x –n.x|+ |end.y –n.y|这里end表示迷宫的目标点，n表示当前点，很明显这里h（n）<=h（n）*。

g（n）容易表示，即每走一步的代价是1，所以利用f（n）=g（n）+h（n）这种策略，我们可以不断地逼近目标点，从而找到问题的解。

时间复杂度：m行n列的迷宫矩阵实现算法的时间复杂度为O(m*n).结果演示：源码：#include <queue>#include <vector>#include <iostream>using namespace std;int direc[4][2]={{0,1},{-1,0},{0,-1},{1,0}};enum Flag{SEAL,OPEN,UNVISITED};typedef struct node{int _x,_y; //节点坐标(x,y)int _G; //实际已开销Gint _H; //探测将开销Hint _F; //优先级_F=_G+_H struct node *pre; //前驱顶点}Queue_Node;typedef struct{Flag flag;Queue_Node *point;}Seal;class A_Star{public://构造函数A_Star(){input();}~A_Star(){for(int i=1;i<=_len;++i){for(int j=1;j<=_wid;++j){if(_seal[i][j].point!=NULL){delete _seal[i][j].point;}}}for(i=0;i<=_len;++i){delete []_seal[i];delete []_maze[i];}delete []_seal;delete []_maze;}void input(){cout<<"输入: 迷宫左边长,上边宽! 例如：30 20"<<endl;cin>>_len>>_wid;_seal=new Seal*[_len+1];_maze=new unsigned char*[_len+1];for(int i=0;i<=_len;++i){_seal[i]=new Seal[_wid+1];_maze[i]=new unsigned char[_wid+1];}cout<<"从下一行开始输入迷宫信息："<<endl;for( i=1;i<=_len;++i){for(int j=1;j<=_wid;++j){cin>>_maze[i][j];_seal[i][j].flag=UNVISITED;_seal[i][j].point=NULL;}}cout<<"输入起点坐标,目标点坐标,例如:1 1 30 20"<<endl;cin>>_sx>>_sy>>_ex>>_ey;if(_maze[_sx][_sy]=='1'||_maze[_ex][_ey]=='1'||bound(_sx,_sy)==false||bound(_ex,_ey)==fal se){cout<<"不可能存在这样的情况！"<<endl;return;}cout<<"调用A*算法打印结果如下："<<endl;A();}//A*核心算法void A(){//源点放入开放列表Queue_Node *p_node=new Queue_Node;p_node->pre=NULL;p_node->_H=get_H(_sx,_sy);p_node->_G=0;p_node->_x=_sx;p_node->_y=_sy;p_node->_F=p_node->_H+p_node->_G;_open.push(p_node);_seal[_sx][_sy].flag=OPEN;_seal[_sx][_sy].point=p_node;while(!_open.empty()){p_node=_open.top();_open.pop();int x=p_node->_x;int y=p_node->_y;_seal[x][y].flag=SEAL;for(int i=0;i<4;++i){int tx=x+direc[i][0];int ty=y+direc[i][1];if(bound(tx,ty)==false||_maze[tx][ty]=='1'||_seal[tx][ty].flag==SEAL){continue;}if(_seal[tx][ty].flag==UNVISITED){if(tx==_ex&&ty==_ey){print(p_node);cout<<"("<<tx<<","<<ty<<")"<<endl;cout<<"总共走了:"<<p_node->_F<<"步"<<endl;return;}Queue_Node *temp=new Queue_Node;_seal[tx][ty].flag=OPEN;_seal[tx][ty].point=temp;temp->pre=p_node;temp->_G=p_node->_G+1;temp->_x=tx;temp->_y=ty;temp->_H=get_H(tx,ty);temp->_F=temp->_G+temp->_H;_open.push(temp);}else{Queue_Node *temp=_seal[tx][ty].point;if(p_node->_G+1<temp->_G){temp->_G=p_node->_G+1;temp->pre=p_node;temp->_F=temp->_G+temp->_H;}}}}cout<<"没有从("<<_sx<<","<<_sy<<")--->"<<"("<<_ex<<","<<_ey<<")的路径"<<endl;}//打印路径void print(Queue_Node *p){if(p==NULL){return;}print(p->pre);cout<<"("<<p->_x<<","<<p->_y<<"),";}bool bound(int x,int y){return (x<=_len)&&(x>=1)&&(y<=_wid)&&(y>=1);}int get_H(int x,int y){return ab(x-_ex)+ab(y-_ey);}int ab(int i){return i<0 ? -i:i;}private:struct cmp{bool operator()(Queue_Node *n1,Queue_Node *n2){return n1->_F>n2->_F;}};priority_queue<Queue_Node *,vector<Queue_Node *>,cmp> _open;//最小堆(开放列表) int _len,_wid;//迷宫左边长,上边宽int _sx,_sy,_ex,_ey;Seal **_seal;//动态开辟封闭列表unsigned char **_maze;//迷宫地图};int main(){A_Star test;return 0;}。

深度优先搜索算法和A＊算法在迷宫搜索中的仿真研究

能通过传感器感测到目标点所在的大致位置，然
这些路径中找到最快到达目标点的一条路径，原始的泛洪算法不适合本次实验中的搜救应用，于是，我们在实验中是用深度优先搜索算法进行比较研究。Ｔｋｙｌｔ，Ｔｋｓｉｏａａ究了ＡａａｕＧｏｏａｅｈｓｋ研ｄＫ以及Ｄ算法在ＩＳ（能运输系统）和机器人路Ｔ智
后根据算法一步一步的搜索到目标物。从出发点处找到目标物时所耗的时间我们记录为搜索迷宫
所用的时间，当然，搜救的目的不仅仅是为了找到目标物，同时是需要在找到目标物后将目标物
法要优于深度优先搜索算法。关键词：迷宫搜索；深度优先搜索算法；Ａ＋算法
中囤分类号：Ｔ０．Ｐ３１６文献标识码：Ａ文章编号：１０—０（０１６上）１１０９１４２１）（一００ — ３０３
Ｄｏｉ３６／．ｓ．０－０４２１．（Ｉ．０：１９９Ｊｉｎ１９１．０１６－）３０．ｓ０３
一
１实验研究
１１实验研究方法．
实验研究目的是将算法用于现实搜救中，既然是为了搜救，那么时间是关键，搜索迷宫所用时间的长短就成为评价算法优劣的主要因素。对

迷宫任意两点最优解算法

迷宫任意两点最优解算法迷宫游戏一般是一种思维和逻辑性训练的游戏，最常见的问题是如何找到从起点到终点的最短路径。

为了找到迷宫任意两点的最优解，我们可以采用一定的算法来实现。

1. 定义问题在进行算法设计之前，首先需要确定问题的定义。

问题的输入应该包括迷宫的大小、起点和终点的位置以及障碍物的位置。

问题的输出应该是起点到终点的最短路径。

2. 搜索算法搜索算法是寻找从起点到终点的最短路径的一种常见算法。

其中，广度优先搜索算法（BFS）和深度优先搜索算法（DFS）是比较常用的两种算法。

BFS算法可以保证找到从起点到终点的最短路径，但是需要存储所有可能的路径，因此比较消耗内存。

DFS算法则只需要存储当前路径，可以节省内存，但是不能保证找到最短路径。

3. A*算法A*算法是一种启发式搜索算法，通常被认为是解决迷宫最短路径问题的最佳算法之一。

A*算法使用估价函数来估计到终点的距离，并根据估价函数的值来选择下一步的搜索方向。

与BFS和DFS不同，A*算法只需存储最优的路径，比BFS更节省内存。

与DFS不同，A*算法可以保证找到最短路径。

4. 实现算法在实现算法时，可以使用数据结构来存储迷宫的信息和路径。

通常使用二维数组来表示迷宫，但是也可以使用其他数据结构。

在应用A*算法时，需要选择合适的估价函数。

常用的估价函数包括曼哈顿距离和欧几里德距离等。

较好地估价函数可以提高算法的效率和准确性。

5. 代码实例下面是一个基于A*算法的Python代码实例：```pythonfrom queue import PriorityQueuedef heuristic(a, b):return abs(b[0] - a[0]) + abs(b[1] - a[1])def astar(array, start, goal):neighbors = [(0,1),(0,-1),(1,0),(-1,0)]close_set = set()came_from = {}gscore = {start:0}fscore = {start:heuristic(start, goal)}queue = PriorityQueue()queue.put((0, start))while not queue.empty():current = queue.get()[1]if current == goal:data = []while current in came_from:data.append(current)current = came_from[current]data.append(start)return data[::-1]close_set.add(current)for i, j in neighbors:neighbor = current[0] + i, current[1] + jtentative_g_score = gscore[current] +heuristic(current, neighbor)if 0 <= neighbor[0] < array.shape[0]:if 0 <= neighbor[1] < array.shape[1]:if array[neighbor[0]][neighbor[1]] == 1: continueelse:continueelse:continueif neighbor in close_set andtentative_g_score >= gscore.get(neighbor, 0):continueif tentative_g_score < gscore.get(neighbor, 0) or neighbor not in [i[1]for i in queue.queue]:came_from[neighbor] = currentgscore[neighbor] = tentative_g_scorefscore[neighbor] = tentative_g_score + heuristic(neighbor, goal)queue.put((fscore[neighbor], neighbor)) return False```以上是一个较为基础的A*算法代码实现，可以根据具体需要和问题进行修改和调整。

迷宫算法集锦范文

迷宫算法集锦范文迷宫算法是一种常见的图论算法，通过和回溯技巧来解决在迷宫中寻找路径的问题。

在迷宫中，通常会存在一个起点和一个终点，任务就是找到从起点到终点的路径。

下面我将介绍几种常见的迷宫算法。

1.深度优先（DFS）：深度优先是一种常用的图算法，它遵循一个简单的原则：当达到一些节点时，尽可能深入这个节点的未被访问过的邻居节点。

对于迷宫问题来说，可以通过递归来实现DFS。

从起点开始，每次选择一个未被访问过的邻居节点进行探索，直到找到终点或者无路可走。

2.广度优先（BFS）：广度优先也是一种常用的图算法，不同的是它会首先离起点较近的节点。

在迷宫问题中，BFS可以通过队列来实现。

将起点加入队列，然后依次取出队列中的节点，并将其未被访问过的邻居节点加入队列，直到找到终点或者队列为空。

3. Dijkstra算法：Dijkstra算法是一种解决带权重图最短路径问题的常用算法。

在迷宫问题中，可以将迷宫转化为无权重图，将每个迷宫单元格视为图的一个节点，如果两个单元格相邻且可以通过，则它们之间有一条边。

然后使用Dijkstra算法找到起点到终点的最短路径。

4. A*算法：A*算法是一种常用的启发式算法，结合了BFS和Dijkstra算法的思想。

它通过评估每个节点的代价函数来优化路径，其中代价函数的值由节点到终点的预计距离和节点到起点的实际距离共同决定。

在迷宫问题中，可以使用欧几里得距离或曼哈顿距离作为代价函数。

5.回溯算法：回溯算法是一种通过尝试所有可能的解来解决问题的算法。

在迷宫问题中，可以通过递归和回溯的方式来找到路径。

从起点开始，按照其中一种策略选择一个方向前进，如果不能到达终点，则回溯到上一个节点重新选择方向。

以上是几种常见的迷宫算法。

不同的算法有着不同的优劣势，适用于不同的问题场景。

在实际应用中，根据具体情况选择合适的算法可以提高效率和准确性。

迷宫算法作为图论算法的一种，也可以用于其他问题的求解，如路径规划、图像识别等领域。

迷宫游戏知识点

迷宫游戏知识点迷宫游戏是一种非常受欢迎的游戏类型，它考验着玩家的智力和思考能力。

通过解决迷宫中的难题，玩家需要找到通往出口的路径。

在这篇文章中，我们将介绍迷宫游戏的一些关键知识点。

1.迷宫的基本概念：迷宫是由通道和墙壁组成的。

通道通常是玩家可以通过的路径，而墙壁则是不可穿越的障碍物。

迷宫的目标是找到从起点到终点的路径。

2.深度优先搜索算法：深度优先搜索（DFS）是解决迷宫问题的一种常用算法。

该算法通过不断探索迷宫的每一个分支，直到找到出口或者所有路径都被探索完为止。

DFS使用栈来保存当前路径的状态，并递归地探索每一个可能的方向。

3.广度优先搜索算法：广度优先搜索（BFS）也是解决迷宫问题的一种常用算法。

与DFS不同，BFS使用队列来保存当前路径的状态，并按照层级顺序探索迷宫的每一个分支。

这种方法可以保证找到最短路径。

4.A搜索算法： A搜索算法是一种启发式搜索算法，可以在迷宫问题中找到最佳路径。

它通过估算每个可能路径的代价来进行搜索。

A*算法使用一个启发函数来评估路径的优先级，并选择当前最有希望达到目标的路径进行探索。

5.回溯算法：回溯算法是一种解决迷宫问题的经典方法。

它通过尝试每一种可能的路径来找到一个可行的解决方案。

当遇到死路时，回溯算法会回到上一个分支点，并尝试其他路径。

6.迷宫生成算法：除了解决迷宫问题，我们还可以使用算法生成迷宫。

迷宫生成算法可以创建出各种形状和难度级别的迷宫。

其中，递归分割法和随机洗牌法是两种常用的迷宫生成算法。

7.最佳路径算法：解决迷宫问题的一个重要目标是找到最佳路径。

对于给定的迷宫，可以使用Dijkstra算法或者贝尔曼-福特算法来找到最短路径。

这些算法会考虑路径上每个点的权重，并选择最小权重的路径。

通过了解这些关键知识点，你可以更好地理解迷宫游戏的背后原理，并提高在解决迷宫问题时的思考能力。

希望这篇文章能对你有所帮助！。

解决迷宫问题的算法

解决迷宫问题的算法
迷宫问题是一个经典的计算机科学问题，它在很多领域中都有广泛的应用，包括搜索、路径规划、人工智能等等。

解决迷宫问题的算法有很多种，其中最常见的是深度优先搜索和广度优先搜索。

深度优先搜索算法是一种递归的算法，通过不断地向下探索路径，直到找到终点或者到达死胡同为止。

该算法在实现上比较简单，但是可能会陷入死循环，因此需要特判。

广度优先搜索算法则是一种迭代的算法，通过按照层次逐步扩展搜索范围，最终找到终点。

该算法的实现较为复杂，但是能够找到最短路径。

除了深度优先搜索和广度优先搜索，还有其他一些算法可以用来解决迷宫问题，例如A*算法、IDA*算法等等。

这些算法都有各自的
优缺点和适用范围，需要根据具体情况进行选择。

总之，解决迷宫问题的算法有很多种，每一种都有其特点和适用范围。

在实际应用中，我们需要根据具体情况来选择合适的算法，以便更好地解决问题。

- 1 -。

迷宫实验报告范文

迷宫实验报告范文**迷宫实验报告****一、实验目的**1.理解迷宫问题的背景和相关概念；2.熟悉迷宫实验的规则和步骤，培养解决问题的能力；3.探究迷宫问题的求解方法及其效果。

**二、实验原理**1.迷宫问题：在一个固定的区域内，寻找从起点到终点的路径，期间避免碰到障碍物；2.深度优先算法（DFS）：从起点出发，每次选择一个没有访问过的相邻节点继续深入，直到找到终点或者无路可走；3.广度优先算法（BFS）：从起点出发，按照距离逐层，直到找到终点；4.A*算法：结合了启发函数和广度优先。

**三、实验步骤**1.首先，我们创建一个M*N的矩阵，用来表示迷宫。

其中，起点用"S"表示，终点用"E"表示，空格用"."表示，障碍物用"#"表示；2.然后，我们使用深度优先算法和广度优先算法分别求解迷宫问题；2.1深度优先算法（DFS）：从起点出发，每次选择一个没有访问过的相邻节点继续深入，直到找到终点或者无路可走；2.2广度优先算法（BFS）：从起点出发，按照距离逐层，直到找到终点；3.最后，我们使用A*算法求解迷宫问题。

A*算法结合了广度优先和启发函数，其中，启发函数用来估计每个节点到终点的距离。

**四、实验结果及分析**我们使用以上三种方法求解迷宫问题，并将结果进行比较：1.深度优先算法（DFS）：该算法能够找到至少一条路径，但是并不能保证找到最短路径。

它倾向于选择一个方向一直走下去，直到无路可走，然后回溯到上一个节点继续探索。

这种算法在迷宫问题中很容易陷入局部最优解，但是效率较高。

2.广度优先算法（BFS）：该算法可以保证找到最短路径，但是需要更长的时间和更大的空间。

它按照距离逐层，直到找到终点。

由于要保存每一层的节点，所以空间复杂度较高。

3.A*算法：该算法结合了广度优先和启发函数，能够找到最短路径，并且效率高。

启发函数用来估计每个节点到终点的距离，通过这个估计值，可以优先选择离终点更近的节点进行，从而提高效率。