8数码问题之深度优先算法
深度优先遍历的算法

深度优先遍历的算法深度优先遍历(Depth-First Search,DFS)是一种用来遍历或树或图的算法。
它以一个起始节点开始,沿着路径尽可能深地,直到到达最深处或无法继续为止,然后回溯到上一个节点,继续其他路径。
DFS通过栈来实现,每次访问一个节点时,将其标记为已访问,并将其相邻的未访问节点压入栈中。
然后从栈中弹出节点,重复这个过程,直到栈为空为止。
1.创建一个栈,用来存储待访问的节点。
2.将起始节点标记为已访问,并将其压入栈中。
3.当栈不为空时,执行以下步骤:-弹出栈顶节点,并输出该节点的值。
-将该节点的未访问的相邻节点标记为已访问,并将其压入栈中。
4.重复步骤3,直到栈为空为止。
-深度优先遍历是一种先序遍历,即先访问节点本身,然后访问其子节点。
-深度优先遍历可以用来求解连通图、查找路径等问题。
-深度优先遍历的时间复杂度为O(V+E),其中V为节点数,E为边数。
1.求解连通图:深度优先遍历可以用来判断一个图是否连通,即从一个节点是否能够访问到所有其他节点。
2.查找路径:深度优先遍历可以找到两个节点之间的路径。
当遇到目标节点时,即可停止遍历,返回路径结果。
3.拓扑排序:深度优先遍历可以进行拓扑排序,即将有依赖关系的任务按一定的顺序排列。
深度优先遍历的实现可以通过递归或迭代方式来完成。
递归方式更加简洁,但在处理大规模图时可能导致栈溢出。
迭代方式则可以采用栈来避免栈溢出问题。
无论是递归方式还是迭代方式,其核心思想都是通过访问节点的相邻节点来进行深入,直至遍历完整个图或树的节点。
总而言之,深度优先遍历是一种常用的图遍历算法,它以一种深入优先的方式遍历路径。
在实际应用中,深度优先遍历可以用来求解连通图、查找路径和拓扑排序等问题,是图算法中的重要工具之一。
深度优先算法
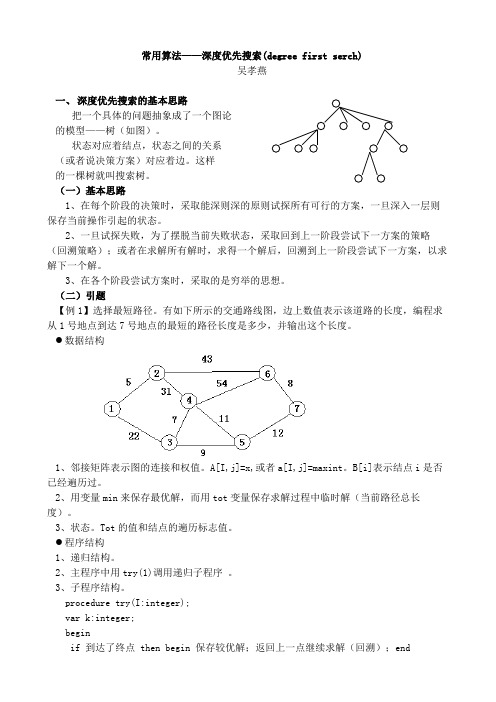
常用算法——深度优先搜索(degree first serch)吴孝燕一、深度优先搜索的基本思路把一个具体的问题抽象成了一个图论的模型——树(如图)。
状态对应着结点,状态之间的关系(或者说决策方案)对应着边。
这样的一棵树就叫搜索树。
(一)基本思路1、在每个阶段的决策时,采取能深则深的原则试探所有可行的方案,一旦深入一层则保存当前操作引起的状态。
2、一旦试探失败,为了摆脱当前失败状态,采取回到上一阶段尝试下一方案的策略(回溯策略);或者在求解所有解时,求得一个解后,回溯到上一阶段尝试下一方案,以求解下一个解。
3、在各个阶段尝试方案时,采取的是穷举的思想。
(二)引题【例1】选择最短路径。
有如下所示的交通路线图,边上数值表示该道路的长度,编程求从1号地点到达7号地点的最短的路径长度是多少,并输出这个长度。
●数据结构1、邻接矩阵表示图的连接和权值。
A[I,j]=x,或者a[I,j]=maxint。
B[i]表示结点i是否已经遍历过。
2、用变量min来保存最优解,而用tot变量保存求解过程中临时解(当前路径总长度)。
3、状态。
Tot的值和结点的遍历标志值。
●程序结构1、递归结构。
2、主程序中用try(1)调用递归子程序。
3、子程序结构。
procedure try(I:integer);var k:integer;beginif 到达了终点 then begin 保存较优解;返回上一点继续求解(回溯);endelsebegin穷举从I出发当前可以直接到达的点k;if I到k点有直接联边并且 k点没有遍历过 thenthen begin把A[I,K]累加入路径长度tot;k标记为已遍历;try(k); 现场恢复;end;end;●子程序procedure try(i:integer);var k:integer;beginif i=n then begin if tot<min then min:=tot;exit;endelsebeginfor k:=1 to n doif (b[k]=0) and (i<>k) and (a[i,k]<32700) thenbeginb[k]:=1;tot:=tot+a[i,k];try(k);b[k]:=0;tot:=tot-a[i,k]; end;end;end;●主程序数据输入readln(fi,n);for i:=1 to n dobeginfor j:=1 to n do read(fi,a[i,j]);readln(fi);end;close(fi);●主程序预处理和调用子程序tot:=0;min:=maxint;b[1]:=1;try(1);writeln('tot=',min);(三)递归程序结构框架Procedure try(i:integer);Var k:integer;BeginIf 所有阶段都已求解 thenBegin比较最优解并保存;回溯;endelsebeginfor k:=i 深度可能决策范围;do begin穷举当前阶段所有可能的决策(方案、结点)kif k方案可行 then begin记录状态变化;try(i+1);状态恢复(回溯); endend;end;End;二、深度优先搜索的应用例1:有A,B,C,D,E 5本书,要分给张、王、刘、赵、钱5位同学,每人只选一本。
人工智能实验总结

总结
宽度优先搜索法
在有解的情形总能保证搜索到最短路经,也 就是移动最少步数的路径。但宽度优先搜索法的 最大问题在于搜索的结点数量太多,因为在宽度 优先搜索法中,每一个可能扩展出的结点都是搜 索的对象。随着结点在搜索树上的深度增大,搜 索的结点数会很快增长,并以指数形式扩张,从 而所需的存储空间和搜索花费的时间也会成倍增 长。
1 2
0 1 0 1
0 0 1 1
0 1 1 0
神经网络设计
用两层神经网络来实现,其中隐层为随机 感知器层(net1),神经网络元数目设计为 3,其权值和阈值是随机的,它的输出作为 输出层(分类层)的输入;输出层为感知 器层(net2),其神经元数为1,这里仅对 该层进行训练。
程序运行结果
随机感知器层的权值向量 iw1 = 0.4267 -0.6556 -0.5439 0.9376 -0.1007 -0.2886 随机感知器层的阈值向量 b1 = 0.4074 0.0441 0.8658
运行结果分析
上面实验结果可以看出,城市数目为30的 时候,当迭代次数为100,算法收敛慢,在 迭代次数内最优解没有达到稳定,没有搜 索到最好的解。 迭代次数为200和250的时候,算法基本达 到收敛,最优解在100代以后趋于稳定,表 明搜索到问题的最优解。
运行结果
当城市数目改变的时候: CityNum=50;最大代数gnmax=100;
程序运行结果
第二层感知器层的权值向量和阈值向量 iw2 = -3 -2 2 b2 = 2
深度优先搜索和广度优先搜索

二、 重排九宫问题游戏
在一个 3 乘 3 的九宫中有 1-8 的 8 个数及一个空格随机摆放在其中的格子里。如下面 左图所示。现在要求实现这样的问题:将该九宫调整为如下图右图所示的形式。调整规则是: 每次只能将与空格(上,下或左,右)相临的一个数字平移到空格中。试编程实现。
|2|8 |3|
|1|2|3|
from = f; to = t; distance = d; skip = false; } } class Depth { final int MAX = 100; // This array holds the flight information. FlightInfo flights[] = new FlightInfo[MAX]; int numFlights = 0; // number of entries in flight array Stack btStack = new Stack(); // backtrack stack public static void main(String args[]) {
下面是用深度优先搜索求解的程序:
// Find connections using a depth-first search. import java.util.*; import java.io.*; // Flight information. class FlightInfo {
String from; String to; int distance; boolean skip; // used in backtracking FlightInfo(String f, String t, int d) {
int dist; FlightInfo f; // See if at destination. dist = match(from, to); if(dist != 0) {
八数码难题(8puzzle)深度优先和深度优先算法

⼋数码难题(8puzzle)深度优先和深度优先算法1 搜索策略搜索策略是指在搜索过程中如何选择扩展节点的次序问题。
⼀般来说,搜索策略就是采⽤试探的⽅法。
它有两种类型:⼀类是回溯搜索,另⼀类是图搜索策略。
2 盲⽬的图搜索策略图搜索策略⼜可分为两种:⼀种称为盲⽬的图搜索策略,或称⽆信息图搜索策略;⽽另⼀种称为启发式搜索策略,⼜称为有信息的图搜索策略。
最常⽤的两种⽆信息图搜索策略是宽度优先搜索和深度优先搜索。
2.1 宽度优先搜索它是从根节点(起始节点)开始,按层进⾏搜索,也就是按层来扩展节点。
所谓按层扩展,就是前⼀层的节点扩展完毕后才进⾏下⼀层节点的扩展,直到得到⽬标节点为⽌。
这种搜索⽅式的优点是,只要存在有任何解答的话,它能保证最终找到由起始节点到⽬标节点的最短路径的解,但它的缺点是往往搜索过程很长。
2.2 深度优先搜索它是从根节点开始,⾸先扩展最新产⽣的节点,即沿着搜索树的深度发展下去,⼀直到没有后继结点处时再返回,换⼀条路径⾛下去。
就是在搜索树的每⼀层始终先只扩展⼀个⼦节点,不断地向纵深前进直到不能再前进(到达叶⼦节点或受到深度限制)时,才从当前节点返回到上⼀级节点,沿另⼀⽅向⼜继续前进。
这种⽅法的搜索树是从树根开始⼀枝⼀枝逐渐形成的。
由于⼀个有解的问题树可能含有⽆穷分枝,深度优先搜索如果误⼊⽆穷分枝(即深度⽆限),则不可能找到⽬标节点。
为了避免这种情况的出现,在实施这⼀⽅法时,定出⼀个深度界限,在搜索达到这⼀深度界限⽽且尚未找到⽬标时,即返回重找,所以,深度优先搜索策略是不完备的。
另外,应⽤此策略得到的解不⼀定是最佳解(最短路径)。
3 “⼋”数码难题的宽度优先搜索与深度优先搜索3.1“⼋”数码难题的宽度优先搜索步骤如下:1、判断初始节点是否为⽬标节点,若初始节点是⽬标节点则搜索过程结束;若不是则转到第2步;2、由初始节点向第1层扩展,得到3个节点:2、3、4;得到⼀个节点即判断该节点是否为⽬标节点,若是则搜索过程结束;若2、3、4节点均不是⽬标节点则转到第3步;3、从第1层的第1个节点向第2层扩展,得到节点5;从第1层的第2个节点向第2层扩展,得到3个节点:6、7、8;从第1层的第3个节点向第2层扩展得到节点9;得到⼀个节点即判断该节点是否为⽬标节点,若是则搜索过程结束;若6、7、8、9节点均不是⽬标节点则转到第4步;4、按照上述⽅法对下⼀层的节点进⾏扩展,搜索⽬标节点;直⾄搜索到⽬标节点为⽌。
“八”数码问题的宽度优先搜索与深度优先搜索

“八”数码问题的宽度优先搜索与深度优先搜索我在观看视频和查看大学课本及网上搜索等资料才对“八”数码问题有了更进一步的了解和认识。
一、“八”数码问题的宽度优先搜索步骤如下:1、判断初始节点是否为目标节点,若初始节点是目标节点则搜索过程结束;若不是则转到第2步;2、由初始节点向第1层扩展,得到3个节点:2、3、4;得到一个节点即判断该节点是否为目标节点,若是则搜索过程结束;若2、3、4节点均不是目标节点则转到第3步;3、从第1层的第1个节点向第2层扩展,得到节点5;从第1层的第2个节点向第2层扩展,得到3个节点:6、7、8;从第1层的第3个节点向第2层扩展得到节点9;得到一个节点即判断该节点是否为目标节点,若是则搜索过程结束;若6、7、8、9节点均不是目标节点则转到第4步;4、按照上述方法对下一层的节点进行扩展,搜索目标节点;直至搜索到目标节点为止。
二、“八”数码问题的深度优先搜索步骤如下:1、设置深度界限,假设为5;2、判断初始节点是否为目标节点,若初始节点是目标节点则搜索过程结束;若不是则转到第2步;3、由初始节点向第1层扩展,得到节点2,判断节点2是否为目标节点;若是则搜索过程结束;若不是,则将节点2向第2层扩展,得到节点3;4、判断节点3是否为目标节点,若是则搜索过程结束;若不是则将节点3向第3层扩展,得到节点4;5、判断节点4是否为目标节点,若是则搜索过程结束;若不是则将节点4向第4层扩展,得到节点5;6、判断节点5是否为目标节点,若是则搜索过程结束;若不是则结束此轮搜索,返回到第2层,将节点3向第3层扩展得到节点6;7、判断节点6是否为目标节点,若是则搜索过程结束;若不是则将节点6向第4层扩展,得到节点7;8、判断节点7是否为目标节点,若是则结束搜索过程;若不是则将节点6向第4层扩展得到节点8;9、依次类推,知道得到目标节点为止。
三、上述两种搜索策略的比较在宽度优先搜索过程中,扩展到第26个节点时找到了目标节点;而在深度优先搜索过程中,扩展到第18个节点时得到了目标节点。
深度宽度优先搜索---八数码
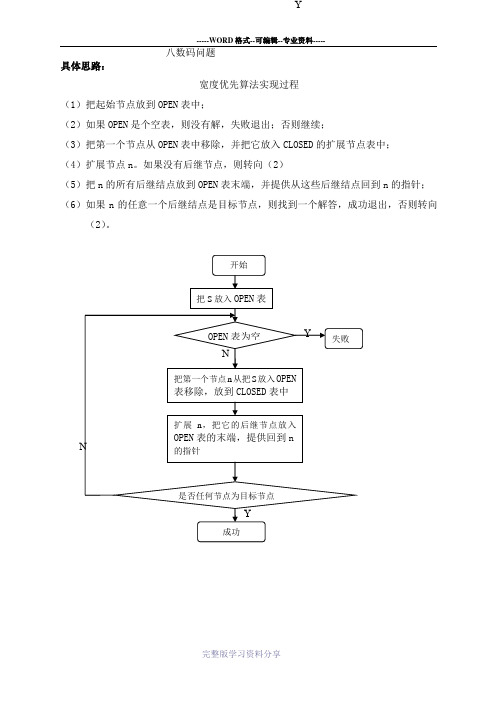
Y-----WORD格式--可编辑--专业资料-----八数码问题具体思路:宽度优先算法实现过程(1)把起始节点放到OPEN表中;(2)如果OPEN是个空表,则没有解,失败退出;否则继续;(3)把第一个节点从OPEN表中移除,并把它放入CLOSED的扩展节点表中;(4)扩展节点n。
如果没有后继节点,则转向(2)(5)把n的所有后继结点放到OPEN表末端,并提供从这些后继结点回到n的指针;(6)如果n的任意一个后继结点是目标节点,则找到一个解答,成功退出,否则转向(2)。
深度优先实现过程(1)把起始节点S放入未扩展节点OPEN表中。
如果此节点为一目标节点,则得到一个解;(2)如果OPEN为一空表,则失败退出;(3)把第一个节点从OPEN表移到CLOSED表;(4)如果节点n的深度等于最大深度,则转向(2);(5)扩展节点n,产生其全部后裔,并把它们放入OPEN表的前头。
如果没有后裔,则转向(2);(6)如果后继结点中有任一个目标节点,则得到一个解,成功退出,否则转向(2)。
方法一:用C语言实现#include <stdio.h>#include <string.h>#include<stdlib.h>typedef long UINT64;typedef struct{char x; //位置x和位置y上的数字换位char y; //其中x是0所在的位置} EP_MOVE;#define SIZE 3 //8数码问题,理论上本程序也可解决15数码问题,#define NUM SIZE * SIZE //但move_gen需要做很多修改,输入初始和结束状态的部分和check_input也要修改#define MAX_NODE 1000000#define MAX_DEP 100#define XCHG(a, b) { a=a + b; b=a - b; a=a - b; }#define TRANS(a, b)/*{ long iii; (b)=0; for(iii=0; iii < NUM; iii++) (b)=((b) << 4) + a[iii]; }*/ //将数组a转换为一个64位的整数b#define RTRANS(a, b) \{ \long iii; \UINT64 ttt=(a); \for(iii=NUM - 1; iii >= 0; iii--) \{ \b[iii]=ttt & 0xf; \ttt>>=4; \} \} //将一个64位整数a转换为数组b//typedef struct EP_NODE_Tag{ UINT64 v; //保存状态,每个数字占4个二进制位,可解决16数码问题struct EP_NODE_Tag *prev; //父节点struct EP_NODE_Tag *small, *big;} EP_NODE;EP_NODE m_ar[MAX_NODE];EP_NODE *m_root;long m_depth; //搜索深度EP_NODE m_out[MAX_DEP]; //输出路径//long move_gen(EP_NODE *node, EP_MOVE *move){long pz; //0的位置UINT64 t=0xf;for(pz=NUM - 1; pz >= 0; pz--){if((node->v & t) == 0){ break; //找到0的位置}t<<=4;}switch(pz){case 0:move[0].x=0;move[0].y=1;move[1].x=0;move[1].y=3;return 2;case 1:move[0].x=1;move[0].y=0;move[1].x=1;move[1].y=2;move[2].x=1;move[2].y=4;return 3;case 2:move[0].x=2;move[0].y=1;move[1].x=2;move[1].y=5;return 2;case 3:move[0].x=3;move[0].y=0;move[1].x=3;move[1].y=6;move[2].x=3;move[2].y=4;return 3;case 4:move[0].x=4;move[0].y=1;move[1].x=4;move[1].y=3;move[2].x=4;move[2].y=5;move[3].x=4;move[3].y=7;return 4;case 5:move[0].x=5;move[0].y=2;move[1].x=5;move[1].y=4;move[2].x=5;move[2].y=8;return 3;case 6:move[0].x=6;move[0].y=3;move[1].x=6;move[1].y=7;return 2;case 7:move[0].x=7;move[0].y=6;move[1].x=7;move[1].y=4;move[2].x=7;move[2].y=8;return 3;case 8:move[0].x=8;move[0].y=5;move[1].x=8;move[1].y=7;return 2;}return 0;}long mov(EP_NODE *n1, EP_MOVE *mv, EP_NODE *n2) //走一步,返回走一步后的结果{char ss[NUM];RTRANS(n1->v, ss);XCHG(ss[mv->x], ss[mv->y]);TRANS(ss, n2->v);return 0;}long add_node(EP_NODE *node, long r){EP_NODE *p=m_root;EP_NODE *q;while(p){ q=p;if(p->v == node->v) return 0;else if(node->v > p->v) p=p->big;else if(node->v < p->v) p=p->small;}m_ar[r].v=node->v;m_ar[r].prev=node->prev;m_ar[r].small=NULL;m_ar[r].big=NULL;if(node->v > q->v){ q->big= &m_ar[r];}else if(node->v < q->v){ q->small= &m_ar[r];}return 1;}/*得到节点所在深度*/long get_node_depth(EP_NODE *node){ long d=0;while(node->prev){ d++;node=node->prev;}return d;}/*返回值:成功-返回搜索节点数,节点数不够-(-1),无解-(-2)*/ long bfs_search(char *begin, char *end){ long h=0, r=1, c, i, j;EP_NODE l_end, node, *pnode;EP_MOVE mv[4]; //每个局面最多4种走法TRANS(begin, m_ar[0].v);TRANS(end, l_end.v);m_ar[0].prev=NULL;m_root=m_ar;m_root->small=NULL;m_root->big=NULL;while((h < r) && (r < MAX_NODE - 4)){ c=move_gen(&m_ar[h], mv);for(i=0; i < c; i++){ mov(&m_ar[h], &mv[i], &node);node.prev= &m_ar[h];if(node.v == l_end.v){ pnode= &node;j=0;while(pnode->prev){ m_out[j]=*pnode;j++;pnode=pnode->prev;}m_depth=j;return r;}if(add_node(&node, r)) r++; //只能对历史节点中没有的新节点搜索,否则会出现环}h++;printf("\rSearch...%9d/%d @ %d", h, r, get_node_depth(&m_ar[h]));}if(h == r){ return -2; }else{return -1; }}long check_input(char *s, char a, long r){ long i;for(i=0; i < r; i++){ if(s[i] == a - 0x30) return 0; }return 1;}long check_possible(char *begin, char *end){ char fs;long f1=0, f2=0;long i, j;for(i=0; i < NUM; i++){ fs=0;for(j=0; j < i; j++){if((begin[i] != 0) && (begin[j] != 0) && (begin[j] < begin[i])) fs++;}f1+=fs;fs=0;for(j=0; j < i; j++){ if((end[i] != 0) && (end[j] != 0) && (end[j] < end[i])) fs++;}f2+=fs;}if((f1 & 1) == (f2 & 1)) return 1;elsereturn 0;}void output(void){ long i, j, k;char ss[NUM];for(i=m_depth - 1; i >= 0; i--){ RTRANS(m_out[i].v, ss);for(j=0; j < SIZE; j++){ for(k=0; k < SIZE; k++){ printf("%2d", ss[SIZE * j + k]);}printf("\n");}printf("\n");}}int main(void){ char s1[NUM];char s2[NUM];long r;char a;printf("请输入开始状态:");r=0;while(r < NUM){ a=getchar();if(a >= 0x30 && a < 0x39 && check_input(s1, a, r)) { s1[r++]=a - 0x30;printf("%c", a);}}printf("\n请输入结束状态:");r=0;while(r < NUM){ a=getchar();if(a >= 0x30 && a < 0x39 && check_input(s2, a, r)) { s2[r++]=a - 0x30;printf("%c", a);}}printf("\n");if(check_possible(s1, s2)){ r=bfs_search(s1, s2);printf("\n");if(r >= 0){ printf("查找深度=%d,所有的方式=%ld\n", m_depth, r); output();}else if(r == -1){ printf("没有找到路径.\n");}else if(r == -2){printf("这种状态变换没有路径到达.\n");}else{printf("不确定的错误.\n");}}else{ printf("不允许这样移动!\n");}return 0;}方法二:用MATLAB实现program 8no_bfs; {八数码的宽度优先搜索算法} ConstDir : array[1..4,1..2]of integer {四种移动方向,对应产生式规则} = ((1,0),(-1,0),(0,1),(0,-1));n=10000;TypeT8no = array[1..3,1..3]of integer;TList = recordFather : integer; {父指针}dep : byte; {深度}X0,Y0 : byte; {0的位置}State : T8no; {棋盘状态 }end;VarSource,Target : T8no;List : array[0..10000] of TList; {综合数据库 }Closed,open,Best : integer { Best表示最优移动次数}Answer : integer; {记录解}Found : Boolean; {解标志}procedure GetInfo; {读入初始和目标节点}var i,j : integer;beginfor i:=1 to 3 dofor j:=1 to 3 do read(Source[i,j]);for i:=1 to 3 dofor j:=1 to 3 do read(Target[i,j]);end;procedure Initialize; {初始化}var x,y : integer;beginFound:=false;Closed:=0;open:=1;with List[1] do beginState:=Source;dep:=0;Father:=0;For x:=1 to 3 doFor y:=1 to 3 doif State[x,y]=0 then Begin x0:=x;y0:=y; End;end;end;Function Same(A,B : T8no):Boolean; {判断A,B状态是否相等 }Var i,j : integer;BeginSame:=false;For i:=1 to 3 do for j:=1 to 3 do if A[i,j]<>B[i,j] then exit;Same:=true;End;Function not_Appear(new : tList):boolean;{判断new是否在List中出现 }var i : integer;beginnot_Appear:=false;for i:=1 to open do if Same(new.State,List[i].State) then exit;not_Appear:=true;end;procedure Move(n : tList;d : integer;var ok : boolean;var new : tList); {将第d条规则作用于n得到new,OK是new是否可行的标志 }var x,y : integer;beginX := n.x0 + Dir[d,1];Y := n.y0 + Dir[d,2];{判断new的可行性}if not ((X > 0) and ( X < 4 ) and ( Y > 0 ) and ( Y < 4 )) then begin ok:=false;exit end;OK:=true;new.State:=n.State; {new=Expand(n,d)}new.State[X,Y]:=0;new.State[n.x0,n.y0]:=n.State[X,Y];new.X0:=X;new.Y0:=Y;end;procedure Add(new : tList); {插入节点new}beginif not_Appear(new) then Begin {如果new没有在List出现 }Inc(open); {new加入open表 }List[open] := new;end;end;procedure Expand(Index : integer; var n : tList); {扩展n的子节点}var i : integer;new : tList;OK : boolean;Beginif Same(n.State , Target) then begin {如果找到解}Found := true;Best :=n.Dep;Answer:=Index;Exit;end;For i := 1 to 4 do begin {依次使用4条规则} Move(n,i,OK,new);if not ok then continue;new.Father := Index;new.Dep :=n.dep + 1;Add(new);end;end;procedure GetOutInfo; {输出}procedure Outlook(Index : integer); {递归输出每一个解} var i,j : integer;beginif Index=0 then exit;Outlook(List[Index].Father);with List[Index] dofor i:=1 to 3 do beginfor j:=1 to 3 do write(State[i,j],' ');writeln;end;writeln;end;beginWriteln('Total = ',Best);Outlook(Answer);end;procedure Main; {搜索主过程}beginRepeatInc(Closed);Expand(Closed,List[Closed]); {扩展Closed}Until (Closed>=open) or Found;if Found then GetOutInfo {存在解}else Writeln('no answer'); {无解}end;BeginAssign(Input,'input.txt');ReSet(Input);Assign(Output,'Output.txt');ReWrite(Output);GetInfo;Initialize;Main;Close(Input);Close(Output);End.五、实验结果六、实验总结通过实验问题的求解过程就是搜索的过程,采用适合的搜索算法是关键的,因为对求解过程的效率有很大的影响,包括各种规则、过程和算法等推理技术。
深度优先递归算法

深度优先递归算法深度优先递归算法是一种常用的算法,它可以用来解决许多问题。
在这篇文章中,我们将介绍深度优先递归算法的基本原理和应用。
深度优先递归算法是一种递归算法,它的基本思想是从根节点开始,沿着一条路径一直走到底,直到找到目标节点或者无法继续走下去为止。
如果无法继续走下去,就返回上一个节点,继续沿着另一条路径走下去,直到找到目标节点或者遍历完整个图为止。
深度优先递归算法的实现通常使用递归函数来实现。
递归函数的基本结构是:```void dfs(int u) {// 处理节点ufor (int v : adj[u]) {if (!visited[v]) {visited[v] = true;dfs(v);}}}```其中,`u`表示当前节点,`adj[u]`表示与节点`u`相邻的节点集合,`visited[v]`表示节点`v`是否已经被访问过。
在处理节点`u`时,我们可以进行一些操作,比如更新最短路径、计算连通块等等。
然后,我们遍历与节点`u`相邻的节点,如果这些节点没有被访问过,就递归调用`dfs`函数,处理这些节点。
深度优先递归算法的应用非常广泛,比如:1. 图的遍历:深度优先递归算法可以用来遍历图,找到所有连通块、最短路径等信息。
2. 拓扑排序:深度优先递归算法可以用来进行拓扑排序,找到有向无环图的拓扑序列。
3. 回溯算法:回溯算法是一种搜索算法,它可以用深度优先递归算法来实现。
回溯算法通常用来解决一些组合问题,比如八皇后问题、数独问题等等。
4. 生成树:深度优先递归算法可以用来生成树,比如最小生成树、最大生成树等等。
深度优先递归算法是一种非常重要的算法,它可以用来解决许多问题。
在实际应用中,我们需要根据具体问题选择合适的算法,并进行适当的优化,以提高算法的效率。
深度优先递归算法

深度优先递归算法
深度优先递归算法(Depth-First Recursive Algorithm,DFS)是一种常用的图论算法,它能够快速地搜索一个图中的节点,从而找到最佳路径。
这种算法也常被用来解决迷宫问题。
深度优先递归算法的原理是,使用一个指针(或者说游标)来遍历图中的所有节点,并依次进行深度优先搜索。
它的基本思想就是,将当前节点放在栈的顶部,然后寻找它的相邻节点,将相邻节点也放入栈中,直到找到满足条件的目标节点,再从栈中弹出节点。
深度优先递归算法需要使用一个栈来存储已经访问过的节点。
当算法从一个新节点开始时,会将当前节点放入栈中,然后检查该节点的所有相邻节点,如果存在未访问过的节点,就将其放入栈中,重复上述步骤,直到找到终点,或者栈为空。
深度优先递归算法的特点是,它能够快速地搜索图中的所有节点,并且可以找到最佳路径。
它也比较容易理解,不需要复杂的数据结构,只需要一个栈即可。
但是,深度优先递归算法也有一些缺点,其中一个就是它容易出现堆栈溢出,尤其是在处理大型图时,算法的时间复杂度会很高,因此,它的效率不是很高。
总的来说,深度优先递归算法是一种简单而有效的图搜索算法,在处理一些小型图时,它的效率还是很高的。
深度宽度优先搜索---八数码
Y.八数码问题具体思路:宽度优先算法实现过程(1)把起始节点放到OPEN表中;(2)如果OPEN是个空表,则没有解,失败退出;否则继续;(3)把第一个节点从OPEN表中移除,并把它放入CLOSED的扩展节点表中;(4)扩展节点n。
如果没有后继节点,则转向(2)(5)把n的所有后继结点放到OPEN表末端,并提供从这些后继结点回到n的指针;(6)如果n的任意一个后继结点是目标节点,则找到一个解答,成功退出,否则转向(2)。
深度优先实现过程(1)把起始节点S放入未扩展节点OPEN表中。
如果此节点为一目标节点,则得到一个解;(2)如果OPEN为一空表,则失败退出;(3)把第一个节点从OPEN表移到CLOSED表;(4)如果节点n的深度等于最大深度,则转向(2);(5)扩展节点n,产生其全部后裔,并把它们放入OPEN表的前头。
如果没有后裔,则转向(2);(6)如果后继结点中有任一个目标节点,则得到一个解,成功退出,否则转向(2)。
方法一:用C语言实现#include <stdio.h>#include <string.h>#include<stdlib.h>typedef long UINT64;typedef struct{char x; //位置x和位置y上的数字换位char y; //其中x是0所在的位置} EP_MOVE;#define SIZE 3 //8数码问题,理论上本程序也可解决15数码问题,#define NUM SIZE * SIZE //但move_gen需要做很多修改,输入初始和结束状态的部分和check_input也要修改#define MAX_NODE 1000000#define MAX_DEP 100#define XCHG(a, b) { a=a + b; b=a - b; a=a - b; }#define TRANS(a, b)/*{ long iii; (b)=0; for(iii=0; iii < NUM; iii++) (b)=((b) << 4) + a[iii]; }*/ //将数组a转换为一个64位的整数b#define RTRANS(a, b) \{ \long iii; \UINT64 ttt=(a); \for(iii=NUM - 1; iii >= 0; iii--) \{ \b[iii]=ttt & 0xf; \ttt>>=4; \} \} //将一个64位整数a转换为数组b//typedef struct EP_NODE_Tag{ UINT64 v; //保存状态,每个数字占4个二进制位,可解决16数码问题struct EP_NODE_Tag *prev; //父节点struct EP_NODE_Tag *small, *big;} EP_NODE;EP_NODE m_ar[MAX_NODE];EP_NODE *m_root;long m_depth; //搜索深度EP_NODE m_out[MAX_DEP]; //输出路径//long move_gen(EP_NODE *node, EP_MOVE *move){long pz; //0的位置UINT64 t=0xf;for(pz=NUM - 1; pz >= 0; pz--). {if((node->v & t) == 0){ break; //找到0的位置}t<<=4;}switch(pz){case 0:move[0].x=0;move[0].y=1;move[1].x=0;move[1].y=3;return 2;case 1:move[0].x=1;move[0].y=0;move[1].x=1;move[1].y=2;move[2].x=1;move[2].y=4;return 3;case 2:move[0].x=2;. move[0].y=1;move[1].x=2;move[1].y=5;return 2;case 3:move[0].x=3;move[0].y=0;move[1].x=3;move[1].y=6;move[2].x=3;move[2].y=4;return 3;case 4:move[0].x=4;move[0].y=1;move[1].x=4;move[1].y=3;move[2].x=4;move[2].y=5;move[3].x=4;move[3].y=7;return 4;. case 5:move[0].x=5;move[0].y=2;move[1].x=5;move[1].y=4;move[2].x=5;move[2].y=8;return 3;case 6:move[0].x=6;move[0].y=3;move[1].x=6;move[1].y=7;return 2;case 7:move[0].x=7;move[0].y=6;move[1].x=7;move[1].y=4;move[2].x=7;move[2].y=8;return 3;.case 8:move[0].x=8;move[0].y=5;move[1].x=8;move[1].y=7;return 2;}return 0;}long mov(EP_NODE *n1, EP_MOVE *mv, EP_NODE *n2) //走一步,返回走一步后的结果{char ss[NUM];RTRANS(n1->v, ss);XCHG(ss[mv->x], ss[mv->y]);TRANS(ss, n2->v);return 0;}long add_node(EP_NODE *node, long r){EP_NODE *p=m_root;EP_NODE *q;. while(p){ q=p;if(p->v == node->v) return 0;else if(node->v > p->v) p=p->big;else if(node->v < p->v) p=p->small;}m_ar[r].v=node->v;m_ar[r].prev=node->prev;m_ar[r].small=NULL;m_ar[r].big=NULL;if(node->v > q->v){ q->big= &m_ar[r];}else if(node->v < q->v){ q->small= &m_ar[r];}return 1;}/*得到节点所在深度*/long get_node_depth(EP_NODE *node) { long d=0;while(node->prev).{ d++;node=node->prev;}return d;}/*返回值:成功-返回搜索节点数,节点数不够-(-1),无解-(-2)*/ long bfs_search(char *begin, char *end){ long h=0, r=1, c, i, j;EP_NODE l_end, node, *pnode;EP_MOVE mv[4]; //每个局面最多4种走法TRANS(begin, m_ar[0].v);TRANS(end, l_end.v);m_ar[0].prev=NULL;m_root=m_ar;m_root->small=NULL;m_root->big=NULL;while((h < r) && (r < MAX_NODE - 4)){ c=move_gen(&m_ar[h], mv);for(i=0; i < c; i++){ mov(&m_ar[h], &mv[i], &node);node.prev= &m_ar[h];if(node.v == l_end.v){ pnode= &node;j=0;while(pnode->prev){ m_out[j]=*pnode;j++;pnode=pnode->prev;}m_depth=j;return r;}if(add_node(&node, r)) r++; //只能对历史节点中没有的新节点搜索,否则会出现环}h++;printf("\rSearch...%9d/%d @ %d", h, r, get_node_depth(&m_ar[h]));}if(h == r){ return -2; }else{return -1; }}long check_input(char *s, char a, long r){ long i;for(i=0; i < r; i++){ if(s[i] == a - 0x30) return 0; }return 1;}long check_possible(char *begin, char *end){ char fs;long f1=0, f2=0;long i, j;for(i=0; i < NUM; i++){ fs=0;for(j=0; j < i; j++){if((begin[i] != 0) && (begin[j] != 0) && (begin[j] < begin[i])) fs++; }f1+=fs;fs=0;for(j=0; j < i; j++){ if((end[i] != 0) && (end[j] != 0) && (end[j] < end[i])) fs++;}f2+=fs;}if((f1 & 1) == (f2 & 1)) return 1;. elsereturn 0;}void output(void){ long i, j, k;char ss[NUM];for(i=m_depth - 1; i >= 0; i--){ RTRANS(m_out[i].v, ss);for(j=0; j < SIZE; j++){ for(k=0; k < SIZE; k++){ printf("%2d", ss[SIZE * j + k]);}printf("\n");}printf("\n");}}int main(void){ char s1[NUM];char s2[NUM];long r;char a;printf("请输入开始状态:");r=0;while(r < NUM){ a=getchar();if(a >= 0x30 && a < 0x39 && check_input(s1, a, r)) { s1[r++]=a - 0x30;printf("%c", a);}}printf("\n请输入结束状态:");r=0;while(r < NUM){ a=getchar();if(a >= 0x30 && a < 0x39 && check_input(s2, a, r)) { s2[r++]=a - 0x30;printf("%c", a);}}printf("\n");if(check_possible(s1, s2)){ r=bfs_search(s1, s2);printf("\n");if(r >= 0){ printf("查找深度=%d,所有的方式=%ld\n", m_depth, r);output();}else if(r == -1){ printf("没有找到路径.\n");}else if(r == -2){printf("这种状态变换没有路径到达.\n");}else{printf("不确定的错误.\n");}}else{ printf("不允许这样移动!\n");}return 0;}方法二:用MATLAB实现program 8no_bfs; {八数码的宽度优先搜索算法} ConstDir : array[1..4,1..2]of integer {四种移动方向,对应产生式规则} = ((1,0),(-1,0),(0,1),(0,-1));n=10000;TypeT8no = array[1..3,1..3]of integer;TList = recordFather : integer; {父指针}dep : byte; {深度}X0,Y0 : byte; {0的位置}State : T8no; {棋盘状态}end;VarSource,Target : T8no;List : array[0..10000] of TList; {综合数据库}Closed,open,Best : integer { Best表示最优移动次数} Answer : integer; {记录解}Found : Boolean; {解标志}procedure GetInfo; {读入初始和目标节点}var i,j : integer;beginfor i:=1 to 3 dofor j:=1 to 3 do read(Source[i,j]);for i:=1 to 3 dofor j:=1 to 3 do read(Target[i,j]);end;procedure Initialize; {初始化}var x,y : integer;beginFound:=false;Closed:=0;open:=1;with List[1] do beginState:=Source;dep:=0;Father:=0;For x:=1 to 3 doFor y:=1 to 3 doif State[x,y]=0 then Begin x0:=x;y0:=y; End;end;end;Function Same(A,B : T8no):Boolean; {判断A,B状态是否相等} Var i,j : integer;BeginSame:=false;For i:=1 to 3 do for j:=1 to 3 do if A[i,j]<>B[i,j] then exit; Same:=true;End;Function not_Appear(new : tList):boolean;{判断new是否在List中出现}var i : integer;beginnot_Appear:=false;for i:=1 to open do if Same(new.State,List[i].State) then exit;not_Appear:=true;end;procedure Move(n : tList;d : integer;var ok : boolean;var new : tList);{将第d条规则作用于n得到new,OK是new是否可行的标志}var x,y : integer;beginX := n.x0 + Dir[d,1];Y := n.y0 + Dir[d,2];{判断new的可行性}if not ((X > 0) and ( X < 4 ) and ( Y > 0 ) and ( Y < 4 )) then begin ok:=false;exit end;OK:=true;new.State:=n.State; {new=Expand(n,d)}new.State[X,Y]:=0;new.State[n.x0,n.y0]:=n.State[X,Y];new.X0:=X;new.Y0:=Y;end;procedure Add(new : tList); {插入节点new}beginif not_Appear(new) then Begin {如果new没有在List出现} Inc(open); {new加入open表}List[open] := new;end;end;procedure Expand(Index : integer; var n : tList); {扩展n的子节点}var i : integer;new : tList;OK : boolean;Beginif Same(n.State , Target) then begin {如果找到解}Found := true;Best :=n.Dep;Answer:=Index;Exit;end;For i := 1 to 4 do begin {依次使用4条规则} Move(n,i,OK,new);if not ok then continue;new.Father := Index;new.Dep :=n.dep + 1;Add(new);end;end;procedure GetOutInfo; {输出} procedure Outlook(Index : integer); {递归输出每一个解} var i,j : integer;beginif Index=0 then exit;Outlook(List[Index].Father);with List[Index] dofor i:=1 to 3 do beginfor j:=1 to 3 do write(State[i,j],' ');writeln;end;writeln;end;beginWriteln('Total = ',Best);Outlook(Answer);end;procedure Main; {搜索主过程} beginRepeatInc(Closed);Expand(Closed,List[Closed]); {扩展Closed} Until (Closed>=open) or Found;if Found then GetOutInfo {存在解}else Writeln('no answer'); {无解}end;BeginAssign(Input,'input.txt');ReSet(Input);Assign(Output,'Output.txt');ReWrite(Output);GetInfo;Initialize;Main;Close(Input);Close(Output);End.五、实验结果六、实验总结通过实验问题的求解过程就是搜索的过程,采用适合的搜索算法是关键的,因为对求解过程的效率有很大的影响,包括各种规则、过程和算法等推理技术。
八数码——深度优先搜索+判重

八数码——深度优先搜索八数码难题(Eight-puzzle)。
在3X3的棋盘上,摆有8个棋子,在每个棋子上标有1~8中的某一数字。
棋盘中留有一个空格。
空格周围的棋子可以移到空格中。
要求解的问题是,给出一种初始布局(初始状态)和目标布局(目标状态),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
初始状态和目标状态如下:初始状态目标状态2 83 1 2 31 6 4 8 47 5 7 6 5看到题目,我想到用0表示空格。
然后用深度优先搜索解决问题。
程序如下:typear=array[1..3,1..3]of integer;consts:ar=((2,8,3),(1,6,4),(7,0,5));z:ar=((1,2,3),(8,0,4),(7,6,5));fx:array[1..4,1..2]of integer=((-1,0),(1,0),(0,-1),(0,1));vara:array[1..100]of recordb:ar;end;function dd(a:ar):boolean;vari,j:integer;begindd:=true;for i:=1 to 3 dofor j:=1 to 3 doif a[i,j]<>z[i,j] thenexit(false);end;function pd(h,l,i:integer):boolean;beginpd:=true;if h+fx[i,1]=4 thenexit(false);if h+fx[i,1]=0 thenexit(false);if l+fx[i,2]=0 thenexit(false);if l+fx[i,2]=4 thenexit(false);end;function fan(n:integer):integer;begincase n of1:exit(2);2:exit(1);3:exit(4);4:exit(3);end;end;procedure p(n:integer);vari,j,k:integer;beginfor i:=1 to n dobeginfor j:=1 to 3 dobeginfor k:=1 to 3 dowrite(a[i].b[j,k],' ');writeln;end;writeln;end;end;procedure dfs(dep,h,l,f:integer);varj,x,y:integer;beginif dd(a[dep].b) thenbeginp(dep);close(output);halt;end;for j:=1 to 4 doif pd(h,l,j)and(j<>f) thenbeginx:=h+fx[j,1];y:=l+fx[j,2];a[dep+1]:=a[dep];a[dep+1].b[h,l]:=a[dep].b[x,y];a[dep+1].b[x,y]:=0;if dep<6 thendfs(dep+1,x,y,fan(j));end;end;beginassign(output,'bsm.out');rewrite(output);a[1].b:=s;dfs(1,3,2,0);end.运行程序,输出:2 8 31 6 47 0 52 8 31 0 47 6 52 0 31 8 47 6 50 2 31 8 47 6 51 2 30 8 47 6 51 2 38 0 47 6 5这个程序对是对了。
人工智能结课作业-DFSBFSAstar解决八数码问题

⼈⼯智能结课作业-DFSBFSAstar解决⼋数码问题如果帮到你了,希望给个star⿎励⼀下1 深度优先遍历搜索(DFS)1.1算法介绍深度优先搜索算法(Depth-First-Search,DFS)是⼀种⽤于遍历或搜索树或图的算法。
沿着树的深度遍历树的节点,尽可能深的搜索树的分⽀。
当节点v的所在边都⼰被探寻过,搜索将回溯到发现节点v的那条边的起始节点。
这⼀过程⼀直进⾏到已发现从源节点可达的所有节点为⽌。
如果还存在未被发现的节点,则选择其中⼀个作为源节点并重复以上过程,整个进程反复进⾏直到所有节点都被访问为⽌。
属于盲⽬搜索。
以上图为例,简述DFS的过程。
⾸先从根节点"1"出发,按⼀定的顺序遍历其⼦节点,这⾥我们假设优先遍历左边的。
所以,在遍历"1"之后,我们到了节点"2",此时"2"仍有⼦节点,所以应继续向下遍历,下⼀个节点是"3",然后是"4"。
到了"4"之后,没有⼦节点了,说明我们已经将这⼀条路遍历完了,接着我们应该回溯,应该回到"4"的⽗节点,也就是"3"。
因为"3"还有⼀个⼦节点"5"没有遍历,所以下⼀个我们应该遍历的是"5"。
遍历完"5"之后⼜发现⼀条路到头了,再次回溯依然回溯到其⽗节点"3",此时"3"的所有⼦节点都已经遍历完了,因该接着回溯到"3"的⽗节点"2",然后检查"2"是否有没有遍历完的⼦节点。
按照这样的规则,完成所有节点的遍历。
最终得到的遍历顺序是"1-2-3-4-5-6-7-8-9-10-11-12"在介绍了DFS在遍历树的应⽤后,我们将其应⽤于⼋数码问题的解决。
深度优先算法与广度优先算法的比较

深度优先算法与广度优先算法的比较深度优先算法以深度为优先,从一个节点开始,逐个遍历其邻居节点直至最深处,然后回溯到上一个节点,再继续遍历其他分支。
它是通过栈来实现的,先进后出的特性决定了深度优先算法是一个递归算法。
深度优先算法在过程中,不需要记住所有的路径,只需要记住当前路径上的节点即可。
对于树而言,深度优先算法通常沿着左子树一直深入,直到最深的叶节点,然后再回溯到前一个节点继续右子树的遍历。
广度优先算法以广度为优先,从一个节点开始,逐层遍历其所有邻居节点,然后再遍历下一层的节点,直至遍历完所有节点。
它是通过队列来实现的,先进先出的特性决定了广度优先算法是一个非递归算法。
广度优先算法在过程中,需要记住每一层的节点,并且按照先进先出的顺序进行遍历。
对于树而言,广度优先算法会先遍历根节点,然后是根节点的子节点,再然后是子节点的子节点,按照层次逐层遍历。
以下是深度优先算法和广度优先算法的比较:1.方式:深度优先算法通过一条路径一直遍历到最深处,然后回溯到上一个节点,再继续遍历其他分支。
广度优先算法逐层遍历,先遍历当前层的节点,再遍历下一层的节点。
2.存储结构:深度优先算法使用栈进行遍历,而广度优先算法使用队列进行遍历。
3.内存占用:深度优先算法只需要记住当前路径上的节点,所以内存占用较小。
而广度优先算法需要记住每一层的节点,所以内存占用较大。
4.时间效率:深度优先算法通常适用于解决单个解或路径的问题,因为它首先深入其中一个分支,整个分支再回溯,因此它可能会浪费一些时间在不必要的路径上。
而广度优先算法通常适用于解决最短路径或最小步数的问题,因为它遍历一层后再遍历下一层,所以找到的解很可能是最优解。
5.应用场景:深度优先算法适用于解决迷宫问题、拓扑排序和连通性等问题。
广度优先算法适用于解决最短路径、社交网络中的人际关系、图的遍历和等问题。
总结起来,深度优先算法和广度优先算法都有各自的特点和适用场景。
深度优先算法适合解决单个解或路径的问题,而广度优先算法适合解决最短路径或最小步数的问题。
简述深度优先算法的基本思想

简述深度优先算法的基本思想从认知学习理论出发,研究了深度优先算法的基本思想。
深度优先算法( Depth-First Algorithm),也称为深度平面搜索法,它是由J.H.Bayes在1956年提出来的。
它是一种先进的启发式搜索算法。
它具有启发性强、搜索空间大等特点,能够避免传统算法只会沿着固定路径搜索的缺点。
它既适合于处理规则少、结构简单的问题,又适合处理规则多、结构复杂的问题。
( 1)在一个有向图中找到一个点,要求这个点所在的线段不得多于所有向下或者向上可能路径的总和;( 2)找到所有最短路径的路径;( 3)把最短路径的路径作为深度优先搜索的搜索路径;( 4)计算每一个线段中前进方向与原来方向之间的距离;( 5)若前进方向与原来方向之间的距离小于某一特定值,则跳过此路径。
( 2)从该点向左或向右边采用步长为1的线段作为搜索路径。
设当前从点向右搜索路径长为L,则上一步搜索到从该点向右搜索路径长为l;( 3)计算当前第i个向下可能路径的步数,然后计算各可能向下路径到第i个最近点之间的距离。
由距离最小原则选择上一步的最短路径,如果该步最短路径不是从该点向右,就不是好的路径,继续从第一个方向重新开始,直到找到更好的路径。
( 4)将两种路径进行交叉比较。
,记第i个向下路径对应的可能向下路径序列为: p(i=1, 2,3, 4, 5),其中j为第j个最近点,其值为(2-i, i-j);每一个线段中前进方向与原来方向之间的距离,记为d。
显然,对任何一个( p(i=1, 2, 3, 4, 5), p(i=1, 2, 3, 4, 5)),由(4)式可知有p(i=1, 2, 3, 4, 5)- p(i=1, 2, 3, 4, 5)+d>0,即p(i=1, 2, 3, 4, 5)>0,所以可以舍弃这一条线段而选择另一条线段;根据“前进方向与原来方向之间的距离最小”原则,从该点向右前进。
( 5)如果向左或向右采用的路径相同,则采用向左或向右搜索。
深度优先搜索算法

深度优先搜索算法深度优先搜索算法是一种经典的算法,它在计算机科学领域中被广泛应用。
深度优先搜索算法通过沿着一个分支尽可能的往下搜索,直到搜索到所有分支的末端后,返回上一层节点,再继续往下搜索其它分支。
在搜索过程中,深度优先搜索算法采用递归的方式进行,它的工作原理与树的先序遍历算法相似。
本文将介绍深度优先搜索算法的基本原理、应用场景、实现方式及其优缺点等内容。
一、深度优先搜索算法的基本原理深度优先搜索算法是一种基于贪心法的搜索算法,它的目标是在搜索过程中尽可能的向下搜索,直到遇到死路或者找到了目标节点。
当搜索到一个节点时,首先将该节点标记为已访问。
然后从它的相邻节点中选择一个未被访问过的节点继续搜索。
如果没有未被访问过的节点,就返回到前一个节点,从该节点的其它相邻节点开始继续搜索。
这样不断地递归下去,直到搜索到目标节点或者搜索完所有的节点。
深度优先搜索算法的实现方式通常是通过递归函数的方式进行。
假设我们要搜索一棵树,从根节点开始进行深度优先搜索。
可以采用以下的伪代码:```function depthFirstSearch(node)://标记节点为已访问node.visited = true//递归搜索该节点的相邻节点for each adjacentNode in node.adjacentNodes:if adjacentNode.visited == false:depthFirstSearch(adjacentNode)```这段代码表示了深度优先搜索算法的基本思想。
在搜索过程中,首先将当前节点标记为已访问,然后递归搜索该节点的相邻节点。
如果相邻节点未被访问过,就以该节点为起点继续深度优先搜索。
通过递归函数不断往下搜索,最终遍历完整棵树。
二、深度优先搜索算法的应用场景深度优先搜索算法在计算机科学领域中有很多应用,例如图论、路径查找、迷宫和游戏等领域。
下面介绍一些具体的应用场景。
1.图论深度优先搜索算法被广泛应用于图论中。
九宫八数问题的四种深度优先编程方法

九宫八数问题的四种深度优先编程方法马旭【摘要】Optimized programming on the storage mode of the grid matrix and mobile path can effectively improve the time complexity and space complexity of the ″eight-number and nine-grid ″programming.The paper provides two C language programming and compares the methodof ″square matrix storage″and ″string storage method″.Experimental data analysis shows that the ″string storage method″is superior to the ″square matrix storage method″in the time-space efficiency of the program.In addition,a programming method is proposed to establish path identification matrix,which can simplify programming code and improve readability.It also proposes a recursive programming method of retaining path information,which can effectively reduce the recursive stack space,significantly reduce program space complexity, reduce program running time,and improve program efficiency.%在方格矩阵及移动路径的存储方式上优化编程,可以有效地改进"九宫八数"编程的时间复杂度及空间复杂度.采用C语言编程,比较"方阵存储法"与"字串存储法"两种方格矩阵存储方法.实验数据分析可知,"字串存储法"比"方阵存储法"在程序时空效率上更优越.提出建立路径标识矩阵的编程方法,可以有效地简化程序设计代码,提高程序可读性.提出保留路径信息的递归编程方法,可以有效地减少递归压栈空间,显著降低程序空间复杂度,缩短程序运行时间,提高程序效率.【期刊名称】《计算机应用与软件》【年(卷),期】2018(035)005【总页数】6页(P10-14,84)【关键词】九宫八数问题;深度优先编程方法;方阵存储法;字串存储法;路径标识矩阵;时空复杂度【作者】马旭【作者单位】辽宁大学创新创业学院辽宁沈阳110036【正文语种】中文【中图分类】TP311.110 引言M×N方格矩阵中移子类智能游戏是高级程序设计人员必备的程序设计训练题目[1-4]。
深度优先算法与广度优先算法

深度优先算法与⼴度优先算法深度优先搜索和⼴度优先搜索,都是图形搜索算法,它两相似,⼜却不同,在应⽤上也被⽤到不同的地⽅。
这⾥拿⼀起讨论,⽅便⽐较。
⼀、深度优先搜索深度优先搜索属于图算法的⼀种,是⼀个针对图和树的遍历算法,英⽂缩写为DFS即Depth First Search。
深度优先搜索是图论中的经典算法,利⽤深度优先搜索算法可以产⽣⽬标图的相应拓扑排序表,利⽤拓扑排序表可以⽅便的解决很多相关的图论问题,如最⼤路径问题等等。
⼀般⽤堆数据结构来辅助实现DFS算法。
其过程简要来说是对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌,⽽且每个节点只能访问⼀次。
基本步奏(1)对于下⾯的树⽽⾔,DFS⽅法⾸先从根节点1开始,其搜索节点顺序是1,2,3,4,5,6,7,8(假定左分枝和右分枝中优先选择左分枝)。
(2)从stack中访问栈顶的点;(3)找出与此点邻接的且尚未遍历的点,进⾏标记,然后放⼊stack中,依次进⾏;(4)如果此点没有尚未遍历的邻接点,则将此点从stack中弹出,再按照(3)依次进⾏;(5)直到遍历完整个树,stack⾥的元素都将弹出,最后栈为空,DFS遍历完成。
⼆、⼴度优先搜索⼴度优先搜索(也称宽度优先搜索,缩写BFS,以下采⽤⼴度来描述)是连通图的⼀种遍历算法这⼀算法也是很多重要的图的算法的原型。
Dijkstra单源最短路径算法和Prim最⼩⽣成树算法都采⽤了和宽度优先搜索类似的思想。
其别名⼜叫BFS,属于⼀种盲⽬搜寻法,⽬的是系统地展开并检查图中的所有节点,以找寻结果。
换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为⽌。
基本过程,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。
如果所有节点均被访问,则算法中⽌。
⼀般⽤队列数据结构来辅助实现BFS算法。
基本步奏(1)给出⼀连通图,如图,初始化全是⽩⾊(未访问);(2)搜索起点V1(灰⾊);(3)已搜索V1(⿊⾊),即将搜索V2,V3,V4(标灰);(4)对V2,V3,V4重复以上操作;(5)直到终点V7被染灰,终⽌;(6)最短路径为V1,V4,V7.作者:安然若知链接:https:///p/bff70b786bb6来源:简书简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
回溯算法(DFS:深度优先)

回溯算法(DFS:深度优先)1. ⼋皇后问题⼋皇后问题,是⼀个古⽼⽽著名的问题,是回溯算法的典型案例。
该问题是国际西洋棋棋⼿马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放⼋个皇后,使其不能互相攻击,即任意两个皇后都不能处于同⼀⾏、同⼀列或同⼀斜线上,问有多少种摆法。
思路:使⽤⼀个数组gEightQueen存储第i⾏的皇后摆在第gEightQueen[i]列的位置上步骤⼀:对于第0⾏,⼀共有⼋个位置可以选择,逐⼀选择步骤⼆:对于以后的每⼀⾏,⼀共有⼋个位置可以选择,确定位置后需要判断该位置放置元素是否与前⾯的⾏冲突,如果冲突,继续在剩余的位置中选择测试。
如果不冲突,则继续向下递归,递归结束后应当将改⾏的元素置0。
步骤三:当递归到第7⾏,选择位置不冲突则找到了⼀种情况,将总的情况统计数加1。
#include<iostream>using namespace std;static int gEightQueen[8] = { 0 }, gCount = 0;void print()//输出每⼀种情况下棋盘中皇后的摆放情况{for (int i = 0; i < 8; i++){int inner;for (inner = 0; inner < gEightQueen[i]; inner++)cout << "0";cout <<"#";for (inner = gEightQueen[i] + 1; inner < 8; inner++)cout << "0";cout << endl;}cout << "==========================\n";}int check_pos_valid(int loop, int value)//检查是否存在有多个皇后在同⼀⾏/列/对⾓线的情况{int index;int data;for (index = 0; index < loop; index++){data = gEightQueen[index];if (value == data)return0;if ((index + data) == (loop + value))return0;if ((index - data) == (loop - value))return0;}return1;}void eight_queen(int index){int loop;for (loop = 0; loop < 8; loop++){if (check_pos_valid(index, loop)){gEightQueen[index] = loop;if (7 == index){gCount++, print();gEightQueen[index] = 0;return;}eight_queen(index + 1);gEightQueen[index] = 0;}}}int main(int argc, char*argv[]){eight_queen(0);cout << "total=" << gCount << endl;return0;}2. 数独问题解法:只需要求出⼀个解,solve()返回布尔类型对于判断是否完成解⼗分有⽤步骤⼀:依此遍历数独中所有的元素,如果不存在'.',说明已经获得了解,如果存在'.',说明需要继续向下求解。
深度优先搜索算法DFS

深度优先搜索算法DFS= = =1.首先选定图的类别(有向图、无向图),再选定图的存储结构,根据输入的顶点或者边建立图;并把相应的邻接表或者邻接矩阵输出;2.根据已有的邻接矩阵或邻接表用递归方法编写深度优先搜索遍历算法,并输出遍历结果;[dfs.rar] - 深度优先搜索算法解决八码难题[Draw1Doc.rar] - 简单的绘图程序,能画点,直线,多边形等,比较简单= = = =这里的图的深度优先算法利用了栈来实现。
图的深度遍历原则:1 如果有可能,访问一个领接的未访问的节点,标记它,并把它放入栈中。
2 当不能执行规则1 时,如果栈不为空,则从栈中弹出一个元素。
3 如果不能执行规则1 和规则2 时,则完成了遍历。
代码中的图使用的是Graph 图-邻接矩阵法来表示,其他的表示法请见:Graph 图-邻接表法代码中的Stack为辅助结构,用来记载访问过的节点。
栈的详细描述可以见:ArrayStack 栈,LinkedStack 栈。
Vertex表示图中的节点,其中包含访问,是否访问,清除访问标志的方法。
Graph.main:提供简单测试。
代码可以以指定下标的节点开始作深度遍历。
代码比较简单,除了Graph.dsf(int i)深度优先遍历算法外没有过多注释。
= = = =深度优先搜索DFS正如算法名称那样,深度优先搜索所遵循的搜索策略是尽可能“深”地搜索图。
在深度优先搜索中,对于最新发现的顶点,如果它还有以此为起点而未探测到的边,就沿此边继续汉下去。
当结点v的所有边都己被探寻过,搜索将回溯到发现结点v有那条边的始结点。
这一过程一直进行到已发现从源结点可达的所有结点为止。
如果还存在未被发现的结点,则选择其中一个作为源结点并重复以上过程,整个进程反复进行直到所有结点都被发现为止。
和宽度优先搜索类似,每当扫描已发现结点u的邻接表从而发现新结点v时,深度优先搜索将置v的先辈域π[v]为u。
和宽度优先搜索不同的是,前者的先辈子图形成一棵树,而后者产生的先辈子图可以由几棵树组成,因为搜索可能由多个源顶点开始重复进行。
深度优先算法和广度优先算法

深度优先算法和广度优先算法
深度优先算法(Depth-first search, DFS)是搜索树根节点开始,跟据一定的搜索规则,逐深搜索解空间树上的每一个分支,直至找到合适的叶节点,然后返回,再回到上一层,沿另一条分支继续搜索直到解空间树上所有的叶节点都搜索完毕,从而求出一个最优解的算法。
广度优先算法(Breadth-first search, BFS)是利用队列实现的,其基本思想是从根节点开始,按层次一次搜索解空间树上每一层的所有节点,当某一层节点全部被搜索时,再继续搜索下一层节点,直至所有节点搜索完毕,当一个节点被访问时,其所有没有被访问过的邻居节点入队列,从而求出最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
return deapth; } int get_evafun(void) {
return eva_function; } void set_num(int other_num[9]); void show(void); eight_num& operator=(eight_num&); eight_num& operator=(int other_num[9]); int operator==(eight_num&); int operator==(int other_num[9]); };
return 0; else {
num[i] = num[i + 1]; num[i + 1] = 0; return 1; } }
//判断可否解出 int icansolve(int num[9], int target[9]) {
int i, j; // int count_num,count_target; int count_num = 0, count_target = 0; for (i = 0; i<9; i++) for (j = 0; j<i; j++) {
void eight_num::get_numbers_to(int other_num[9])
{ for (int i = 0; i<9; i++) other_num[i] = num[i];
}
void eight_num::set_num(int other_num[9]) {
for (int i = 0; i<9; i++) num[i] = other_num[i];
// 8数码之深度优先 //编译环境:VS2013
#include "stdafx.h" #include <iostream> #include <time.h> #include <stdio.h> #include <dos.h> #include <conio.h>
static int target[9] = { 1, 2, 3, 8, 0, 4, 7, 6, 5 }; int i = 0; //static int target[9]={1,2,3,4,5,6,7,8,0};
for (int i = 0; i<9; i++)
num[i] = i;
}
void cul_para(void);
void get_numbers_to(int other_num[9]); int get_nipn(void) {
return not_in_position_num; } int get_deapth(void) {
}
void eight_num::show() {
cout << num[0]; cout << " "; cout << num[1]; cout << " "; cout << num[2]; cout << "\n"; cout << num[3]; cout << " "; cout << num[4]; cout << " "; cout << num[5]; cout << "\n"; cout << num[6]; cout << " "; cout << num[7]; cout << " "; cout << num[8]; cout << "\n"; }
//空格向下移 int move_down(int num[9]) {
for (int i = 0; i<9; i++) if (num[i] == 0)
break; if (i>5)
return 0; else {
num[i] = num[i + 3]; num[i + 3] = 0; return 1; } } //空格向左移 int move_left(int num[9]) { for (int i = 0; i<9; i++) if (num[i] == 0) break; if (i == 0 || i == 3 || i == 6) return 0; else { num[i] = num[i - 1]; num[i - 1] = 0; return 1; } } //空格向右移 int move_right(int num[9]) { for (int i = 0; i<9; i++) if (num[i] == 0) break; if (i == 2 || i == 5 || i == 8)
flag = 1; if (target[i]<0 || target[i]>8 || flag == 1) {
i--; cout << "Illegle number!\tReinput!\n"; } } } eight_num S(num), Target(target); //S 为初始节点,Target为目标节点 S.parent = S.open_pre = NULL; S.cul_para(); memery_used++; cout << "初始数组是:\n"; S.show(); cout << "目标数组是:\n"; Target.show();
//主函数开始 int main(void) {
int max_step = 30; double time; clock_t Start, Finish; int memery_used = 0, step = 0; int num[9]; int flag = 0;//是否输入错误标志,1表示输入错误 int bingo = 0;//是否查找成功标志,1表示成功 int new_flag = 0;//是否有新节点生成,1表示有 int i, j; cout << "郭文涛 S201402233\n请输入初始数组(0代表空白):\n"; for (i = 0; i<9; i++) {
{
num[0] = num1;
num[1] = num2;
num[2] = num3;
num[3] = num4;
num[4] = num5;
num[5] = num6;
num[6] = num7;
num[7] = num8;
num[8] = num9;
}
eight_num(voiFra bibliotek)//构造函数
{
using namespace std;
//class definition class eight_num { private:
int num[9]; int not_in_position_num; int deapth; int eva_function;
public: eight_num* parent; eight_num* open_pre;
flag = 0; cin >> num[i]; for (j = 0; j<i; j++) if (num[i] == num[j])
flag = 1; if (num[i]<0 || num[i]>8 || flag == 1) {
i--; cout << "非法数组!\请重新输入\n"; } } cout << "你确定要转换(是Y/否N)?"; char input; cin >> input; if (input == 'y' || input == 'Y') { cout << "\n请输入新数组:\n"; for (i = 0; i<9; i++) { flag = 0; cin >> target[i]; for (j = 0; j<i; j++) if (target[i] == target[j])
if (num[j]<num[i] && num[j] != 0) count_num++;
if (target[j]<target[i] && target[j] != 0) count_target++;
} count_num = count_num - 2 * (count_num / 2); count_target = count_target - 2 * (count_target / 2); if ((count_num == 1 && count_target == 1) || (count_num == 0 && count_target == 0))
}
eight_num& eight_num::operator=(eight_num& another_8num) {
for (int i = 0; i<9; i++) num[i] = another_8num.num[i];
