汽车理论matl新编作业

合集下载

汽车理论课后作业答案MATLAB

汽车理论作业MA TLAB过程汽车驱动力与阻力平衡图加速度倒数-速度曲线图0 10 20 30 40 50 60 70 80 90 100u汽车功率平衡图u/(km/h)最高档等速百公里油耗曲线Ua/(km/h)燃油积极性-加速时间曲线源程序：《第一章》m=3880;g=9.8;r=0.367;x=0.85;f=0.013;io=5.83;CdA=2.77;lf=0.218;Iw1=1.798;Iw2=3.598;Iw=lw1+lw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比L=3.2;a=1.947;hg=0.9;n=600:1:4000;T=-19.313+295.27* n/1000-165.44*(门/1000)人2+40.874*(门/1000)人3-3.8445*( n/IOOO).%;Ft1=T*ig(1)*io*x/r; %计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F仁m*g*f+CdA*u”2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.A2/21.15;F3=m*g*f+CdA*u3.A2/21.15;F4=m*g*f+CdA*u4.A2/21.15;figure(1);plot(u1,Ft1, '-r' ,u2,Ft2, '-m' ,u3,Ft3, '-k' ,u4,Ft4, '-b' ,u1,F1, '-r' ,u2,F2, '-m' ,u3,F3, ' k' ,u4,F4, '-b' , 'LineWidth' ,2) title( ' 汽车驱动力与阻力平衡图' );xlabel( 'u_{a}/km.hA{-1}' )ylabel( 'F/N' )gtext( 'F_{t1}' )gtext( 'F_{t2}' )gtext( 'F_{t3}' )gtext( 'F_{t4}' )gtext( 'F_{f}+F_{w}' )%由汽车驱动力与阻力平衡图知，他们无交点，u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp( ' 假设是后轮驱动' );C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*rA2)+If*ig(1)*rA2*ioA2*x/(m*rA2);delta2=1+(Iw1+Iw2)/(m*rA2)+If*ig(2)*rA2*ioA2*x/(m*rA2);delta3=1+(Iw1+Iw2)/(m*rA2)+If*ig(3)*rA2*ioA2*x/(m*rA2);delta4=1+(Iw1+Iw2)/(m*rA2)+If*ig(4)*rA2*ioA2*x/(m*rA2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4, 'LineWidth',2);title( ' 加速度倒数- 速度曲线图xlabel( 'u' )ylabel( '1/a' )gtext( '1/a1' )gtext( '1/a2' )gtext( '1/a3' )gtext( '1/a4' )%由加速度倒数- 速度曲线图可知u1min=min(u1);u1max=max(u1); u2min=u1max; u2min=min(u2);u2max=max(u2); u3min=u2max;u3max=max(u3); u4min=u3max; u4max=70;x1=[]; x2=[]; x3=[]; x4=[];y=3401; for i=1:3401;if u3(i)<=u3min;x1=[i];end end q1=max(x1); ua3=u3(q1:y); a3=h3(q1:y); for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];end end q2=max(x2); q3=max(x3); ua4=u4(q2:q3); a4=h4(q2:q3); s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp( ' 积分得' ) t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600; %计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x); %计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1, '-r' ,u2,Pe2, '-m' ,u3,Pe3, '-k' ,u4,Pe4, '-b' ,u1,P1, 'k' ,u2,P2, 'k' ,u3,P3, 'k' u4,P4, 'k' ,'linewidth' ,2);gtext( 'Pe1' )gtext( 'Pe2' )gtext( 'Pe3' )gtext( 'Pe4' )xlabel( 'u/(km/h)' );ylabel( 'P/kW' );title( ' 汽车功率平衡图' );n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.A2; 算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x); %计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215]; B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230 -0.000038568];b1=(B0⑴)+(B1(1)*Pe(1))+(B2(1)*Pe(1f2)+(B3(1)*Pe⑴T)+(B4(1)*Pe⑴人4); b2=(B0(2))+(B1(2)*Pe (2))+(B2(2)*Pe(2)A2)+(B3(2)*Pe(2)A3)+(B4(2)*Pe(2)A4);b3=(B 0(3) )+(B1(3)*Pe(3))+(B2 (3)*Pe(3)A2)+(B3(3)*Pe(3)A3)+(B4(3)*Pe(3)A4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)A2)+(B3(4)*Pe(4)A3)+(B4(4)*Pe(4)A4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)A2)+(B3(5)*Pe(5)A3)+(B4(5)*Pe(5)A4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)A2)+(B3(6)*Pe(6)A3)+(B4(6)*Pe(6)A4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)A2)+(B3(7)*Pe(7)A3)+(B4(7)*Pe(7)A4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)A2)+(B3(8)*Pe(8)A3)+(B4(8)*Pe(8)A4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig 4)*io); %卩表示车速QS=polyval(M,UA); %0表示油耗figure(4);plot(UA,QS, 'linewidth' ,2);title( '最高档等速百公里油耗曲线' );xlabel( 'Ua/(km/h)' );ylabel( 'Qs/L' );《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档，较高转速(n取3401 )，最经济负荷(即90%负荷大约46.9366KW )行驶时油耗' ) qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g); qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g); qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185]; %加速时间：(这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间) 因与题 1.3 第三问求法相同，这里不在累述，可直接有计算机求得：figure(5);plot(qs,st, '+' ,'lineWidth' ,2)hold on plot(qs,st,); gtext( 517') gtext( 543') gtext( 583') gtext( 617') gtext( 633')title('燃油积极性-加速时间曲线’); xlabel('燃油经济性(qs/L)'); ylabel('动力性--原地起步加速时间(st/s)');《第四章》4-31)时：前轮先抱死 0时：后轮先抱死利用MATLAB 作图得到下图:前轴利用附着系数为:L z b zh g后轴利用附着系数为:L 1 zazh g空载时： 03.95 0.38 1.85所以满载时：ohg0.8450.413空载时后轮总是先抱死。

汽车理论 matlab编程作业答案

4.3（1）利用附着系数空载时前轴的利用附着系数φf1：φf1=βz1L b+zh g=0.38z13.951.85+0.845z空载时后轴的利用附着系数φr1：φr1=(1−β)z1L a−zh g=(1−0.38)z13.952.1−0.845z满载时前轴的利用附着系数φf2：φf2=βz1L b+zh g=0.38z13.951.0+1.17z满载时后轴的利用附着系数φr2：φr2=(1−β)z1L a−zh g=(1−0.38)z13.952.95−1.17zMatlab程序：clcclearsyms z;f1=0.38*z/((1/3.95)*(1.85+0.845*z));r1=(1-0.38)*z/((1/3.95)*(2.1-0.845*z)); f2=0.38*z/((1/3.95)*(1.0+1.17*z));r2=(1-0.38)*z/((1/3.95)*(2.95-1.17*z)); f=z;ezplot(f1);hold on;ezplot(f2);ezplot(r1);ezplot(r2);ezplot(f);axis([0 1.0 0 1.0]);title('利用附着系数曲线');xlabel('制动强度z');ylabel('利用附着系数');text(0.38,0.8,'Ør(空载)');text(0.6,0.9,'Ør(满载)');text(0.8,0.45,'Øf(空载)');text(0.8,0.6,' Øf(满载)');text(0.85,0.9,'Ø=z')制动效率空载时前轴的制动效率E f1：E f1=bLβ−φf gL=1.85/3.95f空载时后轴的制动效率E r1：E r1=aL(1−β)−φr gL=2.1/3.95r满载时前轴的制动效率E f2：E f2=bLβ−φf gL=1.0/3.950.38−φf∙1.17/3.95满载时后轴的制动效率E r2：E r2=aL(1−β)−φr gL=2.95/3.95rMatlab程序：clearsyms x;Er1=2.1/3.95/(1-0.38+x*0.845/3.95); Ef2=1.0/3.95/(0.38-x*1.17/3.95);Er2=2.95/3.95/(1-0.38+x*1.17/3.95); ezplot(Ef2);hold on;ezplot(Er1);ezplot(Er2);axis([0 1.0 0 1.0]);title('前后轴制动效率曲线'); xlabel('附着系数'); ylabel('制动效率（%）'); text(0.35,0.9,'Ef'); text(0.8,0.9,'Er'); text(0.55,0.78,'Er'); text(0.65,0.94,'满载'); text(0.55,0.65,'空载');(2)①由图可得：空载时，在φ=0.8时的制动效率为0.7，则其制动减速度为0.8g*0.7=0.56g 。

汽车理论大作业(2)

汽车理论大作业20100410420车辆四班杨江林1.内容本文在MATLAB/Simulink中搭建ABS莫型，将ABS寸整车的性能影响进行仿真，并对仿真结果进行分析来证明方法的可行性。

2原理由轮胎纵向力特性可知，车轮的滑移率 b s决定了制动力和侧向力的大小。

公式1给出了车轮滑移率b s的定义。

式中，丿宀为车速，对应线速度，V V为汽车线速度，r R为车轮半径，为车轮线速度。

如图1所示为车辆在制动行使时，地面作用于车轮的制动力sb F和侧向力yF随车轮制动滑移率b s的变化关系。

可以看出，侧向力随滑移率bs的增加而下降，当滑移率从1降为0时，制动力开始随滑移率的增加而迅速增加；当滑移率增至某值opt s时，制动力则随滑移率的增加而迅速减少。

公式1说明了车速与轮速的关系：当滑移率为1时，车速与轮速相等；当滑移率为0时，车轮已经处于抱死状态。

车轮抱死滑移时，不仅制动力减少，制动强度降低，而且车轮侧向附着力也大大减少。

因此，当前轮抱死滑移时，车辆丧失转向能力；而后轮抱死滑移则属于不稳定工况，易引起车辆急速甩尾的危险。

根据制动时附着系数与滑移率的关系曲线可知，当把车轮滑移率的值控制在最佳滑移率20%附近时，汽车将能够获得最好的制动效能同时还拥有较好的方向稳定性。

附着系数的数值主要取决于道路的材料、路面的状况、轮胎的结构、胎面花纹、材料以及车速等因素。

因此对于不同的路面来说，附着系数与滑移率的关系是不同的。

图2是不同路面的附着系数与滑移率的关系。

0 20 40 60 80 100^滑移率'图2不同路面的附着系数与滑移率的关系利用车轮滑移率的门限值及参考滑移率设计控制逻辑，使得车轮的滑移率保持在峰值附着系数附近，从而获得最大的地面制动力和最小的制动距离。

制动时的侧向稳定性。

3. 模型由于汽车动力学模型建立是个复杂的过程，采用单轮模型建立汽车动力学模型。

简化的单轮模型如图3。

同时获得较大的侧向力，保证由图可得到车辆的动力方程:车辆运动方程：dv m— dt车轮运动方程：dI FR T b dt车辆纵向摩擦力：F N（1）（2）式中, m为1/4整车质量（kg）；F为地面制动力（N）；R为车轮半径（m）; I为车轮转动惯量（kg?m2）；Tb为制动力矩（N?m), m); v 为车身速度(m/s); w 为车轮角速度（rad • s ）; N 为地面对车轮的法向反作用力（ N ）;卩为地面摩擦系数。

汽车理论大作业

二自由度轿车模型的有关参数如下：总质量 m ＝1818．2kg绕z o 轴转动惯量 23885z I kg m =⋅轴距 L=3.048m质心至前轴距离 a=1.463m质心至后轴距离 b=1.585m前轮总侧偏刚度 rad N k /626181-=后轮总侧偏刚度 2110185k =- /N rad转向系总传动比 i=20试求：1)稳定性因数K 、特征车速ch u 。

2)稳态横摆角速度增益曲线r ωδ)s ----a u 车速u=22.35m/s 时的转向灵敏度r swωδ。

3)静态储备系数S.M.，侧向加速度为0．4g 时的前、后轮侧偏角绝对值之差12a a -与转弯半径的比值R/R 0(R 0=15m)。

4)车速u=30.56m/s,瞬态响应的横摆角速度波动的固有(圆)频率0ω、阻尼比ζ、反应时间τ与峰值反应时间ε。

提示： 1) 稳定性系数：⎪⎪⎭⎫ ⎝⎛-=122k b k a L m K =0.002422/m s 特征车速Ku ch 1==20.6s m /=74.18km/h 2) 转向灵敏度21KuL u s r +=⎪⎭⎫δω=0.618 3) ()211αα-=L a K y ⇒ 21αα-=0.0281rad δL R =0 ()21ααδ--=LR ⇒0R R =1.16 4) 固有圆频率 m c '=0ω=5.58rad/s.0f =0.8874Hz 阻尼比m h '=02ωξ=0.5892 反应时间ωτΦ-== 0.1811s 峰值反应时间 ωξωωεΦ-=0arctg=0.3899sMATLAB程序m=1818.2 ; Iz=3885 ; L=3.048 ;a=1.463 ; b=1.585 ;k1=-62618 ; k2=-110185 ;i=20 ; R0=15 ;t=0:0.05:8 ;K=m/(L*L)*(a/k2-b/k1);u_ch=(1/K)^0.5 ;q0=L/R0 ;u=30;w_r0=u./L*q0./(1+K.*u.*u) ;w0=L./u.*(k1.*k2.*(1+K.*u.*u)/(m.*Iz)).^0.5 ;zuni=(-m.*(a.*a.*k1+b.*b*k2)-Iz*( k1+k2))./(2*L.*(m.*Iz.*k1.*k2.*(1+K.*u.*u)).^0.5) ;Q=atan((1-zuni.^2).^0.5./( m.*u.*a.*w0/L/k2+zuni )) ;w=w0.*(1-zuni.^2).^0.5 ;w_r=w_r0.*(1+(1./(1-zuni.*zuni).*( (-m.*u*a/(L*k2)).^2.*w0.^2 + 2*m.*u*a.*zuni.*w0/(L*k2) +1 )).^0.5.*exp(-zuni.*w0.*t).*sin(w.*t+Q));plot(t,w_r);利用5.11的数据，在MATLAB 分别画出横摆角速度瞬态响应曲线。

汽车理论作业(一)

∴
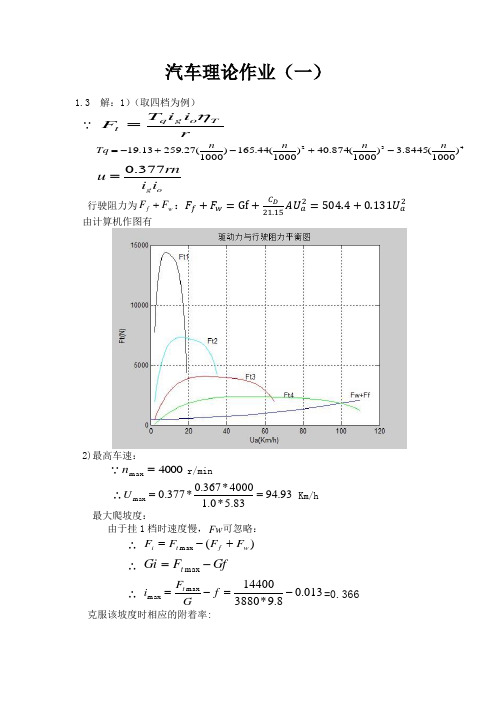
用Matlab软件采用梯形法求积分，计算求出加速时间为27.4156s。
1.8解：①1挡时，
由于忽略滚动阻力和空气阻力，则
∴
∴将出现打滑现象，故在加速过程中发动机扭矩不能否充分发挥。
②由题意知，
∵ ,且
∴解得b=1704.6mm
∴前轴负荷率为：
2.1答：不正确。（1）由燃油消耗率曲线知：汽车在中等转速、较大档位上才是最省油的。此时，后备功率较小，发动机负荷率较高燃油消耗率低，百公里燃油消耗量较小。（2）发动机负荷率高只是汽车省油的一个方面，另一方面汽车的质量利用系数（即装载质量与整备质量之比）大小也关系汽车是否省油。
汽车理论作业（一）
1.3解：1）（取四档为例）
∵
行驶阻力为：
由计算机作图有
2)最高车速：
∵ r/min
∴ Km/h
最大爬坡度：
由于挂1档时速度慢，可忽略:
在求最大坡度时，，故：等效坡度
∴
3）①由 ,
绘制汽车行驶加速倒数曲线（已装货）：
②汽车由2档起步加速行驶至70km/h的加速时间。
2.7解：①∵
由以上三个关系式，可以绘出各个档位下发动机的有效功率图。

汽车理论作业 1.3 Matlab 作图

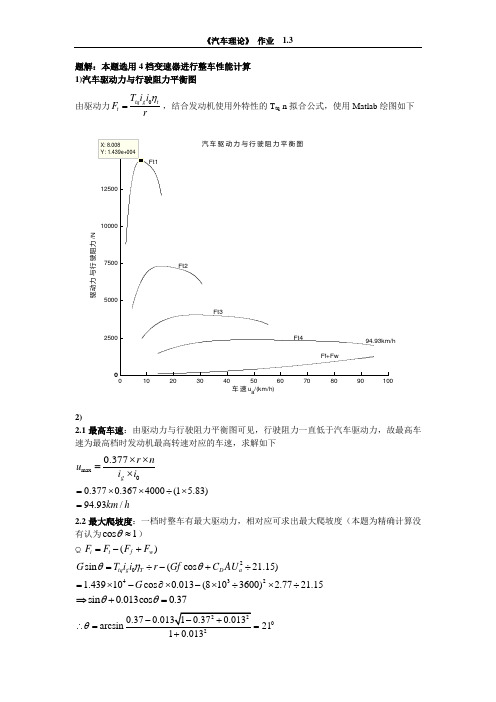
题解：本题选用4档变速器进行整车性能计算1)汽车驱动力与行驶阻力平衡图由驱动力0tq g tt T i i F r η=，结合发动机使用外特性的T tq -n 拟合公式，使用Matlab 绘图如下2) 2.1最高车速：由驱动力与行驶阻力平衡图可见，行驶阻力一直低于汽车驱动力，故最高车速为最高档时发动机最高转速对应的车速，求解如下max 00.3770.3674000(1 5.83)94.93/0.377g km hu r n i i =⨯⨯÷⨯=⨯⨯=⨯2.2最大爬坡度：一档时整车有最大驱动力，相对应可求出最大爬坡度（本题为精确计算没有认为cos 1θ≈）20432()sin (cos 21.15)1.43910cos 0.013(8103600) 2.7721.15i t f w tq g T D a F F F F G T i i r Gf C AU G θηθ=-+=÷-+÷=⨯-∂⨯-⨯÷⨯÷Qsin 0.013cos 0.37θθ⇒+=020.37arcsin 2110.013θ-∴==+于是最大爬坡度0tan tan 200.384i θ===2.3最大爬坡度对应的附着率：由于轻型货车一般为后轮驱动，故选用以下公式进行计算 /(//)0.384(1.947 3.20.90.384 3.2)0.536g i a L h i L C ϕ=+=÷÷+⨯÷=3)间：根据汽车行驶加速度倒数曲线，汽车由二档起步至加速到二档最高速度30.7214km/h ，用时t1=25.9478/3.6 s ；此时换位三档，从车速30.7214 km/h ，加速到三档最高速度55.5140 km/h ，用时t2=28.5747/3.6s ；此时换为四档，继续加速到最高速度70 km/h ，用时t3=26.7305/3.6s ；故汽车用2档起步加速行驶至70 km/h 的加速时间为t=t 1+t 2+t 3=25.9478/3.6+28.5747/3.6+26.7305/3.6=22.5703s。

汽车理论课程综合设计书

《汽车理论》课程设计作业要求
题目1. 确定某一轻型货车的动力性能（车辆参数见《汽车理论》第五版课后习题1.3和2.7）采用matlab编制程序，对汽车动力性进行计算。

要求得到以下数据和图形。

数据：
（1）最高车速；（2）加速时间t （3）最大爬坡度
图形：
（1）驱动力-行驶阻力平衡图
（2）汽车加速时间曲线
（3）动力特性曲线
（4）功率平衡图
要求：
（1）写出程序应为通用式，在给定了足够参数时能自动计算得到以上所有数据和图形，并能保证其计算精度。

程序具有通用性。

（2）需上交课程设计任务书，封面模板已给。

（3）有设计过程及其对应程序。

吉林大学汽车理论第一次作业

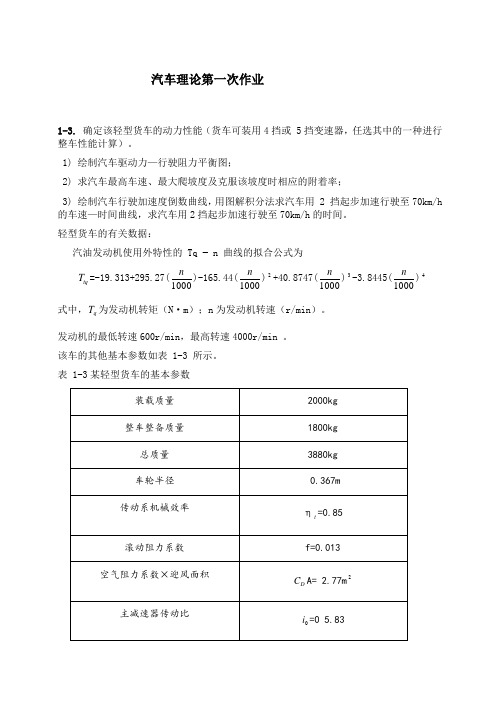
汽车理论第一次作业1-3. 确定该轻型货车的动力性能（货车可装用4挡或 5挡变速器，任选其中的一种进行整车性能计算）。

1) 绘制汽车驱动力—行驶阻力平衡图；2) 求汽车最高车速、最大爬坡度及克服该坡度时相应的附着率；3) 绘制汽车行驶加速度倒数曲线，用图解积分法求汽车用 2 挡起步加速行驶至70km/h 的车速—时间曲线，求汽车用2挡起步加速行驶至70km/h 的时间。

轻型货车的有关数据：汽油发动机使用外特性的 Tq − n 曲线的拟合公式为 tq T =-19.313+295.27(1000n )-165.44(1000n )2+40.8747(1000n )3-3.8445(1000n )4 式中，q T 为发动机转矩（N·m）；n 为发动机转速（r/min ）。

发动机的最低转速600r/min ，最高转速4000r/min 。

该车的其他基本参数如表 1-3 所示。

表 1-3某轻型货车的基本参数装载质量 2000kg 整车整备质量 1800kg 总质量 3880kg 车轮半径 0.367m 传动系机械效率ηt =0.85 滚动阻力系数 f=0.013空气阻力系数×迎风面积D C A= 2.77m 2主减速器传动比0i =0 5.83飞轮转动惯量f I =0.2182m kg ⋅二前轮转动惯量1w I =1.7982m kg ⋅四后轮转动惯量2w I =3.598 2m kg ⋅轴距L=3.2m 质心距前轴距离（满载）a=1.947m质心高（满载）g h =0.9m变速器（4挡和 5挡）的传动比g i 如表 1-4所示。

解：1）绘制汽车驱动力与行驶阻力平衡图。

驱动力矩tq T =-19.313+295.27(1000n )-165.44(1000n )2+40.8747(1000n )3-3.8445(1000n )4 主减速器传动比 0i =5.83车速 Ua=0.377n*r/(g i *i0) 驱动力 Ft=tq T *g i *0i *ηt /r变速器传动比 1 挡 2 挡 3 挡 4 挡 5 挡四档变速器 6.09 3.09 1.71 1.00 -- 五挡变速器 5.562.7691.6441.00.793行驶阻力（不考虑爬坡因素，加速阻力） Ff+Fw=Gf+A C D *Ua^2/21.15 整合以上信息可得当一档行驶时：g i =5.56时， 2.561≦Ua ≦17.074 当二挡行驶时：g i =2.769时，5.142≦<Ua ≦34.283 当三挡行驶时：g i =1.664时， 8.661≦Ua ≦57.74 当四挡行驶时：g i =1.00时，14.239≦Ua ≦94.929 当五挡行驶时：g i =0.793时，17.956≦Ua ≦119.709接下来，用MATLAB 编程进行编程（程序在最后），绘制出图像：2）求汽车最高车速、最大爬坡度及克服该坡度时相应的附着率。

(完整版)汽车理论课后作业答案MATLAB

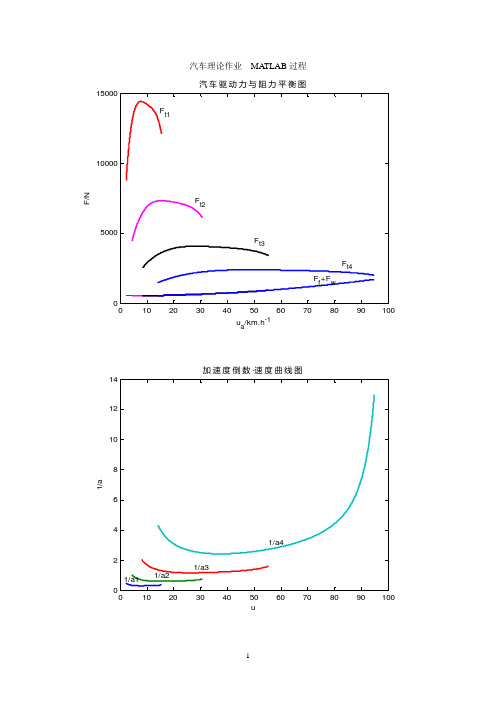
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序：《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知，他们无交点，u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档，较高转速（n取3401 ），最经济负荷（即90%负荷大约 46.9366Kw）行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间：（这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间）因与题1.3第三问求法相同，这里不在累述，可直接有计算机求得：figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31）前轴利用附着系数为：gf zh b zL +=βϕ后轴利用附着系数为： ()gr zh a zL --=βϕ1空载时：g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。

汽车理论作业

汽车理论作业姓名：陈洪平学号：021100701班级：车辆一班1.3解：（1）绘制驱动力与行驶阻力平衡图的Matlab程序：i0=5.83;r=0.367;nt=0.85;m=3880;g=9.8;f=0.013;CdA=2.27;ig=[6.09 3.09 1.71 1];n=600:1:4000;ua=0:1:120;ua1=0.377.*r.*n./ig(1)./i0;ua2=0.377.*r.*n./ig(2)./i0;ua3=0.377.*r.*n./ig(3)./i0;ua4=0.377.*r.*n./ig(4)./i0;N=n./1000;Tq=-19.313+295.27.*N-165.44.*N.^2+40.874.*N.^3-3.8445.*N.^4;Ft1=Tq.*ig(1).*i0.*nt./r;Ft2=Tq.*ig(2).*i0.*nt./r;Ft3=Tq.*ig(3).*i0.*nt./r;Ft4=Tq.*ig(4).*i0.*nt./r;F=m*g*f+CdA/21.15*ua.^2;plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua,F);set(gca, 'XTick',[0 40 80 120 ] );set(gca,'YTick',[0 2000 4000 6000 8000 10000 12000 14000 16000]); gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gtext('Ft4'),gtext('Ff+Fw'); title('汽车驱动力-行驶阻力平衡图');xlabel('Ua/(km/h)');ylabel('Ft/N');Matlab运行结果：(2)由驱动力与行驶阻力平衡图可得=94.93km/h求汽车最大爬坡度是可根据公式再根据换算成最大爬坡度。

(完整word版)汽车理论课后作业matlab编程详解(带注释)(word文档良心出品)

1.3matlab程序：（1）%驱动力-行驶阻力平衡图%货车相关参数。

m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.000.793];y=0.85;r=0.367;f=0.013;CdA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;n=600:10:4000;%发动机转数转换成汽车行驶速度。

ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;%计算各档位驱动力。

Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.84 45*(n/1000).^4;Ft1=Tq*ig(1)*i0*y/r;Ft2=Tq*ig(2)*i0*y/r;Ft3=Tq*ig(3)*i0*y/r;Ft4=Tq*ig(4)*i0*y/r;Ft5=Tq*ig(5)*i0*y/r;%计算行驶阻力。

Fz1=m*g*f+2.77*ua1.^2/21.15;Fz2=m*g*f+2.77*ua2.^2/21.15;Fz3=m*g*f+2.77*ua3.^2/21.15;Fz4=m*g*f+2.77*ua4.^2/21.15;Fz5=m*g*f+2.77*ua5.^2/21.15;%驱动力-行驶阻力平衡图。

plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua5,Ft5,ua1,Fz1,'k',ua2,Fz2,'k', ua3,Fz3,'k',ua4,Fz4,'k',ua5,Fz5,'k');title('驱动力-行驶阻力平衡图');xlabel('ua(km/s)');ylabel('Ft(N)');legend('Ft1','Ft2','Ft3','Ft4','Ft5','Ff+Fw')%求最高车速。

汽车理论大作业综述

汽车理论大作业20100410420车辆四班杨江林1.内容本文在MATLAB/Simulink中搭建ABS模型，将ABS对整车的性能影响进行仿真，并对仿真结果进行分析来证明方法的可行性。

2.原理由轮胎纵向力特性可知，车轮的滑移率b s 决定了制动力和侧向力的大小。

公式1给出了车轮滑移率b s 的定义。

式中，为车速，对应线速度，V V 为汽车线速度，r R 为车轮半径，为车轮线速度。

如图1所示为车辆在制动行使时，地面作用于车轮的制动力sb F 和侧向力y F 随车轮制动滑移率b s 的变化关系。

可以看出，侧向力随滑移率b s 的增加而下降，当滑移率从1降为0时，制动力开始随滑移率的增加而迅速增加；当滑移率增至某值opt s 时，制动力则随滑移率的增加而迅速减少。

公式1说明了车速与轮速的关系：当滑移率为1时，车速与轮速相等；当滑移率为0时，车轮已经处于抱死状态。

车轮抱死滑移时，不仅制动力减少，制动强度降低，而且车轮侧向附着力也大大减少。

因此，当前轮抱死滑移时，车辆丧失转向能力；而后轮抱死滑移则属于不稳定工况，易引起车辆急速甩尾的危险。

图1滑移率与附着系数的关系根据制动时附着系数与滑移率的关系曲线可知，当把车轮滑移率的值控制在最佳滑移率20%附近时，汽车将能够获得最好的制动效能同时还拥有较好的方向稳定性。

附着系数的数值主要取决于道路的材料、路面的状况、轮胎的结构、胎面花纹、材料以及车速等因素。

因此对于不同的路面来说，附着系数与滑移率的关系是不同的。

图2是不同路面的附着系数与滑移率的关系。

利用车轮滑移率的门限值及参考滑移率设计控制逻辑，使得车轮的滑移率保持在峰值附着系数附近，从而获得最大的地面制动力和最小的制动距离。

同时获得较大的侧向力，保证制动时的侧向稳定性。

ABS 工作原理图3. 模型由于汽车动力学模型建立是个复杂的过程，采用单轮模型建立汽车动力学模型。

简化的单轮模型如图3。

图3 单车轮模型由图可得到车辆的动力方程：车辆运动方程：dvmF dt =- （1）车轮运动方程：b d IFR T dt ω=- （2）车辆纵向摩擦力：F N μ= （3）式中，m 为1/4整车质量（kg ）；F 为地面制动力（N ）；R 为车轮半径（m ）；I 为车轮转动惯量（kg •m2）；Tb 为制动力矩（N •m ），m ）；v 为车身速度（m/s ）；ω 为车轮角速度（rad ·s ）；N 为地面对车轮的法向反作用力（N ）；μ为地面摩擦系数。

汽车理论课后作业matlab编程详解(带注释)【范本模板】

1。

3matlab程序:(1）%驱动力—行驶阻力平衡图％货车相关参数.m=3880；g=9.8;nmin=600;nmax=4000;G=m*g;ig=［5。

56 2。

769 1.644 1。

00 0.793]；y=0。

85；r=0。

367；f=0。

013；CdA=2。

77；i0=5。

83；L=3。

2;a=1。

947；hg=0。

9；If=0.218;Iw1=1.798；Iw2=3.598；n=600：10:4000;％发动机转数转换成汽车行驶速度。

ua1=0。

377＊r*n/ig(1）/i0;ua2=0.377＊r＊n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0；ua4=0.377＊r*n/ig（4）/i0;ua5=0。

377*r*n/ig（5）/i0；%计算各档位驱动力。

Tq=-19。

313+295.27*（n/1000)-165.44＊（n/1000）。

^2+40。

874＊（n/1000)。

^3—3.8445*(n/1000）.^4；Ft1=Tq*ig（1)*i0*y/r；Ft2=Tq*ig（2）*i0＊y/r;Ft3=Tq*ig（3）＊i0*y/r;Ft4=Tq＊ig(4）*i0＊y/r;Ft5=Tq＊ig(5)*i0＊y/r；%计算行驶阻力。

Fz1=m＊g*f+2.77＊ua1.^2/21。

15；Fz2=m*g＊f+2.77＊ua2。

^2/21。

15；Fz3=m*g*f+2.77＊ua3.^2/21。

15；Fz4=m＊g＊f+2。

77＊ua4.^2/21。

15；Fz5=m＊g＊f+2。

77＊ua5.^2/21.15；%驱动力—行驶阻力平衡图.plot（ua1,Ft1,ua2,Ft2,ua3，Ft3,ua4，Ft4,ua5，Ft5，ua1，Fz1,’k',ua2，Fz2，’k’,ua3，Fz3,'k'，ua4,Fz4，'k'，ua5，Fz5，'k'）；title（’驱动力-行驶阻力平衡图'）；xlabel（’ua（km/s)’）;ylabel('Ft（N）’）;legend（’Ft1’，’Ft2'，'Ft3','Ft4’,’Ft5’，’Ff+Fw'）%求最高车速。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

汽车理论m a t l新编作业Document number：BGCG-0857-BTDO-0089-2022一、确定一轻型货车的动力性能。

已知数据略。

（参见《汽车理论》习题第一章第3题）解题程序如下:用Matlab语言(1)绘制汽车驱动力与行驶阻力平衡图m1=2000; m2=1800; mz=3880;g=; r=; CdA=; f=; nT=;ig=[ ]; i0=;If=; Iw1=; Iw2=;Iw=2*Iw1+4*Iw2;for i=1:69n(i)=(i+11)*50;Ttq(i)=+*(n(i)/1000)*(n(i)/1000)^2+*(n(i)/1000)^*(n(i)/1000)^4; endfor j=1:5for i=1:69Ft(i,j)=Ttq(i)*ig(j)*i0*nT/r;ua(i,j)=*r*n(i)/(ig(j)*i0);Fz(i,j)=CdA*ua(i,j)^2/+mz*g*f;endendplot(ua,Ft,ua,Ff,ua,Ff+Fw)title('汽车驱动力与行驶阻力平衡图'); xlabel('ua(km/h)');ylabel('Ft(N)');gtext('Ft1')gtext('Ft2')gtext('Ft3')gtext('Ft4')gtext('Ft5')gtext('Ff+Fw')(2)求最大速度和最大爬坡度for k=1:175n1(k)=3300+k*;Ttq(k)=+*(n1(k)/1000)*(n1(k)/1000)^2 +*(n1(k)/1000)^*(n1(k)/1000)^4;Ft(k)=Ttq(k)*ig(5)*i0*nT/r;ua(k)=*r*n1(k)/(ig(5)*i0);Fz(k)=CdA*ua(k)^2/+mz*g*f;E(k)=abs((Ft(k)-Fz(k)));endfor k=1:175if(E(k)==min(E))disp('汽车最高车速=');disp(ua(k));disp('km/h');endendfor p=1:150n2(p)=2000+p*;Ttq(p)=+*(n2(p)/1000)*(n2(p)/1000)^2+*(n2(p)/1000) ^*(n2(p)/1000)^4;Ft(p)=Ttq(p)*ig(1)*i0*nT/r;ua(p)=*r*n2(p)/(ig(1)*i0);Fz(p)=CdA*ua(p)^2/+mz*g*f;af(p)=asin((Ft(p)-Fz(p))/(mz*g));endfor p=1:150if(af(p)==max(af))i=tan(af(p));disp('汽车最大爬坡度=');disp(i);endend汽车最高车速=h汽车最大爬坡度=（3）计算2档起步加速到70km/h所需时间for i=1:69n(i)=(i+11)*50;Ttq(i)=+*(n(i)/1000)*(n(i)/1000)^2+*(n(i)/1000)^*(n(i)/1000)^4; endfor j=1:5for i=1:69deta=1+Iw/(mz*r^2)+If*ig(j)^2*i0^2*nT/(mz*r^2);ua(i,j)=*r*n(i)/(ig(j)*i0);a(i,j)=(Ttq(i)*ig(j)*i0*nT/r-CdA*ua(i,j)^2/-mz*g*f)/(deta*mz);if(a(i,j)<=0)a(i,j)=a(i-1,j);endif(a(i,j)>b1(i,j)=a(i,j);u1(i,j)=ua(i,j);elseb1(i,j)=a(i-1,j);u1(i,j)=ua(i-1,j);endb(i,j)=1/b1(i,j);endendx1=u1(:,1);y1=b(:,1);x2=u1(:,2);y2=b(:,2);x3=u1(:,3);y3=b(:,3);x4=u1(:,4);y4=b(:,4);x5=u1(:,5);y5=b(:,5);plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5); title('加速度倒数时间曲线');axis([0 120 0 30]);xlabel('ua(km/h)');ylabel('1/aj');gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext('1/a5')for i=1:69 A=ua(i,3)-ua(69,2); if (A<1&A>0)j=i;endB=ua(i,4)-ua(69,3);if(B<2&B>0)k=i;endif(ua(i,4)<=70)m=i;endendt=ua(1,2)*b(1,2);for p1=2:69t1(p1)=(ua(p1,2)-ua(p1-1,2))*(b(p1,2)+b(p1-1,2))*;t=t+t1(p1);endfor p2=j:69t2(p2)=(ua(p2,3)-ua(p2-1,3))*(b(p2,3)+b(p2-1,3))*;t=t+t2(p2);endfor p3=k:mt3(p3)=(ua(p3,4)-ua(p3-1,4))*(b(p3,4)+b(p3-1,4))*;t=t+t3(p3);endt=t+(ua(j,3)-ua(69,2))*b(69,2)+(ua(k,4)-ua(69,3))*b(69,3) +(70-ua(m,4))*b(m,4);tz=t/;disp('加速时间=');disp(tz);disp('s');加速时间=二、计算与绘制题1 中货车的1）汽车功率平衡图；2）最高档与次高档的等速百公里油耗曲线。

已知数据略。

（参见《汽车理论》习题第二章第7题）解题程序如下:用Matlab语言m1=2000; m2=1800; mz=3880; g=;r=; CdA=; f=; nT=;ig=[ ];i0=; If=; Iw1=; Iw2=;n1=[815 1207 1614 2012 2603 3006 3403 3804];Iw=2*Iw1+4*Iw2;nd=400; Qid=;for j=1:5for i=1:69n(i)=(i+11)*50;Ttq(i)=+*(n(i)/1000)*(n(i)/1000)^2+*(n(i)/1000)^*(n(i)/1000)^4; Pe(i)=n(i)*Ttq(i)/9549;ua(i,j)=*r*n(i)/(ig(j)*i0);Pz(i,j)=(mz*g*f*ua(i,j)/3600.+CdA*ua(i,j)^3/76140.)/nT;endend plot(ua,Pe,ua,Pz);title('汽车功率平衡图)'); xlabel('ua(km/h)');ylabel('Pe,Pz(kw)'); gtext('I')gtext('II')gtext('III')gtext('IV')gtext('V')gtext('P阻')for j=1:5for i=1:8Td(i)=+*(n1(i)/*(n1(i)/^2+*(n1(i)/10 ^*(n1(i)/^4;Pd(i)=n1(i)*Td(i)/9549;u(i,j)=*n1(i)*r/(ig(j)*i0);endendb(1)=*Pd(1)^*Pd(1)^3+*Pd(1)^*Pd(1)+; b(2)=*Pd(2)^*Pd(2)^3+*Pd(2)^*Pd(2)+; b(3)=*Pd(3)^*Pd(3)^3+*Pd(3)^*Pd(3)+; b(4)=*Pd(4)^*Pd(4)^3+*Pd(4)^*Pd(4)+; b(5)=*Pd(5)^*Pd(5)^3+*Pd(5)^*Pd(5)+; b(6)=*Pd(6)^*Pd(6)^3+*Pd(6)^*Pd(6)+; b(7)=*Pd(7)^*Pd(7)^3+*Pd(7)^*Pd(7)+; b(8)=*Pd(8)^*Pd(8)^3+*Pd(8)^*Pd(8) +;u1=u(:,1)';u2=u(:,2)';u3=u(:,3)';u4=u(:,4)';u5=u(:,5)';B1=polyfit(u1,b,3);B2=polyfit(u2,b,3);B3=polyfit(u3,b,3);B4=polyfit(u4,b,3);B5=polyfit(u5,b,3);for q=1:69bh(q,1)=polyval(B1,ua(q,1));bh(q,2)=polyval(B2,ua(q,2));bh(q,3)=polyval(B3,ua(q,3));bh(q,4)=polyval(B4,ua(q,4));bh(q,5)=polyval(B5,ua(q,5));endfor i=1:5for q=1:69Q(q,i)=Pz(q,i)*bh(q,i)/*ua(q,i)*; endendplot(ua(:,4),Q(:,4),ua(:,5),Q(:,5));title('四档五档等速百公里油耗图');xlabel('ua(km/h)');ylabel('Qs(L/100km)');三、改变题中轻型货车的主减速器传动比，做出0i为、、、、时的燃油经济性—加速时间曲线，讨论不同0i值对汽车性能的影响。

Matlab程序：m1=2000 ;m2=1800 ;m=3880 ;r0= ;gt= ;f= ;CDA= ;i0= ;If= ;Iw1= ;Iw2= ;Ig5=[ ];Ig0=[ ];B=[ ;;;;;;;;];n=[815 1207 1614 2012 2603 3006 3403 3804];for i=1:5for k=1:8ua(i,k)=**n(k)/(Ig0(i)*Ig5(5));Ttq(i)=+.*(n(i)/1000).*(n(i)/1000).^2+.*(n(i)/1000).^.*(n(i)/10 00).^4;F5(i,k)=*3880*+.*ua(i,k)^2/;Pe(i,k)=F5(i,k)*ua(i,k)/(3600*;b5(i,k)=B(k,1)+B(k,2)*Pe(i ,k)+B(k,3)*Pe(i,k)^2+B(k,4)*Pe(i,k)^ 3+B(k,5)*Pe(i,k)^4;endendua1=25; s1=50;Fa5=*3880*+.*ua1.^2/;Pe5=Fa5.*ua1/(3600*;d1=polyfit(Pe(1,:),b5(1,:),3);ba1=polyval(d1,Pe5);d2=polyfit(Pe(2,:),b5(2,:),3);ba2=polyval(d2,Pe5);d3=polyfit(Pe(3,:),b5(3,:),3);ba3=polyval(d3,Pe5);d4=polyfit(Pe(4,:),b5(4,:),3);ba4=polyval(d4,Pe5);d5=polyfit(Pe(5,:),b5(5,:),3);ba5=polyval(d5,Pe5) ;ba=[ba1 ba2 ba3 ba4 ba5];Qa1=Pe5.*ba*50/(ua1*102*7)ua2=25:40;Q2=1+(2*Iw1+4*Iw2)/(m*r0^2)+If*Ig5(2).^2*Ig0(2)^2*gt/(m*r0^2)Fb5=*3880*+.*ua2.^2/+Q2*m*;Pb5=Fb5.*ua2/(3600*;db1=polyfit(Pe(1,:),b5(1,:),3); bb1=polyval(db1,Pb5);db2=polyfit(Pe(2,:),b5(2,:),3); bb2=polyval(db2,Pb5);db3=polyfit(Pe(3,:),b5(3,:),3); bb3=polyval(db3,Pb5);db4=polyfit(Pe(4,:),b5(4,:),3); bb4=polyval(db4,Pb5);db5=polyfit(Pe(5,:),b5(5,:),3); bb5=polyval(db5,Pb5);bb=[bb1bb2bb3bb4bb5];Pb=[Pb5Pb5Pb5Pb5Pb5];Qb=Pb.*bb/*7);for i=1:5for j=1:15qb(i,j)=Qb(i,j)+Qb(i,j+1); endendQb2=sum(qb')ua3=40; s2=250;Fc5=*3880*+.*ua3.^2/;Pc5=Fc5.*ua3/(3600*;dc1=polyfit(Pe(1,:),b5(1,:),3);bc1=polyval(dc1,Pc5);dc2=polyfit(Pe(2,:),b5(2,:),3);bc2=polyval(dc2,Pc5);dc3=polyfit(Pe(3,:),b5(3,:),3);bc3=polyval(dc3,Pc5);dc4=polyfit(Pe(4,:),b5(4,:),3);bc4=polyval(dc4,Pc5);dc5=polyfit(Pe(5,:),b5(5,:),3);bc5=polyval(dc5,Pc5) ;bc=[bc1 bc2 bc3 bc4 bc5];Qc3=Pc5.*bc*250/(ua3*102*7)ua4=40:50;Q4=1+(2*Iw1+4*Iw2)/(m*r0^2)+If*Ig5(4).^2*Ig0(4)^2*gt/(m*r0^2) Fd5=*3880*+.*ua4.^2/+Q4*m*;Pd5=Fd5.*ua4/(3600*;dd1=polyfit(Pe(1,:),b5(1,:),3);bd1=polyval(dd1,Pd5);dd2=polyfit(Pe(2,:),b5(2,:),3);bd2=polyval(dd2,Pd5);dd3=polyfit(Pe(3,:),b5(3,:),3);bd3=polyval(dd3,Pd5);dd4=polyfit(Pe(4,:),b5(4,:),3);bd4=polyval(dd4,Pd5);dd5=polyfit(Pe(5,:),b5(5,:),3);bd5=polyval(dd5,Pd5);bd=[bd1bd2bd3bd4bd5];Pd=[Pd5Pd5Pd5Pd5Pd5];Qd=Pd.*bd/*7);for i=1:5for j=1:10qd(i,j)=Qd(i,j)+Qd(i,j+1); endendQd4=sum(qd')ua5=50; s2=250;Ff5=*3880*+.*ua5.^2/;Pf5=Ff5.*ua5/(3600*;df1=polyfit(Pe(1,:),b5(1,:),3);bf1=polyval(df1,Pf5);df2=polyfit(Pe(2,:),b5(2,:),3);bf2=polyval(df2,Pf5);df3=polyfit(Pe(3,:),b5(3,:),3);bf3=polyval(df3,Pf5);df4=polyfit(Pe(4,:),b5(4,:),3);bf4=polyval(df4,Pf5);df5=polyfit(Pe(5,:),b5(5,:),3);bf5=polyval(df5,Pf5) ;bf=[bf1 bf2 bf3 bf4 bf5];Qf5=Pf5.*bf*250/(ua3*102*7)Qi=;Qg=(50-25)/*;Qg6=[Qg Qg Qg Qg Qg]Q=[Qa1Qb2Qc3Qd4Qf5Qg6];Qz=sum(Q)/1075*100for k=1:5for i=1:3401;for j=1:5;n(i)=i+599;ua(i,j)=*r0*n(i)./(Ig5(j)*Ig0(k));Q(j)=1+(2*Iw1+4*Iw2)/(m*r0^2)+If*Ig5(j).^2*Ig0(k)^2*gt/(m*(r0)^ 2);endenduamax=max(ua);uamin=min(ua);ua2=uamin(2):uamax(2);n=ua2*Ig0(k)*Ig5(2)/*;Ttq=+*(n/1000)*(n/1000).^2+*(n/1000).^*(n/1000).^4;Ft2=Ttq*Ig0(k)*Ig5(2)*;F2=*3880*+*ua2.^2/;a2=(Ft2-F2)./(Q(2)*m);t2=trapz(ua2,1./a2)/;ua3=uamax(2):uamax(3);n3=ua3*Ig0(k)*Ig5(3)/*;Ttq3=+*(n3/1000)*(n3/1000).^2+*(n3/1000).^*(n3/1000).^4; Ft3=Ttq3*Ig0(k)*Ig5(3)*;F3=*3880*+*ua3.^2/;a3=(Ft3-F3)./(Q(3)*m);t3=trapz(ua3,1./a3)/;ua4=uamax(3):70;n4=ua4*Ig0(k)*Ig5(4)/*;Ttq4=+*(n4/1000)*(n4/1000).^2+*(n4/1000).^*(n4/1000).^4; Ft4=Ttq4*Ig0(k)*Ig5(4)*;F4=*3880*+*ua4.^2/;a4=(Ft4-F4)./(Q(4)*m);t4=trapz(ua4,1./a4)/;t(k)=t2+t3+t4;endf=polyfit(Qz,t,2);QQ=Qz(1)::Qz(5);b=polyval(f,QQ)plot(QQ,b,Qz,t,'*')gtext('')gtext('')gtext('')gtext('')gtext('')title('燃油经济性-动力性曲线') xlabel('燃油经济性/[L(100km)-1]') ylabel('t/s')四、一中型货车装有前后制动器分开的双管路制动系，其有关参数如下：1）计算并绘制利用附着系数曲线和制动效率曲线2）求行驶车速Ua ＝30km/h ，在ϕ＝路面上车轮不抱死的制动距离。

汽车理论matl新编作业

汽车理论课后作业答案MATLAB

最新汽车理论matlab作业

汽车理论 matlab编程作业答案

汽车理论大作业(2)

汽车理论大作业

汽车理论作业(一)

汽车理论作业 1.3 Matlab 作图

汽车理论课程综合设计书

吉林大学汽车理论第一次作业

(完整版)汽车理论课后作业答案MATLAB

汽车理论作业

(完整word版)汽车理论课后作业matlab编程详解(带注释)(word文档良心出品)

汽车理论大作业综述

最新汽车理论大作业17050

汽车理论课后作业matlab编程详解(带注释)【范本模板】

汽车理论matl新编作业

汽车理论课后作业答案MATLAB

最新汽车理论matlab作业

汽车理论 matlab编程 作业答案

汽车理论大作业(2)

汽车理论大作业

汽车理论作业(一)

汽车理论 作业 1.3 Matlab 作图

汽车理论课程综合设计书

吉林大学汽车理论第一次作业

(完整版)汽车理论课后作业答案MATLAB

汽车理论作业

(完整word版)汽车理论课后作业matlab编程详解(带注释)(word文档良心出品)

汽车理论大作业综述

最新汽车理论大作业17050

汽车理论课后作业matlab编程详解(带注释)【范本模板】

汽车理论 matlab编程作业答案

汽车理论作业 1.3 Matlab 作图