高中圆锥曲线二级结论
高中数学圆锥曲线最常用二级结论总结

圆锥曲线的常用二级结论一、椭圆的常用二级结论1.(1)与椭圆22221x y a b +=共焦点的椭圆的方程可设为()222221,0x y b a b λλλ+=+>++.(2)与椭圆22221x y a b +=有相同的离心率的椭圆可设为2222x y a b λ+=,()2222,0x y b aλλ+=>.2.椭圆的两焦点分别为12,F F ,P 是椭圆上任意一点,则有以下结论成立:(1)122PF PF a +=;(2)1a c PF a c -≤≤+;(3)2212b PF PF a ≤⋅≤;(4)焦半径公式10||PF a ex =+,20||PF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).3.椭圆的方程为22221x y a b +=(a >b >0),左、右焦点分别为12,F F ,()00,P x y 是椭圆上任意一点,则有:(1)()()22222222000022,b a y a x x b y a b =-=-;(2)参数方程()00cos sin x a y b θθθ=⎧⎨=⎩为参数;4.设P 点是椭圆上异于长轴端点的任一点,F 1、F 2为其焦点记12F PF θ∠=,则(1)2122||||1cos b PF PF θ=+.(2)焦点三角形的面积:122||=tan2PF F P S c y b θ∆=.(3)当P 点位于短轴顶点处时,θ最大,此时12PF F S ∆也最大;(4).21cos 2e -≥θ(5)点M 是21F PF ∆内心,PM 交21F F 于点N ,则caMN PM =||||.5.有关22b a-的经典结论(椭圆中的垂径定理)(1).AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a⋅=-.(2).椭圆的方程为22221x y a b+=(a >b >0),过原点的直线交椭圆于,A B 两点,P 点是椭圆上异于,A B 两点的任一点,则有22PA PBb K K a=-(3).椭圆的方程为22221x y a b+=(a >b >0),过原点的直线交椭圆于,A B 两点,F 1,F 2点是椭圆上两焦点,则有四边形AF 1BF 2至少为平行四边6.若000(,)P x y 在椭圆22221x y a b+=上,则(1)以000(,)P x y 为切点的切线斜率为2020b x k a y =-;(2)过0P 的椭圆的切线方程是00221x x y ya b+=.7.若000(,)P x y 在椭圆22221x y a b+=外,则过000(,)P x y 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.8.椭圆的两个顶点为1(,0)A a -,2(,0)A a ,与y 轴平行的直线交椭圆于P 1、P 2时A 1P 1与A 2P 2交点的轨迹方程是22221x y a b-=.9.过椭圆上任一点00(,)A x y 任意作两条倾斜角互补的直线交椭圆于B,C 两点,则直线BC 有定向且2020BC b x k a y =(常数).10.若P 为椭圆上异于长轴端点的任一点,F 1,F 2是焦点,12PF F α∠=,21PF F β∠=,则()sin sin sin c e a αβαβ+==+.11.P 为椭圆上任一点,F 1,F 2为二焦点,A 为椭圆内一定点,则2112||||||2||a AF PA PF a AF -≤+≤+,当且仅当2,,A F P 三点共线时,等号成立.12.O 为坐标原点,P 、Q 为椭圆上两动点,且OP OQ ⊥.(1)22221111||||OP OQ a b +=+;(2)|OP|2+|OQ|2的最大值为22224a b a b +;(3)OPQ S ∆的最小值是2222a b a b +.13.已知A 、B 、是椭圆上的两点,线段AB 的垂直平分线与x 轴相交于点0(,0)P x ,则22220a b a b x a a ---<<.14.过焦点且垂直于长轴的弦叫通经,其长度为ab 2215.从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线必经过椭圆的另一个焦点.16.若椭圆方程为22221(0)x y a b a b+=>>,半焦距为c ,焦点()()12,0,,0F c F c -,设(1).过1F 的直线l 的倾斜角为α,交椭圆于A 、B 两点,则有①2211,cos cos b b AF BF a c a c αα==-+;②2cos ab AB a c α=-2222(2).若椭圆方程为22221(0)x y a b a b+=>>,半焦距为c ,焦点()()12,0,,0F c F c -,设过F 2的直线l 的倾斜角为α,交椭圆于A 、B 两点,则有:①22,cos cos b b AF BF a c a c αα==22+-;②22cos ab AB a c α=-222结论:椭圆过焦点弦长公式:()()222cos 2sin ab x a c AB ab y a c αα⎧⎪⎪-=⎨⎪⎪-⎩222222焦点在轴上焦点在轴上17.若AB 是过焦点F 的弦,设,AF m BF n ==,则2112amnb+=18、过圆锥曲线的焦点F 作直线交圆锥曲线于A 、B 两点,若λ=BFAF ,则有下列结论:1、椭圆、双曲线(直线与双曲线两个交点在一支上)、抛物线(离心率e=1)(焦比公式)①焦点在x 轴上时:11cos +-=λλθe ,1112+-+=λλk e ;②焦点在y 轴上时:11sin +-=λλθe ,11112+-+=λλk e 。
数学圆锥曲线二级结论大全

数学圆锥曲线二级结论大全
《数学圆锥曲线二级结论大全》
一、圆锥曲线关于它的一级结论:
1、圆锥曲线的象限是双对称的,在其主象限内都有自己明显的特征。
2、圆锥曲线的终点处离原点越远,它的凹凸性越明显,终点越近,它的凹凸性越不明显。
3、圆锥曲线的宽度随着它距离原点的距离而增大,离原点越远,它的宽度越宽。
4、圆锥曲线的长度随着它距离原点的距离而减小,离原点越近,它的长度越短。
二、圆锥曲线的二级结论:
1、圆锥曲线的起点与终点位于原点的对称轴上,其宽度和长度的变化规律也同样遵循这一原则。
2、圆锥曲线的宽度和长度是由它的凹凸性来决定的,凹凸性越明显,宽度和长度越小,反之亦然。
3、圆锥曲线的宽度和长度还受长短轴的影响,长短轴越大,圆锥曲线的宽度和长度也就越大。
4、圆锥曲线的起点处和终点处的宽度和长度总是比较接近的,而在它们之间的距离就会随着它们离原点的距离变化而变化。
圆锥曲线二级结论大全及证明过程

圆锥曲线二级结论大全及证明过程
一般圆锥曲线(也称为双曲线)的定义为:在空间中,任一点到光源的距离(可以取
为两个焦点)的和等于它到曲线的距离。
因此,讨论一般圆锥曲线的两个焦点的性质则成
为讨论圆锥曲线二级结论的基础。
1. 一般圆锥曲线的两个焦点处都有曲线切线:
证明:设$F_1,F_2$分别为曲线$C$的两个焦点。
令$P$为曲线$C$上一点,$a$为$P$到$F_1F_2$的距离,则$P$到$F_1$的距离记为$b$,$P$到$F_2$的距离记为$c$。
又由距离公式,记$P$到曲线$C$的距离为$d$,有$b + c = a + d$
将直线$F_1F_2$上点$Q$作曲线上$P$的切线,由距离公式可得:$PQ = d$
由于$F_1,F_2$都是$C$的焦点,有$F_1P + F_2P = a$,令$PQ = b$
可得$F_1Q + F_2Q = a - b$
证明:设圆锥曲线$C$的两个焦点为$F_1,F_2$,当$F_1$和$F_2$越靠近时,曲线
$C$的形状越扁平。
当$F_1$和$F_2$在靠近时,$a$接近于0,则$F_1P + F_2P接近于0$,即$F_1P 接近
于- F_2P$,由弦距定义可知,$F_1P$ 和$F_2P$ 分别成正负对称,由此可知当$F_1$ 和$F_2$ 相越靠近时,直线$F_1F_2$ 和曲线$C$ 的斜率越加小,曲线$C$ 的形状越扁平。
综上所述,证明一般圆锥曲线的两焦点越近,曲线形状越扁平。
圆锥曲线常用二级结论 -回复

圆锥曲线常用二级结论 -回复
圆锥曲线的二级结论包括以下几点:
1. 椭圆的离心率e满足0<e<1,其中e越接近于0,椭圆形状越细长,e越接近于1,椭圆形状越圆。
2. 椭圆的长轴是短轴的两倍或多倍,且两轴的中点为椭圆的中心。
3. 双曲线的离心率e大于1,其中e越大,双曲线的形状越细长。
4. 双曲线的两支曲线无交点,且无端点或渐近线。
5. 抛物线的离心率为1,其焦点在顶点的对称轴上。
6. 抛物线的两面从焦点出发,无限延伸,无交点。
这些二级结论是在圆锥曲线的基础上通过观察和推理得出的,对于分析和解决一些几何问题具有重要的指导意义。
高中数学圆锥曲线二级结论

高中数学圆锥曲线二级结论高中数学二级结论1.任意的简单n 面体内切球半径为表S V 3(V 是简单n 面体的体积,表S 是简单n 面体的表面积) 2.在任意ABC △内,都有tan A +tan B +tan C =tan A ·tan B ·tan C 推论:在ABC △内,若tan A +tan B +tan C <0,则ABC △为钝角三角形3.斜二测画法直观图面积为原图形面积的42倍 4.过椭圆准线上一点作椭圆的两条切线,两切点连线所在直线必经过椭圆相应的焦点5.导数题常用放缩1+≥x e x 、1ln 11-≤≤-<-x x xx x 、)1(>>x ex e x 6.椭圆)0,0(12222>>=+b a by a x 的面积S 为πab S = 7.圆锥曲线的切线方程求法:隐函数求导推论:①过圆222)()(r b y a x =-+-上任意一点),(00y x P 的切线方程为200))(())((r b y b y a x a x =--+--①过椭圆)0,0(12222>>=+b a by a x 上任意一点),(00y x P 的切线方程为12020=+b yy a xx ①过双曲线)0,0(12222>>=-b a by a x 上任意一点),(00y x P 的切线方程为12020=-b yy a xx 8.切点弦方程:平面内一点引曲线的两条切线,两切点所在直线的方程叫做曲线的切点弦方程①圆022=++++F Ey Dx y x 的切点弦方程为0220000=++++++F E y y D x x y y x x ①椭圆)0,0(12222>>=+b a b y a x 的切点弦方程为12020=+by y a x x ①双曲线)0,0(12222>>=-b a b y a x 的切点弦方程为12020=-by y a x x ①抛物线)0(22>=p px y 的切点弦方程为)(00x x p y y +=①二次曲线的切点弦方程为0222000000=++++++++F y y E x x D y Cy x y y x B x Ax 9.①椭圆)0,0(12222>>=+b a by a x 与直线)0·(0≠=++B A C By Ax 相切的条件是22222C b B aA =+ ②双曲线)0,0(12222>>=-b a by a x 与直线)0·(0≠=++B A C By Ax 相切的条件是22222C b B a A =- 10.若A 、B 、C 、D 是圆锥曲线(二次曲线)上顺次四点,则四点共圆(常用相交弦定理)的一个充要条件是:直线AC 、BD 的斜率存在且不等于零,并有0=+BD AC k k ,(AC k ,BD k 分别表示AC 和BD 的斜率)11.已知椭圆方程为)0(12222>>=+b a by a x ,两焦点分别为1F ,2F ,设焦点三角形21F PF 中θ=∠21F PF ,则221cos e -≥θ(2m ax 21cos e -=θ)12.椭圆的焦半径(椭圆的一个焦点到椭圆上一点横坐标为0x 的点P 的距离)公式02,1ex a r ±=13.已知1k ,2k ,3k 为过原点的直线1l ,2l ,3l 的斜率,其中2l 是1l 和3l 的角平分线,则1k ,2k ,3k 满足下述转化关系:3222223321212k k k k k k k k +-+-=,31231231312)()1(1k k k k k k k k k +++-±-=,2122221123212k k k k k k k k +-+-= 14.任意满足r by ax n n =+的二次方程,过函数上一点),(11y x 的切线方程为r y by x ax n n =+--1111 15.已知f (x )的渐近线方程为y=ax+b ,则a x x f x =∝+→)(lim ,b ax x f x =-∝+→])([lim 16.椭圆)0(12222>>=+b a b y a x 绕Ox 坐标轴旋转所得的旋转体的体积为πab V 34= 17.平行四边形对角线平方之和等于四条边平方之和18.在锐角三角形中C B A C B A cos cos cos sin sin sin ++>++19.函数f (x )具有对称轴a x =,b x =)(b a ≠,则f (x )为周期函数且一个正周期为|22|b a -20.y=kx+m 与椭圆)0(12222>>=+b a b y a x 相交于两点,则纵坐标之和为22222bk a mb + 21.已知三角形三边x ,y ,z ,求面积可用下述方法(一些情况下比海伦公式更实用,如27,28,29) AC C B B A S z A C y C B x B A ?+?+?==+=+=+222222.圆锥曲线的第二定义:椭圆的第二定义:平面上到定点F 距离与到定直线间距离之比为常数e (即椭圆的偏心率,ac e =)的点的集合(定点F 不在定直线上,该常数为小于1的正数)双曲线第二定义:平面内,到给定一点及一直线的距离之比大于1且为常数的点的轨迹称为双曲线23.到角公式:若把直线1l 依逆时针方向旋转到与2l 第一次重合时所转的角是θ,则21121tan k k k k θ=+- 24.A 、B 、C 三点共线?nm n m +=+=1,(同时除以m+n ) 25.过双曲线)0,0(12222>>=-b a b y a x 上任意一点作两条渐近线的平行线,与渐近线围成的四边形面积为2ab。
圆锥曲线常用二级结论及推导

圆锥曲线常用二级结论及推导
一级定理:
圆锥曲线以圆锥为开口的曲面,可以分为无穷类:双曲线、抛物线、圆环等,它们具有相同的曲线性质:
其曲线方程与相应圆锥的椭球坐标方程有关;
1. 每条曲线都由两个圆锥内切,且两个圆锥圆心恒定;
2. 每条曲线都内切于两个椭球相同的u轴对称,且保证轴线恒定;
3. 每条曲线都具有特定的v轴对称性,即它的曲线的曲线的v值是它的相反数;
4. 各曲线的曲率系数及曲率半径都是椭球坐标系中固定的;
5.曲线的凹凸性及其轮廓都是椭圆的图形而不受其开口的圆锥影响。
1. 椭圆圆锥曲线的抛物线曲线方程:
uV=C。
其中,C为椭球坐标系中定义的一个常量,用来表示曲线定义的空间维度。
证明:由三维圆锥的椭球坐标方程u2/ a2+v2 /b2=1,得到uV/a2b2=1,即uV=a2b2,故结论得证。
圆锥曲线定点定值二级结论

圆锥曲线定点定值二级结论圆锥曲线是高等数学中的一个重要概念,它是平面上所有点到两个定点的距离之比等于常数的点的集合。
圆、椭圆、双曲线和抛物线都是圆锥曲线的特例。
在研究圆锥曲线时,我们经常需要考虑定点和定值的问题,而圆锥曲线定点定值二级结论就是一个非常有用的定理。
圆锥曲线定点定值二级结论是指,对于一个圆锥曲线上的点P,以该点为焦点的任意圆锥曲线都经过该点,并且该点到该圆锥曲线的另一个焦点的距离为定值。
这个定值就是该点到圆锥曲线的直线的距离,也就是该点到该圆锥曲线的切线的距离。
这个定理对于研究圆锥曲线的性质和应用非常重要,下面我们将详细介绍。
首先,我们来证明圆锥曲线定点定值二级结论的第一个部分,即以该点为焦点的任意圆锥曲线都经过该点。
我们可以采用反证法,假设存在一个以该点为焦点的圆锥曲线,它不经过该点。
那么,该圆锥曲线上必然存在一个点Q,它到该点的距离不等于该点到该圆锥曲线的另一个焦点的距离。
这与圆锥曲线的定义矛盾,因此假设不成立,即以该点为焦点的任意圆锥曲线都经过该点。
接下来,我们来证明圆锥曲线定点定值二级结论的第二个部分,即该点到该圆锥曲线的另一个焦点的距离为定值。
我们可以采用向量法,设圆锥曲线的方程为F(x,y)=0,其中F(x,y)是一个二次函数。
设该点为P(x0,y0),该圆锥曲线的另一个焦点为F(xf,yf),则有:F(x0,y0) = c * PF^2其中PF表示点P到焦点F的距离,c为常数。
我们可以将F(x,y)在点P处进行泰勒展开,得到:F(x,y) = F(x0,y0) + Fx(x0,y0) * (x - x0) + Fy(x0,y0) * (y - y0) + ...其中Fx和Fy分别表示F(x,y)对x和y的偏导数。
由于点P在圆锥曲线上,所以F(x0,y0) = 0,且Fx(x0,y0) * (x - x0) + Fy(x0,y0) * (y - y0) = 0。
这意味着点P到圆锥曲线的切线垂直于向量(Fx(x0,y0),Fy(x0,y0)),即该向量是圆锥曲线在点P处的法向量。
圆锥曲线中的几个常用二级结论

结论 2 椭圆、双曲线共焦点
已知 F1,F2 是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且∠F1PF2=θ,e1, e2 分别是椭圆和双曲线的离心率,则sien2122θ+coes2222θ=1.
2 (1)已知共焦点的椭圆和双曲线,焦点为 F1,F2,记它们其中的一个交点为 P,
且∠F1PF2=23π,则该椭圆离心率 e1 与双曲线离心率 e2 必定满足的关系式为( C )
点,F1,F2 分别为左、右焦点,若∠F1PF2=θ,∠PF1F2=α,∠PF2F1
=β,则
S△PF1F2= b2θ,离心率 tan2
e=|sinαs-inθsinβ|x22+by22=1(a>b>0)上的一点,F1,F2 分别为左、右焦点,若 P→F1·P→F2=0,tan∠PF1F2=12,则椭圆的离心率为___3_5__.
【解析】 因为 tan∠PF1F2=12,P→F1·P→F2=0,所以 sin∠PF1F2=sinα= 15,sin∠PF2F1
=sinβ=
25,sin∠F1PF2=sinθ=1,所以
e=sinαs+inθsinβ=
1
1 +
2
=
35.
55
3 (2)已知 F1,F2 是双曲线x42-y2=1 的两个焦点,点 P 在双曲线上,且P→F1· P→F2=0,则△PF1F2 的面积为__1___.
2 (2)已知 F1,F2 为椭圆 C1:ax221+by221=1(a1>b1>0)与双曲线 C2:ax222-by222=1(a2>
0,b2>0)的公共焦点,M 是它们的一个公共点,且∠F1MF2=π3,e1,e2 分别为 C1,
C2 的离心率,则 e1e2 的最小值为
( A)
圆锥曲线的常用二级结论

圆锥曲线的常用二级结论圆锥曲线是由平面上一固定点(焦点)和一条固定直线(准线)构成的几何图形。
它们包括椭圆、双曲线和抛物线。
在学习圆锥曲线的过程中,常用的二级结论有以下几个:一、椭圆的性质1. 椭圆的离心率小于1:椭圆是由一个固定点(焦点)到平面上所有点到另一个固定点(焦点)的距离之和等于一个常数的所有点构成的集合。
这个常数就是椭圆的长轴长度,而短轴长度等于长轴长度乘以离心率。
因此,椭圆的离心率小于1。
2. 椭圆的两个焦点在长轴上:椭圆的两个焦点与长轴垂直,并且它们都在长轴上。
3. 椭圆是对称图形:椭圆具有对称性,即如果将它绕着中心旋转180度,它仍然保持不变。
4. 椭圆的周长公式:设椭圆长轴为2a,短轴为2b,则椭圆周长公式为C=π(a+b)。
二、双曲线的性质1. 双曲线的离心率大于1:双曲线是由一个固定点(焦点)到平面上所有点到另一个固定点(焦点)的距离之差等于一个常数的所有点构成的集合。
这个常数就是双曲线的长轴长度,而短轴长度等于长轴长度乘以离心率。
因此,双曲线的离心率大于1。
2. 双曲线有两条渐近线:双曲线有两条渐近线,它们与双曲线趋近于无限远时重合。
3. 双曲线不具有对称性:与椭圆不同,双曲线不具有对称性。
4. 双曲线的渐近线方程:设双曲线方程为x^2/a^2-y^2/b^2=1,则它的两条渐近线方程分别为y=±(b/a)x。
三、抛物线的性质1. 抛物线是对称图形:抛物线具有轴对称性,即如果将它绕着轴旋转180度,它仍然保持不变。
2. 抛物线焦点和准线相等距离:抛物线是由平面上所有点到一条直线(准线)的距离等于这些点到一个固定点(焦点)的距离的所有点构成的集合。
它的焦点和准线相等距离。
3. 抛物线方程:设抛物线方程为y=ax^2+bx+c,则它的焦点坐标为(-b/2a,1/4a),准线方程为y=-1/4a。
4. 抛物线与直线交点坐标:如果抛物线与直线y=kx+m相交,则交点坐标为(x,y)=(k^2a+bk+c-m,-ka^2-kb+m)。
圆锥曲线常用的二级结论

圆锥曲线常用的二级结论有:1.离心率定义式:$e = \frac{\sqrt{a^2 - b^2}}{a}$,其中$a$ 为长半轴,$b$ 为短半轴。
2.曲率公式:$\kappa = \frac{|\text{二阶导数}|}{(1 + y'^2)^{\frac{3}{2}}}$,其中$\kappa$ 为曲率,$y'$ 为导数。
3.两点之间的弦长公式:$L = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$,其中$(x_1,y_1)$ 和$(x_2, y_2)$ 为两点的坐标。
4.圆锥曲线的极坐标方程:$r = \frac{p}{1 + e\cos\theta}$,其中$r$ 为点到焦点的距离,$\theta$ 为点的极角,$p$ 为直线到焦点的距离,$e$ 为离心率。
5.焦点公式:$F = \sqrt{a^2 - b^2}$,其中$a$ 为长半轴,$b$ 为短半轴,$F$ 为焦点到中心的距离。
6.弦的中点公式:$(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2})$,其中$(x_1, y_1)$ 和$(x_2, y_2)$ 为弦两个端点的坐标。
7.椭圆的标准方程:$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$,其中$a$ 为长半轴,$b$ 为短半轴。
8.双曲线的标准方程:$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$,其中$a$ 为长半轴,$b$ 为短半轴。
9.抛物线的标准方程:$y = ax^2$,其中$a$ 为常数。
10.焦半径公式:$r_f = \frac{p}{e}$,其中$p$ 为直线到焦点的距离,$e$ 为离心率,$r_f$ 为以焦点为圆心,$p$ 为半径的圆的半径长度。
圆锥曲线常用的二级结论包括但不限于以下内容:1.设直线$l$ 与圆锥曲线$C$ 相交于两点$P,Q$,则$P,Q$ 间的线段垂直于轴线。
圆锥曲线常用的二级结论

圆锥曲线常用的二级结论圆锥曲线是数学中的一个重要分支,研究圆锥曲线的性质和特点对于解决实际问题具有重要意义。
在研究圆锥曲线的过程中,我们常常会遇到一些二级结论,它们对于理解和应用圆锥曲线的知识起到了关键的作用。
本文将介绍一些圆锥曲线常用的二级结论,并探讨其应用。
一、椭圆的二级结论椭圆是圆锥曲线中的一种。
通过对椭圆的研究,我们可以得到以下几个常用的二级结论:1. 椭圆的离心率范围为0到1,离心率越接近于0,则椭圆越接近于圆形;离心率越接近于1,则椭圆越扁平。
这个结论告诉我们椭圆的形状是由其离心率确定的。
当离心率接近于0时,可以认为椭圆近似于一个圆;而当离心率接近于1时,椭圆则会变得更加扁平。
2. 椭圆的两个焦点到椭圆上任意一点的距离之和是一个常数,等于长轴的长度。
这个结论称为椭圆的焦点定理,它表明椭圆上任意一点到两个焦点的距离之和是一个常数。
这个常数即为椭圆的长轴的长度。
这个结论在许多实际问题中都有着重要的应用,比如卫星轨道的设计等。
3. 椭圆的切线与其法线垂直。
这个结论告诉我们椭圆上任意一点的切线和法线是垂直的。
利用这个性质,我们可以求解椭圆上某一点的切线方程和法线方程,进而研究椭圆曲线的切线和法线的性质。
二、双曲线的二级结论双曲线是圆锥曲线中的另一种。
通过对双曲线的研究,我们可以得到以下几个常用的二级结论:1. 双曲线的离心率范围大于1,离心率越大,则双曲线越扁平。
这个结论与椭圆的结论类似,不同之处在于双曲线的离心率始终大于1。
离心率越大,双曲线越扁平。
2. 双曲线的两个焦点至双曲线上任意一点的距离之差是一个常数,等于双曲线的距离。
这个结论称为双曲线的焦点定理,它表明双曲线上任意一点到两个焦点的距离之差是一个常数。
这个常数等于双曲线的距离。
3. 双曲线上的切线和法线不垂直。
与椭圆不同的是,双曲线上的切线和法线不垂直。
这个性质给了我们研究双曲线其他性质的线索。
三、抛物线的二级结论抛物线是圆锥曲线中的另一种。
圆锥曲线二级结论高中

圆锥曲线二级结论高中
圆锥曲线是高中数学中的重要内容之一,其二级结论也是备考中不可或缺的一部分。
这些结论可以帮助考生简化解题过程、加快解题速度,从而提高考试成绩。
以下是一些常见的圆锥曲线二级结论:
1. 过曲线上的点 P(x,y) 的切线方程为 y = mx + b,其中 m 为切线与曲线的斜率,b 为切线与曲线的截距。
2. 直线与圆锥曲线相交的弦长公式为:|AB| = |AC| ×√
(1-e^2),其中 A、B、C 分别表示直线与曲线相交的三点,e 为直线的倾斜角度。
3. 涉及到曲线上的点 A、B 及线段 AB 的中点 M 的关系时,可以利用点差法:设 MP = x,则 MP + PM = 2x,即 x = (MP + PM) / 2。
4. 圆锥曲线的两类对称问题:曲线关于点成中心对称的曲线是本身;曲线关于直线成轴对称的曲线是圆。
这些二级结论在高考圆锥曲线题目中经常会被用到,掌握它们可以帮助考生更好地应对高考考试。
同时,考生也应该注重对这些结论的推导和熟练掌握,以在实际考试中快速、准确地运用它们。
圆锥曲线常用二级结论汇总

圆锥曲线常用二级结论汇总以下是圆锥曲线常用的二级结论汇总,包括椭圆、双曲线和抛物线的性质和特点。
详细解析如下:1.椭圆(Ellipse):-定义:椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。
-主要性质:-焦点与直径关系:椭圆的焦点到任意点的距离之和等于该点到直径的距离之和。
-长轴和短轴:椭圆的长轴是通过两个焦点的直线,短轴是垂直于长轴且通过中心点的直线。
-离心率:椭圆的离心率定义为焦距与长轴长度之比,介于0和1之间。
-对称性:椭圆具有x轴对称和y轴对称性。
2.双曲线(Hyperbola):-定义:双曲线是平面上到两个定点F1和F2的距离之差等于常数2a的点P的轨迹。
-主要性质:-焦点与直径关系:双曲线的焦点到任意点的距离之差等于该点到直径的距离之差。
-长轴和短轴:双曲线的长轴是通过两个焦点的直线,短轴是垂直于长轴且通过中心点的直线。
-离心率:双曲线的离心率定义为焦距与长轴长度之比,大于1。
-渐近线:双曲线有两条渐近线,与曲线趋于无穷远时相交。
3.抛物线(Parabola):-定义:抛物线是平面上到定点F的距离等于点P到定直线l的距离的点P的轨迹。
-主要性质:-焦点与直径关系:抛物线的焦点是位于开口方向上的对称点,与焦点距离相等的两条直线互相平行。
-对称性:抛物线具有顶点对称性,焦点、顶点和直线l三者共线。
-方程形式:抛物线的标准方程为y=ax^2+bx+c,其中a为常数且不为0。
4.曲线参数方程:-椭圆的参数方程:x=a*cosθ,y=b*sinθ,其中a和b分别为长轴和短轴的一半,θ是参数。
-双曲线的参数方程:x=a*coshθ,y=b*sinhθ,其中a和b分别为长轴和短轴的一半,θ是参数。
-抛物线的参数方程:x=at^2,y=2at,其中a为常数,t是参数。
5.曲线图像和方程:-椭圆的标准方程:(x/a)^2+(y/b)^2=1,其中a和b分别为长轴和短轴的一半。
-双曲线的标准方程:(x/a)^2-(y/b)^2=1,其中a和b分别为长轴和短轴的一半。
数学圆锥曲线二级结论

数学圆锥曲线二级结论
数学圆锥曲线的二级结论主要包括以下几个内容:
1. 曲线相关定理:包括焦点、准线、直角等定理。
例如,椭圆的焦点定理指出,椭圆上任意一点到焦点的距离之和是一个定值。
2. 极坐标方程:用极坐标方程表示圆锥曲线。
例如,椭圆的极坐标方程为$r = \frac{p}{1-e\cdot\cos\theta}$,其中$r$为极径,$p$为半焦距,$e$为离心率。
3. 集中思路:圆锥曲线的性质与方程的意义。
例如,双曲线的方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,其中$a$为横轴
半径,$b$为纵轴半径。
根据这个方程可以得到双曲线的离心
率$e=\sqrt{1+\frac{b^2}{a^2}}$,并且根据离心率可以确定双
曲线的形状。
4. 曲线的性质:包括切线、法线、渐近线、对称性等。
例如,椭圆的切线与法线切点形成的角度为直角;双曲线的两支曲线的渐近线方程为$y=\frac{\pm b}{a}x$。
5. 常见问题:周长、面积、焦距、离心率等计算问题。
例如,椭圆的面积为$S=\pi a b$,焦距为$f=\sqrt{a^2-b^2}$。
总的来说,数学圆锥曲线二级结论是指对圆锥曲线的进一步研究,包括基本定理的推导、曲线的性质和相关问题的解答等。
这些二级结论可以帮助我们更深入地理解和运用圆锥曲线。
高考数学圆锥曲线常用的二级结论
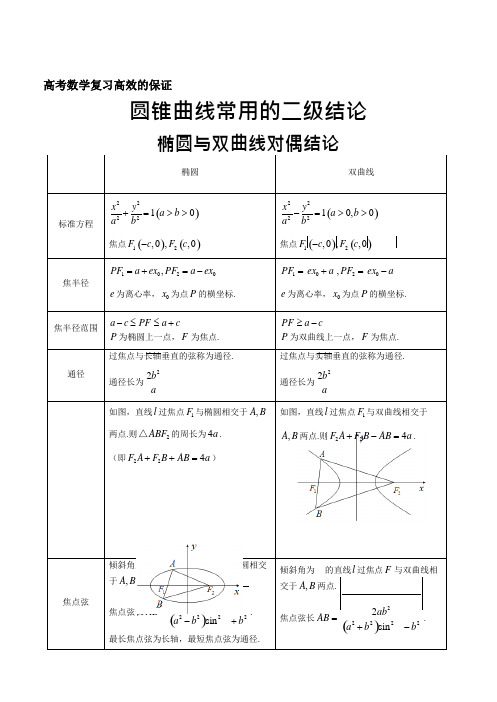
椭圆双曲线标准方程x2 y2+=1(a >b > 0)a2 b 2焦点F1 (-c, 0), F2 (c, 0)x2 y2-=1(a > 0, b> 0)a2 b2焦点F1 (-c, 0), F2 (c, 0)焦半径PF1=a +ex, PF2=a -exe 为离心率,x为点P 的横坐标.PF1=ex+a , PF2=ex-ae 为离心率,x为点P 的横坐标.焦半径范围a -c ≤PF ≤a +cP 为椭圆上一点,F 为焦点.PF ≥a -cP 为双曲线上一点,F 为焦点.通径过焦点与长轴垂直的弦称为通径.2b2通径长为a过焦点与实轴垂直的弦称为通径.2b2通径长为a如图,直线l 过焦点F1 与椭圆相交于A, B两点.则△ABF2 的周长为4a .(即F2 A+F2B +AB = 4a )如图,直线l 过焦点F1 与双曲线相交于A, B 两点.则F2A+F2B -AB = 4a .焦点弦倾斜角为的直线l 过焦点F 与椭圆相交于A, B 两点.2ab2焦点弦长AB =.(a2 -b2 )s i n 2 +b2最长焦点弦为长轴,最短焦点弦为通径.倾斜角为的直线l 过焦点F 与双曲线相交于A, B 两点.2ab2焦点弦长AB =.(a2 +b2 )s i n 2 -b2高考数学复习高效的保证圆锥曲线常用的二级结论椭圆与双曲线对偶结论AF 与BF 数量关系直线l 过焦点F 与椭圆相交于A, B 两点,1 1 2a则+=.AF BF b2直线l 过焦点F 与双曲线相交于A, B 两点,则1+1=2a.AF BF b2已知点P 是椭圆上一点,O 坐标原点,则b ≤PO ≤a .已知点P 是双曲线上一点,O 坐标原点,则PO ≥a .焦三角形如图,P 是椭圆上异于长轴端点的一点,已知∠F1PF2 =,∠PF1F2 =,∠PF2F1=,则(1)S =b2 tan;sin(2)离心率e =.sin+s i n如图,P 是双曲线上异于实轴端点的一点,已知∠F PF =,∠PF F =,1 2 1 2∠PF2F1=,则b2(1)S =b2 cot =;△PF1F2 2tan2s i n(2)离心率e =.sin-s i n垂径定理如图,已知直线l 与椭圆相交于A, B 两点,点M 为AB 的中点,O 为原点,则b2kOMkAB=-2.a如图,已知直线l 与双曲线相交于A, B 两点,点M 为AB 的中点,O 为原点,则b2kOMkAB=2.a(注:直线l 与双曲线的渐近线相交于A, B 两点,其他条件不变,结论依然成立)△PF1F2 2周角定理如图,已知点A, B 椭圆长轴端点(短轴端点),P 是椭圆上异于A, B 的一点,b2则k k =-.推广:如图,已知点A, B 是椭圆上关于原点对称的两点,P 是椭圆上异于A, B 的一点,若直线PA, PB 的斜率存在且不为零,b2kPAkPB=-2a如图,已知点A, B 双曲线实轴端点,P 是双曲线上异于A, B 的一点,b2则k k =.推广:如图,已知点A, B 是双曲线上关于原点对称的两点,P 是双曲线上异于A, B的一点,若直线PA, PB 的斜率存在且不为零,b2kPAkPB=2.a直线l 过焦点F (c, 0)与椭圆相交于A, B⎛a2 ⎫两点,点Pc,0⎪,则∠APF =∠BPF (即k PA +k PB = 0 ).直线l 过焦点F (c, 0)与双曲线相交于⎛a2 ⎫A, B 两点,点Pc,0⎪,则∠APF =∠BPF (即k PA +k PB = 0 ). 切线方程已知点P(x0 , y0 )是椭圆上一点,则椭圆在点P 处的切线方程为xx+yy=1.a2 b2已知点P(x0 , y0 )是双曲线上一点,则双曲线在点P 处的切线方程为xx-yy=1 .a2 b2PA PB a2PA PB a2⎝⎭⎝⎭- 2 2 22 - 2 2 22 - 2 2 22 - 2 2 22 双曲线的结论1.过定点(定点在双曲线外且不在渐近线上)的直线与双曲线交点个数问题:设斜率为 k 的直线 l 过定点 P (0, t )(t ≠ 0),双曲线方程为 x y= 1(a > 0, b > 0),过点P 与双曲 a b线相切时的斜率为 k 0 .(1)当 0 ≤ k b< b 时,直线 l 与双曲线有两个交点,且这两交点在双曲线的两支上;a(2)当 kb= 时,直线l 与双曲线只有一个交点; a(3)当 < k a< k 0 时,直线 l 与双曲线有两个交点,且这两交点在双曲线的同一支上;(4)当 k= k 0时,直线 l 与双曲线只有一个交点;(5)当 k > k 0 时,直线 l 与双曲线没有交点.2.如图, F (c , 0)是双曲线 x y= 1(a > 0, b > 0)的焦点,过点F 作 FH 垂直双曲线的其中一条 a b渐近线,垂足为 H , O 为原点,则 OH = a , FH = b .3.点 P 是双曲线 x y= 1(a > 0, b > 0)上任意一点,则点P 到双曲线的渐近线的距离之积为定值 a ba 2b 2. a 2 + b 24.点 P 是双曲线 x y= 1(a > 0, b > 0)上任意一点,过点P 作双曲线的渐近线的平行线分别与渐 a b近线相交于 M , N 两点, O 为原点,则平行四边形 OMPN 的面积为定值ab .22⎨2 抛物线的结论如图,抛物线方程为 y = 2 p x ( p > 0),准线 x = - p与 x 轴相交于点 P ,过焦点 F ⎛ p , 0 ⎫的直线 l 与2 2⎪⎝⎭抛物线相交于 A (x 1 , y 1 ), B (x 2 , y 2 )两点, O 为原点,直线 l 的倾斜角为.⎧ p 1. ⎪ x 1 x 2 = 4 , ⎪ y y = - p 2 . ⎩ 1 2p p2.焦半径: AF = x 1 + , BF = x 2 + , AB = x 1 + x 2 + p .2 2 2 p3.焦点弦: AB = .s i n 24. AF , BF 的数量关系: 1 + 1= 2 , AF ⋅ BF = p .AF BF p sin 25.三角形 AOB 的面积 S △AOBp 2= . 2 s i n6.以焦点弦 AB 为直径的圆与准线相切;以焦半径 AF 为直径的圆与 y 轴相切.7.直线 PA , PB 的斜率之和为零( k PA + k PB = 0 ),即 ∠APF = ∠BPF . 8.点 A , O , N 三点共线;点 B , O , M 三点共线.9.如图,点 A , B 是抛物线 y = 2 p x ( p > 0), O 为原点,若∠AOB = 90o ,则直线 AB 过定点 (2 p , 0).圆锥曲线部分二级结论一:1:定圆上一动点与圆内一定点的线段的垂直平分线,与动点和圆心之间的半径交点的轨迹是椭圆。
圆锥曲线二级结论大全常用

圆锥曲线二级结论大全常用圆锥曲线是数学中的一个重要分支,包括椭圆、双曲线和抛物线三种类型。
在研究圆锥曲线时,有一些常用的二级结论可以帮助我们更好地理解和应用这些曲线。
下面是一些常用的二级结论:1. 椭圆的焦点定理,对于椭圆,任意一点到两个焦点的距离之和等于常数2a,其中a是椭圆的半长轴。
2. 双曲线的焦点定理,对于双曲线,任意一点到两个焦点的距离之差的绝对值等于常数2a,其中a是双曲线的半长轴。
3. 抛物线的焦点和准线定理,对于抛物线,焦点到准线的距离等于焦距的一半。
4. 椭圆的离心率,椭圆的离心率定义为焦点到准线的距离与长轴长度的比值,通常用字母e表示。
离心率越接近于0,椭圆越接近于圆形;离心率越接近于1,椭圆越扁平。
5. 双曲线的离心率,双曲线的离心率定义为焦点到准线的距离与焦点到顶点的距离之比,通常用字母e表示。
离心率大于1的双曲线是开口向外的,离心率小于1的双曲线是开口向内的。
6. 抛物线的离心率,抛物线的离心率定义为焦点到准线的距离与焦点到焦点之间的距离的比值,通常用字母e表示。
抛物线的离心率恒为1,表示抛物线是所有圆锥曲线中离心率固定的一种。
7. 椭圆的参数方程,椭圆可以用参数方程表示,其中x=acos(t)和y=bsin(t),其中a和b分别是椭圆的半长轴和半短轴。
8. 双曲线的参数方程,双曲线可以用参数方程表示,其中x=acosh(t)和y=bsinh(t),其中a和b分别是双曲线的半长轴和半短轴。
9. 抛物线的参数方程,抛物线可以用参数方程表示,其中x=t和y=t^2。
10. 椭圆的焦点和直径关系,椭圆的焦点和直径之间有一个重要的关系,即直径的中点恰好是焦点连线的中垂线的交点。
这些是圆锥曲线中常用的二级结论,它们可以帮助我们更好地理解和应用椭圆、双曲线和抛物线。
当然,圆锥曲线还有许多其他的性质和结论,这里只列举了一部分常用的二级结论。
圆锥曲线常用的二级结论

圆锥曲线常用的二级结论圆锥曲线是一个非常重要的数学话题,它被广泛地应用于各种科学领域中。
在圆锥曲线的研究中,有很多二级结论是非常重要的。
这些结论与圆锥曲线的方程有关,可以帮助我们更好地理解这些曲线的性质和特点。
下面,我们将介绍一些常用的二级结论。
1. 判别式在研究二次曲线的性质时,很重要的一个问题是如何判断其类型。
一个二次曲线的类型取决于其方程的系数。
比如,二次曲线的方程可以表示为:Ax² + Bxy + Cy² + Dx + Ey + F = 0其中,A、B、C、D、E和F都是常数。
二次曲线的类型如下:如果B² - 4AC > 0,则为双曲线。
如果B² - 4AC = 0,则为抛物线。
如果B² - 4AC < 0,则为椭圆。
这个判别式非常有用,可以帮助我们快速地判断一个二次曲线的类型。
在实际应用中,我们可以用这个结论来分析椭圆、双曲线和抛物线这些曲线的性质。
2. 焦半径公式圆锥曲线中最常见的二次曲线就是椭圆和双曲线。
在研究这些曲线的性质时,焦半径公式是非常重要的一个结论。
对于一个椭圆或双曲线,假设其焦点为F1和F2,离心率为e,焦距为2a,则任何一点P到F1和F2的距离之和等于2a。
即:PF1 + PF2 = 2a这个式子可以用来计算与椭圆或双曲线相关的各种参数。
比如,我们可以用这个式子计算出椭圆的周长和面积。
在应用中,我们经常需要用这个结论来计算椭圆和双曲线的各种参数。
3. 长短轴公式对于一个椭圆,它有两个特殊的轴,分别称为长轴和短轴。
这两个轴对于椭圆的性质有很大的影响。
在研究椭圆的性质时,长短轴公式是非常重要的一个结论。
对于一个椭圆,设其长轴长为2a,短轴长为2b,则有以下两个关系式:a² = b² + c²其中,c是椭圆的焦距,即焦点到中心的距离。
这个结论可以帮助我们计算椭圆的长轴和短轴长度。
在实际应用中,我们经常需要用这个结论来计算各种椭圆的参数。
圆锥曲线常用的二级结论

通径长为
a
如图,直线 l 过焦点 F1 与椭圆相交于 A, B 如图,直线 l 过焦点 F1 与双曲线相交于
两点.则 △ABF2 的周长为 4a .
A, B 两点.则 F2 A F2B AB 4a .
(即 F2 A F2B AB 4a )
焦点弦
倾斜角为 的直线 l 过焦点 F 与椭圆相交 于 A, B 两点.
.
则 kPAkPB
b2 a2
.
周角定理
推广:如图,已知点 A, B 是椭圆上关于原 推广:如图,已知点 A, B 是双曲线上关于 点对称的两点, P 是椭圆上异于 A, B 的一 原点对称的两点, P 是双曲线上异于 A, B
点,若直线 PA, PB 的斜率存在且不为零
,
kPAkPB
b2 a2
(2)当
k
b a
时,直线
l
与双曲线只有一个交点;
(3)当
b a
k
k0
时,直线 l 与双曲线有两个交点,且这两交点在双曲线的同一支上;
(4)当 k k0 时,直线 l 与双曲线只有一个交点;
(5)当 k k0 时,直线 l 与双曲线没有交点.
2.如图, F c, 0是双曲线
x2 a2
.
欢迎关注微信公众号(QQ群):高中数学解题研究群416652117
4.点 P 是双曲线
x2 a2
y2 b2
1a
0, b
0上任意一点,过点 P 作双曲线的渐近线的平行线分别与渐
近线相交于
M
,
N
两点, O
为原点,则平行四边形 OMPN
