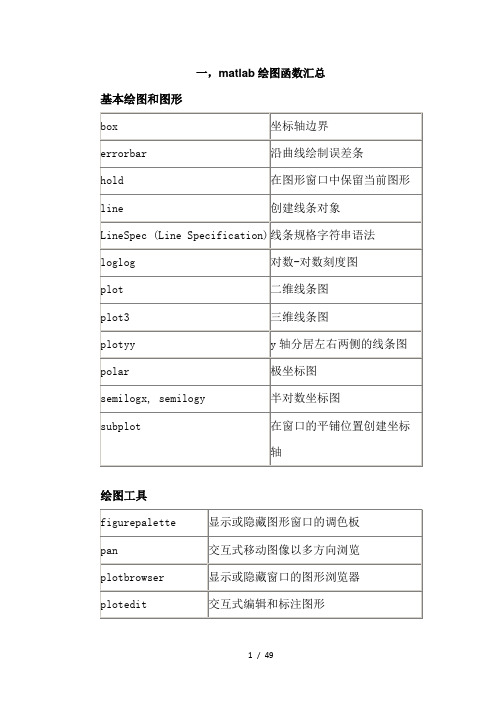
数学建模MATLAB程序汇总

建模MATLAB程序汇总
求特征值、特征向量、权向量
A=input('A=');
E=eig(A)
[V,D]=eig(A)
t=max(E);
disp(t);
for i=1:1:3
if E(i)==t;
m=i;
end
end
X=V(:,m);
mt=X./sum(X);
disp(mt)
求π
n=1;s=0;
while 1/(2*n-1)>10^(-6)
s=s+(-1)^(n+1)/(2*n-1);
n=n+1;
end
pai=4*s
求e
n=1;s=1;
while 1/prod(1:n)>10^(-6)
s=s+1/prod(1:n);
n=n+1;
end
e=s
回归分析、
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
X=[ones(16,1) x];
[b,bint,r,rint,stats]=regress(Y,X,0.025);
b,bint,stats
rcoplot(r,rint)
z=b(1)+b(2)*x
plot(x,Y,'k+',x,z,'r')
回归曲线
x=[2:16];
y=[6.42 8.20 9.58 9.50 9.70 10 9.93 09.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
x1=1./x;
y1=log(y);
p=polyfit(x1,y1,1)
a=exp(p(2))
b=p(1)
z=a.*exp(b./x)
plot(x,y,'k+',x,z,'r')
回归预测
x=[20 25 30 35 40 45 50 55 60 65]';
Y=[13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3]';
X=[ones(10,1) x];
[b,bint,r,rint,stats]=regress(Y,X,0.05);
b,bint,stats
rcoplot(r,rint)
z=b(1)+b(2)*x
rstool(x,Y,'purequadratic')
灰色GM(1,1)
clc,clear
x0=[8438.73 9398.53 9959.17 10949.99 11145.92 11800 12700];
n=length(x0);
lamda=x0(1:n-1)./x0(2:n)
range=minmax(lamda)
x1=cumsum(x0)
for i=2:n
z(i)=0.5*(x1(i)+x1(i-1));
end
B=[-z(2:n)',ones(n-1,1)];
Y=x0(2:n)';
u=B\Y
x=dsolve('Dx+a*x=b','x(0)=x0');
x=subs(x,{'a','b','x0'},{u(1),u(2),x1(1)});
yuce1=subs(x,'t',[0:n-1]);
digits(6),y=vpa(x) %为提高预测精度，先计算预测值，再显示微分方程的解yuce=[x0(1),diff(yuce1)]
epsilon=x0-yuce %计算残差
delta=abs(epsilon./x0) %计算相对误差
rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda %计算级比偏差值
求余
for n=1:5000
k=n^3;
if rem(k,10000)==8888
n
end
end
人口预测模型
k=197.273; %xm=197.273
r=0.03134; % r=0.03134
t=0:10:160; %时间间隔为10年
n0=3.929;
n1=[3.929 5.308 7.240 7.638 12.866 17.069 23.192 31.443 38.558 50.156 62.948 75.995 91.972 105.711 122.775 131.669 150.697];% 实际统计资料
n2=n0*exp(r*t); % Malthus模型
n3=k./(1+((k/n0)-1).*exp(-r.*t)); %Logistic模型
t=t+1790;
plot(t,n1,'k*-',t,n2,'go-',t,n3)
水仙花数
for a=1:9
for b=0:9
for c=0:9
abc=a*100+b*10+c*1;
if abc==a.^3+b.^3+c.^3
disp(abc)
end
end
end
end
主成分分析
X = [40 10 120 250 120 10 40 270 280 170 180 130 220 160 220 140 220 40 20 120;
2 1.5
3 4.5 3.5 1.5 1
4 3.
5 3 3.5 2 1.5 1.5 2.5 2 2 1 1 2;
5 5 13 18 9 12 19 13 11 9 14 30 17 35 14 20 14 10 12 20;
20 30 50 0 50 50 40 60 60 60 40 50 20 60 30 20 10 0 60 0]'
[pc,score,variance,t2] = princomp(X)
Z=zscore(X);
mean(X,1)
std(X,0,1)
回归模型y= ax1+bx2+cx3+dx4+ex5+fx6
1．对回归模型建立M文件model.m如下:
function yy=model(beta0,X)
a=beta0(1);
b=beta0(2);
c=beta0(3);
d=beta0(4);
e=beta0(5);
f=beta0(6);
x1=X(:,1);
x2=X(:,2);
x3=X(:,3);
x4=X(:,4);
x5=X(:,5);
x6=X(:,6);
yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;
X=[598.00 349.00 461.00 57482.00 20729.00 44.00
…………………………………………………………..
2927.00 6862.00 1273.00 100072.0 43280.00 496.00];
y=[184.00 216.00 248.00 254.00 268.00 286.00 357.00 444.00 506.00 ... 271.00 230.00 266.00 323.00 393.00 466.00 352.00 303.00 447.00 ... 564.00 638.00 658.00 691.00 655.00 692.00 657.00 723.00 922.00 ... 890.00 826.00 810.0]';
beta0=[0.50 -0.03 -0.60 0.01 -0.02 0.35];
betafit = nlinfit(X,y,'model',beta0)。