四年级奥数讲义-等积变形二 通用版
奥数-等积变形

奥数-教学教案
授课时间:年月日备课时间年月日年级五课程类别课时学生姓名
授课主题三角形等积变形授课教师
教学目标理解和掌握三角形形状变化但是面积不变
教学
重难点
理解三角形形状变化但是面积不变
教学方法讲练结合
教学过程1、课程导入/错题讲解:
点
拨
教学过程2.知识点讲解
学
习
札
记
教学过程
3、例题分析:
1、如图所示三角形ABC,D为AC上一点,CD=2AD。
问:三角形ABC的面积是三角形
ADB的几倍?方法与技巧
2.如图平行四边形ABCD,E为AB中点,F为DB中点。
已知三角形BEF面积为4平方厘米,问:平行四边形ABCD面积是多少平方厘米?
教学过程4、随堂练习
小
提
本课小结
及下节预告。
四下奥数-等积变形.doc
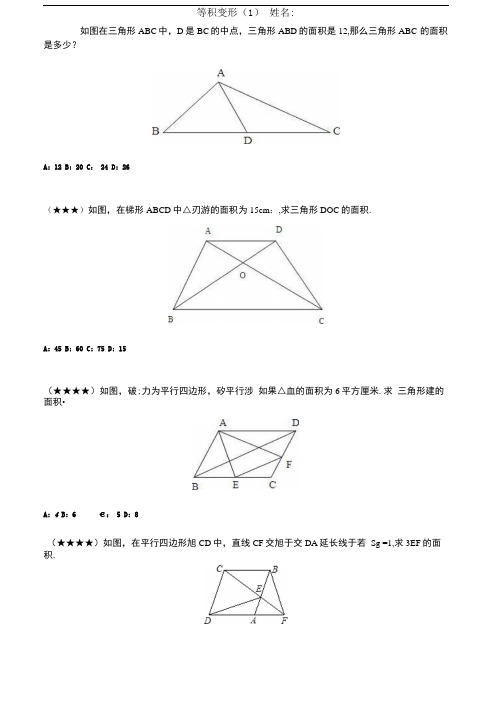
等积变形(1)姓名:如图在三角形ABC中,D是BC的中点,三角形ABD的面积是12,那么三角形ABC 的面积是多少?A: 12 B: 20 C: 24 D: 26(★★★)如图,在梯形ABCD中△刃游的面积为15cm:,求三角形DOC的面积.A: 45 B: 60 C: 75 D: 15(★★★★)如图,破;力为平行四边形,矽平行涉如果△血的面积为6平方厘米.求三角形建的面积•A: 4 B: 6 €: 5 D: 8(★★★★)如图,在平行四边形旭CD中,直线CF交旭于交DA延长线于若Sg =1,求3EF的面积.A: 1 B: 2 C: 3 D: 4(★★★★)如图:已知三角形ABC的面积是88平方厘米,是平行四边形Z)EFC的2倍, 求阴影部分的面积。
A: 44 B: 31 C: 22 D; 30(★★★)如图是由大、小两个正方形组成的,小正方形的询长是占厘米,求三角形NBC 的面积.A: 4 B: 8 C: 16 D: 20(★★★)如图,与AEFG均为正方形,三角形如丑的面积为6平方厘米,图中阴影部分的面积为•DA: 3 B: 6 C:9 D: 123 D等积变形(2) 姓名:BD 长4厘米,DC 长16厘米,B 、C 和D 在同一条直线上.则三角形ABC 的面积是三角 形ABD 面积的( )倍;三角形ADC 的面积是三角形ABD 面积的( )倍。
A; 3 , 4 B; 4 , 3 C : 5 , 3 D; S , 4如图,在三角形ABC 中,BC=10厘米,高是6厘米,D 、E 分别为AB 和AC 的中点,那么三角形DEB 的面积是( )平方厘米。
A: 6 B: 6, 5 (': 7 D: 7. 5三角形.4SC 中,DC = 23D, CE = 3北,三角形如)E 的面积是20平方厘米,三角形.45(? 的面积是( )平方厘米。
A:90 B: 100 C; 120 D: 150A; 30B;40 C : 50 D : 60 如图, 的面积是( 三角形ECD 的面积为3,其中CE=3AE, 3D = 4CD,三角形ABC)0 A: 10B; 12 C : 15 P: 16 如图, X13C 的面积是10平方厘米,将一纺、BC 、 得到一个新的SDEF ,则少EF 的面积为( 分别延长一倍到D 、E. F 且两两 )平方厘米。
小学四年级奥数竞赛班讲义 第44讲:等积变形(二)
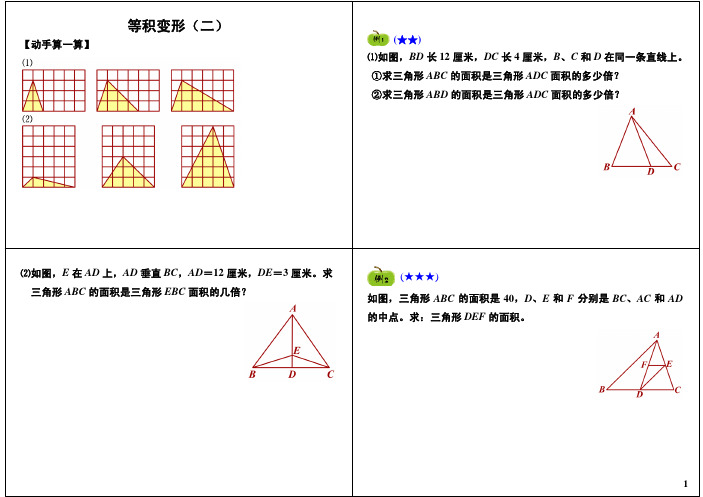
等积变形(二)【动手算一算】⑴如图,BD长12厘米,DC长4厘米,B、C和D在同一条直线上。
①求三角形ABC的面积是三角形ADC面积的多少倍?②求三角形ABD的面积是三角形ADC面积的多少倍?(★★)⑵如图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
求三角形ABC的面积是三角形EBC面积的几倍?如图,三角形ABC的面积是40,D、E和F分别是BC、AC和AD的中点。
求:三角形DEF的面积。
(★★★)1如图,在三角形ABC中,BC=8厘米,高是6厘米,E、F分别为AB和AC的中点,那么三角形EBF的面积是多少平方厘米?(★★★)如图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为10平方厘米。
平行四边形ABCD的面积是多少平方厘米?(★★★)如图,三角形ABC被分成了甲、乙两部分,BD=DC=4,BE=3,AE=6,乙部分面积是甲部分面积的几倍?(★★★★)如图,三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形BDE的面积是多少?(★★★)2如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=BC;延长CA至F,使AF=2AC,求三角形DEF的面积。
(★★★★)如图,D是三角形ABC一边上的中点,两个长方形分别以B、D为顶点,并且有一个公共顶点E,已知两块阴影部分的面积分别是100和120,则三角形BDE的面积是多少?(★★★★★)【大海点睛】一、重要结论1.结论㈠:等底等高的两个三角形面积相等结论㈠拓展:夹在平行线间的一组同底三角形面积相等如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,那么S△ACD=S△BCD2.结论㈡⑴若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
⑵若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
小学奥数等积变形2

奥数拓展:等积变形2【例1】重叠面积中的等积变形1.如图是有两个相同的直角梯形重叠而成(单位:厘米),阴影部分的面积是()平方厘米.2.如图,两个完全一样的直角三角形重叠一部分,图中阴影部分面积是()平方厘米.A.90 B.75 C.52 D.30【例2】等积变形的灵活运用1.如图,长方形ABCD的面积是56平方厘米,点E、F、G分别是长方形ABCD边上的中点,H为AD边上的任意一点,求阴影部分的面积.2.将三角形ABC的BA边延长1倍到D;CB边延长2倍到E,AC边延长3倍到F,如果三角形ABC的面积等于2,那么三角形DEF的面积是_____。
备用图1 备用图23.如图直角三角形中的空白部分是正方形,正方形的一个顶点将这个直角三角形的斜边分成两部分,阴影部分的面积是6 平方厘米,DB长厘米.EBA三.出门考1. 一个等腰三角形的两条边长分别是51米和21米,这个三角形的周长是( )米。
2. 如下图,ABCD 为平行四边形,E 、F 分别为AD 、DC 的中点,如果△BFC 的面积为4平方厘米,则△AEB 的面积是( )平方厘米.3. 如图是由两个相同的直角梯形重叠而成的,图中只标出三个数据(单位:厘米),图中阴影部分的面积是多少平方厘米?4*.如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)四.课后作业1. 计算,能简算的要简算。
435177-- 4847157+- 74512712⎛⎫-- ⎪⎝⎭ 4357910910+++ 41327373-+-2. 一根长2米的绳子,先用去41米,又用去21米,这根绳子短了多少米?3. 光明小学拥有一块公顷的菜地,其中青菜占菜地的,黄瓜占菜地的.剩下的种西红柿,西红柿占菜地的几分之几?4. 光明小学拥有一块公顷的菜地,其中种青菜的有公顷,种黄瓜的有公顷.剩下的种西红柿,西红柿有多少公顷?5. 如图将△ABC 的AB 边延长到D ,BC 边延长到E ,CA 边延长到F ,使DB=AB ,EC=2BC ,FA=2AC ,如果三角形ABC 的面积是5平方厘米,那么三角形DEF 的面积是平方厘米.6. 探索规律并计算=-4131 =-5131 =-6151 =-8151 =+4131 =+5131 =+6151 =+8151 我发现每日一练第一天:周天(5月20日)1. 三根电线共长87米,第一根和第二根共长43米,第二根和第三根共长31米。
小学奥数全国推荐四年级奥数通用学案附带练习题解析答案32三角形的等积变形(二)

年 级 四年级 学 科 奥数版 本通用版课程标题三角形的等积变形(二)上一讲我们学习了三角形的面积与底和高之间的关系,在这个基础上,这节课,我们再一起学习一下平行线间的等积变形。
夹在一组平行线间的等积变形:如下图,ACD ∆和BCD ∆夹在一组平行线之间,且有公共底边CD 那么BCD ACD S S ∆∆=;反之,如果BCD ACD S S ∆∆=,则可知直线AB 平行于CD 。
例1 如图,把四边形ABCD 改成一个等积的三角形。
分析与解:本题有两点要求:一是把四边形改成一个三角形;二是改成的三角形与原四边形面积相等。
我们可以利用三角形等积变形的方法,如下图把顶点A 移到CB 的延长线上的点A ′处,△A ′BD 与△ABD 的面积相等,从而△A ′DC 的面积与原四边形ABCD 的面积相等。
这样就把四边形ABCD 等积地改成了△A ′DC 。
问题是A ′位置的选择是依据三角形的等积变形原则。
过A 作一条和DB 平行的直线与CB 的延长线交于A ′点。
具体做法:连接BD ,过A 作BD 的平行线,与CB 的延长线交于A ′。
连接A ′D ,则△A ′CD 与四边形ABCD 等积。
例2 如图,ABCD 为平行四边形,EF 平行于AC ,如果△ADE 的面积为4平方厘米。
求△CDF 的面积。
分析与解:连接AF 、CE 。
∴ADE S △=ACE S △,CDF S △=ACF S △。
又∵AC 与EF 平行,∴ACE S △=ACF S △。
∴ ADE S △=CDF S △=4(平方厘米)。
例3 如图,已知正方形ABCD 和正方形CEFG ,且正方形ABCD 的边长为10厘米,则图中阴影部分的面积为多少平方厘米?分析与解:解法一 :△BEF 的面积 = BE ×EF ÷2,梯形EFDC 的面积=(EF +CD )×CE ÷2=BE ×EF ÷2=△BEF 的面积 ,而四边形CEFH 是它们的公共部分,所以 △DHF 的面积=△BCH 的面积,进而可得阴影部分△BDF 的面积=△BCD 的面积=10×10÷2=50(平方厘米)。
等积变形2讲义

D
知识大总结 1 等高模型: 1. 等高模型:“二合一”模型 二合 模型. ⑴ 从顶点出发,一分为二. ⑵ 面积之比=底边长度之比. 面积之比=底边长度之比 2. 平行线性质: 【今日讲题】 【今 讲题】 例3,例4,例5 【讲题心得】
B
A O
D
C
6. 并排正方形:同方向的一组对角线平行. 并排 方 方向的 组对角线
A
C
1
4. 二合一模型: 模 ⑴ 从顶点出发,将一个三角形分成两个三角形. ⑵ 两个小三角形的面积之比=底边长度之比. ABD BD ADC DC 【例3】(★★★) 如图 在平行四边形ABCD中, 如图,在平行四边形 中 E为AB中点, 中点 AF=2CF,△ △AFE的 面积为10平方厘米,问:平行四边形ABCD的面积是多少?
等积变形(二)
本讲主线 1. 等高模型. 2. 添加辅助线 . 3. 平行线的等积变形.
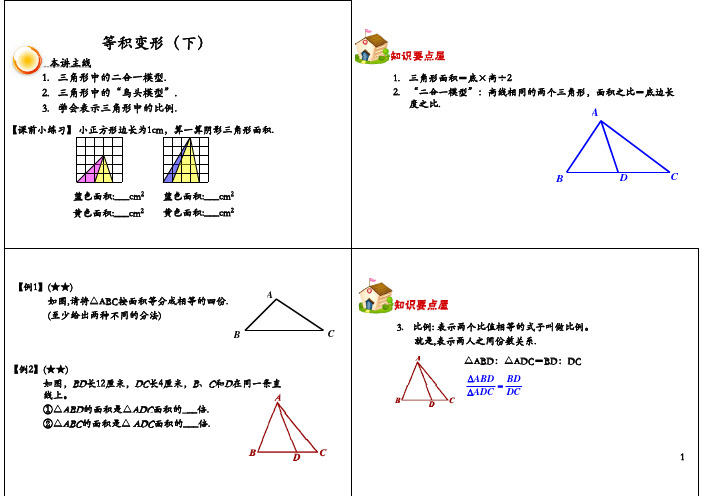
1. 三角形面积=底×高÷2 2. 等高模型:高线相同,底边相等的两个三角形,面积相等. 3. 比:一种份数关系的表达方式. A 2 ⑴ 形式: A : B 2 :1 或 B 1 ⑵ 化简:同时除以相同的因数. △ABD:△ADC=BD:DC
D F E B C
【例4】(★★★☆) 图, ABC的面积为2,其中 ,其中AE=3AB,BD=2BC, ,△BDE的面 如图,△ 积是多少?
5.平行线性质:夹在平行线间的等底三角形,面积相等. 线 质 夹在 线 的等底 角 相等
A O B
Dபைடு நூலகம்
A
C
【例5】 (★★★☆) 图,在平行 形ABCD中,EF平行AC, ,连接BE、AE、CF、 如图,在平行四边形 BF. 那么,与△BFC面积相等的三角形一共有哪几个?
2011年学而思春季第二讲(等积变形)
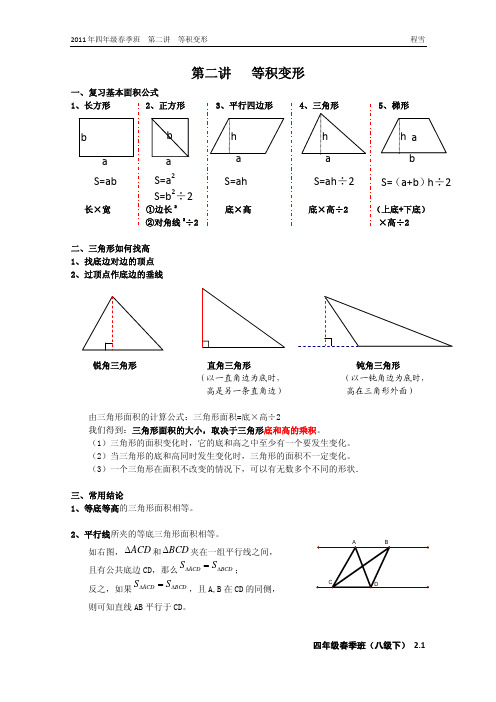
第二讲 等积变形一、复习基本面积公式二、三角形如何找高 1、找底边对边的顶点 2、过顶点作底边的垂线锐角三角形 直角三角形 钝角三角形 (以一直角边为底时, (以一钝角边为底时, 高是另一条直角边) 高在三角形外面)由三角形面积的计算公式:三角形面积=底×高÷2我们得到:三角形面积的大小,取决于三角形底和高的乘积。
(1)三角形的面积变化时,它的底和高之中至少有一个要发生变化。
(2)当三角形的底和高同时发生变化时,三角形的面积不一定变化。
(3)一个三角形在面积不改变的情况下,可以有无数多个不同的形状.三、常用结论1、等底等高的三角形面积相等。
2、平行线所夹的等底三角形面积相等。
如右图,ACD Δ和BCD Δ夹在一组平行线之间, 且有公共底边CD,那么BCD ACD S S ΔΔ=;反之,如果BCD ACD S S ΔΔ=,且A,B 在CD 的同侧,则可知直线AB 平行于CD。
S=ab3、梯形的两条对角线及两腰所夹的两个三角形面积相等。
由上一条结论,△ACD 与△BCD 的面积相等,同时减去 △OCD 的面积,余下的面积也应该相等,即BOD AOC S S ΔΔ=4、等高看底:若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.等底看高:若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.四、例题讲解 例1 如图,BD 长12厘米,DC 长4厘米,B,C,D 在同一条直线上。
(1)求三角形ABC 的面积是三角形ADC 面积的多少倍? (2)求三角形ABD 的面积是三角形ADC 面积的多少倍? 解析:(1)观察三角形ABC 与三角形ADC 有什么联系——同高!注意:怎样判断同高 ①有1个公共顶点②该顶点所对边共线根据“等高看底”,它俩的面积比其实就是底边的比,只是要注意底边的数据: 三角形ABC 的底边是BC=12+4=16(厘米)三角形ADC 的底边是DC=4厘米16÷4=4,三角形ABC 的面积是三角形ADC 面积的4倍(2)同理,三角形ABD 与三角形ADC 也是同高的,其面积比等于12÷4=3例2 如图,E 在AD 上,AD 垂直于BC,AD=12厘米,DE=3厘米,求三角形ABC 的面积是三角形EBC 面积的多少倍?解析:显然,三角形ABC 与三角形EBC 有相同的底边BC。
小学奥数四年级奥数经典讲义第2讲三角形等积变形 提高教师

第二讲 三角形的等积变形内容概述我们已经知道三角形面积的计算公式:三角形面积=底×高÷2从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。
这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ① 等底等高的两个三角形面积相等.②若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.③夹在一组平行线之间的等积变形,如下图,ACD ∆和BCD ∆夹在一组平行线之间,且有公共底边CD 那么BCD ACD S S ∆∆=;反之,如果BCD ACD S S ∆∆=,则可知直线AB 平行于CD 。
例题精讲【例1】 如右图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线长。
① 求三角形ABC 的面积是三角形ABD 面积的多少倍? ② 求三角形ABD 的面积是三角形ADC 面积的多少倍?分析:因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等。
于是: 三角形ABD 的面积=12×高÷2=6×高三角形ABC 的面积=(12+4)×高÷2=8×高 三角形ADC 的面积=4×高÷2=2×高所以,三角形ABC 的面积是三角形ABD 面积的4/3倍;三角形ABD 的面积是三角形ADC 面积的3倍。
第十一讲 等积变形讲义

第十一讲等积变形讲义1、让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2、在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3、进一步积累解决问题的经验,增强解决问题的“转化”意识,提高学好数学的信心。
例1、(运用转化的策略巧算周长)求下面图形的周长。
(单位:厘米)分析与解:求这个图形的周长,就是求围成这个图形的所有线段的长度和。
图中有的线段的长度不知道,可以将其中的4条线段进行平移(如下图),平移之后形成一个长方形,长方形的周长和原来图形的周长是相等的。
因此求原来图形周长的问题就转化成了求下图这个长方形的周长。
例2、(将复杂的图形转化成简单的图形后计算面积)如图1是一块长方形草地,长方形的长是16米,宽是10米。
中间有两条道路,一条是长方形,一条是平行四边形。
草地部分的面积有多大?图1 图2分析与解:求草地部分的面积,可以用大长方形的面积减去两条道路的面积,但要考虑两条道路的重叠部分,因此计算比较复杂。
可以将图1转化成图2,两条道路转化到了长方形草地的边上,很明显,图2草地部分(阴影部分)的面积和图1相等,现在求草地的面积转化成了求长方形的面积,计算比较简单。
解答:(16 - 2 )×(10 - 2) = 112(平方米)答:草地部分的面积是112平方米。
例三.一个底面半径是4厘米,高6厘米的圆柱,里面盛满水,现倒入一个长12厘米,宽6.28厘米的水槽内,求圆柱的高。
例四.两个底面半径是6厘米的圆锥高都是9厘米,现把它熔铸成一个底面半径是9厘米的圆柱,求圆柱的高。
奥数几何专题:等积变形(基础篇)

等积变形(上)
例1
(★★)
⑴图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
⑵图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
⑶图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
例2
(★★★)
如图,在梯形ABCD中,共有八个三角形,其中面积相等的三角形共有哪几对?
例3
(★★★)
正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?
例4
(★★★)
下图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC的面积。
例5
(★★★★)
如图,有三个正方形的顶点D、G、K恰好在同一条直线上,其中正方形GFEB的边长为10厘米,求阴影部分的面积。
例6
(★★★)
在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积。
例7
(★★★★)
如图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米。
求三角形CDF的面积。
⑴夹在一组平行线之间的等积变形,如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,反之,如果S△ACD=S△BCD,且A、B在CD同侧,则可知直线AB平行于CD。
⑵平行线藏在哪里?
——并列正方形的同方向对角线
【先睹为快】
(★★★★)
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=BC;延长CA至F,使AF=2AC,求三角形DEF的面积。
第二讲等积变形
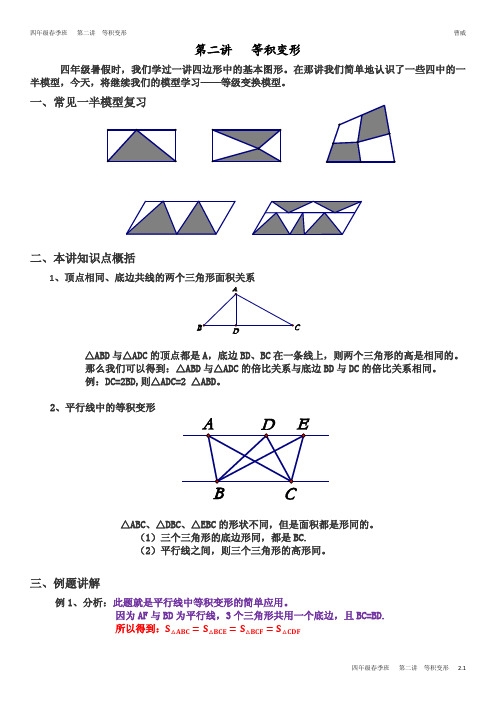
第二讲 等积变形四年级暑假时,我们学过一讲四边形中的基本图形。
在那讲我们简单地认识了一些四中的一半模型,今天,将继续我们的模型学习——等级变换模型。
一、常见一半模型复习二、本讲知识点概括1、顶点相同、底边共线的两个三角形面积关系△ABD 与△ADC 的顶点都是A ,底边BD 、BC 在一条线上,则两个三角形的高是相同的。
那么我们可以得到:△ABD 与△ADC 的倍比关系与底边BD 与DC 的倍比关系相同。
例:DC=2BD,则△ADC=2 △ABD 。
2、平行线中的等积变形△ABC 、△DBC 、△EBC 的形状不同,但是面积都是形同的。
(1)三个三角形的底边形同,都是BC.(2)平行线之间,则三个三角形的高形同。
三、例题讲解例1、分析:此题就是平行线中等积变形的简单应用。
因为AF 与BD 为平行线,3个三角形共用一个底边,且BC=BD. 所以得到:B丙甲乙BEAC B例2、分析:3对,分别是:,,例3、分析:如图:梯形ABCD中若AE∥BC,则可得到平行四边形ABCE.那么在平行四边形ABCE 中的甲乙两个三角形满足一边模型。
则平行四边形ABCE面积可求。
梯形面积可求。
解题如下:2丙=20(平方厘米),丙=10(平方厘米)平行四边形面积=2(甲+乙)=2×20=40(平方厘米)梯形ABCD面积=平行四边形面积+丙=40+10=50(平方厘米)拓展练习:如图在梯形ABDE中,BC=CD=AE,F是CE的中点,△ABC的面积为6平方厘米,求梯形ABDE的面积?例4、(1)△ABC与△ABD都以A为顶点,底边BC、BD共线,且BC=BD,所以△ABD与△ADE都以D为顶点,底边AB、AE共线,且ABC=AE,所以所以拓展练习:(1)如图△ABC的面积为24平方厘米,E、F分别是AB和AC的中点,那么△EBF的面积是多少平方厘米?提示:找顶点相同,底边共线的三角形,利用底边的倍比关系求解。
四年级奥数之等积变形(下)
ABD BD ADC DC
1
【例3】(★★★) 如图,△ABC中,DC=2BD,CE=3AE,△ADE的面积是20cm2, △ABC的面积是多少?
【例4】(★★★) 如图,△ABC的面积是40,D、E和F分别是BC、 AC和AD的中点。求: △DEF的面积。
4. “鸟头”模型:有角共线的两个三角形,它们的面积之比等于相 应边长乘积之比。
A D
E
E C
D
D
A
B
C
B
A
E
B
C
ห้องสมุดไป่ตู้
ABC AB AC ADE AD AE
2
【今日讲题】 例3,例5,超常大挑战
【讲题心得】 ___________________________________________ __________________________________________。
A
C
E
D E
D
D
A
B
CB
ABC AB AC ADE AD AE
A
E
B
C
【例5】(★★★★) 如图,△ABC中,AB是AD的5倍,AC是AE的3倍,如果△ADE的面 积等于1,那么△ABC的面积是多少?
等积变形(下)
1. 三角形中的“二合一”模型。 2. 三角形中的“鸟头”模型。
【超常大挑战】(★★★★) 如图,△ABC的面积为2,其中AE=3AB,BD= 2BC,△BDE的面积是多少?
【家长评价】
____________________________________________ ____________________________________________ ________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等积变形(二)
【动手算一算】
⑴如图,BD长12厘米,DC长4厘米,B、C和D在同一条直线上。
①求三角形ABC的面积是三角形ADC面积的多少倍?
②求三角形ABD的面积是三角形ADC面积的多少倍?
(★★)
⑵如图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
求
三角形ABC的面积是三角形EBC面积的几倍?
如图,三角形ABC的面积是40,D、E和F分别是BC、AC和AD
的中点。
求:三角形DEF的面积。
(★★★)
1
如图,在三角形ABC中,BC=8厘米,高是6厘米,E、F分别为AB
和AC的中点,那么三角形EBF的面积是多少平方厘米?
(★★★)
如图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三
角形AFE(图中阴影部分)的面积为10平方厘米。
平行四边形ABCD
的面积是多少平方厘米?
(★★★)
如图,三角形ABC被分成了甲、乙两部分,BD=DC=4,BE=3,
AE=6,乙部分面积是甲部分面积的几倍?
(★★★★)
如图,三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形
BDE的面积是多少?
(★★★)
2
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长
BC至E,使CE=BC;延长CA至F,使AF=2AC,求三角形DEF
的面积。
(★★★★)
如图,D是三角形ABC一边上的中点,两个长方形分别以B、D为顶
点,并且有一个公共顶点E,已知两块阴影部分的面积分别是100和
120,则三角形BDE的面积是多少?
(★★★★★)
【大海点睛】
一、重要结论
1.结论㈠:等底等高的两个三角形面积相等
结论㈠拓展:夹在平行线间的一组同底三角形面积相等
如下图,△ACD和△BCD夹在一组平行线之间,且有公共底
边CD,那么S△ACD=S△BCD
2.结论㈡
⑴若两个三角形的高相等,其中一个三角形的底是另一个三角形的
几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
⑵若两个三角形的底相等,其中一个三角形的高是另一个三角形的
几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
二、技巧方法
1.平行线的来源
⑴平行四边形(包括长方形和正方形)和梯形
⑵已知平行
⑶并排摆放的正方形的同方向对角线
2.已知做底边,等高优先找
三、经典例题
等积变形(上):例3,例5,例6,例7
等积变形(下):例2,例4,例5,例7
3。
