生物统计学 方差分析共62页
合集下载
精选生物统计学方差分析讲义.

Ck2
k! 2!(k
次 2)!
例如4个样本均数需比较次数为6次。
假设每次比较所确定的检验水准为0.05,
则每次检验拒绝H0不犯第一类错误的概率为1-0.05=0.95; 那么6次检验都不犯第一类错误的概率为(1-0.05)6=0.7351,
而犯第一类错误的概率为0.2649
第七页,共166页。
方差分析的意义
解:(1)假设 H 0: 0 3,0 即该棉花品种纤维长度不能达到纺织
品生产要求含量。对
H A : 0
(2)选取显著水平 0.05
(3)检验计算 s s 2.5 0.125
x n 400
u x 30.2 30.0 1.6
sx
0.125
(4)推断 u<u0.05=1.64, P>0.05 ,显著水平上接受H0,拒绝HA。
例 2.2 为了探讨不同窝的动物的出生重是 否存在差异,随机选取4窝动物,每窝中均有4只 幼仔,结果如下:
动物号
1 2 3 4 和 平均数
表2-2 4窝动物的出生重(克)
窝
别
Ⅰ
Ⅱ
Ⅲ
34.7
33.2
27.1
33.3
26.0
23.3
26.2
28.6
27.8
31.6
32.3
26.7
125.8
120.1
104.9
解为不同来源的平方和及自由度
3、计算不同方差估计值的比值
4、检验各样本所属的平均数是否相等 • 实际上是观察值变异原因的数量分析
第十二页,共166页。
方差分析的应用条件和用途
方差分析应用条件:
1、各样本须是相互独立的随机样本
生物统计第三节单因素试验资料的方差分析

C T / N 460.5 / 25 8482.41
2
2
上一张 下一张 主 页
退 出
SST x C
2
ij
(21.5 2 19.5 2 17.0 2 16.0 2 ) 8482 . 41
8567 . 75 8482 . 41
Байду номын сангаас85.34
MSE
P
⑥ 列出方差分析表
df
3、确定P值、下结论
•从上表得F=14.32,查附表5(方差分析界值表,
单侧),自由度相同时,F界值越大,P值越小。
因F0.01,2,27= 5.49;故P<0.01,按α=0.05水准
拒绝H0,接受HA,可认为三个不同时期切痂对
ATP含量的影响有统计显著性差异。
方差分析的结果只能总的来说多组间是否
S,即
x
得各最小显著极差,所得结果列于表6-15。
上一张 下一张 主 页
退 出
表6-15 SSR值及LSR值
dfe
上一张 下一张 主 页
退 出
将表6-14中的差数与表6-15中相应的最小显
著极差比较并标记检验结果。
检验结果表明:5号品种母猪的平均窝产仔数
极显著高于2号品种母猪,显著高于4号和1号品
③ 计算总的变异及总的自由度
SST x C
2
ij
dfT kn 1 N 1
④ 计算组间变异及相应的自由度
SSB Ti 2 / ni C
df b k 1
⑤ 计算组内变异及相应的自由度
SSE SST SSB
df e dfT df b
N k
生物统计学课件方差分析一

详细描述
例如,研究不同品种的玉米在不同施肥条件下产量的差异。通过单因素方差分析 ,可以判断不同品种的玉米在相同施肥条件下是否存在显著产量差异。
双因素方差分析实例
总结词
用于比较两个分类变量与一个连续变量的关系
详细描述
例如,研究不同饲料类型和不同饲养密度对猪生长速度的影响。通过双因素方差分析,可以判断饲料类型和饲养 密度对猪生长速度是否存在显著影响。
判断差异显著性
根据F值和概率P值判断各组间是否 存在显著差异。通常,如果P值小于 预设的显著性水平(如0.05),则认 为各组间存在显著差异。
如果拒绝零假设,则需要进行进一步 的组间比较或使用其他统计方法来了 解差异的性质和方向。
04 方差分析的应用实例
单因素方差分析实例
总结词
用于比较一个分类变量与一个连续变量的关系
02 方差分析的数学模型与假 设检验
方差分析的数学模型
数学模型建立
方差分析通过建立数学模型,将 多组数据之间的差异分解为组间 和组内两部分,以评估各组之间 的差异是否具有统计学显著性。
线性模型
方差分析所使用的数学模型通常是 线性模型,将数据的变化与自变量 关联起来,以解释和预测因变量的 变化。
模型假设
方差齐性
各组数据的方差应大致相等,避免 出现极端值或离群点。
03
02
正态性
数据应符合正态分布,否则可能需 要采用其他统计方法。
样本量
确保样本量足够大,以提高统计检 验的效能和准确性。
04
方差分析的局限性
前提假设严格 交互作用 多元比较
Байду номын сангаас异常值影响
方差分析的前提假设较为严格,如正态分布、方差齐性和独立 性等,如果不能满足这些假设,结果可能不准确。
例如,研究不同品种的玉米在不同施肥条件下产量的差异。通过单因素方差分析 ,可以判断不同品种的玉米在相同施肥条件下是否存在显著产量差异。
双因素方差分析实例
总结词
用于比较两个分类变量与一个连续变量的关系
详细描述
例如,研究不同饲料类型和不同饲养密度对猪生长速度的影响。通过双因素方差分析,可以判断饲料类型和饲养 密度对猪生长速度是否存在显著影响。
判断差异显著性
根据F值和概率P值判断各组间是否 存在显著差异。通常,如果P值小于 预设的显著性水平(如0.05),则认 为各组间存在显著差异。
如果拒绝零假设,则需要进行进一步 的组间比较或使用其他统计方法来了 解差异的性质和方向。
04 方差分析的应用实例
单因素方差分析实例
总结词
用于比较一个分类变量与一个连续变量的关系
02 方差分析的数学模型与假 设检验
方差分析的数学模型
数学模型建立
方差分析通过建立数学模型,将 多组数据之间的差异分解为组间 和组内两部分,以评估各组之间 的差异是否具有统计学显著性。
线性模型
方差分析所使用的数学模型通常是 线性模型,将数据的变化与自变量 关联起来,以解释和预测因变量的 变化。
模型假设
方差齐性
各组数据的方差应大致相等,避免 出现极端值或离群点。
03
02
正态性
数据应符合正态分布,否则可能需 要采用其他统计方法。
样本量
确保样本量足够大,以提高统计检 验的效能和准确性。
04
方差分析的局限性
前提假设严格 交互作用 多元比较
Байду номын сангаас异常值影响
方差分析的前提假设较为严格,如正态分布、方差齐性和独立 性等,如果不能满足这些假设,结果可能不准确。
生物统计学 第六章 方差分析

������������������
������
F分布右尾从F 到+∞的概率为:
P( F F ) 1 F ( F )
F
f ( F )dF
方差分析
图6-1 F分布密度曲线
F分布的取值范围是(0,+∞),其平均值为������������ =1。 附表4列出了不同自由度条件下的右尾概率。 应用举例 当������������1 =3, ������������2 =18时,������0.05(3,18) =?? 方差分析
方差分析
第四步
列出方差分析表 方差分析表
平方和 (SS) 24.3215 0.0060 24.3275 自由度 (df) 3 16 19
变异来源 处理间 处理内 总变异
均方(MS) 8.1072 0.0004
F值 20268**
方差分析
5.多重比较 F检验的结果显著,仅说明k个平均数间有显著差异, 但不能说明哪些平均数间有显著差异。 定义:判断不同处理平均数两两间差异的显著性, 每个处理的平均数都要与其他的处理进行比较, 这个种差异显著性检验方法就叫做多重比较。 方法:主要有(1)最小显著差数法LSD,(2) 最小显著极差法LSR(q检验法和邓肯检验法)
方差分析
线性数学模型 ������������������ = ������ + ������������ + ������������������ ������������������ = ������.. + (������������. − ������.. ) + (������������������ − ������������. ) kn观测值的总变异=处理间的变异+处理内的变异 其中第i处理j个观测值分解为:全试验观测值总体的 平均数(������)、第i个处理的效应(������������ )和试验误差(������������������ )。 ������������������ 相互独立且服从正态分布,所以各处理A������ 所属总 体也服从正态分布N(������������ ,������ 2 )。 基本假定 效应的可加性、分布的正态性、方差 的同质性(各处理的方差相等)。
生物统计学 第14讲 方差分析

If H0成立,A的k个水平的均值μi相等,因素A发生变 化时,指标Xi~N(μ,σ2),因素A对指标没有作用,称 因素A没有效应。
因素A的效应
29
xij i ij
1
xi. = ni
ni j1
x) i i.
j1
x..
• 为研究某中药对肿瘤重量的影响,以便选定最佳抑 癌作用剂量. 今先将一批小白鼠致癌,然后随机分 成四组(每组10只)分别实施三种剂量的药物注射 及适量的生理盐水注射,经过相同的实验期之后, 测定四组鼠的肿瘤重量.
多个总体的比较
6
Kruskal-Wallis秩和检验 k个独立总体(k ≥ 2) 总体分布未知 有序数据
X i ~ N (i , 2 ) (i 1, 2, , k )
xij ~ N (i , 2 ) (i 1, 2, , k; j 1, 2, , ni )
xij i ij
ij
~
N (0,
2)
H0 : 1 2 k H A : i不全相等
H0:各个总体分布相同
优点:普适性广 缺点:效率低
方差分析 k个独立总体+正态+方差相等(k ≥ 2)
H0:μ1=μ2=……=μk
方差分析解决的问题:多个正态总体均值的比较
7
第一节 单因素方差分析 检验多个正态总体均值是否有差异的一种假 设检验方法.
• 方差分析解决的问题 • 方差分析模型 • 方差分析
1 N
k i 1
ni
xij
j1
1 N
k i 1
ni
(
j1
i
方差分析(共66张PPT)

18~岁 21.65 20.66
… … 18.82 16 22.07 8.97
30~岁 27.15 28.58
… … 23.93 16 25.94 8.11
45~60岁 20.28 22.88 … … 26.49 16 25.49 7.19
基本步骤
(1)建立假设,确定检验水准
H0:三个总体均数相等,即三组工作人员的 体重指数总体均数相等
单因素方差分析
例1 在肾缺血再灌注过程的研究中,将36只雄性大鼠随机等分成三组, 分别为正常对照组、肾缺血60分组和肾缺血60分再灌注组,测得 各个体的NO数据见数据文件,试问各组的NO平均水平是否相同?
单因素方差分析
分析:
对于单因素方差分析,其资料在SPSS中的数据结构应当由两 列数据构成,其中一列是观察指标的变量值,另一列是用以表 示分组变量。实际上,几乎所有的统计分析软件,包括SAS, STATA等,都要求方差分析采用这种数据输入形式,这一点也暗 示了方差分析与线性模型间千丝万缕的联系。
H1:三个总体均数不等或不全相等
(2)计算检验统计量F值
变异来源
SS 自由度(df)
MS
F
组间 组内 总变异
143.406 363.86 507.36
2
71.703
8.87
45
8.09
47
(3)确定p值,作出统计推断
,本次F值处于F界值之外,说明组间均方组内 均方比值属于小概率事件,因此拒绝H0,接受 H1,三个总体均数不等或不全相等
分凝血活酶时间有无不同?
方差分析步骤 :
(1)提出检验假设,确定检验水准
H0:μ1=μ2=μ3 H1:μ1,μ2,μ3不全相同 a=
生物统计学 第六章 方差分析

(1)LSD法
该法是最小显著差数(Least significant difference) 法的简称,是Fisher 1935年提出的,多用于检验某一对 或某几对在专业上有特殊探索价值的均数间的两两比 较,并且在多组均数的方差分析没有推翻无效假设H0 时也可以应用。该方法实质上就是t检验,检验水准无 需作任何修正,只是在标准误的计算上充分利用了样 本信息,为所有的均数统一估计出一个更为稳健的标 准误,因此它一般用于事先就已经明确所要实施对比 的具体组别的多重比较。
xij i ij
它是方差分析的基础。
6.2 方差分析的原理
方差分析的基本原理是认为不同处理组的均数间 的差别基本来源有两个: (1) 随机误差,如测量误差造成的差异或个体间的差 异,称为组内差异,用变量在各组的均值与该组内变 量值之偏差平方和的总和表示,记作 SS e ,组内自由度 df e 。 (2) 实验条件,即不同的处理造成的差异,称为组间 差异。用变量在各组的均值与总均值之偏差平方和表 示,记作 SSt ,组间自由度 df t 。 总偏差平方和 SST SSt SSe 。
6.1 方差分析的相关术语
研究马氏珠母贝三亚、印度品系在不同地区的生 长差异,选择同一批繁殖的两品系马氏珠母贝的稚贝, 分别在海南黎安港、广东流沙港、广西防城港三个海 区进行养殖,每个地区每个品系养殖1000个,1年后 测定马氏珠母贝壳高与总重,比较生长差异。 这里壳高与总重称为试验指标,在试验中常会测定 日增重、产仔数、产奶量、产蛋率、瘦肉率、某些生 理生化和体型指标(如血糖含量、体高、体重)等,这些 都是试验指标,就是我们需要测量的数据。
6.4 均值间的两两比较
对完全随机设计多组平均水平进行比较时,当资料满 足正态性和方差齐性,就可以尝试方差分析,若得到 P>α的结果,不拒绝零假设,认为各组样本来自均数相 等的总体,即不同的处理产生的效应居于同一水平, 分析到此结束; 若方差分析结果P≤α,则拒绝零假设, 接受备择假设,认为各处理组的总体均数不等或不全 相等,即各个处理组中至少有两组的总体均数居于不 同水平。这是一个概括性的结论,研究者往往希望进 一步了解具体是哪两组的总体均数居于不同水平,哪 两组的总体均数相等,这就需要进一步作两两比较来 考察各个组别之间的差别。
该法是最小显著差数(Least significant difference) 法的简称,是Fisher 1935年提出的,多用于检验某一对 或某几对在专业上有特殊探索价值的均数间的两两比 较,并且在多组均数的方差分析没有推翻无效假设H0 时也可以应用。该方法实质上就是t检验,检验水准无 需作任何修正,只是在标准误的计算上充分利用了样 本信息,为所有的均数统一估计出一个更为稳健的标 准误,因此它一般用于事先就已经明确所要实施对比 的具体组别的多重比较。
xij i ij
它是方差分析的基础。
6.2 方差分析的原理
方差分析的基本原理是认为不同处理组的均数间 的差别基本来源有两个: (1) 随机误差,如测量误差造成的差异或个体间的差 异,称为组内差异,用变量在各组的均值与该组内变 量值之偏差平方和的总和表示,记作 SS e ,组内自由度 df e 。 (2) 实验条件,即不同的处理造成的差异,称为组间 差异。用变量在各组的均值与总均值之偏差平方和表 示,记作 SSt ,组间自由度 df t 。 总偏差平方和 SST SSt SSe 。
6.1 方差分析的相关术语
研究马氏珠母贝三亚、印度品系在不同地区的生 长差异,选择同一批繁殖的两品系马氏珠母贝的稚贝, 分别在海南黎安港、广东流沙港、广西防城港三个海 区进行养殖,每个地区每个品系养殖1000个,1年后 测定马氏珠母贝壳高与总重,比较生长差异。 这里壳高与总重称为试验指标,在试验中常会测定 日增重、产仔数、产奶量、产蛋率、瘦肉率、某些生 理生化和体型指标(如血糖含量、体高、体重)等,这些 都是试验指标,就是我们需要测量的数据。
6.4 均值间的两两比较
对完全随机设计多组平均水平进行比较时,当资料满 足正态性和方差齐性,就可以尝试方差分析,若得到 P>α的结果,不拒绝零假设,认为各组样本来自均数相 等的总体,即不同的处理产生的效应居于同一水平, 分析到此结束; 若方差分析结果P≤α,则拒绝零假设, 接受备择假设,认为各处理组的总体均数不等或不全 相等,即各个处理组中至少有两组的总体均数居于不 同水平。这是一个概括性的结论,研究者往往希望进 一步了解具体是哪两组的总体均数居于不同水平,哪 两组的总体均数相等,这就需要进一步作两两比较来 考察各个组别之间的差别。
生物统计学中-方差分析与平均数的比较58页PPT

生物统计学中-方差分析与平均数的比
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 Nhomakorabea克罗维 乌斯
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
较
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 Nhomakorabea克罗维 乌斯
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
较
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
生物统计学各处理重复数不等的方差分析课件PPT
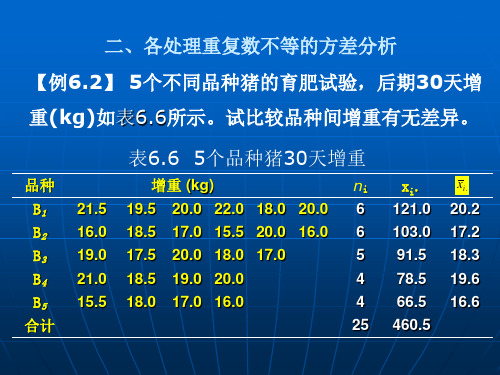
表6.16 表6.15资料各处理组合平均数的LSR值(新复极差测验)
表6.16 表6.14资料各处理组合平均数的新复极差测验
② 各肥类平均数的比较:肥类间的F测验极显著。求得肥类 平均数的标准误:
故有各肥类平均数的LSR 值表6.17,显著性测验结果表6.18 。
表6.17 表6.14资料肥类平均数的LSR值
二、各处理重复肥试验,后期30天增
重(kg)如表6.6所示。试比较品种间增重有无差异。 表6.6 5个品种猪30天增重
品种 增重 (kg) ni 6 6 5
B1
B2 B3
21.5
16.0 19.0
19.5
18.5 17.5
20.0 22.0 18.0 20.0
ix表665个品种猪30天增重1计算各项平方和与自由度2列出方差分析表进行f检验变异来源平方和自由度均方f值值f临界值显著性品种间465041163599f005420287f001420443品种内388420194总变异8534表675个品种育肥猪增重方差分析表3多重比较因为各处理重复数不等应先计算出平均重复次数n0根据dfe20秩次距k2345从附表6中查出005与001的临界ssr值乘以063即得各最小显著极差所得结果列于表68xs表68ssr值及lsr值表将各平均数差数与表68中相应的最小显著极差比较作出推断
(1) 自由度和平方和的分解 根据上表,将各项变异来源的自由度填于表6.15。以下 分解平方和,求得:
(2) F 测验
将上述结果录于表6.15, 求得肥类×土类间的F=4.81/0.928 =5.18>F0.01; 求得肥类间的F=89.69/0.928=96.65>F 0.01; 求得土类间的F=1.98/0.928=2.13<F0.05。 所以该试验肥类×土类的互作和肥类的效应间差异都是 极显著的,而土类间无显著差异。
表6.16 表6.14资料各处理组合平均数的新复极差测验
② 各肥类平均数的比较:肥类间的F测验极显著。求得肥类 平均数的标准误:
故有各肥类平均数的LSR 值表6.17,显著性测验结果表6.18 。
表6.17 表6.14资料肥类平均数的LSR值
二、各处理重复肥试验,后期30天增
重(kg)如表6.6所示。试比较品种间增重有无差异。 表6.6 5个品种猪30天增重
品种 增重 (kg) ni 6 6 5
B1
B2 B3
21.5
16.0 19.0
19.5
18.5 17.5
20.0 22.0 18.0 20.0
ix表665个品种猪30天增重1计算各项平方和与自由度2列出方差分析表进行f检验变异来源平方和自由度均方f值值f临界值显著性品种间465041163599f005420287f001420443品种内388420194总变异8534表675个品种育肥猪增重方差分析表3多重比较因为各处理重复数不等应先计算出平均重复次数n0根据dfe20秩次距k2345从附表6中查出005与001的临界ssr值乘以063即得各最小显著极差所得结果列于表68xs表68ssr值及lsr值表将各平均数差数与表68中相应的最小显著极差比较作出推断
(1) 自由度和平方和的分解 根据上表,将各项变异来源的自由度填于表6.15。以下 分解平方和,求得:
(2) F 测验
将上述结果录于表6.15, 求得肥类×土类间的F=4.81/0.928 =5.18>F0.01; 求得肥类间的F=89.69/0.928=96.65>F 0.01; 求得土类间的F=1.98/0.928=2.13<F0.05。 所以该试验肥类×土类的互作和肥类的效应间差异都是 极显著的,而土类间无显著差异。
生物统计学 方差分析

缺点:加大犯I型错误的概率
Duncan多范围检验
P341
§8.5 方差分析应具备的条件
多个方差齐性检验
了解
Bartlett 检验(Bartlett test)
Levene 检验( Levene test)
作业
P157
8.2(用C=80来编码) 8.8 (用C=4来编码)
请翻译以下术语/Try
§8.4 多重比较(multiple comparison)
目的:
哪些处理之间存在显著差异,平均数之 间进行一对一比较。
LSD法
Duncan法(SSR)
S-N-K法
/s/blog_54b63 97501014fz3.html
最小显著差数检验(LSD)检验
附:生物统计学
第九章 两因素及多因素 方差分析
2012.5
§9.2 固定效应模型
线性统计模型(linear
statistical model)
同一处理的处理效应是相同的
简易计算方法
statistical model)
如何做到?
§8.2 固定效应模型
线性统计模型
平方和与自由度的分解
艾塔
重要
组间 组内
简易计算方法
学习小组任务
自学并讲解表8-3及其计算式。
自学并讲解公式8.1的组成及含义
(p144-148)。 自学并讲解p149例题 。 课后阅读p152-154内容,或自行上网查 资料,说明多重比较是做什么的?常用 多重比较有哪些?
to translate these terms
please: One-factor ANOVA,固定因素,significant, 多重比较
第三节 两因素完全随机设计试验资料的方差分析 《生物统计学》课件

N(0,σ2)。
上一张 下一张 主 页 退 出
(αβ)ij为Ai与Bj的互作效应
()ij ij i. . j
i , j , ij 分别为Ai、Bj、AiBj观测值总体
平均数;且
a
b
Байду номын сангаас
n
b
ab
i 0, j 0, ( )ij ( )ij
( )ij 0
i1
j 1
i1
j 1
i1 j1
上一张 下一张 主 页 退 出
因试验资料的总变异可分解为水平组合间 变异与水平组合内变异 即 误差两部分 ,若 记
A、B 水平组合间的平方和与自由度为 SSAB, dfAB,则两因素有重复观测值试验资料方差分
析平方和与自由度的分解式可表示为 :
SST SSAB SSe
dfT dfAB dfe
αi=μi-μ,βj=μj-μ
μi、μj分别为Ai、Bj观测值总体平均数,
且Σαi=0,Σβj=0; εij 为随机误差 ,相互独立 ,且服从
N (0,σ2)。
上一张 下一张 主 页 退 出
两因素交叉分组单个观测值的试验资料,
A因素的每个水平有b次重复,B 因素的每个 水平有a次重复,每个观测值同时受到A、B
上一张 下一张 主 页 退 出
A的效应随着B因素水平的不同而不同,反 之亦然,此时称A、B两因素间存在交互作用, 记为A×B。
或者说,某一因素的简单效应随着另一因 素水平的变化而变化时,则称该两因素间存在 交互作用。
互作效应可由(A1B1+A2B2-A1B2-A2B1)/2来估计。
表5-28中的互作效应为: (470+512-480-472)/2=15
上一张 下一张 主 页 退 出
(αβ)ij为Ai与Bj的互作效应
()ij ij i. . j
i , j , ij 分别为Ai、Bj、AiBj观测值总体
平均数;且
a
b
Байду номын сангаас
n
b
ab
i 0, j 0, ( )ij ( )ij
( )ij 0
i1
j 1
i1
j 1
i1 j1
上一张 下一张 主 页 退 出
因试验资料的总变异可分解为水平组合间 变异与水平组合内变异 即 误差两部分 ,若 记
A、B 水平组合间的平方和与自由度为 SSAB, dfAB,则两因素有重复观测值试验资料方差分
析平方和与自由度的分解式可表示为 :
SST SSAB SSe
dfT dfAB dfe
αi=μi-μ,βj=μj-μ
μi、μj分别为Ai、Bj观测值总体平均数,
且Σαi=0,Σβj=0; εij 为随机误差 ,相互独立 ,且服从
N (0,σ2)。
上一张 下一张 主 页 退 出
两因素交叉分组单个观测值的试验资料,
A因素的每个水平有b次重复,B 因素的每个 水平有a次重复,每个观测值同时受到A、B
上一张 下一张 主 页 退 出
A的效应随着B因素水平的不同而不同,反 之亦然,此时称A、B两因素间存在交互作用, 记为A×B。
或者说,某一因素的简单效应随着另一因 素水平的变化而变化时,则称该两因素间存在 交互作用。
互作效应可由(A1B1+A2B2-A1B2-A2B1)/2来估计。
表5-28中的互作效应为: (470+512-480-472)/2=15
