聚类分析实例
R语言聚类分析实例教程

R语言聚类分析实例教程R语言是一种广泛应用于数据分析和统计建模的开源编程语言。
聚类分析是一种无监督学习的技术,可以帮助我们发现数据中的隐藏模式和结构。
下面是一个使用R语言进行聚类分析的实例教程。
首先,我们使用一个虚拟的数据集来说明聚类分析的步骤。
假设我们有一个包含100个样本和5个变量的数据集。
我们可以使用以下代码来生成这个数据集:```Rset.seed(123)data <- matrix(rnorm(100*5), ncol = 5)```接下来,我们需要对数据进行预处理。
这包括标准化数据以确保每个变量具有相似的尺度。
我们可以使用以下代码对数据进行标准化:```Rscaled_data <- scale(data)```接下来,我们可以使用K均值聚类算法来对数据进行聚类。
K均值算法将数据集分成K个不同的簇,每个簇包含与其质心最近的样本。
我们可以使用以下代码来执行K均值聚类:```Rkmeans_result <- kmeans(scaled_data, centers = 3)```在这个例子中,我们将数据分成3个簇。
请注意,你可以根据数据的特点选择不同的簇数。
接下来,我们可以检查聚类结果,并将其可视化。
我们可以使用以下代码来绘制数据点,并使用不同的颜色表示不同的聚类:```Rlibrary(ggplot2)df <- data.frame(scaled_data, cluster =as.factor(kmeans_result$cluster))ggplot(df, aes(x = X1, y = X2, color = cluster)) +geom_point( +labs(x = "Variable 1", y = "Variable 2", title = "Cluster Analysis")```上述代码创建了一个散点图,其中x轴和y轴表示数据集的两个变量,颜色表示不同的聚类。
货运企业客户价值聚类分析实例

远 高 于 现 期水 平 , 5分 ; 高 成 互 补 关 系 , 是对 企 业 有 利 的 同盟 者 , 5分 ; 企业 对
2
。…
2 期 3
对运 量 相 对 较 大 的 l 5家 典 型 客 户进 行 分 析 。各 项 无专 门 的研 发 机 构 , 品质 量 一般 , 分 。 产 1 评价 指 标 的 打分 标 准 如 下 : ( ) 同时问 1合 ( 3 有 效 订舱 率 1) 9 %以上 , 0 5分 ; 0 8 %以上 , 4
、
O l 37 3 0 0l l 7
0OI 7l
墨
.
,
O 0 26 .5
禹2
01 34 .0 nO 1 l 0
不 同价 值 的客 户 制 定差 异 化 营销 策 略 。
I
基
OO 32 .2
yl 1 0f 42 1 7
0加 59 I
yl _ O lO8 2
0 o 66 .S
∞
00 67 2
00 267
【0 93 1 0
0( 93 m
1 客 户 价 值 评 价 指 标 体 系 的 构 成
客 户 价 值 评 价 指 标 体 系 由直接 价 值 和 潜 在 价
值构 成 , 中 : 其 直接 价 值 包括 交 易 、 用 、 信 特征 等方
9%以上 , 0 5分 ;0 7 %以上 , 4
对 企 业 价 值较 大 , 企 业 形 与
( ) 润贡献率 5利
分 ;0 5 %以上 , ; 0 3分 3 %以上 , ;0 2分 3 %以 下 , 。 1分
3分 ; 低 , 较 2分 ; 低 , 分 。 很 1 ( ) 来箱挝预期 6未
聚类分析实例分析题(推荐文档)

5.2酿酒葡萄的等级划分5.2.1葡萄酒的质量分类由问题1中我们得知,第二组评酒员的的评价结果更为可信,所以我们通过第二组评酒员对于酒的评分做出处理。
我们通过excel计算出每位评酒员对每支酒的总分,然后计算出每支酒的10个分数的平均值,作为总的对于这支酒的等级评价。
通过国际酿酒工会对于葡萄酒的分级,以百分制标准评级,总共评出了六个级别(见表5)。
在问题2的计算中,我们求出了各支酒的分数,考虑到所有分数在区间[61.6,81.5]波动,以原等级表分级,结果将会很模糊,不能分得比较清晰。
为此我们需要进一步细化等级。
为此我们重新细化出5个等级,为了方便计算,我们还对等级进行降序数字等级(见表6)。
通过对数据的预处理,我们得到了一个新的关于葡萄酒的分级表格(见表7):考虑到葡萄酒的质量与酿酒葡萄间有比较之间的关系,我们将保留葡萄酒质量对于酿酒葡萄的影响,先单纯从酿酒葡萄的理化指标对酿酒葡萄进行分类,然后在通过葡萄酒质量对酿酒葡萄质量的优劣进一步进行划分。
5.2.2建立模型在通过酿酒葡萄的理化指标对酿酒葡萄分类的过程,我们用到了聚类分析方法中的ward 最小方差法,又叫做离差平方和法。
聚类分析是研究分类问题的一种多元统计方法。
所谓类,通俗地说,就是指相似元素的集合。
为了将样品进行分类,就需要研究样品之间关系。
这里的最小方差法的基本思想就是将一个样品看作P 维空间的一个点,并在空间的定义距离,距离较近的点归为一类;距离较远的点归为不同的类。
面对现在的问题,我们不知道元素的分类,连要分成几类都不知道。
现在我们将用SAS 系统里面的stepdisc 和cluster 过程完成判别分析和聚类分析,最终确定元素对象的分类问题。
建立数据阵,具体数学表示为:1111...............m n nm X X X X X ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(5.2.1) 式中,行向量1(,...,)i i im X x x =表示第i 个样品;列向量1(,...,)'j j nj X x x =’,表示第j 项指标。
SPSS聚类分析加具体案例
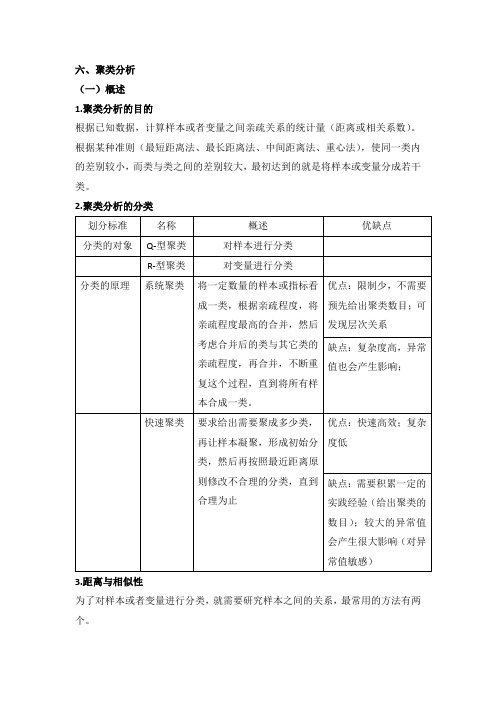
六、聚类分析(一)概述1.聚类分析的目的根据已知数据,计算样本或者变量之间亲疏关系的统计量(距离或相关系数)。
根据某种准则(最短距离法、最长距离法、中间距离法、重心法),使同一类内的差别较小,而类与类之间的差别较大,最初达到的就是将样本或变量分成若干类。
2.聚类分析的分类3.距离与相似性为了对样本或者变量进行分类,就需要研究样本之间的关系,最常用的方法有两个。
(二)系统聚类1.系统聚类的步骤距离的具体定义及计算方式计算n各样本两两之间的距离将距离接近的数据依次合并为一类,再计算,再合并 画聚类图,解释类与类之间的关系2.亲疏程度度量方法3.系统聚类的分类4.SPSS操作及实例SPSS采用的是凝聚法。
案例:根据30个省的23个主要行业的平均工资情况,通过聚类分析来判断哪些地区平均工资水平高。
SPSS操作及结果:打开SPSS上方菜单栏中的分析->分类->系统聚类选择变量->勾选统计量->在绘制里选择树状图和冰柱图勾选方法(通常使用组间联接)->度量区间->选择标准化方式(全距从0到1)下图为近似矩阵表,标注了相关系数,数值越大,距离越接近下图为聚类分析结果表,第一类表示这是聚类分析的第几步,第二三列表示该步中那几个样本或者小类聚成一类,第四列表示距离,第五六列表示本步骤中参与的是个体还是小类(0表示样本,非0表示第n步生成的小类),第七列表示本步骤的聚类结果将在以下第几步中用到。
下面是冰柱图和树状图的结果,根据树状图可以看出,如果分为三类的话,第一类包括北京上海,第二类包括天津、广东、浙江、江苏、西藏,剩下的归为一类。
(三)快速聚类(适合大样本聚类)1.快速聚类的步骤指定聚类数目K确定K个初始类的中心(自定义或者根据数据中心初步确定)根据距离最近的原则进行分类根据新的中心位置,重新计算每一记录距离新的类别中心的的距离,并重新分类重复步骤4,直到达到标准2.SPSS操作及实例打开SPSS上方菜单栏中的分析->分类->K-均值聚类选择变量->勾选统计量->定义变量值选择迭代次数->选项(勾选初始聚类中心、每个个案的聚类信息)->定义变量值->保存(勾选聚类成员、聚类中心距离)下图为输出的初始聚类中心下图为最终距离中心,第一类平均工资最高,第二类次之,第三类最低下图为每个聚类中的案例数和聚类成员。
SPSS聚类分析实例讲解

SPSS聚类分析实例讲解SPSS是一款功能强大的统计分析软件,可用于数据清洗、描述统计分析、假设检验和聚类分析等。
聚类分析是一种无监督学习方法,其目标是按照数据的相似性度量,将样本数据划分为多个不同的群组。
下面将以一个实例来讲解如何使用SPSS进行聚类分析。
实例描述:假设有一个超市的销售数据,包含了不同商品的销售额、销售量和利润等信息。
我们希望将商品进行聚类分析,找出相似销售特征的商品群组。
步骤一:数据准备首先,将销售数据保存为一个.SP文件,然后打开SPSS软件。
在主界面上选择“文件”-“打开”-“数据库”-“从SPSS文件”,打开数据文件。
步骤二:变量选择在数据文件中,选择出要进行聚类分析的变量。
在“数据视图”中,选择那些代表销售特征的变量,例如“销售额”、“销售量”和“利润”。
在变量列上按住“Ctrl”键,同时点击这些变量名,选中它们。
步骤三:聚类分析点击菜单上的“数据”-“服务”-“聚类分析”进行聚类分析操作。
会弹出“聚类分析”对话框。
在对话框中,将选中的变量移到右侧的“变量”框中,并选择“K均值聚类”作为聚类方法。
K值是指要分成的群组数量,可以根据实际情况设定。
这里假设将商品分成3个群组,因此设置为3步骤四:聚类结果解读点击“确定”按钮,SPSS将自动进行聚类分析。
完成后,SPSS会在数据文件中生成一个新的变量,用于表示每个样本所属的群组。
在下方的“结果视图”中,可以看到聚类结果的统计数据、聚类中心和变量间的距离。
此外,在“分类变量资料”中,还可以看到每个样本所属的群组编号。
步骤五:聚类结果可视化为了更好地理解聚类结果,可以进行可视化展示。
点击菜单上的“图形”-“散点图”,在对话框中依次选择所属群组变量和销售额、销售量这两个变量。
点击“确定”按钮,即可生成散点图。
散点图可以清楚地显示出不同群组之间的差异和相似性。
根据散点图,可以对聚类结果进行解读。
例如,如果不同群组之间的点比较分散,则说明聚类效果较差;而如果不同群组之间的点比较集中,则说明聚类效果较好。
NTSYS软件进行聚类分析——UPGMA实例

NTSYS软件进行聚类分析——UPGMA实例第一部分说明文档Cluster analysis 聚合分析NTSYSpc最常见的使用是对某些相似或相异矩阵进行各种聚类分析。
以下是一个批处理例子;首先,标准化数据矩阵,其次,计算各列之间的距离系数,第三,采用单链路聚类方法,第四,计算表面值(超度量)矩阵和相关系数,第五,以散点图形式显示结果并同时输出距离矩阵。
" Standardize the variables*stand o=data.nts r=sdata.nts" Compute a distance matrix*simint o=sdata.nts r=dist.nts c=dist" Do a single-link cluster analysis of the distance matrix*sahn o=dist.nts r=tree.nts cm=single" Compute cophenetic values*coph o=tree.nts r=coph.nts" Compute the cophenetic correlation*mxcomp x=coph.nts y=dist.nts" Display phenogram*tree o=tree.nts" Display distance matrix*output o=dist.nts第二部分实例解析如果你的数据集包含量纲不一致的变量,则必须要先经过标准化处理,可以用STAND 组件完成。
如下图指明了标准化窗口。
Test.nts文件将被按行(意味着行为变量)标准化,并输出标准化文件名为teststand.nts。
如果你的变量量纲一致(如,基因序列)或者是定性数据则不需要标准化处理。
输出结果如下(5个变量的简单统计)下一步,相似或非相似矩阵数据集必须要在标准化后的数据集上构建,用来衡量各OTUS(列)两两之间的相似/非相似程度。
聚类分析及其应用实例ppt课件

Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
聚类分析及其应用实例.ppt

Gp Gq
D pq ? max{ d ij | i ? G p , j ? G q }
类平均距离( average linkage ):
Gp和Gq中每两两样本间距离的平均值作为两个类之间的距离。
Gp Gq
?? D pq
?
1 t ptq
tp i?1
? 相似系数----常用于对变量的聚类
? Pearson相关系数:两个连续变量间呈线性相关 ? Spearman相关系数:利用两变量的秩次大小作线性相关分析 ? Kendall等级相关系数,。。。
凝聚的层次聚类示意图
C3
X4 X3
C4
X5 X2
X1
X1:Gibbon (长臂猿) X2:Symphalangus (合趾猿) X3:Human (人) X4:Gorilla (大猩猩) X5:Chimpanzee (黑猩猩)
tq
X (q) i i ?1
用Gp和Gq表示两个类,它们所包含的样本数目分别为tp和tq,类Gp和Gq之间
的距离用Dpq表示。
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
Gq
D 2 ? WM ? W p ? Wq
凝聚的层次聚类示意图
Oh?
X4 X3
X5 X2
X1
X1:Gibbon (长臂猿) X2:Symphalangus (合趾猿) X3:Human (人) X4:Gorilla (大猩猩) X5:Chimpanzee (黑猩猩)
常用的聚类统计量
多元统计聚类分析方法实例

多元统计聚类分析方法实例
一、概述
多元统计聚类分析是一种建立数据从不同特征维度上的理解和描述的
方法。
它是通过对多维数据进行聚类分析,将具有共同特征的不同数据项
归纳到一组中,以便进一步分析和解释这些数据项之间的相似性和差异性,从而达到更深入地理解和把握数据特征的目的。
二、基本多元统计聚类分析步骤
1、数据准备
首先,在开始进行多元统计聚类分析之前,需要准备足够的数据,以
便进行模型的建立和应用。
在进行数据准备时,要注意把握数据的准确性,避免数据准备过程中的错误,以保证后续步骤正确的进行。
2、聚类分析
在进行聚类分析时,需要根据实际的数据情况,确定聚类的参数,并
计算不同类簇之间的距离,作为聚类的依据。
在此过程中,要根据聚类的
具体目的,采用相应的聚类分析方法,以便达到更理想的聚类效果。
3、聚类评价
接下来,需要对聚类结果进行评价,以识别聚类的质量和准确性,并
可以根据评价结果,对聚类的方法和参数进行调整,以获得更理想的聚类
结果。
4、聚类结果应用
最后,在聚类分析完成后,可以将聚类结果应用到实际的问题中,以获得有效的决策依据。
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
如何使用聚类分析进行市场细分

如何使用聚类分析进行市场细分市场细分是指根据消费者的特征和需求将市场划分为若干具有一定相似性的细分市场。
通过市场细分可以更好地了解消费者的需求并制定相应的营销策略,以提高市场竞争力和销售业绩。
聚类分析是一种常用的市场细分方法,可以帮助我们发现消费者群体中的相似特征并进行细分。
本文将介绍如何使用聚类分析进行市场细分。
一、聚类分析的原理聚类分析是一种无监督学习方法,通过对样本数据进行分类,将相似度高的样本划分到同一类别中。
其基本原理是通过计算样本之间的相似度或距离,将相似度高的样本归为一类。
二、聚类分析的步骤1. 收集数据:首先需要收集市场相关的数据,包括消费者的基本信息、消费行为、偏好等。
这些数据可以通过市场调研、问卷调查等方式获得。
2. 数据预处理:对收集到的数据进行预处理,包括数据清洗、缺失值处理、数据标准化等。
确保数据的准确性和可靠性。
3. 确定聚类变量:根据实际需求选择适合的聚类变量,一般选择与市场细分相关的特征指标,如购买频率、客单价、消费偏好等。
4. 选择聚类方法:根据数据的特点选择合适的聚类方法,常用的有层次聚类、K均值聚类、密度聚类等。
不同的方法对数据的要求和聚类效果可能会有所不同,需要根据具体情况选择。
5. 进行聚类分析:根据选定的聚类方法进行数据分析,将样本数据划分到不同的类别中。
可以使用统计软件进行聚类计算和可视化展示。
6. 评价结果:对聚类结果进行评价,包括聚类的合理性、稳定性和可解释性等。
如果聚类结果不理想,可以调整聚类方法或者变量选择,重新进行分析。
7. 市场细分应用:根据聚类结果制定相应的市场细分策略。
可以根据每个细分市场的特征和需求制定差异化的产品、定价、促销和渠道策略,提高市场竞争力和销售业绩。
三、聚类分析的应用实例以某电商平台为例,假设我们想要对购买者进行市场细分,将消费者划分为不同的购买群体,并制定相应的营销策略。
1. 数据收集:收集购买者的基本信息和购买行为数据,如性别、年龄、购买频率、客单价等。
聚类分析简单例子

聚类结果优化策略
特征选择
选择与聚类任务相关的特征,去除冗余和无 关特征,提高聚类效果。
选择合适的聚类算法和参数
针对数据集的特点选择合适的聚类算法,并 调整算法参数以达到最佳聚类效果。
特征变换
通过降维或升维技术,将原始特征转换为更 有利于聚类的特征空间。
集成聚类
将多个聚类结果集成起来,得到更稳定和可 靠的聚类结果。
聚类结果的解释性
当前聚类算法往往缺乏对聚类结果的解释性,使 得用户难以理解聚类结果的含义。未来可以研究 如何提高聚类结果的解释性,使得聚类分析更加 易于理解和应用。
高维数据聚类
随着数据维度的增加,传统聚类算法可能会面临 “维数灾难”的问题。未来可以研究专门针对高 维数据的聚类算法,以提高聚类的准确性和效率 。
初始化
选择K个点作为初始聚类中心。
分配数据点
计算每个数据点与K个聚类中心 的距离,将其分配给最近的聚 类中心。
更新聚类中心
重新计算每个聚类的中心点, 即该类中所有数据点的均值。
迭代
重复分配数据点和更新聚类中 心的步骤,直到聚类中心不再 发生变化或达到最大迭代次数
。
层次聚类算法原理
01
02
03
04
初始化
将每个数据点视为一个独立的 簇。
合并簇
计算每对簇之间的距离,将距 离最近的两个簇合并为一个新
的簇。
更新距离
重新计算新簇与其余簇之间的 距离。
迭代
重复合并簇和更新距离的步骤 ,直到达到预设的簇数量或簇 之间的距离超过某个阈值。
DBSCAN算法原理
初始化
选择任意一个未访问过的数据点作为种子 点。
标记噪声点
数据准备
Matlab中的时间序列聚类分析方法与实例

Matlab中的时间序列聚类分析方法与实例时间序列聚类分析是一种重要的数据挖掘技术,利用时间序列数据的特征进行聚类可以帮助我们理解和发现数据中的模式和规律。
在Matlab中,提供了丰富的工具和函数来进行时间序列聚类分析,并且可以直观地展示聚类结果。
本文将介绍一些常用的时间序列聚类方法,并给出相应的实例。
一、基于距离的时间序列聚类方法基于距离的时间序列聚类方法是将时间序列看作向量,通过计算不同时间序列之间的距离来进行聚类。
常用的方法有欧氏距离、曼哈顿距离和动态时间规整(DTW)等。
1. 欧氏距离:欧氏距离衡量两个时间序列在每个时刻上数值的差异,然后将每个时刻上的差异进行平方求和并开平方根,即为欧氏距离。
在Matlab中,可以使用pdist函数来计算欧氏距离。
```matlabdata = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 假设有三个时间序列dist = pdist(data, 'euclidean');```2. 曼哈顿距离:曼哈顿距离是将两个时间序列上对应时刻数值的差的绝对值进行求和,即为曼哈顿距离。
在Matlab中,可以使用pdist函数来计算曼哈顿距离。
```matlabdata = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 假设有三个时间序列dist = pdist(data, 'cityblock');```3. 动态时间规整(DTW):DTW是一种基于时间序列形状相似度的距离度量方法,它考虑了时间上的不对齐。
在Matlab中,可以通过调用dtw函数来计算DTW距离。
```matlabx = [1, 2, 3, 4, 5]; % 第一个时间序列y = [2, 3, 4]; % 第二个时间序列dist = dtw(x, y);```二、基于相似度的时间序列聚类方法基于相似度的时间序列聚类方法是通过计算不同时间序列之间的相似度来进行聚类。
聚类分析实例讲解

聚类分析实例讲解Lab 6 聚类分析一、分析背景Chrysler公司为了赢得市场竞争地位,打算推出新产品Viper,该种产品的目标客户是雅皮士阶层。
为了进一步了解这种人群的心理特征,定位自己的产品,吸引目标客户,Chrysler公司举行了一次市场调研。
讨论者使用九点量表测量400名被试者对30项陈述的态度,从而了解这些目标客户的心理特征。
调研还咨询被试者对Dodge Viper型汽车的态度来测量标准变量,标准变量的测量通过九点量表来测试消费者对“我情愿购买Chrysler公司生产的Dodge Viper型汽车”的态度。
本次分析的目的是:通过聚类分析,将原始变量分离聚成三类和四类,比较两种办法的效果。
同时,比较使用原始变量得到的聚类结果和使用因子得分得到的聚类结果,看哪一种办法能更好地解释数据。
二、分析结果1、按照原始变量举行的聚类分析首先按照原始变量举行聚类分析,因为样本数较大,采纳迭代聚类法,分离将样本聚为三类和四类,下面是聚类分析的结果比较。
表1 聚为三类后的组重心表2 聚为四类后的组重心表3 聚为三类的每组样本数表聚为四类的每组样本数表5 聚为三类后组重心之间的距离表6 聚为四类后组重心之间的距离由方差分析的结果(结果略)可知,在聚为三类和四类的分析中,V8,V9,V18,V19,V20和V27的组间差异均大于0.05,结果不显著。
2、按照因子得分举行的聚类分析以下是按照因子得分,采纳迭代法将样本聚为三类和四类的结果:表7 聚为三类后的组重心-.45298 .16364 .29950 .36038 -.22794 -.15239 .28739-.32881 .00765 .25444 .70915 -.87203 .52946 -.29355-.26021 .18363 .11953 -.28471 .00228 .20936 -.18616 .56772-.64844.01414消费因子时尚因子社会因子爱国因子期望因子偏好因子共性因子家庭因子12 3 Cluster表8 聚为三类时的样本数137.000 123.000 140.000400.000 .0001 2 3ClusterValidMissing以下是按照因子得分聚为四类的结果:从以上用因子得分的结果可以看出,聚为三类和四类时八个因子的组间差异都很显著。
多元统计聚类分析方法实例

三种系统聚类方法对24款8600GT 进行分类的应用0082807段超波 0082796童善杰(江西财经大学信息管理学院08管理科学1班,江西,南昌220032)摘要:我们知道在SAS 系统中提供了很多种系统聚类过程中确定类别与类别之间距离的方法,像类平均法(AVE )、最短距离法(SIN )、离差平方和法(WARD )、最长距离法(COM )、重心法(CEN )等,从而影响最终的分类结果。
到底哪一种方法更合理更符合实际呢?通过用类平均法(AVE )、最短距离法(SIN )和离差平方和法(WARD )3种方法对24款8600GT 进行分类,来对比一下这三种方法的分类效果。
关键词:聚类分析 类平均法 最短距离法 离差平方和法Three Kinds of Clustering Method in 8600GT Classification of 24 of theApplicationAbstract: we know in the SAS system provides a variety of system clustering process to determine the distance between classes and category of methods, like Average linkage (AVE), Single linkage (SIN), WARD (WARD), Complete method (COM), Centroid method (CEN) etc, thus influence the final classification results. Which method is more reasonable more accord with actual? Through using class average method (AVE), Single linkage (SIN) and WARD (WARD), three methods for the 24 8600GT classification, to compare these three methods of classification effect. Keywords: Cluster Analysis Average linkage WARD Single linkage.在现实生活中,需要对复杂的对象依据一定的标准进行分类,通常情况下,人们根据事物现象的一个指标或者某一方面就可以进行分类活动,而实际上,需考虑的事物或对象不只包含单一指标,因此,很可能还需通过许多侧面或者指标来进行分类。
机器学习中的聚类分析技术

机器学习中的聚类分析技术机器学习是一种通过计算机程序从数据中提取规律和模式的技术。
聚类分析是机器学习的一个分支,通过将数据分成相似的群组来解决问题。
在本文中,我们将讨论机器学习中的聚类分析技术,以及它们在现实中的应用。
一、什么是聚类分析聚类分析是一种无监督学习方法,用于将一组数据按其相似度进行分组。
相似的数据被分配到同一组中,而不同的数据被分配到不同的组中。
在聚类分析中,没有给定任何类别标签或事先定义的目标,而是通过分析数据本身的特性,确定数据的分组方式。
例如,我们可以使用聚类分析来对人口数据进行分组,将人们根据其年龄,职业,收入和教育水平等因素进行分类。
这种分类方式有助于我们理解不同群体之间的差异和特征,并帮助我们更好地了解不同群体的需求和利益。
二、聚类分析的类型在聚类分析中,有几种不同的方法和算法可以使用。
以下是一些常用的聚类算法:1. KMeans算法:KMeans算法是一种基于距离度量的聚类算法,它通过计算数据之间的距离来确定数据之间的相似度。
该算法将数据分成K个组,在每个组中尽量使数据之间的距离最小。
KMeans算法在图像处理、文本挖掘和数据分析等领域得到了广泛应用。
2. 层次聚类算法:层次聚类算法通常用于小型数据集,将数据分成多个层次结构,并在每个层次上确定数据之间的相似程度。
这种算法可以帮助我们发现数据之间的关系,并提供更深入的分析。
3. 密度聚类算法:密度聚类算法是一种基于密度度量的聚类算法,它利用每个数据点周围的密度来确定数据之间的相似度。
这种算法可以在处理具有噪声数据和离群点的数据时表现出更好的表现力。
三、聚类分析的应用聚类分析在各种领域中都有广泛的应用,包括自然语言处理、医疗诊断、金融分析和市场营销等领域。
以下是几个应用聚类分析的实例:1. 自然语言处理:在自然语言处理中,聚类分析可以用于识别文档中的主题和关键字,并将文档分成相关主题的群组。
2. 医疗诊断:在医疗诊断中,聚类分析可以用于将症状和疾病进行分类和分组,以便更好地了解不同疾病之间的相似性和差异性。
系统聚类分析

0.26
0.04
0.00
0.15
0.00
0.00
二、距离的计算
常见的距离有 ① 绝对值距离
d ij xik x jk
② 欧氏距离
d ij ( xik x jk ) 2
k 1 n
n
(i, j 1,2,, m)
(3.4.5)
i 1
(i, j 1,2,, m)
(3.4.6)
计算原来各类与新类之间的距离,这样就得到 一个新的(m-1)阶的距离矩阵; 再从新的 距离矩阵中选出最小者dij,把Gi和Gj归并成新 类;再计算各类与新类的距离,这样一直下去, 直至各分类对象被归为一类为止。
例题:以下根据式(3.4.9)中的距离矩阵,
用最短距离聚类法对某地区的9个农业区进行 聚类分析。
1 m x j xij 0 m i 1 sj 1 m ( xij x ) 2 1 j m i 1
③ 极大值标准化,即
xij xij max{xij }
i
(i 1,2, , m; j 1,2, , n)
(3.4.3)
经过这种标准化所得的新数据,各要素的 极大值为1,其余各数值小于1。
假设有m 个聚类的对象,每一个聚类对象 都有n个要素构成。它们所对应的要素数据可 用表3.4.1给出。
表3.4.1 聚类对象与要素数据
要 聚 类 对 象 素
x1
x11 x21 xi1 xm1
x2 x j
x12 x22 xi 2 x1 j xij
xn
x1n xin xmn
d8,10=min{d84,d89}= min{1.29,1.40}=1.29
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k-means聚类”——数据分析、数据挖掘
一、概要
分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应。
但是很多时候上述条件得不到满足,尤其是在处理海量数据的时候,如果通过预处理使得数据满足分类算法的要求,则代价非常大,这时候可以考虑使用聚类算法。
聚类属于无监督学习,相比于分类,聚类不依赖预定义的类和类标号的训练实例。
本文介绍一种常见的聚类算法——k 均值和k 中心点聚类,最后会举一个实例:应用聚类方法试图解决一个在体育界大家颇具争议的问题——中国男足近几年在亚洲到底处于几流水平。
二、聚类问题
所谓聚类问题,就是给定一个元素集合D,其中每个元素具有n 个可观察属性,使用某种算法将D 划分成k 个子集,要求每个子集内部的元素之间相异度尽可能低,而不同子集的元素相异度尽可能高。
其中每个子集叫做一个簇。
与分类不同,分类是示例式学习,要求分类前明确各个类别,并断言每个元素映射到一个类别,而聚类是观察式学习,在聚类前可以不知道类别甚至不给定类别数量,是无监督学习的一种。
目前聚类广泛应用于统计学、生物学、数据库技术和市场营销等领域,相应的算法也非常的多。
本文仅介绍一种最简单的聚类算法——k 均值(k-means)算法。
三、概念介绍
区分两个概念:
hard clustering:一个文档要么属于类w,要么不属于类w,即文档对确定的类w是二值的1或0。
soft clustering:一个文档可以属于类w1,同时也可以属于w2,而且文档属于一个类的值不是0或1,可以是这样的小数。
K-Means就是一种hard clustering,所谓K-means里的K就是我们要事先指定分类的个数,即K个。
k-means算法的流程如下:
1)从N个文档随机选取K个文档作为初始质心
2)对剩余的每个文档测量其到每个质心的距离,并把它归到最近的质心的类
3)重新计算已经得到的各个类的质心
4)迭代2~3步直至满足既定的条件,算法结束
在K-means算法里所有的文档都必须向量化,n个文档的质心可以认为是这n 个向量的中心,计算方法如下:
这里加入一个方差RSS的概念:
RSSk的值是类k中每个文档到质心的距离,RSS是所有k个类的RSS值的和。
算法结束条件:
1)给定一个迭代次数,达到这个次数就停止,这好像不是一个好建议。
2)k个质心应该达到收敛,即第n次计算出的n个质心在第n+1次迭代时候位置不变。
3)n个文档达到收敛,即第n次计算出的n个文档分类和在第n+1次迭代时候文档分类结果相同。
4)RSS值小于一个阀值,实际中往往把这个条件结合条件1使用
回过头用RSS讨论质心的计算方法是否合理
为了取得RSS的极小值,RSS对质心求偏导数应该为0,所以得到质心
可见,这个质心的选择是合乎数学原理的。
K-means方法的缺点是聚类结果依赖于初始选择的几个质点位置,看下面这个例子:
如果使用2-means方法,初始选择d2和d5那么得到的聚类结果就是{d1,d2,d3}{d4,d5,d6},这不是一个合理的聚类结果
解决这种初始种子问题的方案:
1)去处一些游离在外层的文档后再选择
2)多选一些种子,取结果好的(RSS小)的K个类继续算法
3)用层次聚类的方法选择种子。
我认为这不是一个合适的方法,因为对初始N 个文档进行层次聚类代价非常高。
以上的讨论都是基于K是已知的,但是我们怎么能从随机的文档集合中选择这个k值呢
我们可以对k去1~N分别执行k-means,得到RSS关于K的函数下图:
当RSS由显著下降到不是那么显著下降的K值就可以作为最终的K,如图可以选择4或9。
四、算法及示例
k 均值算法的计算过程非常直观:
1、从D 中随机取k 个元素,作为k 个簇的各自的中心。
2、分别计算剩下的元素到k 个簇中心的相异度,将这些元素分别划归到相异度最低的簇。
3、根据聚类结果,重新计算k 个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。
4、将D 中全部元素按照新的中心重新聚类。
5、重复第4 步,直到聚类结果不再变化。
6、将结果输出。
由于算法比较直观,没有什么可以过多讲解的。
下面,我们来看看k-means 算法一个有趣的应用示例:中国男足近几年到底在亚洲处于几流水平
今年中国男足可算是杯具到家了,几乎到了过街老鼠人人喊打的地步。
对于目前中国男足在亚洲的地位,各方也是各执一词,有人说中国男足亚洲二流,有人说三流,还有人说根本不入流,更有人说其实不比日韩差多少,是亚洲一流。
既然争论不能解决问题,我们就让数据告诉我们结果吧。
下图是采集的亚洲15 只球队在2005 年-2010 年间大型杯赛的战绩(由于澳大利亚是后来加入亚足联的,所以这里没有收录)。
其中包括两次世界杯和一次亚洲杯。
我提前对数据做了如下预处理:对于世界杯,进入决赛圈则取其最终排名,没有进入决赛圈的,打入预选赛十强赛赋予40,预选赛小组未出线的赋予50。
对于亚洲杯,前四名取其排名,八强赋予5,十六强赋予9,预选赛没出现的赋予17。
这样做是为了使得所有数据变为标量,便于后续聚类。
下面先对数据进行[0,1]规格化,下面是规格化后的数据:
其中包括两次世界杯和一次亚洲杯。
我提前对数据做了如下预处理:对于世界杯,进入决赛圈则取其最终排名,没有进入决赛圈的,打入预选赛十强赛赋予40,预选赛小组未出线的赋予50。
对于亚洲杯,前四名取其排名,八强赋予5,十六强赋予9,预选赛没出现的赋予17。
这样做是为了使得所有数据变为标量,便于后续聚类。
下面先对数据进行[0,1]规格化,下面是规格化后的数据:
从做到右依次表示各支球队到当前中心点的欧氏距离,将每支球队分到最近的簇,可对各支球队做如下聚类:
中国C,日本A,韩国A,伊朗A,沙特A,伊拉克C,卡塔尔C,阿联酋C,乌兹别克斯坦B,泰国C,越南C,阿曼C,巴林B,朝鲜B,印尼C。
第一次聚类结果:
A:日本,韩国,伊朗,沙特;
B:乌兹别克斯坦,巴林,朝鲜;
C:中国,伊拉克,卡塔尔,阿联酋,泰国,越南,阿曼,印尼。
下面根据第一次聚类结果,调整各个簇的中心点。
A 簇的新中心点为: {+0++/4=,(0+++/4=,+++/4=} = {, , }
用同样的方法计算得到B 和C 簇的新中心点分别为{, , },{1, ,}。
用调整后的中心点再次进行聚类,得到:
第二次迭代后的结果为:
中国C,日本A,韩国A,伊朗A,沙特A,伊拉克C,卡塔尔C,阿联酋C,乌兹别克斯坦B,泰国C,越南C,阿曼C,巴林B,朝鲜B,印尼C。
结果无变化,说明结果已收敛,于是给出最终聚类结果:
亚洲一流:日本,韩国,伊朗,沙特
亚洲二流:乌兹别克斯坦,巴林,朝鲜
亚洲三流:中国,伊拉克,卡塔尔,阿联酋,泰国,越南,阿曼,印尼
看来数据告诉我们,说国足近几年处在亚洲三流水平真的是没有冤枉他们,至少从国际杯赛战绩是这样的。
其实上面的分析数据不仅告诉了我们聚类信息,还提供了一些其它有趣的信息,例如从中可以定量分析出各个球队之间的差距,例如,在亚洲一流队伍中,日本与沙特水平最接近,而伊朗则相距他们较远,这也和近几年伊朗没落的实际相符。
另外,乌兹别克斯坦和巴林虽然没有打进近两届世界杯,不过凭借预算赛和亚洲杯上的出色表现占据B 组一席之地,而朝鲜由于打入了2010 世界杯决赛圈而有幸进入B 组,可是同样奇迹般夺得2007年亚洲杯的伊拉克却被分在三流,看来亚洲杯冠军的分量还不如打进世界杯决赛圈重啊。
其它有趣的信息,有兴趣的朋友可以进一步挖掘。
