精密形位误差的测试与数据处理实验报告讲解
形位误差测量实验心得

形位误差测量实验心得
形位误差测量实验心得:在进行仪器的检查和维护时
形位误差测量实验心得:在进行仪器的检查和维护时,一定要按照规范来操作。
要注意这些内容不能省略,对于有问题或异常现象应该加以说明和记录。
而且为了防止出错,还需要写下“记”字。
当然有些是必须做到的事情,而有些则可以自己决定,根据自身情况来考虑。
如果仅仅只是一般的校准就可以避免很多麻烦,如此简单也好控制。
2.按照顺序工作首先应把设备摆放整齐,使其方便操作。
即便使用同样的软件、工具及标准,但由于各人的习惯不同,因此排列顺序也会存在着差别,所以无论如何都要养成良好的习惯,切勿混乱。
3.保持清洁要随时擦拭机械表面的灰尘,不让脏物堆积在设备上。
尤其是电子元器件等金属零件,否则极易导致故障产生。
4.定期进行校准虽然看起来简单,却是最重要的部分之一。
除了与设计值比较外,还要反复核对日常读数。
例如温度传感器输入端是0。
5V,输出端1。
0 V,那么经过一个月后,至少也应再检查一次它的输出值,确认没有任何变化才算合格。
- 1 -。
精密形位误差的测试与数据处理实验报告

精密形位误差的测试与数据处理实验报告实验目的:1.学习精密形位误差测试的方法和步骤;2.掌握精密形位误差数据的处理方法;3.了解精密形位误差对工件加工精度的影响。
实验仪器与材料:1.精密测量仪器(如三坐标测量仪);2.待测试零件。
实验步骤:1.准备待测试的零件,并对其进行表面清洁处理,以保证测量的准确性;2.将待测试零件放置在三坐标测量仪的工作台上,并进行初始定位;3.选择合适的测量方法,对待测试零件的形位误差进行测量,如平面度、圆度、直线度等;4.根据测量结果,将数据记录下来,并进行数据处理;5.根据实验要求,对数据进行统计分析,计算形位误差的平均值、标准差等统计指标;6.根据形位误差的统计指标,对待测试零件的加工质量进行评估。
数据处理:1.对测量数据进行去离群值处理,排除异常值对数据结果的干扰;2.计算形位误差的平均值,即所有测量结果的算术平均数,用于评估待测试零件的整体形位误差;3.计算形位误差的标准差,用于评估待测试零件的形位误差分布的离散程度;4.绘制形位误差的统计图表,如直方图、箱线图等,以直观展示数据分布情况;5.根据形位误差的统计指标,评估待测试零件的加工质量,并提出改善建议。
实验结果与分析:根据实验数据处理的结果,我们可以得出以下结论:1.待测试零件的形位误差平均值为X,标准差为Y,表明待测试零件的整体形位误差较小/较大;2.待测试零件的形位误差分布较为集中/分散,表明待测试零件的加工精度较高/较低;3.形位误差主要集中在一些特定特征上,如圆度误差较大、直线度误差较小等;4.待测试零件的形位误差对其功能和性能的影响较小/较大,需要在实际应用中进行进一步调整和改进。
结论:通过本次实验,我们学习并掌握了精密形位误差测试的方法和步骤,并对测量数据进行了详细的处理和分析。
实验结果表明,形位误差对工件加工精度有着重要的影响,对于要求高精度的工件加工,需要采取相应的措施来控制和改善形位误差。
精密模具误差分析报告

精密模具误差分析报告1. 概述本报告旨在对精密模具误差进行详尽的分析,以评估其质量和性能,并为模具制造过程的优化提供指导。
通过对模具构成要素的误差进行分析,可以揭示出模具制造过程中存在的问题和改进的空间。
2. 误差来源精密模具的误差来源多种多样,主要包括材料性质、制造工艺、加工设备和操作人员等方面。
其中,材料性质的误差包括材料的成分不均匀性、热胀冷缩等因素引起的尺寸变化。
制造工艺的误差则涉及到模具的设计、加工和装配过程中的不精确性。
加工设备的误差主要表现在加工精度和稳定性方面,而操作人员的误差通常与操作技术和经验有关。
3. 误差类型精密模具的误差类型主要包括尺寸误差、形状误差、位置误差和表面质量误差等。
尺寸误差是指模具中各个尺寸参数与设计要求之间的差异。
形状误差则涉及到模具的几何形状特征,如平面度、圆度、直线度等误差。
位置误差主要描述模具中不同要素之间的相对位置关系是否满足要求。
表面质量误差则是指模具的表面光洁度、粗糙度等方面的误差。
4. 误差评估方法为了对精密模具的误差进行全面的评估,可以采用多种评估方法。
常用的方法包括测量与检测、数值模拟和统计分析等。
测量与检测方法通过使用精密测量设备对模具尺寸和形状进行实际测量,以获取具体的数值。
数值模拟方法通过建立适当的数学模型,对模具在应力、热变形等方面的行为进行仿真计算,以预测模具的误差情况。
统计分析方法则通过对一组模具样品的测量结果进行统计处理,以评估模具误差的整体分布情况。
5. 误差控制措施为了减小精密模具的误差,可以采取一系列的控制措施。
首先,需要对材料进行充分的检测和筛选,以保证材料的质量和均匀性。
其次,在制造工艺方面,应严格控制每个制造环节的精度要求,并合理安排加工顺序和工艺参数。
此外,对于特定的误差类型,可以针对性地采取相应的控制措施,如增加装配精度、优化模具设计和加工工艺等。
6. 结论精密模具误差的分析是模具制造中至关重要的一环,它可以为改善模具的质量和性能提供重要的依据。
精密测量中的误差分析与处理

精密测量中的误差分析与处理在现代科学与工程领域中,精密测量是非常重要的一项技术。
通过测量,我们可以获取到各种物理量的准确数值,从而帮助我们更好地理解和控制自然界的规律。
然而,任何一项测量都无法完全避免误差的存在。
误差对精密测量结果的准确性和可靠性有着重要的影响。
因此,对误差的分析与处理是精密测量中不可或缺的一环。
一、误差的来源误差可以来自多个方面,其中最主要的包括环境条件、仪器设备、人为操作等。
在环境条件方面,如温度、湿度、气压等的变化会对测量设备产生影响,从而引入误差。
而仪器设备本身的制造工艺和精度也会对测量结果产生误差。
同时,人为因素如操作不当、读数不准确等也是误差产生的重要原因。
二、误差的分类根据误差的性质和产生原因,我们可以将误差分为系统误差和随机误差两类。
1. 系统误差系统误差是由于固有的原因引起的,它们在多次测量中表现出一致的偏差,不受环境条件和操作方式的影响。
系统误差的存在会导致测量结果偏离真值。
常见的系统误差包括仪器偏差、传感器非线性、装置移位等。
为了减小系统误差,我们可以通过校正仪器、调整环境条件或者采用更精密的仪器设备等手段进行处理。
2. 随机误差随机误差是由于各种未知因素引起的,它们在多次测量中呈现出不一致的分散分布。
随机误差是不可避免的,但可以通过多次重复测量来降低其影响。
常见的随机误差包括个体差异、测量读数的不确定度等。
为了处理随机误差,我们可以利用统计学方法进行数据处理,如计算平均值、标准差等。
三、误差的分析在测量过程中,我们需要对误差进行分析,以评估测量结果的准确性和可靠性。
误差分析可通过以下几方面进行:1. 系统误差的分析针对系统误差,我们需要对仪器设备的性能进行全面的评估。
可以通过校准、验收测试等方法来确定系统误差的大小和特性。
同时,还需关注系统误差的来源,以便通过改进设备和操作方式来减小其影响。
2. 随机误差的分析随机误差的分析需要借助统计学方法。
可以通过重复测量同一物理量,并对数据进行处理,计算出平均值和标准差等统计指标,以评估测量结果的稳定性和可靠性。
形位误差和表面粗糙度测量实验结果及分析

形位误差和表面粗糙度测量实验结果及分析
形位误差和表面粗糙度测量实验可以采用不同的实验方法和仪器,因此实验结果也会有所不同。
以下是一般实验结果和分析:
形位误差实验结果:
形位误差实验通常通过三坐标测量仪或者影像测量仪进行,常用的参数包括平面度、圆度、直线度、平行度、垂直度等。
实验结果一般以数字形式给出,例如:
平面度误差:0.005mm
圆度误差:0.003mm
直线度误差:0.008mm
平行度误差:0.007mm
垂直度误差:0.006mm
形位误差的实验结果可以直观反映出被测物体在各维度方面的精度和准确度,进一步为后续的工艺加工提供基础参数。
表面粗糙度实验结果:
表面粗糙度实验通常使用表面粗糙度测试仪器进行,常用的参数包括Ra、Rz、Rq等。
实验结果一般以数字形式给出,例如:
Ra值:0.25μm
Rz值:3.25μm
Rq值:1.68μm
表面粗糙度的实验结果可以直观反映出被测物体表面的平滑度和粗糙度,对于一些需要精确表面加工的产品或部件而言,这些参数的掌握是非常重要的。
分析:
形位误差和表面粗糙度都是反映被测物体精度和准确度的重要参数,通过实验结果的分析和对比,可以找出其中存在的问题和不足,通过进一步的调整和改进加工工艺,提高被测物体的精度和准确度,最终提高产品的质量。
精密形位误差的测试与数据处理实验报告(2015年最新)讲解
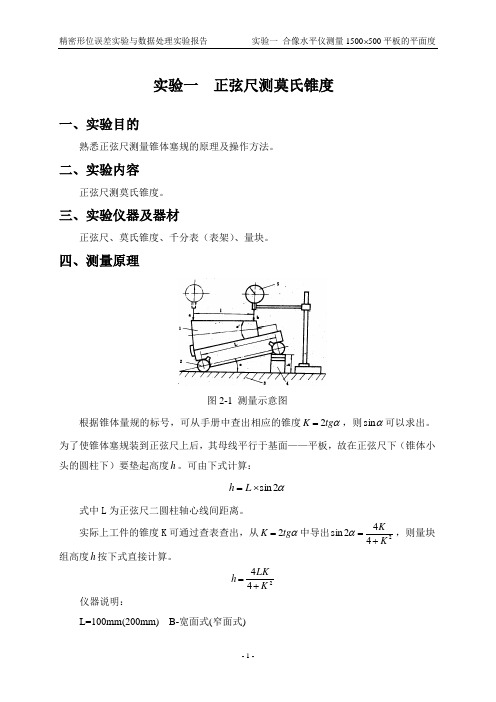
实验一 正弦尺测莫氏锥度一、实验目的熟悉正弦尺测量锥体塞规的原理及操作方法。
二、实验内容正弦尺测莫氏锥度。
三、实验仪器及器材正弦尺、莫氏锥度、千分表(表架)、量块。
四、测量原理图2-1 测量示意图根据锥体量规的标号,可从手册中查出相应的锥度αtg K 2=,则αsin 可以求出。
为了使锥体塞规装到正弦尺上后,其母线平行于基面——平板,故在正弦尺下(锥体小头的圆柱下)要垫起高度h 。
可由下式计算:α2sin ⨯=L h式中L 为正弦尺二圆柱轴心线间距离。
实际上工件的锥度K 可通过查表查出,从αtg K 2=中导出2442sin K K+=α,则量块组高度h 按下式直接计算。
244KLKh +=仪器说明:L=100mm(200mm) B-宽面式(窄面式)五、实验步骤1. 根据被测锥度塞规的公称锥角2α及正弦尺柱中心距L ,由 h=Lsin 2α计算量块组的尺寸,并组合好量块,在正弦尺下(锥体小头的圆柱下)要垫起高度h 。
本实验选用4号塞规,查表得2α=2°58’ 31’’=2.9753°,则h=Lsin 2α=100*sin2.9753°=5.19 mm ,选用4+1.19的量块组合。
2. 将圆锥塞规稳放在正弦尺的工作面上(应使圆锥塞规轴线垂直于正弦尺的圆柱轴线),选取a 、b 两测量点,这里a 、b 两点的固定距离用一个宽度l =10 mm 的量块保证。
3. 用带架千分表测出a 、b 两点高度差H ∆。
在被测圆锥塞规素线上距离l 的a 、b 两点进行测量和读数,将指示表在第一参考点处前后推移,记下最大读数。
测量的指示表的测头应先压缩1~2 mm 。
重复15次,取平均值。
4. 按lHK ∆=∆算出锥体误差,再根据查表所得K ∆来判断适用性。
六、实验记录在试验过成中记录的数据如表2-1所示。
表2-1 莫式锥度测量数据表序号1 2 3 4 5 6 7 8 9 10 a 点0.904 0.896 0.897 0.905 0.906 0.903 0.904 0.902 0.906 0.903 b 点 0.934 0.936 0.941 0.943 0.944 0.938 0.941 0.941 0.943 0.940 序号11 12 13 14 15 a 点0.904 0.903 0.899 0.901 0.900 b 点0.9380.9440.9360.9370.936七、数据处理及实验分析1.在a 点处千分表测得的15组数求平均值:0.00430.0040.0030.0050.00620.00330.0020.0010.0010.9000.9022()15mm ⨯+-+-++⨯+⨯++-++=()()()在b 点处千分表测得的十组数求平均值:0.0340.03630.04130.04320.04420.03820.0400.0370.9000.9395()15mm +⨯+⨯+⨯+⨯+⨯+++=2. a 、b 两点高差为:0.93950.90220.0373()mm -=。
位置误差的测量——实验报告

位置误差的测量——实验报告实验报告:位置误差的测量一、实验目的本实验旨在通过比较实际值与理论值之间的差异,测量位置误差,并分析误差产生的原因,以评估生产过程中的质量控制情况。
二、实验原理位置误差是指零件或产品的实际位置与理论位置之间的偏差。
在生产过程中,位置误差可能受到多种因素的影响,如机床精度、工件定位、操作人员技能等。
通过测量位置误差,可以了解生产过程中存在的问题,并采取相应的措施进行改进。
三、实验步骤1.准备实验器材:千分尺、量块、标准件、待测工件等。
2.将待测工件放置在量块上,保证工件与量块平行。
3.使用千分尺测量待测工件的实际位置,记录数据。
4.将实际值与理论值进行比较,计算位置误差。
5.分析误差产生的原因,提出改进措施。
6.重复以上步骤,对多个工件进行测量。
四、实验结果及分析实验数据如下表所示:根据实验数据,我们发现工件的实际位置与理论位置存在一定的偏差。
其中,工件1和工件3的位置误差为+10μm和+20μm,表现为正向误差;工件2和工件5的位置误差为-10μm和-20μm,表现为负向误差;工件4的位置误差为+30μm。
进一步分析发现,正向误差可能与机床精度、操作人员技能等因素有关;负向误差可能与工件定位、装夹等因素有关;而工件4的误差较大,可能受到多种因素的影响。
针对这些问题,可以采取相应的措施进行改进,如提高机床精度、加强操作人员技能培训、优化工件定位和装夹方式等。
五、结论本实验通过比较实际值与理论值之间的差异,测量了位置误差,并分析了误差产生的原因。
实验结果表明,在生产过程中存在一定的位置误差,这些误差可能受到多种因素的影响。
为了提高产品质量和生产效率,需要采取相应的措施进行改进,如提高机床精度、加强操作人员技能培训、优化工件定位和装夹方式等。
同时,对于大批量生产而言,可以考虑采用自动化检测设备来提高检测效率和精度。
位置误差的测量——实验报告

位置误差的测量实验报告一、实验目的1. 熟悉零件有关位置误差的含义和基准的体现方法。
2. 掌握有关通用量仪的使用方法。
二、实验用量具齿轮跳动检查仪、平板、千分表、百分表、千分表架、V型块、直角尺、钢板尺等三、实验内容及说明1、平行度误差的测。
连杆小孔轴线对大孔轴线的平行度1)连杆孔的平行度要求如图1-15所示2)测量方法如图1-16所示平行度误差为将零件转位使之处于图中0度位置,使两心轴中心与平板等高,然后在测出0度位置的平行度误差。
根据测量结果判断零件平行度误差是否合格2. 垂直度误差的测量十字头孔轴线对孔轴线以及对侧面B的垂直度要求,如图1-17所示。
1)轴线对轴线的垂直度误差的测量如图1-18所示。
将测量表架安装在基准孔心轴上部,在距离为L2两端用千分表测得读数分别为M1,M2,则该零件轴线对轴线的垂直度误差为:2) 轴线对侧面B的垂直度误差测量如图1-19所示。
被测孔轴线用心轴模拟,先将心轴穿入零件被测孔,以零件顶面为支撑面,放在三个千斤顶上。
再用一直角尺,使其一面放在平板上,另一面与基准面B靠拢,同时调节千斤顶使其与基准面贴合为止,这说明基准面B与平板垂直。
然后用千分表分别测出图中L2长度两端读数M1,M2,则垂直度误差为根据以上结果,判断两项垂直度要求是否合格3. 圆跳动误差的测量被测零件圆跳动公差要求如图1-23所示,其测量方法如图1-24所示1)径向圆跳动误差的测量:将工件旋转一周,记下千分表读数的最大差值。
共测三个截面,取其中最大跳动量作为该表面的径向圆跳动误差值,并判断该指标是否合格2)端面圆跳动误差的测量:分别在端面靠近最大直径处和较小直径处测量,每测一处,转动工件一转,读取指示表的最大最小读数差,取其较大者作为该端面的圆跳动误差值图1-15图1-16图1-17图1-18中国石油大学(华东)四、数据分析1. 单位(mm)实验内容L1L21L22L2M1M2F允许值是否合格孔轴线平行度0度位置36.262.059.0157.2 1.191 1.1950.000920.25合格孔轴线平行度90度位置36.279.578.5194.2 1.981 2.4650.09020.1合格孔轴线与端面垂直度93.860.060.0213.80.7100.5260.08070.06不合格孔轴线与孔轴线垂直度93.878.077.8249.60.8390.8890.01880.06合格图1-19图1-23图1-242. 单位(µm )3. 单位(µm )五、思考题1. 求垂直度、平行度误差时为什么要有L1/L2,L1、L2分别指什么?L2指被测心轴长度;L1指被测工件孔的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一用合像水平仪测量1500⨯500平板的平面度一、实验目的1. 了解合像水平仪的结构和工作原理。
2. 加深对平面度定义的理解。
3. 掌握用水平仪测量平板平面度方法及测量数据处理。
4.掌握平面度的判定标准及数据处理方法。
二、实验内容用合像水平仪测量平板平面度误差。
三、实验仪器及器材合像水平仪,标准平面平板、桥板。
四、测量原理1. 合像水平仪的使用原理1-底板;2-杠杆;3-支承;4-壳体;5-支承架;6-放大镜;7-棱镜;8-水准器;9-微分筒;10-测微螺杆;11-放大镜;12-刻线尺图1-1 合像水平仪合像水平仪是一种精密测角仪器,用自然水平面为测量基准。
合像水平仪的结构见图1-1,它的水准器8是一个密封的玻璃管,管内注入精镏乙醚,并留有一定量的空气,以形成气泡,管的内壁在长度方向具有一定的曲率半径。
气泡在管中停住时,气泡的位置必然垂直于重力方向。
就是说,当水平仪倾斜时,气泡本身并不倾斜,而始终保持水平位置。
利用这个原理,将水平仪放在桥板上使用,便能测出实际被测直线上相距一个桥板跨距的两点间高度差,如图1-2所示。
I-桥板;Ⅱ-水平仪;Ⅲ-实际被测直线;L-桥板跨距;0,1,2,…,n-测点序号图1-2用水平仪测量直线度误差时的示意图在水准器玻璃管管长的中部,从气泡的边缘开始向两端对称地按弧度值(mm/m)刻有若干条等距刻线。
水平仪的分度值i用[角]秒和mm/m表示。
合像水平仪的分度值为2",该角度相当于在1m长度上,对边高0.01mm的角度,这时分度值也用0.01mm/m 或0.01/1000表示。
测量时,合像水平仪水准器8中的气泡两端经棱镜7反射的两半像从放大镜6观察。
当桥板两端相对于自然水平面无高度差时,水准器8处于水平位置。
则气泡在水准器8的中央,位于棱镜7两边的对称位置上,因此从放大镜6看到的两半像相合(如图1—3(a)所示)。
如果桥板两端相对于自然水平面有高度差,则水平仪倾斜一个角度α,因此,气泡不在水准器8的中央,从放大镜6看到的两半像是错开的(如图1—3(b)所示),产生偏移量△。
(a)相合 (b)错开图1-3 气泡的两半像为了确定气泡偏移量A的数值,转动测微螺杆10使水准器8倾斜一个角度α,以使气泡返回到棱镜7两边的对称位置上。
从放大镜中观察到气泡的两半像恢复成图1-3(a)所示相合的两半像。
偏移量A先从放大镜11由刻线尺12读数,它反映测微螺杆10转动的整圈数;再从测微螺杆手轮9(微分筒)的分度盘读数(该盘每格为刻线尺一格的百分之一);它是螺杆10转动不足一圈的细分读数。
读数取值的正负由测微螺杆手轮9指明。
2. 平面度误差的评定方法平面度公差用以限制平面的形状误差。
其公差带是距离为公差值的两平行平面之间的区域。
并规定,理想形状的位置应符合最小条件,常见的平面度测量方法有用指示表测量、用光学平晶测量平面度、用水平仪测量平面度及用自准仪和反射镜测量平面度误差。
用各种不同的方法测得的平面度测值,应进行数据处理,然后按一定的评定准则处理结果。
平面度误差的评定方法有:1. 最小包容区域法,由两平行平面包容实际被测要素时,实现至少四点或三点接触。
且具有下列形式之一者,即为最小包容区域,其平面度误差值最小。
最小包容区域的判别方法有下列三种形式,分别如图1-4(a)、1-4(b)、1-4(c)所示图1-4 平面度误差的最小区域判别法2. 三角形法是以通过被测表面上相距最远且不在一条直线上的3个点建立一个基准平面,各测点对此平面的偏差中最大值与最小值的绝对值之和为平面度误差。
实测时,可以在被测表面上找到3个等高点,并且调到零。
在被测表面上按点测量,与三角形基准平面相距最远的最高和最低点间的距离为平面度误差值。
3.对角线法是通过被测表面的一条对角线作另一条对角线的平行平面,该平面即为基准平面。
偏离此平面的最大值和最小值的绝对值之和为平面度误差。
五、实验步骤1. 量出被测表面总长,确定相邻两点之间的距离(节距),按节距L调整桥板的两圆柱中心距。
2.将合象水平仪放于桥板上,然后将桥板依次放在各节距的位置。
每放一个节距后,要旋转微分筒合象,使放大镜中出现如下图b所示的情况,此时即可进行读数。
先在放大镜处读数,它是反映螺杆的旋转圈数;微分筒(标有+、-旋转方向)的读数则是螺杆10旋转一圈(100格)的细分读数;如此顺测(从首点至终点)、回测(由终点至首点)各一次。
回测时桥板不能调头。
各测点两次读数的平均值作为该点的测量数据。
必须注意,如某测点两次读数相差较大,说明测量情况不正常,应检查原因并加以消除后重测,测量位置示意图如图1-5所示。
图1-5 测量位置示意图六、实验记录在实验过程中数据记录如表1-1所示。
其中测量桥距为:L=25.00cm表1-1 平面度测量数据表桥段1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 数值-0.855 -0.825 1.025 1.025 1.025 0.980 0.905 0.890 0.235 桥段10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 数值0.240 -1.295 -1.245 -1.255 -1.200 -1.210 -1.180 0.755 0.690 桥段19-20 20-21 21-22 22-23 23-24 24-25 25-26 26-27 27-28 数值0.710 0.640 0.640 0.640 0.275 0.265 -1.140 -1.210 -1.130 桥段28-29 29-30 30-31 31-32 32-1数值-1.055 -1.070 -1.050 0.665 0.750由桥距:250mm,分度值:0.01/1000mm计算得相对高差H=0.01/1000mm*250*数值,则各测量点间相对高差如表1-2所示。
表1-2 处理后的数据记录表桥段1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 H -0.00214 -0.00206 0.002563 0.002563 0.002563 0.00245 0.002263 0.002225 0.000588 桥段10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 H 0.0006 -0.00324 -0.00311 -0.00314 -0.003 -0.00303 -0.00295 0.001888 0.001725 桥段19-20 20-21 21-22 22-23 23-24 24-25 25-26 26-27 27-28 H 0.001775 0.0016 0.0016 0.0016 0.000688 0.000663 -0.00285 -0.00303 -1.130 桥段28-29 29-30 30-31 31-32 32-1H -0.00264 -0.00268 -0.00263 0.001663 0.001875七、数据处理及分析本次试验采用最小包容区域法来计算测量平板的平面度,根据表1-2中的数据进行处理,通过matlab编程实现数据的处理计算,程序的流程图如下所示。
按照测量顺序图,各个点坐标为:y = [0 250 500 750 1000 1250 1500 1500 1500 1250 1000 750 500 250 0 0 1262.83 1025.66 788.49551.32 314.146 76.975 1262.83 1025.66 788.49 314.146 76.975 76.975]';z = [0 -0.00214 -0.00420 -0.001637 0.000926 0.003408 0.005938 0.0082 0.010425 0.011013 0.0116130.008375 0.005263 0.002125 -0.0088 -0.0039 0.005938 0.002988 0.004876 0.006601 0.008376 0.0099760.012025 0.012713 0.013375 0.0075 0.004675 0.001875]';x = [0 0 0 0 0 0 0 250 500 500 500 500 500 500 500 250 79.57 158.11 237.17 316.23 395.285 500 500395.285 316.23 158.11 79.59 250]'; 单位mm其中长为y,宽为x,起伏为z用matlab处理数据,代码如下:y = [0 250 500 750 1000 1250 1500 1500 1500 1250 1000 750 500 250 0 0 1262.83 1025.66 788.49551.32 314.146 76.975 1262.83 1025.66 788.49 314.146 76.975 76.975]';z = [0 -0.00214 -0.00420 -0.001637 0.000926 0.003408 0.005938 0.0082 0.010425 0.011013 0.0116130.008375 0.005263 0.002125 -0.0088 -0.0039 0.005938 0.002988 0.004876 0.006601 0.008376 0.0099760.012025 0.012713 0.013375 0.0075 0.004675 0.001875]';x = [0 0 0 0 0 0 0 250 500 500 500 500 500 500 500 250 79.57 158.11 237.17 316.23 395.285 500 500395.285 316.23 158.11 79.59 250]';scatter3(x,y,z,'filled')hold onX = [ones(28,1) x y];b = regress(z,X)xfit = min(x):1:max(x);yfit = min(y):10:max(y);[XFIT,YFIT]= meshgrid (xfit,yfit);ZFIT = b(1) + b(2) * XFIT + b(3) * YFIT;mesh (XFIT,YFIT,ZFIT)结果:b =-0.00251020.000000030.00000004则平面方程为:0.00000003x+0.0000004y+z=-0.0025102然后计算点到平面的距离:For i=1:1:28D=(b(2)*x(i)+b(3)*y(i)+1*z(i)+b(1))/sqrt(b(2)^2+b(3)^2+1^2)End得出结果如下-0.0025 -0.0032 -0.0039 0.00018 0.0041 0.008 0.012 0.0175 0.023 0.022 0.0213 0.0167 0.0121 0.0076 -0.0034 0.0117 0.0084 0.0100 0.0114 0.0128 0.0144 0.0233 0.0212 0.0195 0.0088 0.0036 0.003可以得出Dmax=0.023 mm,Dmin=-0.034 mm因此平面度:Dmax-Dmin=0.057 mm=57 um实验二 正弦尺测莫氏锥度一、实验目的熟悉正弦尺测量锥体塞规的原理及操作方法。
