最新A卷答案

合集下载

A卷人际沟通与交流参考答案

A卷人际沟通与交流参考答案某某学院2021-2021学年第一学期期终考试（2021.11）2021级会展专业人际沟通与交流试卷a卷参考答案一、单选题（8小题，每题2分后，共16分后)1、“一句话可以说得叫人笑，一句话也可以说得叫人跳。

”说得叫人笑的人具有（b）。

a、幽默感b、会沟通c、亲和力d、圆滑世俗2、与上级沟通的重要性表现在（c）。

a、做错事情时能获得上司原谅b使上司看见你的不懈努力c、较好的沟通交流有利于工作进展d可以获得上司的尊重3、语言沟通交流中的抒发技巧存有：（b）a、从容b、果断c、急躁d、谈判4、以下选项中，不属于沟通的6c原则的一项是（b）。

a、清晰b、简单c、准确d、礼貌5、下列选项不属于沟通的步骤的是（d）。

a、信息策划b、信息传输c、信息反馈d、信息技术6、以下婉拒上级的作法中，恰当的一项就是（c）。

a、为上级出谋划策b、直接告诉上级说“我不去”、“我干不了”c、以直截了当的方式抒发自己的立场d、为了整体表现自己或害怕触怒上级而一味地遵从7、较好的沟通交流能力，并不是天生具有的，而是通过（c）赢得的。

a、上级培育b、领导剥夺c、自学d、后天移殖8、以下有关同事之间相处的方法中，不正确的一项是（c）。

a、与同事一点一滴的日常相处中为自己累积最大限度的“人缘”，同时也可以给对方存有相当大的回旋余地。

b、给别人留面子，其实也就是给自己赚面子。

c、常喜欢摆架子、我行我素、挑剔、恫吓、在众人面前指责同事或下属d、应努力营造愉快融洽的气氛，学会与同事和平相处、友好合作。

二、多选题（6小题，每题3分后，共18分后)1、开发跨文化沟通的技能应该做到（abcd）。

a、主动沟通交流b、学会宽容c、特别注意细节d、轮转思索2、语言的谋略存有：（abc）。

a、幽默的语言表达b、巧妙的攀谈c、恰当地问话与结束谈话d、把握语速3、与同事沟通的技巧（abcd）。

a、经常赞美你的同事b、特别注意同事的语言习惯，防止误会c、不要展现自己的优越感d、防止敏感话题4、有效率的跨文化沟通交流，必须秉持以下几条原则（abc）a、尊重原则b、平等原则c、属地原则d、技术原则5、与上下级沟通的禁忌有（abd）。

2024年陕西省中考英语真题(A卷)(含答案)

试卷类型：A2024年陕西省初中学业水平考试英语试卷注意事项：1.本试卷分为第一部分(听力)和第二部分(笔试)。

全卷共10页，总分120分。

考试时间120分钟。

2.领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号，同时用2B铅笔在答题卡上填涂对应的试卷类型信息点(A或B)。

3.请在答题卡上各题的指定区域内作答，否则作答无效。

4.考试结束，本试卷和答题卡一并交回。

第一部分（听力共30分）Ⅰ.听选答案（共15小题，计20分）第一节：听下面10段对话，每段对话后有一个问题，读两遍。

请根据每段对话的内容和后面的问题，从所给的三个选项中选出问题的正确答案。

（共10小题，计10分）1.A.Saying hello. B.Saying sorry. C.Saying thanks.2.A.A hat. B.A book. C.A toy.3.A.On the sofa. B.Under the sofa. C.Behind the sofa.4.A.A scientist. B.A writer. C.A teacher.5.A.Go to the party. B.Go to the club. C.Go to the museum.6.A.Excited. B.Tired. C.Surprised.7.A.Black. B.White. C.Yellow.8.A.Jason. B.Bob. C.Eric.9.A.For four years. B.For three years. C.For seven years.10.A.He agrees with the girl.B.He doesn’t agree with the girl.C.He cares little about the girl’s opinion.第二节：听下面两段材料，包括一篇独白和一段对话，每段材料后有几道小题。

2023-2024学年北京市丰台区高一上学期期中联考地理试卷A卷含答案

丰台区2023-2024学年度第一学期期中练习高一地理（A卷）考试时间：90分钟第I卷（选择题共60分）本部分共30小题，每小题2分，共60分。

在每小题给出的四个选项中，选出最符合题意的一项。

凌日和冲日是两种天文现象。

太阳系中的行星在绕日运行过程中有时会处在太阳与地球之间，这时，地球上的观测者可看到一个小黑圆点在日面缓慢移动，这就是凌日现象。

所谓的冲日，通常是指在地球上观察的行星和太阳的位置相差180度，即该行星和太阳分别在地球的两侧，行星、地球、太阳排成一条直线。

读图1，回答第1、2题。

某行星凌日图某行星冲日图图11．地球两侧相邻的是A．木星与土星 B．金星与火星 C．金星与木星 D．火星与土星2．下列说法正确的是A．位于地球公转轨道外侧的行星，可发生凌日现象B．位于地球公转轨道内侧的行星，可发生冲日现象C．位于地球公转轨道内侧的行星，可发生凌日现象D．在地球上既可看到火星凌日，也可看到火星冲日图2为一段时间内太阳黑子数与我国江淮地区梅雨强度的相关系数分布图。

读图，回答第3、4题。

图23．太阳黑子数与梅雨强度A．在湖北省的东南部呈正相关B．在安徽省的大部分地区呈负相关C．在图中西北部的相关性最小D．正相关最大值出现在图中东北部4．太阳黑子数达最大值时A．通信卫星信号易受干扰B．江淮地区梅雨强度增大C．漠河地区出现极昼现象D．耀斑爆发强度减弱地球上生命出现后，生物多样性随着地理环境的改变会出现变化。

图3示意古生代至新生代生物多样性和地表温度的变化。

读图，回答第5～7题。

图35．地表温度从石炭纪到白垩纪A．持续下降B．波动下降C．持续上升D．波动上升6．图中A．展示了从元古宙到新生代生物多样性越来越丰富B．二叠纪比三叠纪生物多样性丰富C．寒武纪植物以被子植物为主并且是哺乳类动物繁盛时期D．推动生物演化的主要动力来自于地球内部的炽热岩浆7．乙时期物种大灭绝最有可能A．与地表升温有关B．与地磁变化有关C．与植物中毒有关D．与陨石撞击有关图4为地球内部地震波传播速度与圈层结构示意（①～④表示地球内部圈层）。

2023年公务员省考之行测综合检测试卷A卷含答案

2023年公务员省考之行测综合检测试卷A卷含答案单选题（共50题）1、填入划横线部分最恰当的一项是春晚相声《新虎口遐想》的出现，其最现实的意义就在于它实现了相声本质的回归，讽刺的分寸感好，对社会不良现象反思有力。

只是________春晚时间的限制，结尾比较仓促，实在是美中不足的遗憾。

但是________，它回归了本质，找回了初心。

A.由于大醇小疵B.囿于瑕不掩瑜C.困于毋庸置疑D.缘于不言而喻【答案】 B2、一批零件如果全部都交由甲厂加工，正好在计划时间完成，如果全部交由乙厂加工，要超过计划时间5天才能完成，如果甲乙两厂合作加工3天，再由乙厂单独加工，正好也是在计划时间完成，则加工完这批零件计划时间是（）A.5B.7C.7.5D.8.5【答案】 C3、元宵节∶端午节∶中秋节A.玫瑰∶百合∶康乃馨B.元朝∶明朝∶清朝C.奥巴马∶林肯∶布什D.大象∶长颈鹿∶梅花鹿【答案】 B4、现有26棵树苗，要分值于5块绿地上，若使每块绿地上的树苗数都不相同，则分得树苗最多的绿地至少可以分得几株树苗。

A.8B.7C.6D.5【答案】 A5、党的十八大以来，习近平主席在国际国内多个重要场合提出构建人类命运共同体，并对其丰富内涵和实践路径作了深入阐述。

人类命运共同体理念明确回答了世界向何处去、崛起的中国向何处去、新形势下中国怎样办外交等重大命题，是当代中国外交理论的重大创新成果之一，也是马克思主义中国化的最新成果之一。

人类命运共同体理念超越了西方主流国际关系理论，蕴含着重大理论意义和实践价值，必将有力促进人类和平与发展的崇高事业。

任何重大理论创新都不是无源之水、无本之木，往往都是在继承前人思想精髓的基础上，结合新的现实条件和具体实践发展起来的。

人类命运共同体理念是在继承马克思主义与中华传统文化思想精髓的基础上所形成的理论创新成果。

A.“无产阶级联合体”B.“自由人联合体”C.“无产阶级共同体”D.“世界公民联合体”【答案】 B6、下列情形中不属于行政处罚的是（）。

运动控制系统试卷A答案（最新整理）

运动控制系统试卷A答案（最新整理）《运动控制系统》课程试卷（A 卷）答案第1篇直流调速系统（60分）⼀、填空题（每空1分，共23分）1. 运动控制系统由电动机、功率放⼤与变换装置、控制器及相应的传感器等构成。

2. 转矩控制是运动控制的根本问题，磁链控制与转矩控制同样重要。

3. ⽣产机械常见的三种负载是恒转矩负载、恒功率负载和平⽅率负载。

4. 某直流调速系统电动机额定转速，额定速降，1430/min N n r =115/min N n r ?=当要求静差率时，允许的调速范围为5.3，若当要求静差率时，30%s ≤20%s ≤则调速范围为3.1，如果希望调速范围达到10，所能满⾜的静差率是44.6%。

5. 数字测速中，T 法测速适⽤于低速，M 法测速适⽤于⾼速。

6. ⽣产机械对调速系统转速控制的要求有调速、稳速和加减速三个⽅⾯。

7、直流电机调速的三种⽅法是：调压调速、串电阻调速和弱磁调速。

8、双闭环直流调速系统的起动过程分为电流上升阶段、恒流升速阶段和转速调节三个阶段。

9. 单闭环⽐例控制直流调速系统能够减少稳态速降的实质在于它的⾃动调节作⽤，在于它能随着负载的变化⽽相应的改变电枢电压，以补偿电枢回路电阻压降的变化。

⼆、选择题（每题1分，共5分）1、双闭环直流调速系统，ASR 、ACR 均采⽤PI 调节器，其中ACR 所起的作⽤为（D ）。

A 、实现转速⽆静差B 、对负载变化起抗扰作⽤C 、输出限幅值决定电动机允许的最⼤电流D 、对电⽹电压波动起及时抗扰作⽤2、典型I 型系统与典型II 型系统相⽐，（ C ）。

A 、前者跟随性能和抗扰性能均优于后者B 、前者跟随性能和抗扰性能不如后者C 、前者跟随性能好，抗扰性能差D 、前者跟随性能差，抗扰性能好3、转速单闭环调速系统对下列哪些扰动⽆克服能⼒，（ D ）。

A 、电枢电阻B 、负载转矩C 、电⽹电压D 、速度反馈电位器4、下述调节器能消除被控制量稳态误差的为（ C ）。

2024年重庆市中考英语真题(A卷)及答案

重庆市2024年初中学业水平暨高中招生考试英语试题 (A卷）（全卷共九个大题满分：150分考试时间：120分钟）注意事项：1.试题的答案书写在答题卡上，不得在试题卷上直接作答。

2.作答前认真阅读答题卡上的注意事项。

3.考试结束，由监考人员将试题卷和答题卡一并收回。

第Ⅰ卷（共95分）Ⅰ. 听力测试。

（共30分）第一节（每小题1.5分，共9分）听一遍。

根据你所听到的句子，从A、B、C三个选项中选出最恰当的答语，并把答题卡上对应题目的答案标号涂黑。

1. 【此处可播放相关音频，请去附件查看】A. Nice to meet you, too.B. Good afternoon.C. I’m fine.2. 【此处可播放相关音频，请去附件查看】A. Thank you.B. This is Jane.C. What a pity.3. 【此处可播放相关音频，请去附件查看】A. That’s all right.B. Yes, please.C. Never mind.4. 【此处可播放相关音频，请去附件查看】A. It’s red.B. It’s long.C. It’s 20 yuan.5. 【此处可播放相关音频，请去附件查看】A. It doesn’t matter.B. Good idea.C. Not at all.6. 【此处可播放相关音频，请去附件查看】A. Well done.B. Have fun.C. Sure, I will.第二节（每小题1.5分，共9分）听一遍。

根据你所听到的对话和问题，从A、B、C三个选项中选出正确答案，并把答题卡上对应题目的答案标号涂黑。

7. 【此处可播放相关音频，请去附件查看】A. /dres/.B. /desk/.C. /dæns/.8. 【此处可播放相关音频，请去附件查看】A. Cards.B. Flowers.C. Cakes.9. 【此处可播放相关音频，请去附件查看】A. To the zoo.B. To the cinema.C. To the farm.10. 【此处可播放相关音频，请去附件查看】A. Jenny’s father.B. Jenny’s mother.C. Jenny’s sister.11. 【此处可播放相关音频，请去附件查看】A. Because it’s relaxing.B. Because it’s interesting.C. Because it’s exciting.12. 【此处可播放相关音频，请去附件查看】A. B. C.第三节（每小题1.5分，共6分）听两遍。

2023年AMC10美国数学竞赛A卷附中文翻译和答案

2023AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) (B)(C)(D) (E)4. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) (C) (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A∪B, the union of A and B?(A) 5 (B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) (B) (C)(D) (E)8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7 (B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A) (B)(C)(D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13 (B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) (B)(C)(D) (E)15. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A) (B) (C) (D) (E)17. In the eight-term sequence A, B, C, D, E, F, G, H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17 (B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B?(B) (C) (D) (E)(A)19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2023, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) (B) (C) (D) (E)21. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) (B) (C) (D) (E)22. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A) (B) (C) (D) (E)an integer. A point X in the interior of R is25. Let R be a square region andcalled n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500 (B) 1560 (C) 2320 (D) 2480 (E) 25002023AMC10美国数学竞赛A卷1. 某通讯公司手机每月基本费为20美元, 每传送一则简讯收 5美分（一美元=100 美分）。

2023年公务员省考之行测题库练习试卷A卷附答案

2023年公务员省考之行测题库练习试卷A卷附答案单选题（共30题）1、节能∶减排∶环保A.火药∶造纸∶四大发明B.起床∶步行∶上班C.生产∶销售∶管理D.锻炼∶营养∶健康【答案】 D2、创新源泉的另一个重要方向，就是面向历史的发掘，每一次回顾历史都可能是一次观念的清理和创新，研究和发掘新的史料，也是一次价值观的梳理，____，重新发现历史，建立当下社会观念与历史价值的承继关系，这是奠定创新思维的一个重要因素，我们要在前人的肩膀上瞭望未来，不是简单地忽略或者漠视历史积累，不断重复曾经的创新过程。

A.历史无法重来B.与其重读历史，不如创造历史C.一切历史都是当代史D.历史是胜利者的历史【答案】 C3、有我之境：指审美过程中包含客体性的自然景物，蕴藏审美者的主管感受。

即作为观察对象的客观事物染上观察A.明月松间照，清泉石上流B.星垂平野阔，月涌大江流C.片云天共远，永夜月同孤D.明月出天山，苍茫云海间【答案】 C4、"今日到南苑，明日到北海，何日再到古长安？叹黎民膏血全枯，只为一人歌庆有；五十割琉球，六十割台湾，而今又割东三省，痛赤县邦圻益蹙，每逢万寿祝疆无。

”以上对联讽刺的是（）。

A.慈禧B.李鸿章C.袁世凯D.蒋介石【答案】 A5、小华、小玲、小芳、小丽同住一个宿舍。

按规定，晚上最迟回宿舍的同学，应该关掉室外的路灯。

有一天晚上，室外的路灯没有关掉，第二天，宿舍管理员过来查询哪一个同学最迟返回宿舍。

小玲说：“我回来的时候。

小丽已经睡了，我也就睡下了。

”小华说：“我回来的时候，小芳还没有睡。

”小芳说：“我进门的时候，小玲还没有睡。

”小丽说：“我上床就睡着了，什么都不知道。

”这四位同学说的都是事实，请判断以下哪项为真？( )A.小华最迟返回宿舍B.小玲最迟返回宿舍C.小芳最迟返回宿舍D.小丽最迟返回宿舍【答案】 A6、根据以下资料，回答问题题。

A.0.20B.0.21C.0.22【答案】 C7、有专家指出，判断名优白酒的真伪有简单的办法：价格低得离谱的名优白酒肯定都是假的，凡是打着某一名优白酒旗号在外公开销售的定制酒都是假的。

2024年重庆市中考真题(A卷)数学试题(含答案)

重庆市2024年初中学业水平暨高中招生考试数学试题（A卷）（全卷共三个大题，满分150分，考试时间120分钟）注意事项：1.试题的答案书写在答题卡上，不得在试题卷上直接作答；2.作答前认真阅读答题卡上的注意事项；3.作图（包括作辅助线）请一律用黑色2B铅笔完成；4.考试结束，由监考人员将试题卷和答题卡一并收回．参考公式：抛物线()20y ax bx c a=++≠的顶点坐标为24,24b ac ba a⎛⎫-- ⎪⎝⎭，对称轴为2bxa=-．一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧确答案所对应的方框涂黑．1.下列四个数中，最小的数是（）A.2-B.0C.3D.1 2-【答案】A【解析】【分析】本题考查了有理数比较大小，解题的关键是掌握比较大小的法则．根据正数大于0，0大于负数，两个负数比较大小，绝对值大的反而小，即可得到答案．【详解】解：∵13022>>->-，∴最小的数是2-；故选：A．2.下列四种化学仪器的示意图中，是轴对称图形的是（）A.B.C. D.【答案】C【解析】【分析】此题考查了轴对称图形的概念，根据概念逐一判断即可，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线(成轴）对称，熟练掌握知识点是解题的关键．【详解】A 、不是轴对称图形，故本选项不符合题意；B 、不是轴对称图形，故本选项不符合题意；C 、是轴对称图形，故本选项符合题意；D 、不是轴对称图形，故本选项不符合题意；故选：C ．3.已知点()3,2-在反比例函数()0k y k x =≠的图象上，则k 的值为（）A.3- B.3 C.6- D.6【答案】C【解析】【分析】本题考查了待定系数法求反比例解析式，把()3,2-代入()0k y k x=≠求解即可．【详解】解：把()3,2-代入()0k y k x =≠，得326k =-⨯=-．故选C ．4.如图，AB CD ∥，165∠=︒，则2∠的度数是（）A.105︒B.115︒C.125︒D.135︒【答案】B【解析】∠=∠=︒，由邻补角性质得【分析】本题主要考查了平行线的性质，根据平行线的性质得3165∠+∠=︒，然后求解即可，熟练掌握两直线平行，同位角相等是解题的关键．23180【详解】解：如图，∥，∵AB CD∠=∠=︒，∴3165∠+∠=︒，∵23180∠=︒，∴2115故选：B．5.若两个相似三角形的相似比是1:3，则这两个相似三角形的面积比是（）A.1:3B.1:4C.1:6D.1:9【答案】D【解析】【分析】此题考查了相似三角形的性质，根据“相似三角形的面积比等于相似比的平方”解答即可．【详解】解：两个相似三角形的相似比是1:3，则这两个相似三角形的面积比是1:9，故选：D．6.烷烃是一类由碳、氢元素组成的有机化合物质，下图是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子．第1种如图①有4个氢原子，第2种如图②有6个氢原子，第3种如图③有8个氢原子，……按照这一规律，第10种化合物的分子结构模型中氢原子的个数是（）A.20B.22C.24D.26【答案】B【解析】【分析】本题考查数字的变化类，根据图形，可归纳出规律表达式的特点，再解答即可．【详解】解：由图可得，第1种如图①有4个氢原子，即2214+⨯=第2种如图②有6个氢原子，即2226+⨯=第3种如图③有8个氢原子，即2238+⨯=⋯，∴第10种化合物的分子结构模型中氢原子的个数是：221022+⨯=；故选：B ．7.已知m =，则实数m 的范围是（）A.23m << B.34m << C.45m << D.56m <<【答案】B【解析】【分析】此题考查的是求无理数的取值范围，二次根式的加减运算，掌握求算术平方根的取值范围的方法是解决此题的关键．先求出m ==，即可求出m 的范围．【详解】解：∵m ====，∵34<<，∴34m <<，故选：B ．8.如图，在矩形ABCD 中，分别以点A 和C 为圆心，AD 长为半径画弧，两弧有且仅有一个公共点．若4=AD ，则图中阴影部分的面积为（）A.328π- B.4πC.324π- D.8π【答案】D【解析】【分析】本题考查扇形面积的计算，勾股定理等知识．根据题意可得28AC AD ==，由勾股定理得出AB =2个扇形的面积即可得到结论．【详解】解：连接AC ，根据题意可得28AC AD ==，∵矩形ABCD ，∴4AD BC ==，90ABC ∠=︒，在Rt ABC △中，AB ==，∴图中阴影部分的面积2904428360ππ⨯=⨯⨯=．故选：D ．9.如图，在正方形ABCD 的边CD 上有一点E ，连接AE ，把AE 绕点E 逆时针旋转90︒，得到FE ，连接CF 并延长与AB 的延长线交于点G ．则FG CE 的值为（）A. B.C.2 D.2【答案】A【解析】【分析】过点F 作DC 延长线的垂线，垂足为点H ，则90H ∠=︒，证明ADE EHF ≌，则1AD EH ==，设DE HF x ==，得到HF CH x ==，则45HCF ∠=︒，故CF =，同理可求CG ==则)1FG CG CF x =-=-，因此)11x FG CE x -==-．【详解】解：过点F 作DC 延长线的垂线，垂足为点H ，则90H ∠=︒，由旋转得,90EA EF AEF =∠=︒，∵四边形ABCD 是正方形，∴90D Ð=°，DC AB ∥，DA DC BC ==，设1DA DC BC ===，∴D H ∠=∠，∵12AEH AEF D ∠=∠+∠=∠+∠，∴12∠=∠，∴ADE EHF ≌，∴DE HF =，1AD EH ==，设DE HF x ==，则1CE DC DE x =-=-，∴()11CH EH EC x x =-=--=，∴HF CH x ==，而90H ∠=︒，∴45HCF ∠=︒，∴2sin 45HF CF ==︒，∵DC AB ∥，∴45HCF G ∠=∠=︒，同理可求22CG BC ==∴)2221FG CG CF x x =-==-，∴)2121x FG CE x-==-，故选：A ．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，解直角三角形，旋转的性质，正确添加辅助线，构造“一线三等角全等”是解题的关键．10.已知整式1110:n n n n M a x a x a x a --++++ ，其中10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ．下列说法：①满足条件的整式M 中有5个单项式；②不存在任何一个n ，使得满足条件的整式M 有且只有3个；③满足条件的整式M 共有16个．其中正确的个数是（）A.0B.1C.2D.3【答案】D【解析】【分析】本题考查的是整式的规律探究，分类讨论思想的应用，由条件可得04n ≤≤，再分类讨论得到答案即可．【详解】解：∵10,,,n n a a - 为自然数，n a 为正整数，且1105n n n a a a a -+++++= ，∴04n ≤≤，当4n =时，则2104345a a a a a +++++=，∴41a =，23100a a a a ====，满足条件的整式有4x ，当3n =时，则210335a a a a ++++=，∴()()3210,,,2,0,0,0a a a a =，()1,1,0,0，()1,0,1,0，()1,0,0,1，满足条件的整式有：32x ，32x x +，3x x +，31x +，当2n =时，则21025a a a +++=，∴()()210,,3,0,0a a a =，()2,1,0，()2,0,1，()1,2,0，()1,0,2，()1,1,1，满足条件的整式有：23x ，22x x +，221x +，22x x +，22x +，21x x ++；当1n =时，则1015a a ++=，∴()()10,4,0a a =，()3,1，()1,3，()2,2，满足条件的整式有：4x ，31x +，3x +，22x +；当0n =时，005a +=，满足条件的整式有：5；∴满足条件的单项式有：4x ，32x ，23x ，4x ，5，故①符合题意；不存在任何一个n ，使得满足条件的整式M 有且只有3个；故②符合题意；满足条件的整式M 共有1464116++++=个．故③符合题意；故选D二、填空题：（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上．11.计算：011(3)(2π--+＝_____．【答案】3【解析】【分析】根据零指数幂和负指数幂的意义计算．【详解】解：011(3)()1232π--+=+=，故答案为：3．【点睛】本题考查了整数指数幂的运算，熟练掌握零指数幂和负指数幂的意义是解题关键．12.如果一个多边形的每一个外角都是40︒，那么这个多边形的边数为______．【答案】9【解析】【分析】本题考查了多边形的外角和定理，用外角和360︒除以40︒即可求解，掌握多边形的外角和等于360︒是解题的关键．【详解】解：360409︒÷︒=，∴这个多边形的边数是9，故答案为：9．13.重庆是一座魔幻都市，有着丰富的旅游资源．甲、乙两人相约来到重庆旅游，两人分别从A 、B 、C 三个景点中随机选择一个景点游览，甲、乙两人同时选择景点B 的概率为_____．【答案】19【解析】【分析】本题考查了画树状图法或列表法求概率，根据画树状图法求概率即可，熟练掌握画树状图法或列表法求概率是解题的关键．【详解】解：画树状图如下：由图可知，共有9种等可能的情况，其中甲、乙两人同时选择景点B 的情况有1种，∴甲、乙两人同时选择景点B 的的概率为19，故答案为：19．14.随着经济复苏，某公司近两年的总收入逐年递增．该公司2021年缴税40万元，2023年缴税48.4万元，该公司这两年缴税的年平均增长率是______．【答案】10%【解析】【分析】本题主要考查一元二次方程的应用．设平均增长率为x ，然后根据题意可列方程进行求解．【详解】解：设平均增长率为x ，由题意得：()240148.4x +=，解得：10.110%x ==，2 2.1x =-（不符合题意，舍去）；故答案为：10%．15.如图，在ABC 中，延长AC 至点D ，使CD CA =，过点D 作DE CB ∥，且DE DC =，连接AE 交BC 于点F ．若CAB CFA ∠=∠，1CF =，则BF =______．【答案】3【解析】【分析】先根据平行线分线段成比例证AF EF =，进而得22DE CD AC CF ====，4AD =，再证明CAB DEA ≌，得4BC AD ==，从而即可得解．【详解】解：∵CD CA =，过点D 作DE CB ∥，CD CA =，DE DC =，∴1FA CA FE CD==，CD CA DE ==，∴AF EF =，∴22DE CD AC CF ====，∴4AD AC CD =+=，∵DE CB ∥，∴CFA E ∠∠=，ACB D ∠∠=，∵CAB CFA ∠=∠，∴CAB E ∠∠=，∵CD CA =，DE CD =，∴CA DE =，∴CAB DEA ≌，∴4BC AD ==，∴3BF BC CF =-=，故答案为：3，【点睛】本题主要考查了平行线的性质，三角形的中位线定理，平行线分线段成比例以及全等三角形的判定及性质，熟练掌握三角形的中位线定理，平行线分线段成比例以及全等三角形的判定及性质是解题的关键．16.若关于x 的不等式组()411321x x x x a -⎧<+⎪⎨⎪+≥-+⎩至少有2个整数解，且关于y 的分式方程13211a y y -=---的解为非负整数，则所有满足条件的整数a 的值之和为______．【答案】16【解析】【分析】本题考查了分式方程的解，以及解一元一次不等式组．先解不等式组，根据关于x 的一元一次不等式组至少有两个整数解，确定a 的取值范围8a ≤，再把分式方程去分母转化为整式方程，解得22a y -=，由分式方程的解为非负整数，确定a 的取值范围2a ≥且4a ≠，进而得到28a ≤≤且4a ≠，根据范围确定出a 的取值，相加即可得到答案．【详解】解：()411321x x x x a -⎧<+⎪⎨⎪+≥-+⎩①②，解①得：4x <，解②得：23a x -≥，关于x 的一元一次不等式组至少有两个整数解，∴223a -≤，解得8a ≤，解方程13211a y y -=---，得22a y -=，关于y 的分式方程的解为非负整数，∴202a -≥且212a -≠，2a -是偶数，解得2a ≥且4a ≠，a 是偶数，∴28a ≤≤且4a ≠，a 是偶数，则所有满足条件的整数a 的值之和是26816++=，故答案为：16．17.如图，以AB 为直径的O 与AC 相切于点A ，以AC 为边作平行四边形ACDE ，点D 、E 均在O 上，DE 与AB 交于点F ，连接CE ，与O 交于点G ，连接DG ．若10,8AB DE ==，则AF =______．DG =______．【答案】①.8②.13【解析】【分析】连接DO 并延长，交O 于点H ，连接GH ，设CE 、AB 交于点M ，根据四边形ACDE 为平行四边形，得出∥DE AC ，8AC DE ==，证明AB DE ⊥，根据垂径定理得出142DF EF DE ===，根据勾股定理得出3OF ==，求出538AF OA OF =+=+=；证明EFM CAM ∽，得出EF FM AC AM =，求出83FM =，根据勾股定理得出4133EM ===，证明EFM HGD ∽，得出FM EM DG DH =，求出201313DG =．【详解】解：连接DO 并延长，交O 于点H ，连接GH ，设CE 、AB 交于点M ，如图所示：∵以AB 为直径的O 与AC 相切于点A ，∴AB AC ⊥，∴90CAB ∠=︒，∵四边形ACDE 为平行四边形，∴∥DE AC ，8AC DE ==，∴90BFD CAB ==︒∠∠，∴AB DE ⊥，∴142DF EF DE ===，∵10AB =，∴152DO BO AO AB ====，∴3OF ==，∴538AF OA OF =+=+=；∵∥DE AC ，∴EFM CAM ∽，∴EF FMAC AM =，∴48FM AF FM =-，即488FM FM =-，解得：83FM =，∴3EM ===，∵DH 为直径，∴90DGH ∠=︒，∴DGH EFM ∠=∠，∵ DGDG =，∴DEG DHG =∠∠，∴EFM HGD ∽，∴FM EM DG DH=，即84133310DG =，解得：201313DG =．故答案为：8；201313．【点睛】本题主要考查了平行四边形的性质，垂径定理，圆周角定理，切线的性质，勾股定理，三角形相似的判定和性质，解题的关键是作出辅助线，熟练掌握三角形相似的判定方法．18.我们规定：若一个正整数A 能写成2m n -，其中m 与n 都是两位数，且m 与n 的十位数字相同，个位数字之和为8，则称A 为“方减数”，并把A 分解成2m n -的过程，称为“方减分解”．例如：因为26022523=-，25与23的十位数字相同，个位数字5与3的和为8，所以602是“方减数”，602分解成26022523=-的过程就是“方减分解”．按照这个规定，最小的“方减数”是______．把一个“方减数”A 进行“方减分解”，即2A m n =-，将m 放在n 的左边组成一个新的四位数B ，若B 除以19余数为1，且22m n k +=（k 为整数），则满足条件的正整数A 为______．【答案】①.82②.4564【解析】【分析】本题考查了新定义，设10m a b =+，则108n a b =+-（19a ≤≤，08b ≤≤）根据最小的“方减数”可得10,18m n ==，代入，即可求解；根据B 除以19余数为1，且22m n k +=（k 为整数），得出34719a b ++为整数，308a b ++是完全平方数，在19a ≤≤，08b ≤≤，逐个检验计算，即可求解．【详解】①设10m a b =+，则108n a b =+-（19a ≤≤，08b ≤≤）由题意得：()()2210108m n a b a b -=+-+-，∵19a ≤≤，“方减数”最小，∴1a =，则10m b =+，18n b =-，∴()()2222101810020188221m n b b b b b b b -=+--=++-+=++，则当0b =时，2m n -最小，为82，故答案为：82；②设10m a b =+，则108n a b =+-（19a ≤≤，08b ≤≤）∴10001001081010998B a b a b a b =+++-=++∵B 除以19余数为1，∴1010997a b ++能被19整除∴134********B a b a b -++=++为整数，又22m n k +=（k 为整数）∴()210108308a b a b a b +++-=++是完全平方数，∵19a ≤≤，08b ≤≤∴308a b ++最小为49，最大为256即716k ≤≤设34719a b t ++=，t 为正整数，则13t ≤≤当1t =时，3412a b +=，则334b a =-，则330830384a b a a ++=+-+是完全平方数，又19a ≤≤，08b ≤≤，无整数解，当2t =时，无整数解，当3t =时，3450a b +=，则5034a b -=，则5033083084a ab a -++=++是完全平方数，经检验，当6,8a b ==时，3473648757193a b ++=⨯+⨯+==⨯，23068819614⨯++==，3,14t k ==，∴68,60m n ==，∴268604564A =-=故答案为：82，4564．三、解答题：（本大题8个小题，第19题8分，其余每小题10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．19.计算：（1）()()22x x y x y -++；（2）22111a a a a -⎛⎫+÷ ⎪+⎝⎭．【答案】（1）222x y +；（2）11a a +-．【解析】【分析】（1）根据单项式乘以多项式和完全平方公式法则分别计算，然后合并同类项即可；（2）先将括号里的异分母分式相减化为同分母分式相减，再算分式的除法运算得以化简；本题考查了单项式乘以多项式，完全平方公式和分式的化简，熟练掌握运算法则是解题的关键．【小问1详解】解：原式22222x xy x xy y =-+++，222x y =+；【小问2详解】解：原式()()()1111a a a a a a +-+=÷+，()()()11·11a a a a a a ++=+-，11a a +=-．20.为了解学生的安全知识掌握情况，某校举办了安全知识竞赛．现从七、八年级的学生中各随机抽取20名学生的竞赛成绩（百分制）进行收集、整理、描述、分析．所有学生的成绩均高于60分（成绩得分用x 表示，共分成四组：A ．6070x <≤；B ．7080x <≤；C ．8090x <≤；D ．90100x <≤），下面给出了部分信息：七年级20名学生的竞赛成绩为：66，67，68，68，75，83，84，86，86，86，86，87，87，89，95，95，96，98，98，100.八年级20名学生的竞赛成绩在C 组的数据是：81，82，84，87，88，89．七、八年级所抽学生的竞赛成绩统计表年级七年级八年级平均数8585中位数86b 众数a 79根据以上信息，解答下列问题：（1）上述图表中=a ______，b =______，m =______；（2）根据以上数据分析，你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好？请说明理由（写出一条理由即可）；（3）该校七年级有400名学生，八年级有500名学生参加了此次安全知识竞赛，估计该校七、八年级参加此次安全知识竞赛成绩优秀()90x >的学生人数是多少？【答案】（1）86，87.5，40；（2）八年级学生竞赛成绩较好，理由见解析；（3）该校七、八年级参加此次安全知识竞赛成绩优秀的学生人数是320人．【解析】【分析】（1）根据表格及题意可直接进行求解；（2）根据平均分、中位数及众数分析即可得出结果；（3）由题意可得出参加此次竞赛活动成绩优秀的百分比，然后可进行求解；本题主要考查扇形统计图及中位数、众数、平均数，熟练掌握扇形统计图及中位数、众数、平均数是解题的关键．【小问1详解】根据七年级学生竞赛成绩可知：86出现次数最多，则众数为86，八年级竞赛成绩中A 组：2010%2⨯=（人），B 组：2020%4⨯=（人），C 组：6人，所占百分比为6100%30%20⨯=D 组：202468---=（人）所占百分比为%110%20%30%40%m =---=，则40m =，∴八年级的中位数为第1011、个同学竞赛成绩的平均数，即C 组第45、个同学竞赛成绩的平均数878887.52b +==，故答案为：86，87.5，40；【小问2详解】八年级学生竞赛成绩较好，理由：七、八年级的平均分均为85分，八年级的中位数高于七年级的中位数，整体上看八年级学生竞赛成绩较好；【小问3详解】640040%50032020⨯+⨯=（人），答：该校七、八年级参加此次安全知识竞赛成绩优秀的学生人数是320人．21.在学习了矩形与菱形的相关知识后，小明同学进行了更深入的研究，他发现，过矩形的一条对角线的中点作这条对角线的垂线，与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形，可利用证明三角形全等得到此结论．根据他的想法与思路，完成以下作图与填空：（1）如图，在矩形ABCD 中，点O 是对角线AC 的中点．用尺规过点O 作AC 的垂线，分别交AB ，CD 于点E ，F ，连接AF ，CE ．（不写作法，保留作图痕迹）（2）已知：矩形ABCD ，点E ，F 分别在AB ，CD 上，EF 经过对角线AC 的中点O ，且EFAC ⊥．求证：四边形AECF 是菱形．证明：∵四边形ABCD 是矩形，∴AB CD ．∴①，OCF OAE ∠=∠．∵点O 是AC 的中点，∴②．∴CFO AEO ≅△△（AAS ）．∴③．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．进一步思考，如果四边形ABCD 是平行四边形呢？请你模仿题中表述，写出你猜想的结论：④．【答案】（1）见解析（2）①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形【解析】【分析】本题主要考查了矩形的性质，平行四边形的性质与判定，菱形的判定，垂线的尺规作图：（1）根据垂线的尺规作图方法作图即可；（2）根据矩形或平行四边形的对边平行得到OFC OEA ∠=∠，OCF OAE ∠=∠，进而证明()AAS CFO AEO ≌，得到OF OE =，即可证明四边形AECF 是平行四边形．再由EF AC ⊥，即可证明四边形AECF 是菱形．【小问1详解】解：如图所示，即为所求；【小问2详解】证明：∵四边形ABCD 是矩形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．猜想：过平行四边形的一条对角线的中点作这条对角线的垂线，与平行四边形两边相交的两点和这条对角线的两个端点构成的四边形是菱形；证明：∵四边形ABCD 是平行四边形，∴AB CD ．∴OFC OEA ∠=∠，OCF OAE ∠=∠．∵点O 是AC 的中点，∴OA OC =．∴()AAS CFO AEO ≌．∴OF OE =．又∵OA OC =，∴四边形AECF 是平行四边形．∵EF AC ⊥，∴四边形AECF 是菱形．故答案为：①OFC OEA ∠=∠；②OA OC =；③OF OE =；④四边形AECF 是菱形．22.为促进新质生产力的发展，某企业决定投入一笔资金对现有甲、乙两类共30条生产线的设备进行更新换代．（1）为鼓励企业进行生产线的设备更新，某市出台了相应的补贴政策．根据相关政策，更新1条甲类生产线的设备可获得3万元的补贴，更新1条乙类生产线的设备可获得2万元的补贴．这样更新完这30条生产线的设备，该企业可获得70万元的补贴．该企业甲、乙两类生产线各有多少条？（2）经测算，购买更新1条甲类生产线的设备比购买更新1条乙类生产线的设备需多投入5万元，用200万元购买更新甲类生产线的设备数量和用180万元购买更新乙类生产线的设备数量相同，那么该企业在获得70万元的补贴后，还需投入多少资金更新生产线的设备？【答案】（1）该企业甲类生产线有10条，则乙类生产线各有20条；（2）需要更新设备费用为1330万元【解析】【分析】本题考查的是一元一次方程的应用，分式方程的应用，理解题意，确定相等关系是解本题的关键．（1）设该企业甲类生产线有x 条，则乙类生产线各有()30x -条，再利用更新完这30条生产线的设备，该企业可获得70万元的补贴，再建立方程求解即可；（2）设购买更新1条甲类生产线的设备为m 万元，则购买更新1条乙类生产线的设备为()5m -万元，利用用200万元购买更新甲类生产线的设备数量和用180万元购买更新乙类生产线的设备数量相同，再建立分式方程，进一步求解．【小问1详解】解：设该企业甲类生产线有x 条，则乙类生产线各有()30x -条，则()323070x x +-=，解得：10x =，则3020x -=；答：该企业甲类生产线有10条，则乙类生产线各有20条；【小问2详解】解：设购买更新1条甲类生产线的设备为m 万元，则购买更新1条乙类生产线的设备为()5m -万元，则2001805m m =-，解得：50m =，经检验：50m =是原方程的根，且符合题意；则545m -=，则还需要更新设备费用为10502045701330⨯+⨯-=（万元）；23.如图，在ABC 中，6AB =，8BC =，点P 为AB 上一点，过点P 作PQ BC ∥交AC 于点Q ．设AP 的长度为x ，点P ，Q 的距离为1y ，ABC 的周长与APQ △的周长之比为2y．（1）请直接写出1y ，2y 分别关于x 的函数表达式，并注明自变量x 的取值范围；（2）在给定的平面直角坐标系中画出函数1y ，2y 的图象；请分别写出函数1y ，2y 的一条性质；（3）结合函数图象，直接写出12y y >时x 的取值范围．（近似值保留一位小数，误差不超过0.2）【答案】（1）()()124606063y x x y x x =<≤=<≤，（2）函数图象见解析，1y 随x 增大而增大，2y 随x 增大而减小（3）2.26x <≤【解析】【分析】本题主要考查了一次函数与反比例函数综合，相似三角形的性质与判定：（1）证明APQ ABC ∽，根据相似三角形的性质得到APQABC C PQ APC BC AB ==△△，据此可得答案；（2）根据（1）所求利用描点法画出对应的函数图象并根据函数图象写出对应的函数图象的性质即可；（3）找到一次函数图象在反比例函数图象上方时自变量的取值范围即可．【小问1详解】解：∵PQ BC ∥，∴APQ ABC ∽，∴APQABC C PQ APC BC AB ==△△，∴12686y x AB y AP x===，∴()()124606063y x x y x x =<≤=<≤，；【小问2详解】解：如图所示，即为所求；由函数图象可知，1y 随x 增大而增大，2y 随x 增大而减小；【小问3详解】解：由函数图象可知，当12y y >时x 的取值范围2.26x <≤．24.如图，甲、乙两艘货轮同时从A 港出发，分别向B ，D 两港运送物资，最后到达A 港正东方向的C 港装运新的物资．甲货轮沿A 港的东南方向航行40海里后到达B 港，再沿北偏东60︒方向航行一定距离到达C 港．乙货轮沿A 港的北偏东60︒方向航行一定距离到达D 港，再沿南偏东30︒方向航行一定距离到达C港．（参考数据： 1.41≈ 1.73≈ 2.45≈）（1）求A ，C 两港之间的距离（结果保留小数点后一位）；（2）若甲、乙两艘货轮的速度相同（停靠B 、D 两港的时间相同），哪艘货轮先到达C 港？请通过计算说明．【答案】（1）A ，C 两港之间的距离77.2海里；（2）甲货轮先到达C 港．【解析】【分析】（1）过B 作BE AC ⊥于点E ，由题意可知：45GAB ∠=︒，60EBC ∠=︒，求出cos AE AB BAE =∠=tan CE BE EBC =∠=（2）通过三角函数求出甲行驶路程为：4056.496.4AB BC +=+=，乙行驶路程为：66.838.6105.4AD CD +=+=，然后比较即可；本题考查了方位角视角下的解直角三角形，构造直角三角形，熟练掌握锐角三角函数是解题的关键．【小问1详解】如图，过B 作BE AC ⊥于点E，∴90AEB CEB ∠=∠=︒，由题意可知：45GAB ∠=︒，60EBC ∠=︒，∴45BAE ∠=︒，∴cos 40cos 45AE AB BAE =∠=⨯︒=∴tan 60CE BE EBC =∠=︒=∴201.4120 2.4577.2AC AE CE =+=⨯+⨯≈（海里），∴A ，C 两港之间的距离77.2海里；【小问2详解】由（1）得：45BAE ∠=︒，60EBC ∠=︒，77.2AC =，∴sin 40sin 45BE AB BAE =∠=⨯︒=∴56.41cos cos 602BE BC EBC ====≈∠︒，由题意得：60ADF ∠=︒，30CDF ∠=︒，∴90ADC ∠=︒，∴1177.238.622CD AC ==⨯=， 1.73cos3077.266.82AD AC =︒=⨯≈（海里），∴甲行驶路程为：4056.496.4AB BC +=+=（海里），乙行驶路程为：66.838.6105.4AD CD +=+=（海里），∵96.4105.4<，且甲、乙速度相同，∴甲货轮先到达C 港．25.如图，在平面直角坐标系中，抛物线()240y ax bx a =++≠经过点()1,6-，与y 轴交于点C ，与x 轴交于A B ，两点（A 在B 的左侧），连接tan 4AC BC CBA ∠=，，．（1）求抛物线的表达式；（2）点P 是射线CA 上方抛物线上的一动点，过点P 作PE x ⊥轴，垂足为E ，交AC 于点D ．点M 是线段DE 上一动点，MN y ⊥轴，垂足为N ，点F 为线段BC 的中点，连接AM NF ，．当线段PD 长度取得最大值时，求AM MN NF ++的最小值；（3）将该抛物线沿射线CA 方向平移，使得新抛物线经过（2）中线段PD 长度取得最大值时的点D ，且与直线AC 相交于另一点K ．点Q 为新抛物线上的一个动点，当QDK ACB ∠∠=时，直接写出所有符合条件的点Q 的坐标．【答案】（1）234y x x =--+；（2）AM MN NF ++的最小值为4122+；（3）符合条件的点Q 的坐标为()1,2--或1943,416⎛⎫-⎪⎝⎭．【解析】【分析】（1）利用正切函数求得1OB =，得到()1,0B ，再利用待定系数法即可求解；（2）求得()4,0A -，利用待定系数法求得直线AC 的解析式，设()2,34P p p p --+，求得PD 最大，点()2,6P -，再证明四边形AMNE 是平行四边形，得到AM EN =，推出当E N F 、、共线时，EF 取最小值，即AM MN NF ++取最小值，据此求解即可；（3）求得()2,2D -，再利用平移的性质得到新抛物线的解析式278y x x '=---，再分两种情况讨论，计算即可求解．【小问1详解】解：令0x =，则4y =，∴()0,4C ，∴4OC =，∵tan 4CBA ∠=，∴4OC OB =，∴1OB =，∴()1,0B ，将()1,0B 和()1,6-代入24y ax bx =++得6404a b a b =-+⎧⎨=++⎩，解得13a b =-⎧⎨=-⎩，∴抛物线的表达式为234y x x =--+；【小问2详解】解：令0y =，则2034x x =--+，解得4x =-或1x =，∴()4,0A -，设直线AC 的解析式为4y mx =+，代入()4,0A -，得044m =-+，解得1m =，∴直线AC 的解析式为4y x =+，设()2,34P p p p --+（40p -<<），则(),4D p p +，∴()()2234424PD p p p p =--+-+=-++，∵10-<，∴当2p =-时，PD 最大，此时()2,6P -，∴2AE =，2MN OE ==，()2,0E -，∴AE MN =，AE MN ∥，连接EN ，∴四边形AMNE 是平行四边形，∴AM EN =，∴AM MN NF EN MN NF MN EF ++=++≥+，∴当E N F 、、共线时，EF 取最小值，即AM MN NF ++取最小值，∵点F 为线段BC 的中点，∴1,22F ⎛⎫ ⎪⎝⎭，∴412EF ==，∴AM MN NF ++的最小值为4122+；【小问3详解】解：由（2）得点D 的横坐标为2-，代入4y x =+，得2y =，∴()2,2D -，∴新抛物线由234y x x =--+向左平移2个单位，向下平移2个单位得到，∴()()222324278y x x x x =-+-++-=---'，过点D 作1DQ BC ∥交抛物线y '于点1Q ，∴1Q DK BCA ∠=∠，同理求得直线BC 的解析式为44y x =-+，∵1DQ BC ∥，∴直线1DQ 的解析式为46y x =--，联立得28476x x x =-----，解得11x =-，22x =-，当=1x -时，=2y -，∴()11,2Q --，作1DQ 关于直线AC 的对称线得2DQ 交抛物线y '于点2Q ，∴21Q DK Q DK BCA ∠=∠=∠，设1DQ 交x 轴于点G ，由旋转的性质得到DG DG '=，过点D 作DR x ∥轴，作DH x ⊥轴于点H ，作G H DR ''⊥于点H '，当0y =时，046x =--，解得32x =-，∴3,02G ⎛⎫- ⎪⎝⎭∵()4,0A -，()0,4C ，∴OA OC =，∴45OAC OCA ∠=∠=︒，∵DR x ∥轴，∴45RDA DAH ADH ∠=∠=∠=︒，∴'G DH GDH '∠=∠，∵''90G H D GHD ∠=∠=︒，'DG DG=∴GD H GDH ''≌△△，∴31222G H GH ''==-=，2DH DH '==，∴54,2G ⎛⎫- ⎪⎝⎭'，同理直线2DQ 的解析式为4213=-+y x ，联立2134278x x x =--+--，解得2x =-或194x =-，当194x =-时，11934344216y ⎛⎫=-⨯-+= ⎪⎝⎭，∴21943,416Q ⎛⎫- ⎪⎝⎭，综上，符合条件的点Q 的坐标为()1,2--或1943,416⎛⎫-⎪⎝⎭．【点睛】本题是二次函数综合问题，考查二次函数的图象及性质，待定系数法确定函数关系式，熟练掌握二次函数的图象及性质，轴对称的性质，直角三角形的性质，数形结合是解题的关键．26.在ABC 中，AB AC =，点D 是BC 边上一点（点D 不与端点重合）．点D 关于直线AB 的对称点为点E ，连接,AD DE ．在直线AD 上取一点F ，使EFD BAC ∠∠=，直线EF 与直线AC 交于点G ．（1）如图1，若60,,BAC BD CD BAD α∠=︒<∠=，求AGE ∠的度数（用含α的代数式表示）；（2）如图1，若60,BAC BD CD ∠=︒<，用等式表示线段CG 与DE 之间的数量关系，并证明；（3）如图2，若90BAC ∠=︒，点D 从点B 移动到点C 的过程中，连接AE ，当AEG △为等腰三角形时，请直接写出此时CG AG的值．【答案】（1）60α︒+（352+【解析】【分析】（1）由三角形内角和定理及外角定理结合EFD BAC ∠∠=即可求解；（2）在CG 上截取CM BD =，连接,BM BE ，BM 交AD 于点H ，连接,BE AE ，先证明，再证明四边形EBMG 是平行四边形，可得2CG BD =，记AB 与DE 的交点为点N ，则由轴对称可知：DE AB ⊥，NE ND =，再解Rt BND △即可；（3）连接BE ，记AB 与DE 的交点为点N ，由轴对称知EAB DAB ∠=∠，DE AB ⊥，NE ND =，45EBA DBA ∠=∠=︒，当点G 在边AC 上时，由于90EAG ∠>︒，当AEG △为等腰三角形时，只能是AE AG =，由（1）得BAD ∠=α，60AGE α∠=︒+，Rt AFG △中，290αα+=︒，解得30α=︒，然后AF x =，解直角三角形，表示出2AG x =，)1CG x =，即可求解；当点G 在CA 延长线上时，只能是GE GA =，设BAD BAE β∠=∠=，在Rt AFE 中，90180290ββ︒-+︒-=︒，解得60β=︒，设GF x =，解直角三角形求出(5CG x =+，即可求解．【小问1详解】解：如图，∵EFD BAC ∠∠=，60BAC ∠=︒，∴60EFD ∠=︒∵11EFD BAD α∠=∠+∠=∠+，∴160α∠=︒-，∵1180AGE BAC ∠+∠+∠=︒，∴1806011201AGE ∠=︒-︒-∠=︒-∠，∴()1206060AGE αα∠=︒-︒-=︒+；【小问2详解】在CG 上截取CM BD =，连接,,BM BE AE ，BM 交AD 于点H ，∵,60AB AC BAC =∠=︒，∴BCA V 为等边三角形，∴60,ABC C BC AB ∠=∠=︒=，∴ABD BCM △≌△，∴3=4∠∠，∵35AHM ∠=∠+∠，∴4560AHM ∠=∠+∠=︒，∵60EFD BAC ∠=∠=︒，∴AHM EFD ∠=∠，∴EG BM ∥，∵点D 关于直线AB 的对称点为点E ，∴,,60AE AD BE BD ABE ABC ==∠=∠=︒，∴120EBC ∠=︒，∴180EBC C ∠+∠=︒，∴EB AC ∥，∴四边形EBMG 是平行四边形，∴BE GM =，∴BE GM BD CM ===，∴2CG BD =，记AB 与DE 的交点为点N ，。

第1章丰富的图形世界七年级上册数学北师大版(2024)单元质检A卷(含答案)

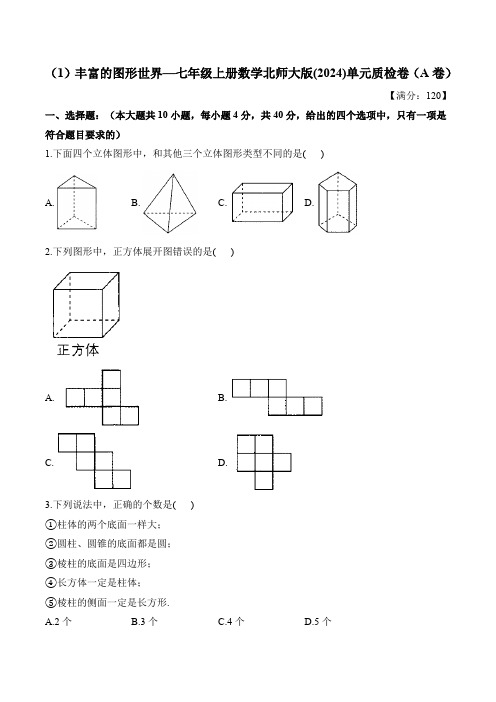
（1）丰富的图形世界—七年级上册数学北师大版(2024)单元质检卷（A卷）【满分：120】一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.下面四个立体图形中，和其他三个立体图形类型不同的是( )A. B. C. D.2.下列图形中，正方体展开图错误的是( )A. B.C. D.3.下列说法中，正确的个数是( )①柱体的两个底面一样大；②圆柱、圆锥的底面都是圆；③棱柱的底面是四边形；④长方体一定是柱体；⑤棱柱的侧面一定是长方形.A.2个B.3个C.4个D.5个4.如图，一个几何体上半部为正四棱锥，下半部为正方体，且有一个面涂有颜色，该几何体的表面展开图可能是( )A. B. C. D.5.从正面、左面、上面观察某个立体图形,得到如图所示的平面图形,那么这个立体图形是( )A. B. C. D.6.下列说法错误的是( )A.长方体、正方体都是棱柱B.三棱柱的侧面是三角形C.直六棱柱有六个侧面，侧面均为长方形D.从正面、左面、上面看球体得到的图形均为同样大小的圆形7.用一个平面去截一个几何体，得到的截面形状是长方形，那么这个几何体不可能是( )A长方体 B.圆柱 C.圆锥 D.正方体8.如图是的正方形网格，选择一空白小正方形，能与阴影部分组成正方体展开图的方法有( )A.1种B.2种C.3种D.4种9.某棱柱共有14个顶点，用一个平面去截该棱柱，截面不可能是( )A.十一边形B.五边形C.三角形D.九边形10.一个不透明小立方块的六个面上分别标有数字1，2，3，4，5，6，其展开图如图1所示.在一张不透明的桌子上，按图2方式将三个这样的小立方块搭成一个几何体，则该几何体能看得到的面上数字之和最小是( )A.31B.32C.33D.34二、填空题（每小题4分，共20分）11.如图所示的立体图形是由___________个面组成的；面与面相交成___________条线；其中有___________条线是曲的.12.如图，这是由若干个大小相同的小正方体组合而成的几何体，那么从三个方向看到的平面图形中，面积最大的是从________面看.（填“上”“前”或“左”）13.如图，节日的焰火可以看成由点运动形成的，这可以说__________.14.一个立方体木块，6个面都涂上红色，然后把它切成大小相等的27个小立方体，其中有两个面是红色的小立方体有__________个.15.在综合实践课学习中，老师要求用长为12厘米，宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.甲、乙、丙三位同学分别以下列方式在长方形纸片上截去两角（图中阴影部分），然后沿虚线折成一个无盖的长方体纸盒.甲：如图1，盒子底面的四边形是正方形乙：如图2，盒子底面的四边形是正方形丙：如图3，盒子底面的四边形是长方形，请将这三位同学所折成的无盖长方体的容积（）按从大到小的顺序排列：____________.三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）写出下列立体图形的名称：17.（8分）如图,左面立.体图形中四边形表示平面截正方体的截面,请在右面展开图中画出四边形的四条边.18.（10分）如图，这是一个由小正方体所搭的几何体从上面观察所得到的形状图，正方形中的数字表示在该位置上小正方体的个数，请你画出从正面、左面观察该几何体所看到的形状图.19.（10分）已知一个直棱柱有15条棱，它的底面边长都相等.(1)该直棱柱是几棱柱？它有几个面？侧面是什么图形？(2)用一个平面去截该直棱柱，截面形状可能是；（写出一种即可）(3)若该直棱柱的底面周长为，侧棱长为，求它的所有侧面的面积之和.20.（12分）如图所示，在长方形ABCD中，，.现绕这个长方形的一边所在直线旋转一周得到一个几何体.请解决以下问题：（1）说出旋转得到的几何体的名称？（2）如果用一个平面去截旋转得到的几何体，那么截面有哪些形状（至少写出3种）？（3）求以CD边所在直线进行旋转所得几何体的体积？（结果保留）21.（12分）（1）如图所示的长方体，长、宽、高分别为4，3，6.若将它的表面沿某些棱剪开，展成一个平面图形，则下列图形中，可能是该长方体表面展开图的有________（填序号）.（2）图A，B分别是题（1）中长方体的两种表面展开图，求得图A的外围周长为52，请你求出图B的外围周长.（3）第（1）题中长方体的表面展开图还有不少，聪明的你能画出一个使外围周长最大的表面展开图吗？请画出这个表面展开图，并求出它的外围周长.答案以及解析1.答案：B解析：B选项是棱锥，A，C，D选项是棱柱，所以和其他三个立体图形类型不同的是B选项.故选B.2.答案：D解析：由正方体展开图的知识可知，四个小正方形绝对不可能展开成“田”字形，故D选项的展开图错误.故选D.3.答案：B解析：①柱体包括圆柱、棱柱；柱体的两个底面一样大；故此选项正确，②圆柱、圆锥的底面都是圆，正确；③棱柱的底面可以为任意多边形，错误；④长方体符合柱体的条件，一定是柱体，正确；⑤棱柱分为直棱柱和斜棱柱，直棱柱的侧面应是长方形，故错误；共有3个正确，故选：B.4.答案：B解析：根据涂有颜色一面的位置，排除A，C项；D中的图形不是这个几何体的表面展开图，排除D.5.答案：C解析：一个立体图形从正面、左面看到的平面图形是长方形,从上面看到的平面图形是一个三角形,则这个立体图形是有两个底面是三角形的三棱柱.故选：C.6.答案：B解析：A、长方体和正方体都是特殊的四棱柱，故本选项不符合题意；B、三棱柱的底面是三角形，侧面是矩形或平行四边形，故本选项符合题意；C、直六棱柱有六个侧面，侧面都是矩形，本选项不符合题意；D、从正面、左面、上面看球体得到的图形均为同样大小的圆形，本选项不符合题意；故选B.7.答案：C解析：A.长方体的截面可以是长方形，不符合题意；B.用垂直于地面的一个平面截圆柱截面为长方形，不符合题意；C.圆锥由一个平面和一个曲面，截面最多有三条边，截面不可能是长方形，符合题意；D.正方体的截面可以是长方形，不符合题意.故选：C.8.答案：B解析：如图所示：共有2种方法，故选：B.9.答案：A解析：因为该棱柱共有14个顶点，所以该棱柱是7棱柱，所以用一个平面去截该棱柱，截面可能是三角形、五边形、九边形，但不可能是十一边形.10.答案：B解析：由正方体表面展开图的“相间、Z端是对面”可知，“1”与“3”，“2”与“4”，“5”与“6”是对面，因此要使题图2中几何体能看得到的面上数字之和最小，最右边的那个正方体所能看到的4个面的数字为1，2，3，5，最上边的那个正方体所能看到的5个面的数字为1，2，3，4，5，左下角的那个正方体所能看到的3个面的数字为1，2，3，所以该几何体能看得到的面上数字之和最小为.11.答案：5；9；2解析：由立体图形可以看出立体图形由5个面组成的，面与面相交成9条线，其中曲线有2条.故答案为：5；9；2.12.答案：上解析：所给的几何体从前面看由5个小正方形组成；从左面看由5个小正方形组成；从上面看由6个小正方形组成.故面积最大的是从上面看.故答案为上.13.答案：点动成线解析：节日的焰火可以看成由点运动形成的，这可以说点动成线；故答案为：点动成线.14.答案：12解析：两面涂色的在每条棱长上（除去顶点处的小正方体），有：（个）；答：其中有两个面是红色的小立方体有12个.故答案为：12.15.答案：解析：由图1可得：盒子底面的正方形的边长为（厘米），高为（厘米），则甲所折成的无盖长方体的容积为：（立方厘米），由图2可得：盒子底面的正方形的边长为（厘米），高为（厘米），则乙所折成的无盖长方体的容积为：（立方厘米），由图3可得：盒子底面的长方形的边长为（厘米），（厘米），高为（厘米），则丙所折成的无盖长方体的容积为：（立方厘米），.故答案为：.16.答案：球；圆柱；圆锥；长方体；三棱柱解析：如图所示：故答案为球，圆柱，圆锥，长方体，三棱柱.17.答案：图见解析解析：截面的线在展开图中,如图18.答案：见解析解析：由图例，可画从正面、左面观察该几何体所看到的形状图，如下图所示：从正面看：从左面看：19.答案：(1)该直棱柱为五棱柱，它有7个面，侧面是长方形(2)五边形(3)它的所有侧面的面积之和为解析：（1），所以该直棱柱为五棱柱，它有7个面，侧面是长方形;（2）用一个平面去截该直棱柱，截面形状可能是五边形，故答案为：五边形（答案不唯一）；（3），，即它的所有侧面的面积之和为.20.答案：（1）圆柱（2）长方形或圆形或梯形（3）解析：（1）长方形绕一边旋转一周，得到圆柱；（2）如果用一个平面去截这个圆柱，则截面可能是：长方形或圆形或梯形；（3）当以CD为边所在直线进行旋转，得到的是底面半径为6 cm，高为8 cm的圆柱，则体积为：.21.答案：（1）①②③（2）58（3）70，图见解析解析：（1）根据长方体展开图的特征可得答案为：①②③；（2）由已知可以给图B标上尺寸如下：图B的外围周长为.（3）能.如图所示.外围周长为.。

2024-2025学年五年级数学上册秋季开学摸底考A卷(答案解析)(北师大版)

2024-2025学年五年级数学上册秋季开学摸底考A卷答案解析一．填空题（满分20分，每小题2分）1．（2分）在桌面上有一个用正方体木块搭成的立体图形，从正南方向看如图（1），从正东方向看如图（2），要搭成一个这样的立体图形最多用20 个正方体木块，最少用个正方体木块。

（正方体之间至少有一个面重合）【分析】底层最少有7个小正方体，上层最少2个小正方体；底层最多有16个小正方体，最多4个小正方体，据此写出答案。

【解答】解：在桌面上有一个用正方体木块搭成的立体图形，从正南方向看如图（1），从正东方向看如图（2），要搭成一个这样的立体图形最多有20个正方体木块，最少用9个正方体木块。

（正方体之间至少有一个面重合）故答案为：20；9。

【点评】本题考查的是用正方体搭立体图形，关键是明确只有从三个方向才能确定小正方体的个数。

2．（2分）小明在本子上写了一个小数，先把这个小数的小数点向左移动一位，再向右移动三位后是36.29，小明最初在本上写的这个小数是0.3629 。

【分析】先把这个小数的小数点向左移动一位，再向右移动三位，相当于原数的小数点向右移动两位，是36.29，那么把36.29的小数点向左移动两位就是原数，据此解答。

【解答】解：由分析可得，把36.29的小数点向左移动两位为原数，即0.3629，所以小明最初在本上写的这个小数是0.3629。

故答案为：0.3629。

【点评】掌握小数点位置移动引起数的大小变化规律是解答本题的关键。

3．（2分）用0，4，7和小数点写两位小数（一个数中，同一个数字不重复用），按从小到大的顺序排列是0.470.74 4.07 4.707.047.40<<<<<。

【分析】求用0、4、7和小数点可以组成多少个不同的两位小数，先把0写在个位上，可以写出2个两位小数；再把4写在个位上，可以写出2个两位小数；再把7写在个位上，可以写出2个两位小数；然后根据小数的大小比较方法，由小到大排列即可。

2023年重庆市中考数学真题(A卷)(答案解析)

重庆市2023年初中学业水平暨高中招生考试数学试题（A 卷）一、选择题：（本大题10个小题，每小题4分，共40分）1.【答案】A【解析】解：8的相反数是8-，故选A ．2.【答案】D【解析】从正面看第一层是2个小正方形，第二层右边1个小正方形，故选：D ．3.【答案】C【解析】解：A 选项，将1x =代入反比例函数4y x =-得到14y =-≠，故A 项不符合题意；B 选项，项将1x =-代入反比例函数4y x =-得到44y =≠-，故B 项不符合题意；C 选项，项将=−2代入反比例函数4y x =-得到22y ==，故C 项符合题意；D 选项，项将2x =代入反比例函数4y x=-得到22y =-≠，故D 项不符合题意；故选C ．4.【答案】B【解析】解：∵两个相似三角形周长的比为1:4，∴相似三角形的对应边比为1:4，故选B ．5.【答案】A【解析】解：∵AB CD ∥，155∠=︒，∴18055125CAB Ð=°-°=°，∵AD AC ⊥，∴90CAD ∠=︒，∴21259035CAB CAD Ð=Ð-Ð=°-°=°，故选：A ．6.【答案】B+=4=+∵2 2.5<<，∴45<<，∴849<+，故选：B ．7.【答案】B【解析】解：第①个图案用了459+=根木棍，第②个图案用了45214+⨯=根木棍，第③个图案用了45319+⨯=根木棍，第④个图案用了45424+⨯=根木棍，……，第⑧个图案用的木棍根数是45844+⨯=根，故选：B ．8.【答案】C【解析】解：连接OB ，∵AC 是O 的切线，B 为切点，∴OB AC ⊥，∵30A ∠=︒，AB =∴在Rt OAB 中，3tan 23OB AB A =⋅∠==，∵3BC =，∴在Rt OBC 中，OC ==，故选C ．9.【答案】A【解析】将ADF 绕点A 逆时针旋转90︒至ABH，∵四边形ABCD 是正方形，∴AB AD =，90B D BAD C ∠=∠=∠=∠=︒，由旋转性质可知：DAF BAH ∠=∠，90D ABH ∠=∠=︒，AF AH =，∴180AHB ABC ∠+∠=︒，∴点H B C ，，三点共线，∵BAE α∠=，45EAF ∠=︒，90BAD HAF ∠=∠=︒，∴45DAF BAH α∠=∠=︒-，45EAF EAH ∠=∠=︒，∵90AHB BAH ∠+∠=︒，∴45AHB α∠=︒+，在AEF 和AEH 中AF AH FAE HAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴()AFE AHE SAS ≌，∴45AHE AFE α∠=∠=︒+，∴45AHE AFD AFE α∠=∠=∠=︒+，∴902DFE AFD AFE α∠=∠+∠=︒+，∵90DFE FEC C FEC ∠=∠+∠=∠+︒，∴2FEC α∠=，故选：A ．10.【答案】C【解析】解：x y z m n x y z m n ----=----，故说法①正确．若使其运算结果与原多项式之和为0，必须出现x -，显然无论怎么添加绝对值，都无法使x 的符号为负，故说法②正确．当添加一个绝对值时，共有4种情况，分别是x y z m n x y z m n ----=----；x y z m n x y z m n ----=-+--；||x y z m n x y z m n ----=--+-；x y z m n x y z m n ----=---+．当添加两个绝对值时，共有3种情况，分别是x y z m n x y z m n ----=--+-；x y z m n x y z m n ----=---+；x y z m n x y z m n ----=-+-+．共有7种情况；有两对运算结果相同，故共有5种不同运算结果，故说法③不符合题意．故选：C ．二、填空题：（本大题8个小题，每小题4分，共32分）11.【答案】1.5【解析】1023-+=11=1.52+.故答案为1.5.12.【答案】36°【解析】正五边形内角和：（5﹣2）×180°＝3×180°＝540°∴5401085B ︒︒∠==，∴180B 1801083622BAC ︒︒︒︒-∠-∠===.故答案为36°．13.【答案】19【解析】解：根据题意列表如下：红球白球蓝球红球（红球，红球）（白球，红球）（蓝球，红球）白球（红球，白球）（白球，白球）（蓝球，白球）蓝球（红球，蓝球）（白球，蓝球）（蓝球，蓝球）由表知，共有9种等可能结果，其中两次都摸到红球的有1种结果，所以两次摸到球的颜色相同的概率为19，故答案为：19．14.【答案】()2150111815x +=【解析】解：设七、八两个月提供就业岗位数量的月平均增长率为x ，根据题意得，()2150111815x +=，故答案为：()2150111815x +=．15.【答案】3【解析】解：∵90BAC ∠=︒，∴90EAB EAC ∠+∠=︒，∵BE AD ⊥，CF AD ⊥，∴90AEB AFC ∠=∠=︒，∴90ACF EAC ∠+∠=︒，∴ACF BAE ∠=∠，在AFC △和BEA △中：AEB CFA ACF BAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS AFC BEA ≌△△，∴4,1AF BE AE CF ====，∴413EF AF AE =-=-=，故答案为：3．16.【答案】25124π-【解析】解：连接BD ，∵四边形ABCD 是矩形，∴BD 是O 的直径，∵4,3AB AD ==，∴5BD ==，∴O 的半径为52，∴O 的面积为254π，矩形的面积为3412⨯=，∴阴影部分的面积为25124π-；故答案为25124π-；17.【答案】4【解析】解：+34222x x a ⎧≤⎪⎨⎪-≥⎩①②解不等式①得：5x ≤，解不等式②得：1+2a x ≥，∴不等式的解集为1+52a x ≤≤，∵不等式组至少有2个整数解，∴1+42a ≤，解得：6a ≤；∵关于y 的分式方程14222a y y-+=--有非负整数解，∴()1422a y ---=解得：12a y -=，即102a -≥且122a -≠，解得：1a ≥且5a ≠∴a 的取值范围是16a ≤≤，且5a ≠∴a 可以取：1，3，∴134+=，故答案为：4．18.【答案】①.4312②.8165【解析】解：∵a312是递减数，∴1033112a +-=，∴4a =，∴这个数为4312；故答案为：4312∵一个“递减数”的前三个数字组成的三位数abc 与后三个数字组成的三位数bcd 的和能被9整除，∴101010a b b c c d +--=+，∵1001010010abc bcd a b c b c d +=+++++，∴110010110100110001abc bcd a b c b b a b a b c +=++++++--=，∵()11010199112a b a b a b +=+++，能被9整除，∴112a b +能被9整除，∵各数位上的数字互不相等且均不为0，∴12345678,,,,,,,87654321a a a a a a a ab b b b b b b b ========⎧⎧⎧⎧⎧⎧⎧⎧⎨⎨⎨⎨⎨⎨⎨⎨========⎩⎩⎩⎩⎩⎩⎩⎩，∵最大的递减数，∴8,1a b ==，∴1089110c c d ⨯-⨯-=+，即：1171c d +=，∴c 最大取6，此时5d =，∴这个最大的递减数为8165．故答案为：8165．三、解答题：（本大题8个小题，第19题8分，其余每题各10分，共78分）19.【答案】（1）21a -（2）11x +【解析】（1）解：原式2221a a a =-+-21a =-；（2）原式()222.11x x x x x x ⎛⎫+-=÷ ⎪++⎝⎭()22211x x x x =÷++()22211x x x x +=⋅+11x =+．20.【答案】作图：见解析；FAO ∠；AO CO =；FOA ∠；被平行四边形一组对边所截，截得的线段被对角线中点平分【解析】解：如图，即为所求；证明：∵四边形ABCD 是平行四边形，∴DC AB ∥．∴ECO ∠=FAO ∠．∵EF 垂直平分AC ，∴AO CO =．又EOC ∠=FOA ∠．∴()COE AOF ASA ≅ ．∴OE OF =．故答案为：FAO ∠；AO CO =；FOA ∠；由此得到命题：过平行四边形对角线中点的直线被平行四边形一组对边所截，截得的线段被对角线中点平分，故答案为：被平行四边形一组对边所截，截得的线段被对角线中点平分．21.【答案】（1）72，70.5，10；（2）B 款智能玩具飞机运行性能更好；因为B 款智能玩具飞机运行时间的方差比A 款智能玩具飞机运行时间的方差小，运行时间比较稳定；（3）两款智能玩具飞机运行性能在中等及以上的大约共有192架．【解析】（1）解：由题意可知10架A 款智能玩具飞机充满电后运行最长时间中，只有72出现了三次，且次数最多，则该组数据的众数为72，即72a =；由B 款智能玩具飞机运行时间的扇形图可知，合格的百分比为40%，则B 款智能玩具飞机运行时间合格的架次为：1040%4⨯=（架）则B 款智能玩具飞机运行时间优等的架次为：10451--=（架）则B 款智能玩具飞机的运行时间第五、第六个数据分别为：70,71，故B 款智能玩具飞机运行时间的中位数为：707170.52+=B 款智能玩具飞机运行时间优等的百分比为：1100%10%10⨯=即10m =故答案为：72，70.5，10；（2）B 款智能玩具飞机运行性能更好；因为B 款智能玩具飞机运行时间的方差比A 款智能玩具飞机运行时间的方差小，运行时间比较稳定；（3）200架A 款智能玩具飞机运行性能在中等及以上的架次为：620012010⨯=（架）200架A 款智能玩具飞机运行性能在中等及以上的架次为：61207210⨯=（架）则两款智能玩具飞机运行性能在中等及以上的共有：12072192+=架，答：两款智能玩具飞机运行性能在中等及以上的大约共有192架．22.【答案】（1）购买杂酱面80份，购买牛肉面90份（2）购买牛肉面60份【解析】（1）解：设购买杂酱面x 份，则购买牛肉面()170x -份，由题意知，()152********x x +⨯-=，解得，80x =，∴17090x -=，∴购买杂酱面80份，购买牛肉面90份；（2）解：设购买牛肉面a 份，则购买杂酱面1.5a 份，由题意知，1260120061.5a a+=，解得60a =，经检验，60a =是分式方程的解，∴购买牛肉面60份．23.【答案】（1）当04t <≤时，y t =；当46t <≤时，122y t =-；（2）图象见解析，当04t <≤时，y 随x 的增大而增大（3）t 的值为3或4.5【解析】（1）解：当04t <≤时，连接EF ，由题意得AE AF =，60A ∠=︒，∴AEF △是等边三角形，∴y t =；当46t <≤时，122y t =-；（2）函数图象如图：当04t <≤时，y 随t 的增大而增大；（3）当04t <≤时，3y =即3t =；当46t <≤时，3y =即1223t -=，解得 4.5t =，故t 的值为3或4.5．24.【答案】（1）AD 的长度约为14千米（2）小明应该选择路线①，理由见解析【解析】（1）解：过点D 作DF AB ⊥于点F ，由题意可得：四边形BCDF 是矩形，∴10DF BC ==千米，∵点D 在点A 的北偏东45︒方向，∴45DAF DAN Ð=Ð=°，∴14sin 45DF AD ==°千米，答：AD 的长度约为14千米；（2）由题意可得：10BC =，14CD =，∴路线①的路程为：14102438AD DC BC ++=+=+（千米），∵10DF BC ==，45DAF DAN Ð=Ð=°，90DFA ∠=︒，∴DAF △为等腰直角三角形，∴10AF DF ==，∴101424AB AF BF AF DC =+=+=+=，由题意可得60EBS Ð=°，∴60E ∠=︒，∴tan 60AB AE ==°，sin 60AB BE ==°，所以路线②的路程为：42AE BE +=千米，∴路线①的路程<路线②的路程，故小明应该选择路线①．25.【答案】（1）213222y x x =-++（2）PDE △周长的最大值65105+，此时点()2,3P （3）以点A ，P ，M ，N 为顶点的四边形是菱形时59,22N ⎛⎫- ⎪⎝⎭或137,22⎛ ⎝⎭或137,22⎛⎫- ⎪ ⎪⎝⎭【解析】（1）把()1,3、()1,0A -代入22y ax bx =++得，3202a b a b =++⎧⎨=-+⎩，解得1232a b ⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线的表达式为213222y x x =-++；（2）延长PE 交x 轴于F，∵过点P 作PD BC ⊥于点D ，过点P 作y 轴的平行线交直线BC 于点E ，∴DEP BCO ∠=∠，90PDE COB ∠=∠=︒，∴DPE OBC ，∴DPE PEOBC BC =周长周长，∴PEDPE OBC BC =⋅周长周长，∴当PE 最大时PDE △周长的最大∵抛物线的表达式为213222y x x =-++，∴()4,0B ，∴直线BC 解析式为122y x =-+，BC ==设213,222P m m m ⎛⎫-++ ⎪⎝⎭，则1,22E m m ⎛⎫-+ ⎪⎝⎭∴()222131112222222222PE m m m m m m ⎛⎫=-++--+=-+=--+ ⎪⎝⎭，∴当2m =时2PE =最大，此时()2,3P ∵BOC周长为6OC OB BC ++=+，∴PDE △(651065++=，此时()2,3P ，即PDE △周长的最大值65105+，此时点()2,3P ；（3）∵将该抛物线沿射线CB方向平移个单位长度，可以看成是向右平移2个单位长度再向下平移一个单位长度，∴平移后的解析式为()()221317222142222y x x x =--+-+-=-+-，此抛物线对称轴为直线72x =，∴设7,2M n ⎛⎫ ⎪⎝⎭，(),N s t ∵()2,3P ，()1,0A -∴218PA =，()()22227923324PM n n ⎛⎫=-+-=+- ⎪⎝⎭，()22227811024AM n n ⎛⎫=++-=+ ⎪⎝⎭，当PA 为对角线时，此时以点A ，P ，M ，N 为顶点的四边形是菱形∴PA 与MN 互相平分，且PM AM=∴()22981344n n +-=+，解得32n =-∵PA 中点坐标为2130,22-+⎛⎫ ⎪⎝⎭，MN 中点坐标为72,22s n t ⎛⎫+ ⎪+ ⎪ ⎪⎝⎭，∴7123s n t ⎧+=⎪⎨⎪+=⎩，解得5292s t ⎧=-⎪⎪⎨⎪=⎪⎩，此时59,22N ⎛⎫- ⎪⎝⎭；当PA 为边长且AM 和PN 是对角线时，此时以点A ，P ，M ，N 为顶点的四边形是菱形∴AM 与PN 互相平分，且PMPA =∴()293184n +-=，解得3732n =±∵PN 中点坐标为23,22s t ++⎛⎫ ⎪⎝⎭，AM 中点坐标为7102,22n ⎛⎫- ⎪+ ⎪ ⎪⎝⎭，∴721230s t n ⎧+=-⎪⎨⎪+=+⎩，解得122s t ⎧=⎪⎪⎨⎪=±⎪⎩，此时137,22N ⎛⎫ ⎪ ⎪⎝⎭或137,22N ⎛- ⎝⎭；同理，当PA 为边长且AN 和PM 是对角线时，此时以点A ，P ，M ，N 为顶点的四边形是菱形∴AN 和PM 互相平分，且AM PA =281184n +=，此方程无解；综上所述，以点A ，P ，M ，N 为顶点的四边形是菱形时59,22N ⎛⎫- ⎪⎝⎭或137,22⎛⎫ ⎪ ⎪⎝⎭或137,22⎛- ⎝⎭；26.【答案】（1）（2）见解析（3）435【解析】（1）解：在Rt ABC 中，90ACB ∠=︒，=60B ∠︒，∴sin 32AC AB B ===，∵BD =，∴AD AB BD =-=（2）证明：如图所示，延长FB 使得FH FG =，连接EH ，∵F 是DE 的中点则DF FE =，FH FG =，GFD HFE ∠=∠，∴()SAS GFD HFE ≌，∴H G ∠=∠，∴EH GC ∥，∴60HEC ECD ∠=∠=︒∵DEC 是等边三角形，∴60DEC EDC ∠=∠=︒，∵60DEC DBC ==︒∠∠，∴,,,B C D E 四点共圆，∴EDB BCE ∠=∠，BEC BDC ∠=∠，∴6060BEH BEC BDC EDB ∠=︒-∠=︒-∠=∠，∵G BCE BDE H ∠=∠=∠=∠，∴H BEH ∠=∠，∴EB BH =，∴FH FG BF BH BF EB ==+=+；（3）解：如图所示，在CD 取得最小值的条件下，即CD AB ⊥，设4AB a =，则2BC a =，AC =，∴24AC BC a CD AB a⨯⨯===，12BD BC a ==，∵将BEM 沿BM 所在直线翻折至ABC 所在平面内得到BNM ．∴BE BN=∴点N 在以B 为圆心，a 为半径的圆上运动，取AB 的中点S ，连接SP ，则SP 是ABN 的中位线，∴P 在半径为12a 的S 上运动，当CP 取最大值时，即,,P S C 三点共线时，此时如图，过点P 作PTAC ⊥于点T ，过点N 作NR AC ⊥于点R ，∵S 是AB 的中点，60ABC ∠=︒∴SC SB BC ==，∴BCS △是等边三角形，则60PCB ∠=︒，∴30PCA ACB BCP ∠=∠-∠=︒，∵2BC a =，4AB a =，∴2CS BC a ==，12PS a =∴52PC a =，15sin 24PT PC PCT PC a =⨯∠==，TC ==∵AC =，∴AT =，如图所示，连接PQ ，交NR 于点U ，则四边形PURT是矩形，∴PU AR ∥，P 是AN 的中点，∴1NU NP UR PA==即PD 是ANR 的中位线，同理可得PT 是ANR 的中位线，∴54NU UR PT a ===，12PU AR AT ===∵BCS △是等边三角形，将BCP 沿BC 所在直线翻折至ABC 所在平面内得到BCQ ，∴2120QCP BCP ∠=∠=︒∴PQ ===则UQ PQ PU =-=-=在Rt NUQ中，432NQ a =∴43432552a NQ CP a ==．。

2024年重庆市中考语文真题A卷(含答案)

重庆市2024年初中学业水平暨高中招生考试语文试题（A卷）（全卷共四个大题，满分150分，考试时间120分钟）注意事项：1．试题的答案书写在答题卡上，不得在试题卷上直接作答。

2．作答前认真阅读答题卡上的注意事项。

3．考试结束，由监考人员将试题卷和答题卡一并收回。

一、语文知识及运用（30分）学校开展“革命精神代代传”主题活动，请你完成以下任务。

任务一：探访英雄城市一踏上重庆的土地，你定会感到无比震撼：巍峨yì______立的大山如刚毅果敢的男子，蜿蜒流淌的江水似妩媚多情的女子，他们互相níng______望，彼此衬托，相得益彰。

就是这样的一座山城，孕育了情感燥热，性格刚勇的重庆人。

他们逢山开路，遇水架桥，将重庆建成了一座令人目眩神迷的魔幻之都。

他们血脉里的勇毅来自哪里？既来自地域文化的熏陶，又来自革命精神的浇灌。

①日本飞机的狂轰滥炸吓不倒重庆人，他们挖掘了无数的防空洞来抵御；②国民党的独裁统治压不垮重庆人，红岩先烈用生命和鲜血做出了响亮的回答。

瞻仰曾家岩50号，我们似乎看到了周恩来忙碌的身影；参观渣滓洞、白公馆，③我们似乎听到了革命先辈的殷殷嘱托……高山巍巍，江流有声。

④将在这里继续演绎英雄的故事，传承革命精神！1.根据拼音写汉字，给加点字注音。

yì（）立蜿．蜒（）妩．媚（）níng（）望2.文段中画横线的词语使用不当的一项是（）A.相得益彰B.孕育C.燥热D.目眩神迷3.文段中画波浪线的句子有语病的一项是（）A.①B.②C.③D.④4.请从以下三个诗句中任选一句，进行引用或化用，写一段话来讴歌先烈。

示例仅供参考，句式不限。

示例：革命前路山重水复，你们以坚定的信念，穿越重重迷雾，终于迎来柳暗花明。

（化用“山重水复疑无路，柳暗花明又一村”）备选诗句：①千磨万击还坚劲，任尔东西南北风。

（郑燮《竹石》）②人生自古谁无死？留取丹心照汗青。

（文天祥《过零丁洋》③长风破浪会有时，直挂云帆济沧海。

统编版2024七年级语文上册-第四单元 A卷-提升卷(原卷版+答案)

第四单元A卷·提升卷（考试时间：70分钟试卷满分：100分）（一）积累与运用（36分）1.阅读下面的材料，完成下面小题。

（15分）一个外国人，毫无利己的动机，把中国人民的解放事业当作他自己的事业，这是什么精神？这是国际主义的精神，这是共产主义的精神，每一个中国共产党员都要学习这种精神。

列宁主义认为[A]资本主义国家的无产阶级要拥护殖民地半殖民地人民的解放斗争[B]殖民地半殖民地的无产阶级要拥护资本主义国家的无产阶级的解放斗争[C]世界革命才能胜利[D]白求恩同志是实践了这一条列宁主义路线的。

我们中国共产党员也要实践这一条路线。

我们要和一切资本主义国家的无产阶级________起来，才能打倒．帝国主义，解放我们的民族和人民，解放世界的民族和人民。

这就是我们的国际主义，这就是我们用以________狭隘．民族主义和狭隘爱国主义的国际主义。

白求恩同志毫不利己专门利人的精神，表现在他对工作的极端的负责任，对同志对人民的极端的热忱．。

每个共产党员都要学习他。

不少的人对工作不负责任，________，把重担子推给人家，自己挑轻的。

①一事当前，先替自己打算，然后再替别人打算。

②出了一点力就觉得了不起，喜欢自吹，生怕人家不知道。

③对同志对人民不是满腔热忱，而是冷冷清清，________，麻木不仁．。

④从前线回来的人说到白求恩，没有一个不佩服，没有一个不为他的精神所感动。

晋察冀边区的军民，凡亲眼受过白求恩医生的治疗和亲身看过白求恩医生的工作的，无人为之感动。

每一个共产党员，一定要学习白求恩同志的这种真正共产主义者的精神。

（1）下列加点字的字音或字形，不正确．．．的一项是（）（3分）A．打倒．B．狭隘．（yì）C．热忱．（chén）D．麻木不仁．（2）依次填入文中横线处的词语，恰当．．的一项是（）（3分）A．结合反抗拈轻怕重漠不关心B．联合反对拈轻怕重漠不关心C．联合反抗漠不关心拈轻怕重D．结合反对漠不关心拈轻怕重（3）文中方括号中填入的标点符号，不正确．．．的一项是（）（3分）列宁主义认为[A]资本主义国家的无产阶级要拥护殖民地半殖民地人民的解放斗争[B]殖民地半殖民地的无产阶级要拥护资本主义国家的无产阶级的解放斗争[C]世界革命才能胜利[D]白求恩同志是实践了这一条列宁主义路线的。

【单元测试】最新人教部编版小学五年级上册语文第二单元分层训练A卷【基础篇含答案】

【单元测试】五年级语文上册第二单元分层训练A卷（基础篇）时间：90分钟满分：100分班级：姓名：得分： .第一部分：积累运用(48分)一、看拼音，写词语。

（6分）lǎn duò pínɡhénɡyǔn nuò（）（）（）dǎn qièzhào jí yǐn bì（）（）（）二、把下列词语补充完整，并完成练习。

(9分)难．( )( )信．()发冲()同()()尽()()不提1．描写神态的词语是______________，这样的词语我也能写两个：__________________、__________________。

(3分)2．将加点词语的意思用具体的情景表现出来。

(2分)________________________________________________________________________________________________________________________________________________________________________三、选择题。

(12分)1．[字音]下列词语中，加点字的读音完全正确的一项是()。

A．汛．期(xùn) 上卿．(qīng)游隼．(sǔn) 吆．喝(yāo)B．大臣．(chén) 允诺．(ruò) 浩瀚．( hàn) 侵略．(lùe)C．侮辱．(rǔ) 冠．军(guàn) 任．丘(rèn) 人影绰．绰(zhuó)D. 强．逼(qiáng) 间．隔(jiàn) 孑．口( jié) 搁．东西(gē)2．[字音]“髎”可能与()读音相同。

A．渺B．廖C．鹘D．榾3．[字形]下列词语中，书写完全正确的一项是()。

A．暴发联洁称赞同心协力B．胆怯防碍平衡完壁归赵C．隐敝唯独俯冲无穷无尽D．召集修筑职位难以置信4．[字义]会意字“嘦”的意思最可能是()。