概率统计分布表常用
(最全)高中数学概率统计知识点总结

概率与统计一、普通的众数、平均数、中位数及方差1、 众数 :一组数据中,出现次数最多的数。
2、平均数 : ①、常规平均数:xx 1x 2x n②、加权平均数: xx 1 1 x 2 2x nnn12n3、中位数: 从大到小或者从小到大排列,最中间或最中间两个数的平均数 。
4、方差: s 21[( x 1 x) 2 ( x 2 x )2( x nx )2 ]n二、频率直方分布图下的频率1、频率 =小长方形面积: f S y 距 d ;频率 =频数 / 总数2、频率之和 : f 1f 2f n 1 ;同时 S 1 S 2S n1 ;三、频率直方分布图下的众数、平均数、中位数及方差1、众数: 最高小矩形底边的中点。
2、平均数: x x 1 f 1 x 2 f 2 x 3 f 3 x n f nx x 1 S 1 x 2 S 2x 3 S 3x n S n3、中位数: 从左到右或者从右到左累加,面积等于0.5 时 x 的值。
4、方差: s 2( x 1x )2 f 1 ( x 2 x) 2 f 2( x n x) 2 f n四、线性回归直线方程 : ? ? ?bxy an(x ix )( y iy )nx i y i nxy??其中: b i 1i 1,a?ybxnn( x i x )2x i 2nx 2i 1i11、线性回归直线方程必过样本中心( x , y ) ;??0 : 负相关。
2、 b 0 : 正相关; b?3、线性回归直线方程: y? ?bx a?的斜率 b 中,两个公式中分子、分母对应也相等;中间可以推导得到。
五、回归分析?i1、残差 : ?iy i?i 越小越好;ey (残差 =真实值—预报值)。
分析:e2、残差平方和 :n? )2(y i,i 1y in( y iy )2( y 1 y )2 ( yy )2( yy )2分析:①意义:越小越好;②计算:?i?12?2n?ni 1n ?i )23、拟合度(相关指数) : R 21( yy ,分析:① . R 20,1②. 越大拟合度越高;i 1的常数;ny)2i ( y i1nn4、相关系数 : ri ( x i x )( y i y)x i y i nx y1i 1nx)2 ny) 2 nx) 2 ny )2i 1( x i i ( y i( x i ( y i1i 1i 1分析:① . r[ 1,1]的常数;② . r 0: 正相关; r0: 负相关③. r[0,0.25] ;相关性很弱;r(0.25,0.75) ;相关性一般;r [0.75,1] ;相关性很强;六、独立性检验 x 1 x 21、2×2 列联表 :合计2、独立性检验公式 bc)2y 1 a b a b ①. k 2(an( add )y 2cdc db)(c d )(a c)(b合计a cb dn②.犯错误上界 P 对照表3、独立性检验步骤①.计算观察值n(ad bc) 2k : k;(a b)(c d )(a c)(b d )②.查找临界值 k0:由犯错误概率P,根据上表查找临界值k0;③.下结论: k k0:即犯错误概率不超过P 的前提下认为:, 有 1-P 以上的把握认为:;k k0:即犯错误概率超过P 的前提认为:,没有 1-P 以上的把握认为:;【经典例题】题型 1 与茎叶图的应用例 1( 2014 全国)某市为考核甲、乙两部门的工作情况,学科网随机访问了50 位市民。
t分布表_精品文档

t分布表1. 什么是t分布表t分布表是一种统计学中常用的工具,用于计算t分布的累积概率。
t分布是一种概率分布,通常用于小样本(样本量较小)情况下对样本均值的推断。
t分布表中列出了在给定自由度和置信水平下的t值和对应的累积概率。
2. t分布表的用途t分布表主要用于解决以下两个问题:a. 给定t值,计算对应的累积概率在统计学中,我们经常需要计算一个t值对应的累积概率,即给定某个t值,求该t值以下的面积。
这可以用t分布表来完成。
用户只需要在t分布表中找到对应的自由度和置信水平,即可得到该t值以下的累积概率。
b. 给定累积概率,计算对应的t值在一些统计推断问题中,我们需要给定累积概率,求该累积概率对应的t值。
例如,在假设检验中,我们常常需要计算一个t临界值,该值将样本均值与总体均值进行比较。
t分布表可以帮助我们找到给定累积概率下的t值。
3. 如何使用t分布表在使用t分布表时,我们需要知道两个关键的输入参数:自由度和置信水平。
a. 自由度自由度(degrees of freedom)是t分布中的一个重要参数。
对于给定的问题,自由度等于样本中独立观察值的数量减1。
例如,若样本容量为10个,则自由度为9。
b. 置信水平置信水平是统计推断中常用的一个指标,用于表示结果的可靠性。
常见的置信水平有0.95(95%置信水平)和0.99(99%置信水平)等。
较高的置信水平意味着对结果的可靠性更高。
使用t分布表的步骤如下:1.确定问题中的自由度和置信水平;2.在t分布表中找到相应的自由度;3.在该行中找到置信水平对应的列;4.交叉点的数值即为t值。
4. t分布表的局限性在使用t分布表时,需要注意其一些局限性:•只能用于正态分布情况下的小样本(样本量较小)推断;•对于较大的自由度,t分布和正态分布的差异较小,所以在样本量大的情况下,通常可以使用正态分布近似代替t分布;•t分布表只给出了常见自由度和置信水平下的数值,若需要计算其他自由度或置信水平下的值,需要使用统计软件或计算工具进行计算。
常见的离散型随机变量的概率分布标准版文档

(II) 贝努里概型 和 二项分布 例6 设生男孩的概率为p,生女孩的概率为 q=1-p,令X表示随机抽查出生的4个婴儿 中“男孩”的个数.
我们来求X的概率分布.
X表示随机抽查的4个婴儿中男孩的个数,
生男孩的概率为 p.
男女
X=0 X =1 X =2 X =3 X =4
X的概率分布是:
X可取值0,1,2,3,4.
X()=
1, = 1 0, = 2
例 5 200件产品中,有196件是正品,4
件是次品,今从中随机地抽取一件,若规
定
1, 取到合格品
X()=
0, 取到不合格品
则 P{X=1}=196/200=0.98, P{X=0}=4/200=0.02
故 X服从参数为0.98的两点分布 . 即 X ∼ B(1,0.98).
注: 贝努里概型对试验结果没有等可能 的要求,但有下述要求: (1)每次试验条件相同;
(2)每次试验只考虑两个互逆结果A或 A ,
且P(A)=p ,P(A)1p; (3)各次试验相互独立.
二项分布描述的是n重贝努里试验中出现 “成功”次数X的概率分布.
例8 某类灯泡使用时数在2000小时以上视为正 品.已知有一大批这类的灯泡,其次品率是0.2. 随机抽出20只灯泡做寿命试验,求这20只灯泡 中恰有3只是次品的概率.
X= X1+X2+ +Xn 其密度函数和分布函数常用 和
表示:
~N(0,1)
(IV)、标准正态分布
0,1的正态分布称为标准正态分布.
其密度函数和分布函数常用 (x)和(x)表示:
(x)
1
x2
e2,
x
2
(x) 1
概率分布与统计图表

心,左右对称。 2. 在 在 处取得概率密度函数的最大值, 处有拐点,表现为 钟形曲线。即正
对称。即态分布以均数为中
态曲线在横轴上方均数处最高。
2018/10/26
6
3. 正态分布有两个参数,即均数µ 和标准差σ。
µ 是位置参数,σ是变异度参数(形状参数)。常用
N(µ ,σ2)表示均数为μ ,标准差为σ的正态分布;用
( 2)
2018/10/26
16
( 3)
查附表1,标准正态分布曲线下左侧面积为0.10所对应
的Z值为-1.28,所以80%的8岁男孩身高值集中在
X 1.28S 区间内,即116.9cm~129.2cm
2018/10/26
17
练习:
查附表,求标准正态分布曲线下的面积。 (-∞,-1.96),( -∞ ,-2.58), (-1.96,1.96),(-1,1),( -∞ ,0.00)。
,
S=4.79 cm ,估计(1)该地8岁男孩身高在130 cm以上者占该地8岁 男孩总数的百分比;(2)身高界于120cm~128cm者占该地8岁男孩
总数的比例;(3)该地80%男孩身高集中在哪个范围?
先做标准化变化:
理论上该地8岁男孩身高在130 cm以上者占该地8岁男孩 总数的7.21%。
2018/10/26 15
分析:正常人的血红蛋白过高过低均为异常,要制
定双侧正常值范围。
该指标的95%医学参考值范围为
2018/10/26 21
例4 某地调查110名正常成年男子的第一秒肺通 气量,得均数为4.2 L,标准差为0.7 L ,试估计该地 正常成年男子第一秒肺通气量的95%参考值范围。
分析:正常人的第一秒肺通气量近似正态分布,且只
卡方分布表

卡方分布表
卡方分布表是数学、统计学中常用的一种工具,它用于
帮助人们计算卡方分布的概率值。
卡方分布是一种重要的概率分布,它在统计学中具有广泛的应用。
卡方分布表中所列出的数值代表着不同自由度下的卡方
统计量与对应的概率值。
卡方统计量是用来衡量观察值与期望值之间的差异程度的,它的计算方式需要使用到频数和期望频数,因此广泛应用于假设检验和拟合优度检验等领域。
卡方分布表一般是按照不同自由度分别列出来的,常见
的有1自由度、2自由度、3自由度等,数值从0开始,依次
递增。
使用卡方分布表时,我们可以通过查找对应的自由度和相应的卡方统计量来得到概率值。
例如在1自由度下,如果卡方统计量为3.84,它对应的概率值为0.05,这表示了卡方统
计量为3.84时,有5%的概率出现在1自由度下。
在实际应用中,卡方分布表被广泛应用于各种统计分析中,比如拟合优度检验、协方差分析、参数估计等,它可以帮助人们计算出卡方统计量的概率值,并且从而进行假设检验。
比如,在进行拟合优度检验时,我们可以通过计算观察频数和期望频数之间的卡方统计量,并通过查找卡方分布表来获取对应的概率值,进而决定是否拒绝原假设。
总体来说,卡方分布表是一种十分有用的统计学工具,
它在统计分析中发挥着重要的作用,能够帮助人们进行各种假设检验并进行数据分析。
需要注意的是,在使用卡方分布表时,我们要根据具体的实际情况选择对应自由度的卡方分布表,并
且正确地解读概率值。
通过充分理解和运用卡方分布表,可以更好地进行数据分析和统计研究。
概率统计分布表(常用)
标准正态表.n\p 0.005 0.010 0.025 0.050 0.100 0.250 0.750 0.900 0.950 0.975 0.990 0.995.T分布....F分布.P= 0.99.......Excel公式1.正态分布函数Excel计算正态分布时,使用NORMDIST函数,其格式如下:NORMDIST(a,μ,σ,累积)其中,“累积”:若为TRUE,则输出分布函数值,即P{X≤a};若为FALSE,则为概率密度函数值.示例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式NORMDIST(500, 600, 100, TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.2、正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(p,μ ,σ ),此公式计算a,使P{X ≤a}=p3标准正态分布反函数=NORMSINV(0.975)3、t分布Excel计算t分布的值,采用TDIST函数,格式如下:TDIST(a,自由度,侧数)其中,“侧数”:指明分布为单侧或双侧:.若为1,为单侧;此命令输出P{ T >a }若为2,为双侧.此命令输出P{ |T| >a}示例:设T服从自由度为24的t分布,求P(T>1.711).已知t=1.711,df=24,采用单侧,则T分布的值:TDIST(1.711,24,1)得到0.05,即P(T > 1.711)=0.05.4. t分布的反函数Excel使用TINV函数得到t分布的反函数,格式如下:TINV(α,自由度)输出T 分布的α / 2 分位点:t_α/2_(n)若求临界值tα(n),则使用公式=TINV(2*α, n)5.返回F分布的函数是FDISTFDIST(x,degrees_freedom1,degrees_freedom2)函数FDIST 的计算公式为FDIST=P( F>x ),5.F分布的反函数FINV(probability,deg_freedom1,deg_freedom2)已知probability=P( F>x ),求x.。
正态分布概率表95%

正态分布概率表95%
正态分布概率表是一种统计学中常用的概率分布表,它可以用来描述一组数据的分布情况。
正态分布概率表95%是指,在正态分布中,95%的数据位于平均值的两个标准差之内。
正态分布概率表95%的应用非常广泛,它可以用来分析一组数据的分布情况,从而更好地了解数据的特征。
此外,正态分布概率表95%还可以用来估计一组数据的概率分布,从而更好地预测数据的变化趋势。
正态分布概率表95%也可以用来评估一组数据的稳定性,如果95%的数据都位于平均值的两个标准差之内,则说明数据的分布情况较为稳定,可以更好地进行分析和预测。
正态分布概率表95%也可以用来评估一组数据的可靠性,如果95%的数据都位于平均值的两个标准差之内,则说明数据的可靠性较高,可以更好地进行分析和预测。
总之,正态分布概率表95%是一种非常有用的统计工具,它可以用来分析一组数据的分布情况,从而更好地了解数据的特征,并可以用来评估数据的稳定性和可靠性。
(卫生统计学)第四章 常用概率分布

第二节 Poisson分布的概念与特征
一、Poisson分布概念与特征
若某一随机变量X的取值为0,1,2,…,且X=k 的概率为:
P(X k) k e
k!
记作 X~P( λ )
其中 自然数e≈2.7182; λ 是大于0的常数,称X服从以λ 为参数的Poisson分布。
Poisson分布主要用于描述在单位时间(空间)内稀有事件的发生数。例如:放 射性物质在单位时间内的放射次数、单位容积内充分摇匀的水中的细菌数、染色 体异变数等。
350 300 250 200
人数
150 100
50 0
109 111 113 115 117 119 121 123 125 127 129 131 133 135 137 139 141 143
不同参数µ和σ下的正态分布曲线
正态分布函数
1.Gauss函数 (Gauss, 1777~1855 德国人)
某地正常成人心率(次/分)的频率分布
频数 1 5 12 13 26 31
组段 75~ 80~ 85~ 90~ 95~ 100~105
频数 24 15 9 7 5 2
心率频数分布
35
30
25
20
人数
15
10
5
0
45
50
55
60
65
70
75
80
85
90
95 100~105
正态曲线
例4-10 某地1986年120名8岁男孩身高频数图
百分位数法
例4-13
282名正常人尿汞值(g/L)测量结果
尿汞值 0~ 8.0~
16.0~ 24.0~ 32.0~ 40~ 48.0~ 56.0~ 64.0~72.0
常用概率分布间简介

其中 c 为常数,解方程(1)得
f ( ) c f ( )
f
(
)
k
e
1 2
c
2
,
k
为常数.
为使 f ( ) 为概率密度函数,
f
( )d
1,
即
k
e
1 2
c
2
dy
1
故必须 c 0 ,不妨令 c 1 ( 0 ),代入(2)解得 2
k 1 , 2 Biblioteka 于是f ( ) 1
2
e2 2 , R ,
2
这是均值为 0,方差为 2 的正态分布的概率密度函数.
.
X
~
N(0, 2)
,
则Y
X2
~
Ga(
1 2
,
1 2
2
)
.
(1) (2)
Ga( n , 1) 2(n) . 22
m
Xi ~ N(0,1) , i 1,2,,n 且相互独立 , 则 X
X
2 i
~
2(n) .
i 1
⒊ 相当误差(比率)的概率分布
m
设
Xi
~
N(0, 2 ) ,i
1,2,, m,m 1,,m n且相互独立,则
i 1
二、随机误差的概率分布
⒈ 高斯随机误差模型 随机变量的高斯分解
可观测的指标
X
不可观测的随机干扰
指标的标准值(生产控制参数,理论均值)
原始测量误差的概率分布
由棣莫弗提出,高斯推证,拉普拉斯再证,原始测量误差的概率分布为:
~ N (0 , 2 )
高斯的推证要点如下:
设测量误差 X 的密度函数为 f ( ) ,由“最大后验概率”的原则得
第3节 常用统计分布(三个常用分布)

例2
设X
~
N
(
,
2
),
Y
2
~
2 (n),且X ,Y相互独立,
试求 T X 的概率分布.
Yn
解 因为X ~ N(, 2),所以 X ~ N(0,1)
又Y
2
~
2 (n),且X ,Y独立,则
X
与Y
2
独立,
由定理得
T (X ) / X ~ t(n) (Y / 2) / n Y n
n
事实上,它们受到一个条件的约束:
Xi nX
i 1
n
i 1
Xi
X
1
n
(
i 1
Xi
nX )
1
0
0.
例1
设X1 ,
X 2 ,
,
X
为
6
来
自
正
态
总
体N
(0,1)的
一
组
样
本,
求C1
,
C
使
2
得
Y C1( X1 X 2 )2 C2( X 3 X4 X5 X6 )2
服 从 2分 布.
解
X1
2
4
则C1 1 2 ,C2 1 4 .
3. t 分布 定义 设 X ~ N (0, 1), Y ~ 2 (n), 且 X , Y
独立,则称随机变量 T X 服从自由度为 n Y /n
的 t 分布, 记为T ~ t(n).
t 分布又称学生氏(Student)分布. t(n) 分布的概率密度函数为
2. 2分布(卡方分布)
定义、设 X1, X 2 ,L , X n 相互独立,同服从 N (0, 1)
概率论与数理统计第四章_几种重要的分布

ξ
0
1
2
3
4
p 0.0016 0.0256 0.1536 0.4096 0.4096
4.2超几何分布(了解)
主要内容: (一)了解超几何分布的概念 (二)了解超几何分布的期望和方差
4.2超几何分布
例1 某班有学生20名,其中有5名女同学,今从 班上任选4名学生去参观展览,被选到的女同学数ξ
k1 (k 1)!(n k)!
n
(k 11)n! pk (1 p)nk
k1 (k 1)!(n k)!
n
(k 1)n!
n
pk (1 p)nk
n!
pk (1 p)nk
k1 (k 1)!(n k)!
k1 (k 1)!(n k)!
n
n!
n
pk (1 p)nk
n!
pk (1 p)nk
k2 (k 2)!(n k)!
解 可以取0,1,2,3这4个值。
P(
=k)=
C3k
C4k 17
C420
(k=0,1,2,3,)
列成概率分布如下
ξ
0
1
2
3
p 0.4912 0.4211 0.0842 0.0035
定义42 设N个元素分为两类,有N1个属于第一类, N2个属于第二类(N1+N2=N)。从中按不重复抽 样取n个,令ξ表示这n个中第一(或二)类元素的个数,
k1 (k 1)!(n k)!
n2
n1
n(n 1)Cnl 2 pl2 (1 p)n2l nCnj1 p j1(1 p)n1 j
l0
j0
n2
n(n 1)Cnl 2 pl2 (1 p)n2l l0
第4章 几种常见的概率分布

6. 正态分布的单双侧临界值
面积为,已知 上侧临界值 P(U> u )= α ,下侧临界值 P (U <- u )= α (附表 3 上侧临界值)
若将一定曲线下面积α,平分到两侧尾区,则每侧曲线下面积为α/2,
即 P(
U U 2
)=
α,
U 这时的
U
2
称为α的双侧临界值。
面积为,已知
u 称为的上侧临界值。 附表3 (256页)给出了u的值。
N(0,1)
x=0 时,φ(x) 达到最大值
(1) 关于点(0,0.5)对称,该点也
是它的拐点
(2)x 取值离原点越远,φ (x) 值越小 (2) 曲线以 y = 0 和 y = 1 为渐近线;
(3)关于 y 轴对称,即φ(x)= φ (- x)
(3) Ф(1.960)-Ф(-1.960) = 0.95
种变量有它各自的概率而组成一个分布。这个分布就叫做二项概率分布,或简称二项分布
(binomial distribution) 由此得到计算二项分布任何一项概率的通式为:p(x) =Cnx φ
x(1- φ)n-x
二项分布是一种离散型随机变量的概率分布
性质
n
Cnx x (1 )nx 1
x0
m
一指定时间范围内或在指定的面积或体积内某一事件出现的个体数的分布 泊松分布是一种离散型随机变量的概率分布
实例 调查某种猪场闭锁育种群仔猪畸形数,共记录 200 窝, 畸形仔猪数的分布情况如下表所
示。试判断畸形仔猪数是否服从泊松分布。 畸形仔猪数统计分布
解:根据泊松分布的平均数与方差相等这一特征,若畸形仔猪数服从泊松分布,则由观察数 据计算的平均数和方差就近于相等。样本均数和方差 S2 计算结果如下:
第5章 常用概率分布2

正态分布的参数
1
2
3
图9 标准差相同、均数不同的正态分布曲线
正态分布的参数
σ1 σ2 σ3 σ1<σ2<σ3
图10 均数相同、标准差不同的正态分布曲线
正态分布
二、正态概率密度曲线下的面积规律
正态曲线下面积总和为1;
正态曲线关于均数对称;对称的区域内面积相等; 对任意正态曲线,按标准差为单位,对应的面积相 等;
计算z值:
z1 x1
( 1.96 )
1.96
z2
x2
( 1.96 )
1.96
0.025 1.96
查附表1:确定概率 结论:95%
0.025 -1.96
正态分布
例 已知X服从均数为 、标准差 为的正态分布, 1 .96 试估计:(1)X取值在区间 上的概率; (2)X 取值在区间 上的概率。 2.58
记为N(0,1)。 标准正态分布是一条曲线。
标准正态分布曲线下的面积
μ±1范围内的面积为68.27% μ±1.96范围内的面积为95%
μ±2.58范围内的面积占99%
图12 正态曲线下的面积分布示意
标准正态分布曲线下的面积的计算
求z值,用z值查表,得到所求区间面积占总面
积的比例。 曲线下对称于0的区间,面积相等。 曲线下总面积为100%或1。
计算z值:
Z 130 123 .02 1.46 4.79
查附表1:确定概率
0.0721 0.0721 1.46
结论:7.21%
-1.46
概率论与数理统计几种重要的分布

二、二项分布
例1、一批产品的合格率为0.9,重复抽取三次, 每次一件, 连续3次,求3次中取到的合格品件数 X的分布.
如果在一次试验中,事件A成功的概率为 p(0 p 1), 则在n重贝努里试验中事件 A成功的次数 X的分布为 :
P(X
k)
C
k n
pkqnk .
1、定义 X ~ B(n, p)
P(X
k)
C
k 3
C 4 17
k
C
4 20
(k 0,1,2,3)
1、定义 X ~ H (n, M , N )
设N个元素分为两类,
其中N
1个属于第一类,
N
个属于
2
第二类, 从中不放回抽取n个, 令X表示这n个中第一类
元素的个数,则称X的分布为超几何分布 :
P(X
m)
C C m nm N1 N N1
若X的分布为P( X
k)
C
k n
pkqnk , k
0,1,, n
其中0 p 1, q 1 p,则称X ~ B(n, p)。
2、数字特征
EX
n
kC
k n
k 0
pkqnk
n
k
k0
n! k!(n k)!
pk q nk
n
n (n 1)!
p p q k 1 (n1)(k 1)
k1 (k 1)! (n 1) (k 1) !
kkekxpk01只有两个互逆结果的n次独立重复试验n1pmin10nmllkccckxpnnknnmkm10211kppkxpk无穷次伯努利试验中a首次发生的试验次数对含有两类元素的有限总体进行不放回抽样时某类元素个数的概率分布在一定时间内出现在给定区域的随机质点的个数一均匀分布1定义
标准泊松分布表

标准泊松分布表
介绍
标准泊松分布是概率论和统计学中常用的一种离散性概率分布。
它描述了在一定时间内一个事件发生的次数的概率分布情况,适用
于一些与时间相关的事件,如电话的呼叫次数、邮件的收件次数等。
计算方法
计算标准泊松分布的概率可以借助泊松分布表来进行。
泊松分
布表是一个包含了不同事件发生次数的概率值的表格,可以用于计
算特定事件发生次数的概率。
标准泊松分布表一般以参数λ表示,其中λ为单位时间内该事
件平均发生的次数。
通过查表,可以找到给定λ值和特定事件发生
次数的概率。
使用示例
假设某项事件在一分钟内平均发生5次,我们想要知道在该分
钟内发生0次、1次、2次等事件的概率。
我们可以通过标准泊松
分布表来找到相应的概率。
使用该表格,我们可以快速找到特定事件发生次数的概率,从而对事件发生的概率进行分析和预测。
注意事项
在使用标准泊松分布表时,需要确保所使用的λ值符合标准泊松分布的要求。
此外,使用该表格进行计算时,需要注意查找正确的事件发生次数和相应的概率值。
总结
标准泊松分布表是一种用于计算标准泊松分布概率的工具。
通过查表,可以快速找到特定事件发生次数的概率,从而进行概率分析和预测。
在使用该表格时,需要注意参数λ的正确性和查找准确的概率值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
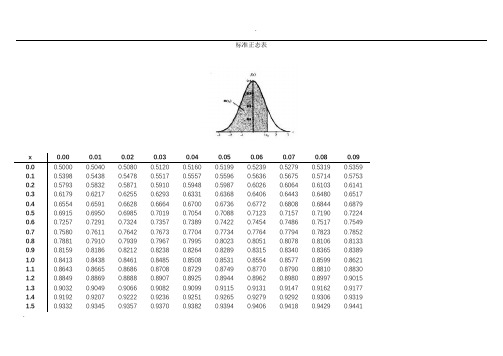
标准正态表x 0.00 0.01 0.02 0.03 0.04 0.05 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.82891.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.96781.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.97442.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.98422.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.99782.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.99843.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.99963.4 0.9997 0.9997 0.9997 0.9997 0.9997 0.99973.5 0.9998 0.9998 0.9998 0.9998 0.9998 0.99983.6 0.9998 0.9998 0.9999 0.9999 0.9999 0.99993.7 0.9999 0.9999 0.9999 0.9999 0.9999 0.99993.8 0.9999 0.9999 0.9999 0.9999 0.9999 0.99993.9 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000n\p 0.005 0.010 0.025 0.050 0.100 0.250 0.750 0.900 0.9501 0.0000 0.0002 0.0010 0.0039 0.0158 0.1015 1.3233 2.7055 3.84152 0.0100 0.0201 0.0506 0.1026 0.2107 0.5754 2.7726 4.6052 5.99153 0.0717 0.1148 0.2158 0.3518 0.5844 1.2125 4.1083 6.2514 7.81474 0.2070 0.2971 0.4844 0.7107 1.0636 1.9226 5.3853 7.7794 9.48775 0.4117 0.5543 0.8312 1.1455 1.6103 2.6746 6.6257 9.2364 11.07050.6757 0.8721 1.2373 1.6354 2.2041 3.4546 7.8408 10.6446 12.59160.9893 1.2390 1.6899 2.1673 2.8331 4.2549 9.0371 12.0170 14.06711.3444 1.64652.1797 2.73263.4895 5.0706 10.2189 13.3616 15.50731.73492.0879 2.70043.32514.16825.8988 11.3888 14.6837 16.91902.1559 2.55823.2470 3.94034.8652 6.7372 12.5489 15.9872 18.30702.60323.0535 3.81574.57485.5778 7.5841 13.7007 17.2750 19.67513.0738 3.57064.40385.22606.3038 8.4384 14.8454 18.5493 21.02613.56504.10695.0088 5.8919 7.0415 9.2991 15.9839 19.8119 22.36204.0747 4.66045.62876.57067.7895 10.1653 17.1169 21.0641 23.68484.60095.22936.26217.26098.5468 11.0365 18.2451 22.3071 24.99585.1422 5.81226.90777.9616 9.3122 11.9122 19.3689 23.5418 26.29625.69726.40787.5642 8.6718 10.0852 12.7919 20.4887 24.7690 27.58716789 10 111213141516176.26487.01498.23079.3905 10.8649 13.6753 21.6049 25.9894 28.86936.84407.63278.9065 10.1170 11.6509 14.5620 22.7178 27.2036 30.14357.4338 8.2604 9.5908 10.8508 12.4426 15.4518 23.8277 28.4120 31.41048.0337 8.8972 10.2829 11.5913 13.2396 16.3444 24.9348 29.6151 32.67068.6427 9.5425 10.9823 12.3380 14.0415 17.2396 26.0393 30.8133 33.92449.2604 10.1957 11.6886 13.0905 14.8480 18.1373 27.1413 32.0069 35.17259.8862 10.8564 12.4012 13.8484 15.6587 19.0373 28.2412 33.1962 36.415010.5197 11.5240 13.1197 14.6114 16.4734 19.9393 29.3389 34.3816 37.652511.1602 12.1981 13.8439 15.3792 17.2919 20.8434 30.4346 35.5632 38.885111.8076 12.8785 14.5734 16.1514 18.1139 21.7494 31.5284 36.7412 40.113312.4613 13.5647 15.3079 16.9279 18.9392 22.6572 32.6205 37.9159 41.337113.1211 14.2565 16.0471 17.7084 19.7677 23.5666 33.7109 39.0875 42.557018192021 22 2324252627282913.7867 14.9535 16.7908 18.4927 20.5992 24.4776 34.7997 40.2560 43.773014.4578 15.6555 17.5387 19.2806 21.4336 25.3901 35.8871 41.4217 44.985315.1340 16.3622 18.2908 20.0719 22.2706 26.3041 36.9730 42.5847 46.194315.8153 17.0735 19.0467 20.8665 23.1102 27.2194 38.0575 43.7452 47.399916.5013 17.7891 19.8063 21.6643 23.9523 28.1361 39.1408 44.9032 48.602417.1918 18.5089 20.5694 22.4650 24.7967 29.0540 40.2228 46.0588 49.801817.8867 19.2327 21.3359 23.2686 25.6433 29.9730 41.3036 47.2122 50.998518.5858 19.9602 22.1056 24.0749 26.4921 30.8933 42.3833 48.3634 52.192319.2889 20.6914 22.8785 24.8839 27.3430 31.8146 43.4619 49.5126 53.383519.9959 21.4262 23.6543 25.6954 28.1958 32.7369 44.5395 50.6598 54.572220.7065 22.1643 24.4330 26.5093 29.0505 33.6603 45.6160 51.8051 55.758521.420822.9056 25.2145 27.3256 29.9071 34.5846 46.6916 52.9485 56.942430 313233 34 35363738394041T分布0.75 0.80 0.85 0.90 0.95 0.997 0.999 0.9990.975 0.990 0.995p 0 0 0 0 0 5 0 5A1.00 1.37 1.96 3.07 6.31 12.70 31.82 63.65 127.32 318.30 636.61100 642677 386205 67 1388920.81 1.06 1.38 1.88 2.92 4.302 6.964 9.924 14.089 22.327 31.599 265 07 62 56 00 7 6 8 0 1 10.76 0.97 1.24 1.63 2.35 3.182 4.540 5.840 10.214 12.924 3 7.453349 85 98 77 34 4 7 9 5 04 0.74 0.941.18 1.532.13 2.7763.7464.6045.5976 7.1732 8.610342 22.1385 23.6501 25.9987 28.1440 30.7654 35.5099 47.7663 54.0902 58.124043 22.8595 24.3976 26.7854 28.9647 31.6255 36.4361 48.8400 55.2302 59.303544 23.5837 25.1480 27.5746 29.7875 32.4871 37.3631 49.9129 56.3685 60.480945 24.3110 25.9013 28.3662 30.6123 33.3504 38.2910 50.9849 57.5053 61.656207 10 96 32 181.151.472.01 2.5703.3644.0324.77335.8934 5859506 910.72 0.91 5 67956.8688 1.431.942.4463.142 9832970.71 0.90 1.13 6 7657423.7074.31685.2076 45.9588 0.71 0.89 1.11 7 1160921.892.364 2.9983.4994.0293 4.7853 46651.41 495.4079 1.391.852.306 2.896 689550.70 0.88 1.10 8 6489813.3553.83254.5008 45.0413 1.381.832.262 2.821 3031 2 40.70 0.88 1.09 9 2734973.2493.68974.2968 84.7809 0.69 0.87 1.09 1.37 10989131221.812.228 2.7633.1693.58144.1437 251 834.58690.69 0.87 1.081.36 11745577 341.792.2012.7183.1053.49664.0247 59184.43700.69 0.87 1.08 1.35 1.78 2.178 2.6813.0543.4284 3.92964.317855 263262238 050.690.871.071.351.772.1602.6503.0123.3725 3.85204.220838029502094330.69 0.861.071.341.762.1442.624 2.9763.3257 3.78744.1405 24 81 63 50 13 8 580.69 0.861.071.341.752.1312.602 2.9463.2860 3.73284.0728 12 62 35 06 31 4 570.69 0.861.071.331.742.1192.583 2.9203.2520 3.68624.0150 01 47 11 68 59 9 580.68 0.861.061.331.732.1092.566 2.8983.2224 3.6458 3.9651 92 33 90 34 96 8 920.68 0.861.061.331.732.1002.552 2.8783.1966 3.6105 3.921684207204419440.68 0.861.061.321.722.0932.539 2.8603.1737 3.5794 3.8834 761055 77 91 0 5912131415161718190.68 0.86 1.06 1.32 1.72 2.086 2.528 2.8453.1534 3.5518 3.8495 70 0040534730.680.851.061.321.722.0792.517 2.8313.1352 3.5272 3.819364912732076640.68 0.851.061.321.712.0732.508 2.8183.1188 3.5050 3.7921 58 83 14 12 71 9 380.68 0.851.061.311.712.0682.499 2.8073.1040 3.4850 3.7676 53 75 03 95 39 7 930.68 0.851.051.311.712.0632.492 2.7963.0905 3.4668 3.7454 48 69 93 78 09 9 290.68 0.851.051.311.702.0592.485 2.7873.0782 3.4502 3.7251 44 62 84 63 81 5 140.68 0.851.051.311.702.0552.478 2.7783.0669 3.4350 3.706640577550565670.68 0.851.051.311.702.0512.472 2.7703.0565 3.4210 3.6896 3751 67 37 33 8 7720212223242526270.68 0.85 1.05 1.31 1.70 2.048 2.467 2.7633.0469 3.4082 3.6739 2834 46 60 25 1130.68 0.85 1.05 1.312930 42 53 14 1.69 2.045 2.462 2.7563.0380 3.3962 3.6594 91 2 0 40.68 0.85 1.05 1.313028 38 47 04 1.69 2.042 2.457 2.7503.0298 3.3852 3.6460 73 3 3 00.68 0.85 1.05 1.33125 34 41 95 1.69 2.039 2.452 2.7443.0221 3.3749 3.6335 55 5 8 00.68 0.85 1.05 1.3 3222 30 35 86 1.69 2.036 2.448 2.7383.0149 3.3653 3.6218 39 9 7 50.68 0.85 1.05 1.33320 26 30 77 1.69 2.034 2.444 2.7333.0082 3.3563 3.6109 24 5 8 30.68 0.85 1.05 1.33418 23 25 70 1.69 2.032 2.441 2.7283.0020 3.3479 3.6007 09 2 1 40.68 0.85 1.05 1.33516 20 20 62 1.68 2.030 2.437 2.7232.99603.3400 3.5911 96 1 7 80.68 0.85 1.05 1.30 1.68 2.028 2.434 2.71936 2.9905 3.3326 3.582114 17 16 55 830.68 0.85 1.05 1.33712 14 12 49 1.68 2.026 2.431 2.7152.98523.3256 3.5737 71 2 4 40.68 0.85 1.05 1.33810 12 08 42 1.68 2.024 2.428 2.7112.98033.3190 3.5657 60 4 6 63940 0.68 0.85 1.05 1.30 1.68 2.022 2.42508 09 04 36 492.7072.97563.3128 3.558190.68 0.85 1.05 1.30 1.68 2.021 2.42307 07 00 31 392.7042.97123.3069 3.551050.68 0.85 1.04 1.34105 05 97 25 1.68 2.019 2.420 2.7012.96703.3013 3.5442 29 5 8 20.68 0.85 1.04 1.34204 03 94 20 1.68 2.018 2.418 2.6982.96303.2960 3.5377 20 1 5 10.68 0.85 1.04 1.34302 01 91 16 1.68 2.016 2.416 2.6952.95923.2909 3.5316 11 7 3 10.68 0.84 1.04 1.30 1.68 2.015 2.414 2.6922.95553.2861 3.525801998811024130.680.841.041.301.672.0142.412 2.6892.95213.2815 3.520300978506941160.67 0.841.041.301.672.0122.410 2.6872.94883.2771 3.5150 99 95 83 02 87 9 20.670.841.041.291.672.0112.408 2.6842.94563.2729 3.509997938098797360.67 0.841.041.291.672.0102.406 2.6822.94263.2689 3.5051 96 92 78 94 72 6 620.670.841.041.291.672.0092.404 2.6802.93973.2651 3.50049590759166690.670.841.041.291.672.0082.403 2.6772.93703.2614 3.496094897387596380.67 0.841.041.291.672.0072.401 2.6752.93433.2579 3.4918 9387 71 84 53 6 7744454647484950510.67 0.84 1.04 1.29 1.67 2.006 2.400 2.67352 2.9318 3.2545 3.487792 86 69 80 47 70.67 0.84 1.04 1.295391 85 67 77 1.67 2.005 2.398 2.6712.92933.251341 7 8 83.48380.67 0.84 1.04 1.295491 83 65 74 1.67 2.004 2.397 2.6702.92703.24836 9 4 03.48000.67 0.84 1.04 1.295590 82 63 71 1.67 2.004 2.396 2.6682.92473.24530 0 1 23.47640.67 0.84 1.04 1.2 5689 81 61 69 1.67 2.003 2.394 2.6662.92253.242325 2 8 53.47290.67 0.84 1.04 1.295788 80 59 66 1.67 2.002 2.393 2.6642.92043.239520 5 6 93.46960.67 0.84 1.04 1.295887 79 58 63 1.67 2.001 2.392 2.6632.91843.236816 7 4 33.46630.67 0.84 1.04 1.295987 78 56 61 1.67 2.001 2.391 2.6612.91643.234211 0 2 83.46320.67 0.84 1.04 1.296086 77 55 58 1.67 2.000 2.390 2.6602.91463.2317 3.4602 06 3 1 30.67 0.84 1.04 1.296185 76 53 56 1.67 1.999 2.389 2.6582.91273.2293 3.4573 02 6 0 90.67 0.84 1.04 1.296285 75 52 54 1.66 1.999 2.388 2.6572.91103.2270 3.4545 98 0 0 50.67 0.84 1.04 1.296384 74 50 51 1.66 1.998 2.387 2.6562.90933.2247 3.4518 94 3 0 10.67 0.84 1.04 1.296483 73 49 49 1.66 1.997 2.386 2.6542.90763.22253.4491 90 7 0 90.67 0.84 1.04 1.296583 72 48 47 1.66 1.997 2.385 2.6532.90603.2204 3.4466 86 1 1 60.67 0.84 1.04 1.296682 71 46 45 1.66 1.996 2.384 2.6522.90453.21843.4441 83 6 2 40.67 0.84 1.04 1.296782 70 45 43 1.66 1.996 2.383 2.6512.90303.2164 3.4417 79 0 3 20.67 0.84 1.04 1.29 1.66 1.995 2.382 2.65068 2.9015 3.2145 3.4394697081 69 44 41 760.67 0.84 1.04 1.291.6681 69 43 39 720.67 0.84 1.04 1.291.6680 68 42 38 690.67 0.84 1.04 1.29 1.667180 67 41 36 660.67 0.84 1.04 1.27279 66 40 340.67 0.84 1.04 1.297379 66 38 330.67 0.84 1.04 1.297478 65 37 310.67 0.84 1.04 1.297578 64 36 295 4 11.9942.381 2.6492.90013.2126 3.4372 9 6 01.9942.380 2.6472.89873.2108 3.4350 4 8 91.9932.380 2.6462.89743.2090 3.4329 9 0 91.66 1.9932.379 2.6452.89613.2073 3.4308 63 5 3 91.66 1.9932.378 2.6442.89493.2057 3.4289 60 0 5 91.66 1.9922.377 2.6432.89363.2041 3.4269 57 5 8 91.66 1.9922.377 2.6432.89243.2025 3.4250 54 1 1 00.67 0.84 1.04 1.29 1.66 1.991 2.376 2.6422.89133.2010 3.4232 77 643628527 410.670.841.041.291.661.9912.375 2.6412.89023.1995 3.421477633526493820.67 0.841.041.291.661.9902.375 2.6402.88913.1980 3.4197 76 63 34 25 46 8 130.67 0.841.041.291.661.9902.374 2.6392.88803.1966 3.4180 76 62 33 24 44 5 550.67 0.841.041.291.661.9902.373 2.6382.88703.1953 3.4163 76 61 32 22 41 1 970.67 0.841.041.291.661.9892.373 2.6372.88603.1939 3.4147 75 61 31 21 39 7 390.67 0.841.041.291.661.9892.372 2.6372.88503.1926 3.413275603020363710.67 0.841.041.291.661.9892.372 2.6362.88403.1913 3.4116 756029 18 34 0 1476777879808182830.67 0.84 1.04 1.29 1.66 1.988 2.371 2.6352.88313.1901 3.4102 74 592917326 660.670.841.041.291.661.9882.371 2.6342.88223.1889 3.40877459281630390.67 0.841.041.291.661.9872.370 2.6342.88133.1877 3.4073 74 58 27 15 28 9 520.67 0.841.041.291.661.9872.370 2.6332.88043.1866 3.4059 73 58 26 14 26 6 050.67 0.841.041.291.661.9872.369 2.6322.87953.1854 3.4045 73 57 26 12 24 3 590.67 0.841.041.291.661.9872.369 2.6322.87873.1843 3.4032 73 57 25 11 22 0 020.67 0.841.041.291.661.9862.368 2.6312.87793.1833 3.401972562410207560.670.841.041.291.661.9842.364 2.6252.87073.1737 3.3905 70 52 18 01 02 0 298485868788899010 012 0.67 0.84 1.04 1.28 1.65 1.979 2.357 2.6172.85993.1595 3.373530.9039.8649.5053.5955.8357.2459.4 61.2261.7462.2658.91459.869.08.539.16 9.24 9.29 9.35 9.37 9.38 9.42 9.44 9.465.45.5465.39 5.34 5.31 5.27 5.25 5.24 5.20 5.18 5.1765 46 09 86 77 4F分布10 15 20 302.864.34.54 4.06 3.78 3.59 3.46 3.36 3.29 3.23 3.73.43.23.13.02.94.193.623.293.072.922.812.732.66 4.113.523.182.962.812.692.612.544.053.453.112.882.732.612.522.453.983.373.012.782.622.512.412.343.953.342.982.752.592.472.382.303.943.322.962.722.562.442.352.273.873.242.872.632.462.342.242.173.843.212.842.592.422.302.202.123.823.172.802.562.382.252.162.08456 7891 01122.613.18 12.61 2.482.392.83.14 62.56 2.432.352.73.10 32.52 2.392.31 2.73.07 02.492.362.272.73.05 72.46 2.332.242.63.03 42.442.312.222.63.012.992.62.42 2.292.202.40 2.272.182.282.242.212.102.062.23 2.202.162.052.012.011.962.192.152.122.011.96 2.16 2.122.091.97 1.921.911.872.132.092.061.941.89 2.10 2.062.031.91 1.861.841.812.082.062.042.001.891.841.782.021.981.861.811.761 21 31 41 51 61 71 81 9P= 0.9992.38 2.252.162.042.001.961.841.791.742.52.36 2.232.142.021.981.951.831.781.7272.52.35 2.222.132.011.971.931.811.761.7062.52.33 2.192.101.981.941.911.781.731.6742.52.31 2.172.081.961.921.881.761.711.6522.52.29 2.162.061.941.901.871.741.691.632.42.28 2.142.051.931.881.851.721.671.612.52.97 2.96 2.95 2.93 2.91 2.89 2.8892 02 12 22 42 62 83 012 3 5 6 7 8 10 12 14 16 18 205 16.2627m62499562 576 592602 610 6146194052.540359816170089.54.53.68.32.46.32.61.5 18.35 .07.10 .78567273399 98.5034.1221.2012.0 11. 10. 10. 10.2 10. 9.8 9.79.6 9.68 9. 63997469169715513.99.99.1 99. 99. 99. 99.3 99. 99. 99. 99.4 99. .4 00 25 30 36 39 42 43 44 26 30. 29.4 28. 28. 27. 27.4 27. 27. 26. 26.8 26. .682712467350592751418.16.6 15. 15. 14. 14.8 14. 14. 14. 14.1 14..0009852986637250810. 9.18.7 8.2 7.97.7 7.6 7.47.7.2 5.6 5.3 4.8 4.6 4.4 4.2 4.1 4.6.224.744.2117 2 9 3 09 5 10 119.656 13.75 9.78 92 5 5 8.106 8 2 7.52 0 5 40 712.259.58.4557.87.4 566.96.84 96.7 6.4 276.36.28 66.2 6. 1 168.67.0 6.6 6.1811.267.5951385.9 5.6 5.55.4 5.6.035.481761368.06.4 6.0 5.65.3 5.1 910.566.995.472261515.04.8 4.4.92168110 10.047.56.5565.9 5.6 945.25.06 04.9 4.7 414.64.52 04.4 4. 6416.95.4 5.0 4.64.3 4.1 129.335.954.503164964.03.93.3.9751866.75.2 4.8 4.44.1 139.075.744.3016493.93.83.7 3.3.7866266006.55.04.6 4.2 4.0 3.8 3.73.5 3.5.564.143.62149836 51148.864.6 4.3 3.93.6 3.4 3.33.2 3. 5.183.793.277438651166.1178.4015.84.4 4.1 3.73.4 3.2 3.1208.104.94 3.56536332.9 2.3.05 9946.34.8 4.5 4.1158.685.4269643.8 3.6 3.53.4 3.4.003.49976237168.536.25.2934.74.4 744.03.89 33.7 3.5 853.43.37 53.3 3. 1266.04.5 4.2 3.8 188.295.093.7118543.63.3 3.23.13.3.19773 08198.185.94.5 4.1 3.73.5 3.3 3.13.0 3. 5.013.633.125.74.3 4.0 3.63.4 3.1 218.024.873.518 7 4 4 0 73.02.92.2.9973 885.64.2 3.9 3.2 3.0 2.9 2.74.723.362.851263397424 7.824.03.7 3.33.0 2.8 2.72.6 2.3.172.662 07440 555.3307.564.5195.7 4.33.5 3.33.1 227.95 4.823.452 1 9 9 5 23.02.82.2.942 8 83 237.885.64.7664.2 3.9 643.53.41 43.3 3.0 072.92.89 72.8 2. 378257.775.54.6874.1 3.8 853.43.32 63.2 2.9 292.82.81 92.7 2. 570267.725.54.6434.1 3.8 423.43.29 23.1 2.9 862.82.78 62.7 2.2 665.44.1 3.7 3.33.1 277.684.603.26918952.92.82.6 2.2.7532863287.645.44.5754.0 3.7 753.33.23 63.1 2.9 22.72.72 92.6 2. 560297.605.44.5424.03.7 433.33.20 33.0 2.8 972.72.69 72.6 2. 357Excel公式1. 正态分布函数Excel计算正态分布时,使用NORMDIS函数,其格式如下: NORMDISTa,y,c,累积)其中,“累积”:若为TRUE则输出分布函数值,即P{X W a}; 若为FALSE则为概率密度函数值.示例:已知X服从正态分布,卩=600,c= 100,求P{X< 500}.输入公式NORMDIST(5OO, 600, 100, TRUE)得到的结果为0.158655,即P{X< 500}=0.158655 .2、正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMIN函数,格式如下:NORMIN(p,卩,(T ),此公式计算a,使P{X <a}=p 3标准正态分布反函数=NORMSINV(0.975)3、t分布Excel计算t分布的值,采用TDIST函数,格式如下:TDIST(a,自由度,侧数)其中,“侧数”:指明分布为单侧或双侧:若为1,为单侧;此命令输出P{ T >a }若为2,为双侧•此命令输出P{ |T| >a}示例:设T服从自由度为24的t分布,求P(T>1.711).已知t = 1.711 , df=24,采用单侧,贝U T分布的值:TDIST(1.711,24,1)得到0.05,即卩P(T > 1.711)=0.054. t分布的反函数Excel使用TINV函数得到t分布的反函数,格式如下:TINV (a,自由度)输出T分布的a / 2 分位点:t_ a /2_(n)若求临界值t a (n),则使用公式=TINV(2* a , n) 5. 返回F分布的函数是FDISTFDIST(x,degrees_freedom1,degrees_freedom2) 函数FDIST的计算公式为FDIST=P( F>x ),5.F分布的反函数FINV(probability,deg_freedom1,deg_freedom2) 已知probability=P( F>x ) ,求x。
