全等三角形经典培优题型(含问题详解)
八年级数学全等三角形(培优篇)(Word版含解析)

八年级数学全等三角形(培优篇)(Word版含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在菱形ABCD中,ZABC=120° , AB=10cm,点P是这个菱形内部或边上的一点.若以P,B f C为顶点的三角形是等腰三角形,则P, A(P, A两点不重合)两点间的最短距离为____________ c m .【答案】1OJJ-1O【解析】解:连接3D,在菱形A3CD中,T Z ABC=120° , AB=BC=AD=CD=10 , :. Z A=Z C=60° ,二△ ABD , △ BCD都是等边三角形,分三种情况讨论:①若以边8C为底,则3C垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了"直线外一点与直线上所有点连线的线段中垂线段最短",即当点P与点D重合时,必最小,最小值^4=10 ;②若以边P3为底,ZPCB为顶角时,以点C为圆心,BC长为半径作圆,与AC相交于一点,则弧3D (除点8外)上的所有点都满足APBC是等腰三角形,当点P在AC上时,AP 最小,最小值为lOjJ-10 ;③若以边PC为底,ZPBC为顶角,以点3为圆心,BC为半径作圆,则弧AC上的点&与点D均满足APBC为等腰三角形,当点P与点A重合时,必最小,显然不满足题意,故此种情况不存在;综上所述,必的最小值为10>/3-10 (cm).故答案为:10x/I—10 .点睹:本题考查菱形的性质、等边三角形的性质,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.2.在等腰△遊中,肋丄肚交直线%于点以若妙丄万G则△磁的顶角的度数为【答案】30。
或150。
或90°【解析】试题分析:分两种情况:①3C为腰,②BC为底,根据直角三角形30。
角所对的直角边等于斜边的一半判断岀ZACD=3O°,然后分AD在^ABC内部和外部两种情况求解即可.解:①BC为腰,VAD丄 BC 于点D t AD= - BC f2:.ZACD二30。
第1章 全等三角形-解答题中考经典常考题)-江苏省2023-2024学年上学期八年级数学单元培优专题

第1章全等三角形-解答题(中考经典常考题)-江苏省2023-202 4学年上学期八年级数学单元培优专题练习(苏科版)一.全等三角形的判定与性质(共5小题)1.(2023•南通)如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC.求证:∠1=∠2.小虎同学的证明过程如下:证明:∵∠ADC=∠AEB=90°,∴∠DOB+∠B=∠EOC+∠C=90°.∵∠DOB=∠EOC,∴∠B=∠C.……第一步又OA=OA,OB=OC,∴△ABO≌△ACO.……第二步∴∠1=∠2.……第三步(1)小虎同学的证明过程中,第 步出现错误;(2)请写出正确的证明过程.2.(2023•淮安)已知:如图,点D为线段BC上一点,BD=AC,∠E=∠ABC,DE∥AC.求证:DE=BC.3.(2023•苏州)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.(1)求证:△ADE≌△ADF;(2)若∠BAC=80°,求∠BDE的度数.4.(2022•淮安)已知:如图,点A、D、C、F在一条直线上,且AD=CF,AB=DE,∠BAC =∠EDF.求证:∠B=∠E.5.(2021•无锡)已知:如图,AC,DB相交于点O,AB=DC,∠ABO=∠DCO.求证:(1)△ABO≌△DCO;(2)∠OBC=∠OCB.第1章全等三角形-解答题(中考经典常考题)-江苏省2023-202 4学年上学期八年级数学单元培优专题练习(苏科版)参考答案与试题解析一.全等三角形的判定与性质(共5小题)1.(2023•南通)如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC.求证:∠1=∠2.小虎同学的证明过程如下:证明:∵∠ADC=∠AEB=90°,∴∠DOB+∠B=∠EOC+∠C=90°.∵∠DOB=∠EOC,∴∠B=∠C.……第一步又OA=OA,OB=OC,∴△ABO≌△ACO.……第二步∴∠1=∠2.……第三步(1)小虎同学的证明过程中,第 二 步出现错误;(2)请写出正确的证明过程.【答案】(1)二;(2)证明见解答过程.【解答】(1)解:小虎同学的证明过程中,第二步出现错误,故答案为:二;(2)证明:∵∠ADC=∠AEB=90°,∴∠BDC=∠CEB=90°,在△DOB和△EOC中,,∴△DOB≌△EOC(AAS),∴OD=OE,在Rt△ADO和Rt△AEO中,,∴Rt△ADO≌Rt△AEO(HL),∴∠1=∠2,方法二:∵OD=OE,∠ADC=∠AEB=90°,∴∠1=∠2.2.(2023•淮安)已知:如图,点D为线段BC上一点,BD=AC,∠E=∠ABC,DE∥AC.求证:DE=BC.【答案】证明见解析.【解答】证明:∵DE∥AC,∴∠EDB=∠C,在△BDE和△ACB中,,∴△BDE≌△ACB(AAS),∴DE=BC.3.(2023•苏州)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A圆心,AD 长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.(1)求证:△ADE≌△ADF;(2)若∠BAC=80°,求∠BDE的度数.【答案】见试题解答内容【解答】(1)证明:∵AD是△ABC的角平分线,∴∠BAD=∠CAD.由作图知:AE=AF.在△ADE和△ADF中,,∴△ADE≌△ADF(SAS);(2)解:∵∠BAC=80°,AD为△ABC的角平分线,∴∠EAD=∠BAC=40°,由作图知:AE=AD.∴∠AED=∠ADE,∴∠ADE=×(180°﹣40°)=70°,∵AB=AC,AD为△ABC的角平分线,∴AD⊥BC.∴∠BDE=90°﹣∠ADE=20°.4.(2022•淮安)已知:如图,点A、D、C、F在一条直线上,且AD=CF,AB=DE,∠BAC =∠EDF.求证:∠B=∠E.【答案】见解析.【解答】证明:∵AD=CF,∴AD+CD=CF+CD,∴AC=DF.在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),∴∠B=∠E.5.(2021•无锡)已知:如图,AC,DB相交于点O,AB=DC,∠ABO=∠DCO.求证:(1)△ABO≌△DCO;(2)∠OBC=∠OCB.【答案】见试题解答内容【解答】证明:(1)在△ABO和△DCO中,,∴△ABO≌△DCO(AAS);(2)由(1)知,△ABO≌△DCO,∴OB=OC∴∠OBC=∠OCB.。
全等三角形专题培优(带答案)

全等三角形专题培优考试总分: 110 分考试时间: 120 分钟卷I(选择题)一、选择题(共 10 小题,每小题 2 分,共 20 分)1.如图为个边长相等的正方形的组合图形,则A. B.C. D.2.下列定理中逆定理不存在的是()A.角平分线上的点到这个角的两边距离相等B.在一个三角形中,如果两边相等,那么它们所对的角也相等C.同位角相等,两直线平行D.全等三角形的对应角相等3.已知:如图,,,,则不正确的结论是()A.与互为余角B.C.D.4.如图,是的中位线,延长至使,连接,则的值为()A. B. C. D.5.如图,在平面直角坐标系中,在轴、轴的正半轴上分别截取、,使;再分别以点、为圆心,以大于长为半径作弧,两弧交于点.若点的坐标为,则与的关系为()A. B.C. D.6.如图,是等边三角形,,于点,于点,,则下列结论:①点在的角平分线上;②;③;④.正确的有()A.个B.个C.个D.个7.如图,直线、、″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有()A.一处B.二处C.三处D.四处8.如图,是的角平分线,则等于()A. B.C. D.9.已知是的中线,且比的周长大,则与的差为()A. B.C. D.10.若一个三角形的两条边与高重合,那么它的三个内角中()A.都是锐角B.有一个是直角C.有一个是钝角D.不能确定卷II(非选择题)二、填空题(共 10 小题,每小题 2 分,共 20 分)11.问题情境:在中,,,点为边上一点(不与点,重合),交直线于点,连接,将线段绕点顺时针方向旋转得第1页,共7页第2页,共7页………外………○……………………○……………………○※※请※※不※※答※※题※………内………○……………………○……………………○到线段(旋转角为),连接.特例分析:如图.若,则图中与全等的一个三角形是________,的度数为________.类比探究:请从下列,两题中任选一题作答,我选择________题. :如图,当时,求的度数; :如图,当时,①猜想的度数与的关系,用含的式子表示猜想的结果,并证明猜想;②在图中将“点为边上的一点”改为“点在线段的延长线上”,其余条件不变,请直接写出的度数(用含的式子表示,不必证明)12.如图,正方形纸片的边长为,点、分别在边、上,将、分别沿、折叠,点、恰好都落在点处,已知,则的长为________.13.在中,为的平分线,于,于,面积是,,,则的长为________.14.在中,,的垂直平分线与所在的直线相交所得到锐角为,则等于________.15.如图,平分,于,于,,则图中有________对全等三角形.16.如图,在中,,点从点出发沿射线方向,在射线上运动.在点运动的过程中,连结,并以为边在射线上方,作等边,连结. 当________时,;请添加一个条件:________,使得为等边三角形; ①如图,当为等边三角形时,求证:;②如图,当点运动到线段之外时,其它条件不变,①中结论还成立吗?请说明理由.17.如图,从圆外一点引圆的两条切线,,切点分别为,.如果,,那么弦的长是________.18.如图,在中,,,是的平分线,平分交于,则________.19.阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图,在中,,平分,, 求的长.小聪思考:因为平分,所以可在边上取点,使,连接.这样很容易得到,经过推理能使问题得到解决(如图). 请回答:是________三角形.的长为________.参考小聪思考问题的方法,解决问题: 如图,已知中,,,平分,,.求的长.20.如图,在和中,,,若要用“斜边直角边..”直接证明,则还需补充条件:________.三、解答题(共 7 小题 ,每小题 10 分 ,共 70 分 )21.如图,已知为等边三角形,为延长线上的一点,平分,,求证:为等边三角形.22.尺规作图(不要求写作法,保留作图痕迹)如图,作①的平分线;②边上的中线;22.一块三角形形状的玻璃破裂成如图所示的三块,请你用尺规作图作一个三角形,使所得的三角形和原来的三角形全等.(不要求写作法,保留作图痕迹.不能在原图上作三角形)22.如图:在正方形网格中有一个,按要求进行下列画图(只能借助于网格):①画出中边上的高(需写出结论).②画出先将向右平移格,再向上平移格后的.23.平行四边形中,,点为边上一点,连结,点在边所在直线上,过点作交于点.如图,若为边中点,交延长线于点,,,,求;如图,若点在边上,为中点,且平分,求证:;如图,若点在延长线上,为中点,且,问中结论还成立吗?若不成立,那么线段、、满足怎样的数量关系,请直接写出结论.24.如图,直线与轴、轴分别交于、两点,直线与直线关于轴对称,已知直线的解析式为,求直线的解析式;过点在的外部作一条直线,过点作于,过点作于,请画出图形并求证:;沿轴向下平移,边交轴于点,过点的直线与边的延长线相交于点,与轴相交于点,且,在平移的过程中,①为定值;②为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.25.如图:,,过点,于,于,.求证:.第3页,共7页第4页,共7页26.如图,点,在上,,,,与交于点.求证:;试判断的形状,并说明理由.27.如图,已知点是平分线上一点,,,垂足为、吗?为什么?是的垂直平分线吗?为什么? 答案 1.B 2.D 3.D 4.A 5.B 6.D 7.D 8.A 9.B 10.B11.[ “”, “” ][ “” ] 12.[ “” ] 13.[ “” ] 14.[ “或” ]15.[ “” ] 16.[ “;” ][ "添加一个条件,可得为等边三角形; 故答案为:;①∵与是等边三角形, ∴,,, ∴, 即, 在与中, , ∴, ∴;②成立,理由如下; ∵与是等边三角形, ∴,,, ∴, 即, 在与中, , ∴, ∴." ] 17.[ “” ] 18.[ “” ]19.[ "解:是等腰三角形, 在与中,, ∴, ∴,, ∵, ∴, ∴,∴是等腰三角形;" ][ "的长为, ∵中,,, ∴, ∵平分, ∴,在边上取点,使,连接, 则,∴, ∴, ∴,在边上取点,使,连接, 则, ∴,, ∵, ∴, ∴, ∵,∴." ]\"go题库\"20.[ “” ]21.证明:∵为等边三角形,∴,,即,∵平分,∴,在和中,,∴,∴,,又,∴,∴为等边三角形.22.解:如图所示:;如图所示:即为所求;;①如图所示:即为所求;②如图所示:即为所求;..23.解:如图,在平行四边形中,,∴,∵在中,为的中点,,∴,又∵,∴,故可设,,则中,,解得,∴,又∵,,∴为的中点,∴;如图,延长交的延长线于点,则,∵,∴,又∵平分,∴,∴是等腰直角三角形,∴,又∵,∴,∴,,又∵为的中点,∴,∴,∴,∵,∴;第5页,共7页第6页,共7页…○…………装订…………○…※※请※※不※※内※※答※※题※※…○…………装订…………○…若点在延长线上,为中点,且,则中的结论不成立,正确结论为:. 证明:如图,延长交的延长线于点,则,∵, ∴, ∴, 又∵, ∴, ∴,,又∵为的中点, ∴, ∴, ∴, ∵, ∴.24.解:∵直线与轴、轴分别交于、两点, ∴,,∵直线与直线关于轴对称, ∴∴直线的解析式为:;如图..∵直线与直线关于轴对称, ∴,∵与为象限平分线的平行线, ∴与为等腰直角三角形, ∴, ∵, ∴ ∴ ∴,,∴;①对,过点作轴于,直线与直线关于轴对称∵,, 又∵, ∴, 则, ∴ ∴ ∴ ∴ ∴.25.证明:连接, ∵, ∴, ∵, ∴, ∴, ∵,, ∴, 在和中,∴.26.证明:∵,∴,即.又∵,,∴,∴.解:为等腰三角形理由如下:∵,∴,∴,∴为等腰三角形.27.解:.理由:∵是的平分线,且,,∴,∴;是的垂直平分线.理由:∵,在和中,,∴,∴,由,,可知点、都是线段的垂直平分线上的点,从而是线段的垂直平分线.第7页,共7页。
人教版 八年级数学 第12章 全等三角形 培优训练 (含答案)

人教版八年级数学第12章全等三角形培优训练一、选择题1. 下列各组的两个图形属于全等图形的是()2. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE相交于点M,则∠DCE等于()A.∠B B.∠A C.∠EMF D.∠AFB3. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PF A的依据是()A.HL B.ASA C.SSS D.SAS4. 根据下列条件,能画出唯一的△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=50°D.∠A=30°,∠B=70°,∠C=80°5. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是()A.点O在点A的南偏东60°方向上B.点B在点A的北偏东30°方向上C.点B在点O的北偏东60°方向上D.点B在点O的北偏东30°方向上6. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是()7. 现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,OA=a,AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点A为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确,小雷的作法错误B.小雷的作法正确,小惠的作法错误C.两人的作法都正确D.两人的作法都错误8. 如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF 于点H.若∠AFB=40°,则∠BCF的度数为()A.40°B.50°C.55°D.60°二、填空题9. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=°.10. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.11. 如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.12. 在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD 的面积之比是________.13. (2019•南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.14. 如图所示,已知AD∥BC,则∠1=∠2,理由是________________;又知AD =CB,AC为公共边,则△ADC≌△CBA,理由是______,则∠DCA=∠BAC,理由是__________________,则AB∥DC,理由是________________________________.15. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.16. 如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC =2,则S△ABC=.三、解答题17. 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20 m,AC=10 m,分别求一串红与鸡冠花两种花草的种植面积.18. 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上.若AD=16,BC=10,求AB的长.19. 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是筝形,其中AB=AD,CB=CD,P是对角线AC上除A,C外的任意一点.求证:∠ABP =∠ADP.20. 如图,已知AP∥BC,∠P AB的平分线与∠CBA的平分线相交于点E,过点E 的直线分别交AP,BC于点D,C.求证:AD+BC=AB.21. (1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.人教版八年级数学第12章全等三角形培优训练-答案一、选择题1. 【答案】A2. 【答案】A[解析] ∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,∴∠DCE=∠B.故选A.3. 【答案】A4. 【答案】C[解析] 对于选项A来说,AB+BC<AC,不能画出△ABC;对于选项B来说,可画出△ABC为锐角三角形或者钝角三角形;对于选项C来说,已知两边及其夹角,△ABC是唯一的;对于选项D来说,△ABC的形状可确定,但大小不确定.5. 【答案】D[解析] 如图,由题意知∠AOD=30°,∠COD=90°,∴∠AOC=120°.由作图可知,OB平分∠AOC,∴∠AOB=∠AOC=60°.∴∠DOB=30°.∴点B在点O的北偏东30°方向上.6. 【答案】C[解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项C中,如图①,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.这两个角所对的边是BE和CF,而已知条件给的是BD=CF=3,故不能判定两个小三角形全等.选项D中,如图②,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.又∵BD=CE=2,∠B=∠C,∴△BDE≌△CEF.故能判定两个小三角形全等.7. 【答案】A[解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.8. 【答案】B[解析] 如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.∵AF平分∠BAC,FZ⊥AE,FW⊥AB,∴FZ=FW.同理FW=FY.∴FZ=FY.又∵FZ⊥AE,FY⊥CB,∴∠FCZ=∠FCY.由∠AFB=40°,易得∠ACB=80°.∴∠ZCY=100°.∴∠BCF=50°.二、填空题9. 【答案】125[解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.10. 【答案】AB =AC11. 【答案】20[解析] 如图,过点D 作射线AF.在△BAD 和△CAD 中,⎩⎨⎧AB =AC ,AD =AD ,BD =CD ,∴△BAD ≌△CAD(SSS). ∴∠BAD =∠CAD ,∠B =∠C.∵∠BDF =∠B +∠BAD ,∠CDF =∠C +∠CAD , ∴∠BDF +∠CDF =∠B +∠BAD +∠C +∠CAD , 即∠BDC =∠B +∠C +∠BAC. ∵∠BAC =80°,∠BDC =120°, ∴∠B =∠C =20°.12. 【答案】4∶3【解析】如解图,过D 作DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,∵AD 是∠BAC 的平分线,∴DE =DF(角平分线上的点到角两边的距离相等),设DE=DF=h,则S△ABDS△ACD =12AB·h12AC·h=43.13. 【答案】70【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,在Rt△ABE和Rt△CBF中,AB CBAE CF=⎧⎨=⎩,∴Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.14. 【答案】两直线平行,内错角相等SAS全等三角形的对应角相等内错角相等,两直线平行15. 【答案】20[解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB =AE+EB=AB.16. 【答案】7[解析] 过点P作PF⊥BC于点F,PG⊥AB于点G ,连接AP.∵△ABC的两条外角平分线BP,CP相交于点P,∴PF=PG=PE=2.∵S△BPC=2,∴BC·2=2,解得BC=2.∵△ABC的周长为11,∴AC+AB=11-2=9.∴S △ABC =S △ACP +S △ABP -S △BPC =AC ·PE+AB ·PG-S △BPC =×9×2-2=7.三、解答题17. 【答案】解:如图,过点D 作DE ⊥AB 于点E ,DF ⊥AC 于点F. ∵AD 是∠BAC 的平分线,∴DE =DF. ∵AB =20 m ,AC =10 m ,∴S △ABC =12×20×10=12×20·DE +12×10·DF ,解得DE =203(m).∴△ACD 的面积=12×10×203=1003(m 2),△ABD 的面积=12×20×203=2003(m 2).故一串红的种植面积为2003 m 2,鸡冠花的种植面积为1003 m 2.18. 【答案】解:∵△ACF ≌△DBE ,∴AC=DB.∴AC-BC=DB-BC ,即AB=CD.∵AD=16,BC=10,∴AB=CD=(AD-BC )=3.19. 【答案】证明:在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,AC =AC ,CB =CD , ∴△ABC ≌△ADC.∴∠BAP =∠DAP.在△BAP 和△DAP 中,⎩⎨⎧AB =AD ,∠BAP =∠DAP ,AP =AP , ∴△BAP ≌△DAP.∴∠ABP =∠ADP.20. 【答案】证明:如图,在AB 上截取AF =AD ,连接EF.∵AE 平分∠PAB ,∴∠DAE =∠FAE.在△DAE 和△FAE 中,⎩⎨⎧AD =AF ,∠DAE =∠FAE ,AE =AE ,∴△DAE ≌△FAE(SAS).∴∠AFE =∠ADE.∵AD ∥BC ,∴∠ADE +∠C =180°.又∵∠AFE +∠EFB =180°,∴∠EFB =∠C.∵BE 平分∠ABC ,∴∠EBF =∠EBC.在△BEF 和△BEC 中,⎩⎨⎧∠EFB =∠C ,∠EBF =∠EBC ,BE =BE ,∴△BEF ≌△BEC(AAS).∴BF =BC.∴AD +BC =AF +BF =AB.21. 【答案】解:(1)证明:∵BD ⊥直线m ,CE ⊥直线m , ∴∠BDA =∠AEC =90°.∴∠BAD +∠ABD =90°.∵∠BAC =90°,∴∠BAD +∠CAE =90°. ∴∠CAE =∠ABD.在△ADB 和△CEA 中,⎩⎨⎧∠ABD =∠CAE ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.(2)成立.证明:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠EAC =180°-α. ∴∠DBA =∠EAC.在△ADB 和△CEA 中,⎩⎨⎧∠DBA =∠EAC ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.。
培优专题03 证明三角形全等的基本思路-解析版

∴ VACE ≌ VDCE
∴ AE = DE ,
∴S△ACE:S△ACD=1:2,
同理可得,S△ABE:S△ABD=1:2,
∵S△ABC=12 cm2 ,
∴阴影部分的面积为
S△ACE+S△ABE=
1 2
S△ABC=
1 2
×12=6 cm2 .
故答案为 6.
【点睛】本题主要考查了全等三角形的判定与性质及三角形面积的等积变换,解题关键是明确三角形的中
(
)
A.DF∥ AC
B.∠A=∠D
C.CF=BE
D.AC=DF
【答案】D
【分析】直接利用三角形全等判定条件逐一进行判断即可.
【详解】A. 由 DF∥AC 可得∠ACB=∠DFE,由 AB∥DE,可得∠ABC=∠DEF,又因 AB=DE,利用 AAS
可得△ABC≌△DEF,故本选项不符合题意;
B. 由 AB∥DE,可得∠ABC=∠DEF,又因∠A=∠D,AB=DE,利用 ASA 可得△ABC≌△DEF,故本选项
B.0.8cm
C.4.2cm
D.1.5cm
【答案】B
【分析】根据 BE ^ CE , AD ^ CE 得 ÐE = ÐADC ,则 ÐCAD + ÐACD = 90° ,再由 ÐACB = 90° ,得
ÐBCE + ÐACD = 90° ,则∠BCE = ∠CAD,从而证出 DBCE≌DCAD ,进而得出 BE 的长.
ìBD = CD ïíÐADB = ÐEDC , ïî AD = DE
\DABD≌DECD(SAS) , \CE = AB = 3 , 在 DACE 中, CE - AC < AE < CE + AC ,
初二上数学培优专题(3)三角形全等

三角形全等例1:已知,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,(1)如图1,求C点的坐标;(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y 轴的负半轴上沿负方向运动时,以下两个结论:①m﹣n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.例2:已知△ABC中、∠ABC=∠ACB=40°,BD是∠ABC的平分线,延长BD至点E,使得DE=AD,求∠ECA的度数。
例3.已知∠GOH=90°,A、C分别是OG、OH上的点,且OA=OC=4,以OA为边长作正方形OABC.(1)E是边OC上一点,作∠AEF=90°使EF交正方形的外角平分线CF于点F(如图1),求证:EF=AE.(2)现将正方形OABC绕O点顺时针旋转,当A点第一次落在∠GOH的角平分线OP上时停止旋转;旋转过程中,AB边交OP于点M,BC边交OH于点N(如图2),①旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;②设△MBN的周长为p,在正方形OABC的旋转过程中,p值是否有变化?请证明你的结论.例4:如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由点B出发向C点运动,同时,点Q在线段CA上由点C出发向A点运动.设运动时间为t(s).(1)若点P的运动速度为3cm/s,则t(s)时,BP= cm,CP= cm,(用含t的代数式表示).若点Q的运动速度与点P的运动速度相等,经过几秒后,△BPD与△CQP是否全等?请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,且点P的速度比点Q的速度慢1cm/s,则点Q的速度为多少时,能够使△BPD与△CQP全等?(3)若点Q以(2)中的速度从点C出发,点P以(2)中的运动速度从点B同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P与点Q第一次相遇,相遇点在△ABC的哪条边上?1.∆ABC中,高AD和BE交于点H,且BH=AC,则∠ABC=_____2.如图∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN ⑤EM=FN.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个 2题3.下列条件中能作出唯一的三角形的是()A.已知两边及一边的对角B.已知两边及第三边上的中线C.已知两角D.已知两边及第三边上的高线4.下列判断正确的是()A.有两边及其中一边的对角对应相等的两个三角形全等.B.有两边对应相等,且有一个角为30°的两个等腰三角形全等.C.有一个角和一边对应相等的两个直角三角形全等 .D.有两角和一边对应相等的两个三角形全等. 5题5.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③AO=CO=AC④四边形ABCD的面积=AC•BD,其中正确的结论有 .6.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述结论一定正确的是()A.①②③ B.②③④ C.①③⑤ D.①③④7.下列叙述:①任意一个三角形的三条高至少有一条在三角形内部;②以a,b,c为边(a,b,c都大于0,且a+b>c)一定可以构成一个三角形;③一个三角形内角之比为3:2:1,此三角形为直角三角形;④两个角和其中一角的对边对应相等的两个三角形全等;⑤两条边和其中一边的对角对应相等的两个三角形全等;⑥三个角对应相等的两个三角形全等;⑦两边和其中一边上的高分别相等的两个三角形全等。
人教版八年级数学上册《全等三角形》培优专题训练(含答案)

《全等三角形》培优专题训练1 全等三角形的概念两个能够完全重合的三角形叫做全等三角形.把两个全等三角形重合在一起,重合的角叫做对应角,重合的边叫做对应边.全等三角形的对应角相等,对应边相等. 经典例题如图所示,ABC DEF ∆≅∆,30A ∠=︒,50B ∠=︒,2BF =.求DFE ∠的度数与EC 的长.解题策略在ABC ∆中,+180A B ACB ∠∠+∠=︒ (三角形内角和为180°).因为30A ∠=︒,50B ∠=︒(已知),所以1803050100ACB ∠=︒-︒-︒=︒ 因为ABC DEF ∆≅∆ (已知),所以ACB DFE ∠=∠(全等三角形对应角相等) BC EF =(全等三角形对应边相等), 因此100DFE ∠=︒,所以2EC EF FC BC FC BF =-=-== 画龙点睛1. 在解答与全等三角形有关的问题时,要充分利用全等三角形的定义所得到的对应边相等、对应角相等的结论.2. 在本题中求EC 的长时,不能直接求,可将之转化为两条线段的差,这也是将来求线段长的一种常用的转化方法.举一反三1. 如图,若ABC ADE ∆≅∆,则这对全等三角形的对应边是 ;对应角是 .2. 如图,若ABD ACD ∆≅∆,试说明AD 与BC 的位置关系.3. 如图所示,斜折一页书的一角,使点A 落在同一页书内'A 处,DE 为折痕,作DF平分'A DB ∠,试猜想FDE ∠等于多少度,并说明理由.融会贯通4. 如图,ABE ∆和ACD ∆是ABC ∆分别沿着AB 、AC 边翻折180°形成的,若θ∠的度数50°,则BAC ∠的度数是 .2 三角形全等的判定判断两个三角形全等,并非需要证明两个三角形的三条边以及三个角均对应相等,而只需满足全等三角形的判定定理就可以了. 经典例题已知:如图,AO 平分EAD ∠和EOD ∠,求证:(1)AOE AOD ∆≅∆;(2) BOE COD ∆≅∆.解题策略证明:(1)因为AO 平分EAD ∠和EOD ∠,所以OAD OAE ∠=∠,AOE AOD ∠=∠,又因为AO AO =,所以AOE AOD ∆≅∆ ( ASA).(2)由AOE AOD ∆≅∆,得OE OD =,且AEO ADO ∠=∠.又180BEO AEO ∠=︒-∠,180CDO ADO ∠=︒-∠,所以B E O C D O ∠=∠.在AOE ∆和AOD ∆中,因为B E O C D O ∠=∠,OE OD =,BOE COD ∠=∠,所以B O E C O D ∆≅∆(ASA). 画龙点睛1. 判定两个三角形全等,往往需要三个条件,根据题目已知的条件可以得到两个条件(要注意公共角及公共边),这时.设法证明所缺的条件也成立就是证题的关键了. 2. 要证明两条线段或者两个角相等,常用的方法是证明它们是一对全等三角形的对应边或者对应角.举一反三1. 如图,已知AB AD =,那么添加下列一个条件后,仍无法判定ABC ADC ∆≅∆的是( ).(A) CB CD = (B)BAC DAC ∠=∠ (C)BCA DCA ∠=∠ (D)90B D ∠=∠=︒2. 如图所示,点D 、C 在BF 上,//AB EF ,A E ∠=∠,BC DF =.求证AB EF =.3. 如图,AB 交CD 于点O ,AD 、CB 的延长线相交于点E ,且OA OC =,EA EC =,你能证明A C ∠=∠吗?点O 在AEC ∠的平分线上吗?融会贯通4. 如图所示,已知BD 、CE 分别是ABC ∆的边AC 和AB 上的高,点P 在BD 的延长线上,BP AC =,点Q 在CE 上,CQ AB =.求证:(1)AP AQ =;(2)AP AQ ⊥.3 全等三角形的应用全等三角形的判定和性质被广泛地应用于几何证明题中。
华师大二附中八年级数学上册第十二章《全等三角形》经典题(培优)

一、选择题1.如图,在ABC 和AEF 中,EAC BAF ∠=∠,EA BA =,添加下面的条件:①EAF BAC ∠=∠;②E B ∠=∠;③AF AC =;④EF BC =,其中可以得到ABC AEF ≌△△的有( )个.A .1B .2C .3D .4B解析:B【分析】 根据EAC BAF ∠=∠,EAF EAC CAF ∠=∠+∠,BAC BAF CAF ∠=∠+∠,经推到得EAF BAC ∠=∠;再结合全等三角形判定的性质分析,即可得到答案.【详解】∵EAC BAF ∠=∠,EAF EAC CAF ∠=∠+∠,BAC BAF CAF ∠=∠+∠ ∴EAF BAC ∠=∠E B ∠=∠,即E B EAF BAC EA BA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC AEF ≌△△()ASA ,故②符合题意;AF AC =,即AF AC EAF BAC EA BA =⎧⎪∠=∠⎨⎪=⎩∴ABC AEF ≌△△()SAS ,故③符合题意; ①和④不构成三角形全等的条件,故错误;故选:B .【点睛】本题考查了全等三角形的知识;解题的关键是熟练掌握全等三角形的性质,从而完成求解.2.如图,AB ⊥CD ,且AB =CD .E 、F 是AD 上两点,CE ⊥AD ,BF ⊥AD .若CE =a ,BF =b,EF=c,则AD的长为( )A.a+c B.b+cC.a+b-c D.a-b+c C解析:C【分析】由“AAS”可证△ABF≌△CDE,根据全等三角形的性质可得AF=CE=a,BF=DE=b,则可推出AD=AF+DF=a+(b−c)=a+b−c.【详解】解:∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,∴∠A=∠C,∵AB=CD,∴△ABF≌△CDE(AAS),∴AF=CE=a,BF=DE=b,∵EF=c,∴AD=AF+DF=a+(b−c)=a+b−c.故选:C.【点睛】本题考查了全等三角形的判定和性质,解题的关键是掌握全等三角形的判定方法并准确寻找全等三角形解决问题.3.如图,AB=AC,AD=AE,∠A=105°,∠D=25°,则∠ABE等于()A.65°B.60°C.55°D.50°D解析:D【分析】依据SAS即可得判定△ABE≌△ACD,再根据全等三角形的性质,得出∠D=∠E=25°,由三角形内角和定理可求出答案.【详解】解:在△ABE和△ACD中,AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ACD (SAS ),∴∠D =∠E ,∵∠D =25°,∴∠E =25°,∴∠ABE =180°﹣∠A ﹣∠E =180°﹣105°﹣25°=50°.故选:D .【点睛】本题考查了全等三角形的判定与性质,三角形内角和定理,熟练掌握全等三角形的判定与性质是解题的关键.4.如图,ABC 的面积为26cm ,AP 垂直B 的平分线BP 于P ,则PBC 的面积为( )A .21cmB .22cmC .23cmD .24cm C解析:C【分析】 延长AP 交BC 于E ,根据AP 垂直∠B 的平分线BP 于P ,即可求出△ABP ≌△BEP ,又知△APC 和△CPE 等底同高,可以证明两三角形面积相等,即可证明三角形PBC 的面积.【详解】解:延长AP 交BC 于E ,∵AP 垂直∠B 的平分线BP 于P ,∴∠ABP =∠EBP ,∠APB =∠BPE =90∘,在△APB 和△EPB 中∠=∠⎧⎪=⎨⎪∠=∠⎩APB EPB BP BPABP EBP ∴△APB ≌△EPB (ASA ),∴APB EPB S S =△△,AP =PE ,∴△APC 和△CPE 等底同高,∴APC PCE S S =,∴PBC PCE PCE S S S =+△△△=12ABC S=1632⨯= 故选C .【点睛】本题考查了三角形的面积和全等三角形的性质和判定的应用,关键是求出PBC PCE PCE S S S =+△△△=12ABC S .5.如图,123,,l l l 是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.A .1B .2C .3D .4D解析:D【分析】 到三条相互交叉的公路距离相等的地点应是三条角平分线的交点,把三条公路的中心部位看作三角形,那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求.【详解】(1)三角形两个内角平分线的交点,共一处(2)三个外角两两平分线的交点,共三处,共四处,故选:D ..【点睛】此题考查角平分线的性质:角平分线上的点到角两边的距离相等,熟记性质是正确解题的关键.6.如图,在OAB 和OCD 中,OA OB =,OC OD =,OA OC >,40AOB COD ∠=∠=︒,连接AC 、BD 交于点M ,连接OM ,下列结论:①AC BD =;②40AMB ∠=︒;③OM 平分BOC ∠;④MO 平分BMC ∠,其中正确的为( )A .①②③B .①②④C .②③④D .①②③④B解析:B【分析】 由SAS 证明AOC BOD ≅得出OCA ODB ∠=∠,=AC BD ,①正确;由全等三角形的性质得出OAC OBD ∠=∠,由三角形的外角性质得:AMB OAC AOB OBD ∠+∠=∠+∠,得出40AOB COD ∠=∠=︒,②正确;作OG MC ⊥于G ,OH MB ⊥于H ,如图所示:则90OGC OHD ∠=∠=,由AAS 证明OCG ODH ≅(AAS ),得出OG=OH ,由角平分线的判定方法得出MO 平分BOC ∠,④正确;由AOB COD ∠=∠,得出当∠=∠DOM AOM 时,OM 平分BOC ∠,假设∠=∠DOM AOM ,由AOC BOD ≅得出COM BOM ,由MO 平分BMC ∠得出∠=∠CMO BMO ,推出COM BOM ≅,得出OB=OC ,OA=OB ,所以OA=OC ,而OA OC >,故③错误;即可得出结论.【详解】∵40AOB COD ∠=∠=︒,∴AOB AOD COD AOD ∠+∠=∠+∠即AOC BOD ∠=∠在AOC △和BOD 中OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴AOC BOD ≅(SAS )∴OCA ODB ∠=∠,=AC BD ,①正确;∴OAC OBD ∠=∠,由三角形的外角性质得:AMB OAC AOB OBD ∠+∠=∠+∠,∴40AOB COD ∠=∠=︒,②正确;作OG MC ⊥于G ,OH MB ⊥于H ,如图所示:则90OGC OHD ∠=∠=,在OCG 和ODH 中OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴OCG ODH ≅(AAS ),∴OG=OH∴MO 平分BOC ∠,④正确;∴AOB COD ∠=∠∴当∠=∠DOM AOM 时,OM 平分BOC ∠,假设∠=∠DOM AOM∵AOC BOD ≅∴COM BOM ,∵MO 平分BMC ∠∴∠=∠CMO BMO ,在COM 和BOM 中 OCM BOM OM OMCMO BMO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴COM BOM ≅(ASA )∴OB=OC ,∵OA=OB ,∴OA=OC ,与OA OC >矛盾,∴③错误;正确的有①②④;故选:B【点睛】本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识;证明三角形全等是解题的关键.7.如图,在下列条件中,不能判断△ABD ≌△BAC 的条件是( )A .∠D=∠C , ∠BAD=∠ABCB .BD=AC , ∠BAD=∠ABC C .∠BAD=∠ABC , ∠BAD=∠ABCD .AD=BC ,BD=AC B解析:B【分析】 本题已知条件是两个三角形有一公共边,只要再加另外两边对应相等或有两角对应相等即可,如果所加条件是一边和一角对应相等,则所加角必须是所加边和公共边的夹角对应相等才能判定两个三角形全等;【详解】A 、符合AAS ,能判断两个三角形全等,故该选项不符合题意;B 、符合SSA ,∠BAD 和∠ABC 不是两条边的夹角,不能判断两个三角形全等,故该选项符合题意;C 、符合AAS ,能判断两个三角形全等,故该选项不符合题意;D 、符合SSS ,能判断两个三角形全等,故该选项不符合题意;故选:B .【点睛】本题考查了全等三角形的判定方法,三角形判定定理中,最容易出错的是“边角边”定理,这里强调的是夹角,不是任意角;8.如图,在四边形ABCD 中,//,AB CD AE 是BAC ∠的平分线,且AE CE ⊥.若,AC a BD b ==,则四边形ABDC 的周长为( )A .1.5()a b +B .2a b +C .3a b -D .2+a b B解析:B【分析】 在线段AC 上作AF=AB ,证明△AEF ≌△AEB 可得∠AFE=∠B ,∠AEF=∠AEB ,再证明△CEF ≌△CED 可得CD=CF ,即可求得四边形ABDC 的周长.【详解】解:在线段AC 上作AF=AB ,∵AE 是BAC ∠的平分线,∴∠CAE=∠BAE ,又∵AE=AE ,∴△AEF ≌△AEB (SAS ),∴∠AFE=∠B ,∠AEF=∠AEB ,∵AB ∥CD ,∴∠D+∠B=180°,∵∠AFE+∠CFE=180°,∴∠D=∠CFE ,∵AE CE ⊥,∴∠AEF+∠CEF=90°,∠AEB+∠CED=90°,∴∠CEF=∠CED ,在△CEF 和△CED 中∵D CFE CEF CED CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△CEF ≌△CED (AAS )∴CE=CF ,∴四边形ABDC 的周长=AC+AB+BD+CD=AC+AF+CF+BD=2AC+BD=2a b +,故选:B .【点睛】本题考查全等三角形的性质和判断.能正确作出辅助线构造全等三角形是解题关键. 9.如图,在Rt ABC 和Rt ADE △中,90,,ACB AED AB AD AC AE ∠=∠===,则下列说法不正确的是( )A .BC DE =B .BAE DAC ∠=∠ C .OC OE =D .EAC ABC ∠=∠ D解析:D【分析】 根据HL 定理分别证明Rt △ABC ≌Rt △ADE 和Rt △AEO ≌Rt △ACO ,根据全等三角形的性质可判断各选项.【详解】解:解:∵90,,ACB AED AB AD AC AE ∠=∠===,∴Rt △ABC ≌Rt △ADE (HL )∴BC DE =,∠BAC=∠DAE ,故A 选项正确;∴∠BAC-∠EAC=∠DAE-∠EAC ,即BAE DAC ∠=∠,故B 选项正确;连接AO ,∵AE=AC ,AO=AO ,∴Rt △AEO ≌Rt △ACO (HL ),∴OC OE =,故C 选项正确;无法得出EAC ABC ∠=∠,故D 选项错误;故选:D .【点睛】本题全等三角形的性质与判断.掌握证明直角三角形全等的HL 定理是解题关键.10.如图,AD 是ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且DE DF =,连结BF ,CE .下列说法:①CE BF =;②ACE △和CDE △面积相;③//BF CE ;④BDF CDE ≌.其中正确的有( )A .1个B .2个C .3个D .4个C解析:C【分析】 根据“SAS”可证明△CDE ≌△BDF ,则可对④进行判断;利用全等三角形的性质可对①进行判断;由于AE 和DE 不能确定相等,则根据三角形面积公式可对②进行判断;根据全等三角形的性质得到∠ECD=∠FBD ,则利用平行线的判定方法可对③进行判断;【详解】∵ AD 是△ABC 的中线,∴ CD=BD ,∵ DE=DF ,∠CDE=∠BDF ,∴ △CDE ≌△BDF(SAS),所以④正确;∴ CE=BF ,所以①正确;∵ AE 与DE 不能确定相等,∴ △ACE 和△CDE 面积不一定相等,所以②错误;∵ △CDE ≌△BDF ,∴∠ECD=∠FBD ,∴BF ∥CE ,所以③正确;故选:C .【点睛】本题考查了全等三角形的判定与性质,三角形的面积 ,熟练掌握三角形全等的判定方法并准确识图是解题的关键.二、填空题11.如图,△ABC 中,∠ACB =90°,点D 在边AC 上,DE ⊥AB 于点E ,DC =DE ,∠A =32°,则∠BDC 的度数为________.61°【分析】首先利用直角三角形的性质求得∠ABC 的度数然后利用角平分线的判定方法得到BD 为∠ABC 的平分线再求出∠ABD 的度数根据三角形外角的性质进而求得结论【详解】解:∵∠A=32°∠ACB=9解析:61°【分析】首先利用直角三角形的性质求得∠ABC 的度数,然后利用角平分线的判定方法得到BD 为∠ABC 的平分线,再求出∠ABD 的度数,根据三角形外角的性质进而求得结论.【详解】解:∵∠A=32°,∠ACB =90°,∴∠CBA=58°,∵DE ⊥AB ,DC ⊥BC ,DC=DE ,∴BD 为∠ABC 的平分线,∴∠CBD=∠EBD ,∴∠CBD=12∠CBA=12×58°=29°, ∴∠BDC=∠A+∠ABD=32°+29°=61°.故答案为:61°.【点睛】本题考查了角平分线的判定与性质,解题的关键是根据已知条件得到BD 为∠ABC 的平分线,难度不大.12.如图,已知四边形,90,3,4,5,ABCD B AB BC AC ︒∠====180BAD CAD ︒∠+∠=,180BCD ACD ︒∠+∠=,则四边形ABCD 的面积是_________.21【分析】如图作DHBA 交BA 的延长线于H 作DFBC的延长线于F 作DEAC 于E 首先证明利用面积法求出DE 即可解决问题【详解】解:作DHBA 交BA 的延长线于H 作DFBC 的延长线于F 作DEAC 于E 设则 解析:21【分析】如图,作DH ⊥BA 交BA 的延长线于H ,作DF ⊥BC 的延长线于F ,作DE ⊥AC 于E ,首先证明DH DE DF ==,利用面积法求出DE ,即可解决问题.【详解】解:作DH ⊥BA 交BA 的延长线于H ,作DF ⊥BC 的延长线于F ,作DE ⊥AC 于E ,180,180 BAD CAD BAD DAH∠+∠=︒∠+∠=︒,CAD DAH∴∠=∠,180,180 BCD ACD BCD DCF∠+∠=︒∠+∠=︒,ACD DCF∴∠=∠,,,DH BH DE AC DF BF⊥⊥⊥,DH DE DF∴==,设DH DE DF x===,则有:11112222AB DH BC DF AB BC AC DE ⋅⋅+⋅⋅=⋅⋅+⋅⋅,∴34125x x x+=+,6x∴=,∴S四边形ABCD=1111345621 2222AB CB AC DE⋅+⋅=⨯⨯+⨯⨯=.故答案为:21.【点睛】本题考查了角平分线的性质、三角形的面积等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.13.已知在△ABC中,AB=9,中线AD=4,那么AC的取值范围是____1<AC<17【分析】作出图形延长AD至E使DE=AD然后利用边角边证明△ABD和△ECD全等根据全等三角形对应边相等可得AB=CE再利用三角形的任意两边之和大于第三边三角形的任意两边之差小于第三边解析:1<AC<17【分析】作出图形,延长AD至E,使DE=AD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得AB=CE,再利用三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出AC的取值范围.【详解】如图,延长AD至E,使DE=AD,∵AD 是△ABC 的中线,∴BD =CD ,在△ABD 和△ECD 中,BD CD ADB EDC AD DE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ECD (SAS ),∴AB =CE ,∵AD =4,∴AE =4+4=8,∵AC +CE >AC >CE -AE ,∴9-8<AC <8+9,∴1<AC <17,故答案为:1<AC <17.【点睛】本题考查了全等三角形的判定与性质,三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.14.如图,在△ABC 中,∠C =90°,AD 是∠BAC 的角平分线,若BC =8cm ,BD =5cm ,AB=10cm,则S △ABD =______.15cm2【分析】过点D 作DE ⊥AB 于E 根据角平分线的性质可得DE=CD 根据三角形的面积公式即可求得△ABD 的面积【详解】解:过点D 作DE ⊥AB 于E ∵AD 是∠BAC 的角平分线∠C =90°DE ⊥AB ∴解析:15cm 2【分析】过点D 作DE ⊥AB 于E ,根据角平分线的性质可得DE=CD ,根据三角形的面积公式即可求得△ABD 的面积.【详解】解:过点D 作DE ⊥AB 于E ,∵AD 是∠BAC 的角平分线,∠C =90°,DE ⊥AB∴DE=DC ,∵BC =8cm ,BD =5cm ,∴DE=DC=3cm ,∴S △ABD =12·AB·DE=12×10×3=15(cm 2), 故答案为:15cm 2.【点睛】本题考查角平分线的性质、三角形的面积公式,熟练掌握角平分线的性质是解答的关键. 15.如图所示,在ABC 中,AB AC =,AD 是ABC 的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F .则下面结论中(1)DA 平分EDF ∠;(2)AE AF =,DE DF =;(3)AD 上的点到B ,C 两点的距离相等;(4)图中共有3对全等三角形.正确的有________ .(1)(2)(3)(4)【分析】在△ABC 中AB=ACAD 是△ABC 的平分线可知直线AD 为△ABC 的对称轴再根据图形的对称性逐一判断【详解】解:(1)∵在中是的角平分线∴∵∴∴∴平分故(1)正确;(解析:(1)(2)(3)(4)【分析】在△ABC 中,AB=AC ,AD 是△ABC 的平分线,可知直线AD 为△ABC 的对称轴,再根据图形的对称性,逐一判断.【详解】解:(1)∵在ABC 中,AB AC =,AD 是ABC 的角平分线,∴BAD CAD ∠=∠.∵DE AB ⊥,DF AC ⊥,∴ADE 90BAD ∠∠=︒-,ADF 90CAD ∠∠=︒-,∴ADE ADF ∠∠=, ∴DA 平分EDF ∠,故(1)正确;(2)由(1)可知,ADE ADF ∠∠=,在AED 和AFD 中,EAD FAD,AD AD,ADE ADF,∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AED AFD ASA ≅,∴AE AF =,DE DF =,故(2)正确;(3)在AD 上取一点M ,连结BM ,CM .在ABM 和ACM 中,AB AC BAD CAD AM AM =⎧⎪∠=∠⎨⎪=⎩∴()ABM ACM SAS ≅,∴BM CM =,故(3)正确;(4)在ABD 和ACD 中,AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∴()ABD ACD SAS ≅.∵DE AB ⊥,DF AC ⊥,∴∠AED=∠AFD=90°在ADE 和ADF 中,AED=AFD BAD CAD AD AD ∠∠⎧⎪∠=∠⎨⎪=⎩∴()ADE ADF AAS ≅. ∵ABD ACD ≅∴∠ABC=∠ACB ,BD=CD ,∵DE AB ⊥,DF AC ⊥,∴∠BED=∠CFD在BED 和CFD △中,EBD FCD BED CFD BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BED CFD AAS ≅,∴图中共有3对全等三角形,故(4)正确.故答案为:(1)(2)(3)(4).【点睛】本题考查了等腰三角形的性质,利用三角形全等是正确解答本题的关键.16.在Rt △ABC 中,∠C =90°,AC =15cm ,BC =8cm ,AX ⊥AC 于A ,P 、Q 两点分别在边AC 和射线AX 上移动.当PQ =AB ,AP =_____时,△ABC 和△APQ 全等.8cm 或15cm 【分析】分情况讨论:①AP =BC =8cm 时Rt △ABC ≌Rt △QPA (HL );②当P 运动到与C 点重合时Rt △ABC ≌Rt △PQA (HL )此时AP =AC =15cm 【详解】解:①当P 运动解析:8cm 或15cm【分析】分情况讨论:①AP =BC =8cm 时,Rt △ABC ≌Rt △QPA (HL );②当P 运动到与C 点重合时,Rt △ABC ≌Rt △PQA (HL ),此时AP =AC =15cm .【详解】解:①当P 运动到AP =BC 时,如图1所示:在Rt △ABC 和Rt △QPA 中,AB QP BC PA=⎧⎨=⎩, ∴Rt △ABC ≌Rt △QPA (HL ),即AP =B =8cm ;②当P 运动到与C 点重合时,如图2所示:在Rt △ABC 和Rt △PQA 中,AB PQ AC PA=⎧⎨=⎩, ∴Rt △ABC ≌Rt △PQA (HL ),即AP =AC =15cm .综上所述,AP 的长度是8cm 或15cm .故答案为:8cm 或15cm .【点睛】本题考查了三角形全等的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键,注意分类讨论,以免漏解.17.如图,ABC 中,∠C =90°,AD 平分∠BAC , AB =5,CD =2,则ABD △的面积是______5【分析】根据角平分线的性质求出DE根据三角形的面积公式计算即可;【详解】如图:作DE⊥AB于点E∵AD平分∠BAC∠C=90°DE⊥AB∴DE=DC=2∵AB=5∴△ABD的面积=×AB×DE=5解析:5【分析】根据角平分线的性质求出DE,根据三角形的面积公式计算即可;【详解】如图:作DE⊥AB于点E,∵AD平分∠BAC,∠C=90°,DE⊥AB,∴DE=DC=2,∵AB=5∴△ABD的面积=1×AB×DE=5,2故答案为:5.【点睛】本题考查了角平分线的性质,掌握角平分线上的点到角的两边的距离相等是解题的关键; 18.如图,12∠=∠,要用“SAS ”判定ADC BDC ≌△△,则可加上条件__________.AD=BD 【分析】要判定△BCD ≌△ACD 已知∠1=∠2CD是公共边具备了一边一角对应相等注意SAS 的条件;两边及夹角对相等只能选AD=BD 【详解】解:由图可知只能是AD=BD 才能组成SAS 故答案为 解析:AD=BD【分析】要判定△BCD ≌△ACD ,已知∠1=∠2,CD 是公共边,具备了一边一角对应相等,注意“SAS”的条件;两边及夹角对相等,只能选AD=BD.【详解】解:由图可知,只能是AD=BD ,才能组成“SAS”,故答案为:AD=BD.【点睛】本题考查了全等的判定,掌握“SAS”的条件是两边及夹角对相等是解题的关键. 19.ABC 中,4AB =,6AC =, 则第三边BC 边上的中线m 的取值范围是______.【分析】如图延长AD 至点E 使得DE=AD 可证△ABD ≌△CDE 可得AB=CEAD=DE 在△ACE 中根据三角形三边关系即可求得AE 的取值范围即可解题【详解】解:延长AD 至点E 使得DE=AD ∵点D 是BC解析:15a <<【分析】如图延长AD 至点E ,使得DE=AD ,可证△ABD ≌△CDE ,可得AB=CE ,AD=DE ,在△ACE 中,根据三角形三边关系即可求得AE 的取值范围,即可解题.【详解】解:延长AD 至点E ,使得DE=AD ,∵点D 是BC 的中点,∴BD=CD在△ABD 和△CDE 中,AD DE ADB CDE BD CD ⎧⎪∠∠⎨⎪⎩===,∴△ABD ≌△CDE (SAS ),∴AB=CE ,∵△ACE 中,AC-CE <AE <AC+CE ,即:AC-AB <AE <AC+AB ,∴2<AE <10,∴1<AD <5.故答案为:1<AD <5.【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD ≌△CDE 是解题的关键.20.如图,在△ABC 和△DBC 中,∠ACB=∠DBC=90°,E 是BC 的中点,DE ⊥AB ,垂足为F ,AB=DE .若BD=8cm ,则AC 的长为_________.4cm 【分析】由DE ⊥AB 可得∠BFE=90°由直角三角形两锐角互余可得∠ABC+∠DEB=90°由∠ACB=90°由直角三角形两锐角互余可得∠ABC+∠A=90°根据同角的余角相等可得∠A=∠DE解析:4cm .【分析】由DE ⊥AB ,可得∠BFE=90°,由直角三角形两锐角互余,可得∠ABC+∠DEB=90°,由∠ACB=90°,由直角三角形两锐角互余,可得∠ABC+∠A=90°,根据同角的余角相等,可得∠A=∠DEB ,然后根据AAS 判断△ABC ≌△EDB ,根据全等三角形的对应边相等即可得到BD=BC ,AC=BE ,由E 是BC 的中点,得到BE=12BC=12BD=4. 【详解】解:∵DE ⊥AB ,可得∠BFE=90°,∴∠ABC+∠DEB=90°,∵∠ACB=90°,∴∠ABC+∠A=90°,∴∠A=∠DEB ,在△ABC 和△EDB 中, ACB DBC A DEBAB DE ∠∠⎧⎪∠∠⎨⎪⎩===, ∴△ABC ≌△EDB (AAS ),∴BD=BC ,AC=BE ,∵E 是BC 的中点,BD=8cm ,∴BE=12BC=12BD=4cm , ∴AC=4cm .故答案为:4cm .【点睛】此题考查了全等三角形的判定与性质,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,本题是一道较为简单的题目,找准全等的三角形是解决本题的关键.三、解答题21.如图1是一个平分角的仪器,其中OD=OE ,FD=FE .(1)如图2,将仪器放置在△ABC 上,使点O 与顶点A 重合,D 、E 分别在边AB 、AC 上,沿AF 画一条射线AP ,交BC 于点P .则AP 就是∠BAC 的平分线吗?请给出判断并说明理由.(2)如图3,在(1)的前提下,过点P 作PQ ⊥AB 于点Q ,已知PQ=4,AC=7,△ABC 的面积是32,求AB 的长.解析:(1)AP 是∠BAC 的平分线,理由见解析;(2)AB=9【分析】(1)利用“SSS”证明△ADF ≌△AEF 即可证明AP 是∠BAC 的平分线;(2)利用角平分线的性质得到PG=PQ=4,再根据三角形的面积公式即可求解.【详解】解:(1)AP 是∠BAC 的平分线,理由如下:在△ADF 和△AEF 中,AD AE AF AF DF EF =⎧⎪=⎨⎪=⎩,∴△ADF ≌△AEF (SSS ),∴∠DAF=∠EAF ,即AP 平分∠BAC ;(2)过点P 作PG ⊥AC 于点G ,∵AP 平分∠BAC ,PQ ⊥AB ,PG ⊥AC ,∴PG=PQ=4, ∵11 22ABC ABP APC SS S AB PQ AC PG =+=⋅+⋅ ∴114743222AB ⨯+⨯⨯=, ∴AB=9.【点睛】本题考查了全等三角形的判定及性质,角平分线的判定和性质.熟练掌握确定三角形的判定方法,正确的识别图形是解题的关键.22.如图,点E ,F 在线段BD 上,已知AF BD ⊥,CE BD ⊥,//AD CB ,DE BF =,求证:AF CE =.解析:见解析【分析】根据ASA 定理证明三角形全等,从而利用全等三角形的性质求解.【详解】证明:∵DE=BF ,∴DE+EF=BF+EF ;∴DF=BE ;∵AF BD ⊥,CE BD ⊥∴∠AFD=∠CEB=90°∵//AD CB∴∠B=∠D在Rt △ADF 和Rt △BCE 中B D DF BE AFD CEB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴Rt △ADF ≌Rt △BCE∴AF CE =【点睛】本题考查了三角形全等的判定及性质;由DE=BF 通过等式的性质得DF=BE 在三角形全等的证明中经常用到,应注意掌握应用.23.如图,在Rt ABC △和Rt DEF △中,90C F ∠=∠=︒,点A 、E 、B 、D 在同一直线上,BC 、EF 交于点M ,AC DF =,AB DE =.求证:(1)CBA FED ∠=∠;(2)AM DM =.解析:(1)见解析;(2)见解析【分析】(1)根据HL 定理可得Rt △ABC ≌ Rt △DEF ,从而得到∠CBA=∠FED ;(2)由(1)所得结论和已知条件可以证得△AEM ≌△DBM ,从而可得AM=DM .【详解】证明:(1)在Rt ABC △和Rt DEF △中,90C F ∠=∠=︒AC DF AB DE =⎧⎨=⎩∴()Rt Rt HL ABC DEF ≌△△∴CBA FED ∠=∠.(2)∵CBA FED ∠=∠∴ME MB =,且AEMDBM ∠=∠ 又∵AB DE =∴AB EB DE EB -=-即AE DB =在AEM △和DBM △中AE DB AEM DBM ME MB =⎧⎪∠=∠⎨⎪=⎩∴()AEM DBM SAS △≌△∴AM DM =.【点睛】本题考查三角形全等的判定和性质,熟练掌握三角形全等的判定定理HL 、SAS 及三角形全等的性质是解题关键.24.如图,在ABC ∆中,90,C ∠=︒点D 在BC 上,过点D 作DE AB ⊥于点,E 点F 是AC 边上一点,连接DF .若,BD DF CF EB ==,求证:AD 平分BAC ∠.解析:证明见解析【分析】由已知可得RT △DCF ≌RT △DEB ,从而得到DC=DE ,又由已知可得DC ⊥AC ,DE ⊥AB ,所以由角平分线的判定定理即可得解.【详解】证明:由题意可得,在Rt DCF ∆和Rt DEB ∆中,CF EB BD DF =⎧⎨=⎩Rt DCF Rt DEB ∴∆≅∆,DC DE ∴=90,C ∠=︒,DC AC ∴⊥,DE AB ⊥AD ∴平分BAC ∠.【点睛】本题考查角平分线与直角三角形的综合运用,熟练掌握角平分线的判定与直角三角形的判定和性质是解题关键.25.已知:如图,120AOB ∠=︒,过点O 作射线OP ,若OM 平分AOP ∠,ON 平分BOP ∠,AOP α∠=(1)如图1,补全图形,直接写出MON ∠=____________︒(2)如图2,若4BOM BON ∠=∠,求α的值.解析:(1)图形见解析,60;(2)144︒【分析】(1)根据尺规作图,以点O 为圆心,任意长度为半径画弧,交角的两边于C 、D ,然后再分别以C 、D 为圆心,大于CD/2长度为半径用圆规画圆弧;即可得到点M ,连接OM ,BOP ∠的角平分线同理可得,由已知条件120AOB ∠=︒,然后根据角平分线的性质即可求得MON ∠的度数;(2)根据题目已知条件可知120POB α∠=-︒,根据角平分线的性质可知2AOM POM α∠=∠=,112022PON BON POB α-∠=∠=∠=,再根据 4BOM BON ∠=∠,120AOB ∠=︒即可求得α的值.【详解】(1)根据尺规作图,首先以O 为圆心,任意长度为半径画弧,交AOP ∠两边于C 、D ,然后以C 为圆心,大于CD/2长度为半径用圆规画圆弧,接着以D 为圆心,同以上步骤一样的长度为半径用圆规画圆弧,最后两圆弧交于M 点,连接顶点O 和M ,OM 即为角平分线.BOP ∠的角平分线同理可得;∵OM 平分AOP ∠,ON 平分BOP ∠, ∴12POM AOM AOP ∠=∠=∠, 12BON PON BOP ∠=∠=∠, ∵AOB AOP BOP ∠=∠+∠,∵MON POM PON ∠=∠+∠,∴11()6022MON AOP BOP AOB ∠=∠+∠=∠=︒;(2)∵AOP α∠=,120AOB ∠=︒,OM 平分AOP ∠,ON 平分BOP ∠,∴120POB α∠=-︒,2AOM POM α∠=∠=,112022PON BON POB α-∠=∠=∠=, ∵4BOM BON ∠=∠,∴)12021204(2αα+=-︒,解得:144.【点睛】 本题考查了尺规作图、角平分线的性质,解题的关键是找准等量关系列出方程. 26.如图,AB AD =,AC AE =,CAE BAD ∠=∠.求证:B D ∠=∠.解析:见解析【分析】先证明BAC DAE ∠=∠,再根据“SAS”证明ABC ADE △≌△即可.【详解】证明:CAE BAD ∠=∠,CAE EMB BAD EAB ∴∠+∠=∠+∠,即BAC DAE ∠=∠.在ABC 和ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,()ABC ADE SAS ∴≌.B D ∴∠=∠.【点睛】题主要考查了全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.27.如图,BC ⊥AD 于C ,EF ⊥AD 于F ,AB ∥DE ,分别交BC 于B ,交EF 于E ,且BC =EF .求证:AF =CD .解析:证明见解析.【分析】由BC ⊥AD ,EF ⊥AD 得∠EFD =∠BCA =90°,由AB ∥DE ,得∠D =∠A ,又BC =EF ,从而△ABC ≌△DEF ,则AC =FD , AF =CD .【详解】证明:∵BC ⊥AD ,EF ⊥AD ,∴∠EFD =∠BCA =90°∵AB ∥DE ,∴∠D =∠A∵BC =EF ,∴△ABC ≌△DEF ,∴AC =FD ,∴AF =CD .【点睛】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键. 28.如图,点E ,F 在BC 上,A D ∠=∠,AF DE =,AFC DEB ∠=∠.求证:BE CF =.解析:见详解【分析】先证明∠AFB=∠DEC ,再根据ASA 证明∆AFB ≅∆DEC ,进而即可得到结论. 【详解】∵AFC DEB ∠=∠,∴∠AFB=∠DEC ,又∵A D ∠=∠,AF DE =,∴∆AFB ≅∆DEC (ASA ),∴BF=CE ,∴BF-EF= CE-EF,.∴BE CF【点睛】本题主要考查三角形全等的判定和性质定理,熟练掌握ASA证明三角形全等,是解题的关键.。
全等三角形(培优2动点问题)

培优部分(一)与全等相关的动点问题例1如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到D、E处,请问(1)在爬行过程中,CD和BE始终相等吗?(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中∠CQE的大小保持不变.请利用图(2)情形,求证:∠ CQE =60°;(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图(3),则爬行过程中,DF始终等于EF是否正确.练习、如图,已知△ABC 中,AB=AC=10cm ,BC=8cm ,点D 为AB 的中点.如果点P 在线段BC 上以3cm/s 的速度由点B 向C 点运动,同时,点Q 在线段CA 上由点C 向A 点运动.(1)若点Q 的运动速度与点P 的运动速度相等,经过1秒后,△BPD 与△CQP 是否全等,请说明理由.(2)若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?如图,等边△ABC 中,点D 、E 、F 分别同时从点A 、B 、C 出发,以相同的速度在AB 、BC 、CA 上运动,连结DE 、EF 、DF .(1)证明:△DEF 是等边三角形;(2)在运动过程中,当△CEF 是直角三角形时,试求DEF ABCS S △△的值.例2已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B、点C重合).以AD为边作等边三角形ADE,连接CE.(1)如图1,当点D在边BC上时.①求证:△ABD≌△ACE;②直接判断结论BC=DC+CE 是否成立;(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC、DC、CE之间存在的数量关系,并写出证明过程;(3)如图3,当点D在边CB的延长线上时,且点A、点E分别在直线BC的异侧,其他条件不变,直接写出BC、DC、CE之间存在的数量关系已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由..在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.(1)如图(1),点D在线段BC上移动时,角α与β之间的数量关系是;证明你的结论;(2)如图(2),点D在线段BC的延长线上移动时,角α与β之间的数量关系是,请说明理由;(3)当点D在线段BC的反向延长线上移动时,请在图(3)中画出完整图形并猜想角α与β之间的数量关系是(1)学完全等三角形以后,老师布置了这样一道题:如图1,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q.试说明:∠BQM=60°.(2)小丽做完后,进行了反思,提出了许多问题,如图2:①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?②如图2若将题中的点M、N分别移动到BC、CA的延长线上,是否仍能得到∠BQM=60°?如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是;(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;.。
初二数学 数学全全等三角形截长补短的专项培优练习题(含答案

初二数学 数学全全等三角形截长补短的专项培优练习题(含答案一、全等三角形截长补短1.已知ABC 是等边三角形,6AB =.(1)如图1,点M 是BC 延长线上一点,60AMN ∠=︒,MN 交ABC 的外角平分线于点N ,求CN CM -的值;(2)如图2,过点A 作AD BC ⊥于点D ,点P 是直线AD 上一点,以CP 为边,在CP 的下方作等边CPQ ,连接DQ ,求DQ 的最小值.2.数学课上,小白遇到这样一个问题:如图1,在等腰Rt ABC ∆中,90BAC ∠=︒,AB AC =,AD AE =,求证ABE ACD ∠=∠;在此问题的基础上,老师补充:过点A 作AF BE ⊥于点G 交BC 于点F ,过F 作FP CD ⊥交BE 于点P ,交CD 于点H ,试探究线段BP ,FP ,AF 之间的数量关系,并说明理由.小白通过研究发现,AFB ∠与HFC ∠有某种数量关系;小明通过研究发现,将三条线段中的两条放到同一条直线上,即“截长补短”,再通过进一步推理,可以得出结论.阅读上面材料,请回答下面问题:(1)求证ABE ACD ∠=∠;(2)猜想AFB ∠与HFC ∠的数量关系,并证明;(3)探究线段BP ,FP ,AF 之间的数量关系,并证明.3.如图①,ABC 和BDC 是等腰三角形,且AB AC =,BD CD =,80BAC ∠=︒,100∠=︒BDC ,以D 为顶点作一个50︒角,角的两边分别交边AB ,AC 于点E 、F ,连接EF .(1)探究BE 、EF 、FC 之间的关系,并说明理由;(2)若点E 、F 分别在AB 、CA 延长线上,其他条件不变,如图②所示,则BE 、EF 、FC 之间存在什么样的关系?并说明理由.4.如图,ABC ∆中,BE ,CD 分别平分ABC ∠和ACB ∠,BE ,CD 相交于点F ,60A ∠=︒.(1)求BFD ∠的度数;(2)判断BC ,BD ,CE 之间的等量关系,并证明你的结论.5.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD ,以D 为顶点作MDN ∠,交边AC ,BC 于点M ,N .(1)如图(1),若30ACD ∠=︒,60MDN ∠=︒,当MDN ∠绕点D 旋转时,AM ,MN ,BN 三条线段之间有何种数量关系?证明你的结论;(2)如图(2),当90ACD MDN ∠+∠=︒时,AM ,MN ,BN 三条线段之间有何数量关系?证明你的结论;(3)如图(3),在(2)的条件下,若将M ,N 分别改在CA ,BC 的延长线上,完成图(3),其余条件不变,则AM ,MN ,BN 之间有何数量关系(直接写出结论,不必证明).6.(1)方法选择如图①,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD ,AB BC AC ==,求证:BD AD CD =+.小颖认为可用截长法证明:在DB 上截取DM AD =,连接AM ……小军认为可用补短法证明:延长CD 至点N ,使得DN AD =……请你选择一种方法证明.(2)类比探究探究1如图②,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD ,若BC 是⊙O 的直径,AB AC =,试用等式表示线段AD ,BD ,CD 之间的数量关系,并证明你的结论. 探究2如图③,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .若BC 是⊙O 的直径,::::BC AC AB a b c =,则线段AD ,BD ,CD 之间的等量关系式是______.7.如图,在正方形ABCD 中,点F 是CD 的中点,点E 是BC 边上的一点,且AF 平分DAE ∠,求证:AE EC CD =+.8.如图所示,平行四边形ABCD 和平行四边形CDEF 有公共边CD ,边AB 和EF 在同一条直线上,AC ⊥CD 且AC=AF ,过点A 作AH ⊥BC 交CF 于点G ,交BC 于点H ,连接EG .(1)若AE=2,CD=5,则△BCF 的面积为 ;△BCF 的周长为 ;(2)求证:BC=AG+EG .9.已知,在ABCD 中,AB BD AB BD E ⊥=,,为射线BC 上一点,连接AE 交BD 于点F .(1)如图1,若E 点与点C 重合,且25AF =,求AD 的长;(2)如图2,当点E 在BC 边上时,过点D 作DG AE ⊥于G ,延长DG 交BC 于H ,连接FH .求证:AF DH FH =+.(3)如图3,当点E 在射线BC 上运动时,过点D 作DG AE ⊥于G M ,为AG 的中点,点N 在BC 边上且1BN =,已知42AB =,请直接写出MN 的最小值.10.如图1,在ABC ∆中,ACB ∠是直角,60B ∠=︒,AD 、CE 分别是BAC ∠、BCA ∠的平分线,AD 、CE 相交于点F .(1)求出AFC ∠的度数;(2)判断FE 与FD 之间的数量关系并说明理由.(提示:在AC 上截取CG CD =,连接FG .)(3)如图2,在△ABC ∆中,如果ACB ∠不是直角,而(1)中的其它条件不变,试判断线段AE 、CD 与AC 之间的数量关系并说明理由.【参考答案】***试卷处理标记,请不要删除一、全等三角形截长补短1.(1)6;(2)32【分析】(1)在CN 上截取点H ,使CH=CM ,先证出△CMH 为等边三角形,然后利用ASA 证出△AMC ≌△NMH ,从而得出AC=NH ,从而求出结论;(2)连接BQ ,利用SAS 证出△QCB ≌△PCA ,从而得出∠CBQ=∠CAP ,然后根据三线合一和等量代换即可求出∠CBQ=30°、∠ABQ =90°,从而判断出点Q 的运动轨迹,然后根据垂线段最短即可得出当DQ ⊥BQ 时,DQ 最短,然后利用30°所对的直角边是斜边的一半即可得出结论.【详解】解:(1)在CN 上截取点H ,使CH=CM ,连接MH∵△ABC 为等边三角形∴∠ACB=60°,AC=AB=6∴∠ACM=180°-∠ACB=120°∵CN 平分∠ACM∴∠MCN=12∠ACM=60° ∴△CMH 为等边三角形 ∴CM=HM ,∠CMH=∠CHM=60°∴∠NHM=180°-∠CHM=120°,∠AMC +∠AMH=60°∴∠ACM=∠NHM∵60AMN ∠=︒∴∠NMH +∠AMH=60°∴∠AMC=∠NMH在△AMC 和△NMH 中AMC NMH CM HMACM NHM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AMC ≌△NMH∴AC=NH∴CN CM -=CN -CH=NH=AC=6(2)连接BQ∵△ABC 和△CPQ 都是等边三角形∴BC=AC ,QC=PC ,∠PCQ =∠ACB=∠ABC=∠BAC =60°∴∠PCQ -∠PCB=∠ACB -∠PCB∴∠QCB=∠PCA在△QCB 和△PCA 中BC AC QCB PCA QC PC =⎧⎪∠=∠⎨⎪=⎩∴△QCB ≌△PCA∴∠CBQ=∠CAP∵AD BC ⊥∴∠CAP=12∠BAC=30°,BD=12BC=3 ∴∠CBQ=30°∴∠ABQ=∠ABC +∠CBQ=90°∴点Q 在过点B 作AB 的垂线上运动 根据垂线段最短可得:当DQ ⊥BQ 时,DQ 最短此时在Rt △BDQ 中,∠QBD=30°∴DQ=12BD=32即DQ 的最小值为32.【点睛】此题考查的是全等三角形的判定及性质、等边三角形的判定及性质、直角三角形的性质和垂线段最短的应用,掌握构造全等三角形的方法、全等三角形的判定及性质、等边三角形的判定及性质、30°所对的直角边是斜边的一半和垂线段最短是解决此题的关键. 2.(1)见解析;(2)HFC BFA ∠=∠,证明见解析;(3)BP AF PF =+,证明见解析【分析】(1)利用SAS 证明ABE ACD ≅可得结论;(2)设ABE ACD x ∠=∠=,推出=45BFA x ∠︒+,=45HFC x ∠︒+,即可证明HFC BFA ∠=∠;(3)过点C 作CM AC ⊥交AF 延长线于点M ,延长FP 交AC 于点N ,证明△ABE ≌△CAM ,得出BE AM =和M BEA ∠=∠,从而证明△NFC ≌△MFC ,得到FM FN =和M FNC ∠=∠,可得PN=PE ,从而得出BP=AF+PF.【详解】解:(1)∵在△ABE 和△ACD 中,==AB AC A A AE AD ⎧⎪∠=∠⎨⎪⎩,ABE ACD ∴∆≅∆(SAS ),ABE ACD ∴∠=∠;(2)设ABE ACD x ∠=∠=,AF BE ⊥,90BAF x ∴∠=︒-,()=9045=45BFA x x ∴∠︒-︒-︒+,ACD x ∠=,45HCF x ∴∠=︒-,FP CD ⊥,()9045=45HFC x x ∴∠=︒-︒-︒+,HFC BFA ∴∠=∠;(3)过点C 作CM AC ⊥交AF 延长线于点M ,延长FP 交AC 于点N ,90BAF FAC ∠+∠=︒,90BAF ABG ∠+∠=︒,FAC ABG ∴∠=∠,在△ABE 和△CAM 中,===BAE ACM AB AC ABE CAM ∠∠⎧⎪⎨⎪∠∠⎩, ABE CAM ∴∆≅∆(ASA ),BE AM ∴=,M BEA ∠=∠,BFA MFC NFC ∠=∠=∠,FC FC =,45ACB BCM ∠=∠=︒,NFC MFC ∴∆≅∆(ASA ),FM FN ∴=,M FNC ∠=∠,FNC BEA ∴∠=∠,PN PE ∴=,∴BP BE PE AM PE AF FM PE =-=-=+-AF FN PN AF PF =+-=+.【点睛】本题考查了全等三角形的判定和性质、等腰直角三角形的性质以及等角对等边等知识点,解题的关键是根据截长补短法添加适当的辅助线,构造全等三角形证明结论,有一定难度. 3.(1)EF=BE+FC ;(2)EF=FC-BE .【分析】(1)由等腰三角形的性质,解得50ABC ACB ∠=∠=︒,40DBC DCB ∠=∠=︒,延长AB 至G ,使得BG=CF ,连接DG ,进而证明GBD △()FCD SAS ≅,再根据全等三角形对应边相等的性质解得DG FD =,再结合等腰三角形的性质可证明DEF ()DGE SAS ≅,最后根据全等三角形的性质解题即可;(2)在CA 上截取CG=BE,连接DG ,由等腰三角形的性质,可得50ABC ACB ∠=∠=︒,40DBC DCB ∠=∠=︒,进而证明BED ≅()CGD SAS 得到DG DE =,据此方法再证明EDF ≅()GDF SAS ,最后根据全等三角形的性质解题即可.【详解】 (1)ABC 和BDC 是等腰三角形, ABC ACB ∴∠=∠DBC DCB ∴∠=∠80BAC AB AC ∠=︒=,50ABC ACB ∴∠=∠=︒100BDC BD CD ∠=︒=,40DBC DCB ∴∠=∠=︒90ABD ACD DCF ∴∠=∠=︒=∠延长AB 至G ,使得BG=CF ,连接DG18090GBD ABD ∠=︒-∠=︒在GBD △和FCD 中,BG=CF ,GBD DCF BD FD ∠=∠=,∴GBD △()FCD SAS ≅,DG FD ∴=BDG CDF ∴∠=∠50100EDF BDC ∴∠=︒∠=︒,50BDE CDF ∴∠+∠=︒50GDE BDG BDE CDF BDE ∠=∠+∠=∠+∠=︒在DEF 和DGE △中,DE=DE ,EDF GDE DF GD ∠=∠=,∴DEF ()DGE SAS ≅,EF EG BE GB BE CF ∴==+=+(2)在CA 上截取CG=BE,连接DGABC 是等腰三角形,80BAC ∠=︒50ABC ACB ∴∠=∠=︒100BDC BD CD ∠=︒=,40DBC DCB ∴∠=∠=︒90EBD GCD ∴∠=∠=︒CG BE BD CD ==,在BED 和CGD △中,CG=BE ,EBD GCD BD CD ∠=∠=,BED ∴≅()CGD SASDG DE ∴=在EDF 和GDF 中,FD=FD ,GDF EDF ED GD ∠=∠=,EDF ∴≅()GDF SASEF FG FC CG FC BE ∴==-=-【点睛】本题考查等腰三角形的性质、全等三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.4.(1)∠BFD =60°;(2)BC =BD +CE ;证明见解析【分析】(1)根据角平分线和外角性质求解即可;(2)在BC 上截取BG =BD ,连接FG ,证明△BDF ≌△BGF ,△CGF ≌△CEF ,即可得到结果;【详解】(1)∵BE ,CD 分别平分ABC ∠和ACB ∠,BE ,∴ABE CBE ∠=∠,ACD BCD ∠=∠,∵60A ∠=︒,∴120ABC ACB ∠+∠=︒,∴60FBC FCB ∠+∠=︒,∴60DFB ∠=︒.(2)BC =BD +CE ;证明方法:在BC 上截取BG =BD ,连接FG ,在△BDF 和△BGF 中,BD BG DBF GBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴()△△BDF BGFSAS ≅, ∴60DFB BFG ∠=∠=︒,又∵GCF ECF ∠=∠,∴△CGF ≌△CEF (ASA ),∴CE =CG ,∴BC =BD +CE .【点睛】本题主要考查了三角形内角和定理、外角定理、三角形全等应用,准确分析是解题的关键.5.(1)AM BN MN +=;证明见解析;(2)AM BN MN +=;证明见解析;(3)补图见解析;BN AM MN -=;证明见解析.【分析】(1)延长CB 到E ,使BE=AM ,证△DAM ≌△DBE ,推出∠BDE=∠MDA ,DM=DE ,证△MDN ≌△EDN ,推出MN=NE 即可;(2)延长CB 到E ,使BE=AM ,证△DAM ≌△DBE ,推出∠BDE=∠MDA ,DM=DE ,证△MDN ≌△EDN ,推出MN=NE 即可;(3)在CB 截取BE=AM ,连接DE ,证△DAM ≌△DBE ,推出∠BDE=∠MDA ,DM=DE ,证△MDN ≌△EDN ,推出MN=NE 即可.【详解】(1)AM BN MN +=.证明如下:如图,延长CB 到E ,使BE AM =,连接DE .90A CBD ∠=∠=︒,90A EBD ∴∠=∠=︒.ADC BDC ≌,AD BD ∴=.在DAM △和DBE 中,AM BE A DBE AD BD =⎧⎪∠=∠⎨⎪=⎩,()DAM DBE SAS ∴≌,BDE MDA ∴∠=∠,DM DE =.MDN ADC BDC ∠=∠=∠,ADM NDC BDE ∴∠=∠=∠,MDC NDB ∠=∠,MDN NDE ∴∠=∠.在MDN △和EDN △中,DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩,()MDN EDN SAS ∴△≌△,MN NE ∴=.NE BE BN AM BN =+=+,AM BN MN ∴+=;(2)AM BN MN +=.证明如下:如图,延长CB 到E ,使BE AM =,连接DE .90A CBD ∠=∠=︒,90A DBE ∴∠=∠=︒.ADC BDC ≌,AD BD ∴=,ADC CDB ∠=∠.在DAM △和DBE 中,AM BE A DBE AD BD =⎧⎪∠=∠⎨⎪=⎩,()DAM DBE SAS ∴≌,BDE MDA ∴∠=∠,DM DE =.90MDN ACD ∠+∠=︒,90ACD ADC ∠+∠=︒,ADC CDB ∠=∠,NDM ADC CDB ∴∠=∠=∠,ADM CDN BDE ∴∠=∠=∠,CDM NDB ∠=∠,MDN NDE ∴∠=∠.在MDN △和EDN △中,DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩,()MDN EDN SAS ∴△≌△,MN NE ∴=.NE BE BN AM BN =+=+,AM BN MN ∴+=;(3)补充完成题图,如图所示.BN AM MN -=.证明如下:如上图,在CB 上截取BE=AM ,连接DE .90CDA ACD ∠+∠=︒,90MDN ACD ∠+∠=︒,MDN CDA ∴∠=∠,MDA CDN ∴∠=∠.90B CAD ∠=∠=︒,90B DAM ∴∠=∠=︒.在DAM △和DBE 中,AM BE DAM DBE AD BD =⎧⎪∠=∠⎨⎪=⎩,()DAM DBE SAS ∴≌,BDE ADM CDN ∴∠=∠=∠,DM DE =.ADC BDC MDN ∠=∠=∠,ADN CDE ∴∠=∠,MDN EDN ∴∠=∠.在MDN △和EDN △中,DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩,()MDN EDN SAS ∴△≌△,MN NE ∴=.NE BN BE BN AM =-=-,BN AM MN ∴-=.【点睛】本题考查了全等三角形的性质和判定的应用,作出辅助线构造全等三角形是解题的关键.6.(1)见解析;(2)①BD CD =+,见解析,②c a BD CD AD b b=+ 【分析】 (1)根据题中所给的截长法或补短法思路解题,利用全等三角形的性质解题即可.(2)探究1 要求AD 、BD 、CD 之间的数量关系,结合(1)中所给方法,在BD 上截取BM CD =,再利用全等三角形及等腰直角三角形的性质进行求解.探究2 要求AD 、BD 、CD 之间的数量关系,以AD 为边构造直角三角形,再利用相似的性质求解.【详解】(1)截长法 证明:如图①-1,在DB 上截取DM AD =,连接AM ,AB BC AC ==,ABC ∴是等边三角形,60ABC ACB BAC ∴∠=∠=∠=︒.60ADB ACB ∴∠=∠=︒,DM AD =,AMD ∴△是等边三角形,60MAD ∴∠=︒,AM AD =.BAM CAD ∴∠=∠,()BAM CAD SAS ∴△≌△,BM CD ∴=,BD DM BM AD CD ∴=+=+;补短法 证明:如图①-2,延长CD 至点N ,使得DN AD =,DAN DNA ∴∠=∠.AB AC BC ==,ABC ∴为等边三角形,60ABC ACB BAC ∠=∠=∠=︒.60ADB ACB ∴∠=∠=︒,60BDC BAC ∠=∠=︒,18060ADN BDC ADB ∴∠=︒-∠-∠=︒,ADN ∴为等边三角形,AD AN =,60DAN ∠=︒.BAD CAN ∴∠=∠.在BAD 和CAN △中,AB AC BAD CAN AD AN =⎧⎪∠=∠⎨⎪=⎩,()BAD CAN SAS ∴△≌△,BD CN ∴=,又CN CD DN CD AD =+=+,BD CD AD ∴=+.(2)探究1 解:2BD AD CD =+; 证明:如图②,在BD 上截取BM CD =,连接AM ,BC 是O 的直径,AB AC =,90BAC ∴∠=︒,45ABC ACB ∠=∠=︒.45ADM ACB ∴∠=∠=︒,在BAM 和CAD 中,,AB AC ABM ACD BM CD =⎧⎪∠=∠⎨⎪=⎩()BAM CAD SAS ∴△≌△,AM AD ∴=,BAM CAD ∠=∠.45AMD ADM ∴∠=∠=︒,90MAD ∠=︒.AMD ∴△是等腰直角三角形,2MD AD ∴=.BD MD BM =+,2BD AD CD ∴=+;探究2 解:c a BD CD AD b b=+. 如图③,过点A 作AM AD ⊥交BD 于点M ,BC 是O 的直径,90BAC ∴∠=︒,BAC MAD ∴∠=∠,BAM CAD ∴∠=∠,ABM DCA ∠=∠,BAM CAD ∴△∽△,BM AB c CD AC b ∴==,c BM CD b ∴=, 又ADM ACB ∠=∠,MAD BAC ∠=∠,ADM ACB ∴△∽△,DM BC a AD AC b ∴==,a DM AD b∴=, BD BM MD =+,c a BD CD AD b b∴=+.【点睛】本题是圆的综合题,考查了圆周角定理,全等三角形的判定和性质,相似三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的判定与性质,正确作出辅助线,熟练运用图形的性质是解题的关键.7.见解析【分析】过F 作FH ⊥AE 于H ,得出FH=FD ,然后证明△FHE ≌△FCE ,再通过等价转换可证得AE=EC+CD .【详解】证明:过F 作FH ⊥AE 于H ,如图,∵AF 平分∠DAE ,∠D=90°,FH ⊥AE ,∴∠DAF=∠EAF ,FH=FD ,又∵DF=FC=FH ,FE 为公共边,∴△FHE ≌△FCE (HL ).∴HE=CE .∵AE=AH+HE ,AH=AD=CD ,HE=CE ,∴AE=EC+CD .【点睛】本题考查角平分线的性质,角平分线上的点到角的两边距离相等,也考查了等量代换的思想,属于比较典型的题目.8.(1)3,23234++;(2)见解析【分析】(1)根据平行和垂直的特点求出BF ,AF ,再根据勾股定理求出CD ,根据FP 与BA 的比值求出面积,再根据勾股定理求CF ,BC 即可得到周长. (2)在AD 上截取AM=AG ,连接CM ,证△FAG ≌△CAM ;证△EFG ≌△DCM .【详解】解:(1)面积为3;周长为23234++∵四边形ABCD 和四边形CDEF 都是平行四边形,∴EF=CD ,AB=CD ,AB ∥CD∴EF=AB=CD=5∴AE=EF-AE=5-2=3 ∴BF=5-3=2过F 作FP ⊥BC则FP :AH=BF :AB=2:5,∴::2:5BCF BCA S S FP AH == , ∵AC ⊥CD ,AB ∥CD,∴AB ⊥AC ,即∠BAC=90°,∵AC=AF=3,∴223332+= ,223534+=,∴2213552BCF BCA S S CD AC ==⨯⨯=∴△BCF 的面积为3,△BCF 周长为23234+(2)在AD 上截取AM=AG ,连接CM ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD=BC∵AH ⊥BC∴AD ⊥AH∴∠DAH=90°∵∠BAC=90°∴∠DAH=∠BAC∴∠DAH-∠CAH =∠BAC-∠CAH∴∠BAH=∠CAD∵AF=AC∴△FAG ≌△CAM∴FG=CM ,∠ACM=∠AFG∵四边形CDEF 是平行四边形,∴EF ∥CD ,EF=CD ,∴∠DCF+∠AFC=180°,∵AF=AC , ∠BAC=90°,∴∠AFC=∠ACF=45°,∴∠DCF=180°-∠AFC=135°,∴∠ACM=∠AFG=45°,∴∠DCM=∠FCD-∠ACF-∠ACM=45°,∴∠AFG=∠DCM ,∴△EFG ≌△DCM ,∴EG=DM ,∵AD=AM+DM ,∴AD=AG+EG ,∵AD=BC ,∴BC=AG+EG .【点睛】此题考查平行四边形的性质,平行线分线段成比例和勾股定理的应用.9.(1)42AD =2)见解析;(3)MN 的最小值为3.【分析】(1)如图1中,利用等腰三角形的性质可得90ABD ∠=︒,利用平行四边形的性质可得F 为BD 中点,在Rt ABF ∆中,由勾股定理可求得BF ,则可求得AB ,在Rt ABD∆中,再利用勾股定理可求得AD ;(2)如图2中,在AF 上截取AK HD =,连接BK ,可先证明ABK DBH ∆≅∆,再证明BFK BFH ∆≅∆,可证得结论;(3)连接AN 并延长到Q ,使NQ AN =,连接GQ ,取AD 的中点O ,连接OG ,得到90AGD ∠=︒,于是得到点G 的轨迹是以O 为圆心,以OG 为半径的弧,且4OG =,求得GQ 最小值为6,根据三角形的中位线定理即可得到结论.【详解】(1)45AB BD BAD =∠=︒,,45BDA BAD ∴∠=∠=︒90 ABD ∴∠=︒,四边形ABCD 是平行四边形,∴当点E 与点C 重合时,1122BF BD AB == 在Rt ABF 中,222AF AB BF =+()()222252BF BF ∴=+ 24BF AB ∴==,Rt ABD ∴中,42AD =.(2)证明:如图2中,在AF 上截取AK HD =,连接BK ,23AFD ABF FGD ∠=∠+∠=∠+∠,90ABF FGD ∠=∠=︒,23∴∠=∠,在ABK 和DBH ∆中,23AB BD AK HD =⎧⎪∠=∠⎨⎪=⎩, ABK DBH ∴∆≅∆,BK BH ∴=,61∠=∠,AK DH =,四边形ABCD 是平行四边形,//AD BC ∴,41645∴∠=∠=∠=︒,5645ABD ∴∠=∠-∠=︒,51∴∠=∠,在FBK ∆和FBH ∆中,51BF BF BK BH =⎧⎪∠=∠⎨⎪=⎩, FBK FBH ∴∆≅∆,KF FH ∴=,AF AK KF =+,AF DH FH ∴=+;()3解:连接AN 并延长到Q ,使NQ AN =,连接GQ ,取AD 的中点O ,连接OG ,作AK ⊥BC ,交BC 延长线于点K ,作QP ⊥AD ,交AD 延长线于点P .90AGD ∠=︒,∴点G 的轨迹是以O 为圆心,以OG 为半径的弧,且4OG =,根据△ABD 为等腰直角三角形,可得AD 228AB BD +=, ∴AO=142AD =, 根据△ABK 为等腰直角三角形,可得AK =BK =4,可得QE =PE =4,∴PQ =8,∵BK=4,BN =1,∴KN =5,∴KE=AP =10,∴OP =6,10OQ ∴=,4OG =,GQ ∴最小值为6, MN 是AGQ ∆的中位线,MN ∴的最小值为3.【点睛】本题考查四边形综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、中位线定理,解题的关键是学会添加常用辅助线,构造全等三角形.10.(1)∠AFC=120°;(2)FE与FD之间的数量关系为:DF=EF.理由见解析;(3)AC=AE+CD.理由见解析.【分析】(1)根据三角形的内角和性质只要求出∠FAC,∠ACF即可解决问题;(2)根据在图2的 AC上截取CG=CD,证得△CFG≌△CFD (SAS),得出DF= GF;再根据ASA 证明△AFG≌△AFE,得EF=FG,故得出EF=FD;(3)根据(2) 的证明方法,在图3的AC上截取AG=AE,证得△EAF≌△GAF (SAS)得出∠EFA=∠GFA;再根据ASA证明△FDC≌△FGC,得CD=CG即可解决问题.【详解】(1)解:∵∠ACB=90°,∠B=60°,∴∠BAC=90°﹣60°=30°,∵AD、CE分别是∠BAC、∠BCA的平分线,∴∠FAC=15°,∠FCA=45°,∴∠AFC=180°﹣(∠FAC+∠ACF)=120°(2)解:FE与FD之间的数量关系为:DF=EF.理由:如图2,在AC上截取CG=CD,∵CE是∠BCA的平分线,∴∠DCF=∠GCF,在△CFG和△CFD中,CG CD DCF GCF CF CF =⎧⎪∠=∠⎨⎪=⎩,∴△CFG ≌△CFD (SAS ),∴DF =GF .∠CFD =∠CFG由(1)∠AFC =120°得,∴∠CFD =∠CFG =∠AFE =60°,∴∠AFG =60°,又∵∠AFE =∠CFD =60°,∴∠AFE =∠AFG ,在△AFG 和△AFE 中,AFE AFG AF AFEAF GAF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AFG ≌△AFE (ASA ),∴EF =GF ,∴DF =EF ;(3)结论:AC =AE+CD .理由:如图3,在AC 上截取AG =AE ,同(2)可得,△EAF ≌△GAF (SAS ),∴∠EFA =∠GFA ,AG =AE∵∠BAC+∠BCA=180°-∠B=180°-60°=120°∴∠AFC =180°﹣(∠FAC+∠FCA)=180°-12(∠BAC+∠BCA)=180°-12×120°=120°, ∴∠EFA =∠GFA =180°﹣120°=60°=∠DFC ,∴∠CFG =∠CFD =60°,同(2)可得,△FDC ≌△FGC (ASA ),∴CD =CG ,∴AC =AG+CG =AE+CD .【点睛】本题考查了全等三角形的判定和性质的运用,全等三角形的判定和性质是证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.。
(完整版)全等三角形经典培优题型(含答案解析),推荐文档

我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.全等三角形证明经典(答案)1. 延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52证明:连接BF和EF。
因为BC=ED,CF=DF,∠BCF=∠EDF。
所以三角形BCF全等于三角形EDF(边角边)。
所以BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
所以∠EBF=∠BEF。
又因为∠ABC=∠AED。
所以∠ABE=∠AEB。
所以AB=AE。
在三角形ABF和三角形AEF中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以三角形ABF和三角形AEF全等。
所以∠BAF=∠EAF (∠1=∠2)。
3 证明:过E点,作EG//AC,交AD延长线于G则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE(AAS)∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG∴EF=AC4证明:在AC上截取AE=AB,连接ED∵AD平分∠BAC∴∠EAD=∠BAD又∵AE=AB,AD=AD∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB∵AC=AB+BDAC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C5证明:在AE上取F,使EF=EB,连接CF因为CE⊥AB所以∠CEB=∠CEF=90°因为EB=EF,CE=CE,所以△CEB≌△CEF所以∠B=∠CFE因为∠B+∠D=180°,∠CFE+∠CFA=180°所以∠D=∠CFA因为AC平分∠BAD所以∠DAC=∠FAC又因为AC=AC所以△ADC≌△AFC(SAS)所以AD=AF所以AE=AF+FE=AD+BE6证明:在BC上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则⊿ABE≌ΔFBE(SAS),∠EFB=∠A; AB平行于CD,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD.11证明:在AB上找点E,使AE=AC∵AE=AC,∠EAD=∠CAD,AD=AD∴△ADE≌△ADC。
全等三角形经典培优题型(含标准答案)
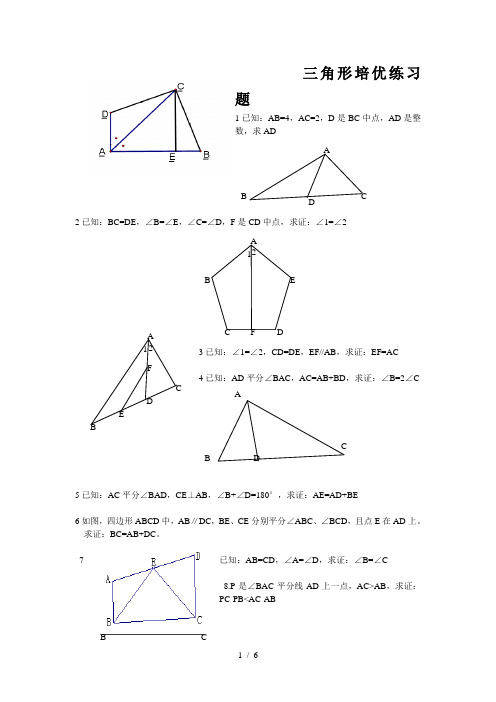
三角形培优练习题1已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C5已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE6如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
已知:AB=CD ,∠A=∠D ,求证:∠B=∠C78.P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-ABCDBA BC DEF 2 1ADBCA B CD ABACDF2 1 E9已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC10.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .11如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B12如图:AE 、BC 交于点M ,F点在AM 上,BE∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
13已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F 。
求证:BE =CD .14在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.15如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。
《全等三角形》培优题型全集解析

《全等三⾓形》培优题型全集解析《全等三⾓形》培优题型全集题型⼀:倍长中线(线段)造全等1、已知:如图,AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且 AE=EF ,求证:AC=BFC2、如图,△ABC 中,AB=5,AC=3,则中线AD 的取值范围是______.DCBA3、在△ABC 中,AC=5,中线AD=7,则AB 边的取值范围是( ) A 、1C 、5D 、94、已知:AD 、AE 分别是△ABC 和△ABD 的中线,且BA=BD ,求证:AE=21AC CE5、已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠ABFDEC题型⼆:截长补短1、已知,四边形ABCD 中,AB ∥CD ,∠1=∠2,∠3=∠4。
求证:BC =AB +CD 。
2、已知:如图,在△ABC 中,∠C =2∠B ,∠1=∠2,求证:AB=AC+CD.3、如图,在△ABC 中,∠BAC=60°, AD 是∠BAC 的平分线,且AC=AB+BD ,求∠ABC 的度数A4、已知ABC ?中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.DOECB ADCB A 12题型三:⾓平分线上的点向⾓两边引垂线段1、如图,在四边形ABCD中,BC>BA,AD=CD,求证:∠BAD+∠C=180°DCBA2、如图,四边形ABCD中,AC平分∠BAD,CE⊥AB于E,AD+AB=2AE,则∠B与∠ADC互补,为什么?3、如图,△ABD和△ACD,BD=CD,∠ABD=∠ACD,求证AD平分∠BAC.4、已知,AB>AD,∠1=∠2,CD=BC。
求证:∠ADC+∠B=180°。
图九21CBAD5、如图,在△ABC中∠A BC,∠A CB的外⾓平分线相交于点P,求证:AP是∠BAC的⾓平分线图⼗⼀1ABC6、如图,∠B=∠C=90°,AM平分∠DAB,DM平分∠ADC。
全等三角形经典培优题型(含答案)

全等三角形经典培优题型(含答案)1.已知三角形ABC中,AB=4,AC=2,D是BC的中点,AD是整数,求AD的长度。
解:由题意可得AD=AB-DB,又BD=DC=AC/2=1,故AB=AD+DB=AD+1,代入AB=4得AD=3.2.已知四边形BCDE中,BC=DE,∠B=∠E,∠C=∠D,F是CD的中点,证明∠1=∠2.解:由于BC=DE,且∠B=∠E,所以△BCE≌△EDC,从而∠1=∠BCE=∠EDC=∠2.3.已知四边形ABCD中,∠1=∠2,CD=DE,EF//AB,证明EF=AC。
解:由于EF//AB,所以△EFC∼△ABC,从而EF/AC=FC/BC,而CD=DE,所以FC=CD,代入得EF/AC=CD/BC,又由于∠1=∠2,所以△BCD∼△ECD,从而CD/BC=ED/AC,代入得EF/AC=ED/AC,即EF=AC。
4.已知三角形ABC中,AD平分∠BAC,AC=AB+BD,证明∠B=2∠C。
解:由于AD平分∠BAC,所以∠BAD=∠CAD,从而∠B=∠BAD+∠ABD=∠CAD+∠ACD,又由于AC=AB+BD,所以BD=AC-AB,代入得∠B=∠CAD+∠ACD=∠CAD+∠ABC,又由于∠CAD=∠CAB,所以∠B=∠CAB+∠ABC=2∠C。
5.已知三角形ABC中,AC平分∠BAD,CE⊥AB,∠B+∠D=180°,证明AE=AD+BE。
解:由于AC平分∠BAD,所以∠CAD=∠CAB,从而△ABE∼△DCE,所以AE/AD=BE/CD,又由于∠B+∠D=180°,所以CD=AB,代入得AE/AD=BE/AB,即AE=AD·(BE/AB),又由于CE⊥AB,所以△CEB为直角三角形,从而BE/AB=CE/AC,代入得AE=AD·(CE/AC),又由于AC平分∠BAD,所以△ACD∼△ABC,从而CE/AC=CD/AB,代入得AE=AD·(CD/AB),又由于CD=AB-BD,所以AE=AD·((AB-BD)/AB),即AE=AD+BE·(AB/AD-1),又由于AB>AD,所以AB/AD-1<AB/AD,从而AE<AD+BE·(AB/AD),即AE<AD+BE。
八年级上册数学 全等三角形(培优篇)(Word版 含解析)

八年级上册数学 全等三角形(培优篇)(Word 版 含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在01A BA △中,20B ∠=︒,01A B A B =,在1A B 上取点C ,延长01A A 到2A ,使得121A A AC =;在2A C 上取一点D ,延长12A A 到3A ,使得232A A A D =;…,按此做法进行下去,第n 个等腰三角形的底角n A ∠的度数为__________.【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律即可得出第n 个等腰三角形的底角∠A n 的度数.【详解】解:∵在△A 0BA 1中,∠B=20°,A 0B=A 1B , ∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°, ∵A 1A 2=A 1C ,∠BA 1 A 0是△A 1A 2C 的外角, ∴∠CA 2A 1= 108022BA A ︒∠= =40°; 同理可得,∠DA 3A 2=20°,∠EA 4A 3=10°,∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律是解答此题的关键.2.如图,△ABC 是等边三角形,高AD 、BE 相交于点H ,3,在BE 上截取BG=2,以GE 为边作等边三角形GEF ,则△ABH 与△GEF 重叠(阴影)部分的面积为_____.【答案】53 【解析】试题分析:如图所示,由△ABC 是等边三角形,BC=43,得到AD=BE=3BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE ﹣BG=6﹣2=4.由GE 为边作等边三角形GEF ,得FG=EG=4,∠EGF=∠GEF=60°,△MHE 是等边三角形;S △ABC =12AC•BE=12AC×EH×3EH=13BE=13×6=2.由三角形外角的性质,得∠BIF=∠FGE ﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG ﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,IN=3.S 五边形NIGHM =S △EFG ﹣S △EMH ﹣S △FIN =223314231442⨯-⨯-⨯⨯=53,故答案为53.考点:1.等边三角形的判定与性质;2.三角形的重心;3.三角形中位线定理;4.综合题;5.压轴题.3.如图,点A,B,C 在同一直线上,△ABD 和△BCE 都是等边三角形,AE,CD 分别与BD,BE 交于点F,G ,连接FG ,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG ;④AD ⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)【答案】①②③⑤【解析】【分析】易证△ABE ≌△DBC ,则有∠BAE =∠BDC ,AE =CD ,从而可证到△ABF ≌△DBG ,则有AF =DG ,BF =BG ,由∠FBG =60°可得△BFG 是等边三角形,证得∠BFG =∠DBA =60°,则有FG ∥AC ,由∠CDB ≠30°,可判断AD 与CD 的位置关系.【详解】∵△ABD 和△BCE 都是等边三角形,∴BD =BA =AD ,BE =BC =EC ,∠ABD =∠CBE =60°. ∵点A 、B 、C 在同一直线上,∴∠DBE =180°﹣60°﹣60°=60°,∴∠ABE =∠DBC =120°. 在△ABE 和△DBC 中,∵BD BA ABE DBC BE BC ∠∠=⎧⎪=⎨⎪=⎩,∴△ABE ≌△DBC ,∴∠BAE =∠BDC ,∴AE =CD ,∴①正确; 在△ABF 和△DBG中,60BAF BDG AB DBABF DBG ∠∠∠∠=⎧⎪=⎨⎪==︒⎩,∴△ABF ≌△DBG ,∴AF =DG ,BF =BG . ∵∠FBG =180°﹣60°﹣60°=60°,∴△BFG 是等边三角形,∴∠BFG =60°,∴②正确; ∵AE =CD ,AF =DG ,∴EF =CG ;∴③正确;∵∠ADB =60°,而∠CDB =∠EAB ≠30°,∴AD 与CD 不一定垂直,∴④错误.∵△BFG 是等边三角形,∴∠BFG =60°,∴∠GFB =∠DBA =60°,∴FG ∥AB ,∴⑤正确. 故答案为①②③⑤.【点睛】本题考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、平行线的判定和性质,证得△ABE ≌△DBC 是解题的关键.4.如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点O ,过点O 作//EF BC 交AB 于E ,交AC 于F ,过点O 作OD AC ⊥于D 下列结论:①EF BE CF =+;②点O 到ABC ∆各边的距离相等;③1902BOC A ∠=+∠;④设OD m =,AE AF n +=,则AEF S mn ∆=;⑤1()2AD AB AC BC =+-.其中正确的结论是.__________.【答案】①②③⑤【解析】【分析】由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC=90°+12∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=12mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.【详解】∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣12∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+12∠A;故③正确;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF.∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥AB于M,作ON⊥BC于N,连接OA.∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=12AE•OM+12AF•OD=12OD•(AE+AF)=12mn;故④错误;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故②正确;∵AO=AO,MO=DO,∴△AMO≌△ADO(HL),∴AM=AD;同理可证:BM=BN,CD=CN.∵AM+BM=AB,AD+CD=AC,BN+CN=BC,∴AD=12(AB+AC﹣BC)故⑤正确.故答案为:①②③⑤.【点睛】本题考查了角平分线的定义与性质,等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.5.等腰三角形一边长等于4,一边长等于9,它的周长是__.【答案】22【解析】【分析】等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形;【详解】解:因为4+4=8<9,0<4<9+9=18,∴腰的不应为4,而应为9,∴等腰三角形的周长=4+9+9=22.故答案为22.【点睛】本题主要考查了等腰三角形的性质和三角形的三边关系;求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.6.如图,ABC ∆中,AB AC =,点D 是ABC ∆内部一点,DB DC =,点E 是边AB 上一点,若CD 平分ACE ∠,100AEC =∠,则BDC ∠=______°【答案】80【解析】【分析】根据角平分线得到∠ACE=2∠ACD,再根据角的和差关系得到∠ECB =∠ACB-2∠ACD,然后利用外角定理得到∠ABC+∠ECB=100°,代换化简得出∠ACB-∠ACD=50°,即∠DCB=50°,从而求出∠BDC即可.【详解】∵CD平分∠ACE,∴∠ACE=2∠ACD=2∠ECD,∴∠ECB=∠ACB-∠ACE=∠ACB-2∠ACD,∵∠AEC=100°,∴∠ABC+∠ECB=100°,∴∠ABC+∠ACB-2∠ACD=100°,∵AB=AC,∴∠ABC=∠ACB,∴2∠ACB-2∠ACD=100°,∴∠ACB-∠ACD=50°,即∠DCB=50°,∵DB=DC,∴∠DBC=∠DCB,∴∠BDC=180°-2∠DCB=180°-2×50°=80°.【点睛】本题考查了角平分线,三角形内角和,外角定理,及等边对等角的性质等知识,熟练掌握基本知识,找出角与角之间的关系是解题的关键.7.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出_____个格点三角形与△ABC成轴对称.【答案】6【解析】【分析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解.【详解】如图,最多能画出6个格点三角形与△ABC成轴对称.故答案为:6.【点睛】本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.8.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC=_____cm.【答案】8cm.【解析】【详解】解:如图,延长ED交BC于M,延长AD交BC于N,作DF∥BC,∵AB=AC ,AD 平分∠BAC ,∴AN ⊥BC ,BN=CN ,∵∠EBC=∠E=60°,∴△BEM 为等边三角形,∴△EFD 为等边三角形,∵BE=6cm ,DE=2cm ,∴DM=4,∵△BEM 为等边三角形,∴∠EMB=60°,∵AN ⊥BC ,∴∠DNM=90°,∴∠NDM=36°,∴NM=2,∴BN=4,∴BC=8.9.如图,D 为ABC ∆内一点,CD 平分ACB ∠,BD CD ⊥,A ABD ∠=∠,若8AC =,5BC =,则BD 的长为_______.【答案】1.5【解析】【分析】延长BD 交AC 边于点E ,根据BD⊥CD,CD 平分∠ACB,得到三角形全等,由此求出AE 的长,再根据A ABD ∠=∠,求出BE 的长即可求得BD.【详解】延长BD 交AC 于点E ,∵BD⊥CD,∴∠BDC=∠EDC=900,∵CD 平分∠ACB,∴∠BCD=∠ECD又∵CD=CD∴△BCD≌△ECD∴BD=ED,CE=BC=5,∴AE=AC -CE=8-5=3,∵A ABD ∠=∠,∴BE=AE=3,∴BD=1.5【点睛】此题考察等腰三角形的性质,延长BD构建全等三角形是证明此题的关键.10.在下列结论中:①有三个角是60︒的三角形是等边三角形;②有一个外角是120︒的等腰三角形是等边三角形;③有一个角是60︒,且是轴对称的三角形是等边三角形;④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形.其中正确的是__________.【答案】①②③④【解析】【分析】依据等边三角形的定义,含有一个600角的等腰三角形是等边三角形判断即可.【详解】有三个角是600的三角形是等边三角形,故①正确;外角是1200时,邻补角为600,即有一个内角是600的等腰三角形是等边三角形,故②正确;轴对称的三角形是等腰三角形,且含有一个600角,因此是等边三角形,故③正确;一腰上的高也是中线,故底边等于腰长,所以此三角形是等边三角形,故④正确.故此题正确的是①②③④.【点睛】此题考查等边三角形的判定方法,熟记方法才能熟练运用.二、八年级数学轴对称三角形选择题(难)11.如图,平面直角坐标系中存在点A(3,2),点B(1,0),以线段AB为边作等腰三角形ABP,使得点P在坐标轴上.则这样的P点有()A.4个B.5个C.6个D.7个【答案】D【解析】【分析】本题是开放性试题,由题意知A 、B 是定点,P 是动点,所以要分情况讨论:以AP 、AB 为腰、以AP 、BP 为腰或以BP 、AB 为腰.则满足条件的点P 可求.【详解】由题意可知:以AP 、AB 为腰的三角形有3个;以AP 、BP 为腰的三角形有2个;以BP 、AB 为腰的三角形有2个.所以,这样的点P 共有7个.故选D .【点睛】本题考查了等腰三角形的判定及坐标与图形的性质;分类别寻找是正确解答本题的关键.12.如图,ABC ,分别以AB 、AC 为边作等边三角形ABD 与等边三角形ACE ,连接BE 、CD ,BE 的延长线与CD 交于点F ,连接AF ,有以下四个结论:①BE CD =;②FA 平分EFC ∠;③FE FD =;④FE FC FA +=.其中一定正确的结论有( )A .1B .2C .3D .4【答案】C【解析】【分析】 根据等边三角形的性质证出△BAE ≌△DAC ,可得BE =CD ,从而得出①正确;过A 作AM ⊥BF 于M ,过A 作AN ⊥DC 于N ,由△BAE ≌△DAC 得出∠BEA =∠ACD ,由等角的补角相等得出∠AEM =∠CAN ,由AAS 可证△AME ≌△ANC ,得到AM =AN ,由角平分线的判定定理得到FA 平分∠EFC ,从而得出②正确;在FA 上截取FG ,使FG =FE ,根据全等三角形的判定与性质得出△AGE ≌△CFE ,可得AG =CF ,即可求得AF =CF +EF ,从而得出④正确;根据CF +EF =AF ,CF +DF =CD ,得出CD ≠AF ,从而得出FE ≠FD ,即可得出③错误.【详解】∵△ABD 和△ACE 是等边三角形,∴∠BAD =∠EAC =60°,AE =AC =EC .∵∠BAE +∠DAE =60°,∠CAD +∠DAE =60°,∴∠BAE =∠DAC ,在△BAE 和△DAC 中,∵AB ADBAE DACAE AC=⎧⎪∠=∠⎨⎪=⎩,∴△BAE≌△DAC(SAS),∴BE=CD,①正确;过A作AM⊥BF于M,过A作AN⊥DC于N,如图1.∵△BAE≌△DAC,∴∠BEA=∠ACD,∴∠AEM=∠ACN.∵AM⊥BF,AN⊥DC,∴∠AME=∠ANC.在△AME和△ANC中,∵∠AEM=∠CAN,∠AME=∠ANC,AE=AC,∴△AME≌△ANC,∴AM=AN.∵AM⊥BF,AN⊥DC,AM=AN,FA平分∠EFC,②正确;在FA上截取FG,使FG=FE,如图2.∵∠BEA=∠ACD,∠BEA+∠AEF=180°,∴∠AEF+∠ACD=180°,∴∠EAC+∠EFC=180°.∵∠EAC=60°,∴∠EFC=120°.∵FA平分∠EFC,∴∠EFA=∠CFA=60°.∵EF=FG,∠EFA=60°,∴△EFG是等边三角形,∴EF=EG.∵∠AEG+∠CEG=60°,∠CEG+∠CEF=60°,∴∠AEG=∠CEF,在△AGE和△CFE中,∵AE ACAEG CEFEG EF=⎧⎪∠=∠⎨⎪=⎩,∴△AGE≌△CFE(SAS),∴AG=CF.∵AF=AG+FG,∴AF=CF+EF,④正确;∵CF+EF=AF,CF+DF=CD,CD≠AF,∴FE≠FD,③错误,∴正确的结论有3个.故选C.【点睛】本题考查了等边三角形的判定与性质以及全等三角形的判定与性质,正确作辅助线是解答本题的关键.13.如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是()A.①②③④B.①④③②C.①④②③D.②①④③【答案】B【解析】【分析】根据尺规作等边三角形的过程逐项判断即可解答.【详解】解:已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②在射线AM上截取AB=a;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④连结AC、BC.△ABC即为所求作的三角形.故选答案为B.本题考查了尺规作图和等边三角形的性质,解决本题的关键是理解等边三角形的作图过程.的正方形网格中,A,B是如图所示的两个格点,如果C也是格点,且14.在一个33ABC是等腰三角形,则符合条件的C点的个数是()A.6B.7C.8D.9【答案】C【解析】【分析】根据题意、结合图形,画出图形即可确定答案.【详解】解:根据题意,画出图形如图:共8个.故答案为C.【点睛】本题主要考查了等腰三角形的判定,根据题意、画出符合实际条件的图形是解答本题的关键.15.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC 于F,AD交CE于G.则下列结论中错误的是( )A.AD=BE B.BE⊥ACC.△CFG为等边三角形D.FG∥BC【答案】B试题解析:A.ABC 和CDE △均为等边三角形,60AC BC EC DC ACB ECD ∴==∠=∠=︒,,,在ACD 与BCE 中,{AC BCACD BCE CD CF =∠=∠=,ACD BCE ∴≌,AD BE ∴=,正确.B .据已知不能推出F 是AC 中点,即AC 和BF 不垂直,所以AC BE ⊥错误,故本选项符合题意.C.CFG 是等边三角形,理由如下:180606060ACG BCA ∠=︒-︒-︒=︒=∠,ACD BCE ≌,CBE CAD ∴∠=∠,在ACG 和BCF 中,{CAG CBFAC BCBCF ACG ∠=∠=∠=∠,ACG BCF ∴≌,CG CH ∴=,又∵∠ACG=60° CFG ∴是等边三角形,正确.D.CFG 是等边三角形,60CFG ACB ∴∠︒=∠﹦,.FG BC ∴ 正确.故选B.16.如图,在△ABC 中,BC 的垂直平分线分别交AC ,BC 于点D ,E ,若△ABC 的周长为24,CE =4,则△ABD 的周长为( )A .16B .18C .20D .24【答案】A【解析】根据线段的垂直平分线的性质和三角形的周长公式进行解答即可.【详解】解:∵DE是BC的垂直平分线,∴DB=DC,BC=2CE=8又∵AABC的周长为24,∴AB+BC+AC=24∴AB+AC=24-BC=24-8=16∴△ABD的周长=AD+BD+AB=AD+CD+AB=AB+AC=16,故答案为A【点睛】本题考查的是线段的垂直平分线的性质,理解并应用线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.17.如图,已知等边△ABC的边长为4,面积为43,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为()A.3 B.2C.3D.3【答案】C【解析】【分析】由题意可知点A、点C关于BD对称,连接AE交BD于点P,由对称的性质可得,PA=PC,故PE+PC=AE,由两点之间线段最短可知,AE即为PE+PC的最小值.【详解】解:∵△ABC是等边三角形,点D为AC的中点,点E为BC的中点,∴BD⊥AC,EC=2,连接AE,线段AE的长即为PE+PC最小值,∵点E是边BC的中点,∴AE⊥BC,∴PE+PC22-=4223AC E C-22故选C.【点睛】本题考查的是轴对称-最短路线问题,熟知等边三角形的性质是解答此题的关键.18.如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第43秒或第83秒时,△PBQ为直角三角形,正确的有几个 ( )A.1 B.2 C.3 D.4【答案】C【解析】【分析】①等边三角形ABC中,AB=BC,而AP=BQ,所以BP=CQ.②根据等边三角形的性质,利用SAS证明△ABQ≌△CAP;③由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠CMQ=60°;④设时间为t秒,则AP=BQ=tcm,PB=(4-t)cm,当∠PQB=90°时,因为∠B=60°,所以PB=2BQ,即4-t=2t故可得出t的值,当∠BPQ=90°时,同理可得BQ=2BP,即t=2(4-t),由此两种情况即可得出结论.【详解】①在等边△ABC中,AB=BC.∵点P、Q的速度都为1cm/s,∴AP=BQ,∴BP=CQ.只有当CM=CQ时,BP=CM.故①错误;②∵△ABC是等边三角形∴∠ABQ=∠CAP,AB=CA,又∵点P、Q运动速度相同,在△ABQ与△CAP中,∵AB CAABQ CAP AP BQ⎧⎪∠∠⎨⎪⎩===,∴△ABQ≌△CAP(SAS).故②正确;③点P、Q在运动的过程中,∠QMC不变.理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC=∠ACP+∠MAC,∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°.故③正确;④设时间为t秒,则AP=BQ=tcm,PB=(4-t)cm,当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,即4-t=2t,t=43,当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4-t),t=83,∴当第43秒或第83秒时,△PBQ为直角三角形.故④正确.正确的是②③④,故选C.【点睛】此题是一个综合性题目,主要考查等边三角形的性质、全等三角形的判定与性质等知识.熟知等边三角形的三个内角都是60°是解答此题的关键.19.如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD 交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为( ) A.1 B.2 C.3 D.4【解析】【分析】根据题意,结合图形,对选项一一求证,即可得出正确选项.【详解】(1)△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,∴AC=BC,EC=DC,∠ACB=∠DCE=60°,∴∠ACE=∠BCD=120°.在△BCD和△ACE中,∵AC BCBCD ACECD CE=⎧⎪∠=∠⎨⎪=⎩,∴△BCD≌△ACE,∴AE=BD,故结论①正确;(2)∵△BCD≌△ECA,∴∠GAC=∠FBC.又∵∠ACG=∠BCF=60°,AC=BC,∴△ACG≌△BCF,∴AG=BF,故结论②正确;(3)∵△ACG≌△BCF,∴CG=CF.∵∠ACB=∠DCE=60°,∴∠ACD=60°,∴△FCG为等边三角形,∴∠FGC=60°,∴∠FGC=∠DCE,∴FG∥BE,故结论③正确;(4)过C作CN⊥AE于N,CZ⊥BD于Z,则∠CNE=∠CZD=90°.∵△ACE≌△BCD,∴∠CDZ=∠CEN.在△CDZ和△CEN中,CZD CNECDZ CENCD CE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CDZ≌△CEN,∴CZ=CN.∵CN⊥AE,CZ⊥BD,∴∠BOC=∠EOC,故结论④正确.综上所述:四个结论均正确.故选D.【点睛】本题综合考查了等边三角形的判定与性质,全等三角形的判定与性质,角平分线的判定定理等重要几何知识点,有一定难度,需要学生将相关知识点融会贯通,综合运用.20.如图,在ABC△中,2B C∠=∠,AH BC⊥,AE平分BAC∠,M是BC中点,则下列结论正确的个数为()(1)AB BE AC+=(2)2AB BH BC+=(3)2AB HM=(4)CH EH AC+=A.1 B.2 C.3 D.4【答案】D【解析】【分析】(1)延长AB取BD=BE,连接DE,由∠D=∠BED,2ABC C∠=∠,得到∠D=∠C,在△ADE和△ACE中,利用AAS证明ADE ACE≌,可得AC=AD=AB+BE;(2)在HC上截取HF=BH,连接AF,可知△ABF为等腰三角形,再根据2ABC AFB C∠=∠=∠,可得出△AFC为等腰三角形,所以FC+BH+HF=AB+2BH=BC;(3)HM=BM-BH,所以2HM=2BM-2BH=BC-2BH,再结合(2)中结论,可得2AB HM=;(4)结合(1)(2)的结论,BC2BH BE BC BH BE BH CH EHAC AB BE=+=-+=-+-=+.【详解】解:①延长AB取BD=BE,连接DE,∴∠D=∠BED,∠ABC=∠D+∠BED=2∠D,∵2ABC C∠=∠,∴∠D=∠C,在△ADE和△ACE中,DAE CAED CAE AE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ADE ACE≌∴AC=AD=AB+BE,故(1)正确;②在HC上截取HF=BH,连接AF,∵AH BC⊥,∴△ABF为等腰三角形,∴AB=AF,∠ABF=∠AFB,∵2ABC C∠=∠,∴∠AFB=2∠C=∠C+∠CAF,∴FC=AF=AB,∴FC+BH+HF=AB+2BH=BC,故(2)正确;③∵HM=BM-BH ,∴2HM=2BM-2BH=BC-2BH ,由②可知BC-2BH=AB ,∴2AB HM =④根据①②结论,可得:BC 2BH BE BC BH BE BH CH EH AC AB BE =+=-+=-+-=+,故(4)正确;故选D.【点睛】本题主要考查了等腰三角形的判定和性质、三角形的外角以及全等三角形的判定和性质,结合实际问题作出合适辅助线是解题关键.。
八年级上册全等三角形(培优篇)(Word版 含解析)

八年级上册全等三角形(培优篇)(Word版含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在长方形ABCD的边AD上找一点P,使得点P到B、C两点的距离之和最短,则点P的位置应该在_____.【答案】AD的中点【解析】【分析】【详解】分析:过AD作C点的对称点C′,根据轴对称的性质或线段垂直平分线的性质得出AC=PC′,从而根据两点之间线段最短,得出这时的P点使BP+PC的之最短.详解:如图,过AD作C点的对称点C′,根据轴对称的性质可得:PC=PC′,CD=C′D∵四边形ABCD是矩形∴AB=CD∴△ABP≌△DC′P∴AP=PD即P为AD的中点.故答案为P为AB的中点.点睛:本题考查了轴对称-最短路线问题,矩形的性质,两点之间线段最短的性质.得出动点P所在的位置是解题的关键.2.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有_____个.【答案】4【解析】【分析】由A点坐标可得OA=22,∠AOP=45°,分别讨论OA为腰和底边,求出点P在x轴正半轴和负半轴时,△APO是等腰三角形的P点坐标即可.【详解】(1)当点P在x轴正半轴上,①如图,以OA为腰时,∵A的坐标是(2,2),∴∠AOP=45°,OA=22,当∠AOP为顶角时,OA=OP=22,当∠OAP为顶角时,AO=AP,∴OPA=∠AOP=45°,∴∠OAP=90°,∴OP=2OA=4,∴P的坐标是(4,0)或(22,0).②以OA为底边时,∵点A的坐标是(2,2),∴∠AOP=45°,∵AP=OP,∴∠OAP=∠AOP=45°,∴∠OPA=90°,∴OP=2,∴P点坐标为(2,0).(2)当点P在x轴负半轴上,③以OA为腰时,∵A的坐标是(2,2),∴OA=22,∴OA=OP=22,∴P的坐标是(﹣22,0).综上所述:P的坐标是(2,0)或(4,0)或(22,0)或(﹣22,0).故答案为:4.【点睛】此题主要考查等腰三角形的判定及坐标与图形性质的综合运用,注意分类讨论思想的运用是解题关键.3.如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为______.【答案】2.【解析】【分析】【详解】过点D作DF⊥B′E于点F,过点B′作B′G⊥AD于点G,∵∠B=60°,BE=BD=4,∴△BDE 是等边三角形,∵△B′DE ≌△BDE ,∴B′F=12B′E=BE=2,DF=23, ∴GD=B′F=2, ∴B′G=DF=23,∵AB=10,∴AG=10﹣6=4,∴AB′=27.考点:1轴对称;2等边三角形.4.在ABC ∆中,边AB 、AC 的垂直平分线分别交边BC 于点D 、点E ,20DAE ∠=︒,则BAC ∠=______°.【答案】80或100【解析】【分析】根据题意,点D 和点E 的位置不确定,需分析谁靠近B 点,则有如下图(图见解析)两种情况:(1)图1中,点E 距离点B 近,根据垂直平分线性质可知,,BD AD AE CE ==,从而有1,2B DAE C DAE ∠=∠+∠∠=∠+∠,再根据三角形的内角和定理可得180B C BAC ∠+∠+∠=︒,联立即可求得;(2)图2中,点D 距离点B 近,根据垂直平分线性质可知,,BD AD AE CE ==,从而有3,4B C ∠=∠∠=∠,由三角形的内角和定理得180B C BAC ∠+∠+∠=︒,联立即可求得.【详解】由题意可分如下两种情况:(1)图1中,根据垂直平分线性质可知,,BD AD AE CE ==,1,2B DAE C DAE ∴∠=∠+∠∠=∠+∠(等边对等角),两式相加得12B C DAE DAE ∠+∠=∠+∠+∠+∠,又12DAE BAC ∠+∠+∠=∠20B C BAC DAE BAC ∴∠+∠=∠+∠=∠+︒,由三角形内角和定理得180B C BAC ∠+∠+∠=︒,20180BAC BAC ∴∠+︒+∠=︒,80BAC ∴∠=︒;(2)图2中,根据垂直平分线性质可知,,BD AD AE CE ==,3,4B C ∴∠=∠∠=∠(等边对等角),两式相加得34B C ∠+∠=∠+∠,又34DAE BAC ∠+∠+∠=∠,3420BAC DAE BAC ∴∠+∠=∠-∠=∠-︒,20B C BAC ∴∠+∠=∠-︒由三角形内角和定理得180B C BAC ∠+∠+∠=︒,20180BAC BAC ∴∠-︒+∠=︒,100BAC ∴∠=︒.故答案为80或100.【点睛】本题考查了垂直平分线的性质(垂直平分线上的点到线段两端点的距离相等)、等腰三角形的定义和性质(等边对等角)、以及三角形内角和定理,本题的难点在于容易漏掉第二种情况,出现漏解.5.在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,∆为等腰三角形,符合条件的C点有36∠=︒,在x轴或y轴上取点C,使得ABCABO__________个.【答案】8【解析】【分析】观察数轴,按照等腰三角形成立的条件分析可得答案.【详解】解:如下图所示,若以点A为圆心,以AB为半径画弧,与x轴和y轴各有两个交点,但其中一个会与点B重合,故此时符合条件的点有3个;若以点B为圆心,以AB为半径画弧,同样与x轴和y轴各有两个交点,但其中一个与点A重合,故此时符合条件的点有3个;线段AB的垂直平分线与x轴和y轴各有一个交点,此时符合条件的点有2个.∴符合条件的点总共有:3+3+2=8个.故答案为:8.【点睛】本题考查了等腰三角形的判定,可以观察图形,得出答案.6.如图,将ABC ∆沿着过AB 中点D 的直线折叠,使点A 落在BC 边上的1A 处,称为第1次操作,折痕DE 到BC 的距离记为1h ,还原纸片后,再将ADE ∆沿着过AD 中点1D 的直线折叠,使点A 落在DE 边上的2A 处,称为第2次操作,折痕11D E 到BC 的距离记为2h ,按上述方法不断操作下去…经过第2020次操作后得到的折痕20192019D E 到BC 的距离记为2020h ,若11h =,则2020h 的值为______.【答案】2019122-【解析】【分析】根据中点的性质及折叠的性质可得DA=DA ₁=DB,从而可得∠ADA ₁=2∠B,结合折叠的性质可得.,∠ADA ₁=2∠ADE,可得∠ADE=∠B,继而判断DE// BC,得出DE 是△ABC 的中位线,证得AA ₁⊥BC,AA ₁=2,由此发现规律:01 2122h =-=-₁同理21122h =-3211122222h =-⨯=-…于是经过第n 次操作后得到的折痕Dn-1 En-1到BC 的距离1122n n h -=-,据此求得2020h 的值. 【详解】解:如图连接AA ₁,由折叠的性质可得:AA ₁⊥DE, DA= DA ₁ ,A ₂、A ₃…均在AA ₁上 又∵ D 是AB 中点,∴DA= DB ,∵DB= DA ₁ ,∴∠BA ₁D=∠B ,∴∠ADA ₁=∠B +∠BA ₁D=2∠B,又∵∠ADA ₁ =2∠ADE ,∴∠ADE=∠B∵DE//BC,∴AA ₁⊥BC ,∵h ₁=1∴AA ₁ =2, ∴012122h =-=-₁ 同理:21122h =-; 3211122222h =-⨯=-; …∴经过n 次操作后得到的折痕D n-1E n-1到BC 的距离1122n n h -=-∴20202019122h =-【点睛】本题考查了中点性质和折叠的性质,本题难度较大,要从每次折叠发现规律,求得规律的过程是难点.7.如图,在直角坐标系中,点()8,8B -,点()2,0C -,若动点P 从坐标原点出发,沿y 轴正方向匀速运动,运动速度为1/cm s ,设点P 运动时间为t 秒,当BCP ∆是以BC 为腰的等腰三角形时,直接写出t 的所有值__________________.【答案】2秒或46秒或14秒【解析】【分析】分两种情况:PC为腰或BP为腰.分别作出符合条件的图形,计算出OP的长度,即可求出t的值.【详解】解:如图所示,过点B作BD⊥x轴于点D,作BE⊥y轴于点E,分别以点B和点C为圆心,以BC长为半径画弧交y轴正半轴于点F,点H和点G∵点B(-8,8),点C(-2,0),∴DC=6cm,BD=8cm,由勾股定理得:BC=10cm∴在直角三角形COG中,OC=2cm,CG=BC=10cm,∴22-=,10246(cm)当点P运动到点F或点H时,BE=8cm,BH=BF=10cm,∴EF=EH=6cm∴OP=OF=8-6=2(cm)或OP=OH=8+6=14(cm),故答案为:2秒,6秒或14秒.【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用,通过作图找出要求的点的位置,利用勾股定理来求解是本题的关键.8.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△A n B n A n+1的边长为_____.【答案】2n.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.【详解】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∵OA2=4,∴OA1=A1B1=2,∴A2B1=2,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2=32,以此类推△A n B n A n+1的边长为 2n.故答案为:2n.【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.9.如图,△ABC中,AC=DC=3,BD垂直∠BAC的角平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为________.【答案】9 2【解析】【分析】首先证明两个阴影部分面积之差=S△ADC,当CD⊥AC时,△ACD的面积最大.【详解】延长BD交AC于点H.设AD交BE于点O.∵AD⊥BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠H+∠HAD=90°,∵∠BAD=∠HAD,∴∠ABD=∠H,∴AB=AH,∵AD⊥BH,∴BD=DH,∵DC=CA,∴∠CDA=∠CAD,∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,∴∠CDH=∠H,∴CD=CH=AC,∵AE=EC,∴S△ABE=14S△ABH,S△CDH=14S△ABH,∵S△OBD−S△AOE=S△ADB−S△ABE=S△ADH−S△CDH=S△ACD,∵AC=CD=3,∴当DC⊥AC时,△ACD的面积最大,最大面积为12×3×3=92.故填:92.【点睛】本题考查等腰三角形的判定和性质,三角形中线的性质等知识,解题的关键是学会用转化的思想思考问题.10.如图,在△ABC 中,AB=AC ,AB 边的垂直平分线DE 交AC 于点D .已知△BDC 的周长为14,BC=6,则AB=___.【答案】8【解析】试题分析:根据线段垂直平分线的性质,可知AD=BD ,然后根据△BDC 的周长为BC+CD+BD=14,可得AC+BC=14,再由BC=6可得AC=8,即AB=8.故答案为8.点睛:此题主要考查了线段的垂直平分线的性质,解题时,先利用线段的垂直平分线求出BD=AD ,然后根据三角形的周长互相代换,即可其解.二、八年级数学轴对称三角形选择题(难)11.如图,在射线OA ,OB 上分别截取11OA OB =,连接11A B ,在11B A ,1B B 上分别截取1212B A B B =,连接22A B ,按此规律作下去,若11A B O α∠=,则1010A B O ∠=( )A .102aB .92aC .20aD .18a 【答案】B【解析】【分析】根据等腰三角形两底角相等用α表示出22A B O ∠,依此类推即可得到结论.【详解】解:1212B A B B =,11A B O α∠=,2212A B O α∴∠=,同理332111222A B O αα∠=⨯=, 44312A B O α∠=, 112n n n A B O α-∴∠=, 101092A B O α∴∠=,故选:B .【点睛】本题考查了等腰三角形两底角相等的性质,图形的变化规律,依次求出相邻的两个角的差,得到分母成2的指数次幂变化,分子不变的规律是解题的关键.12.如图所示,△ABP 与△CDP 是两个全等的等边三角形,且PA ⊥PD ,有下列四个结论:①∠PBC =15°,②AD ∥BC ,③PC ⊥AB ,④四边形ABCD 是轴对称图形,其中正确的个数为( )A .1个B .2个C .3个D .4个【答案】D【解析】【分析】根据周角的定义先求出∠BPC 的度数,再根据对称性得到△BPC 为等腰三角形,∠PBC 即可求出;根据题意:有△APD 是等腰直角三角形;△PBC 是等腰三角形;结合轴对称图形的定义与判定,可得四边形ABCD 是轴对称图形,进而可得②③④正确.【详解】根据题意,BPC 36060290150∠=-⨯-= , BP PC =,()PBC 180150215∠∴=-÷=,①正确;根据题意可得四边形ABCD 是轴对称图形,④正确;∵∠DAB+∠ABC=45°+60°+60°+15°=180°,∴AD//BC ,②正确;∵∠ABC+∠BCP=60°+15°+15°=90°,∴PC ⊥AB ,③正确,所以四个命题都正确,故选D .【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、等腰三角形的判定与性质、轴对称图形的定义与判定等,熟练掌握各相关性质与定理是解题的关键.13.如图,△ABC中,AB=AC,且∠ABC=60°,D为△ABC内一点,且DA=DB,E 为△ABC 外一点,BE =AB,且∠EBD=∠CBD,连DE,CE. 下列结论:①∠DAC=∠DBC;②BE⊥AC ;③∠DEB=30°. 其中正确的是()A.①... B.①③... C.② ... D.①②③【答案】B【解析】【分析】连接DC,证ACD BCD DAC DBC∠∠≅=得出①,再证BED BCD≅,得出BED BCD30∠∠==︒;其它两个条件运用假设成立推出答案即可.【详解】解:证明:连接DC,∵△ABC是等边三角形,∴AB=BC=AC,∠ACB=60°,∵DB=DA,DC=DC,在△ACD与△BCD中,AB BCDB DADC DC=⎧⎪=⎨⎪=⎩,∴△ACD≌△BCD (SSS),由此得出结论①正确;∴∠BCD=∠ACD=1302ACB∠=︒∵BE=AB,∴BE=BC,∵∠DBE=∠DBC,BD=BD,在△BED与△BCD中,BE BCDBE DBCBD BD=⎧⎪∠=∠⎨⎪=⎩,∴△BED≌△BCD (SAS),∴∠DEB=∠BCD=30°.由此得出结论③正确;∵EC∥AD,∴∠DAC=∠ECA,∵∠DBE=∠DBC,∠DAC=∠DBC,∴设∠ECA=∠DBC=∠DBE=∠1,∵BE=BA,∴BE=BC,∴∠BCE=∠BEC=60°+∠1,在△BCE中三角和为180°,∴2∠1+2(60°+∠1)=180°∴∠1=15°,∴∠CBE=30,这时BE是AC边上的中垂线,结论②才正确.因此若要结论②正确,需要添加条件EC∥AD.故答案为:B.【点睛】本题考查的知识点主要是全等三角形的判定与性质以及等边三角形的性质,通过已知条件作出恰当的辅助线是解题的关键点.14.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,在直线AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有()A.6个B.5个C.4个D.3个【答案】C【解析】【分析】根据等腰三角形的判定定理即可得到结论.【详解】解:根据题意,∵△PAB为等腰三角形,∴可分为:PA=PB,PA=AB,PB=AB三种情况,如图所示:∴符合条件的点P共有4个;故选择:C.【点睛】本题考查了等腰三角形的判定来解决实际问题,其关键是根据等腰三角形的判定定理解答.15.如图,在Rt△ABC中,AC=BC,∠ACB=90°,D为AB的中点,E为线段AD上一点,过E点的线段FG交CD的延长线于G点,交AC于F点,且EG=AE,分别延长CE,BG交于点H,若EH平分∠AEG,HD平分∠CHG则下列说法:①∠GDH=45°;②GD=ED;③EF=2DM;④CG=2DE+AE,正确的是()A.①②③B.①②④C.②③④D.①②③④【答案】B【解析】【分析】首先证明△AEC≌△GEC(SAS),推出CA=CG,∠A=∠CGE=45°,推出DE=DG,故②正确;再证明△EDC≌△GDB,推出∠CED=∠BGD,ED=GD,由三角形外角的性质得出∠HDG=∠HDE,进而得出∠GDH=∠EDH=45°,即可判断①正确;通过证明△EDC和△EMD是等腰直角三角形,得到ED2MD,再通过证明△EFC≌△EDC,得到EF=ED,从而可判断③错误;由CG=CD+DG,CD=AD,ED=GD,变形即可判断④正确.【详解】∵AC=BC,∠ACB=90°,AD=DB,∴CD⊥AB,CD=AD=DB,∠A=∠CBD=45°.∵EH平分∠AEG,∴∠AEH=∠GEH.∵∠AEH+∠AEC=180°,∠GEH+∠CEG=180°,∴∠AEC=∠CEG.∵AE=GE,EC=EC,∴△AEC≌△GEC(SAS),∴CA=CG,∠A=∠CGE=45°.∵∠EDG=90°,∴∠DEG=∠DGE=45°,∴DE=DG,∠AEF=∠DEG=∠A=45°,故②正确;∵DE=DG,∠CDE=∠BDG=90°,DC=DB,∴△EDC≌△GDB(SAS),∴∠CED=∠BGD,ED=GD.∵HD平分∠CHG,∴∠GHD=∠EHD.∵∠CED=∠EHD+∠HDE,∠BGD=∠GHD+∠HDG,∴∠HDG=∠HDE.∵∠EDG=∠ADC=90°,∴∠GDH=∠EDH=45°,故①正确;∵∠EDC=90°,ED=GD,∴△EDC是等腰直角三角形,∴∠DEG=45°.∵∠GDH=45°,∴∠EDH=45°,∴△EMD是等腰直角三角形,∴ED MD.∵∠AEF=∠DEG=∠A=45°,∴∠AFE=∠CFG=90°.∵∠EDC=90°,∴∠EFC=∠EDC=90°.∵EH平分∠AEG,∴∠AEH=∠GEH.∵∠FEC=∠GEH,∠DEC=∠AEH,∴∠FEC=∠DEC.∵EC=EC,∴△EFC≌△EDC,∴EF=ED,∴EF MD.故③错误;∵CG=CD+DG=AD+ED=AE+ED+ED,∴CG=2DE+AE,故④正确.故选B.【点睛】本题考查了等腰直角三角形的性质和判定,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.16.如图,Rt ABC ∆中,90ACB ∠=,3AC =,4BC =,5AB =,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B ′处,两条折痕与斜边AB 分别交于点E 、F ,则线段EF 的长为( )A .52B .125C .4D .53【答案】B【解析】【分析】先利用折叠的性质证明出△ECF 是一个等腰直角三角形,因此EF=CE ,然后再根据文中条件综合得出S △ABC =12AC∙BC=12AB∙CE ,求出CE 进而得出答案即可. 【详解】根据折叠性质可知:CD=AC=3,BC=B C '=4,∠ACE=∠DCE ,∠BCF=∠B 'CF ,CE ⊥AB , ∴∠DCE+∠B 'CF=∠ACE+∠BCF ,∵∠ACB=90°,∴∠ECF=45°,又∵CE ⊥AB ,∴△ECF 是等腰直角三角形,∴EF=CE , 又∵S △ABC =12AC∙BC=12AB∙CE , ∴AC∙BC=AB∙CE , ∵3AC =,4BC =,5AB =,∴125CE =, ∴EF 125=. 所以答案为B 选项.【点睛】本题主要考查了直角三角形与等腰三角形性质的综合运用,熟练掌握相关概念是解题关键.17.如果一个三角形能被一条线段分割成两个等腰三角形,那么称这个三角形为特异三角形.若△ABC 是特异三角形,∠A=30°,∠B 为钝角,则符合条件的∠B 有( )个. A .1 B .2 C .3 D .4【解析】【分析】【详解】如下图,当30°角为等腰三角形的底角时有两种情况:∠B=135°或90°,当30°角为等腰三角形的顶角时有一种情况:∠B=112.5°,所以符合条件的∠B有三个.又因为∠B为钝角,则符合答案的有两个,故本题应选B.点睛:因为不确定这个等腰三角形的底边,所以应当以点A为一个确定点进行分类讨论:①当以B为顶点时,即以B为圆心,AB长为半径画弧交AC于点D,构成等腰△BAD;②当以点A为顶点时,即以点A为圆心,AB长为半径画弧,交AC于点D,构成等腰△ABD;或作线段AB的垂直平分线交AC于点D构成等腰△DAB.18.如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形).则∠OCD 等于()A.108°B.114°C.126°D.129°【答案】C【解析】【分析】按照如图所示的方法折叠,剪开,把相关字母标上,易得∠ODC和∠DOC的度数,利用三角形的内角和定理可得∠OCD的度数.解:展开如图,五角星的每个角的度数是,180=36°.5∵∠COD=360°÷10=36°,∠ODC=36°÷2=18°,∴∠OCD=180°-36°-18°=126°,故选C.【点睛】本题主要考查轴对称性质,解决本题的关键是能够理解所求的角是五角星的哪个角,解题时可以结合正五边形的性质解决.19.已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE,试判断下列结论:①AE=BD;②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2,正确的序号有()A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°,∠ACE=∠ACD+60°可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,可得AE=BD,①正确;∠CBD=∠CAE=60°,进而可得∠EAD=60°,②正确,当∠BCD=90°时,可得∠ACD=∠ADC=30°,可得AD=AC,即可得CE2+AD2=AC2+DE2,④正确;当D点在BA延长线上时,∠BDE-∠BDC=60°,根据△BCD≌△ACE可得∠AEC=∠BDC,进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,即可证明∠BDE-∠BDC=∠BDC+∠AED,即∠BDE-∠AED=2∠BDC,当点D在AB上时可证明∠BDE-∠AED=120°,③错误,综上即可得答案.【详解】∵∠BCA=∠DCE=60°,∴∠BCA+∠ACD=∠DCE+∠ACD,∴∠BCD=∠ACE,又∵AC=BC,CE=CD,∴△BCD≌△ACE,∴AE=BD ,∠CBA=∠CAE=60°,∠AEC=∠BDC ,①正确,∴∠BAE=120°,∴∠EAD=60°,②正确,∵∠BCD=90°,∠BCA=60°,∴∠ACD=∠ADC=30°,∴AC=AD ,∵CE=DE ,∴CE 2+AD 2=AC 2+DE 2,④正确,当D 点在BA 延长线上时,∠BDE-∠BDC=60°,∵∠AEC=∠BDC ,∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC ,如图,当点D 在AB 上时,∵△BCD ≌△∠ACE ,∴∠CAE=∠CBD=60°,∴∠DAE=∠BAC+∠CAE=120°,∴∠BDE-∠AED=∠DAE=120°,③错误故正确的结论有①②④,故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握20.如图,ABC △中,60BAC ∠=︒,ABC ∠、ACB ∠的平分线交于E ,D 是AE 延长线上一点,且120BDC ∠=︒.下列结论:①120BEC ∠=︒;②DB DE =;③2BDE BCE ∠=∠.其中所有正确结论的序号有( ).A .①②B .①③C .②③D .①②③【答案】D【解析】 分析:根据三角形内角和等于180°求出∠ABC+∠ACB ,再根据角平分线的定义求出∠EBC+∠ECB ,然后求出∠BEC=120°,判断①正确;过点D 作DF ⊥AB 于F ,DG ⊥AC 的延长线于G ,根据角平分线上的点到角的两边的距离相等可得DF=DG ,再求出∠BDF=∠CDG ,然后利用“角边角”证明△BDF 和△CDG 全等,根据全等三角形对应边相等可得BD=CD ,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ,根据等角对等边可得BD=DE ,判断②正确,再求出B ,C ,E 三点在以D 为圆心,以BD 为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ,判断③正确.详解:∵60BAC ∠=︒,∴18060120ABC ACB ∠+∠=︒-︒=︒,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴12EBC ABC ∠=∠,12ECB ACB ∠=∠, ∴11()1206022EBC ECB ABC ACB ∠+∠=∠+∠=⨯︒=︒, ∴180()18060120BEC EBC ECB ∠=︒-∠+∠=︒-︒=︒, 故①正确.如图,过点D 作DF AB ⊥于F ,DG AC ⊥的延长线于G ,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴AD 为BAC ∠的平分线,∴DF DG =,∴36090260120FDG ∠=︒-︒⨯-︒=︒,又∵120BDC ∠=︒,∴120BDF CDF ∠+∠=︒,120CDG CDF ∠+∠=︒.∴BDF CDG ∠=∠,∵在BDF 和CDG △中,90BFD CGD DF DGBDF CDG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ∴BDF ≌()CDG ASA ,∴DB CD =, ∴1(180120)302DBC ∠=︒-︒=︒, ∴30DBC DBC CBE CBE ∠=∠+∠=︒+∠,∵BE 平分ABC ∠,AE 平分BAC ∠,∴ABE CBE ∠=∠,1302BAE BAC ∠=∠=︒, 根据三角形的外角性质, 30DEB ABE BAE ABE ∠=∠+∠=∠+︒,∴DEB DBE ∠=∠,∴DB DE =,故②正确.∵DB DE DC ==,∴B 、C 、E 三点在以D 为圆心,以BD 为半径的圆上,∴2BDE BCE ∠=∠,故③正确,综上所述,正确结论有①②③,故选:D .点睛:本题考查了角平分线的性质,全等三角形的判定与性质,等角对等边的性质,圆内接四边形的判定,同弧所对的圆周角等于圆心角的一半性质,综合性较强,难度较大,特别是③的证明.。
三角形全等培优证明题100题(有答案)
全等三角形证明题专项练习(100题)1.已知如图,△ABC≌△ADE,∠B=30°,∠E=20°,∠BAE=105°,求∠BAC的度数.∠BAC=_________.2.已知:如图,四边形ABCD中,AB∥CD,AD∥BC.求证:△ABD≌△CDB.3.如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE 的道理.4.如图,△ABC的两条高AD,BE相交于H,且AD=BD.试说明下列结论成立的理由.(1)∠DBH=∠DAC;(2)△BDH≌△ADC.5.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,则AB=AC,并说明理由.6.如图,AE是∠BAC的平分线,AB=AC,D是AE反向延长线的一点,则△ABD与△ACD全等吗?为什么?7.如图所示,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证:△AEF≌△BCD.8.如图,已知AB=AC,AD=AE,BE与CD相交于O,△ABE与△ACD全等吗?说明你的理由.9.如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明它们为什么是全等的.10.如图所示,CD=CA,∠1=∠2,EC=BC,求证:△ABC≌△DEC.11.已知AC=FE,BC=DE,点A、D、B、F在一条直线上,要使△ABC≌△FDE,应增加什么条件?并根据你所增加的条件证明:△ABC≌△FDE.12.如图,已知AB=AC,BD=CE,请说明△ABE≌△ACD.13.如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,连接BB1.设CB1交AB于D,A1B1分别交AB,AC于E,F,在图中不再添加其他任何线段的情况下,请你找出一对全等的三角形,并加以证明.(△ABC与△A1B1C1全等除外)14.如图,AB∥DE,AC∥DF,BE=CF.求证:△ABC≌△DEF.15.如图,AB=AC,AD=AE,AB,DC相交于点M,AC,BE相交于点N,∠DAB=∠EAC.求证:△ADM≌△AEN.16.将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.求证:△ABE≌△ACD.17.如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.请在图中找出所有全等的三角形,用符号“≌”表示,并选择一对加以证明.18.如图,已知∠1=∠2,∠3=∠4,EC=AD.(1)求证:△ABD≌△EBC.(2)你可以从中得出哪些结论?请写出两个.19.等边△ABC边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)求当AD取何值时,DE=EF.20.巳知:如图,AB=AC,D、E分别是AB、AC上的点,AD=AE,BE与CD相交于G.(Ⅰ)问图中有多少对全等三角形?并将它们写出来.(Ⅱ)请你选出一对三角形,说明它们全等的理由(根椐所选三角形说理难易不同给分,即难的说对给分高,易的说对给分低)21.已知:如图,AB=DC,AC=BD,AC、BD相交于点E,过E点作EF∥BC,交CD于F,(1)根据给出的条件,可以直接证明哪两个三角形全等?并加以证明.(2)EF平分∠DEC吗?为什么?22.如图,己知∠1=∠2,∠ABC=∠DCB,那么△ABC与△DCB全等吗?为什么?23.如图,B,F,E,D在一条直线上,AB=CD,∠B=∠D,BF=DE.试证明:(1)△DFC≌△BEA;(2)△AFE≌△CEF.24.如图,AC=AE,∠BAF=∠BGD=∠EAC,图中是否存在与△ABE全等的三角形?并证明.25.如图,D是△ABC的边BC的中点,CE∥AB,E在AD的延长线上.试证明:△ABD≌△ECD.26.如图,已知AB=CD,∠B=∠C,AC和BD相交于点O,E是AD的中点,连接OE.(1)求证:△AOB≌△DOC;(2)求∠AEO的度数.27.如图,已知AB∥DE,AB=DE,AF=DC.(1)求证:△ABF≌△DEC;(2)请你找出图中还有的其他几对全等三角形.(只要直接写出结果,不要证明)28.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:△ABD≌△GCA;(2)请你确定△ADG的形状,并证明你的结论.29.如图,点D、F、E分别在△ABC的三边上,∠1=∠2=∠3,DE=DF,请你说明△ADE≌△CFD的理由.30.如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点F在线段BE上,∠1=∠2,点D在线段EC上,给出两个条件:①DF∥BC;②BF=DF.请你从中选择一个作为条件,证明:△AFD≌△AFB.31.如图,在△ABC中,点D在AB上,点E在BC上,AB=BC,BD=BE,EA=DC,求证:△BEA≌△BDC.32.阅读并填空:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.请说明△ADC≌△CEB的理由.解:∵BE⊥CE于点E(已知),∴∠E=90°_________,同理∠ADC=90°,∴∠E=∠ADC(等量代换).在△ADC中,∵∠1+∠2+∠ADC=180°_________,∴∠1+∠2=90°_________.∵∠ACB=90°(已知),∴∠3+∠2=90°,∴_________.在△ADC和△CEB中,.∴△ADC≌△CEB (A.A.S)33.已知:如图所示,AB∥DE,AB=DE,AF=DC.(1)写出图中你认为全等的三角形(不再添加辅助线);(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.34.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.试说明下列结论正确的理由:(1)∠C=∠E;(2)△ABC≌△ADE.35.如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是斜边AB上的一点,AE⊥CD于E,BF⊥CD交CD的延长线于F.求证:△ACE≌△CBF.36.如图,在△ABC中,D是BC的中点,DE∥CA交AB于E,点P是线段AC上的一动点,连接PE.探究:当动点P运动到AC边上什么位置时,△APE≌△EDB?请你画出图形并证明△APE≌△EDB.37.已知:如图,AD∥BC,AD=BC,E为BC上一点,且AE=AB.求证:(1)∠DAE=∠B;(2)△ABC≌△EAD.38.如图,D为AB边上一点,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,CA=CB,CD=CE,图中有全等三角形吗?指出来并说明理由.39.如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:△ABD≌△ACE.40.如图,已知D是△ABC的边BC的中点,过D作两条互相垂直的射线,分别交AB于E,交AC于F,求证:BE+CF>EF.41.如图所示,在△MNP中,H是高MQ与NE的交点,且QN=QM,猜想PM与HN有什么关系?试说明理由.42.如图,在△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥GF,交AB于点E,连接EG.(1)求证:BG=CF;(2)请你判断BE+CF与EF的大小关系,并证明你的结论.43.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.44.如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,BC=AD,请说明:∠A=∠C的道理,小明动手测量了一下,发现∠A确实与∠C相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.45.如图,AD是△ABC的中线,CE⊥AD于E,BF⊥AD,交AD的延长线于F.求证:CE=BF.46.如图,已知AB∥CD,AD∥BC,F在DC的延长线上,AM=CF,FM交DA的延长线上于E.交BC于N,试说明:AE=CN.47.已知:如图,△ABC中,∠C=90°,CM⊥AB于M,AT平分∠BAC交CM于D,交BC于T,过D作DE∥AB 交BC于E,求证:CT=BE.48.如图,已知AB=AD,AC=AE,∠BAE=∠DAC.∠B与∠D相等吗?请你说明理由.49.D是AB上一点,DF交AC于点E,DE=EF,AE=CE,求证:AB∥CF.50.如图,M是△ABC的边BC上一点,BE∥CF,且BE=CF,求证:AM是△ABC的中线.51.四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.52.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.53.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.54.如图,点O是线段AB和线段CD的中点.(1)求证:△AOD≌△BOC;(2)求证:AD∥BC.55.如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.56.如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.求证:AE=BC.57.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.58.如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.59.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.60.如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.61.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.62.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.63.如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.64.如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.65.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;(2)若AD=2,∠DAC=30°,求AC的长.66.如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.67.如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△ABC≌△BAD.68.已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:△ABC≌△DEF.69.已知:点A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.(1)你添加的条件是:;(2)证明:.70.如图,AB=AC,AD=AE.求证:∠B=∠C.71.如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.72.一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.73.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:;结论:.(均填写序号)证明:74.如图,在△ABC和△DEF中,AB=DE,BE=CF,∠B=∠1.求证:AC=DF.(要求:写出证明过程中的重要依据)75.如图,已知AB=DC,AC=DB.求证:∠1=∠2.76.如图,D、E分别为△ABC的边AB、AC上的点,BE与CD相交于O点.现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD.(1)请你选出两个条件作为题设,余下的两个作为结论,写出一个正确的命题:命题的条件是和,命题的结论是和(均填序号);(2)证明你写出的命题.77.如图,已知AB∥DE,AB=DE,AF=DC,请问图中有哪几对全等三角形并任选其中一对给予证明.78.如图所示,在梯形ABCD中,AD∥BC,∠B=∠C,点E是BC边上的中点.求证:AE=DE.79.如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.80.已知:如图,∠ACB=90°,AC=BC,CD是经过点C的一条直线,过点A、B分别作AE⊥CD、BF⊥CD,垂足为E、F,求证:CE=BF.81.如图,在△ABC中,AC⊥BC,AC=BC,D为AB上一点,AF⊥CD交于CD的延长线于点F,BE⊥CD于点E,求证:EF=CF﹣AF.82.如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,EC⊥MN于E.(1)求证:BD=AE;(2)若将MN绕点A旋转,使MN与BC相交于点O,其他条件都不变,BD与AE边相等吗?为什么?(3)BD、CE与DE有何关系?83.已知:如图,△ABC中,AB=AC,BD和CE为△ABC的高,BD和CE相交于点O.求证:OB=OC.84.在△ABC中,∠ACB=90°,D是AB边的中点,点F在AC边上,DE与CF平行且相等.试说明AE=DF的理由.85.如图,在△ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连接DE,已知DE=2cm,BD=3cm,求线段BC的长.86.如图:已知∠B=∠C,AD=AE,则AB=AC,请说明理由.87.如图△ABC中,点D在AC上,E在AB上,且AB=AC,BC=CD,AD=DE=BE.(1)求证△BCE≌△DCE;(2)求∠EDC的度数.88.已知:∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E.求证:BD=2CE.89.如图,已知:AB=CD,AD=BC,过BD上一点O的直线分别交DA、BC的延长线于E、F.(1)求证:∠E=∠F;(2)OE与OF相等吗?若相等请证明,若不相等,需添加什么条件就能证得它们相等?请写出并证明你的想法.90.如下图,AD是∠BAC的平分线,DE垂直AB于点E,DF垂直AC于点F,且BD=DC.求证:BE=CF.91.如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B 落在点F处,连接FC,(1)求CF的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的提高拓展训练全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等. 寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的判定方法:(1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等.(4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线. 拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.全等三角形证明经典题1已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2ADBC3已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C5已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE6 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
CDB AB A CDF2 1 E7已知:AB=CD ,∠A=∠D ,求证:∠B=∠C8 P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB9已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DCA BC D P D ACB FAE DC B10.(5分)如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .11(6分)如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B12(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
PEDCBAD CB AMFECBA13已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F ,求证:BE =CD .14在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.AC B DEF15如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。
求证:(1)EC=BF ;(2)EC ⊥BF16.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等吗?请说明理由17.如图9所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .A EB MCFA B C D EF图9全等三角形证明经典(答案)1. 延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52证明:连接BF和EF。
因为 BC=ED,CF=DF,∠BCF=∠EDF。
所以三角形BCF全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
所以∠EBF=∠BEF。
又因为∠ABC=∠AED。
所以∠ABE=∠AEB。
所以 AB=AE。
在三角形ABF和三角形AEF中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以三角形ABF和三角形AEF全等。
所以∠BAF=∠EAF (∠1=∠2)。
3 证明:过E点,作EG//AC,交AD延长线于G则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE(AAS)∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG∴EF=AC4证明:在AC上截取AE=AB,连接ED∵AD平分∠BAC∴∠EAD=∠BAD又∵AE=AB,AD=AD∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB∵AC=AB+BDAC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C5证明:在AE上取F,使EF=EB,连接CF因为CE⊥AB所以∠CEB=∠CEF=90°因为EB=EF,CE=CE,所以△CEB≌△CEF所以∠B=∠CFE因为∠B+∠D=180°,∠CFE+∠CFA=180°所以∠D=∠CFA因为AC平分∠BAD所以∠DAC=∠FAC又因为AC=AC所以△ADC≌△AFC(SAS)所以AD=AF所以AE=AF+FE=AD+BE6证明:在BC上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则⊿ABE≌ΔFBE(SAS),∠EFB=∠A;AB平行于CD,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD.7证明:设线段AB,CD所在的直线交于E,(当AD<BC时,E点是射线BA,CD的交点,当AD>BC 时,E点是射线AB,DC的交点)。
则:△AED是等腰三角形。
所以:AE=DE而AB=CD所以:BE=CE (等量加等量,或等量减等量)所以:△BEC是等腰三角形所以:角B=角C.8作B 关于AD 的对称点B‘,因为AD 是角BAC 的平分线,B'在线段AC 上(在AC 中间,因为AB 较短)因为PC<PB’+B‘C,PC -PB’<B‘C,而B'C=AC-AB'=AC-AB,所以PC-PB<AC-AB9作AG ∥BD 交DE 延长线于G AGE 全等BDE AG=BD=5 AGF ∽CDF AF=AG=5所以DC=CF=210证明:做BE 的延长线,与AP 相交于F 点, ∵PA//BC∴∠PAB+∠CBA=180°,又∵,AE ,BE 均为∠PAB 和∠CBA 的角平分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB 为直角三角形 在三角形ABF 中,AE ⊥BF ,且AE 为∠FAB 的角平分线 ∴三角形FAB 为等腰三角形,AB=AF,BE=EF 在三角形DEF 与三角形BEC 中,∠EBC=∠DFE,且BE=EF ,∠DEF=∠CEB ,∴三角形DEF 与三角形BEC 为全等三角形,∴DF=BC ∴AB=AF=AD+DF=AD+BC11证明:在AB 上找点E ,使AE=AC ∵AE=AC ,∠EAD=∠CAD ,AD=AD∴△ADE ≌△ADC 。
DE=CD ,∠AED=∠C ∵AB=AC+CD ,∴DE=CD=AB-AC=AB-AE=BE ∠B=∠EDB∠C=∠B+∠EDB=2∠B12证明: ∵BE ‖CFP D ACB∴∠E=∠CFM,∠EBM=∠FCM∵BE=CF∴△BEM≌△CFM∴BM=CM∴AM是△ABC的中线.13证明:因为 AB=AC,所以∠EBC=∠DCB因为 BD⊥AC,CE⊥AB所以∠BEC=∠CDBBC=CB (公共边)则有三角形EBC全等于三角形DCB所以 BE=CD14(1)证明:∵∠AC B=90°,∴∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE.在Rt△ADC和Rt△CEB中,{∠ADC=∠CEB∠ACD=∠CBE AC=CB,∴Rt△ADC≌Rt△CEB(AAS),∴AD=CE,DC=BE,∴DE=DC+CE=BE+AD;(2)不成立,证明:在△ADC和△CEB中,{∠ADC=∠CEB=90°∠ACD=∠CBE AC=CB,∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE,∴DE=CE-CD=AD-BE;15(1)证明;因为AE垂直AB所以角EAB=角EAC+角CAB=90度因为AF垂直AC所以角CAF=角CAB+角BAF=90度所以角EAC=角BAF因为AE=AB AF=AC..所以三角形EAC和三角形FAB全等所以EC=BF角ECA=角F(2)延长FB与EC的延长线交于点G因为角ECA=角F(已证)所以角G=角CAF因为角CAF=90度所以EC垂直BF16在AB上取点N ,使得AN=AC∠CAE=∠EAN ,AE为公共边,所以三角形CAE全等三角形EAN 所以∠ANE=∠ACE又AC平行BD所以∠ACE+∠BDE=180而∠ANE+∠ENB=180所以∠ENB=∠BDE∠NBE=∠EBNBE为公共边,所以三角形EBN全等三角形EBD所以BD=BN所以AB=AN+BN=AC+BD17证明:作CG平分∠ACB交AD于G∵∠ACB=90°∴∠ACG= ∠DCG=45°∵∠ACB=90° AC=BC∴∠B=∠BAC=45°∴∠B=∠DCG=∠ACG∵CF⊥AD∴∠ACF+∠DCF=90°∵∠ACF+∠CAF=90°∴∠CAF=∠DCF∵ AC=CB ∠ACG=∠B∴△ACG≌△CBE∴CG=BE∵∠DCG=∠B CD=BD∴△CDG ≌△BDE∴∠ADC=∠BDE. 下载可编辑.。
