对勾函数最值的十种求法

对勾函数

对勾函数图象性质对勾函数 :数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一 ) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+ （接下来写作f(x)=ax+b/x ）。

当 a≠0， b≠0时， f(x)=ax+b/x 是正比例函数 f(x)=ax 与反比例函数 f(x)= b/x 叠“加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当 a ， b 同号时，f(x)=ax+b/x 的图象是由直线y＝ ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：a>0 b>0 a<0 b<0对勾函数的图像（ ab 同号）当 a ，b 异号时， f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）对勾函数的图像（ab 异号）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0 ， b>0 。

之后当a<0，b<0 时，根据对称就很容易得出结论了。

1(二 ) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当 x>0 时，。

当 x<0 时，。

即对勾函数的定点坐标：(三 ) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四 ) 对勾函数的单调性y(五 ) 对勾函数的渐进线O Xy=ax由图像我们不难得到：(六 ) 对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、类耐克函数性质探讨函数y ax b，在 a0或b0时为简单的单调函数，不予讨论。

对勾函数讲解与例题解析

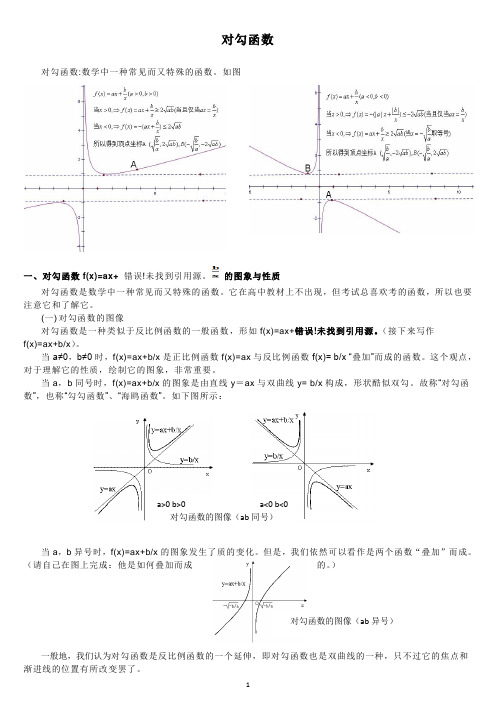
对勾函数对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+错误！未找到引用源。

的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+错误！未找到引用源。

（接下来写作f(x)=ax+b/x ）。

当a≠0，b≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

a>0 b>0 a<0 b<0 对勾函数的图像（ab 同号）对勾函数的图像（ab 异号）接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，错误！未找到引用源。

当x<0时，错误！未找到引用源。

即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到： (六)对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、均值不等式(基本不等式）对勾函数性质的研究离不开均值不等式。

对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+ 错误!未找到引用源。

的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+错误!未找到引用源。

（接下来写作f(x)=ax+b/x）。

当a≠0，b≠0时，f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a，b同号时，f(x)=ax+b/x的图象是由直线y＝ax与双曲线y= b/x构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：a>0 b>0 a<0 b<0对勾函数的图像（ab同号）当a，b异号时，f(x)=ax+b/x的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）对勾函数的图像（ab异号）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，错误!未找到引用源。

当x<0时，错误!未找到引用源。

即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到： (六)对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、均值不等式(基本不等式）对勾函数性质的研究离不开均值不等式。

对勾函数讲解与例题解析(完整资料).doc

【最新整理，下载后即可编辑】对勾函数对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一)对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x）。

当a≠0，b≠0时，f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a，b同号时，f(x)=ax+b/x的图象是由直线y＝ax与双曲线y= b/x构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：a>0 b>0 a<0 b<0对勾函数的图像（ab同号）当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，。

当x<0时，。

即对勾函数的定点坐标： (三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到：(六) 对勾函数的奇偶性：对勾函数在定义域内是奇函数，对勾函数的图像（ab 异号） yXOy=ax二、均值不等式(基本不等式）对勾函数性质的研究离不开均值不等式。

对勾函数最值横坐标

对勾函数最值横坐标
对于一个二次函数f(x) = ax^2 + bx + c，其中 a ≠0，最值横坐标可以通过以下步骤求得：
首先，判断二次函数的开口方向。

如果 a > 0，则开口向上，最小值在顶点处取得；如果a < 0，则开口向下，最大值在顶点处取得。

求出顶点的横坐标。

顶点的横坐标可以通过公式x = -b / (2a) 求得。

所以，对于一个对勾函数，如果是开口向上的，则最小值的横坐标为-b / (2a)；如果是开口向下的，则最大值的横坐标也是-b / (2a)。

请注意，这个结论只适用于二次函数。

对于其他类型的函数，最值横坐标的求解方法可能不同。

对勾函数详细分析

对勾函数的性质及应用一.对勾函数的图像与性质：1.定义域：（-∞，0）∪（0，+∞）2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即4.图像在一、三象限, 当时，2√ab（当且仅当取等号），即在x=时，取最小值由奇函数性质知：当x<0时，在x=时，取最大值5.单调性：增区间为（），（）,减区间是（0，），（,0）1、对勾函数的变形形式类型一：函数的图像与性质1.定义域：2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，在x=时，取最小值；当时，在x=时，取最大值5.单调性：增区间为（0，），（,0）减区间是（），（）,类型二：斜勾函数①作图如下1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-，0），（0，+）.②作图如下：1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-，0），（0，+）.类型三：函数。

此类函数可变形为，可由对勾函数上下平移得到练习1.函数的对称中心为类型四：函数此类函数可变形为，则可由对勾函数左右平移，上下平移得到练习 1.作函数与的草图2.求函数在上的最低点坐标3. 求函数的单调区间及对称中心类型五：函数。

此类函数定义域为，且可变形为a.若，图像如下：1．定义域： 2. 值域：3.奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最大值，当x<0时，在x=时，取最小值5. 单调性：减区间为（），（）；增区间是练习1.函数的在区间上的值域为b. 若，作出函数图像：1．定义域： 2. 值域：3.奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最小值，当x<0时，在x=时，取最大值5. 单调性：增区间为（），（）；减区间是练习1.如，则的取值范围是类型六：函数.可变形为，则可由对勾函数左右平移，上下平移得到练习1.函数由对勾函数向（填“左”、“右”）平移单位，向（填“上”、“下”）平移单位.2.已知，求函数的最小值；3.已知，求函数的最大值类型七：函数练习1.求函数在区间上的最大值；若区间改为则的最大值为2.求函数在区间上的最大值类型八：函数.此类函数可变形为标准形式：练习1.求函数的最小值；2．求函数的值域；3.求函数的值域类型九：函数。

对勾函数

对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x ）。

当a≠0，b≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，。

当x<0时，。

即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到：a>0 b>0 a<0 b<0对勾函数的图像（ab 同号）对勾函数的图像（ab 异号） yXOy=ax(六) 对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、类耐克函数性质探讨函数xbax y +=，在时或00==b a 为简单的单调函数，不予讨论。

对勾函数详细分析教学指导

对勾函数的性质及应用一.对勾函数的图像与性质：1.定义域：（-∞，0）∪（0，+∞）2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即4.图像在一、三象限, 当时，2√ab（当且仅当取等号），即在x=时，取最小值由奇函数性质知：当x<0时，在x=时，取最大值5.单调性：增区间为（），（）,减区间是（0，），（,0）1、对勾函数的变形形式类型一：函数的图像与性质1.定义域：2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，在x=时，取最小值；当时，在x=时，取最大值5.单调性：增区间为（0，），（,0）减区间是（），（）,类型二：斜勾函数①作图如下1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-，0），（0，+）.②作图如下：1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-，0），（0，+）.类型三：函数。

此类函数可变形为，可由对勾函数上下平移得到练习1.函数的对称中心为类型四：函数此类函数可变形为，则可由对勾函数左右平移，上下平移得到练习 1.作函数与的草图2.求函数在上的最低点坐标3. 求函数的单调区间及对称中心类型五：函数。

此类函数定义域为，且可变形为a.若，图像如下：1．定义域： 2. 值域：3. 奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最大值，当x<0时，在x=时，取最小值5. 单调性：减区间为（），（）；增区间是练习1.函数的在区间上的值域为b. 若，作出函数图像：1．定义域： 2. 值域：3. 奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最小值，当x<0时，在x=时，取最大值5. 单调性：增区间为（），（）；减区间是练习1.如，则的取值范围是类型六：函数.可变形为，则可由对勾函数左右平移，上下平移得到练习1.函数由对勾函数向（填“左”、“右”）平移单位，向（填“上”、“下”）平移单位.2.已知，求函数的最小值；3.已知，求函数的最大值类型七：函数练习1.求函数在区间上的最大值；若区间改为则的最大值为2.求函数在区间上的最大值类型八：函数.此类函数可变形为标准形式：练习1.求函数的最小值；2．求函数的值域；3.求函数的值域类型九：函数。

对勾函数详细分析

对勾函数的性质及应用一.对勾函数的图像与性质：1.定义域：（-∞，0）∪（0，+∞）2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即4.图像在一、三象限, 当时，2√ab（当且仅当取等号），即在x=时，取最小值由奇函数性质知：当x<0时，在x=时，取最大值5.单调性：增区间为（），（）,减区间是（0，），（,0）1、对勾函数的变形形式类型一：函数的图像与性质1.定义域：2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，在x=时，取最小值；当时，在x=时，取最大值5.单调性：增区间为（0，），（,0）减区间是（），（）,类型二：斜勾函数①作图如下1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-，0），（0，+）.②作图如下：1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-，0），（0，+）.类型三：函数。

此类函数可变形为，可由对勾函数上下平移得到练习1.函数的对称中心为类型四：函数此类函数可变形为，则可由对勾函数左右平移，上下平移得到练习 1.作函数与的草图2.求函数在上的最低点坐标3. 求函数的单调区间及对称中心类型五：函数。

此类函数定义域为，且可变形为a.若，图像如下：1．定义域： 2. 值域：3. 奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最大值，当x<0时，在x=时，取最小值5. 单调性：减区间为（），（）；增区间是练习1.函数的在区间上的值域为b. 若，作出函数图像：1．定义域： 2. 值域：3. 奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最小值，当x<0时，在x=时，取最大值5. 单调性：增区间为（），（）；减区间是练习1.如，则的取值范围是类型六：函数.可变形为，则可由对勾函数左右平移，上下平移得到练习1.函数由对勾函数向（填“左”、“右”）平移单位，向（填“上”、“下”）平移单位.2.已知，求函数的最小值；3.已知，求函数的最大值类型七：函数练习1.求函数在区间上的最大值；若区间改为则的最大值为2.求函数在区间上的最大值类型八：函数.此类函数可变形为标准形式：练习1.求函数的最小值；2．求函数的值域；3.求函数的值域类型九：函数。

对勾函数表达式

对勾函数表达式：
对勾函数知识点总结如下：
1、对号函数又称“对勾函数”、“双勾函数”、“勾函数”。

表达式：y=x+p/x
当函数表达式为y=qx+p/x，我们可以提取出q，使它成为y=q(x+p/qx)，这样依旧可以由性质上去观察函数。

2、函数性质：
（1）奇偶性
当p>0时，它的图象是分布在一、三象限的两条抛物线，都不能与X 轴、Y轴相交，为奇函数。

当p<0时，它的图象是分布在二、四象限的两条抛物线，都不能与X 轴、Y轴相交，也为奇函数。

（2）单调性
对于第一象限的情况：以（√p,2√p）为顶点，在（0，√p]上是减函数，在[√p，+∞）上是增函数，开口向上；
第三象限内以（-√p,-2√p）为顶点，在（－∞，-√p]，是增函数，在[-√p,0）是减函数，开口向下。

其中顶点的纵坐标是由对函数使用均值不等式后得到的。

3、值得注意的是：在第一象限的图像，当x越小，即越接近于0时，图像左侧就越趋向Y轴+∞,但不相交；当x越大，即越趋向+∞时，图像右侧就越接近直线y=x正半支，但不相交。

4、同理，在第三象限的图像，当x越大，即越接近于0时，图像右
侧就越趋向Y轴-∞，但不相交；当x越小，即越趋向-∞时，图像左侧就越接近直线y=x负半支，但不相交。

即渐近线有Y轴，和直线y=x。

5、最值：最值的求法一是利用函数的单调性，二是均值不等式，三是特殊的单调性如求函数Y=(X+5)/√(X+4)的最值。

双钩函数最值

双钩函数最值
1.概念：双勾（也称对勾）函数的一般形式为f(x)=x + a²/x (a>0).
2.奇偶性与单调性：容易得出，对勾函数是奇函数。

对勾函数的单调性可由求导的方法或直接利用定义判断得到，它有四个单调区间。

在(-∞，-a]和[a，+∞)上是增函数；在[-a，0)和(0，
a]上是减函数。

3.图像：①由于是奇函数，所以图像关于原点对称，再根据单调性，可以得到函数的图像。

②对勾函数的图像有两个顶点，它们关于原点对称，分别是A(a，2a)和B(-a，-2a)。

③对勾函数的图像有两条渐近线，分别是y轴和直线y=x，对勾函数的图像夹在渐近线之间，形状像两个对称的“勾”。

4.用对勾函数求最值应用举例
已知 a，b∈R+，且a+b=1，求ab+1/(ab)的最小值。

由基本不等式，得ab≤[(a+b)/2]²=1/4，令x=ab，则x∈(0，1/4],f(x)=ab+1/(ab)=x+1/x，
由对勾函数的单调性易知，f(x)在（0，1/4]上是减函数(实际上在（0，1）上都是减的），所以最小值为f(1/4)=17/4 。

从而 ab+1/(ab)的最小值为17/4.。

对勾函数最值的十种求法

关于求函数y = x • 1 x . 0最小值的十种解法 x一、均值不等式1 1x 0, . y=x ・一_2，当且仅当x ，即x=1的时候不等式取到“=”。

x x当X =1的时候，y min =2 二、厶法1 2 y=x — : x -yx1=0 x若y 的最小值存在，则厶=y 2 -4亠0必需存在，即y 亠2或y _ -2 （舍）找到使y =2时，存在相应的x 即可。

通过观察当x =1的时候，y min =2三、单调性定义1 1 f X 1 - f X2 = x 1 -X 2 X 1 X 2 当对于任意的X 1,X 2，只有X 1,X 2三〔0,1时，f X 1 - f X 2 2 0, •此时f x 单调递增; 当对于任意的x 1,x 2，只有X —X 2三［时，f x 1 - f x 2 ::： 0，•此时f X 单调递减。

当X - 1取到最小值，『min = f 1 =2四、复合函数的单调性t = Jx ——2在（0,母）单调递增，y =t 2 +2在（—°°,0 ｝单调递减；在 b,畑）单调递增 x 又 x 三〔0,1 二 t '：L ~0 x 1, • ：： = t 0,::-原函数在 0,1上单调递减；在1, 上单调递增即当X =1取到最小值，丫皿山二f 1 =2= ：［X1-X 2 1 二 X 1 -X 2 3 X 1X 2y =x 12 x五、求一阶导1 ' 1y = X — ： y =1 2 XX 当 10,1时，y' :：: 0，函数单调递减；当 X ，1, 时，y' .0,函数单调递增。

当X =1取到最小值，y min = f 1 =2六、二角代换厂兀） 1 a € 0, — 1,则一 =COta I 2丿X广JI 、 a = 0,— 1= 2a E （0,兀）I 2丿 '八、图象相减11 ，即y 表示函数y = x 和y 两者之间的距离X X求y min ，即为求两曲线竖直距离的最小值1平移直线y = x ，显然当y = x 与y 相切时，两曲线竖直距离最小。

对勾函数

对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x ）。

当a≠0，b≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和a>0 b>0 a<0 b<0 对勾函数的图像（ab 同号）对勾函数的图像（ab 异号）渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，。

当x<0时，。

即对勾函数的定点坐标：(三)对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到：(六)对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、类耐克函数性质探讨函数xbaxy+=，在时或00==ba为简单的单调函数，不予讨论。

一道运用对勾函数求最值问题的研究性学习

• 18 •中学数学研究2020年第6期2sinBcosA - sinC = 2sinBcosA - sin (A + B) =sinBcosA - sinAcosB = sin(B - A).以下同解法 1.学生4：直接利用余弦定理的另外一种形式，解法2和解法3都可以进行简化.解法4：由余弦定理戻=a +c - 2accosB ,代入(4)式整理得 ac = c 2 - 2accosB ,即 a = c -2acosB(5).由正弦定理上式为sinA = sinC -2sirk4cos_B = sin (A + B) - 2sinAcosB = sinBcosA -cosBsinA = sin(B - A).以下同解法 1.解法5：由余弦定理戸=a +c -2accosB,代入(4)式得 ac = 2bcosA - / ,即 a = 2bcosA - c(6).以下同解法3.教师：(5)式和(6)式可以联想到锐角三角形中的什么定理？学生5：由(5)式和(6)式可以联想到锐角三角形中的射影定理.解法6：由锐角三角形中的射影定理得c =acosB + bcosA.结合由(5)式或(6)式，化简即a =bcosA - acosB.由正弦定理可化为 sinA = sinBcosA-sinAcosB = sin(B - A).以下同解法 1.感悟:数学教师在实施课堂教学的过程中，要让学生能够把自己所学的所积累的解题经验总结并加工，并让它保存在自己的记忆当中，当遇到一个新的问题时，能够辨识它是属于哪一类基本问题,联想到这个已经解决的问题，以此为索引，在脑子里提取出解决这个问题的方法，为学生构建一条“从具体到抽象,从个别到一般，由此及彼”的思维通道，这一策略体现了“转化与化归”的重要的数学思想方法.一道运用对勾函数求最值问题的研究性学习”陕西师范大学附属中学(710061) 曹艳陕西师范大学附属中学分校(710061) 董强试题已知正数a 和6满足a + b = 1,求(a +丄)(6 +g)的最小值.a b这是学完基本不等式后留给同学们的一道练习题，学生的解答情况不尽一致，出现了不同解法的同时也呈现了一些典型的错误，笔者将其整理希望对同学们的日后学习有所帮助.典型错误1：因为a >0,6 >0,所以(a+-)(6a4- £)=必+4+色 + ¥工2+2 = 4,所以(a +b ab a b丄)3+*)的最小值为4.*项目来源:本文系陕西师范大学教师教育研究专项资助成果《基于核心素养视域下的初中数学单元教学设计研究》(项目编号:JCJY019)阶段性研究成果之一.a b典型错误2：因为a > Q,b > Q,a +b = 1,所以(a + —) (b+£) =aZ»+-y+ — + -7- = aZ»+-y + a b ab a b ab(a + 0)： -2ab =〃+W_2m 2Q-2,所以(a +ab ab—)(6 + 的最小值为2^2 - 2.a b错误评析：以上两类错误均来源于对基本不等式等号成立条件的不重视所致，看到两个正数而且有了定值，马上就去使用基本不等式，而不去检验等号是否成立，这往往是学习基本不等式过程中出现错误频率最高的一个方面.实际上，上述问题中，因为 a > Q,b > 0,a +b = 1,所以 ab W ”_ J_,当且仅当a = b = *时取等号，即必e (0,*],错误1中等号如要成立须有a = b = 1，这不可能，错误2中等号如要成立须有必=也不可能.事实上，上述两种解法均未能求出相应的最小值.解法1：因为a >0,6 >0,a+b = 1,所以必W2020年第6期中学数学研究• 19・(中 )2 =*，当且仅当a = b=+时取等号，即必e (0,*],由对勾函数的性质可知当且仅当a = b=寺时,(a+丄)3+壬)=必+三-2有最小值2a b ab为孚解法 2： (a + 丄)(b + +)= (a+° + l)(b +a b a-y- + 1) 二 ab + —— + —— + -y- + —— + 3 M cib + 2 Jab b baba + 2+3 = (/^ + l 「+4,因为 M e (0,y],所以(烦+ if +4 M 孚，当且仅当烦二!，即a=b 二+时，(。

对勾函数最值的十种求法

对勾函数最值的十种求法 Prepared on 22 November 2020关于求函数()01>+=x x x y 最小值的十种解法一、均值不等式0>x ，∴21≥+=x x y ，当且仅当x x 1=，即1=x 的时候不等式取到“=”。

∴当1=x 的时候，2min =y二、∆法若y 的最小值存在，则042≥-=∆y 必需存在，即2≥y 或2-≤y （舍）找到使2=y 时，存在相应的x 即可。

通过观察当1=x 的时候，2min =y三、单调性定义设210x x <<当对于任意的21,x x ，只有21,x x (]1,0∈时，()()21x f x f -0>，∴此时()x f 单调递增；当对于任意的21,x x ，只有21,x x ()+∞∈,1时，()()21x f x f -0<，∴此时()x f 单调递减。

∴当1=x 取到最小值，()21min ==f y四、复合函数的单调性x x t 1-=在()+∞,0单调递增，22+=t y 在()0,∞-单调递减；在[)+∞,0单调递增又 ∈x ()1,0()0,∞-∈⇒t ∈x [)+∞,1[)+∞∈⇒,0t ∴原函数在()1,0上单调递减；在[)+∞,1上单调递增即当1=x 取到最小值，()21min ==f y五、求一阶导当()1,0∈x 时，0'<y ，函数单调递减；当[)+∞∈,1x 时，0'>y ，函数单调递增。

∴当1=x 取到最小值，()21min ==f y六、三角代换令αtan =x ，⎪⎭⎫ ⎝⎛∈2,0πα，则αcot 1=x∴当4πα=，即22πα=时，()12sin max =α，2min =y ，显然此时1=x七、向量()1,1,1,=⎪⎭⎫ ⎝⎛=b x x ab a x x x x y ⋅=⋅+⋅=+=1111，根据图象，a 为起点在原点，终点在x y 1=()0>x 图象上的一个向量，θcos a 的几何意义为a 在b 上的投影，显然当b a =时，θcos a 取得最小值。

对勾函数

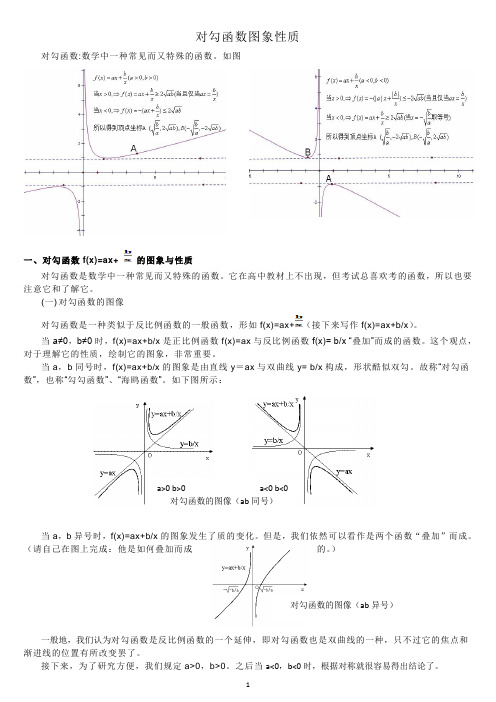
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x ）。

当a≠0，b≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

a>0 b>0 a<0 b<0 对勾函数的图像（ab 同号）对勾函数的图像（ab 异号）(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，。

当x<0时，。

即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到：(六) 对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、类耐克函数性质探讨函数xbax y +=，在时或00==b a 为简单的单调函数，不予讨论。

对勾函数求最值方法

对勾函数求最值方法对勾函数求最值？嘿，这可是个超厉害的数学大招！你想不想轻松搞定最值问题？那就赶紧来看看对勾函数的神奇之处吧！咱先说说对勾函数求最值的步骤。

首先得认识对勾函数的样子，它就像一个调皮的小钩子，有自己独特的形状。

然后呢，通过分析函数的特点，找到关键的转折点。

这就好比在迷宫里找到那条正确的路，一旦找到了，就能顺利求出最值。

注意啦，可不能马虎，每个步骤都要仔细认真，不然就容易出错。

你想想，要是因为一点小马虎求错了最值，那得多郁闷啊！再讲讲安全性和稳定性。

嘿，对勾函数求最值那可是相当靠谱的！只要你按照正确的方法来，就像走在坚实的大路上，不会有啥危险。

它就像一个忠实的小伙伴，稳稳地帮你解决最值问题。

不用担心它会突然“发脾气”，给你带来麻烦。

那对勾函数都能用在啥场景呢？哎呀呀，那可多了去了！比如在经济学里，要计算成本和利润的最值。

这时候对勾函数就像一把神奇的钥匙，能打开最值的大门。

在物理学中，也能用来求一些最值问题，就像一个超级英雄，拯救你于难题之中。

它的优势可不少呢！简单易懂，只要掌握了方法，就能轻松应对各种最值问题。

而且通用性强，不管是数学考试还是实际生活中的问题，都能派上用场。

举个实际案例吧！比如说有一家工厂，要生产一种产品。

已知成本函数是个对勾函数的形式。

通过分析对勾函数的特点，找到了成本最低的生产方案。

哇塞，这效果简直太棒了！不仅节省了成本，还提高了效益。

你说，对勾函数是不是很厉害？还有在学习中，同学们经常会遇到求最值的问题。

用对勾函数的方法，就能快速准确地找到答案。

就像有了一把魔法宝剑，能斩断难题的荆棘。

对勾函数求最值真的是个超棒的方法！它能让你在数学的海洋里畅游无阻，轻松解决各种最值问题。

赶紧掌握起来吧，让你的数学学习更上一层楼！。