四种方法解根的分布问题

合集下载

备《一元二次方程的实根分布问题》

想一想,怎样求函数的零点呢？
求函数的零点有两种方法： ①代数法:求方程f(x)=0的实数根； ②几何法:将它与函数y=f(x)的图象联
系起来,并利用函数的性质找出零点。
连续函数在某个区间上存在零点的判别方法：
如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线，并且有 f(a)·f(b)<0，那么，函数y=f(x)在区间 (a,b)内有零点.即存在c∈(a,b)，使得 f(c )=0，这个c也就是方程f(x)=0的根.
如右图知
O 24 x
f f
(2) (4)
3m 5m
2 4
0 0
m
4 5
问题已知方程x²+(m–3)x+m=0，求实数m的取值范围。
条件8：若方程有一个正根，一个负根且正根的绝对值较大。
y
分析设f(x)=x²+(m–3)x+m
如右图知
O
x
f
(0) m m3
2
0
0
m0
小结
分析设f(x)=x²+(m–3)x+m
y
如右图知
(m 3)24m 0
0
m
3
2
2
f (0) m 0
f (2) 3m 2 0
O
2 m1 3
2x
问题已知方程x²+(m–3)x+m=0，求实数m的
取值范围。条件5：若方程的两个根有且仅有一个在( 0，2)内。
分析设f(x)=x²+(m–3)x+m
例1、若关于x的方程3kx2-2x-4k-2=0的两根一个小于1，另一根
大于1，试求实数k 的取值范围。

求解一元二次方程根的分布问题的途径

丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳丳一元二次方程根的分布问题，通常会给出一元二次方程根的分布区间，要求方程中参数的取值范围.解答此类问题，常需利用一元二次方程根的判别式、韦达定理以及一元二次函数的图象、性质.下面重点谈一谈一元二次方程根的分布问题的解法.一、采用直接法一元二次方程的根能够直接用配方法或因式分解法求出来，可采用直接法，将一元二次方程的根直接求出来，然后根据方程的根所在的区间建立不等式，解不等式即可确定参数的取值范围.例1.要使关于x的方程x2-2mx+m2-1=0的两个实根介于-1和4之间，求实数m的取值范围.分析：方程x2-2mx+m2-1=0的两个实根很容易用配方法或因式分解法求出来，可采用直接法求解.解：x2-2mx+m2-1=()x-m-1()x-m+1=0，解得x1=m-1，x2=m+1，由题意得-1＜m-1＜m+1＜4，解得0＜m＜3.有时可运用求根公式求得方程的根，但要注意对判别式的符号进行讨论.二、利用函数法一元二次方程与一元二次函数之间的联系紧密，若一元二次函数为f（x）=ax2+bx+c（a≠0），当函数f（x）=0时，它就会变成一元二次方程ax2+bx+c=0(a≠0).而解方程实质上是求对应函数的零点，即函数图象与x轴交点的横坐标，所以在解答一元二次方程根的分布问题时，可构造一元二次函数，借助图象来讨论函数零点的位置或取值，以明确方程根的分布情况.例2.关于x的方程2kx2-2x-3k-2=0的两实根一个大于1，一个小于1，求实数k的取值范围.解：设f（x）=2kx2-2x-3k-2，画出如图1、2所示的函数图象，图1图2根据题意可得{k>0,f()1<0,或{k<0,f()1>0,即{k>0,-k-4<0,或{k<0,-k-4>0,解得k＞0或k＜-4.根据所给的一元二次方程构造一元二次函数，便可将问题转化为函数问题，采用函数法来求解.对一元二次函数的开口方向和两根的取值范围进行讨论，便能快速建立关于k的不等式，求得问题的答案.三、分离参数对于一些含参一元二次方程，可将参数分离，运用分离参数法来求参数的取值范围.利用分离参数法求解一元二次方程根的分布问题，需在分离参数后，构造函数模型，将问题转化为求函数的值域或函数图象的交点问题.例3.若方程x2+ax-2=0在区间[]1,5上有解，则实数a的取值范围为（）.A.（-235，+∞）B.（1，+∞）C.éëùû-235，1 D.（-∞，-235）解：因为x∈[]1,5，所以方程x2+ax-2=0可以变形为a=2x-x，令f(x)=2x-x，g(x)=a，故原方程在区间[]1,5上有解⇔f(x)与g(x)的图象在区间x∈[]1,5上有交点，由图3知f(x)=2x-x在[]1,5上单调递减，其值域为éëùû-235，1，所以实数a的取值范围是éëùû-235,1，本题应选C项.将方程x2+ax-2=0变形为a=2x-x，就能将参数分离，再构造函数f(x)、g(x)，便将问题转化为f(x)与g(x)的图象在区间x∈[]1,5上有交点的问题.总之，对于简单的一元二次方程根的分布的问题，可采用直接法求解；对于较为复杂的问题，就需灵活运用函数法和分离参数法求解.而每种方法的适用情况均不相同，同学们需根据解题需求选择合适的方法来求解，这样才能有效提升解题的效率.（作者单位：江苏省盐城市龙冈中学）赵爱华图3探索探索与与研研究究50。

方程根的分布问题

一元二次方程根的分布一元二次方程根的分布是二次函数中的重要内容。

这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用。

函数与方程思想：若y =()f x 与x 轴有交点0x ⇔f (0x )=0若y =f (x )与y =g (x )有交点(0x ，0y )⇔()f x =()g x 有解0x 。

下面我们将主要结合二次函数图象的性质，分两种情况系统地介绍一元二次方程实根分布的充要条件及其运用。

一．一元二次方程根的基本分布——零分布所谓一元二次方程根的零分布，指的是方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧。

设一元二次方程02=++c bx ax（0≠a ）的两个实根为1x ，2x ，且21x x ≤。

【定理1】01>x ，02>x (两个正根)⇔21212400b ac b x x ac x x a⎧∆=-≥⎪⎪⎪+=->⎨⎪⎪=>⎪⎩，推论：01>x ，02>x ⇔⎪⎪⎩⎪⎪⎨⎧<>=>≥-=∆00)0(0042b c f a ac b 或⎪⎪⎩⎪⎪⎨⎧><=<≥-=∆00)0(0042b c f a ac b 上述推论结合二次函数图象不难得到。

【例1】若一元二次方程0)1(2)1(2=-++-m x m x m 有两个正根，求m 的取值范围。

分析：依题意有24(1)4(1)02(1)0101m m m m m mm ⎧⎪∆=++-≥⎪+⎪->⎨-⎪-⎪>⎪-⎩0<m <1。

【定理2】01<x ，02<x ⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<-=+≥-=∆000421212ac x x ab xx ac b ，推论：01<x ，02<x ⇔⎪⎪⎩⎪⎪⎨⎧>>=>≥-=∆00)0(0042b c f a ac b 或⎪⎪⎩⎪⎪⎨⎧<<=<≥-=∆00)0(0042b c f a ac b 由二次函数图象易知它的正确性。

微专题11 二次函数根的分布问题(解析版)

微专题11二次函数根的分布问题【方法技巧与总结】1、实系数一元二次方程20(0)ax bx c a ++=≠的实根符号与系数之间的关系（1）方程有两个不等正根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=->⎨⎪⎪=>⎪⎩（2）方程有两个不等负根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=-<⎨⎪⎪=>⎪⎩（3）方程有一正根和一负根，设两根为12,x x ⇔120cx x a=<2、一元二次方程20(0)ax bx c a ++=≠的根的分布问题一般情况下需要从以下4个方面考虑：（1）开口方向；（2）判别式；（3）对称轴2bx a=-与区间端点的关系；（4）区间端点函数值的正负．设12,x x 为实系数方程20(0)ax bx c a ++=>的两根，则一元二次20(0)ax bx c a ++=>的根的分布与其限定条件如表所示．根的分布图像限定条件12m x x <<02()0b m a f m ∆>⎧⎪⎪->⎨⎪⎪>⎩12x m x <<()0f m <12x x m<<02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪>⎩在区间(,)m n 内没有实根∆<12120x x m x x m∆==≤=≥或02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪≥⎩02()0b n a f n ∆>⎧⎪⎪->⎨⎪⎪≥⎩()0()0f m f n ≤⎧⎨≤⎩在区间(,)m n 内有且只有一个实根()0()0f m f n >⎧⎨<⎩()0()0f mf n<⎧⎨>⎩在区间(,)m n内有两个不等实根2()0()0bm naf mf n∆>⎧⎪⎪<-<⎪⎨⎪>⎪>⎪⎩【题型归纳目录】题型一：正负根问题题型二：根在区间的分布问题题型三：整数根问题题型四：范围问题【典型例题】题型一：正负根问题例1．（2022·河南·郑州市回民高级中学高一阶段练习）已知m为实数，命题甲：关于x的不等式240mx mx+-<的解集为R；命题乙：关于x的方程22200x mx m-++=有两个不相等的负实数根．若甲、乙至少有一个为真命题，求实数m的取值范围为_______．【答案】(20,0]-【解析】由命题甲：关于x的不等式240mx mx+-<的解集为R，当0m=时，不等式40-<恒成立；当0m≠时，则满足2160mm m<⎧⎨∆=+<⎩，解得160m-<<，综上可得160m-<≤．由命题乙：关于x的方程22200x mx m-++=有两个不相等的负实数根，则满足2121244(20)020200m m x x m x x m ⎧∆=-+>⎪+=<⎨⎪=+>⎩，整理得2200020m m m m ⎧-->⎪<⎨⎪>-⎩，所以45020m m m m <->⎧⎪<⎨⎪>-⎩或，解得204m -<<-．所以甲、乙至少有一个为真命题时，有160m -<≤或204m -<<-，可得200m -<≤，即实数m 的取值范围为(20,0]-．故答案为：(20,0]-．例2．（2022·全国·高一单元测试）关于x 的方程2210ax x ++=的实数根中有且只有一个负实数根的充要条件为____________.【答案】0a ≤或1a =【解析】若方程2210ax x ++=有且仅有一个负实数根，则当0a =时，12x =-，符合题意.当0a ≠时，方程2210ax x ++=有实数根，则440a ∆=-≥，解得1a ≤，当1a =时，方程有且仅有一个负实数根1x =-，当1a <且0a ≠时，若方程有且仅有一个负实数根，则10a<，即0a <.所以当0a ≤或1a =时，关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根.综上，“关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根”的充要条件为“0a ≤或1a =”.故答案为：0a ≤或1a =.例3．（2022·甘肃·兰化一中高一阶段练习）若一元二次方程2330kx kx k ++-=的两根都是负数，求k 的取值范围为___________.【答案】125k ≤-或3k >【解析】首先0k ≠，设方程2330kx kx k ++-=的两根为12,x x ，则12121200,00x x x x x x +<⎧<<⇔⎨>⎩，所以2Δ94(3)03030k k k kkk k⎧⎪=--≥⎪⎪-<⎨⎪-⎪>⎪⎩，又0k ≠，解得125k ≤-或3k >．故答案为：125k ≤-或3k >．例4．（2022·全国·高一专题练习）已知关于x 的二次方程2(21)210m x mx m +-+-=有一正数根和一负数根，则实数m 的取值范围是_____．【答案】112m -<<【解析】由题意知，二次方程有一正根和一负根，得2101021m m m +≠⎧⎪-⎨<⎪+⎩，解得112m -<<.故答案为：112m -<<例5．（2022·河南·高一阶段练习）（1）若不等式210ax bx +-<的解集是113x x ⎧⎫-<<⎨⎬⎩⎭∣，求,a b 的值；（2）若31b a =--，且关于x 的方程210+-=ax bx 有两个不同的负根，求a 的取值范围.【解析】（1）由题意可得1-和13是方程210+-=ax bx 的两个实根，则11,31113b a a ⎧-+=-⎪⎪⎨-⎪-⨯=⎪⎩解得3,2a b ==.（2）因为31b a =--，所以()23110ax a x -+-=，由题可知Δ0>，则1a <-或19a >-，由题意，方程有两个负根，即310,10,a a a +⎧<⎪⎪⎨-⎪>⎪⎩解得103-<<a .综上，实数a 的取值范围是109aa ⎧⎫-<<⎨⎬⎩⎭∣.例6．（2022·辽宁·沈阳市第八十三中学高一阶段练习）已知1x ､2x 是一元二次方程24410kx kx k -++=的两个实数根．(1)若1x ､2x 均为正根，求实数k 的取值范围；(2)是否存在实数k ，使得()()12123222x x x x --=-成立？若存在，求出k 的值；若不能存在，请说明理由．【解析】（1）由题意，一元二次方程有两个正根1x ､2x 故20,(4)16(+1)0k k k k ≠∆=-≥，即0k ≤，且121210104x x k x x k +=>⎧⎪+⎨=>⎪⎩，解得：1k <-．（2）由题意，当0∆≥，即0k ≤时，有121211,4k x x x x k++==()()2221212121212129(1)93222+252()92442k k x x x x x x x x x x x x k k ++--=-=+-=-=-=-解得：95k =，与0k ≤矛盾.故不存在实数k ，使得()()12123222x x x x --=-成立题型二：根在区间的分布问题例7．（2022·全国·高一专题练习）已知一元二次方程x 2＋ax ＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a 的取值范围为________．【答案】5(,2)2--【解析】设f (x )＝x 2＋ax ＋1，由题意知(0)10(1)20(2)520f f a f a =>⎧⎪=+<⎨⎪=+>⎩，解得－52<a <－2.故答案为：5(,2)2--.例8．（2022·全国·高一课时练习）已知关于x 的方程220x x a -+=．(1)当a 为何值时，方程的一个根大于1，另一个根小于1？(2)当a 为何值时，方程的一个根大于1-且小于1，另一个根大于2且小于3？(3)当a 为何值时，方程的两个根都大于0？【解析】（1）二次函数22y x x a =-+的图象是开口向上的抛物线，故方程220x x a -+=的一个根大于1，另一个根小于1，则2120a -+<，解得1a <，所以a 的取值范围是{}1a a <．（2）方程220x x a -+=的一个根大于1-且小于1，另一个根大于2且小于3，作满足题意的二次函数22y x x a =-+的大致图象，由图知，120120440960a a a a ++>⎧⎪-+<⎪⎨-+<⎪⎪-+>⎩，解得30a -<<．所以a 的取值范围是{}30a a -<<．（3）方程220x x a -+=的两个根都大于0，则Δ4400a a =-≥⎧⎨>⎩，解得01a <≤，所以a 的取值范围是{}01a a <≤．例9．（2022·全国·高一专题练习）已知关于x 的一元二次方程2220x ax a -++=，当a 为何值时，该方程：有不同的两根且两根在(1,3)内．【解析】令2()22f x x ax a =-++，因为方程2220x ax a -++=有不同的两根且两根在(1,3)内，所以213Δ44(2)0(1)30(3)1150a a a f a f a <<⎧⎪=-+>⎪⎨=->⎪⎪=->⎩，解得1125<<a ，故答案为：112,5⎛⎫⎪⎝⎭例10．（2022·江苏·高一专题练习）已知二次函数()2221R y x tx t t =-+-∈.(1)若该二次函数有两个互为相反数的零点，解不等式22210x tx t -+-≥；(2)若关于x 的方程22210x tx t -+-=的两个实根均大于2-且小于4，求实数t 的取值范围．【解析】（1）设二次函数()2221y x tx t t =-+-∈R 的两个零点分别为1x ，2x ，由已知得120x x +=，而122x x t +=，所以20t =，故0=t ，不等式22210x tx t -+-≥即210x -≥，解得1≥x 或1x ≤-，故不等式的解集为{1x x ≥或}1≤-x .（2）因为方程22210x tx t -+-=的两个实根均大于2-且小于4，所以()()()()222222Δ2t 4t 102t 422t 2t 1042t 4t 10⎧=---≥⎪⎪-<<⎨⎪--⨯-+->⎪-⨯+->⎩，即2240244308150t t t t t ≥⎧⎪-<<⎪⎨++>⎪⎪-+>⎩，解得：13t -<<，即实数t 的取值范围为{}13t t -<<.例11．（2022·全国·高一单元测试）求实数m 的范围，使关于x 的方程()221 260.x m x m +-++=(1)有两个实根，且一个比2大，一个比2小；(2)有两个实根 αβ，，且满足014αβ<<<<；(3)至少有一个正根.【答案】(1)1m <-(2)7554m -<<-(3)1m ≤-【分析】设()()22126y f x x m x m ==+-++，一元二次方程根的分布主要从对称轴、判别式、端点值、开口方向这几个方面来确定.（1）设()()22126y f x x m x m ==+-++．依题意有()20f <，即()441260m m +-++<，得1m <-．（2）设()()22126y f x x m x m ==+-++．依题意有()()()02601450410140f m f m f m ⎧=+>⎪=+<⎨⎪=+>⎩，解得7554m -<<-．（3）设()()22126y f x x m x m ==+-++．方程至少有一个正根，则有三种可能：①有两个正根，此时可得()()Δ0002102f m ⎧⎪≥⎪⎪>⎨⎪-⎪>⎪-⎩，即153.311m m m m m ≤-≥⎧⎪>-∴-<≤-⎨⎪<⎩或．②有一个正根，一个负根，此时可得()00f <，得3m <-．③有一个正根，另一根为0，此时可得()6203210m m m +=⎧∴=-⎨-<⎩，．综上所述，得1m ≤-．例12．（2022·上海市七宝中学高一阶段练习）方程()2271320x a x a a -++--=的一个根在区间()0,1上，另一个根在区间()1,2上，则实数a 的取值范围为___________.【答案】()()2,13,4--【解析】令()()227132f x x a x a a =-++--，因为程()2271320x a x a a -++--=的一个根在区间()0,1上，另一个根在区间()1,2上，所以()()()001020f f f ⎧>⎪<⎨⎪>⎩，即()22220713202821320a a a a a a a a ⎧-->⎪--+--<⎨⎪-++-->⎩，解得21a -<<-或34a <<，所以实数a 的取值范围为()()2,13,4--.故答案为：()()2,13,4--.例13．（2022·全国·高一专题练习）关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根，则实数a 的取值范围是_____．【答案】16(5,]3【解析】关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根，令()()214f x x a x =--+，则有()()()2Δ1160113216031630a a f a f a ⎧=-->⎪-⎪<<⎪⎨⎪=-≥⎪=-≥⎪⎩，解得1653a <≤，所以实数a 的取值范围是16(5,]3.故答案为：16(5,]3例14．（2022·全国·高一单元测试）方程()2250x a x a --+-=的两根都大于2，则实数 a 的取值范围是_____．【答案】54a -<≤-【解析】由题意，方程()2250x a x a +=－－－的两根都大于 2，令()()225f x x a x a =+－－－，可得()020222f a⎧⎪≥⎪>⎨⎪-⎪>⎩，即2165024a a a ⎧≥⎪+>⎨⎪->⎩，解得54a <≤－－．故答案为：54a -<≤-.例15．（2022·全国·高一专题练习）已知关于x 的方程220ax x ++=的两个实根一个小于0，另一个大于1，则实数a 的取值范围是_____．【答案】()3,0-【解析】显然0a ≠，关于x 的方程220ax x ++=对应的二次函数()22f x ax x =++当0a >时，二次函数()22f x ax x =++的图象开口向上，因为220ax x ++=的两个实根一个小于0，另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0，另一个大于1，所以()()0010f f ⎧<⎪⎨<⎪⎩，即2030a <⎧⎨+<⎩，解得a ∈∅；②当0a <时，二次函数()22f x ax x =++的图象开口向下，因为220ax x ++=的两个实根一个小于0，另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0，另一个大于1，所以()()0010f f ⎧>⎪⎨>⎪⎩，即2030a >⎧⎨+>⎩，解得30a -<<．；综上所述，实数a 的范围是()3,0-．故答案为：()3,0-．例16．（2022·全国·高一专题练习）已知方程()()22110x a x a a -+++=的两根分别在区间()0,1，()1,3之内，则实数a 的取值范围为______．【答案】()0,1.【解析】方程()()()()2211010x a x a a x a x a ⎡⎤+++=⇒--+=⎣⎦－∴方程两根为12,1x a x a ==+，若要满足题意，则01113a a <<⎧⎨<+<⎩，解得01a <<，故答案为：()0,1.例17．（2022·上海·高一专题练习）方程2240x ax -+=的两根均大于1，则实数a 的取值范围是_______【答案】5[2,)2【解析】2240x ax -+=的两个根都大于121520Δ4160a a a >⎧⎪∴->⎨⎪=-≥⎩，解得522a ≤<可求得实数a 的取值范围为5[2,2故答案为：5[2,)2例18．（2022·湖北·华中师大一附中高一开学考试）关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x <<，那么a 的取值范围是（）A ．2275a -<C ．27a <-D ．2011a -<<【答案】D【解析】当0a =时，()2290ax a x a +++=即为20x =，不符合题意；故0a ≠，()2290ax a x a +++=即为22190x x a ⎛⎫+++= ⎪⎝⎭，令2219y x x a ⎛⎫=+++ ⎪⎝⎭，由于关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x <<，则()229y ax a x a =+++与x 轴有两个交点，且分布在1的两侧，故1x =时，0y <，即211190a ⎛⎫++⨯+< ⎪⎝⎭，解得211a<-，故2011a -<<，故选：D例19．（2022·全国·高一课时练习）关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内，则实数m 的取值范围是（）A ．13,22⎡⎤⎢⎥⎣⎦B ．12,23⎛⎤ ⎥⎝⎦C ．1,22⎡⎫⎪⎢⎣⎭D．{12,623⎛⎤⋃- ⎥⎝⎦【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为：()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1)，则需要满足：①()()010f f ⋅<，()()21320m m --<，解得：1223m <<；②函数()f x 刚好经过点()0,0或者()1,0，另一个零点属于(0,1)，把点()0,0代入()2(2)21f x x m x m =+-+-，解得：12m =，此时方程为2302x x -=，两根为0，32，而()30,12∉，不合题意，舍去把点()1,0代入()2(2)21f x x m x m =+-+-，解得：23m =，此时方程为23410x x -+=，两根为1，13，而()10,13∈，故符合题意；③函数与x 轴只有一个交点，横坐标属于(0,1)，()2(2)4210m m ∆=---=，解得6m =±当6m =+2(2)210x m x m +-+-=的根为2-若6m =-2(2)210x m x m +-+-=2，符合题意综上：实数m的取值范围为{12,623⎛⎤⋃- ⎥⎝⎦故选：D题型三：整数根问题例20．（2022·上海市实验学校高一开学考试）已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ，使得()()12123222x x x x --=-成立？若存在，求出k 的值；若不存在，请说明理由；(2)求使12212x x x x +-的值为整数的实数k 的整数值.【解析】（1）假设存在实数k ，使得()()12123222x x x x --=-成立，一元二次方程24410kx kx k -++=的两个实数根，()2400Δ(4)441160k k k k k k ≠⎧∴⇒<⎨=--⋅+=-⎩，(不要忽略判别式的要求)，由韦达定理得1212114x x k x x k +=⎧⎪+⎨=⎪⎩，()()()()2221212121212129322252942k x x x x x x x x x x x x k +∴--=+-=+-=-=-，95k ⇒=但0k <，∴不存在实数k ，使得()()12123222x x x x --=-成立.（2）()22212121221121244224411x x x x x x k x x x x x x k k +++-==-=-=-++，∴要使其值是整数，只需要1k +能被4整除，故1124k +=±±±，，，即021335k =---，，，，，，0k <，235k ∴=---，，.例21．（2022·上海·高三专题练习）已知,a Z ∈关于x 的一元二次不等式260x x a -+≤的解集中有且仅有3个整数，则所有符合条件的a 的值之和是（）A ．13B ．18C ．21D ．26【答案】C【解析】设2()6f x x x a =-+，其图象为开口向上，对称轴为3x =的抛物线，根据题意可得，3640a ∆=->，解得9a <，因为()0f x ≤解集中有且仅有3个整数，结合二次函数的对称性可得(2)0(1)0f f ≤⎧⎨>⎩，即4120160a a -+≤⎧⎨-+>⎩，解得58a <≤，又,a Z ∈所以a =6，7，8，所以符合题意的a 的值之和6+7+8=21.故选：C例22．（多选题）（2022·全国·高一课时练习）已知a ∈Z ，关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数，则a 的值可以是（）A ．5B ．6C ．7D ．9【答案】BC【解析】设()26f x x x a =-+，函数图象开口向上，且对称轴为3x =，因此关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数时，需满足()()2010f f ⎧≤⎪⎨>⎪⎩，即2226201610a a ⎧-⨯+≤⎨-⨯+>⎩，解得58a <≤，又因为a ∈Z ，所以6a =或7或8，故选：BC.例23．（2022·全国·高一专题练习）若方程()22460x kx x --+=有两个不相等的实根，则k 可取的最大整数值是______.【答案】1【解析】方程化为()221860k x x --+=，由()Δ6424210k =-->，12k ≠解得116k <，所以k 最大整数值是1.故答案为：1.题型四：范围问题例24．（2022·上海·高一专题练习）已知t 是实数，若a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，则()()2211a b --的最小值是___________.【答案】3-【解析】a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，∴可得2a b +=，10ab t =-≥，1t ∴≥，又()4410t ∆=--≥，可得2t ≤，12t ∴≤≤，又()()()()()()222222211121a b ab a b ab a b ab --=-++=-+++()()()()2221114211a b t t ∴--=--+-+，24t =-，又12t ≤≤，2340t ∴-≤-≤，故答案为：3-．例25．（2022·吉林省实验中学高一阶段练习）设方程240x mx m -+=的两实根分别为12,x x .(1)当1m =时，求1211+x x 的值；(2)若120,0x x >>，求实数m 的取值范围及124x x +的最小值.【解析】（1）当1m =时，方程为2410x x -+=，2(4)4120∆=--=>，所以12124,1x x x x +=⋅=，122112114x x x x x x ∴+⋅+==.（2）因为240x mx m -+=两根120,0x x >>，所以21212Δ1640400m m x x m x x m ⎧=-≥⎪+=>⎨⎪⋅=>⎩，解得14m ≥.因为12124x x x x +=，120,0x x >>，所以12114x x +=，所以211212121241111194(4)()(5)54444x x x x x x x x x x ⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭，当且仅当21124x x x x =，即1233,48x x ==时等号成立，此时91324m =>符合题意，124x x ∴+的最小值为94.例26．（2022·北京海淀·高一期末）已知函数()22f x x bx c =++（b ，c 为实数），()()1012f f -=.若方程()0f x =有两个正实数根1x ，2x ，则1211+x x 的最小值是（）A ．4B ．2C ．1D ．12【答案】B【解析】因为函数()22f x x bx c =++（b ，c 为实数），()()1012f f -=，所以1012200288b c b c +=++-，解得4b =-，所以()224f x x x c -+=，因为方程()0f x =有两个正实数根1x ，2x ，所以()Δ168000c f c =-≥⎧⎨=>⎩，解得02c <≤，所以121212112422x x c x x x x c =++==≥，当c =2时，等号成立，所以其最小值是2，故选：B例27．（2022·江苏·高一）已知关于x 的方程230x kx k -++=有两个正根，那么两个根的倒数和最小值是（）A ．-2B ．23C ．89D ．1【答案】B【解析】由题意可得∆2()4(3)0k k =--+ ，解得6k 或2k ≤-，设两个为1x ，2x ，由两根为正根可得12120·30x x k x x k +=>⎧⎨=+>⎩，解得0k >，综上知，6k .故两个根的倒数和为12121211x x x x x x ++=1331k k k==++，6k ，∴1106k < ，3102k < ，故33112k <+，∴12331k+，故两个根的倒数和的最小值是23.故选：B例28．（2022·上海·华师大二附中高一期中）已知实数a b <，关于x 的不等式()210x a b x ab -+++<的解集为()12,x x ，则实数a 、b 、1x 、2x 从小到大的排列是()A ．12a x x b <<<B ．12x a b x <<<C ．12a x b x <<<D ．12x a x b<<<【答案】A【解析】由题可得：12x x a b +=+，121x x ab =+.由a b <，12x x <，设1x a m =+，则2x b m =-.所以212()()()1a m b m ab m b a m ab x x =+-=+--=+，所以2()1m b a m --=，21m m b a+=-.又a b <，所以0b a ->，所以0m >.故1x a >，2x b <.又12x x <，故12a x x b <<<.故选：A.例29．（2022·福建厦门·高一期末）已知函数()()11f x x x a =-⋅--，a R ∈．(1)若0a =，解不等式()1f x <；(2)若函数()f x 恰有三个零点1x ，2x ，3x ，求123111x x x ++的取值范围．【解析】(1)当0a =时，原不等式可化为()120x x -⋅-<…①．（ⅰ）当0x ≥时，①式化为220x x --<，解得12x -<<，所以02x ≤<；（ⅱ）当0x <时，①式化为220x x -+>，解得x ∈R ，所以0x <．综上，原不等式的解集为(),2-∞．(2)依题意，()()()2211,11,x a x a x af x x a x a x a ⎧-++--<⎪=⎨-++-≥⎪⎩．因为()10f a =-<，且二次函数()211y x a x a =-++-开口向上，所以当x a ≥时，函数()f x 有且仅有一个零点．所以x a <时，函数()f x 恰有两个零点．所以()()()21,21410,10.a a a a f a +⎧<⎪⎪⎪=+-+>⎨⎪=-<⎪⎪⎩解得3a >．不妨设123x x x <<，所以1x ，2x 是方程()2110x a x a -++--=的两相异实根，则12121,1x x a x x a +=+⎧⎨=+⎩，所以121212111x x x x x x ++==．因为3x 是方程()2110x a x a -++-=的根，且312a x +>，由求根公式得3x =因为函数()g a ()3,+∞上单调递增，所以()332x g >=31012x <<-．所以123111x x x ++．所以a 的取值范围是21,22⎛- ⎝⎭．【过关测试】一、单选题1．（2022·江苏·高一专题练习）已知p ：a m <（其中R a ∈，m ∈Z ），q ：关于x 的一元二次方程2210ax x ++=有一正一负两个根.若p 是q 的充分不必要条件，则m 的最大值为（）A ．1B ．0C ．1-D ．2【答案】C【解析】因为2210ax x ++=有一正一负两个根，所以224010a a ⎧∆=->⎪⎨<⎪⎩，解得0a <.因为p 是q 的充分不必要条件，所以0m <，且m ∈Z ，则m 的最大值为1-.故选：C2．（2022·江苏·高一专题练习）已知方程2(2)50x m x m +-+-=有两个不相等的实数根，且两个实数根都大于2，则实数m 的取值范围是（）A ．(5,4)(4,)--+∞B ．(5,)-+∞C ．(5,4)--D ．(4,2)(4,)--+∞【答案】C【解析】令()2(2)5mf x m x x =+-+-由题可知：()()()()2Δ02450442222242250520m m m m m m m m m m f >⎧⎧--⨯->><-⎧⎪⎪-⎪⎪>⇒<-⇒<-⎨⎨⎨⎪⎪⎪+-⨯+->>-⎩>⎩⎪⎩或则54m -<<-，即(5,4)m ∈--故选：C3．（2021·北京·北师大实验中学高一期中）设方程2610x x -+=的两个不等实根分别为12,x x ，则12||x x -=（）A ．3B ．6C．D．【答案】D【解析】2610x x -+=，364320∆=-=>，故121261x x x x +=⎧⎨=⎩，12||x x -===.故选：D.4．（2021·江苏·高一课时练习）设a 为实数，若方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解，则a 的取值范围是（）.A ．(,0)(1,)-∞⋃+∞B ．(1,0)-C ．1,03⎛⎫- ⎪⎝⎭D ．1,0(1,)3⎛⎫-+∞ ⎪⎝⎭【答案】C【解析】令2()2g x x ax a =-+，由方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解可得244011(1)0(1)0a a a g g ⎧∆=->⎪-<<⎪⎨->⎪⎪>⎩，即011131a a a a <⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩或111131a a a a >⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩，解得103-<<a ，故选：C5．（2022·全国·高一课时练习）一元二次方程()22100ax x a ++=≠有一个正实数根和一个负实数根的一个充分不必要条件是()A ．0a C ．1a <-D ．2a <【答案】C【解析】由题意，不妨设2()21f x ax x =++，因为(0)10=>f ，且()22100ax x a ++=≠有一个正实数根和一个负实数根，所以2()21f x ax x =++的图像开口向下，即0a <，故对于选项ABCD ，只有C 选项：1a <-是0a <的充分不必要条件.故选：C.6．（2021·四川·树德中学高一阶段练习）设集合{}2320A x x x =-+<，集合{}2210B x ax x =--=，若A B ⋂≠∅，则实数a 的取值范围是（）A ．34,43⎡⎫⎪⎢⎣⎭B ．5,34⎛⎫ ⎪⎝⎭C ．3,4⎡⎫+∞⎪⎢⎣⎭D ．(1,)+∞【答案】B【解析】由题意，{}2320{|12}A x x x x x =-+<=<<若AB ⋂≠∅，即方程2210ax x --=存在根在区间(1,2)（1）若102102a x x =∴--=∴=-，不成立；（2）若0a ≠，由于0x =不为方程的根，故0x ≠，则222221211210(1)1x ax x a x x x x+--=⇔==+=+-由于21115(1,2)(,1)(1)1(,3)24x x x ∈∴∈∴+-∈综上，实数a 的取值范围是5,34⎛⎫⎪⎝⎭故选：B7．（2022·全国·高一课时练习）要使关于x 的方程()22120x a x a +-+-=的一根比1大且另一根比1小，则实数a 的取值范围是（）A ．{}12a a -<【答案】B【解析】由题意可得()2211220a a a a +-+-=+-<，解得21a -<<.故选：B.8．（2021·甘肃·天水市第一中学高一阶段练习）已知一元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，则m 的值为（）A ．4-B ．5-C ．6-D ．7-【答案】A【解析】因为元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，令2()(1)1f x x m x =+++，则由题意可得(0)0(1)0(3)0f f f >⎧⎪<⎨⎪>⎩，即10,30,1330,m m >⎧⎪+<⎨⎪+>⎩解得1333m -<<-，又m Z ∈，可得4m =-.故选：A 二、多选题9．（2022·江苏南通·高一开学考试）已知不等式20(0)x ax b a ++>>的解集是{}|x x d ≠，则下列四个结论中正确的是（）.A ．24a b=B ．若不等式2+x ax b c +<的解集为(3,1)-，则7a b c ++=C ．若不等式20x ax b +-<的解集为12(,)x x ，则120x x >D ．若不等式2x ax b c ++<的解集为12(,)x x ，且12||4x x -=，则4c =【答案】ABD【解析】由题意，不等式20(0)x ax b a ++>>的解集是{}|x x d ≠，所以240a b ∆=-=，24a b ∴=，所以A 正确；对于B ：2+x ax b c +<变形为2+0x ax b c +-<，其解集为(3,1)-，所以231 314 a b c a b -+=-⎧⎪-⨯=-⎨⎪=⎩，得214a b c =⎧⎪=⎨⎪=⎩，故7a b c ++=成立，所以B 正确；对于C ：若不等式20x ax b +-<的解集为12(,)x x ，由韦达定理知：21204a x xb =-=-<，所以C 错误；对于D ：若不等式2x ax bc ++<的解集为12(,)x x ，即20x ax b c ++-<的解集为12(,)x x ，由韦达定理知：21212,4a x x a x x b c c +=-=-=，则12||4x x -==，解得4c =，所以D 正确.故选：D.10．（2021·江苏·海安高级中学高一阶段练习）一元二次方程240x x m -+=有正数根的充分不必要条件是（）A ．4m =B ．5m =C ．1m =D ．12=-m 【答案】ACD【解析】设()24f x x x m =-+，则二次函数()f x 的图象的对称轴为2x =．当4m =时，方程即()224420x x x -+=-=，求得2x =，满足方程有正根，但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故4m =是方程240x x m -+=有正数根的充分不必要条件，故A 满足条件；当5m =时，方程即()224521x x x -+=-=-，求得x ∈∅，不满足方程有正实数根，故5m =不是方程240x x m -+=有正数根的充分条件，故排除B ．当1m =时，方程即()224123x x x -+=-=，求得2=±x 但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故1m =方程240x x m -+=有正数根的充分不必要条件，故C 满足条件；当12=-m 时，方程即24120x x --=，求得2x =-，或6x =，满足方程有正根，但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故12=-m 方程240x x m -+=有正数根的充分不必要条件，故D 满足条件，故选：ACD ．11．（2022·湖南湖南·高一期末）若方程220x x λ++=在区间()1,0-上有实数根，则实数λ的取值可以是（）A ．3-B ．18C ．14D ．1【答案】BC【解析】由题意22x x λ=--在(1,0)-上有解．∵(1,0)x ∈-，∴222(1)1(0,1)x x x λ=--=-++∈，故选：BC ．12．（2021·全国·高一专题练习）已知关于x 的方程()230x m x m +-+=，则下列结论中正确的是（）A ．方程()230x m x m +-+=有一个正根一个负根的充要条件是{}0m m m ∈D ．当m =3时，方程()230x m x m +-+=的两个实数根之和为0【答案】AB【解析】对A ，当0x =时，函数2(3)y x m x m =+-+的值为m ，由二次函数的图象知，方程有一正一负根的充要条件是{}|0m m m ∈<，故A 正确；对B ，若方程()230x m x m +-+=有两个正实数根1x ，2x ，即()2121234030,0,m m x x m x x m ⎧∆=--≥⎪+=->⎨⎪=>⎩解得：01m <≤，故B 正确；对C ，方程()230x m x m +-+=无实数根，即()2340m m ∆=--<，解得：19m <<，方程()230x m x m +-+=无实数根的充要条件是{}19m m m ∈<<，故C 错误；对D ，当3m =时，方程为230x +=，无实数根，故D 错误.故答案为：AB.13．（2021·江苏·高一专题练习）已知一元二次方程()()21102x m x m Z +++=∈有两个实数根12,x x ，且12013x x <<<<，则m 的值为（）A ．-2B ．-3C ．-4D ．-5【答案】BC 【解析】设()()2112f x x m x =+++，由12013x x <<<<，可得()()()()10200110110230193102f f m f m ⎧>⎪⎧>⎪⎪⎪<⇒+++<⎨⎨⎪⎪>⎩⎪+++>⎪⎩，解得：25562m -<<-，又因为m Z ∈，得3m =-或4m =-，故选：BC.三、填空题14．（2022·安徽省蚌埠第三中学高一开学考试）关于x 的方程210x ax ++=的一根大于1，一根小于1，则a 的取值范围是：__________________．【答案】a <-2【解析】∵关于x 的方程210x ax ++=的一根大于1，另一根小于1，令2()1=++f x x ax ，则(1)20f a =+<，求得2a <-，故答案为：2a <-15．（2021·北京师大附中高一期中）若关于x 的一元二次方程2240x ax -+=有两个实根，且一个实根小于1，另一个实根大于2，则实数a 的取值范围是________．【答案】（52，＋∞）【解析】设2()24f x x ax =-+，由题意2Δ4160(1)1240(2)4440a f a f a ⎧=->⎪=-+<⎨⎪=-+<⎩，解得52a >，故答案为：5(,)2+∞．16．（2021·上海·复旦附中高一期中）若关于x 的方程220x kx -+=的一根大于－1，另一根小于－1，则实数k 的取值范围为______．【答案】(),3-∞-【解析】由题意，关于x 的方程220x kx -+=的一根大于-1，另一根小于-1，设()22f x x kx =-+，根据二次函数的性质，可得()130f k -=+<，解得3k <-，所以实数k 的取值范围为(),3-∞-.故答案为：(),3-∞-.17．（2020·上海·高一专题练习）已知集合()(){}2|320,A x x x x x R =-+-≤∈，{}2|120,B x x ax x R =--≤∈，若A B ⊆，则实数a 的取值范围是______________．【答案】[]1,1-【解析】由()()2320x x x -+-≤，得23020x x x ⎧-≥⎪⎨+-≤⎪⎩或23020x x x ⎧-≤⎪⎨+-≥⎪⎩，解得13x ≤≤，所以集合{|31A x x =-≤≤-或}13x ≤≤，因为A B ⊆，令()212f x x ax =--，则()()3030f f ⎧-≤⎪⎨≤⎪⎩，即9312093120a a +-≤⎧⎨--≤⎩，解得11a -≤≤，所以实数a 的取值范围是[]1,1-故答案为：[]1,1-四、解答题18．（2022·全国·高一期中）命题:p 关于x 的方程20x x m ++=有两个相异负根；命题():0,q x ∃∈+∞，2390x mx -+<．(1)若命题q 为假命题，求实数m 的取值范围；(2)若这两个命题有且仅有一个为真命题，求实数m 的取值范围．【解析】（1）若命题q 为假命题，则对()0,x ∀∈+∞，2390x mx -+≥为真命题；239mx x ∴≤+，即93m x x ≤+；96x x +≥（当且仅当9x x =，即3x =时取等号），36m ∴≤，解得：2m ≤，∴实数m 的取值范围为(],2-∞.（2）由（1）知：若命题q为真命题，则2m >；若命题p 为真命题，则Δ1400m m =->⎧⎨>⎩，解得：104m <<；若p 真q 假，则104m <<；若p 假q 真，则2m >；综上所述：实数m 的取值范围为()10,2,4⎛⎫+∞ ⎪⎝⎭.19．（2022·湖南·高一课时练习）若一元二次方程2570x x a --=的一个根在区间()1,0-内，另一个根在区间()1,2内，求实数a 的取值范围．【解析】令2()57f x x x a =--，则根据题意得(1)057012(0)000(1)0202(2)0201406f a a f a a f a a f a a ->⇒+->⇒<⎧⎪<⇒-⇒⎪⎨<⇒--⇒-⎪⎪>⇒-->⇒<⎩，∴06a <<.故实数a 的取值范围(0,6).20．（2021·辽宁·昌图县第一高级中学高一期中）1.已知()()2213f x x a x =+-+．(1)如果方程()0f x =在()0,3有两个根，求实数a 的取值范围；(2)如果[]1,2x ∃∈，()0f x >成立，求实数a 的取值范围．【解析】(1)()()2213f x x a x =+-+的对称轴为1x a=-要想方程()0f x =在()0,3有两个根，需要满足()()()100001330f a f a f ⎧-<⎪>⎪⎨<-<⎪⎪>⎩解得：(1,1a ∈--(2)[]1,2x ∃∈，()22130x a x +-+>成立，即3122x a x ⎛⎫->-+ ⎪⎝⎭在[]1,2x ∈上有解，只需1a -大于()322x g x x ⎛⎫=-+ ⎪⎝⎭的最小值，其中()322x g x x ⎛⎫=-+ ⎪⎝⎭为对勾函数，在x ⎡∈⎣上单调递增，在)x ∈上单调递减，又()131222g ⎛⎫=-+=- ⎪⎝⎭，()2372244g ⎛⎫=-+=- ⎪⎝⎭，所以最小值为()12g =-故12a ->-，解得：1a >-，实数a 的取值范围为()1,-+∞21．（2021·上海市七宝中学高一阶段练习）设二次函数()2f x ax bx c =++，其中R a b c ∈、、.(1)若()21,94b a c a =+=+，且关于x 的不等式()28200-+<x x f x 的解集为R ，求a 的取值范围；(2)若Z a b c ∈、、，且()()01f f 、均为奇数，求证：方程()0f x =无整数根；(3)若21,21,a b k c k ==-=，当方程()0f x =有两个大于1的不等根时求k 的取值范围.【解析】（1）∵()22820440x x x -+=-+>∴()()221940f x ax a x a =++++<在R 上恒成立∵0a ≠，则()()20Δ414940a a a a <⎧⎪⎨=+-+<⎪⎩，解得12a <-综上所述：a 的取值范围为1,2⎛⎫-∞- ⎪⎝⎭.（2）∵()()0,1f c f a b c ==++，则c 为奇数，a b +为偶数当Z x ∈时，则有：1.若a b 、均为偶数时，则2ax bx +为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根2.若a b 、均为奇数时，则有①若x 为偶数时，则2ax bx +为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根②若x 为奇数时，则()2ax bx x ax b +=+为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根综上所述：方程()0f x =无整数根（3）()()2221f x x k x k =+-+由题意可得()()222Δ21402112120k k k f k k ⎧=-->⎪-⎪->⎨⎪=+>⎪⎩，解得2k <-则k 的取值范围为(),2∞--.。

不等式专题：一元二次方程根的分布问题-【题型分类归纳】高一数学上学期同步讲与练(解析版)

一元二次方程根的分布问题一、二次函数相关知识对于形如()20=++≠y ax bx c a 的二次函数，有以下性质：1、判别式：ac b 42-=∆；求根公式：aacb b x 242-±-=；2、韦达定理：a b x x -=+21，acx x =21；3、二次函数对称轴a b x 2-=，定点坐标（a b 2-，ac b ac 442-）．二、一元二次方程根的0分布方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧.0分布结合判别式，韦达定理以及0处的函数值列不等式，即可求出参数的取值范围。

三、一元二次方程根的k 分布k x k x <<21,k x k x >>21,21x k x <<()0∆>⎧⎩()0∆>⎧⎩0∆>0∆>kkk∆>()0f m⎧> 0∆>⎧题型一 R 上根的分布情况【例1】设k 为实数，若关于x 的一元二次方程210x kx k +++=没有实数根，则k 的取值范围是___.【答案】(222,222-+.【解析】∵关于x 的一元二次方程210x kx k +++=没有实数根∴()2Δ410k k =-+<∴2440k k --<解得：222222k -<<+【变式1-1】关于x 的方程()2210mx m x m +++=有两个不等的实根，则m 的取值范围是（）A ．1,4⎛⎫-+∞ ⎪⎝⎭B ．1,4⎛⎫-∞- ⎪⎝⎭C ．1,4⎡⎤-+∞⎢⎥⎣⎦D ．()1,00,4⎛⎫-+∞ ⎪⎝⎭【答案】D【解析】因为关于x 的方程()2210mx m x m +++=有两个不等的实根0m ≠且>0∆，即：()22214410m m m +-=+>且0m ≠，解得14m >-且0m ≠.故选：D.【变式1-2】关于x 的一元二次方程2310kx x +-=有实根，则k 的取值范围是（） A ．94k ≤- B ．94k ≥-且0k ≠ C ．94k ≥- D ．94k >-且0k ≠【答案】B【解析】由题可知：240k +≥△=3，所以94k ≥-，又因为0k ≠，所以94k ≥-且0k ≠.故选：B.【变式1-3】若关于x 的一元二次方程2(1)0x m x m -+-=有两个不相等的实根，则m 的取值范围为（） A ．()(),232232,-∞---++∞ B ．()322322---+，C ．()(),322322,-∞---++∞ D ．()232232---+，【答案】C【解析】由关于x 的一元二次方程2(1)0x m x m -+-=有两个不相等的实根，所以2(1)40m m ∆=++=，即26+10m m +> 解得：322m >-+或322m <--故选：C.题型二根的“0”分布【例2】若关于x 的方程2210ax ax -+=有两个不同的正根，则实数a 的取值范围是（） A ．()0,1 B ．()0,∞+ C ．()1,+∞ D ．(),0-∞ 【答案】C【解析】因为关于x 的方程2210ax ax -+=有两个不同的正根，所以2044010a a a a ⎧⎪≠⎪∆=->⎨⎪⎪>⎩，解得1a >，故实数a 的取值范围是()1,+∞.故选：C【变式2-1】若一元二次方程2330kx kx k ++-=的两根都是负数，求k 的取值范围为___________. 【答案】125k ≤-【解析】首先0k ≠，设方程2330kx kx k ++-=的两根为12,x x ，则12121200,00x x x x x x +<⎧<<⇔⎨>⎩，所以2Δ94(3)03030k k k kkk k⎧⎪=--≥⎪⎪-<⎨⎪-⎪>⎪⎩，又0k ≠，解得125k ≤-．故答案为：125k ≤-．【变式2-2】已知关于x 的二次方程2(21)210m x mx m +-+-=有一正数根和一负数根，则实数m 的取值范围是_____．【答案】112m -<<【解析】由题意知，二次方程有一正根和一负根，得2101021m m m +≠⎧⎪-⎨<⎪+⎩，解得112m -<<.【变式2-3】一元二次方程24260x mx m -++=有两个不等的非正根，则实数m 的范围为（） A ．30m -<⎪<⎨⎪+≥⎩，解得31m -≤<-，故选：C【变式2-4】若方程()2250x m x m ++++=只有正根，则m 的取值范围是（）A ．4m ≤-或4m ≥B ．54m -<≤-C ．54m -≤≤-D ．52m -<<- 【答案】B【解析】方程()2250x m x m ++++=只有正根，则1（）当()()22450m m ∆=+-+=，即4m =±时，当4m =-时，方程为()210x -=时，1x =，符合题意；当4m =时，方程为()230x +=时，3x =-不符合题意.故4m =-成立；2（）当()()22450m m ∆=+-+>，解得4m <-或4m >，则()()()224502050m m m m ⎧∆=+-+>⎪-+>⎨⎪+>⎩，解得54m -<<-. 综上得54m -<≤-.故选B.题型三根的“k ”分布【例3】已知方程2(2)50x m x m +-+-=有两个不相等的实数根，且两个实数根都大于2，则实数m 的取值范围是（）A ．(5,4)(4,)--+∞B ．(5,)-+∞C ．(5,4)--D ．(4,2)(4,)--+∞ 【答案】C【解析】令()2(2)5m f x m x x =+-+-由题可知：()()()()2Δ02450442222242250520m m m m m m m m m m f >⎧⎧--⨯->><-⎧⎪⎪-⎪⎪>⇒<-⇒<-⎨⎨⎨⎪⎪⎪+-⨯+->>-⎩>⎩⎪⎩或则54m -<<-，即(5,4)m ∈--，故选：C【变式3-1】方程2240x ax -+=的两根均大于1，则实数a 的取值范围是_______ 【答案】5[2,)2【解析】2240x ax -+=的两个根都大于121520Δ4160a a a >⎧⎪∴->⎨⎪=-≥⎩，解得522a ≤<可求得实数a 的取值范围为5[2,)2，故答案为：5[2,)2【变式3-2】若关于x 的方程220x kx -+=的一根大于－1，另一根小于－1，则实数k 的取值范围为______．【答案】(),3-∞-【解析】由题意，关于x 的方程220x kx -+=的一根大于-1，另一根小于-1，设()22f x x kx =-+，根据二次函数的性质，可得()130f k -=+<，解得3k <-，所以实数k 的取值范围为(),3-∞-.【变式3-3】若关于x 的方程20x x a ++=的一个根大于1、另一个根小于1，则实数a 的取值范围为_____. 【答案】(,2)-∞-【解析】关于x 的方程20x x a ++=的一个根大于1、另一个根小于1，令2()f x x x a =++，则()120f a =+<，解得2a <-，题型四根在区间上的分布【例4】关于x 方程2210ax x --=在01x <<内恰有一解，则（） A ．1a <- B ．1a > C ．11a -<< D ．01a <≤ 【答案】B【解析】当0a =时，1(0,1)x =-∉，不合题意；∴0a ≠，令2()21f x ax x =--，有(0)1f =-，(1)2(1)f a =-，要使()f x 在01x <<内恰有一个零点， ∴(0)(1)0f f <即可，则1a >，故选：B【变式4-1】（多选）已知一元二次方程()()21102x m x m Z +++=∈有两个实数根12,x x ，且12013x x <<<<，则m 的值为（）A ．-2B ．-3C ．-4D ．-5【答案】BC【解析】设()()2112f x x m x =+++，由12013x x <<<<，可得()()()()10200110110230193102f fm f m ⎧>⎪⎧>⎪⎪⎪<⇒+++<⎨⎨⎪⎪>⎩⎪+++>⎪⎩，解得：25562m -<<-，又因为m Z ∈，得3m =-或4m =-，故选：BC.【变式4-2】若关于x 的一元二次方程2240x ax -+=有两个实根，且一个实根小于1，另一个实根大于2，则实数a 的取值范围是________．【答案】（52，＋∞）【解析】设2()24f x x ax =-+，由题意2Δ4160(1)1240(2)4440a f a f a ⎧=->⎪=-+<⎨⎪=-+<⎩，解得52a >，故答案为：5(,)2+∞．【变式4-3】已知一元二次方程x 2＋ax ＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a 的取值范围为________．【答案】5(,2)2--【解析】设f (x )＝x 2＋ax ＋1，由题意知(0)10(1)20(2)520f f a f a =>⎧⎪=+<⎨⎪=+>⎩，解得－52<a <－2.【变式4-4】关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内，则实数m 的取值范围是（）A ．13,22⎡⎤⎢⎥⎣⎦ B ．12,23⎛⎤ ⎥⎝⎦ C ．1,22⎡⎫⎪⎢⎣⎭ D ．{12,623⎛⎤⋃- ⎥⎝⎦【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为：()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1)，则需要满足： ①()()010f f ⋅<，()()21320m m --<，解得：1223m <<； ②函数()f x 刚好经过点()0,0或者()1,0，另一个零点属于(0,1)，把点()0,0代入()2(2)21f x x m x m =+-+-，解得：12m =，此时方程为2302x x -=，两根为0，32，而()30,12∉，不合题意，舍去把点()1,0代入()2(2)21f x x m x m =+-+-，解得：23m =，此时方程为23410x x -+=，两根为1，13，而()10,13∈，故符合题意； ③函数与x 轴只有一个交点，横坐标属于(0,1)，()2(2)4210m m ∆=---=，解得6m =±当6m =+2(2)210x m x m +-+-=的根为2- 若6m =-2(2)210x m x m +-+-=2，符合题意综上：实数m 的取值范围为{12,623⎛⎤⋃- ⎥⎝⎦，故选：D【变式4-5】关于x 的一元二次方程2210x kx k ++-=在区间(1,2)-内、外各有一个实数根，则实数k 的取值范围是___________. 【答案】3,04⎛⎤- ⎥⎝⎦【解析】2210x kx k ++-=在区间(1,2)-内、外各有一个实数根，令()221f x x kx k =++-，当1,2x x =-=不是方程的根时，所以()()()24210120k k f f ⎧∆=-->⎪⎨-⋅<⎪⎩，解得：304k -<<；当1x =-是方程的根时，得12100k k k -+-=⇒=，此时方程变为：210x -=，解得：1x =或1x =-，1x =在区间(1,2)-内，1x =-在区间(1,2)-外，符合题意；当2x =是方程的根时，得3422104k k k ++-=⇒=-，此时方程变为：23344210x x ⎛⎫+⨯-= ⎪⎝⎭--，解得：2x =或54x =-，此时方程的两根均在区间(1,2)-外，不符合题意；所以实数k 的取值范围是3,04⎛⎤- ⎥⎝⎦.。

专题一元二次方程根的分布(解析版)

专题04 一元二次方程根的分布二次方程()200ax bx c a ++=≠的根从几何意义上来说就是二次函数()c bx ax x f ++=2与x 轴交点的横坐标，所以研究02=++c bx ax 的实根的情况，可从函数()c bx ax x f ++=2的图象上进行研究.若在()+∞∞-,内研究方程02=++c bx ax 的实根情况，只需考查()c bx ax x f ++=2与x 轴交点的个数以及交点横坐标的符号，根据判别式以及韦达定理，由∆、21x x +、21x x ⋅的值与符号，从而判断出实根的情况.若在区间()n m ,内研究二次方程02=++c bx ax ，则需由二次函数图象与区间关系来确定.知识梳理分布情况两个负根即两根都小于0 ()120,0x x << 两个正根即两根都大于0 ()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（0>a ）知识结模块一：得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩()00<f大致图象（0<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩()00>f综合结论（不讨论）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩()00<⋅f a【例1】已知方程()2210x m x m -++=有两个不等正实根，求实数m 的取值范围．【难度】★★ 【答案】见解析【解析】由典例剖析()()0102200m f ∆>⎧⎪-+⎪->⎨⎪>⎪⎩⇒()218010m m m m ⎧+->⎪>-⎨⎪>⎩⇒330m m m ⎧<->+⎪⎨>⎪⎩⇒03m <<-3m >+即为所求的范围．【例2】若方程05)2(2=-+-+m x m x 的根满足下列条件，分别求出实数m 的取值范围．（1）方程两实根均为正数；（2）方程有一正根一负根．【难度】★★ 【答案】见解析【解析】分析讨论二次方程根的分布，应在二次方程存在实根的条件下进行．代数方法与图象法是研究二次方程根的分布问题的主要方法．解1 （1）由题意，得.45244050)2(0)5(4)2(00022121-≤⇒⎪⎩⎪⎨⎧<<≥-≤⇒⎪⎩⎪⎨⎧>->--≥---⇒⎪⎩⎪⎨⎧>>+≥∆m m m m m m m m m x x x x 或所以，当4-≤m 时，原方程两实根均为正数；（2）由题意，得.5050021>⇒<-⇒⎩⎨⎧<≥∆m m x x所以，当5>m 时，原方程有一正根一负根．解2 二次函数m x m x y -+-+=5)2(2的图象是开口向上的抛物线．（1）如图，由题意，得4052)2(4)2(022050)2(020)0(22-≤⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-+--->-->-⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤->->m m m m m m a b f a b f 。

二次函数图像解题——根的分布

2
其交点横坐标便是方程的解，由图知： k 4时，无解； k = 4或k 3时，有两解； 4 k 3时有四个解； k 3时有三个解.
3
4
y
x
结论：一元二次方程 ax2 bx c 0(a 0) 在区间上的
实根分布问题.
（） 1 一元二次方程有且仅有一个实根属于（m, n）的充要条件是： f (m) f (n) 0. b 2 4ac 0 a f ( m) 0 a f ( n) 0 m b n 2a
(6) x1，x2有且只有一个根在（k1 , k2）内
k1
k2
f (k1 ) f (k2 ) 0
k1
k2
0 或 b k1 k2 2a
k1
k2
f ( k1 ) 0 或 b k1 k2 k1 2a 2
k1
f ( k2 ) 0 或 k1 k2 b 2 2a k2 k2
(2) 一元二次方程两个实根都属于（m, n）的充要条件是：
(3) 一元二次方程两个实根分别在（m, n）两侧的
a f ( m) 0 充要条件是： a f ( n) 0 （4）一元二次方程两个实根分别在（m, n）同一侧的充要条件是：分两类： b 2 4ac 0 （）在（m, n）右侧 a f (n) 0 b n 注：前提 m,n 2a 不是方程（1） b 2 4ac 0 （）在（m, n）左侧 a f (m) 0 b m 2a
不等式组
2 x 变式题：m为何实数值时，关于x的方程 mx (3 m) 0
有两个大于1的根.

高一数学二次函数根的分布专题归类精练

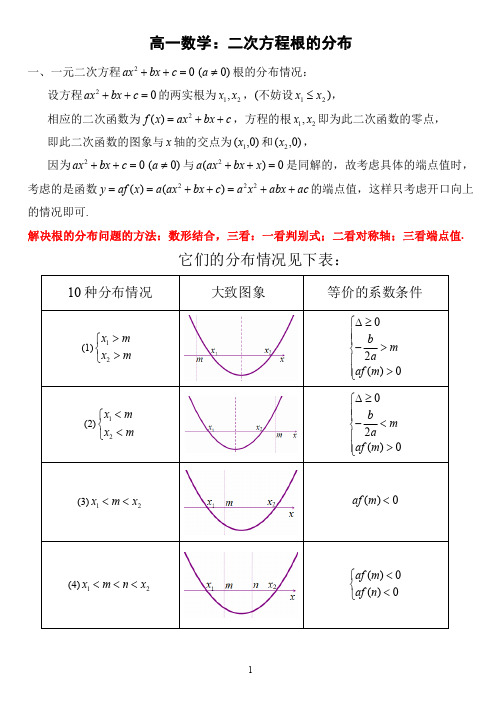
高一数学：二次方程根的分布一、一元二次方程02=++c bx ax )0(≠a 根的分布情况：设方程02=++c bx ax 的两实根为12,x x ，(不妨设21x x ≤)，相应的二次函数为c bx ax x f ++=2)(，方程的根12,x x 即为此二次函数的零点，即此二次函数的图象与x 轴的交点为)0,(1x 和)0,(2x ，因为02=++c bx ax )0(≠a 与0)(2=++x bx ax a 是同解的，故考虑具体的端点值时，考虑的是函数ac abx x a c bx ax a x af y ++=++==222)()(的端点值，这样只考虑开口向上的情况即可.解决根的分布问题的方法：数形结合，三看：一看判别式；二看对称轴；三看端点值.它们的分布情况见下表：如上图，只是可以过两端点，注注2：对于端点值是否可取，最好单独讨论；注3：以上11种情况都有相应的等价形式，对于具体题中的条件，往往是几种情况合在一起的，这时需要分类讨论，此时莫忘注1，注2 .特别注意下列两种情况：一. 函数)(x f 在()n m ,内仅有一个零点，可分：（1）方程0)(=x f 有且只有一根（两根重合时），且这个根在区间()n m ,内，即0∆=，此时由0∆=可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数的值.（2）若()0f m =，可以确定的求出相应的系数（或得到一个关系），从而可以求出另外一根，若这另外的一根在区间()n m ,内，则满足条件；若不在，则这种情况不成立.（3）若()0f n =时，同理.（4）以上三种都讨论完了，只剩下一种情况，即只要0)()(<n f m f 即可.例1：已知624)(2++-=m mx x x f 在区间()3,0-内有且仅有一个零点，求m 的取值范围.解：①当0∆=时，即()2164260m m -+=，得出1m =-或32m =，当1m =-时，根()23,0x =-∈-，即1m =-满足题意；当32m =时，根()33,0x =∉-，故32m =不满足题意； ②当0151462129)3(=+=+++=-m m m f ，解得：1415-=m ，由韦达定理的两根之积为72767156232=+-=+=⨯-m x ，即)0,3(792-∈-=x ，满足条件，故1415-=m 合适； ③当062)0(=+=m f ，解得：3-=m ，由韦达定理的两根之和为12402-==+m x ，即)0,3(122-∉-=x ，不满足条件，故3-=m （舍）；④当0)0()3(<⋅-f f 时，即0)62)(1514(<++m m ，得出14153-<<-m ，必满足条件. 综上所述所求m 的取值范围是：14153-≤<-m ，或1m =-. 注：你能发现这个题的巧解吗？二. 函数)(x f 在],[n m 内仅有一个零点，可同上分析.即先讨论0=∆（即方程两根重合）时的情况，验证相应的根是否合适；再看取到端点值时的情况，此时已知一根，由韦达定理易得另一根，验证是否满足条件；最后0)()(<n f m f 即可！熟练之后，此次序可以灵活变通，只是请注意分类要不重不漏！例2：已知624)(2++-=m mx x x f 在区间]0,3[-内有且仅有一个零点，求m 的取值范围. 解：①当0∆=时，即()2164260m m -+=，得出1m =-或32m =，当1m =-时，根]0,3[2-∈-=x ，即1m =-满足题意；当32m =时，根]0,3[3-∉=x ，故32m =不满足题意； ②当0151462129)3(=+=+++=-m m m f ，解得：1415-=m ，由韦达定理的两根之积为72767156232=+-=+=⨯-m x ，即)0,3(792-∈-=x ，不满足条件，故1415-=m （舍）；③当062)0(=+=m f ，解得：3-=m ，由韦达定理的两根之和为12402-==+m x ，即)0,3(122-∉-=x ，满足条件，故3-=m 合适；④当0)0()3(<⋅-f f 时，即0)62)(1514(<++m m ，得出14153-<<-m ，必满足条件. 综上所述所求m 的取值范围是：14153-<≤-m ，或1m =-. 注：你能发现这个题的巧解吗？注：讨论端点时，如果遇到下列情况，前参看下列题的处理办法！例3：已知方程02)2(2=++-x m mx 在区间()1,3上有一根，求m 的取值范围. 解：当0=m 时，易知方程仅有一个根为1，不满足条件当0≠m 时，令2)2()(2++-=x m mx x f ，因为()10f =，所以()()()22212mx m x x mx -++=--，故另一根为2m，由213m <<，得223m <<即为所求. 例4：已知方程02)2(2=++-x m mx 在区间]3,1[上有一根，求m 的取值范围. 解：当0=m 时，易知方程仅有一个根为1，满足条件；当0≠m 时，令)2)(1(2)2()(2--=++-=mx x x m mx x f ，必有一根为1 故另一根2m ，当12=m，即2=m 时合适；否则必须满足：12<m 或32>m ，解得：0<m ，或320<<m ，或2>m综上所述，所求m 的取值范围是32<m 或2≥m .注：你能发现这两个题的巧解吗？以后再赘述吧，先抱歉了！二．根的分布经典题归类讲解例1、①m 取何实数值时，方程0)1(22=++-m x m x 有两个不等正实根.②m 取何实数值时，方程013422=-++m mx x 有两个负数根.③m 取何实数值时，关于x 的方程05)2(2=-+-+m x m x 的两个实根都大于2. 解：①令=)(x f m x m x ++-)1(22，其图像开口向上，对称轴为41+=m x ，判别式为168)1(22+-=-+=∆m m m m原条件⎪⎪⎩⎪⎪⎨⎧>=>+>+-=∆⇔0)0(0410162m f m m m 解得：2230-<<m 或223+>m ，即为所求.②令=)(x f 13422-++m mx x ，其图像开口向上，对称轴为m x -=，判别式为)1)(21(16)2123(16)13(81622--=+-=--=∆m m m m m m . 原条件⎪⎪⎩⎪⎪⎨⎧>-=<-≥--=∆⇔013)0(00)1)(21(16m f m m m 解得：2131≤<m 或1≥m ，即为所求.③令=)(x f m x m x -+-+5)2(2，其图像开口向上，对称轴为21m x -=，判别式为)4)(4(16)5(4)2(22-+=-=---=∆m m m m m .原条件⎪⎪⎩⎪⎪⎨⎧>+=-+-+=>-≥-+=∆⇔055424)2(2210)4)(4(m m m f m m m 解得：45-≤<-m ，即为所求.例2、①已知二次方程012)12(2=-+-+m mx x m 有一正根和一负根，求实数m 的取值范围.②已知二次函数33)42()2(2+++-+=m x m x m y 与x 轴有两个交点，一个在1=x 的左侧，一个在1=x 的右侧，求实数m 的取值范围.③m 取何实数值时，关于x 的方程05)2(2=-+-+m x m x 的一个实根大于2，另一个实根小于2.解：①令=)(x f 12)12(2-+-+m mx x m ，其图像开口方向不明，原条件0)1)(12()0()12(<-+=+⇔m f m ，解得：21->m . 即为所求. 注：利用两个之积012121<+-=m x x ，也可以快速得出！②令=)(x f 33)42()2(2+++-+m x m x m ，其图像开口方向不明，原条件0)12)(2()33422)(2()1()2(<++=++--++=+⇔m m m m m m f m ，解得：212-<<-m . 即为所求. 注：利用0)1)(1(21<--x x ，即021212422331)(2121<++=+++-++=++-m m m m m m x x x x 也可得.③令=)(x f m x m x -+-+5)2(2，其图像开口向上，原条件055424)2(<+=-+-+=⇔m m m f 解得：5-<m ，即为所求.注：利用0)2)(2(21<--x x ，即054)2(254)(22121<+=+---=++-m m m x x x x 也可得. 例3．①已知关于x 的方程：022=+-a ax x 有两个实根βα,，且满足2,10><<βα，求实数a 的取值范围．②已知关于x 的方程：062)1(22=-++--m m mx x m 有两个实根βα,，且满足βα<<<10，求实数m 的取值范围．③已知关于x 的方程：0532=+-a x x 有两个实根βα,，且满足)3,1(),0,2(∈-∈βα，求实数a 的取值范围．解：①令=)(x f a ax x +-22，其图像开口向上，画图可得：原条件⎪⎩⎪⎨⎧<-=<-=>=⇔034)2(01)1(0)0(a f a f a f 解得：34>a ，即为所求.②令=)(x f 62)1(22-++--m m mx x m ，其图像开口方向不明，画图可得：原条件⎩⎨⎧<->-⇔0)1()1(0)0()1(f m f m ，即⎪⎩⎪⎨⎧<-++--->-+-⇔0)621)(1(0)6)(1(22m m m m m m m m即⎩⎨⎧<+-->+--⇔0)7)(7)(1(0)3)(2)(1(m m m m m m 解得：73-<<-m 或72<<m ，即为所求.③令=)(x f a x x +-532，其图像开口向上，画图可得：原条件⎪⎪⎩⎪⎪⎨⎧>+=+-=<-=+-=<=>+=++=-⇔0121527)3(022)1(0)0(0221012)2(a a f a a f a f a a f 解得：012<<-a ，即为所求.例4、①已知方程03222=+++m mx x 的两个不等实根都在区间)2,0(内，求实数m 的取值范围.②已知方程03222=+++m mx x 的两个不等实根都在区间]2,0[之外，求实数m 的取值范围. 解：令322)(2+++=m mx x x f ，其图像开口向上，对称轴为m x -=，由判别式0)3)(1(4)32(4)32(4422>-+=--=+-=∆m m m m m m ，得：1-<m 或3>m①的条件⎪⎪⎩⎪⎪⎨⎧>+=>+=<-<>∆⇔076)2(032)0(200m f m f m ，即⎪⎪⎪⎩⎪⎪⎪⎨⎧->-><<->-<⇔67230231m m m m m 或解得：167-<<-m 即为所求.②的条件可分为：两根都小于0，或两根都大于2，或一根小于0，一根大于2，三种情况故⎪⎩⎪⎨⎧>+=<->∆⇔032)0(00m f m 或⎪⎩⎪⎨⎧>+=>->∆076)2(20m f m 或⎩⎨⎧<+=<+=076)2(032)0(m f m f解得：3>m ，或无解，或23-<m ，故所求m 的取值范围是：23-<m 或3>m . 例5：已知集合}0107|{2≤+-=x x x A ，}05)2(|{2≤-+--=m x m x x B ，且A B ⊆，求实数m 的取值范围.解：首先}52|{≤≤=x x A ；当∅=B 时，即不等式05)2(2≤-+--m x m x 无解，即0)5(4)2(2<---=∆m m 即：0162<-m ，解得：44<<-m ； -----（1）当∅≠B 时，即不等式05)2(2≤-+--m x m x 有解，其形式必为21x x x ≤≤；其中21,x x 为方程05)2(2=-+--m x m x 的两个根，（不妨设21x x ≤）按条件，只要5221≤≤≤x x 即可满足A B ⊆；按照根的分布的理论，此时只要满足：⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-+--=≥-+--=≤-≤≥-=∆05)2(525)5(05)2(24)2(52220162m m f m m f m m即⎪⎪⎩⎪⎪⎨⎧-≥-≥-≤≤-≥-≤55284,4m m m m m 或，解得：45-≤≤-m ，-----（2）由（1）（2）可得：所求的m 的取值范围是45≤≤-m .三．自己练习巩固提升1．设有一元二次方程02)1(22=++-+m x m x ．试问：(1)m 为何值时，有一正根、一负根．(2)m 为何值时，有一根大于1、另一根小于1． (3)m 为何值时，有两正根． (4)m 为何值时，有两负根．(5)m 为何值时，仅有一根在[1，4]内.2. 关于x 的方程012=-++a ax x 有异号的两个实根，求a 的取值范围.3.如果方程032)3(22=-+++a x a x 的两个实根中一根大于3,另一根小于3，求实数a 的取值范围. 4.若方程07)1(82=-+++m x m x 有两个负根，求实数a 的取值范围. 5. 关于x 的方程0422=-+-a ax x 有两个正根，求a 的取值范围.6.设关于x 的方程0)(44222=+++-n m x n m x 有一个实根大于-1，另一个实根小于-1，则n m ,必须满足什么关系.7. 设关于x 的方程023222=---k x kx 有两个实根都在]0,2[-之间，求k 的取值范围.8.关于x 的方程02)13(72=--+-m x m x 的两个实根21,x x 满足2021<<<x x ，求m 的范围. 9.①已知方程065)9(222=+-+-+a a x a x 的一根小于0，另一根大于2，求实数a 的取值范围.②已知方程065)9(222=+-+-+a a x a x 的存在小于2的根，求实数a 的取值范围.。

淡谈方程根的分布问题

浅谈方程根的分布问题瑞丽一中杨世泽一元二次不等式是高中数学中极其重要的内容，这段内容与一元二次方程、二次函数等内容有着直接而密切的联系，老师讲解一元二次不等式时，不能不涉及一元二次方程根的分布。

尽管这段内容现被列为了选学内容，但它是老师进行数形结合教学，培养学生分类讨论思想的良好素材。

因此老师不仅要讲解这段内容，而且还要达到一定的深度，使学生对这段内容有一个较为全面透彻的理解。

学生要学好一元二次方程根的分布，首先应掌握好一元一次方程根的分布。

一、一元一次方程根的分布问题研究一元一次方程在指定区间上的根的问题有以下二种常见解法。

1、求根→列出相关的不等式组→解不等式组2、利用数形结合列出不等式例1、关于x 的方程01=+kx 的根在（１，２）内，求k 的取值范围。

解：法一：原方程的根为kx 1-=得，211<-<k⇒211->>-k ⇒211-<<-k∴实数k 的取值范围是{}211-<<-k k法二：设1)(+=kx x f ，利用数形结合，因方程01=+kx 的根在（１，２）内，则1)1(+=k f 、12)2(+=k f 的值必一正一负，得0)12)(1(<++k k ⇒211-<<-k∴实数k 的取值范围是{}211-<<-k k二、一元二次方程根的分布问题一元二次方程在指定区间上的实根分布问题有以下三类常见解法。

第一类：求根→列出相关的不等式组→解不等式组。

此方法一般用于方程的根可用十字相乘法求出的题。

例2、方程()001222>=-+-m ，m x x 的两根在（-2，3）内，求m 的取值范围。

解：原方程可化为()()110,(0)x m x m m --⋅-+=>⎡⎤⎡⎤⎣⎦⎣⎦x∴原方程的两根为：m x -=11，21x m =+，得0213213m m m >⎧⎪-<-<⎨⎪-<+<⎩解得20<<m ∴实数m 的取值范围是{}02m m <<第二类：利用根与系数的关系及符号法则列出不等式组。

二次方程根的分布情况归纳(完整版)

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200axbx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）k k k根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

如方程()2220mx m x -++=在区间()1,3上有一根，因为()10f =，所以()()()22212mx m x x mx -++=--，另一根为2m，由213m <<得223m <<即为所求； 2︒ 方程有且只有一根，且这个根在区间()n m ,内，即0∆=，此时由0∆=可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数。

如方程24260x mx m -++=有且一根在区间()3,0-内，求m的取值范围。

分析：①由()()300f f -<即()()141530m m ++<得出15314m -<<-；②由∆=即()2164260m m -+=得出1m =-或32m =，当1m =-时，根()23,0x =-∈-，即1m =-满足题意；当32m =时，根()33,0x =∉-，故32m =不满足题意；综上分析，得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根，求实数m 的取值范围。

四阶方程根的分布

四阶方程根的分布一、引言四阶方程是数学领域中一类重要的多项式方程，其在科学研究、工程设计及日常生活等多个方面有着广泛的应用。

四阶方程的根分布问题，即求解方程在复平面上的根的位置，一直是数学家们关注的重点。

本文将详细探讨四阶方程根的分布及其相关性质。

二、四阶方程的基本概念四阶方程是指最高次数为四的多项式方程，一般形式为：a_4x^4 + a_3x^3 + a_2x^2 + a_1x + a_0 = 0其中，a_4, a_3, a_2, a_1, a_0 为常数，且a_4 ≠0。

该方程的根可以是实数，也可以是复数。

三、四阶方程的根的分布1. 根的个数：根据代数基本定理，四阶方程在复数域内有且仅有四个根（包括重根）。

2. 实根与复根：四阶方程的根可以是实数或复数。

当方程的系数均为实数时，其复根必成对出现，即若z 是方程的根，则其共轭复数ȳ也是方程的根。

3. 根的位置：四阶方程的根在复平面上的位置是不确定的，与方程的系数密切相关。

通过求解方程，可以确定根的具体位置。

四、四阶方程根的性质1. 根的和与积：对于四阶方程，其根的和等于-a_3/a_4，根的积等于a_0/a_4。

2. 根的稳定性：在动态系统等领域中，四阶方程的根的稳定性是一个重要问题。

当所有根的实部均为负时，系统被认为是稳定的；否则，系统可能不稳定。

3. 根的对称性：在某些特殊情况下，四阶方程的根可能具有对称性。

例如，当方程系数满足一定条件时，其根可能在复平面上呈现出对称分布。

五、求解四阶方程的方法求解四阶方程的方法主要包括：1. 公式法：对于一般的四阶方程，由于其求解公式较为复杂且不易记忆，实际应用中较少使用。

但在特定情况下（如系数满足某些关系时），可以利用公式直接求解。

2. 数值法：利用数值计算方法（如牛顿法、迭代法等）可以求解四阶方程的近似根。

这种方法适用于无法获得精确解或对方程的解有较高精度要求的情况。

3. 图形法：通过绘制四阶方程的图像（如函数图像、极坐标图像等），可以直观地观察根的分布情况。

(解析版)二次不等式与二次方程根的分布问题考点串讲+重点剖析

专题04 二次不等式与二次方程根的分布问题一、知识梳理1.三个“二次”间的关系判别式Δ＝b2－4acΔ＞0Δ＝0Δ＜0 二次函数y＝ax2＋bx＋c(a＞0)的图象一元二次方程ax2＋bx＋c＝0 (a＞0)的根有两相异实根x1，x2(x1＜x2)有两相等实根x1＝x2＝－b2a没有实数根ax2＋bx＋c＞0❶(a＞0)的解集{x|x＜x1或x＞x2}⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x⎪⎪⎪x≠－b2aRax2＋bx＋c＜0(a＞0)的解集{x|x1＜x＜x2}∅∅不等式解集a＜b a＝b a＞b(x－a)·(x－b)＞0{x|x＜a或x＞b}{x|x≠a}{x|x＞a或x＜b}(x－a)·(x－b)＜0{x|a＜x＜b}∅{x|b＜x＜a}3.二次方程ax2+bx+c=0的根的分布问题的策略策略一:构造相应的二次函数y=ax2+bx+c,，根据题意画出图象，然后以下三个方面：（1）判别式△的符号，（2）对称轴x=－b2a与所给区间的位置关系，（3）区间端点处的函数值的符号.列出相应的不等式（组）；策略二：分离参数法，运用函数思想求解；策略三：用求根公式求出两根加以限制；策略四：灵活运用韦达定理建立不等式组.其中策略三和策略四的运算量较大或技巧太高不便于操作，我们习惯用策略一与策略二处理此类问题.二、例题讲解考点一解不等式问题例1求下列关于x的不等式的解集:（Ⅰ）x2−4x−5<0,(Ⅱ) 3−4x −x 2<0,（Ⅲ）2ax 2−(a −2)x −1<0分析：二次不等式的求解是高中数学的运算基石，我们要能在准确求解二次方程的基础上，结合二次函数的图象快速写出不等式的解. 【解析】（Ⅰ）x 2−2x −3<0, 不等式可化为：(x +1)(x −3)<0，我们不难看出其对应的方程的根为-1和3，对应的二次函数开口向上，在草稿纸上画出草图当−1<x <3时，函数值为负数，即不等式x 2−2x −3<0的解集为（−1，3）. (Ⅱ) 3−2x −x 2<0,不等式可化为：(1−x )(3+x )<0，我们不难看出其对应的方程的根为-3和1，对应的二次函数开口向下，在草稿纸上画出草图当x <−3,或x >1时，函数值为负数，即不等式 3−2x −x 2<0的解集为(−∞，−3)∪（1，+∞）. （Ⅲ）2ax 2−(a −2)x −1<0不等式可化为：(2x −1)(ax +1)<0，⑴ 当0a =时，不等式化为210x -<，解得：12x <⑵ 当0a >时，由于112a -<，所以112x a -<<； ⑶ 当0a <时，①当2a =-时，得：()2210x ->，所以12x ≠ ②当20a -<<时，这时112a -<，解得：1x a <-，或12x >；③当2a <-时，这时112a ->，解得：12x <，或1x a>-.综上可得：当0a >时，不等式的解集为112a ⎛⎫- ⎪⎝⎭，；当0a =时，不等式的解集为1,2⎛⎫-∞ ⎪⎝⎭；当20a -<<时，不等式的解集为11,+2a ⎛⎫⎛⎫-∞-∞ ⎪ ⎪⎝⎭⎝⎭，；当2a =-时，不等式的解集为11,+22⎛⎫⎛⎫-∞∞ ⎪⎪⎝⎭⎝⎭，；当2a <-时，不等式的解集为11,+2a ⎛⎫⎛⎫-∞-∞ ⎪⎪⎝⎭⎝⎭，. 点评：从函数观点理解方程和不等式是数学的一种常用的基本思想方法，高中许多问题的解决都依赖于一元二次不等式及一元二次方程，解二次不等式在整个高中学习中具有很强的基础性作用，是一个重要工具.因此我们通过梳理知识达到知识整合、模块系统化、方法简洁化的目的. 针对练习一1．【2019年高考全国Ⅰ卷理数】已知集合2|42{|60}{},M x x N x x x =-<<=--<，则M N =A ．}{43x x -<0}，B ={x |x –1<0}，则A ∩B =A ．(–∞，1)B ．(–2，1)C ．(–3，–1)D ．(3，+∞)【答案】A【解析】由题意得，2{560|}{2|A x x x x x =-+><=或3}x >，{10}{1|}|B x x x x =-<=<，则{|1}(,1)A B x x =<=-∞．故选A ．3．【2019年高考全国Ⅲ卷理数】已知集合2{1,0,1,2},{|1}A B x x =-=≤，则A B =A ．{}1,0,1-B ．{}0,1C ．{}1,1-D ．{}0,1,2【答案】A【解析】∵21,x ≤∴11x -≤≤，∴{}11B x x =-≤≤，又{1,0,1,2}A =-，∴{}1,0,1A B =-.故选A ．4.(高二高三)【2019年高考天津理数】设x ∈R ，则“250x x -<”是“|1|1x -<”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件【答案】B【解析】由250x x -<可得05x <<，由|1|1x -<可得02x <<，易知由05x <<推不出02x <<，由02x <<能推出05x <<，故05x <<是02x <<的必要而不充分条件，即“250x x -<”是“|1|1x -<”的必要而不充分条件. 故选B.5.若m ，n ∈R 且m +n >0，则关于x 的不等式(m −x)(n +x)>0的解集为( )A. {x|x <−n 或x >m}B. {x|−n <x <m}C. {x|−m <x <n}D. {x|x <−m 或x >n} 【答案】B【解析】因为(m −x)(n +x)>0，所以(x −m)(n +x)<0，因为m +n >0，所以m >−n ，则(x −m)(n +x)<0的解集为{x|−n <x <m}，故选B ． 6. 不等式x －3x －1≤0的解集为( ) A ．{x |x ＜1或x ≥3} B ．{x |1≤x ≤3} C ．{x |1＜x ≤3} D ．{x |1＜x ＜3}【答案】C【解析】由x －3x －1≤0，得⎩⎪⎨⎪⎧x －3x －1≤0，x －1≠0，解得1＜x ≤3.故选C 项．7.求关于x 的不等式2ax 2+(a −2)x −1>0的解集.【解析】不等式可化为：(2x +1)(ax −1)>0，（1）当0a =时，不等式化为210x -<，解得：12x <-（2）当0a >时，由于112a >-，所以112x x a<->,或；（3）当0a <时，①当2a =-时，得：()22+10x <，无解，②当20a -<<时，这时112a<-，解得：112x a <<-； ③当2a <-时，这时112a >-，解得：112x a-<<. 综上可得：不等式的解集：当0a >时，为11,+2a ⎛⎫⎛⎫-∞-∞ ⎪ ⎪⎝⎭⎝⎭，；当0a =时，为1,2⎛⎫-∞-⎪⎝⎭；当20a -<<时，为112a ⎛⎫- ⎪⎝⎭，；当2a =-时，为∅；当2a <-时，为112a ⎛⎫- ⎪⎝⎭，.8.（高二高三用）求函数f (x )=[2ax 2−(3a +2)x +(3a +1)]e x 的增区间. 【解析】f′(x)=[ 2ax 2+(a −2)x −1] e x =(2x +1)(ax −1)e x由5题可知：当0a >时，f (x )的增区间为11,+2a ⎛⎫⎛⎫-∞-∞ ⎪ ⎪⎝⎭⎝⎭，，；当0a =时，f (x )的增区间为为1,2⎛⎫-∞-⎪⎝⎭；当20a -<<时，f (x )的增区间为为112a⎛⎫- ⎪⎝⎭，；当2a =-时，f (x )的无增区间；当2a <-时，f (x )的增区间为为112a ⎛⎫- ⎪⎝⎭，.考点二三个“二次”的联系例2 关于x 的不等式ax 2+bx +c >0的解集为(−∞,−2)∪(−1,+∞)，则不等式 cx 2+bx +a <0的解集为___________________.分析：本题主要考查已知一元二次不等式的解集的端点值就是相应方程的方程的根这一关系，结合韦达定理可求出参数的值.【解析】∵关于x 的不等式ax 2+bx +c >0的解集为(−∞,−2)∪(−1,+∞)， ∴ax 2+bx +c =0的两个根为−2，−1，且a >0， ∴由韦达定理，得{−2−1=−ba−2×(−1)=c a ，解得{b =3a c =2a，∴cx 2+bx +a <0，可化为2ax 2+3ax +a <0,即2x 2+3x +1<0， ∴(2x +1)(x +1)<0， ∴−1<x <−12，∴原不等式解集为：（−1，−12）.点评;一元二次方程ax 2+bx +c =0，二次函数y =ax 2+bx +c 与二次不等式ax 2+bx +c >0关系密切，二次函数是核心.二次函数的零点是对应方程的根，是对应的二次不等式的解集端点. 针对练习二1.关于x 的不等式ax −b >0的解集是(−∞,−1)，则关于x 的不等式(ax +b)(x +3)>0的解集为_________. 【答案】(−3,1)【解析】由ax −b >0的解集为(−∞,−1)，可知a <0且ba =−1．令(ax +b )(x −3)=0，解得x 1=1，x 2=−3． ∵a <0，∴(ax +b)(x +3)>0的解集为(−3,1).2.已知关于x 的不等式ax 2−x +c <0的解集为{x|−2<x <1}，则a +c 等于( )A. −1B. 1C. −3D. 3 【答案】B【解析】根据题意知a ≠0，且−2，1是方程ax 2−x +c =0的两实根； ∴将x =1带入方程得a +c −1=0； ∴a +c =1．故选B ．3.关于x 的不等式ax 2+bx +c >0的解集为(1，3)，则 bx 2−cx +a <0的解集为___________________. 【答案】（−1，14）【解析】∵关于x 的不等式ax 2+bx +c >0的解集为(1，3)，∴ax 2+bx +c =0的两个根为1，3，且a <0， ∴由韦达定理，得{−b a =1+3=4c a =3，解得{b =−4ac =3a，∴ bx 2−cx +a <0，可化为-4ax 2−3ax +a <0,即4x 2+3x −1<0， ∴(4x −1)(x +1)<0， ∴−1<x <−14，∴原不等式解集为：（−1，14）.4. 若关于x 的不等式x−a b x−b b >0(a,b ∈R)的解集为(－∞，1)∪(4，＋∞)，则a +b ＝_____，ab ＝____.【答案】5 4【解析】若关于x 的不等式x−a bx−b b >0(a,b ∈R)的解集为(－∞，1)∪(4，＋∞)，则a ＝1，b ＝4或a ＝4，b ＝1，则a ＋b ＝5，ab ＝4.5.已知不等式ax 2+5x −2>0的解集是M ．(1)若2∈M ，求a 的取值范围;(2)若M ={x|12<x <2}，求不等式ax 2−5x +a 2−1>0的解集．【解析】(1)∵2∈M ， ∴a ×22+5×2−2>0，解得a >−2．∴a 的取值范围为(−2,+∞). (2)∵M ={x|12<x <2}，∴12，2是方程ax 2+5x −2=0的两个根， ∴{12+2=−5a 12×2=−2a，解得a =−2．∴不等式ax 2−5x +a 2−1>0可化为−2x 2−5x +3>0，其解集为{x|−3<x <12}.考点三二次方程根的分布问题例3 （1）若方程4x 2−4ax +a 2−2a +2=0在区间[0,2]上有两根不等实根，则实数a 的取值范围是( ) A. (1,5−√7] B. (1,5−√7) C. (1,5+√7] D. (1,5+√7)（2）方程x 2−4x +a =0的一个跟比1大，另一个比1小，则实数a 的范围为____________________. （1）【答案】A. 【解析】由题意，令f(x)=4x 2−4ax +a 2−2a +2，则f(x)区间[0,2]上有两个零点，则{△=16a 2−16(a 2−2a +2)>00<a 2<2f (0)=a 2−2a +2≥0f (2)=a 2−10a +18≥0，即{a >10<a <4a ∈Ra ≤5−√7或a ≥5+√7解得1<a ≤5−√7，故选A ．（2）【答案】 a <3【解析】令f(x)=x 2−4x +a ，则f(x)有两个零点分别在1的两侧，则f (1)=1−4+a <0,即：a <3. 点评：二次方程的根的分布求参数范围问题常构造相应的二次函数，画出正确的图象列出从以下三方面列出不等式(组)：（1）判别式△的符号，（2）对称轴x=－b2a与所给区间的位置关系，（3）区间端点处的函数值的符号.列出相应的不等式（组），有时只需部分就可，如方程x 2−4x +a =0的一个跟比2大，另一个比2小，求a 的范围，令f(x)=x 2−4x +a 只需f (x )=4−8+a <0即可求出a <4.例4 方程x 2＋ax －2＝0在区间[1,5]上有根，则实数a 的取值范围为_________. 【答案】−235≤a ≤1.【解析】方法一由题意，令f (x )=x 2+ax −2，（1）方程区间[1,5]上恰好有两个实根，则{ f (1)≥0f(5)≥01<−a 2<5f(−a 2)<0，即{1+a −2≥025+5a −2≥01<−a 2<5(−a2)2+a(−a 2)−2<0, { a ≥1a ≥−235−10<a <−2a ∈R ，不等式组无解.(2) 方程区间[1,5]上恰好有一个实根，则{f (1)≤0f(5)≥0，即{1+a −2≤025+5a −2≥0, 解得:−235≤a ≤1，综上可知：−235≤a ≤1.方法二由于x ∈[1,5]，所以方程x 2＋ax －2＝0可化为a =−x +2x ,令g (x )=−x +2x ,显然g (x )为[1,5]上的减函数，所以g (5)≤g (x )≤g (1)，又g (5)=−235，g (1)=1，所以−235≤g (x )≤1，，即−235≤a ≤1.点评：当二次方程在某区间的解的个数确定时，解法一比较简单，当二次方程在某区间内有解，而解的个数不定时，常运用分离参数法解法二比较简单.针对练习三1．已知函数f(x)=x 2−kx −6的两个零点均在区间(−3,4)内，则k 的取值范围是( ) A. (−1,8)B. [−1,52] C. (−∞,−1)∪(52,+∞) D. (−1,52)【答案】D【解析】函数f(x)=x 2−kx −6图像的对称轴为直线x =k2．若f(x)的两个零点均在区间(−3,4)内，必有{△≥0−3<k 2<4f (−3)>0f (4)>0，即{−3<k 2<49+3k −6>016−4k −6>0,可得−1<k <52，即k 的取值范围是(−1,52).故选D ．2.若关于x 的方程x 2+2(a −1)x +2a +6=0有两个实根，且两根都在区间(1,+∞)内, 求实数a 的范围. 【解析】令f(x)=x 2+2(a −1)x +2a +6，由题意可得：{△=4(a −1)2−4(2a +6)≥01−a >1f (1)=1+2(a −1)+2a +6>0，即{(a +1)(a −5)≥0a <0a >−54,{a ≥5或a ≤−1a <0a >−54所以−54<a ≤−1.3. 已知a 是实数，函数f (x )=−x 2+ax −3在区间(0,1)与(2,4)上各有一个零点，求a 的取值范围．【解析】令f (x )=−x 2+ax −3，由题意可得：{f (0)=−3<0f (1)=a −4>0f (2)=2a −7>0f (4)=4a −19<0必有,{a >4a >72a <194所以4< a <194. 所以−54<a ≤−1.4. （高二高三用）函数f (x )=x 3+ax 2+(a +6)x +1在区间(-2，2)上既有最大值又有最小值，求a 的取值范围．【解析】函数f (x )=x 3+ax 2+(a +6)x +1在区间(-2，2) 上既有最大值又有最小值，即函数f (x )=x 3+ax 2+(a +6)x +1在区间(-2，2) 上既有极大值又有极小值，所以 f ′(x )=3x 2−2ax +a +6=0在区间(−2，2) 上有两个不等的实根，{ △=4a 2−4×3(a +6)>0−2<−a 3<2 f ′(−2)=−3a +18>0f ′(2)=5a +18>0解得：−185<a <−3.考点四不等式恒问题例5 （Ⅰ）关于x 的不等式kx 2+3kx +k −2≤0对任意x ∈R 恒成立，则实数k 的取值范围是( ) A. {k|−45≤k <0} B. {k|−85≤k <0} C. {k|−45≤k ≤0}D. {k|−85≤k ≤0}（Ⅱ）当x ∈(1,2)时，不等式x 2+mx +4<0恒成立，则m 的取值范围是( )A. (−∞,−4]B.C. (−∞,−5]D. (−5,−4)（Ⅲ）已知a ∈[－1,1]时不等式x 2＋(a －4)x ＋4－2a ＞0恒成立，则x 的取值范围为( ) A ．(－∞，2)∪(3，＋∞) B ．(－∞，1)∪(2，＋∞) C ．(－∞，1)∪(3，＋∞) D ．(1,3)（Ⅰ）【答案】D【解析】当k =0时，不等式恒成立，符合题意;当k ≠0时，需满足k <0且9k 2−4k(k −2)=5k 2+8k ≤0，所以−85≤k <0．综上，实数k 的取值范围是{k|−85≤k ≤0}．故选D ．（Ⅱ）【答案】C【解析】解法一由不等式x 2+mx +4<0，得，因为x ∈(1,2)，所以，即，令y =x +4x ，则该函数在(1,2)上单调递减，所以值域为(4,5)，所以z =−(x +4x )的值域为(−5,−4)，其最小值无限逼近−5，但不会等于−5，要使在(1,2)上恒成立，需要m 小于z =−(x +4x )的最小值，故m ≤−5，故答案为C ．解法二令f (x )=x 2+mx +4<0对x ∈(1,2)恒成立，只需{ f (1)=m +5≤0f (2)=2m +8≤0解得：{m ≤−5m ≤−4,所以m ≤−5. （Ⅲ）【答案】C【解析】把不等式的左端看成关于a 的一次函数，记 f (a )＝(x －2)a ＋x 2－4x ＋4，则由f (a )＞0对于任意的a ∈[－1,1]恒成立，得f (－1)＝x 2－5x ＋6＞0，且f (1)＝x 2－3x ＋2＞0即可，解不等式组⎩⎪⎨⎪⎧ x 2－5x ＋6＞0，x 2－3x ＋2＞0，得x ＜1或x ＞3.故选C 项．不等式恒成立问题的求解方法(1)x ∈R 的不等式确定参数的范围时，结合二次函数的图象，利用判别式来求解．如果二次项系数含有参数，注意验证为0时是否符合题意.(2)x ∈[a ，b ]的不等式确定参数的范围时，①根据函数的单调性，求其最值，让最值大于等于或小于等于0，从而求出参数的范围；②数形结合，利用二次函数在端点a ，b 处的取值特点确定不等式，从而求出参数的范围．(3)已知参数m ∈[a ，b ]的不等式确定x 的范围，要注意变换主元，一般地，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．针对练习四1.若不等式x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，则实数a 的取值范围是( )A ．[－1,4]B ．(－∞，－2]∪[5，＋∞)C ．(－∞，－1]∪[4，＋∞)D ．[－2,5] 【答案】A【解析】由于x 2－2x ＋5＝(x －1)2＋4的最小值为4，所以x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，只需a 2－3a ≤4，解得－1≤a ≤4.故选A.2.已知函数f (x )＝x 2＋mx －1，若对于任意x ∈[m ，m ＋1]，都有f (x )<0成立，则实数m 的取值范围是________.【答案】⎝ ⎛⎭⎪⎫－22，0 【解析】二次函数f (x )对于任意x ∈[m ，m ＋1]，都有f (x )<0成立，则{f (m )<0f (m +1)<0解得－22<m <0. 3.若不等式x 2＋ax ＋4≥0对一切x ∈(0,1]恒成立，则a 的取值范围为________.【答案】[－5，＋∞)【解析】由题意，分离参数后得a ≥－⎝ ⎛⎭⎪⎫x ＋4x .设f (x )＝－⎝ ⎛⎭⎪⎫x ＋4x ，x ∈(0,1]，则只要a ≥f (x )max 即可．由于函数 f (x )在区间(0,1]上单调递增，所以f (x )max ＝f (1)＝－5，故a ≥－5.4.若对任意实数p ∈[－1,1]，不等式px 2＋(p －3)x －3>0成立，则实数x 的取值范围为________.【答案】(－3，－1)【解析】不等式可变形为(x 2＋x )p －3x －3＞0，令f (p )＝(x 2＋x )·p －3x －3，p ∈[－1,1]．原不等式成立等价于f (p )＞0，p ∈[－1,1]，则{f(−1)>0f(1)>0即⎩⎪⎨⎪⎧ －x 2－x －3x －3＞0，x 2＋x －3x －3＞0，解得－3＜x ＜－1. 5．设函数f (x )＝mx 2－mx －1.若对于x ∈[1,3]，f (x )<－m ＋5恒成立，求m 的取值范围.【解析】要使f (x )<－m ＋5在x ∈[1,3]上恒成立，即m ⎝ ⎛⎭⎪⎫x －122＋34m －6<0在x ∈[1,3]上恒成立. 令g (x )＝m ⎝ ⎛⎭⎪⎫x －122＋34m －6，x ∈[1,3]. 当m >0时，g (x )在[1,3]上是增函数，所以g (x )max ＝g (3)⇒7m －6<0，所以m <67，所以0<m <67；当m ＝0时，－6<0恒成立；当m <0时，g (x )在[1,3]上是减函数，所以g (x )max ＝g (1)⇒m －6<0，所以m <6，所以m <0.综上所述：m 的取值范围是{m |m <67}.。

三角函数根的分布问题

三角函数根的分布问题全文共四篇示例，供读者参考第一篇示例：三角函数在数学中是非常重要的一部分，它涉及到了角度和三角形的关系，同时也在各个领域中有着广泛的应用。

在三角函数中，我们经常会遇到根的问题，即在什么条件下，三角函数的值会等于零。

这个问题往往涉及到了角度的范围、周期性以及三角函数的性质等方面，对于理解三角函数的性质和应用至关重要。

三角函数根的分布问题，即研究三角函数在某一区间内根的位置和数量。

这个问题涉及到了三角函数的周期性和性质，因此在解决这个问题时，我们需要充分了解三角函数的周期性和特点。

在本文中，我们将深入探讨三角函数根的分布问题，包括不同类型三角函数的根的分布规律，以及如何通过图像和计算来确定根的位置和数量。

首先，我们需要了解三角函数的基本性质。

在数学中，常见的三角函数包括正弦函数、余弦函数、正切函数等。

这些函数在不同的区间内都具有周期性，即它们的函数值在一定区间内会重复出现。

例如，正弦函数的周期是2π，余弦函数的周期也是2π，而正切函数的周期是π。

这个周期性是三角函数根的分布问题的关键，因为根的位置和数量都受到周期性的影响。

正弦函数和余弦函数是最常见的三角函数，它们在数学中起到了非常重要的作用。

正弦函数的图像是一条波浪线，它在[0, 2π]区间内有无数个根，即正弦函数在这个区间内有无数个解。

余弦函数的图像也是一条波浪线，它和正弦函数的图像有些许不同，但在[0, 2π]区间内同样有无数个根。

这说明正弦函数和余弦函数在一个周期内有无限个根。

在实际计算中，我们往往需要确定三角函数在某一区间内的根的位置和数量，这时我们可以通过图像来判断。

以正弦函数为例，我们可以画出正弦函数在一个周期内的图像，然后找出所有的根的位置。

通过观察图像，我们可以大致确定根的大致位置和数量。

除了通过图像外，我们还可以通过计算来确定三角函数的根。

以正弦函数为例，我们知道正弦函数的周期是2π，即正弦函数在[0, 2π]区间内有一个周期。

一元二次方程根的分布问题的认知分析和教学对策

一元二次方程根的分布问题认知分析和教学对策430070 武汉市关山中学张璟怡摘要：一元二次方程根的分布问题是我们教师很熟悉的问题,但是学生解决这类问题常常有些困难，笔者由三类不同解法着手研究，分别谈谈他们的特点、难点及难点如何突破及教学启示.关键词：一元二次方程根的分布问题解法分析认知分析及难点突破教学启示一元二次方程根的分布问题是我们教师很熟悉的问题,但是学生解决这类问题常常不是那样的得心应手,畅快淋漓.是哪些原因禁锢了学生的思维，让他们止步不前.笔者饶有兴趣地进行了一番探究，有些心得与同行共商.引例:已知关于x 的一元二次方程()04312=+-+a ax x a 的两根均大于1，求a 的取值范围. 1 解法分析一元二次方程根的分布问题大致有如下三类解法：解法一：由韦达定理，利用21x x +及21x x 的关系，列出有关a 的不等式组，求取a 的范围. 解法二：利用求根公式aac b b x 2422.1-±-=，由已知两根都大于1，即小根1242>---aac b b ，列出有关a 的不等式，通过解根式不等式，求取a 的范围. 解法三：利用一元二次函数，根据条件画出去大致图像，然后列出图像的充要条件，得到有关a 的不等式组，求取a 的范围.2 认知分析及难点突破上述三类解法从不同方面着手研究，涉及知识点、思想方法都有所不同，难点当然也有所不同.下面就三类解法分别谈谈他们的特点、难点及难点如何突破.（1）解法一是用韦达定理解决根的分布问题.怎样正确的利用韦达定理.首先来看看解题一过程中经常犯的一个错误，⎩⎨⎧>>1121x x ，故⎩⎨⎧>>+122121x x x x ；其次来看看错误的根源在哪里及是受到那些知识的影响形成的思维定势，造成的错误.不妨用反例驳倒上述结论.当21,321==x x 时，221>+x x ，121>x x ，但两根不全大于1，所以上述结论有误.另外，学生将⎩⎨⎧>>1121x x 等价转化时是利用一元二次方程)0(02≠=++a c bx ax 有两正根⎩⎨⎧>>0021x x 的充要条件是⎩⎨⎧>>+002121x x x x 进行了知识的负迁移，得到上述结论；再次来寻找⎩⎨⎧>>1121x x 的充要条件.⎩⎨⎧>>1121x x 可等价转化为⎩⎨⎧>->-010121x x ，它的充要条件是()()()()⎩⎨⎧>-->-+-0110112121x x x x ，即()⎩⎨⎧>+->+12212121x x x x x x ，再由韦达定理⎪⎩⎪⎨⎧+=+=+a a x x a a x x 14132121及0≥∆可得1716-≤≤-a ；最后为突破上述难点作如下拓展: 拓展一将引例中一元二次方程有两根改为均小于a 的充要条件是⎩⎨⎧<<a x a x 21⇔⎩⎨⎧<-<-0021a x a x ⇔()()()()⎩⎨⎧>--<-+-002121a x a x a x a x ⇔()⎩⎨⎧>++-<-+0022212121a x x a x x a x x ，拓展二将引例中一元二次方程有两根改为一根大于a ，另一根小于a 的充要条件是⎩⎨⎧<>a x a x 21⇔⎩⎨⎧<->-0021a x a x ⇔()()021<--a x a x ⇔()022121<++-a x x a x x ，拓展三将引例中一元二次方程有两根改为一根小于a 之间，另一根大于b(a<b)的充要条件是⎪⎪⎩⎪⎪⎨⎧>-<->-<-00002121b x b x a x a x ⇔()()()()⎩⎨⎧<--<--002121b x b x a x a x ⇔()()⎩⎨⎧<++-<++-0022********b x x b x x a x x a x x . 小结：（1）对于一元二次方程有两根，两根均大于a 、两根均小于a 及一根大于a ，另一根小于a 利用韦达定理解题较方便；（2）两根均大于a 、两根均小于a 及一根大于a ，另一根小于a 的充要条件寻找过程就是将问题等价转化为两根之积、两根之和的不等关系的过程，即保证能用利用韦达定理解决问题；（3）上述拓展三⎪⎩⎪⎨⎧<>-<-b a b x a x 0021⇔()()021<--b x a x ⇔02121<+--ab ax bx x x ，因为此条件无法进一步利用韦达定理解决.（2）解法二是用求根公式解决根的分布问题.由于求根公式带有根式，并且对根式不等式的解法的不熟练成为用此种方法解决问题的拦路虎.在高中阶段由于解根式不等式的要求不断降低，因此用求根公式解决根的分布问题着实困难,解题过程中需要注意下列两个充要条件:)()(x g x f <的充要条件⎪⎩⎪⎨⎧≥≥<0)(0)()()(2x f x g x g x f ；)()(x g x f >的充要条件⎪⎩⎪⎨⎧≥≥>0)(0)()()(2x f x g x g x f 或⎩⎨⎧<≥0)(0)(x g x f ，但如果一元二次方程能因式分解，即用求根公式不存在根号时，此法不失为解决根的分布问题的一种好方法.如方程0222=-+a ax x 在[]1,1-上有解，求a 的范围？()()02=+-a x a x 2a x =∴或a x -=，故121≤≤-a 或11≤-≤-a ，得22≤≤-a 或11≤≤-a ，即22≤≤-a .（3）解法三是用一元二次函数的观念来解决根的分布问题.在初中阶段学生就已经接触过函数.不过，那时学生对函数的认识大多停留在初步和感性的层面，表现为重在运算，即进去一个自变量，出来一个对应的唯一函数值.进入高中，学生开始接触函数的性质，但由于函数性质的抽象性，导致许多学生惧怕函数.那么如何能使学生主动地、有意识的利用一元二次函数观点解决根的分布问题呢?首先二次函数的所有性质都可以借助其图像表现出来,因此必须借助二次函数的图像，以减轻学生的思维负担，从而克服函数的抽象性.那么帮助学生全面考虑问题，画出满足题意的所有二次函数图像是关键的一步；其次由图像概括归纳出图像的共性，实现由图像语言转化为数学符号语言的目的.在初中我们已经掌握了二次函数c bx ax y ++=2（1）图像开口方向与二次函数的二次项系数a 有关；（2）图像与x 轴交点个数问题与∆有关；（3）函数图像顶点的位置与对称轴ab x 2-=有关；此外，（4）图像与x 轴交点的具体位置还受到函数值()0x f 的正负影响，如开口向上的二次函数()x f ，函数图像与x 轴的两个不同交点都在y 轴的左侧或右侧，则⎩⎨⎧>∆>00)0(f ；函数图像与x 轴的两个不同交点一个在y 轴的左侧另一个在y 轴右侧，则⎩⎨⎧>∆<00)0(f .因此若已知函数的零点落在某个区域内,即已知方程根分布的区域，必须考虑区域端点函数值与0的关系.这样满足某类特征的二次函数图像可以由上述四个方面唯一确定，有时这四个方面有从属关系，只需研究其中几个方面即可.最后,还应该通过更新条件,让学生自己在题目的变化中逐步认识和接纳数形结合的数学思想,同时提高学生诸如分类、概括等的解题能力.如将引例中一元二次方程有两根均大于1作如下变化：变化一：两根均小于1，求a 的取值范围; 变化二：一根在()1,0之间，另一根在()3,1之间,求a 的取值范围; 变化三：在()3,0之间有且仅有一根, 求a 的取值范围; 变化四：在()3,0之间有根, 求a 的取值范围; 变化五：方程在[]3,0之间有根, 求a 的取值范围.3 教学启示如果站在学生的角度，我们会发现一元二次方程根的分布问题并不简单，首先教学要注意讲思想，一元二次方程根的分布问题涵盖了许多数学思想，如数形结合的数学思想、分类讨论的数学思想、函数与方程的数学思想、化归的数学思想，如果不讲这些思想而把它们形式化，学生会认为这是种解题技巧，会出现一听就懂，听过就忘的情形；其次教学要注重过程，解题的过程就是一个对知识理解的过程，只有理解了，才能将知识内化到原有的知识体系中去，也只有经历解题的全过程学生才会有更多的感悟；最后教学重视解题的方法，授之以鱼不如授之以渔.不同解的介绍可以满足不同层次学生的需要，熟悉求根公式能够的学生更容易接受解法二；熟悉韦达定理的法学生更容易接受解法一；对函数性质理解较透彻的学生更容易接受解法三.不同解法的比较可以让学生认识到各种解法的优缺点，以及应用的局限性，从而解决类似问题时能提出多种不同解决预案，再由已知条件进行筛选，从而选择最优解法.参考文献刘秀华数学问题解决中的思维障碍及教学对策山东师范大学2008。

第一课时根的分布

解决一元二次方程ax2+bx+c=0(a＞0)实根分布的方法、步骤：（1）确定方程根分布在同一区间还是不同区间；（2）方程根分布在同一区间时利用四要素列出不等式组；（3）方程根分布在不同区间时利用端点函数值列出不等式(组)；（4）求解不等式即得相应参数的范围。
注意：与原点有关的根的分布问题用韦达定理法求解更简单一些！
（1）开口方向
（2）判别式 b2 4ac
（3）对称轴
x b 2a
（4）区间端点函数值的符号
根的分布的四要素
问题1:关于x的一元二次方程x2＋(m－3)x＋m=0有两个正根,求m的范围。
用以前学过的解法：
解：设方程的两实根分别为x1、x2，则
( m 3 )2 4m 0 m2 10m 9 0
f
(0)
m
0
f (4) 5m 4 0
m 0
m
4
m
4 5
m
0
y
5
-2 O
4x
问题12：方程满足下列条件x2+（m-3)x+m=0，求m的范围。
（12）一个根小于2，一个根大于4
解：x2＋(m－3)x＋m=0一个根小于2，一个根大于4，即一根在
(-∞,2)上,另一根在(4,+∞)上,由图象知只需满足以下条件：
m 0
-2 O 1
3x
问题11：方程满足下列条件x2+（m-3)x+m=0，求m的范围。
（11）一个根在（-2 ,0）内，另一个根在（0 ,4）内
解：x2＋(m－3)x＋m=0一个根在（-2 ,0）内，另一个根在（0 ,4）
内，由图象知只需满足以下条件：
f (2) m 10 0 m 10

多项式的根的分布问题

第1章绪论在数论、代数的组成和数值代数等多个学科里面，都会将多项式作为它们知识网络的基础之一．多项式作为一个可以孤立的体系，也可以与其他的学科体系相联系，并与它们形成一个复杂而又明了的知识网络．在理论和实际应用方面，多项式有着多种多样的内容和作用，一般情况下，它在实际应用研究方面通常会对于某类特定情形下的多项式在一些概括的概念或特定的问题中帮助其求出答案；而在理论方面，就显得有较强的针对性，究其原因，还是取决于多项式它的封闭性、齐次性、可分解性、可约性等其它推导的各种性质．另外，在一些线性或非线性微分方程、常系数微分方程乃至其它微分动力系统中，我们可以利用多项式已知的各种性质来求得问题的近似解或者说是解的取值范围，得到它们特定式子根的实部情况，使所联系的系统达到稳定即可，而不用一定要得出所列多项式的精确解和它们的一切根．本文首先介绍多项式的相关理论基础（罗尔定理和零点定理），然后根据相关定理得到多项式的根的存在性以及根的确定性，其次介绍由笛卡尔符号原则得到多项式的正根、负根的个数的方法，并举出实例，解决多项式的正根、负根的个数的问题．通过总结整理多项式的根的分布问题，可以帮助我们快速准确的选解决多项式的根的问题，从而进一步加深我们对多项式的根的分布的掌握，把多项式的根的分布问题进行细致归纳．第2章多项式根的存在性2.1相关定理介绍罗尔定理和零点定理是高等数学微积分理论中的两个重要定理．在实际问题里，罗尔定理讨论多项式根中的应用非常多，主要取决于多项式的连续求导、次数随求导次数依次降级的性质．零点定理反映了闭区间上连续函数的一个性质，在有关方程根的存在性方面有着重要的应用．罗尔定理如果函数f(x)满足：（1）在闭区间[a,b]上连续；（2）在开区间(a,b)内可导；（3）f(a)=f(b)，那么在开区间(a,b)内至少有一点ξ(a<ξ<b)，使得f′(ξ)=0．[1]运用点一：如果想要讨论一个函数它的导数根是否存在，或当根存在时其取值范围和具体有哪几个，那么这个函数在定义域内是连续可导的，由罗尔定理不难看出，其导数方程至少有一个根会存在于多项式方程两个根之间．运用点二：若是将罗尔定理反过来看的话，我们可以发现：如果多项式方程f(x)=0没有解出来根，则方程f(x)=0最多有一个根．可以根据已知函数方程的根来求其它函数方程的跟，然后再根据零点定理，就可以得到“如果方程f′(x)=0没有根，则方程f(x)=0只有一个根．”这样的结论．零点定理设函数f(x)在闭区间[a,b]上连续，且f(a)与f(b)异号（即f(a)∙f(b)<0），则在开区间(a,b)内至少有函数f(x)的一个零点，即至少有一点ζ(a<ζ<b)，使f(ζ)=0．[2]应用根据所给方程作辅助函数，再寻找闭区间，是辅助函数在该区间端点处的函数值异号．2.2例题总结例2.1 设函数f(x)=(x−1)(x−2)(x−3)(x−4)，讨论方程f′(x)=0有几个实根，并分别指出他们所在的区间．分析：令f(x)=0，则 x=1、2、3、4，可得f(1)=f(2)=f(3)=f(4)=0，再利用罗尔定理，即可得出结论．解：函数f(x)在（−∞,+∞）内处处可导，并且满足f(1)=f(2)=f(3)= f(4)=0，f(x)在区间[1,2]，[2,3]，[3,4]上分别满足罗尔定理的三个条件因此至少存在一点ξ1∈(1,2)，ξ2∈(2,3)，ξ3∈(3,4)使得f′(ξ1)=f′(ξ2)=f′(ξ3)=0即ξ1，ξ2，ξ3是f′(x)=0的三个实根，又因为f′(x)=0是三次方程，至多有三个实根，故f′(x)=0只有三个实根，分别在区间(1,2)，(2,3)，(3,4)内．例2.2 证明方程6x7+2x+a=0至多有一个根，其中a为任意常数．分析：用反证法，假设方程有两个不同的实根，再由罗尔定理可知其导数方程至少有一个根，从而产生矛盾，即可得出结论．证明：方程6x7+2x+a=0的导数方程42x6+2=0没有根假设方程6x7+2x+a=0有两个根，由罗尔定理可知其导数方程42x6+2=0至少有一个根．产生矛盾．所以方程6x7+2x+a=0有一个根．例2.3 证明方程2x3−5x2+1=0在区间(0,1)内至少有一个根．分析：在解决此类问题时，要牢记方程的根=函数的零点．通过区间端点值的正负来判断是否存在零点，即方程的根．证明：函数f(x)=2x3−5x2+1在闭区间[0,1]上连续又f(0)=1>0，f(1)=−2<0根据零点定理，在(0,1)内至少有一点ζ，使得f(ζ)=0即2ζ3−5ζ2+1=0(0<ζ<1)因此方程2x3−5x2+1=0在区间(0,1)内至少有一个根．第3章多项式的根的确定性3.1奇次多项式的根的确定性例3.1 奇次多项式必至少有一个实根．证明：设f(x)=a n x n+a n−1x n−1+⋯+a1x+a0(其中n为奇数)明显有f(x)为连续函数，当a n<0时有：lim(x→−∞)，f(x)=−∞lim(x→+∞)，f(x)=+∞由于f(x)是连续函数，所以f(x)至少有一个零点即f(x)至少有一个实数根．当a n<0时有：lim(x→−∞)，f(x)=+∞lim(x→+∞)，f(x)=−∞由于f(x)是连续函数，所以f(x)至少有一个零点即f(x)至少有一个实数根．综上所述：奇次多项式必至少有一个实根．3.2偶次多项式的根的确定性定理3.1 任何实系数四次方程ax4+bx3+cx2+dx+e=0如果满足下列两个条件之一：（1）a>0，e>0，c−14a b2−14ed2>0；（2）a<0，e<0，c−14a b2−14ed2<0；则方程无实根．[3]定理3.2 任意实系数六次方程a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0=0如果满足下列两个条件之一：（1）a6>0，a0>0，a4−14a6a52>0，a2−14(a4−14a6a52)a32−14a0a12>0；（2）a6>0，a0>0，a4−14a6a52>0，a2−1a4−14a6a52a32−14a0a12>0；则方程无实根．[3]定理3.3 任意实系数2 n次（n≥3为正整数）方程a2n x2n+a2n−1x2n−2+⋯+a1x+a0=0如果满足下列两个条件之一：（1）a2n>0，a0>0，a′2n−2=a2n−2−14a2n a2n−12>0，a′2n−4=a2n−4−14a′2n−2a2n−32>0，a′2n−6=a2n−6−14a′2n−4a2n−52>0，……，a′4=a4−14a′6a52>0 ，a′2=a2−14a′4a32−1(4a0)a12>0 ；（2）a2n<0，a0<0，a′2n−2<0，a′2n−4<0，a′2n−6<0，……，a′4<0，a′2<0，则方程无实根．[3]除定理3.1，定理3.2，定理3.3所述的情况方程无实根外，其他情况均有实根．当多项式的根的精确解得不到时，则用二分法得到近似解并估计误差．在数学分析中，若函数f在区间[a,b]上连续，且f(a)与f(b)异号（即f(a)∙f(b)<0），则至少存在一点x∗∈(a,b)，使得f(x∗)=0，即方程f(x)=0在(a,b)内至少有一个根，这就是根的存在定理．二分法求方程的近似实根基于根的存在定理的第一个方法称作二分法(或逐次分半法)．假设f是定义在区间[a,b]上的连续函数，且f(a)与f(b)反号．根据根的存在定理，在(a,b)内至少存在一个数x∗使得f(x∗)=0．为了简单起见设在这个区间内的根是唯一的．这种方法要求将[a,b]的子区间反复减半，在每一步找出含有x∗的那一半，直到区间长度不大于预设进度ε．二分法求方程根的步骤：第一步：输入有根区间端点a，b和计算精度ε；第二步：取区间[a,b]的中点x0；第三步：计算函数值f(a)，f(x0)，若f(x0)=0，则x0就为所求实根，输出x0结束算法，否则转第四步；第四步：若f(a)∙f(x0)<0，记a=a，b=x0；否则记a=x0，b=b，转第五步；，结束算法，否则转第二步．第五步：若|b−a|≤ε，则输出x0=a+b2二分法求方程根的MATLAB程序：function x=agui_bisect(fname,a,b,ε);fa=feval(fname,a);fb=feval(fname,b);if fa*fb>0 error(‘两端函数值为同号’)；endk=0;x0=(a+b)/2;while |b−a|≤εfx=feval(fname,x);if fa*fx<0;b=x;fb=fx;elsea=x;fa=fx;endk=k+1;x=(a+b)/2end例3.2 利用计算器，求方程lgx=3−x的一个近似解（精确到0.1）．分析：分别画函数y=lgx和y=3−x的图像，在两个函数图像的交点处，函数值相等．这个点的横坐标就是方程lgx=3−x的解．有函数y=lgx与y=3−x的图像可发现，方程lgx=3−x有唯一解，记为x1，并且这个解在区间(2,3)内．解：设f(x)=lgx+x−3，利用计算器计算得f(2)<0，f(3)>0⇒x1∈(2,3)；f(2.5)<0，f(3)>0⇒x1∈(2.5,3)；f(2.5)<0，f(2.75)>0⇒x1∈(2.5,2.75)；f(2.5)<0，f(2.625)>0⇒x1∈(2.5,2.625)；f(2.5626)<0，f(2.625)>0⇒x1∈(2.5626,2.625)因为2.5625与2.625精确到0.1的近似值都为2.6，所以此方程的近似解为x1≈2.6．图1第4章笛卡尔符号原则设实系数多项式函数f(x)=a0x n+a1x n−1+⋯+a i x n−i+⋯+a n(a0≠0) (1)定理4.1 n次多项式f(x)至多有n个不同的根．[5]定理4.2（笛卡尔符号原则）对于多项式函数f(x)，它的正实根个数等于f(x)的非零系数的符号变化个数，或者等于比该变化个数小一个偶数的，数；f(x)的负实根个数等于f(−x)的非零系数的符号变化个数，或者等于比该变化个数小一个偶数的数．[6]定理4.3 设f(x)为实系数多项式，D(f)为f(x)的根的判别式，则当D(f)=0时，方程f(x)=0有重根；当D(f)<0时，方程f(x)=0无重根，且有奇数对虚根；当D(f)>0时，方程f(x)=0无重根，且有偶数对虚根．[6]对（1）式中的f(x)，D(f)定义为:D(f)=(−1)n(n−1)2a0−1R(f,f′)，其中f′为f(x)的导函数，R(f,f′)称为f和f′的结式,是由f(x)的各项系数确定的一个2n−1阶方阵R的行列式．如果当k>0或k<0时记a k=0，则R的第i行第j列的元素为r ij={a j−i, 当 1≤i≤n−1,(i−j+1)a j+n−i−1,当 n≤i≤2n−1.定理4.4(根的上下界定理) 设(1)式中a0>0，（1）若存在正实数M，当用x−M去对f(x)作综合除法时第三行数字仅出现正数或0，那么M就是f(x)的根的一个上界；（2）若存在不大于0的实数m，当用x−m去对f(x)作综合除法时第三行数字交替地出现正数（或0）和负数（或0）时，那么m就是f(x)的根的一个下界．定理4.5（判断根上下界的牛顿法）设有实数k，使f(k)，f′(k)，⋯，f m(k)，⋯，f n(k)均为非负数，或均为非正数，则方程f(x)=0的实根都小于k，这里f m(k)表示f(x)的m阶导数．[6]4.1多项式的正根想要求一个多项式的根，并且是正根，那么该怎样求呢？（1）通过定理4.1先求有多少个解；（2）通过定理4.2知道其中有几个可能是对的正实数根；（3）通过定理4.3计算该多项式的判别式，判别它有没有重根；若无重根，则根据定理4.3，当判别式大于零时，方程的根的个数与n相差4的倍数；反之，方程的根的个数与n−2相差4的倍数．（4）若判别式等于零，用辗转相除法求出f(x)和f′(x)的最大公因式(f(x),f′(x))，该公因式的根即为f(x)的重根，用带余除法将多项式将次．（5）利用定理4.4、定理4.5或用改写方程的方法找出多项式的根的上下界．例4.1 求多项式函数f(x)=x5−5x4+14x3−34x2+48x−24的实数根．分析：根据寻找多项式函数正根的方法及步骤，分步计算，即可求得该多项式函数的实根．解：由定理4.1知f(x)至多有5个实根；由定理4.2知f(x)有5个或3个或1个正根；计算D(f)，算出R(f,f′)≈4×10−8，因其绝对值远小于1，用矩阵的初等变换求出(f(x),f′(x))=x−2，知2为多项式的一个重根．用(x−2)2除原多项式，将多项式将次，得g(x)=x3−x2+6x−6；=x2+6．显然x2+6计算g(1)=0，知1为多项式的一个根，计算g(x)x−1无实根，故原多项式的实根为1和二重根2．4.2多项式的负根想要求一个多项式的根，并且是负根，那么该怎样求呢？（1）通过定理4.1先求有多少个解；（2）通过定理4.2知道其中有几个可能是对的负实数根；（3）通过定理4.3计算该多项式的判别式，判别它有没有重根；若无重根，则根据定理4.3，当判别式大于零时，方程的根的个数与n相差4的倍数；反之，方程的根的个数与n−2相差4的倍数．（4）若判别式等于零，用辗转相除法求出f(x)和f′(x)的最大公因式(f(x),f′(x))，该公因式的根即为f(x)的重根，用带余除法将多项式将次．（5）利用定理4.4、定理4.5或用改写方程的方法找出多项式的根的上下界．例4.2 求多项式函数f(x)=3x5−2x4−15x3+10x2+12x−8的实数根．分析：根据寻找多项式函数负根的方法及步骤，分步计算，即可求得该多项式函数的实根．解：由定理4.1知f(x)至多有5个实数根；由定理4.2知f(x)有3个或1个正根，有2个或0个负根；计算D(f)，算出R(f,f′)≈4×10−8，从而知D(f)>0，方程有1个或5个实根；因为f(x)=x3(3x2−2x−15)+(10x2+12x−8)，所以(1+√46)是f(x)的一个上界．3又因为f(x)=3x(x4−5x2+4)−2(x4−5x2+4)，所以-2是f(x)的一个下界；又f(x)=(3x−2)(x4−5x2+4)=(3x−2)(x2−1)(x2−4)即得到f(x)的所有实根有2、1、-1、2、-2．3图2第5章总结本文通过相关资料的收集与整理，对多项式的根的分布问题的相关理论和方法的介绍以及这些理论和方法在例题中的应用进行阐述．对于多项式的根的分布问题，先根据罗尔定理及零点定理判断根是否存在，并讨论根的确定性，当精确解得不到时，则用二分法得到多项式的近似解并估计误差，最后由笛卡尔原则得到多项式根的个数（多项式正实根个数等于f(x)的非零系数的符号变化个数，或者等于比该变化个数小一个偶数的数；多项式负实根个数等于f(−x)的非零系数的符号变化个数，或者等于比该变化个数小一个偶数的数．），由此解决多项式的根的分布问题．具体在求多项式函数实根的问题中，应根据题意选择具体简洁的步骤求解．学习数学的时候，数学思维是非常重要的，不断地学习数学理论和讨论数学实际问题，不但能锻炼思维能力，还能培养我们学习数学的兴趣．知识会越用越活，我们的大脑也越用越聪明．参考文献[1]李娟，关晓红．罗尔定理在讨论多项式方程的根中的应用[J]．牡丹江教育学院学报，2010(04)．114-114[2]闫广霞．零点定理的推广及其应用[J]．河北工业大学成人教育学院学报．2002年6月．17（2）1-2[3]杨宗培．实系数一元偶次代数方程无实根的判别法则[J]．南昌大学学报（工科版）．1982（1）：56-61[4]鲍克元．基于MATLAB中随机函数的求方程实根的方法探析[J]．数学之友．2016(24):3-3[5]张禾瑞，郝鈵新．高等代数[M]．第4版．北京：高等教育出版社，1999[6]黄永，康道坤．求多项式函数实数根的方法[J]．邵通学院学报．2007年．29（5）：8-11[7]周伯壎．高等代数[M]．第4版．北京：人民教育出版社，1966。

多种方法解答一元二次方程根的分布问题

多种方法解答一元二次方程根的分布问题
赵彦伍
【期刊名称】《数理天地（初中版）》
【年(卷),期】2024()11
【摘要】一元二次方程根的分布问题是初中数学代数类问题中较难的一种题型.很多学生在遇到这类题目时常常没有思路,其主要原因就是没有理解方程根的本质和这类题目的解题方法.本文将结合几道典型例题来谈解答一元二次方程根的分布问题的多种方法,以供读者参考.
【总页数】2页(P18-19)
【作者】赵彦伍
【作者单位】山东省莒县峤山镇中心初级中学
【正文语种】中文
【中图分类】G63
【相关文献】
1.两招妙解一元二次方程根的分布问题
2.四种方法直击一元二次方程根的分布问题
3.追根化困惑,问底见本质r——用"缩分"法解一元二次方程根的分布问题
4.含参数一元二次方程根的分布问题的思考
5.一元二次方程根的分布问题
因版权原因，仅展示原文概要，查看原文内容请购买。

一元二次解法恒成立、根的分布情况

④原不等式的解集为{x|-1＜x＜2或2＜x＜3}.
例7 解不等式 ( x 1)( x x 6) 0 .
2
解：原不等式 ( x 1)(x 3)(x 2) 0
( x 2)(x 1)(x 3) 0

-2
.

1
.

.

3
∴原不等式的解集为：
{x | x 2，或1 x 3}.
例题选讲
题型五. 恒成立问题
2 ( a 2 ) x 2(a 2) x 4 0 例5.不等式
对一切 x R 恒成立，则a的取值范围。变式1.不等式(a 2 4) x2 (a 2) x 1 0 的解集为空集，求a的取值范围。
变式2.若函数 f ( x) kx 2 6kx ( k 8) 的定义域为R,求实数k的取值范围.
例题选讲
题型四. 一元二次不等式的解与系数的关系(韦达定理)
例4.不等式 ax bx 2 0 的解集为
2
1 1 {x | x }, 求 a, b. 2 3 1 1 2 , 是方程 ax bx 2 0 解:由题意可得,
2 3
的两个根,且a<0.
1 1 b 2 3 a 1 1 2 2 3 a
并将各因式x的系数化“+”
②求根，并在数轴上表示出来(注意空心?实心?)
③由右上方穿线，经过数轴上表示各根的点
④若不等式是“＞0”,则找“线”在x轴上方的区间；若不等式是“＜0”,则找“线”在x轴下方的区间.
穿线的原则：奇穿偶不穿
例5：解不等式 x(x-3)(2-x)(x+1)＞0.
解：①将原不等式化为x(x-3)(x-2)(x+1)＜0

代数法解决一元二次方程两类根的分布问题

m ＜n＜p＜q)分布模型
p~q(
４．
２其他分布模型的解法
(
１)
m ~n(
m ＜n)分布模型的解法
一元二次方程两不等实根 x１ ,
x２在数轴上分布
在 m,
n 的两侧、之间或同一侧,有以下六种情况．
①x１＜m ＜x２＜n:两根分布在 m 的两侧且分布
ìΔ＞０,
布模型,并对其解法进行探究．
１题目假设
假设实系数一元二次方程 ax ＋bx ＋c＝０(
a≠
)
,
,
有两不等实根
且
０
x１ x２
x１＜x２．
２
２零分布
一元二次方程 ax２＋bx ＋c＝０(
a≠０)的两不等
实根 x１ ,
x２分布在数轴上０的不同侧或同一侧,有以
要激发学生全方面的潜能,而且还能在技能、感官及
同评价的占比,尽量丰富评价内容,确保学生学习习
认知上给予学生全方位的启迪．
惯、解题能力和数学思想等内容的有机结合,不断提
升学生综合能力．
４结语
综上所述,在新课程改革标准的积极影响下,初
师能够在高视角下观察与分析,不难发现数学课堂教
可适当延伸评价思路,使学生在研究数学问题的同时
学内容均围绕交流活动展开,但唯独缺少了学生间的
提升思想境界,促进学生现有数学知识的延伸,深刻