如何将WGS84矢量地图反纠偏后与高德地图叠加

合集下载

解决矢量地图与卫星地图叠加有偏移的两种方法

解决矢量地图与卫星地图叠加有偏移的两种方法1概述众所周知，谷歌地图除了在从国外服器下载的卫星地图以外，其它地图与实际坐标都是有偏移的。

另外，如高德地图、雅虎地图、SOSO地图等同样存在坐标偏移的问题。

这样就给我们要将矢量数据和影像数据进行叠加带来了麻烦，因为影像数据的“先天不足”（偏差）会导致与矢量数据叠加产生错位。

以下我们提供两种解决叠加产生错位的解决方案。

方案一：对影像数据进行纠偏后与矢量地图数据叠加该方法的优点是坐标与实际坐标吻合，可以叠加GPS采集的矢量数据；缺点是转换影像地图数据的工作量比较大，耗时比较长，如果影像图上有地名和道路名等文字的话，文字会有一定变形，从而影像地图美观。

当要求坐标与真实坐标一定要吻合时，可以采用此种方法。

对影像地图数据进行纠偏的方法请参阅本文第3节《如何对影像地图数据进行纠偏》。

方案二：对矢量数据进行反纠偏后与影像地图数据叠加该方法的优点是影像地图不会变形，与原图一样美观，对矢量数据的转换工作量十分小；缺点是坐标与实际坐标不吻合。

当比较关心叠加效果而可以忽略坐标与实际坐标的偏差时，可以采用此种方法。

对矢量地图数据进行反纠偏的方法请参阅本文第4节《如何对矢量地图数据进行反纠偏》。

s2如何对影像地图数据进行纠偏2.1准备工作安装水经注万能地图下载器，如果你没有安装该软件，可以到水经注软件的官方网站去下载。

安装ESRI ArcGIS 10.0，我们会用到该产品中的ArcMap软件，如果你没有安装，可以在百度中搜索一下，很多地方都可以下载破解版的，该软件比较大，有4个多G，因此下载之前，您得作好心里准备。

2.2下载谷歌卫星地图启动水经注万能地图下载器，软件启动时列出了本软件所能下载的所有地图类型的列表，这里我们只需要勾选“卫星.谷歌”，并点击“确定”按钮就可以了，如下图所示。

由于我们需要准确的坐标，这里我们需要在服务器菜单中选择国外服务器（国内服务器下载的数据是有偏移的），如下图所示。

【高德地图API】如何解决坐标转换，坐标偏移？

【高德地图API】如何解决坐标转换，坐标偏移？摘要：各种坐标体系之间如何转换？到底有哪些坐标体系？什么是火星坐标？为什么我的坐标，在地图上显示会有偏移？本文详细解答以上问题。

最后给出坐标拾取工具。

---------------------------------------------------------------------------------------------------------------------------一、坐标体系首先我们要明白，开发者能接触到哪些坐标体系呢？第一种分类：1、 GPS，WGS-84，原始坐标体系。

一般用国际标准的GPS记录仪记录下来的坐标，都是GPS的坐标。

很可惜，在中国，任何一个地图产品都不允许使用GPS坐标，据说是为了保密。

GPS坐标形式如图，度分秒形式的经纬度：2、 GCJ-02，国测局02年发布的坐标体系。

又称“火星坐标”。

在中国，必须至少使用GCJ-02的坐标体系。

比如谷歌，腾讯，高德都在用这个坐标体系。

GCJ-02也是国内最广泛使用的坐标体系。

3、其他坐标体系。

一般都是由GCJ-02进过偏移算法得到的。

这种体系就根据每个公司的不同，坐标体系都不一样了。

比如，百度和搜狗就使用自己的坐标体系，与其他坐标体系不兼容。

第二种分类：首先明白，所有坐标体系的原点，都是非洲。

1、经纬度。

这个是球面坐标，对于北京来说，就是(116.38817139.935961)这样的坐标。

比如腾讯、高德、百度都是这样的经纬度坐标。

谷歌是经纬度顺序写反的经纬度坐标。

如果是度分秒坐标，需要进行转换，才能得到这样的经纬度坐标。

详见坐标转换。

2、墨卡托坐标。

平面坐标，相当于是直线距离，数字一般都比较大，像这样的。

(215362.00021333335 99526.00034912192) 墨卡托坐标，主要用于程序的后台计算。

直线距离嘛，加加减减几乎计算方便。

搜狗地图API就是直接使用的墨卡托坐标。

150107_如何在谷歌卫星地图中叠加等高线并打印

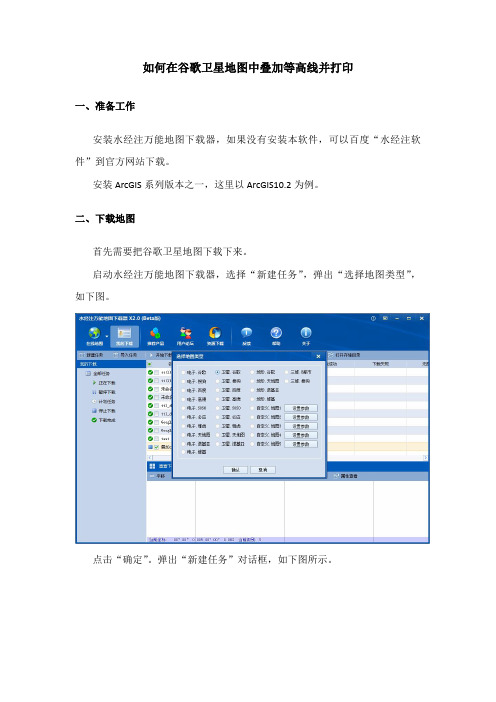
如何在谷歌卫星地图中叠加等高线并打印一、准备工作安装水经注万能地图下载器，如果没有安装本软件，可以百度“水经注软件”到官方网站下载。

安装ArcGIS系列版本之一，这里以ArcGIS10.2为例。

二、下载地图首先需要把谷歌卫星地图下载下来。

启动水经注万能地图下载器，选择“新建任务”，弹出“选择地图类型”，如下图。

点击“确定”。

弹出“新建任务”对话框，如下图所示。

输入坐标，并选择级别。

在级别列表中，你可以选择任何级别，但一般来讲城区选择19级，郊区选择16级比理想，但选择级别之前，最好在在线地图浏览中先查看所想要下载的级别是否有数据，这里我们以15级为例。

选择好级别后，点击确定开始下载。

下载完成后会弹出对话框询问是否要立即导出，选择“是”，然后显示“导出图片数据”对话框，如下图所示。

在该对话框中，不需要作任何设置，点击“输出”按钮以默认参数导出数据即可。

默认导出路径为“D:\SGDownload\叠加dem_拼接[默认]\L15”。

三、将dem转换成等高线首先启动ArcMap，打开ArcToolbox，选择3D分析工具->栅格表面->等值线，弹出窗口，如下图所示。

输入栅格：我们准备好的dem（水经注软件公司可以为广大用户有偿提供全球30米分辨率的DEM高程数据，也可以提供等高线高程数据的各种生成处理服务）。

输出折线要素：输出路径，并带折线要素名称。

等值线间距：比如100。

点击确定，等待系统处理。

处理完成后，加载等高线，如下图所示。

四、影像叠加等高线并打印输出把我们下载的谷歌卫星地图也加载进来，如下图所示。

选择菜单“视图”->“布局视图”，如下图所示。

调整好布局后，选择“文件”->”导出地图”，弹出“导出地图”对话框，如下图所示。

选择保存类型以及分辨率等信息，点击“保存”。

保存成功后，我们在桌面打开保存的图片，如下图所示。

将结果打印出来。

大规模矢量地图与多分辨率DEM 快速叠加的方法

引用格式:杨玲,张立强,康志忠,等.大规模矢量地图与多分辨率DEM 快速叠加的方法.中国科学:信息科学,2010,40:801–808论文中国科学:信息科学2010年第40卷第6期:801∼808 大规模矢量地图与多分辨率DEM 快速叠加的方法杨玲x ,张立强x ∗,康志忠y ,肖志强x ,彭军还y ,张兴明x ,刘骝xx 北京师范大学遥感科学国家重点实验室,北京100875y 中国地质大学(北京)土地科学技术学院,北京100083*通信作者.E-mail:zhanglq@收稿日期:2009–01–19;接受日期:2009–07–13国家自然科学基金(批准号:60502008)、国家高技术研究发展计划(批准号:2006AA12Z220,2007AA12Z226)、教育部新世纪优秀人才支持计划(批准号:NCET-07-0099)和国家海洋局开放研究基金(批准号:KP2007007)资助项目摘要高分辨率矢量地图数据与数字高程模型的无缝可视化,能增强两者在空间信息表达和分析中的作用.如何实现两者高精度实时无缝三维可视化是地理信息科学的一个重要研究内容.文中提出一种基于利用帧缓存和Voronoi 图的方法,实现了大规模矢量地图的快速简化,并有效保持了简化前后拓扑关系的一致性,以此为基础建立了矢量地图的多细节层次模型,完成了视点相关多分辨率的叠加操作.此方法普适于各种DEM 多分辨率模型,且可视化的性能不受地形数据集复杂度的影响,同时利用视景体裁剪和区域索引技术,降低了矢量地图数据规模对叠加效率的影响,使叠加耗时始终控制在一定范围内,从而实现了大规模矢量地图与多分辨率DEM 无缝快速叠加显示.关键词大规模矢量地图多分辨率模型视点相关无缝渲染1引言矢量数据是编码地理空间实体(如道路交通网、植被和土壤类型)的主要方式,它通常由(半)自动方式通过遥感影像、GPS 测量或者人工输入的方式获取.二维矢量数据与地形叠加分析是空间分析内容,对不同要素的图层进行空间叠加分析,有助于进行专题操作,帮助人们更清晰直观地认知空间事物,并可相互增强两者在空间信息表达和分析中的作用.如将不同时间序列的海岸线图层进行叠加,可观察海岸线的沉陷、位置偏移等;将跨空间连续变化的雨量信息的降雨专题图与数字高程模型(DEM)叠加,可以形成各行政区划内的平均或最大降雨量图.随着遥感及相关技术的发展,如机载激光扫描仪、高分辨率卫星影像等,使得高分辨率矢量数据的获取成为可能,人们获取空间数据的数据量也呈摩尔定律的速度增长,远远超出了计算机设备和网络的实时传输能力.对高分辨率、大规模的矢量数据来说,为了更好地实现其快速渲染和高质量的空间分析,需要对矢量数据进行多分辨率描述和表达,减少数据量和参与计算的顶点数目.传统的矢量地图数据与DEM(digital elevation model)叠加算法顾及了地形复杂性以及DEM 简化时所采用的杨玲等:大规模矢量地图与多分辨率DEM快速叠加的方法LOD(level of detail)算法,在实现LOD模型构建的同时,完成矢量地图数据和地形的叠加过程.但是,不同的应用系统采用的LOD算法不尽相同,而且LOD模型的动态变化会引起叠加过程的重新构建,所以该方法缺少通用性,消耗大量的计算机内存,而且随着数据量的增加,算法的复杂度也迅速增长.为了实现大规模矢量(面状和线状)地图与DEM的无缝、实时叠加,本文在保持拓扑关系不变的前提下,研究了矢量地图的快速简化算法,建立了矢量地图的LOD模型,同时结合视景体裁剪及区域索引的方法,实现了大数据量多分辨率矢量地图与细节层次DEM的实时动态叠加.该方法的优点在于不会产生像基于纹理叠加技术的走样现象,并且与DEM内在几何关系及所采用的LOD模型无关,叠加的性能不受地形数据集的影响,只与矢量数据复杂性有关.2相关工作2.1矢量地图的简化方法随着数据采集技术飞速发展,人们获取的矢量地图数据的范围和分辨率增长速度已经远超出了计算机软硬件的更新速度.对于WEBGIS和3DGIS来说,如此巨大的数据难以满足网络的实时传输和快速可视化的需要.在保证视觉精度和拓扑关系不变的前提下,采用简化方法,去除冗余数据,是加快网络传输和快速可视化的一种行之有效的途径,同时也能减少渲染所需开销.Douglas和Peuker[1]提出了Douglas-Peuker折线简化法,效率较高,且可保持线要素的重要几何特征,因此得到广泛应用.但在简化过程中会导致拓扑关系发生改变,造成简化后的线要素出现如图1所示的三种拓扑关系不一致[2].对于面要素来说,若以多边形为基本单位,则简化后还可出现如图2所示的邻接关系改变.为避免上述现象,还需在简化过程中加入一定的约束条件.Buttenﬁeld[3](2002)基于Douglas-Peucker算法对曲线进行化简预处理,利用Strip树结构存储简化结果,为保持拓扑关系一致性,Buttenﬁeld用曲线的凸包来描述曲线,虽然部分增加了计算代价,但是对于曲线的概括描述更精确.Mustafa等[4]提出了一种基于Voronoi图方法,Voronoi图的计算和简化结果的初步获得都利用了图形硬件,故计算效率较高,且避免了线要素之间错误的相交,但不能避免自相交.Mantler等[5]也利用了Voronoi图求得了折线的安全集,在安全集内应用Douglas-Peuker算法可避免自相交错误的出现.此算法计算Voronoi图的时间复杂度为O(n log n),计算安全集的时间复杂度为O(n),加上Douglas-Peuker算法本身的时间复杂度O(n2),使得对于大规模数据的简化耗时较长.2.2矢量地图与地形叠加的方法矢量数据通常又分为点状、线状和面状.点状矢量数据的叠加易于实现,故大多研究只针对线状和面状数据.目前的研究基本可分为两类[6∼9],一类是基于几何的,一类是基于纹理的.第1类方法是指在原数据上加入高程信息,并求出与地形转折处交点的高程信息,将其加入原始数据中.由于高分辨率DEM多采用LOD技术可视化,细节处的起伏信息随视点改变实时变化,因此需先求算出矢量数据和细节层次下地形转折处的交点.但细节层次改变时,容易造成两者之间产生裂缝.另一方面,渲染过程中根据当前细节层次实时计算交点,占用一定的计算时间,延迟了可视化的速度.另外,交点的求法以DEM所采用的LOD算法为基础,很难找到一种普适的求交算法.基于纹理方法的主要思想是由矢量数据生成一张纹理图,然后通过纹理映射将其叠加到地形上.但是,随着视点的拉近,边界比较模糊.若显示大区域的矢量数据,就必须采用大尺寸的纹理,或者生成并存储多张纹理图,会耗费大量纹理802中国科学:信息科学第40卷第6期图1折线简化法可能导致的3种拓扑不一致现象[2]图2折线简化法可能导致的邻接关系改变内存.Schneider等[6]引入了阴影锥算法.把矢量数据作为悬于地形上空的遮蔽物,垂直向下投射阴影,再将地形上落入阴影中的部分渲染出来,即为矢量数据与地形的叠加结果.此方法克服了前两种传统方法的缺点,较好地实现了小规模矢量数据与三维地形的快速精确叠加,并且也适用于凹多边形和带洞的多边形.更重要的是它独立于DEM所采用的LOD算法,具有很强的通用性.不足之处在于,渲染大数据量的矢量地图,需要内存较大,无法实时渲染.本文将主要采用此方法对矢量地图进行叠加,并结合矢量地图的LOD模型及其他辅助技术实现了实时动态叠加.3基于Voronoi图的矢量地图简化方法本文在Mustafa等[4]的方法基础上,提出了如下简化方法:首先清空各个帧缓存,使其值均为0.在模板缓存中渲染整幅地图的宽为ε的Voronoi图,每个线要素的Voronoi区域的模板缓存值与要素序列号i一一对应.连接要素c i上不相邻的两顶点,在颜色缓存中渲染此捷径.渲染时开启模板检测,要求模板缓存值不等于i的部分才能渲染到颜色缓存中,并且每条捷径与一种颜色一一对应.对于c i,定义其所有捷径组成集合为S i,初始时,S i包括所有捷径.渲染完所有要素的所有捷径后,逐像素检查颜色缓存,若一像素的RGBA值不全为0,则将与此颜色对应的捷径从S i中剔除.颜色缓存检查完毕后,逐一计算S i中剩余的捷径和其对应的原线段组的距离,若大于ε,则也需从S i剔除.最后按照最短路径,将S i中剩余捷径相连,即得到简化结果c.对于面要素,可将其看作线要素加以简化.i将整幅地图同时渲染在帧缓存中,若地图范围很大,则每个要素会被显著地缩小,只对应十几个甚至几个像素,此时矢量要素的捷径相互覆盖,致使先渲染的捷径被后渲染的捷径完全覆盖.为解决此问题,首先可将地图分幅渲染.设地图平均采样间距为d,屏幕宽度为w个像素,地图宽度为W,横向上地图应被分成n个子区间,n=(int)(2·W)/(d·w)+1,纵向也同样处理.另一方法是避免渲染不必要的捷径.通常,一个顶点与相隔较远顶点的连线很可能超出缓冲区,故无需对所有点两两连线,只需连接较近的m个点即可,若矢量地图采样点较密,m值可较大,反之,可较小.针对图1(b)所示的位置改变现象,即线要素被简化后,位于线一侧的点v可能会错误地位于线的另一侧,解决此问题可利用Voronoi图快速实现.在生成线要素的Voronoi图后,生成点要素宽度为ε的缓冲区,并且在渲染其缓冲区时,减少其深度值,使其在模板缓存中覆盖原Voronoi图,得到完全渲染,则经过点缓冲区的捷径将从S i剔除.针对图1(c)所示错误,本文认为线要素在简化后产生自相交,是由于线要素生成的Voronoi图自相交.故研究重点集中于如何去除Voronoi图中因自相交而重叠的区域.此类区域的去除,也可利用模板缓存.先求得由一组四边形组成的线要素的缓冲区,宽度为ε.在生成矢量地图的Voronoi图后,关闭深度缓存的写操作,而后渲染每个要素的缓冲区.假设矢量要素c i对应的模板缓存值为i,则渲染缓冲区时,模板缓存值要大于或等于i的地方其缓存值加1,其他地方值不变.此后在渲染捷径时,要求模板值不为i+1的地方才可通过检测得到渲染.803杨玲等:大规模矢量地图与多分辨率DEM快速叠加的方法此外,还有一种拓扑关系需要保持,即图2所示的多边形的邻接关系.两个多边形共用一条边时,若简化以多边形为基本单位,则此公共边将被简化两次,两次简化结果可能不同,使得这两个多边形边界不再完全重合.为消除这种错误,对于可以得知邻接关系的面状数据,简化时应以组成多边形的弧段为基本单位.在渲染时,也以弧段为基本单位,判断一个多边形的各个组成弧段是否应该被简化,然后再由简化过或未简化过的弧段组成多边形,用阴影锥的方法渲染.此方法耗时较小;其更重要的优点是可以避开复杂的算法,简单而有效地保拓扑关系.4矢量地图与多分辨率DEM无缝快速叠加4.1矢量数据的精确叠加Schneider等[6]借用阴影锥技术[10],渲染矢量数据在地形上投射的阴影,此阴影即为叠加结果.由矢量数据生成的阴影锥是一个柱形包围体,其侧面垂直于水平面,如图3所示.面要素基于地形的最低点和最高点生成包围体,上下底面平行于水平面,其他各面与水平面垂直,以确保要素覆盖区域全部位于此包围体内.而线要素在水平面内要拓宽成狭长的面,此步可采用要素简化时生成的缓冲区,对其宽度进行缩放即可.然后找出其每条线段经过地形的最高点和最低点,由这些最高点和最低点连接生成包围体(图4),这样就最大限度减少了包围体的面积,从而减少了渲染的开销.本研究采用上述方法,只是线要素生成包围体时,采用和面状数据一样的方法.因在简化的过程中将会生成一些新的线段,其所经过的地形高度范围可能超出原包围体的范围,从而造成渲染错误;若重新计算包围体,则需增加简化过程所需时间和存储空间.该方法可实现精确叠加,且与DEM采用的LOD模型无关,但当矢量地图数据规模很大时,即使是渲染简化后的矢量要素,也需花费大量的时间.故叠加距离视点远的要素时,本文改用近似叠加的方法.4.2线要素的快速叠加当线要素离视点很远时,即使与地形叠加是有缝的,也不会影响可视化的逼真性,所以为加快叠加的速度,可将线要素按照一定步长进行插值,对于格网DEM数据,使用是格网间距的一半作为步长.求算并存储原有点和新插入点的高程,在当线要素远离视点时,将这些点连接成三维的线,即可把矢量数据叠加在地形上.此方法所需计算量,存储空间和叠加耗时都较小.为避免“Z-buﬀerﬁghting”现象,以及部分叠加线段嵌入地面以下,可对求得高程加一个微小偏移量,使其略高于地面.4.3面要素的快速叠加在物体远离视点时,采用纹理映射代替复杂的几何模型渲染是常用的方法,如公告牌(Billboard)技术.为加快面状数据的叠加显示速度,在最低细节层次改用纹理映射方法.首先由所有面要素生成纹理图,每个要素对应特定颜色,其余地方设为透明,然后使用多重纹理的方法将其和其他纹理一起映射在地形上.此方法的关键在于纹理图的实时更新.因离视点近的区域纹理映射会产生严重的走样,故应根据视点变化,实时确定离视点较近的矢量要素,并检查该要素在纹理图上对应区域的像素值,若一像素的RGB值等于该要素设定的RGB值,则令该像素的Alpha值为255,即使其变为透明.此时纹理图上将不再显现该要素,可改用阴影锥的方法精确叠加.对于离视点较远的要素,按照同样方法检查纹理图上对应区域是否未透明的,若为透明,将其改为不透明,此时用纹理映射渲染的要素可能会边界模糊,804中国科学:信息科学第40卷第6期图3由面要素生成包围体的三维示意图图4由线要素生成包围体的二维示意图[6]但因距视点远,模糊程度将被降低到视觉可接受的范围内.5视景体裁剪及区域索引的算法大多数情况下,只有部分矢量要素位于视域范围内,故可利用视景体裁剪算法剔除视景体之外的要素,以降低渲染的开销.但因裁剪算法本身也要耗时,若整体数据量很大,但每个要素复杂度较小,则对效率提高改进不多,故本文结合区域索引的方法来减少调用裁剪算法的次数.将整个区域分为若干子区域,并记录其包含的要素.再判断每一子区域与视景体的位置关系:生成子区域的包围盒,盒高为地形的整体高度差,判断包围盒位于视景体的外部或内部,或与视景体相交1).首先生成视景体的各裁剪面,并使其法向量指向内部.如图5所示,判断包围盒8个顶点在裁剪面法向量上投影值最大的点p和值最小的点n.第i个裁剪面的方程为A i x+B i y+C i z+D i=0,p点坐标为(x p,y p,z p),将p点代入方程,定义p到面的距离为d p=A i x p+B i y p+C i z p+D i,若d p<0,则认为包围盒在裁剪面外侧,也在视景体外侧.否则同理定义d n,若d n>0则在裁剪面内侧,若d p>0且d n<0,则与裁剪面相交.记录当前位置关系,继续检查其他面.若位于任何一个面的外侧,即可认为是在视景体外侧,否则又分两种情况,一种是在每个裁剪面的内侧,则该子区域完全在视景体内;否则和视景体相交.若子区域和视景体相交,采用包围球的方法2)判断此子区域中的各要素和视景体的关系.如图6所示,计算球心到裁剪面的距离d和球的半径r,若d<−r,则在裁减面外部,若d>r则在内部,否则与裁剪面相交.此处采用包围球,因其与包围盒相比计算复杂度较低.采取上述方法,可将渲染开销始终控制在一定范围内.当视点较近时,可裁剪大多数要素,大大减少渲染开销.当距视点较远时,多数要素需被渲染,但同时远处的要素可以用更粗糙的方法渲染,在保持较好的视觉效果的同时也控制了渲染所需开销.1)S´y kora D,Jel´ınek J.Eﬃcient view frustum Culling./CESCG-2002/DSykoraJJelinek/index. html.20022)Morley M.Frustum culling in openGL.http://www.cg.tuwien.ac.at/studentwork/CESCG/CESCG-2002/DSykora-JJel-inek.2000805杨玲等:大规模矢量地图与多分辨率DEM快速叠加的方法图5包围盒VFC算法示意图图6包围球VFC算法示意图6实验为了证明本文提出方法的可行性,进行实验验证.机器配置为:CPU为Intel(R)Pentium(R)4,速度为3993MHz,内存大小为768MB,显卡型号为Intel(R)82865G Graphics controller,开发语言为VC++.NET和OpneGL.为了检验地形数据和矢量地图对渲染效果的影响,选取了两个地区的地形数据和矢量地图.对于每个地区,均采用Roettger3)的算法和Seumas[11]的算法构建DEM的多分辨率LOD模型,在其上用本文提出的方法实现矢量数据与DEM的叠加.第一幅地形数据为夏威夷岛的数字高程模型数据,文件来源为/Implemen-tation/Formats/BT.html,格式为BT文件.网格大小:1025×1025,网格间距:130.99m×149.14m.与之相应的矢量地图来自/dbedt/gis/lulc.htm,用于表示夏威夷州的土地覆盖和土地利用类型,原文件格式为ESRI的shapeﬁle.截取了位于夏威夷岛的部分,使用ArcGIS为其建立拓扑关系后,生成线状和面状两幅shapeﬁle格式的矢量地图,其中线状地图包含2906个线要素,面状地图包含1197个面要素,两幅地图包含顶点数均为168667个.两幅矢量地图均以弧段为基本单位进行简化,缓冲区宽度设为130m,只针对相邻的100个顶点进行简化,简化后保留了9771个顶点,简化程度约为5%,简化时间为约为47s.叠加效果如图7∼10所示.漫游时帧速率的变化曲线如图7和8所示.图中同时给出了对比实验结果,即完全采用阴影锥技术叠加原始地图时的帧速率变化情况.第二幅地形数据来自美国地质调查局1:25万数字高程模型,为北京及其周边地区的数字高程模型数据,范围为北纬39◦∼42◦,东京115◦∼118◦.网格大小为4097×4097.矢量地图来自全国1:1万土壤地图数据,文件格式为shapeﬁle.实验中截取相应地区的矢量数据,使用ArcGIS为其建立拓扑关系后,生成线状和面状两幅shapeﬁle格式的矢量地图,其中线状地图包含4909个线要素,面状地图包含1742个面要素,两幅地图包含顶点数均为83642个.缓冲区宽度设为124m,只针对相邻的100个顶点进行简化,简化后保留了32492个顶点,简化程度约为39%,简化时间为约为27s.帧速率如图11和12.以上叠加效果图上没有明显的缝隙和边界模糊,视觉效果比较理想.同时采用了矢量地图的LOD 模型后,漫游时的帧速率约是没采用LOD模型的两倍.更重要的事,渲染效率基本不受地形数据和矢3)Mcnally S.Binary triangle trees and terrian tessellation./McNally/progbinri.html. 2000806中国科学:信息科学第40卷第6期图7线状地图叠加效果图图8面状地图叠加效果图图9Roettger算法渲染夏威夷地形时的帧速率图图10Seumas算法渲染夏威夷地形时的帧速率图图11Roettger算法渲染北京地形时的帧速率图图12Seumas算法渲染北京地形时的帧速率图807杨玲等:大规模矢量地图与多分辨率DEM快速叠加的方法量地图的数据量的影响,同时,在视点快速变化时,可能保持较高的帧速率.移除捷径时,Mustafa等[4]的方法在要素内两两点相连形成捷径时间复杂度为O(n2),而本文方法只连接较近的m个点,其时间复杂度为O(n).由第一类捷径生成最短路径时,我们从第一个点开始,连接符合条件的距其最远的点,直到最后一点为止,故其时间复杂度也为O(n),因此本文的方法总的时间复杂度为O(n).随着数据量的增加,本方法的优势随之显现出来.由此可见,本文提出的简化方法效率较高,且保持了拓扑关系的一致性;叠加方法独立于DEM所采用的LOD模型,渲染开销可始终控制在一定范围内.7结论本文主要研究了大数据量矢量地图与多分辨率地形的无缝快速叠加显示.借助图形硬件和Voronoi 图实现了矢量数据的简化,并保持了拓扑关系的正确性.在保持简化前后拓扑关系一致和满足数据精度的前提下,本文的方法能够快速的对矢量数据进行简化,同时也能够按照简化过程的逆变换实现数据的快速重建,较好地实现了大规模量矢量地图数据的综合.以此为基础,建立了矢量数据的细节层次模型,中高层次上利用了阴影锥技术实现了矢量数据与地形的叠加渲染,在最低细节层次上,采用了较粗糙但更快速的方法替代阴影锥技术,并建立了多分辨率模型的确定标准,得到了较好的视觉效果.同时结合了视景体裁剪和区域索引等技术,提出了独立于多分辨率DEM模型的叠加算法,实现了大规模矢量地图与三维地形的精确实时叠加显示.下一步工作主要是在本文算法的基础上,研究大规模矢量地图和DEM的网络传输以及快速叠加可视化.参考文献1Douglas D H,Peucker T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature.Canad Cartogr,1973,10:112–1222Crow F.Shadow algorithms for computer graphics.P Siggraph,1977,11:242–2483Buttenﬁeld B.Transmitting vector geospatial data across the Internet.In:Proceedings of the2nd International Conference on Geographic Information Science,2002.51–644Mustafa N,Krishnan N S,Varadhan G,et al.Dynamic simpliﬁcation and visualization of large maps.Int J Geogr Inf Sci,2006,20:273–3205Mantler A,Snoeyink J.Safe sets for line simpliﬁcation.In:Abstracts of10th Annual Fall Workshop on Computational Geometry.New York:ACM,20006Schneider M,Klein R.Eﬃcient and accurate rendering of vector data on virtual landscapes.J Comput Graph Visual Comput Vis,2007,15:59–667Schneider M,Guthe M,Klein R.Real-time rendering of complex vector data on3D terrain models.In:Proceedings of the11th International Conference on VirtualSystems and Multimedia.Ghent:Archaeolingua,2005.573–5828Wartell Z,Kang E,Wasilewski T,et al.Rendering vector data over global multiresolution3D terrain.In:Proceedings on the Symposium on Data Visualization.Grenoble:Eurographics Association,2003.213–2229Wahl R,Massing M,Degener P,et al.Scalable compression of textured terrain data.J Comput Graph Visual Comput Vis,2004,12:521–52810HoﬀK E,Culver T,Keyser J,et al.Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware.In:Computer Graphics Simpliﬁcation of large maps301(SIGGRAPH’99Proceedings),1999.33:277–28611Roettger S,Heidrich W,Slusallek P,et al.Real-time generation of continuous levels of detail for heightﬁelds.In: Skala V,ed.Proceedings of International on Conference in Central Europe on Computer Graphics,Visualization and Computer Vision.Plzen:Union Agency Science,1998.315–322808。

利用SRTM数据绘制地形图及在Google Earth 中叠加显示

工程技术科技创新导报 Science and Technology Innovation Herald85美国G o o g l e 公司在2005年推出Google Ear th 软件，用户可以通过它浏览全球范围内任何一处地点的卫星影像, 包括建筑物或地形的三维图像。

这使得用户能在快速容易地查看特定区域的卫星图像和地形地貌等信息。

它的出现促进了相关行业从业人员的工作方式的改进和进步。

它已经在地质[1-5]、地理教学[6,7]、路线工程[8]、石油勘查与灾害调查[9-11]、地震[12-15]等领域应用。

随着Google Earth版本的更新和新功能的加入，相信应用前景会更加广泛。

但由于国防原因或客观条件所限，G o o g l e E a r t h 在某些地段数据量不够,其图像资料分辨率低。

拍摄角度不同也造成了部分地物轮廓不清，形状变形。

且它不能提供准确的高程数据，不利于进行地物地貌的分辨和分析。

在很多时候，还是要依赖地形图进行下一步的工作。

但地形图一般为涉密文件，不易获得，且时间上有一定的滞后性，其采用的坐标系也与G o og le E a r t h 不同，在对比应用时可能会出现偏差。

为解决上述问题，笔者下载了美国SRT M数据，应用Globa l Mapper软件进行地形图的绘制和格式转换，可以实现地形图在G oo g le E a r t h 软件界面上的叠加显示。

将卫星图像与地形图的特点相结合，更好地为实际工作服务。

1 SRTM数据介绍SRTM的全称是Shuttle Radar Top og raphy M is s ion，即航天飞机雷达地形测绘任务。

2000年2月11日上午11时44分，美国“奋进”号航天飞机在佛罗里达州卡那维拉尔角的航天发射中心发射升空，“奋进”号上搭载的S RT M系统共计进行了222小时23分钟的数据采集工作，获取北纬60度至南纬56度之间，面积超过1.19亿平方公里的9.8万亿字节的雷达影像数据，覆盖全球陆地表面的80%以上，该测量数据已覆盖中国全境。

万能地图下载器中的叠加信息设置

万能地图下载器中的叠加信息设置
许多朋友在浏览地图的时候除了浏览地图上原有的标注信息以外还希望在上面叠加一些信息并对这些信息进行管理，本文讲解的就是水经注万能地图下载器中相关叠加信息的管理。

工具/原料
水经注万能地图下载器
方法/步骤
1.把鼠标放在左上方的工具栏上可以看到相关的叠加类型信息（图1）。

图1
2.首先是“标签”，标签即为地图上的道路和文字标注等信息，关闭后地图上的文字和道路等标注信息就会关闭（图2）。

图2
3.“标注”指的是自己在地图上做的一些标注信息，勾选上即可把标注叠加在地
图上（图3）。

图3
4.“拍摄时间”可以显示地图拍摄的时间，但是需要将地图切换到“谷歌地球”
和“谷歌地球历史影像”才可以显示，勾选即可显示（图4）。

图4
5.某些地图有大字体地图比如谷歌卫星、高德电子、百度卫星和百度电子，当勾
选上“大字体”后，地图会显示成大字体地图（图5）。

图5
6.如果需要显示经纬网可以勾选上“经纬网络”，勾选后地图上会显示出经纬网
（图6）。

图6
7.同经纬网一样，如果需要显示瓦片网络，可以勾选上“瓦片网络”，这样就会
显示出来瓦片网格及其编号（图7）。

图7
8.以上就是水经注万能地图下载器中叠加信息的相关介绍，希望对大家有所帮
助。

使用js对WGS-84，GCJ-02与BD-09的坐标进行转换

使⽤js对WGS-84，GCJ-02与BD-09的坐标进⾏转换获取到经纬度在⽤百度地图进⾏定位时，却发现⾏驶轨迹的路线定到海⾥⾯去了。

从⽹上查阅，知道此⽅法。

⼀。

在进⾏地图开发过程中，我们⼀般能接触到以下三种类型的地图坐标系： 1.WGS－84原始坐标系，⼀般⽤国际GPS纪录仪记录下来的经纬度，通过GPS定位拿到的原始经纬度，Google和⾼德地图定位的的经纬度（国外）都是基于WGS－84坐标系的；但是在国内是不允许直接⽤WGS84坐标系标注的，必须经过加密后才能使⽤； 2.GCJ－02坐标系，⼜名“⽕星坐标系”，是我国国测局独创的坐标体系，由WGS－84加密⽽成，在国内，必须⾄少使⽤GCJ－02坐标系，或者使⽤在GCJ－02加密后再进⾏加密的坐标系，如百度坐标系。

⾼德和Google在国内都是使⽤GCJ－02坐标系，可以说，GCJ－02是国内最⼴泛使⽤的坐标系； 3.百度坐标系:bd-09，百度坐标系是在GCJ－02坐标系的基础上再次加密偏移后形成的坐标系，只适⽤于百度地图。

(⽬前百度API提供了从其它坐标系转换为百度坐标系的API，但却没有从百度坐标系转为其他坐标系的API) ⼆。

为什么会发⽣偏移？ 1.由于坐标系之间不兼容，如在百度地图上定位的经纬度拿到⾼德地图上直接描点就肯定会发⽣偏移；只考虑国内的情况，⾼德地图和Google地图是可以不经过转换也能够准确显⽰的（在国内⽤的都是GCJ－02坐标系）；下⾯是收录了⽹上的WGS－84，GCJ－02，百度坐标系(bd-09)之间的相互转换的⽅法，经测试，是转换后相对准确可⽤的：var GPS = {PI : 3.14159265358979324,x_pi : 3.14159265358979324 * 3000.0 / 180.0,delta : function (lat, lon) {// Krasovsky 1940//// a = 6378245.0, 1/f = 298.3// b = a * (1 - f)// ee = (a^2 - b^2) / a^2;var a = 6378245.0; // a: 卫星椭球坐标投影到平⾯地图坐标系的投影因⼦。

高德轨迹纠偏逻辑

高德轨迹纠偏逻辑随着科技的发展和定位系统的不断完善，人们的出行方式越来越依赖于导航软件。

其中，高德地图作为国内领先的导航提供商，其轨迹纠偏逻辑的设计与实现显得尤为重要。

本文将对高德轨迹纠偏逻辑进行详细解析，以帮助读者更好地了解这一技术原理。

一、概述轨迹纠偏，也称为轨迹矫正或路径调整，是指根据一定的算法和规则，对原始轨迹数据进行处理，使其更加符合实际情况的过程。

在实际应用中，由于受到定位误差、道路信息更新等因素的影响，用户实际行驶的轨迹可能会与规划路径存在一定的偏差。

为了提高导航的准确性和用户体验，需要对这些偏差进行纠正。

二、高德轨迹纠偏逻辑1.数据预处理在纠偏之前，需要对原始轨迹数据进行预处理，包括数据清洗、格式转换、坐标系转换等。

数据清洗主要是去除无效、异常数据，保证数据的准确性和可靠性；格式转换是将原始轨迹数据转换成统一的格式，便于后续处理；坐标系转换则是将轨迹数据从一种坐标系转换到另一种坐标系，以便与地图数据对齐。

2.路径规划在进行轨迹纠偏时，需要先进行路径规划。

高德地图采用先进的路径规划算法，根据起点和终点之间的道路网络信息，为用户规划出最优路径。

路径规划算法需要考虑多种因素，如道路长度、道路等级、交通状况等。

在规划过程中，高德地图会根据实时交通信息和历史数据预测路况，为用户提供更加准确的路径规划结果。

3.轨迹匹配在完成路径规划后，高德地图会将原始轨迹数据与规划路径进行匹配。

这一过程主要采用动态规划算法，将原始轨迹点按照距离和方向等相似度指标分配到规划路径上。

在匹配过程中，高德地图会考虑道路曲率、交叉路口等因素，以确保匹配的准确性和可靠性。

4.纠偏处理根据匹配结果，高德地图会对原始轨迹数据进行纠偏处理。

对于偏离规划路径的轨迹点，高德地图会根据道路网络信息和实时交通状况对其进行调整，使其更加符合实际情况。

纠偏处理算法会考虑多种因素，如道路宽度、交叉路口转向限制等，以保证纠偏后的轨迹更加准确和可靠。

MapGIS地图应用系列之MapGIS地图及Google地图叠加

MapGIS地图应用系列（三）--MapGIS地图与Google地图叠加SOA架构的应用极大地促进了GIS行业的发展，各种功能以服务的方式提供也成了现阶段GIS的一个发展方向和应用热点。

现在的Web开发中，用Google地图等在线地图作为底图，在其上叠加自有的矢量地图，实现相应的功能已经成为WebGIS开发者不二的选择，这篇文章主要介绍怎样使自己的MapGIS地图与Google在线地图实现无缝叠加。

MapGIS数据采用的投影的椭球以及投影方式与Google均不同，是以在进行叠加之前，需要进行投影变换。

要实现MapGIS地图与Google地图叠加，需要经过如下个步骤：（1）新建用于投影变换的用户自定义坐标系google坐标系。

打开GDB企业管理器，在地理数据库中点击"空间参照系"-"用户自定义坐标系"-"创建"，打开"空间属性"对话框："坐标系"选项卡下设置"空间参照系类型"为"投影平面直角坐标系"，设置"空间参照系名称"为"google坐标系"；"地理坐标系"选项卡下，设置"标准椭球"为"WGS-84"，设置"角度单位"-"单位"为，设置"本初子午线"-"名称"为格林威治；"投影坐标系"选项卡下，设置"投影"-“类型"为"WEB墨卡托投影"，设置"长度单位"为米；"坐标轴设置"选项卡下，设置"坐标轴维数"为2，分别设置XY轴的单位为米，精度为9；"高程坐标系设置"选项卡下，设置"大地水准面类型"为"1985国家高程基准"。

百度地图和高德地图坐标系的互相转换

百度地图和⾼德地图坐标系的互相转换GPS、⾕歌、百度、⾼德坐标相互转换⼀、在进⾏地图开发过程中，我们⼀般能接触到以下三种类型的地图坐标系：1.WGS－84原始坐标系，⼀般⽤国际GPS纪录仪记录下来的经纬度，通过GPS定位拿到的原始经纬度，Google和⾼德地图定位的的经纬度（国外）都是基于WGS－84坐标系的；但是在国内是不允许直接⽤WGS84坐标系标注的，必须经过加密后才能使⽤；2.GCJ－02坐标系，⼜名“⽕星坐标系”，是我国国测局独创的坐标体系，由WGS－84加密⽽成，在国内，必须⾄少使⽤GCJ－02坐标系，或者使⽤在GCJ－02加密后再进⾏加密的坐标系，如百度坐标系。

⾼德和Google在国内都是使⽤GCJ－02坐标系，可以说，GCJ－02是国内最⼴泛使⽤的坐标系；3.百度坐标系:bd-09，百度坐标系是在GCJ－02坐标系的基础上再次加密偏移后形成的坐标系，只适⽤于百度地图。

(⽬前百度API提供了从其它坐标系转换为百度坐标系的API，但却没有从百度坐标系转为其他坐标系的API)⼆、为什么会发⽣偏移？1.由于坐标系之间不兼容，如在百度地图上定位的经纬度拿到⾼德地图上直接描点就肯定会发⽣偏移；只考虑国内的情况，⾼德地图和Google地图是可以不经过转换也能够准确显⽰的（在国内⽤的都是GCJ－02坐标系）；下⾯是收录了⽹上的WGS－84，GCJ－02，百度坐标系(bd-09)之间的相互转换的⽅法，经测试，是转换后相对准确可⽤的。

三、代码Java：package com.zehin.map.util;public class GPSUtil {public static double pi = 3.1415926535897932384626;public static double x_pi = 3.14159265358979324 * 3000.0 / 180.0;public static double a = 6378245.0;public static double ee = 0.00669342162296594323;public static double transformLat(double x, double y) {double ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y+ 0.2 * Math.sqrt(Math.abs(x));ret += (20.0 * Math.sin(6.0 * x * pi) + 20.0 * Math.sin(2.0 * x * pi)) * 2.0 / 3.0;ret += (20.0 * Math.sin(y * pi) + 40.0 * Math.sin(y / 3.0 * pi)) * 2.0 / 3.0;ret += (160.0 * Math.sin(y / 12.0 * pi) + 320 * Math.sin(y * pi / 30.0)) * 2.0 / 3.0;return ret;}public static double transformLon(double x, double y) {double ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1* Math.sqrt(Math.abs(x));ret += (20.0 * Math.sin(6.0 * x * pi) + 20.0 * Math.sin(2.0 * x * pi)) * 2.0 / 3.0;ret += (20.0 * Math.sin(x * pi) + 40.0 * Math.sin(x / 3.0 * pi)) * 2.0 / 3.0;ret += (150.0 * Math.sin(x / 12.0 * pi) + 300.0 * Math.sin(x / 30.0* pi)) * 2.0 / 3.0;return ret;}public static double[] transform(double lat, double lon) {if (outOfChina(lat, lon)) {return new double[]{lat,lon};}double dLat = transformLat(lon - 105.0, lat - 35.0);double dLon = transformLon(lon - 105.0, lat - 35.0);double radLat = lat / 180.0 * pi;double magic = Math.sin(radLat);magic = 1 - ee * magic * magic;double sqrtMagic = Math.sqrt(magic);dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * sqrtMagic) * pi);dLon = (dLon * 180.0) / (a / sqrtMagic * Math.cos(radLat) * pi);double mgLat = lat + dLat;double mgLon = lon + dLon;return new double[]{mgLat,mgLon};}public static boolean outOfChina(double lat, double lon) {if (lon < 72.004 || lon > 137.8347)return true;if (lat < 0.8293 || lat > 55.8271)return true;return false;}/*** 84 to ⽕星坐标系 (GCJ-02) World Geodetic System ==> Mars Geodetic System** @param lat* @param lon* @return*/public static double[] gps84_To_Gcj02(double lat, double lon) {if (outOfChina(lat, lon)) {return new double[]{lat,lon};}double dLat = transformLat(lon - 105.0, lat - 35.0);double dLon = transformLon(lon - 105.0, lat - 35.0);double radLat = lat / 180.0 * pi;double magic = Math.sin(radLat);magic = 1 - ee * magic * magic;double sqrtMagic = Math.sqrt(magic);dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * sqrtMagic) * pi);dLon = (dLon * 180.0) / (a / sqrtMagic * Math.cos(radLat) * pi);double mgLat = lat + dLat;double mgLon = lon + dLon;return new double[]{mgLat, mgLon};}/*** * ⽕星坐标系 (GCJ-02) to 84 * * @param lon * @param lat * @return* */public static double[] gcj02_To_Gps84(double lat, double lon) {double[] gps = transform(lat, lon);double lontitude = lon * 2 - gps[1];double latitude = lat * 2 - gps[0];return new double[]{latitude, lontitude};}/*** ⽕星坐标系 (GCJ-02) 与百度坐标系 (BD-09) 的转换算法将 GCJ-02 坐标转换成 BD-09 坐标** @param lat* @param lon*/public static double[] gcj02_To_Bd09(double lat, double lon) {double x = lon, y = lat;double z = Math.sqrt(x * x + y * y) + 0.00002 * Math.sin(y * x_pi);double theta = Math.atan2(y, x) + 0.000003 * Math.cos(x * x_pi);double tempLon = z * Math.cos(theta) + 0.0065;double tempLat = z * Math.sin(theta) + 0.006;double[] gps = {tempLat,tempLon};return gps;}/*** * ⽕星坐标系 (GCJ-02) 与百度坐标系 (BD-09) 的转换算法 * * 将 BD-09 坐标转换成GCJ-02 坐标 * * @param * bd_lat * @param bd_lon * @return*/public static double[] bd09_To_Gcj02(double lat, double lon) {double x = lon - 0.0065, y = lat - 0.006;double z = Math.sqrt(x * x + y * y) - 0.00002 * Math.sin(y * x_pi);double theta = Math.atan2(y, x) - 0.000003 * Math.cos(x * x_pi);double tempLon = z * Math.cos(theta);double tempLat = z * Math.sin(theta);double[] gps = {tempLat,tempLon};return gps;}/**将gps84转为bd09* @param lat* @param lon* @return*/public static double[] gps84_To_bd09(double lat,double lon){double[] gcj02 = gps84_To_Gcj02(lat,lon);double[] bd09 = gcj02_To_Bd09(gcj02[0],gcj02[1]);return bd09;}public static double[] bd09_To_gps84(double lat,double lon){double[] gcj02 = bd09_To_Gcj02(lat, lon);double[] gps84 = gcj02_To_Gps84(gcj02[0], gcj02[1]);//保留⼩数点后六位gps84[0] = retain6(gps84[0]);gps84[1] = retain6(gps84[1]);return gps84;}/**保留⼩数点后六位* @param num* @return*/private static double retain6(double num){String result = String .format("%.6f", num);return Double.valueOf(result);}}c#：public class GpsUtil{public static double pi = 3.1415926535897932384626;public static double x_pi = 3.14159265358979324 * 3000.0 / 180.0;public static double a = 6378245.0;public static double ee = 0.00669342162296594323;public static double TransformLat(double x, double y){double ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y+ 0.2 * Math.Sqrt(Math.Abs(x));ret += (20.0 * Math.Sin(6.0 * x * pi) + 20.0 * Math.Sin(2.0 * x * pi)) * 2.0 / 3.0;ret += (20.0 * Math.Sin(y * pi) + 40.0 * Math.Sin(y / 3.0 * pi)) * 2.0 / 3.0;ret += (160.0 * Math.Sin(y / 12.0 * pi) + 320 * Math.Sin(y * pi / 30.0)) * 2.0 / 3.0; return ret;}public static double TransformLon(double x, double y){double ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1* Math.Sqrt(Math.Abs(x));ret += (20.0 * Math.Sin(6.0 * x * pi) + 20.0 * Math.Sin(2.0 * x * pi)) * 2.0 / 3.0;ret += (20.0 * Math.Sin(x * pi) + 40.0 * Math.Sin(x / 3.0 * pi)) * 2.0 / 3.0;ret += (150.0 * Math.Sin(x / 12.0 * pi) + 300.0 * Math.Sin(x / 30.0* pi)) * 2.0 / 3.0;return ret;}public static double[] transform(double lat, double lon){if (OutOfChina(lat, lon)){return new double[] { lat, lon };}double dLat = TransformLat(lon - 105.0, lat - 35.0);double dLon = TransformLon(lon - 105.0, lat - 35.0);double radLat = lat / 180.0 * pi;double magic = Math.Sin(radLat);magic = 1 - ee * magic * magic;double SqrtMagic = Math.Sqrt(magic);dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * SqrtMagic) * pi);dLon = (dLon * 180.0) / (a / SqrtMagic * Math.Cos(radLat) * pi);double mgLat = lat + dLat;double mgLon = lon + dLon;return new double[] { mgLat, mgLon };}public static bool OutOfChina(double lat, double lon){if (lon < 72.004 || lon > 137.8347)return true;if (lat < 0.8293 || lat > 55.8271)return true;return false;}/*** 84 to ⽕星坐标系 (GCJ-02) World Geodetic System ==> Mars Geodetic System ** @param lat* @param lon* @return*/public static double[] Gps84ToGcj02(double lat, double lon){if (OutOfChina(lat, lon)){return new double[] { lat, lon };}double dLat = TransformLat(lon - 105.0, lat - 35.0);double dLon = TransformLon(lon - 105.0, lat - 35.0);double radLat = lat / 180.0 * pi;double magic = Math.Sin(radLat);magic = 1 - ee * magic * magic;double SqrtMagic = Math.Sqrt(magic);dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * SqrtMagic) * pi);dLon = (dLon * 180.0) / (a / SqrtMagic * Math.Cos(radLat) * pi);double mgLat = lat + dLat;double mgLon = lon + dLon;return new double[] { mgLat, mgLon };}/*** * ⽕星坐标系 (GCJ-02) to 84 * * @param lon * @param lat * @return* */public static double[] Gcj02ToGps84(double lat, double lon){double[] gps = transform(lat, lon);double lontitude = lon * 2 - gps[1];double latitude = lat * 2 - gps[0];return new double[] { latitude, lontitude };}/// <summary>/// ⽕星坐标系 (GCJ-02) 与百度坐标系 (BD-09) 的转换算法将 GCJ-02 坐标转换成 BD-09 坐标 /// ⾼德⾕歌转为百度/// </summary>/// <param name="lat"></param>/// <param name="lon"></param>/// <returns></returns>public static double[] Gcj02ToBd09(double lat, double lon){double x = lon, y = lat;double z = Math.Sqrt(x * x + y * y) + 0.00002 * Math.Sin(y * x_pi);double theta = Math.Atan2(y, x) + 0.000003 * Math.Cos(x * x_pi);double tempLon = z * Math.Cos(theta) + 0.0065;double tempLat = z * Math.Sin(theta) + 0.006;double[] gps = { tempLat, tempLon };return gps;}/// <summary>/// ⽕星坐标系 (GCJ-02) 与百度坐标系 (BD-09) 的转换算法 * * 将 BD-09 坐标转换成GCJ-02 坐标 /// 百度坐标转为⾼德⾕歌坐标/// </summary>/// <param name="lat"></param>/// <param name="lon"></param>/// <returns></returns>public static double[] Bd09ToGcj02(double lat, double lon){double x = lon - 0.0065, y = lat - 0.006;double z = Math.Sqrt(x * x + y * y) - 0.00002 * Math.Sin(y * x_pi);double theta = Math.Atan2(y, x) - 0.000003 * Math.Cos(x * x_pi);double tempLon = z * Math.Cos(theta);double tempLat = z * Math.Sin(theta);double[] gps = { tempLat, tempLon };return gps;}/// <summary>/// gps84转为bd09/// GPS坐标转为百度坐标/// </summary>/// <param name="lat"></param>/// <param name="lon"></param>/// <returns></returns>public static double[] Gps84ToBd09(double lat, double lon){double[] gcj02 = Gps84ToGcj02(lat, lon);double[] bd09 = Gcj02ToBd09(gcj02[0], gcj02[1]);return bd09;}/// <summary>/// 百度坐标转成GPS坐标/// </summary>/// <param name="lat"></param>/// <param name="lon"></param>/// <returns></returns>public static double[] Bd09ToGps84(double lat, double lon){double[] gcj02 = Bd09ToGcj02(lat, lon);double[] gps84 = Gcj02ToGps84(gcj02[0], gcj02[1]);//保留⼩数点后六位gps84[0] = Retain6(gps84[0]);gps84[1] = Retain6(gps84[1]);return gps84;}/// <summary>/// 保留⼩数点后六位/// </summary>/// <param name="num"></param>/// <returns></returns>private static double Retain6(double num){String result = String.Format("%.6f", num); return Double.Parse(result);}}。

ArcGIS中将WGS84坐标转换为北京54或者西安80坐标系

ArcGIS中将WGS84坐标转换为北京54或者西安80坐标系导读ArcGIS的投影变换结合空间调整功能实现不同坐标系统的相对精确的转换。

GPS（全球定位系统）在资源与环境调查中的应用日益广泛。

然而在这些数据与国内其他来源的地理数据进行叠合分析时，都面临着坐标系统转换的难题。

美国GPS采用的是WGS84坐标系统，而国内的地图数据多是北京54，西安80坐标系以及地方自己定义的坐标系统。

不同坐标系统之间的转换有严格的数学定义和转换方程。

如3参数法，7参数法，10参数（arcgis），只有获得当地的精确地参考坐标，才能将这些参数求出来，进行精确的转换。

然而对大多数非测绘类的用户，很难获得这些参数。

因此经常见到对定位不太精确的用户，在软件中随便选择一个参数进行转换。

作者尝试利用ArcGIS的投影变换结合空间调整功能实现不同坐标系统的相对精确的转换。

由于ArcGIS中提供6个地方的转换方式，Beijing_1954_To_WGS_1984_1 15918 China - Orduz basin （适用鄂尔多斯盆地）Beijing_1954_To_WGS_1984_2 15919 China - offshore Yellow Sea （黄海地区）Beijing_1954_To_WGS_1984_3 15920 China - offshore South China Sea - Pearl River basin （南海及珠江盆地）Beijing_1954_To_WGS_1984_4 15921 China - south and west Tarim basin （西南塔里木盆地）Beijing_1954_To_WGS_1984_5 15935 China - south and west Tarim basin （西南塔里木盆地）Beijing_1954_To_WGS_1984_6 15936 China - Orduz basin （鄂尔多斯盆地）其中1,4,6为3参数法转换，2，3，5为7参数转换。

矢量面 84坐标系转高德坐标系

矢量面 84坐标系转高德坐标系矢量面 84坐标系转高德坐标系：深度解析与实践应用1. 矢量面 84坐标系的基本概念与特点在地理信息系统（GIS）领域中，矢量面 84坐标系是一种地理坐标系，通常用于描述地球表面上的点、线和面。

它采用经度和纬度作为坐标单位，以地球椭球体为基准，广泛应用于地图制作、空间分析和位置服务等领域。

矢量面 84坐标系具有高精度、全球通用性和易于存储和传输等特点，因此在地理信息数据处理与管理中占据重要地位。

2. 高德坐标系的概念及与矢量面 84坐标系的对比高德坐标系是一种由中国高德地图开发的地理坐标系，其基准系统与矢量面 84坐标系不尽相同。

高德坐标系采用平面直角坐标系，以国内地图为基准，具有更好的适应性和精度，特别适用于国内的地理信息服务与应用。

与矢量面 84坐标系相比，高德坐标系更贴合国内实际情况，因此在大众导航、地图检索和位置定位等方面有更好的效果。

3. 矢量面 84坐标系转高德坐标系的需求及实际应用随着定位技术和地图服务的迅速发展，矢量面 84坐标系转高德坐标系的需求也日益凸显。

在实际应用中，由于矢量面 84坐标系与高德坐标系的基准系统不同，需要通过对坐标数据进行转换，以便在高德地图平台上进行准确地理位置展示和查询。

这种转换不仅涉及坐标系的转换计算，还需要考虑地图投影、数据精度和误差控制等因素，因此具有一定的技术难度和挑战性。

4. 矢量面 84坐标系转高德坐标系的计算方法与工具实现矢量面 84坐标系向高德坐标系的转换，通常可以借助专业的地理信息处理软件或在线地图服务平台。

其中，常用的转换方法包括数学计算法、投影转换法和基于开放接口的在线转换服务等。

这些方法各有优劣，需要根据具体情况选择合适的工具和技术方案，以确保转换结果的准确性和可靠性。

5. 个人观点和实际应用建议从个人角度看，矢量面 84坐标系转高德坐标系是一个复杂而有挑战的技术问题，需要深入了解地理信息坐标系的原理与转换方法，并结合实际需求选择合适的转换工具和策略。

84坐标转高德坐标函数

要将84坐标（通常是WGS84坐标系）转换为高德坐标（通常是中国大地坐标系），需要进行一系列的地理坐标转换。

这里是一个简化的流程，并给出相应的Python函数：1.转换流程:o将WGS84的经纬度转换为笛卡尔坐标（X, Y, Z）。

o使用坐标转换模型将笛卡尔坐标转换为高德坐标。

2.使用Python进行转换:首先，你需要安装一些Python库：pyproj和numpy。

bash复制代码pip install pyproj numpy然后，你可以使用以下代码进行转换：python复制代码import pyprojimport numpy as npdef wgs84_to_gcj02(lon, lat):# 设置WGS84和GCJ02的投影转换wgs84 = pyproj.Proj(proj='latlong', datum='WGS84')gcj02 = pyproj.Proj(proj='latlong', datum='GCJ02')# 转换经纬度到GCJ02x, y = pyproj.transform(wgs84, gcj02, lon, lat)return x, y3.使用方法:如果你有一个点的经纬度坐标，你可以这样转换：python复制代码lon = 116.397428# 示例经度值，你可以替换为其他值lat = 39.9042# 示例纬度值，你可以替换为其他值x, y = wgs84_to_gcj02(lon, lat)print(f"GCJ02 coordinates: {x}, {y}")注意：这只是一个简化的转换方法，对于更精确的转换，可能需要使用更复杂的模型和考虑其他因素。

wkid=4326,4490,cgcs2000,坐标系总结（高德爬取的坐标叠加到84上是什么样）

wkid=4326,4490,cgcs2000,坐标系总结（⾼德爬取的坐标叠加到84上是什么样）⾼德爬取的坐标叠加到84上是什么样坐标是偏移的，要转⼀下哈，这⾥给⼀个流⾏的python# -*- coding: utf-8 -*-import jsonimport mathimport arcpyimport osx_pi = 3.14159265358979324 * 3000.0 / 180.0pi = 3.1415926535897932384626 # πa = 6378245.0 # 长半轴ee = 0.00669342162296594323 # 扁率def gcj02towgs84(lng, lat):"""GCJ02(⽕星坐标系)转GPS84:param lng:⽕星坐标系的经度:param lat:⽕星坐标系纬度:return:"""if out_of_china(lng, lat):return lng, latdlat = transformlat(lng - 105.0, lat - 35.0)dlng = transformlng(lng - 105.0, lat - 35.0)radlat = lat / 180.0 * pimagic = math.sin(radlat)magic = 1 - ee * magic * magicsqrtmagic = math.sqrt(magic)dlat = (dlat * 180.0) / ((a * (1 - ee)) / (magic * sqrtmagic) * pi)dlng = (dlng * 180.0) / (a / sqrtmagic * math.cos(radlat) * pi)mglat = lat + dlatmglng = lng + dlngreturn [lng * 2 - mglng, lat * 2 - mglat]def transformlat(lng, lat):ret = -100.0 + 2.0 * lng + 3.0 * lat + 0.2 * lat * lat + \0.1 * lng * lat + 0.2 * math.sqrt(math.fabs(lng))ret += (20.0 * math.sin(6.0 * lng * pi) + 20.0 *math.sin(2.0 * lng * pi)) * 2.0 / 3.0ret += (20.0 * math.sin(lat * pi) + 40.0 *math.sin(lat / 3.0 * pi)) * 2.0 / 3.0ret += (160.0 * math.sin(lat / 12.0 * pi) + 320 *math.sin(lat * pi / 30.0)) * 2.0 / 3.0return retdef transformlng(lng, lat):ret = 300.0 + lng + 2.0 * lat + 0.1 * lng * lng + \0.1 * lng * lat + 0.1 * math.sqrt(math.fabs(lng))ret += (20.0 * math.sin(6.0 * lng * pi) + 20.0 *math.sin(2.0 * lng * pi)) * 2.0 / 3.0ret += (20.0 * math.sin(lng * pi) + 40.0 *math.sin(lng / 3.0 * pi)) * 2.0 / 3.0ret += (150.0 * math.sin(lng / 12.0 * pi) + 300.0 *math.sin(lng / 30.0 * pi)) * 2.0 / 3.0return retdef out_of_china(lng, lat):"""判断是否在国内，不在国内不做偏移:param lng::param lat::return:"""if lng < 72.004 or lng > 137.8347:return Trueif lat < 0.8293 or lat > 55.8271:return Truereturn Falseif__name__ == '__main__':# [lng,lat]=[120.769927,32.042828]# [dstlng, dstlat] = gcj02towgs84(lng, lat)# print(dstlng, dstlat)#创建featureclass poi3#添加字段path=r'E:\nanxxx_gcj02.gdb\poi3'spatialref=arcpy.SpatialReference(4326)fc=arcpy.CreateFeatureclass_management(os.path.dirname(path), os.path.basename(path),"POINT", "", "", "",spatialref)arcpy.AddField_management(fc, "name", "TEXT","","",250,"","NULLABLE")arcpy.AddField_management(fc, "type1", "TEXT","","",50,"","NULLABLE")arcpy.AddField_management(fc, "type2", "TEXT","","",50,"","NULLABLE")arcpy.AddField_management(fc, "type3", "TEXT","","",50,"","NULLABLE")arcpy.AddField_management(fc, "address", "TEXT","","",150,"","NULLABLE")cur2=arcpy.da.InsertCursor(fc, ["SHAPE@","name","type1","type2","type3","address"])gcj02=r'E:\nantonxxxgcj02.gdb\poi2'with arcpy.da.SearchCursor(gcj02,["SHAPE@XY","name","type1","type2","type3","address"]) as cursor:for row in cursor:x,y=row[0][lng, lat] = gcj02towgs84(x, y)point = arcpy.Point(lng, lat)cur2.insertRow([point,row[1],row[2],row[3],row[4],row[5]])del cur2print'over'View Code国内的常⽤坐标系1、WGS-84坐标系：地⼼坐标系，GPS原始坐标体系在中国，任何⼀个地图产品都不允许使⽤GPS坐标，据说是为了保密。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如何将WGS84矢量地图反纠偏后与高德地图叠加
这里以成都为例，说明如何将WGS84坐标系的矢量地图进行反纠偏和进行墨卡托坐标系转换后与高德地图进行叠加的方法。

首先，请到水经注软件官网下载安装水经注矢量地图转换器，然后请按以下步聚进行操作。

第一步：导入源数据
在软件中点击“输入”按钮，如下图所示。

在显示的“输入矢量地图文件”对话框中点击“添加”按钮，选择添加成都的所有矢量图层文件，如下图所示。

在该对话框中点击“确定”按钮完成文件选择。

第二步：设置输出路径
点击“输出”按钮，如下图所示。

在显示的“浏览文件夹”中选择保存路径，如下图所示。

这里我们选择“D:\Test”目录，点击“确定”按钮完成设置。

第三步：设置转换参数
软件默认只选择“反纠偏”选项，这里我们把“生成墨卡托坐标系”也选择上，如下图所示。

第四步：数据转换
点击“转换”按钮，开始对所有文件进行反纠偏和进行墨卡托坐标系转换处理，如下图所示。

第五步：结果验证
用《水经注高德卫星地图下载器》下载成都二环路以内数据第19级数据，如下图所示。

下载完成后，将卫星地图导出为GeoTIFF(*.tif)文件，这里选择不叠加标签数据。

众所周知，高德地图和谷歌的国内服务器的卫星地图一样是有一定偏移的，这里我们没有对该卫星地图进行任何纠偏校正处理，以保证原有的清晰度和坐标系。

启动ArcMap将下载的卫星地图在ArcMap中打开，在右下角可以看到当前卫星地图坐标是墨卡托坐标（也可通过图层属性查看），如下图所示。

图所示。