2020年高考卷数学(浙江卷)附答案

合集下载

浙江省杭州市(新版)2024高考数学统编版(五四制)测试(综合卷)完整试卷

浙江省杭州市（新版）2024高考数学统编版（五四制）测试(综合卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题已知平面向量，且，则（）A．2B．-2C．D．第(2)题设，，，则（）A．B．C．D．第(3)题函数y＝sin2x＋cos 2x的最小正周期为（）A．B．C．πD．2π第(4)题已知为等比数列，，且，则的公比的取值范围是（）A．B．C．D．第(5)题下列选项中，所得到的结果为4的是（）A．双曲线的焦距B．的值C．函数的最小正周期D．数据的下四分位数第(6)题将函数图象上所有点的横坐标缩小为原来的，再向右平移个单位长度，得到函数的图象，若在上有两个不同的零点，，则（）A．B．C．D．第(7)题样本数据16，20，21，24，22，14，18，28的分位数为（）A．16B．14C．23D．22第(8)题已知点在关于x，y的不等式所表示的平面区域内，则的最小值为（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题如图，已知函数的图象，，则（）A．B．C．D．第(2)题某保险公司销售某种保险产品，根据2020年全年该产品的销售额（单位：万元）和该产品的销售额占总销售额的百分比，绘制出如图所示的双层饼图．根据双层饼图，下列说法正确的是（）A．2020年第四季度的销售额为280万元B．2020年上半年的总销售额为500万元C．2020年2月份的销售额为60万元D．2020年12个月的月销售额的众数为60万元第(3)题已知平面向量，且，满足，若﹐则可能的取值为（）A．4B．8C．12D．16三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题若正数x，y满足，则的最小值是___________.第(2)题不等式的解集是 .第(3)题在三角形ABC中，角A、B、C的对边分别为a、b、c，且∠BAC的平分线交BC于D，若，则的最小值为________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题设函数．（1）当时，求不等式的解集；（2）若，，，证明．第(2)题为了促进消费，某商场针对会员客户推出会员积分兑换商品活动：每位会员客户可在价值80元，90元，100元的，，三种商品中选择一种使用积分进行兑换，每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1000积分，且甲兑换，，三种商品的概率分别为，，，乙兑换，，三种商品的概率分别为，，，且他们兑换何种商品相互独立.(1)求甲、乙两人兑换同一种商品的概率；(2)记为两人兑换商品后的积分总余额，求的分布列与期望第(3)题如图，在直三棱柱中，底面是以为底边的等腰直角三角形，，.(1)求证：平面平面；(2)求点到平面的距离.第(4)题如图，在三棱柱中，是等边三角形，侧面底面，且，，M是的中点．(1)证明：．(2)求二面角的正弦值．第(5)题已知为等差数列的前项和，且，当时，．(1)求数列的通项公式；(2)若，求数列的前项和．。

专题07 平面向量解析版(2016-2020)高考数学(理)真题分项详解

专题07 平面向量【2020年】1.（2020·新课标Ⅲ）已知向量a ，b 满足||5a =，||6b =，6a b ⋅=-，则cos ,=+a a b （） A. 3135-B. 1935-C.1735D.1935【答案】D 【解析】5a =，6b =，6a b ⋅=-，()225619a a b a a b ∴⋅+=+⋅=-=.()22222526367a b a ba ab b +=+=+⋅+=-⨯+=，因此，()1919cos ,5735a a ba ab a a b⋅+<+>===⨯⋅+. 2.（2020·山东卷）已知P 是边长为2的正六边形ABCDEF 内的一点，则AP AB ⋅ 的取值范用是（） A. ()2,6- B. (6,2)- C. (2,4)- D. (4,6)-【答案】A 【解析】AB 的模为2，根据正六边形的特征，可以得到AP 在AB 方向上的投影的取值范围是(1,3)-，结合向量数量积的定义式，可知AP AB ⋅等于AB 的模与AP 在AB 方向上的投影的乘积，所以AP AB ⋅的取值范围是()2,6-，3.（2020·北京卷）已知正方形ABCD 的边长为2，点P 满足1()2AP AB AC =+，则||PD =_________；PB PD ⋅=_________．【答案】 (1).5 (2). 1-【解析】以点A 为坐标原点，AB 、AD 所在直线分别为x 、y 轴建立如下图所示的平面直角坐标系，则点()0,0A 、()2,0B 、()2,2C 、()0,2D ，()()()()1112,02,22,1222AP AB AC =+=+=，则点()2,1P ，()2,1PD ∴=-，()0,1PB =-，因此，()22215PD =-+=，()021(1)1PB PD ⋅=⨯-+⨯-=-.4.（2020·天津卷）如图，在四边形ABCD 中，60,3B AB ︒∠==，6BC =，且3,2AD BC AD AB λ=⋅=-，则实数λ的值为_________，若,M N 是线段BC 上的动点，且||1MN =，则DM DN ⋅的最小值为_________．【答案】 (1). 16 (2). 132【解析】AD BC λ=，//AD BC ∴，180120BAD B ∴∠=-∠=，cos120AB AD BC AB BC AB λλ⋅=⋅=⋅1363922λλ⎛⎫=⨯⨯⨯-=-=- ⎪⎝⎭，解得16λ=，以点B 为坐标原点，BC 所在直线为x 轴建立如下图所示的平面直角坐标系xBy ，()66,0BC C =∴，,∵3,60AB ABC =∠=︒，∴A 的坐标为3332A ⎛ ⎝⎭,∵又∵16AD BC =,则533,22D ⎛⎫ ⎪ ⎪⎝⎭，设(),0M x ，则()1,0N x +（其中05x ≤≤）， 533,2DM x ⎛=- ⎝⎭，333,2DN x ⎛=- ⎝⎭，()222533321134222222DM DN x x x x x ⎛⎛⎫⎛⎫⋅=--+=-+=-+ ⎪⎪ ⎝⎭⎝⎭⎝⎭，所以，当2x =时，DM DN ⋅取得最小值132. 5.（2020·浙江卷）设1e ，2e 为单位向量，满足21|22|-≤e e ，12a e e =+，123b e e =+，设a ，b 的夹角为θ，则2cos θ的最小值为_______．【答案】2829【解析】12|2|2e e -≤，124412e e ∴-⋅+≤，1234e e ∴⋅≥， 222121222121212(44)4(1)()cos (22)(106)53e e e e a b e e e e e e a bθ+⋅+⋅⋅∴===+⋅+⋅+⋅⋅12424228(1)(1)3332953534e e =-≥-=+⋅+⨯. 6.（2020·江苏卷）在△ABC 中，43=90AB AC BAC ==︒，，∠，D 在边BC 上，延长AD 到P ，使得AP =9，若3()2PA mPB m PC =+-（m 为常数），则CD 的长度是________．【答案】185【解析】∵,,A D P 三点共线， ∴可设()0PA PD λλ=>， ∵32PA mPB m PC ⎛⎫=+- ⎪⎝⎭，∴32PD mPB m PC λ⎛⎫=+- ⎪⎝⎭，即32m m PD PB PC λλ⎛⎫- ⎪⎝⎭=+，若0m ≠且32m ≠，则,,B D C 三点共线， ∴321m m λλ⎛⎫- ⎪⎝⎭+=，即32λ=， ∵9AP =，∴3AD =，∵4AB =,3AC =,90BAC ∠=︒， ∴5BC =，设CD x =，CDA θ∠=，则5BD x =-，BDA πθ∠=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD θ+-==⋅，()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-，∵()cos cos 0θπθ+-=，∴()()2570665x x x --+=-，解得185x =，∴CD 的长度为185.当0m =时， 32PA PC =，,C D 重合，此时CD 的长度为0，当32m =时，32PA PB =，,B D 重合，此时12PA =，不合题意，舍去.7.（2020·新课标Ⅱ）已知单位向量a ，b 的夹角为45°，ka –b 与a 垂直，则k =__________.【答案】2【解析】由题意可得：211cos 452a b →→⋅=⨯⨯=，由向量垂直的充分必要条件可得：0k a b a →→→⎛⎫-⋅= ⎪⎝⎭，即：202k a a b k →→→⨯-⋅=-=，解得：2k =.8.（2020·新课标Ⅰ）设,a b 为单位向量，且||1+=a b ，则||a b -=______________.【解析】因为,a b 为单位向量，所以1a b == 所以()2222221a b a b a a b b a b +=+=+⋅+=+⋅=解得：21a b ⋅=- 所以()22223a b a b a a b b -=-=-⋅+=【2019年】1．【2019年高考全国I 卷理数】已知非零向量a ，b 满足||2||=a b ，且()-a b ⊥b ，则a 与b 的夹角为A ．π6 B ．π3C ．2π3D ．5π6【答案】B【解析】因为()-a b ⊥b ，所以2()-⋅=⋅-a b b a b b =0，所以2⋅=a b b ，所以cos θ=22||12||2⋅==⋅a b b a b b ，所以a 与b 的夹角为π3，故选B ．2．【2019年高考全国II 卷理数】已知AB →=(2,3)，AC →=(3，t )，BC →=1，则AB →·BC →= A ．−3 B ．−2 C ．2D ．3【答案】C【解析】由BC →=AC →—AB →=（1，t-3），211BC ==，得3t =，则(1,0)BC =，(2,3)(1,0)21302AB BC ==⨯+⨯=．故选C ．3．【2019年高考北京卷理数】设点A ，B ，C 不共线，则“AB →与AC →的夹角为锐角”是“||||AB AC BC +>”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】AB 与AC 的夹角为锐角，所以2222||||2||||2AB AC AB AC AB AC AB AC ++⋅>+-⋅，即22||||AB AC AC AB +>-，因为AC AB BC -=，所以|AB +AC |>|BC |；当|AB +AC |>|BC |成立时，|AB +AC |2>|AB -AC |2AB ⇒•AC >0，又因为点A ，B ，C 不共线，所以AB 与AC 的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件,故选C ．4．【2019年高考全国III 卷理数】已知a ，b 为单位向量，且a ·b =0，若2=c a ，则cos ,=a c ___________. 【答案】23【解析】因为2=c a ，0⋅=a b ，所以22⋅=⋅a c a b 2=，222||4||5||9=-⋅+=c a b b ，所以||3=c ，所以cos ,=a c 22133⋅==⨯⋅a c a c ．5．【2019年高考天津卷理数】在四边形ABCD 中，,5,30AD BC AB AD A ==∠=︒∥，点E在线段CB 的延长线上，且AE BE =，则BD AE ⋅=_____________．【答案】1-【解析】建立如图所示的直角坐标系，∠DAB =30°，23,5,AB AD ==则(23,0)B ，535(,)22D . 因为AD ∥BC ，30BAD ∠=︒，所以30ABE ∠=︒，因为AE BE =，所以30BAE ∠=︒，所以直线BE 的斜率为33，其方程为3(23)3y x =-，直线AE 的斜率为33-，其方程为33y x =-. 由3(23),333y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩得3x =，1y =-，所以(3,1)E -.所以35(,)(3,1)122BD AE =-=-.6．【2019年高考江苏卷】如图，在ABC △中，D 是BC 的中点，E 在边AB 上，BE =2EA ，AD 与CE 交于点O .若6AB AC AO EC ⋅=⋅，则ABAC的值是_____.【答案】3.【解析】如图，过点D 作DF //CE ，交AB 于点F ，由BE =2EA ，D 为BC 的中点，知BF =FE =EA ,AO =OD ．()()()3632AO EC AD AC AE AB AC AC AE =-=+-，()223131123233AB AC AC AB AB AC AB AC AB AC ⎛⎫⎛⎫=+-=-+- ⎪ ⎪⎝⎭⎝⎭22223211323322AB AC AB AC AB AC AB AC AB AC ⎛⎫=-+=-+= ⎪⎝⎭，得2213,22AB AC =即3,AB AC =故3ABAC=【2018年】1．【2018·全国I 卷】在ABC △中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC -B ．1344AB AC - C ．3144AB AC +D ．1344AB AC +【答案】A【解析】根据向量的运算法则，可得()111111222424BE BA BD BA BC BA BA AC =+=+=++ 1113124444BA BA AC BA AC =++=+，所以3144EB AB AC =-. 故选A.2．【2018·全国II 卷】已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b A ．4 B ．3 C ．2 D ．0【答案】B【解析】因为()()22222||1213⋅-=-⋅=--=+=a a b a a b a 所以选B.3．（2018·浙江卷）已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为π3，向量b 满足b 2−4e ·b +3=0，则|a −b |的最小值是 A ．3−1 B ．3+1 C ．2 D ．2−3【答案】A【解析】设，则由得，由b 2−4e ·b +3=0得因此|a −b |的最小值为圆心到直线的距离23=32减去半径1，为选A.4．【2018·天津卷】如图，在平面四边形ABCD 中，,,120,AB BC AD CD BAD ⊥⊥∠=1,AB AD ==若点E 为边CD 上的动点，则AE BE ⋅的最小值为A ．2116 B ．32C ．2516D ．3【答案】A【解析】连接AD ,取AD 中点为O ,可知ABD △为等腰三角形，而,AB BC AD CD ⊥⊥，所以BCD △为等边三角形，3BD =. 设()01DE tDC t =≤≤AE BE ⋅ ()()()2232AD DE BD DE AD BD DE AD BD DE BD DE DE =+⋅+=⋅+⋅++=+⋅+ =233322t t -+ ()01t ≤≤ 所以当14t =时，上式取最大值2116，故选A.5．【2018·北京卷】设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】C 【解析】222222699+63333-=+-=⇔⇔-++⋅=⋅+a a b a b a b a b a b b a a b b ，因为a ，b 均为单位向量，所以2222699+6=0-⋅+=⋅+⇔⋅⇔a a b b a a b b a b a ⊥b ，即“33-=+a b a b ”是“a ⊥b ”的充分必要条件.故选C.6．【2018·全国III 卷】已知向量()=1,2a ，()=2,2-b ，()=1,λc ．若()2∥c a +b ，则λ=___________．【答案】12【解析】由题可得()24,2+=a b ，()2∥c a +b ，()=1,λc ，420λ∴-=，即12λ=，故答案为12.7．【2018·上海卷】在平面直角坐标系中，已知点()10A -，、()20B ，，E 、F 是y 轴上的两个动点，且||2EF =，则AE BF ⋅的最小值为___________．【答案】-3【解析】根据题意，设E （0，a ），F （0，b ）； ∴2EF a b =-=； ∴a =b +2，或b =a +2；且()()1,2,AE a BF b ==-，； ∴2AE BF ab ⋅=-+；当a =b +2时，()22222AE BF b b b b ⋅=-++⋅=+-； ∵b 2+2b ﹣2的最小值为8434--=-； ∴AE BF ⋅的最小值为﹣3，同理求出b =a +2时，AE BF ⋅的最小值为﹣3．故答案为：﹣3．8．【2018·江苏卷】在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，()5,0B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=，则点A 的横坐标为___________．【答案】3【解析】设(),2(0)A a a a >，则由圆心C 为AB 中点得5,,2a C a +⎛⎫⎪⎝⎭易得()()():520C x x a y y a --+-=，与2y x =联立解得点D 的横坐标1,D x =所以()1,2D .所以()55,2,1,22a AB a a CD a +⎛⎫=--=-- ⎪⎝⎭，由0AB CD ⋅=得()()()2551220,230,32a a a a a a a +⎛⎫--+--=--== ⎪⎝⎭或1a =-，因为0a >，所以 3.a =【2017年】1．【2017·全国III 卷】在矩形ABCD 中，AB =1，AD =2，动点P 在以点C 为圆心且与BD 相切的圆上.若AP AB AD λμ=+，则λμ+的最大值为 A ．3B ．22C ．5D ．2【答案】A【解析】如图所示，建立平面直角坐标系.设()()()()()0,1,0,0,2,0,2,1,,A B C D P x y ，易得圆的半径5r =C 的方程是()22425x y -+=，()()(),1,0,1,2,0AP x y AB AD =-=-=，若满足AP AB AD λμ=+，则21x y μλ=⎧⎨-=-⎩ ，,12x y μλ==-，所以12xy λμ+=-+，设12x z y =-+，即102x y z -+-=，点(),P x y 在圆()22425x y -+=上，所以圆心(20),到直线102xy z -+-=的距离d r ≤21514z -≤+，解得13z ≤≤，所以z 的最大值是3，即λμ+的最大值是3，故选A ．2．【2017·全国II 卷】已知ABC △是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是 A ．2-B ．32-C ．43-D ．1-【答案】B【解析】如图，以BC 为x 轴，BC 的垂直平分线DA 为y 轴，D 为坐标原点建立平面直角坐标系，则3)A ，(1,0)B -，(1,0)C ，设(,)P x y ，所以(3)PA x y =-，(1,)PB x y =---，(1,)PC x y =--，所以(2,2)PB PC x y +=--，22()22(3)22(PA PB PC x y y x y ⋅+=-=+-2333)22-≥-，当3P 时，所求的最小值为32-，故选B ．3．【2017·北京卷】设m ,n 为非零向量，则“存在负数λ，使得λ=m n ”是“0<⋅m n ”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A【解析】若0λ∃<，使λ=m n ，则两向量,m n 反向，夹角是180︒，那么cos180⋅=︒=m n m n0-<m n ；若0⋅<m n ，那么两向量的夹角为(]90,180︒︒，并不一定反向，即不一定存在负数λ，使得λ=m n ，所以是充分而不必要条件，故选A.4．【2017·全国I 卷】已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2b |=___________．【答案】23【解析】方法一：222|2|||44||4421cos60412+=+⋅+=+⨯⨯⨯+=a b a a b b ，所以|2|1223+==a b 方法二：利用如下图形，可以判断出2+a b 的模长是以2为边长，一夹角为60°的菱形的对角线的长度，则为235．【2017·江苏卷】如图，在同一个平面内，向量OA ，OB ，OC 的模分别为1，1，2，OA 与OC 的夹角为α，且tan α=7，OB 与OC 的夹角为45°．若OC mOA nOB =+(,)m n ∈R ，则m n +=___________．【答案】3【解析】由tan 7α=可得72sin α=2cos α= 易得cos 45cos 2sin 45sin 0n m n m αα⎧︒+=⎪⎨︒-=⎪⎩2222720210n m ⎧=⎪⎪-=⎪⎩，即510570n m n m +=⎧⎨-=⎩，即得57,44m n ==，所以3m n +=．6．【2017·天津卷】在ABC △中，60A =︒∠，3AB =，2AC =．若2BD DC =，AE AC λ=-()AB λ∈R ，且4AD AE ⋅=-，则λ的值为___________．【答案】311【解析】由题可得1232cos 603,33AB AC AD AB AC ⋅=⨯⨯︒==+，则12()33AD AE AB AC ⋅=+2123()34934333311AC AB λλλλ-=⨯+⨯-⨯-⨯=-⇒=． 7．【2017·山东卷】已知12,e e 123-e e 与12λ+e e 的夹角为60︒，则实数λ的值是___________．【解析】∵221212112122)()λλλλ-⋅+=⋅-⋅-e e e e e e e ，12|2-==e ，12||λ+===e e ，cos60λ=︒=λ=． 8．【2017·浙江卷】已知向量a ，b 满足1,2,==a b 则++-a b a b 的最小值是________，最大值是___________．【答案】4，【解析】设向量,a b 的夹角为θ，则-==a b+==a b则++-=a b a b令y =[]21016,20y =+，据此可得：()()maxmin 4++-==++-==a b a ba b a b ，即++-a b a b 的最小值是4，最大值是【2016年】1.【2016高考山东理数】已知非零向量m ，n 满足4│m │=3│n │，cos<m ，n >=13.若n ⊥（t m +n ），则实数t 的值为（）（A ）4 （B ）–4 （C ）94（D ）–94【答案】B【解析】由43=m n ，可设3,4(0)k k k ==>m n ，又()t ⊥+n m n ，所以22221()cos ,34(4)41603t t n n t t k k k tk k ⋅+=⋅+⋅=⋅+=⨯⨯⨯+=+=n m n n m m n m n n , 所以4t =-，故选B.2.【2016高考新课标2理数】已知向量(1,)(3,2)a m a =-，=，且()a b b ⊥+，则m =（）（A ）－8 （B ）－6 （C ）6 （D ）8 【答案】D【解析】向量a b (4,m 2)+=-，由(a b)b +⊥得43(m 2)(2)0⨯+-⨯-=，解得m 8=，故选D.3.【2016高考新课标3理数】已知向量1(2BA = ，31()2BC = ，则ABC ∠=（） (A)30︒ (B)45︒ (C)60︒ (D)120︒【答案】A【解析】由题意，得112222cos 11||||BA BC ABC BA BC ⋅∠===⨯，所以30ABC ∠=︒，故选A ． 4.【2016年高考北京理数】设a ，b 是向量，则“||||a b =”是“||||a b a b +=-”的（） A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件【答案】D【解析】由22||||()()0a b a b a b a b a b a b +=-⇔+=-⇔⋅=⇔⊥，故是既不充分也不必要条件，故选D.5.【2016高考天津理数】已知△ABC 是边长为1的等边三角形，点E D ,分别是边BC AB ,的中点，连接DE 并延长到点F ，使得EF DE 2=，则BC AF ⋅的值为（）（A ）85-（B ）81 （C ）41 （D ）811【答案】B【解析】设BA a =，BC b =，∴11()22DE AC b a ==-，33()24DF DE b a ==-， 1353()2444AF AD DF a b a a b =+=-+-=-+，∴25353144848AF BC a b b ⋅=-⋅+=-+=，故选 B.6.【2016年高考四川理数】在平面内，定点A ，B ，C ，D 满足DA=DB =DC ,DA ⋅DB =DB ⋅DC =DC ⋅DA =-2，动点P ，M 满足AP =1，PM =MC ，则2BM 的最大值是( ) （A ）434 （B ）494 （C ）37634+ （D ）372334+ 【答案】B【解析】甴已知易得1220,DA ADC ADB D D BDC B C ∠=∠====∠=︒.以D 为原点，直线DA 为x 轴建立平面直角坐标系，如图所示，则()()()2,0,1,3,1,3.A B C ---设(),,P x y 由已知1AP =，得()2221x y -+=，又13133,,,,,2222x y x y PM MC M BM ⎛⎫⎛⎫-+++=∴∴= ⎪ ⎪⎝⎭⎝⎭()()222+1334x y BM ++∴=，它表示圆()2221x y -+=上的点()x y ，与点()1,33--的距离的平方的14，()()2222max149333144BM⎛⎫∴=++= ⎪⎝⎭，故选B.7.【2016高考新课标1卷】设向量a =(m ,1),b =(1,2),且|a +b |2=|a |2+|b |2,则m = . 【答案】－2【解析】由222||||||+=+a b a b ,得⊥a b ,所以1120m ⨯+⨯=,解得2m =-.8.【2016高考江苏卷】如图，在ABC ∆中，D 是BC 的中点，,E F 是,A D 上的两个三等分点，4BC CA ⋅=，1BF CF ⋅=- ，则BE CE ⋅ 的值是 ▲ .【答案】78【解析】因为222211436=42244AD BC FD BC BA CA BC AD BC AD --⋅=-⋅--==（）（）， 2211114123234FD BCBF CF BC AD BC AD -⋅=-⋅--==-（）（），因此22513,82FD BC ==，2222114167.22448ED BC FD BC BE CE BC ED BC ED --⋅=-⋅--===（）（） 9.【2016高考浙江理数】已知向量a 、b , ｜a ｜ =1，｜b ｜ =2，若对任意单位向量e ，均有｜a ·e ｜+｜b ·e ｜≤,则a ·b 的最大值是．【答案】12【解析】221|(a b)||a ||b |6|a b |6|a ||b |2a b 6a b 2e e e +⋅≤⋅+⋅≤⇒+≤⇒++⋅≤⇒⋅≤，即最大值为12。

横看成岭侧成峰远近高低各不同——2020年高考数学浙江卷第19题线面角问题的多角度分析

数理化解题研究2021年第01期总第494期横看成岭侧成峰远近高低各不同2020年高考数学浙江卷第19题线面角问题的多角度分析章显联(浙江省绍兴鲁迅高级中学312000)摘要：本文对2020年高考数学浙江卷第19题线面角问题进行多角度分析：非坐标形式的向量法(基底法)、三余弦定理法、等体积法、纯几何法、空间直角坐标系法.给出了复习的两个建议：关注最小，秒杀线面；重视非坐标形式的向量法.关键词：非坐标形式的向量法；线面角；两个原理中图分类号:G632 文献标识码：A 文章编号：1008 -0333(2021)01 -0036 -04一、典型考题所成角为0 ,由已知，得0C 与平面DBC 所成角也为0.由公式，得例1（2020年浙江第19题）如图1,在三棱台ABC-DEF 中，平面 ACFD 丄平面 ABC , /ACB - /ACD -45°,DC -2B C.(1) 证明：EF 丄DB ；(2) 求直线DF 与平面DBC 所成角的正弦值.本题主要考查空间直线互相垂直的判定和性质，以及直线与平面所成角的几何计算问题，考查了空间想象能力和思维能力，平面与空间互相转化能力,几何计算能力，以及逻辑推理能力，本题属综合性较强的中档题.笔者认为此题无论图1是试题难度、试题背景、命题立意,还是对数学核心素养的考查，都很到位,可谓简约不简单.它也是一道解题训练的优质题,横看成岭侧成峰，很有研究价值.解法1非坐标形式的向量法(基底法)过点D 作D0丄AC 于点0,以｛ C B ，C B ,CD ｝为基底. 不妨设 DC - 2B C -2,贝V DB - 3 , C0 - 2 , / 0CB -：,/0CD - n , /DCB - n ,设平面DBC 的法向量为n - %-CD -0,（• C B -0 得｛2% + y + 4z - 0,% + y + z - 0.C O + y C B + zC B ，贝V 由所以n - -3 C0 +2 B + CD.设直线DF 与平面DBC解法2三余弦定理法过点D 作D0丄AC 于点0,由已知,得0在平面DBC 的射影H 在/DCB 的角平分线上,设直线DF 与平面DBC 所成角为0,由已知,得0C 与平面DBC 所成角也为0.由三余弦定理，得 cos n - cos n • cos 0,cos 0 - f •463所以sin 0 -耳.解法3等体积法.过点D 作D0丄AC 于点0,设直线DF 与平面DBC 所成角为0,由已知，得0C 与平面DBC 所成角也为0.由 % - DBC 二 % - 0BC ，解得 h 二专,sin 0 二豊二专.解法4坐标形式的向量法以0为原点,0D 为Z 轴,0C 为Y 轴,在平面ABC 内, 过点0作0C 垂线为Z 轴，易求D ,C ,B 坐标，从而求得平面DBC 的法向量，利用线面角公式sin 0 - 3 •解法5纯几何法分析(1)题根据已知条件，作DH 丄AC ,根据面面垂直，可得DH 丄BC ,进一步根据直角三角形的知识可判断收稿日期：2020 -10 -05作者简介:章显联(1972. 12 -)，男，浙江省龙港人，本科，中学高级教师，从事高中数学教学研究.—36—2021年第01期总第494期数理化解题研究出厶BHC是直角三角形，且Z HBC_90°,则HB丄BC,从而可证出BC丄面DHB,最后根据棱台的定义有EF〃BC,根据平行线的性质可得EF丄DB.（2）题可先设BC_1,根据解直角三角形可得BH_1,HC_2,DH_2,DC_2,DB_3,然后找到CH与面DBC的夹角即为Z HCG,根据棱台的特点可知DF与面DBC所成角与CH与面DBC的夹角相图2等，通过计算乙HCG的正弦值，即可得到DF与面DBC所成角的正弦值.二、考题赏析本题建系有些困难,不存在明显的过同一点的两两垂直的直线.这种情况下，非坐标形式的向量法（基底法）显得更实用.本题解法以｛CO,C B,CD｝为基底，因为它们不共面长度可求,且它们的夹角也可求.应用此法，可使求解过程更自由.若CO,C B,CD是单位向量且两两垂直,就是通常的坐标形式的向量法了.坐标形式的向量法可以看作是非坐标形式的向量法的一种特殊情形.解法2中0在平面DBC的射影H在Z DCB的角平分线上，利用三余弦定理可求出0C与平面DBC所成角.B图4三正弦定理（最大角定理）设二面角M-AB-N的度数为Y,在平面M上有一条射线AC,它和棱AB所成的角为0,和平面N所成的角为//a,贝V sin a_si叩•sin y.（为了力便于记忆，我们约定:0为线棱角,a为线面角，Y为二面角）证明如图4,C0丄平面N,0B丄AB,BC丄AB,0C△0BC,△0AC,△ABC均为直角三角形,sin y_,si叩_BCBCAC，sin a_器，易得sin a_sin S•sin y.说明由sin a_sin S•sin y且sin S W1,知sin a W sin y,a W y，所以二面角的半平面M内的任意一条直线与另一个半平面N所成的线面角不大于二面角,即二面角是线面角中最大的角.若平面斜线上异于斜足的点在平面上的射影不易确定，则可转换为其他点如是操作或利用等体积法求出垂线段的长，利用公式sin O_h求得.如本题解法3.其实不管是纯几何法还是坐标形式的向量法,都能解决线面角问题，高考试题的参考答案一贯都是纯几何法与坐标形式的向量法,每种方法的学习都可促进学生能力的提高,只是各有侧重.如解法4与解法5.三余弦定理（最小角定理或爪子定理）设点A为平面a上一点，过点A的斜线在平面a上的射影为B0,BC为平面a上的任意直线,那E么Z ABC,乙0BC,乙0BA三、复习建议三角的余弦关系为cosZ ABC图3_cos Z0BC•cos Z0BA.即斜线与平面内一条直线夹角0的余弦值等于斜线与平面所成角a的余弦值乘以射影与平面内直线夹角O的余弦值,cos0_cos a-cos O.（为了便于记忆,我们约定:0为斜线角,a为线面角,O为射影角）证明如图3,^0AB,△0BC,△ABC均为直角三角形,cosQ BCAB，cosaB0AB，cosO B0，易知cosQ_cos a•cos O，得证.说明这三个角中，角0是最大的,其余弦值最小,等于另外两个角的余弦值之积.斜线与平面所成角a是斜线与平面内所有直线所成角中最小的角.1.紧扣最小，秒杀线面在研究空间角的最值与求值问题时，我们应关注最大角与最小角定理,三余弦公式与三正弦公式.这样的考查在近几年的学考、高考试题中已多次出现：例2（2019年浙江高考第8题）设三棱锥V-ABC 的底面是正三角形,侧棱长均相等,P是棱VA上的点（不含端点）.记直线PB与直线AC所成的角为a,直线PB与平面ABC所成的角为S,二面角P-AC-B的平面角为Y，则（）.A.S<Y,a<yB.S<a,0<yC.S<a,y<aD.a<0,y<0解法1由最小角原理，得S<a，记二面角V-AB-C的平面角为y'（显然y_y'），由最大角原理，得S<y，故选B.解法2（特殊位置）取V-ABC为正四面体,P是棱VA上的中点，算出a,0,y的正弦值，可得选项B.例3（2018年浙江高考第8题）已知四棱锥S-ABCD的底面是正方形，侧棱长均相等,E是线段—37—数理化解题研究2021年第01期总第494期AB上的点（不含端点）,设SE与BC所成的角为O],SE 与平面ABCD所成的角为O2,二面角S-AB-C的平面角为O3,则（）•A.O1W O2W O3B.O3W O2W O1C.O1W O3W O2D.O2W O3W O1解法1作出三个角，通过定量计算得出答案为D.解法2由最小角与最大角原理知：O1M O2,O3M O2,故选D.例4（2014年浙江高考第17题）如图5,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面的射击线CM-移动，此人为了准确瞄准目标点P,需计算由点A观察点P的仰角O的大小•若AB=15m,图5AC=25m,Z BCM=30°,贝卩tan O的最大值解析由线面角W面面角,求tan O的最大值转化为求二面角M-AC-Q的平面角•易求最大值为5j•例5（2018年11月浙江学考）四边形ABCD为矩形，沿AC将A ADC翻折成A AD'C.设二面角D'-AB-C 的平面角为O,直线AD'与BC所成的角为O1,直线AD'与平面ABC所成的角为O2,当O为锐角时，有（）•A.O2W O1W OB.O2W O W O1C.O1W O2W OD.O W O2W O1解析由最小角原理，得O1M O2,由最大角原理，得O M O2,下面比较O]与O的大小即可•故选B.例6（2018年全国高考n卷理科第20题）如图6,在三棱锥P-ABC中,AB=BC=22,PA=PB=PC=4,0为AC的中点•（1）证明：PO丄平面ABC；（2）若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面图6PAM所成角的正弦值.解析（1）略.（2）由题意，知线棱角Z CPA=60°,二面角M-PA-C为30°，由三正弦定理，得sin a=sin60°sin30°=例7（2009年浙江高考理科第17题）如图7,在长方形ABCD中,AB=2,BC=1,E为DC的中点，F为线段EC（端点除外）上一动点•现将△AFD沿AF折起,使平面—38—ABD丄平面ABC.在平面ABD内过点D作DK丄AB,K为垂足•设AK=£,则t的取值范围是•」___E.$____C d/一A B A K B图7解析由三余弦定理及已知，得cos Z DAF= cosZ DAK・cosZ BAF,又Z DAF+Z BAF二;，则cos Z DAK=tan Z BAF.在Rt△DAK中t=cos Z DAB,因此t=tanZ BAF,又由折叠前的图形，知0<Z CAB<Z BAFn<Z EAB=；.4所以tan Z CAB<tan Z BAF<tan Z EAB.所以1<t<1.考查这类空间角的大小是命题者难以割舍的情结,其本质是考查线面角与面面角定义的合理性,是考查学生数学核心素养的有效途径•2.非坐标形式的向量法非坐标形式的向量法比坐标形式的向量法应用更自由，更广泛•相比较纯几何法可避免令人深感畏惧的辅助线的添加技巧等.当然,解题方法中的选择也是当用则用，不分彼此,有时多种方法可揉合于同一道题中,特别是向量与几何的紧密联系与转化•应用非坐标形式的向量法解题的基本步骤：（1）会选基底.只需要不共面的三条线段长度可求，且它们的夹角也可求即可.（2）会表示•会用基底表示其他向量,一般只涉及向量的三角形式及其推广（闭合回路）,数乘与平行,数量积与垂直两个定理•特别是要掌握好平面法向量的求法，方法可参考高考真题解法1•（3）会用公式•运算过程中无论是平面向量还是空间向量操作完全一致，运用的公式与坐标形式的向量法一致.笔者尝试用非坐标形式的向量法研究高考数学卷，发现非坐标向量法作为解答立体几何的方法有着诸多的可取之处.例8（2018年浙江高考第19题）如图8,已知多面体ABCA1B1C1中，A1A,B1B,C1C均垂直于平面ABC, Z ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.（1）证明:AB】丄平面A]B]C]；（2）求直线AC】与平面ABB]所成的角的正弦值.解析以｛BA,B C,B—｝为基底，可证明（1）,也可求2021年第01期总第494期数理化解题研究得直线AC]与平面ABB1所成的角的正弦值为晋•例9(2019年浙江高考第19题)如图9,已知三棱柱ABC-A1B1C1,平面A1ACC1丄平面ABC,/ABC-90°,/BAC-30°,A1A二A1C-AC,E,F分别是AC,A]B]的中点(1)证明：EF丄BC；(2)求直线EF与平面A1BC所成角的余弦值.解析以｛E b]c B,C B｝为基底,可证明(1)，也可求得直线EF与平面A]BC所成角的余弦值是3•我们研究的向量是自由向图9量，运用非坐标形式的向量法无需考虑建立空间直角坐标系所需要的特殊要求,使解题过程更自由•例10(2009年浙江高考理科第17题)如图10,在长方形ABCD中,AB-2,BC-1,E为DC的中点,F为线段EC(端点除外)上一动点•现将△AFD沿AF折起，使平面ABD丄平面ABC.在平面ABD内过点D作DK丄AB,K为垂足•设AK-t，则t的取值范围是•图10解析以｛K4,KD,KF｝为基底，设DF-m,抓住折叠过程中的不变量AD-1,AB-2,由于平面ABD丄平面ABC,DK丄AB,从而DK丄平面ABC.由DF二D A+AF二d K+k A+AF，得m2二(d K+K4+AF)2.化简,得mt-1,即t——.由1<m<2,得<t<1.m2利用非坐标形式的向量法进行的上述解答,化动为静，简捷别致，令人耳目一新.例11(2000年全国高考理科第18题)如图11,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形，且/C1CB-/C1CD-/BCD-60°.(1)证明：C]C丄BD；3(2)假定CD-2,CC]-3，记Bi Ai图11面C]BD为a,面CBD为0,求二面角a-BD-0的平面角的余弦值；(3)当CD的值为多少时，能使A]C丄平面C]BD?请给出证明.解析以｛Cc1，CD,C B｝为基底，则CA]-C c]+CD+CB.(1)由BD-CD-CB,得C2C・BD-0,所以C2C丄BD.(2)易知平面a的法向量为C B；--8CC]+CD+C B，所以平面S的法向量为n--4CC]+CD+C B,从而求得a-D-S的平面角的余弦值为3•(3)当CD-1时,能使A]C丄平面C]BD.设CD-2,可证A]C丄BD,再由A]C丄BC2求得CC2-2.例12(2015年浙江省高考理科第13题)如图12,三棱锥A-BCD中，AB二AC二BD二CD-3,AD-BC-2,点M,N分别是AD,BC的中点，则异面直线AN,CM所成的角的余弦值是•解析以｛BA,BC,BD｝为基底，在△ABD,由余弦定理得cos图12/ABD-7,同理得cos/CBD-[,cos/ABC-[,BA・933B C-2,BA・B D-7,B C・BD-2.用基底表示A N,C M,AN--BA+2BC,C M-2(BD+BA-2BC),异面直线AN,CM所成的角的余弦值是简]CM-T•平面向量仅是空间向量的一种特殊情形•“平面向量”可向“空间向量”自然转化.用向量方法求解空间角度与距离问题,为某些位置关系的判断问题创立了一种新的方法•在向量的运算中,要注意数形结合,灵活运用图形的几何意义、向量的几何意义去解题.《新课程标准(2017年版)》对空间向量的应用提出了更多、更高的要求,可见非坐标形式的向量法用于解决立体几何问题,完全符合新课程标准对学生的要求•如何使非坐标形式的向量法成为学生解决立体几何问题的又一个通用的好方法,还需要我们建一步地探索与总结•参考文献:[1]章显联.高考复习要注意回归教材[J].数理化解题研究，2020(13)：15-18.[责任编辑:李璟]—39—。

5、2020年浙江省高考数学试卷及答案详情

则的零点为，， .
当时，则，，
要使，必有且，
即且，所以；
当时，则，，要使，必有 .
综上一定有 .
故选 .
【点评】
此题暂无点评
10.
【答案】
A
【考点】
并集及其运算
【解析】
此题暂无解析
【解答】
解：若取，则，
此时，包含个元素，排除选项；
若取，则，
此时，包含个元素，排除选项；
【答案】
解：当时，的方程为，
故抛物线的焦点坐标为 .
设，
，，
由
，
∴ ，
， .
由在抛物线上，
∴ .
又
，
∴ ，
∴ ，
∴ .
由，
即
，
∴ ，，，
∴ 的最大值为 .
【考点】
直线与抛物线结合的最值问题
抛物线的性质
直线与椭圆结合的最值问题
抛物线的标准方程
【解析】
此题暂无解析
【解答】
解：当时，的方程为，
3.
【答案】
B
【考点】
求线性目标函数的最值
【解析】
此题暂无解析
【解答】
解：由约束条件作出可行域如图：
联立
解得
由图可得：平移直线到点时，
有最小值，
∴ 的取值范围为 .
故选 .
【点评】
此题暂无点评
4.
【答案】
A
【考点】
函数的图象
【解析】
此题暂无解析
【解答】
解：令，
∴
，
∴函数是奇函数，故选项错误.

2020年浙江省高考数学试卷试题+答案详解

2020年普通高等学校招生全国统一考试（浙江卷）
数学
本试题卷分选择题和非选择题两部分.全卷共4页，选择题部分1至2页；非选择题部分3至4页.满分150分.考试用时120分钟、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.
2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效.
球的表面积公式
球的体积公式
其中表示球的半径
选择题部分（共40分）
一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.已知集合，，则P Q=（）
A. B. C. D.
2.已知a∈R，若a–1+(a–2)i(i为虚数单位)是实数，则a=（）
A. 1B. –1C. 2D. –2
17.设，为单位向量，满足，，，设，的夹角为，则的最小值为_______．
三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.
18.在锐角△ABC中，角A，B，C的对边分别为a，b，c，且．
（I）求角B；
（II）求cosA+cosB+cosC的取值范围．
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
7.已知等差数列{an}的前n项和Sn，公差，．记b1=S2，bn+1=Sn+2–S2n，，下列等式不可能成立的是（）
A. 2a4=a2+a6B. 2b4=b2+b6C. D.
8.已知点O（0，0），A（–2，0），B（2，0）．设点P满足|PA|–|PB|=2，且P为函数y= 图像上的点，则|OP|=（）

2020年浙江省高考数学试卷-解析版

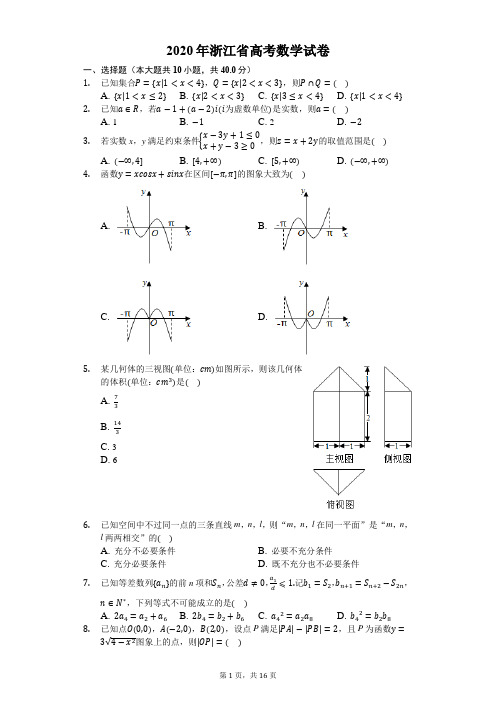
2020年浙江省高考数学试卷一、选择题（本大题共10小题，共40.0分）1. 已知集合P ={x|1<x <4}，Q ={x|2<x <3}，则P ∩Q =( )A. {x|1<x ≤2}B. {x|2<x <3}C. {x|3≤x <4}D. {x|1<x <4}2. 已知a ∈R ，若a −1+(a −2)i(i 为虚数单位)是实数，则a =( )A. 1B. −1C. 2D. −2 3. 若实数x ，y 满足约束条件{x −3y +1≤0x +y −3≥0，则z =x +2y 的取值范围是( )A. (−∞,4]B. [4,+∞)C. [5,+∞)D. (−∞,+∞)4. 函数y =xcosx +sinx 在区间[−π,π]的图象大致为( )A.B.C.D.5. 某几何体的三视图(单位：cm)如图所示，则该几何体的体积(单位：cm 3)是( )A. 73 B. 143 C. 3 D. 66. 已知空间中不过同一点的三条直线m ，n ，l ，则“m ，n ，l 在同一平面”是“m ，n ，l 两两相交”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 已知等差数列{a n }的前n 项和S n ，公差d ≠0，a1d⩽1.记b 1=S 2，b n+1=S n+2−S 2n ，n ∈N ∗，下列等式不可能成立的是( )A. 2a 4=a 2+a 6B. 2b 4=b 2+b 6C. a 42=a 2a 8D. b 42=b 2b 8 8. 已知点O(0,0)，A(−2,0)，B(2,0)，设点P 满足|PA|−|PB|=2，且P 为函数y =3√4−x 2图象上的点，则|OP|=( )A. √222B. 4√105C. √7D. √109.已知a，b∈R且a，b≠0，若(x−a)(x−b)(x−2a−b)≥0在x≥0上恒成立，则()A. a<0B. a>0C. b<0D. b>010.设集合S，T，S⊆N∗，T⊆N∗，S，T中至少有两个元素，且S，T满足：①对于任意x，y∈S，若x≠y，都有xy∈T；②对于任意x，y∈T，若x<y，则yx∈S；下列命题正确的是()A. 若S有4个元素，则S∪T有7个元素B. 若S有4个元素，则S∪T有6个元素C. 若S有3个元素，则S∪T有5个元素D. 若S有3个元素，则S∪T有4个元素二、填空题（本大题共7小题，共36.0分）11.我国古代数学家杨辉、宋世杰等研究过高阶等差数列求和问题，如数列{n(n+1)2}就是二阶等差数列，数列{n(n+1)2}，(n∈N∗)的前3项和______．12.二项展开式(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a4=______；a1+a2+a3=______．13.已知tanθ=2，则cos2θ=______；tan(θ−π4)=______．14.已知圆锥的侧面积(单位：cm2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是______．15.已知直线y=kx+b(k>0)与圆x2+y2=1和圆(x−4)2+y2=1均相切，则k=______，b=______．16.盒中有4个球，其中1个红球，1个绿球，2个黄球，从盒中随机取球，每次取1个不放回，直到取出红球为止，设此过程中取到黄球的个数为ξ，则P(ξ=0)=______，E(ξ)=______．17.已知平面向量e1⃗⃗⃗ ，e2⃗⃗⃗ 满足|2e1⃗⃗⃗ −e2⃗⃗⃗ |≤√2，设a⃗=e1⃗⃗⃗ +e2⃗⃗⃗ ，b⃗ =3e1⃗⃗⃗ +e2⃗⃗⃗ ，向量a⃗，b⃗ 的夹角为θ，则cos2θ的最小值为______．三、解答题（本大题共5小题，共74.0分）18.在锐角△ABC中，角A,B,C的对边分别为a,b,c.已知2bsinA−√3a=0．(1)求角B；(2)求cosA+cosB+cosC的取值范围．19.如图，三棱台ABC−DEF中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC=2BC．(1)证明：EF⊥DB；(2)求DF与面DBC所成角的正弦值．⋅20.已知数列{a n}，{b n}，{c n}满足a1=b1=c1=1，c n+1=a n+1−a n，c n+1=b nb n+2c n(n∈N∗)．(1)若{b n}为等比数列，公比q>0，且b1+b2=6b3，求q的值及数列{a n}的通项公式；(2)若{b n}为等差数列，公差d>0，证明：c1+c2+c3+⋯+c n<1+1，n∈N∗．d21.如图，已知椭圆C1：x2+y2=1，抛物线C2：y2=2px(p>0)，点A是椭圆C1与2抛物线C2的交点．过点A的直线l交椭圆C1于点B，交抛物线C2于点M(B,M不同于A)．(1)若p=1，求抛物线C2的焦点坐标；16(2)若存在不过原点的直线l使M为线段AB的中点，求p的最大值．22.已知1<a≤2，函数f(x)=e x−x−a.其中e=2.718281828459…为自然对数的底数．(1)证明：函数y=f(x)在(0,+∞)上有唯一零点；(2)记x0为函数y=f(x)在(0,+∞)上的零点，证明：(ⅰ)√a−1≤x0≤√2(a−1)；(ⅰ)x0f(e x0)≥(e−1)(a−1)a．答案和解析1.【答案】B【解析】解：集合P ={x|1<x <4}，Q ={x|2<x <3}，则P ∩Q ={x|2<x <3}．故选：B ．直接利用交集的运算法则求解即可．此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． 2.【答案】C【解析】【分析】本题考查复数的基本概念，是基础题．利用复数的虚部为0，求解即可．【解答】解：a ∈R ，若a −1+(a −2)i(i 为虚数单位)是实数，可得a −2=0，解得a =2．故选：C ．3.【答案】B【解析】解：画出实数x ，y 满足约束条件{x −3y +1≤0x +y −3≥0所示的平面区域，如图：将目标函数变形为−12x +z2=y ，则z 表示直线在y 轴上截距，截距越大，z 越大，当目标函数过点A(2,1)时，截距最小为z =2+2=4，随着目标函数向上移动截距越来越大，故目标函数z =2x +y 的取值范围是[4,+∞)．故选：B ．作出不等式组表示的平面区域；作出目标函数对应的直线；结合图象判断目标函数z =x +2y 的取值范围．本题考查画不等式组表示的平面区域、考查数形结合求函数的最值．4.【答案】A【解析】解：y =f(x)=xcosx +sinx ，则f(−x)=−xcosx −sinx =−f(x)，∴f(x)为奇函数，函数图象关于原点对称，故排除B ，D ，当x =π时，y =f(π)=πcosπ+sinπ=−π<0，故排除B ，故选：A ．先判断函数的奇偶性，再判断函数值的特点．本题考查了函数图象的识别，掌握函数的奇偶性额函数值得特点是关键，属于基础题．5.【答案】A【解析】解：由题意可知几何体的直观图如图，下部是直三棱柱，底面是斜边长为2的等腰直角三角形，棱锥的高为2，上部是一个三棱锥，一个侧面与底面等腰直角三角形垂直，棱锥的高为1，所以几何体的体积为：12×2×1×2+13×12×2×1×1=73．故选：A．画出几何体的直观图，利用三视图的数据求解几何体的体积即可．本题考查三视图求解几何体的体积，判断几何体的形状是解题的关键．6.【答案】B【解析】【分析】本题借助空间的位置关系，考查了充分条件和必要条件，属于基础题．由m，n，l在同一平面，则m，n，l相交或m，n，l有两个平行，另一直线与之相交，或三条直线两两平行，根据充分条件，必要条件的定义即可判断．【解答】解：空间中不过同一点的三条直线m，n，l，若m，n，l在同一平面，则m，n，l相交或m，n，l有两个平行，另一直线与之相交，或三条直线两两平行．故m，n，l在同一平面”是“m，n，l两两相交”的必要不充分条件，故选：B．7.【答案】B【解析】解：在等差数列{a n}中，a n=a1+(n−1)d，S n+2=(n+2)a1+(n+2)(n+1)2d，S2n=2na1+2n(2n−1)2d，b1=S2=2a1+d，b n+1=S n+2−S2n=(2−n)a1−3n2−5n−22d．∴b2=a1+2d，b4=−a1−5d，b6=−3a1−24d，b8=−5a1−55d．A.2a4=2(a1+3d)=2a1+6d，a2+a6=a1+d+a1+5d=2a1+6d，故A正确；B.2b4=−2a1−10d，b2+b6=a1+2d−3a1−24d=−2a1−22d，若2b4=b2+b6，则−2a1−10d=−2a1−22d，即d=0不合题意，故B错误；C.若a42=a2a8，则(a1+3d)2=(a1+d)(a1+7d)，即a12+6a1d+9d2=a12+8a1d+7d2，得a1d=d2，∵d≠0，∴a1=d，符合a1d⩽1，故C正确；D.若b42=b2b8，则(−a1−5d)2=(a1+2d)(−5a1−55d)，即2(a1d )2+25a1d+45=0，则a1d有两不等负根，满足a1d⩽1，故D正确．∴等式不可能成立的是B．故选：B．由已知利用等差数列的通项公式判断A与C；由数列递推式分别求得b2,b4,b6,b8，分析B，D成立时是否满足公差d≠0，a1d⩽1判断B与D．本题考查数列递推式，等差数列的通项公式与前n项和，考查转化思想和计算能力，是中档题．8.【答案】D【解析】解：点O(0,0)，A(−2,0)，B(2,0).设点P满足|PA|−|PB|=2，可知P的轨迹是双曲线x21−y23=1的右支上的点，P为函数y=3√4−x2图象上的点，即y236+x24=1在第一象限的点，联立两个方程，解得P(√132,3√32)，所以|OP|=√134+274=√10．故选：D．求出P满足的轨迹方程，求出P的坐标，即可求解|OP|．本题考查圆锥曲线的综合应用，曲线的交点坐标以及距离公式的应用，是中档题．9.【答案】C【解析】【分析】本题考查不等式恒成立问题，注意三次函数的图象，考查分类讨论思想和转化思想，属于中档题．先由x=0时，不等式ab(−2a−b)⩾0恒成立，可得1a +2b⩽0，则a,b至少有一个是小于0的，再按a<0,b<0，a<0,b>0，a>0,b<0，讨论可得结论．【解答】解：由题意知，x=0时，不等式ab(−2a−b)⩾0恒成立，即ab(2a+b)⩽0，∵ab≠0，∴可得1a +2b⩽0，则a,b至少有一个是小于0的，(1)若a<0,b<0，由图象知，(x−a)(x−b)(x−2a−b)⩾0在x⩾0时恒成立，符合题意；(2)若a<0,b>0，2a+b>0，(x−a)(x−b)(x−2a−b)⩽0在x≥0上恒成立，则b=2a+b，得a=0，矛盾，不符合题意．(3)若a>0,b<0，(x−a)(x−b)(x−2a−b)⩾0在x⩾0时恒成立，则a=2a+b，则a+b=0，符合题意．综合，b<0成立．故选：C．10.【答案】A【解析】【分析】本题考查命题的真假的判断与应用，集合的基本运算，利用特殊集合排除选项是选择题常用方法，属于较难题．利用特殊集合排除选项，推出结果即可．【解答】解：取：S ={1,2，4}，则T ={2,4，8}，S ∪T ={1,2，4，8}，4个元素，排除C ． S ={2,4，8}，则T ={8,16，32}，S ∪T ={2,4，8，16，32}，5个元素，排除D ； S ={2,4，8，16}则T ={8,16，32，64，128}，S ∪T ={2,4，8，16，32，64，128}，7个元素，排除B ；故选：A ．11.【答案】10【解析】【分析】本题考查数列求和，数列通项公式的应用，是基本知识的考查．求出数列的前3项，然后求解即可．【解答】解：数列{a n }满足a n =n(n+1)2，可得a 1=1，a 2=3，a 3=6，所以S 3=1+3+6=10．故答案为：10．12.【答案】80；130【解析】【分析】本题考查二项式定理的应用，只有二项式定理系数以及项的系数的区别，属于基础题．直接利用二项式定理的通项公式，求解即可．【解答】解：∵(1+2x)5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5，则a 4=C 54⋅24=80．a 1+a 2+a 3=C 51⋅2+C 52⋅4+C 53⋅8=130．故答案为：80；130．13.【答案】−35， 13【解析】解：tanθ=2，则cos2θ=cos 2θ−sin 2θcos 2θ+sin 2θ=1−tan 2θ1+tan 2θ=1−41+4=−35． tan(θ−π4)=tanθ−tanπ41+tanθtanπ4=2−11+2×1=13．故答案为：−35；13．利用二倍角公式以及同角三角函数基本关系式求解第一问，利用两角和与差的三角函数转化求解第二问．本题考查二倍角公式的应用，两角和与差的三角函数以及同角三角函数基本关系式的应用，是基本知识的考查．14.【答案】1【解析】解：∵圆锥侧面展开图是半圆，面积为2π，设圆锥的母线长为a ，则12×a 2π=2π，∴a =2，∴侧面展开扇形的弧长为2π，设圆锥的底面半径OC =r ，则2πr =2π，解得r =1．故答案为：1．利用圆锥的侧面积，求出母线长，求解底面圆的周长，然后求解底面半径．本题考查圆锥的母线长的求法，注意利用圆锥的弧长等于底面周长这个知识点．15.【答案】√33 ；−2√33【解析】解：由条件得C 1(0,0)，r 1=1，C 2(4,0)，r 2=1，因为直线l 与C 1，C 2都相切，故有d 1=√1+k 2=1，d 2=√1+k 2=1，则有√1+k 2=√1+k 2，故可得b 2=(4k +b)2，整理得k(2k +b)=0，因为k >0，所以2k +b =0，即b =−2k ，代入d 1=√1+k 2=1，解得k =√33，则b =−2√33，故答案为：√33；−2√33．根据直线l 与两圆都相切，分别列出方程d 1=√1+k2=1，d 2=√1+k 2=1，解得即可．本题考查直线与圆相切的性质，考查方程思想，属于中档题．16.【答案】13 ；1【解析】解：由题意知，随机变量ξ的可能取值为0，1，2；计算P(ξ=0)=14+14×13=13；P(ξ=1)=1 2×13 +14×23×12+24×13×12=13；P(ξ=2)=1−13−13=13；所以E(ξ)=0×13+1×13+2×13=1．故答案为：13，1．由题意知随机变量ξ的可能取值为0，1，2；分别计算P(ξ=0)、P(ξ=1)和P(ξ=2)，再求E(ξ)的值．本题考查了离散型随机变量的分布列与数学期望的计算问题，是中档题．17.【答案】2829【解析】【分析】本题考查了平面向量的数量积与夹角的运算问题，是中档题．设e1⃗⃗⃗ 、e2⃗⃗⃗ 的夹角为α，由题意求出cosα≥34；再求a⃗，b⃗ 的夹角θ的余弦值cos2θ的最小值即可．【解答】解：设e1⃗⃗⃗ 、e2⃗⃗⃗ 的夹角为α，由e1⃗⃗⃗ ，e2⃗⃗⃗ 为单位向量，满足|2e1⃗⃗⃗ −e2⃗⃗⃗ |≤√2，所以4e1⃗⃗⃗ 2−4e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=4−4cosα+1≤2，解得cosα≥34；又a⃗=e1⃗⃗⃗ +e2⃗⃗⃗ ，b⃗ =3e1⃗⃗⃗ +e2⃗⃗⃗ ，且a⃗，b⃗ 的夹角为θ，所以a⃗⋅b⃗ =3e1⃗⃗⃗ 2+4e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=4+4cosα，a⃗2=e1⃗⃗⃗ 2+2e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=2+2cosα，b⃗ 2=9e1⃗⃗⃗ 2+6e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=10+6cosα；则cos2θ=(a⃗ ⋅b⃗)2a⃗2×b⃗2=(4+4cosα)2(2+2cosα)(10+6cosα)=4+4cosα5+3cosα=43−835+3cosα，所以cosα=34时，cos2θ取得最小值为43−835+3×34=2829．故答案为2829．18.【答案】解：(1)∵2bsinA=√3a，∴2sinBsinA=√3sinA，∵sinA≠0，∴sinB=√32，，∴B=π3，(2)∵△ABC为锐角三角形，B=π3，∴C=2π3−A，，△ABC为锐角三角形，，，解得，，，，∴cosA+cosB+cosC的取值范围为(√3+12,32 ]．【解析】本题考查了正弦定理，三角函数的化简，三角函数的性质，考查了运算求解能力和转化与化归能力，属于中档题．(1)根据正弦定理可得sinB=√32，结合角的范围，即可求出，(2)根据两角和差的余弦公式，以及利用正弦函数的性质即可求出．19.【答案】解：(1)证明：作DH⊥AC，且交AC于点H，∵面ADFC⊥面ABC，面ADFC∩面ABC=AC，DH⊂面ADFC，∴DH⊥面ABC，BC⊂面ABC，∴DH⊥BC，∴在Rt△DHC中，CH=CD⋅cos45°=√22CD，∵DC=2BC，∴CH=√22CD=√22⋅2BC=√2⋅BC，∴BCCH =√22，又∠ACB=45°，∴△BHC是直角三角形，且∠HBC=90°，∴HB⊥BC，又∵DH⊂面DHB，HB⊂面DHB，DH∩HB=H，∴BC⊥面DHB，∵DB⊂面DHB，∴BC⊥DB，∵在三棱台DEF−ABC中，EF//BC，∴EF⊥DB．(2)设BC=1，则BH=1，HC=√2，在Rt△DHC中，DH=√2，DC=2，在Rt△DHB中，DB=√DH2+HB2=√2+1=√3，作HG⊥BD于G，∵BC⊥面DHB，HG⊂面DHB，∴BC⊥HG，而BC⊂面BCD，BD⊂面BCD，BC∩BD=B，∴HG⊥面BCD，∵GC⊂面BCD，∴HG⊥GC，∴△HGC是直角三角形，且∠HGC=90°，设DF与面DBC所成角为θ，则θ即为CH与面DBC的夹角，且sinθ=sin∠HCG=HGHC =√2，∵在Rt△DHB中，DH⋅HB=BD⋅HG，∴HG=DH⋅HBBD =√2⋅13=√63，∴sinθ=√2=√63√2=√33．【解析】本题主要考查空间直线互相垂直的判定和性质，以及直线与平面所成角的几何计算问题，考查了空间想象能力和思维能力，平面与空间互相转化是能力，几何计算能力，以及逻辑推理能力，本题属综合性较强的中档题．(1)题根据已知条件，作DH⊥AC，根据面面垂直，可得DH⊥BC，进一步根据直角三角形的知识可判断出△BHC是直角三角形，且∠HBC=90°，则HB⊥BC，从而可证出BC⊥面DHB，最后根据棱台的定义有EF//BC，根据平行线的性质可得EF⊥DB；(2)题先可设BC=1，根据解直角三角形可得BH=1，HC=√2，DH=√2，DC=2，DB=√3，然后找到CH与面DBC的夹角即为∠HCG，根据棱台的特点可知DF与面DBC 所成角与CH与面DBC的夹角相等，通过计算∠HCG的正弦值，即可得到DF与面DBC 所成角的正弦值．20.【答案】(1)解：由题意，b2=q，b3=q2，∵b1+b2=6b3，∴1+q=6q2，整理，得6q2−q−1=0，解得q=−13(舍去)，或q=12，∴c n+1=b nb n+2⋅c n=1b n+2b n⋅c n=1q2⋅c n=1(12)2⋅c n=4⋅c n，∴数列{c n}是以1为首项，4为公比的等比数列，∴c n=1⋅4n−1=4n−1，n∈N∗．∴a n+1−a n=c n+1=4n，则a1=1，a2−a1=41，a3−a2=42，……a n−a n−1=4n−1，各项相加，可得a n=1+41+42+⋯+4n−1=1−4n1−4=4n−13．(2)证明：依题意，由c n+1=b nb n+2⋅c n(n∈N∗)，可得b n+2⋅c n+1=b n⋅c n，两边同时乘以b n+1，可得b n+1b n+2c n+1=b n b n+1c n，∵b1b2c1=b2=1+d，∴数列{b n b n+1c n}是一个常数列，且此常数为1+d，b n b n+1c n=1+d，∴c n=1+db n b n+1=1+dd⋅db n b n+1=(1+1d)⋅b n+1−b nb n b n+1=(1+1d)(1b n−1b n+1)，∴c1+c2+⋯+c n=(1+1d)(1b1−1b2)+(1+1d)(1b2−1b3)+⋯+(1+1d)(1b n−1b n+1)=(1+1d)(1b1−1b2+1b2−1b3+⋯+1b n−1b n+1)=(1+1d)(1b1−1b n+1)=(1+1d)(1−1b n+1)<1+1d，∴c1+c2+⋯+c n<1+1d，故得证．【解析】本题主要考查数列求通项公式，等差数列和等比数列的基本量的运算，以及和式不等式的证明问题．考查了转化与化归思想，整体思想，方程思想，累加法求通项公式，裂项相消法求和，放缩法证明不等式，以及逻辑推理能力和数学运算能力，属于综合题．(1)先根据等比数列的通项公式将b2=q，b3=q2代入b1+b2=6b3，计算出公比q的值，然后根据等比数列的定义化简c n+1=b nb n+2⋅c n可得c n+1=4c n，则可发现数列{c n}是以1为首项，4为公比的等比数列，从而可得数列{c n}的通项公式，然后将通项公式代入c n+1=a n+1−a n，可得a n+1−a n=c n+1=4n，再根据此递推公式的特点运用累加法可计算出数列{a n}的通项公式；(2)通过将已知关系式c n+1=b nb n+2⋅c n不断进行转化可构造出数列{b n b n+1c n}，且可得到数列{b n b n+1c n}是一个常数列，且此常数为1+d，从而可得b n b n+1c n=1+d，再计算得到c n=1+db n b n+1，根据等差数列的特点进行转化进行裂项，在求和时相消，最后运用放缩法即可证明不等式成立．21.【答案】解：(1)p =116，则 p 2=132，则抛物线C 2的焦点坐标(132,0)，(2)由题意可设直线l ：x =my +t (m ≠0,t ≠0)，点A (x 0,y 0)，将直线l 的方程代入椭圆C 1：x 22+y 2=1得(m 2+2)y 2+2mty +t 2−2=0∴点M 的纵坐标y M =−mtm 2+2。

2022年浙江省新高考数学试题及参考答案

2022年普通高等学校招生全国统一考试（浙江卷）数学本试题卷分选择题和非选择题两部分。

全卷共4页，选择题部分1至3页；非选择题部分3至4页．满分150分，考试时间120分钟。

考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。

2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：如果事件A ，B 互斥，则柱体的体积公式()()()P A B P A P B +=+ V Sh =如果事件A ，B 相互独立，则其中S 表示柱体的底面积，h 表示柱体的高()()()P AB P A P B =⋅ 锥体的体积公式若事件A 在一次试验中发生的概率是p ，则n 次 13V Sh =独立重复试验中事件A 恰好发生k 次的概率其中S 表示锥体的底面积，h 表示锥体的高()C (1)(0,1,2,,)k k n k n n P k p p k n -=-= 球的表面积公式台体的体积公式 24S R =π()112213V S S S S h =球的体积公式其中12,S S 表示台体的上、下底面积， 343V R =π h 表示台体的高其中R 表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合{1,2},{2,4,6}A B ==，则A B =（）A ．{2}B ．{1,2}C ．{2,4,6}D ．{1,2,4,6} 2．已知,,3i (i)i a b a b ∈+=+R （i 为虚数单位），则（）A ．1,3a b ==-B ．1,3a b =-=C ．1,3a b =-=-D ．1,3a b ==3．若实数x ，y 满足约束条件20,270,20,x x y x y -≥⎧⎪+-≤⎨⎪--≤⎩则34z x y =+的最大值是（）A ．20B ．18C ．13D ．64．设x ∈R ，则“sin 1x =”是“cos 0x =”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A ．22πB ．8πC ．22π3 D ．16π36．为了得到函数2sin3y x =的图象，只要把函数π2sin 35y x ⎛⎫=+ ⎪⎝⎭图象上所有的点（） A ．向左平移π5个单位长度 B ．向右平移π5个单位长度 C ．向左平移π15个单位长度 D ．向右平移π15个单位长度7．已知825,log 3ab ==，则34a b-=（）A ．25B ．5C ．259D ．538．如图，已知正三棱柱1111,ABC A B C AC AA -=，E ，F 分别是棱11,BC AC 上的点．记EF 与1AA 所成的角为α，EF 与平面ABC 所成的角为β，二面角F BC A --的平面角为γ，则（）A ．αβγ≤≤B ．βαγ≤≤C ．βγα≤≤D ．αγβ≤≤ 9．已知,a b ∈R ，若对任意,|||4||25|0x a x b x x ∈-+---≥R ，则（）A ．1,3a b ≤≥B ．1,3a b ≤≤C ．1,3a b ≥≥D ．1,3a b ≥≤10．已知数列{}n a 满足()21111,3n n n a a a a n *+==-∈N ，则 A ．100521002a << B ．100510032a << C ．100731002a << D ．100710042a <<非选择题部分（共110分）二、填空题：本大题共7小题，单空题每题4分，多空题每空3分，共36分．11．我国南宋著名数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白．如果把这个方法写成公式，就是222222142c a b S c a ⎡⎤⎛⎫+-=-⎢⎥ ⎪⎢⎥⎝⎭⎣⎦，其中a ，b ，c 是三角形的三边，S 是三角形的面积．设某三角形的三边2,3,2a b c ===，则该三角形的面积S =___________．12．已知多项式42345012345(2)(1)x x a a x a x a x a x a x +-=+++++，则2a =__________，12345a a a a a ++++=___________．13．若3sin sin 10,2παβαβ-=+=，则sin α=__________，cos2β=_________．14．已知函数22,1,()11,1,x x f x x x x ⎧-+≤⎪=⎨+->⎪⎩则12f f⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭________；若当[,]x a b ∈时，1()3f x ≤≤，则b a -的最大值是_________．15．现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为ξ，则(2)P ξ==__________，()E ξ=_________．16．已知双曲线22221(0,0)x y a b a b -=>>的左焦点为F ，过F 且斜率为4b a的直线交双曲线于点()11,A x y ，交双曲线的渐近线于点()22,B x y 且120x x <<．若||3||FB FA =，则双曲线的离心率是_________．17．设点P 在单位圆的内接正八边形128A A A 的边12A A 上，则222182PA PA PA +++的取值范围是_______．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18．（本题满分14分）在ABC △中，角A ，B ，C 所对的边分别为a ，b ，c ．已知345,cos 5a c C ==．（Ⅰ）求sin A 的值；（Ⅱ）若11b =，求ABC △的面积．19．（本题满分15分）如图，已知ABCD 和CDEF 都是直角梯形，AB DC ∥，DC EF ∥，5AB =，3DC =，1EF =，60BAD CDE ∠=∠=︒，二面角F DC B --的平面角为60︒．设M ，N 分别为,AE BC 的中点．（Ⅰ）证明：FN AD ⊥；（Ⅱ）求直线BM 与平面ADE 所成角的正弦值．20．（本题满分15分）已知等差数列{}n a 的首项11a =-，公差1d >．记{}n a 的前n 项和为()n S n *∈N．（Ⅰ）若423260S a a -+=，求n S ；（Ⅱ）若对于每个n *∈N ，存在实数n c ，使12,4,15n n n n n n a c a c a c +++++成等比数列，求d 的取值范围．21．（本题满分15分）如图，已知椭圆22112x y +=．设A ，B 是椭圆上异于(0,1)P 的两点，且点10,2Q ⎛⎫ ⎪⎝⎭在线段AB 上，直线,PA PB 分别交直线132y x =-+于C ，D 两点．（Ⅰ）求点P 到椭圆上点的距离的最大值；（Ⅱ）求||CD 的最小值．22．（本题满分15分）设函数e()ln (0)2f x x x x=+>．（Ⅰ）求()f x 的单调区间；（Ⅱ）已知,a b ∈R ，曲线()y f x =上不同的三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b ．证明：（ⅰ）若e a >，则10()12e a b f a ⎛⎫<-<- ⎪⎝⎭；（ⅱ）若1230e,a x x x <<<<，则22132e 112e e 6e 6ea a x x a --+<+<-．是自然对数的底数）（注：e 2.718282022年普通高等学校招生全国统一考试（浙江卷）数学参考答案选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. D2. B3. B4. A5. C6. D7. C8. A9. D 10. B非选择题部分（共110分）二、填空题：本大题共7小题，单空题每题4分，多空题每空3分，共36分．11.234. 12.①. 8 ②. 2- 13. ①.310②. 4514. ①. 3728②. 333+3 15.①.1635， ②. 127##51716.3617. [1222,16]+三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18.（15；（2）22．19.（1）过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H ． ∵四边形ABCD 和EFCD 都是直角梯形，//,//,5,3,1AB DC CD EF AB DC EF ===，60BAD CDE ∠=∠=︒，由平面几何知识易知，2,90DG AH EFC DCF DCB ABC ==∠=∠=∠=∠=︒，则四边形EFCG 和四边形DCBH 是矩形，∴在Rt EGD 和Rt DHA ，23EG DH ==∵,DC CF DC CB ⊥⊥，且CF CB C ⋂=，∴DC ⊥平面,BCF BCF ∠是二面角F DC B --的平面角，则60BCF ∠=， ∴BCF △是正三角形，由DC ⊂平面ABCD ，得平面ABCD ⊥平面BCF ，∵N 是BC 的中点，∴FN BC ⊥，又DC ⊥平面BCF ，FN ⊂平面BCF ，可得FN CD ⊥，而BC CD C ⋂=，∴FN ⊥平面ABCD ，而AD ⊂平面ABCD FN AD ∴⊥．（25720.（1）235(N )2n n nS n *-=∈（2）12d <≤ 21.（11211；（265． 22.（1）()f x 的减区间为e 02⎛⎫ ⎪⎝⎭,，增区间为e ,2⎛⎫+∞⎪⎝⎭. （2）（ⅰ）因为过(),a b 有三条不同的切线，设切点为()(),,1,2,3i i x f x i =，故()()()i i i f x b f x x a '-=-，故方程()()()f x b f x x a '-=-有3个不同的根，该方程可整理为()21e e ln 022x a x b x x x ⎛⎫----+= ⎪⎝⎭，设()()21e e ln 22g x x a x b x x x ⎛⎫=----+ ⎪⎝⎭，则()()22321e 1e 1e 22g x x a x x x x x x⎛⎫'=-+-+--+ ⎪⎝⎭ ()()31e x x a x=---，当0e x <<或x a >时，0g x ；当e x a <<时，0g x ，故()g x 在()()0,e ,,a +∞上为减函数，在()e,a 上为增函数，因为()g x 有3个不同的零点，故()e 0g <且()0>g a ，故()21e e e ln e 0e 2e 2e a b ⎛⎫----+<⎪⎝⎭且()21e e ln 022a a a b a a a ⎛⎫----+> ⎪⎝⎭，整理得到：12e a b <+且()e ln 2b a f a a>+=，此时()1e 13e11ln ln 2e 2e 22e 222a a a b f a a a a a ⎛⎫⎛⎫---<+-+-+=-- ⎪ ⎪⎝⎭⎝⎭，设()3e ln 22u a a a =--，则()2e-202a u a a '=<，故()u a 为()e,+∞上的减函数，故()3eln e 022eu a <--=，故()1012e a b f a ⎛⎫<-<- ⎪⎝⎭. （ⅱ）当0e a <<时，同（ⅱ）中讨论可得：故()g x 在()()0,,e,a +∞上为减函数，在(),e a 上为增函数，不妨设123x x x <<，则1230e x a x x <<<<<，因为()g x 有3个不同的零点，故()0g a <且()e 0g >，故()21e e e ln e 0e 2e 2e a b ⎛⎫----+>⎪⎝⎭且()21e e ln 022a a a b a a a ⎛⎫----+< ⎪⎝⎭，整理得到：1ln 2e 2ea ab a +<<+，因为123x x x <<，故1230e x a x x <<<<<，又()2e e 1ln 2a ag x x b x x+=-+-+，设e t x =，()0,1eam =∈，则方程2e e 1ln 02a a x b x x +-+-+=即为： 2e ln 0e 2e a a t t t b +-+++=即为()21ln 02mm t t t b -++++=，记123123e e e,,,t t t x x x === 则113,,t t t 为()21ln 02m m t t t b -++++=有三个不同的根，设3131e1x t k t x a ==>>，1ea m =<，要证：22122e 112e e 6e 6e a a x x a --+<+<-，即证13e 2e e 26e 6ea a t t a --+<+<-，即证：13132166m mt t m --<+<-，即证：131********m m t t t t m --⎛⎫⎛⎫+-+-+< ⎪⎪⎝⎭⎝⎭，即证：()()()2131313122236m m m t t m m t t --++--<+，而()21111ln 02m m t t t b -++++=且()23331ln 02m m t t t b -++++=，故()()()22131313ln ln 102m t t t t m t t -+--+-=，故131313ln ln 222t t t t m m t t -+--=-⨯-，故即证：()()()21313131312ln ln 236m m m t t m t t m t t --+--⨯<-+，即证：()()()1213313ln1312072t t t m m m t t t +--++>-即证：()()()213121ln 0172m m m k k k --+++>-，记()()1ln ,11k k k k k ϕ+=>-，则()()2112ln 01k k k kk ϕ⎛⎫'=-->⎪⎝⎭-，设()12ln u k k k k =--，则()2122210u k k k k k'=+->-=即()0k ϕ'>，故()k ϕ在()1,+∞上为增函数，故()()k m ϕϕ>，所以()()()()()()22131213121ln 1ln 172172m m m m m m k k m m k m --+--++++>+--，记()()()()()211312ln ,01721m m m m m m m m ω---+=+<<+，则()()()()()()()2232322132049721330721721m m m m m mm m m m m ω---+-+'=>>++，所以()m ω在0,1为增函数，故()()10m ωω<=，故()()()()211312ln0721m m m mmm---++<+即()()()213121ln172m m mm mm--+++>-，故原不等式得证：。

2022年普通高等学校招生全国统一考试浙江卷数学(含答案)

★启用前2022年普通高等学校招生全国统一考试〔浙江卷〕数学本试题卷分选择题和非选择题两局部。

全卷共4页，选择题局部1至2页；非选择题局部3至4页。

总分值150分。

考试用时120分钟。

考生注意：1．答题前，请务势必自己的姓名、。

2．答题时，请按照答题纸上“考前须知〞的要求，在答题纸相应的位置上标准作答，在本试题卷上的作答一律无效。

参考公式：假设事件A ，B 互斥，那末()()()P A B P A P B +=+ 假设事件A ，B 相互独立，那末()()()P AB P A P B = 假设事件A 在一次试验中发生的概率是p ，那末n 次独立重复试验中事件A 恰好发生k 次的概率()C (1)(0,1,2,,)k k n k nnP k p p k n -=-=台体的体积公式11221()3V S S S S h =++其中12,S S 分别表示台体的上、下底面积，h 表示台体的高柱体的体积公式V Sh =其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积，h 表示锥体的高球的外表积公式 24S R =π球的体积公式343V R =π其中R 表示球的半径选择题局部〔共40分〕一、选择题：本大题共10小题，每题4分，共40分。

在每题给出的四个选项中，惟独一项为哪一项符合题目要求的。

1．全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，那末()UA B =A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1,3-2．渐近线方程为x ±y =0的双曲线的离心率是A ．22B ．1C ．2D ．23．假设实数x ，y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，那末z =3x +2y 的最大值是A ．1-B ．1C ．10D ．124．祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，那末积不容异〞称为祖暅原理，利用该原理可以得到柱体的体积公式V 柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高．假设某柱体的三视图如下图〔单位：cm 〕，那末该柱体的体积〔单位：cm 3〕是A ．158B ．162C ．182D ．3245．假设a >0，b >0，那末“a +b ≤4〞是 “ab ≤4〞的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件6y =1xa ，y =log a (x +12)(a >0，且a ≠1)的图象可能是7．设0＜a ＜1，那末随机变量X 的分布列是那末当a 在〔0,1〕内增大时， A ．D 〔X 〕增大B ．D 〔X 〕减小C ．D 〔X 〕先增大后减小D ．D 〔X 〕先减小后增大8．设三棱锥V –ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点〔不含端点〕．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P –AC –B 的平面角为γ，那末 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β9．,a b ∈R 32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩．()y f x ax b =--恰有3个零点，那末 A ．a <–1，b <0 B ．a <–1，b >0 C ．a >–1，b <0D ．a >–1，b >010．设a ，b ∈R ，数列{a n }满足a 1=a ，a n +1=a n 2+b ，b *∈N ，那末A ．当b =12时，a 10>10B ．当b =14时，a 10>10C ．当b =–2时，a 10>10D ．当b =–4时，a 10>10非选择题局部〔共110分〕二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2020年浙江省普通高中高考数学模拟试卷(二)(5月份)(有答案解析)

A. 5
B. -5
C. -2
D. 2
3. 若 α∈（，π），sin（π-α）= ，则 cosα=（）
A.
B.
C.
D.
4. lg（）2=（）
A. -4
B. 4
5. 下列函数中，最小正周期为的是（
A. y=2018sinx
C. y=-cos2x
C. Байду номын сангаас0
）
D. -10
B. y=sin2018x D. y=sin（4x+ ）
考查函数定义域的概念及求法，指数函数的定义域．
7.答案：C
解析：解：直线 y=x，即 x -y=0，它与直线 x-y+2=0 的距离为 = ，
故选：C．由题意利用两条平行直线间的距离公式，求得结果．本题主要考查两条平行直线间的距离公式的应用，注意未知数的系数必需相同，属于基础题．
8.答案：C
解析：解：∵1=log44＜log49＜log416=2， ∴1＜a＜2，
2020 年浙江省普通高中高考数学模拟试卷（二）（5 月份）
一、选择题（本大题共 18 小题，共 54.0 分） 1. 已知集合 P={-3，-2，-1，0}，Q={x∈N|-2＜x＜2}，那么集合 P∪Q 中元素的个数是
（）
A. 2
B. 3
C. 4
D. 5
2. 已知向量 =（-1，1）， =（3，-2），则 =（）
6. 函数 f（x）=2x
的定义域为（
A. [-2，2] C. （-∞，-2]∪[2，+∞）
7. 直线 y=x 与直线 x-y+2=0 的距离为（
A. 2
B.

2020年浙江省高考数学试卷(原卷版)

17.设，为单位向量，满足，，，设，的夹角为，则的最小值为_______．
三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.
18.在锐角△ABC中，角A，B，C 对边分别为a，b，c，且．
（I）求角B；
（II）求cosA+cosB+cosC 取值范围．
21.如图，已知椭圆，抛物线，点A是椭圆与抛物线的交点，过点A的直线l交椭圆于点B，交抛物线于M（B，M不同于A）．
（Ⅰ）若，求抛物线的焦点坐标；
（Ⅱ）若存在不过原点直线l使M为线段AB的中点，求p的最大值．
22.已知，函数，其中e=2.71828…为自然对数的底数．
（Ⅰ）证明：函数在上有唯一零点；
参考公式：
如果事件A，B互斥，那么
如果事件A，B相互独立，那么
如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中事件A恰好发生k次的概率
台体的体积公式
其中分别表示台体的上、下底面积，表示台体的高
柱体的体积公式
其中表示柱体的底面积，表示柱体的高
锥体的体积公式
其中表示锥体的底面积，表示锥体的高
A. 1B. –1C. 2D. –2
3.若实数x，y满足约束条件，则z=2x+y的取值范围是（）
A. B. C. D.
4.函数y=xcosx+sinx在区间[–π，+π]的图象大致为（）
A. B.
C. D.
5.某几何体的三视图（单位：cm）如图所示，则该几何体的体积（单位：cm3）是（）
A. B. C. 3D. 6
A. 2a4=a2+a6B. 2b4=b2+b6C. D.

2020年浙江省高考数学试题(学生版)

2020年普通高等学校招生全国统一考试(浙江卷)数学本试题卷分选择题和非选择题两部分.全卷共4页，选择题部分1至2页；非选择题部分3至4页.满分150分.考试用时120分钟. 考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效. 参考公式：选择题部分(共40分)一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合P ={|14}<<x x ，{}23Q x =<<，则P Q =( ) A. {|12}x x <≤ B. {|23}x x << C. {|34}x x ≤<D. {|14}<<x x2.已知a ∈R ，若a –1+(a –2)i (i 为虚数单位)是实数，则a =( )A. 1B. –1C. 2D. –23.若实数x ，y 满足约束条件31030x y x y -+≤⎧⎨+-≥⎩，则z =x +2y 的取值范围是( )A. (,4]-∞B. [4,)+∞C. [5,)+∞D. (,)-∞+∞4.函数y =x cos x +sin x 在区间[–π，+π]的图象大致为( )A. B.C. D.5.某几何体的三视图(单位：cm )如图所示，则该几何体的体积(单位：cm 3)是()A.73B.143C. 3D. 66.已知空间中不过同一点的三条直线m ，n ，l ，则“m ，n ，l 在同一平面”是“m ，n ，l 两两相交”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件D. 既不充分也不必要条件7.已知等差数列{a n }的前n 项和S n ，公差d ≠0，11a d≤．记b 1=S 2，b n+1=S 2n+2–S 2n ，n *∈N ，下列等式不可能成立的是( ) A 2a 4=a 2+a 6B. 2b 4=b 2+b 6C. 2428a a a = D. 2428b b b =8.已知点O (0，0)，A (–2，0)，B (2，0)．设点P 满足|P A |–|PB |=2，且P 为函数y =|OP |=( )A.B.C.D.9.已知a ，b ∈R 且ab ≠0，若(x –a )(x –b )(x –2a –b )≥0在x ≥0上恒成立，则( ) A. a <0B. a >0C. b <0D. b >010.设集合S ，T ，S ⊆N *，T ⊆N *，S ，T 中至少有两个元素，且S ，T 满足： ①对于任意x ，y ∈S ，若x ≠y ，都有xy ∈T ②对于任意x ，y ∈T ，若x <y ，则yx∈S ；下列命题正确的是( )A. 若S 有4个元素，则S ∪T 有7个元素B. 若S 有4个元素，则S ∪T 有6个元素C. 若S 有3个元素，则S ∪T 有4个元素D. 若S 有3个元素，则S ∪T 有5个元素非选择题部分(共110分)二、填空题：本大题共7小题，共36分.多空题每小题6分，单空题每小题4分.11.已知数列{a n }满足(1)=2n n n a +，则S 3=________． 12.设()2345125345612 x a a x a x a x a x a x +=+++++，则a 5=________；a 1+a 2 + a 3=________． 13.已知tan 2θ=，则cos2θ=________；πtan()4θ-=______． 14.已知圆锥展开图的侧面积为2π，且为半圆，则底面半径为_______．15.设直线:(0)l y kx b k =+>，圆221:1C x y +=，222:(4)1C x y -+=，若直线l 与1C ，2C 都相切，则k =_______；b =______．16.一个盒子里有1个红1个绿2个黄四个相同的球，每次拿一个，不放回，拿出红球即停，设拿出黄球的个数为ξ，则(0)P ξ==_______；()E ξ=______．17.设1e ，2e 为单位向量，满足21|22|-≤e e ，12a e e =+，123b e e =+，设a ，b 的夹角为θ，则2cos θ的最小值为_______．三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.18.在锐角△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且2sin 3b A a =． (I )求角B ；(II )求cos A +cos B +cos C 的取值范围．19.如图，三棱台DEF —ABC 中，面ADFC ⊥面ABC ，∠ACB =∠ACD =45°，DC =2BC ．(I )证明：EF ⊥DB ；(II )求DF 与面DBC 所成角的正弦值．20.已知数列{a n }，{b n }，{c n }中，1111121,,()nn n n n n n b a b c c a a c c n b +++====-=⋅∈*N ． (Ⅰ)若数列{b n }为等比数列，且公比0q >，且1236b b b +=，求q 与a n 的通项公式； (Ⅱ)若数列{b n }为等差数列，且公差0d >，证明：1211n c c c d+++<+． 21.如图，已知椭圆221:12x C y +=，抛物线22:2(0)C y px p =>，点A 是椭圆1C 与抛物线2C 的交点，过点A 的直线l 交椭圆1C 于点B ，交抛物线2C 于M (B ，M 不同于A )．(Ⅰ)若116=p ，求抛物线2C 焦点坐标；(Ⅱ)若存在不过原点的直线l 使M 为线段AB 的中点，求p 的最大值．22.已知12a <≤，函数()e xf x x a =--，其中e =2.71828…为自然对数底数．(Ⅰ)证明：函数()y f x =在(0)+∞，上有唯一零点；(Ⅱ)记x 0为函数()y f x =在(0)+∞，上的零点，证明：(ⅰ0x ≤≤； (ⅱ)00(e )(e 1)(1)x x f a a ≥--．。

2020年高考浙江卷数学试题(含解析)

1.已知集合{|14}P x x =<<，{|23}Q x x =<<，则P Q =（） A.{|12}x x <≤ B.{|23}x x << C.{|34}x x ≤< D.{|14}x x << 【答案】B【解析】由题易知，{|23}P Q x x =<<，故选B.2.已知a R ∈，若1(2)a a i -+-（i 是虚数单位）是实数，则a =（） A.1 B.1- C.2 D.2- 【答案】C【解析】因为1(2)a a i -+-是实数，则虚部为0，所以20a -=，即2a =.故选C.3.若实数x ，y 满足约束条件31030x y x y -+≤⎧⎨+-≥⎩，则2z x y =+的取值范围是（）A.(,4]-∞B.[4,)+∞C.[5,)+∞D.(,)-∞+∞【答案】B【解析】根据约束条件，画出可行域，如图所示，将2z x y =+化为22x zy =-+，由图可知，当直线22x zy =-+经过点(2,1)时，截距z 最小，此时，z 取得最小值，即min 2214z =+⨯=，z 的最大值可取到无穷大，则2z x y =+的取值范围为[4,)+∞.故选B.4.函数cos sin y x x x =+在区间[,]ππ-上的图象可能是（）A. B.C. D.【解析】函数()cos sin f x x x x =+，则()cos()sin()cos sin ()f x x x x x x x f x -=--+-=--=-，则()f x 为奇函数，可排除C ，D 项；当x π=时，()cos sin 0f πππππ=+=-<，故选A.5.某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：3cm ）是（）A.73 B.143 C.3 D.6 【答案】A【解析】由三视图易知，原几何体由一个三棱锥和一个三棱柱两部分组成，该几何体的直观图如图所示，三棱锥的体积1111211323V =⨯⨯⨯⨯=，三棱柱的体积2121222V =⨯⨯⨯=，则该几何体的体积为1217233V V V =+=+=.故选A.6.已知空间中不过同一点的三条直线,,l m n ，“,,l m n 共面”是“,,l m n 两两相交”的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B【解析】,,m n l 两两相交⇒,,m n l 在同一平面内，,,m n l 在同一平面内,,m n l ⇒两两相交，比如////m n l ，所以,,m n l 在同一平面内是,,m n l 两两相交的必要不充分条件.故选B.7.已知等差数列{}n a 的前n 项和为n S ，公差0d ≠，且11ad≤.记12b S =，*1222,n n n b S S n N ++=-∈，下列等式不可能成立的是（）A.4262a a a =+B.4262b b b =+C.2428a a a =D.2428b b b = 【答案】D【解析】等差数列{}n a 的通项公式为1(1)n a a n d =+-，因为1n n b b +-222222()()n n n n S S S S +-=---2221221()4(2)n n n n a a a a d n ++-=+-+=≥，又214b b d -=，所以{}n b 是公差为4d 的等差数列，11(1)42(43)n b b n d a n d =+-⋅=+-，选项A ，B 由等差数列性质可知正确；选项C ，若2428a a a =，则2111(3)()(7)a d a d a d +=++，化简得21a d d =，满足0d ≠，11ad≤，所以C 正确；选项D ，若2428b b b =，则2111(213)(25)(229)a d a d a d +=++，化简得2123a d d =，不满足0d ≠，11ad≤，所以D 正确.故选D.8.已知点(0,0)O ，(2,0)A -，(2,0)B .设点P 满足||||2PA PB -=，且P为函数y =图象上的点，则||OP =（）【答案】D【解析】由题知，(2,0)A -，(2,0)B ，点P 满足||||2PA PB -=，由双曲线的定义可知，则22a =，即1a =，又||42AB c ==，则2c =，b ，所以点P 在双曲线22113x y -=右支上，而y =229(4)y x =-，则2222162y x +=，所以点P 又在椭圆221436x y +=上半部分(0)y ≥，联立2222131436y x x y ⎧-=⎪⎪⎨⎪+=⎪⎩，解得x y ⎧=⎪⎪⎨⎪=⎪⎩P ，则||OP ==故选D. 9.已知a ，b R ∈且0ab ≠，对于任意0x ≥均有()()(2)0x a x b x a b ----≥，则（） A.0a < B.0a > C.0b < D.0b > 【答案】C【解析】根据标根法分类讨论，三个根分别为123,,2x a x b x a b ===+，①当1230,0,0x x x ≤≤≤时，0,0a b ≤≤； ②当1230,x x x ≤=时，0,a b R =∈；③当2130,x x x ≤=时，0,b a b ≤=-，即0,0b a ≤≥； ④当3120,x x x ≤=时，0b ≤或0a ≤；综上，0b ≤.10.设集合S ，T ，*S N ⊆，*T N ⊆，S ，T 中至少有2个元素，且S ，T 满足： ①对于任意的,x y S ∈，若x y ≠，则xy T ∈；②对于任意的,x y T ∈，若x y <，则yS x∈.下列命题正确的是（）A.若S 有4个元素，则S T 有7个元素B.若S 有4个元素，则S T 有6个元素C.若S 有3个元素，则S T 有5个元素D.若S 有3个元素，则S T 有4个元素【答案】A【解析】取{1,2,4}S =，{2,4,8}T =，此时{1,2,4,8}S T =有4个元素，排除D ；取{2,4,8}S =，{8,16,32}T =，此时{2,4,8,16,32}S T =有5个元素，排除C ；取{2,4,8,16}S =，{8,16,32,64,128}T =，此时{2,4,8,16,32,64,128}S T =有7个元素，排除B.故选A. 二、填空题11.我国古代数学家杨辉，朱世杰等研究过高阶等差数列的求和问题，如数列(1){}2n n +就是二阶等差数列，数列*(1){}()2n n n N +∈的前3项和是 . 【答案】10【解析】设(1)2n n n a +=，则11212a ⨯==，22332a ⨯==，33462a ⨯==，∴313610S =++=.12.二项展开式52345102354(12)x a a x a x a x a x a x +=+++++，则4a = ，315a a a ++= . 【答案】80,122【解析】444445(2)5280C x x x =⨯⨯=，∴480a =，15(2)10C x x =，3533(2)80C x x ⋅=，5555(2)32C x x =，∴110a =，380a =，532a =， ∴513122a a a =++.13.已知tan 2θ=，则cos2θ= ；)an(t 4πθ-= .【答案】35-,13【解析】222222cos sin 1tan 143cos2cos sin 1tan 145θθθθθθθ---====-+++，tan tan2114tan 412131tan t (n 4)a πθπθπθ---===+⨯+. 14.已知圆锥的侧面积（单位：2cm ）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm ）是 . 【答案】1【解析】设圆锥母线长为l ，底面半径为r ，由圆锥展开图的侧面积为2π可得2rl ππ=，由圆锥展开图的侧面为半圆可得1222r l ππ=⋅⋅，可解得1r =.15.已知直线(0)y kx b k =+>与圆221x y +=和圆22(4)1x y -+=均相切，则k = ；b【解析】根据对称性直线AB 过线段12O O 中点(2,0)C ，故直线:(2)AB y k x =-，再由1||1O A =，且190O AC ∠=，得1230O CA O CB ∠=∠=，所以2tan k O CB =∠=，故b =16.盒中有4个球，其中1个红球，1个绿球，2个黄球.从盒中随机取球，每次取1个，不放回，直到取出红球为止，设此过程中取到黄球的个数为ξ，则(0)P ξ== ，()E ξ= .【答案】13,1【解析】第一次红球114P =，第一次绿球第二次红球21114312P =⨯=，111(0)4123P ξ==+=，红球在两黄球左边，中间，右边的概率为13，当红球在两黄球之外之内不同位置所取出的黄球数不同，∴111()0121333E ξ=⨯+⨯+⨯=.17.已知平面单位向量12,e e 满足12|2|2e e -≤，设12a e e =+，123b e e =+，设,a b 夹角为θ，则2cos θ的最小值为 .【答案】2829【解析】法一：22121122|2|24()4()2e e e e e e -≤⇒-⋅+≤，∴1234e e ⋅≥， ()()2212222121244()cos 22(106)||||e e a b e e e e a b θ+⋅⋅==⋅++⋅⋅，令1234k e e =⋅≥，则224(1)4(1)424228cos 113(1)(53)533533295()()34k k k k k k θ++===⋅-≥-=+++++⨯. 法二：设1(1,0)e =，2(cos ,sin )e αα=， 2212|2|2(2cos )sin 2e e αα-≤⇒-+≤，∴3cos 4α≥， ||||cos ,a b a b a b ⋅=⨯⨯〈〉22(44cos )cos ,(22cos )(106cos )a b ααα+⇒〈〉=++88cos 44cos 106cos 53cos αααα++==++.设443(14()53)x f x x x +=≤≤+， 4(1)424228()113533533()(2)9534x f x x x +==⋅-≥-=+++⨯，即2min 28cos (9)2θ=. 三、解答题18.在锐角ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，已知2sin 0b A=. （1）求角B 的大小；（2）求cos cos cos A B C ++的取值范围.【解析】（1）由正弦定理得2sin sin B A A ，故sin B 3B π=.（2）由A B C π++=得23C A π=-，由ABC ∆是锐角三角形得(,)62A ππ∈，由21cos cos()cos 32C A A A π=-=-+得1113cos cos cos cos sin()]22622A B C A A A π++=++=++∈.故cos cos cos A B C ++的取值范围是3]2.19.如图，在三棱台ABC DEF -中，平面ACFD ⊥面ABC ，45ACB ACD ∠=∠=︒，2DC BC =. （1）证明：EF DB ⊥；（2）求直线DF 与平面DBC 所成角的正弦值.【解析】（1）如图，过点D 作DO AC ⊥，交直线AC 于点O ，连结OB .由45ACD ∠=︒，DO AC ⊥得CD ，由平面ACFD ⊥平面ABC 得DO ⊥平面ABC ，所以DO BC ⊥.由45ACB ∠=︒，12BC CD ==得BO BC ⊥，所以BC ⊥平面BDO ，故BC DB ⊥.由三棱台ABC DEF -得//BC EF ，所以EF DB ⊥.（2）方法一：过点O 作OH BD ⊥，交直线BD 于点H ，连结CH . 由三棱台ABC DEF -得//DF CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角. 由BC ⊥平面BDO 得OH BC ⊥，故OH ⊥平面BCD ，所以OCH ∠为直线CO 与平面DBC 所成角.设CD =，由2DO OC ==，BO BC ==得BD =，OH =sin OH OCH OC ∠==，因此，直线DF 与平面DBC . 方法二：由三棱台ABC DEF -得//DF CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角，记为θ.如图，以O 为原点，分别以射线OC ，OD 为y ，z 轴的正半轴，建立空间直角坐标系O xyz -.设22CD =.由题意知各点坐标如下：(0,0,0)O ，(1,1,0)B ，(0,2,0)C ，(0,0,2)D . 因此(0,2,0)OC =，(1,1,0)BC =-，(0,2,2)CD =-. 设平面BCD 的法向量(,,)n x y z =，由00n BC n CD ⎧⋅=⎪⎨⋅=⎪⎩，即0220x y y z -+=⎧⎨-+=⎩，可取(1,1,1)n =，所以||3sin |cos ,|3||||OCn OC n OC n θ⋅=<>==⋅. 因此，直线DF 与平面DBC . 20.已知数列{}n a ，{}n b ，{}n c 满足1111a b c ===，1n n n c a a +=-，12nn n n b c c b ++=，*()n N ∈. （1）若数列{}n b 为等比数列，公比0q >，且1236b b b +=，求q 的值及数列{}n a 的通项公式；（2）若数列{}n b 为等差数列，公差0d >，证明：*12311,n c c c c n N d++++<+∈….【解析】（1）由1236b b b +=得216q q +=，解得12q =，由14n n c c +=得14n n c -=.由114n n n a a -+--得121421443n n n a a --+=++++=. （2）由12n n n n b c c b ++=得12111111()nn n n n b b c d c b b d b b +++==-，所以123111(1)n n d c c c c d b ++++++=-，由11b =，0d >得10n b +>，因此12311n c c c c d++++<+，*n N ∈. 21.如图，已知椭圆221:12x C y +=，抛物线22:2(0)C y px p =>，点A 是椭圆1C 与抛物线2C 的交点，过点A 的直线l 交椭圆1C 于点B ，交抛物线2C 于点M （,B M 不同于A ）.（1）若116p =，求抛物线2C 的焦点坐标；（2）若存在不过原点的直线l 使M 为线段AB 的中点，求p 的最大值.【解析】（1）由116p =得2C 的焦点坐标是1(,0)32.（2）由题意可设直线l ：x my t =+（0m ≠，0t ≠），点00(,)A x y .将直线l 的方程代入椭圆1C ：2212x y +=得222(2)220m y mty t +++-=，所以点M 的纵坐标22M mty m =-+. 将直线l 的方程代入抛物线2C ：22y px =得2220y pmy pt --=，所以02M y y pt =-，解得202(2)p m y m +=，因此，22022(2)p m x m +=. 由220012x y +=得2421224()2()160m m p m m =+++≥，所以当m t =时，p . 22.已知12a <≤，函数()x f x e x a =--，其中 2.71828e =是自然对数的底数.（1）证明：函数()y f x =在(0,)+∞上有唯一零点；（2）记0x 是函数()y f x =在(0,)+∞上的零点，证明：（i 0x ≤（ii ）()00(1)(1)xx f e e a a ≥--.【解析】（1）因为(0)10f a =-<，22(2)240f e a e =--≥->，所以()y f x =在(0,)+∞上存在零点.因为()1x f x e '=-，所以当0x >时，()0f x '>，故函数()f x 在[0,)+∞上单调递增，所以函数()y f x =在(0,)+∞上有唯一零点.（2）（i ）令21()1(0)2xg x e x x x =---≥，()1()1x g x e x f x a '=--=+-，由（1）知函数()g x '在[0,)+∞上单调递增，故当0x >时，()(0)0g x g ''>=，所以函数()g x 在[0,)+∞单调递增，故()(0)0g x g ≥=.由0g ≥得00()f a f x =-≥=，因为()f x 在[0,)+∞0x ≥. 令1()21(01)x h x e x x =--≤≤，1()2x h x e '=-，所以故当01x <<时，1()0h x <，即1()0h x '<，所以()h x 在[0,1]单调递减，因此当01x ≤≤时，()(0)0h x h ≤=.由0h ≤得00()f a f x =≤=，因此()f x 在[0,)+∞0x ≤.0x ≤≤（ii ）令()(1)1x u x e e x =---，()(1)x u x e e '=--，所以当1x >时，()0u x '>，故函数()u x 在区间[1,)+∞上单调递增，因此()(1)0u x u ≥=.由00x e x a =+可得022000000()()(1)(2)(1)x a a x f e x f x a e x a e x e ax =+=-+-≥-，由0x ≥得00()(1)(1)x x f e e a a ≥--.。

2022年高考真题—数学(浙江卷)【含答案及解析】

年普通⾼等学校招⽣全国统⼀考试（浙江卷）数学参考公式：如果事件A ，B 互斥，则柱体的体积公式()()()P A B P A P B +=+V Sh=如果事件A ，B 相互独立，则其中S 表示柱体的底面积，h 表示柱体的高()()()P AB P A P B =×锥体的体积公式若事件A 在一次试验中发生的概率是p ，则n 次13V Sh=独立重复试验中事件A 恰好发生k 次的概率其中S 表示锥体的底面积，h 表示锥体的高()(1)(0,1,2,,)k k n k n n P k C p p k n -=-=L 球的表面积公式台体的体积公式24S R p=()1213V S S h =++球的体积公式其中12,S S 表示台体的上、下底面积，343V R p =h 表示台体的高其中R 表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合{1,2},{2,4,6}A B ==，则A B È=（）A.{2}B.{1,2}C.{2,4,6}D.{1,2,4,6}2.已知,,3i (i)i a b a b Î+=+R （i 为虚数单位），则（）A.1,3a b ==- B.1,3a b =-= C.1,3a b =-=- D.1,3a b ==3.若实数x ，y 满足约束条件20,270,20,x x y x y -³ìï+-£íï--£î则34z x y =+的最大值是（）A 20B. 18C. 13D. 64.设x ÎR ，则“sin 1x =”是“cos 0x =”的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）.A.22πB.8πC.22π3D.16π36.为了得到函数2sin 3y x =的图象，只要把函数π2sin 35y x æö=+ç÷èø图象上所有的点（）A.向左平移π5个单位长度 B.向右平移π5个单位长度C.向左平移π15个单位长度 D.向右平移π15个单位长度7.已知825,log 3ab ==，则34a b -=（）A.25B.5C.259 D.538.如图，已知正三棱柱1111,ABC A B C AC AA -=，E ，F 分别是棱11,BC A C 上的点．记EF 与1AA 所成的角为a ，EF 与平面ABC 所成的角为b ，二面角F BC A --的平面角为g ，则（）A.a b g££ B.b a g ££ C.b g a££ D.a g b££9.已知,a b ÎR ，若对任意,|||4||25|0x a x b x x Î-+---³R ，则（）A.1,3a b £³ B.1,3a b ££ C.1,3a b ³³ D.1,3a b ³£10.已知数列{}n a 满足()21111,3n n n a a a a n *+==-ÎN ，则（）A.100521002a <<B.100510032a << C.100731002a <<D.100710042a <<非选择题部分（共110分）二、填空题：本大题共7小题，单空题每题4分，多空题每空3分，共36分．11.我国南宋著名数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白．如果把这个方法写成公式，就是S =，其中a ，b ，c 是三角形的三边，S 是三角形的面积．设某三角形的三边2a b c ===，则该三角形的面积S =___________．12已知多项式42345012345(2)(1)x x a a x a x a x a x a x +-=+++++，则2a =__________，12345a a a a a ++++=___________．13.若3sin sin 2pa b a b -=+=，则sin a =__________，cos 2b =_________．14.已知函数()22,1,11,1,x x f x x x x ì-+£ï=í+->ïî则12f f æöæö=ç÷ç÷èøèø________；若当[,]x a b Î时，1()3f x ££，则b a -的最大值是_________．15.现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为x ，则(2)P x ==__________，()E x =_________．16.已知双曲线22221(0,0)x y a b a b -=>>的左焦点为F ，过F 且斜率为4b a的直线交双曲线于点()11,A x y ，交双曲线的渐近线于点()22,B x y 且120x x <<．若||3||FB FA =，则双曲线的离心率是_________．17.设点P 在单位圆的内接正八边形128A A A L 的边12A A 上，则222182PA PA PA +++u u u r u u L u r u u u r 的取值范围是_______．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18.在ABC V 中，角A ，B ，C 所对的边分别为a ，b ，c．已知34,cos 5a C ==．（1）求sin A 的值；（2）若11b =，求ABC V 面积．.的19.如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE Ð=Ð=°，二面角F DC B --的平面角为60°．设M ，N 分别为,AE BC 的中点．（1）证明：FN AD ^；（2）求直线BM 与平面ADE 所成角的正弦值．20.已知等差数列{}n a 的首项11a =-，公差1d >．记{}n a 的前n 项和为()n S n *ÎN ．（1）若423260S a a -+=，求n S ；（2）若对于每个n *ÎN ，存在实数n c ，使12,4,15n n n n n n a c a c a c +++++成等比数列，求d 的取值范围．21.如图，已知椭圆22112x y +=．设A ，B 是椭圆上异于(0,1)P 的两点，且点0,21Q æöç÷èø在线段AB上，直线,PA PB 分别交直线132y x =-+于C ，D 两点．（1）求点P 到椭圆上点距离的最大值；（2）求||CD 的最小值．22.设函数e()ln (0)2f x x x x=+>．（1）求()f x 的单调区间；（2）已知,a b ÎR ，曲线()y f x =上不同三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b ．证明：（ⅰ）若e a >，则10()12e a b f a æö<-<-ç÷èø；（ⅱ）若1230e,a x x x <<<<，则22132e 112e e 6e 6ea a x x a --+<+<-．（注：e 2.71828=L是自然对数的底数）的的答案及解析选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合{1,2},{2,4,6}A B ==，则A B È=（）A.{2}B.{1,2}C.{2,4,6}D.{1,2,4,6}【答案】D 【解析】【分析】利用并集的定义可得正确的选项.【详解】{}1,2,4,6A B =U ，故选：D.2.已知,,3i (i)i a b a b Î+=+R （i 为虚数单位），则（）A.1,3a b ==- B.1,3a b =-= C.1,3a b =-=- D.1,3a b ==【答案】B 【解析】【分析】利用复数相等的条件可求,a b .【详解】3i 1i a b +=-+，而,a b 为实数，故1,3a b =-=，故选：B.3.若实数x ，y 满足约束条件20,270,20,x x y x y -³ìï+-£íï--£î则34z x y =+的最大值是（）A. 20B. 18C. 13D. 6【答案】B 【解析】【分析】在平面直角坐标系中画出可行域，平移动直线34z x y =+后可求最大值.【详解】不等式组对应的可行域如图所示：当动直线340x y z +-=过A 时z 有最大值.由2270x x y =ìí+-=î可得23x y =ìí=î，故()2,3A ，故max 324318z =´+´=，故选：B.4.设x ÎR ，则“sin 1x =”是“cos 0x =”的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A 【解析】【分析】由三角函数的性质结合充分条件、必要条件的定义即可得解.【详解】因为22sin cos 1x x +=可得：当sin 1x =时，cos 0x =，充分性成立；当cos 0x =时，sin 1x =±，必要性不成立；所以当x ÎR ，sin 1x =是cos 0x =的充分不必要条件.故选：A.5.某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A.22πB.8πC.22π3D.16π3【答案】C 【解析】【分析】根据三视图还原几何体可知，原几何体是一个半球，一个圆柱，一个圆台组合成的几何体，即可根据球，圆柱，圆台的体积公式求出．【详解】由三视图可知，该几何体是一个半球，一个圆柱，一个圆台组合成的几何体，球的半径，圆柱的底面半径，圆台的上底面半径都为1cm ，圆台的下底面半径为2cm ，所以该几何体的体积(322214122ππ1π122π2π12333V =´´+´´+´´´+´+=3cm ．故选：C ．6.为了得到函数2sin 3y x =的图象，只要把函数π2sin 35y x æö=+ç÷èø图象上所有的点（）A. 向左平移π5个单位长度 B.向右平移π5个单位长度C. 向左平移π15个单位长度 D. 向右平移π15个单位长度【答案】D【解析】【分析】根据三角函数图象的变换法则即可求出．【详解】因为ππ2sin 32sin 3155y x x éùæö==-+ç÷êúèøëû，所以把函数π2sin 35y x æö=+ç÷èø图象上的所有点向右平移π15个单位长度即可得到函数2sin 3y x =的图象．故选：D.7.已知825,log 3ab ==，则34a b -=（）A. 25B. 5C.259D.53【答案】C 【解析】【分析】根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出．【详解】因为25a=，821log 3log 33b ==，即323b =，所以()()22323232452544392a aa bb b -====．故选：C.8.如图，已知正三棱柱1111,ABC A B C AC AA -=，E ，F 分别是棱11,BC A C 上的点．记EF 与1AA 所成的角为a ，EF 与平面ABC 所成的角为b ，二面角F BC A --的平面角为g ，则（）A.a b g££ B.b a g ££ C.b g a££ D.a g b££【答案】A 【解析】【分析】先用几何法表示出a b g ，，，再根据边长关系即可比较大小．【详解】如图所示，过点F 作FP AC ^于P ，过P 作PM BC ^于M ，连接PE ，则EFP a =Ð，FEP b =Ð，FMP g =，tan 1PE PE FP AB a ==£，tan 1FP AB PE PE b ==³，tan tan FP FPPM PEg b =³=，所以a b g ££，故选：A ．9.已知,a b ÎR ，若对任意,|||4||25|0x a x b x x Î-+---³R ，则（）A 1,3a b £³ B.1,3a b ££ C.1,3a b ³³ D.1,3a b ³£【答案】D 【解析】【分析】将问题转换为|||25||4|a x b x x -³---，再结合画图求解．【详解】由题意有：对任意的x ÎR ，有|||25||4|a x b x x -³---恒成立．设()||f x a x b =-，()51,2525439,421,4x x g x x x x x x x ì-£ïïï=---=-<<íï-³ïïî，即()f x 的图象恒在()g x 的上方（可重合），如下图所示：.由图可知，3a ³，13b ££，或13a £<，3143b a££-£，故选：D ．10.已知数列{}n a 满足()21111,3n n n a a a a n *+==-ÎN ，则（）A.100521002a <<B.100510032a << C.100731002a <<D.100710042a <<【答案】B 【解析】【分析】先通过递推关系式确定{}n a 除去1a ，其他项都在()0,1范围内，再利用递推公式变形得到1111133n n n a a a +-=>-，累加可求出11(2)3n n a >+，得出1001003a <，再利用11111111333132n n n a a a n n +æö-=<=+ç÷-+èø-+，累加可求出()111111113323n n a n æö-<-++++ç÷èøL ，再次放缩可得出10051002a >．【详解】∵11a =，易得()220,13a =Î，依次类推可得()0,1n aÎ由题意，1113n n n a a a +æö=-ç÷èø，即()1131133n n n n n a a a a a +==+--，∴1111133n n n a a a +-=>-，即211113a a ->，321113a a ->，431113a a ->，…，1111,(2)3n n n a a -->³，累加可得()11113n n a ->-，即11(2),(2)3n n n a >+³，∴()3,22n a n n <³+，即100134a <，100100100334a <<,又11111111,(2)333132n n n n a a a n n +æö-=<=+³ç÷-+èø-+，∴211111132a a æö-=+ç÷èø，321111133a a æö-<+ç÷èø，431111134a a æö-<+ç÷èø，…，111111,(3)3n n n a a n -æö-<+³ç÷èø，累加可得()11111111,(3)3323n n n a n æö-<-++++³ç÷èøL ，∴10011111111133334943932399326a æöæö-<++++<+´+´<ç÷ç÷èøèøL ，即100140a <，∴100140a >，即10051002a >；综上：100510032a <<．故选：B ．【点睛】关键点点睛：解决本题的关键是利用递推关系进行合理变形放缩.非选择题部分（共110分）二、填空题：本大题共7小题，单空题每题4分，多空题每空3分，共36分．11.我国南宋著名数学家秦九韶，发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白．如果把这个方法写成公式，就是S =，其中a ，b ，c 是三角形的三边，S 是三角形的面积．设某三角形的三边2a b c ===，则该三角形的面积S =___________．【答案】4.【解析】【分析】根据题中所给的公式代值解出．【详解】因为S =，所以4S ==．故答案为：4.12.已知多项式42345012345(2)(1)x x a a x a x a x a x a x +-=+++++，则2a =__________，12345a a a a a ++++=___________．【答案】①.8②.2-【解析】【分析】第一空利用二项式定理直接求解即可，第二空赋值去求，令0x =求出0a ，再令1x =即可得出答案．【详解】含2x 项为：()()3232222244C 12C 14128x x x x x x ×××-+×××-=-+=，故28a =；令0x =，即02a =，令1x =，即0123450a a a a a a =+++++，∴123452a a a a a ++++=-，故答案为：8；2-．13.若3sin sin 2pa b a b -=+=，则sin a =__________，cos 2b =_________．【答案】①.10②.45【解析】【分析】先通过诱导公式变形，得到a 的同角等式关系，再利用辅助角公式化简成正弦型函数方程，可求出a ，接下来再求b ．【详解】2pa b +=，∴sin cos b a =，即3sin cos a a -=的sin cos1010a aö-=÷÷øsin10q=，cos10q=，()a q-=，∴22k k Zpa q p-=+Î，，即22kpa q p=++，∴sin sin2cos210kpa q p qæö=++==ç÷èø，则224cos22cos12sin15b b a=-=-=．故答案为：10；45．14.已知函数()22,1,11,1,x xf xx xxì-+£ï=í+->ïî则12f fæöæö=ç÷ç÷èøèø________；若当[,]x a bÎ时，1()3f x££，则b a-的最大值是_________．【答案】①.3728②.3【解析】【分析】结合分段函数的解析式求函数值，由条件求出a的最小值,b的最大值即可.【详解】由已知2117()2224fæö=-+=ç÷èø，77437()144728f=+-=，所以137()228f féù=êúëû，当1x£时，由1()3f x££可得2123x£-+£，所以11x-££，当1x>时，由1()3f x££可得1113xx£+-£，所以12x<£1()3f x££等价于12x-££+，所以[,][1,2a bÍ-+，所以b a-的最大值为3.故答案为：3728，315.现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为x，则(2)P x==__________，()E x=_________．【答案】①.1635，②.127##517【解析】【分析】利用古典概型概率公式求(2)P x =，由条件求x 分布列，再由期望公式求其期望.【详解】从写有数字1,2,2,3,4,5,6的7张卡片中任取3张共有37C 种取法，其中所抽取的卡片上的数字的最小值为2的取法有112424C C C +种，所以11242437C C C 16(2)C 35P x +===，由已知可得x 的取值有1，2，3，4，2637C 15(1)C 35P x ===，16(2)35P x ==，，()()233377C 31134C 35C 35P P x x ======，所以15163112()1234353535357E x =´+´+´+´=,故答案为：1635，127.16.已知双曲线22221(0,0)x y a b a b -=>>的左焦点为F ，过F 且斜率为4b a的直线交双曲线于点()11,A x y ，交双曲线的渐近线于点()22,B x y 且120x x <<．若||3||FB FA =，则双曲线的离心率是_________．【答案】4【解析】【分析】联立直线AB 和渐近线2:bl y x a=方程，可求出点B ，再根据||3||FB FA =可求得点A ，最后根据点A 在双曲线上，即可解出离心率．【详解】过F 且斜率为4b a 的直线:()4b AB y x c a=+，渐近线2:bl y x a =，联立()4b y x c ab y xa ì=+ïïíï=ïî，得,33c bc B a æöç÷èø，由||3||FB FA =，得5,,99c bc A a æö-ç÷èø而点A 在双曲线上，于是2222222518181c b c a a b -=，解得：228124c a =，所以离心率e 4=.故答案为：4．17.设点P 在单位圆的内接正八边形128A A A L 的边12A A 上，则222182PA PA PA +++u u u r u u L u r u u u r 的取值范围是_______．【答案】[12+【解析】【分析】根据正八边形的结构特征，分别以圆心为原点，37A A 所在直线为x 轴，51A A 所在直线为y 轴建立平面直角坐标系，即可求出各顶点的坐标，设(,)P x y ，再根据平面向量模的坐标计算公式即可得到()2222212888PA PA PA x y +++=++u u u r u u u r u u u r L ，然后利用cos 22.5||1OP ££o 即可解出．【详解】以圆心为原点，37A A 所在直线为x 轴，51A A 所在直线为y 轴建立平面直角坐标系，如图所示：则1345726(0,1),,,(1,0),,,(0,1),,,(1,0)222222A A A A A A A æöææ-----ç÷ççç÷ç÷ç÷èøèøèø,822A æö-ç÷ç÷èø，设(,)P x y ,于是()2222212888PA PA PA x y +++=++u u u r u u u r u u u r L ，因为cos 22.5||1OP ££o，所以221cos 4512x y +£+£o ，故222128PA PA PA +++u u u r u u u r u u u r L 的取值范围是[12+.故答案为：[12+．三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤．18.在ABC V 中，角A ，B ，C 所对的边分别为a ，b ，c．已知34,cos 5a C ==．（1）求sin A 的值；（2）若11b =，求ABC V 的面积．【答案】（1；（2）22．【解析】【分析】（1）先由平方关系求出sin C ，再根据正弦定理即可解出；（2）根据余弦定理的推论222cos 2a b c C ab+-=以及4a =可解出a ，即可由三角形面积公式in 12s S ab C =求出面积．【小问1详解】由于3cos 5C =，0πC <<，则4sin 5C =．因为4a =，由正弦定理知4sin A C =，则sin sin 45A C ==．【小问2详解】因为4a =，由余弦定理，得2222221612111355cos 22225a a a abc C ab a a +--+-====，即26550a a +-=，解得5a =，而4sin 5C =，11b =，所以ABC V 的面积114sin 51122225S ab C ==´´´=．19.如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE Ð=Ð=°，二面角F DC B --的平面角为60°．设M ，N 分别为,AE BC 的中点．（1）证明：FN AD ^；（2）求直线BM 与平面ADE 所成角的正弦值．【答案】（1）证明见解析；（2）14．【解析】【分析】（1）过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H ，由平面知识易得FC BC =，再根据二面角的定义可知，60BCF Ð=o ，由此可知，FN BC ^，FN CD ^，从而可证得FN ^平面ABCD ，即得FN AD ^；（2）由（1）可知FN ^平面ABCD ，过点N 做AB 平行线NK ，所以可以以点N 为原点，NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz -，求出平面ADE 的一个法向量，以及BM uuu u r，即可利用线面角的向量公式解出．【小问1详解】过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H ．∵四边形ABCD 和EFCD 都是直角梯形，//,//,5,3,1AB DC CD EF AB DC EF ===，60BAD CDE Ð=Ð=°，由平面几何知识易知，2,90DG AH EFC DCF DCB ABC ==Ð=Ð=Ð=Ð=°，则四边形EFCG 和四边形DCBH 是矩形，∴在Rt EGD V 和Rt DHA V ，EG DH ==∵,DC CF DC CB ^^，且CF CB C Ç=，∴DC ^平面,BCF BCF Ð是二面角F DC B --的平面角，则60BCF Ð=o ，∴BCF △是正三角形，由DC Ì平面ABCD ，得平面ABCD ^平面BCF ，∵N 是BC 的中点，\FN BC ^，又DC ^平面BCF ，FN Ì平面BCF ，可得FN CD ^，而BC CD C Ç=，∴FN ^平面ABCD ，而AD Ì平面ABCD FN AD \^．【小问2详解】因为FN ^平面ABCD ，过点N 做AB 平行线NK ，所以以点N 为原点，NK ，NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz -，设(3,(1,0,3)A B D E，则33,,22M æöç÷ç÷èø，33,,,(2,(22BM AD DE æö\=-=--=-ç÷ç÷èøu u u u r u u ur u u u r 设平面ADE 的法向量为(,,)n x y z =r由00n AD n DE ì×=í×=îu u u v r u u u v r，得20230x x z ì--=ïí-++=ïî，取n =-r ，设直线BM 与平面ADE 所成角为q ，∴||sin cos ,14|||n BM n BM n BM q ×=áñ====×u uu u r r u uu u r r uu u u r r ．20.已知等差数列{}n a 的首项11a =-，公差1d >．记{}n a 的前n 项和为()n S n *ÎN ．（1）若423260S a a -+=，求n S ；（2）若对于每个n *ÎN ，存在实数n c ，使12,4,15n n n n n n a c a c a c +++++成等比数列，求d 取值范围．【答案】（1）235(N )2n n nS n *-=Î（2）12d <£【解析】【分析】（1）利用等差数列通项公式及前n 项和公式化简条件，求出d ，再求n S；的(2)由等比数列定义列方程，结合一元二次方程有解的条件求d 的范围.【小问1详解】因为42312601S a a a -+==-，，所以()()46211260d d d -+--+-++=，所以230d d -=，又1d >，所以3d =，所以34n a n =-，所以()213522n na a n n n S +-==，【小问2详解】因为n n a c +，14n n a c ++，215n n a c ++成等比数列，所以()()()212415n n n n n n a c a c a c +++=++，()()()2141115n n n nd c nd d c nd d c -+=-+-+-+++，22(1488)0n n c d nd c d +-++=，由已知方程22(1488)0n n c d nd c d +-++=的判别式大于等于0，所以()22148840d nd d D =-+-³，所以()()168812880d nd d nd -+-+³对于任意的n *ÎN 恒成立，所以()()212320n d n d ----³éùéùëûëû对于任意的n *ÎN 恒成立，当1n =时，()()()()21232120n d n d d d ----=++³éùéùëûëû，当2n =时，由()()2214320d d d d ----³，可得2£d 当3n ³时，()()21232(3)(25)0n d n d n n ---->--³éùéùëûëû，又1d >所以12d <£21.如图，已知椭圆22112x y +=．设A ，B 是椭圆上异于(0,1)P 的两点，且点0,21Q æöç÷èø在线段AB 上，直线,PA PB 分别交直线132y x =-+于C ，D 两点．（1）求点P 到椭圆上点的距离的最大值；（2）求||CD 的最小值．【答案】（1）11；（2）5．【解析】【分析】（1）设,sin )Q q q 是椭圆上任意一点,再根据两点间的距离公式求出2||PQ ，再根据二次函数的性质即可求出；（2）设直线1:2AB y kx =+与椭圆方程联立可得1212,x x x x +，再将直线132y x =-+方程与PA PB 、的方程分别联立，可解得点,C D 的坐标，再根据两点间的距离公式求出CD ，最后代入化简可得231CD k =×+，由柯西不等式即可求出最小值．【小问1详解】设,sin )Q q q 是椭圆上任意一点,(0,1)P ,则222221144144||12cos (1sin )1311sin 2sin 11sin 111111PQ q q q q q æö=+-=--=-+£ø+ç÷è，当且仅当1sin 11q =-时取等号，故||PQ 的最大值是11.【小问2详解】设直线1:2AB y kx =+,直线AB 方程与椭圆22112x y +=联立,可得22130124k x kx æö++-=ç÷èø,设()()1122,,,A x y B x y ，所以12212211231412k x x k x x k ì+=-ï+ïïíï=-æöï+ç÷ïèøî，因为直线111:1y PA y x x -=+与直线132y x =-+交于C ,则111114422(21)1C x x x x y k x ==+-+-,同理可得,222224422(21)1D x x x x y k x ==+-+-.则||CD ====231555k =×=³=+，当且仅当316k =时取等号，故CD的最小值为5.【点睛】本题主要考查最值计算，第一问利用椭圆的参数方程以及二次函数的性质较好解决，第二问思路简单，运算量较大，求最值的过程中还使用到柯西不等式求最值，对学生的综合能力要求较高，属于较难题．22.设函数e()ln (0)2f x x x x=+>．（1）求()f x 的单调区间；（2）已知,a b ÎR ，曲线()y f x =上不同三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b ．证明：（ⅰ）若e a >，则10()12e a b f a æö<-<-ç÷èø；（ⅱ）若1230e,a x x x <<<<，则22132e 112e e 6e 6ea a x x a --+<+<-．（注：e 2.71828=L 是自然对数的底数）【答案】（1）()f x 的减区间为e 02æöç÷èø,，增区间为e ,2æö+¥ç÷èø.的的（2）（ⅰ）见解析；（ⅱ）见解析.【解析】【分析】（1）求出函数的导数，讨论其符号后可得函数的单调性.（2）（ⅰ）由题设构造关于切点横坐标的方程，根据方程有3个不同的解可证明不等式成立，（ⅱ）31x k x =，1eam =<，则题设不等式可转化为()()()2131313122236m m m t t m m t t --++--<+，结合零点满足的方程进一步转化为()()()()211312ln 0721m m m m m m ---++<+，利用导数可证该不等式成立.【小问1详解】()22e 12e 22xf x x x x -¢=-+=，当e 02x <<，()0f x ¢<；当e2x >，()0f x ¢>，故()f x 的减区间为e 02æöç÷èø,，()f x 的增区间为e ,2æö+¥ç÷èø.【小问2详解】（ⅰ）因为过(),a b 有三条不同的切线，设切点为()(),,1,2,3i i x f x i =，故()()()i i i f x b f x x a ¢-=-，故方程()()()f x b f x x a ¢-=-有3个不同的根，该方程可整理为()21e e ln 022x a x b x x x æö----+=ç÷èø，设()()21e e ln 22g x x a x b x x x æö=----+ç÷èø，则()()22321e 1e 1e22g x x a x x x x x xæö¢=-+-+--+ç÷èø()()31e x x a x=---，当0e x <<或x a >时，()0g x ¢<；当e x a <<时，()0g x ¢>，故()g x 在()()0,e ,,a +¥上为减函数，在()e,a 上为增函数，因为()g x 有3个不同的零点，故()e 0g <且()0>g a ，故()21e e e ln e 0e 2e 2e a b æö----+<ç÷èø且()21e e ln 022a a a b a a a æö----+>ç÷èø，整理得到：12e a b <+且()eln 2b a f a a>+=，此时()1e 13e11ln ln 2e 2e 22e 222a a a b f a a a a aæöæö---<+-+-+=--ç÷ç÷èøèø，设()3e ln 22u a a a =--，则()2e-202au a a ¢=<，故()u a 为()e,+¥上的减函数，故()3eln e 022eu a <--=，故()1012e a b f a æö<-<-ç÷èø.（ⅱ）当0e a <<时，同（ⅰ）中讨论可得：故()g x 在()()0,,e,a +¥上为减函数，在(),e a 上为增函数，不妨设123x x x <<，则1230e x a x x <<<<<，因为()g x 有3个不同的零点，故()0g a <且()e 0g >，故()21e e e ln e 0e 2e 2e a b æö----+>ç÷èø且()21e e ln 022a a a b a a a æö----+<ç÷èø，整理得到：1ln 2e 2ea ab a +<<+，因为123x x x <<，故1230e x a x x <<<<<，又()2e e 1ln 2a ag x x b x x+=-+-+，设e t x =，()0,1e a m =Î，则方程2e e 1ln 02a ax b x x+-+-+=即为：2e ln 0e 2e a a t t t b +-+++=即为()21ln 02mm t t t b -++++=，记123123e e e,,,t t t x x x ===则113,,t t t 为()21ln 02m m t t t b -++++=有三个不同的根，设3131e 1x t k t x a ==>>，1eam =<，要证：22122e 112e e 6e 6e a a x x a --+<+<-，即证13e 2e e 26e 6e a a t t a --+<+<-，即证：13132166m mt t m --<+<-，即证：131********m m t t t t m --æöæö+-+-+<ç÷ç÷èøèø，即证：()()()2131313122236m m m t t m m t t --++--<+，而()21111ln 02m m t t t b -++++=且()23331ln 02mm t t t b -++++=，故()()()22131313ln ln 102m t t t t m t t -+--+-=，故131313ln ln 222t t t t m m t t -+--=-´-，故即证：()()()21313131312ln ln 236m m m t t m t t m t t --+--´<-+，即证：()()()1213313ln1312072t t t m m m t t t +--++>-即证：()()()213121ln 0172m m m k k k --+++>-，记()()1ln ,11k k k k k j +=>-，则()()2112ln 01k k k k k j æö¢=-->ç÷èø-，设()12ln u k k k k =--，则()2122210u k k k k k¢=+->-=即()0k j ¢>，故()k j 在()1,+¥上为增函数，故()()k m j j >，所以()()()()()()22131213121ln 1ln 172172m m m m m m k k m m k m --+--++++>+--，记()()()()()211312ln ,01721m m m m m m m m w ---+=+<<+，则()()()()()()()2232322132049721330721721m mm m m mm m m m m w ---+-+¢=>>++，所以()m w 在()0,1为增函数，故()()10m w w <=，故()()()()211312ln 0721m m m m m m ---++<+即()()()213121ln 0172m mm m m m --+++>-，故原不等式得证：【点睛】思路点睛：导数背景下的切线条数问题，一般转化为关于切点方程的解的个数问题，而复杂方程的零点性质的讨论，应该根据零点的性质合理转化需求证的不等式，常用的方法有比值代换等.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020
1.已知集合，，则
A
B
C
D
2.已知，若（i为虚数单位）是实数，则a＝
A1
B-1
C2
D-2
3.若实数x，y满足约束条件，则的取值范围是A
B
C
D
4. 函数在区间的图像大致为
A
B
C
D
5. 某几何体的三视图（单位：）如图所示，则该几何体的体积（单位：
）是
A
B
C
D
6. 已知空间中不过同一点的三条直线则“在同一平面” 是“两两相交”的
A充分不必要条件
B必要不充分条件
C充分必要条件
D既不充分也不必要条件
7.已知等差数列的前项的和，公差，.记
下列等式不可能成立的是
A
B
C
D
8.已知点, ,.设点满足，且为函数
的图像上的点，则
A
B
C
D
9．已知，若在上恒成立，则A
B
C
D
A若S有4个元素，则有7个元素
B若S有4个元素，则有6个元素
C若S有3个元素，则有4个元素
D若S有3个元素，则有5个元素
11.已知数列满足，则______
12.设，则=_______；
_______.
13．已知=2，则=______；=______.
14．已知圆锥展开图的侧面积为2π，且为半圆，则底面半径为______.
15．设直线l:y=kx+b(k>0)，圆:，:，若直线l与,
都相切,则k=______;b=______.
16.一个盒子里有1个红1个绿2个黄四个相同的球，每次拿一个，不放回，拿出红球即停，设拿出黄球的个数为，则；；
17.设，为单位向量，满足，，，设的
夹角为，则的最小值为.
18.（本题满分14分）
19（本题满分15分）
如图，三棱台中，面面，，。

（Ⅰ）证明：；
（Ⅱ）求与面所成角的正弦值。

（第19题图）
20.(本题满分15分)
已知中，.
（I）若数列为等比数列，且公比，且，求与的通项公式；
（Ⅱ）若数列为等差数列，且公差，证明：
21.（15分）
如图，已知椭圆，抛物线，点是椭圆与抛物线的交点，过点的直线交椭圆于点，交抛物线于（
不同于）.
（I）若，求抛物线的焦点坐标；
（Ⅱ）若存在不过原点的直线使为线段的中点；求的最大值. 22.（本题满分15 分）
已知函数，其中为自然对数的底数．（Ⅰ）证明：函数在上有唯一零点；
（Ⅱ）记为函数在上的零点，证明:
（i）
（ⅱ）.
参考答案
1.B
2.C
3.B
4.A
5.A
6.B
7.D
8.D
9.C 10.A 11.10 12.80 ,122
13. 14.1 15. 16.
17.28
29
18 正确答案及相关解析
正确答案
19 正确答案及相关解析正确答案
20 正确答案及相关解析正确答案
21 正确答案及相关解析正确答案
22 正确答案及相关解析正确答案。