第二节 单自由度体系的运动方程
合集下载
第二节 单自由度体系的运动方程

m y ( t ) c y ( t ) k y ( t ) P ( t ) 11
式表明,若建立体系的运动方程时以静平衡位置作为计算位移 的起点,则所得动位移的微分方程与重力无关。以后在建立体 系的运动方程时,将不标出重力W及其产生的静位移 st 。 上述方法是直接利用达朗贝尔原理建立质点m在任一瞬时的动 力平衡方程,它要用到结构的刚度系数k11,所以又称为刚度法。
3 11 l l l 2 l ) 1 P ( EI 2 22 4 EI
运动方程 为
EI 1 y ( t ) 3y ( t ) P ( t ) ml 4 m
图 ) R ( t ) P ( t ) 11
即
1 m y ( t ) c y ( t ) y ( t ) P ( t )
11
式中 11 为柔度系数,它表示在质点上沿质点运动方向施加单位力引起 质点沿运动方向的静位移。柔度系数与刚度系数k11互为倒数.由于建 立运动方程要用到体系的柔度系数,所以又称为柔度法。
一、列动力平衡方程(刚度法) 利用平衡条件建立运动方程
图11-10
在振动的任一时刻t取质点m为隔离体作用在质点上的力有(各力以指向y(t)的正 方向为正): (1)重力W。 (2)动力荷载P(t)。
图11-10
(3)弹性恢复力 S(t)。它是由于杆件的弹性变形而施加于质点的力,它的大 小与质点的位移成正比,但方向相反,即
§11-2 单自由度体系的运动方程
• 动力计算的基本未知量是质点的位移,它是时间t的函数。为
了 求出动力反应,应先列出求解质点位移的方程。描述体系 振动时质点动位移的数学方程,称为体系的运动方程(或振动方 程)。
动力学(第1章)
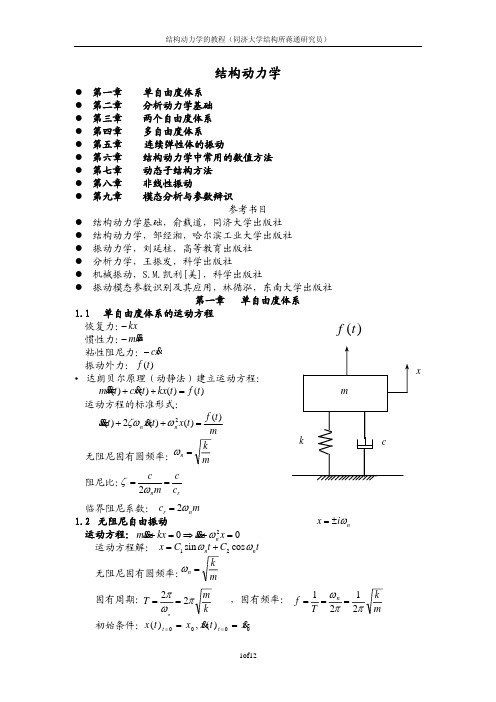
f
(t)
=
2P0
ωt π
∫ ∫ bi
=
2 T
T 0
f (t) sin(iωt)dt = 4ω π
π 2ω 0
f
(t) sin(iωt)dt
=
8P0 i2π 2
i −1
(−1) 2 (i
= 1,3,5,⋅⋅⋅)
6of12
结构动力学的教程(同济大学结构所蒋通研究员)
∑ 取
i=1~3
β1 算得:
=
1
−
1 ω2
= 1−ω
2ζω 3 2 + (2ζω )2
1+ 4ζ 2ω 2 (1− ω 2 )2 + (2ζω )2
5of12
结构动力学的教程(同济大学结构所蒋通研究员)
隔振要求: 频率比: ω
=
ω
>
2⇒
ωn
阻尼比小:ζ ↓⇒ A ↓
B
A <1 B
但过小通过共振区不利
主动隔振:将振源隔开,使振动传播不出去(隔振器)
+ϕ)
振幅与相位角: A=
x02
+
⎜⎜⎝⎛
x&0 ωn
⎟⎟⎠⎞2
,ϕ
=
arctg
ωn x0 x&0
x
A
x&0
x0
t ϕ /ωn
t t +T
例题 1-1 求图示体系的固有频率
悬臂梁刚度:k1
=
3EI l3
与 K2 并联后等效刚度:k = k1 + k2 固有频率:ωn = k / m (串联弹簧)
l m
• •
能量守衡:We +Wd + Wf = 0 → ω = ωn →
结构力学-单自由度体系的自由振动

mh3 T 2 24 EI
Vibration Characteristic
y(t ) Asin( t )
Acceleration: Inertia Force:
(t ) A 2 sin(t ) y (t ) mA 2 sin(t ) I (t ) m y
这是一个齐次方程,其通解为
y(t ) C1 cost C2 sin t
C1 和 C2 可由初始条件确定,设初始位移和初始速度分别为
y(0) y0 C1 y0
(0) v0 y
C2
v0
v0
,
y (t ) y0 cos t
sin t
y (t ) y0 cos t
在无阻尼自由振动中,位移、加速度和惯性力都按正弦规律
变化,且作相位相同的同步运动,即它们在同一时刻均达极值,
而且惯性力的方向与位移的方向一致。
幅值产生于
sin(t ) 1 时,其值分别为:
y A
A 2 y
I mA
2
由于在运动的任一瞬时质体都处于平衡状态,在幅值出现时
l
1 m
EA ml
st Wl T 2 2 g EAg
例: 求图示结构自振频率 。(EI 为常数,杆件自身 质量不计) [分析] 图乘法求位移
A m C l h
1 1 2 2 1 2 h2 B ( h h hl h) (h l ) EI 2 3 2 3 3EI
y y
v0
sin t
T
0
t
y cos t
-y
y
12.2单自由度体系的运动方程

(
&& + k B b 2α = 0 m1 a + m2 l α
2 2
)
All Rights Reserved
重庆大学土木工程学院®
【例12-3】试用柔度法建立图 】试用柔度法建立图12-14a所示静定刚架受动力荷载 所示静定刚架受动力荷载 作用的运动方程。 作用的运动方程。 M (t) M (t)
重庆大学土木工程学院®
All Rights Reserved
3EI 1 m&& + 3 y = M ( t ) y 2l 4l
l
m
y
M( EI B
C
EI A
也可写作
m&& + k11 y = FE (t ) y
为等效动力荷载
l
FE (t )
FE (t ) = (δ1P δ11)M(t )
&& FI1 = −m1 (aα ) &&) FI 2 = −m2 (lα
FB = k B (bα )
All Rights Reserved 重庆大学土木工程学院®
解:由∑MA=0,得 , 整理后, 整理后,得运动方程
&& && m1 a 2α + m2 l 2α + k B b 2α = 0
y = δ11 FI + δ11 FC + δ11 FP ( t )
All Rights Reserved 重庆大学土木工程学院®
(12-6)
y = δ11 FI + δ11 FC + δ11 FP ( t )
(12-6)
结构动力学 -单自由度体系的振动

负号表示等效力的方向和地面加速度方向相反。
13
§2.2 无阻尼自由振动
自由振动(free vibration) :无外界干扰的体系振动形 态称为自由振动(free vibration)。振动是由初始位 移或初始速度或两者共同影响下所引起的。 无阻尼自由振动:如果阻尼系数等于零,则这种自由 振动称为无阻尼自由振动(undamped free vibration)。 假设由于外界干扰,质点离开平衡位置,干扰消失后, 质点将围绕静力平衡点作自由振动。
或:m y ( t) c y ( t) k ( t) y m y g ( t) P e( f t) f
Peff (t ) :等效荷载,即在地面加速度yg (t )影响下,结构的响
应就和在外荷载p (t )作用下的响应一样,只是外荷载 p (t )
等于质量和地面加速度的乘积。
干扰力的大小只能影响振幅A的大小,而对结构自
振周期T的大小没影响。
(2)自振周期与质量平方根成正比,质量越大,则
周期越大;自振周期与刚度的平方根成反比,刚度
越大,则周期越小。要改变结构的自振周期,只有
改变结构的质量或刚度。
24
§2.2 无阻尼自由振动
k g
m
st
(3)把集中质点放在结构上产生最大位移的地方,则可
1、位移以静力平衡位置作为基准的,而这样确定的位移 即为动力响应。
2、在求总挠度和总应力时,要把动力分析的结果与静
力分析结果相加。
9
§2.1运动方程的建立
3、支座运动的影响 结构的动位移和动应力既可以由动荷载引起,也
可以由结构支座的运动而产生。 1)由地震引起建筑物基础的运动; 2)由建筑物的振动而引起安置在建筑物内的设备 基底的运动等等。
13
§2.2 无阻尼自由振动
自由振动(free vibration) :无外界干扰的体系振动形 态称为自由振动(free vibration)。振动是由初始位 移或初始速度或两者共同影响下所引起的。 无阻尼自由振动:如果阻尼系数等于零,则这种自由 振动称为无阻尼自由振动(undamped free vibration)。 假设由于外界干扰,质点离开平衡位置,干扰消失后, 质点将围绕静力平衡点作自由振动。
或:m y ( t) c y ( t) k ( t) y m y g ( t) P e( f t) f
Peff (t ) :等效荷载,即在地面加速度yg (t )影响下,结构的响
应就和在外荷载p (t )作用下的响应一样,只是外荷载 p (t )
等于质量和地面加速度的乘积。
干扰力的大小只能影响振幅A的大小,而对结构自
振周期T的大小没影响。
(2)自振周期与质量平方根成正比,质量越大,则
周期越大;自振周期与刚度的平方根成反比,刚度
越大,则周期越小。要改变结构的自振周期,只有
改变结构的质量或刚度。
24
§2.2 无阻尼自由振动
k g
m
st
(3)把集中质点放在结构上产生最大位移的地方,则可
1、位移以静力平衡位置作为基准的,而这样确定的位移 即为动力响应。
2、在求总挠度和总应力时,要把动力分析的结果与静
力分析结果相加。
9
§2.1运动方程的建立
3、支座运动的影响 结构的动位移和动应力既可以由动荷载引起,也
可以由结构支座的运动而产生。 1)由地震引起建筑物基础的运动; 2)由建筑物的振动而引起安置在建筑物内的设备 基底的运动等等。
201单自由度体系运动方程(力学)

yst yd
k
静平衡位置
c
m m
注意:质点的位移、速度和加速度以向下为正。
k m
c
k m
c
yst
k m
c
yst
y = yst + yd
yd
y y , y ,
静平衡位置
FP(t)
y y st yd y yd d y y
位
移
displacement
速 度
velocity
讨论:同一体系,激励位置不同,质量m的 运动方程是否相同?
m m
FP(t)) 11 FI ( t ) FS ( t ) 1P FP ( t )
1P mu ku FP ( t ) 11
1P FE ( t ) FP ( t ) 11
1. 建立体系运动方程方法
为什么要研究单自由度体系? 1. 许多动力问题常可按单自由度体系进行计算或进行 初步估算 2. 单自由度体系的分析是多自由度体系分析的基础 3. 许多概念由单自由度分析引出
单自由度体系运动方程的一般形式:
m k 水平运动模型 k m
m m
k
竖向运动模型
2. 刚度法(列动力平衡方程)
m cy y
1
y FP ( t )
1 k
与刚度法推出的运动方程相比较可见
4. 虚功法(对于刚体系特别方便)
δy k
FI y FD y FS y FP y 0
FP(t)
c
FI FD FS FP y 0
FI FD FS FP 0
加速度 acceleration
单自由度体系的自由振动

令
ω2 = k
m
y + ω 2 y = 0
运动方程的解 y + ω 2 y = 0 可由振动的初 2
始条件来确定
常系数的线性齐次微分方程,其通解为
y(t) = A1 cosωt + A2 sinωt
若当 t = 0 时 y = y0 初位移
y(0) = y0 = A1 cosω × 0 + A2 sin ω × 0
因此,自振周期(或频率)的计算十分重 要。
例 计算自振频率
14
EI=常数
如果让振动体系沿振动方向发生单位位移时,所有刚 结点都不能发生转动(如横梁刚度为无穷大的刚架) 计算刚度系数方便。
两端刚结的杆的侧移刚度为:12EI
l3
一端铰结的杆的侧移刚度为:3EI
l3
例 计算自振频率
1
k11
EI=常数
12 EI l3
y = y0 初速度
y(0) = y0 = −ωA1 sinω × 0 + ωA2 cosω × 0
A1 = y0
A2
=
y0
ω
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
位移的多项表达式
位移、速度的单项表达式
3
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
若令
y(t) = a sinϕ cosωt + a cosϕ sin ωt
结构自振周期、频率
6
自振周期的倒数称为工程频率 f = 1
(或频率),记作 f
T
频率 f 表示单位时间内的振动次数,其常用单位
2-1结构动力学(单自由度)

c 2 m
O
t
这条曲线仍具有衰减性,但不具有波动性。
1, cr 2m
c 2m
c cr
阻尼比
(2)ξ> 1(强阻尼)情况
1,2 2 1 0
y t C1e1t C2e2t
t
y( t )
O
y (t ) e t C1 sinh 2 1 t C 2 cosh 2 1 t
g y st
y st m T 2 2 k g
频率只取决于体系的质量和刚度,而与外界因素 无关,是体系本身固有的属性,所以又称为固有频率
(natural frequency)。
(3)简谐自由振动的特性
y(t ) Asin( t )
(t ) A 2 sin(t ) y 加速度为: 惯性力为: FI (t ) m (t ) mA 2 sin(t ) y
特征根 一般解
2 2 2 0
1, 2 2 1
y(t ) C1e
1t
C2 e
2t
(1)ξ= 1(临界阻尼)情况
1,2
y C1 C2 t e t
y( t )
tan v
t
y y0 (1 t ) v0t e
d
阻尼对自振频率、周期的影响
,
d
Td T
在工程结构问题中,若0.01<ξ<0.1,可近似取:
d , Td T
y(t ) e t Asin ( d t )
阻尼对振幅的影响
yk Aetk Td e y k 1 Ae (tk Td )
O
t
这条曲线仍具有衰减性,但不具有波动性。
1, cr 2m
c 2m
c cr
阻尼比
(2)ξ> 1(强阻尼)情况
1,2 2 1 0
y t C1e1t C2e2t
t
y( t )
O
y (t ) e t C1 sinh 2 1 t C 2 cosh 2 1 t
g y st
y st m T 2 2 k g
频率只取决于体系的质量和刚度,而与外界因素 无关,是体系本身固有的属性,所以又称为固有频率
(natural frequency)。
(3)简谐自由振动的特性
y(t ) Asin( t )
(t ) A 2 sin(t ) y 加速度为: 惯性力为: FI (t ) m (t ) mA 2 sin(t ) y
特征根 一般解
2 2 2 0
1, 2 2 1
y(t ) C1e
1t
C2 e
2t
(1)ξ= 1(临界阻尼)情况
1,2
y C1 C2 t e t
y( t )
tan v
t
y y0 (1 t ) v0t e
d
阻尼对自振频率、周期的影响
,
d
Td T
在工程结构问题中,若0.01<ξ<0.1,可近似取:
d , Td T
y(t ) e t Asin ( d t )
阻尼对振幅的影响
yk Aetk Td e y k 1 Ae (tk Td )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柔度法) 二、列位移方程(柔度法 列位移方程 柔度法 对于不便于计算刚度系数的体系, 对于不便于计算刚度系数的体系,也可改用结构的柔度系数来建 立运动方程。这种方法以整个休系为研究对象,如图所示, 立运动方程。这种方法以整个休系为研究对象,如图所示,在振 动的任一时刻t,质点m上除作用有动力荷载 上除作用有动力荷载P(t)外,还有惯性力 动的任一时刻 ,质点 上除作用有动力荷载 外 I(t)、阻尼力R(t),不考虑重力,又由于弹性恢复力是内力,故图 、阻尼力 ,不考虑重力,又由于弹性恢复力是内力, 中未标出。质点m的动位移 看成是由于动力荷载、 的动位移y(t)看成是由于动力荷载 中未标出。质点 的动位移 看成是由于动力荷载、惯性力和阻 尼力共同引起的,根据叠加原理, 尼力共同引起的,根据叠加原理,可得
§11-2 单自由度体系的运动方程
• 动力计算的基本未知量是质点的位移,它是时间t的函数。为
了 求出动力反应,应先列出求解质点位移的方程。描述体系 振动时质点动位移的数学方程,称为体系的运动方程(或振动方 程)。
•建立运动方程常用的方法是动静法。根据达朗贝尔原理,将惯
性力假想地作用在质点上,在振动的每一瞬时,惯性力与结构 受到的动荷载、约束反力等在形式上组成一平衡力系(动平衡), 于是就可以利用静力学中的方法建立运动方程。
即
建立图示体系的运动方程。图中质点m 例11-1 建立图示体系的运动方程。图中质点 1=2m、m2=m,弹 、 , 性支座B的刚度系数为 忽略阻尼影响和刚性杆的分布质量 的刚度系数为k 忽略阻尼影响和刚性杆的分布质量。 性支座 的刚度系数为 1,忽略阻尼影响和刚性杆的分布质量。
解:这是两个质点的单自由度体系。设在振动的任一时刻t刚性 这是两个质点的单自由度体系。设在振动的任一时刻 刚性 杆绕铰A的转角为 顺时针为正,则质点m 杆绕铰 的转角为α (t ) ,顺时针为正,则质点 1、m2的惯性力 分别为 3 3 l && && I 2 (t ) = − m2 ⋅ lα (t ) = − mlα (t ) &&(t ) = − ml α&(t ) & I1 (t ) = − m1 ⋅ α 2 2 2
刚度法) 一、列动力平衡方程(刚度法 列动力平衡方程 刚度法 利用平衡条件建立运动方程
图11-10
在振动的任一时刻t取质点 为隔离体作用在质点上的力有 各力以指向y(t)的正 在振动的任一时刻 取质点m为隔离体作用在质点上的力有 各力以指向 的正 取质点 为隔离体作用在质点上的力有(各力以指向 方向为正): 方向为正 : (1)重力 。 重力W。 重力 (2)动力荷载 动力荷载P(t)。 动力荷载 。
图示体系,各杆EI=常数,忽略杆件的分布质量和阻 常数, 例11-2 图示体系,各杆 常数 尼影响,建立其运动方程。 尼影响,建立其运动方程。
图11-13
解:图示体系为静定结构,求柔度系数比较方便,宜列位移 图示体系为静定结构,求柔度系数比较方便, 方程。 方程。
y (t ) = δ11[− m&&(t )] + δ1P ⋅ P(t ) y
1 1 2 2 1 2 l3 δ11 = ( ×l × l + ×l ×2l × ×l) = EI 2 3 2 3 EI 1 1 l l l3 δ1P = ( × 2l × × ) = EI 2 2 2 4EI
运动方程 为
&&( t ) + y
EI 1 y (t ) = P (t ) 3 ml 4m
y 沿动位移 沿动位移y(t)的正向作用。 的正向作用。 惯性力 −m&&(t ) 的正向作用
(5)阻尼力 阻尼力R(t)。关于阻尼力的理论有多种,这里采用计算较简单 阻尼力 。关于阻尼力的理论有多种, 的粘滞阻尼理论。它假定阻尼力R(t)与质点速度成正比,方向与速 与质点速度成正比, 的粘滞阻尼理论。它假定阻尼力 与质点速度成正比 度的方向相反, 度的方向相反,即
图11-11
y (t ) = δ11[I (t ) + R(t ) + P(t )]
即
& m&&(t ) + cy (t ) + y 1
δ11
y (t ) = P (t )
为柔度系数, 式中 δ11为柔度系数,它表示在质点上沿质点运动方向施加单位力引起 质点沿运动方向的静位移。柔度系数与刚度系数k 互为倒数. 质点沿运动方向的静位移。柔度系数与刚度系数 11互为倒数.由于建 立运动方程要用到体系的柔度系数,所以又称为柔度法。 立运动方程要用到体系的柔度系数,所以又称为柔度法。
弹性支座B的反力 弹性支座 的反力 为
RB = k1lα (t )
得由Leabharlann ΣM A = 0I1 (t ) ⋅
l 3 + I 2 (t ) ⋅ l − RB ⋅ l = 0 2 2
将I1(t)、I2(t)和RB的表达式代 入上式并整理得运动方程 、 和
4k1 && α (t ) + α (t ) = 0 11m
因质点重力W与由其引起的静位移 ∆ st 的关系为 W = k11∆ st , 因质点重力 与由其引起的静位移 于是得出质点振动的运动微分方程为
& m&&(t ) + cy (t ) + k11 y (t ) = P(t ) y
式表明, 式表明 ,若建立体系的运动方程时以静平衡位置作为计算位移 的起点,则所得动位移的微分方程与重力无关。 的起点 , 则所得动位移的微分方程与重力无关 。 以后在建立体 系的运动方程时,将不标出重力W及其产生的静位移 系的运动方程时,将不标出重力 及其产生的静位移∆ st 。 上述方法是直接利用达朗贝尔原理建立质点m在任一瞬时的动 上述方法是直接利用达朗贝尔原理建立质点 在任一瞬时的动 力平衡方程,它要用到结构的刚度系数k 所以又称为刚度法。 力平衡方程,它要用到结构的刚度系数 11,所以又称为刚度法。
图11-10
(3)弹性恢复力 弹性恢复力S(t)。它是由于杆件的弹性变形而施加于质点的力,它的大 弹性恢复力 。它是由于杆件的弹性变形而施加于质点的力, 小与质点的位移成正比,但方向相反, 小与质点的位移成正比,但方向相反,即
S (t ) = −k11 [∆ st + y (t )]
为刚度系数, 式中 k11 为刚度系数,其意义是使质点沿运动方向产生单位静位移而需在质 点上沿运动方向施加的力。 点上沿运动方向施加的力。 (4)惯性力 。其大小为质点质量 与质点加速度的乘积,方向与加速度的 惯性力I(t)。其大小为质点质量m与质点加速度的乘积 与质点加速度的乘积, 惯性力 方向相反, 方向相反,即 I (t ) = − m&&(t ) y
& R (t ) = −cy (t )
式中c称为粘滞阻尼系数。 式中 称为粘滞阻尼系数。 称为粘滞阻尼系数 考虑质点m的动力平衡 考虑质点 的动力平衡ΣY=0,应有 的动力平衡 ,
I (t ) + R (t ) + S (t ) + P (t ) + W = 0
即
& m&&(t ) + cy (t ) + k11[∆ st + y (t )] = P (t ) + W y
