第3章-习题、答案
电工安全 第3章课后习题答案

第三章 电网运行的安全技术1、判断题1双重绝缘是指除了基本绝缘外,还有一层独立的附加绝缘。
答案:正确2加强绝缘是指绝缘材料的机械强度和绝缘性能都加强了的基本绝缘。
答案:正确3固体绝缘材料发生电击穿后,如除去电压,绝缘性能还能恢复,不过有所降低。
答案:错误4网眼遮栏的高度应不低于1.7m,下部距地面应不大干0.1m,网眼应不大于40×40ram2。
答案:正确5网眼遮栏与裸导体的距离、对于低压应不小于0.15m,对于10KV设备应不小于0.35m。
答案:正确650m档距的低压架空线路,导线间的最小距离为0.4mo答案:正确7通过居民区和道路的低压架空线路,距地面应不低于6m。
答案:正确8低压线路与树木之间的最小垂直和水平距离均为lm。
答案:正确910KV架空导线与建筑物间的最小水平距离为2m,最小垂直距离为3 m。
答案:正确10低压和10KV线路的接户线和进户线的最低高度和线间最小距离都有严格规定,施工时必须严格遵守。
答案:正确11户内线路与煤气管、热水管、上下水管等各种工业管道之间的最小距离都有严格规定,施工时必须严格遵守。
答案:正确12Y接三相绕组的公共联结点,因其对三绕组另一端的电压绝对值相等,故称为中点。
答案:正确13通过接地装置与大地相连接的的中点称为零点。
答案:正确14由零点引出、与相线并行、作为三相不平衡电流和单相短电流通道的线称为零线。
答案:正确15零线有工作零线和保护零线之分。
答案:正确16在三相四线接地电网中,工作零线只用于通过三相不平衡电流。
答案:错误17三相五线制也是接地电网。
答案:错误18三相五线制中的保护零线只能通过短路电流和漏电电流,而不通过工作电流。
答案:正确19三相不平衡电流是工作电流而非短路或漏电电流。
答案:正确20接零保护是不接地电网中的主要安全措施之一。
答案:正确21在中点接地的三相四线制电网中,以接零保护作为电网运行的主要安全措施之一;而对接地保护—般不作要求。
马原,第三章习题及答案

第三章 人类社会及其发展规律(课后练习题)一、单项选择题1 .人类社会历史发展的决定力量是( )A .生产方式B .地理条件C .社会意识D .人口因素2 .社会意识相对独立性的最突出表现是它( )A .同社会存在发展的不同步性B .具有历史的继承性C .对社会存在具有能动的反作用D .同社会经济的发展具有不平衡性3 .在生产关系中起决定作用的是( )A .生产资料所有制B .产品的分配和交换C .在生产中人与人的关系D .管理者和生产者的不同地位4 . “手推磨产生的是封建主的社会,蒸汽磨产生的是工业资本家的社会” 这句话揭示了 ( )A .生产工具是衡量生产力水平的重要尺度B .科学技术是第一生产力C .社会形态的更替有其一定的顺序性D .物质生产的发展需要建立相应的生产关系5 .十一届三中全会以来,我党制定的一系列正确的路线、方针、政策促进了我国经济的 迅猛发展,这说明( )A .经济基础发展的道路是由上层建筑决定的B .上层建筑的发展决定经济基础的发展 方向C .上层建筑对经济基础具有积极的能动作用D .社会主义社会的发展不受经济基础决定上层建筑规律的制约6 .一定社会形态的经济基础是( )A .生产力B .该社会的各种生产关系C .政治制度和法律制度D .与一定生产力发展阶段相适应的生产关系的总和7 .上层建筑是指( )A .社会的经济制度B .科学技术C .社会生产关系D . 建立在一定社会经济基础之上的意识形态及相应的制度和设施8 .社会形态是( )A .生产力和生产关系的统一B .同生产力发展一定阶段相适应的经济基础和上层建筑 的统一体C .社会存在和社会意识的统一D .物质世界和精神世界的统一9 .人类社会发展的一般规律是( A .生产方式内部的矛盾规律 B10 .阶级斗争对阶级社会发展的推动作用突出表现在( ) A .生产力的发展 B .生产关系的变革 C .社会形态的更替 D .科技的进步 11 .社会革命根源于( ) A .人口太多 B .少数英雄人物组织暴动C .先进思想和革命理论的传播D .社会基本矛盾的尖锐化12 .社会主义改革的根本目的在于( )A .改变社会主义制度B .完善社会主义制度C .解放和发展生产力D .实现社会公平 13 . “蒸汽、电力和自动纺织机甚至是比巴尔贝斯、拉斯拜尔和布朗基诸位公民更危险万 分的革命家。
逻辑第三章习题参考答案(0710)

30
III. 三、2. P94
【原题】 ⒉ 已知“有S不是p”为假
【参考答案】
SP
SOP
0
例S 蕃茄
例P 西红柿
2021/4/14
PS
SP
0
1
美国人
人
SP
1
SP
1
31
III. 三、3. P94
【原题】 ⒊ 已知“有S是P”为真
【参考答案】
SP
SIP
1
例S 蕃茄
2021/4/14
36
III. 四、2. P94
【原题】 ⒉ 这架飞机上的乘客都是去英国旅游的。
【参考答案】
整理:所有乘客是去英国旅游的。SAP为真
SIP:有的乘客是去英国旅游的。 真 SOP:有的乘客不是去英国旅游的。假 SEP:所有乘客不是去英国旅游的。假
【参考答案】
不表达判断
因为是一般疑问句,是有疑而问,无所断定。
2021/4/14
3
III. 一、2. P93
【原题】 ⒉ 没有耕耘,哪来收获?
【参考答案】
间接表达判断:没有耕耘就没有收获。 因为是反诘句。
2021/4/14
第三章练习题
(共一讲)
III. 一、P93 (共 10 小题)
【原题】 一、下列语句是否表达判断?为什么?
【知识点】
语句和判断的关系 何种语句表达判断?何种语句不表达判断?
2021/4/14
2
III. 一、1. P93
【原题】 ⒈ 为什么说社会主义制度有无比的优越性?
2021/4/14
15
III. 二、3. P93
大学数据库-第3章习题解答

生产厂家的数据有:厂名、地址、向商店提供的商品价格
请设计该百货商店的概念模型,再将概念模型转换为关系模型。注意某些信息可用属性 表示,其他信息可用联系表示。 答:概念模型如图所示。
题 3.22 E-R 图
图中:
职工:职工号,姓名,住址 商品部:商品部号,名称 商品:商品代号,价格,型号,出厂价格 生产厂家:厂名,地址
〖3.19〗 请设计一个图书馆数据库,此数据库中对每个借阅 者保存记录,包括:读者号、姓名、地址、性别、 年龄、单位。对每本书,保存有:书号、书名、作 者、出版社。对每本被借出的书保存有读者号、借 出日期和应还日期。要求:给出该图书馆数据库的 E-R 图,再将其转换为关系模型。
答:该图书馆数据库的 E-R 图如图所示。 其中:
〖3.16〗 为什么要从两层 C/S 结构发展成三层 C/S 结构? 答:为了减轻两层 C/S 结构中客户机的负担,从客户机和服务器各抽一部分功能,组成应用 服务器,成为三层 C/S 结构。 〖3.17〗 叙述数据字典的主要任务。 答:数据字典的任务就是管理有关数据的信息,主要包括:描述数据库系统的所有对象,并 确定其属性;描述数据库系统对象之间的各种交叉联系;登记所有对象的完整性及安全性限 制等;对数据字典本身的维护、保护、查询与输出。 〖3.18〗 现有一个局部应用,包括两个实体“出版社”和“作者”,这两个实体是多对多的
答:概念结构设计的结果用数据库的信息模型表示。信息模型的主要特点和设计策略是:信 息模型是现实世界的一个真实模型,能真实、充分地反映现实世界,能满足用户对数据的处 理要求;信息模型应当易于理解;信息模型应当易于更改,有利于修改和扩充;信息模型易 于向特定的数据模型转换。 〖3.8〗 什么是数据抽象?试举例说明。 答:① 数据抽象就是抽取现实世界的共同特性,忽略非本质的细节,并把这些共同特性用 各种概念精确地加以描述,形成某种数据模型。
数据与计算机通信答案(第3章)

而对于数字彩色电视机,相当不错了。如果不提高数据率,还可以通过降低分辨率或刷新速 率,来换取色彩数的提高,但这也不实用的方法。
已知视频带宽 B=5MHz,所以有 5=P/105,则每行的像素数 P=5x105=525。 然而,通常 CCIR-M/NTSC 制式每行只约有 450 像素,带宽 B=P/105=450/105=4.3MHz (实 际技术指标 4.2Hz) 。 带宽由 4.2MHz 增加到 5MHz 时,水平分辨率约增加 75 像素,增幅 16.7%。 (2)计算垂直分辨率的增幅 由于信号最高频率 fH=5MHz,即最短的信号周期 1/fH=0.2υs。 又因为每个最短周期包含 2 个像素,则有 225 周期/行。那么,每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs,每行往返扫描时间为 56υs ,即 56x10-6 s, 假定每屏 V 行,每秒扫描 30 场(帧、屏),则每秒扫描行数为 30V。 因此对于画面刷新,有 30V×56x10-6 = 1s,V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行,增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以, f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t
第3章练习题(答案)

第三章练习题(答案)一、填空题常用光源LD是以受激辐射为基础发相干(激)光,LED以自发辐射为基础发非相干(荧)光。
光与物质的粒子体系的相互作用主要有三个过程是:受激吸收,自发辐射,受激辐射;产生激光的最主要过程是:受激辐射。
激光器由工作物质、激励源(泵浦源)和光学谐振腔三部分组成。
激光振荡器必须包括增益介质、激励源和光学谐振腔。
LD的P-I特性具有阈值特性,其阈值电流随温度升高而升高,当其增大至原来的 1.5 倍时,LD寿命告终。
在半导体激光器P-I曲线中,工作电流小于阈值电流的范围对应于荧光区,工作电流大于阈值电流的范围对应于激光。
光电检测器的作用是进行光/电转换,PIN管本质上是外加反向(或负)偏压的PN结。
常用的导体光电检测器主要有PIN光电二极管(PIN-PD)和雪崩光电二极管(APD)两种,基本原理是通过受激吸收(光电效应)过程实现光电转换。
无源器件主要有光纤连接器、光耦合器、光隔离器、光波分复用器、和光波长转换器、光开关等。
光纤连接器的主要性能指标有插入损耗(介入损耗)、回波损耗、互换性、插拔寿命、重复性、稳定性等。
表示光纤耦合器性能指标的参数有隔离度、插入损耗和分光比等。
二、选择题光纤通信系统中使用的光器件主要有:( D )A 激光器、发光二极管;B 分布反馈激光器、PIN光电二极管;C 半导体激光器、光检测器、分布反馈激光器;D 光源、光检测器、光放大器。
光纤通信系统中常用的光检测器主要有:( B )A. 激光器、发光二极管B. PIN光电二极管、APD雪崩光电二极管C.分布反馈激光器、PIN光电二极管D. PIN光电二极管、半导体激光器LD光源的作用是:( B )A 产生输入光波信号;B 将电信号电流变换为光信号功率,即实现电-光转换;C 产生输入光功率;D 光波对电信号进行调制,使其载荷信息在光纤中传输。
发光二极管LED产生的光:( A )A 是荧光而不是激光;B 是激光而不是荧光;C 是自然光而不是激光;D 是相干光而不是荧光。
大学物理第三章课后习题答案

L 时时, (1)摩擦力做功多少? (2)弹性力做功多少? (3)其他力做功多少? (4)外力做的总功是多少? 8. 小球系于细绳的一端,质量为 m ,并以恒定的角速
度 ω 0 在光滑水平面上围绕一半径为 R 的圆周运动。细 绳穿过圆心小孔, 若手握绳的另一端用力 F 向下拉绳,使小球运转的半径减小一半, 求 力对小球所做的功。 9. 如图所示, 一小车从光滑的轨道上某处由
9. 解:由题意知小车飞越 BC 缺口时做斜抛运动,其射程 BC = 2 R sin α 。 设小车在 B 点时的速度为 υ B , 欲使小车 刚 好 越 过 BC , 应 满 足 2υ B ⋅ sin α g
-7-
2 R sin α = υ B ⋅ cos α ⋅
自治区精品课程—大学物理学
题库
gR (1) cos α 由 A 点运动到 B 点时机械能守恒得: 1 2 mgh = mg ( R + R cos α ) + mυ B (2) 2 由式(1)与(2)得 1 h = (1 + cos α + )R 2 cos α
自治区精品课程—大学物理学
题库
第三章 功和能
一、 填空 1. 功等于质点受的 和 的标量积,功是 变化的量度。 2. 物理学中用 来描述物体做功的快慢。力的瞬时功率等于 与 的标积。对于一定功率的机械,当速度小时,力就 (填“大”或“小” ) , 速度大时,力必定 (填“大”或“小” ) 。 3. 合外力对质点所做的功等于质点动能的增量,此即 定理。 4. 质点动能定理的微分形式是 。 5. 质点动能定理的积分形式是 。 6. 按做功性质,可以将力分为 和 。 7. 所做的功只取决于受力物体的初末位置,与物体所经过的路径无 关。做功与路径有关的力叫做 。 8. 物体在 力作用下,沿任意闭合路径绕一周所做的功等于零。 9. 保守力做功与物体势能改变量之间的关系是 。 10. 若保守力做正功,则势能 ( “增加”或“减少” ) ,若保守力做负功, 则 势能 ( “增加”或“减少” ) 。 11. 势能的增量与势能零点的选取 (填“有关”或“无关” ) ,势能的大小 与势能零点的选取 (填“有关”或“无关” ) 。 12. 质点系内各质点之间的相互作用力称为 ,质点系以外的其他物体对 质点系内各质点的作用力称为 。 13. 质点系在运动过程中, 所做的功与 所做的功的总 和等于质点系的机械能的增量,此即质点系的 原理。 14. 在只 有 做功 的情 况下, 质点 系的机 械能 保持不 变, 这就是 定律。 15. 行星沿 轨道绕太阳运行, 太阳位于椭圆的一个 上; 对任一行星, 以 太阳 中 心为 参 考点 , 行星 的 位置 矢 量在 相 等的 时 间内 扫 过的 面 积填 ( “相 等 ”或 “ 不 相等 ” ) ; 行星 绕 太阳 运 动的 和 椭圆 轨 道的 成正比。 16. 第一宇宙速度是 所需要 的速度。 17. 第二宇宙速度是 所需要的 最小速度。 18. 第三宇宙速度是 所需的 最小速度。 二、 简答 1. 2. 3. 4. 5. 简述质点动能定理的内容,并写出其微分形式和积分形式。 简述保守力做功与物体势能改变量之间的关系。 简述质点系功能原理的内容。 简述机械能守恒定律的内容。 简述行星运动的三大定律的内容。
第3章《自测题、习题》参考答案

第 3 章 场效应管及其基本放大电路自测题3.1填空题1.按照结构,场效应管可分为 。
它属于 型器件,其最大的优点是 。
2.在使用场效应管时,由于结型场效应管结构是对称的,所以 极和 极可互换。
MOS 管中如果衬底在管内不与 极预先接在一起,则 极和 极也可互换。
3.当场效应管工作于线性区时,其漏极电流D i 只受电压 的控制,而与电压 几乎无关。
耗尽型D i 的表达式为 ,增强型D i 的表达式为 。
4.某耗尽型MOS 管的转移曲线如题3.1.4图所示,由图可知该管的DSS I = ,U P = 。
5.一个结型场效应管的电流方程为2GS D 161(mA)4U I ⎛⎫=⨯- ⎪⎝⎭,则该管的DSS I = , U P = ;当GS 0u =时的m g = 。
6.N 沟道结型场效应管工作于放大状态时,要求GS 0u ≥≥ ,DS u > ;而N 沟道增强型MOS 管工作于放大状态时,要求GS u > ,DS u > 。
7.耗尽型场效应管可采用 偏压电路,增强型场效应管只能采用 偏置电路。
8.在共源放大电路中,若源极电阻s R 增大,则该电路的漏极电流D I ,跨导m g ,电压放大倍数 。
9.源极跟随器的输出电阻与 和 有关。
答案:1.结型和绝缘栅型,电压控制,输入电阻高。
2.漏,源,源,漏,源。
3.GS u ,DS u ,2GS D DSS P 1u i I U ⎛⎫=- ⎪⎝⎭,2GS D DO T 1u i I U ⎛⎫=- ⎪⎝⎭。
4.4mA ,-3V 。
5.16mA ,题3.1.4图4V ,8ms 。
6.p U ,GS P u U -,T U ,GS T u U -。
7.自给,分压式。
8.减小,减小,减小。
9.m g ,s R 。
3.2选择题1.P 沟道结型场效应管中的载流子是 。
A .自由电子;B .空穴;C .电子和空穴;D .带电离子。
2.对于结型场效应管,如果GS P |||U U >,那么管子一定工作于 。
第三章习题参考答案
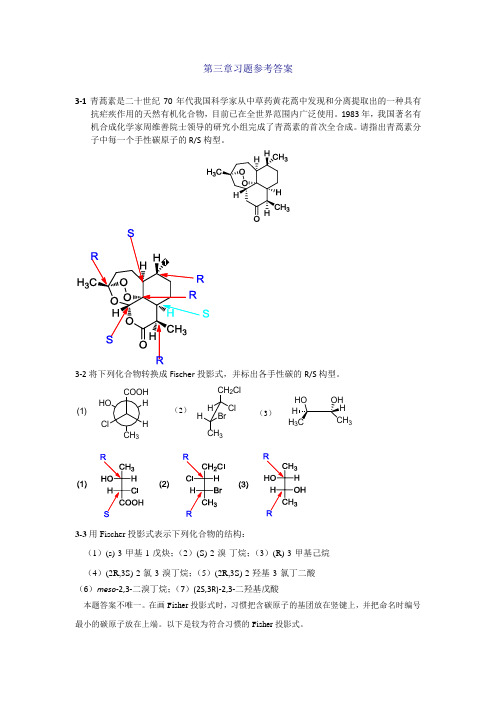
第三章习题参考答案3-1青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrH3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔;(2)(S)-2-溴-丁烷;(3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷;(7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher 投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher 投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(.Chem.2013,78,6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
(R)-A(S)-A3-6山梗烷定是从印度烟叶中分离到的一种化合物,它没有旋光性,也不可被拆分。
第3章习题解答

《数字通信系统原理》教材习题解答第三章练习题33-1 填空(1)模拟信号在数字通信系统中的传输,首先必须把模拟信号转变为 数字信号 ,转换的方法有 脉冲编码调制 和增量调制等。
(2)衡量量化性能好坏的常用指标是 量化信噪比。
此值越大,说明量化性能越 好。
(3)非均匀量化的PCM 中,信号功率小时,量化噪声功率 小,适用于动态范围较宽的信号。
(4)目前,数字通信系统中采用两种压扩特性:一种是A 律压扩特性:另一种是 μ律压扩特性 。
(5)采用增量调制的目的是 简化模拟信号的数字化方法 :采用自适应增量调制的目的是 提高小信号的量化信噪比。
补充题:1.线性PCM 的量化噪声与信号功率大小有关吗?无关,它适用于动态范围小的信号。
2.在对数PCM 中,量化噪声功率与信号功率的定性关系是信号功率小,量化噪声功率就小,适用于动态范围大的信号。
在对数M 中,信号在某一段落内变化时,量化噪声功率是否变化?不变。
3.在对数PCM 和自适应增量调制中,抗噪声能力强的是自适应增量调制,量化噪声小的是对数PCM 。
4.均匀量化器的量化信噪比与编码位数的关系是编码增加1位,量化信噪比增大6dB ,非均匀量化器可以提高小信号的量化信噪比。
5.若A 律13折线PCM 编码器输入信号为直流且幅度等于最小量化间隔的1.5倍,则编码器的输出为10000001。
6.线性PCM 编码器的抽样信号频率为8kHz ,当信息速率由80kbit/s 下降到56kbit/s 时,量化信噪比增大18dB 。
3-2 试画出PCM 通信的原理图,并简述PCM 通信的过程。
3-3 PAM 信号、量化信号和PCM 信号属于什么类型的信号?3-4 对基带信号t t t g ππ4cos 3cos 2)(+=进行理想抽样。
(1)为了在接收端不失真地从已抽样信号中恢复出,怎样选取抽样间隔?(2)若抽样间隔为0.2s ,试画出已抽样信号的频谱。
解:(1)基带信号可以看成是低通信号,由于Hz f m 2=根据抽样定理,得Hz f f m s 42=≥(2)由已知得,抽样频率为Hz f s 52.01==。
电工技术第3章习题答案

第3章习题答案3.2.1 选择题1.晶体管能够放大的外部条件是___C______。
(a) 发射结正偏,集电结正偏 (b) 发射结反偏,集电结反偏(c) 发射结正偏,集电结反偏2.当晶体管工作于饱和状态时,其__A_______。
(a) 发射结正偏,集电结正偏 (b) 发射结反偏,集电结反偏(c) 发射结正偏,集电结反偏3. 测得晶体管三个电极的静态电流分别为0.06mA,3.66mA和3.6mA。
则该管的为___C______。
(a) 40 (b) 50 (c) 604.反向饱和电流越小,晶体管的稳定性能___A______。
(a) 越好 (b) 越差 (c) 无变化5.温度升高,晶体管的电流放大系数b___A______。
(a) 增大 (b) 减小 (c) 不变6.温度升高,晶体管的管压降|UBE|__B_______。
(a) 升高 (b) 降低 (c) 不变7.对PNP型晶体管来说,当其工作于放大状态时,__C______极的电位最低。
(a) 发射极 (b) 基极 (c) 集电极8.温度升高,晶体管输入特性曲线____B____。
(a) 右移 (b) 左移 (c) 不变9.温度升高,晶体管输出特性曲线___A_____。
(a) 上移 (b) 下移 (c) 不变10.温度升高,晶体管输出特性曲线间隔___C_____。
(a) 不变 (b) 减小 (c) 增大11.晶体管共射极电流放大系数b随集电极电流iC___B_____。
(a) 不变化 (b) 有一定变化 (c) 无法判断12.当晶体管的集电极电流时,下列说法正确的是__C_____。
(a) 晶体管一定被烧毁 (b) 晶体管的(c) 晶体管的一定减小13.对于电压放大器来说,___B____越小,电路的带负载能力越强。
(a) 输入电阻 (b) 输出电阻 (c) 电压放大倍数14.在单级共射放大电路中,若输入电压为正弦波形,则输出与输入电压的相位___B____。
3第三章 电子商务与合同法习题答案-精品

课后练习:一、名词解释:1、电子合同是电子商务活动中基本的契约形式,契约是保障当事人各方权利义务的有效方式2、电子代理人所谓电子代理人是指在没有人的参与的情况下,独立采取某种措施对某个电子信息作出反应的某个计算机程序、电子的或其他的自动手段3、电子要约电子商务方式发出的要约4、电子承诺电子商务方式发出的要约5、电子格式合同电子合同是电子商务活动中基本的契约形式,契约是保障当事人各方权利义务的有效方式。
二、选择题1、我国属于(A)的国家,在合同的概念上,也是将合同理解为一种合意。
A、大陆法系B、英美法系2、合同是当事人(B)的结果。
A、行为一致B、意思表示自愿真实一致C、思想一致D、结果一致3、电子合同是当事人的意思表示的(A)反映。
A、真实B、格式化C、电子化D、自动化4、我国《合同法》的第32条规定:“当事人采用合同书形式订立合同的,自双方当事人(D)时合同成立。
”A、电子邮件B、传真C、电话D、签字或者盖章5、在拟定《电子商务示范法》的过程中,针对各国法律规定的(C)形式的要求,国际贸易法委员会认为没有必要取消各国的这一法律规定,而只要扩大法律对(A)一词所下的定义,使电子数据能被纳入书面范畴。
A、口头B、公证C、书面D、代理6、根据我国《合同法》的规定,因欺诈订立的电子合同,只要不是损害国家利益的,亦应属于(A)合同。
A、无效B、有效C、可撤销D、可变更7、(B)年5月25日,国家外经贸部正式宣布,我国决定于7月1日在网上正式推出“中国商品市场”,并宣称外经贸部的目标是将“中国商品市场”发展为中国“最大的网上购物系统”。
A、1997B、1998C、1999D、20008、在电子数据传输过程中,(C)是一个十分重要的问题。
A、数据B、信息C、安全D、内容9、对电子证据的收集,按照“谁主张,谁举证”的原则,应是(B)自身的权利与义务。
A、法官B、当事人C、第三人D、代理人10、根据我国最高人民法院的解释,由于行为人对行为的性质、标的物的品种、数量、质量、规格,以及行为的相对人发生错误认识,使行为的后果与行为人的意思相背离,并造成较大损失的,是(D),行为人可以主张撤销合同。
蒋立源编译原理 第三版 第三章 习题与答案(修改后)
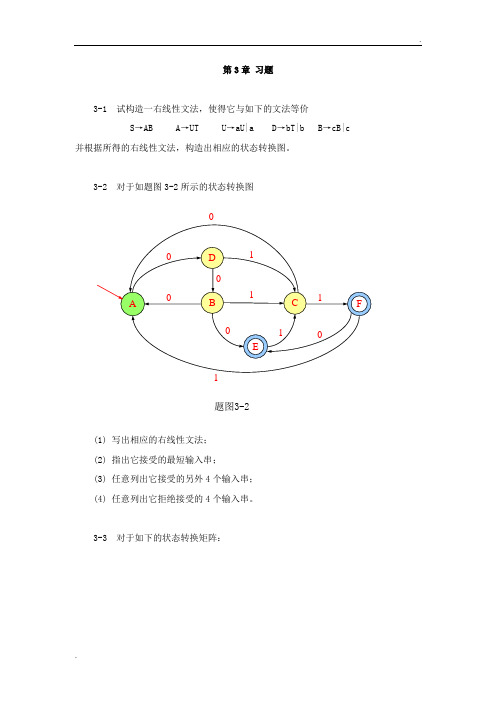
第3章习题3-1 试构造一右线性文法,使得它与如下的文法等价S→AB A→UT U→aU|a D→bT|b B→cB|c 并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图3-2所示的状态转换图(1) 写出相应的右线性文法;(2) 指出它接受的最短输入串;(3) 任意列出它接受的另外4个输入串;(4) 任意列出它拒绝接受的4个输入串。
3-3 对于如下的状态转换矩阵:(1) 分别画出相应的状态转换图;(2) 写出相应的3型文法;(3) 用自然语言描述它们所识别的输入串的特征。
3-4 将如下的NFA确定化和最小化:3-5 将如题图3-5所示的具有ε动作的NFA确定化。
题图3-5 具有ε动作的NFA3-6 设有文法G[S]:S→aA A→aA|bB B→bB|cC|c C→cC|c 试用正规式描述它所产生的语言。
3-7 分别构造与如下正规式相应的NFA。
(1) ((0* |1)(1* 0))*(2) b|a(aa*b)*b3-8 构造与正规式(a|b)*(aa|bb)(a|b)*相应的DFA。
第3章习题答案3-1 解:根据文法知其产生的语言是:L[G]={a m b n c i| m,n,i≧1}可以构造与原文法等价的右线性文法:S→aA A→aA|bB B→bB|cC|c C→cC|c 其状态转换图如下:3-2 解:(1) 其对应的右线性文法是G[A]:A →0D B→0A|1C C→0A|1F|1D→0B|1C E→0B|1C F→1A|0E|0(2) 最短输入串为011(3) 任意接受的四个输入串为:0110,0011,000011,00110(4) 任意拒绝接受的输入串为:0111,1011,1100,10013-3 解:(1) 相应的状态转换图为:(2) 相应的3型文法为:(ⅰ) S→aA|bS A→aA|bB|b B→aB|bB|a|b(ⅱ) S→aA|bB|a A→bA|aC|a|b B→aB|bC|b C→aC|bC|a|b(ⅲ) S→aA|bB|b A→aB|bA|a B→aB|bB|a|b(ⅳ) S→bS|aA A→aC|bB|a B→aB|bC|b C→aC|bC|a|b(3) 用自然语言描述的输入串的特征为:(ⅰ) 以任意个(包括0个)b开头,中间有任意个(大于1)a,跟一个b,还可以有一个由a,b组成的任意字符串。
概率论与数理统计第三章课后习题及参考答案

概率论与数理统计第三章课后习题及参考答案1.设二维随机变量),(Y X 只能取下列数组中的值:)0,0(,)1,1(-,31,1(-及)0,2(,且取这几组值的概率依次为61,31,121和125,求二维随机变量),(Y X 的联合分布律.解:由二维离散型随机变量分布律的定义知,),(Y X 的联合分布律为2.某高校学生会有8名委员,其中来自理科的2名,来自工科和文科的各3名.现从8名委员中随机地指定3名担任学生会主席.设X ,Y 分别为主席来自理科、工科的人数,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:(1)由题意,X 的可能取值为0,1,2,Y 的可能取值为0,1,2,3,则561)0,0(3833====C C Y X P ,569)1,0(381323====C C C Y X P ,569)2,0(382313====C C C Y X P ,561)3,0(3833====C C Y X P ,283)0,1(382312====C C C Y X P ,289)1,1(38131312====C C C C Y X P ,283)2,1(382312====C C C Y X P ,0)3,1(===Y X P ,563)0,2(381322====C C C Y X P ,563)1,2(381322====C C C Y X P ,0)2,2(===Y X P ,0)3,2(===Y X P .),(Y X 的联合分布律为:(2)X 的边缘分布律为X 012P1452815283Y 的边缘分布律为Y 0123P285281528155613.设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其他.,0,42,20),6(),(y x y x k y x f 求:(1)常数k ;(2))3,1(<<Y X P ;(3))5.1(<Y P ;(4))4(≤+Y X P .解:方法1:(1)⎰⎰⎰⎰--==+∞∞-+∞∞-422d d )6(d d ),(1yx y x k y x y x f ⎰--=42202d |)216(y yx x x k k y y k 8d )210(42=-=⎰,∴81=k .(2)⎰⎰∞-∞-=<<31d d ),()3,1(y x y x f Y X P ⎰⎰--=32102d d )216(yx yx x x ⎰--=32102d |)216(81y yx x x 83|)21211(81322=-=y y .(3)),5.1()5.1(+∞<<=<Y X P X P ⎰⎰+∞∞-∞---=5.1d d )6(81yx y x ⎰⎰--=425.10d d )6(81y x y x y yx x x d )216(81422⎰--=3227|)43863(81422=-=y y .(4)⎰⎰≤+=≤+4d d ),()4(y x y x y x f Y X P ⎰⎰---=2042d )6(d 81x y y x x ⎰+-⋅=202d )812(2181x x x 32|)31412(1612032=+-=x x x .方法2:(1)同方法1.(2)20<<x ,42<<y 时,⎰⎰∞-∞-=yxv u v u f y x F d d ),(),(⎰⎰--=y xv u v u 20d d )6(81⎰--=y xv uv u u 202d |)216(81⎰--=y v xv x x 22d )216(81y xv v x xv 222|)21216(81--=)1021216(81222x xy y x xy +---=,其他,0),,(=y x F ,∴⎪⎩⎪⎨⎧<<<<+---=其他.,0,42,20),1021216(81),(222y x x x xy y x xy y x F 83)3,1()3,1(==<<F Y X P .(3))42,5.1(),5.1()5.1(<<<=+∞<<=<Y X P Y X P X P )2,5.1()4,5.1(<<-<<=Y X P Y X P 3227)2,5.1()4,5.1(=-=F F .(4)同方法1.4.设随机变量),(Y X 的概率密度为⎩⎨⎧>>=--其他.,0,0,0,e ),(2y x A y x f y x 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)⎰⎰⎰⎰+∞+∞--+∞∞-+∞∞-==02d d e d d ),(1yx A y x y x f y x ⎰⎰+∞+∞--=002d e d e y x A y x2|)e 21(|)e (020A A y x =-⋅-=∞+-∞+-,∴2=A .(2)0>x ,0>y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰--=yxv u vu 02d d e 2yv x u 020|)e 21(|)e (2---⋅-=)e 1)(e 1(2y x ----=,其他,0),(=y x F ,∴⎩⎨⎧>>--=--其他.,0,0,0),e 1)(e 1(),(2y x y x F y x .5.设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=其他.,0,10,10,),(y x Axy y x f 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)2121d d d d ),(11010⋅⋅===⎰⎰⎰⎰+∞∞-+∞∞-A y y x x A y x y x f ,∴4=A .(2)10≤≤x ,10≤≤y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰=yxv u uv 0d d 4220202||y x v u yx =⋅=,10≤≤x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4xv u uv 210202||x v u x =⋅=,10≤≤y ,1>x 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4yu v uv 202102||y v u y =⋅=,1>x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=101d d 4v u uv 1||102102=⋅=v u,其他,0),(=y x F ,∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>≤≤>>≤≤≤≤≤≤=其他.,0,1,1,1,10,1,,1,10,,10,10,),(2222y x y x y y x x y x y x y x F .6.把一枚均匀硬币掷3次,设X 为3次抛掷中正面出现的次数,Y 表示3次抛掷中正面出现次数与反面出现次数之差的绝对值,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:由题意知,X 的可能取值为0,1,2,3;Y 的可能取值为1,3.易知0)1,0(===Y X P ,81)3,0(===Y X P ,83)1,1(===Y X P ,0)3,1(===Y X P 83)1,2(===Y X P ,0)3,2(===Y X P ,0)1,3(===Y X P ,81)3,3(===Y X P 故),(Y X 得联合分布律和边缘分布律为:7.在汽车厂,一辆汽车有两道工序是由机器人完成的:一是紧固3只螺栓;二是焊接2处焊点,以X 表示由机器人紧固的螺栓紧固得不牢的数目,以Y 表示由机器人焊接的不良焊点的数目,且),(Y X 具有联合分布律如下表:求:(1)在1=Y 的条件下,X 的条件分布律;(2)在2=X 的条件下,Y 的条件分布律.解:(1)因为)3,3()1,2()1,1()1,0()1(==+==+==+====Y X P Y X P Y X P Y X P Y P 08.0002.0008.001.006.0=+++=,所以43)1()1,0()1|0(=======Y P Y X P Y X P ,81)1()1,1()1|1(=======Y P Y X P Y X P ,101)1()1,2()1|2(=======Y P Y X P Y X P ,401)1()1,3()1|3(=======Y P Y X P Y X P ,故在1=Y 的条件下,X 的条件分布律为X 0123P4381101401(2)因为)2,2()1,2()0,2()2(==+==+====Y X P Y X P Y X P X P 032.0004.0008.002.0=++=,所以85)2()0,2()2,0(=======X P Y X P X Y P ,4)2()1,2()2,1(=======X P Y X P X Y P ,81)2()2,2()2,2(=======X P Y X P X Y P ,故在2=X 的条件下,Y 的分布律为:Y 012P8541818.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=+-其他.,0,0,0,e ),()2(y x c y x f y x 求:(1)常数c ;(2)X 的边缘概率密度函数;(3))2(<+Y X P ;(4)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)⎰⎰⎰⎰+∞+∞+-+∞∞-+∞∞-==0)2(d d e d d ),(1yx c y x y x f y x⎰⎰+∞+∞--=002d e d ey x c y x2|)e (|)e 21(002c c y x =-⋅-=∞+-∞+-,∴2=c .(2)0>x 时,⎰+∞∞-=y y x f x f X d ),()(⎰+∞+-=0)2(d e 2y y x x y x 202e 2|)e (e 2-+∞--=-=,0≤x 时,0)(=x f X ,∴⎩⎨⎧≤>=-.0,0,0,e 2)(2x x x f x X ,同理⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)⎰⎰<+=<+2d d ),()2(y x y x y x f Y X P ⎰⎰---=2202d d e 2xy x yx 422202e e 21d e d e 2-----+-==⎰⎰xy x y x .(4)由条件概率密度公式,得,当0>y 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e 2,0,0,e e 2)(),()|(22|x x y f y x f y x f xy y x Y Y X ,0≤y 时,0)|(|=y x f Y X ,所以⎩⎨⎧>>=-其他.,0,0,0,e 2)|(2|y x y x f x Y X ;同理,当0>x 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e ,0,0,2e e 2)(),()|(22|y y x f y x f x y f yx y x X X Y 0≤x 时,0)|(|=x y f X Y ,所以⎩⎨⎧>>=-其他.,0,0,0,e )|(|y x x y f y X Y .9.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<=其他.,0,0,10,3),(x y x x y x f求:(1)关于X 、Y 的边缘概率密度函数;(2)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)10<<x 时,⎰+∞∞-=y y x f x f X d ),()(203d 3x y x x==⎰,其他,0)(=x f X ,∴⎩⎨⎧<<=其他.,0,10,3)(2x x x f X ,密度函数的非零区域为}1,10|),{(}0,10|),{(<<<<=<<<<x y y y x x y x y x ,∴10<<y 时,⎰+∞∞-=x y x f y f Y d ),()()1(23d 321y x x y-==⎰,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<-=其他.,0,10),1(23)(2y y y f Y .(2)当10<<y 时,有⎪⎩⎪⎨⎧<<-=⎪⎪⎩⎪⎪⎨⎧<<-==其他.其他.,0,1,12,0,1,)1(233)(),()|(22|x y y x x y y xy f y x f y x f Y Y X ,其他,0)|(|=y x f Y X ,故⎪⎩⎪⎨⎧<<<<-=其他.,0,10,1,12)|(2|y x y y xy x f Y X .当10<<x 时,有⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==其他.其他.,0,0,1,0,0,33)(),()|(2|x y x x y x x x f y x f x y f X X Y ,其他,0)|(|=x y f X Y ,故⎪⎩⎪⎨⎧<<<<=其他.,0,10,0,1)|(|x x y x x y f X Y .10.设条件密度函数为⎪⎩⎪⎨⎧<<<=其他.,0,10,3)|(32|y x yx y x f Y X Y 的概率密度函数为⎩⎨⎧<<=其他.,0,10,5)(4y y y f Y 求21(>X P .解:⎩⎨⎧<<<==其他.,0,10,15)|()(),(2|y x y x y x f y f y x f Y X Y ,则6447d )(215d d 15d d ),(21(121421211221=-===>⎰⎰⎰⎰⎰>x x x x y y x y x y x f X P xx .11.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<<<+=其他.,0,20,10,3),(2y x xyx y x f 求:(1)),(Y X 的边缘概率密度;(2)X 与Y 是否独立;(3))),((D Y X P ∈,其中D 为曲线22x y =与x y 2=所围区域.解:(1)10<<x 时,x x y xy x y y x f x f X 322d )3(d ),()(222+=+==⎰⎰+∞∞-,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<+=其他.,0,10,322)(2x x x x f X ,20<<y 时,⎰+∞∞-=x y x f y f Y d ),()(316)d 3(12+=+=⎰y x xy x ,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<+=其他.,0,20,316)(y y y f Y .(2)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(3)}22,10|),{(2x y x x y x D ≤≤<<=,∴⎰⎰+=∈102222d d )3()),((x xx y xy x D Y X P 457d )32238(10543=--=⎰x x x x .12.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=-其他.,0,0,0,e )1(),(2y x y x y x f x试讨论X ,Y 的独立性.解:当0>x 时,xx x X x yx y y x y y x f x f -∞+-∞+-∞+∞-=+-=+==⎰⎰e |11e d )1(e d ),()(002,当0≤x 时,0)(=x f X ,故⎩⎨⎧≤>=-.0,0,0,e )(x x x x f x X ,同理,可得⎪⎩⎪⎨⎧≤>+=.0,0,0,)1(1)(2y y y y f Y ,因为)()(),(y f x f y x f Y X =,所以X 与Y 相互独立.13.设随机变量),(Y X 在区域}|),{(a y x y x g ≤+=上服从均匀分布,求X 与Y 的边缘概率密度,并判断X 与Y 是否相互独立.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其他.,0,,21),(2a y x a y x f ,当0<<-x a 时,有)(1d 21d ),()(2)(2x a ay a y y x f x f xa x a X +===⎰⎰++-+∞∞-,当a x <≤0时,有)(1d 21d ),()(2)(2x a a y a y y x f x f x a x a X -===⎰⎰---+∞∞-,当a x ≥时,0d ),()(==⎰+∞∞-y y x f x f X ,故⎪⎩⎪⎨⎧≥<-=.a x a x x a a x f X ,0,),(1)(2,同理,由轮换对称性,可得⎪⎩⎪⎨⎧≥<-=.a y a y y a a y f Y ,0,),(1)(2,显然)()(),(y f x f y x f Y X ≠,所以X 与Y 不相互独立.14.设X 和Y 时两个相互独立的随机变量,X 在)1,0(上服从均匀分布,Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY (1)求X 和Y 的联合概率密度;(2)设含有a 的二次方程为022=++Y aX a ,试求a 有实根的概率.解:(1)由题可知X 的概率密度函数为⎩⎨⎧<<=其他.,0,10,1)(x x f X ,因为X 与Y 相互独立,所以),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧><<==-其他.,0,0,10,e 21)()(),(2y x y f x f y x f yY X ,(2)题设方程有实根等价于}|),{(2X Y Y X ≤,记为D ,即}|),{(2X Y Y X D ≤=,设=A {a 有实根},则⎰⎰=∈=Dy x y x f D Y X P A P d d ),()),(()(⎰⎰⎰---==1021002d )e 1(d d e 2122xx y x x y⎰--=102d e12x x ⎰--=12e 21212x x ππππ23413.01)]0()1([21-=Φ-Φ-=.15.设i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,求行列式4321X X X X X =的分布律.解:由i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,易知41X X ~)84.0,16.0(b ,32X X ~)84.0,16.0(b .因为1X ,2X ,3X ,4X 相互独立,所以41X X 与32X X 也相互独立,又32414321X X X X X X X X X -==,则X 的所有可能取值为1-,0,1,有)1()0()1,0()1(32413241======-=X X P X X P X X X X P X P 1344.016.084.0=⨯=,)1,1()0,0()0(32413241==+====X X X X P X X X X P X P )1()1()0()0(32413241==+===X X P X X P X X P X X P 7312.016.016.084.084.0=⨯+⨯=,)0()1()0,1()1(32413241=======X X P X X P X X X X P X P 1344.084.016.0=⨯=,故X 的分布律为X 1-01P1344.07312.01344.016.设二维随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-其他.,0,0,0,e 2),()2(y x y x f y x 求Y X Z 2+=的分布函数及概率密度函数.解:0≤z 时,若0≤x ,则0),(=y x f ;若0>x ,则0<-=x z y ,也有0),(=y x f ,即0≤z 时,0),(=y x f ,此时,0d d ),()2()()(2==≤+=≤=⎰⎰≤+zy x Z y x y x f z Y X P z Z P z F .0>z 时,若0≤x ,则0),(=y x f ;只有当z x ≤<0且02>-=xz y 时,0),(≠y x f ,此时,⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 2d d ),()2()()(⎰⎰-+-=zx z y x y x 020)2(d e 2d z z z ----=e e 1.综上⎩⎨⎧≤>--=--.0,0,0,e e 1)(z z z z F z z Z ,所以⎩⎨⎧≤<='=-.0,0,0,e )()(z z z z F z f z Z Z .17.设X ,Y 是相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤=其他.,0,10,1)(x x f X ,⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y 求Y X Z +=的概率密度.解:0<z 时,若0<x ,则0)(=x f X ;若0≥x ,则0<-=x z y ,0)(=-x z f Y ,即0<z 时,0)()(=-x z f x f Y X ,此时,0d )()()(=-=⎰+∞∞-x x z f x f z f Y X Z .10≤≤z 时,若0<x ,则0)(=x f X ;只有当z x ≤≤0且0>-=x z y 时0)()(≠-x z f x f Y X ,此时,z zx z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e 1d e d )()()(0)(.1>z 时,若0<x ,0)(=x f X ;若1>x ,0)(=x f X ;若10≤≤x ,则0>-=x z y ,此时,0)()(≠-x z f x f Y X ,z x z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e )1e (d e d )()()(1)(.综上,⎪⎩⎪⎨⎧<>-≤≤-=--.0,0,1,e )1e (,10,e 1)(z z z z f z z Z .18.设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=+-其他.,0,0,0,e)(21),()(y x y x y x f y x (1)X 和Y 是否相互独立?(2)求Y X Z +=的概率密度.解:(1)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(2)0≤z 时,若0≤x ,则0)(=x f X ;若0>x ,则0<-=x z y ,0),(=y x f ,此时,0d ),()(=-=⎰+∞∞-x x z x f z f Z .0≥z 时,若0≤x ,则0)(=x f X ;只有当z x <<0且0>-=x z y 时0),(≠y x f ,此时,⎰+∞∞--=x x z x f z f Z d ),()(⎰+-+=zy x x y x 0)(d e )(21⎰-=z z x z 0d e 21z z -=e 212,所以⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2z z z z f zZ .19.设X 和Y 时相互独立的随机变量,它们都服从正态分布),0(2σN .证明:随机变量22Y X Z +=具有概率密度函数⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.解:因为X 与Y 相互独立,均服从正态分布),0(2σN ,所以其联合密度函数为2222)(2e 121),(σσπy x y xf +-⋅=,(+∞<<∞-y x ,)当0≥z 时,有⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 22d d ),()()()(22⎰⎰≤++-⋅=zy x y x y x 22222d e 1212)(2σσπ⎰⎰-⋅=πσθσπ2022d ed 12122zr r r ⎰-=zr r r 022d e122σσ,此时,2222e)(σσz Z z z f -=;当0<z 时,=≤+}{22z Y X ∅,所以0)()()(22=≤+=≤=z Y X P z Z P z F Z ,此时,0)(=z f Z ,综上,⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.20.设),(Y X 在矩形区域}10,10|),{(≤≤≤≤=y x Y X G 上服从均匀分布,求},min{Y X Z =的概率密度.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他.,0,20,10,21),(y x y x f ,易证,X ~]1,0[U ,Y ~]2,0[U ,且X 与Y 相互独立,⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(x x x x x F X ,⎪⎪⎩⎪⎪⎨⎧≥<≤<=.2,1,20,2,0,0)(y y yy y F Y ,可得)](1)][(1[1)(z F z F z F Y X Z ---=)()()()(z F z F z F z F Y X Y X -+=⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.1,1,10,223,0,02z z z z z ,求导,得⎪⎩⎪⎨⎧<<-=其他.,0,10,23)(z z z f Z .21.设随机变量),(Y X 的概率密度为⎩⎨⎧+∞<<<<=+-其他.,0,0,10,e ),()(y x b y x f y x (1)试确定常数b ;(2)求边缘概率密度)(x f X 及)(y f Y ;(3)求函数},max{Y X U =的分布函数.解:(1)⎰⎰⎰⎰+∞+-+∞∞-+∞∞-==01)(d d e d d ),(1yx b y x y x f y x ⎰⎰+∞--=10d e d e y x b y x)e 1(|)e(|)e (10102-+∞---=-⋅=b b y x ,∴1e11--=b .(2)10<<x 时,1)(1e1e d e e 11d ),()(--∞++--∞+∞--=-==⎰⎰x y x X y y y x f x f ,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<-=--其他.,0,10,e 1e )(1x x f xX ,0>y 时,⎰+∞∞-=x y x f y f Y d ),()(yy x x -+--=-=⎰e d e e 1110)(1,0≤y 时,0)(=y f Y ,∴⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)0≤x 时,0)(=x F X ,10<<x 时,101e1e 1d e 1e d )()(----∞---=-==⎰⎰xxt xX X t t t f x F ,1≥x 时,1)(=x F X ,∴⎪⎪⎩⎪⎪⎨⎧≥<<--≤=--.1,1,10,e 1e1,0,0)(1x x x x F x X ;0≤y 时,0)(=y F Y ,0>y 时,y yv y Y Y v v v f y F --∞--===⎰⎰e 1d e d )()(0,∴⎩⎨⎧≤>-=-.0,0,0,e 1)(y y y F y Y ,故有)()()(y F x F u F Y X U =⎪⎪⎩⎪⎪⎨⎧≥-<≤--<=---.1,e 1,10,e 1e1,0,01u u u uu .。
(完整版)第3章资本和剩余价值(习题及答案)

第3章资本和剩余价值一、单选题1.货币转化为资本的前提条件是:A.在流通中进行不等价交换B.劳动力成为商品C.小商品生产者的两极分化D.劳动起家勤俭节约2.个别资本家之所以要不断改进技术,因为:A.追求超额剩余价值B.生产相对剩余价值C.降低劳动力价值D.生产绝对剩余价值3.剩余价值率用公式来表示为:A.m′=v/mB.m′=m/vC.m′=m/cD.m′=m/(c+v)4.剩余价值的产生条件是:A.既不在流通中产生,也不能离开流通而产生B.在流通中产生C.不在流通中产生D.在商品交换中产生二、多选题1.劳动力成为商品必须具备的条件是:A.劳动力所有者是小生产者B.劳动力所有者必须具有人身自由C.劳动力所有者是一无所有的D.劳动力所有者是一无所有的奴隶2.资本家生产剩余价值的两种基本方法是:A.绝对剩余价值生产B.超额剩余价值生产C.相对剩余价值生产D.一般剩余价值生产3.资本主义工资的基本形式是:A.计件工资B.名义工资C.计时工资D.实际工资4.资本主义生产过程的两重性是:A.生产使用价值的劳动过程B.生产剩余价值的价值增值过程C.价值形成过程D.商品生产过程5.马克思根据资本在价值增值过程中的不同作用分为:A.不变资本B.商业资本C.可变资本D.生产资本6.在等价交换原则基础上缩短必要劳动时间的办法是:A.降低劳动力的价值B.提高两大部类的劳动生产率C.降低劳动力所必需的生活资料价值D.把工人工资压低到劳动力价值以下7.劳动力商品的价值包括:A.维持劳动者自身生存所必需的生活资料价值B.维持劳动者家属所必需的生活资料价值C.劳动力买卖过程中所需的费用D.劳动者掌握生产技术所必需的教育和训练费用8.作为反映资本家对工人剥削程度的剩余价值率是:A.剩余价值与可变资本的比率B.剩余劳动与必要劳动的比率C.剩余劳动时间与必要劳动时间的比率D.可变资本与不变资本的比率9.资本主义工资:A.掩盖了劳动力商品买卖的实质B.掩盖了劳动与劳动力的区别C.掩盖了资本主义剥削关系D.掩盖了剩余价值的真正来源10.价值增值过程是超过一定点的价值形成过程,这个“一定点”是指:A.劳动过程的起点B.价值形成过程的起点C.必要劳动的终点D.劳动者所必需生活资料价值的时间终点11.机器人不能创造剩余价值的原因是:A.机器人是先进的机器B.机器人本身的价值渐次转移到新产品中去C.机器人属于不变资本D.机器人要依靠技术人员来操纵三、名词解释1.劳动力商品价值2.绝对剩余价值3.相对剩余价值4. 超额剩余价值5. 不变资本6. 可变资本7.资本主义工资四、分析判断1.工人给资本家做工,资本家付给工人工资,因此工资是工人劳动的价值或价格。
数字通信技术第3章习题及答案

所谓同步,就是要求通信的收发双方在时间基准上保持一致,即开始时间、位边界、重复频率。常用的方式有:载频同步、位同步、帧同步、网同步。
3-22、什么是载波同步?简述载波同步常见得实现方法?
在接收设备中产生一个和接收信号的载波同频同相的本地振荡,供给解调器作为相干解调用。实现的方法有:插入导频法;直接法。
3-7PSK信号、2DPSK信号的调制和解调工作原理?
2PSK信号调制:是相位选择法进行调相的原理。在这种方法里预先把所需要的相位准备好,然后根据基带信号的规律性选择相位得到相应的输出。见下图。
2DPSK信号调制:
3-8已知数字信息为1101001,并设码元宽度是载波周期的两倍,试画出绝对码、相对码、2PSK信号、2DPSK信号的波形。
以载波的不同相位直接去表达相应二进制数字信号的调制方式,成为绝对相移调制;利用前后相邻码元的载波相对相位变化传递二进制数字信号的调制方式,成为相对相移调制。他们都是利用载波的相位变化来传递数字信号的调制方式,不同的是绝对相移是以未调制的载波的相位作为参考基准的,而相对相移是以相邻码元的载波相位为参考基准的。
二进制FSK信号的解调方法常采用非相干检测法和相干检测法等如下图所示。
3-5己知某2FSK系统的码元传输速率为1200Baud,发“0”时载频为2400Hz,发“1”时载频为4800Hz,若发送的数字信息序列为011011010,试画出2FSK信号波形图。
3-6什么是绝对移相调制?什么是相对移相调制?它们之间有什么不同点?
3-25、什么是网同步?简述网同步常见得实现方法?
在数字通信网和计算机网络中各站点为了进行分路和并路,必须调整各个方向送来的信码的速率和相位,使之步调一致,这种调整过程称为网同步。网同步常见得实现方法:(1)主从同步法、(2)相互同步法、(3)分级的主从同步法、(4)独立时钟法
第三章连接课后习题参考答案

第三章连接课后习题参考答案第三章连接课后习题参考答案焊接连接参考答案一、概念题3.1 从功能上分类,连接有哪几种基本类型?3.2 焊缝有两种基本类型—对接坡口焊缝和贴角焊缝,二者在施工、受力、适用范围上各有哪些特点?3.3 对接接头连接需使用对接焊缝,角接接头连接需采用角焊缝,这么说对吗?3.4 h和lw相同时,吊车梁上的焊缝采用正f面角焊缝比采用侧面角焊缝承载力高?3.5 为何对角焊缝焊脚尺寸有最大和最小取值的限制?对侧面角焊缝的长度有何要求?为什么?【答】(1)最小焊脚尺寸:角焊缝的焊脚尺寸不能过小,否则焊接时产生的热量较小,致使施焊时冷却速度过快,导致母材开裂。
《规范》规定:h f≥1.5t,式中:t2——较厚焊件厚度,单2位为mm。
计算时,焊脚尺寸取整数。
自动焊熔深较大,所取最小焊脚尺寸可减小1mm;T形连接的单面角焊缝,应增加1mm;当焊件厚度小于或等于4mm时,则取与焊件厚度相同。
(2)最大焊脚尺寸:为了避免焊缝区的主体金属“过热”,减小焊件的焊接残余应力和残余变形,角焊缝的焊脚尺寸应满足12.1t h f式中: t 1——较薄焊件的厚度,单位为mm 。
(3)侧面角焊缝的最大计算长度侧面角焊缝在弹性阶段沿长度方向受力不均匀,两端大而中间小,可能首先在焊缝的两端破坏,故规定侧面角焊缝的计算长度l w ≤60h f 。
若内力沿侧面角焊缝全长分布,例如焊接梁翼缘与腹板的连接焊缝,可不受上述限制。
3.6 简述焊接残余应力产生的实质,其最大分布特点是什么? 3.7 画出焊接H 形截面和焊接箱形截面的焊接残余应力分布图。
3.8 贴角焊缝中,何为端焊缝?何为侧焊缝?二者破坏截面上的应力性质有何区别?3.9 规范规定:侧焊缝的计算长度不得大于焊脚尺寸的某个倍数,原因何在?规范同时有焊缝最小尺寸的规定,原因何在? 3.10 规范禁止3条相互垂直的焊缝相交,为什么。
3.11 举3~5例说明焊接设计中减小应力集中的构造措施。
仪器分析第三章习题参考答案

仪器分析第三章习题参考答案第三章思考题解答第三章思考题解答1.从分离原理、仪器构造及应用范围上简要比较气相色谱及液相色谱的异同点。
解:二者都是根据样品组分与流动相和固定相相互作用力的差别进行分离的。
从仪器构造上看,液相色谱需要增加高压泵以提高流动相的流动速度,克服阻力。
同时液相色谱所采用的固定相种类要比气相色谱丰富的多,分离方式也比较多样。
气相色谱的检测器主要采用热导检测器、氢焰检测器和火焰光度检测器等。
而液相色谱则多使用紫外检测器、荧光检测器及电化学检测器等。
但是二者均可与MS等联用。
二者均具分离能力高、灵敏度高、分析速度快,操作方便等优点,但沸点太高的物质或热稳定性差的物质难以用气相色谱进行分析。
而只要试样能够制成溶液,既可用于HPLC分析,而不受沸点高、热稳定性差、相对分子量大的限制。
2.液相色谱中影响色谱峰展宽的因素有哪些? 与气相色谱相比较,有哪些主要不同之处?解:液相色谱中引起色谱峰扩展的主要因素为涡流扩散、流动的流动相传质、滞留的流动相传质以及柱外效应。
在气相色谱中径向扩散往往比较显著,而液相色谱中径向扩散的影响较弱,往往可以忽略。
另外,在液相色谱中还存在比较显著的滞留流动相传质及柱外效应。
3. 在液相色谱中, 提高柱效的途径有哪些?其中最有效的途径是什么?解:液相色谱中提高柱效的途径主要有:1.提高柱内填料装填的均匀性;2.改进固定相减小粒度; 选择薄壳形担体; 选用低粘度的流动相;适当提高柱温其中,减小粒度是最有效的途径.4. 液相色谱有几种类型?它们的保留机理是什么? 在这些类型的应用中,最适宜分离的物质是什么?解:液相色谱有以下几种类型:液-液分配色谱; 液-固吸附色谱; 化学键合色谱;离子交换色谱; 离子对色谱; 空间排阻色谱等.其中;液-液分配色谱的保留机理是通过组分在固定相和流动相间的多次分配进行分离的。
可以分离各种无机、有机化合物。
液-固吸附色谱是通过组分在两相间的多次吸附与解吸平衡实现分离的.最适宜分离的物质为中等相对分子质量的油溶性试样,凡是能够用薄层色谱分离的物质均可用此法分离。
课后习题答案_第3章_门电路

数字电子技术基础第三章习题答案3-1 如图3-63a~d所示4个TTL门电路,A、B端输入的波形如图e所示,试分别画出F1、F2、F3和F4的波形图。
略3-2 电路如图3-64a所示,输入A、B的电压波形如图3-64b所示,试画出各个门电路输出端的电压波形。
略3-3 在图3-7所示的正逻辑与门和图3-8所示的正逻辑或门电路中,若改用负逻辑,试列出它们的逻辑真值表,并说明F和A、B之间是什么逻辑关系。
答:(1)图3-7负逻辑真值表F与A、B之间相当于正逻辑的“或”操作。
(2)图3-8负逻辑真值表F与A、B之间相当于正逻辑的“与”操作。
3-4 试说明能否将与非门、或非门、异或门当做反相器使用?如果可以,各输入端应如何连接?答:三种门经过处理以后均可以实现反相器功能。
(1)与非门: 将多余输入端接至高电平或与另一端并联;(2)或非门:将多余输入端接至低电平或与另一端并联;(3) 异或门:将另一个输入端接高电平。
3-5 为了实现图3-65所示的各TTL 门电路输出端所示的逻辑关系,请合理地将多余的输入端进行处理。
答:a )多余输入端可以悬空,但建议接高电平或与另两个输入端的一端相连;b)多余输入端接低电平或与另两个输入端的一端相连;c) 未用与门的两个输入端至少一端接低电平,另一端可以悬空、接高电平或接低电平;d )未用或门的两个输入端悬空或都接高电平。
3-6 如要实现图3-66所示各TTL 门电路输出端所示的逻辑关系,请分析电路输入端的连接是否正确?若不正确,请予以改正。
答:a )不正确。
输入电阻过小,相当于接低电平,因此将Ω50提高到至少2K Ω。
b) 不正确。
第三脚V CC 应该接低电平。
c )不正确。
万用表一般内阻大于2K Ω,从而使输出结果0。
因此多余输入端应接低电平,万用表只能测量A 或B 的输入电压。
3-7 (修改原题,图中横向电阻改为6k Ω,纵向电阻改为3.5 k Ω,β=30改为β=80) 为了提高TTL 与非门的带负载能力,可在其输出端接一个NPN 晶体管,组成如图3-67所示的开关电路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)1.目的练习材料按定额费用的比例分配。
2.资料某企业生产甲、乙两种产品,耗用原材料费用共计62 400元。
本月投产甲产品220件,乙产品256件。
单件原材料费用定额:甲产品120元,乙产品100元。
3.要求采用原材料定额费用比例分配甲、乙产品实际耗用原材料费用。
解:(1)计算每种产品的材料定额消耗额甲产品材料定额消耗量=220×120=26 400(元)乙产品材料定额消耗量=256×100=25 600(元)(2)材料费用分配率=62400 2640025600+=1.2(3)每种产品应分配的材料费用甲产品应分配的材料费用=26400×1.2=31 680(元)乙产品应分配的材料费用=25600×1.2=30 720(元)(二)1.目的练习材料按定额消耗量的比例分配法。
2.资料某企业生产A、B两种产品,本月两种产品共同领用主要材料12 375千克,单价20元,共计247500元。
本月投产A产品为425件,B产品为525件,A产品的材料消耗定额为20千克,B产品的材料消耗定额为10千克。
3.要求按材料定额消耗量比例分配材料费用。
解:(1)计算每种产品的材料定额消耗量A产品材料定额消耗量=425×20=8500(千克)B产品材料定额消耗量=525×10=5250(千克)(2)材料消耗量分配率=12375 85005250+=0.9(3)每种产品应分配的材料数量A产品应分配的材料数量=8500×0.9=7 650(千克)B产品应分配的材料数量=5250×0.9=4 725(千克)(4)每种产品应分配的材料费用A产品应分配的材料费用=7 650×20=153 000(元)B产品应分配的材料费用=4 725×20=94 500(元)(三)1.目的练习直接材料费用分配的系数分配法。
2.资料某厂生产A1、A2、A3、A4,和A5五种产品,五种产品单位产品甲材料消耗定额分别为30、27.5、25、20、17.5元,本月实际产量分别为400、500、1 000、200、160件,本月实际消耗甲材料59 850元,见表。
2.资料某厂加工车间所产甲产品中,发现可修复废品80件,已修复验收入库。
根据本月“耗用材料汇总表”、“直接人工费用分配表”和“制造费用分配表”提供的资料,本月修复甲产品领用材料8 000元,修复甲产品实际耗用工时1 000小时,小时工资分配率为11元(不含应提取的应付福利费),小时制造费用分配率为6元;本月修复废品应分配人工费用12 540元,其中生产工人工资11 000元,提取应付福利费1 540元;应分配制造费用6 000元。
按规定,本月发生的80件废品应由过失人赔偿1 200元。
解:(1)编制发生可修复废品修复费用的会计分录如下:借:废品损失26 540贷:原材料8 000应付工资11 000应付福利费 1 540制造费用 6 000(2)编制应收过失人赔款的会计分录如下:借:其他应收款 1 200贷:废品损失 1 200(3)结转本月废品净损失的会计分录如下:借:基本生产成本——甲产品(废品损失)25 340贷:废品损失25 340(三)1.目的练习废品损失的核算。
2.资料某企业规定不可修复废品成本按定额成本计价。
某月某产品的不可修复废品40件,每件直接材料定额为30元;40件废品的定额工时共为260小时。
每小时的费用定额为:直接人工10元,制造费用14元。
该月产品的可修复废品的修复费用为:直接材料1 000元,直接人工720元,制造费用1 600元。
废品的残料作为辅助材料入库,计价200元。
应由责任售货员赔偿的废品损失400元。
废品净损失由当月同种产品成本负担。
解:(1)计算不可修复废品的生产成本:不可修复废品的材料成本=40×30=1 200(元)不可修复废品的人工成本=260×10=2 600(元) .不可修复废品的制造费用=260×14=3 640(元)不可修复废品的生产成本=1 200+2 600+3 640=7 440(元)(2)计算全部废品的净损失:全部废品的净损失=不可修复废品的生产成本+可修复废品的修复费用-残料价值-应收赔款=7 440+1 000+720+1 600-200-400=l0 160(元)(3)编制归集废品修复费用,以及结转不可修复废品生产成本、废品残值、应收赔款和废品净损失的会计分录如下:借:废品损失 3 320贷:原材料 1 000应付工资720制造费用 1 600借:废品损失7 440贷:基本生产成本7 440借:原材料200贷:废品损失200借:其他应收款400贷:废品损失400借:基本生产成本10 160贷:废品损失10 160(五)1.目的练习约当产量法。
2.资料某厂生产的甲产品本月完工验收入库数量为4 000件,月末盘点在产品数量为800件,在产品完工程度为50%,材料系开工时一次投入,甲产品生产成本明细账归集的生产费用表明,月初在产品成本为800 000元,其中直接材料600 000元,直接人工88 000元,制造费用112 000元,甲产品本月发生的生产费用为6 871 200元,其中直接材料为4 866 200元,直接人工为882 200元,制造费用为1 122 800元。
解:(1)采用约当产量法计算甲产品月末在产品成本和本月完工产品成本如下表:产品成本计算单(2)借:库存商品——甲产品 6 559 712.4贷:基本生产成本——甲产品 6 559 712.4(六)1.目的练习约当产量法。
2.资料某基本生产车间生产甲产品,采用约当产量比例法分配费用。
甲产品单件工时定额20小时,经三道工序制造。
各工序工时定额:第一道工序4小时,第二道工序8小时,第三道工序8小时。
各道工序内均按50%的完工程度计算。
本月完工200件,在产品120件,其中:第一道工序20件,第二道工序40件,第三道工序60件。
月初加本月发生费用合计分别为:原材料16 000元,工资及福利费7 980元,制造费用8 512元,原材料在生产开始时一次投入。
解:(1)第一道工序加工程度=450%488⨯++×100%=10%第二道工序加工程度=4850%488+⨯++×100%=40%第三道工序加工程度=48850%488++⨯++×100%=80%(2)在产品的约当产量为:投料程度的约当产量为120;加工程度的约当产量=20×10%+40×40%+60×80%=66(3)完工产品成本=16000÷(200+120)×200+7980÷(200+66)×200+8512÷(200+66)×200=22400(元)在产品成本=16000+7980+8512-22400=10092(元)(七)1.目的练习约当产量法。
2.资料某企业生产的丁产品分三道工序制成,各道工序的原材料消耗定额为:第一道工序100千克,第二道工序60千克,第三道工序40千克。
在产品数量:第一道工序150件,第二道工序200件,第三道工序250件。
解:(1)原材料在每道工序开始时一次投料,则各工序的投料程度为:第一道工序=100÷(100+60+40)×100%=50%第二道工序=(100+60)÷(100+60+40)×100%=80%第三道工序=(100+60+40)÷(100+60+40)×100%=100%各工序约当产量是:第一道工序=150×50%=75(件)第二道工序=200×80%=160(件)第三道工序=250×100%=250(件)(2)原材料陆续投料投料程度为:第一道工序=l00×50%÷(100+60+40)×100%=25%第二道工序=(]00+60×50%)÷(100+60+40)×100%=65%第三道工序=(100+60+40×50%)÷(100+60+40)×100%=90%各工序约当产量是:第一道工序=150×25%=37.5(件)第二道工序=200×65%=130(件)第三道工序=250×90%=225(件)(八)1.目的练习定额比例法。
2.资料某企业采用定额比例法分配费用,9月份丙产品生产成本明细账的有关资料如下表:3.要求计算完工产品和月末在产品成本。
解:(1)计算定额原材料费用:完工产品=100×80=8 000(元)在产品=3 000+7 000-8 000=2 000(元)(2)计算定额工时:完工产品=100×40=4 000(小时)在产品=2 000+3 000-4 000=1000(小时)(3)计算定额比例:直接材料分配率=(3 500+7 500)÷(8 000+2 000)=1.1直接工资分配率=(2 500+3 500)÷(4 000+1 000)=1.2制造费用分配率=(1 500+2 500)÷(4 000+1 000)=0.8(4)1.目的练习定额比例法。
2.资料某企业生产甲产品采用定额比例法分配费用,原材料费用按定额费用比例分配,3.要求(1)计算各项费用分配率。
(2)分配计算完工产品和月末在产品成本。
(3)登记甲产品成本明细账。
解:(1)计算各项费用分配率:材料费用分配率=10 010÷(5 600+3 500)=1.1人工费用分配率=8 550÷(3 860+1 880)=1.4895制造费用分配率=7 462÷(3 860+1 880)=1.3(2)分配计算完工产品和月末在产品成本:完工产品应负担的材料费用=5 600×1.1=6 160(元)完工产品应负担的人工费用=3 860×1.4895=5 749.47(元)完工产品应负担的制造费用=3 860× 1.3=5 018(元)完工产品成本=6 160+5 749.47+5 018=16 927.47(元)在产品应负担的材料费用=3 500×1.1=3 850(元)在产品应负担的人工费用=8 550-5 749.47=2 800.53(元)在产品应负担的制造费用=1 880×1.3=2 444(元)在产品成本=3 850+2 800.53+2 444=9 094.53(元)(3)1.目的练习在产品按定额成本计价法。
