小学六年级奥数专题训练:不规则图形的面积求法
小学奥数:不规则图形的面积.专项练习

本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 你有什么好的方法计算所给图形的面积呢?(单位:厘米)3994399439943994图1 图2 图3【巩固】如图是学校操场一角,请计算它的面积(单位:米)30203040【巩固】如右图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积. 例题精讲4-2-6.不规则图形的面积F【巩固】求图中五边形的面积.6453【例 2】这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?【例 3】有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?【例 4】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【例 5】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA【例 6】 如图,李大伯给一块长方形田地喷药,喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长2米的正方形区域,他从图中的A 点出发,沿最短路线(图中虚线)走,走过88米到达B 点,恰好把这块田地全部喷完,这块田地的面积是多少平方米?BA 1米1米【例 7】 右图中甲的面积比乙的面积大__________平方厘米.6厘米8厘米4厘米【例 8】 右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF的面积大9平方厘米,求ED 的长.AB CDE F【巩固】如图所示,4CA AB ==厘米,ABE △比CDE △的面积小2平方厘米,求CD 的长为多少厘米?ABE C D【巩固】如图,平行四边形ABCD 种,10BC cm =,直角三角形ECB 的边8EC cm =,已知阴影部分的总面积比三角形EFG 的面积大210cm ,求平行四边形ABCD 的面积.G FEDCBA【例 9】 如图,ABCD 是74⨯的长方形,DEFG 是102⨯的长方形,求BCO 与EFO 的面积差.O BC D GFE A【例 10】 有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?680平方米2720平方米60【巩固】有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?2【例 11】 一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?【例 12】 一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?【巩固】一块长方形纸片,在长边剪去5cm,宽边剪去2cm后(如图),得到的正方形面积比原长方形面积少231cm.求原长方形纸片的面积.52【巩固】一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?66【例 13】一块正方形的钢板,先截去一个宽5分米的长方形,又截去一个宽8分米的长方形(如图),面积就比原来正方形减少181平方分米.原正方形的边长是多少分米?85【巩固】一张长方形纸片,先把长剪去8厘米,这时面积减少了72平方厘米,又把宽剪去5厘米,这时面积又减少了60平方厘米,原来这张长方形纸片的面积是多少平方厘米?5【巩固】如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽7分米的长方形,所得图形的面积比原正方形减少301平方分米.原正方形的边长是______分米.11【例 14】如图长方形被分成两部分,已知阴影面积比空白部分面积大34平方厘米,求阴影部分的面积.10cm【例 15】一张长方形纸片,把它的右上角往下折叠(如图甲),阴影部分面积占原纸片面积的27;再把左下角往上折叠(如图乙),乙图中阴影部分面积占原纸片面积的________(答案用分数表示).甲乙【巩固】折叠后,原平行四边形面积是折叠后图形面积的1.5倍.已知阴影部分面积之和为1,则重叠部分(即空白部分)的面积是多少?【巩固】如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?5【例 16】如图,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例 17】如图所示,直角三角形中有一个长方形,求长方形的面积?44 4【例 18】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积?【巩固】如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是.第6题【巩固】图中有6个正方形,较小的正方形都由较大的正方形的4边中点连接而成.已知最大的正方形的边长为16厘米,那么最小的正方形的面积等于多少平方厘米?【例 19】已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米?【巩固】如图所示,外侧大正方形的边长是10cm,在里面画两条对角线、一个圆、两个正方形,阴影的总面积为226cm,最小的正方形的边长为多少厘米?【例 20】有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形.求图中阴影部分的面积?【例 21】如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为.第2题【例 22】 下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)6【巩固】如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?【例 23】 甲、乙、丙三个正方形,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?108 6丙乙甲【巩固】将20张边长为10厘米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候,要求后摆的纸片必须有一个顶点与前一张的中心重合,且每一张只与其前一张和后一张有重合部分(右图表示已经摆好的5张).地板被这20张纸片所覆盖部分的面积是多少?【例 24】有2个大小不同的正方形A和B.如下左图所示的那样,在将B正方形的对角线的交点与A正方形的一个顶点相重叠时,相重叠部分的面积为A正方形面积的19.求A与B的边长之比.如果当按下右图那样,将A和B反向重叠的话,所重叠部分的面积是B的几分之几?左图右图【例 25】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?【巩固】一块长方形草坪(图中阴影部分)长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米?【例 26】如图所示,一个长方形广场的正中央有一个长方形的水池.水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.水池【例 27】用四个相同的长方形拼成一个面积为2100cm的大正方形,每个长方形的周长是多少平方厘米?【巩固】如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例 28】四个完全相同的长方形拼成右图,大正方形的面积是l00平方分米,小正方形的面积是l6平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?16【巩固】如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为厘米,宽厘米.第19题【例 29】街心花园里有一个正方形花坛,四周有一条宽1米的甬道(如图),如果甬道的面积是12平方米,那么中间花坛的面积是多少平方米?1米【巩固】在一个正方形的小花园周围,环绕着宽5米的水池,水池面积为300平方米,那么正方形花园的面积是多少平方米?5【巩固】有大、小两个长方形(如图),对应边的距离均为1cm,已知两个长方形之间部分的面积是216cm,且小长方形的长是宽的2倍,求大长方形的面积.A【例 30】已知大正方形比小正方形边长多4厘米,大正方形面积比小正方形面积大96平方厘米.问大、小正方形面积各是多少?【巩固】两个正方形的面积相差29cm,边长相差1cm.求两个正方形的面积和.C BA【巩固】有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米.小正方形的面积是多少平方厘米?【例 31】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差16厘米,面积相差96平方厘米,求小正方形的面积是多少平方厘米?(1)(2)c bca【例 32】用两块长方形纸片和一块正方形纸片拼成一个大正方形,长方形纸片面积分别为44平方厘米与28平方厘米,原正方形纸片面积是多少平方厘米?【例 33】计划修建一个正方形的花坛,并在花坛周围种上3米宽的草坪,草坪的面积为300平方米,那么修建这个花坛需要占地多少平方米?(1)(2)【巩固】有大、小两个长方形(右图),对应边的距离均为1厘米,已知两个长方形之间部分的面积是16平方厘米,且小长方形的长是宽的2倍,求大长方形的面积.【巩固】一块长方形的草坪(见图中阴影部分),长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路,求草坪的总面积是多少平方米?【例 34】一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?3030【例 35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?【巩固】从一个正方形的木板上锯下宽1m的一个长方形木条后,剩下的长方形面积为26m,问锯下的长方形木条面积是多少?【巩固】从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米?【例 36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.【例 37】有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?图a图b【例 38】 如图,边长是整数的四边形AFED 的面积是48平方厘米,FB 为8厘米.那么,正方形ABCD 的面积是 平方厘米.A BCDEF 488【例 39】 如图,一个正方形被分成4个小长方形,它们的面积分别是110平方米、15平方米、310平方米和25平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?【例 40】 长方形ABCD 的周长是30厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290平方厘米,那么长方形ABCD 的面积是多少平方厘米?C 1D 1E 1A 1EBC DA【巩固】如图,长方形ABCD 的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方厘米,求长方形ABCD 的面积?A B C D IH G FEAB C D【例 41】 一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是2厘米,这条手帕白色部分的面积是多少?【例 42】 用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?图1图2【例 43】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?24【巩固】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?【例 44】如右图所示,在长方形ABCD中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.B【例 45】 若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例 46】 一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A 和B 的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?ABA BCDE FGH【巩固】如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为281cm ,请问这个矩形之面积为多少平方厘米?【巩固】图中的长方形被分割成6个正方形,已知中央小正方形的面积是1平方厘米,求原来长方形的面积.【巩固】9个边长分别为1、4、7、8、9、10、14、15、18的正方形拼成一个长方形,问这个长方形的长和宽是多少?并请画出这个长方形的拼接图.1518141094781【例 47】 图中数字分别表示两个长方形和一个直角三角形的面积,另一个三角形的面积是 .51215A 51215【例 48】 如图,一个矩形被分成八个小矩形,其中有五个矩形的面积如图中所示(单位:平方厘米),问大矩形的面积是多少平方厘米?1230201636G FEDC B AS 3S 2S 11230201636G FEDC B A【巩固】阳阳用四块小长方形恰好拼成了一个大的长方形,如图所示.现在知道其中三块长方形的面积分别为48平方厘米、24平方厘米、30平方厘米,那么,阴影部分的面积是多少?302448【巩固】如图,矩形ABCD 被分割成9个小矩形.其中有5个小矩形的面积如图所示.矩形ABCD 的面积为 .164221CBD A【例 49】 有红、黄、绿三块大小一样的正方形纸片,放在一个底面为正方形的盒内,它们之间相互叠合(见下图).已知露在外面的部分中,红色面积是20,黄色面积是14,绿色面积是10.求正方形盒底的面积.绿黄红绿黄红【例 50】 如图所示,在正方形ABCD 内,红色、绿色正方形的面积分别是48和12,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点.那么黄色正方形的面积是 .DCBA绿黄红 312【巩固】如图所示,在正方形ABCD 中,红色,绿色正方形的面积分别是52和13,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,求黄色正方形面积.绿黄红D C BA【例 51】 如图,三个一样大小的正方形放在一个长方形的盒内,A 和B 是两个正方形的重叠部分,C 、D 、E 是空出的部分,每一部分都是矩形,它们的面积比是A :B :C :D :E =1:2:3:4:5,那么这个长方形的长与宽之比是________.【例 52】 如图如果长方形的面积为56平方厘米,且2MD =厘米、3QC =厘米、5CP =厘米、6BN =厘米,那么请你求出四边形MNPQ 的面积是多少厘米?CP2552PC【巩固】长方形的广告牌长为10米,宽为8米,A,B,C,D分别在四条边上,并且C 比A低5米,D在B的左边2米,四边形ABCD的面积是平方米.DCBADCBA【例 53】直角三角形PQR的直角边为5厘米,9厘米,问:图中三个正方形的面积之和比4个三角形的面积之和大多少?DFCCFD【例 54】如图所示,甲、乙、丙、丁四个长方形拼成一个正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是232cm,四边形ABCD的面积是220cm.⑴求正方形EFGH的边长?⑵求甲、乙、丙、丁四个长方形周长的总和?FEGDBABCDGH E Fhgfe d cba图1 图2 图3【例 55】 如图,平面上CDEF 是正方形,ABCD 是等腰梯形,它的上底23AD =厘米,下底35BC =厘米.求三角形ADE 的面积.FECB DAH 2H 1HADBCEF【例 56】 右图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例 57】 把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形.再将这个六角形的六个”角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样就得到如右图所示的图形.如果所作的最小的小正三角形的面积为1平方厘米,求如图中整个图形的面积.图a中中中大图b【例 58】 如图,长方形的面积是小于100的数.它的内部有三个边长是整数的正方形.正方形②的边长是长方形长的512,正方形①的边长是长方形宽的18.那么,图中阴影部分的面积是。
不规则图形的面积计算
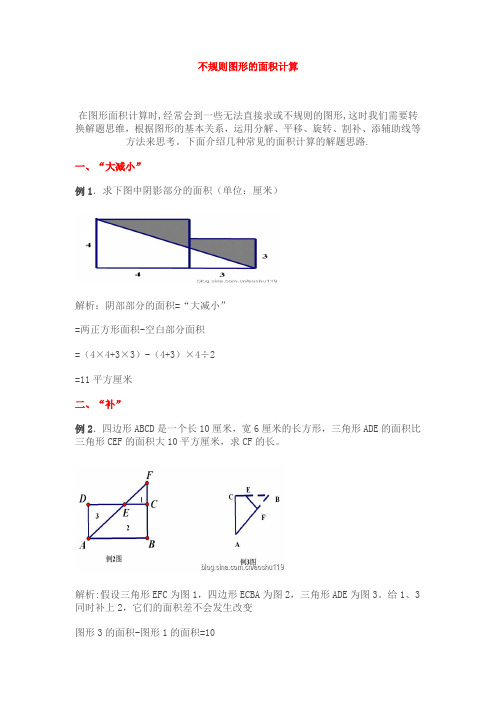
不规则图形的面积计算在图形面积计算时,经常会到一些无法直接求或不规则的图形,这时我们需要转换解题思维,根据图形的基本关系,运用分解、平移、旋转、割补、添辅助线等方法来思考。
下面介绍几种常见的面积计算的解题思路.一、“大减小”例1.求下图中阴影部分的面积(单位:厘米)解析:阴部部分的面积=“大减小”=两正方形面积-空白部分面积=(4×4+3×3)-(4+3)×4÷2=11平方厘米二、“补”例2.四边形ABCD是一个长10厘米,宽6厘米的长方形,三角形ADE的面积比三角形CEF的面积大10平方厘米,求CF的长。
解析:假设三角形EFC为图1,四边形ECBA为图2,三角形ADE为图3。
给1、3同时补上2,它们的面积差不会发生改变图形3的面积-图形1的面积=10(图形3+图形2)-(图形1+图形2)=即长方形ABCD的面积-三角形ABF的面积=10那么,三角形ABF的面积=60-10=50=AB×BF÷2可算出 BF=10厘米,所以CF=10-6=4厘米例3.如图,四边形ACEF中,角ACE=角EFA=90°,角CAF=45°,AC=8厘米,EF=2厘米,求四边形ACEF的面积解析:分别延长AF、CE,交于B点在三角形ABC中,很明显,它是个等腰直角三角形,面积=8×8÷2=32平方厘米在三角形EFB中,很明显,它也是一个等腰直角三角形,面积=2×2÷2=2平方厘米所以,S四边形ACEF=S△ABC-S△EFB=32-2=30平方厘米三、“移”例4.如图所示(1图),四边形ABCD是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求路的面积。
解析:小路是曲折的,不规则图形,可用采用“移”的思路来解决把图1下面空白部分往上、往左移,使它与上面空白部分连接在一起,就成了图2中的空白部分,是一个长方形,长是20-2=18米,宽是14-2=12米,这个长方形的面积=18×12=216平方米,小路的面积=大长方形的面积-空白长方形的面积=20×14-216=64平方米例5.如图,AE=ED,AF=FC,已知三角形ABC的面积是100平方厘米,求阴影部分的面积解析:由于两阴影部分不在一起,我们可以考虑用“移”的思维把阴影变成一个整体。
不规则图形面积的计算(实用课件)

8
“割”、“补”的方法是我们今后计算复 杂图形时常用的方法,方法越简单越好。
❖ 在进行图形计算割补时,要注意以下几点:
(1)要根据原来图形的特点进行思考。
(2)要便于利用已知条件计算简单图形的面积。
(3)可以用不同的方法进行割补。
不规则图形面积的计算(实用课件)
9
练一练:
1、校园里有一个花圃(如图),你能算出 它的面积是多少平方米?
❖
3×6÷2=9㎡
❖ 草坪的面积:120+9=129㎡
❖ 答:这块草坪的不面规则图积形面是积的1计2算(9实㎡用课件)
6
12m
方法三:分割法 4m
10m
15m
❖ 草坪的面积=梯形面积+三角形面积 ❖ 梯形的面积:(4+10)×12÷2=84㎡ ❖ 三角形的面积:10-4=6m,15×6÷2=45㎡ ❖ 草坪的面积:84+45=129㎡ ❖ 答:这块草坪的面积是129㎡
不规则图形面积的计算
感谢您的阅览
不规则图形面积的计算(实用课件)
你还记得吗?
长 方 形 的 面 积 = 长 ×宽
S=ab
正 方 形 的 面 积 = 边长×边长
S=a×a
平行四边形的面积= 底×高
S=ah
三 角 形 的 面 积 = 底×高÷2
S=ah÷2
梯 形 的 面 积 = (上底+下底)×高÷2 S=(a+b)h÷2
17
作业
课本23页练习四1到4题
不规则图形面积的计算(实用课件)
18
45cm 60cm
学校开运动会要制作一 些锦旗,式样如右图。 一面锦旗需要多少平方 厘米面料?
(60+45) ×(30÷2) ÷2×2 =105×15÷2×2 =1575(㎝²)
不规则图形面积的计算

Excellent handout template
Special lecture notes
1、草坪的面积有多少平方米
Excellent handout template
Special lecture notes
2、现在要给小路铺上地砖,如果9块 地砖正好铺1m2,那么至少需要多少 块地砖
中队旗面积 = 长方形面积 — 三角形面积
Excellent handout template
Special lecture notes
小结
方法:一分图形 二找条件 三算面积
关键:学会运用分割与添补的方 法计算组合图形面积.
Excellent handout template
作业
Special lecture notes
课本23页练习四1到4题
Excellent handout template
学校开运动会要制作一 些锦旗,式样如右图。一 面锦旗需要多少平方厘 米面料
60+45 × 30÷2 ÷2×2 =105×15÷2×2
=1575 ㎝²
答:一面锦旗需要1575平方厘 米面料。
45cm 60cm
Special lecture notes
不规则图形面积的计算
This template is the internal standard courseware template of the enterprise
Special lecture notes
不规则图形面积的计算
Excellent handout template
你还记得吗
❖ 正方形面积=边长×边长用字母表示为
❖S=a×a= a 2
Excellent handout template
六年级数学-不规则图形面积计算

不规则图形面积计算(1)我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形. 我们的面积及周长都有相应的公式直接计算. 如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算. 一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了、例题与方法指导例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10 厘米和12厘米. 求阴影部分的面积。
思路导航:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ ABG、△BDE、△ EFG)的面积之和。
例 2 如右图,正方形 ABCD 的边长为 6 厘米,△ ABE 、△ ADF 与四边形 AECF 的面积 彼此相等,求三角形 AEF 的面积 .1∴四边形AECF 的面积与△ ABE 、△ ADF 的面积都等于正方形 ABCD 的 。
3在△ ABE 中,因为 AB=6.所以 BE=4,同理 DF=4,因此 CE=CF=2, ∴△ ECF 的面积为 2×2÷ 2=2。
所以 S △ AEF=S 四边形 AECF-S △ECF=12-2=10(平方厘米)。
例 3 两块等腰直角三角形的三角板,直角边分别是 10 厘米和 6 厘米。
如右图那样在等腰直角三角形 ABC 中 ∵AB=10∵EF=BF=AB-AF=10-6=4,∴阴影部分面积 =S △ ABG-S △ BEF=25-8=17(平方厘米)。
例 4 如右图, A 为△ CDE 的 DE 边上中点, BC=CD ,若△ ABC (阴影部分)面积为 5平方厘米 .求△ ABD 及△ ACE 的面积 .思路导航:取 BD 中点 F ,连结 AF.因为△ ADF 、△ ABF 和△ ABC 等底、等高,所以它们的面积相等,都等于 5 平方厘米 .∴△ ACD 的面积等于 15 平方厘米,△ ABD 的面积等于 10 平方厘米。
(专题)圆中不规则图形面积解法(含答案解析)

专题圆中不规则图形面积解法方法一公式法例题11. 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形的面积为_____;若将此扇形围成一个无底的圆锥(不计接头),则圆锥底面半径为_____.【答案】①. π ①. 1 2【解析】【分析】由勾股定理求扇形的半径,再根据扇形面积公式求值;根据扇形的弧长等于底面周长求得底面半径即可.【详解】解:连接BC,由∠BAC=90°得BC为⊙O的直径,∴BC=,在Rt△ABC中,由勾股定理可得:AB=AC=2,∴S扇形ABC=904360π=π;∴扇形的弧长为:902180π⨯=π,设底面半径为r,则2πr=π,解得:r=12,故答案为:π,12.【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.变式12. 如图,将边长为3的正六边形铁丝框ABCDEF (面积记为1S )变形为以点D 为圆心,CD 为半径的扇形(面积记为2S ),则1S 与2S 的关系为( )A. 12S S >B. 12S SC. 12S S <D. 12π3S S =【答案】A 【解析】【分析】由正六边形的性质出EAC 的长,根据扇形面积公式=12×弧长×半径,可得结果【详解】解:由题意:12EAC = ①2112318,2S =⨯⨯=①2163,42S =⨯= ∴12S S > 故选:A【点睛】本题考查了正多边形和圆、正六边形的性质、扇形面积公式;熟练掌握正六边形的性质,求出弧长是解决问题的关键.变式23. 如图,在ABCD 中,E 为BC 的中点,以E 为圆心,BE 长为半径画弧交对角线AC 于点F ,若60BAC ∠=︒,100ABC ∠=︒,4BC =,则扇形BEF 的面积为________.【答案】4π9【解析】【分析】根据三角形内角和、三角形的外角以及等腰三角形性质求出BEF ∠,然后根据扇形面积公式计算.【详解】解:∵60BAC ∠=︒,100ABC ∠=︒, ∴20ACB ∠=︒,∵E 为BC 的中点,EB 、EF 为半径, ∴20EFC ECF ∠=∠=︒, ∴=40BEF ∠︒, ∵4BC =, ∴2BE =,∴扇形BEF ①①①240243609ππ⨯==. 【点睛】本题主要考查的是扇形面积计算,三角形内角和定理,等腰三角形性质,掌握扇形面积计算公式是解题的关键.变式34. 如图,在每个小正方形的边长为1的网格中,每个小正方形的顶点叫格点,ABC 的三个顶点均在格点上,把ABC 绕着点A 按逆时针方向旋转到AB C ''△.(1)求BAC ∠的正切值. (2)求扇形CAC '的面积. 【答案】(1)1tan 3BAC ∠=;(2)10πCAC S '=扇形. 【解析】【分析】(1)过点C 作CD ⊥AB ,交AB 的延长线于D ,如图,根据正切的定义求解; (2)连接CC ´,如图,先利用勾股定理的逆定理证明△ACC 为直角三角形,则∠CAC=90°,然后根据扇形的面积公式计算.【详解】解:(1)过点C 作CD AB ⊥,交AB 的延长线于D ,则2CD =,6AD =, ∴在Rt ACD △中,21tan 63CD BAC AD ∠===. (2)连接CC ',2224880C C '=+=,22222640C A CA '==+=,∵22280C A CA C C ''+==,∴ACC '△为直角三角形,90CAC '∠=︒, ∴290π90π4010π360360CAC AC S '⋅⨯===扇形.【点睛】本题考查了作图一旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.方法二 直接和差法特征:阴影部分是几个常见图形组合而成. 计算方法:S S S =±阴影常见图形常见图形一、直接和差法:ACB-AOB-AOBAB -半圆AB S 半圆ADEACB例题25. 某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED 与母线AD 长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB AC =,AD BC ⊥.将扇形AEF 围成圆锥时,AE ,AF 恰好重合.(1)求这种加工材料的顶角BAC ∠的大小(2)若圆锥底面圆的直径ED 为5cm ,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)【答案】(1)BAC ∠=90°;(2)S 阴影=(100-25π)cm 2. 【解析】【分析】(1)设ED =x ,则AD =2x ,根据圆的周长求 EF 弧长,利用弧长公式求90n =︒即可;(2)由AB AC =,BAC ∠=90°,可得△ABC 为等腰直角三角形,由AD BC ⊥可求BD =CD =AD =10cm , 利用三角形面积公式求S △BAC =12BC AD ⨯,利用扇形面积公式求=25EF S π扇形,利用面积差求S 阴影即可. 【详解】解:(1)设ED =x ,则AD =2x , ∴EF 弧长222180x n xππ⨯=⨯=, ∴90n =︒, ∴BAC ∠=90°; (2)∵ED =5cm , ∴AD =2ED =10cm , ∵AB AC =,BAC ∠=90°, ∴△ABC 为等腰直角三角形, ∵AD BC ⊥, ∴BD =CD =AD =10cm , ∴BC =BD +CD =20cm①∴S △BAC =11201010022BC AD ⨯=⨯⨯=cm 2,∴EFS 扇形29010==25360ππ⨯⨯,∴S 阴影= S △BAC -EF S 扇形=(100-25π)cm 2.【点睛】本题考查圆锥,侧面展开图,扇形面积公式,等腰直角三角形判定与性质,利用割补法求阴影面积,掌握圆锥,侧面展开图,扇形面积公式,等腰直角三角形判定与性质,利用割补法求阴影面积是解题关键.变式46. 如图,在扇形OAB 中,已知90AOB ∠=︒,2OA =,过AB 的中点C 作CD OA ⊥,CE OB ⊥,垂足分别为点D ,E ,则图中阴影部分的面积为( )A. π1-B. π2-C. π4-D.π12- 【答案】B 【解析】【分析】根据矩形的判定定理得到四边形ODCE 是矩形,连接OC ,根据全等三角形的性质得到OD=OE ,然后得到矩形ODCE 是正方形,最后利用扇形和正方形的面积公式计算即可. 【详解】如图所示,连接OC∵90AOB ∠=︒,CD OA ⊥,CE OB ⊥ ∴四边形ODCE 是矩形 ∵点C 是AB 的中点 ∴COA COB ∠=∠ ∴COD COE ≌ ∴OD OE =∴四边形ODCE 是正方形 ∴OD CD = ∴2222OD CD += ∴22OD = 即2ODCE S =正方形由扇形的面积公式可得:AOB S π=扇形 ∴=-2S π阴影 故选:B【点睛】本题主要考查矩形的判定定理和性质、正方形的判定定理和性质、全等三角形的判定和性质、扇形面积的计算公式,熟练掌握相应的判定定理和性质是解题的关键.变式57. 如图,在O 中,3OA =,45C ∠=︒,则图中阴影部分的面积是_________.(结果保留π)【答案】9942π- 【解析】【分析】由45C ∠=︒,根据圆周角定理得出90AOB ∠=︒,根据S 阴影=S 扇形AOB -AOBS 可得出结论.【详解】解:∵45C ∠=︒, ∴90AOB ∠=︒, ∴S 阴影=S 扇形AOB -AOBS29031=333602π⨯⨯-⨯⨯99=42π-, 故答案为:9942π-. 【点睛】本题主要考查圆周角定理、扇形的面积计算,根据题意求得三角形与扇形的面积是解答此题的关键.变式68. 如图,在ABC ∆中,BC =4,且ABC ∆的面积为4,以点A 为圆心,2为半径的⊙A 交AB 于E ,交AC 于F ,点P 是⊙A 上一点,且∠EPF =45°.(1)求证:BC 为⊙A 的切线; (2)求图中阴影部分的面积. 【答案】(1)证明见详解;(2)4π-. 【解析】【分析】(1)作AD ⊥BC ,根据三角形的面积,可求出AD =2=半径且为BC 边上的高,即可判定;(2)再根据圆周角定理得∠EAF =2∠EPF =90°,而S 阴=ABCSS -扇形EAF ,然后利用扇形的面积公式:S =2360n R π和三角形的面积公式即可计算出图中阴影部分的面积.【详解】解:(1)过点A 作AD ⊥BC ,如图,∵BC=4,S △ABC =4,∴114422BC AD AD ⨯⨯=⨯⨯=, ∴AD=2,又⊙A 的半径为2,∴BC 与⊙A 相切,切点为点D ,(2)∵由(1)可知⊙A 与BC 相切于点D ,∴AD ⊥BC ,且AD =2, 又∵∠EPF =45° ∴∠BAC=90°, 而BC =4,4ABCS =,∴S 阴=ABCSS -扇形EAF =12BC×AD ﹣2902360π⨯=4π-. 【点睛】本题考查了扇形的面积公式:S =2360n R π(其中n 为扇形的圆心角的度数,R 为圆的半径),或S =12lR ,l 为扇形的弧长,R 为半径.同时考查了切线的性质定理和圆周角定理.二、构造和差法:OCE-ODC-SBOC例题39. 如图,已知⊙O 的半径是4,点A,B,C 在⊙O 上,若四边形OABC 为菱形,则图中阴影部分面积为① ①A. 83π- B.163π- C.163π- D. 83π-【答案】B 【解析】【分析】连接OB 和AC 交于点D ,根据菱形及直角三角形的性质先求出AC 的长及∠AOC 的度数,然后求出菱形ABCO 及扇形AOC 的面积,则由S 扇形AOC -S 菱形ABCO 可得答案.【详解】连接OB 和AC 交于点D ,如图所示:∵圆的半径为4① ∴OB=OA=OC=4① 又四边形OABC 是菱形, ∴OB ⊥AC①OD=12OB=2① 在Rt △COD 中利用勾股定理可知:CD=224223,243AC CD -===,∵sin ∠COD=CD OC = ∴∠COD=60°①∠AOC=2∠COD=120°①∴S 菱形ABCO=11422OB AC ⨯=⨯⨯= ∴S 扇形=21204163603ππ⨯⨯=,则图中阴影部分面积为S 扇形AOC -S 菱形ABCO =163π-. 故选B.【点睛】考查扇形面积的计算及菱形的性质,解题关键是熟练掌握菱形的面积=12a•b(a 、b 是两条对角线的长度);扇形的面积=2360n r π.变式7【2019·泰安】10. 如图,90AOB ∠=︒,30B ∠=︒,以点O 为圆心,OA 为半径作弧交AB 于点A ,点C ,交OB 于点D ,若3OA =,则阴影部分的面积为_____.【答案】34π【解析】【分析】根据题意连接OC ,可得阴影部分的面积等于两个阴影部分面积之和,再根据弧AC 所对的阴影部分面积等于弧AC 所对圆心角的面积减去OAC ∆的面积,而不规则图形BCD 的面积等于OBC ∆的面积减去弧DC 所对圆心角的面积.进而可得阴影部分的面积.【详解】解:根据题意连接OC,90903060OA OC OAB B ︒︒︒︒=∠=-∠=-=ACO ∴∆为等边三角形60AOC ︒∴∠=∴阴影部分面积1=26013333cos3036022ππ︒⨯⨯-⨯⨯=∴阴影部分面积2=2133033223604ππ⨯-⨯⨯=-∴阴影部分面积=阴影部分面积1+阴影部分面积2=34π故答案为34π.【点睛】本题只要考查圆弧的面积计算,关键在于阴影部分面积的分割.变式811. 如图,A ,C 是双曲线1y x=上关于原点对称的点,B ,D 是双曲线3y x=-上关于原点对称的点,圆弧BAD 与BCD 围成了一个封闭图形,当线段AC 与BD 都最短时,图中阴影部分的面积为________.【答案】163π-【解析】【分析】设点A 1x x ⎛⎫⎪⎝⎭,,要使当线段AC 与BD 都最短,就是使OA 最短,利用勾股定理表示出OA 与x 的函数解析式,将其函数解析式转化为顶点式,利用二次函数的性质可求出OA 的最小值,即可求出AC 的值;再利用同样的方法可求出BC 的长;再证明△ABC 是等边三角形,然后利用扇形的面积公式和三角形的面积公式可求出阴影部分的面积.【详解】解:设点A 1x x ⎛⎫⎪⎝⎭,, 要使当线段AC 与BD 都最短,就是使OA 最短,∴OA ==∴当10x x-=时,OA ,∴x =1(负值舍去),∴点A (1,1),点()1,1C --;∴AC =,设点B 3m m ⎛⎫- ⎪⎝⎭, , 要使当线段BD 都最短,就是使OB 最短,∴OB ==∴当30x x-=时,OB ,∴x ,∴点B ( , 点D-;∵点B 和点D ,点A 和点C 关于原点对称, ∴BC =AB =CD =AD ,∴BC ==∴△ABC 是等边三角形, ∴BC =AC =AB ,∴r =∴S 阴影部分=(211164623ππ⎛-⨯=- ⎝故答案为:163π-【点睛】本题考查了反比例函数,线段最值,二次函数求最值,等边三角形,弓形面积的计算,解题关键在于求出线段的最值.变式92019·新抚区三模】12. 如图,AB =AC ,⊙O 为△ABC 的外接圆,AF 为⊙O 的直径,四边形ABCD 是平行四边形.(1)求证:AD 是⊙O 的切线;(2)若∠BAC =45°,AF =2,求阴影部分的面积.【答案】(1)证明见解析;(2)124π+-. 【解析】【分析】(1)由题意根据垂径定理得到AF ⊥BC ,根据平行四边形的性质得到AD ∥BC ,求得AD ⊥AF ,于是得到AD 是⊙O 的切线;(2)根据题意连接OC ,OB ,根据圆周角定理得到∠BOC=90°,根据勾股定理得到,连接OE ,根据梯形和扇形的面积公式即可得到结论.【详解】解:(1)①AB =AC , ①AB AC =, ①AF 为①O 的直径, ①AF①BC ,①四边形ABCD 是平行四边形, ①AD①BC , ①AD①AF , ①AD 是①O 的切线; (2)连接OC ,OB ,①①BAC =45°, ①①BOC =90°, ①AF =2,①OB =OC =1,①BC①四边形ABCD 是平行四边形,①AD =BC , 连接OE , ①AB①BD ,①①ACE =①BAC =45°, ①①AOE =2①ACE =90°, ①OA =OE =1,①阴影部分的面积=S 梯形AOED ﹣S 扇形AOE =12()×1﹣2901360π⨯=124π-. 【点睛】本题考查切线的判定,等腰三角形的性质,平行四边形的性质,扇形的面积的计算,正确的作出辅助线是解题的关键.方法三:重叠法特征:几个常见图形经过一次性重叠组成 常见图形,从而重叠部分是阴影部分. 计算方法:12n S S S S S =++-阴影图形图形图形组成图形例题413. 如图,正方形的边长为a ,以各边为直径在正方形内画半圆.求图中阴影部分的面积.【答案】222a π-【解析】【分析】阴影部分的面积为正方形的面积减去四空白的面积.而正方形的面积减去两个半圆的面积就得两个空隙的面积,正方形的面积为a 2,半圆的面积为21122a π⎛⎫ ⎪⎝⎭π. 【详解】解:如图,图中四个半圆都通过正方形的中心,用正方形的面积减去四空白的面积,剩下的就是阴影部分的面积,而正方形的面积减去两个半圆的面积就得两个空隙的面积, ∴2=S a 正方形,221=224a S a ππ⎛⎫=⎪⎝⎭半圆 ∴22=22=22a S S S a π--正方形半圆4个空白∴2222222==2222a a S S S a a a a πππ⎛⎫----=-= ⎪⎝⎭阴影正方形4个空白 【点睛】本题考查了圆的面积以及不规则的几何图形的面积的求法,将不规则图形转化为规则的几何图形的面积的和与差是解题的关键.变式1014. ①①①①Rt ABC ①①∠BCA=90° 4,2AC BC ==①①①①①,AC BC ①①①①①①①①①①①①①①①① ①A.542π- B. 104π- C. 108π- D.582π- 【答案】A 【解析】【详解】①①①①①①①①①①S 1、S 2、S 3、S 4、S 5①①①①①①∵①①①①①①①①①①S 1+S 5+S 4+S 2+S 3+S 4①△ABC①①①①S 3+S 4+S 5①①①①① ①①①①S 1+S 2+S 4①∴①①①①①①①①①①①①①①①①①①①①①①①①①① ①①①①①①①①=12π×4+12π×1-4×2÷2=52π-4① ①①A.变式1115. 正三角形的边长为2,分别以A 、B 、C 为圆心,以1为半径在三角形形内作弧,作ABC 内切圆,求阴影部分面积.【答案】56π-【解析】【分析】根据切线长定理求出①OBD =①OBF =30°,由切线的性质得①ODB =90°,根据勾股定理求出OD ,然后根据S 圆中间空白= 6S ①BDO - 3S 扇形BDF 和S 阴影=S ⊙O - S 圆中间空白求解即可.【详解】解:连接OD ,OB ,由题意知BD =1, ①①ABC 是等边三角形, ①①ABC =60°,①①O 是①ABC 的内切圆,①①OBD =①OBF =30°,①ODB =90°, ①OB =2OD , ①OD 2+BD 2=OB 2,①OD 2+12=4OD 2,①OD S 圆中间空白= 6S ①BDO - 3S 扇形BDF=2160161323360π⨯⨯⨯⨯-⨯12π,①S 阴影=S ⊙O - S 圆中间空白=212ππ⎫⨯-⎪⎭⎝⎭=56π故答案为:56π-【点睛】本题考查了切线长定理,切线的性质,含30°角的直角三角形的性质,等边三角形的性质,勾股定理,以及扇形面积公式,熟练掌握各知识点是解答本题的关键.方法四 割补法特征:把阴影部分某一部分图形,改变它的位置后,从新组成一个常见图形. 计算方法:S S =阴影组成图形例如:例题516. 如图,在⊙O中,直径2AB=,AC切O于A,BC交⊙O于D,若∠=︒,则阴影部分的面积为______.45C【答案】1【解析】【分析】根据题意连接AD,得到ABC为等腰直角三角形,推出AB=BD,则弓形BD的面积=弓形AD的面积,故阴影部分的面积=△ACD的面积,可解出最终结果.【详解】连接AD ,=45C ∠︒,AC 切⊙O 于A 点,=90BAC ∴∠︒,ABC 为等腰直角三角形,又=90ADB ∠︒,∴AD=BD ,弓形BD 的面积=弓形AD 的面积,故阴影部分的面积=△ACD 的面积,AB=2,S △ACD=12CD×AD=12,即阴影部分的面积是1.【点睛】本题考查圆的性质及切线和弓形面积的知识,属于综合题,需要充分掌握圆的基础知识,学会运用圆的性质进行解题是关键.变式1217.CFD 的圆心C 是AB 的中点,且扇形CFD 绕着点C 旋转,半径AE ,CF 交于点G ,半径BE ,CD 交于点H ,则图中阴影面积等于( )A. 12π-B.22π- C. 1π- D. 2π-【答案】D 【解析】【分析】先根据扇形面积公式求出两扇形面积,再过C 分别作CM ⊥AE 于M ,CN ⊥BE于N ,连接EC ,再证明△CMG ≌△CNH的正方形CMEN 得面积,进而可求得阴影部分的面积.2π=,过C 分别作CM ⊥AE 于M ,CN ⊥BE 于N ,连接EC ,则四边形CMEN 是矩形, ∵C 是AB 的中点,∴∠AEC =①BEC ,即EC 平分∠AEB , ∴CM =CN ,∴四边形CMEN 是正方形, ∴∠CMG =∠MCN =①CNH ,∴∠MCG +∠GCN =①NCH +①GCN =90°, ∴∠MCG =①NCH , ∴△CMG ≌△CNH (ASA ),的正方形CMEN 的面积,∴空白部分面积为112=,∴阴影部分面积为21π2π-⨯=-, 故选:D .【点睛】本题考查扇形面积公式、圆的有关性质、角平分线的性质、正方形的判定与性质、全等三角形的判定与性质,熟记扇形面积公式,熟练掌握角平分线的性质定理和全等三角形的判定与性质,求出空白部分面积是解答的关键.变式1318. 如图,在Rt △ABC 中,∠C =90°,AB =6,AD 是∠BAC 的平分线,经过A ,D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.若圆半径为2,则阴影部分面积=_____.【答案】2 3【解析】【分析】连接OD,OF.首先证明OD∥AC,推出S阴影=S扇形OF A,再证明△AOF是等边三角形即可解决问题.【详解】解:连接OD,OF.∵AD是∠BAC的平分线,∴∠DAB=∠DAC,∵OD=OA,∴∠ODA=∠OAD,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴S①AFD=S①OFA,∴S阴影=S扇形OF A,∵OD=OA=2,AB=6,∴OB=4,∴OB =2OD , ∴∠B =30°, ∴∠BAC =60°, ∵OF =OA ,∴△AOF 是等边三角形, ∴∠AOF =60°,∴S 阴影=S 扇形OF A =260223603ππ⋅=. 故答案为:23π. 【点睛】本题考查扇形的面积,等边三角形的判定和性质,解直角三角形等知识,解题的关键是添加常用辅助线,运用转化的思想思考问题.变式1419. 如图,AB 是⊙O 的直径,E 是⊙O 上一点,AC 平分BAE ∠,过点C 作CD AE ⊥交AE 延长线于点D .(1)求证:CD 是⊙O 的切线;(2)若6AB =,30BAC ∠=︒,求阴影部分的面积. 【答案】(1)见解析;(2)3π2【解析】【分析】(1)连接OC ,根据等腰三角形的性质得到∠BAC =∠ACO ,推出AD //OC ,根据平行线的性质得到∠OCD =90°,于是得到CD 是⊙O 的切线; (2)求出∠OEA =∠EOC =60°,由扇形的面积公式可得出答案. 【详解】(1)连接OC , ∵OC =OA ,∴∠BAC =∠ACO , ∵AC 是∠BAD 的平分线, ∴∠DAC =∠BAC , ∴∠DAC =∠ACO , ∴AD //OC , ∴∠OCD +∠D =180°, ∵CD AE ⊥ ∴∠CDA =90°, ∴∠OCD =90°, ∴CD 是⊙O 的切线.(2)连接CE ,OE , ∵6AB =, ∴3OC OE ==,∵30BAC DAC ∠=∠=︒,OA OE =, ∴60OEA EOC ∠=∠=︒,AOE ∴和EOC △为等边三角形60OEC AOE EOC ∴∠=∠=∠=︒∴//CE AB , ∴CEO CAE S S =△△, ∴60π93π3602EOC S S ⋅⋅===阴扇.【点睛】本题考查了切线的判定与性质,等腰三角形的性质,扇形的面积的计算,正确的作出辅助线是解题的关键.方法五等积法特征:阴影部分图形在不改变面积的前提下,改变它的形状后,是一个常见图形.计算方法:=S S阴影常见图形一、平移法例题620. 直径为4 cm的圆O1,平移5 cm到圆O2,则图中阴影部分面积为( )A. 20 cm2B. 10 cm2C. 25 cm2D. 16 cm2【答案】A【解析】【详解】分析:通过平移,把⊙O2的半圆向左平移到⊙O1的位置,则圆中阴影部分面积等于一个矩形的面积,然后根据面积公式计算即可.详解:圆中阴影部分面积=5×4=20①cm2①①故选A①点睛:本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.二、旋转法例题7【2019·扬州】21. 如图,将四边形ABCD绕顶点A顺时针旋转45︒至四边形AB C D'''的位置,若4cmAB=,则图中阴影部分的面积为________2cm.【答案】2π【解析】【分析】由旋转的性质得:∠BAB'=45°,四边形AB'C'D'≌四边形ABCD,图中阴影部分的面积=四边形ABCD的面积+扇形ABB'的面积-四边形AB'C'D'的面积=扇形ABB'的面积,代入扇形面积公式计算即可.【详解】解:由旋转的性质得:∠BAB'=45°,四边形AB'C'D'≌四边形ABCD,则图中阴影部分的面积=四边形ABCD的面积+扇形ABB'的面积-四边形AB'C'D'的面积=扇形ABB'的面积=2 454 360π⨯=2π;故答案为:2π.【点睛】本题考查了旋转的性质、扇形面积公式;熟练掌握旋转的性质,得出阴影部分的面积=扇形ABB'的面积是解题的关键.变式1822. 如图,A,B,C,D,E相互外离,它们的半径都是2,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是()A. 6πB. 5πC. 4πD. 3π【答案】A 【解析】【分析】求出五个扇形的圆心角之和,利用扇形面积公式求解即可. 【详解】(52)180540-⨯︒=︒ ∴254026360S ππ=⨯= 故选A .【点睛】本题考查了多边形内角和,扇形面积公式,理解题意是解题的关键.变式1923. 如图,已知2),1),将△AOB 绕着点O 逆时针旋转,使点A旋转到点A′(-2,的位置,则图中阴影部分的面积为________.【答案】34π【解析】【详解】试题分析:①A (2)、B (1),①OA=4,①由A (2)使点A 旋转到点A′(﹣2,,①①A′OA=①B′OB=90°,根据旋转的性质可得,''OB C OBC S S ∆∆=,①阴影部分的面积等于S 扇形A'OA ﹣S 扇形C'OC =2211444ππ⨯-⨯=34π,故答案为34π.考点:1.扇形面积的计算;2.坐标与图形变化-旋转. 视频变式2024. 如图,在平面直角坐标系中,ABC 的三个顶点坐标分别为(1,1),(4,2),(3,4)A B C ---.(1)作出ABC 关于原点对称的111A B C △;(2)将ABC 绕点A 逆时针旋转90︒,根据三角形扫过的痕迹,求图中阴影部分的面积.【答案】(1)所作图形如图所示,见解析;(2)图中阴影部分的面积为134π. 【解析】【分析】(1)根据关于原点对称的点的坐标特征得到A 1、B 1、C 1,然后描点即可; (2)由题意,阴影部分的面积等于线段AC 绕点A 逆时针旋转90°所得到的扇形面积,即可求出答案.【详解】解:(1)所作图形如图所示:(2)由题意可知,∵AC ==所求阴影部分的面积等于线段AC 绕点A 逆时针旋转90°所得到的扇形面积:211344S ππ=⨯⨯=扇形. 【点睛】本题考查了作图——旋转变换,旋转的性质,熟练掌握网格结构准确找出对应点的位置是解题的关键.也考查了三角形的面积和扇形面积公式.三、对称法 ACDOAB S = ADC例题8【2018·山西】25. 如图,正方形ABCD 内接于①O①①O 的半径为2,以点A 为圆心,以AC 长为半径画弧交AB 的延长线于点E ,交AD 的延长线于点F ,则图中阴影部分的面积为( )A. 4π①4B. 4π①8C. 8π①4D. 8π①8【答案】A【解析】 【分析】利用对称性可知:阴影部分的面积=扇形AEF 的面积-△ABD 的面积.【详解】利用对称性可知:阴影部分的面积=扇形AEF 的面积-△ABD 的面积=290413602π⨯⨯-×4×2=4π-4① 故选A①【点睛】本题考查扇形的面积公式、正方形的性质等知识,解题的关键是学会用转化的思想思考问题.变式2126. 如图,AB 是圆O 的直径,弦CD ⊥AB ,∠BCD =30°,CD =S 阴影=_____.【答案】83π 【解析】【分析】根据垂径定理求得CE ED ==,然后由圆周角定理知∠DOE=60°,然后通过解直角三角形求得线段OD 、OE 的长度,最后将相关线段的长度代入S 阴影=S 扇形ODB -S △DOE +S △BEC .【详解】解:如图,假设线段CD 、AB 交于点E ,∵AB 是⊙O 的直径,弦CD ⊥AB ,∴CE =ED =又∵∠BCD =30°,∴∠DOE =2∠BCD =60°,∠ODE =30°,∴OE =DE•cot60°=2,OD =2OE =4, ∴S 阴影=S 扇形ODB ﹣S △DOE +S △BEC =2600D 118OE DE BE CE 360223ππ⨯-⨯+⋅=-=83π. 故答案为83π.【点睛】此题考查了垂径定理、扇形面积的计算,解题的关键是学会利用分割法求阴影部分面积,用转化的思想思考问题,属于中考常考题型.变式2227. 如图,在菱形ABCD 中,对角线AC 和BD 交于点O ,30ABD ∠=︒,4AB =,分别以点A 、点C 为圆心,以OA 的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为________.(结果保留π)【答案】43π 【解析】【分析】根据菱形的性质得到AC ⊥BD ,∠ABC =2∠ABD =60°,即可得出∠BAD =120°,根据直角三角形的性质求出AO 、BD ,根据扇形面积公式、三角形面积公式计算即可.【详解】解:∵四边形ABCD 是菱形,∠ABD =30°,∴AC ⊥BD ,∠ABC =2∠ABD =60°,∴∠BAD =120°,OA =12AB =12×4=2,由勾股定理得,OB =∴BD =∴阴影部分的面积=12×2120243603ππ⨯=,故答案为:43π. 【点睛】本题考查的是扇形面积计算、菱形的性质,掌握扇形面积公式是解题的关键.变式2328. 如图,平行四边形ABCD 中,AB=AC=4,AB①AC ,O 是对角线的交点,若①O 过A 、C 两点,则图中阴影部分的面积之和为_____.【答案】4.【解析】【详解】①①AOB=①COD ,①S 阴影=S ①AOB .①四边形ABCD 是平行四边形, ①OA=12AC=12×4=2. ①AB①AC , ①S 阴影=S ①AOB =12OA•AB=12×2×4=4. 【点睛】本题考查了扇形面积的计算.四、等底等高变形例题929. 如图,在Rt ABC 中,90C ∠=︒,6AB =,AD 是BAC ∠的平分线,经过A ,D 两点的圆的圆心O 恰好落在AB 上,O 分别与AB 、AC 相交于点E 、F .若圆半径为2.则阴影部分面积( ).A. 13π B. 43π C. 23π 3 【答案】C【解析】 【分析】连接OD ,OF .首先证明OD ∥AC ,推出S 阴=S 扇形OFA ,再证明△AOF 是等边三角形即可解决问题.【详解】解:连接OD ,OF .∵AD 是∠BAC 的平分线,∴∠DAB=∠DAC,∵OD=OA,∴∠ODA=∠OAD,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴S△AFD=S△OFA,∴S阴=S扇形OFA,∵OD=OA=2,AB=6,∴OB=4,∴OB=2OD,∴∠B=30°,∴∠A=60°,∵OF=OA,∴△AOF是等边三角形,∴∠AOF=60°,∴S阴=S扇形OFA=2 6022= 3603.故选:C.【点睛】本题考查扇形的面积,等边三角形的判定和性质,解直角三角形等知识,解题的关键是添加常用辅助线,用转化的思想思考问题.变式2430. 如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC①2,则图中阴影部分的面积为________①【答案】2 3π【解析】【详解】整体分析:连接OC①OB①则①OAB为等边三角形,由BC①OA①得S①OCB①S①PCB①把阴影部分的面积转化为扇形OBC的面积.解①连接OC①OB.①OB①OC①BC①2①①①OAB为等边三角形,①①COB①60°.∵BC①OA①①S①OCB①S①PCB①①S阴影①S扇形OBC①2602360π⨯①23π.变式2531. 如图,在半径为2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在弧QN 上有一动点P,且点P到弦MN所在直线的距离为x.(1)求弦MN的长;(2)试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围;(3)试分析比较,阴影部分面积y 与OMN S 扇形的大小关系.【答案】(1)MN =2;(2)2π023y x x =+-≤≤+;(3)见解析 【解析】【分析】①1)根据有一个角是60°的等腰三角形是等边三角形,可得出△OMN 是等边三角形,即OM=ON=MN =2,①2)根据三角形的面积公式,即可列出y、x 的函数关系式,①3①根据等底等高的三角形的面积相等,可以过点O 作OP′①MN ,以此线段为分界线进行分情况讨论.【详解】(1) ∵OM =ON ,∠MON =60°,∴△MON 是等边三角形,∴MN =OM =ON =2.(2) 作OH ⊥MN 于H 点,∴112MH MN ==.在Rt △OHN 中,222OH ON NH =- ,∴OH =.2π3OMN OMN S S S=-=-弓形扇形∴21π232PMN y S S x =+=⨯弓形,即2π023y x x =+≤≤+.(3) 令OMN y S =扇形,即22ππ33x +=,∴x =当x =,OMN y S =扇形;当0x ≤<,OMN y S <扇形;2x ≤+时,OMN y S >扇形.【点睛】本题主要考查了圆的综合题,解题时,利用了勾股定理、垂径定理、等边三角形的判定与性质以及扇形面积的计算,解决本题的关键是要熟练利用相关几何定理和性质.。
请计算六年级奥数阴影形状的面积。

请计算六年级奥数阴影形状的面积。
请计算六年级奥数阴影形状的面积介绍本文档将介绍如何计算六年级奥数题目中给定阴影形状的面积。
我们将使用简单的几何形状,并提供详细的步骤和计算公式。
计算步骤1. 确定阴影形状的几何形状类型。
常见的几何形状包括矩形、三角形和圆形。
2. 根据形状类型,选择相应的计算方法。
矩形的面积计算1. 矩形的面积计算公式为:面积 = 长 ×宽。
2. 如果题目已经给出了矩形的长度和宽度,则直接将两个数值相乘即可得到面积。
三角形的面积计算1. 三角形的面积计算公式为:面积 = 底 ×高 ÷ 2。
2. 如果题目已经给出了三角形的底和高,则将底和高相乘后再除以2即可得到面积。
圆形的面积计算1. 圆形的面积计算公式为:面积= π × 半径²,其中π 的近似值为3.14。
2. 如果题目已经给出了圆形的半径,则将半径的平方乘以π 即可得到面积。
示例题目题目一阴影部分是一个边长为5 cm的正方形,请计算该阴影形状的面积。
解答1. 根据题目描述,该阴影形状是一个正方形,边长为5 cm。
2. 使用矩形的面积计算公式,将边长相乘:面积 = 5 cm × 5 cm = 25 cm²。
3. 所以,该阴影形状的面积为25 cm²。
题目二阴影部分是一个底边长为10 cm、高为8 cm的三角形,请计算该阴影形状的面积。
解答1. 根据题目描述,该阴影形状是一个三角形,底边长为10 cm,高为8 cm。
2. 使用三角形的面积计算公式,将底和高相乘后再除以2:面积 = 10 cm × 8 cm ÷ 2 = 40 cm²。
3. 所以,该阴影形状的面积为40 cm²。
题目三阴影部分是一个半径为6 cm的圆形,请计算该阴影形状的面积。
解答1. 根据题目描述,该阴影形状是一个圆形,半径为6 cm。
2. 使用圆形的面积计算公式,将半径的平方乘以π:面积 =3.14 × 6 cm × 6 cm = 113.04 cm²。
六年级数学-不规则图形面积计算

实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
例2如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.
思路导航:
∵△ABE、△ADF与四边形AECF的面积彼此相等,
∴四边形 AECF的面积与△ABE、△ADF的面积都等于正方形ABCD的 。
在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,
∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。如右图那样重合.求重合部分(阴影部分)的面积。
思路导航:
在等腰直角三角形ABC中
∵AB=10
∵EF=BF=AB-AF=10-6=4,
∴阴影部分面积=S△ABG-S△BEF=25-8=17(平方厘米)。
例4如右图,A为△CDE的DE边上中点,BC=CD,若△ABC(阴影部分)面积为5平方厘米.
求△ABD及△ACE的面积.
思路导航:
取BD中点F,连结AF.因为△ADF、△ABF和△ABC等底、等高,
所以它们的面积相等,都等于5平方厘米.
一、 相加法:
这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.
不规则图形面积的计算

2、现在要给小路铺上地砖,如果9块 地砖正好铺1m2,那么至少需要多少 块地砖?
复习旧知:
平行四边形的面积=底×高 用字母表示为S=a×h 三角形面积=底×高÷2 用字母表示为S=a×h÷2 梯形面积=(上底+下底)×高÷2 用字母表示为S=(a+b)h÷2 长方形面积=长×宽用字母表示为S=a×b 正方形面积=边长×边长用字母表示为
S=a×a= a 2
下面是某自然保护区一个湖泊的平面图 (每个小方格表示1公顷)。你能估计这 个湖泊的面积大约是多少公顷吗?
你准备怎样估计?
先数整格,再数不满整格, 不满整格作半格计算。
不规则图形面积的计算
你还记得吗?
长 方 形 的 面 积 = 长 ×宽
S=ab
正 方 形 的 面 积 = 边长×边长
S=a×a
平行四边形的面积= 底×高
S=ah
三 角 形 的 面 积 = 底×高÷2
S=ah÷2
梯 形 的 面 积 = (上底+下底)×高÷2 S=(a+b)h÷2
生活中有许多不规则的图形
法计算组合图形面积.
作业
课本23页练习四1到4题
学校开运动会要制作一 些锦旗,式样如右图。 一面锦旗需要多少平方 厘米面料?
(60+45) ×(30÷2) ÷2×2 =105×15÷2×2 =1575(㎝²)
答:一面锦旗需要1575平方厘 米面料。
45cm 60cm
30cm
1、草坪的面积有多少平方米?
小 喷泉 湖
草坪
假山
游乐场
例如:华丰校园里有一块草坪(如图) 它的面积是多少平方米?
12m
4m 10m
方法一:分割法
小学六年级奥数专题训练:不规则图形的面积求法

一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
不规则图形面积的计算

2、现在要给小路铺上地砖,如果9块 地砖正好铺1m2,那么至少需要多少 块地砖?
下面是某自然保护区一个湖泊的平面图 (每个小方格表示1公顷)。你能估计这 个湖泊的面积大约是多少公顷吗?
你准备怎样估计?
先数整格,再数不满整格, 不满整格作半格计算。
答:这块草坪的面积是129㎡
方法二:分割法
12m
4m 10m
15m
草坪的面积=长方形的面积+三角形的面积
长方形的面积:12×10=120㎡
三角形的面积:15-12=3m,10-4=6m
3×6÷2=9㎡
草坪的面积:120+9=129㎡
答:这块草坪的面积是129㎡
12m
方法三:分割法 4m
法计算组合图形面积.
作业
课本23页练习四1到4题
学校开运动会要制作一 些锦旗,式样如右图。 一面锦旗需要多少平方 厘米面料?
(60+45) ×(30÷2) ÷2×2 =105×15÷2×2 =1575(㎝²)
答:一面锦旗需要1575平方厘 米面料。
45cm 60cm
30cm
1、草坪的面积有多少平方米?
10m
15m
草坪的面积=梯形面积+三角形面积 梯形的面积:(4+10)×12÷2=84㎡ 三角形的面积:10-4=6m,15×6÷2=45㎡ 草坪的面积:84+45=129㎡ 答:这块草坪的面积是129㎡
方法四:补的方法
12m
4m
10m
15m
草坪的面积=长方形的面积-梯形的面积 长方形的面积:15×10=150㎡ 梯形的面积:15-12=3m,(4+10) ×3÷2=21㎡ 草坪的面积:150-21=129㎡ 答:这块草坪的面积是129㎡.
不规则图形面积的计算

你还记得吗?
长 方 形 的 面 积 = 长 ×宽 正 方 形 的 面 积 = 边长×边长
S=ab
S=a×a S=ah S=ah÷2
平行四边形的面积= 底×高
三 角 形 的 面 积 = 底×高÷2
梯 形 的 面 积 = (上底+下底)×高÷2 S=(a+b)h÷2
生活中有许多不规则的图形
草坪
喷泉 小 湖
假山 游乐场
例如:华丰校园里有一块草坪(如图) 它的面积是多少平方米?
12m
4m
10m
方法一:分割法
15m
草坪的面积=长方形的面积+梯形的面积
长方形的面积:12×4=48㎡ 梯形的面积:10-4=6m (12+15) ×6=81㎡ 草坪的面积:48+81=129㎡ 答:这块草坪的面积是129㎡
正方形面积=边长×边长用字母表示为 2 S=a×a=
a
下面是某自然保护区一个湖泊的平面图 (每个小方格表示1公顷)。你能估计这 个湖泊的面积大约是多少公顷吗?
你准备怎样估计?
先数整格,再数不满整格, 不满整格作半格计算。
爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”
六年级奥数图形题2

六年级奥数图形题2例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了(如图)。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可(如图)。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了(如图)。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了(如图)。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如图)。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半(如图).七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形(如图)。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积(如图).九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB 在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积(如图)。
不规则图形面积的求法

不规则图形面积的求法求不规则图形面积的基本思路是通过分割、重叠、等积替换等方法把不规则图形转化为规则图形或规则图形面积的和差。
一、等积替换(1)三角形等积替换依据:等底等高的三角形面积相等或全等的三角形面积相等。
例1、如图1所示,半圆O 中,直径AB 长为4,C 、D 为半圆O 的三等分点.,求阴影部分的面积.解:连结OC 、OD , 由C 、D 为半圆O 的三等分点知:∠COD=60°,且∠ADC=∠DAB=30°, ∴CD ∥AB ,所以ODC ADC S S ∆∆=(同底等高的三角形面积相等)∴==扇形阴影O CD S S ππ323602602=⨯⨯例2、如图2所示,在矩形ABCD 中,AB=1,以AD 为直径的半圆与BC 切于M 点,求阴影部分面积.解:由AB =1,半圆与BC 相切,得AD =2 取AD 的中点O ,则OD =BM =1。
连结OM 交 BD 于E; 则△OED ≌△MEB∴MEB OED S S ∆∆= (全等三角形面积相等)∴==扇形阴影O M D S S 43601902ππ=⨯⨯ (2)弓形等积替换依据:等弧所对的弓形面积相等。
例3、 在RT △ABC 中,∠B=90°,AB=BC=4,AB 为直径的⊙O 交AC 于点D, 求图中两个阴影部分的面积之和.解:连结BD ,由AB 为⊙O 的直径得∠ADB =90°, RT △ABC 中∠B =90°AB =BC =4,得∠A =45°且AC=AD =BD =CD=∴A D BnD S S 弓形m 弓形=∴CDB 11S CD BD 422S ∆⨯⨯⨯阴影===例4、点A、B、C、D是圆周上四点,且 AB + CD= AC + BD , 弦AB=8,CD=4,求两个阴影部分的面积之和。
解:作⊙ O 的直径BE 连结AE ,则∠BAE =90°,AB AE =+半圆;A图2图4又∵ AB + CD= AC + BD = 1AB CD AC BD 2(+++)=半圆, ∴ AE = CD ,所以A E C DS m n S 弓形弓形=,AE=CD=4。
不规则图形面积的计算练习题及详细讲解教学提纲

精品文档第一讲不规则图形面积的计算(一)习题一(及详细答案)一、填空题(求下列各图中阴影部分的面积):二、解答题:1.如右图,ABCD为长方形,AB=10厘米,BC=6厘米,E、F分别为AB、AD中点,且FG=2GE.求阴影部分面积。
2.如右图,正方形ABCD与正方形DEFG的边长分别为12厘米和6厘米.求四边形CMGN(阴影部分)的面积.精品文档.精品文档3.如右图,正方形ABCD的边长为5厘米,△CEF的面积比△ADF的面积大5平方厘米.求CE的长。
4.如右图,已知CF=2DF,DE=EA,三角形BCF的面积为2,四边形BEDF的面积为4.求三角形ABE的面积.5.如右图,直角梯形ABCD的上底BC=10厘米,下底AD=14厘米,高CD=5厘米.又三角形ABF、三角形BCE和四边形BEDF的面积相等。
求三角形DEF的面积.6.如右图,四个一样大的长方形和一个小的正方形拼成一个大正方形,其中大、小正方形的面积分别是64平方米和9平方米.求长方形的长、宽各是多少?7.如右图,有一三角形纸片沿虚线折叠得到右下图,它的面积与原三角形面积之比为2:3,已知阴影部分的面积为5平方厘米.求原三角形面积.8.如右图,ABCD的边长BC=10,直角三角形BCE的直角边EC长8,已知阴影部分的面积比△EFG的面积大10.求CF的长.精品文档.精品文档习题一解答一、填空题:二、解答题:精品文档.精品文档厘米..CE=73可求出BE=12.所以CE=BE-5=7厘米.4.3.提示:加辅助线BD∴CE=4,DE=CD-CE=5-4=1。
同理AF=8,DF=AD-AF=14-8=6,6.如右图,大正方形边长等于长方形的长与宽的和.中间小正方形的边长等于长方形的长与宽的差.而大、小正方形的边长分别是8米和3米,所以长方形的宽为(8-3)÷2=2.5(米),长方形的长为8-2.5=5.5(米).7.15平方厘米.解:如右图,设折叠后重合部分的面积为x平方厘米,x=5.所以原三角形的面积为2×5+5=15平方厘米.精品文档.精品文档GEF S△∴阴影部分面积是:10x-40+阴影部分面积,+10=△由题意:S GEF. (厘米)x=5,∴10x-40=10精品文档.。
不规则图形面积的计算(方法总结及详解)

不规则图形计算的方法总结总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可.三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了.五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
几种不规则图形面积的解题方法

对于不规则图形面积的计算问题,一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出组合图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:(平方厘米)2.相加、相减求面积:这种方法是将组合图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出该图形的面积。
例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:5×5+4×4=41(平方厘米)三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)除了以上这两种方法,还有其他的几种方法,同学们不妨了解了解。
3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
例3:平行四边形ABCD的边BC长8厘米,直角三角形ECB的直角边EC长为6厘米。
已知阴影部分的总面积比三角形EFG的面积大8平方厘米,平行四边形ABCD的面积是多少?解答:阴影部分的总面积比三角形EFG的面积大8平方厘米,分别加上梯形FBCG,得出的平行四边形ABCD比三角形EBC的面积大8平方厘米。
平行四边形ABCD的面积:8×6÷2+8=32(平方厘米)4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
例4:下图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2平方厘米,CD的长是多少?解答:结合已知条件看图,很难有思路,连接DA,就可以发现:三角形ABE比三角形CDE的面积大2平方厘米,分别加上三角形DAE得到的三角形ABD比三角形CDA的面积大2平方厘米。
沪教版 六年级数学 不规则图形面积的求法

不规则图形面积的求法课前测试【题目】课前测试如图,已知大圆半径为6cm,四个小圆的面积相等,求阴影部分的面积是多少平方厘米?【答案】72【解析】试题分析:每个小圆中有两个空白椭圆形,将它们平均分成两部分,则圆中的阴影部分可以补到空白部分,那么每个小圆都可以是一样的操作,最后求3个小正方形的面积即可,正方形的面积=对角线×对角线÷2解答。
总结:本题通过割补法将不规则图形转化为规则图形求面积。
【难度】3【题目】课前测试四边形ABCD中,M为AB的中点,N为CD的中点,如果四边形ABCD的面积是80平方厘米,求阴影部分BNDM的面积是多少?【答案】40cm²【解析】试题分析:连接BD,由于M、N分别是AB、CD边的中点,根据三角形同底等高面积相等,则有三角形ADM的面积等于三角形BDM的面积,三角形BCN的面积等于三角形BDN的面积,因此阴影部分的面积就是四边形ABCD面积的一半。
总结:本题主要利用分割法以及三角形同底等高面积相等进行转化、计算。
【难度】3知识定位适用范围:沪教版,六年级,成绩中等以及中等以下知识点概述:不规则图形求面积是考题中常见的一种题型,我们要通过所学知识将不规则图形与规则图形建立联系求出面积,从中培可以养学生的语言表达能力和合作探究精神,发展学生思维的灵活性适用对象:成绩中等以及中等以下注意事项:大部分学生试听这个内容主要想听分割法、拼接法、填补法重点选讲:①分割法求面积②拼接法求面积③填补法求面积知识梳理知识梳理1:分割法求面积请回忆我们学过图形的面积公式:长方形面积=长×宽正方形面积=边长×边长平行四边形面积=底×高三角形面积=底×高÷2梯形面积=(上底+下底)×高÷2圆的面积=π×半径²扇形的面积=n°/360°×π×半径²分割法求面积:知识梳理2:拼接法求面积拼接法求面积:知识梳理3:填补法求面积例题精讲题型1:分割法求面积如图,已知三角形ABC的周长是30cm,三角形内一点到三角形三条边的距离都是3cm,求三角形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助
线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.
七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.
九、对称添补法:这种方法是作出原图形的对称图形,从而得到一
个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
十、重叠法:这种方法是将所求的图形看成是两个或两个以上图形的重叠部分,然后运用“容斥原理”(SA∪B=SA+SB-SA∩B)解决。
例如,欲求右图中阴影部分的面积,可先求两个扇形面积的和,减去正方形面积,因为阴影部分的面积恰好是两个扇形重叠的部分.。
