动态平衡中的三力问题宁波市鄞州中学
高中物理力学提升专题06三力动态平衡问题的处理技巧2

专题06 三力动态平衡问题的处理技巧【专题概述】在分析力的合成与分解问题的动态变化时,用公式法讨论有时很繁琐,而用作图法解决就比较直观、简单,但学生往往没有领会作图法的实质和技巧,或平时对作图法不够重视,导致解题时存在诸多问题.用图解法和相似三角形来探究力的合成与分解问题的动态变化有时可起到事半功倍的效果动态平衡”是指物体所受的力一部分是变力,是动态力,力的大小和方向均要发生变化,但变化过程中的每一时刻均可视为平衡状态,所以叫动态平衡,这是力平衡问题中的一类难题.解决这类问题的一般思路是:化“动”为“静”,“静”中求“动”,【典例精讲】1. 图解法解三力平衡图解法分析物体动态平衡问题时,一般物体只受三个力作用,且其中一个力大小、方向均不变,另一个力的方向不变,第三个力大小、方向均变化典例1如图所示,小球用细绳系住放在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,细绳上的拉力将( )A.逐渐增大 B.逐渐减小C.先增大后减小 D.先减小后增大【答案】D典例2、如图所示,一小球用轻绳悬于O点,用力F拉住小球,使悬线保持偏离竖直方向75°角,且小球始终处于平衡状态.为了使F有最小值,F与竖直方向的夹角θ应该是( )A.90° B.45° C.15° D.0°【答案】C2 . 相似三角形解动态一般物体只受三个力作用,且其中一个力大小、方向均不变,另外两个力的方向都在发生变化,此时就适合选择相似三角形来解题了,物体受到三个共点力的作用而处于平衡状态,画出其中任意两个力的合力与第三个力等值反向的平行四边形中,可能有力三角形与题设图中的几何三角形相似,进而得到力三角形与几何三角形对应边成比例,根据比值便可计算出未知力的大小与方向典例3 半径为R的球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,滑轮到球面B的距离为h,轻绳的一端系一小球,靠放在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止,如图所示,现缓慢地拉绳,在使小球由A到B的过程中,半球对小球的支持力F N和绳对小球的拉力F T的大小变化的情况是( )A. F N不变,F T变小B. F N不变, F T先变大后变小C. F N变小,F T先变小后变大D. F N变大,F T变小【答案】A【解析】以小球为研究对象,分析小球受力情况:重力G,细线的拉力F T和半球面的支持力F N,作出F N、F T的合力F,典例4 如图所示,不计重力的轻杆OP能以O为轴在竖直平面内自由转动,P端挂一重物,另用一根轻绳通过滑轮系住P端,当OP和竖直方向的夹角α缓慢增大时(0<α<π),OP杆所受作用力的大小( )A.恒定不变B.逐渐增大C.逐渐减小D.先增大后减小【答案】A【解析】在OP杆和竖直方向夹角α缓慢增大时(0<α<π),结点P在一系列不同位置处于静态平衡,以结点P为研究对象,如图甲所示,3. 辅助圆图解法典例5 如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA绳中的拉力F1和CB绳中的拉力F2的大小发生变化,即 ( )A.F1先变小后变大 B.F1先变大后变小C.F2逐渐减小 D.F2最后减小到零【答案】BCD【解析】从上述图中可以正确【答案】是:BCD【提升总结】用力的矢量三角形分析力的最小值问题的规律(1)若已知F合的方向、大小及一个分力F1的方向,则另一分力F2的最小值的条件为F1⊥F2;(2)若已知F合的方向及一个分力F1的大小、方向,则另一分力F2的最小值的条件为F2⊥F合。
2024届浙江省宁波市鄞州区东钱湖、李关弟、实验中学物理八下期末预测试题含解析

2024届浙江省宁波市鄞州区东钱湖、李关弟、实验中学物理八下期末预测试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、单选题1.放在水平桌面上的书,所受的力中属于平衡力的是[ ]A.书对桌面的压力与书所受的重力;B.书对桌面的压力与桌面对书的支持力;C.书所受的重力与桌面对书的支持力;D.书对桌面的压力加上书的重力与桌面对书的支持力.2.“估测”是物理学中常用的一种方法。
小华同学尝试估测了与自己身体相关的一些物理量,其中不合理的是A.脉搏跳动频率为68HzB.体积约为50LC.双脚站立时,对地面的压强约为1.5×104PaD.步行的速度约为4km/h3.如图所示,用力快速打击桌面上一摞相同棋子中间的某个,该棋子由静止开始沿水平方向飞出,则下列关于棋子的说法中正确的是A.没动的棋子惯性较大B.没动的棋子受到的重力较大C.棋子飞出过程中其惯性增大D.打击力改变了飞出棋子的运动状态4.中空的铁球、木球、铝球、铅球,形状完全相同,质量和外观体积都相等,则其中空心部分最大的是(ρ铅>ρ铁>ρ铝>ρ木)A.铁球B.铅球C.铝球D.木球5.关于力对物体做功,下列说法正确的是A.电灯吊挂在天花板上静止,拉力对电灯做了功B.从树上下落的苹果,重力对苹果做了功C.小球从斜面上向下滚动的过程中,支持力对小球做了功D.踢出去的足球,在水平地面上滚动,在滚动过程中,踢力对足球做了功6.下列实验中,没有采用控制变量法的是A.探究二力平衡的条件B.探究重力的大小跟质量的关系C.探究影响压力作用效果的因素D.探究物体的动能跟哪些因素有关7.如图所示,体重为510N的人,用滑轮组拉重500N的物体A沿水平方向以0.02m/s 的速度匀速运动.运动中物体A受到地面的摩擦阻力为200N.动滑轮重为20N(不计绳重和摩擦,地面上的定滑轮与物体A相连的绳子沿水平方向,地面上的定滑轮与动滑轮相连的绳子沿竖直方向,人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,).则下列计算结果中正确的是A.人对地面的压力为400NB.绳子自由端受到的拉力大小是100NC.人对地面的压力为250ND.绳子自由端运动速度是0.06m/s8.杜甫有诗云“八月秋高风怒号,卷我屋上三重茅”,秋风“卷”走屋顶茅草的原因是流过屋顶外侧的空气A.流速大,压强大B.流速大,压强小C.流速小,压强小D.流速小,压强大二、多选题9.只用量筒、长方体小木块、长细针、水、密度未知的盐水,能测出的物理量是(温馨提示:长方体小木块不吸水,ρ木<ρ水)()A.木块的质量B.木块的密度C.木块的高度D.盐水的密度10.小明沿水平方向推箱子前行,如图甲所示.推箱子过程中,其F﹣t和v﹣t的图象分别如图乙、丙所示.则下列判断正确的是A.0~3s,箱子受到地面的静摩擦力为3NB.t=5s时,箱子受到地面的滑动摩擦力为6NC.t=8s时,箱子受到的推力和摩擦力是一对平衡力D.9~12s,推力的功率为18W三、填空题11.如图所示,氦气球释放后,若它的运动可看成是匀速上升,则上升过程中氦气球的动能,机械能(均选填“增大”、“不变”或“减小”)。
动态平衡受力分析专题

专题动态平衡中的三力问题图解法分析动态平衡在相关物体平衡的问题中.冇一类涉及动态平衡c 这类问題中的一部分力足变力.是动态力.力的大小和方向 均耍发生变化.故这是力平衡问惣中的一类难趣c 縣决这类问题的一般思路足:把“动”化为“焙”,“焙”中 求“动”。
根据现行髙考耍求.物体受到往往足三个共点力问趣,利用三力平衡特点讨论动态平衡问题足力学 中一个重点和逼点.很多问学因不能学握其规律往往无从下手.很多多考书的讨论常忽略几中倩况.作者楚理 后介绍如下。
伶点:三用形图赛法则适用于物体所受的三个力中.冇一力的大小、方向均不变(通常为重力. 也可能是 其它力).另一个力的方向不变.大小变化. 笫三个力则大小、方向均发生变化的问题。
方独:先准确分折物体所受的三个力. 将三个力的矢好甘足相连构成闭合三用形。
然后将方向不变的力的 矢录延长. 根据物体所受三个力中二个力变化而又维対平衡关系时. 这个闭合三用形总足存升. 只不过形状发 生改变而已. 比校这些不间形状的矢母三用形.各力的大小及变化就一目了然了。
P 例1・1如ES 1所示.一个童力G 的匀质球放在光 滑斜面上.斜面倾用为.在斜面上升一光滑的不 计厚反的木板挡住球. 使之处于舲止状态° 今使 板与斜面的夹用媛慢增大.问:在此过程中.扌当 板和斜面对球的压力大小如何变化?鮮析:取球为研究对寥,如图1-2所示,球受还力 态.故三个力的合力始终为零,将三个力矢好构成封闭的三用形。
用的方向不变.但方向不变.始终与斜面垂Ac E 的大小、方向均改变. 瓯若挡板逆时针耳专动时.E 的方向也逆时针转动. 动态矢好三用形图1-3中一画 出的一系列虚线表示变化的庄Q 由此可知.E 先减小后增大.巧随增大而始终减小° 同ft典SSL :例1・2所示.小球械轻质细绳系若.斜吊若放在光滑斜面上.小球质好 为 m 9 斜面倾用为 夕.向右缓慢推动斜面,宜到细线与斜面平行. 在这个过程.中. 绳上张力、斜面对小球的支対力的变化倩况?(答案:绳上张力减小.斜面对小球 的支持力增大)轸点:相似三用形法适用于物体所受的三个力中. 一个力大小、方向不变. 其 它二个力的方向均发生变化,且三个力中没冇二力保持垂克关系.但能够找到力构成的矢好三用形相似的几何 三用形的问题 M3K :先准确分析物体的受力,画出受力分析EQ. 将三个力的矢漳首尾相连构成闭合三用开勺 卉寻找与 力的三用形相似的几何三用形.利用相似三用形的性质. 建立比例关系. 把力的大小变化问憑转化为几何三用 瑶析:取B0杆的B 端为研究对致.受到绳子拉力(大小为 R 、B0杆的支対力 尺料悬挂重物的绳子的拉力(大小 为G )的作用.将尺与G 合成.其合力与尸芳值反向.如图2-2所示.将三个力矢好构成封 闭的三用形(如图中画斜线部分),力的三用形与几何三用形OBA 相似.利用相似三用形对 应边成比例可得:(如图2-2所示.设A0高为圧B0长为厶 绳长厶)° _ /,_ F .式 H L I中 G H. Z 均不变,[遥渐变小,所以可知尺不变.尸逐渐变小。
2024届高考物理微专题:动态平衡问题

微专题13动态平衡问题1.三力动态平衡常用解析法、图解法、相似三角形法、正弦定理法等:(1)若一力恒定还有一个力方向不变,第三个力大小、方向都变时可用图解法;(2)若另两个力大小、方向都变,且有几何三角形与力的三角形相似的可用相似三角形法;(3)若另外两个力大小、方向都变,且知道力的三角形中各角的变化规律的可用正弦定理;(4)若另外两个力大小、方向都变,且这两个力的夹角不变的可用等效圆周角不变法或正弦定理.2.多力动态平衡问题常用解析法.1.光滑斜面上固定着一根刚性圆弧形细杆,小球通过轻绳与细杆相连,此时轻绳处于水平方向,球心恰位于圆弧形细杆的圆心处,如图所示.将悬点A 缓慢沿杆向上移动,直到轻绳处于竖直方向,在这个过程中,轻绳的拉力()A .逐渐增大B .大小不变C .先减小后增大D .先增大后减小答案C 解析方法一图解法:在悬点A 缓慢向上移动的过程中,小球始终处于平衡状态,小球所受重力mg 的大小和方向都不变,支持力的方向不变,对小球进行受力分析如图甲所示,由图可知,拉力F T 先减小后增大,C 正确.方法二解析法:如图乙所示,由正弦定理得F T sin α=mg sin β,得F T =mg sin αsin β,由于mg 和sin α不变,而sin β先增大后减小,可得F T 先减小后增大,C 正确.2.质量为m 的球置于倾角为θ的光滑固定斜面上,被与斜面垂直的光滑挡板挡着,如图所示.当挡板从图示位置沿逆时针缓慢转动至水平位置的过程中,挡板对球的弹力F N1和斜面对球的弹力F N2的变化情况是()A.F N1先增大后减小B.F N1先减小后增大C.F N2逐渐增大D.F N2逐渐减小答案D解析对球受力分析如图,当挡板逆时针缓慢转动到水平位置时,挡板对球的弹力逐渐增大,斜面对球的弹力逐渐减小,故选D.3.(2023·湖南郴州市质检)如图所示,斜面体置于粗糙水平面上,光滑小球被轻质细线系住放在斜面上,细线另一端跨过光滑定滑轮,用力拉细线使小球沿斜面缓慢向上移动一小段距离,斜面体始终静止.则在小球移动过程中()A.细线对小球的拉力变大B.斜面体对小球的支持力变大C.斜面体对地面的压力变大D.地面对斜面体的摩擦力变大答案A解析对小球受力分析并合成矢量三角形.如图所示,重力大小、方向不变,支持力方向不变,细线拉力方向由图甲中实线变为虚线,细线对小球的拉力增大,斜面体对小球的支持力减小,A正确,B错误;甲乙对斜面体受力分析,正交分解:F N′sinα=F f,F N地=F N′cosα+Mg,根据牛顿第三定律,小球对斜面体的压力F N′减小,所以地面对斜面体的摩擦力减小,地面对斜面体的支持力减小,根据牛顿第三定律,斜面体对地面的压力减小,C、D错误.4.(多选)(2023·安徽蚌埠市高三月考)如图,轻杆一端连在光滑的铰链上,另一端固定着质量为m的小球,初始时,在球上施加作用力F使杆处于水平静止,力F和杆的夹角α=120°.现保持α角不变,改变力F的大小缓慢向上旋转轻杆,直至杆与水平方向成60°角,在这个过程中()A.力F逐渐增大B.力F逐渐减小C.杆对小球的弹力先增大后减小D.杆对小球的弹力先减小后增大答案BD解析由于轻杆一端连在光滑的铰链上,故杆对小球的作用力始终沿着杆的方向,设转动过程中杆与竖直方向夹角为θ,由平衡条件可得,垂直杆方向满足F sin60°=mg sinθ,杆转过60°过程,θ从90°减小到30°,可知力F逐渐减小,A错误,B正确;沿杆方向满足F杆=F cosmg·sin(θ-60°),可知当θ=60°时,F杆=0,故θ60°-mg cosθ,联立上述两式可得F杆=233从90°减小到30°的过程,杆对小球的弹力先减小为零后反向增大,C错误,D正确.5.在一些地表矿的开采点,有一些简易的举升机械,利用图示装置,通过轻绳和滑轮提升重物.轻绳a端固定在井壁的M点,另一端系在光滑的轻质滑环N上,滑环N套在光滑竖直杆上.轻绳b的下端系在滑环N上并绕过定滑轮.滑轮和绳的摩擦不计.在右侧地面上拉动轻绳b使重物缓慢上升过程中,下列说法正确的是()A.绳a的拉力变大B.绳b的拉力变大C.杆对滑环的弹力变大D.绳b的拉力始终比绳a的小答案D解析设a绳子总长为L,左端井壁与竖直杆之间的距离为d,动滑轮左侧绳长为L1,右侧绳长为L2.由于绳子a上的拉力处处相等,所以两绳与竖直方向夹角相等,设为θ则由几何知识,得d =L 1sin θ+L 2sin θ=(L 1+L 2)sin θ,L 1+L 2=L 得到sin θ=d L,当滑环N 缓慢向上移动时,d 、L 没有变化,则θ不变.绳子a 的拉力大小为F T1,重物的重力为G .以动滑轮为研究对象,根据平衡条件得2F T1cos θ=G ,解得F T1=G 2cos θ,故当θ不变时,绳子a 拉力F T1不变,A 错误;以滑环N 为研究对象,绳b 的拉力为F T2,则F T2=F T1cos θ保持不变;杆对滑环的弹力F N =F T1sin θ保持不变,B 、C 错误;绳b 的拉力F T2=F T1cos θ,所以绳b 的拉力F T2始终比绳a 的拉力F T1小,D 正确.6.某小区晾晒区的并排等高门形晾衣架A ′ABB ′-C ′CDD ′如图所示,AB 、CD 杆均水平,不可伸长的轻绳的一端M 固定在AB 中点上,另一端N 系在C 点,一衣架(含所挂衣物)的挂钩可在轻绳上无摩擦滑动.将轻绳N 端从C 点沿CD 方向缓慢移动至D 点,整个过程中衣物始终没有着地.则此过程中轻绳上张力大小的变化情况是()A .一直减小B .先减小后增大C .一直增大D .先增大后减小答案B 解析轻绳N 端由C 点沿CD 方向缓慢移动至D 点的过程中,衣架两侧轻绳与水平方向的夹角先增大后减小,设该夹角为θ,轻绳上的张力为F ,由平衡条件有2F sin θ=mg ,故F =mg 2sin θ,可见张力大小先减小后增大,B 项正确.7.如图所示,半径为R 的圆环竖直放置,长度为R 的不可伸长的轻细绳OA 、OB ,一端固定在圆环上,另一端在圆心O 处连接并悬挂一质量为m 的重物,初始时OA 绳处于水平状态,把圆环沿地面向右缓慢转动,直到OA 绳处于竖直状态,在这个过程中()A .OA 绳的拉力逐渐增大B .OA 绳的拉力先增大后减小C .OB 绳的拉力先增大后减小D .OB 绳的拉力先减小后增大答案B 解析以重物为研究对象,重物受到重力mg 、OA 绳的拉力F 1、OB 绳的拉力F 2三个力而平衡,构成矢量三角形,置于几何圆中如图所示.在转动的过程中,OA 绳的拉力F 1先增大,转过直径后开始减小,OB 绳的拉力F 2开始处于直径上,转动后一直减小,B 正确,A 、C 、D 错误.8.(2023·山东青岛市模拟)我国的新疆棉以绒长、品质好、产量高著称于世,目前新疆地区的棉田大部分是通过如图甲所示的自动采棉机采收.自动采棉机在采摘棉花的同时将棉花打包成圆柱形棉包,通过采棉机后侧可以旋转的支架平稳将其放下,这个过程可以简化为如图乙所示模型:质量为m 的棉包放在“V ”型挡板上,两板间夹角为120°固定不变,“V ”型挡板可绕O 轴在竖直面内转动.在使OB 板由水平位置顺时针缓慢转动到竖直位置过程中,忽略“V ”型挡板对棉包的摩擦力,已知重力加速度为g ,下列说法正确的是()A .棉包对OA 板的压力逐渐增大B .棉包对OB 板的压力先增大后减小C .当OB 板转过30°时,棉包对OB 板的作用力大小为mgD .当OB 板转过60°时,棉包对OA 板的作用力大小为mg答案D 解析对棉包受力分析如图,(a)由正弦定理可得mg sin 120°=F OB sin β=F OA sin α,棉包在旋转过程中α从0逐渐变大,β从60°逐渐减小,因此OB 板由水平位置缓慢转动60°过程中,棉包对OA 板压力逐渐增大,对OB 板压力逐渐减小;OB 板继续转动直至竖直的过程中,棉包脱离OB 板并沿OA 板滑下,棉包对OA 板压(b)力随板转动逐渐减小,故A 、B 错误;当OB 板转过30°时,两板与水平方向夹角均为30°,两板支持力大小相等,与竖直方向夹角为30°,如图(b),可得F OA ′=F OB ′=33mg ,故C 错误;当OB 板转过60°时,OA 板处于水平位置,棉包只受到受力和OA 板的支持力,由二力平衡得F OA ″=mg ,故D 正确.9.(2023·上海市模拟)如图所示,细绳一端固定在A 点,另一端跨过与A 等高的光滑定滑轮B 后悬挂一个砂桶Q (含砂子).现有另一个砂桶P (含砂子)通过光滑挂钩挂在A 、B 之间的细绳上,稳定后挂钩下降至C 点,∠ACB =120°,下列说法正确的是()A .若只增加Q 桶中的砂子,再次平衡后P 桶位置不变B .若只增加P 桶中的砂子,再次平衡后P 桶位置不变C .若在两桶内增加相同质量的砂子,再次平衡后P 桶位置不变D .若在两桶内增加相同质量的砂子,再次平衡后Q 桶位置上升答案C 解析对砂桶Q 分析有,Q 受到细绳的拉力大小F T =G Q ,设AC 、BC 之间的夹角为θ,对C点分析可知C 点受三个力而平衡,由题意知,C 点两侧的绳张力相等,故有2F T cosθ2=G P ,联立可得2G Q cos θ2=G P ,故只增加Q 桶中的砂子,即只增加G Q ,夹角θ变大,P 桶上升,只增加P 桶中的砂子,即只增加G P ,夹角θ变小,P 桶下降,故A 、B 错误;由2G Q cosθ2=G P ,可知,当θ=120°时有G Q =G P ,此时若在两砂桶内增加相同质量的砂子,上式依然成立,则P 桶的位置不变,故C 正确,D 错误.10.如图所示,一光滑的轻滑轮用细绳OO ′悬挂于O 点.另一细绳跨过滑轮,左端悬挂物块a ,右端系一位于水平粗糙桌面上的物块b .外力F 向右上方拉b ,整个系统处于静止状态.若保持F 的方向不变,逐渐增大F 的大小,物块b 仍保持静止状态,则下列说法中正确的是()A .桌面受到的压力逐渐增大B.连接物块a、b的绳子张力逐渐减小C.物块b与桌面间的摩擦力一定逐渐增大D.悬挂于O点的细绳OO′中的张力保持不变答案D解析由于整个系统处于静止状态,所以滑轮两侧连接a和b的绳子的夹角不变;物块a只受重力以及绳子的拉力,由于物块a平衡,则连接a和b的绳子张力F T保持不变;由于绳子的张力及夹角均不变,所以OO′中的张力保持不变,B错误,D正确;对b分析可知,b处于静止即平衡状态,设绳子和水平方向的夹角为θ,力F和水平方向的夹角为α,对b受力分析,由平衡条件可得F N+F sinα+F T sinθ=mg,可得F N=mg-F sinα-F T sinθ,θ与α均保持不变,绳子拉力不变,力F增大,则桌面给物块b的支持力减小,根据牛顿第三定律,桌面受到的压力逐渐减小;在水平方向上,当力F的水平分力大于和绳子拉力F T的水平分力时,则有F cosα=F f+F T cosθ,此时摩擦力随着F增大而增大,当力F的水平分力小于和绳子拉力的水平分力时,则有F cosα+F f=F T cosθ,此时摩擦力随着F的增大而减小,A、C错误.11.(多选)(2023·陕西渭南市模拟)质量为m的物体,放在质量为M的斜面(倾角为α)体上,斜面体放在水平粗糙的地面上,物体和斜面体均处于静止状态,如图所示.当在物体上施加一个水平力F,且F由零逐渐加大到F m的过程中,物体和斜面体仍保持静止状态.在此过程中,下列判断正确的是()A.斜面体对物体的支持力逐渐增大B.斜面体对物体的摩擦力逐渐增大C.地面受到的压力逐渐增大D.地面对斜面体的摩擦力由零逐渐增大到F m答案AD解析对物体进行研究,物体受到重力mg、水平推力F、斜面的支持力F N1(如图甲,摩擦力F f1不确定)当F=0时,物体受到的静摩擦力大小为F f1=mg sinα,方向沿斜面向上,支持力F N1=mg cos α.在F不为零时,斜面体对物体的支持力F N1=mg cosα+F sinα,所以支持力逐渐增大;对于静摩擦力,当F cosα≤mg sinα时,静摩擦力大小F f1=mg sinα-F cosα,可见随F的增大而减小,当F cos α>mg sin α时,静摩擦力F f1=F cos α-mg sin α,随F 的增大而增大,故A 正确,B 错误;对于整体,受到总重力(M +m )g 、地面的支持力F N2、静摩擦力F f2和水平推力F ,如图乙,由平衡条件得F N2=(m +M )g ,地面的摩擦力F f2=F ,可见,当F 增大时,F f2逐渐增大.由牛顿第三定律得知,地面受到的压力保持不变,地面对斜面体的摩擦力由零逐渐增大到F m ,故C 错误,D 正确.12.(2023·河南洛阳市模拟)《大国工匠》节目中讲述了王进利用“秋千法”在1000kV 的高压线上带电作业的过程.如图所示,绝缘轻绳OD 一端固定在高压线杆塔上的O 点,另一端固定在兜篮D 上.另一绝缘轻绳跨过固定在杆塔上C 点的定滑轮,一端连接兜篮,另一端由工人控制.身穿屏蔽服的王进坐在兜篮里,缓慢地从C 点运动到处于O 点正下方E 点的电缆处.绳OD 一直处于伸直状态,兜篮、王进及携带的设备总质量为m ,可看作质点,不计一切阻力,重力加速度大小为g .关于王进从C 点缓慢运动到E 点的过程中,下列说法正确的是()A .绳OD 的拉力一直变小B .工人对绳的拉力一直变大C .OD 、CD 两绳拉力的合力小于mgD .当绳CD 与竖直方向的夹角为30°时,工人对绳的拉力为33mg 答案D 解析对兜篮、王进及携带的设备整体受力分析,绳OD 的拉力为F 1,与竖直方向的夹角为θ;绳CD 的拉力为F 2,与竖直方向的夹角为α,则由几何关系得α=45°-θ2.由正弦定理可得F 1sin α=F 2sin θ=mg sin π2+α ,解得F 1=mg tan α,F 2=mg sin θcos α=mg cos 2αcos α=mg (2cos α-1cos α),α增大,θ减小,则F 1增大,F 2减小,A 、B 错误;两绳拉力的合力大小等于mg ,C 错误;当α=30°时,则θ=30°,根据平衡条件有2F 2cos 30°=mg ,可得F 2=33mg ,D 正确.。
一道动态平衡高考题的两种解法

一道动态平衡高考题的两种解法作者:张守柏来源:《新课程》2021年第23期在物體平衡问题中,有一类动态平衡问题,这类问题的特点是一部分力是变力,是动态力,力的大小和方向随平衡态发生变化。
这类题目难度大,对学生而言是一个难点,但是在高考中考查频率非常高。
解决物体动态平衡问题时,我们常用的方法有数学解析法、三角形图解法、相似三角形法等。
但在动态平衡问题中有一种情形:在三个共点力作用下而处于平衡状态的物体,这三个共点力其中有一个力是大小和方向都保持不变的恒力,而另外两个力的大小和方向都随平衡态发生变化,但这两个力的夹角(不等于90°)保持不变。
这种动态平衡问题,解题的难度最大,若找不到恰当的解法则很难解答,尤其若采用以上常规解法来解,则难以解决,但此时若用数学知识正弦定理或三角形外接圆法则就容易多了。
用数学知识来解决物理问题,这正是高考对学生的一种基本能力的考查要求。
因此,我们在教学过程中应该加强对学生这一能力的培养。
下面我以2017年理综全国卷Ⅰ第21题为例加以说明。
题目:(多选)现有一柔软轻质细绳ON的O端点固定不动,在细绳中间某处M点拴一重物,用手拉住绳的另一端点N。
如图1所示,开始时,绳OM段保持竖直状态,绳MN段则刚好被拉直,绳OM与MN之间的夹角为α(其中角α>90°)。
现将重物向右上方缓慢拉起,但保持夹角α不变,直到绳OM被拉至水平,则在此过程中下列说法正确的是()A.绳OM段的拉力先变小后变大B.绳MN段的拉力逐渐变大C.绳OM段的拉力先变大后变小D.绳MN段的拉力保持不变解法一:利用数学知识——正弦定理基本思路:如图2所示,当物体受到三个共点力作用而保持平衡状态时,这三个力就可以构成一个封闭的三角形,那么此时这三个共点力中任何一个力的大小与这力所对角的补角的正弦值之比都相等,即有下面我们就用此种方法来解答,具体解法如下:解法二:作三角形外接圆解题思路:当物体受到三个共点力作用而处于平衡状态时,这三个共点力可以构成一个封闭的三角形,这个三角形就有一个对应外接圆。
微专题13 解决”动态平衡“问题的几种方法

1.三力动态平衡常用图解法、相似三角形法、正弦定理法、等效圆周角不变法等,三个力中重力一般不变:(1)若还有一个力方向不变,第三个力大小方向都变时可用图解法;(2)若另外两个力大小方向都变,且有几何三角形与力的三角形相似的可用相似三角形法;(3)若另外两个力大小方向都变,且知道力的三角形中各角的变化规律的可用正弦定理;(4)若另外两个力大小方向都变,且这两个力的夹角不变的可用等效圆周角不变法或正弦定理.2.多力动态平衡问题常用解析法.3.涉及到摩擦力的时候要注意静摩擦力与滑动摩擦力的转换.1.(2019·重庆市沙坪坝等主城六区第一次调研抽测)如图1,轻绳一端系在小球A上,另一端系在圆环B上,B套在粗糙水平杆PQ上.现用水平力F作用在A上,使A从图中实线位置(轻绳竖直)缓慢上升到虚线位置,但B仍保持在原来位置不动.则在这一过程中,杆对B的摩擦力F1、杆对B的支持力F2、绳对B的拉力F3的变化情况分别是()图1A.F1逐渐增大,F2保持不变,F3逐渐增大B.F1逐渐增大,F2逐渐增大,F3逐渐增大C.F1保持不变,F2逐渐增大,F3逐渐减小D.F1逐渐减小,F2逐渐减小,F3保持不变2.(2020·河北衡水中学调研)如图2所示,有一质量不计的杆AO,长为R,可绕A自由转动,用轻绳在O点悬挂一个重力为G的物体,另一根轻绳一端系在O点,O点为圆弧的圆心,另一端系在圆弧形墙壁上的C点,当该轻绳端点由点C逐渐沿圆弧CB向上移动的过程中(保持OA与地面夹角θ不变),OC绳拉力的大小变化情况是()图2A.逐渐减小B.逐渐增大C.先减小后增大D.先增大后减小3.(多选)(2017·全国卷Ⅰ·21)如图3,图3柔软轻绳ON 的一端O 固定,其中间某点M 拴一重物,用手拉住绳的另一端N .初始时,OM竖直且MN 被拉直,OM 与MN 之间的夹角为α(α>π2).现将重物向右上方缓慢拉起,并保持夹角α不变.在OM 由竖直被拉到水平的过程中( )A .MN 上的张力逐渐增大B .MN 上的张力先增大后减小C .OM 上的张力逐渐增大D .OM 上的张力先增大后减小4.(2019·山东大联考三模)如图4,用硬铁丝弯成的光滑半圆环竖直放置,直径竖直,O 为圆心,最高点B 处固定一光滑轻质滑轮,质量为m 的小环A 穿在半圆环上.现用细线一端拴在A 上,另一端跨过滑轮用力F 拉动,使A 缓慢向上移动.小环A 及滑轮B 大小不计,在移动过程中,关于拉力F 以及半圆环对A 的弹力N 的说法正确的是( )图4A .F 逐渐增大B .N 方向始终指向圆心OC .N 逐渐变小D .N 大小不变5.(多选)(2019·山东烟台市第一学期期末)如图5所示,一质量为m 、半径为r 的光滑球A 用细绳悬挂于O 点,另一质量为M 、半径为R 的半球形物体B 被夹在竖直墙壁和A 球之间,B 的球心到O 点之间的距离为h ,A 、B 的球心在同一水平线上,A 、B 处于静止状态.重力加速度为g .则下列说法正确的是( )图5A .A 对B 的压力大小为R +r hmg B .竖直墙壁对B 的摩擦力可能为零C .当只轻轻把球B 向下移动一点距离,若A 、B 再次保持静止,则A 对B 的压力大小保持不变,细绳拉力增大D .当只轻轻把球B 向下移动一点距离,若A 、B 再次保持静止,则A 对B 的压力减小,细绳拉力减小6.(2020·河南开封市模拟)在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A ,A 与竖直墙之间放另一截面也为半圆的光滑柱状物体B ,整个装置处于静止状态,截面如图6所示.设墙对B 的作用力为F 1,B 对A 的作用力为F 2,地面对A 的作用力为F 3.在B 上加一物体C ,整个装置仍保持静止,则( )图6A.F1保持不变,F3增大B.F1增大,F3保持不变C.F2增大,F3增大D.F2增大,F3保持不变7.(多选)(2019·安徽省A10联盟开年考)如图7,倾角为30°的斜面体放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的柔软轻绳与小球B连接,O点为轻绳与定滑轮的接触点.初始时,小球B在水平向右的拉力F作用下使轻绳OB段与水平拉力F的夹角θ=120°,整个系统处于静止状态.现将小球向右上方缓慢拉起,并保持夹角θ不变,从初始到轻绳OB段水平的过程中,斜面体与物块A均保持静止不动,则在此过程中()图7A.拉力F逐渐增大B.轻绳上的张力先增大后减小C.地面对斜面体的支持力逐渐增大D.地面对斜面体的摩擦力先增大后减小8.(2019·湖南衡阳市第一次联考)如图8所示的装置中,在A端用外力F把一个质量为m的小球沿倾角为30°的光滑斜面匀速向上拉动,已知在小球匀速运动的过程中,拴在小球上的绳子与水平固定杆之间的夹角从45°变为90°,斜面体与水平地面之间是粗糙的,并且斜面体一直静止在水平地面上,不计滑轮与绳子之间的摩擦.则在小球匀速运动的过程中,下列说法正确的是()图8A.外力F一定增大B.地面对斜面体的静摩擦力始终为零C.绳子对水平杆上的滑轮的合力一定大于绳子的拉力D.绳子A端移动的速度大小等于小球沿斜面运动的速度大小9.(2019·湖北省黄冈中学第三次模拟)哥伦比亚大学的工程师研究出一种可以用于人形机器人的合成肌肉,可模仿人体肌肉做出推、拉、弯曲和扭曲等动作.如图9所示,连接质量为m 的物体的足够长细绳ab一端固定于墙壁,用合成肌肉做成的“手臂”ced的d端固定一滑轮,c端固定于墙壁,细绳绕过滑轮,c和e类似于人手臂的关节,由“手臂”合成肌肉控制.设cd与竖直墙壁ac夹角为θ,不计滑轮与细绳的摩擦,下列说法正确的是()图9A.若保持θ不变,增大cd长度,细绳ad部分拉力变大B.若保持θ=90°,增大cd长度,细绳对滑轮的力始终沿dc方向C.若保持ac等于ad,增大cd长度,细绳对滑轮的力始终沿dc方向D.若θ从90°逐渐变为零,cd长度不变,且保持ac>cd,则细绳对滑轮的力先减小后增大10.(2020·山东临沂市质检)如图10所示,一光滑的轻滑轮用细绳OO′悬挂于O点;另一细绳跨过滑轮,其一端悬挂质量为m的物块A,另一端系一位于固定光滑斜面上的质量为2m 的物块B,斜面倾角θ=45°,外力F沿斜面向上拉物块B,使物块B由滑轮正下方位置缓慢运动到和滑轮等高的位置,则()图10A.细绳OO′的拉力逐渐增大B.细绳对物块B的拉力逐渐变大C.斜面对物块B的支持力逐渐变大D.外力F逐渐变大11.(2019·安徽省皖北协作区联考)如图11所示,两块固定且相互垂直的光滑挡板POQ,OP 竖直放置,OQ水平,小球a、b固定在轻弹簧的两端,现有一个水平向左的推力,作用于b 上,使a、b紧靠挡板处于静止状态.现用力F推动小球b,使之缓缓到达b′位置,则()图11A.推力F变大B.b对OQ的压力变大C.弹簧长度变短D.弹簧长度变长12.(多选)(2019·湖南长沙一中月考)《大国工匠》节目中讲述了王进利用“秋千法”在1 000 kV的高压线上带电作业的过程.如图12所示,绝缘轻绳OD一端固定在高压线杆塔上的O点,另一端固定在兜篮上.另一绝缘轻绳跨过固定在杆塔上C点的定滑轮,一端连接兜篮,另一端由工人控制.身穿屏蔽服的王进坐在兜篮里,缓慢地从C点运动到处于O点正下方E点的电缆处.绳OD一直处于伸直状态,兜篮、王进及携带的设备总质量为m,不计一切阻力,重力加速度大小为g.关于王进从C点运动到E点的过程中,下列说法正确的是()图12 A.工人对绳的拉力一直变大B.绳OD的拉力一直变小C.OD、CD两绳拉力的合力大小等于mgD.当绳CD与竖直方向的夹角为30°时,工人对绳的拉力为33mg答案精析1.A[设小球A的质量为m,圆环B的质量为M,对A受力分析,如图甲所示,甲乙由平衡条件可得F3′cos α=mg,F=mg tan α,故随α增大,F增大,则F3′增大,即F3增大;再对两者的整体受力分析,如图乙所示,有:F1=F,F2=(M+m)g,则F2不变,F1增大,故选A.]2.C[对物体受力分析,物体受力平衡,则竖直绳的拉力等于物体的重力G,故竖直绳的拉力不变;再对O点分析,O点总受竖直绳的拉力、OA的支持力F及OC绳的拉力而处于平衡状态,受力分析如图所示,F和OC绳的拉力的合力与G大小相等,方向相反,则在OC绳端点上移的过程中,平行四边形的对角线保持不变,由图可知OC绳的拉力先减小后增大,故C正确.]3.AD[以重物为研究对象,受重力mg、OM绳上拉力F2、MN上拉力F1,由题意知,三个力的合力始终为零,矢量三角形如图所示,F1、F2的夹角为π-α不变,在F2转至水平的过程中,矢量三角形在同一外接圆上,由图可知,MN上的张力F1逐渐增大,OM上的张力F2先增大后减小,所以A、D正确,B、C错误.]4.D [在小环A 缓慢向上移动的过程中,小圆环A 处于三力平衡状态,根据平衡条件知mg 与N 的合力与T 等大反向共线,作出mg 与N 的合力,如图,由三角形相似得:mg BO =N OA =T AB由于最高点B 处固定一光滑轻质滑轮,则F =T ,可得:F =T =AB BOmg ,AB 变小,BO 不变,则F 变小,故A 错误;N =OA BOmg ,AO 、BO 都不变,则N 不变,方向始终背离圆心,故B 、C 错误,D 正确.]5.AD [分析A 球的受力情况,如图所示,N 与mg 的合力与T 等大反向共线,根据两个阴影三角形相似有:N R +r =mg h =T OA,得:N =R +r h mg ,T =OA h mg ,由牛顿第三定律知A 对B 的压力大小为:N ′=N =R +r hmg ,故A 正确;B 在竖直方向受到重力,而A 、B 间无摩擦,由平衡条件知竖直墙壁对B 一定有摩擦力,故B 错误;当只轻轻把球B 向下移动一点距离,分析A 球的受力情况,如图乙所示:N 与T 的合力与mg 等大反向共线,根据两个阴影三角形相似得:N R +r =mg L =T OA可得:N =R +r L mg ,T =OA Lmg ,由于L >h ,可知,N 减小,T 减小,由牛顿第三定律知A 对B 的压力减小,故C 错误,D 正确.]6.C [先对B 、C 整体受力分析,受重力、墙壁支持力和A 的支持力,根据平衡条件,三个力可以构成首尾相连的矢量三角形,如图所示,在B上加一C物体,相当于整体的重力增加了,故墙对B的作用力F1增加,A对B的支持力也增加,根据牛顿第三定律,B对A的作用力F2增加;再对A、B、C整体分析,受重力、地面的支持力、地面的静摩擦力、墙壁的支持力,根据平衡条件,地面的支持力等于整体的重力,故加上C物体后,地面的支持力和摩擦力均变大,则F3变大,故A、B、D错误,C 正确.]7.AD[小球B受重力mg、轻绳OB的拉力T和拉力F,由题意可知,三个力的合力始终为零,矢量三角形如图.在T转至水平的过程中,轻绳OB的拉力T逐渐减小,拉力F逐渐变大,故选项A正确,B 错误;整体(含斜面体,物块A和小球B)受向下的重力,向上的支持力,向左的摩擦力和拉力四个力的作用,根据小球的受力分析可知,拉力F的竖直分力逐渐增大,水平分力先增大后减小,所以支持力逐渐减小,摩擦力先增大后减小,故选项C错误,D正确.]8.A9.C[细绳ad、bd的拉力大小等于物体的重力,如终不变,选项A错误;若保持θ=90°,因T ad=T db=mg,则ad绳和bd绳拉力的合力方向指向左下方∠adb角平分线的方向,则细绳对滑轮的力方向指向左下方,不沿dc方向,选项B错误;若保持ac=ad,则∠acd=∠adc =∠cdb,则此时ad绳和bd绳拉力的合力方向沿dc方向,即使增大cd长度,上述关系仍然不变,即细绳对滑轮的力始终沿dc方向,选项C正确;若θ从90°逐渐变为零,cd长度不变,且保持ac>cd,则ad与ac的夹角先增大后减小,ad与db的夹角先减小后增大,则ad绳和bd绳拉力的合力先增大后减小,即细绳对滑轮的力先增大后减小,选项D错误.]10.D[由题可知,物块缓慢移动整体都处于平衡状态,则绳OO′的拉力等于下面绳对A的拉力和绳对B的拉力的合力,由于绳对A的拉力和绳对B的拉力大小相等,都等于物块A 的重力的大小,但是由于物块B上移,导致二者之间的夹角变大,则根据平行四边形定则可知合力变小,即绳OO′的拉力逐渐减小,故选项A、B错误;物块B未运动前,对物块B 受力分析如图所示,当物块B上移时,α先减小后增大,在垂直斜面方向根据平衡方程可知:斜面对物块B的支持力先减小后增大,在沿斜面方向根据平衡条件可知外力F逐渐变大,故选项C错误,D正确.]11.D [隔离a 分析受力,设此时a 、b 间作用力与水平方向的夹角为θ,如图甲所示,由力的平衡条件可得:F ′=mg sin θ,N =mg tan θ小球到达b ′位置,当a 、b 重新处于静止状态时,由几何关系可知,θ增大,则sin θ、tan θ增大,F ′减小,N 减小,根据胡克定律可知弹簧的形变量变小,所以弹簧长度变长,故D 正确,C 错误;对a 、b 的整体受力分析如图乙所示:由共点力的平衡条件可知,a 、b 重新处于静止状态前后,OQ 挡板对b 的支持力始终和a 、b 的总重力大小相等,保持不变,推力F =N 在减小,故A 、B 错误.]12.CD [对兜篮、王进及携带的设备整体受力分析如图所示,绳OD 的拉力为F 1,与竖直方向的夹角为θ,绳CD 的拉力为F 2,与竖直方向的夹角为α.根据几何知识可知θ+2α=90°,由正弦定理可得,F 1sin α=F 2sin θ=mg sin ()180°-θ-α=mg sin (90°+α),王进从C 点运动到E 点的过程中,α增大,θ减小,则F 1增大,F 2减小,选项A 、B 错误;两绳拉力的合力大小等于mg ,选项C 正确;当绳CD 与竖直方向的夹角为α=30°时,θ=30°,2F 2cos 30°=mg ,可得F 2=33mg ,即工人对绳的拉力为33mg ,选项D 正确.]。
三力动态平衡中的两个最小值

三力动态平衡中的两个最小值
皮曙兴
【期刊名称】《数理天地:高中版》
【年(卷),期】2010(000)010
【摘要】三力平衡中的动态平衡问题,通常是物体受三个力作用(如图1)而处于一系列平衡状态中,物体受到的三个力有如下特征:
【总页数】2页(P33-33,32)
【作者】皮曙兴
【作者单位】学大教育广州白云校区,510403
【正文语种】中文
【中图分类】G633.7
【相关文献】
1.用图解法求解三力动态平衡问题
2.三力动态平衡问题的几种解法
3.动态物理问题分析(一)——三力作用下物体的动态平衡问题
4.把握"三力",寻求"教"与"学"的动态平衡
5.体验式教学视域下进阶式建模的研究——以“三力动态平衡”一轮复习为例
因版权原因,仅展示原文概要,查看原文内容请购买。
三力平衡动态分析

三力平衡动态分析三力平衡动态分析是通过对物体在运动过程中三个力的平衡关系进行综合分析,推导物体的运动状态和性质。
三力平衡动态分析是力学中的基础内容,广泛应用于物体的运动、物体的加速度、绳索和滑轮等力学问题的解决和分析。
在三力平衡动态分析中,我们需要考虑三个力的平衡关系,即合力、重力和惯性力之间的关系。
合力是作用在物体上的所有力的矢量和,重力是物体受到地球引力的作用产生的力,惯性力是物体自身受到加速度作用产生的力。
首先,我们来看一下三力平衡动态分析的条件。
当物体处于平衡状态时,合力为零,即F=0这意味着物体处于静止状态或匀速直线运动状态。
其次,我们来介绍一下三力平衡动态分析的步骤。
首先,我们需要确定物体所受的所有力,包括重力、合力和惯性力。
其次,我们需要建立力的平衡方程,即将所有力的矢量和置为零,得到F=0通过解这个方程,我们可以求解出物体的加速度。
最后,我们需要根据加速度的大小和方向,判断物体的运动状态和性质。
三力平衡动态分析可以应用于各种物理问题。
例如,我们可以用它来分析物体在斜坡上滑动的情况。
在这种情况下,物体受到重力和斜坡提供的力的作用,我们可以根据物体在斜坡上的运动状态,确定它的加速度和滑动的速度。
再例如,我们可以用三力平衡动态分析来分析电梯的运动情况。
在电梯上,乘客受到地球引力、电梯提供的力和惯性力的作用。
通过对这些力进行平衡分析,我们可以判断电梯的加速度和乘客在电梯中的体验。
总之,三力平衡动态分析是力学中重要的一部分,它通过对物体受力平衡关系的综合分析,推导出物体的运动状态和性质。
它广泛应用于物体的运动、物体的加速度、绳索和滑轮等力学问题的解决和分析。
在实际应用中,我们需要根据具体情况,确定所受的力和力的平衡方程,进而求解物体的加速度和运动状态。
巧解变动中的三力平衡问题范文

巧解变动中的三力平衡问题在中学阶段,力的平衡问题,多为三力平衡,按平衡条件,合力必为零,将三力首尾相联即围成一封闭三角形。
一般来说,只要所给条件能满足解这个三角形的条件(如已知两边夹一角或两角夹一边)就能按解三角形的方法解出这力三角形中要求的物理量。
常遇到一类变动中的三力平衡问题。
一般是其中一个力大小和方向确定;另一个力的方向确定,大小可变;第三个力大小和方向均变化。
要依据所给条件,确定后两力的变化规律。
为了帮助学生们很好地理解,采用力三角形来解答,现举几例如下:[例题1]一个光滑的圆球搁在光滑的斜面和竖直的档板之间(图1),斜面和档板对圆球的弹力随斜面倾角α变化而变化的范围是:A.斜面弹力N1变化范围是(mg,+∞)B.斜面弹力N1变化范围是(0,+∞)C.档板的弹力N2变化范围是(0, +∞)D.档板的弹力N2变化范围是(mg,+∞)答:[A、C]解:圆球受三个力,其中重力的大小和方向均为确定的,档板对圆球的弹力N2的方向始终是水平的,亦为确定的。
而斜面对圆球的作用力的大小和方向均在变化中,但不论α如何变动,只要α取一个确定的值,圆球就在三力作用下处于平衡状态,则此三力就组成一个封闭的三角形,如图2所示:由于0<α<90°,所以mg<N1<+∞,0<N2<+∞解出。
[例题2]如图3所示,用两根绳子系住一重物,绳OA与天花板夹角θ不变,且θ>45°,当用手拉住绳OB,使绳OB由水平慢慢转向OB′过程中,OB绳所受拉力将A.始终减少 B.始终增大C.先增大后减少 D.先减少后增大答:[D]解:重物受三个力,其中重力大小方向确定,OA方向不变,OB绳受力的大小方向变化。
在变化过程中,重物所受三力平衡,可组成一个封闭三角形,现图示如下:从图中可很直观地得出结论。
由于θ>45°,θ+α=90°所以α<45°,此时T OB取得最小值。
[例题3]如图4所示,一重球用细线悬于O点,一光滑斜面将重球支持于A点,现将斜面沿水平面向右慢慢移动,那么细线对重球的拉力T 及斜面对重球的支持力N的变化情况是:A.T逐渐增大,N逐渐减小;B.T逐渐减小,N逐渐增大;C.T先变小后变大,N逐渐减小;D.T逐渐增大,N先变大后变小。
专题12三力平衡中的动态平衡问题及最小值问题(解析版)—2023届高三物理一轮复习重难点突破

专题12三力平衡中的动态平衡问题及最小值问题1、三个力的动态平衡问题:一个力恒定,另外两个力的大小或(和)方向不断变化,但物体仍然平衡,关键词——缓慢转动、缓慢移动……2、三个力的动态平衡问题的解法1)解析法——画好受力分析后,对力进行分解列平衡方程,然后由角度变化分析力的变化规律.2)图解法——画好受力分析图后,将三个力按顺序首尾相接构成力的封闭三角形,由于三角形的边的长短反映力的大小,从动态三角形边的长度变化规律看出力的变化规律.3、图解法分析的一般顺序:封闭的矢量三角形→等腰三角形→相似三角形→圆与矢量三角形相结合或正弦定理→圆与矢量三角形相结合考点一解析法分析三个力的动态平衡问题解析法:对研究对象进行受力分析,列平衡方程,根据角度变化分析力的变化规律.1.(2022·江苏南通·高二期末)如图所示,半球形碗静止于水平地面上,一只可视为质点的蚂蚁在碗内缓慢从b点爬到a点的过程中()A.蚂蚁受到的弹力逐渐变大B.蚂蚁受到的摩擦力逐渐变大C.蚂蚁受到的合力逐渐变大D.地面对碗的摩擦力逐渐变大【答案】B【详解】AB.设蚂蚁所在位置的切线与水平方向夹角为,对蚂蚁分析得支持力和静摩擦力分别为N=mcos,=msin故A错误,B正确;C.蚂蚁缓慢上爬的过程中变大,可知蚂蚁受到的支持力减小,静摩擦力增大。
又因为蚂蚁缓慢移动,视为平衡状态,故所受合力为零保持不变,故C错误;D.系统保持平衡状态,则地面对碗的摩擦力为零保持不变,故D错误。
2.(多选)如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙之间放一光滑圆球B,已知A的圆半径为球B的半径的3倍,球B所受的重力为G,整个装置处于静止状态.设墙壁对B的支持力为F1,A对B的支持力为F2,若把A向右移动少许后,它们仍处于静止状态,则F1、F2的变化情况分别是()A.F1减小B.F1增大C.F2增大D.F2减小【答案】AD【详解】解析以球B为研究对象,受力分析如图所示,可得出F1=G tanθ,F2=Gcosθ,当A向右移动少许后,θ减小,则F1减小,F2减小,故A、D正确.考点二矢量三角形法分析三个力的动态平衡问题矢量三角形法常用于三个力中只有一个力的方向发生变化的情况.3.质量为m的物体用轻绳AB悬挂于天花板上。
动态平衡中的三力问题宁波市鄞州中学

动态平衡中的三力问题物理组 王高波在有关物体平衡的问题中,有一类涉及动态平衡;这类问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,故这是力平衡问题中的一类难题;解决这类问题的一般思路是:把“动”化为“静”,“静”中求“动”;根据现行高考要求,物体受到往往是三个共点力问题,利用三力平衡特点讨论动态平衡问题是力学中一个重点和难点,许多同学因不能掌握其规律往往无从下手,许多参考书的讨论常忽略几中情况,笔者整理后介绍如下; 方法一:三角形图解法;特点:三角形图象法则适用于物体所受的三个力中,有一力的大小、方向均不变通常为重力,也可能是其它力,另一个力的方向不变,大小变化,第三个力则大小、方向均发生变化的问题;方法:先正确分析物体所受的三个力,将三个力的矢量首尾相连构成闭合三角形;然后将方向不变的力的矢量延长,根据物体所受三个力中二个力变化而又维持平衡关系时,这个闭合三角形总是存在,只不过形状发生改变而已,比较这些不同形状的矢量三角形,各力的大小及变化就一目了然了;例 如图1所示,一个重力G 的匀质球放在光滑斜面上,斜面倾角为α,在斜面上有一光滑的不计厚度的木板挡住球,使之处于静止状态;今使板与斜面的夹角β缓慢增大,问:在此过程中,挡板和斜面对球的压力大小如何变化解析:取球为研究对象,如图1-2所示,球受重力G 、斜面支持力F 1、挡板支持力F 2;因为球始终处于平衡状态,故三个力的合力始终为零,将三个力矢量构成封闭的三角形;F 1的方向不变,但方向不变,始终与斜面垂直;F 2的大小、方向均改变,随着挡板逆时针转动时,F 2的方向也逆时针转动,动态矢量三角形图1-3中一画出的一系列虚线表示变化的F 2;由此可知,F 2先减小后增大,F 1随β增大而始终减小;同种类型:例所示,小球被轻质细绳系着,斜吊着放在光滑斜面上,小球质量为m ,斜面倾角为θ,向右缓慢推动斜面,直到细线与斜面平行,在这个过程中,绳上张力、斜面对小球的支持力的变化情况方法二:相似三角形法;特点:相似三角形法适用于物体所受的三个力中,一个力大小、方向不变,其它二个力的方向均发生变化,且三个力中没有二力保持垂直关系,但可以找到力构成的矢量三角形相似的几何三角形的问题原理:先正确分析物体的受力,画出受力分析图,将三个力的矢量首尾相连构成闭合三角形,再寻找与力的三角形相似的几何三角形,利用相似三角形的性质,建立比例关系,把力的大小变化问题转化为几何三角形边长的大小变化问题进行讨论;例2.一轻杆BO ,其O 端用光滑铰链固定在竖直轻杆AO 上,B 端挂一重物,且系一细绳,细绳跨过杆顶A 处的光滑小滑轮,用力F 拉住,如图2-1所示;现将细绳缓慢往左拉,使杆BO 与杆A O 间的夹角θ逐渐减少,则在此过程中,拉力F 及杆BO 所受压力F N 的大小变化情况是A .F N 先减小,后增大 始终不变 C .F 先减小,后增大 始终不变图1-1图1-2F 1GF 2图1-3图2-1图2-2图1-4解析:取BO 杆的B 端为研究对象,受到绳子拉力大小为F 、BO 杆的支持力F N 和悬挂重物的绳子的拉力大小为G 的作用,将F N 与G 合成,其合力与F 等值反向,如图2-2所示,将三个力矢量构成封闭的三角形如图中画斜线部分,力的三角形与几何三角形OBA 相似,利用相似三角形对应边成比例可得:如图2-2所示,设AO 高为H ,BO 长为L ,绳长l ,lF L F HG N ==,式中G 、H 、L 均不变,l 逐渐变小,所以可知F N 不变,F 逐渐变小;正确答案为选项B 同种类型:如图2-3所示,光滑的半球形物体固定在水平地 面上,球心正上方有一光滑的小滑轮,轻绳的一端系一小球,靠放在半球上的A 点,另一端绕过定滑轮,后用力拉住,使小球静止.现缓慢地拉绳,在使小球沿球面由A 到半球的顶点B 的过程中,半球对小球的支持力N 和绳对小球的拉力T 的大小变化情况是 D ;A N 变大,T 变小,B N 变小,T 变大C N 变小,T 先变小后变大D N 不变,T 变小方法三:作辅助圆法特点:作辅助圆法适用的问题类型可分为两种情况:①物体所受的三个力中,开始时两个力的夹角为90°,且其中一个力大小、方向不变,另两个力大小、方向都在改变,但动态平衡时两个力的夹角不变;②物体所受的三个力中,开始时两个力的夹角为90°,且其中一个力大小、方向不变,动态平衡时一个力大小不变、方向改变,另一个力大小、方向都改变,原理:先正确分析物体的受力,画出受力分析图,将三个力的矢量首尾相连构成闭合三角形,第一种情况以不变的力为弦作个圆,在辅助的圆中可容易画出两力夹角不变的力的矢量三角形,从而轻易判断各力的变化情况;第二种情况以大小不变,方向变化的力为直径作一个辅助圆,在辅助的圆中可容易画出一个力大小不变、方向改变的的力的矢量三角形,从而轻易判断各力的变化情况;例3、如图3-1所示,物体G 用两根绳子悬挂,开始时绳OA 水平,现将两绳同时顺时针转过90°,且保持两绳之间的夹角α不变)90(0>α,物体保持静止状态,在旋转过程中,设绳OA 的拉力为F 1,绳OB 的拉力为F 2,则 ;A F 1先减小后增大B F 1先增大后减小C F 2逐渐减小D F 2最终变为零解析:取绳子结点O 为研究对角,受到三根绳的拉力,如图3-2所示分别为F 1、F 2、F 3,将三力构成矢量三角形如图3-3所示的实线三角形CDE,需满足力F 3大小、方向不变,角∠ CDE 不变因为角α不变,由于角∠DCE 为直角,则三力的几何关系可以从以DE 边为直径的圆中找,则动态矢量三角形如图3-3中一画出的一系列虚线表示的三角形;由此可知,F 1先增大后减小,F 2随始终减小,且转过90°时,当好为零; 正确答案选项为B 、C 、D另一种类型:如图3-4所示,在做“验证力的平行四边形定则”的实验时,用M 、N 两个测力计通过细线拉橡皮条的结点,使其到达O 点,此时α+β= 90°.然后保持M 的读数不变,而使α角减小,为保持结点位置不变,可采用的办法是 A ; A 减小N 的读数同时减小β角 B 减小N 的读数同时增大β角 C 增大N 的读数同时增大β角D 增大N 的读数同时减小β角图3-1图3-2 图3-3图2-3 图3-4方法四:解析法 特点:解析法适用的类型为一根绳挂着光滑滑轮,三个力中其中两个力是绳的拉力,由于是同一根绳的拉力,两个拉力相等,另一个力大小、方向不变的问题;原理:先正确分析物体的受力,画出受力分析图,设一个角度,利用三力平衡得到拉力的解析方程式,然后作辅助线延长绳子一端交于题中的界面,找到所设角度的三角函数关系;当受力动态变化是,抓住绳长不变,研究三角函数的变化,可清晰得到力的变化关系;例4.如图4-1所示,在水平天花板与竖直墙壁间,通过不计质量的柔软绳子和光滑的轻小滑轮悬挂重物G =40N,绳长L =2.5m,OA =1.5m,求绳中张力的大小,并讨论: 1当B 点位置固定,A 端缓慢左移时,绳中张力如何变化2当A 点位置固定,B 端缓慢下移时,绳中张力又如何变化解析:取绳子c 点为研究对角,受到三根绳的拉力,如图4-2所示分别为F 1、F 2、F 3,延长绳AO 交竖直墙于D 点,由于是同一根轻绳,可得:21F F =,BC 长度等于CD,AD 长度等于绳长;设角∠OAD 为θ;根据三个力平衡可得:θsin 21G F =;在三角形AOD 中可知,ADOD=θsin ;如果A 端左移,AD 变为如图4-3中虚线A ′D ′所示,可知A ′D ′不变,OD ′减小,θsin 减小,F 1变大;如果B 端下移,BC 变为如图4-4虚线B ′C ′所示,可知AD 、OD 不变,θsin 不变,F 1不变;同种类型:如图4-5所示, 长度为5cm 的细绳的两端分 别系于竖立地面上相距为4m 的两杆的顶端A 、B ,绳子上 挂有一个光滑的轻质钩,其 下端连着一个重12N 的物体, 平衡时绳中的张力多大图4-1图4-2 图4-3′ 图4-4 图4-5。
3.6二、三力平衡问题、动态分析ppt课件

最低点顺时针转动至水平位置,求转动过程
中,小球对挡板的压力F1和对斜面的压力F2 分别怎样变A化C ?( )
A、F1 先减小,后增大 C、F2 不断减小
B、F1 不断减大 D、F2 先变大,后减小
练习:
15、如图所示,球面光滑的半径为R的半球固定在
水平面上,球心的正上方固定一小滑轮,跨过滑题意,选择电灯受力分析,它分别受
到重力G,两细绳OA、OB的拉力FA、FB ,可
画出其受力图,由于电灯处于平衡状态,则
两细绳OA、OB的拉力FA、FB 的合力F与重力
大小相等,方向相反,构成一对平衡力。
可得:FA = G/cosθ,FB = Gtanθ
注意箭头的长度与绳子长度无关。
例题4:如右图所示,重力为G的电灯通过两根细绳OB与OA悬挂于 两墙之间,细绳OB的一端固定于左墙B点,且OB沿水平方向,细 绳OA挂于右墙的A点。
A、3N、4N、5N
B、1N、3N、5N
C、1N、4N、7N
D、2N、5N、8N
9、如图,两根杆子构成的一个架子下面挂着一个
B
重为G=6N的重物,已知AB杆长5cm,BC杆长7cm,AC A
距离3cm。假设杆子只在沿杆的方向有力的作用。
CG
求AB杆,BC杆的受力大小?(用相似三角形解)
FAB 10N
木块匀速下滑:m (sin cos )M
7、用轻绳把一个小球悬挂在O点,用力拉小球使轻绳偏离竖
直方向30°,小球处于静止状态,力F与竖直方向成角θ,
如图所示,若要使拉力F取最小值,则角θ应是( B )
A、30° B、60° C、90° D、0°
O 30°
练习:
8、下列各组力能使物体作匀速直线运动的是( A )
2019-2023年高一物理力学专题提升专题06三力动态平衡问题的处理技巧

2019-2023年高一物理力学专题提升专题06三力动态平衡问题的处理技巧三力动态平衡问题是高一物理力学中的一大难点。
在这个专题中,学生需要掌握处理三力动态平衡问题的相关技巧。
下面将介绍几种常见的处理技巧。
首先,我们要了解三力动态平衡问题的基本概念。
三力动态平衡是指物体在受到三个力的作用下,保持平衡并保持其速度恒定的状态。
在这种情况下,物体受到的合力为零,即三个力的矢量和为零,并且物体的合动量为零。
处理三力动态平衡问题的第一步是绘制力的示意图。
根据题目给出的条件,将物体与所受力的方向和大小用矢量表示,并在图上标注清楚。
第二步是分解力的矢量。
将图中的力矢量分解为两个垂直的分力,通常选择一个与物体运动方向一致的分力,称为平行力分量,以及一个垂直于运动方向的分力,称为垂直力分量。
这样,我们可以将三个力分解为六个分力,分别对应物体在平行和垂直方向上的受力情况。
第三步是分析力的平衡条件。
根据物体处于动态平衡状态的条件,我们可以得出以下结论:在平行方向上,物体受到的平行力分量的代数和为零;在垂直方向上,物体受到的垂直力分量的代数和为零。
换句话说,分别对平行和垂直方向上的力分别应用牛顿第二定律和牛顿第一定律,得出平行和垂直方向上的受力平衡条件。
第四步是计算未知量。
根据所给的条件和力的平衡条件,我们可以列出相关的方程。
通过求解这些方程,我们可以计算出未知量,如物体的加速度、速度、力的大小等。
最后,我们要注意解题的思路和方法。
处理三力动态平衡问题时,我们应该将问题转化为代数形式,运用力的平衡条件和运动方程进行分析和求解。
此外,我们还应该注意题目中的附加条件,并根据实际情况进行合理的假设和近似处理。
综上所述,处理三力动态平衡问题需要掌握绘制力的示意图、分解力的矢量、分析力的平衡条件和计算未知量的技巧。
通过熟练掌握这些技巧,我们可以有效地解决三力动态平衡问题,并提升自己的物理学习能力。
希望同学们能够通过不断练习和思考,掌握这些技巧,并取得良好的成绩。
9、三力动态平衡及验证力的平行四边形定则
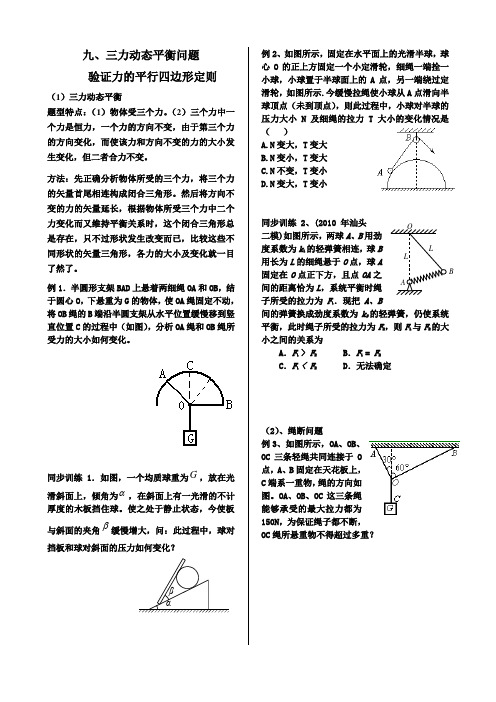
βLLOAB九、三力动态平衡问题验证力的平行四边形定则(1)三力动态平衡题型特点:(1)物体受三个力。
(2)三个力中一个力是恒力,一个力的方向不变,由于第三个力的方向变化,而使该力和方向不变的力的大小发生变化,但二者合力不变。
方法:先正确分析物体所受的三个力,将三个力的矢量首尾相连构成闭合三角形。
然后将方向不变的力的矢量延长,根据物体所受三个力中二个力变化而又维持平衡关系时,这个闭合三角形总是存在,只不过形状发生改变而已,比较这些不同形状的矢量三角形,各力的大小及变化就一目了然了。
例1.半圆形支架BAD上悬着两细绳OA和OB,结于圆心O,下悬重为G的物体,使OA绳固定不动,将OB绳的B端沿半圆支架从水平位置缓慢移到竖直位置C的过程中(如图),分析OA绳和OB绳所受力的大小如何变化。
同步训练1.如图,一个均质球重为G,放在光滑斜面上,倾角为α,在斜面上有一光滑的不计厚度的木板挡住球。
使之处于静止状态,今使板与斜面的夹角β缓慢增大,问:此过程中,球对挡板和球对斜面的压力如何变化?例2、如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮,如图所示.今缓慢拉绳使小球从A点滑向半球顶点(未到顶点),则此过程中,小球对半球的压力大小N及细绳的拉力T大小的变化情况是()A.N变大,T变大B.N变小,T变大C.N不变,T变小D.N变大,T变小同步训练2、(2010年汕头二模)如图所示,两球A、B用劲度系数为k1的轻弹簧相连,球B用长为L的细绳悬于O点,球A固定在O点正下方,且点OA之间的距离恰为L,系统平衡时绳子所受的拉力为F1.现把A、B间的弹簧换成劲度系数为k2的轻弹簧,仍使系统平衡,此时绳子所受的拉力为F2,则F1与F2的大小之间的关系为A.F1> F2 B.F1 = F2C.F1< F2 D.无法确定(2)、绳断问题例3、如图所示,OA、OB、OC三条轻绳共同连接于O点,A、B固定在天花板上,C端系一重物,绳的方向如图。
三力动态平衡

张 健
受力分析
木块A在水平拉力F作用下处于静止状态,分析受力情况
受力分析
分析步骤: 1、确定研究对象 2、分析重力和已经给出的力 3、确定接触面个数,分析每个接触面的弹力N 和摩擦力f(防止少力) 4、确定每一个力的施力物体(防止多力)
受力分析
水平方向:T2-T1sinθ=0 竖直方向:T1cosθ-G=0
三力动态分析
动态平衡即通过控制某一物理量 , 使物体的状态发生 缓慢的变化 , 而在这个过程中物体又始终处于一系列 的平衡状态
三力动态分析
受力情况:重力G为恒力,另外两个弹力有一个弹力的方 向保持不变
在木板的支持下,小球在光滑的斜面上,处于静止状态,现缓慢的倾斜木板, 分析斜面对小球的支持力FN1和木板对小球的支持力FN2的变化(不计摩擦力)
三力动态分析
图解法:运用力的平移得到力的三角形,在三角形中讨论边的长 短变化,即力的大小变化
FN1变小,FN2先变小后变大
三力动态分析
在木板的支持下,小球在光滑的墙壁上处于静止状态,现缓慢 的向下调节木板,分析墙面对小球的支持力 FN1 和木板对小球 的支持力FN2的变化(不计摩擦力)
三力动态分析
受力情况:重力G为恒力,另外两个弹力的方向均发生变化
在光滑的半球面上,质量为 m 的小 球用轻绳绕过定滑轮缓慢拉动,小 球在球面上缓慢移动,分析在移动 过程中,球面对小球的支持力 FN和 绕过定滑轮轻绳的拉力T的变化
三力动态分析
相似法 : 力的三角形与另外确定的三角形相似 , 对应边成比 例来讨FN不变
谢谢!
浙江省宁波市鄞州中学2025届高一物理第一学期期中达标测试试题含解析
浙江省宁波市鄞州中学2025届高一物理第一学期期中达标测试试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:(1-6题为单选题7-12为多选,每题4分,漏选得2分,错选和不选得零分)1、下面能正确表示做自由落体运动的物体下落的速度v随时间t变化的图象的是A.B.C.D.2、我国杭州城市获得2022年亚运会主办权,在下列训练中,考察运动员的训练成绩时,运动员可视为质点的是A.马拉松B.跳水C.击剑D.体操3、改革开放以来,人们的生活水平得到了很大的改善,快捷、方便、舒适的家用汽车作为代步工具正越来越多的走进寻常百姓家中.汽车起动的快慢和能够达到的最大速度,是衡量汽车性能的指标体系中的两个重要指标.汽车在一条平直公路上,若从静止启动到最大速度的时间内做匀加速直线运动,则汽车做匀加速直线运动的加速度大小为A.2.5m/s B.5m/s C.4.17m/s D.9m/s4、由图的图像中可以判断物体做的是匀速直线运动的是()A.B.C.D.5、下列速度中,指平均速度的是()A.汽车通过长江大桥全程的速度B.雨滴落地时的速度C.子弹射出枪口时的速度D.运动员冲过终点时的速度6、关于速度和加速度,下列说法正确的是( )A.加速度方向一定与速度方向相同B.物体的速度为零时,其加速度也一定为零C.物体的速度减小时,其加速度也一定减小D.物体的速度变化越快,其加速度越大7、一个质点做直线运动,其速度随时间变化的函数关系为v=kt。
其中k=0.3m/s2,下列说法正确的是()A.质点做匀速直线运动B.质点的速度变化量大小是0.3m/sC.质点做匀加速直线运动D.质点的加速度为0.3m/s8、如图所示为某质点做直线运动的位移图像,其中0-5s和10-15s均为倾斜的直线,由图可知这个质点的运动情况的正确说法是( )A.0-5s内物体做匀加速直线运动B.10-15s内物体做匀减速直线运动C.物体在0-15s内位移的大小为10mD.10-15s内物体做匀速直线运动,速度的方向与0-5s内的方向相反9、甲、乙两质点在同一时刻从原点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止.甲、乙两质点在运动过程中的x−v(位置—速度)图象如图所示(虚线与对应的坐标轴垂直),则()A.质点甲的加速度大小a1=2m/s2B.质点乙的加速度大小a2=2m/s2C.图线a、b的交点表示两质点同时到达同一位置D.在x−v图象中,图线a表示质点甲的运动,质点乙的初速度v0=6m/s10、如图所示,某人用手握住一个油瓶使其始终在竖直方向保持静止,则下列说法中正确的是( )A.手握得越紧,油瓶受到的摩擦力越大B.手握得越紧,油瓶与手之间的最大静摩擦力越大C.不管手握得多紧,油瓶受到的摩擦力总是一定的D.油瓶受到的摩擦力必须大于其重力才能静止11、关于速度、速度的变化和加速度的关系,下列说法中正确的是()A.速度变化的方向为正,加速度的方向也为正B.物体加速度增大,速度一定越来越大C.速度越来越大,加速度一定越来越大D.加速度为负值,物体也可能做加速运动12、A、B两物块的质量分别为2m和m,静止叠放在水平地面上.A、B 间的动摩擦因数为μ,B与地面间的动摩擦因数为12μ.最大静摩擦力等于滑动摩擦力,重力加速度为g.现对A施加一水平拉力F,则()A.当52F mgμ=时,A的加速度为13gμB.当F<2μmg 时,A、B 都相对地面静止C.当F>3 μmg 时,A相对B滑动D.无论F为何值,B的加速度不会超过12g μ二、实验题(本题共16分,答案写在题中横线上)13、(6分)如图是“验证力的合成的平行四边形定则”实验示意图。
物体的动态平衡问题课件-高一上学期物理人教版(2019) 必修第一册

角度2:力的极大值
方法: 辅助圆法——直径是圆中最长的一条弦
范例2.已知物体在共点、共面的三个力F、F1、F2的作用下处于平衡状态,其中
F=10N,F1、F2的夹角为1500,则F2的最大值是 B
A、10N
B、20N
C、30N
D、40N
F2 30o
F1
F2=2F=20N
F
类型二 角度极大值
方法: 辅助圆法,作圆的切线——切线张角最大
试分析两绳上的张பைடு நூலகம்变化情况
TB
OA绳上的张力TA先变小在变大
TA
OB绳上的张力TB一直变小
TG
2.如图,保持OA绳方向不动。OB绳的B端在半圆形支架上逆时针滑至竖直方向,
试分析两绳上的张力变化情况
TB
OA绳上的张力TA一直变小 OB绳上的张力TB一直变小
TA TG
3.(教材改编)在光滑墙壁上用网兜把足球挂在A点,足球与墙壁的接触点为 B。若
范例1、一质量为m的物体在外力F的作用下恰能静置与倾角为30°的光滑斜面上,
则外力F的值可能为( BD )
A.0.2mg B.1.5mg
FN
C. mg D. mg
变式训练
可得:Fmin=
F mg
1、将一质量m=1kg的小球用细线悬挂于固定点O,小球在一外力F的作用下平衡时 拉线与竖直方向的夹角θ=30°,则该F的大小(取g=10m/s2)可能是( AB ) A、7N B、5N C、3N/C D、1N
FTMN θ
θ= π-α
D.OM上的张力先增大后减小
FTMN= 0
θ
θ
FTMN
FT=G
FTMN
2.如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N,
三力动态平衡问题的几种解法

三力动态平衡问题的几种解法物体在几个力的共同作用下处于平衡状态, 如果其中的某一个力或某几个力发生缓慢的变化,其他的力也随之发生相应的变化,在变化过程中物体仍处于平衡状态,我们称这种平衡为动态平衡。
因为物体受到的力都在发生变化, 是动态力,所以这类问题是力学中比较难的一类问题。
因为在整个过程中物体一直处于平衡状态, 所以过程中的每一瞬间物体所受到的合力都是零,这是我们解这类题的根据・下面就举例介绍几种这类题的解题方法 ・一,三角函数法例1. ( 2014年全国卷1 )如图,用橡皮筋将一小球悬挂在小车的架子上,系绕处于平衡状态。
现使 小车从静止开始向左加速,加速度从零开始逐渐增大到某一值, 然后保持此值,小球稳定地偏离竖直方向某一角度(橡皮筋在弹性限度内) 小球的高度( )A.—定升高B.—定降低C.保持不变D.升高或降低由橡皮筋的劲度系数决定解析:设L0为橡皮筋的原长,k%橡皮筋的劲度系数,小车静止时,对小球受力分析得:F1二mg 弹簧的伸长点的距离为 ,当小车的加速度稳定在一定值时5对小球进行受力分析 如图:<订22 • •夕■■,弹簧的伸长:0二哑上k,贝y 小球与悬挂点的竖直方向的距禺为:“二(厶十工」cas or = Lj+ —< L*,即小球在竖直方向上到悬挂点的距离减小,所以小球一定升高,故A 正确,:BCD 错误•故选A.点评:这种方法适用于有两个力垂直的情形,这样才能构建直角三角形,从而根据直角三角形中的边角尖系解题。
与稳定在竖直位置时相比,七疋,即小球与悬挂得:】图解法例2 •如图所示,半圆形支架为G 的物体,使0A 绳固定不动,将0B 绳的B 端沿半圆支架从水平位置逐渐移至 竖直的位置C 的过程中,如图所示,0A 绳受力大小变化情况是 ,0B 绳受力大小变化情况是n\D O______________________________解析:对0点受力分析,根据0点合力是零可知绳OA 和绳0B 上拉力的合力跟重力大小相等,方向相 反,也就是说这个合力的大小不变方向竖直向上。
浙江省宁波市鄞州中学2023-2024学年高一下学期期中考试物理试题(选考)

浙江省宁波市鄞州中学2023-2024学年高一下学期期中考试物理试题(选考)学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列描述电场的物理量中与试探电荷无关且是失量的是( )A.电场强度B.电势能C.电势D.电势差2.电鳗是一种能通过自身发出的生物电获取食物、威胁敌害、保护自己的深海动物。
若某,可击昏敌害。
则身电鳗的头尾相当于两个电极,它在海水中产生的电场强度达到310N/C长60cm的电鳗,在放电时产生的瞬间电压可达()A.60V B.600V C.6000V D.60000V3.如图,A、B、C、D、P为正方体的顶点,有一正点电荷固定在P点,则 ( )A.顶点A、C的电场强度相同B.顶点D的场强小于B的场强C.正方体侧面ABCD为等势面D.带正电的粒子沿AC移动,电势能先增大后减小4.如图为一压路机的示意图,其大轮半径是小轮半径的1.5倍。
A B、分别为大轮和小轮边缘上的点,C为O和A连线的中点。
在压路机前进时( )1A .无论0v 多大,小B .若04v gR >则小C .若02gR v <<D .只要小球能做完整圆周运10.如图所示,一个半径为R的半圆形轨道竖直固定放置,直径POQ水平,滑块与轨道内表面间的动摩擦因数为μ,一质量为m的小滑块自P点正上方由静止释放,释放高度为R,小滑块恰好从P点进入轨道,小滑块滑到轨道最低点N时对轨道的压力为4mg,重力加速度大小为g,用W表示小滑块从P点运动到Q点的过程中克服摩擦力所做的功,则()A.小滑块恰好可以到达Q点B.小滑块能到达Q点继续向上运动C.W=mgRD.W>mgR11.如图所示为两个点电荷的电场,虚线为一带电粒子只在电场力作用下的运动轨迹,a、b为轨迹上两点,下列说法中正确的是( )A.两个点电荷为左正右负,且右边点电荷所带电荷量多B.带电粒子带正电C.带电粒子在a点的加速度大于在b点的加速度D.带电粒子在a点的电势能大于在b点的电势能12.玉米是我国重要的农作物,收割后脱粒玉米用如图甲所示的传送带装置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态平衡中的三力问题---宁波市鄞州中学
————————————————————————————————作者: ————————————————————————————————日期:
ﻩ
动态平衡中的三力问题
物理组 王高波
在有关物体平衡的问题中,有一类涉及动态平衡。
这类问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,故这是力平衡问题中的一类难题。
解决这类问题的一般思路是:把“动”化为“静”,“静”中求“动”。
根据现行高考要求,物体受到往往是三个共点力问题,利用三力平衡特点讨论动态平衡问题是力学中一个重点和难点,许多同学因不能掌握其规律往往无从下手,许多参考书的讨论常忽略几中情况,笔者整理后介绍如下。
方法一:三角形图解法。
特点:三角形图象法则适用于物体所受的三个力中,有一力的大小、方向均不变(通常为重力,也可能是其它力),另一个力的方向不变,大小变化,第三个力则大小、方向均发生变化的问题。
方法:先正确分析物体所受的三个力,将三个力的矢量首尾相连构成闭合三角形。
然后将方向不变的力的矢量延长,根据物体所受三个力中二个力变化而又维持平衡关系时,这个闭合三角形总是存在,只不过形状发生改变而已,比较这些不同形状的矢量三角形,各力的大小及变化就一目了然了。
例1.1 如图1所示,一个重力G 的匀质球放在光滑斜面上,斜面倾角为α,在斜面上有一光滑的不计厚度的木板挡住球,使之处于静止状态。
今使板与斜面的夹角β缓慢增大,问:在此过程中,挡板和斜面对球的压力大小如何变化?
解析:取球为研究对象,如图1-2所示,球受重力G、斜面支持力F 1
、挡板支持力F 2。
因为球始终处于
平衡状态,故三个力的合力始终为零,将三个力矢量构成封闭的三角形。
F 1的方向不变,但方向不变,始终与
斜面垂直。
F 2的大小、方向均改变,随着挡板逆时针转动时,F 2的方向也逆时针转动,动态矢量三角形图1-3中一画出的一系列虚线表示变化的F 2。
由此可知,F 2先减小后增大,F 1随β增大而始终减小。
同种类型:例1.2所示,小球被轻质细绳系着,斜吊着放在光滑斜面上,小球质量为m,斜面倾角为θ,向右缓慢推动斜面,直到细线与斜面平行,在这个过程中,绳上张力、斜面对小球的支持力的变化情况?(答案:绳上张力减小,斜面对小球的支持力增大)
β
α
图
图
β
α
G
F 1
F 2 F 1 G
F 2 图θ
F
方法二:相似三角形法。
特点:相似三角形法适用于物体所受的三个力中,一个力大小、方向不变,其它二个力的方向均发生变化,且三个力中没有二力保持垂直关系,但可以找到力构成的矢量三角形相似的几何三角形的问题
原理:先正确分析物体的受力,画出受力分析图,将三个力的矢量首尾相连构成闭合三角形,再寻找与力的三角形相似的几何三角形,利用相似三角形的性质,建立比例关系,把力的大小变化问题转化为几何三角形边长的大小变化问题进行讨论。
例2.一轻杆BO ,其O 端用光滑铰链固定在竖直轻杆AO上,B 端挂一重物,且系一细绳,细绳跨过杆顶A 处的光滑小滑轮,用力F 拉住,如图2-1所示。
现将细绳缓慢往左拉,使杆BO 与杆A O 间的夹角θ逐渐减少,则在此过程中,拉力F 及杆B O所受压力FN 的大小变化情况是( )
A .F N 先减小,后增大 B.FN 始终不变 C.F先减小,后增大 D.F 始终不变
解析:取BO 杆的B端为研究对象,受到绳子拉力(大小为F )、BO 杆的支持力F N 和悬挂重物的绳子的拉力(大小为G )的作用,将F N 与G合成,其合力与F 等值反向,如图2-2所示,将三个力矢量构成封闭的三角形(如图中画斜线部分),力的三角形与几何三角形OBA 相似,利用相似三角形对应边成比例可得:(如图2-2所示,设AO
高为H ,BO 长为L ,绳长l ,)l
F L F H
G N ==,式中G 、H、L均不变,l 逐渐变小,所以可知F N不变,F 逐渐变小。
正确答案为选项B
同种类型:如图2-3所示,光滑的半球形物体固定在
水平地
面上,球心正上方有一光滑的小滑轮,轻绳的一
端系一小球,靠放在半球上的A 点,另一端绕过定滑轮,后用力拉住,使小球静止.
现缓慢地拉绳,在使小球
A
F
B
O
θ
图
A
F B O θ
G
F N F L l H 图
A
C
B O
沿球面由A 到半球的顶点B 的过程中,半球对小球的支持力N 和绳对小球的拉力T 的大小变化情况是( D )。
(A)N变大,T 变小, (B)N 变小,T变大
(C)N 变小,T先变小后变大 (D)N不变,T 变小 方法三:作辅助圆法
特点:作辅助圆法适用的问题类型可分为两种情况:①物体所受的三个力中,开始时两个力的夹角为90°,且其中一个力大小、方向不变,另两个力大小、方向都在改变,但动态平衡时两个力的夹角不变。
②物体所受的三个力中,开始时两个力的夹角为90°,且其中一个力大小、方向不变,动态平衡时一个力大小不变、方向改变,另一个力大小、方向都改变,
原理:先正确分析物体的受力,画出受力分析图,将三个力的矢量首尾相连构成闭合三角形,第一种情况以不变的力为弦作个圆,在辅助的圆中可容易画出两力夹角不变的力的矢量三角形,从而轻易判断各力的变化情况。
第二种情况以大小不变,方向变化的力为直径作一个辅助圆,在辅助的圆中可容易画出一个力大小不变、方向改变的的力的矢量三角形,从而轻易判断各力的变化情况。
例3、如图3-1所示,物体G 用两根绳子悬挂,开始时绳OA 水平,现将两绳同时顺时针转过90°,且保持两绳之间的夹角α不变)90(0
>α,物体保持静止状态,在旋转过程中,设绳OA 的拉力为F 1,绳OB 的拉力为
F 2,则( )。
(A)F 1先减小后增大
(B)F1先增大后减小 (C )F 2逐渐减小 (D)F 2最终变为零
解析:取绳子结点O为研究对角,受到三根绳的拉力,如图3-2所示分别为F 1、F 2、F 3,将三力构成矢量三角形(如图3-3所示的实线三角形CD E),需满足力F 3大小、方向不变,角∠ CDE 不变(因为角α不变),由于角∠DCE 为直角,则三力的几何关系可以从以DE 边为直径的圆中找,则动态矢量三角形如图3-3中一画出的一系列虚线表示的三角形。
由此可知,F1先增大后减小,F 2随始终减小,且转过90°时,当好为零。
A B
α
O G
图3-1 A
B
α
O G
F F F
图3-2
F F F C D E
D D
D
图3-3
正确答案选项为B 、C、D
另一种类型:如图3-4所示,在做“验证力的平行四边形定则”的实验时,用M 、N 两个测力计通过细
线拉橡皮条的结点,使其到达O点,此时α+β= 90°.然后保持M 的读数不变,而使α角减小,为保持结点位置不变,可采用的办法是( A )。
(A)减小N的读数同时减小β角 (B )减小N 的读数同时增大β角 (C)增大N的读数同时增大β角 (D)增大N 的读数同时减小β角
方法四:解析法
特点:解析法适用的类型为一根绳挂着光滑滑轮,三个力中其中两个力是绳的拉力,由于是同一根绳的拉力,两个拉力相等,另一个力大小、方向不变的问题。
原理:先正确分析物体的受力,画出受力分析图,设一个角度,利用三力平衡得到拉力的解析方程式,然后作辅助线延长绳子一端交于题中的界面,找到所设角度的三角函数关系。
当受力动态变化是,抓住绳长不变,
研究三角函数的变化,可清晰得到力的变化关系。
例4.如图4-1所示,在水平天花板与竖直墙壁间,通过不计质量的柔软绳子和光滑的轻小滑轮悬挂重物G =40N,绳长L =2.5m ,OA =1.5m,求绳中张力的大小,并讨论: (1)当B 点位置固定,A 端缓慢左移时,绳中张力如何变化?
(2)当A 点位置固定,B 端缓慢下移时,绳中张力又如何变化?
解析:取绳子c 点为研究对角,受到三根绳的拉力,如图4-2所示分别为F 1、F 2、F3,延长绳AO 交竖直墙于
D 点,由于是同一根轻绳,可得:21F F ,BC 长度等于CD ,A D长度等于绳长。
设角∠O AD 为θ;根据三
图4-
A B C G O
A B C G D F F F
O θ
图4
A B C G D F F F
O θ
A ′ D ′ 图4
A B
C G D
F F F
O
θ
C ′
B ′ 图4
M
N
O α
β 图
个力平衡可得:θsin 21G F =
;在三角形A OD 中可知,AD
OD
=θsin 。
如果A 端左移,AD 变为如图4-3中虚
线A ′D ′所示,可知A′D ′不变,OD ′减小,θsin 减小,F1变大。
如果B 端下移,BC 变为如图4-4虚线B ′C ′所示,可知AD 、OD不变,θsin 不变,F 1不变。
同种类型:如图4-5所示, 长度为5cm 的细绳的两端分 别系于竖立地面上相距为4m 的两杆的顶端A 、B ,绳子上 挂有一个光滑的轻质钩,其 下端连着一个重12N 的物体, 平衡时绳中的张力多大?
图4。
