杆件计算基本公式
圆钢管杆件重量计算公式

圆钢管杆件重量计算公式圆钢管是我们在生活和工程中经常会见到的一种材料,比如说建筑结构里、一些机械装置中。
要知道它的重量,那就得用到一个特别的计算公式。
咱先来说说这个公式哈,圆钢管杆件重量的计算公式是:M =π×ρ×(D - t)×t×L 。
这里面的 M 表示的是圆钢管杆件的质量(重量),单位通常是千克(kg);π呢,就是那个大家都熟悉的圆周率,约等于3.14159 ;ρ是材料的密度,比如说常见的钢材,密度大概是 7850 千克/立方米;D 是圆钢管的外径,t 是圆钢管的壁厚,L 是圆钢管的长度。
我给您举个例子哈,就说有一根圆钢管,外径是 50 毫米,壁厚是 5 毫米,长度是 2 米。
那先把单位统一一下,50 毫米等于 0.05 米,5 毫米等于 0.005 米。
咱们按照公式来算算,先算 (D - t)×t ,那就是 (0.05 - 0.005)×0.005 = 0.00225 平方米。
然后再乘以长度 2 米,得到体积是 0.0045 立方米。
接着乘以密度 7850 千克/立方米,再乘以圆周率 3.14159 ,最后算出来这根圆钢管的重量大约是 10.83 千克。
有一次我去一个建筑工地,正好看到工人们在搬运一堆圆钢管。
我就好奇地问其中一个师傅,他们是怎么知道这些钢管够不够重量的。
师傅笑着跟我说,他们就是靠这个计算公式来估算的。
还现场拿了一根钢管给我比划,告诉我外径、壁厚这些该怎么量。
看着师傅熟练的样子,我就知道这公式在他们工作中那可是常用得不能再常用啦。
在实际应用中,这个公式能帮我们解决不少问题呢。
比如说要搭建一个架子,得先算好钢管的重量,才能确定支撑结构是不是足够稳固。
又或者在采购的时候,能根据重量来判断价格是不是合理。
总之,这个圆钢管杆件重量计算公式虽然看起来有点复杂,但只要搞清楚每个参数的含义,用起来还是挺顺手的。
您学会了吗?。
杆件的强度计算公式

杆件的强度计算公式 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT杆件的强度、刚度和稳定性计算1.构件的承载能力,指的是什么答:构件满足强度、刚度和稳定性要求的能力称为构件的承载能力。
(1)足够的强度。
即要求构件应具有足够的抵抗破坏的能力,在荷载作用下不致于发生破坏。
(2)足够的刚度。
即要求构件应具有足够的抵抗变形的能力,在荷载作用下不致于发生过大的变形而影响使用。
(3)足够的稳定性。
即要求构件应具有保持原有平衡状态的能力,在荷载作用下不致于突然丧失稳定。
2.什么是应力、正应力、切应力应力的单位如何表示答:内力在一点处的集度称为应力。
垂直于截面的应力分量称为正应力或法向应力,用σ表示;相切于截面的应力分量称切应力或切向应力,用τ表示。
应力的单位为Pa。
1Pa=1N/m2工程实际中应力数值较大,常用MPa或GPa作单位1MPa=106Pa1GPa=109Pa3.应力和内力的关系是什么答:内力在一点处的集度称为应力。
4.应变和变形有什么不同答:单位长度上的变形称为应变。
单位纵向长度上的变形称纵向线应变,简称线应变,以ε表示。
单位横向长度上的变形称横向线应变,以ε/表示横向应变。
5.什么是线应变什么是横向应变什么是泊松比答:(1)线应变单位长度上的变形称纵向线应变,简称线应变,以ε表示。
对于轴力为常量的等截面直杆,其纵向变形在杆内分布均匀,故线应变为l l∆=ε(4-2)拉伸时ε为正,压缩时ε为负。
线应变是无量纲(无单位)的量。
(2)横向应变拉(压)杆产生纵向变形时,横向也产生变形。
设杆件变形前的横向尺寸为a ,变形后为a 1,则横向变形为横向应变ε/为 a a∆=/ε(4-3)杆件伸长时,横向减小,ε/为负值;杆件压缩时,横向增大,ε/为正值。
因此,拉(压)杆的线应变ε与横向应变ε/的符号总是相反的。
(3)横向变形系数或泊松比试验证明,当杆件应力不超过某一限度时,横向应变ε/与线应变ε的绝对值之比为一常数。
杆件承载力计算公式

杆件承载力计算公式
在工程设计中,经常需要计算杆件的承载力。
杆件承载力的计算公式是根据材料力学理论和结构力学原理推导出来的。
以下是常见的杆件承载力计算公式:
1.压杆的计算公式:
如果杆件为压杆,那么其承载力的计算公式为:
Pc=Ac*Fc*σc
其中,Pc为杆件的承载力,Ac为杆件的截面面积,Fc为截面的调整系数,σc为相应材料的抗压强度。
2.拉杆的计算公式:
如果杆件为拉杆,那么其承载力的计算公式为:
Pt=At*Ft*σt
其中,Pt为杆件的承载力,At为杆件的截面面积,Ft为截面的调整系数,σt为相应材料的抗拉强度。
3.弯曲杆件的计算公式:
如果杆件受到弯曲作用,那么其承载力的计算公式为:
M=σb*W
其中,M为杆件的弯矩,σb为相应材料的弯曲强度,W为截面的抵抗弯曲矩的有效宽度。
4.扭转杆件的计算公式:
如果杆件受到扭转作用,那么其承载力的计算公式为:
T=τt*J
其中,T为杆件的扭矩,τt为相应材料的抗扭强度,J为截面的极
惯性矩。
以上是常见杆件承载力的计算公式,但需要根据具体情况选择适用的
公式。
此外,还应根据杆件的实际情况和要求,结合工程经验和相关规范,考虑到其他因素如安全系数、边界条件等进行修正,以确保杆件的安全可靠。
杆件正应力怎么求计算公式

杆件正应力怎么求计算公式杆件正应力的计算公式。
在工程力学中,杆件正应力是指在杆件内部由外部加载引起的正向拉伸或压缩应力。
正应力的计算是工程设计中非常重要的一部分,它可以帮助工程师确定杆件是否能够承受外部加载,并且可以帮助工程师选择合适的材料和尺寸来设计结构。
杆件正应力的计算公式可以通过简单的力学原理推导得出。
在这篇文章中,我们将介绍杆件正应力的计算公式,并且讨论一些实际应用中的例子。
杆件正应力的计算公式可以表示为:σ = P / A。
其中,σ表示杆件的正应力,P 表示施加在杆件上的外部力,A 表示杆件的横截面积。
这个公式的推导可以通过简单的力学原理来进行。
当一个外部力 P 作用在杆件上时,杆件内部会产生一个与外部力方向相反的内部应力。
根据牛顿第三定律,这个内部应力的大小与外部力的大小相等,方向相反。
而杆件的横截面积 A 则可以用来表示内部应力的分布情况。
因此,杆件的正应力可以表示为外部力 P 与横截面积 A 的比值。
在实际应用中,杆件正应力的计算可以通过这个简单的公式来进行。
例如,当一个钢杆承受一个拉力时,我们可以通过测量钢杆的横截面积和外部拉力来计算钢杆的正应力。
这个计算可以帮助工程师确定钢杆是否能够承受这个拉力,并且可以帮助工程师选择合适的钢材来设计结构。
除了上面提到的简单拉力的情况,杆件正应力的计算公式也可以应用在其他复杂的情况中。
例如,在梁的设计中,梁的横截面积不是均匀的,因此我们可以通过积分的方法来计算梁的正应力分布。
这个计算可以帮助工程师确定梁在不同位置的正应力大小,并且可以帮助工程师选择合适的梁的尺寸和材料来设计结构。
除了简单的拉力和梁的设计,杆件正应力的计算公式也可以应用在其他工程结构的设计中。
例如,在桥梁的设计中,我们可以通过计算桥梁的正应力来确定桥梁的承载能力,并且可以帮助工程师选择合适的桥梁的尺寸和材料来设计结构。
总之,杆件正应力的计算公式是工程设计中非常重要的一部分。
通过这个简单的公式,工程师可以确定杆件是否能够承受外部加载,并且可以帮助工程师选择合适的材料和尺寸来设计结构。
杆件的刚度计算汇总.

第一节
圆轴扭转时的变形及刚度计算
刚度计算的三方面:
① 校核刚度: ② 设计截面尺寸: ③ 计算许可载荷:
max
T max Ip G[ ]
T
max
GI p[ ]
有时,还可依据此条件进行选材。
6
第一节
[例]
圆轴扭转时的变形及刚度计算
图示阶梯圆轴,受力如图。已知该轴大端直径为
有足够的刚度。如果变形过大,将造成梁不能正常工作,进而
引起梁的破坏。如:高精度车床轴;桥梁;变速箱传动轴等。 绕曲线——梁在载荷作用下发生弯曲变形,梁轴线由直线 弯曲成一条光滑连续曲线。 梁曲线上任一点在垂直于梁变形前轴线方向的线位移 称为该点的挠度 。 梁任一横截面绕其中性轴转动的角度称为该截面的转角。
③ 轴上的绝对值最大的扭矩越小越合理,所以,1轮和
2轮应该换位。换位后,轴的扭矩如图所示,此时,轴的最 大直径才为 75mm。 T (kNm) 2.814 x – 4.21
13
第一节
圆轴扭转时的变形及刚度计算
课堂练习
14
第二节
梁的变形及刚度计算
一、弯曲变形的概念
为了确保梁的正常工作,梁除了满足强度条件外,还要求
D=60mm,小端直径为
d=30mm,已知G=80GPa,
1
0
/m 。试求:
1).校核该轴刚度; 2).A截面相对于C 截 面的扭转角。
解:1.内力分析:
画扭矩图如图所。
7
第一节
圆轴扭转时的变形及刚度计算
2.变形分析及刚度条件:
3.14 604 1012 I P1 1.27 106 (m 4 ) 32 32 d 4 3.14 304 1012 I P2 0.08 106 (m 4 ) 32 32 180 T1 180 2.5 103 0 1 1 . 4 ( /m) 9 6 GI P1 3.14 80 10 1.27 10 180 T2 180 1.5 103 0 2 1 . 35 ( /m) 9 6 GI P 2 3.14 80 10 0.08 10 故 max 1.4( 0 /m)
杆件轴力计算

杆件轴力计算【原创实用版】目录1.引言2.杆件轴力计算的基本原理3.杆件轴力计算的常用方法4.杆件轴力计算的实际应用5.总结正文一、引言杆件轴力计算是土木工程、机械工程等领域中常见的一种力学计算问题。
在实际工程中,为了确保结构的安全性、稳定性以及良好的使用性能,对杆件轴力进行精确计算至关重要。
本文将对杆件轴力计算的基本原理、常用方法及实际应用进行详细介绍。
二、杆件轴力计算的基本原理杆件轴力计算的基本原理主要基于静力学原理,即在平衡状态下,杆件所受的外力之和为零,各个截面上的力矩之和为零。
根据这一原理,可以得到杆件轴力计算的基本公式:F = ΣF_i,其中 F 表示杆件的轴力,F_i 表示作用在杆件上的各个力。
三、杆件轴力计算的常用方法1.直接法:直接法是根据力学平衡方程求解杆件轴力的一种方法,适用于简单结构的计算。
其步骤为:首先列出力学平衡方程,然后解方程得到杆件的轴力。
2.弯矩法:弯矩法是根据弯矩平衡方程求解杆件轴力的一种方法,适用于复杂结构的计算。
其步骤为:首先列出弯矩平衡方程,然后解方程得到杆件的轴力。
3.矩阵法:矩阵法是利用矩阵运算求解杆件轴力的一种方法,适用于复杂结构的计算。
其步骤为:首先建立杆件的力学模型,然后列出力学平衡方程,最后利用矩阵运算求解得到杆件的轴力。
四、杆件轴力计算的实际应用杆件轴力计算在实际工程中有广泛的应用,例如:桥梁结构设计、机械臂结构设计、房屋结构设计等。
通过杆件轴力计算,可以确保结构的安全性、稳定性以及良好的使用性能,为工程项目的顺利实施提供有力保障。
五、总结本文对杆件轴力计算的基本原理、常用方法及实际应用进行了详细介绍。
材料力学 杆件的变形计算
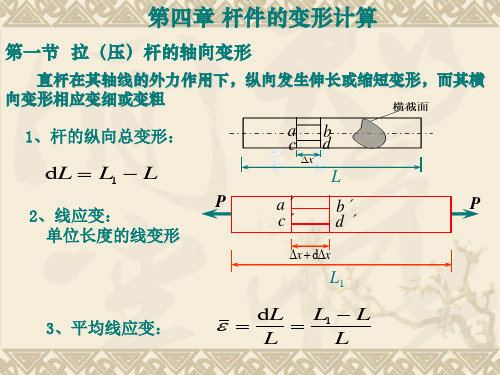
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
杆件轴力计算公式

杆件轴力计算公式在工程力学中,杆件轴力计算是一个非常重要的内容,它可以帮助工程师们准确地计算出杆件在受力情况下的轴力大小。
轴力是指杆件受力时沿着其轴线方向的力,它是杆件受力的重要参数之一。
在实际工程中,我们经常需要计算杆件在受力情况下的轴力大小,这就需要用到杆件轴力计算公式。
杆件轴力计算公式是通过工程力学的理论推导和实验验证得出的,它可以帮助工程师们在设计和施工过程中准确地计算出杆件在受力情况下的轴力大小,从而保证工程的安全性和稳定性。
下面我们将介绍一些常见的杆件轴力计算公式。
1. 杆件轴力计算公式的基本原理。
杆件轴力计算公式是根据杆件受力的基本原理和力学公式推导出来的。
在受力分析中,我们通常会考虑杆件受到的外力和内力,外力包括集中力、分布力和弯矩,内力包括轴力、剪力和弯矩。
杆件轴力计算公式就是通过对杆件受力进行分析,得出杆件在受力情况下的轴力大小的公式。
2. 杆件轴力计算公式的常见形式。
在实际工程中,杆件轴力计算公式有多种形式,常见的有以下几种:(1)集中力作用下的杆件轴力计算公式:当杆件受到集中力作用时,其轴力大小可以通过以下公式计算:N = F。
其中,N为杆件的轴力大小,F为集中力的大小。
(2)分布力作用下的杆件轴力计算公式:当杆件受到分布力作用时,其轴力大小可以通过以下公式计算:N = ∫f(x)dx。
其中,N为杆件的轴力大小,f(x)为分布力的大小,∫表示积分运算。
(3)弯矩作用下的杆件轴力计算公式:当杆件受到弯矩作用时,其轴力大小可以通过以下公式计算:N = M / z。
其中,N为杆件的轴力大小,M为弯矩的大小,z为杆件的截面模量。
3. 杆件轴力计算公式的应用。
杆件轴力计算公式在工程实践中有着广泛的应用,它可以帮助工程师们在设计和施工过程中准确地计算出杆件在受力情况下的轴力大小,从而保证工程的安全性和稳定性。
工程师们可以根据具体的工程情况选择合适的杆件轴力计算公式,进行轴力计算,并根据计算结果进行工程设计和施工。
关于受压杆件长细比的计算

受压杆件的容许长细比 项 次 1 构件名称 柱、桁架和天窗架结构 柱的缀条、吊车梁或吊车桁架以下 的柱间支撑 2 支撑(吊车梁或吊车桁架以下的柱 间支撑除外) 用以减少受压构件长细比的杆件 200 容许长细比 150
关于受压杆件长细比的计算
首先计算出惯性矩 I,对于圆管的惯性矩可根据下列公式计 算:
I=
πD 4
64
(1 − α 4 )
其中 α = d / D ,d 为圆管内径,D 为圆管外径。
i=
I A
πD 2
4 (1 − α ) 2
其中 A 为截面面积,对于圆管截面 A l 为竿的长度,μ为长度因数,其值由竿端约束情况决定。 例如,两端铰支的细长压杆,μ=1;一段固定、一段自由的细长 压杆,μ=2;两端固定的细长压杆,μ=0.5;一段固定一段铰支 的细长压杆,μ=0.7。
杆件屈服应力计算公式

杆件屈服应力计算公式在工程力学中,杆件屈服应力是一个非常重要的参数,它可以帮助工程师确定杆件在受力时是否会发生屈服现象。
屈服现象是指在杆件受到一定的外力作用时,杆件内部会出现塑性变形,导致杆件失去原有的弹性特性。
因此,计算杆件屈服应力是非常重要的,可以帮助工程师选择合适的材料和设计合理的结构。
杆件屈服应力的计算公式可以通过材料的力学性能参数来确定,一般来说,常见的材料力学性能参数包括杨氏模量、屈服强度和断裂强度等。
通过这些参数,可以得到杆件屈服应力的计算公式如下:σ_yield = F_y / A。
其中,σ_yield表示杆件的屈服应力,F_y表示材料的屈服强度,A表示杆件的横截面积。
从这个公式可以看出,杆件的屈服应力与材料的屈服强度和杆件的横截面积有关。
材料的屈服强度越大,杆件的屈服应力也会越大;而杆件的横截面积越大,杆件的屈服应力也会越大。
在实际工程中,工程师需要根据具体的材料和结构设计要求来确定杆件的屈服应力。
一般来说,材料的屈服强度可以通过材料的力学性能表来查找,而杆件的横截面积可以通过几何参数来计算。
在计算杆件的屈服应力时,工程师还需要考虑杆件的受力情况,例如受拉、受压或受弯等情况,这些都会对杆件的屈服应力产生影响。
除了杆件的屈服应力,工程师在设计结构时还需要考虑杆件的安全系数。
安全系数是指杆件的实际强度与设计强度之间的比值,通过安全系数可以评估杆件在受力时的安全性。
一般来说,工程师会根据设计要求和材料的力学性能来确定安全系数的大小,以确保结构在受力时不会发生屈服现象。
总的来说,杆件屈服应力是一个非常重要的参数,在工程设计中起着至关重要的作用。
通过合理计算杆件的屈服应力,可以帮助工程师选择合适的材料和设计合理的结构,从而确保结构在受力时具有足够的强度和稳定性。
同时,工程师还需要考虑安全系数等因素,以确保结构在受力时不会出现屈服现象,从而保障工程的安全性和可靠性。
第四章 杆件的变形计算

3)分别作AC1和BC2的垂线交于C0
A F B 30oC2 C
Cx CC2 0.277mm C y CC1 / sin30 CC 2 cot30
C1
1.44mm
C点总位移:
Cy
C C y C x 1.47mm
(此问题若用圆弧精确求解)
2
2
Cx
C0
T3 C
1)根据题意,首先画出扭矩图
T1 d1 A Mx N· m B T2 d2 C T3
2)AB 段单位长度扭转角:
1400
800
AB
M xAB GI pAB
+
x
1400 4 π 0.06 80 10 9 32 0.01375rad / m
3)BC 段单位长度扭转角: M xBC BC
M xi li j i 1 GI pi
n
请注意单位长度扭转角和相对扭转角的区别
例4-3 一受扭圆轴如图所示,已知:T1=1400N· m, T2=600N· m, T3=800N· m, d1=60mm,d2=40mm,剪切弹性模量G=80GPa,计 算最大单位长度扭转角。
T1 d1 A
T2 d2 B
第四章
• • • • •
杆件的变形计算
本部分主要内容:
拉压杆的轴向变形 圆轴的扭转变形与相对扭转角 梁的弯曲变形、挠曲线近似微分方程 用积分法求梁的弯曲变形 用叠加法求梁的弯曲变形
第一节 拉压杆的轴向变形
直杆在其轴线的外力作用下,纵向发生伸长或缩短变形, 而其横向变形相应变细或变粗 杆件在轴线方向的伸长
泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数, 可以通过实验测得。对于各向同性材料,可以证明三者之间存 在着下面的关系
各类杆件长度计算公式

各类杆件长度计算公式在工程设计和建筑施工中,各类杆件的长度计算是非常重要的一环。
不同类型的杆件,如钢管、钢筋、木材等,其长度计算公式也各不相同。
本文将针对不同类型的杆件,分别介绍其长度计算公式及相关知识。
一、钢管长度计算公式。
1. 直线钢管长度计算公式。
直线钢管的长度计算公式为,L = π D N。
其中,L为钢管的长度,π为圆周率(取3.14),D为钢管的直径,N为钢管的数量。
2. 弯曲钢管长度计算公式。
弯曲钢管的长度计算公式为,L = π D N + (2 R π N)。
其中,L为钢管的长度,π为圆周率,D为钢管的直径,N为钢管的数量,R 为钢管的弯曲半径。
二、钢筋长度计算公式。
钢筋长度计算公式主要根据构件的尺寸和形状来确定。
一般情况下,可以根据以下公式进行计算:1. 直线钢筋长度计算公式。
直线钢筋的长度计算公式为,L = √(X^2 + Y^2 + Z^2)。
其中,L为钢筋的长度,X、Y、Z分别为构件的三个尺寸。
2. 弯曲钢筋长度计算公式。
弯曲钢筋的长度计算公式为,L = √(X^2 + Y^2 + Z^2) + (2 R π)。
其中,L为钢筋的长度,X、Y、Z分别为构件的三个尺寸,R为钢筋的弯曲半径。
三、木材长度计算公式。
木材长度计算公式与其形状和用途有关,一般可根据以下公式进行计算:1. 直线木材长度计算公式。
直线木材的长度计算公式为,L = √(X^2 + Y^2 + Z^2)。
其中,L为木材的长度,X、Y、Z分别为木材的三个尺寸。
2. 弯曲木材长度计算公式。
弯曲木材的长度计算公式为,L = √(X^2 + Y^2 + Z^2) + (2 R π)。
其中,L为木材的长度,X、Y、Z分别为木材的三个尺寸,R为木材的弯曲半径。
以上是针对不同类型杆件长度计算公式的介绍,希望能对工程设计和建筑施工有所帮助。
在实际应用中,除了掌握计算公式外,还需根据具体情况进行合理的调整和计算,以确保杆件的精准使用和安全施工。
杆件计算长度系数

杆件计算长度系数杆件计算长度系数是工程中设计和计算杆件的一个重要参数。
长度系数是指杆件在受压、受拉或弯曲等作用下的稳定性能与其长度之间的关系。
一般情况下,较长的杆件在受力下更容易出现稳定性问题,所以需要引入长度系数来衡量和修正杆件的设计。
杆件的长度系数一般通过极限弯曲载荷来计算。
极限弯曲载荷是指杆件在弯曲加载下承受的最大载荷,超过该载荷后杆件将发生屈曲失稳。
杆件的长度系数可以通过下面的公式计算:KL=(π√(ExI))/K其中KL为杆件的长度系数E为弹性模量I为截面惯性矩K为有效长度系数。
有效长度系数是指将杆件的实际长度与极限弯曲载荷下的临界长度之间的比值,它反映了杆件的支撑和边界条件对其稳定性影响的程度。
有效长度系数一般经验上可以根据杆件的边界条件和支撑方式来确定。
常用的有效长度系数参考值如下:1.简支列柱:KL=12.固定列柱:KL=0.53.在一个端部为固定支座4.对称斜两端支座的柱子:KL=0.855.反对称斜两端支座的柱子:KL=0.65通过以上公式和参考值,可以计算出杆件的长度系数KL。
得到长度系数后,可以通过将杆件的极限弯曲载荷除以长度系数来获得杆件的稳定载荷。
这个稳定载荷即为杆件的临界载荷,超过该载荷的加载将使杆件失去稳定,导致屈曲破坏。
总结起来,杆件的长度系数是一个重要的设计参数,用于衡量杆件在受力下的稳定性能与其长度之间的关系。
根据杆件的类型、边界条件和支撑方式,可以通过特定的公式和参考值计算出杆件的长度系数,从而确定杆件的临界载荷和稳定性能。
设计师需要根据具体情况来选择适当的长度系数,以确保杆件在使用过程中具有足够的稳定性和安全性。
杆件的强度计算公式资料讲解

杆件的强度计算公式资料讲解杆件的强度、刚度和稳定性计算1.构件的承载能⼒,指的是什么?答:构件满⾜强度、刚度和稳定性要求的能⼒称为构件的承载能⼒。
(1)⾜够的强度。
即要求构件应具有⾜够的抵抗破坏的能⼒,在荷载作⽤下不致于发⽣破坏。
(2)⾜够的刚度。
即要求构件应具有⾜够的抵抗变形的能⼒,在荷载作⽤下不致于发⽣过⼤的变形⽽影响使⽤。
(3)⾜够的稳定性。
即要求构件应具有保持原有平衡状态的能⼒,在荷载作⽤下不致于突然丧失稳定。
2.什么是应⼒、正应⼒、切应⼒?应⼒的单位如何表⽰?答:内⼒在⼀点处的集度称为应⼒。
垂直于截⾯的应⼒分量称为正应⼒或法向应⼒,⽤σ表⽰;相切于截⾯的应⼒分量称切应⼒或切向应⼒,⽤τ表⽰。
应⼒的单位为Pa。
1 Pa=1 N/m2⼯程实际中应⼒数值较⼤,常⽤MPa或GPa作单位1 MPa=106Pa1 GPa=109Pa3.应⼒和内⼒的关系是什么?答:内⼒在⼀点处的集度称为应⼒。
4.应变和变形有什么不同?答:单位长度上的变形称为应变。
单位纵向长度上的变形称纵向线应变,简称线应变,以ε表⽰。
单位横向长度上的变形称横向线应变,以ε/表⽰横向应变。
5.什么是线应变?什么是横向应变?什么是泊松⽐?答:(1)线应变单位长度上的变形称纵向线应变,简称线应变,以ε表⽰。
对于轴⼒为常量的等截⾯直杆,其纵向变形在杆内分布均匀,故线应变为l l?=ε(4-2)拉伸时ε为正,压缩时ε为负。
线应变是⽆量纲(⽆单位)的量。
(2)横向应变拉(压)杆产⽣纵向变形时,横向也产⽣变形。
设杆件变形前的横向尺⼨为a,变形后为a1,则横向变形为aaa-=1横向应变ε/为a a=/ε(4-3)杆件伸长时,横向减⼩,ε/为负值;杆件压缩时,横向增⼤,ε/为正值。
因此,拉(压)杆的线应变ε与横向应变ε/的符号总是相反的。
(3)横向变形系数或泊松⽐试验证明,当杆件应⼒不超过某⼀限度时,横向应变ε/与线应变ε的绝对值之⽐为⼀常数。
此⽐值称为横向变形系数或泊松⽐,⽤µ表⽰。
杆件的强度计算公式

杆件的强度、刚度和稳定性计算1.构件的承载能力,指的是什么答:构件满足强度、刚度和稳定性要求的能力称为构件的承载能力。
(1)足够的强度。
即要求构件应具有足够的抵抗破坏的能力,在荷载作用下不致于发生破坏。
(2)足够的刚度。
即要求构件应具有足够的抵抗变形的能力,在荷载作用下不致于发生过大的变形而影响使用。
(3)足够的稳定性。
即要求构件应具有保持原有平衡状态的能力,在荷载作用下不致于突然丧失稳定。
2.什么是应力、正应力、切应力应力的单位如何表示答:内力在一点处的集度称为应力。
垂直于截面的应力分量称为正应力或法向应力,用6表示;相切于截面的应力分量称切应力或切向应力,用T表示。
应力的单位为Pa。
21 Pa=1 N /m2工程实际中应力数值较大,常用MPa或GPa作单位61 MPa=106Pa91 G P a=109P a3.应力和内力的关系是什么答:内力在一点处的集度称为应力。
4.应变和变形有什么不同答:单位长度上的变形称为应变。
单位纵向长度上的变形称纵向线应变,简称线应变,以&表示。
单位横向长度上的变形称横向线应变,以& /表示横向应变。
5.什么是线应变什么是横向应变什么是泊松比答:(1)线应变单位长度上的变形称纵向线应变,简称线应变,以&表示。
对于轴力为常量的等截面直杆,其纵向变形在杆内分布均匀,故线应变为_1l(4-2 )拉伸时&为正,压缩时&为负。
线应变是无量纲(无单位)的量。
(2)横向应变拉(压)杆产生纵向变形时,横向也产生变形。
设杆件变形前的横向尺寸为a,变形后为a i,则横向变形为a a1a横向应变& /为/ _aa(4-3 )杆件伸长时,横向减小,& /为负值;杆件压缩时,横向增大,£/为正值。
因此,拉(压)杆的线应变& 与横向应变& /的符号总是相反的。
(3)横向变形系数或泊松比试验证明,当杆件应力不超过某一限度时,横向应变& /与线应变&的绝对值之比为一常数。
材料力学 杆件的变形计算
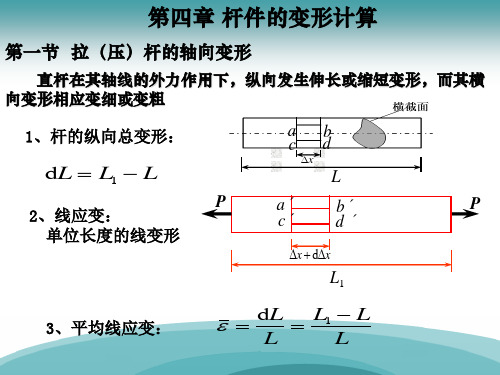
B
30oC2
C
C1
1.44mm
胡:请问,“ 弛其弦,以绳缓援之” 是什么意思 ?
郑:这是讲测量弓力时,先将弓的弦 松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说: 郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
400
400
FN KN 40
2)求伸长量
+
x l l AB lBC
-
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压,AC杆将伸长,而 F BC杆将缩短。
杆件温度伸长量计算公式

杆件温度伸长量计算公式我们需要了解杆件温度伸长量的计算公式。
根据材料力学的基本理论,杆件温度伸长量与杆件长度、温度变化以及杨氏模量有关。
计算公式如下:ΔL = α * L * ΔT其中,ΔL表示温度引起的长度变化,单位为米;α表示材料的线膨胀系数,单位为1/℃;L表示杆件的初始长度,单位为米;ΔT 表示温度变化量,单位为℃。
在实际应用中,我们需要根据具体的材料和温度条件来选择合适的线膨胀系数。
不同材料的线膨胀系数不同,可以通过查阅相关资料或进行实验来获取。
线膨胀系数反映了材料在温度变化下的膨胀或收缩的程度,是材料性质的重要参数。
然后,我们可以通过一个具体的例子来说明杆件温度伸长量的计算方法。
假设有一根铁杆的初始长度为10米,线膨胀系数为12×10^(-6)/℃,温度变化量为100℃,我们来计算温度引起的长度变化。
根据上述公式,我们可以计算出温度伸长量:ΔL = 12×10^(-6)/℃ * 10米* 100℃ = 0.012米因此,铁杆在温度变化100℃时,会引起长度变化为0.012米,即12毫米。
温度伸长量的计算对于工程设计和结构分析非常重要。
在工程实践中,我们需要考虑温度变化对结构的影响,特别是在长跨度结构、高温环境或低温环境下。
通过计算温度伸长量,可以预测结构的变形情况,从而选择合适的材料和结构形式,确保结构的稳定性和安全性。
温度伸长量的计算还可以应用于其他领域。
例如,在轨道铺设过程中,铁轨受到温度变化的影响,会发生伸长或收缩,需要对此进行计算和调整,以保证铁轨的几何稳定性和行车安全。
在管道工程中,温度伸长量的计算可以用于设计管道的伸缩节,以吸收管道在温度变化下的伸长或收缩,避免管道的破裂或变形。
杆件温度伸长量的计算公式为ΔL = α * L * ΔT,其中ΔL表示温度引起的长度变化,α表示材料的线膨胀系数,L表示杆件的初始长度,ΔT表示温度变化量。
温度伸长量的计算对于工程设计和结构分析非常重要,可以用于预测结构的变形情况,选择合适的材料和结构形式,确保结构的稳定性和安全性。
杆件自由长度系数

杆件自由长度系数
杆件自由长度系数是一个重要的概念,它在工程领域中经常被提及。
在设计和分析结构时,了解和计算杆件自由长度系数对于确保结构的稳定性和安全性至关重要。
本文将详细介绍杆件自由长度系数的定义、计算方法以及其在工程实践中的应用。
杆件自由长度系数,又称为杆件的屈曲系数,是指杆件在受到压力作用时能够发生屈曲的能力。
它是一个无量纲的数值,代表了杆件的弯曲能力和稳定性。
杆件自由长度系数越大,表示杆件越能承受压力而不发生屈曲,结构越稳定。
第二节:杆件自由长度系数的计算方法
杆件自由长度系数的计算方法与材料的力学性质和几何形状有关。
一般来说,杆件自由长度系数可以通过以下公式计算:
L/r = (E/σ)^0.5
其中,L为杆件的自由长度,r为杆件的半径或宽度,E为杆件的杨氏模量,σ为杆件的屈服强度。
第三节:杆件自由长度系数的应用
杆件自由长度系数在工程实践中具有广泛的应用。
在结构设计中,通过计算杆件自由长度系数,可以评估杆件的稳定性,并确定合适的杆件尺寸和材料。
此外,杆件自由长度系数还可以用于预测杆件在受到压力作用时可能出现的屈曲情况,从而指导工程设计和施工。
总结:
杆件自由长度系数是一个重要的工程概念,它对于结构的稳定性和安全性具有重要意义。
通过计算杆件自由长度系数,可以评估杆件的稳定性,并指导工程设计和施工。
在实际应用中,我们需要根据杆件的几何形状和材料的力学性质来计算杆件自由长度系数。
希望本文能够对读者理解和应用杆件自由长度系数有所帮助。
