利率期限结构讲解
利率期限结构理论讲解

利率期限结构理论讲解利率期限结构理论,也称为利率结构理论或期限结构理论,是描述不同期限债券的利率之间关系的一种理论框架。
它试图解释为什么不同期限债券的利率不同,以及它们之间的关系如何变化。
利率期限结构理论是金融市场和债券投资者常用的分析工具,有助于理解债券市场的运作和预测未来的利率走势。
在利率期限结构理论中,利率分为短期利率和长期利率。
短期利率指的是短期债券的利率或即期利率,而长期利率指的是长期债券的利率。
利率期限结构曲线是以利率期限为横轴、利率为纵轴,绘制不同期限债券利率的曲线图。
利率期限结构曲线有很多形状,常见的形状包括上升型、下降型和平坦型等。
1.期望理论:该理论认为利率期限结构取决于投资者对未来利率走势的预期。
如果投资者预期未来的利率将上升,他们就要求更高的利率来补偿风险,从而使长期利率高于短期利率。
反之,如果预期未来的利率将下降,投资者就会接受较低的利率,使长期利率低于短期利率。
期望理论解释了利率期限结构曲线上升型和下降型的形状。
2.流动性偏好理论:该理论认为投资者会对长期债券的投资具有风险厌恶,因为长期债券更容易受到利率变动的影响。
因此,投资者要求较高的利率来补偿他们对风险的担忧,使长期利率高于短期利率。
流动性偏好理论解释了利率期限结构曲线上升型的形状。
3.市场分割理论:该理论认为市场上的不同债券投资者有不同的投资偏好,从而导致不同期限债券之间的利率差异。
例如,机构投资者可能更喜欢长期债券,而个人投资者则更偏好短期债券。
因此,市场分割理论认为不同期限债券的利率取决于它们所面对的不同投资者的需求和供给关系。
市场分割理论解释了利率期限结构曲线平坦型的形状。
需要注意的是,利率期限结构理论并不是完美的,它只是提供了一种解释和描述不同期限债券利率之间关系的框架。
实际上,利率期限结构受到很多因素的影响,包括货币政策、通胀预期、经济周期和市场供需等。
因此,利率期限结构的变化和预测并不总是准确,需要综合考虑多种因素进行分析。
利率期限结构

利率期限结构(term structure),是某个时点不同期限的利率所组成的一条曲线.因为在某个时点,零息票债券的到期收益率等于该时期的利率,所以利率期限结构也可以表示为某个时点零息票债券的收益率曲线(yield curve).它是资产定价、金融产品设计、保值和风险管理、套利以及投机等的基准.因此,对利率期限结构问题的研究一直是金融领域的一个基本课题.利率期限结构是一个非常广阔的研究领域,不同的学者都从不同的角度对该问题进行了探讨,从某一方面得出了一些结论和建议.根据不同的角度和方向,这些研究基本上可以分为5类:1)利率期限结构形成假设;2)利率期限结构静态估计;3)利率期限结构自身形态的微观分析;4)利率期限结构动态模型;5)利率期限结构动态模型的实证检验.1利率期限结构形成假设利率期限结构是由不同期限的利率所构成的一条曲线.由于不同期限的利率之间存在差异,所以利率期限结构可能有好几种形状:向上倾斜、向下倾斜、下凹、上凸等.为了解释这些不同形状的利率期限结构,人们就提出了几种不同的理论假设.这些假设包括:市场预期假设(expectation hy-pothesis),市场分割假设(market segmentation hy-pothesis)和流动性偏好假设(liquidity preference hy-pothesis).为了对这些假设进行验证,不同的学者从不同的角度进行了分析.不同的学者利用不同的方法,使用不同国家的数据对利率期限结构形成假设进行了检验.在3个假设中,市场预期假设是最重要的假设,所以大多数的研究都是立足于市场预期假设,并在此基础上考虑流动性溢酬.4)中国市场.庄东辰[19]和宋淮松[20]分别利用非线性回归和线性回归的方法对我国的零息票债券进行分析.唐齐鸣和高翔[21]用同业拆借市场的利率数据对预期理论进行了实证.实证结果表明:同业拆借利率基本上符合市场预期理论,即长短期利率的差可以作为未来利率变动的良好预测,但是短期利率也存在着一些过度反应的现象.此外,还有杨大楷、杨勇[22],姚长辉、梁跃军[23]对国债收益率的研究.但这些研究大部分都是停留在息票债券的到期收益率上,没有研究真正意义上的利率期限结构.2利率期限结构静态估计当市场上存在的债券种类有限时(特别对债券市场不发达国家而言),如何根据有效的债券价格资料对整个利率期限结构进行估计,是进行债券研究的一个重要内容.不同的学者提出了不同的估计方法,其核心就是对贴现函数δ(m)的估计.郑振龙和林海[31]利用McCulloch[25]样条函数和息票剥离法对我国市场利率期限结构进行了静态估计,构造出中国真正的市场利率期限结构.朱世武和陈健恒[32]则使用Nelson-Siege-Svensson[33]方法对我国交易所市场的利率期限结构进行了估计.郑振龙和林海[34]估计出中国债券市场的违约风险溢酬并进行了分析.林海和郑振龙[35]对中国市场利率的流动性溢酬进行了估计和分析.林海和郑振龙[36]对这些问题进行了统一和归纳,并分析了其在中国金融市场的具体运用.3利率期限结构自身形态微观分析利率期限结构的变动也有平行移动和非平行移动.由于利率直接和债券的收益率相关,这些不同方式的移动对债券组合的收益会产生很大的影响,并进而影响债券组合管理的技术.为了衡量利率期限结构的形状变动对债券投资组合的影响并在此基础上进行有效的管理,达到“免疫”的目的,众多的学者对利率期限结构本身的形态作了大量的分析,并对利率期限结构的平行移动和非平行移动条件下的债券组合套期保值的问题进行了深入研究. Zimmermann[40],D'Ecclesia&Zenios[41], Sherris[42],Martellini&Priaulet[43],Maitland[44], Schere&Avellaneda[45]分别对德国、瑞士、意大利、澳大利亚、法国、南非、拉美等国家和地区的利率期限结构进行了主成分和因子分析.朱峰[46]和林海[47]对中国的市场利率期限结构进行了主成分分析,并在此基础上对中国债券组合的套期保值提出了若干建议.4利率期限结构动态模型4.1基本利率期限结构动态模型根据利率期限结构模型的推导过程,可以分为两种类型:第一种类型就是一般均衡模型(Equilibriummodel),根据市场的均衡条件求出利率所必须遵循的一个过程,在这些模型中,相关的经济变量是输入变量,利率水平是输出变量;另一种类型是无套利模型(No arbitrage model),通过相关债券等资产之间必须满足的无套利条件进行分析,此时利率水平是一个输入变量,相关金融工具的价格是输出变量.必须特别指出的是,这些模型都是建立在风险中性世界中,所描述的均是风险中性世界中的利率变动行为.而实证检验都是利用现实世界的利率数据进行的.因此,在将现实世界中的估计结果运用于衍生产品定价时,必须先利用模型相对应的风险价格②通过Girsanov定理将现实世界转换为风险中性世界,然后再利用风险中性世界中的相应结果进行定价.1)一般均衡模型.主要包括Vasicek[66]模型和Cox,Ingersoll&Ross(CIR)[67,68]模型,此外还有Rendleman&Barter[69],Brennan&Schwartz[55]等.2)无套利模型.主要包括HJM[70]模型,Ho&Lee[71]以及Hull&White[72]模型.此外,还有Black,Derman&Toy[73]等.4.2一般化扩展模型1)仿射模型(Affine Model)2)二次高斯模型(Quadratic Gaussian model)3)非线性随机波动模型(Nonlinear StochasticV olatility Model)4)存在跳跃的利率期限结构模型(Diffusion-jump Model)5)机制转换模型(Regime ShiftModel)5利率期限结构动态模型的实证检验在对利率期限结构模型的理论研究基础之上,众多的学者都对不同的期限结构模型进行了实证检验,以对不同的模型进行判别和比较.实证分析可以分成几个类别:(1)对利率单位根问题的检验;(2)对不同期限结构模型的比较研究;(3)对某个特定期限结构模型的分析;(4)对模型可靠性的分析.5.1对利率单位根的检验Wang&Zhang[89]对利率的单位根问题进行了实证分析,以对利率市场的有效性进行验证5.2对不同期限结构模型的比较研究Durham[92]利用Durham&Gallant[93]的计量分析方法对不同的期限结构模型进行了实证检验. 陈典发[108]对Vasicek模型中参数和实际市场数据的一致性问题进行了研究,并探讨了它在公司融资决策中的应用.谢赤和吴雄伟[109]通过一个广义矩方法,使用中国货币市场的数据,对Vasicek模型和CIR模型进行了实证检验.6利率期限结构研究现状总结性分析根据上面对利率期限结构的文献回顾,可以从中发现利率期限结构研究目前的发展方向.(1)在利率期限结构形成假设方面,市场分割假设逐渐地被人们所遗忘,因为随着市场的发展,技术的进步,市场交易规模的扩大,市场已经逐渐形成一个统一的整体;而且市场预期假设如果没有同流动性溢酬相结合,都会被市场资料所拒绝.流动性溢酬呈现出不断变化的特征.因此,今后的研究方向应该是在市场预期假设的模型框架中引入流动性溢酬假设.(2)在利率期限结构静态估计方面,基本上采用样条函数和息票剥离法.为了保证估计的精确性,样条函数的选择越来越复杂.(3)在利率期限结构自身微观形态分析方面,如何通过对久期的进一步修正,从而使之能够地在利率期限结构非平行移动条件下更为有效地达到套期保值的效果,是该领域未来重要的研究方向.但是由于主成分分析受数据的影响很大,结果很不稳定,所以对主成分分析可靠性的检验,也是一个重要的研究内容.(4)根据对利率期限结构动态模型的实证分析,可以发现:1)不同的模型,不同的计量分析方法,不同的数据,所得出的实证结果都会产生差异.因此,对不同的市场,重要的是模型的适用性.2)实证分析也得出一些基本一致的结论:a.漂移率的假设不会对利率期限结构模型产生太大的影响;b.波动率是利率期限结构模型的重要因素;c.多因子模型要比单因子模型表现得好,但是多因子要牺牲自由度,因此,根据实证结果,两因子模型可能是一个比较好的模型.d.利率一般服从一个均值回归过程.3)基于概率密度预测(density forecast)的样本外检验是利率期限结构实证分析未来的发展方向.4)目前大部分对动态模型的检验都是直接利用实际数据在现实世界中进行的,对现实世界和风险中性世界的差异并未引起足够的重视.1.4 利率期限结构模型的最新进展近年来在HJM 模型类的推动下,利率期限结构理论研究的各种新模型层出不穷,如市场模型、随机弦模型、随机域模型、跳跃过程模型和随机折现因子模型等。
利率的期限结构

北京泰和兴投资管理有限公司
1
利率的期限结构
一、什么是利率期限结构
1.概括来说,同一品类的不同期限的利率构成该品类的利率期限结构。
各种利率大多包括期限长短不同的品种,如活期存款利率、一年定期存款利率等。
“期限结构”反映的是利率与期限的相关关系。
2. 一个经济体的利率期限结构,通常选择基准利率——如国债利率——的期限结构代表。
二、即期利率与远期利率 1. “即期利率”与“远期利率”在利率的期限结构中是一对重要的术语、概念。
2. 即期利率是指对不同期限的债权债务所标明的利率(复利);
3. 远期利率则是指隐含在给定的即期利率之中,从未来的某一时点到另一时点的利率。
4. 远期利率使债权债务期限延长的价值具有了定量的说明。
5. 如以 fn 代表第 n 年的远期利率,r 代表即期利率,其一般计算式是:
三、到期收益率
1. 到期收益率相当于投资人按照当前市场价格购买债券并且一直持有到期满时可以获得的年平均收益率。
2. 基本思路:设当前债券的市场价格与“债券现金流的当前价值”相等,即决定当前实际起作用的利率。
“债券现金流的当前价值”是指:从当前到还本时为止,分期支付的利息和最后归还的本金折合成现值的累计额
3. 到期收益率使不同期限从而有不同现金流的债券收益可以相互比较。
4. 设还有n 年到期的国债券,其面值为P ,按票面利率每期支付的利息为C ,当前的市场价格为P m ,到期收益率 y ,可依据下式算出近似值:
文章转自:北京泰和兴投资管理有限公司
2
北京泰和兴投资管理有限公司。
利率期限结构是什么

利率期限结构是什么利率期限结构是指不同期限的借贷利率之间的差异关系。
它是金融市场的一种重要现象,对经济和金融市场的运行具有重要影响。
本文将详细介绍利率期限结构的概念、形成原因以及其在金融市场中的意义。
一、利率期限结构的概念利率期限结构是一种描述不同借贷期限下利率水平和利率之间关系的工具。
在金融市场中,借款人通常可以选择不同期限的借贷方式,而不同期限的借贷利率通常是不同的。
利率期限结构的形成是由市场供求关系、风险偏好以及宏观经济环境等多种因素综合影响的结果。
二、利率期限结构的形成原因1.市场供求关系:供求关系是影响利率期限结构的重要因素之一。
当市场中借款需求大于借款供给时,长期借款的利率往往比短期借款的利率更高,从而形成正斜率的利率期限结构;相反,当借款供给大于需求时,长期借款的利率可能低于短期借款利率,形成负斜率的利率期限结构。
2.风险偏好:借款人对于风险的偏好也会影响利率期限结构。
一般来说,借款期限越长,风险越高,借款人要求的利率也越高。
因此,利率期限结构通常呈现出逐渐上升的形态。
3.宏观经济环境:宏观经济变量对利率期限结构的形成也有一定的影响。
例如,经济增长预期、通货膨胀预期、货币政策等因素都可能对利率期限结构产生影响。
三、利率期限结构的意义1.预测经济走势:利率期限结构可以作为一种预测经济走势的工具。
根据利率期限结构的形态,我们可以得出市场对未来经济走势的预期。
如果利率期限结构呈现出正斜率形态,说明市场预期未来经济将好转;反之,如果利率期限结构呈现负斜率或平坦的形态,说明市场对经济未来不太乐观。
2.引导市场定价:利率期限结构对市场定价也具有指导意义。
借款人和投资者可以根据利率期限结构来确定借贷和投资的最佳期限,从而在市场中获取更优的收益。
3.评估金融风险:利率期限结构的变动可以反映金融市场的风险环境。
例如,当利率期限结构出现倒挂,即长期利率低于短期利率时,可能预示着经济衰退和金融风险上升。
利率期限结构ppt课件

例题
• 策略一 投资于一个两年期债券
1( 1i2t)2 1
1
• 策略二 连续投资于两个一年期债券
i i 1 (1 )(1 e ) 1
t
t 1
1
套利之下,策略一和策略二的收益率趋于相等
(1i2t)2
(1
it
)(1
ie ) t 1
结论
• 简化
e
i i t
t1
i2t
2
• 一般的
•
e ...... e
市场分割假说对三个事实的解释
• 无法解释第一个事实和第二个事实,因为它将不同期限的债券市场看成完全分割的市场。
• 市场分割假说可以解释第三个事实,即典型的收益率曲线总是向上倾斜的。因为在现实经济 中,人们更偏好期限更短,风险较小的债券,而债券发行者一般倾向于发行长期债券以满足 经济发展之需,使得短期债券价格较高,利率较低,长期债券价格较低,利率较高,因此收 益率曲线向上倾斜。
• 利率期限结构是指债券的到期收益率与到期期限之间的关系,该结构可以用收益率曲线表示,或 者说收益率曲线表示的就是债券的利率期限结构。
三个事实
1 不同期限债券利率随时间一起波动 短期利率低,收益率曲线向上倾斜,反之则反
2
收益率曲线几乎都是向上倾斜的,表明长期利率往往高于短期利率
3
纯粹预期假说 分割市场假说 流动性升水假说
• 即典型的收益率曲线总是向上倾斜的。因为投资者偏好短期债券,故随着债券期限延长,期限补偿亦相应 增加,即便未来短期利率预期平均值保持不变,长期利率也将高于短期利率,从而使得收益率曲线总是向 上倾斜。
i i i t t1
t ( n 1)
int
n
对收益率曲线形状的解释
利率的期限结构投资学财经大学

(五)短期利率和收益率曲线斜率
当下一年度短期利率 r2 大于今年得短期利 率r1时, 收益率曲线 向上倾斜。
暗示收益率预计会 上升。
当下一年得短期利率 r2 小于今年得短期利 率r1时, 收益率曲线 会下降。
暗示收益率预计会 下降。
图 15、3 短期利率和即期利率
(六)根据观察到得收益率解出 未来短期利率
(1 y2 )2 (1 r1)[1 E(r2 )]
也就是5%,利率期限结构呈现水平。 如果下一年得期望短期收益率E(r2) 就是6%,
则两年期即期利率y2将就是5、5%,利率期限 结构呈现向上。而下一年得期望短期收益率 E(r2) 如果就是4%,则两年期即期利率y2将就 是4、5%,利率期限结构呈现向下。
例15、1 附息债券得估值
使用表15、1得折现率,计算3年期, 票面利率为 10% 得附息债券(假设面值为$1000)得价值:
价值
$100 1.05
$100 1.062
$1100 1.073
价值 = $1082、17 ,又有:
1082.17
$100 1.0688
$100 1.06882
$1100 1.06883
利率的期限结构投资学财经大学
一、利率期限结构概述
利率期限结构就是不同期限债券贴现现金流得 利率结构。
通常情况下,期限短得现金流用较低得利率贴 现,即要求较低得收益率;期限长得现金流用较 高得利率贴现,即要求较高得收益率。
收益率曲线显示了收益率和期限之间得关系, 所以收益率曲线就是利率期限结构得图形表现。
收益率曲线有四种类型:
从收益率曲线四种类型中可以看到,不同期限债 券得收益率不相同。
收益率曲线在固定收益证券领域有重要得作用。
利率期限结构

利率期限结构利率期限结构是指同一借款主体在不同期限借款时所面临的不同利率水平和利率变化情况。
研究利率期限结构对理解金融市场和货币政策等具有重要意义。
一、利率期限结构的概念利率期限结构是利率和借贷期限之间的关系。
其基本原理是资金成本和市场供求关系上的交互作用,表示了市场对不同期限借款的需求和供应关系及其对借款利率的影响。
在短期内,利率期限结构一般呈现上行趋势。
这是因为短期资金需求呈现急需的状况,供求不平衡,导致利率上涨。
而在长期内,利率期限结构一般呈现平稳或下降趋势。
这是因为长期资金成本相对较低,资金需求量相对较小,导致利率基本稳定或下降。
二、利率期限结构的形状类型利率期限结构的形状主要包括以下三种类型:1. 上凸型利率期限结构:在上凸型利率期限结构中,长期借款利率高于短期借款利率。
这种形状出现的时候,一般反映了市场对未来通货膨胀率和利率相对乐观的预期。
2. 倒挂型利率期限结构:在倒挂型利率期限结构中,短期借款利率高于长期借款利率。
这种形状出现的时候,一般反映了市场对未来经济前景和通货膨胀率相对悲观的预期。
3. 平坦型利率期限结构:在平坦型利率期限结构中,不同期限的借款利率基本相同。
这种形状出现的时候,一般反映了市场对未来通货膨胀率和利率相对中性的预期。
三、利率期限结构的决定因素影响利率期限结构的因素主要包括以下三个方面:1. 货币市场供求关系:货币市场供求关系决定短期利率水平。
2. 预期通货膨胀率:这是决定长期利率水平的根本因素。
市场对未来通货膨胀率的不确定性也会影响长期利率结构的形态和变化。
3. 长短期利率之间的互动关系:长短期利率之间的互动关系也是决定利率期限结构形态和变化的重要因素。
四、利率期限结构对金融市场的影响利率期限结构的形态和变化对金融市场和货币政策等具有深远的影响,主要体现在以下几个方面:1. 对股票市场的影响:当利率期限结构呈现上凸型,即长期利率高于短期利率时,大多数上市公司的借款成本比较高,导致企业利润减少,从而对股票市场产生负面影响。
005.基本理论利率理论(二)
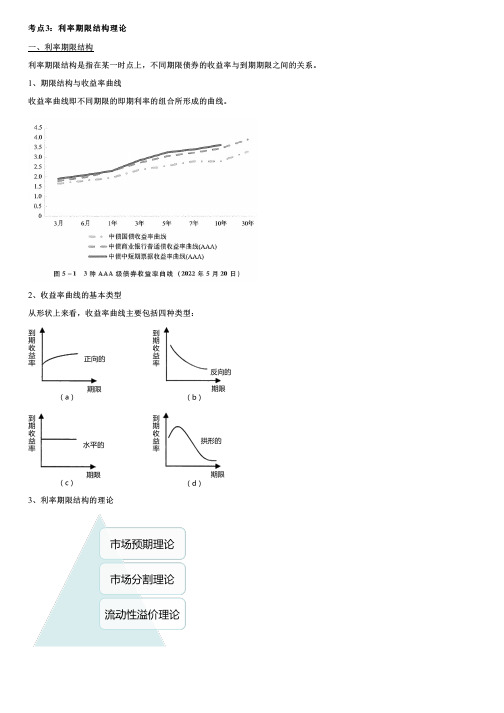
考点3:利率期限结构理论一、利率期限结构利率期限结构是指在某一时点上,不同期限债券的收益率与到期期限之间的关系。
1、期限结构与收益率曲线收益率曲线即不同期限的即期利率的组合所形成的曲线。
2、收益率曲线的基本类型从形状上来看,收益率曲线主要包括四种类型:3、利率期限结构的理论1)市场预期理论又称无偏预期理论,该理论认为利率期限结构完全取决于对未来即期利率的市场预期,长期债券的利率等于长期债券到期日之前各时间段内人们所预期的短期利率的平均值。
如果预期未来即期利率上升,则利率期限结构呈上升趋势;如果预期未来即期利率下降,则利率期限结构呈下降趋势。
在市场预期理论中,某一时点各种期限债券的收益率虽然不同,但是在特定时期内,市场上预计所有债券都取得相同的即期收益率,即长期债券是一组短期债券的理想替代物,长、短期债券取得相同的利率,即市场是均衡的。
【例】人们预期在未来8年中的短期利率平均水平为 9% ,那么按照市场预期理论,8年期债券的利率大致也是9%;如果预期8年后短期利率会升高,预期未来20年中短期利率平均水平为12% , 那么20年期债券的利率大致也是12%。
市场预期理论的前提假定:①投资者对债券的期限没有偏好;②期限不同的债券是完全可以替代的;③投资者的行为取决于预期收益率的变动;④完全替代的债券具有相等的预期收益率。
预期理论可以解释以下事实:①随着时间的推移,不同到期期限的债券利率有同向运动的趋势。
②如果短期利率较低,收益率曲线倾向于向上倾斜;如果短期利率较高,收益率曲线倾向于向下倾斜。
预期理论的缺陷在于无法解释这样一个事实,即收益率曲线通常是向上倾斜的。
因为根据预期理论,典型的收益率曲线应当是平坦的,而非向上倾斜的。
典型的向上倾斜的收益率曲线意味着预期未来短期利率将上升。
事实上,未来短期利率既可能上升,也可能下降。
预期理论还表明,长期利率的波动小于短期利率的波动。
3、利率期限结构的理论2)市场分割理论• 分割市场理论将不同到期期限的债券市场看作完全独立和分割开来的市场。
利率的期限结构

(二)利率的期限结构债券的期限和收益率在某一既定时间存在的关系就称为利率的期限结构,表示这种关系的曲线通常称为收益曲线。
利率期限结构主要讨论金融产品到期时的收益与到期期限这两者之间的关系及变化。
一般而言,随着利率水平的上升,长期收益与短期收益之差将减少或变成负的。
也就是说,当平均利率水平较高时,收益曲线为水平的(有时甚至是向下倾斜的),当利率较低时,收益率曲线通常较陡。
收益率曲线的三种特征:不同期限的债券,其利率经常朝同方向变动。
利率水平较低时,收益率曲线经常呈现正斜率;利率水平较高时,收益率曲线经常出现负斜率。
收益率曲线通常为正斜率。
收益曲线的表现形态有:(1)正常的收益曲线(上升曲线),即常态曲线,指有价证券期限与利率呈正相关关系的曲线;(2)颠倒的收益曲线(下降曲线),指有价证券期限与利率呈负相关关系的曲线。
收益曲线是指那些期限不同、却有着相同流动性、税率结构与信用风险的金融资产的利率曲线。
金融资产收益曲线反映了这样一种现象,即期限不同的有价证券,其利率变动具有相同特征。
曲线的这些特征将通过利率期限结构理论予以解释。
(记住三个理论,理解其含义)1、纯预期理论纯预期理论把当前对未来利率的预期作为决定当前利率期限结构的关键因素。
该理论认为,市场因素使任何期限长期债券的收益率等于当前短期债券收益率与当前预期的超过到期的长期债券收益率的未来短期债券收益率的几何平均。
如果买卖债券的交易成本为零,而且上述假设成立,那么投资者购买长期债券并持有到期进行长期投资时,获得的收益与同样时期内购买短期债券并滚动操作获得的收益相同。
(1)纯预期理论1、该理论把当前对未来的预期是决定当前利率期限结构的关键因素。
2、该理论认为,市场因素使任何期限长期债券的收益率等与当前短期债券收益率与当前预期的超过到期的长期债券收益率的未来短期债券收益率的几何平均。
3、如果买卖债券交易成本为零,上述假设成立的话,该理论结论是:投资者购买长期债券并持有到期所获得的收益与在同样时期内购买短期债券并滚动操作获得的收益相同。
第三章 利率期限结构

• 水平的收益曲线表明债券的收益率与期限长短 无关,不管债券期限如何变化,到期收益率都 是相同的,也就是说长期利率等于短期利率。
二、传统的利率期限结构理论
• 1、纯预期理论 • 纯预期理论最早由费雪提出,其后由希克
斯和卢茨进行了完善,主要内涵可以概括 为:债券的长期利率等于短期利率的预期。
• 仿射指的是若对一个函数F(x)存在常数a、b,使得 对所有x都有F(x)=ax+b,则F(x) 是x的仿射函数。
• 仿射模型通过强调模型设定的数学形式把收益率曲 线表示成状态变量的线性函数,进而求得金融工具 价格的解析解,与多因素模型一样可以将更多风险 因子纳入进来,对利率期限结构进行更好的动态拟 合,且易于操作。
一、利率期限结构概述
• 收益曲线主要有三种形状:向右上方倾斜 的收益曲线,向右下方倾斜的收益曲线, 以及水平的收益曲线益曲线
到期日 反向的收益曲线
到期日
到期日
水平的收益曲线
一、利率期限结构概述
• 向右上方倾斜的收益曲线是最常见的。它表明 期限越长,利率越高,也就是说债券的长期利 率高于短期利率。
三、动态的利率期限结构模型
• 利率期限结构模型主要分为两类:均衡模型和无套利模 型。
• 均衡模型的主要思想是通过假设经济变量,对经济的一 般均衡求解,从而得到短期利率所服从的随机过程,进 而得到债券和其他利率衍生品的价格。其中,宏观经济 相关变量是自变量,当期利率期限结构是因变量。
• 优点:实用性,给定相关的经济变量,它能明确给出一 个均衡,从而把对利率的刻画构建在坚实的微观经济理 论基础上,有助于投资者发现可能的错误定价进而发现 投资机会。
利率的期限结构

利率的期限结构一、利率期限结构的形式债务凭证的期限不同,利率也不同。
利率和债务凭证期限之间的关系,叫做利率的期限结构(term structure of interest rate )。
对于不同的债务凭证来说,利率期限结构可能是不同的。
概括来说,利率的期限结构有三种形式:第一种是利率不随着债务凭证期限的变化而变化。
不论债务凭证的期限是短是长,利率都保持不变。
这种利率期限结构叫做水平的期限结构(flat term structure)。
第二种是利率随着债务凭证期限的延长而提高。
债务凭证的期限越长,利率就越高。
这种利率期限结构叫做上升的期限结构(rising termstructure)。
第三种是利率随着债务凭证期限的延长而下降。
债务凭证的期限越长,利率就越低。
这种利率期限结构叫做下降的期限结构(declining term structure)。
投资者在投资侦务凭证的时候,最关心的是债务凭证的收益率。
虽然债务凭证的收益率和利率有所不同,但是它们存在着正相关的关系。
因此,在研究利率的期限结构时,实际上分析的是收益率的期限结构。
二、利率期限结构的理论解释利率的期限结构的理论有三种:市场预期理论,流动偏好理论和市场分割理论。
1.市场预期理论市场预期理论(The Market Expection Theory)是由费雪(IFisher)在18%年出版的(升值与利息》中提出来的。
希克斯(J. R. Hicks)等人对该理论的发展做出过贡献。
市场预期理论假定,债券投资者只关心如何获得最大利益,而不关心他所持有的债券的期限。
因此,不同期限的债券是可以相互替换的。
购买一张2年期限的债券(上海公积金提取)和先后购买两张1年期限的债券相比较,如果前者的收益率高于后者,投资者将选择前者;如果前者的收益率低于后者,投资者将选择后者。
市场预期理论据此提出,利率的期限结构是由人们对未来市场利率变化的预期决定的。
假设某投资者准备使用100美元进行为期2年的投资时,他可以有两种选择:第一种是购买一张2年期限的债券;第二种是先购买一张1年期限的债券,等待第一年结束时再购买一张I年期限的债券。
利率期限结构课件

市场供求关系是影响利率期限结构的重要因素, 长期债券相对于短期债券风险更大,因此需要更 高的收益率来吸引投资者。
02 经济预期
经济预期也是影响利率期限结构的重要因素,如 果预期未来经济形势好,长期债券收益率会相对 较高。
03 通货膨胀
通货膨胀对利率期限结构的影响主要体现在预期 通货膨胀率上,如果预期通货膨胀率上升,长期 债券收益率也会相应上升。
金融衍生品定价
期权定价
利率期限结构提供了隐含波动率等参 数,用于期权定价模型,如布莱克-舒 尔斯模型。通过这些模型可以计算期 权的理论价值。
利率期货定价
利率期限结构用于确定期货合约的理 论价格。期货合约的未来现金流可以 通过利率期限结构折现到当前价值, 从而计算出期货合约的理论价值。
06
未来研究方向
3
股票市场与货币政策的关系
货币政策通过利率传导机制影响股票市场,央行 可以通过调整利率来调节股票市场的资金供求关 系。
利率期限结构与货币政策
01
货币政策目标与利率期限结构
央行通过货币政策操作影响利率期限结构,以实现经济增长、物价稳定
等政策目标。
02
利率传导机制
央行通过调整短期利率,影响长期利率,进而影响实体经济,这是货币
02
利率期限结构的理论模型
预期理论
总结词
预期理论认为长期债券的利率等于未来短期利率的预期平均值。
详细描述
预期理论认为,投资者会根据对未来短期利率的预期来决定是否购买长期债券。因此,长期债 券的利率应该等于未来短期利率的预期平均值。如果未来短期利率的预期值上升,长期债券的 利率也会相应上升。
市场分割理论
偏好理论认为,投资者对不同期限的债券有不同的风险偏好。对于风险厌恶程度较高的投资者来说,他们更倾向 于购买短期债券;而对于风险偏好较高的投资者来说,他们更倾向于购买长期债券。因此,长期债券的利率与未 来短期利率的关系取决于投资者的风险偏好。
利率期限结构是什么

利率期限结构是什么大家知道什么是利率期限结构吗?它又有什么特点呢?下面就让店铺来为大家介绍一下利率期限结构的相关知识吧。
利率期限结构的概念严格地说,利率期限结构是指某个时点不同期限的即期利率与到期期限的关系及变化规律。
由于零息债券的到期收益率等于相同期限的市场即期利率,从对应关系上来说,任何时刻的利率期限结构是利率水平和期限相联系的函数。
因此,利率的期限结构,即零息债券的到期收益率与期限的关系可以用一条曲线来表示,如水平线、向上倾斜和向下倾斜的曲线。
甚至还可能出现更复杂的收益率曲线,即债券收益率曲线是上述部分或全部收益率曲线的组合。
收益率曲线的变化本质上体现了债券的到期收益率与期限之间的关系,即债券的短期利率和长期利率表现的差异性。
利率期限结构的理论利率的期限结构理论说明为什么各种不同的国债即期利率会有差别,而且这种差别会随期限的长短而变化。
1、预期假说利率期限结构的预期假说首先由欧文·费歇尔(Irving Fisher)(1896年)提出,是最古老的期限结构理论。
预期理论认为,长期债券的现期利率是短期债券的预期利率的函数,长期利率与短期利率之间的关系取决于现期短期利率与未来预期短期利率之间的关系。
如果以Et(r(s))表示时刻t对未来时刻的即期利率的预期,那么预期理论的到期收益可以表达为:因此,如果预期的未来短期债券利率与现期短期债券利率相等,那么长期债券的利率就与短期债券的利率相等,收益率曲线是一条水平线;如果预期的未来短期债券利率上升,那么长期债券的利率必然高于现期短期债券的利率,收益率曲线是向上倾斜的曲线;如果预期的短期债券利率下降,则债券的期限越长,利率越低,收益率曲线就向下倾斜。
这一理论最主要的缺陷是严格地假定人们对未来短期债券的利率具有确定的预期;其次,该理论还假定,资金在长期资金市场和短期资金市场之间的流动是完全自由的。
这两个假定都过于理想化,与金融市场的实际差距太远。
利率期限结构

市场分割假说对三个事实的解释
• 无法解释第一个事实和第二个事实,因为它将不同期限的债券市场看成完全分割的市场。
• 市场分割假说可以解释第三个事实,即典型的收益率曲线总是向上倾斜的。因为在现实经济 中,人们更偏好期限更短,风险较小的债券,而债券发行者一般倾向于发行长期债券以满足 经济发展之需,使得短期债券价格较高,利率较低,长期债券价格较低,利率较高,因此收 益率曲线向上倾斜。
例题
• 策略一 投资于一个两年期债券
1( 1i2t)2 1
1
• 策略二 连续投资于两个一年期债券
i i 1 (1 )(1 e ) 1
t
t 1
1
套利之下,策略一和策略二的收益率趋于相等
(1i2t
)2
(1
it)(1
ie ) t 1
结论
• 简化
e
i i t
t1
i2t
2
• 一般的
•
e ...... e
i i i t t1
t ( n 1)
int
n
对收益率曲线形状的解释
• 若预期的各短期利率高于现行短期利率,则当前长期利率高于短期利率,收益率曲 线向上倾斜。
• 反之,若预期的各短期利率低于现行短期利率,则当前长期利率低于短期利率,收 益率曲线向下倾斜。
纯粹预期假说
• 纯粹预期假说将金融市场视为一个整体,强调不同期限证券间的完全替代性。
假定: • 金融市场不同期限的资产是完全可替代的。人们对于特定的债券没有任何偏好,投
资者仅仅关心债券的预期收益率。(所以,言其“纯粹) • 金融市场是有效率的,人们在不同期限的债券之间进行套利没有转换成本。
结论
利率的风险结构与期限结构讲义

利率的风险结构与期限结构讲义一、利率的风险结构1. 定义:利率的风险结构是指不同期限的借贷利率之间的差异。
在市场经济中,利率是一种重要的金融价格,不同期限的利率会因为市场需求和供给等各种因素的影响而产生差异。
2. 影响因素:- 经济周期:在经济扩张期,资金需求旺盛,市场对短期借贷利率的需求大,短期利率较长期利率更高。
而在经济下行期,市场对长期资金的需求相对较高,长期利率可能较短期利率更高。
- 通货膨胀预期:如果市场预期通货膨胀率将上升,投资者会要求更高的利率来抵消通胀对资金的侵蚀,长期利率可能较短期利率更高。
- 财政政策:政府债券的发行和财政政策的调整,也会对利率的风险结构产生影响。
- 中央银行政策:中央银行通过货币政策调节短期利率,而基准利率的变动也会对其他期限的利率产生影响。
3. 风险结构的形态:- 正常形态:一般情况下,长期利率较短期利率高,但差异不会太大。
这种情况下,市场预期经济状况将保持相对稳定。
- 倒挂形态:在某些特殊情况下,短期利率超过长期利率,通常被视为预示经济衰退的信号。
这可能因为市场预期经济将进入衰退,投资者希望短期内能获得更高的利率。
- 平坦形态:长期利率与短期利率差异较小,通常代表市场对经济走势没有明确的预期。
二、利率的期限结构1. 定义:利率的期限结构是指同一时间点不同期限的借贷利率之间的关系,即短期和长期利率之间的变动情况。
2. 影响因素:- 预期通脱预期:预期通货膨胀率上升,长期利率可能上升;预期通货膨胀率下降,长期利率可能下降。
- 流动性要求:短期利率可能会因为市场对流动性的需求而有所调整。
- 市场情绪:市场对利率的预期、风险偏好和投资者情绪都可能对期限结构产生影响。
3. 期限结构的形态:- 正常形态:短期利率低于长期利率,平均来看,长期利率较高。
这体现了市场对经济状况的预期,即未来经济将保持相对稳定。
- 倒挂形态:短期利率高于长期利率,通常被视为市场对未来经济衰退的担忧,可能预示着经济衰退的到来。
利率期限结构(应用)讲解

• (4)利率期限结构动态模型 • 基本利率期限结构动态模型根据利率期限结构模
型的推导过程,可以分为两种类型:第一种类型就是 一般均衡模型(Equilibriummodel),根据市场的均衡 条件求出利率所必须遵循的一个过程,在这些模型 中,相关的经济变量是输入变量,利率水平是输出变 量;另一种类型是无套利模型(No arbitrage model), 通过相关债券等资产之间必须满足的无套利条件 进行分析,此时利率水平是一个输入变量,相关金融 工具的价格是输出变量.必须特别指出的是,这些模 型都是建立在风险中性世界中,所描述的均是风险 中性世界中的利率变动行为.而实证检验都是利用 现实世界的利率数据进行的.因此,在将现实世界中 的估计结果运用于衍生产品定价时,必须先利用模 型相对应的风险价格通过Girsanov定理将现实世 界转换为风险中性世界,然后再利用风险中性世界 中的相应结果进行定价.
• 一、利率期限结构的现有研究
• 利率期限结构是一个非常广阔的研究领域, 不同的学者都从不同的角度对该问题进行 了探讨,从某一方面得出了一些结论和建议. 根据不同的角度和方向,这些研究基本上可 以分为5类:
• 1)利率期限结构形成假设;
• 2)利率期限结构静态估计;
• 3)利率期限结构自身形态的微观分析;
Zimmermann,D'Ecclesia&Zenios,Sherris,Martellini&Priau let,Maitland,Schere&Avellaneda分别对德国、瑞士、意大 利、澳大利亚、法国、南非、拉美等国家和地区的利率期 限结构进行了主成分和因子分析.朱峰和林海对中国的市 场利率期限结构进行了主成分分析,并在此基础上对中国 债券组合的套期保值提出了若干建议.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:这是前例中的数据。
版权所有:上海财经大学 金融学院 王安兴
11
例:下倾的收益曲线
零息票利率 12% 11.75% 11.25% 10.00% 9.25%
债券到期时间 1 2 3 4 5
版权所有:上海财经大学 金融学院 王安兴
12
例:远期利率——收益曲线下倾
1yr 远期利率
1yr
[(1.1175)2 / 1.12] - 1
版权所有:上海财经大学 金融学院 王安兴
9
四、远期利率与即期利率:计算公式
(1 yn ) n (1 f n ) n 1 (1 yn 1 )
(1 yn ) n (1 yn1 ) n1 (1 f n )
fn = 第n年的远期利率 yn = n年期债券收益率(即期利率)
PVt 1000
1 rt
t
版权所有:上海财经大学 金融学院 王安兴
7
三、付息债券定价
假设付息债券现金流为 ct 、 ct2 、 、 ctn ,则
1
债券价格为:
P
1 r 1 r
t1 t1 t2
ct1
ct2
t2
1 r
tn
ctn
tn
债券到期收益率R为:
版权所有:上海财经大学 金融学院 王安兴
23
流动溢价和收益曲线
收益率
观测到的收 益曲线
远期利率
流动溢价
到期时间
版权所有:上海财经大学 金融学院 王安兴
24
流动溢价和收益曲线
收益率
观测到的收益曲线
远期利率 流动溢价 到期时间
版权所有:上海财经大学 金融学院 王安兴
25
市场分割理论 优先置产理论(Preferred Habitat)
21
流动性偏好理论
长期债券有更大的风险
投资者将要求与长期债券风险相联系的溢价
由于风险溢价的存在,收益率曲线有一个基于长期
利率的向上的偏移 远期利率包含一个流动性溢价且不等于预期未来即 期利率 流动性溢价可能小于零(比较少见)
f n E rn 流动性溢价
版权所有:上海财经大学 金融学院 王安兴
支付一次,则债券价格为:
P 80 80 1080 960.41 2 1.08 1.08995 1.096603
债券到期收益率R为9.59%:
P 80 80 1080 960.41 1.0959 1.09592 1.09593
3年期即期利率为9.660%,大于9.59% 到期收益率与即期利率不同 持有期收益率相同
= 0.115006
2yrs [(1.1125)3 / (1.1175)2] - 1 = 0.102567
3yrs [(1.1)4 / (1.1125)3] - 1
4yrs [(1.0925)5 / (1.1)4] - 1
=
=
0.063336
0.063008
13
版权所有:上海财经大学 金融学院 王安兴
P
1 R
ct1
t1
1 R
ct2
t2
1 R
ctn
tn
付息债券:零息债券的组合 付息债券价格的套利定价:应用套利定价理论 到期收益率与即期利率通常是不同的概念
版权所有:上海财经大学 金融学院 王安兴
8
例:付息债券定价
假设3年期债券面值1000元,息票率8%,每年
例:债券套利定价
面值为1元的3个零息债券,期限分别是1、2和3年,
市场价格分别为0.9元、0.8元和0,7元 面值为1000元的3年期债券,每年付息一次,息票 率为8%,则债券市场价格一定等于
892 0.9 80 0.8 80 0.7 1080
正常的市场没有套利机会
17
预期理论
长期利率是当前即期利率和预期未来即期利率的函
数 长期和短期证券可以完全替代 远期利率是未来即期利率的无偏预测——由长期证 券收益率计算得出的远期利率和预期未来即期利率 一致:市场决定的利率! 预期假设:如果收益曲线向上倾斜,则预期的未来 即期利率大于当前的即期利率;反之,则小于 债券收益率随期限的不同而不同:债券的收益率是 当前即期利率与远期利率的几何平均,而预期的未 来即期利率与当前即期利率可以不同
版权所有:上海财经大学 金融学院 王安兴
29
a. 2年期零息票债券和 2年期息票债券的到期收益率
一年期零息债券的到期收益率:94.34 二年期零息债券的到期收益率:84.99 100 y1 6.000% 1 y1 100
版权所有:上海财经大学 金融学院 王安兴
期限 即期利率(%) 1 2 3.50 4.50
3
4 5
5.00
5.50 6.00
10
6.60
20
预期理论——例
1999年月1日的远期利率
1 y4 1 y3 1 f4 ; 1.055 1.05 1 f4 ; f4 7.01%
22
流动性偏好理论
为了弥补长期债券投资者承担的利率风险,长期债
券的收益比滚动投资短期债券所对应的期望收益高 即使预期将来即期利率下降,如果债券的流动性溢 价足够高,收益曲线依然可以向上倾斜 如果流动性溢价大于零,而收益曲线向下倾斜,则 可以认为预期的未来即期利率小于当前的即期利率 由于通常流动性溢价大于零,因此,远期利率小于 市场对未来即期利率的预期 流动性偏好理论假设:资本市场投资者偏好短期投 资,仅仅当得到溢价补偿时才愿意投资长期证券
版权所有:上海财经大学 金融学院 王安兴
18
预期理论
长期利率可以看作市场预期未来即期利率与期限风
险或流动性溢价之和 预期理论认为流动性溢价为零 因此,远期利率等于市场预期未来即期利率 未来即期利率的市场预测(也就是远期利率)可以从 收益曲线获得 长期期限没有风险溢价(相对于流动性偏好理论) 名义利率
版权所有:上海财经大学 金融学院 王安兴
16
六 、期限结构理论
解释收益曲线形状——经济学解释
分析或预测将来收益曲线变化
(纯)预期理论——未来的看法 流动性偏好理论(流动性溢价理论)——期限溢价 市场分割理论——习惯性偏好 应用——综合???
版权所有:上海财经大学 金融学院 王安兴
版权所有:上海财经大学 金融学院 王安兴
15
案例一、一年期投资:
投资方案二:购买二年期债券,一年后出售 投资者希望未来的即期利率低 案例二、一年期投资: 投资方案一:购买一年期债券,一年后再购买一年 期债券 投资者希望未来的即期利率高 风险溢价??? 远期利率是否等于预期的将来的即期利率,取决于 投资者是否准备承担利率风险,以及投资者是否愿 意持有与他们投资期不一致的债券。
预期的来年1年期利率
年 利率
0 (今天)
1 2 3
8%
10% 11% 11%
版权所有:上海财经大学 金融学院 王安兴
5
债券定价公式: (假设已知未来1年期即期利率)
1 PVn (1 r1 )(1 r2 )...(1 rn )
PVn = 1美元n年后的现值
r1 = 第1年的一年期利率
版权所有:上海财经大学 金融学院 王安兴
14
五、利率不确定性、远期利率与风险
远期利率与将来即期利率——再投资风险与再出售
风险 案例一、一年期投资: 投资方案一:购买一年期债券,持有到期 投资方案二:购买二年期债券,一年后出售 案例二、二年期投资: 投资方案一:购买二年期债券,持有到期 投资方案二:购买一年期债券,一年后再购买一年 期债券
远期利率的无套利决定:应用套利定价理论
版权所有:上海财经大学 金融学院 王安兴
10
例:远期利率
4 yr = 9.993 3yr = 9.660 fn = ? (1.0993)4 = (1.0966)3 (1+fn) (1.46373) / (1.31870) = (1+fn) fn = .10998 或 11%
版权所有:上海财经大学 金融学院 王安兴
27
例:1年期零息票债券的到期收益率为5%,2年期零
息票债券的到期收益率为6%,息票率为12%的2年 期债券(每年付息)的到期收益率为5.8%存在套利机 会吗?如何套利? 息票债券的市场价格 120 1120
p 1.058 1.058
2
1113.98973
短期和长期债券在独立的市场进行交易 在不同市场进行的债券交易决定不同的利率 预期并不直接影响观测到的利率 优先置产
市场分割理论的修正 如果溢价充分大,投资者将转换债券投资的市场 (投资不同到期期限的债券) 收益曲线形状——各市场的供求关系!!!
版权所有:上海财经大学 金融学院 王安兴
4 3 4 3
是对1999年1月1日的1年期即期利率无偏估计的条
件:不同期限的债券完全可替换,没有流动性溢价 或期限溢价 两个使远期利率下降的因素:根据纯预期理论,远 期利率低,说明对应期限内预期的即期利率(名义利 率)低。意味着预期未来实际利率很低,或者预期未 来通货膨胀率很低
版权所有:上海财经大学 金融学院 王安兴
息票债券的无套利价格 套利交易策略
120 1120 p 1111.081727 2 1.05 1.06
版权所有:上海财经大学 金融学院 王安兴
28
例:假定1年期零息票债券面值100元,现价94.34
a. b. c. d.
元,而2年期零息票债券现价84.99元。你正考虑购 买2年期债券,息票率为12% (每年付息),面值 100元 2年期零息票债券的到期收益率是多少? 2年期息 票债券的到期收益率是多少? 第2年的远期利率是多少? 如果纯预期理论成立,则息票债券第一年末的预期 价格和预期持有期收益率是多少? 如果你接受流动性偏好假说,则期望收益率是高还 是低?
