截面的形心静矩培训课件
合集下载
《截面图形几何性质》PPT课件

基本概念
图形对某一对坐标轴y和z取得极值时,图形对该坐标 轴的惯性积为零。 y和z轴称作主惯性轴。图形对主惯性轴的
惯性矩称为主惯性矩。主惯性矩的值是图形对通过同一点的所 有坐标轴的惯性矩的极值。
若主惯性轴通过形心,则该轴称为形心主惯性轴。图 形对形心主惯性轴的惯性矩称为形心主惯性矩。
5.4.1 转轴公式
32
32
圆环形对y(或z)轴的惯性矩为
Iy
Iz
1 2
I
p
64
D4 d 4
由于y轴为对称轴,故
I yz 0
z y
d D
5.2.6 组合图形的惯性矩、惯性积
组合图形对某个坐标轴的惯性矩等于各简单图 形对于同一坐标轴的惯性矩之和;组合图形对某对垂直 坐标轴的惯性积,等于各简单图形对该对坐标轴惯性积 之和,即
4000mm 2
I 20
20
2
2
100
y
Sy S yi Ai zci AI zcI A zII cII
i 1
i 1
4000 45 9000 45 225000mm 3
Sz 210000mm3
5.2 惯性矩 惯性半径 惯性积 Inertial moment, inertial radius & Product of inertia
2
I y1z1
1 2
(
I
y
Iz )sin
2
I yz sin
2
(a)
5.4.2 主惯性轴和主惯性矩(principal moment of inertia)
将式(a)对a求导数,以确定惯性矩的极值
dI y1
d
2
1 2
材料力学课件-10截面的静矩和形心位置

实际应用
静矩在结构设计中的应用
抗弯设计
在结构设计时,需要考虑到截面的抗弯能力。静矩是计算 抗弯能力的重要参数,通过计算截面的静矩,可以确定截 面的抗弯刚度,从而优化结构设计。
稳定性分析
在分析结构的稳定性时,静矩也是一个重要的参数。通过 比较不同截面的静矩,可以判断结构的稳定性,并优化截 面设计。
材料选择
优化设计
通过深入了解静矩和形心位置, 可以更好地优化结构设计,提高 结构的稳定性和安全性践
静矩和形心位置不仅是理论上的 概念,更是指导实践的重要工具 。在实际工程中,这些概念的应 用有助于确保结构的可靠性和安 全性。
THANK YOU
感谢观看
静矩的计算方法
直接积分法
适用于规则截面,通过积分计算得到静矩。
表格法
根据已知的规则截面尺寸和载荷分布,查找表格 中的静矩值。
近似法
对于不规则截面,可以采用近似法估算静矩值。
静矩的性质
静矩具有方向性
根据右手定则判断矩心的方向。
静矩与截面尺寸和形状有关
不同尺寸和形状的截面具有不同的静矩值。
静矩是内力分布的面积分
03
位置,形心位置与截面的形状密切相关。
截面尺寸对形心位置的影响
01
同一形状的截面,尺寸不同时,其形心位置也会发生变化 。
02
例如,矩形截面长度和宽度不同时,其形心位置会有所偏 移。
03
截面尺寸对形心位置的影响:同一形状的截面,尺寸不同时, 其形心位置也会发生变化,但总是位于截面的面积中心。
04
在选择材料时,静矩也是重要的参考因素。不同材料的截 面静矩不同,选择合适的材料可以保证结构的稳定性和安 全性。
形心位置在结构设计中的应用
静矩在结构设计中的应用
抗弯设计
在结构设计时,需要考虑到截面的抗弯能力。静矩是计算 抗弯能力的重要参数,通过计算截面的静矩,可以确定截 面的抗弯刚度,从而优化结构设计。
稳定性分析
在分析结构的稳定性时,静矩也是一个重要的参数。通过 比较不同截面的静矩,可以判断结构的稳定性,并优化截 面设计。
材料选择
优化设计
通过深入了解静矩和形心位置, 可以更好地优化结构设计,提高 结构的稳定性和安全性践
静矩和形心位置不仅是理论上的 概念,更是指导实践的重要工具 。在实际工程中,这些概念的应 用有助于确保结构的可靠性和安 全性。
THANK YOU
感谢观看
静矩的计算方法
直接积分法
适用于规则截面,通过积分计算得到静矩。
表格法
根据已知的规则截面尺寸和载荷分布,查找表格 中的静矩值。
近似法
对于不规则截面,可以采用近似法估算静矩值。
静矩的性质
静矩具有方向性
根据右手定则判断矩心的方向。
静矩与截面尺寸和形状有关
不同尺寸和形状的截面具有不同的静矩值。
静矩是内力分布的面积分
03
位置,形心位置与截面的形状密切相关。
截面尺寸对形心位置的影响
01
同一形状的截面,尺寸不同时,其形心位置也会发生变化 。
02
例如,矩形截面长度和宽度不同时,其形心位置会有所偏 移。
03
截面尺寸对形心位置的影响:同一形状的截面,尺寸不同时, 其形心位置也会发生变化,但总是位于截面的面积中心。
04
在选择材料时,静矩也是重要的参考因素。不同材料的截 面静矩不同,选择合适的材料可以保证结构的稳定性和安 全性。
形心位置在结构设计中的应用
截面的形心静矩课件

截面的几何文档性仅质供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
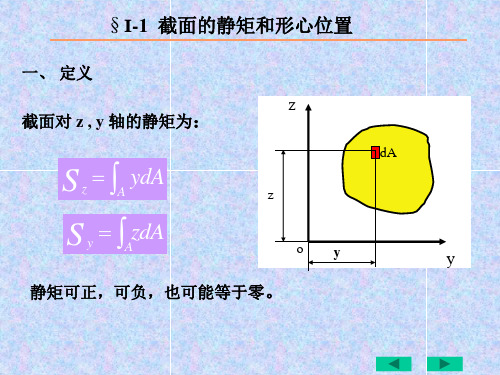
第二节 静矩
一、静距的概念
y 静距是面积与它到轴的距离之积。
dSz ydA dSy zdA
zc=0
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
【例7-2】试求如图7-5所示门字形平面图形的形心坐 标。
解:将平面图形看成是从一个大矩形 中挖去一个小矩形组合而成,每个矩 形的面积和形心坐标分别为: A1=228800××224400==6677220000,,zz11==00,,
在此对称面、对称轴或对称中心上。若平面图形是一个组合 图形,而且各简单图形(如图7-3a、b)的形心容易确定, 则组合形体的形心可按式(7-3)求得,这种求形心的方法为 分割法。另外有些组合图形(如图7-3c、d),可看作为是 从某个简单图形中挖去另一个简单图形而成。则求这类图形 的形心,仍可用分割法,只是切去部分的面积(体积)应取 负值,这种求形心的方法称为负面积法。
另一方面,掌握截面的几何性质的变化规律,就能灵活 机动地为各种构件选取合理的截面形状和尺寸,使构件各部 分的材料能够比较充分地发挥作用,尽可能地做到“物尽其 用”,合理地解决好构件的安全与经济这一对矛盾。
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
重心、形心及静矩
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
【例7-1】试求如图7-4所示工字形截面的形心坐标。
解:将平面图形分割为三个矩形,每个图形的面积 和形心坐标分别为: A1=80×40=3200,z1=0 y1=40+120+40/2=180 A2=120×40=4800, z2=0, y2=40+120/2=100
《截面的几何性质》PPT课件

0
IP
πd 4 32
Iy Iz
另法:
dρ ρ
y
Iy Iz IP
所以
Iy
Iz
πd 4 64
(Properties of Plane Areas)
§10-3 平行移轴公式 (Parallel-axis theorem)
一、平行移轴公式(Parallel-Axis theorem for moment of
Char 10 Properties of Plane Areas
(Properties of Plane Areas)
第10章 截面的几何性质 (Char 10 Properties of plane areas)
§10-1 截面的静矩和形心(The first moments of the area & centroid of an area)
IyC , IzC , IyCzC ̄ 截面对形心轴 yC , zC的惯性矩 和惯性积.
矩形 2
A2 10 80 800mm2
y2
10
80 2
50mm
z2 5mm
所以 y A1 y1 A2 y2 23mm A1 A2
z A1z1 A2z2 38mm A1 A2
z 10
1
y1
z1
2 z2
10
O y2
y
90
(Properties of Plane Areas)
重合
n
y
Ai yi
i 1 n
Ai
A1 y1 A1
A2 y2 A2
i 1
IP
πd 4 32
Iy Iz
另法:
dρ ρ
y
Iy Iz IP
所以
Iy
Iz
πd 4 64
(Properties of Plane Areas)
§10-3 平行移轴公式 (Parallel-axis theorem)
一、平行移轴公式(Parallel-Axis theorem for moment of
Char 10 Properties of Plane Areas
(Properties of Plane Areas)
第10章 截面的几何性质 (Char 10 Properties of plane areas)
§10-1 截面的静矩和形心(The first moments of the area & centroid of an area)
IyC , IzC , IyCzC ̄ 截面对形心轴 yC , zC的惯性矩 和惯性积.
矩形 2
A2 10 80 800mm2
y2
10
80 2
50mm
z2 5mm
所以 y A1 y1 A2 y2 23mm A1 A2
z A1z1 A2z2 38mm A1 A2
z 10
1
y1
z1
2 z2
10
O y2
y
90
(Properties of Plane Areas)
重合
n
y
Ai yi
i 1 n
Ai
A1 y1 A1
A2 y2 A2
i 1
《建筑力学与结构》课件——第五章 截面的几何性质

为零,其单位是m4、cm4、mm4等。
2024/11/13
13
截面的几何性质
建筑力学与结构
4.惯性半径
工程中常把惯性矩表示为平面图形的面积A与某一长度平方的乘积,
即 Iz iz2 A I y iy2 A
惯性半径
iz
Iz A
单位为m、cm、mm等。
iy
Iy A
2024/11/13
14
截面的几何性质
3
图5-1 静矩
截面的几何性质
建筑力学与结构
2.静矩与形心的关系
设平面图形的形心坐标为(zC,yC),平面图形的形心坐标公式为
zdA
zC
A
A
ydA
yC
A
A
静矩与形心的关系式
S z Ayc Sy Azc
平面图形对某轴的静矩等于平面图形的面积乘以其形心到该轴的坐标。
2024/11/13
4
截面的几何性质
解:取参考轴z、y,如图5-2所示。将平面图形分解为两个矩形部分,
这两个矩形部分的形心位置和面积则很容易得出
矩形Ⅰ:
zC1
10 2
5mm
yC1
100 2
50mm
A1 10 100 1000 mm 2
2024/11/13
7
截面的几何性质
矩形Ⅱ:
zC 2
10
70 2
45mm
yC2
10 2
5mm
2024/11/13
17
截面的几何性质
2.计算矩形截面对z轴、y 轴的惯性半径
iz
Iz A
bh3 /12 h bh 2 3
iy
Iy A
《工程力学》课件第6章 截面图形的几何性质

Ip
r2dA A
D 2
r2
2
rdr
D4
0
32
Ip Iy Iz
Iy
பைடு நூலகம்
Iz
Ip 2
D4
64
四、组合截面的惯性矩与惯性积
z
I
例如工字型截面 A AI AII AIII
II
y
III
Iy
z 2 dA
A
z2dA z2dA z2dA
AI
AII
AIII
m
I yI I yII I yIII I yi
包括:形心、静矩、极惯性矩、惯性矩、惯性半径、惯 性积、主轴和形心主轴、主矩和形心主矩等
6.1 静矩和形心
一、静矩
截面对z轴的静矩
z
Sz
ydA
A
截面对y轴的静矩
y
dA
A
z
Sy
zdA
A
o
单位: m3
y
静矩的数值可大于零、等于零或小于零。
二、形心
如图所示均质薄板,重心与形心C重合,
由静力学可知形心坐标在yoz:
何关系, y R sin , dy R cosd ,
dA 2R cosdy 2R2 cos2 d
Sz
A
(2)形心
ydA yC
2 0
Sz A
R sin 2R2 cos2 d
2 R3 3
4R
1 R2 3
zC
2 3
0
R3
2
三、组合截面的静矩和形心 z
D d
y
整个图形对某一轴的静矩等于各个分图形对同一轴的静矩之和。
z1
y1 z
材料力学课件-10截面的静矩和形心位置

材料力学课件ppt-10截面 的静矩和形心位置
本节介绍截面的静矩和形心位置。通过了解截面的定义、静力特征以及形心 的计算方法,我们可以更好地理解材料的行为和性能。
截面的定义
截面是材料在某一位置的横截面形状。了解截面的形状和尺寸对于计算静矩 和形心位置至关重要。
截面的静力特征
1 静矩的定义
静矩是截面内各个点到某一参考轴线的距离乘以该点的截面积的乘积。它示了截面对 外力的抵抗能力。
应用实例
钢梁截面静矩计算
通过计算钢梁截面的静矩和形心位置,可以评估其受力 性能,并确定适当的加固措施。
桥梁截面形心计算
计算桥梁截面的形心位置可以帮助工程师设计合适的支 撑结构,以确保桥梁的稳定性和承载能力。
总结与回顾
本节内容介绍了截面的静矩和形心位置的定义、计算方法以及应用实例。通 过深入理解这些概念,我们可以更好地分析和设计各种结构材料。
2 计算截面的静矩
可以通过积分求解截面的静矩,或者利用几何关系和图形对称性进行简化计算。
形心的定义和计算
1 形心位置的确定方法
2 不规则截面的形心计算
形心是截面上所有点的静矩之和除以截面的总面 积。它表示了截面的重心位置。
对于不规则形状的截面,可以将其分解为几个简 单形状的截面,然后计算各个简单形状的形心, 再进行合成计算。
附录部分课件

由 Ixy
xy d A可知,只要x 轴
A
或y 轴为截面的对称轴,则由于与
该轴对称的任何两个面积元素dA的
惯性积xydA数值相等而正负号相反,
致使整个截面的惯性积必定等于零。
图a所示截面的x 轴和y 轴都是对称
轴,当然Ixy=0。
第四章 弯曲应力
第四章 弯曲应力
例题Ⅰ- 6 图示组合截 面由一个25c号槽钢截面和两 个90 mm×90 mm×12 mm等 边角钢截面组成。试求此截 面分别对于形心轴x和y的惯 性矩Ix 和 Iy 。
至于I x2 则需先求出半圆形对其自身 形心轴的惯性矩。根据平行移轴公式可
得 直径Ix轴xI'(xC图b)23的dπ 惯2 性 πd8矩2,等而于半圆圆形形对对x'轴于
的惯性矩 πd 4 的一半,于是得 64
I xC
I
x
2d 3π
2
πd 2 8
πd 4
2d
2
128 3π
πd 2 8
第四章 弯曲应力
第四章 弯曲应力
解:由型钢规格表查得:
25c号槽钢截面 A 44.91cm2, I xC 3 690 .45 cm4 I yC 218 .415 cm4 形心位置如图所示 90 mm×90 mm×12 mm等边角 钢截面
A 20.30 cm2 I xC I yC 149.22 cm4 形心位置如图所示
1 100 203 100 20 (46.7)2 12
I yC
I1 yC
I2 yC
12.12 106m4
20
yC 1 z2
y
20 140
100 2
第四章 弯曲应力
例题Ⅰ- 5 试求图a所示截 面对于x轴的惯性矩Ix ,对于y轴 的惯性矩Iy ,以及对于x,y轴的 惯性积Ixy 。
截面的静矩和形心位置
Iy
cos 2α
I xy
sin 2α
I y1
Ix
Iy 2
Ix
2
Iy
cos 2α
I xy
sin 2α
I x1 y1
Ix
2
Iy
sin 2α
I xy
cos 2α
y y1
o
x1
x
上式称为转轴公式 显然
I x1 I y1 I x I y
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
C —— 截面形心
a
(a , b ) _____ 形心 c 在 xoy 坐标系下的
坐标。
o
xc , yc ——过截面的形心 c 且与 x , y 轴平 行的坐 标轴(形心轴)
yc
C(a,b)
xc
b
x
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
Ixc ,Iyc , Ixc yc —— 截面对形心轴 xc , yc 的惯性矩和惯性积。
70 20 10
120
y
80
c
x
10
y
Ix
1 12
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
截面对形心轴的静矩等于零。
第七章 静矩及其性质.ppt

z
dA
b
c yc
zc
行于z轴;yc轴平行于y轴。
ay
求:Iz、Iy。
o
z
解:
Iz
y2dA
A
A(yc a)2 dA
A yc2dA
a2dA 2a
A
A ycdA Izc a2 A
Iy
z2dA
A
A (zc
b)2 dA
A zc2dA
2、量纲:[长度]4,单位:m4、mm4。
3、惯性积是对轴而言。
y
z
dA
4、惯性积的取值为正值、负值、零。
y
5、规律:
o
z
两坐标轴中,只要有一个轴为图形的对称轴,则
图形这一对坐标轴的惯性积为零。
17
例2 求图示矩形的 I z ,I y ,I yz ,iy ,iz
z
dz z hc
b
h
I y
之和:
Iz
I zi ,I y
I yi ,I zy
I 24 ziyi
例 求图示直径为d 的半圆对其自身形心轴 xc 的惯性矩。
解: §A-1
y
b( y) 2 R2 y2
b(y) C
yc
d
d
xc
Sx
yd A
A
2 yb( y) d y
0
x
d
2 y2
R2 y2 d y d3
y
求:Iz1、Iy1、Iz1y1。
A dA
dA 在坐标系 ozy 和坐标系oz1y1
的的坐标分别为(z,y )和(z1 ,
材料力学课件(路桥)第5章截面图形的几何性质-PPT精选文档

A
形心轴的惯性矩。 圆
π d Ip I I 2 I y z y c c c 3 2
2
π d4 Iyc Izc 2 6 4
Ip
4 4 4 d π d π d 5 π d I I A B y A c 2 6 4 1 6 6 4
§5-4 惯性矩和惯性积的转轴定理*
截面图形的几何性质
§5–1 静矩和形心
§5–2 惯性矩、极惯性矩、惯性积
§5–3 惯性矩和惯性积的平行移轴定理 §5–4 惯性矩和惯性积的转轴定理* 截面的主惯性轴和主惯性矩
§5-1 静矩和形心 一、静矩:(与力矩类似)是面积与它到轴的距离之积。 z
Sz
y dA z y
ydA
A
S
y
zdA
§5-2 惯性矩、惯性积、极惯性矩 一、惯性矩:(与转动惯量类似) 是面积与它到轴的距离的平方之积。
Iy Iz
z
A
2
dA
z y
y 2d A
ቤተ መጻሕፍቲ ባይዱ
A
dA z y
二、极惯性矩: 是面积对极点的二次矩。
2 Ip d A Iy Iz A
三、惯性积:面积与其到两轴距离之积。
I yz yzd A
A
二、形心: (等厚均质板的质心与形心重合。)
y
质心:
m
ydm m
等厚 均质
A
yt dA t A zt dA t A
A
ydA A zdA A
Sz A Sy A
z
z
m
zdm m
截面的静矩和形心位置及惯性矩的计算课件

数值模拟与优化
利用数值模拟技术,如有限元方法、边界元方法等,可以更精确地计算 截面的静矩和形心位置及惯性矩,并在此基础上进行结构优化设计。
03
多学科交叉
未来研究可以结合多个学科领域,如物理学、化学、生物学等,以更全
面地理解截面的静矩和形心位置及惯性矩的本质和规律,推动相关领域
的发展。
感谢您的观看
THANKS
详细描述
对于任意形状截面,其静矩可以通过对截面进行微分, 然后计算每个微元面积与微元重心到截面边缘的距离乘 积,最后对所有微元的静矩进行积分得到。形心位置可 以通过对截面进行微分,然后计算每个微元的面积与微 元重心坐标的平均值得到。惯性矩可以通过对截面进行 微分,然后计算每个微元的面积、微元重心到截面边缘 的距离以及微元的转动惯量,最后对所有微元的转动惯 量进行积分得到。
矩值。
通过公式计算其半径和 圆周率,得出惯性矩值。
通过公式计算其长轴、 短轴和圆周率,得出惯
性矩值。
不规则截面
需采用数值分析方法进 行近似计算或通过实验
测量得出。
03
截面几何特性的应用
结构强度分析
静矩
静矩是截面内力的一个重要参数,用于计算截面在受力时的稳定性。静矩的计算公式为 ∫(y*dA),其中y为截面各点到截面中心的距离,dA为面积微元。
形心位置
形心是截面的几何中心,其位置决定了截面的质量分布和转动惯量。形心位置可以通过积分 计算得到,公式为∫dA/A∫dxdy,其中A为截面面积。
惯性矩
惯性矩是衡量截面抗弯能力的重要参数,其计算公式为∫y^2dA,其中y为截面各点到形心距 离,dA为面积微元。
结构稳定性分析
结构失稳
当结构受到的外部载荷超 过其承载能力时,结构会 发生失稳,导致结构变形 甚至破坏。
第5章 截面几何性质.ppt

A
y2 d A
A
A
z2
d
A
Iz
Iy
πd 4 32
根据对称性可知,原截面对于形心轴z和y的惯性
矩Iz和Iy是相等的,Iz= Iy,于是得
Iz
Iy
Ip 2
πd 4 64
例:试求图示矩形对z 轴、 y轴的惯性矩Iz、Iy。
y
h y dy
Iz
y2dA
A
h
2 h
y2bdy
2
bh3 12
z
同理
I y
z 2dA
A
b
2 b
z2hdz
2
hb3 12
b
§5-3 惯性矩的平行移轴公式 主轴和主惯性矩
一、惯性矩的平行移轴公式
已知:I z
Iy
y、z轴通
过形心C
y1
求: I z1 I y1
先求 : I z1
z1 y
b
z
C dA A
y z
a y1
Iz
y 2 dA
A
第五章 截面的几何性质
概述 ●截面的几何性质
FN
A
T
Ip
这些与构件横截面的形状、尺寸有关的量统称为
截面的几何性质。
●意义
P
P
截面设计
(a)矩形钢板弯曲
(b)槽形钢ቤተ መጻሕፍቲ ባይዱ弯曲
§5-1 静矩和形心
定义:A ydA 和 A zdA
y
分别称为该截面对z轴和
dA
y轴的静矩
A
y
Sy
zdA
2
y2 d A
A
A
z2
d
A
Iz
Iy
πd 4 32
根据对称性可知,原截面对于形心轴z和y的惯性
矩Iz和Iy是相等的,Iz= Iy,于是得
Iz
Iy
Ip 2
πd 4 64
例:试求图示矩形对z 轴、 y轴的惯性矩Iz、Iy。
y
h y dy
Iz
y2dA
A
h
2 h
y2bdy
2
bh3 12
z
同理
I y
z 2dA
A
b
2 b
z2hdz
2
hb3 12
b
§5-3 惯性矩的平行移轴公式 主轴和主惯性矩
一、惯性矩的平行移轴公式
已知:I z
Iy
y、z轴通
过形心C
y1
求: I z1 I y1
先求 : I z1
z1 y
b
z
C dA A
y z
a y1
Iz
y 2 dA
A
第五章 截面的几何性质
概述 ●截面的几何性质
FN
A
T
Ip
这些与构件横截面的形状、尺寸有关的量统称为
截面的几何性质。
●意义
P
P
截面设计
(a)矩形钢板弯曲
(b)槽形钢ቤተ መጻሕፍቲ ባይዱ弯曲
§5-1 静矩和形心
定义:A ydA 和 A zdA
y
分别称为该截面对z轴和
dA
y轴的静矩
A
y
Sy
zdA
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A3=工40字×形12截0=面48的00形,心z3坐=0标,为y:3=40/2=20
图7-4
y c A A A 1 y y 1 A 1 A A 2 2 y 2 A 3 A 3 y 3 3 2 1 3 0 4 8 2 4 0 8 0 1 0 8 4 0 4 0 0 0 8 0 8 0 2 0 0 1 0 0 0 . 5 5 0
6
若物体是匀质的,即物体的单位体积重量γ是常数。设物 体Δ=体Vγ的的∙nΔ,体重V则积心i,物为坐把体标V此,的公关各重式系微量为带小W入部=式分γ(∙的V7体,-1积每)分一,别微并为小消Δ体去V积γ1、,的Δ则重V得量2、匀Δ…W质、i物
xc
Vx V
yc
Vy V
(7-2)
Vz zc V
可用面积代换。所以薄平板重心的坐标公式为
Ax xc A
yc
Ay A
(7-3)
上式又可称为面积形心的坐标公式。
2/26/2021
截面的形心静矩
8
二、组合图形的形心 若平面图形有对称面、对称轴或对称中心,则它的形心必
在此对称面、对称轴或对称中心上。若平面图形是一个组合 图形,而且各简单图形(如图7-3a、b)的形心容易确定, 则组合形体的形心可按式(7-3)求得,这种求形心的方法为 分割法。另外有些组合图形(如图7-3c、d),可看作为是 从某个简单图形中挖去另一个简单图形而成。则求这类图形 的形心,仍可用分割法,只是切去部分的面积(体积)应取 负值,这种求形心的方法称为负面积法。
A2=200×(280-2×40)=40000 z2=0,
图7-5
y2
200100 2
门字形平面图形的形心坐标为:
y c A A y A 1 y A 1 1 A A 2 2 y 2 67 6 1 2 7 2 4 4 0 20 0 0 0 0 1 0 0 0 0 1 0 00 4 0 09 Zc=0
2/26/2021
截面的形心静矩
3
如图7-1所示,设组成物体的各微小部分所受的 重 重力力分为别 :用ΔW1、ΔW2、…、ΔWn,则物体的总
W=ΔW1+ΔW2+…+ΔWn
2/26/2021
截面的形心静矩
4
取空间直角坐标系Oxyz,设各微小部分重力作
用点的坐标分别为(x1,y1,z1)、(x2,y2,z2)、…、 (xn,yn,zn),物体重心C点的坐标为(xC,,yC,zC)。
由此可见,匀质物体的重心位置与物体的重力无关,取
决于物体的几何形状,与物体的形心重合。
物体的的形心就是它的几何中心。故式(7-2)也是体积
形心的坐标公式。
2/26/2021
截面的形心静矩
7
对于厚度远比其它两个尺寸小得多的匀质薄平板,其 厚度可以略去不计。薄平板的重心就在其所在的平面上,
在薄平板平面内取直角坐标系xoy,故式(7.2)中的体积
zc=0
2/26/2021
截面的形心静矩
10
【例7-2】试求如图7-5所示门字形平面图形的形心坐 标。
解:将平面图形看成是从一个大矩形 中挖去一个小矩形组合而成,每个矩 形的面积和形心坐标分别为: A1=228800××224400==6677220000,,zz11==00,,
y1
20040120 2
截面的几何性质
研究截面几何性质的意义
从上章介绍的应力和变形的计算公式中可以看出,应力 和变形不仅与杆的内力有关,而且与杆件截面的横截面面积 A、极惯性矩IP、抗扭截面系数WP等一些几何量密切相关。 因此要研究构件的的承载能力或应力,就必须掌握截面几何 性质的计算方法。
另一方面,掌握截面的几何性质的变化规律,就能灵活 机动地为各种构件选取合理的截面形状和尺寸,使构件各部 分的材料能够比较充分地发挥作用,尽可能地做到“物尽其 用”,合理地解决好构件的安全与经济这一对矛盾。
对y
my(W)=∑my(ΔW)
即 W∙xC=ΔW1 ∙ x1+ΔW2 ∙ x2+…+ΔWn ∙ xn
所以
xc
Wx W
同理可得:
yc
Wy W
zc
Wz W
2/26/2021
截面的形心静矩
5
因此,一般物体的重心坐标公式为
Wx xc W
yc
Wy W
zc
Wz W
(7-1)
2/26/2021
截面的形心静矩
2/26/2021
截面的形心静矩
11
截面的几何性质
第二节 静矩
一、静距的概念
y 静距是面积与它到轴的距离之积。
dSz ydA dSy zdA
Sz dSz ydA
A
A
S y dS y zdA
A
A
z
dA
y z
平面图形的静矩是对一定的坐标而言的,同一平面图形 对不同的坐标轴,其静矩显然不同。静矩的数值可能为正, 可能为负,也可能等于零。它常用单位是m3或mm3。
2/26/2021截面的形Leabharlann 静矩1重心、形心及静矩
教学目标:
1、理解重心、形心、静矩的概念 2、掌握简单组合图形的形心坐标计算 3、掌握简单组合图形的静矩计算
2/26/2021
截面的形心静矩
2
7.1重心和形心
一、简单图形的重心和形心 地球上的物体都受到重力(地球引力)的作用,
如果把物体看成是由许多微小部分组成的,由于地 球的半径远远大于一般物体的尺寸,可以近似地认 为这些微小部分所受重力是一个空间同向的平行力 系。这个平行力系合力就是物体的重力,其大小即 为物体的总重量。实践证明:无论物体在空间怎样 放置,物体重力的作用线总是通过物体上一个确定 的点,这个点就是物体的重心。(可以说重力合力 的作用点就是物体的重心。)
2/26/2021
截面的形心静矩
12
截面的几何性质
形心
zC
A z A
yC
A
y
A
y
z dA
xC y yC
2/26/2021
zdA
zC
A
A
ydA
yC
A
A
zC
Sy
A
yC
Sz A
Sz A yC
Sy
A zC
平面图形对z轴(或y轴)的 静矩,等于该图形面积A与 其形心坐标yC(或zC)的乘 z 积。
2/26/2021
截面的形心静矩
9
【例7-1】试求如图7-4所示工字形截面的形心坐标。
解:将平面图形分割为三个矩形,每个图形的面积 和形心坐标分别为: A1=80×40=3200,z1=0 y1=40+120+40/2=180 A2=120×40=4800, z2=0, y2=40+120/2=100
图7-4
y c A A A 1 y y 1 A 1 A A 2 2 y 2 A 3 A 3 y 3 3 2 1 3 0 4 8 2 4 0 8 0 1 0 8 4 0 4 0 0 0 8 0 8 0 2 0 0 1 0 0 0 . 5 5 0
6
若物体是匀质的,即物体的单位体积重量γ是常数。设物 体Δ=体Vγ的的∙nΔ,体重V则积心i,物为坐把体标V此,的公关各重式系微量为带小W入部=式分γ(∙的V7体,-1积每)分一,别微并为小消Δ体去V积γ1、,的Δ则重V得量2、匀Δ…W质、i物
xc
Vx V
yc
Vy V
(7-2)
Vz zc V
可用面积代换。所以薄平板重心的坐标公式为
Ax xc A
yc
Ay A
(7-3)
上式又可称为面积形心的坐标公式。
2/26/2021
截面的形心静矩
8
二、组合图形的形心 若平面图形有对称面、对称轴或对称中心,则它的形心必
在此对称面、对称轴或对称中心上。若平面图形是一个组合 图形,而且各简单图形(如图7-3a、b)的形心容易确定, 则组合形体的形心可按式(7-3)求得,这种求形心的方法为 分割法。另外有些组合图形(如图7-3c、d),可看作为是 从某个简单图形中挖去另一个简单图形而成。则求这类图形 的形心,仍可用分割法,只是切去部分的面积(体积)应取 负值,这种求形心的方法称为负面积法。
A2=200×(280-2×40)=40000 z2=0,
图7-5
y2
200100 2
门字形平面图形的形心坐标为:
y c A A y A 1 y A 1 1 A A 2 2 y 2 67 6 1 2 7 2 4 4 0 20 0 0 0 0 1 0 0 0 0 1 0 00 4 0 09 Zc=0
2/26/2021
截面的形心静矩
3
如图7-1所示,设组成物体的各微小部分所受的 重 重力力分为别 :用ΔW1、ΔW2、…、ΔWn,则物体的总
W=ΔW1+ΔW2+…+ΔWn
2/26/2021
截面的形心静矩
4
取空间直角坐标系Oxyz,设各微小部分重力作
用点的坐标分别为(x1,y1,z1)、(x2,y2,z2)、…、 (xn,yn,zn),物体重心C点的坐标为(xC,,yC,zC)。
由此可见,匀质物体的重心位置与物体的重力无关,取
决于物体的几何形状,与物体的形心重合。
物体的的形心就是它的几何中心。故式(7-2)也是体积
形心的坐标公式。
2/26/2021
截面的形心静矩
7
对于厚度远比其它两个尺寸小得多的匀质薄平板,其 厚度可以略去不计。薄平板的重心就在其所在的平面上,
在薄平板平面内取直角坐标系xoy,故式(7.2)中的体积
zc=0
2/26/2021
截面的形心静矩
10
【例7-2】试求如图7-5所示门字形平面图形的形心坐 标。
解:将平面图形看成是从一个大矩形 中挖去一个小矩形组合而成,每个矩 形的面积和形心坐标分别为: A1=228800××224400==6677220000,,zz11==00,,
y1
20040120 2
截面的几何性质
研究截面几何性质的意义
从上章介绍的应力和变形的计算公式中可以看出,应力 和变形不仅与杆的内力有关,而且与杆件截面的横截面面积 A、极惯性矩IP、抗扭截面系数WP等一些几何量密切相关。 因此要研究构件的的承载能力或应力,就必须掌握截面几何 性质的计算方法。
另一方面,掌握截面的几何性质的变化规律,就能灵活 机动地为各种构件选取合理的截面形状和尺寸,使构件各部 分的材料能够比较充分地发挥作用,尽可能地做到“物尽其 用”,合理地解决好构件的安全与经济这一对矛盾。
对y
my(W)=∑my(ΔW)
即 W∙xC=ΔW1 ∙ x1+ΔW2 ∙ x2+…+ΔWn ∙ xn
所以
xc
Wx W
同理可得:
yc
Wy W
zc
Wz W
2/26/2021
截面的形心静矩
5
因此,一般物体的重心坐标公式为
Wx xc W
yc
Wy W
zc
Wz W
(7-1)
2/26/2021
截面的形心静矩
2/26/2021
截面的形心静矩
11
截面的几何性质
第二节 静矩
一、静距的概念
y 静距是面积与它到轴的距离之积。
dSz ydA dSy zdA
Sz dSz ydA
A
A
S y dS y zdA
A
A
z
dA
y z
平面图形的静矩是对一定的坐标而言的,同一平面图形 对不同的坐标轴,其静矩显然不同。静矩的数值可能为正, 可能为负,也可能等于零。它常用单位是m3或mm3。
2/26/2021截面的形Leabharlann 静矩1重心、形心及静矩
教学目标:
1、理解重心、形心、静矩的概念 2、掌握简单组合图形的形心坐标计算 3、掌握简单组合图形的静矩计算
2/26/2021
截面的形心静矩
2
7.1重心和形心
一、简单图形的重心和形心 地球上的物体都受到重力(地球引力)的作用,
如果把物体看成是由许多微小部分组成的,由于地 球的半径远远大于一般物体的尺寸,可以近似地认 为这些微小部分所受重力是一个空间同向的平行力 系。这个平行力系合力就是物体的重力,其大小即 为物体的总重量。实践证明:无论物体在空间怎样 放置,物体重力的作用线总是通过物体上一个确定 的点,这个点就是物体的重心。(可以说重力合力 的作用点就是物体的重心。)
2/26/2021
截面的形心静矩
12
截面的几何性质
形心
zC
A z A
yC
A
y
A
y
z dA
xC y yC
2/26/2021
zdA
zC
A
A
ydA
yC
A
A
zC
Sy
A
yC
Sz A
Sz A yC
Sy
A zC
平面图形对z轴(或y轴)的 静矩,等于该图形面积A与 其形心坐标yC(或zC)的乘 z 积。
2/26/2021
截面的形心静矩
9
【例7-1】试求如图7-4所示工字形截面的形心坐标。
解:将平面图形分割为三个矩形,每个图形的面积 和形心坐标分别为: A1=80×40=3200,z1=0 y1=40+120+40/2=180 A2=120×40=4800, z2=0, y2=40+120/2=100
