(最新)中考数学提优专题:《圆:切割线定理》(含答案)
2021年中考数学必考点培优系列 18 圆与相似:相交线定理、切割线定理(有答案)
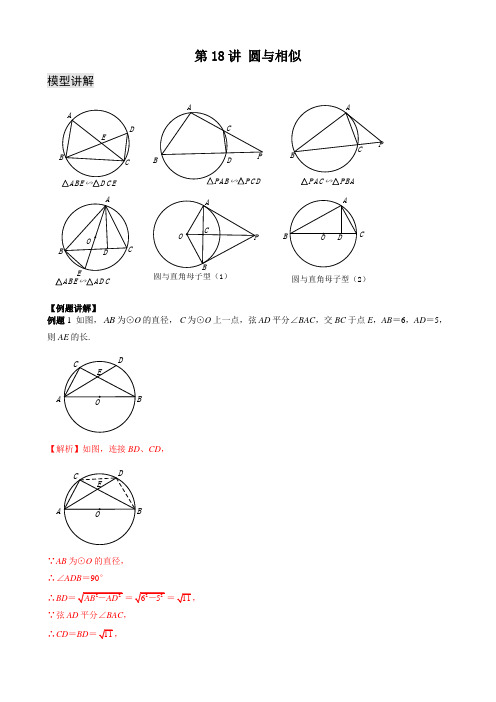
第18讲 圆与相似模型讲解圆与直角母子型(1)圆与直角母子型(2)ABE ∽AD CPAC ∽PBAPAB ∽PC DABE ∽D C EBCDPABCAB CEPDC BA【例题讲解】例题1 如图,AB 为⊙O 的直径, C 为⊙O上一点,弦AD 平分∠BAC ,交BC 于点E ,AB =6,AD =5,则AE 的长.A【解析】如图,连接BD 、CD ,A∵AB 为⊙O 的直径, ∴∠ADB=90°∴BD= ∵弦AD 平分∠BAC , ∴CD =BD∴∠CBD =∠DAB , 在△ABD 和△BED 中, BAD EBD ADB BDE⎧⎨⎩∠=∠∠=∠∴△ABD ∽△BED , ∴DE DB =DBAD解得DE =115. ∴AE =AD -DE =5-115=145. 例题2 如图,在△ABC 中,以AC 边为直径的⊙O 交BC 于点D ,过点B 作BG ⊥AC 交⊙O 于点E 、H ,连AD 、ED 、EC .若BD =8,DC =6,求CE 的长.B【解析】∵AC 为⊙O 的直径, ∴∠ADC =90°, ∵BG ⊥AC ,∴∠BGC =∠ADC =90°, ∵∠BCD =∠ACD , ∴△ADC ∽△BGC , ∴DC CG=ACBC , ∴CG ·AC =DC ·BC =6×14=84, 连接AE ,∵AC 为⊙O 的直径, ∴∠AEC =90°, ∴∠AEC =∠EGC =90°, ∵∠ACE =∠ECG , ∴△CEG ∽△CAE , ∴CG CE =CE AC,∴CE=.B【巩固练习】1.如图,已知D D为等腰三角形ABC的底边BC上的任意一点,AD的延长线交△ABC的外接圆于点E,连接BE、CE,则图中相似三角形共有()A.8对B.6对C.4对D.2对2.如图,AB为⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB交AB于点D,E是OB上一点,直线CE与⊙O交于点F,连接AF交直线CD于点G.若AC=AG·AF=.BA3、如图,已知半圆的直径AB=10,点C在半圆上,CB=6,O为AB的中点,OD⊥AB交AC于点D,则OD=.4.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧AC的中点,BD交AC于点E,若BC=52,CD,则DE = .B5、如图,已知△ABC 内接于⊙0,且AB =AC ,直径AD 交BC 于点E ,F 是OE 的中点,如果BD ∥CF ,BC =,则CD = .BDA(第5题) (第6题) (第7题)6、如图,已知⊙0的半径为4,AB =6,锐角△ABC 内接于⊙0,BD ⊥AC 于点D ,OE ⊥AB于点M ,则sin ∠CBD 的值等于 .7、如图,AD 是圆内接△ABC 的高,AE 是OO 的直径,AB ,AC AE ·AD = .8、如图,△ABC 是⊙0的内接三角形,AB =AC ,BD 平分∠ABC 交⊙0于点D ,连接AD 、C D .作AE ⊥BD 于点E ,若AE =3,DE =1,则△ACD 的面积是 .A9、如图:M 、N 分别为直角坐标系x 、y 正半轴上两点,过M 、N 和原点0三点的圆和直线y =x 交于点P ,(1)试判断△PMN 的形状;(2)连接MN ,设直线y =x 交MN 于点G ,若PG :PN =3:4,△PGN 的周长为6,求△PON 的周长.10、如图,PB 为⊙O 0的切线,B 为切点,直线PO 交⊙O 于点E ,F ,过点B 作PO 的垂线BA ,垂足为点D ,交⊙O 于点A ,延长AO 与⊙O 交于点C ,连接BC 、AF 。
2021年九年级数学中考复习专题之圆:切割线定理综合运用(二)

2021年九年级数学中考复习专题之圆:切割线定理综合运用(二)一.选择题1.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC 等于()A.2 B.3 C.4 D.52.如图,以OB为直径的半圆与半圆O交于点P,A、O、C、B在同一条直线上,作AD⊥AB 与BP的延长线交于点D,若半圆O的半径为2,∠D的余弦值是方程3x2﹣10x+3=0的根,则AB的长等于()A.B.C.8 D.53.如图,两圆相交于C、D,AB是两圆的一条外公切线,A、B为切点,CD的延长线交AB 于M,若CD=9,MD=3,则AB的长为()A.18 B.12 C.13.5 D.6√34.如图:PAB、PCD为⊙O的两条割线,若PA•PB=30,PC=3,则CD的长为()A.10 B.7 C.D.35.如图,点C、O在线段AB上,且AC=CO=OB=5,过点A作以BC为直径的⊙O切线,D 为切点,则AD的长为()A.5 B.6 C.D.106.如图,已知AB、AC分别为⊙O的直径和弦,D为的中点,DE垂直于AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论一定错误的是()A.DE是⊙O的切线B.直径AB长为20cmC.弦AC长为16cm D.C为的中点7.如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为()A.B.C.D.28.如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B、C两点,PB=2cm,BC=8cm,则PA的长等于()A.4cm B.16cm C.20cm D.2cm9.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,CD为直径的⊙O与AB相切于E,则⊙O 的半径是()A.2 B.2.5 C.3 D.410.如图,PA,PB为⊙O的切线,A,B分别为切点,∠APB=60°,点P到圆心O的距离OP =2,则⊙O的半径为()A.B.1 C.D.2二.填空题11.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB=.12.如图,PE是⊙O的切线,E为切点,PAB、PCD是割线,AB=35,CD=50,AC:DB=1:2,则PA=.13.如图,某机械传动装置在静止状态时,连杆PA与点A运动所形成的⊙O交于B点,现测得PB=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是cm.14.如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为.15.如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D,已知∠APB=60°,AC=2,那么CD的长为.三.解答题16.如图,已知矩形ABCD,以A为圆心,AD为半径的圆交AC、AB于M、E,CE的延长线交⊙A于F,CM=2,AB=4.(1)求⊙A的半径;(2)求CE的长和△AFC的面积.17.如图,已知点P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.求证:.18.如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.(1)求证:DA=DC;(2)当DF:EF=1:8,且DF=时,求AB•AC的值;(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O 于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.19.如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直径BD=6,连接CD、AO.(1)求证:CD∥AO;(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;(3)若AO+CD=11,求AB的长.20.如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PE•PF;.(2)当∠BOP=30°,P点为的中点时,求D、E、F、P四个点的坐标及S△DEF参考答案一.选择题1.解:∵PC、PB分别为⊙O的切线和割线,∴PC2=PB•PA,∵OB=3,PB=2,∴PA=8,∴PC2=PB•PA=2×8=16,∴PC=4.故选:C.2.解:∵3x2﹣10x+3=0,∴x=3(不合题意,舍去)或x=.∴cos D=AD:BD=1:3,设AD=x,则BD=3x.∴AB==2x,BC=2x﹣4.∴(2x)2=(2x﹣4)•x.∴x=0(舍去),或x=2.∴AB=2×2=8.故选:C.3.解:∵AB是两圆的一条外公切线,∴MA2=MD•MC,MB2=MD•MC,∵CD=9,MD=3,∴MA=MB=6,∴AB=12,故选:B.4.解:∵PA•PB=PC•PD,PA•PB=30,PC=3,∴PD==10,∴CD=10﹣3=7.故选:B.5.解:∵AD是⊙O的切线,ACB是⊙O的割线,∴AD2=AC•AB,又AC=5,AB=AC+CO+OB=15,∴AD2=5×15=75,∴AD=5.(AD=﹣5不合题意舍去).故选:C.6.解:连接OD,OC.∵D是弧BC的中点,则OD⊥BC,∴DE是圆的切线.故A正确;∴DE2=CE•AE即:36=2AE∴AE=18,则AC=AE﹣CE=18﹣2=16cm.故C正确;∵AB是圆的直径.∴∠ACB=90°,∵DE垂直于AC的延长线于E.D是弧BC的中点,则OD⊥BC,∴四边形CFDE是矩形.∴CF=DE=6cm.BC=2CF=12cm.在直角△ABC中,根据勾股定理可得:AB===20cm.故B正确;在直角△ABC中,AC=16,AB=20,则∠ABC≠30°,而D是弧BC的中点.∴弧AC≠弧CD.故D错误.故选:D.7.解:∵AC是圆O的切线,1∴∠CAB=∠D,又∵∠C=∠C,∴△ACD∽△BCA,∴∴AC2=BC•CD,∵AB=2,BD=3,BC=5,∴AC2=40,AC=2,∵,∴AD=故选:C.8.解:∵PB=2cm,BC=8cm,∴PC=10cm,∵PA2=PB•PC=20,∴PA=2,故选:D.9.解:∵AC,AE为⊙O的切线,∴AC=AE=6,根据勾股定理可知AB=10,∴BE=4;根据切割线定理有,BE2=BD×BC可得,BD=2,∴CD=6,∴⊙O半径为3.故选:C.10.解:连接OA∵PA为⊙O的切线∴PA⊥OA∵∠APO=∠APB=30°∴OA=OP×sin∠APO=2×=1∴⊙O的半径为1故选:B.二.填空题(共5小题)11.解:∵AD•BD=CD•DT,∴TD=,∵CD=2,AD=3,BD=4,∴TD=6,∵PT是⊙O的切线,PA是割线,∴PT2=PA•PB,∵CT为直径,∴PT2=PD2﹣TD2,∴PA•PB=PD2﹣TD2,即(PB+7)PB=(PB+4)2﹣62,解得PB=20.故答案为:20.12.解:设PA=x,∵∠PAC=∠D,∴△PAC∽△PDB,∴=,∵AC:DB=1:2,∴PD=2PA,∴由切割线定理得,PA•PB=PC•PD,即x(x+35)=2x(2x﹣35),解得x=45,故答案为45.13.解:连接PO交圆于C,并延长PO交圆于D;∵PB=4cm,AB=5cm,∴PA=9cm;由割线定理,得:PB•PA=PC•PD;设点P到圆心的距离是xcm,则有:(x﹣4.5)(x+4.5)=36,解得x=7.5cm.故P到O点的距离为7.5cm.14.解:∵PA切⊙O于A,PBC是⊙O的割线,PB=2,PC=4,∴PA2=PB×PC,∴PA==2.故答案为:2.15.解:连接AD,OB,OP;∵PA、PB与⊙O分别相切于点A、点B,∴∠OAP=∠OBP=90°,∠AOB=180°﹣∠P=120°,∴∠AOP=60°,AP=AO tan60°=,∴PC=;∵PA2=PD•PC,∴PD=,∴CD=.三.解答题(共5小题)16.解:(1)四边形ABCD为矩形,AB=4;∴CD=4.在Rt△ACD中,AC2=CD2+AD2;∴(2+AD)2=42+AD2;解得AD=3.(2)过A点作AG⊥EF于G;∵BC=3,BE=AB﹣AE=4﹣3=1.∴CE===.由CE•CF=CD2,得:CF===.又∵∠B=∠AGE=90°,∠BEC=∠GEA,∴△BCE∽△GAE;∴,即=.∴AG=.∴S=CF•AG=××=.△AFC17.证明:连PO交ST于点D,则PO⊥ST;连SO,作OE⊥PB于E,则E为AB中点,于是因为C、E、O、D四点共圆,所以PC•PE=PD•PO又因为Rt△SPD∽Rt△OPS所以即PS2=PD•PO而由切割线定理知PS2=PA•PB所以即18.(1)证明:连接OC,则OC⊥DC,(1分)∴∠DCA=90°﹣∠ACO=90°﹣∠B.∵∠DAC=∠BAE=90°﹣∠B,∴∠DAC=∠DCA.∴DA=DC.(2)解:∵DF:EF=1:8,∵DF=,∴EF=8DF=8.∵DC为⊙O的切线,∴DC2=DF•DE=×9=18.∵DC=3,∴AF=2,AE=6.∴AB•AC=AE•AF=24.(3)解:结论DA=DC仍然成立.理由如下:延长BO交⊙O于K,连接CK,则∠KCB=90°;∵DC为⊙O的切线,∴∠DCA=∠CKB=90°﹣∠CBK.∵∠CBK=∠HBA,∴∠BAH=90°﹣∠HBA=90°﹣∠CBK.∴∠DCA=∠BAH.∴DA=DC.19.(1)证明:连接BC交OA于E点,∵AB、AC是⊙O的切线,∴AB=AC,∠1=∠2.∴AE⊥BC.∴∠OEB=90°.∵BD是⊙O的直径,∴∠DCB=90°.∴∠DCB=∠OEB.∴CD∥AO.(2)解:∵CD∥AO,∴∠3=∠4.∵AB是⊙O的切线,DB是直径,∴∠DCB=∠ABO=90°.∴△BDC∽△AOB.∴=.∴=.∴y=.∴0<x<6.(3)解:由已知和(2)知:,(8分)把x、y看作方程z2﹣11z+18=0的两根,解这个方程得z=2或z=9,∴(舍去).∴AB===.20.(1)证明:连接PB,OP,∵PE⊥AB,PD⊥OB,∴∠BEP=∠PDO=90°,∵AB切⊙O1于B,∠ABP=∠BOP,∴△PBE∽△POD,∴=,同理,△OPF∽△BPD∴=,∴=,∴PD2=PE•PF;(2)解:连接O1B,O1P,∵AB切⊙O1于B,∠POB=30°,∴∠ABP=30°,∴∠O1BP=90°﹣30°=60°,∵O1B=O1P,∴△O1BP为等边三角形,∴O1B=BP,∵P为弧BO的中点,∴BP=OP,即△O1PO为等边三角形,∴O1P=OP=a,∴∠O1OP=60°,又∵P为弧BO的中点,∴O1P⊥OB,在△O1DO中,∵∠O1OP=60°O1O=a,∴O1D=a,OD=a,过D作DM⊥OO1于M,∴DM=OD=a,OM=DM=a,∴D(﹣a,a),∵∠O1OF=90°,∠O1OP=60°∴∠POF=30°,∵PE⊥OA,∴PF=OP=a,OF=a,∴P(﹣a,),F(﹣a,0),∵AB切⊙O1于B,∠POB=30°,∴∠ABP=∠BOP=30°,∵PE⊥AB,PB=a,∴∠EPB=60°∴PE=a,BE=a,∵P为弧BO的中点,∴BP=PO,∴∠PBO=∠BOP=30°,∴∠BPO=120°,∴∠BPE+∠BPO=120°+60°=180°,即OPE三点共线,∵OE=a+a=a,于O,过E作EM⊥x轴于M,∵AO切⊙O1∴∠EOA=30°,∴EM=OE=a,OM=a,∴E(﹣a,a),∵E(﹣a,a),D(﹣a,a),∴DE=﹣a﹣(﹣a)=a,DE边上的高为:a,=×a×a=a2.∴S△DEF故答案为:D(﹣a,a),E(﹣a,a),F(﹣a,0),P(﹣a,);S=a2.△DEF。
2020年中考数学提优专题:《圆:切割线定理》(含答案)

《圆:切割线定理》知识梳理:(1)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT的平方=PA•PB(切割线定理)(2)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.几何语言:∵PBA,PDC是⊙O的割线∴PD•PC=PA•PB(切割线定理推论)(割线定理)由上可知:PT2=PA•PB=PC•PD.一.选择题1.如图,P是⊙O的直径BC延长线上一点,PA切⊙O 于点A,若PC=2,BC=6,则切线PA的长为()A.无限长B.C.4 D.2.如图,PT是⊙O的切线,T为切点,PBA是割线,交⊙O于A、B两点,与直径CT交于点D,已知CD=2,AD=3,BD=4,那么PB等于()A.6 B.C.7 D.203.设H为锐角△ABC的三条高AD、BE、CF的交点,若BC=a,AC=b,AB=c,则AH•AD+BH•BE+CH•CF 等于()A.(ab+bc+ca)B.(a2+b2+c2)C.(ab+bc+ca) D.(a2+b2+c2)4.如图,MN切⊙O于A点,AC为弦,BC为直径,那么下列命题中假命题是()A.∠MAB和∠ABC互余B.∠CAN=∠ABC C.OA=BC D.MA2=MB•BC5.如图,以OB为直径的半圆与半圆O交于点P,A、O、C、B在同一条直线上,作AD⊥AB与BP的延长线交于点D,若半圆O的半径为2,∠D的余弦值是方程3x2﹣10x+3=0的根,则AB的长等于()A.B.C.8 D.56.如图,AB是⊙O直径,AC是⊙O的弦,过弧BC 的中点D作AC的垂线交AC的延长于E,若DE=2,EC=1,则⊙O的直径为()A. B.C.5 D.47.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,AB=PC=2,则PD的长是()A.3 B.7.5 C.5 D.5.58.如图,已知⊙O的弦A B、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=cm,则PE的长为()A.4cm B.3cm C.5cm D.cm9.如图,⊙O1与⊙O2相交于A、B两点,PQ切⊙O1于点P,交⊙O2于点Q、M,交AB的延长线于点N.若MN=1,MQ=3,则NP等于()A.1 B.C.2 D.310.同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆上一点,GE、GF 分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为()A.①③B.②③C.③④D.②④二.填空题11.如图,AB为⊙O的直径,P点在AB的延长线上,PM切⊙O于点M.若OA=a,PM=,那么△PMB 的周长是.12.已知:如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=4,PB=8,则PA =,sin∠P=,CD=.13.如图,PA、PB与⊙O分别相切于点A、点B,AC 是⊙O的直径,PC交⊙O于点D,已知∠APB=60°,AC=2,那么CD的长为.14.如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,若PA=6,PB=4,弧AB的度数为60°,则BC =,∠PCA=度,∠PAB=度.15.如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=.16.如图,AC为⊙O的直径,PA是⊙O的切线,切点为A,PBC是⊙O的割线,∠BAC的平分线交BC于D 点,PF交AC于F点,交AB于E点,要使AE=AF,则PF应满足的条件是(只需填一个条件).17.由⊙O外一点F作⊙O的两条切线,切点分别为B、D,AB是⊙O的直径,连接AD、BD,线段OF交⊙O 于E,交BD于C,连接DE、BE.有下列序号为①~④的四个结论:①BE=DE;②∠EBD=∠EDB;③DE∥AB;④BD2=2AD•FC其中正确的结论有.(把你认为正确结论的序号全部填上)三.解答题18.已知:如图,在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆.(1)求证:AC是⊙O的切线;(2)若AD=6,AE=6,求DE的长.19.如图,圆O是以AB为直径的△ABC的外接圆,D 是劣弧的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;(1)求证:OE=AC;(2)求证:;(3)当AC=6,AB=10时,求切线PC的长.20.如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PE•PF;(2)当∠BOP=30°,P点为的中点时,求D、E、F、P四个点的坐标及S△DEF.参考答案一.选择题1.解:∵PC=2,BC=6,∴PB=8,∵PA2=PC•PB=16,∴PA=4.故选:C.2.解:∵TD•CD=AD•BD,CD=2,AD=3,BD=4,∴TD=6,∵PT2=PD2﹣TD2,∴PT2=PB•PA=(PD﹣BD)(PD+AD),∴PD=24,∴PB=PD﹣BD=24﹣4=20.故选:D.3.解:AH•AD=AC•AE=AC•AB•cos∠BAE=(b2+c2﹣a2),同理BH•BE=(a2+c2﹣b2),CH•CF=(a2+b2﹣c2),故AH•AD+BH•BE+CH•CF=(a2+b2+c2).故选:B.4.解:∵BC是⊙O的直径,∴∠BAC=90°,∴∠MAB+∠CA N=90°;∵MN切⊙O于A,∴MA2=MB•MC,(故D错误)∠CAN=∠CBA,(故B正确)∴∠MAB+∠CBA=90°;(故A正确)∵OA是⊙O的半径,BC是⊙O的直径,∴BC=2OA;(故C正确)故选:D.5.解:∵3x2﹣10x+3=0,∴x=3(不合题意,舍去)或x=.∴cosD=AD:BD=1:3,设A D=x,则BD=3x.∴AB==2x,BC=2x﹣4.∴(2x)2=(2x﹣4)•x.∴x=0(舍去),或x=2.∴AB=2×2=8.故选:C.6.解:连接OD,∵点D是弧BC的中点,∴OD⊥BC,∠OFC=90°,AB是直径,∴∠ACB=90°,DE⊥AE,∴∠E=90°,∴四边形CFDE是矩形,∴∠ODE=90°,∴ED是圆的切线.作OG⊥AC,则OG=CF=ED=2.∵DE2=EC•AE,∴AE=4,AC=3,AG=,∴AO=,∴AB=5.故选:C.7.解:∵PA=3,AB=PC=2,∴PB=5,∵PA•PB=PC•PD,∴PD=7.5,故选:B.8.解:∵PA•PB=PC•PD,PA=4cm,PB=3cm,PC=6cm,∴PD=2;设DE=x,∵AE2=ED•EC,∴x(x+8)=20,∴x=2或x=﹣10(负值舍去),∴PE=2+2=4.故选:A.9.解:∵PN2=NB•NA,NB•NA=NM•NQ,∴PN2=NM•NQ=4,∴PN=2.故选:C.10.解:连接OK,∵EF切小圆于K,∴OK⊥EF,根据垂径定理得EK=FK,∵EP切小圆于P,FQ切小圆于Q,∴EP=EK,FQ=FK,∴EP=FQ,故③正确;∴由切割线定理得,FK2=FN•FG,EK2=EM•EG,∴FN•FG=EM•EG,故④正确;故选:C.二.填空题(共7小题)11.解:连接OM;∵PM切⊙O于点M,∴∠OMP=90°,∵OA=OM=a,PM=,∴tan∠MOP=MP:OM=,∴∠MOP=60°,∴OP=2a,∴PB=OP﹣OB=a;∵OM=OB,∴△OMB是等边三角形,MB=OB=a,∴△PMB的周长是(+2)a.12.解:∵PC切⊙O于点C,割线PAB经过圆心O,PC=4,PB=8,∴PC2=PA•PB.∴PA==2.∴AB=6.∴圆的半径是3.连接OC.∵OC=3,OP=5,∴sin∠P=.∴CE=,∴CD=.13.解:连接AD,OB,OP;∵PA、PB与⊙O分别相切于点A、点B,∴∠OAP=∠OBP=90°,∠AOB=180°﹣∠P=120°,∴∠AOP=60°,AP=AOtan60°=,∴PC=;∵PA2=PD•PC,∴PD=,∴CD=.14.解:∵PA2=PB•PC,PA=6,PB=4;∴PC=9,∴BC=5;∵弧AB的度数为60°,∴∠PCA=30°,∴∠PAB=30°.15.解:由切割线定理得PB•PA=PC•PD,则有8×20=PC(PC+6).解得PC=10.在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.从而AD是圆的直径.由勾股定理,得AD2=AC2+CD2=(PA2﹣PC2)+CD2=202﹣102+62=336.∴AD==4∴R=AD=2.故答案为2.16.解:∵∠PAC=90°,∠ABC=90°,∴90°﹣∠AFP=90°﹣∠BEP,∴∠APF=∠CPF,∴PF平分∠APC.17.解:∵BF,DF是⊙O的两条切线∴OF是∠DFB的角平分线,DF=FB,FO⊥BD,CD=CB∴=∴BE=DE(①正确)∵=∴∠EBD=∠EDB(②正确)∵FB切⊙O于B∴FB⊥OB∵BC⊥OF∵BC2=OC•FC∴(BD)2=OC•CE∵OC为△ABD的中位线∴OC=AD∴(BD)2=AD•CE∴BD2=2AD•FC(④正确)故其中正确的结论有①②④.三.解答题(共3小题)18.(1)证明:连接OE;(1分)∵⊙O是△BDE的外接圆,∠DEB=90°,∴BD是⊙O的直径,(不证直径,不扣分)∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,(2分)∴∠OEB=∠CBE,∴OE∥BC,(3分)∵∠C=90°,∴∠AEO=90°,∴AC是⊙O的切线;(4分)(2)解:∵AE是⊙O的切线,AD=6,AE=6,∴AE2=AD•AB,(5分)∴AB===12,∴BD=AB﹣AD=12﹣6=6;∵∠AED=∠ABE,∠A=∠A,∴△AED∽△ABE,(6分)∴;设DE=x,BE=2x,∵DE2+BE2=BD2,(7分)∴2x2+4x2=36,解得x=±(负的舍去),∴DE=2.(8分)19.(1)证明:∵AB为直径∴∠ACB=90°∴AC⊥BC又D为中点,∴OD⊥BC,OD∥AC,又O为AB中点,∴;(4分)(2)证明:连接CD,PC为切线,由∠PCD=∠CAP,∠P为公共角,∴△PCD∽△PAC,(6分)∴,又CD=BD,∴;(8分)(3)解:∵AC=6,AB=10,∴BC=8,BE=4,OE=3,∴DE=2,∴BD2=DE2+BE2=20,(9分)∴AD2=AB2﹣BD2=80,∴AD=4,(10分)CD=BD=2,由(2),∴,(11分)∴CP2=DP•AP=45×5,∴切线PC=15.(12分)20.(1)证明:连接PB,OP,∵PE⊥AB,PD⊥OB,∴∠BEP=∠PDO=90°,∵AB切⊙O1于B,∠ABP=∠BOP,∴△PBE∽△POD,∴=,同理,△OPF∽△BPD∴=,∴=,∴PD2=PE•PF;(2)解:连接O1B,O1P,∵AB切⊙O1于B,∠POB=30°,∴∠ABP=30°,∴∠O1BP=90°﹣30°=60°,∵O1B=O1P,∴△O1BP为等边三角形,∴O1B=BP,∵P为弧BO的中点,∴BP=OP,即△O1PO为等边三角形,∴O1P=OP=a,∴∠O1OP=60°,又∵P为弧BO的中点,∴O1P⊥OB,在△O1DO中,∵∠O1OP=60°O1O=a,∴O1D=a,OD=a,过D作DM⊥OO1于M,∴DM=OD=a,OM=DM=a,∴D(﹣a,a),∵∠O1OF=90°,∠O1OP=60°∴∠POF=30°,∵PE⊥OA,∴PF=OP=a,OF=a,∴P(﹣a,),F(﹣a,0),∵AB切⊙O1于B,∠POB=30°,∴∠ABP=∠BOP=30°,∵PE⊥AB,PB=a,∴∠EPB=60°∴PE=a,BE=a,∵P为弧BO的中点,∴BP=PO,∴∠PBO=∠BOP=30°,∴∠BPO=120°,∴∠BPE+∠BPO=120°+60°=180°,即OPE三点共线,∵OE=a+a=a,过E作EM⊥x轴于M,∵AO切⊙O1于O,∴∠EOA=30°,∴EM=OE=a,OM=a,∴E(﹣a,a),∵E(﹣a,a),D(﹣a,a),∴DE=﹣a﹣(﹣a)=a,DE边上的高为:a,∴S△DEF=×a×a=a2.故答案为:D(﹣a,a),E(﹣a,a),F(﹣a,0),P(﹣a,);S△DEF=a2.。
2021年中考数学专题关于圆的切线长定理和面积计算习题含答案
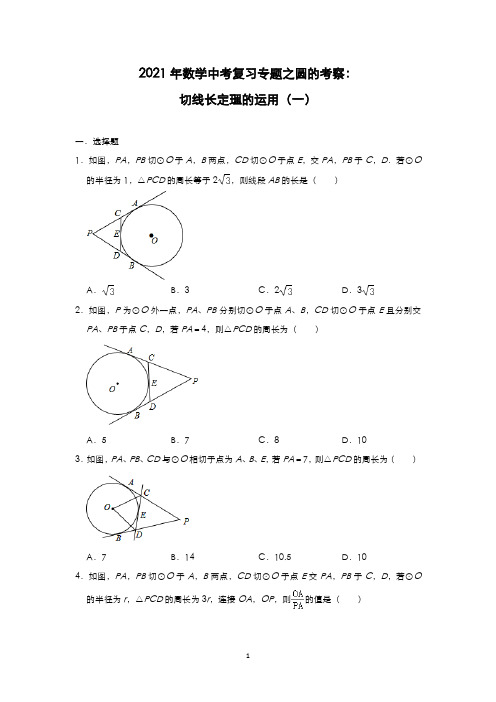
2021年数学中考复习专题之圆的考察:切线长定理的运用(一)一.选择题1.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O 的半径为1,△PCD的周长等于2,则线段AB的长是()A.B.3 C.2D.32.如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E且分别交PA、PB于点C,D,若PA=4,则△PCD的周长为()A.5 B.7 C.8 D.103.如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为()A.7 B.14 C.10.5 D.104.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O 的半径为r,△PCD的周长为3r,连接OA,OP,则的值是()A.B.C.D.5.如图,PA、PB切⊙O于点A、B,PA=8,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是()A.8 B.18 C.16 D.146.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为()A.5,(90°+∠P)B.7,90°+C.10,90°﹣∠P D.10,90°+∠P7.P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是()A.4 B.8 C.12 D.不能确定8.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为()A.20 B.30 C.40 D.509.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35°B.45°C.60°D.70°10.如图,直角梯形ABCD中,以AD为直径的半圆与BC相切于E,BO交半圆于F,DF 的延长线交AB于点P,连DE.以下结论:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4AB•DC.其中正确的是()A.①②③④B.只有①②C.只有①②④D.只有③④二.填空题11.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是cm.12.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD 的周长为.14.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA=cm.15.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是.16.如图,在Rt△ABC中,∠C=90°,BC=5,⊙O与Rt△ABC的三边AB、BC、AC 分别相切于点D、E、F,若⊙O的半径r=2,则Rt△ABC的周长为.三.解答题17.如图,AB、BC、CD分别与⊙O相切于点E、F、G,若∠BOC=90°,(1)求证:AB∥CD;(2)若OB=3,OC=4,求由BE、BC、CG、及弧EFG围成图形的面积(即图中阴影部分).18.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.(1)求∠BAC的度数;(2)当OA=2时,求AB的长.19.如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.(Ⅰ)求∠P的大小;(Ⅱ)若AB=2,求PA的长(结果保留根号).20.如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6.(1)求边AD、BC的长;(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.参考答案一.选择题1.解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,∴AC=EC,DE=DB,PA=PB,∵△PCD的周长等于2,∴PA+PB=2,∴PA=PB=,链接PA和AO,∵⊙O的半径为1,∴tan∠APO===,∴∠APO=30°,∴∠APB=60°,∴△APB是等边三角形,∴AB=PA=PB=.故选:A.2.解:∵PA、PB分别切⊙O于点A、B,∴PB=PA=4,∵CD切⊙O于点E且分别交PA、PB于点C,D,∴CA=CE,DE=DB,∴△PCD的周长=PC+PD+CD=PC+CA+PD+DB=PA+PB=8,故选:C.3.解:∵PA、PB、CD与⊙O相切于点为A、B、E,∴PB=PA=7,CA=CE,DE=DB,∴△PCD的周长=PC+CD+PB=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=14,故选:B.4.解:∵PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,∴CA=CF,DF=DB,PA=PB,∴PC+CF+DF+PD=PA=PB=2PA=3r,∴PA=r,则的值是:=.故选:D.5.解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,∴PB=PA=8,CA=CE,DB=DE,∴△PCD的周长=PC+CE+PD=PC+CE+DE+PC=PC+CA+DB+PD=PA+PB=16.故选:C.6.解:∵PA、PB切⊙O于A、B,CD切⊙O于E,∴PA=PB=10,ED=AD,CE=BC;∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA=10,;如图,连接OA、OE、OB.由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,∵AO=OE=OB,易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),∴∠AOC=∠EOC,∠EOD=∠BOD,∴∠COD=∠AOB,∴∠AOB=180°﹣∠P,∴∠COD=90°﹣∠P.故选:C.7.解:根据题意画出图形,如图所示,由直线DA和直线DC为圆O的切线,得到AD=DC,同理,由直线EC和直线EB为圆O的切线,得到EC=EB,又直线PA和直线PB为圆O的切线,所以PA=PB=4,则△PDE的周长C=PD+DE+PE=PD+DC+EC+PE=PD+DA+EB+PE=PA+PB=4+4=8.故选:B.8.解:据切线长定理有AD=AE,BE=BF,CD=CF;则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40.故选:C.9.解:根据切线的性质定理得∠PAC=90°,∴∠PAB=90°﹣∠BAC=90°﹣35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.故选:D.10.解:∵BA,BE是圆的切线.∴AB=BE,BO是△ABE顶角的平分线.∴OB⊥AE∵AD是圆的直径.∴DE⊥AE∴DE∥OF故①正确;∵CD=CE,AB=BE∴AB+CD=BC故②正确;∵OD=OF∴∠ODF=∠OFD=∠BFP若PB=PF,则有∠PBF=∠BFP=∠ODF而△ADP与△ABO不一定相似,故PB=PF不一定成了.故③不正确;连接OC.可以证明△OAB∽△CDO∴即:OA•OD=AB•CD∴AD2=4AB•DC故④正确.故正确的是:①②④.故选:C.二.填空题(共6小题)11.解:如图所示:菱形ABCD,对角线AC,BD,可得菱形内切圆的圆心即为对角线交点,设AB与圆相切于点E,可得OE⊥AB,∵一个菱形的周长是20cm,两对角线之比是4:3,∴AB=5cm,设BO=4x,则AO=3x,故(4x)2+(3x)2=25,解得:x=1,则AO=3,BO=4,故EO•AB=AO•BO,解得:EO=.故答案为:.12.解:∵PA,PB是⊙O的切线,∴PA=PB,PA⊥OA,∴∠PAB=∠PBA,∠OAP=90°,∴∠PBA=∠PAB=90°﹣∠OAB=90°﹣38°=52°,∴∠P=180°﹣52°﹣52°=76°;故答案为:76.13.解:∵四边形ABCD是⊙O的外切四边形,∴AD+BC=AB+CD=22,∴四边形ABCD的周长=AD+BC+AB+CD=44,故答案为:44.14.解:如图,设DC与⊙O的切点为E;∵PA、PB分别是⊙O的切线,且切点为A、B;∴PA=PB;同理,可得:DE=DA,CE=CB;则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);∴PA=PB=5cm,故答案为:5.15.解:根据切线长定理,得AD=AE,BC=BE,所以梯形的周长是5×2+4=14,故答案为:14.16.解:连接OE、OF,设AD=x,由切线长定理得AF=x,∵⊙O与Rt△ABC的三边AB、BC、AC分相切于点D、E、F,∴OE⊥BC,OF⊥AC,∴四边形OECF为正方形,∵r=2,BC=5,∴CE=CF=2,BD=BE=3,∴由勾股定理得,(x+2)2+52=(x+3)2,解得,x=10,∴△ABC的周长为12+5+13=30,故答案为30.三.解答题(共4小题)17.解:(1)∵∠BOC=90°,∴∠OBC+∠OCB=90°,又BE与BF为圆O的切线,∴BO为∠EBF的平分线,∴∠OBC=∠OBF,同理可得∠OCB=∠OCG,∴∠OBF+∠OCG=90°,∴∠OBC+∠OCB+∠OBE+∠OCG=180°,即∠ABF+∠DCF=180°,∴AB∥CD;(2)连接OE,OF,OG,如图所示:由BE和BF为圆的切线,可得OE⊥AB,OF⊥BC,即∠OEB=∠OFB=90°,∴BE=BF,又OB=OB,∴Rt△OEB≌Rt△OFB(HL),∴∠BOE=∠BOF,S△OEB=S△OFB,∴S扇形OEM=S扇形OFM,∴S△OEB﹣S扇形OEM=S△OFB﹣S扇形OFM,即S阴影BEM=S阴影BFM,同理S阴影NFC=S阴影NCG,由∠BOC=90°,OB=3,OC=4,根据勾股定理得:BC=5,∵BC为圆的切线,∴OF⊥BC,∴OB•OC=BC•OF,即OF=,∴S△BOC=OB•OC=6,S扇形OMN==,则阴影部分面积S=2(S阴影BFM+S阴影NFC)=2(S△BOC﹣S扇形OMN)=12﹣.18.解:(1)∵PA,PB是⊙O的切线,∴AP=BP,∵∠P=60°,∴∠PAB=60°,∵AC是⊙O的直径,∴∠PAC=90°,∴∠BAC=90°﹣60°=30°.(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,∴OP=4,由勾股定理得:,∵AP=BP,∠APB=60°,∴△APB是等边三角形,∴.19.解:(Ⅰ)∵PA是⊙O的切线,AB为⊙O的直径,∴PA⊥AB,∴∠BAP=90°;∵∠BAC=30°,∴∠CAP=90°﹣∠BAC=60°.又∵PA、PC切⊙O于点A、C,∴PA=PC,∴△PAC为等边三角形,∴∠P=60°.(Ⅱ)如图,连接BC,则∠ACB=90°.在Rt△ACB中,AB=2,∠BAC=30°,∵cos∠BAC=,∴AC=AB•cos∠BAC=2cos30°=.∵△PAC为等边三角形,∴PA=AC,∴PA=.20.解:(1)方法1:过D作DF⊥BC于F,在Rt△DFC中,DF=AB=8,FC=BC﹣AD=6,∴DC2=62+82=100,即DC=10.(1分)设AD=x,则DE=AD=x,EC=BC=x+6,∴x+(x+6)=10.∴x=2.∴AD=2,BC=2+6=8.(4分)方法2:连OD、OE、OC,由切线长定理可知∠DOC=90°,AD=DE,CB=CE,设AD=x,则BC=x+6,由射影定理可得:OE2=DE•EC.(2分)即:x(x+6)=16,解得x1=2,x2=﹣8,(舍去)∴AD=2,BC=2+6=8.(4分)(2)存在符合条件的P点.设AP=y,则BP=8﹣y,△ADP与△BCP相似,有两种情况:①△ADP∽△BCP时,∴y=;(6分)②△ADP∽△BPC时,∴y=4.(7分)故存在符合条件的点P,此时AP=或4.(8分)2021年数学中考复习专题之圆的考察:扇形面积的计算的运用(一)一.选择题1.如图,在矩形ABCD中,AB=4,AD=2,分别以点A、C为圆心,AD、CB为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是()A.4﹣2πB.8﹣C.8﹣2πD.8﹣4π2.如图所示,⊙O是以坐标原点O为圆心,4为半径的圆,点P的坐标为(,),弦AB经过点P,则图中阴影部分面积的最小值等于()A.2π﹣4 B.4π﹣8 C.D.3.如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是()A.B.﹣2C.D.﹣4.运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是()A.πB.10πC.24+4πD.24+5π5.如图,在等边△ABC中,AB=2,以点A为圆心,AB为半径画,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为()A.π﹣2 B.π﹣1 C.2π﹣2 D.2π+16.如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为()A.﹣4 B.7﹣4 C.6﹣D.7.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为()A.B.C.+D.8.如图,在扇形AOB中,∠AOB=90°,=,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为()A.2π﹣4 B.4π﹣8 C.2π﹣8 D.4π﹣49.如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为()cm2.A.πB.24﹣πC.24﹣πD.24﹣π10.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D 为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为()A.B.C.D.二.填空题11.如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接EF,则图中阴影部分的面积是.12.如图,⊙O的半径是4,圆周角∠C=60°,点E时直径AB延长线上一点,且∠DEB=30°,则图中阴影部分的面积为.13.如图,Rt△ABC中,∠B=90°,AB=6,BC=8,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A′B′C,则边AB扫过的面积(图中阴影部分)是.14.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是.15.如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是.16.如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是.三.解答题17.如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB 的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.(1)求劣弧PC的长;(结果保留π)(2)求阴影部分的面积.(结果保留π).18.如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交斜边AB于点D.点E为边AC的中点,连接DE并延长交BC的延长线于点F.(1)求证:直线DE⊙O的切线;(2)若∠B=30°,AC=4,求阴影部分的面积.19.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AC,BC.(1)求证:∠A=∠BCD;(2)若CD=4,∠B=60°,求扇形OAC(阴影部分)的面积.20.如图,已知AB,CD是⊙O的两条直径,AE∥CD交⊙O于点E,连结BE交CD于点F.(1)求证:弧BD=弧ED;(2)若⊙O的半径为6,AE=6,求图中阴影部分的面积.参考答案一.选择题1.解:∵矩形ABCD,∴AD=CB=2,∴S阴影=S矩形﹣S半圆=2×4﹣π×22=8﹣2π,故选:C.2.解:由题意当OP⊥AB时,阴影部分的面积最小,∵P(,),∴OP=2,∵OA=OB=4,∴PA=PB=2,∴tan∠AOP=tan∠BOP=,∴∠AOP=∠BOP=60°,∴∠AOB=120°,∴S阴=S扇形OAB﹣S△AOB=﹣•4•2=,故选:D.3.解:连接OC,∵点C是以AB为直径的半圆O的三等分点,∴∠ACB=90°,∠AOC=60°,∠COB=120°,∴∠ABC=30°,∵AC=2,∴AB=2AO=4,BC=2,∴OC=OB=2,∴阴影部分的面积=S扇形﹣S△OBC=﹣×2×1=π﹣,4.解:作直径CG,连接OD、OE、OF、DG.∵CG是圆的直径,∴∠CDG=90°,则DG===8,又∵EF=8,∴DG=EF,∴=,∴S扇形ODG=S扇形OEF,∵AB∥CD∥EF,∴S△OCD=S△ACD,S△OEF=S△AEF,∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=π×52=π.故选:A.5.解:∵等边△ABC中,∠BAD=105°,∴∠CAE=105°﹣60°=45°,∵CE⊥AD,AC=AB=2,∴AE=CE=2,∴S△ACE=2,S扇形ACD==π,∴阴影部分的面积为S扇形ACD﹣S△ACE=π﹣2,6.解:∵⊙O的直径AB=2,∴∠C=90°,∵C是弧AB的中点,∴,∴AC=BC,∴∠CAB=∠CBA=45°,∵AE,BE分别平分∠BAC和∠ABC,∴∠EAB=∠EBA=22.5°,∴∠AEB=180°﹣(∠BAC+∠CBA)=135°,连接EO,∵∠EAB=∠EBA,∴EA=EB,∵OA=OB,∴EO⊥AB,∴EO为Rt△ABC内切圆半径,∴S△ABC=(AB+AC+BC)•EO=AC•BC,∴EO=﹣1,∴AE2=AO2+EO2=12+(﹣1)2=4﹣2,∴扇形EAB的面积==(2﹣),△ABE的面积=AB•EO=﹣1,∴弓形AB的面积=扇形EAB的面积﹣△ABE的面积=,∴阴影部分的面积=⊙O的面积﹣弓形AB的面积=﹣(﹣)=﹣4,故选:A.7.解:连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE==π,∴S阴影=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)=﹣﹣(π﹣×1×)=π﹣π+=+.故选:C.8.解:连接OC,如图所示:∵在扇形AOB中∠AOB=90°,=,∴∠COD=45°,∴OD=CD,∴OC==4,∴阴影部分的面积=扇形BOC的面积﹣△ODC的面积=﹣×(2)2=2π﹣4.故选:A.9.解:∵Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,∴AC==10cm,△ABC的面积是:AB•BC=×8×6=24cm2.∴S阴影部分=×6×8﹣cm2故阴影部分的面积是:24﹣πcm2.故选:D.10.解:连接CD,作DM⊥BC,DN⊥AC.∵CA=CB,∠ACB=90°,点D为AB的中点,∴DC=AB=1,四边形DMCN是正方形,DM=.则扇形FDE的面积是:=.∵CA=CB,∠ACB=90°,点D为AB的中点,∴CD平分∠BCA,又∵DM⊥BC,DN⊥AC,∴DM=DN,∵∠GDH=∠MDN=90°,∴∠GDM=∠HDN,则在△DMG和△DNH中,,∴△DMG≌△DNH(ASA),∴S四边形DGCH=S四边形DMCN=.则阴影部分的面积是:﹣.故选:D.二.填空题(共6小题)11.解:过F作FM⊥BE于M,则∠FME=∠FMB=90°,∵四边形ABCD是正方形,AB=2,∴∠DCB=90°,DC=BC=AB=2,∠DBC=45°,由勾股定理得:BD=2,∵将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,∴∠DCE=90°,BF=BD=2,∠FBE=90°﹣45°=45°,∴BM=FM=2,ME=2,∴阴影部分的面积S=S△BCD+S△BFE+S扇形DCE﹣S扇形DBF=++﹣=6﹣π,12.解:连接OD,∵∠C=60°,∴∠AOD=2∠C=120°,∴∠DOB=60°,∵∠DEB=30°,∴∠ODE=90°,∵OD=4,∴OE=2OD=8,DE=OD=4,∴阴影部分的面积是S=S△ODE﹣S扇形DOB=﹣=8﹣,故答案为:8﹣.13.解:∵∠B=90°,AB=6,BC=8,∴AC=10,∴边AB扫过的面积=﹣=9π,故答案为:9π.14.解:作DH⊥AE于H,∵∠AOB=90°,OA=3,OB=2,∴AB==,由旋转的性质可知,OE=OB=2,DE=EF=AB=,△DHE≌△BOA,∴DH=OB=2,阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=×5×2+×2×3+﹣=8﹣π,15.解:∵四边形ABCD是菱形,∠DAB=60°,∴AD=AB=6,∠ADC=180°﹣60°=120°,∵DF是菱形的高,∴DF⊥AB,∴DF=AD•sin60°=6×=3,∴图中阴影部分的面积=菱形ABCD的面积﹣扇形DEFG的面积=6×3﹣=18﹣9π.故答案为:18﹣9π.16.解:∵四边形ABCD是菱形,∴∠B=∠D=60°,AB=AD=DC=BC=2,∴∠BCD=∠DAB=120°,∴∠1=∠2=60°,∴△ABC、△ADC都是等边三角形,∴AC=AD=2,∵AB=2,∴△ADC的高为,AC=2,∵扇形BEF的半径为1,圆心角为60°,∴∠4+∠5=60°,∠3+∠5=60°,∴∠3=∠4,设AF、DC相交于HG,设BC、AE相交于点G,在△ADH和△ACG中,,∴△ADH≌△ACG(ASA),∴四边形AGCH的面积等于△ADC的面积,∴图中阴影部分的面积是:S扇形AEF﹣S△ACD=﹣×2×=﹣,故答案为:﹣.三.解答题(共4小题)17.解:(1)∵点D是AB的中点,PD经过圆心,∴PD⊥AB,∵∠A=30°,∴∠POC=∠AOD=60°,OA=2OD,∵PF⊥AC,∴∠OPF=30°,∴OF=OP,∵OA=OC,AD=BD,∴BC=2OD,∴OA=BC=2,∴⊙O的半径为2,∴劣弧PC的长===π;(2)∵OF=OP,∴OF=1,∴PF==,∴S阴影=S扇形﹣S△OPF=﹣×1×=π﹣.18.(1)证明:连接OD、CD,∵OC=OD,∴∠OCD=∠ODC,又∵BC是⊙O的直径,∴∠BDC=90°,∴△ACD是直角三角形,又∵点E是斜边AC的中点,∴EC=ED,∴∠ECD=∠EDC又∵∠ECD+∠OCD=∠ACB=90度,∴∠EDC+∠ODC=∠ODE=90°,∴直线DE是⊙O的切线;(2)解:由(1)已证:∠ODF=90°,∴∠B=30°,∴∠DOF=60°,∴∠F=30°,在Rt△ABC中,AC=4,∴BC===4,∴,在Rt△ODF中,,∴阴影部分的面积为:=.19.(1)证明:∵AB是⊙O的直径,弦CD⊥AB,∴=,∴∠A=∠BCD;(2)解:∵OC=OB,∠B=60°,∴△BOC为等边三角形,∴∠BOC=60°,∴∠AOC=120°,∵AB是⊙O的直径,弦CD⊥AB,∴CE=CD=2,在Rt△COE中,OC==4,∴扇形OAC(阴影部分)的面积==π.20.(1)证明:∵AB,CD是⊙O的两条直径,∴∠AOC=∠BOD,∴=,∵AE∥CD,∴=,∴=;(2)解:连接OE,作OH⊥AE于H,则AH=HE=AE=3,cos∠OAH==,∴∠OAH=30°,∴OH=OA=3,∠AOH=60°,∴∠AOE=120°,∴图中阴影部分的面积=﹣×6×3=12π﹣9.。
2021年九年级数学中考复习专题之圆:切割线定理综合运用(一)

2021年九年级数学中考复习专题之圆:切割线定理综合运用(一)一.选择题1.P是⊙O外一点,PA切⊙O于A,割线PBC交⊙O于点B、C,若PB=BC=3,则PA的长是()A.9 B.3 C.D.182.如图,PA切⊙O于点A,PBC是⊙O的一条割线,且PA=2,BC=2PB,那么PB 的长为()A.2 B.C.4 D.3.如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D.已知PA=6,AB=4,PC=5,则CD=()A.B.C.7 D.244.如图,已知P为⊙O外一点,PO交⊙O于点A,割线PBC交⊙O于点B、C,且PB =BC,若OA=7,PA=4,则PB的长等于()A.B.C.6 D.5.如图,PA切⊙O于点A,PBC是⊙O的割线,如果PB=2,PC=8,那么PA的长为()A.2 B.4 C.6 D.6.如图,在▱ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE =5,则DE的长为()A.3 B.4 C.D.7.如图,在以O为圆心的两个同心圆中,A为大圆上任意一点,过A作小圆的割线AXY,若AX•AY=4,则图中圆环的面积为()A.16πB.8πC.4πD.2π8.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=()A.6 B.7 C.8 D.99.以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若,且AB=10,则CB的长为()A.B.C.D.410.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB =60°,PA=8,那么点P与O间的距离是()A.16 B.C.D.二.填空题11.如图,⊙O的半径为,A、B两点在⊙O上,切线AQ和BQ相交于Q,P是AB 延长线上任一点,QS⊥OP于S,则OP•OS=.12.如图,过点P引圆的两条割线PAB和PCD,分别交圆于点A,B和C,D,连接AC,BD,则在下列各比例式中,①;②;③,成立的有(把你认为成立的比例式的序号都填上).13.如图,割线PAB与⊙O交于点A、B,割线PCD与⊙O交于点C、D,PA=PC,PB=3cm,则PD=cm.14.如图,过⊙O外一点P作两条割线,分别交⊙O于A,B和C,D.已知PA=2,PB =5,PD=8,则PC的长是.15.如图,AC为⊙O的直径,PA是⊙O的切线,切点为A,PBC是⊙O的割线,∠BAC 的平分线交BC于D点,PF交AC于F点,交AB于E点,要使AE=AF,则PF应满足的条件是(只需填一个条件).三.解答题16.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E.若AB=CD=2,求CE的长.17.如图所示,⊙O的内接△ABC的AB边过圆心O,CD切⊙O于C,BD⊥CD于D,交⊙O于F,CE⊥AB于点E,FE交⊙O于G.解答下列问题:(1)若BC=10,BE=8,求CD的值;(2)求证:DF•DB=EG•EF.18.如图1,已知Rt△ABC的直角边AC的长为2,以AC为直径的⊙O与斜边AB交于点D,过D点作⊙O的切线(1)求证:BE=DE;(2)延长DE与AC的延长线交于点F,若DF=,求△ABC的面积;(3)从图1中,显然可知BC<AC.试分别讨论在其它条件不变,当BC=AC(图2)和BC>AC(图3)时,直线DE与直线AC还会相交吗?若不能相交,请简要说明理由;若能相交,设交点为F'且DF'=,请再求出△ABC的面积.19.已知:如图,PF是⊙O的切线,PE=PF,A是⊙O上一点,直线AE、AP分别交⊙O 于B、D,直线DE交⊙O于C,连接BC,(1)求证:PE∥BC;(2)将PE绕点P顺时针旋转,使点E移到圆内,并在⊙O上另选一点A,如图2.其他条件不变,在图2中画出完整的图形.此时PE与BC是否仍然平行?证明你的结论.20.如图PAB、PCD是⊙O的两条割线,AB是⊙O的直径.(1)如图甲,若PA=8,PC=10,CD=6.①求sin∠APC的值;②sin∠BOD=;(2)如图乙,若AC∥OD.①求证:CD=BD;②若,试求cos∠BAD的值.参考答案一.选择题1.解:∵PB=BC=3,∴PC=6,∵PA2=PB•PC=18,∴PA=3,故选:C.2.解:设PB=x,则PC=3x,∵PA2=PB•PC,PA=2,BC=2PB,∴x•3x=12,∴x=2.故选:A.3.解:由于PAB、PCD都是⊙O的割线,根据切割线定理可得:PA•PB=PC•PD,即PA•(PA+PB)=PC•PD,∵PA=6,AB=4,PC=5,∴PD=12,即CD=PD﹣PC=7;故选:C.4.解:延长PO交圆于D;设PB=BC=x,∵PB•PC=PA•PD,PB=BC,OA=7,PA=4,∴x•2x=72,∴x=6.故选:C.5.解:∵PA切⊙O于点A,PBC是⊙O的割线,∴PA2=PB•PC=16,即PA=4;故选:B.6.解:连接CE;∵,∴∠BAE=∠EBC+∠BEC;∵∠DCB=∠DCE+∠BCE,由弦切角定理知:∠DCE=∠EBC,由平行四边形的性质知:∠DCB=∠BAE,∴∠BEC=∠BCE,即BC=BE=5,∴AD=5;由切割线定理知:DE=DC2÷DA=,故选:D.7.解:过点A作圆的切线AD,切点是D,∵AD2=AX•AY,AX•AY=4,∴AD=2,∴圆环的面积=πAD2=4π.故选:C.8.解:∵PB,PD是⊙O的割线,∴PA•PB=PC•PD,∵PA=2,PC=CD=3,∴2PB=3×6解得:PB=9.故选:D.9.解:如图,若,且AB=10,∴AD=4,BD=6,作AB关于直线BC的对称线段A′B,交半圆于D′,连接AC、CA′,可得A、C、A′三点共线,∵线段A′B与线段AB关于直线BC对称,∴AB=A′B,∴AC=A′C,AD=A′D′=4,A′B=AB=10.而A′C•A′A=A′D′•A′B,即A′C•2A′C=4×10=40.则A′C2=20,又∵A′C2=A′B2﹣CB2,∴20=100﹣CB2,∴CB=4.故选:A.10.解:连接OA,OP∵PA,PB是⊙O的切线,∠APB=60°,∴∠OPA=∠APB=30°,OA⊥OP,∴OP===,∴点P与O间的距离是.故选:B.二.填空题(共5小题)11.解:连接OQ交AB于M,则OQ⊥AB,连接OA,则OA⊥AQ.∵∠QMP=∠QSP=90°,∴S,P,Q,M四点共圆,故OS•OP=OM•OQ.又∵OM•OQ=OA2=2,∴OS•OP=2.故答案为:2.12.解:∵四边形ABCD是圆内接四边形∴∠PAD=∠C,∠PAD=∠B∴△PAD∽△PCB根据相似三角形的对应边的比相等,得到②③是正确的.13.解:∵PA•PB=PC•PD,PA=PC,PB=3cm∴PB=PD=3cm.14.解:∵PA•PB=PC•PD,PA=2,PB=5,PD=8∴PC==.15.解:∵∠PAC=90°,∠ABC=90°,∴90°﹣∠AFP=90°﹣∠BEP,∴∠APF=∠CPF,∴PF平分∠APC.三.解答题(共5小题)16.解:如图,由切割线定理,得CD2=CB•CA,(2分)CD2=CB(AB+CB),CB2+2CB﹣4=0,解得CB=(负数舍去)连接OD,则OD⊥CD,又EB与⊙O相切,∴EB⊥OC,∴Rt△ODC∽Rt△EBC,(6分)于是,即∴CE=.17.(1)解:∵AB为直径,BD⊥CD∴∠ABC+∠A=90°,∠CBD+∠BCD=90°∵CD为⊙O切线∴∠BCD=∠A∴∠ABC=∠BCD∵CD⊥BD,CE⊥BE∴CE=CD∴CE==6∴CD=6(2)证明:∵CD为切线,BD为割线∴CD2=DF•DB①∵∠ACB=90°,CE⊥AB∴RT△ACE∽RT△CBE∴CE2=EA•EB②∵EG•EF=EA•EB③由①②③及CD=CE得DF•DB=EG•EF.18.(1)证明:连接OD,∴OD⊥DE,∴∠ADO+∠BDE=90°,∵OA=OD,∴∠A=∠ADO,∵∠ACB=90°,∴∠B+∠A=90°,∴∠B=∠BDE,∴BE=DE;(2)解:在直角三角形ODF中,OD=1,DF=,∴∠OFD=30°,∴OF=2,AF=3.∴tan∠A=,∴BC=AC•tan∠A=2×tan30°=.S△ABC=AC•BC=×2×=;(3)解:如图,当BC=AC时,直线DE与直线AC平行;当BC>AC时,在直角三角形ODF′中,OD=1,DF′=,∴∠OF′D=30°,∴OF′=2,AF=1,∴CF′=3,∠BAC=60°,∴tan∠BAC=,∴BC=AC•tan∠BAC=2×tan60°=2.S△ABC=AC•BC=×2×2=2.19.(1)证明:∵PF与⊙O相切,∴PF2=PD•PA.∵PE=PF,∴PE2=PD•PA.∴PE:PD=PA:PE.∵∠APE=∠APE,∴△EPD∽△APE.∴∠PED=∠A.∵∠ECB=∠A,∴∠PED=∠ECB.∴PE∥BC.(2)解:PE与BC仍然平行.证明:画图如图,∵△EPD∽△APE,∴∠PEA=∠D.∵∠B=∠D,∴∠PEA=∠B.∴PE∥BC.20.解:(1)作OE⊥CD于E,连接OC,作DF⊥PB于F.①根据垂径定理,得CE=3.设圆的半径是r.根据勾股定理,得OP2﹣PE2=OC2﹣CE2,(8+r)2﹣169=r2﹣9,解得r=6.则OE=3.则sin∠APC==;②设OF=x.根据勾股定理,得PD2﹣PF2=OD2﹣OF2,256﹣(14+x)2=36﹣x2,解得x=.所以DF=.所以sin∠BOD===.(2)①∵AC∥OD,∴∠1=∠2.又OA=OD,∴∠2=∠3.∴∠1=∠3.所以弧CD=弧BD,所以CD=BD;②∵AC∥OD,∴=.又CD=BD,AB=2OA,∴=.∴cos∠BAD==.。
切割线定理(一)(含解析)

切割线定理(一)© 2011 菁优网一、解答题(共10小题,满分100分,每小题10分)1、(10分)(2010•江汉区)如图,Rt △BDE 中,∠BDE=90°,BC 平分∠DBE 交DE 于点C ,AC ⊥CB 交BE 于点A ,△ABC 的外接圆的半径为r .(1)若∠E=30°,求证:BC•BD=r•ED ;(2)若BD=3,DE=4,求AE 的长.2、(10分)(2009•淄博)如图,两个同心圆的圆心是O ,大圆的半径为13,小圆的半径为5,AD 是大圆的直径.大圆的弦AB ,BE 分别与小圆相切于点C ,F .AD ,BE 相交于点G ,连接BD .(1)求BD 的长;(2)求∠ABE+2∠D 的度数;(3)求BG AG的值.3、(10分)(2008•苏州)如图,在△ABC 中,∠BAC=90度.BM 平分∠ABC 交AC 于M ,以A 为圆心,AM 为半径作⊙A 交BM 于N ,AN 的延长线交BC 于D ,直线AB 交⊙A 于P ,K 两点,作MT ⊥BC 于T .(1)求证:AK=MT ;(2)求证:AD ⊥BC ;(3)当AK=BD 时,求证:BN BP =AC BM .4、(10分)(2008•濮阳)如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交于CA 的延长线于点E ,∠EBC=2∠C .(1)求证:AB=AC ;(2)当AB Bc =√54时,①求tan ∠ABE 的值;②如果AE=2011,求AC 的值.5、(10分)(2007•厦门)已知:如图,PA、PB是⊙O的切线;A、B是切点;连接OA、OB、OP,(1)若∠AOP=60°,求∠OPB的度数;(2)过O作OC、OD分别交AP、BP于C、D两点,①若∠COP=∠DOP,求证:AC=BD;②连接CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.6、(10分)(2007•天津)如图,⊙O和⊙O′都经过点A、B,点P在BA延长线上,过P作⊙O的割线PCD交⊙O于C、D两点,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.(1)求PE的长;(2)求△COD的面积.7、(10分)(2007•庆阳)如图EB是⊙O的直径,A是BE的延长线上一点,过A作⊙O的切线AC,切点为D,过B 作⊙O的切线BC,交AC于点C,若EB=BC=6,求:AD,AE的长.8、(10分)(2007•河池)如图1,已知正方形ABCD的边长为2√3,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.(1)除正方形ABCD的四边和⊙O中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线);(2)求四边形CDPF的周长;(3)延长CD,FP相交于点G,如图2所示.是否存在点P,使BF•FG=CF•OF?如果存在,试求此时AP的长;如果不存在,请说明理由.9、(10分)(2007•安顺)如图,A,B,C,D四点在⊙O上,AD,BC的延长线相交于点E,直径AD=10,OE=13,且∠EDC=∠ABC.(1)计算CEAE =DEBE;(2)计算CE•BE的值;(3)探究:BE的取值范围.10、(10分)(2006•日照)阅读下面的材料:如图(1),在以AB为直径的半圆O内有一点P,AP、BP的延长线分别交半圆O于点C、D.求证:AP•AC+BP•BD=AB2.证明:连接AD、BC,过P作PM⊥AB,则∠ADB=∠AMP=90°,∴点D、M在以AP为直径的圆上;同理:M、C在以BP为直径的圆上.由割线定理得:AP•AC=AM•AB,BP•BD=BM•BA,所以,AP•AC+BP•BD=AM•AB+BM•AB=AB•(AM+BM)=AB2.当点P在半圆周上时,也有AP•AC+BP•BD=AP2+BP2=AB2成立,那么:(1)如图(2)当点P在半圆周外时,结论AP•AC+BP•BD=AB2是否成立?为什么?(2)如图(3)当点P在切线BE外侧时,你能得到什么结论?将你得到的结论写出来.答案与评分标准一、解答题(共10小题,满分100分,每小题10分)1、(10分)(2010•江汉区)如图,Rt △BDE 中,∠BDE=90°,BC 平分∠DBE 交DE 于点C ,AC ⊥CB 交BE 于点A ,△ABC 的外接圆的半径为r .(1)若∠E=30°,求证:BC•BD=r•ED ;(2)若BD=3,DE=4,求AE 的长.考点:切割线定理;直角三角形全等的判定;勾股定理;切线的判定。
2023年九年级中考数学高频考点突破-圆的切线的证明【含答案】

2023年九年级中考数学高频考点突破-圆的切线的证明1.如图,直线AD经过⊙O上的点A,⊙ABC为⊙O的内接三角形,并且⊙CAD=⊙B.(1)判断直线AD与⊙O的位置关系,并说明理由;(2)若⊙CAD=30°,⊙O的半径为1,求图中阴影部分的面积.(结果保留π)2.已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=.BC,AC=12OB(1)求证:AB是⊙O的切线;(2)若∠ACD=45°,OC=2,求弦CD的长.3.如图,△ABC内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.(1)求证:EC是圆O的切线;(2)当∠ABC=22.5°时,连接CF,①求证:AC=CF;②若AD=1,求线段FG的长.4.如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD(1)求证:AC是⊙O的切线;(2)若⊙O的半径为4,求⊙ABC的面积.5.如图,在⊙ABC中,⊙C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE(1)求证:直线DE是⊙O的切线,AC=6,OA=2,求图中阴影部分的面积(2)若BE=10√336.如图,在⊙ABC中,⊙C=90°,⊙ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是⊙BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊙AB,垂足为H,求证:CD=HF;(3)若CD=1,EF= √10,求AF长.7.如图,在⊙ABC中,以AB为直径的⊙O交AC于点M,弦MN⊙BC交AB于点E,且ME=1,AM=2,AE=√3.(1)求证:BC是⊙O的切线;(2)求⊙O的半径.8.如图,AB是⊙O的直径,点P在⊙O上,且PA=PB,点M是⊙O外一点,MB与⊙O相切于点B,连接OM,过点A作AC∥OM交⊙O于点C,连接BC交OM于点D.(1)求证:MC是⊙O的切线;(2)若OB=152,BC=12,连接PC,求PC的长.9.如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且⊙AED=45°.(1)判断CD与⊙O的位置关系,并说明理由;(2)若⊙O半径为6cm,AE=10cm,求⊙ADE的正弦值.10.如图,以Rt⊙ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.(1)DE 与半圆O 相切吗?若相切,请给出证明;若不相切,请说明理由;(2)若AD 、AB 的长是方程x 2﹣10x+24=0的两个根,求直角边BC 的长.11.如图,AB 为⊙O 的直径,C 为⊙O 上一点,⊙ABC 的平分线交⊙O 于点D ,DE⊙BC 于点E .(1)试判断DE 与⊙O 的位置关系,并说明理由;(2)过点D 作DF⊙AB 于点F ,若BE=3 √3 ,DF=3,求图中阴影部分的面积.12.如图,在Rt⊙ABC 中,⊙C =90°,AD 平分⊙BAC 交BC 于点D ,O 为AB 上一点,经过点A ,D 的⊙O 分别交AB ,AC 于点E ,F ,连接DF .(1)求证:BC 是⊙O 的切线;(2)连接DE ,求证:⊙BDE ∼⊙BAD(3)若BE =52,sinB =35,求AD 的长. 13.如图,已知 ΔABC 内接干 ⊙O , AB 是 ⊙O 的直径, ∠CAB 的平分线交 BC 于点 D ,交 ⊙O 于点 E ,连接 EB ,作 ∠BEF =∠CAE ,交 AB 的延长线于点 F .(1)求证:EF是⊙O的切线;(2)若BF=10,EF=20,求⊙O的半径和AD的长.14.如图,在△ABC中,AC=AB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,2∠BCP=∠BAC.(1)求证:CP是⊙O的切线;(2)若BC=6,tan∠BCP=12,求点B到线段AC的距离.15.如图,AB是⊙O的直径,AC是弦,P为AB延长线上一点,⊙BCP=⊙BAC,⊙ACB的平分线交⊙O于点D,交AB于点E,(1)求证:PC是⊙O的切线;(2)求证:⊙PEC是等腰三角形;(3)若AC+BC=2时,求CD的长.16.如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.(1)求证:⊙ABC=⊙D;(2)求AB的长;(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.答案解析部分1.【答案】(1)解:直线AD与⊙O的位置关系是相切,理由是:作直径AE,连接CE,∵AE为直径,∴⊙ACE=90°,∴⊙E+⊙EAC=90°,∵⊙B=⊙DAC,⊙B=⊙E,∴⊙E=⊙DAC,∴⊙EAC+⊙DAC=90°,即OA⊙AD,∵OA过O,∴直线AD与⊙O的位置关系是相切;(2)解:连接OC,过O作OF⊙AC于F,则⊙OFA=90,∵⊙CAD=30°,⊙DAO=90°,∴⊙OAC=60°,∵OC=OA=1,∴⊙OAC是等边三角形,∴AC=OA=1,⊙AOC=60°,∵OA =OC ,OF⊙AC ,∴AF =FC = 12, 由勾股定理得:OF = √12−(12)2=√32, ∴阴影部分的面积为: 60π×12360−12×1×√32=π6−√34【知识点】等边三角形的判定与性质;圆周角定理;切线的判定;扇形面积的计算【解析】【分析】(1)作直径AE ,连接CE ,求出⊙OAD =90°,根据切线的判定得出即可;(2)求出⊙OAC 是等边三角形,再分别求出⊙OAC 和扇形OCA 的面积,即可得出答案.2.【答案】(1)证明:如图,连接OA ; ∵OC =BC,AC =12OB,∴OC=BC=AC=OA. ∴⊙ACO 是等边三角形. ∴∠O =∠OCA =60∘,∵AC=BC , ∴⊙CAB=⊙B , 又⊙OCA 为⊙ACB 的外角, ∴⊙OCA=⊙CAB+⊙B=2⊙B , ∴∠B =30∘, 又 ∠OAC =60∘, ∴∠OAB =90∘,∴AB 是 ⊙O 的切线(2)解:作AE⊙CD 于点E , ∵∠O =60∘,∴∠D =30∘.∵∠ACD =45∘,AC =OC =2,∴在Rt⊙ACE 中, CE =AE =√2;∵∠D =30∘,∴AD =2√2,∴DE =√3AE =√6,∴CD =DE +CE =√6+√2.【知识点】圆周角定理;切线的判定【解析】【分析】(1) 如图,连接OA ,根据题意得出OC =BC =AC =OA . 根据三边相等的三角形是等边三角形得出 ⊙ACO 是等边三角形 ,根据等边三角形的性质得出⊙O=⊙OCA=60°,根据等边对等角得出 ⊙CAB =⊙B , 根据三角形外角的定理得出 ⊙OCA =⊙CAB +⊙B =2⊙B ,故⊙B=30°,根据角的和差得出⊙OAB=90°,故 AB 是 ⊙O 的切线 ;(2) 作AE ⊙CD 于点E ,根据同弧所对的圆周角等于圆心角的一半得出⊙D=30°,然后根据等腰直角三角形的性质及含30°直角三角形的边之间的关系得出CE,DE 的长,进而根据线段的和差即可算出答案。
中考数学知识点过关培优训练:切线长定理(圆)(解析版)

中考数学知识点过关培优训练:切线长定理(圆)一.选择题1.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点A为60°角与直尺交点,点B为光盘与直尺唯一交点,若AB=3,则光盘的直径是()A.6B.3C.6 D.32.如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是()A.32°B.48°C.60°D.66°3.如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是()A.10 B.18 C.20 D.224.如图,PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=40°,则∠PAE+∠PBE的度数为()A.50°B.62°C.66°D.70°5.如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=5,AC=3,则BD的长是()A.4 B.3 C.2 D.16.已知⊙O1和⊙O2外切于M,AB是⊙O1和⊙O2的外公切线,A,B为切点,若MA=4cm,MB=3cm,则M到AB的距离是()A. cm B. cm C. cm D. cm7.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为()A.5 B.7 C.8 D.108.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于()A.13 B.12 C.11 D.109.如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为()A.12cm B.7cmC.6cm D.随直线MN的变化而变化10.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2,则线段AB的长是()A.B.3 C.2D.3二.填空题11.如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE 的周长是.12.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB 于点C、D,若PA=5,则△PCD的周长为.13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为.14.如图,PA、PB切⊙O于A、B,点C在上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是.15.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA=cm.16.如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,且AB=10cm,CD=5cm,则四边形ABCD周长为cm.17.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于.18.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB 均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是.19.已知:PA、PB、EF分别切⊙O于A、B、D,若PA=15cm,那么△PEF周长是cm.若∠P=50°,那么∠EOF=.20.如图所示,⊙D的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.(1)△AEF的周长是;(2)当G为线段AD与⊙D的交点时,连结CD,则五边形DBE FC的面积是.三.解答题21.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.22.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数.23.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.(1)求证:OQ=PQ;(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.24.如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.(1)求△PDE的周长;(2)求∠DOE的度数.25.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB 于D.(1)若PA=6,求△PCD的周长.(2)若∠P=50°求∠DOC.26.如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.参考答案1.解:设三角板与圆的切点为C,连接OA、OB,由切线长定理知AB=AC=3,OA平分∠BAC,∴∠OAB=60°,在Rt△ABO中,OB=AB tan∠OAB=3,∴光盘的直径为6,故选:A.2.解:∵CA、CD是⊙O的切线,∴CA=CD,∵∠ACD=48°,∴∠CAD=∠CDA=66°,∵CA⊥AB,AB是直径,∴∠ADB=∠CAB=90°,∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,∴∠DBA=∠CAD=66°,故选:D.3.解:∵PA、PB切⊙O于点A、B,CD切⊙O于点E,∴PA=PB=10,CA=CE,DE=DB,∴△PCD的周长是PC+CD+PD=PC+AC+DB+PD=PA+PB=10+10=20.故选:C .4.解:∵PA 、PB 、CD 分别切⊙O 于A 、B 、E ,CD 交PA 、PB 于C 、D 两点,∴CE =CA ,DE =DB ,∴∠CAE =∠CEA ,∠DEB =∠DBE ,∴∠PCD =∠CAE +∠CEA =2∠CAE ,∠PDC =∠DEB +∠DBE =2∠DBE ,∴∠CAE =∠PCD ,∠DBE =∠PDC ,即∠PAE =∠PCD ,∠PBE =∠PDC ,∵∠P =40°,∴∠PAE +∠PBE =∠PCD +∠PDC =(∠PCD +∠PDC )=(180°﹣∠P )=70°. 故选:D .5.解:∵AC 、AP 为⊙O 的切线,∴AC =AP =3,∵BP 、BD 为⊙O 的切线,∴BP =BD ,∴BD =PB =AB ﹣AP =5﹣3=2.故选:C .6.解:如图,∵AB 是⊙O 1和⊙O 2的外公切线,∴∠O 1AB =∠O 2BA =90°,∵O 1A =O 1M ,O 2B =O 2M ,∴∠O 1AM =∠O 1MA ,∠O 2BM =∠O 2MB ,∴∠BAM +∠AMO 1=90°,∠ABM +∠BMO 2=90°,∴∠AMB =∠BMO 2+∠AMO 1=90°,∴AM ⊥BM ,∵MA =4cm ,MB =3cm ,∴由勾股定理得,AB =5cm ,由三角形的面积公式,M 到AB 的距离是=cm ,故选:B .7.解:∵PA、PB为圆的两条相交切线,∴PA=P B,同理可得:CA=CE,DE=DB.∵△PCD的周长=PC+CE+ED+PD,∴△PCD的周长=PC+CA+BD+PD=PA+PB=2PA,∴△PCD的周长=10,故选:D.8.解:∵AB∥CD,∴∠ABC+∠BCD=180°,∵CD、BC,AB分别与⊙O相切于G、F、E,∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∴BC==10,∴BE+CG=10(cm).故选:D.9.解:设E、F分别是⊙O的切点,∵△ABC是一张三角形的纸片,AB+BC+AC=17cm,⊙O是它的内切圆,点D是其中的一个切点,BC=5cm,∴BD+CE=BC=5cm,则AD+AE=7cm,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=7(cm).故选:B.10.解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,∴AC=EC,DE=DB,PA=PB,∵△PCD的周长等于3,∴PA+PB=2,∴PA=PB=,链接PA和AO,∵⊙O的半径为1,∴tan∠APO===,∴∠APO=30°,∴∠APB=60°,∴△APB是等边三角形,∴AB=PA=PB=.故选:A.二.填空题(共10小题)11.解:连接OA.∵PA、PB、DE分别切⊙O于A、B、C点,∴BD=CD,CE=AE,PA=PB,OA⊥AP.在直角三角形OAP中,根据勾股定理,得AP=8,∴△PDE的周长为2AP=16.故选答案为16cm.12.解:∵PA、PB切⊙O于A、B,∴PA=PB=5;同理,可得:EC=CA,DE=DB;∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=PA+PB=2PA=10.即△PCD的周长是10.13.解:∵四边形ABCD是⊙O的外切四边形,∴AD+BC=AB+CD=22,∴四边形ABCD的周长=AD+BC+AB+CD=44,故答案为:44.14.解:连接OA、OB,如下图所示:∵PA、PB为圆的两条切线,∴由切线长定理可得:PA=PB,同理可知:DA=DC,EC=EB;∵OA⊥PA,OA=5,PO=13,∴由勾股定理得:PA=12,∴PA=PB=12;∵△PDE的周长=PD+DC+CE+PE,DA=DC,EC=EB;∴△PDE的周长=PD+DA+PE+EB=PA+PB=24,故此题应该填24cm.15.解:如图,设DC与⊙O的切点为E;∵PA、PB分别是⊙O的切线,且切点为A、B;∴PA=PB;同理,可得:DE=DA,CE=CB;则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);∴PA=PB=5cm,故答案为:5.16.解:∵四边形ABCD的边AB、BC、CD、DA和⊙O分别切于L、M、N、P,∴AP=AL,BM=BL,CM=CN,DN=DP,∴AL+BL+DN+CN=AP+BM+DP+CM,即AB+CD=AD+BC,∵AB=10cm,CD=5cm,∴AB+CD=AD+BC=15cm,∴四边形ABCD的周长为30cm.故答案为30.17.解:∵PA、PB是⊙O的两条切线,∴∠APO=∠BPO=∠APB,∠PAO=90°∵∠APB=60°,∴∠APO=30°,∵PO=2,∴AO=1.故答案为:1.18.解:根据切线长定理,得AD=AE,BC=BE,所以梯形的周长是5×2+4=14,故答案为:14.19.解:∵PA、PB、EF分别切⊙O于A、B、D,∴PA=PB=15cm,ED=EA,FD=DB,∴PE+EF+PF=PE+ED+PF+FD=PA+PB=30(cm)即△PEF周长是30cm;∵PA、PB为⊙O的切线,∴∠PAO=∠PBO=90°,而∠P=50°,∴∠AOB=360°﹣90°﹣90°﹣50°=130°;连OD,如图,∴∠ODE=∠ODF=90°,易证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠AOB=65°,则∠EOF=65°.20.解:(1)如图1所示:连接ED,DG,FD,CD,∵AB,AC分别与⊙D相切于点B,C,∴AB=AC,∠ABD=∠ACD=90°,∵⊙D的半径为3,A是圆D外一点且AD=5,∴AB==4,∵过G作⊙D的切线,交AB于点E,交AC于点F,∴BE=EG,FG=FC,则△AEF的周长是:AE+EG+FG+AF=AB+AC=8.故答案为:8;(2)如图2,AG=AD﹣DG=5﹣3=2.∵在△AEG和△ADB中,∠ABD=∠AGD=90°,∠BAD=∠EAG,∴△AEG∽△ADB,∴=,即=,∴EG=,∴EF=2EG=3,∴S△AEF=EF•AG=×3×2=3.又∵S四边形ABDC =2S△ABD=AB•BD=3×4=12,∴S五边形DBEFC=12﹣3=9.故答案是:9.三.解答题(共6小题)21.解:根据切线的性质得:∠PAC=90°,所以∠PAB=90°﹣∠BAC=90°﹣20°=70°,根据切线长定理得PA=PB,所以∠PAB=∠PBA=70°,所以∠P=180°﹣70°×2=40°.22.解:(1)∵CA,CE都是圆O的切线,∴CA=CE,同理DE=DB,PA=PB,∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,即PA的长为6;(2)∵∠P=60°,∴∠PCE+∠PDE=120°,∴∠ACD+∠CDB=360°﹣120°=240°,∵CA,CE是圆O的切线,∴∠OCE=∠OCA=∠ACD;同理:∠ODE=∠CDB,∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,∴∠COD=180﹣120°=60°.23.(1)证明:连接OP.∵PA、PC分别与⊙O相切于点A, C,∴PA=PC,OA⊥PA,∵OA=OC,OP=OP,∴△OPA≌△OPC(SSS),∴∠AOP=∠POC,∵QP⊥PA,∴QP∥BA,∴∠QPO=∠AOP,∴∠QOP=∠QPO,∴OQ=PQ.(2)设OA=r.∵OB=OC,∴∠OBC=∠OCB,∵OB∥QD,∴∠QDC=∠B,∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,∵QO=QP,∴OC=DP=r,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,在Rt△PCQ中,∵PQ2=PC2+QC2,∴(6+r)2=62+(2r)2,r=4或0(舍弃),∴OP==4,∵OB=PD,OB∥PD,∴四边形OBDP是平行四边形,∴BD=OP=4.24.解:(1)∵PA、PB、DE都为⊙O的切线,∴DA=DF,EB=EF,PA=PB=6,∴DE=DA+EB,∴PE+PD+DE=PA+PB=12,即△PDE的周长为12;(2)连接OF,∵PA、PB、DE分别切⊙O于A、B、F三点,∴OB⊥PB,OA⊥PA,∠BOE=∠FOE=∠BOF,∠FOD=∠AOD=∠AOF,∵∠APB=52°,∴∠AOB=360°﹣90°﹣90°﹣52°=128°,∴∠DOE=∠FOE+∠FOD=(∠BOF+∠AOF)=∠BOA=64°.25.解:(1)连接OE,∵PA、PB与圆O相切,∴PA=PB=6,同理可得:AC=CE,BD=DE,△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;(2)∵PA PB与圆O相切,∴∠OAP=∠OBP=90°∠P=50°,∴∠AOB=360°﹣90°﹣90°﹣50°=130°,在Rt△AOC和Rt△EOC中,,∴Rt△AOC≌Rt△EOC(HL),∴∠AOC=∠COE,同理:∠DOE=∠BOD,∴∠COD=∠AOB=65°.26.解:∵PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,∴PA=PB,EA=EQ,FB=FQ,∵PA=8cm,∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm).。
最新2021年九年级数学中考复习专题之圆:切割线定理综合运用(一)

2021年九年级数学中考复习专题之圆:切割线定理综合运用(一)一.选择题1.P是⊙O外一点,PA切⊙O于A,割线PBC交⊙O于点B、C,若PB=BC=3,则PA的长是()A.9 B.3 C.D.182.如图,PA切⊙O于点A,PBC是⊙O的一条割线,且PA=2,BC=2PB,那么PB 的长为()A.2 B.C.4 D.3.如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D.已知PA=6,AB=4,PC=5,则CD=()A.B.C.7 D.244.如图,已知P为⊙O外一点,PO交⊙O于点A,割线PBC交⊙O于点B、C,且PB =BC,若OA=7,PA=4,则PB的长等于()A.B.C.6 D.5.如图,PA切⊙O于点A,PBC是⊙O的割线,如果PB=2,PC=8,那么PA的长为()A.2 B.4 C.6 D.6.如图,在▱ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE =5,则DE的长为()A.3 B.4 C.D.7.如图,在以O为圆心的两个同心圆中,A为大圆上任意一点,过A作小圆的割线AXY,若AX•AY=4,则图中圆环的面积为()A.16πB.8πC.4πD.2π8.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=()A.6 B.7 C.8 D.99.以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若,且AB=10,则CB的长为()A.B.C.D.410.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB =60°,PA=8,那么点P与O间的距离是()A.16 B.C.D.二.填空题11.如图,⊙O的半径为,A、B两点在⊙O上,切线AQ和BQ相交于Q,P是AB 延长线上任一点,QS⊥OP于S,则OP•OS=.12.如图,过点P引圆的两条割线PAB和PCD,分别交圆于点A,B和C,D,连接AC,BD,则在下列各比例式中,①;②;③,成立的有(把你认为成立的比例式的序号都填上).13.如图,割线PAB与⊙O交于点A、B,割线PCD与⊙O交于点C、D,PA=PC,PB=3cm,则PD=cm.14.如图,过⊙O外一点P作两条割线,分别交⊙O于A,B和C,D.已知PA=2,PB =5,PD=8,则PC的长是.15.如图,AC为⊙O的直径,PA是⊙O的切线,切点为A,PBC是⊙O的割线,∠BAC 的平分线交BC于D点,PF交AC于F点,交AB于E点,要使AE=AF,则PF应满足的条件是(只需填一个条件).三.解答题16.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E.若AB=CD=2,求CE的长.17.如图所示,⊙O的内接△ABC的AB边过圆心O,CD切⊙O于C,BD⊥CD于D,交⊙O于F,CE⊥AB于点E,FE交⊙O于G.解答下列问题:(1)若BC=10,BE=8,求CD的值;(2)求证:DF•DB=EG•EF.18.如图1,已知Rt△ABC的直角边AC的长为2,以AC为直径的⊙O与斜边AB交于点D,过D点作⊙O的切线(1)求证:BE=DE;(2)延长DE与AC的延长线交于点F,若DF=,求△ABC的面积;(3)从图1中,显然可知BC<AC.试分别讨论在其它条件不变,当BC=AC(图2)和BC>AC(图3)时,直线DE与直线AC还会相交吗?若不能相交,请简要说明理由;若能相交,设交点为F'且DF'=,请再求出△ABC的面积.19.已知:如图,PF是⊙O的切线,PE=PF,A是⊙O上一点,直线AE、AP分别交⊙O 于B、D,直线DE交⊙O于C,连接BC,(1)求证:PE∥BC;(2)将PE绕点P顺时针旋转,使点E移到圆内,并在⊙O上另选一点A,如图2.其他条件不变,在图2中画出完整的图形.此时PE与BC是否仍然平行?证明你的结论.20.如图PAB、PCD是⊙O的两条割线,AB是⊙O的直径.(1)如图甲,若PA=8,PC=10,CD=6.①求sin∠APC的值;②sin∠BOD=;(2)如图乙,若AC∥OD.①求证:CD=BD;②若,试求cos∠BAD的值.参考答案一.选择题1.解:∵PB=BC=3,∴PC=6,∵PA2=PB•PC=18,∴PA=3,故选:C.2.解:设PB=x,则PC=3x,∵PA2=PB•PC,PA=2,BC=2PB,∴x•3x=12,∴x=2.故选:A.3.解:由于PAB、PCD都是⊙O的割线,根据切割线定理可得:PA•PB=PC•PD,即PA•(PA+PB)=PC•PD,∵PA=6,AB=4,PC=5,∴PD=12,即CD=PD﹣PC=7;故选:C.4.解:延长PO交圆于D;设PB=BC=x,∵PB•PC=PA•PD,PB=BC,OA=7,PA=4,∴x•2x=72,∴x=6.故选:C.5.解:∵PA切⊙O于点A,PBC是⊙O的割线,∴PA2=PB•PC=16,即PA=4;故选:B.6.解:连接CE;∵,∴∠BAE=∠EBC+∠BEC;∵∠DCB=∠DCE+∠BCE,由弦切角定理知:∠DCE=∠EBC,由平行四边形的性质知:∠DCB=∠BAE,∴∠BEC=∠BCE,即BC=BE=5,∴AD=5;由切割线定理知:DE=DC2÷DA=,故选:D.7.解:过点A作圆的切线AD,切点是D,∵AD2=AX•AY,AX•AY=4,∴AD=2,∴圆环的面积=πAD2=4π.故选:C.8.解:∵PB,PD是⊙O的割线,∴PA•PB=PC•PD,∵PA=2,PC=CD=3,∴2PB=3×6解得:PB=9.故选:D.9.解:如图,若,且AB=10,∴AD=4,BD=6,作AB关于直线BC的对称线段A′B,交半圆于D′,连接AC、CA′,可得A、C、A′三点共线,∵线段A′B与线段AB关于直线BC对称,∴AB=A′B,∴AC=A′C,AD=A′D′=4,A′B=AB=10.而A′C•A′A=A′D′•A′B,即A′C•2A′C=4×10=40.则A′C2=20,又∵A′C2=A′B2﹣CB2,∴20=100﹣CB2,∴CB=4.故选:A.10.解:连接OA,OP∵PA,PB是⊙O的切线,∠APB=60°,∴∠OPA=∠APB=30°,OA⊥OP,∴OP===,∴点P与O间的距离是.故选:B.二.填空题(共5小题)11.解:连接OQ交AB于M,则OQ⊥AB,连接OA,则OA⊥AQ.∵∠QMP=∠QSP=90°,∴S,P,Q,M四点共圆,故OS•OP=OM•OQ.又∵OM•OQ=OA2=2,∴OS•OP=2.故答案为:2.12.解:∵四边形ABCD是圆内接四边形∴∠PAD=∠C,∠PAD=∠B∴△PAD∽△PCB根据相似三角形的对应边的比相等,得到②③是正确的.13.解:∵PA•PB=PC•PD,PA=PC,PB=3cm∴PB=PD=3cm.14.解:∵PA•PB=PC•PD,PA=2,PB=5,PD=8∴PC==.15.解:∵∠PAC=90°,∠ABC=90°,∴90°﹣∠AFP=90°﹣∠BEP,∴∠APF=∠CPF,∴PF平分∠APC.三.解答题(共5小题)16.解:如图,由切割线定理,得CD2=CB•CA,(2分)CD2=CB(AB+CB),CB2+2CB﹣4=0,解得CB=(负数舍去)连接OD,则OD⊥CD,又EB与⊙O相切,∴EB⊥OC,∴Rt△ODC∽Rt△EBC,(6分)于是,即∴CE=.17.(1)解:∵AB为直径,BD⊥CD∴∠ABC+∠A=90°,∠CBD+∠BCD=90°∵CD为⊙O切线∴∠BCD=∠A∴∠ABC=∠BCD∵CD⊥BD,CE⊥BE∴CE=CD∴CE==6∴CD=6(2)证明:∵CD为切线,BD为割线∴CD2=DF•DB①∵∠ACB=90°,CE⊥AB∴RT△ACE∽RT△CBE∴CE2=EA•EB②∵EG•EF=EA•EB③由①②③及CD=CE得DF•DB=EG•EF.18.(1)证明:连接OD,∴OD⊥DE,∴∠ADO+∠BDE=90°,∵OA=OD,∴∠A=∠ADO,∵∠ACB=90°,∴∠B+∠A=90°,∴∠B=∠BDE,∴BE=DE;(2)解:在直角三角形ODF中,OD=1,DF=,∴∠OFD=30°,∴OF=2,AF=3.∴tan∠A=,∴BC=AC•tan∠A=2×tan30°=.S△ABC=AC•BC=×2×=;(3)解:如图,当BC=AC时,直线DE与直线AC平行;当BC>AC时,在直角三角形ODF′中,OD=1,DF′=,∴∠OF′D=30°,∴OF′=2,AF=1,∴CF′=3,∠BAC=60°,∴tan∠BAC=,∴BC=AC•tan∠BAC=2×tan60°=2.S △ABC=AC•BC=×2×2=2.19.(1)证明:∵PF与⊙O相切,∴PF2=PD•PA.∵PE=PF,∴PE2=PD•PA.∴PE:PD=PA:PE.∵∠APE=∠APE,∴△EPD∽△APE.∴∠PED=∠A.∵∠ECB=∠A,∴∠PED=∠ECB.∴PE∥BC.(2)解:PE与BC仍然平行.证明:画图如图,∵△EPD∽△APE,∴∠PEA=∠D.∵∠B=∠D,∴∠PEA=∠B.∴PE∥BC.20.解:(1)作OE⊥CD于E,连接OC,作DF⊥PB于F.①根据垂径定理,得CE=3.设圆的半径是r.根据勾股定理,得OP2﹣PE2=OC2﹣CE2,(8+r)2﹣169=r2﹣9,解得r=6.则OE=3.则sin∠APC==;②设OF=x.根据勾股定理,得PD2﹣PF2=OD2﹣OF2,256﹣(14+x)2=36﹣x2,解得x=.所以DF=.所以sin ∠BOD ===.(2)①∵AC ∥OD ,∴∠1=∠2.又OA =OD ,∴∠2=∠3.∴∠1=∠3.所以弧CD =弧BD ,所以CD =BD ; ②∵AC ∥OD ,∴=.又CD =BD ,AB =2OA ,∴=. ∴cos∠BAD ==.1、最困难的事就是认识自己。
2024年中考数学压轴题重难点知识剖析及训练—圆与母子型相似:切割线定理反A模型压轴题专题(含解析)
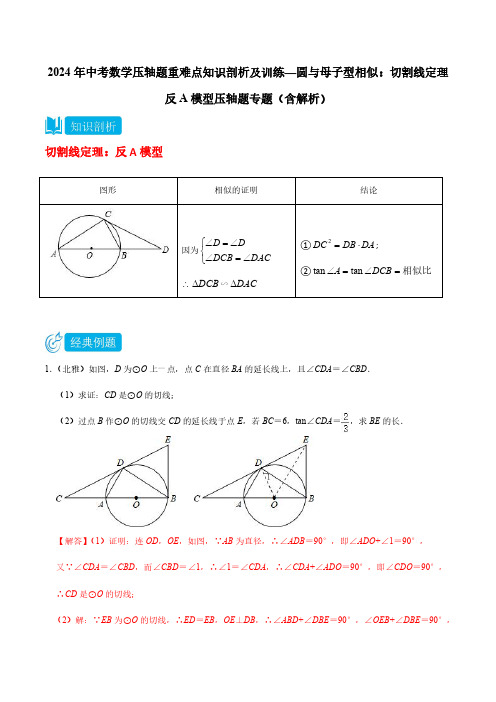
2024年中考数学压轴题重难点知识剖析及训练—圆与母子型相似:切割线定理反A模型压轴题专题(含解析)切割线定理:反A模型1.(北雅)如图,D 为⊙O 上一点,点C 在直径BA 的延长线上,且∠CDA =∠CBD .(1)求证:CD 是⊙O 的切线;(2)过点B 作⊙O 的切线交CD 的延长线于点E ,若BC =6,tan ∠CDA=,求BE的长.【解答】(1)证明:连OD ,OE ,如图,∵AB 为直径,∴∠ADB =90°,即∠ADO +∠1=90°,又∵∠CDA =∠CBD ,而∠CBD =∠1,∴∠1=∠CDA ,∴∠CDA +∠ADO =90°,即∠CDO =90°,∴CD 是⊙O 的切线;(2)解:∵EB 为⊙O 的切线,∴ED =EB ,OE ⊥DB ,∴∠ABD +∠DBE =90°,∠OEB +∠DBE =90°,图形相似的证明结论因为⎩⎨⎧∠=∠∠=∠DACDCB D D ∴DCB ∆∽DAC ∆①DA DB DC ⋅=2;②相似比=∠=∠DCB A tan tan∴∠ABD=∠OEB,∴∠CDA=∠OEB.而tan∠CDA=,∴tan∠OEB==,∵Rt△CDO∽Rt△CBE,∴===,∴CD=×6=4,在Rt△CBE中,设BE=x,∴(x+4)2=x2+62,解得x=.2.(南雅)如图,D为⊙O上一点,点C在直径BA的延长线上,且CD2=CA•CB.(1)求证:CD是⊙O的切线;(2)过点B作⊙O的切线交CD的延长线于点E,若BC=10,,求BE的长.【解答】(1)证明:如图,连接OD,∵CD2=CA•CB,∴,∵∠C=∠C,∴△DCA∽△BCD,∴∠ADC=∠DBC,∵OB=OD,∴∠BDO=∠DBO,∵AB为⊙O的直径,∴∠BDA=90°,∴∠BDO+∠ODA=∠CDA+∠ODA=90°,∴OD⊥CD,∴CD为O0的切线;(2)∵BE、CE是⊙O的切线,∴ED=EB,∵△DCA∽△BCD,∴∠DBA=∠CDA,∴=tan∠DBA=tan∠CDA=,∴CD=BC=6,设BE=x,则DE=x,CE=x+6.在Rt△CBE中,(x+6)2=x2+102,解得:x=,∴BE=.3.(长郡)已知:如图,⊙O的直径AB垂直于弦CD,过点C的切线与直径AB的延长线相交于点P,连结PD.(1)求证:PD是⊙O的切线.(2)求证:2PD PB PA=⋅.(3)若4PD=,1tan2CDB∠=,求直径AB的长.【解答】(1)证明:连接OD,OC,∵PC是⊙O的切线,∴∠PCO=90°,∵AB⊥CD,AB是直径,∴弧BD=弧BC,∴∠DOP=∠COP,在△DOP和△COP中,,∴△DOP≌△COP(SAS),∴∠PDO=∠PCO=90°,∵D在⊙O上,∴PD是⊙O的切线;(2)证明:∵AB是⊙O的直径,∴∠ADB=90°,∵∠PDO=90°,∴∠ADO=∠PDB=90°﹣∠BDO,∵OA=OD,∴∠A=∠ADO,∴∠A=∠PDB,∵∠BPD=∠BPD,∴△PDB∽△PAD,∴,∴PD2=PA•PB;(3)解:∵DC⊥AB,∴∠ADB=∠DMB=90°,∴∠A+∠DBM=90°,∠CDB+∠DBM=90°,∴∠A=∠CDB,∵tan∠CDB=,∴tan A==,∵△PDB∽△PAD,∴===∵PD=4,∴PB=2,PA=8,∴AB=8﹣2=6.4.(明德)如图,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC 平分∠DAB,延长AB交DC于点E,CF⊥AB于点F.(1)求证:直线DE与⊙O相切;(2)若EB=2,EC=4,求⊙O的半径及AC、AD的长;(3)在(2)的条件下,求阴影部分的面积.【解答】解:(1)连接OC;∵AD⊥DC,∴∠DAC+∠ACD=90°;又∵AC平分∠DAB,OA=OC,∴∠DAC=∠CAO,∠CAO=∠ACO,∴∠DAC=∠ACO,∴∠ACD+∠ACO=90°,即OC⊥DC,∴直线DE与⊙O相切.(2)∵EC是⊙O的切线,∴EC2=EB•EA,而EC=4,EB=2,∴EA=8,AB=8﹣2=6;∴⊙O的半径为3.∵AC平分∠DAE,∴,∴,∴AD=2DC(设为x);∵AC平分∠DAB,CD⊥AD,CF⊥AB,∴CD=CF;在△ADC与△AFC中,,∴△ADC≌△AFC(HL),∴AF=AD=2x,BF=6﹣2x;∵AB为⊙O的直径,∴∠ACB=90°;由射影定理得:CF2=AF•BF,即x2=2x(6﹣2x),解得:x=,∴AD=;由勾股定理得:,∴AC=,即⊙O的半径及AC、AD的长分别为3,,.(3)∵,,∴.5.(雅礼)如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.(1)求证:DE是⊙O的切线(2)若tan A=,探究线段AB和BE之间的数量关系,并证明;(3)在(2)的条件下,若OF=1,求⊙O的半径和CD的长.【解答】(1)证明:连接OD,如图,∵EF=ED,∴∠EFD=∠EDF,∵∠EFD=∠CFO,∴∠CFO=∠EDF,∵OC⊥OF,∴∠OCF+∠CFO=90°,∵OC=OD,∴∠OCF=∠ODF,∴∠ODC+∠EDF=90°,即∠ODE=90°,∴OD⊥DE,∵点D在⊙O上,∴DE是⊙O的切线;(2)解;线段AB、BE之间的数量关系为:AB=3BE.证明:∵AB为⊙O直径,∴∠ADB=90°,∴∠ADO=∠BDE,∵OA=OD,∴∠ADO=∠A,∴∠BDE=∠A,而∠BED=∠DEA,∴△EBD∽△EDA,∴,∵Rt△ABD中,tan A==,∴=,∴AE=2DE,DE=2BE,∴AE=4BE,∴AB=3BE;(3)解:设BE=x,则DE=EF=2x,AB=3x,半径OD=x,∵OF=1,∴OE=1+2x,在Rt△ODE中,由勾股定理可得:(x)2+(2x)2=(1+2x)2,∴x=﹣(舍)或x=2,∴AB=3x=6,∴圆O的半径为3.过点O作OH⊥CD,∵OC=OD,∴CD=2CH,在Rt△OCF中,CF==,OH==,在Rt△OCH中,tan∠OCH===,∴CH=3OH=,∴CD=2CH=.6.(青竹湖)如图,已知AB是⊙O的直径,直线AC与⊙O相切于点A,过点B作BD∥OC交⊙O于点D,连接CD并延长交AB的延长线于点E.(1)求证:CD是⊙O的切线.(2)求证:DE2=EB•EA;(3)若BE=1,,求线段AD的长度.【解答】解:(1)∵BD∥OC,∴∠DBO=∠COA,∠ODB=∠COD,∵OB=OD,∴∠DBO=∠ODB,∴∠COA=∠COD,在△COA和△COD中,,∴△COA≌△COD(SAS),∴∠CAO=∠CDO,∵AC是⊙O的切线,∴∠CAO=90°=∠CDO,即OD⊥EC,∵OD是⊙O的半径,∴EC是⊙O的切线;(2)∵EC是⊙O的切线,∴∠ODE=90°,即∠EDB+∠ODB=90°,又∴AB是⊙O的直径,∴∠ADB=90°,∴∠ABD+∠BAD=90°,又∵∠ODB=∠OBD,∴∠EDB=∠EAD,又∵∠E=∠E,∴△EBD∽△EDA,∴=,即DE2=AE•BE;(3)∵∠ACO+∠COA=90°,∠BAD+∠OBD=90°,而∠OBD=∠ODB=∠COD=∠COA,∴∠ABD+∠BAD=90°,∴∠BAD=∠ACO,由△EBD∽△EDA,∴==tan∠BAD=,∵BE=1,∴DE=2,由DE2=AE•BE得,22=1×AE,∴AE=4,∴AB=4﹣1=3,设BD=a,则AD=2a,由勾股定理得,BD2+AD2=AB2,即a2+(2a)2=32,解得a=,∴AD=2a=.7.(北雅)如图①,△ABC内接于⊙O,点P是△ABC的内切圆的圆心,AP交边BC于点D,交⊙O于点E,经过点E作⊙O的切线分别交AB、AC延长线于点F、G.(1)求证:BC∥FG;(2)探究:PE与DE和AE之间的关系;(3)当图①中的FE=AB时,如图②,若FB=3,CG=2,求AG的长.【解答】(1)证明:连接BE,∵点P是△ABC的内心,∴∠BAD=∠CAD.又∵FG切⊙O于E,∴∠BEF=∠BAD.又∵∠DBE=∠CAD,∴∠BEF=∠DBE.∴BC∥FG.(2)解:连接BP,则∠ABP=∠CBP.∵∠BPE=∠BAP+∠ABP=∠PBC+∠EBD,∴∠BPE=∠PBE.∴BE=PE.在△ABE和△BDE中,∠BAE=∠EBD,∠BED=∠AEB,∴△ABE∽△BDE.∴=.∴BE2=AE•DE.∴PE2=AE•DE.(3)解:∵FE2=FB•FA=FB(FB+AB),而FE=AB,∴AB2=3(3+AB).设AB=x,则x2﹣3x﹣9=0,解之得x=.∴AB=(取正值).由(1)在△AFG中,BC∥FG,∴.∴AC==×=1+.∴AG=AC+CG=3+.8.(青竹湖)如图,⊙O经过△ABC的顶点A、C,并与AB边相交于点D,过点D作DF∥BC,交AC于点E,交⊙O于点F,连接DC,点C为弧DF的中点.(1)求证:BC为⊙O的切线;(2)若⊙O的半径为3,DF=4,求CE•CA的值;(3)在(2)的条件下,连接AF,若BD=AF,求AD的长.【解答】(1)证明:连接CO并延长交⊙O于G,连接DG,如图:∵CG为直径,∴∠GDC=90°,∴∠DCG+∠DGC=90°,∵∠DGC=∠BAC,点C为弧DF的中点,∴∠CDF=∠BAC,∴∠DGC=∠CDF,∴∠DCG+∠CDF=90°,∵DF∥BC,∴∠CDF=∠DCB,∴∠DCG+∠DCB=90°,∴OC⊥BC,又∵OC是⊙O的半径,∴BC为⊙O的切线;(2)解:连接OC交DF于M,∵C为弧DF的中,∴OC⊥DF,∴DM=MF=DF=2,∵⊙O的半径为3,∴OM===1,∴CM=OC﹣OM=3﹣1=2,∴DC2=DM2+CM2==12,∵,∴∠DAC=∠CAF,∵∠CDF=∠CAF,∴∠CDF=∠DAC,∵∠DCE=∠ACD,∴△DCE∽△ACD,∴,∴CD2=CE•CA,∴CE•CA=12;(3)解:连接CF,∵四边形ADCF内接于⊙O,∴∠ADC+∠AFC=180°,又∵∠BDC+∠CDA=180°,∴∠AFC=∠BDC,∵,∴CD=CF=2,又∵BD=AF,∴△BDC≌△AFC(SAS),∴BC=AC,∠BCD=∠ACF,∵∠ACF=∠ADF,∴∠BCD=∠ADF,∵DF∥BC,∴∠CDF=∠BCD,∴∠CDF=∠ADF,∴AF=CF,∴,BD=CF=2,∴,∴AC=DF=4=BC,∵∠BCD=∠CDF=∠CAF=∠DAC,∠DBC=∠ABC,∴△DBC∽△CBA,∴,∴BC2=BD•AB,∴•AB,∴AB=,∴AD=AB﹣BD==.9.(麓山国际)如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.【解答】(1)证明:∵PD切⊙O于点C,∴OC⊥PD,又∵AD⊥PD,∴OC∥AD,∴∠ACO=∠DAC.∵OC=OA,∴∠ACO=∠CAO,∴∠DAC=∠CAO,即AC平分∠DAB;(2)证明:∵AD⊥PD,∴∠DAC+∠ACD=90°.又∵AB为⊙O的直径,∴∠ACB=90°.∴∠PCB+∠ACD=90°,∴∠DAC=∠PCB.又∵∠DAC=∠CAO,∴∠CAO=∠PCB.∵CE平分∠ACB,∴∠ACF=∠BCF,∴∠CAO+∠ACF=∠PCB+∠BCF,∴∠PFC=∠PCF,∴PC=PF;(3)解:∵∠PAC=∠PCB,∠P=∠P,∴△PAC∽△PCB,∴=.又∵tan∠ABC=,∴,∴,设PC=4k,PB=3k,则在Rt△POC中,PO=3k+7,OC=7,∵PC2+OC2=OP2,∴(4k)2+72=(3k+7)2,∴k=6(k=0不合题意,舍去).∴PC=4k=4×6=24.10.(青竹湖)如图,AB为⊙O的直径,C为⊙O上一点,D为BA延长线上一点,∠ACD=∠B.(1)求证:DC为⊙O的切线;(2)若⊙O的半径为5,sin B=,求CD和AD的长;(3)在(2)的条件下,线段DF分别交AC,BC于点E,F且∠CEF=45°,求CF的长.【解答】(1)证明:∵AB为⊙O的直径,∴∠ACB=∠BCO+∠OCA=90°,∵OB=OC,∴∠B=∠BCO,∵∠ACD=∠B,∴∠ACD=∠BCO,∴∠ACD+∠OCA=90°,即∠OCD=90°,又∵OC是半径,∴DC为⊙O的切线;(2)解:Rt△ACB中,AB=10,sin B==,∴AC=6,∴BC==8,∵∠ACD=∠B,∠ADC=∠CDB,∴△CAD∽△BCD,∴,设AD=3x,CD=4x,则OD=5+3x,Rt△OCD中,OC2+CD2=OD2,∴52+(4x)2=(5+3x)2,∴x=0(舍)或x=,∴AD=,CD=;(3)解:∵∠CEF=45°,∠ACB=90°,∴CE=CF,设CF=a,∵∠CEF=∠ACD+∠CDE,∠CFE=∠B+∠BDF,∴∠CDE=∠BDF,∵∠ACD=∠B,∴△CED∽△BFD,∴,∴=,∴a=,∴CF=.。
2023年安徽中考数学总复习专题:圆的综合题(切线的性质)(PDF版,有答案)

2023年安徽中考数学总复习专题:圆的综合题1.如图,AB为半圆O的直径,BC切半圆O于点B,连结AC交半圆于点D,点E为AD的中点,连结BE交AC于点F.(1)求证:CB=CF.(2)若EFFB=13,BC=6,求AB的长.2.如图,AB是⊙O的直径,点D是AB延长线上的一点,DC与⊙O相切于点C.连接BC,AC.(1)求证:∠A=∠BCD;(2)若∠D=45°,⊙O的半径为2,求线段AD的长.3.如图,在△ABC中,∠ABC=90°,∠BAC=30°,以AB为直径作⊙O,交AC于点D,过点D作⊙O的切线DM交BC于点M.(1)求证:CM=BM.(2)若AD=23,P为AB上一点,当PM+PD为最小值时,求AP的长.4.如图,⊙O的直径AB垂直于弦DC于点F,点P在AB的延长线上,CP与⊙O相切于点C.(1)求证:∠PCB=∠PAD;(2)若⊙O的直径为4,弦DC平分半径OB,求:图中阴影部分的面积.5.如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O 的切线交AC于点E,交BC的延长线于点F,连接OE.(1)求证:CE=AE;(2)若OB=3,CF=2,求AE的长.6.如图,AB是⊙O的直径,点C、D是⊙O上两点,CE与⊙O相切,交DB延长线于点E,且DE⊥CE,连接AC,DC.(1)求证:∠ABD=2∠A;(2)若DE=2CE,AC=8,求BE的长度.7.如图,在△ABC中,以△ABC的边AB为直径作⊙O,交AC于点D,DE是⊙O的切线,且DE⊥BC,垂足为点E.(1)求证:AB=BC;(2)若DE=3,AC=610,求⊙O的半径.8.如图,AB是⊙O的直径,点C是AB上一点,AC>BC,AC的垂直平分线交⊙O于点E,交AC于点D,过点A作⊙O的切线交CE的延长线于点F.(1)求证:EA=EF;(2)若OD=1,OC=2,求AF的长.9.如图,四边形ABCD是⊙O的内接四边形,且对角线BD为直径,过点A作⊙O的切线AE,与CD的延长线交于点E,已知DA平分∠BDE.(1)求证:AE⊥DE;(2)若⊙O的半径为5,CD=6,求AD的长.10.如图,点C在以AB为直径的⊙O上,过C作⊙O的切线交AB的延长线于E,AD⊥CE 于D,连结AC.(1)求证:∠ACD=∠ABC(2)若tan∠CAD=34,AD=8,求⊙O直径AB的长.11.阅读下列材料,完成相应任务:古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”,它的完美来自对称,其中切弦(chordofcontact)亦称切点弦,是一条特殊弦,从圆外一点向圆引两条切线,连接这两个切点的弦称为切弦.此时,圆心与已知点的连线垂直平分切弦.(1)任务一:为了说明切弦性质的正确性,需要对其进行证明,如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图1,P是⊙O外一点, .求证: .证明:(2)任务二:如图2,在任务一的条件下,CD是⊙O的直径,连接AD、BC,若∠ADC =50°,∠BCD=70°,OC=6,求OP的长.参考答案1.(1)证明:如图,连结AE,∵BC是⊙O的切线,∴BC⊥OB,∴∠ABC=90°,∴∠CBF=90°﹣∠ABE,∴AB是⊙O的直径,∴∠E=90°,∴∠CFB=∠AFE=90°﹣∠DAE,∵点E为AD的中点,∴AE=DE,∴∠ABE=∠DAE,∴90°﹣∠ABE=90°﹣∠DAE,∴∠CBF=∠CFB,∴CB=CF.(2)解:如图,作CG⊥BF于点G,∵BC=CF=6,∴GF=GB=12 FB,∵EFFB=13,∴EF=13 FB,∴EFGF=13FB12FB=23,∵∠FGC=∠E=90°,∠AFE=∠DFG,∴△AFE∽△CFG,∴AFCF=EFGF=23,∴AF=23CF=23×6=4,∴AC=AF+CF=4+6=10,∴AB=AC2―BC2=102―62=8,∴AB的长是8.2.(1)证明:连接OC,∵DC是⊙O的切线,∴∠OCD=90°,即∠BCD+∠OCB=90°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠A+∠OBC=90°,∵OC=OB,∴∠OCB=∠OBC,∴∠A=∠BCD;(2)解:在Rt△OCD中,∠D=45°,OC=2,∴OC=CD=2,∴OD=2OC=22,∴AD=OA+OD=2+22.3.(1)证明:连接OD,OM,∵∠BAC=30°,∴∠DOB=2∠A=60°,∵DM与⊙O相切于点D,∴∠ODM=90°,∵∠ABC=90°,OD=OB,OM=OM,∴Rt△ODM≌Rt△OBM(HL),∴∠DOM=∠BOM=12∠DOB=30°,∴∠A=∠BOM,∴AC∥OM,∵OA=OB,∴BM=CM;解法二:连接BD,∵DM,BC都是⊙O的切线,∴MD=MB,∴∠MBD=∠MDB,∵∠C+∠CBD=90°,∠CDM+∠BDM=90°,∴∠C=∠MDC,∴MC=MD,∴CM=MB.(2)连接DB,过点D作DE⊥AB,垂足为E,并延长交⊙O于点D′,则DE=D′E,∴点D与点D′关于AB对称,连接D′M交AB于点P,连接DP,此时PM+PD的值最小,∵AB是⊙O的直径,∴∠ADB=90°,∵AD=23,∠DAB=30°,∴BD=AD•tan30°=23×33=2,∴AB=2BD=4,∴OA=OB=OD=12AB=2,在Rt△ABC中,BC=AB•tan30°=4×33=433,∴CM=BM=12BC=233,∵∠DOB=60°,∴△DOB是等边三角形,∵DE⊥OB,∴OE=EB=12OB=1,∴DE=3OE=3,∴DE=D′E=3,∵∠D′EP=∠CBP=90°,∠MPB=∠EPD′,∴△MBP∽△D′EP,∴BMD′E=BPEP,∴2333=BP1―BP,∴BP=2 5,∴AP=AB﹣BP=18 5,∴AP的长为18 5.解法二:以B为原点,构造平面直角坐标系.作点D关于x轴的对称点F,连接FM交AB于点P,连接PD,此时PD+PM的值最小.由方法一可知F(﹣1,―3),M(0,233),设直线FM的解析式为y=kx+b,则有―k+b=―3 b=233,∴直线FM放解析式为y=533x+233,令y=0,可得x=―2 5,∴AP=AB﹣PB=18 5.4.(1)证明:连接OC,∵CP与⊙O相切,∴OC⊥PC,∴∠PCB+∠OCB=90°,∵AB⊥DC,∴∠PAD+∠ADF=90°,∵OB=OC,∴∠OBC=∠OCB,由圆周角定理得:∠ADF=∠OBC,∴∠PCB=∠PAD;(2)解:连接OD,在Rt△ODF中,OF=12 OD,则∠ODF=30°,∴∠DOF=60°,∵AB⊥DC,∴DF=FC,∵BF=OF,AB⊥DC,∴S△CFB=S△DFO,∴S阴影部分=S扇形BOD=60π×22360=23π.5.(1)证明:连接CD,∵BC是⊙O的直径,∴∠CDB=∠ADC=90°,∴∠A+∠ACD=90°,∵∠ACB=90°,OC为半径,∴AC是⊙O的切线,∵ED是⊙O的切线,∴DC=ED,∴∠ECD=∠EDC,∵∠EDC+∠ADE=90°,∴∠A=∠ADE,∴AE=DE,∴CE=AE;(2)解:连接OD,∵OB=3,CF=2,∴OB=OC=OD=3,OF=5∵DE是⊙O的切线,∴∠ODF=90°,∴DF=OF2―OD2=4,∵∠ODF=∠ECF=90°,∵∠F=∠F,∴△CEF∽△DOF,∴FCFD=CEDO,即24=CE3,∴CE=3 2,∴AE=CE=3 2.6.(1)证明:连接OC,∵CE与⊙O相切,∴OC⊥CE,∵DE⊥CE,∴OC∥DE,∴∠ABD=∠BOC,由圆周角定理得:∠BOC=2∠A,∴∠ABD=2∠A;(2)解:连接BC,∵AB是⊙O的直径,∴∠ACB=90°,∵DE=2CE,∴tan D=CEDE=12,由圆周角定理得:∠A=∠D,∴tan A=BCAC=12,∴BC=4,∴AB=AC2+BC2=82+42=45,∵∠A=∠BCE,∠ACB=∠CEB,∴△ACB∽△CEB,∴BCBE=ABBC,即4BE=454,解得:BE=45 5.7.(1)证明:连接OD,∵DE是⊙O的切线,∴OD⊥DE,∵DE⊥BC,∴OD∥BC,∴∠ADO=∠C,∵OA=OD,∴∠A=∠ADO,∴∠A=∠C,∴BA=BC;(2)解:连接BD,∵AB是⊙O的直径,∴∠ADB=90°,∵BA=BC,BD⊥AC,∴AD=CD=12AC=310,∵DE⊥BC,∴∠DEC=90°,在Rt△DEC中,DE=3,∴CE=CD2―DE2=(310)2―32=9,∵∠ADB=∠DEC=90°,∠A=∠C,∴△ADB∽△CED,∴ABCD=ADCE,∴AB310=3109,∴AB=10,∴⊙O的半径为5.8.(1)证明:∵AF是⊙O的切线,AB是⊙O的直径,∴AF⊥AB,∴∠CAF=90°,∴∠CAE+∠EAF=90°,∠ACF+∠F=90°,∵ED垂直平分AC,∴EA=CE,∴∠CAE=∠ACE,∴∠F=∠EAF,∴EA=EF;(2)解:连接OE,∵OD=1,OC=2,∴CD=OD+OC=3,∵ED垂直平分AC,∴AD=DC,∴OA=OE=OD+AD=1+3=4,∴DE=OE2―OD2=42―12=15,∵AE=EF,AE=CE,∴EF=CE,又∵AD=CD,∴DE为△ACF的中位线,∴DE=12 AF,∴AF=2DE=215.9.(1)证明:连接OA,∵AE是⊙O切线,∴∠OAE=90°,∵DA平分∠BDE,∴∠ADE=∠ADO,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠ADE,∴OA∥DE,∴∠E=180°﹣∠OAE=90°,∴AE⊥DE;(2)解:过点O作OF⊥CD,垂足为F,∴DF=FC=12DC=3,∠OFD=90°,∵∠OAE=∠E=90°,∴四边形AEFO是矩形,∴EF=OA=5,AE=OF,∴DE=EF﹣DF=5﹣3=2,在Rt△OFD中,OF=OD2―DF2=52―32=4,∴AE=OF=4,在Rt△AED中,AD=AE2+DE2=42+22=25,∴AD的长是25.10.(1)证明:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∵DE与⊙O相切于点C,∴∠DCO=90°,∴∠DCO﹣∠ACO=∠ACB﹣∠ACO,∴∠DCA=∠OCB,∵OC=OB,∴∠OCB=∠ABC,∴∠ACD=∠ABC;(2)解:∵AD⊥CE,∴∠D=90°,∵tan∠CAD=34,AD=8,∴CD=AD•tan∠CAD=8×34=6,∴AC=AD2+CD2=82+62=10,∵∠D=∠ACB=90°,∠ACD=∠ABC,∴△ADC∽△ACB,∴ADAC=ACAB,∴810=10AB,∴AB=25 2,∴⊙O直径AB的长为25 2.11.解:(1)已知:如图1,P是⊙O外一点,PA、PB与⊙O分别相切于点A、B,连接AB、OP,求证:OP垂直平分AB.证明:连接OA、OB,∵PA、PB与⊙O分别相切于点A、B,∴PA=PB,∵OA=OB,∴OP垂直平分AB,故答案为:PA、PB与⊙O分别相切于点A、B,连接AB、OP;OP垂直平分AB;(2)连接OA、OB,∵OA=OD,∴∠ADC=∠DAO=50°,∴∠AOD=180°﹣∠ADC﹣∠DAO=80°,∵OB=OC,∴∠DCB=∠OBC=70°,∴∠BOC=180°﹣∠DCB﹣∠OBC=40°,∴∠AOB=∠180°﹣∠AOD﹣∠BOC=60°,∵PA、PB与⊙O分别相切于点A、B,∴OA⊥PA,∠AOP=∠BOP=30°,∴OP=OAcos∠AOP=632=43.。
2023年中考数学高频考点突破——圆的切线的证明(含解析)

2023年中考数学高频考点突破——圆的切线的证明(1)求证:是的切线;(2)若,的半径为5,求线段2.如图,中,,以(1)求证:是的切线;(2)若,,求3.如图,以的直角边中点,连.(1)请判断是否为的切线,并证明你的结论.(2)当时,4.如图,中,,交于点C ,与交于点A ,与DE O e 1tan 2B =O e ABC V AB AC =DE AB ⊥E ED DE O e tan 2B =103DF =O e Rt ABC △AC DE DE O e :9:16AD DB =8cm DE =EBF △90B Ð=°OF EB形,.(1)求证:为的切线;(2)已知的半径为2,求图中阴影部分的面积.5.如图,已知,在中,,以为直径的分别交,于D ,E 两点,于点F ,且(1)求证:是的切线.(2)若,求的半径.6.如图是直径,是上异于,的一点,点是延长线上一点,连、、,且.(1)求证:直线是的切线;(2)若,求的值;7.如图,四边形为的内接四边形,为直径,平分,过点作的平行线,交的延长线于点.60FOB ∠=︒EF O e O e ABC V AB AC =AC O e AB BC BF CF ⊥.BF BD =FC O e 23BF CE ==,O e CD O e A O e C D B DC AB AC AD BAC ADB ∠=∠AB O e 2BC OC =tan ADB ∠ABCD O e BD AC BAD ∠C BD AD E(1)求证:与相切;(2)求证:.8.如图,在中,,点在边上,以为半径的半圆交于点,交于点,在边上取一点,连接,使得.(1)求证:为半圆的切线;(2)若,,,求半圆的半径长.9.如图,是的直径,点是上的一点,,垂足为,连接,,.(1)求证:;(2)延长交于点,连接,过点作,交的延长线于点.若,求证:直线为的切线.10.如图,以为直径的半圆中,点为圆心,点在圆上,过点作,且.连接,分别交,于点,,与交于点,若.CE O e 2BC AB DE =⋅Rt ABC △90C ∠=︒O AC OA O AB D AC E BC F FD DF BF =DF O 6AC =4BC =1CF =O AB O e C O e CD AB ⊥D AC BC OC 2BOC BCD ∠=∠CD O e E EB C CF EB ⊥EB F 2AC CD =CF O e AB O C C CD AB ∥CD OB =AD OC BC E F O e G =45ABC ∠︒(1)证明:是的切线;(2)求的长.12.如图,是的直径,点D 是直径(1)求证:是的切线;(2)当D 是的中点时,13.如图,点在于点.(1)求证:是的切线.(2)是的切线,为切点,若BC O e EF AB O e EF O e OA D O e AE CD ⊥E CD O e DF O e F(1)求证:是的切线:(2)若,,求15.如图,是的直径,(1)求证:是的切线;(2)求的长.16.如图,在中,上取一点E ,使(1)求证:.(2)求证:是的切线.17.如图,四边形内接于E ,点P 在延长线上,AF O e 35CA AE =10BE =AB O e CD O e DF ABC V AC AE BCD ADE ≌△△DE O e ACBD AB PCB ∠(1)求证:是的切线;(2)求证::18.如图:以的边为直径作,点C 在上,是的弦,,过点C 作于点F ,交于点G ,过点C 作交的延长线于点E .(1)求证:是的切线;(2)求证:.PC O e 2PE PB PA =⋅ABC V AB O e O e BD O e A CBD ∠=∠CF AB ⊥BD CE BD ∥AB EC O e CG BG =参考答案:∴,∴,在中,∴,10AB AC ==ABC C ∠=∠Rt ADC V tan tan AD B C DC ==()222210AD AD +=∵,∴,∵,∴,∴,∴,∵,AB AC =B ACB ∠=∠OD OC =ODC ACB ∠=∠ODC B ∠=∠AB OD ∥DE AB ⊥∵是的直径,,,为的中点,,AC O e 90ADC ∴∠=︒=90BDC ∴∠︒E Q BC 216cm BC DE ∴==∵四边形为菱形,∴,∴、都是等边三角形,∴,∴,AOCD OA DC OC AD OD ====AOD △COD △60AOD COD ∠=∠=︒60BOC ∠=︒是的直径,,,又,,CD Q O e 90CAD ∴∠=︒90OAC OAD ∴∠+∠=︒OA OD =Q OAD ODA ∠=∠∴∵平分,∴,∴;AC BAD ∠»»BC D C =BC DC =【点评】此题重点考查等腰三角形的性质、直角三角形的两个锐角互余、切线的判定定理、勾股定理等知识,正确地作出所需要的辅助线是解题的关键.9.(1)证明见解析(2)证明见解析,., .2AC CD =Q ∴1tan 2CD A AC ==30A ∴∠=︒30E A ︒∴∠=∠=60BOC ∠=︒30OCD ∴∠=︒【点评】本题考查的是切线的判定、圆周角定理、相似三角形的判定和性质,掌握经过半径的外端并且垂直于这条半径的直线是圆的切线是解题的关键.11.(1)见解析(2)165EF=5∵,弦,∴,∵,,OG BF OA BE ⊥⊥BF BE =BG AB =OB OB =∵,∴,∵,∴,∵,∴,CD AB ⊥90DBC C ∠+∠=︒OB OF =OBC OFB ∠=∠EF EC =C EFC ∠=∠,,平分,,OA OC =Q OAC OCA ∴∠=∠AC Q DAE ∠OAC EAC ∴∠=∠∵,FG BC ∥【点评】本题考查了圆的基本性质,圆周角定理,平行线的判定和性质,切线的证明,菱形的判定和性质,以及30︒得到角相等从而证明直线平行,以及菱形的证明.16.(1)见解析(2)见解析【分析】(1)由,得出,又因为,得,即可由定理得出结论;(2)连接,,先求出,从而求得,继而求得,再由,得,然后由,得,根据,可求得,即可得出,从而求得,即可由切线的判定定理得出结论.【解析】(1)证明:∵,∴,∵∴,在与中,,∴;(2)证明:连接,,∵,∴,∵,∴,AC BC =B A ∠=∠AD AC =BC AD =SAS OD OB 45CBA A ∠=∠=︒67.5ACD ADC ∠=∠=︒22.5BCD ACB ACD ∠=∠-∠=︒BCD ADE ≌△△22.5ADE BCD ∠=∠=︒OD OB =ODB OBD ∠=∠245BOD BCD ∠=∠=︒67.5ODB Ð=°22.567.590ADE ODB ∠+∠=︒+︒=︒()18090ODE ADE ODB ∠=︒-∠+∠=︒AC BC =B A ∠=∠AD AC=BC AD =BCD △ADE V BC AD B A BD AE =⎧⎪∠=∠⎨⎪=⎩()SAS BCD ADE V V ≌OD OB AC BC =CBA A ∠=∠90ACB ∠=︒45CBA A ∠=∠=︒∵,∴,∴,由(1),∴,∵,∴∵,∴,∴,∴,∵是的半径,∴是的切线.【点评】本题考查全等三角形的判定与性质,等腰三角形的性质,三角形内角和定理,圆周角定理,切线的判定,熟练掌握全等三角形的判定与性质,等腰三角形的性质,圆周角定理,切线的判定是解题的关键.17.(1)见解析(2)见解析【分析】(1)连接,根据圆周角定理,可得,推出,得到,即可得证;(2)证明,得到,利用等角对等边,得到,即可得证.【解析】(1)证明:连接,∵是直径,AD AC =67.5ACD ADC ∠=∠=︒22.5BCD ACB ACD ∠=∠-∠=︒BCD ADE ≌△△22.5ADE BCD ∠=∠=︒OD OB =ODB OBD∠=∠245BOD BCD ∠=∠=︒67.5ODB Ð=°22.567.590ADE ODB ∠+∠=︒+︒=︒()18090ODE ADE ODB ∠=︒-∠+∠=︒OD O e DE O e OC 90ACB ∠=︒PCB BAC ∠=∠90PCB OCB ∠+∠=︒PCB PAC V V ∽2PC PB PA =⋅PC PE =OC AB∴,∵,∴,∵,∴,∴,∴,∵是半径,∴是的切线;(2)证明:∵,∴,∴,∵平分,∴,∵,∴,∴,∴.【点评】本题考查切线的判定和性质,圆周角定理,相似三角形的判定和性质.熟练掌握直径所对的圆周角是直角,证明三角形相似,是解题的关键.18.(1)证明过程见解析(2)证明过程见解析【分析】(1)连接,根据可得,从而证明,再根据可得,即可得出结论;(2)根据可证,再根据和等腰三角形的判定即可得出结论.【解析】(1)证明:连接,90CAB ABC ∠+∠=︒OC OB =OCB OBC ∠=∠,BDC CAB PCB BDC ∠=∠∠=∠PCB BAC ∠=∠90PCB OCB ∠+∠=︒OC PC ⊥OC PC O e ,PCB PAC P P ∠=∠∠=∠PCB PAC V V ∽2PC PB PA =⋅CD ACB ∠45ACD BCD ∠=∠=︒45,45CEB CAB PCE PCB ∠=∠+︒∠=︒+∠CEB PCE ∠=∠PC PE =2PE PB PA =⋅OC A CBD ∠=∠»»DCCB =OC DB ⊥DB CE ∥OC CE ⊥90ACB CFB ∠=∠=︒BCF A ∠=∠A CBD ∠=∠OC,,,,∵是的半径,,是的切线.(2)证明:为直径 ,,,,,,,又,,.【点评】本题考查了切线的判定、圆周角定理和平行线的性质及等腰三角形的判定,熟练掌握切线的判定和圆周角定理是解决问题的关键.»»=DCCB ∴OC DB ∴⊥DB CE ∥Q OC CE ∴⊥OC O e 90∴∠=︒OCE CE ∴O e AB Q 90ACB ∴∠=︒90A ABC ∴∠+∠=︒CF AB ⊥Q 90CFB ∴∠=︒=90BCF CBA ∴∠+∠︒BCF A ∴∠=∠A CBD ∠=∠Q BCF CBD ∴∠=∠CG GB ∴=。
中考数学总复习《圆的切线的证明》专项提升练习题-附答案

中考数学总复习《圆的切线的证明》专项提升练习题-附答案学校:___________班级:___________姓名:___________考号:___________1.如图,O为菱形 ABCD对角线上一点,⊙O与BC相切于点M.求证:CD与⊙O相切.2.如图,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O,求证:CD是⊙O的切线.3.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC 于点F.(1)求证:AC是⊙O的切线;(2)若BF=6,⊙O的半径为5,求CE的长.4.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连接DB,过点E作EM∥BD,交BA 的延长线于点M.(1)求⊙O的半径;(2)求证:EM是⊙O的切线;(3)若弦DF与直径AB相交于点P,当∠APD=45º时,求图中阴影部分的面积.5.如图,在Rt△ABC中∠C=90°,BD平分∠ABC,交AC于点D,点O是AB边上的点,以BD为弦的⊙O 交AB于点E.(1)求证:AC是⊙O的切线;(2)若∠A=30°,OB=1求阴影部分的面积.6.如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.(1)求证:DE是⊙O的切线;(2)若CD=3cm,DE=2.5cm,求⊙O直径的长.7.如图,AB是⊙O的直径,点C、E在⊙O上,AC平分∠BAE,CM⊥AE于点D.求证:CM是⊙O的切线.8.如图,△ABC是⊙O的内接三角形,D是圆外一点,连接DA,∠DAC=∠ABC连接DC交⊙O于点E.(1)求证:AD是⊙O的切线;(2)若AD=4,E是CD的中点,求CE的长度.9.如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=50°,求证:CD是⊙O的切线.10.如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.(1)直线FC与⊙O有何位置关系?并说明理由;(2)若OB=BG=2,求CD的长.二、综合题11.如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.(1)求证:BD是⊙O的切线;(2)若AB=12,DB=5,求△AOB的面积.⌢的中点,EF∥12.如图,AB是⊙O的直径,AB=6,OC⊥AB,OC=5,BC与⊙O交于点D,点E是BDBC,交OC的延长线于点F.(1)求证:EF是⊙O的切线;(2)CG∥OD,交AB于点G,求CG的长.13.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;(2)过点B作⊙O的切线交CD的延长线于点E,若BC=12,OBBE = 23,求BE的长.14.如图,△BEF内接于⊙O,BE=BF,BO的延长线交EF于点D.C是⊙O外一点,连接OC,BC,OC⊥BE 于点A.已知OA=2,AB=4,AC=8.(1)求证:BC是⊙O的切线.(2)求EF的长.15.如图,△ABC内接于⊙O,AD平分∠BAC交BC边于点E,交⊙O于点D,过点A作AF⊥BC于点F,设⊙O的直径为d,AF=h.(1)过点D作直线MN∥BC,求证:MN是⊙O的切线;(2)若AB=4,AC=3,求dh的值.16.如图,AB是⊙O的直径,点C、D在⊙O上,且AC平分∠BAD,点E为AB的延长线上一点,且∠ECB=∠CAD.(1)填空:∠ACB= ,理由是(2)求证:CE与⊙O相切(3)若AB=6,CE=4,求AD的长17.如图,AB为⊙O的直径,点C在⊙O上,AD⊥CD于点D,且AC平分∠DAB,求证:(1)直线DC是⊙O的切线;(2)AC2=2AD•AO.18.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.(1)求证:AC是⊙D的切线;(2)求线段AC的长.19.如图,已知ΔABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.(1)若E是BD的中点,连结CE,试判断CE与⊙O的位置关系.(2)若AC=3CD,求∠A的大小.20.如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°(1)求证:AE是⊙O的切线;(2)若 AB=AD,AC=2 √2,tan∠ADC=3,求CD的长.21.如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE.(1)判断直线PQ与⊙O的关系;(2)若直径AB的长为4.当四边形AEOP为菱形时,求PE的长.答案1.证明:连接OM,过点O作ON⊥CD于垂足为N∵⊙O与BC相切于点M∴OM⊥BC,OM为半径∴∠OMC=∠ONC=90°∵AC是菱形ABCD的对角线∴∠ACB=∠ACD∵OC=OC∴△OMC≌△ONC(AAS)∴ON=OM=半径,∠ONC=90°∴CD与⊙O相切.2.证明:过点O作OE⊥CD于点E∵在梯形ABCD中,AD∥BC,∠C=90°∴AD⊥CD,BC⊥CD∴AD∥OE∥BC∵OA=OB∴OE是梯形ABCD的中位线(AD+BC)∴OE= 12∵AD+BC=AB∴OE= 1AB2∵以AB为直径作⊙O.∴直线CD是⊙O的切线.3.解:(1)连接OE.∵OE=OB∴∠OBE=∠OEB∵BE平分∠ABC∴∠OBE=∠EBC∴∠EBC=∠OEB∴OE∥BC∴∠OEA=∠C∵∠ACB=90°∴∠OEA=90°∴AC是⊙O的切线;(2)连接OE、OF,过点O作OH⊥BF交BF于H由题意可知四边形OECH为矩形∴OH=CE∵BF=6∴BH=3在Rt△BHO中,OB=5∴OH=4∴CE=4.4.(1)连结OE,如图:∵DE垂直平分半径OA∴OC=∴∠OEC=30°∴(2)由(1)知:∠AOE=60°∴∴∠BDE=60°∵BD∥ME∴∠MED=∠BDE=60°∴∠MEO=90°∴EM是⊙O的切线。
2022年中考数学提优专题:《圆:切割线定理》(含答案)

《圆:切割线定理》知识梳理:(1)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT的平方=PA•PB(切割线定理)(2)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.几何语言:∵PBA,PDC是⊙O的割线∴PD•PC=PA•PB(切割线定理推论)(割线定理)由上可知:PT2=PA•PB=PC•PD.一.选择题1.如图,P是⊙O的直径BC延长线上一点,PA切⊙O 于点A,若PC=2,BC=6,则切线PA的长为()A.无限长B.C.4 D.2.如图,PT是⊙O的切线,T为切点,PBA是割线,交⊙O于A、B两点,与直径CT交于点D,已知CD=2,AD=3,BD=4,那么PB等于()A.6 B.C.7 D.203.设H为锐角△ABC的三条高AD、BE、CF的交点,若BC=a,AC=b,AB=c,则AH•AD+BH•BE+CH•CF 等于()A.(ab+bc+ca)B.(a2+b2+c2)C.(ab+bc+ca) D.(a2+b2+c2)4.如图,MN切⊙O于A点,AC为弦,BC为直径,那么下列命题中假命题是()A.∠MAB和∠ABC互余B.∠CAN=∠ABCC.OA=BC D.MA2=MB•BC5.如图,以OB为直径的半圆与半圆O交于点P,A、O、C、B在同一条直线上,作AD⊥AB与BP的延长线交于点D,若半圆O的半径为2,∠D的余弦值是方程3x2﹣10x+3=0的根,则AB的长等于()A.B.C.8 D.56.如图,AB是⊙O直径,AC是⊙O的弦,过弧BC 的中点D作AC的垂线交AC的延长于E,若DE=2,EC=1,则⊙O的直径为()A.B.C.5 D.47.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,AB=PC=2,则PD的长是()A.3 B.7.5 C.5 D.5.58.如图,已知⊙O的弦A B、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=cm,则PE的长为()A.4cm B.3cm C.5cm D.cm9.如图,⊙O1与⊙O2相交于A、B两点,PQ切⊙O1于点P,交⊙O2于点Q、M,交AB的延长线于点N.若MN=1,MQ=3,则NP等于()A.1 B.C.2 D.310.同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆上一点,GE、GF 分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为()A.①③B.②③C.③④D.②④二.填空题11.如图,AB为⊙O的直径,P点在AB的延长线上,PM切⊙O于点M.若OA=a,PM=,那么△PMB 的周长是.12.已知:如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=4,PB=8,则PA =,sin∠P=,CD=.13.如图,PA、PB与⊙O分别相切于点A、点B,AC 是⊙O的直径,PC交⊙O于点D,已知∠APB=60°,AC=2,那么CD的长为.14.如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,若PA=6,PB=4,弧AB的度数为60°,则BC =,∠PCA=度,∠PAB=度.15.如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=.16.如图,AC为⊙O的直径,PA是⊙O的切线,切点为A,PBC是⊙O的割线,∠BAC的平分线交BC于D 点,PF交AC于F点,交AB于E点,要使AE=AF,则PF应满足的条件是(只需填一个条件).17.由⊙O外一点F作⊙O的两条切线,切点分别为B、D,AB是⊙O的直径,连接AD、BD,线段OF交⊙O 于E,交BD于C,连接DE、BE.有下列序号为①~④的四个结论:①BE=DE;②∠EBD=∠EDB;③DE∥AB;④BD2=2AD•FC其中正确的结论有.(把你认为正确结论的序号全部填上)三.解答题18.已知:如图,在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆.(1)求证:AC是⊙O的切线;(2)若AD=6,AE=6,求DE的长.19.如图,圆O是以AB为直径的△ABC的外接圆,D 是劣弧的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;(1)求证:OE=AC;(2)求证:;(3)当AC=6,AB=10时,求切线PC的长.20.如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PE•PF;(2)当∠BOP=30°,P点为的中点时,求D、E、F、P四个点的坐标及S△DEF.参考答案一.选择题1.解:∵PC=2,BC=6,∴PB=8,∵PA2=PC•PB=16,∴PA=4.故选:C.2.解:∵TD•CD=AD•BD,CD=2,AD=3,BD=4,∴TD=6,∵PT2=PD2﹣TD2,∴PT2=PB•PA=(PD﹣BD)(PD+AD),∴PD=24,∴PB=PD﹣BD=24﹣4=20.故选:D.3.解:AH•AD=AC•AE=AC•AB•cos∠BAE=(b2+c2﹣a2),同理BH•BE=(a2+c2﹣b2),CH•CF=(a2+b2﹣c2),故AH•AD+BH•BE+CH•CF=(a2+b2+c2).故选:B.4.解:∵BC是⊙O的直径,∴∠BAC=90°,∴∠MAB+∠CA N=90°;∵MN切⊙O于A,∴MA2=MB•MC,(故D错误)∠CAN=∠CBA,(故B正确)∴∠MAB+∠CBA=90°;(故A正确)∵OA是⊙O的半径,BC是⊙O的直径,∴BC=2OA;(故C正确)故选:D.5.解:∵3x2﹣10x+3=0,∴x=3(不合题意,舍去)或x=.∴cosD=AD:BD=1:3,设A D=x,则BD=3x.∴AB==2x,BC=2x﹣4.∴(2x)2=(2x﹣4)•x.∴x=0(舍去),或x=2.∴AB=2×2=8.故选:C.6.解:连接OD,∵点D是弧BC的中点,∴OD⊥BC,∠OFC=90°,AB是直径,∴∠ACB=90°,DE⊥AE,∴∠E=90°,∴四边形CFDE是矩形,∴∠ODE=90°,∴ED是圆的切线.作OG⊥AC,则OG=CF=ED=2.∵DE2=EC•AE,∴AE=4,AC=3,AG=,∴AO=,∴AB=5.故选:C.7.解:∵PA=3,AB=PC=2,∴PB=5,∵PA•PB=PC•PD,∴PD=7.5,故选:B.8.解:∵PA•PB=PC•PD,PA=4cm,PB=3cm,PC=6cm,∴PD=2;设DE=x,∵AE2=ED•EC,∴x(x+8)=20,∴x=2或x=﹣10(负值舍去),∴PE=2+2=4.故选:A.9.解:∵PN2=NB•NA,NB•NA=NM•NQ,∴PN2=NM•NQ=4,∴PN=2.故选:C.10.解:连接OK,∵EF切小圆于K,∴OK⊥EF,根据垂径定理得EK=FK,∵EP切小圆于P,FQ切小圆于Q,∴EP=EK,FQ=FK,∴EP=FQ,故③正确;∴由切割线定理得,FK2=FN•FG,EK2=EM•EG,∴FN•FG=EM•EG,故④正确;故选:C.二.填空题(共7小题)11.解:连接OM;∵PM切⊙O于点M,∴∠OMP=90°,∵OA=OM=a,PM=,∴tan∠MOP=MP:OM=,∴∠MOP=60°,∴OP=2a,∴PB=OP﹣OB=a;∵OM=OB,∴△OMB是等边三角形,MB=OB=a,∴△PMB的周长是(+2)a.12.解:∵PC切⊙O于点C,割线PAB经过圆心O,PC=4,PB=8,∴PC2=PA•PB.∴PA==2.∴AB=6.∴圆的半径是3.连接OC.∵OC=3,OP=5,∴sin∠P=.∴CE=,∴CD=.13.解:连接AD,OB,OP;∵PA、PB与⊙O分别相切于点A、点B,∴∠OAP=∠OBP=90°,∠AOB=180°﹣∠P=120°,∴∠AOP=60°,AP=AOtan60°=,∴PC=;∵PA2=PD•PC,∴PD=,∴CD=.14.解:∵PA2=PB•PC,PA=6,PB=4;∴PC=9,∴BC=5;∵弧AB的度数为60°,∴∠PCA=30°,∴∠PAB=30°.15.解:由切割线定理得PB•PA=PC•PD,则有8×20=PC(PC+6).解得PC=10.在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.从而AD是圆的直径.由勾股定理,得AD2=AC2+CD2=(PA2﹣PC2)+CD2=202﹣102+62=336.∴AD==4∴R=AD=2.故答案为2.16.解:∵∠PAC=90°,∠ABC=90°,∴90°﹣∠AFP=90°﹣∠BEP,∴∠APF=∠CPF,∴PF平分∠APC.17.解:∵BF,DF是⊙O的两条切线∴OF是∠DFB的角平分线,DF=FB,FO⊥BD,CD=CB∴=∴BE=DE(①正确)∵=∴∠EBD=∠EDB(②正确)∵FB切⊙O于B∴FB⊥OB∵BC⊥OF∵BC2=OC•FC∴(BD)2=OC•CE∵OC为△ABD的中位线∴OC=AD∴(BD)2=AD•CE∴BD2=2AD•FC(④正确)故其中正确的结论有①②④.三.解答题(共3小题)18.(1)证明:连接OE;(1分)∵⊙O是△BDE的外接圆,∠DEB=90°,∴BD是⊙O的直径,(不证直径,不扣分)∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,(2分)∴∠OEB=∠CBE,∴OE∥BC,(3分)∵∠C=90°,∴∠AEO=90°,∴AC是⊙O的切线;(4分)(2)解:∵AE是⊙O的切线,AD=6,AE=6,∴AE2=AD•AB,(5分)∴AB===12,∴BD=AB﹣AD=12﹣6=6;∵∠AED=∠ABE,∠A=∠A,∴△AED∽△ABE,(6分)∴;设DE=x,BE=2x,∵DE2+BE2=BD2,(7分)∴2x2+4x2=36,解得x=±(负的舍去),∴DE=2.(8分)19.(1)证明:∵AB为直径∴∠ACB=90°∴AC⊥BC又D为中点,∴OD⊥BC,OD∥AC,又O为AB中点,∴;(4分)(2)证明:连接CD,PC为切线,由∠PCD=∠CAP,∠P为公共角,∴△PCD∽△PAC,(6分)∴,又CD=BD,∴;(8分)(3)解:∵AC=6,AB=10,∴BC=8,BE=4,OE=3,∴DE=2,∴BD2=DE2+BE2=20,(9分)∴AD2=AB2﹣BD2=80,∴AD=4,(10分)CD=BD=2,由(2),∴,(11分)∴CP2=DP•AP=45×5,∴切线PC=15.(12分)20.(1)证明:连接PB,OP,∵PE⊥AB,PD⊥OB,∴∠BEP=∠PDO=90°,∵AB切⊙O1于B,∠ABP=∠BOP,∴△PBE∽△POD,∴=,同理,△OPF∽△BPD∴=,∴=,∴PD2=PE•PF;(2)解:连接O1B,O1P,∵AB切⊙O1于B,∠POB=30°,∴∠ABP=30°,∴∠O1BP=90°﹣30°=60°,∵O1B=O1P,∴△O1BP为等边三角形,∴O1B=BP,∵P为弧BO的中点,∴BP=OP,即△O1PO为等边三角形,∴O1P=OP=a,∴∠O1OP=60°,又∵P为弧BO的中点,∴O1P⊥OB,在△O1DO中,∵∠O1OP=60°O1O=a,∴O1D=a,OD=a,过D作DM⊥OO1于M,∴DM=OD=a,OM=DM=a,∴D(﹣a,a),∵∠O1OF=90°,∠O1OP=60°∴∠POF=30°,∵PE⊥OA,∴PF=OP=a,OF=a,∴P(﹣a,),F(﹣a,0),∵AB切⊙O1于B,∠POB=30°,∴∠ABP=∠BOP=30°,∵PE⊥AB,PB=a,∴∠EPB=60°∴PE=a,BE=a,∵P为弧BO的中点,∴BP=PO,∴∠PBO=∠BOP=30°,∴∠BPO=120°,∴∠BPE+∠BPO=120°+60°=180°,即OPE三点共线,∵OE=a+a=a,过E作EM⊥x轴于M,∵AO切⊙O1于O,∴∠EOA=30°,∴EM=OE=a,OM=a,∴E(﹣a,a),∵E(﹣a,a),D(﹣a,a),∴DE=﹣a﹣(﹣a)=a,DE边上的高为:a,∴S△DEF=×a×a=a2.故答案为:D(﹣a,a),E(﹣a,a),F(﹣a,0),P(﹣a,);S△DEF=a2.。
中考数学总复习《圆的切线证明》专题训练(附带答案)

中考数学总复习《圆的切线证明》专题训练(附带答案)学校:___________班级:___________姓名:___________考号:___________⊥于点D,E是AC上一点,以BE为直径的O交1.如图,在ABC中,AB=AC,AD BC∠=︒.BC于点F,连接DE,DO,且90DOB(1)求证:AC是O的切线;(2)若1DF=,DC=3,求BE的长.、2.如图,在O中,BC为非直径弦,点D是BC的中点,CD是ABC的角平分线.∠=∠;(1)求证:ACD ABC(2)求证:AC是O的切线;(3)若1BD=,3BC=时,求弦BD与BD围城的弓形面积.是O的切线;=,且AC BD已知等腰ABC,AB=AC为直径作O交BC于点延长线于点F.是O的切线;CD=2,求O的半径.与O相离,,交O于点A是O上一点,连于点C,且PB(1)求证:PB是O的切线;(2)若25AC=,OP=5,求O的半径.6.如图,点O是ABC的边AC上一点,以点O为圆心,OA为半径作O,与BC相切于点E,连接OB,OE,O交OB于点D,连接AD并延长交CB的延长线于点F,且AOD EOD.∠=∠(1)求证:AB是O的切线;BC=,AC=8,求O的半径.(2)若107.如图,AB 是O 的直径,AC 是O 的弦.(1)尺规作图:过点C 作O 的切线,交AB 的延长线于点D (保留作图痕迹,不写作法);(2)若2BD OB ==,求AC 的长.8.如图,ABCD 的顶点,,A B C 在O 上,AC 为对角线,DC 的延长线交O 于点E ,连接,,OC OE AE .(1)求证:AE BC =;(2)若AD 是O 的切线6,40OC D =∠=︒,求CE 的长.9.如图,Rt ABC △中90C ∠=︒,点E 为AB 上一点,以AE 为直径的O 上一点D 在BC 上,且AD 平分BAC ∠.(1)证明:BC 是O 的切线;(2)若42BD BE ==,,求AB 的长.10.如图,已知O 的弦AB 等于半径,连接OA 、OB ,并延长OB 到点C ,使得BC OB =,连接AC ,过点A 作AE OB ⊥于点E ,延长AE 交O 于点D .(1)求证:AC 是O 的切线;(2)若6BC =,求AD 的长.11.如图,线段AB 经过O 的圆心.O 交O 于A ,C 两点,AD 为O 的弦,连接BD ,30A ABD ∠=∠=︒连接DO 并延长交O 于点E ,连接BE 交O 于点F .(1)求证:BD 是O 的切线;(2)若1BC =,求BF 的长.12.如图,AB 为O 的直径,C 为O 上一点,CD BD ABC CBD ⊥∠=∠.(1)求证:CD 为O 的切线.(2)当1,4BD AB ==时,求CD 的长.13.如图 已知AB 是O 的直径 BC AB ⊥于B E 是OA 上的一点ED BC ∥交O 于D OC AD ∥ 连接AC 交ED 于F .(1)求证:CD 是O 的切线;(2)若8AB = 1AE = 求ED EF 的长.14.如图 AB 是O 的直径 AC BC ,是弦 点D 在AB 的延长线上 且DCB DAC ∠=∠ O 的切线AE 与DC 的延长线交于点E .(1)求证:CD 是O 的切线;(2)若O 的半径为2 30D ∠=︒ 求AE 的长.15.如图 已知AB 是O 的直径 点P 在BA 的延长线上 弦BC 平分PBD ∠且BD PD ⊥于点D .(1)求证:PD 是O 的切线.(2)若8cm 6cm AB BD , 求弧AC 的长.为O的直径在O上连接的延长线交于E.是O的切线;∠tan BDF为O的直径的平分线交O于点E BC的延长线于点(1)求证:DE 为O 切线;(2)若10AB = 6BC = 求DE 的长.18.如图 O 是ABC 的外接圆 点D 在BC 延长线上 且满足CAD B ∠=∠.(1)求证:AD 是O 的切线;(2)若AC 是BAD ∠的平分线 3sin 5B =4BC = 求O 的半径.参考答案:1.【分析】此题重点考查圆周角定理 切线的判定定理 勾股定理 三角形的中位线定理 等腰三角形的“三线合一” 线段的垂直平分线的性质等知识 正确地作出辅助线是解题的关键.是O的切线;+=314是O的直径90︒则22BE=+4(22)⊥AD BC是O的半径是O的切线.)连接EFDC=DF33+=+BD DF∠OE DOBDE=.3是O的直径90︒.中EF=中BE=(3)23312π- 【分析】此题考查了解直角三角形 切线的判定以及扇形的面积.注意掌握辅助线的作法 .(1)点D 是BC 的中点 可以得到BD CD = 即可得到DBC DCB ∠∠= 再根据角平分线的定义得到ACD BCD ∠∠= 进而得到结论;(2)连接OC OD OB 则可得到OD BC ⊥ 然后根据等边对等角可以得到90OCD ACD ∠∠+=︒ 即可得到结论(3)先求出60ODB ∠=︒ 继而利用OBD OBD S S S=-阴影部分扇形求得答案.【详解】(1)解:如图 ∵点D 是BC 的中点∵BD CD =∵DBC DCB ∠∠=又∵CD 是ABC 的角平分线∵ACD BCD ∠∠=∵ACD ABC ∠∠=;(2)证明:如图 连接OC OD OB∵点D 是BC 的中点∵OD BC ⊥∵90ODC BCD ∠∠+=︒∵OD OC =∵ODC OCD ∠∠=又∵ACD BCD ∠∠=∵90OCD ACD ∠∠+=︒即OC AC ⊥∵OC 是O 的半径∵AC 是O 的切线;Rt BDE 中 ODB ∠=60ODB =︒OB OD =∵OBD 是等边三角形BOD ∠=OBD S S==阴影部分.(1)见解析(2)23进而得出BFG 是等边三角形 是O 的切线;)解:如图所示∵OD AC ⊥∵AD CD =∵BD AC =∵BD AC =∵AD BC =∵AD CD BC ==;∵AB 为半圆O 的直径∵90CAB CBA ∠+∠=︒∵30DAC CAB ABD ∠=∠=∠=︒∵60GBF G ∠=∠=︒ 12GB AG =∵BFG 是等边三角形 223AB AG BG BG =-=∵3233BF BG AB ===. 【点睛】本题考查了切线的判定 弧与弦的关系 直径所对的圆周角是直角 勾股定理 等边三角形的性质与判定 垂径定理 熟练掌握以上知识是解题的关键.4.(1)证明(2)233【分析】本题主要考查切线的性质和判定及特殊角的三角函数的应用 掌握切线问题中的辅助线的作法是解题的关键.(1)连接OD 证明ODB C ∠=∠ 推出AC OD ∥ 即可证明结论成立;(2)连接AD 在Rt CED 中 求得利用三角形函数的定义求得30C ∠=︒ 60AOD ∠=︒ 在Rt ADB 中 利用勾股定理列式计算求得圆的半径即可.【详解】(1)证明:连接OD又OB OD=B ODB∴∠=∠ODB∴∠=∠AC OD∥DF AC⊥OD DF∴⊥DF∴是O的切线;(2)连接AD设O半径为Rt CED中3,CE CD=22ED CD∴=-又cosCE CCD ∠=30C∴∠=︒30B∴∠=︒60AOD=∠AB是O的直径.90ADB∴∠=︒12AD AB r ∴== ∵AB AC =∵2CD BD ==又222AD BD AB +=2222(2)r r ∴+=233r ∴=(负值已舍). 5.(1)证明见解析(2)3【分析】本题考查的是勾股定理的应用 等腰三角形的性质 切线的判定 熟练的证明圆的切线是解本题的关键;(1)连接OB 证明PCB PBC ∠=∠ OAB OBA ∠=∠ 再证明90PBC OBA ∠+∠=︒即可;(2)设O 的半径为r 表示()()22222255PC AC AP r =-=-- 222225PB OP OB r =-=- 再利用PB PC =建立方程求解即可.【详解】(1)解:连接OB∵PB PC = OA OB =∵PCB PBC ∠=∠ OAB OBA ∠=∠∵OP l ⊥ OAB PAC ∠=∠∵90BCP CAP BCP OAB ∠+∠=︒=∠+∠∵90PBC OBA ∠+∠=︒∵90OBP ∠=︒∵OB PB ⊥是O 的切线;)设O 的半径为l 2AC =2AC AP =-PB BP 2OP OB =-∵O 的半径为【点睛】.(1)见解析(2)3【分析】本题主要考查切线的判定和性质证AOB EOB ≌ 得出的半径为r 则OE OA =根据AOB EOB ≌得求得4CE = 在Rt OCE 中运用勾股定理列式求出r 的值即可. )证明:在AOB 和EOB 中∵()SAS AOB EOB ≌OAF OEF ∠=∠BC 与O 相切OE BC ⊥90OAB OEB ∠=∠=︒AF是O 的半径是O 的切线;(2)解:在Rt CAB △中 90108CAB BC AC ∠=︒==,,∵22221086AB BC AC =-=-=设圆O 的半径为r 则,OE OA r ==∵8OC r =-∵,AOB EOB ≌∵6BE AB ==∵10,BC =∵1064,CE BC BE =-=-=在Rt OCE 中 222OE CE OC +=∵()22248r r +=-解得3r =.∵O 的半径为3.7.(1)作图见解析(2)4π3【分析】本题考查了作图 复杂作图 切线的性质 等边三角形的判定与性质 弧长的计算 熟练掌握切线的性质 弧长公式是解答本题的关键.(1)根据题意 连接OC 作OC CD ⊥ 交AB 的延长线于点D 由此得到答案. (2)根据题意 得到OBC △是等边三角形 求出120AOC ∠=︒ 再利用弧长公式 得到答案.【详解】(1)解:如图所示 CD 即为所求.(2)如图所示 连接BCBD)证明:在ABCD中AE AD ∴=∵AE BC =.(2)解:连接OA 过点O 作OF CE ⊥于点F 如图所示:AD 是O 的切线OA AD ∴⊥OA BC ∴⊥AB AC ∴=40AEC B D ︒∠=∠=∠=40ACB B ∴∠=∠=︒在ABCD 中 AD BC ∥40DAC ACB ∴∠=∠=︒又180100DAE D AEC ∠=︒-∠-∠=︒60CAE DAE CAD ∴∠=∠-∠=︒2120COE CAE ∴∠=∠=︒OC OE =30OCE ∴∠=︒OF CE ⊥22cos3063CE CF OC ∴==⋅︒=.【点睛】本题主要考查了切线的性质 解直角三角形 圆周角定理 平行四边形的性质垂径定理 等腰三角形的判定 解题的关键是作出辅助线 熟练掌握相关的判定和性质.9.(1)证明详见解析;(2)8.【分析】本题考查了切线的判定 勾股定理等知识 熟练掌握切线的判定定理 勾股定理是解题的关键.(1)连接OD 根据平行线判定推出OD AC ∥ 推出OD BC ⊥ 根据切线的判定推出即可;(2)根据勾股定理求出3OD OA OE === 再根据线段的和差求解即可.【详解】(1)证明:连接OD∵OA OD =∵OAD ODA ∠=∠∵AD 平分BAC ∠∵BAD CAD ∠=∠∵ODA CAD ∠=∠∵OD AC ∥∵180C ODC ∠+∠=︒∵90C ∠=︒∵90ODC ∠=︒∵OD BC ⊥∵OD 为半径∵BC 是O 的切线;(2)解:设OD OE r ==在Rt ODB △中 42BD BE ==,∵2OB r =+由勾股定理 得:()22242r r +=+ 解得:3r =∵3OD OA OE ===∵628AB =+=.10.(1)证明见解析;(2)63.【分析】(1)先证明OAB 是等边三角形 再由性质得出60AOB OAB OBA ∠=∠=∠=︒ 再由BC AB =和角度和差即可求解;(2)先根据等边三角形性质求出132OE OA == 再根据勾股定理求得33AE = 最后由垂径定理即可求解;此题考查了等边三角形的判定与性质 勾股定理和垂径定理 解题的关键是熟练掌握以上知识点的应用.【详解】(1)证明:∵AB OA OB ==∵OAB 是等边三角形∵60AOB OAB OBA ∠=∠=∠=︒∵BC OB =∵BC AB =∵1302BAC BCA OBA ∠=∠=∠=︒ ∵90OAC OAB BAC ∠=∠+∠=︒又∵OA 为O 的半径∵AC 是O 的切线;(2)解:∵6BC =∵6AB OA OB ===∵AD OB ⊥于点E∵30OAE ∠=︒∵132OE OA == ∵2233AE OA OE =-=∵AE OB ⊥∵263AD AE ==.11.(1)见解析∠=)证明:BAD60︒6090︒-︒=OD是O的半径∴直线BD是O的切线;==(2)解:设OD OC△中sin30在Rt BDO解得:1r==+OB OCDE是O的直径∴∠=︒DFE90∠=∠即DFB BDE∠=∠DBF DBE∴△∵BDEBFD△BF BD∴=BD BE337BF ∴= 解得:377BF =. 【点睛】本题考查了切线的判定和性质 相似三角形的性质和判定 圆周角定理 勾股定理等知识点 作出辅助线构造出相似三角形是解题关键.12.(1)见详解(2)3【分析】(1)连接OC 由∠=∠OCB ABC ABC CBD ∠=∠ 得OCB CBD ∠=∠ 则OC BD ∥ 所以18090OCD D ∠=︒-∠=︒ 即可证明CD 为O 的切线;(2)由AB 为的直径 得90ACB ∠=︒ 则ACB D ∠=∠ 而ABC CBD ∠=∠ 所以C ABC BD ∽△△ 则AB CB CB BD = 可求得CB BD AB =⋅ 由勾股定理得22CD CB BD =-.【详解】(1)证明:连接OC 则OC OB =OCB ABC ∴∠=∠ABC CBD ∠=∠OCB CBD ∴∠=∠OC BD ∴∥CD BD ⊥90D ∴∠=︒18090OCD D ∴∠=︒-∠=︒OC 是O 的半径 且CD OC ⊥CD ∴为O 的切线.(2)解:AB 为的直径ABC∠=ABC CBD ∴∽∴AB CBCB BD=1,4BD AB==1 CB BD AB∴=⋅=22CD CB BD∴=-=CD∴的长是【点睛】此题重点考查等腰三角形的性质AD OC∥ADO∴∠OA OD=ADO DAO ∴∠=∠DOC BOC ∴∠=∠OD OB OC OC ==,ODC OBC ∴≌△△∴OBC ODC ∠=∠BC AB ⊥∴90OBC ODC ∠=∠=︒OD 为经过圆心的半径∴CD 是O 的切线;(2)如图所示:作DM BC ⊥交BC 于点M8AB = 1AE =1432OA OB OD AB OE OA AE ∴=====-=, 227DE BM OD OE ==-=令=7CM x CB CD x ==+, 7BE DM ==∴在222Rt DMC CM DM CD +=△,222(7)7x x ∴+=+解得:37x =47BC ∴=DE BC ∥ADE ABC ∴△△∽是O的切线.2)在Rt△是O的切线得出Rt EAD中【详解】(1)证明:连接.是O的直径+∠OCA OCBDCB OCB+∠OCD=︒.90是半径经过O的半径外端∵CD 是O 的切线.(2)解:在Rt OCD △中∵90OCD ∠=︒ 30D ∠=︒ 2OC =∵4OD =.∵6AD AO OD =+=.∵AE 是O 的切线 切点为A∵OA AE ⊥.在Rt EAD 中∵90EAD ∠=︒ 30D ∠=︒ 6AD =∵3tan 306233AE AD =⋅︒=⨯=. 15.(1)见解析(2)4π3【分析】本题考查圆与三角形的综合问题 掌握与圆有关的性质 正确作出辅助线是关键.(1)连接OC 根据条件证明OC BD ∥ 即可证明;(2)根据PCO PDB ∽可得PA 利用余弦值可求出COP ∠ 通过弧长公式求解即可.【详解】(1)证明:连接OC 如图∵OC OB =∵OCB OBC ∠=∠∵弦BC 平分PBD ∠∵DBC OBC ∠=∠∵OCB DBC ∠=∠.∵OC BD ∥∵BD PD ⊥∵OC PD ⊥.为O 的半径是O 的切线;)解:连接OC∵PCO PDB ∽OC PO BD PB= 8cm AB = BD =14cm 2OC AB ==4468PA PA +=+ Rt OCP 中cos COP ∠=60COP =︒AC 的长=(1)证明见解析; 是O 的切线;证明FBD FDA ∽ 得到1tan tan 4BD A BDF AD ∠=∠== 进而得到164DF = 即可求解; 本题考查了切线的判定 相似三角形的判定与性质 等腰三角形的性质 余角性质 根据题意 正确作出辅助线是解题的关键.【详解】(1)证明:连结OD∵CO AB ⊥∵90E C ∠+∠=︒∵FE FD = OD OC =∵E FDE ∠=∠ ∠=∠C ODC∵90FDE ODC ∠+∠=︒∵90ODF ∠=︒∵OD DF ⊥∵FD 是O 的切线;(2)解:连结AD ,OD BD 如图∵AB 为O 的直径∵90ADB ∠=︒∵90∠+∠=︒A ABD∵OB OD =∵OBD ODB ∠=∠∵90A ODB ∠+∠=︒∵FBD FDA ∽DF BD AF AD= 在Rt △ABD 中 tan ∠164DF = 3DF =的平分线交O 于点E∵ED OE ⊥∵DE 为O 切线.(2)过点O 作OM BC ⊥于点M 10AB = 6BC =则132MC MB BC ===,152OB OE AB === 四边形OEDM 时矩形∵DE OM =根据勾股定理 得224DE OM OB BM ==-=.18.(1)见解析(2)103【分析】(1)连接OA OC 与AB 相交于点E 如图 由OA OC = 可得OAC OCA ∠=∠ 根据圆周角定理可得12B AOC ∠=∠ 由已知CAD B ∠=∠ 可得2AOC CAD ∠=∠ 根据三角形内角和定理可得180OCA CAO AOC ∠+∠+∠=︒ 等量代换可得90CAO CAD ∠+∠=︒ 即可得出答案;(2)根据角平分线的定义可得BAC DAC ∠=∠ 由已知可得BAC B =∠∠ 根据垂径定理可得 OC AB ⊥ BE AE = 在Rt BEC △中 根据正弦定理可得3sin 45CE CE B BC === 即可算出CE 的长度 根据勾股定理可算出22BE BC CE =-的长度 设O 的半径为r 则125OE OC CE r =-=- 在Rt AOE △中 222OA OE AE =+ 代入计算即可得出答案. 【详解】(1)证明:连接OA OC 与AB 相交于点E 如图OA OC =OAC ∴∠AC AC =∴12B ∠=CAD ∠=AOC ∴∠=OCA ∠+2CAO ∴∠+CAO ∴∠+OAD ∴∠OA 是O 的半径AD ∴是O 的切线;(2)解:AC 是∠BAC DAC ∴∠=∠CAD B ∠=∠BAC B ∴∠=∠OC AB ∴⊥ BE =在Rt BEC △中4BC =sin CE B BC ∴=125CE ∴=BE BC ∴=设O 的半径为r ,则125OE OC CE r =-=-在Rt AOE △中222OA OE AE =+ 222121655r r ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭ 解得:103r =. 【点睛】本题主要考查了切线的性质与判定,垂径定理,勾股定理及解直角三角形, 熟练掌握切线的性质与判定,垂径定理及解直角三角形的方法进行求解是解决本题的关键.。
2020年中考数学提优专题:《圆:切线长定理》(含答案)

《圆:切线长定理》知识梳理:(1)圆的切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.(2)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.(3)注意:切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.(4)切线长定理包含着一些隐含结论:①垂直关系三处;②全等关系三对;③弧相等关系两对,在一些证明求解问题中经常用到.综合练习:一.选择题1.如图,已知AB为⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若AB=3,ED=2,则BC的长为()A.2 B.3 C.3.5 D.42.既有外接圆,又有内切圆的平行四边形是()A.矩形B.菱形C.正方形D.矩形或菱形3.如图所示,已知PA、PB切⊙O于A、B两点,C是上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=()A.56°B.60°C.62°D.不可求4.已知四边形ABCD是梯形,且AD∥BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是()A.大于B.等于C.小于D.不能确定5.如图,在平行四边形ABCD中,AB=15,过点D作一圆与AB、BC分别相切于G、H,与边AD、CD相交于点E、F,且5AE=4DE,8CF=DF,则BH等于()A.5 B.6 C.7 D.86.如图,PA,PB分别切⊙O于点A和点B,C是上任一点,过C的切线分别交PA,PB于D,E.若⊙O的半径为6,PO=10,则△PDE的周长是()A.16 B.14 C.12 D.107.如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为()A.B.C.D.8.PA、PB、CD分别切⊙O于A、B、E,∠APB=54°,则∠COD=()A.36°B.63°C.126°D.46°9.如图,P A、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35°B.45°C.60°D.70°10.已知:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O 于点E,AE的延长线交BC于点F,连接AD、BD.以下结论:①AD∥OC;②点E为△CDB的内心;③FC=FE;④CE•FB=AB•CF.其中正确的只有()A.①②B.②③④C.①③④D.①②④二.填空题11.如图,PA,PB分别为⊙O的切线,切点分别为A、B,PA=6,在劣弧AB上任取一点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长是.12.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE=.13.如图,四边形ABCD是正方形,以BC边为直径在正方形内作半圆O,再过顶点A作半圆O的切线(切点为F)交CD边于E,则sin∠DAE=.14.如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,AB=6,PA=5.则⊙O的半径.15.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为.16.如图,PA、PB、EF分别切⊙O于A、B、D,若PA=10cm,则△PEF的周长是cm,若∠P=35°,则∠AOB=(度),∠EOF=(度).17.如图,正方形ABCD的边长为4,以AB为直径向正方形内作半圆,CE与DF是半圆的切线,M,N为切点,CE,DF交于点P.则AE=,△PMN的面积是.三.解答题18.如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.(1)求△PDE的周长;(2)求∠DOE的度数.19.如图,P是半径为cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB =3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.(1)求△PDE的周长;(2)若DE=cm,求图中阴影部分的面积.20.已知:AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.①求BC的长;②延长AE交BC的延长线于G点,求EG的长.参考答案一.选择题1.解:由切割线定理,得DE2=EA•EB,∵AB=3,ED=2,∴4=AE(AE+3),解得AE=1或﹣4(舍去),∵CB切⊙O于B,∴∠B=90°,∴根据勾股定理得,BC2+42=(BC+2)2,∴BC=3.故选:B.2.解:A、矩形只有外接圆,没有内切圆,故本选项不符合题意;B、菱形只有内切圆,没有外接圆,故本选项不符合题意;C、正方形既有外接圆,也有内切圆,故本选项符合题意;D、矩形只有外接圆,没有内切圆,菱形只有内切圆,没有外接圆,故本选项不符合题意;故选:C.3.解:∠PMN+∠PNM=180°﹣∠P=124°,∠AMN+∠BNM=360°﹣124°=236°,∵MA、MC是⊙O的切线,∴∠AMO=∠CMO,∵NB、NC是⊙O的切线,∴∠BNO=∠CNO,∴∠CMO+∠CNO=(∠AMN+∠BNM)=118°,∴∠MON=180°﹣118°=62°,故选:C.4.解:连接OF,OA,OE,作AH⊥BC于H.∵AD是切线,∴OF⊥AD,易证四边形AHOF是矩形,∴AH=OF=OE,∵S△AOB=•OB•AH=•AB•OE,∴OB=AB,同理可证:CD=CO,∴AB+CD=BC,故选:B.5.解:由8CF=DF,得CF=15×=,则CH2=CF×DC,故CH=5,设BC=x,则BH=x﹣5=BG,故AG=20﹣x,又∵5AE=4DE,∴DE=x,AE=x,则AG2=AE×AD,则(20﹣x)2=x2,解得:x=12,故BH=BC﹣CH=7.故选:C.6.解:连接OA,∵PA切⊙O于A,∴∠OAP=90°,∴在Rt△OAP中,OP=10,OA=6,由勾股定理得:PA=8,∵PA,PB分别切⊙O于点A和点B,DE切⊙O于C,∴PA=PB=8,DA=DC,EB=EC,∴△PDE的周长是:PD+DE+PE=PD+DC+CE+PE=PD+DA+EB+PE=PA+PB=8+8=16,故选:A.7.解:连接OA,OB.则OA⊥AP,OB⊥PB,∴在四边形APBO中,∠P+∠AOB=180°,又∵∠AOB=2∠ACB,∠ABC=2∠P,设∠ACB=180°﹣2∠ABC=180°﹣4∠P,∴∠AOB=360°﹣8∠P,∴∠P+∠AOB=∠P+(360°﹣8∠P)=180°,∴∠P=,∴∠ACB=180﹣4×=,∴∠ACB的弧度数为.故选:A.8.解:如图,连接OA,OB,OE,∵PA、PB、CD分别切⊙O于A、B、E,∴∠AOC=∠EOC,同理∠BOD=∠DOE,∴∠COD=∠COE+∠DOE=∠AOB,∵∠APB=54°,∴∠AOB=126°,∴∠COD=63°.故选:B.9.解:根据切线的性质定理得∠PAC=90°,∴∠PAB=90°﹣∠BAC=90°﹣35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.故选:D.10.解:连接OD,DE,EB,CD与BC是⊙O的切线,∠ODC=∠OBC=90°,OD=OB,∵OC=OC∴Rt△CDO≌Rt△CBO,∴∠COD=∠COB,∴∠COB=∠DAB=∠DOB,∴AD∥OC,故①正确;∵CD是⊙O的切线,∴∠CDE=∠DOE,而∠BDE=∠BOE,∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,因此E为△CBD的内心,故②正确;若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,∴弧AD=弧BE,而弧AD与弧BE不一定相等,故③不正确;设AE、BD交于点G,由②可知∠EBG=∠EBF,又∵BE⊥GF,∴FB=GB,由切线的性质可得,点E是弧BD的中点,∠DCE=∠BCE,又∵∠MDA=∠DCE(平行线的性质)=∠DBA,∴∠BCE=∠GBA,而∠CFE=∠ABF+∠FAB,∠DGE=∠ADB+∠DAG,∠DAG=∠FAB(等弧所对的圆周角相等),∴∠AGB=∠CFE,∴△ABG∽△CEF,∴CE•GB=AB•CF,又∵FB=GB,∴CE•FB=AB•CF故④正确.因此正确的结论有:①②④.故选:D.二.填空题(共7小题)11.解:∵PA,PB分别为⊙O的切线,∴PA=PB,同理,DA=DC,EB=EC.∴△PDE的周长=PD+DE+PE=PD+DC+CE+PE=PD+AD+PE+BE=PA+PB=2PA=2×6=12.故答案是:12.12.解:∵CD、CE分别与⊙O相切于点D、E,∴CD=CE,∵∠DAC=∠DCA,∴AD=CD,∴AD=CE,∵AD=2,∴CE=2.故答案为:2.13.解:设正方形ABCD的边长为4a,EC=x,∵AF为半圆O的切线,∴AF=AB=4a,EC=EF=x,在Rt△ADE中,DE=4a﹣x,AE=4a+x,∴AE2=AD2+DE2,即(4a+x)2=(4a)2+(4a﹣x)2,解得x=a,∴AE=5a,DE=3a,在Rt△ADE中,sin∠DAE===.故答案为.14.解:连接OP,OB,∵AP为⊙O切线,PB为⊙O切线,∴PA=PB,∵∠APO=∠BPO,PG=PG,∴△APG≌△BPG,∴∠PGA=90°,∵△APO为直角三角形,∠APG=∠APG,∴△PGA∽△PAO,根据垂径定理,得到AG=GB,在R t△PAG中,PG==4,∵△PGA∽△AGO,∴=,∴=,∴AO=.故答案为:.15.解:∵OA=OB,∴∠OAB=∠OBA,∵∠BAC=35°,∴∠AOB=110°,∵PA,PB分别是⊙O的切线,∴∠PAO=∠PBO=90°,∵∠P+∠AOB+∠PAO+∠PBO=360°,∴∠P=70°.故答案为:70°.16.解:∵PA、PB、EF分别切⊙O于A、B、D,∴PA=PB=10cm,ED=EA,FD=DB,∴PE+EF+PF=PE+ED+PF+FD=PA+PB=20(cm);∵PA、PB为⊙O的切线,∴∠PAO=∠PBO=90°,而∠P=35°,∴∠AOB=360°﹣90°﹣90°﹣35°=145°;连OD,如图,∴∠ODE=∠ODF=90°,易证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠AOB=72.5°,∠EOF=72.5°.故答案为20;145;72.5.17.解:(1)由切线长定理知:AE=EM,CM=CB;∵CD=CB,∴CM=CD=4.设AE=EM=x,则DE=4﹣x,CE=CM+EM=4+x;在Rt△CDE中,由勾股定理得:(4﹣x)2+42=(4+x)2,解得x=1;故AE=1.(2)同(1)可求得BF=FN=1,则DF=CE=5,DE=CF=3;则可证得Rt△CDE≌Rt△DCF;∴∠DCP=∠CDP,即DP=CP,∴PM=PN;故△DPC∽△NPM,且MN∥CD;设MN所在直线与AD、BC的交点为R、T,则MR⊥AD,NT⊥BC;在Rt△MRE中,ME=1,则ER=ME•cos∠DEC=,MR=ME•sin∠DEC=;过P作PG⊥MN于G,则RG=GT=2,MG=2﹣RM=;易知RE∥PG,则△REM∽△GPM,∴=()2=;∵S△REM=MR•RE=××=,∴S△PMG=×=,故S△PMN=2S△PMG=.三.解答题(共3小题)18.解:(1)∵PA、PB、DE都为⊙O的切线,∴DA=DF,EB=EF,PA=PB=6,∴DE=DA+EB,∴PE+PD+DE=PA+PB=12,即△PDE的周长为12;(2)连接OF,∵PA、PB、DE分别切⊙O于A、B、F三点,∴OB⊥PB,OA⊥PA,∠BOE=∠FOE=∠BOF,∠FOD=∠AOD=∠AOF,∵∠APB=52°,∴∠AOB=360°﹣90°﹣90°﹣52°=128°,∴∠DOE=∠FOE+∠FOD=(∠BOF+∠AOF)=∠BOA=64°.19.解:(1)∵PA、PB、DE是⊙O的切线,∴PA=PB=3cm,CE=BE,AD=DC,∴△PDE的周长=PE+DE+PD=PE+CE+CD+PD=PE+BE+AD+PD=PA+PB=3cm+3cm=6cm;(2)连接OB、OA、OE,OD,如图,∵PA、PB、OC是⊙O的切线,∴OB⊥PB,OA⊥PA,OC⊥DE,∴∠OBP=∠OPA=90°,∵∠APB=60°,∴∠BOA=120°,∵BE=CE,DC=DA,∴S△OCE=S△OBE,S△OCD=S△ODA,∴S五边AOBED=2S△ODE=2×××=4,∴图中阴影部分的面积=S五边AOBED﹣S扇形AOB=4﹣=(4﹣π)cm2.20.解:①过点D作DF⊥BC于点F,∵AB为⊙O的直径,∠A=∠B=90°,∴四边形ABFD是矩形,AD与BC是⊙O的切线,∴DF=AB=2,BF=AD=2,∵DE与⊙O相切,∴DE=AD=2,CE=BC,设BC=x,则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,在Rt△DCF中,DC2=CF2+DF2,即(2+x)2=(x﹣2)2+(2)2,解得:x=,即BC=;②∵AB为⊙O的直径,∠A=∠B=90°,∴AD∥BC,∴△ADE∽△GCE,∴AD:CG=DE:CE,AE:EG=AD:CG,∵AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,∴AE:EG=4:5,在Rt△ABG中,AG==3,∴EG=AG=.。
中考数学知识点过关培优训练:切线长定理(圆)(解析版)
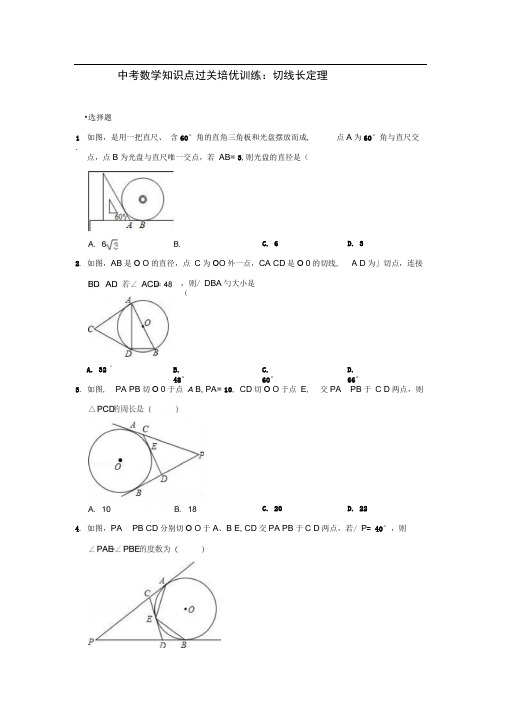
1. 2. 3. 4. 中考数学知识点过关培优训练:切线长定理•选择题 如图,是用一把直尺、 含60°角的直角三角板和光盘摆放而成, 点,点B 为光盘与直尺唯一交点,若 AB= 3,则光盘的直径是( C. 6 点A 为60°角与直尺交D. 3如图,AB 是O O 的直径,点 C 为O O 外一点,CA CD 是O 0的切线, OA. 32 ,则/ DBA 勺大小是(B. 48°C. 60° PA PB 切O 0于点 A B, PA= 10, CD 切O O 于点 E , 如图, C. 20 交PA A D 为」切点,连接D. 66°PB 于 C D 两点,则D. 22PB CD 分别切O O 于A 、B E, CD 交PA PB 于C D 两点,若/ P = 40°,则如图,PAA.50°B. 62C. 66D.70°5.如图,AB AC BD是O O的切线,切点分别是P、C D.若AB= 5, AC= 3, 则BD的长是A. 4B. 3C. 2D. 16.已知O Oi和O Q外切于M AB是O O和O Q的外公切线, A, B为切点,若MA= 4cm MB=3cm贝y M到AB的距离是(A. cm2B.匕cm5 C.cm D.4825cm7.如图,P为O O外一点,PA PB分别切O B,CD切O O于点E,分别交PA PB于A. 5B. 7C.D.10&如图,直线AB CD BC分别与O O相切于E F、G且AB// CD 若OB= 6cm OC= 8cmB. 12C. 11D. 109.如图,△ ABC是一张周长为17 cm的三角形的纸片, BC= 5cm O O是它的内切圆,小明准备用剪刀在O O的右侧沿着与O O相切的任意一条直线MN剪下△AMN则剪下的三角形的周长为(B. 7cmD.随直线MN的变化而变化10.如图,PA PB 切于A , B 两点,CD 切O O 于点E ,交PAPB 于C D.若O O 的半径为1, △ PCD 勺周长等于2二,则线段AB 的长是( ).填空题11.如图,PA PB DE 分别切O O 于A B 、C, O O 的半径为6cm , OP 的长为10cm,则厶PDE12.如图,P 为O O 外一点,PA PB 分别切O O 于A B, CD 切O O 于点E,分别交 PA PB13.如图,四边形 ABCD 是O O 的外切四边形,且 AB= 10, CD= 12,则四边形 ABC 啲周长C. 6cmC. 2 -A. 12cm14•如图,PA PB切O O于A B,点C在上, DE切O O于C,交PA PB于D E已知C D,已知△15.如图,PA PB分别切圆O于A B,并与圆O的切线,分别相交于周长等于10cm贝U PA= _______ cmN、P,且16.如图,四边形ABC[的边AB BC CD DA和O O分别切于L、MCD= 5cm,则四边形ABCC周长为_______ cm18.如图,已知以直角梯形ABCD勺腰CD为直径的半圆O与梯形上底均相切,切点分别是D, C, E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长19.已知:PA PB EF分别切O O于A B、D,若PA= 15cm那么△PEF周长是cm.若/ P= 50°,那么/ EOF= ________ .20.如图所示,O D的半径为3, A是圆D外一点且AD= 5, AB, AC分别与O D相切于点B,C. G是劣弧BC上任意一点,过G作O D的切线,交AB于点E,交AC于点F.(1 )△ AEF的周长是______ ;(2)当G为线段AD与O D的交点时」,连结CD则五边形DBEFC的面积是__________ .三•解答题21.如图,PA PB是O O的切线,A、B为切点,AC是O O的直径,/ BAC= 20°,求/ P的CD切O O于点E △ PCD的周长为12,/ AP申60° .求:(1) PA的长;(2)Z COD勺度数.23.如图,AB为O O直径,PA PC分别与O O相切于点A C, PQL PA PQ交OC的延长线于点Q.(1)求证:OQ= PQ(2 )连BC并延长交PQ于点D, PA= AB,且CQ= 6,求BD的长.24.如图,/ APB= 52°, PA PB DE都为O O的切线,切点分别为A、B、F,且PA= 6.(1 )求厶PDE的周长;(2)求/ DOE勺度数.25.已知PA PB分别切O O于A、B, E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.(1 )若PA= 6,求厶PCD勺周长.(2)若/ P= 50° 求/ DOC26•如图所示,PA PB 是O O 的切线,切点分别是 A B, Q 为O O 上一点,cQ 点作O O 的参考答案1解:设三角板与圆的切点为C,连接OA OBAB由,切线长定理知AB= AC= 3, 0A平分/ BAC•••/ OAB= 60°,在Rt △ ABO中, OB= AB an / OAB= 3 二•光盘的直径为 6 _,故选:A.2 .解:T CA CD是O O的切线,•••CA= CD•••/ ACD= 48°,• / CAD=/ CDA= 66°,•••CALAB AB是直径,•••/ ADB=Z CAB= 90°,•••/ DBA/ DA申90。
2024年中考数字复习 圆中的重要模型-圆幂定理模型(原卷+答案解析)

圆中的重要模型--圆幂定理模型圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理、割线定理、弦切角定理、托勒密定理以及它们推论的统一与归纳。
可能是在19世纪由德国数学家施泰纳(Steiner)或者法国数学家普朗克雷(Poncelet)提出的。
圆幂定理的用法:可以利用圆幂定理求解与圆有关的线段比例、角度、面积等问题。
模型1.相交弦模型条件:在圆O中,弦AB与弦CD交于点E,点E在圆O内。
结论:△CAE∼△BDE⇒ECEB=EAED⇒EC⋅ED=EB⋅EA。
1(2023·广东广州·九年级校考期中)如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,两圆组成的圆环的面积是.2(2023·江西景德镇·九年级校考期末)如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB=.3(2023·江苏·九年级专题练习)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(1)为了说明相交弦定理正确性,需要对其进行证明,如下给出了不完整的“已知”“求证”,请补充完整,并写出证明过程.已知:如图①,弦AB,CD交于点P,求证:.(2)如图②,已知AB是⊙O的直径,AB与弦CD交于点P,且AB⊥CD于点P,过D作⊙O的切线,交BA的延长线于E,D为切点,若AP=2,⊙O的半径为5,求AE的长.模型2.双割线模型条件:如图,割线CH与弦CF交圆O于点E和点G。
结论:△CEG∼△CHF⇒ECCH=CGCF⇒EC⋅FC=GC⋅HC4(2023·浙江·九年级假期作业)如图:PAB、PCD为⊙O的两条割线,若PA∙PB=30,PC=3,则CD的长为()A.10B.7C.510D.35(2023·四川成都·九年级校考阶段练习)如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为.6(2022·河南洛阳·统考一模)我们知道,直线与圆有三种位置关系:相交、相切、相离.当直线与圆有两个公共点(即直线与圆相交)时,这条直线就叫做圆的割线.割线也有一些相关的定理.比如,割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等.下面给出了不完整的定理“证明一”,请补充完整.已知:如图①,过⊙O 外一点P 作⊙O 的两条割线,一条交⊙O 于A 、B 点,另一条交⊙O 于C 、D 点.求证:PA ⋅PB =PC ⋅PD .证明一:连接AD 、BC ,∵∠A 和∠C 为BD 所对的圆周角,∴.又∵∠P =∠P ,∴,∴.即PA ⋅PB =PC ⋅PD .研究后发现,如图②,如果连接AC 、BD ,即可得到学习过的圆内接四边形ABDC .那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示,独立完成证明二.证明二:连接AC 、BD ,模型3.切割线模型条件:如图,CB 是圆O 的切线,CA 是圆O 的割线。
