圆面积的综合应用胡共46页文档
人教版六年级数学上册《圆面积的综合应用》优质课课件

一、创设情景,谈话引入
二、探究新知,解决问题
说说这两种设计有什么联系和区别?
二、探究新知,解决问题
外
外
方
圆
内
内
圆
方
你能利用学具组合出这两个图形吗?
二、探究新知,解决问题
两个圆的半 径都是1 m。
怎样计算正方形和圆 之间部分的面积?
二、探究新知,解决问题
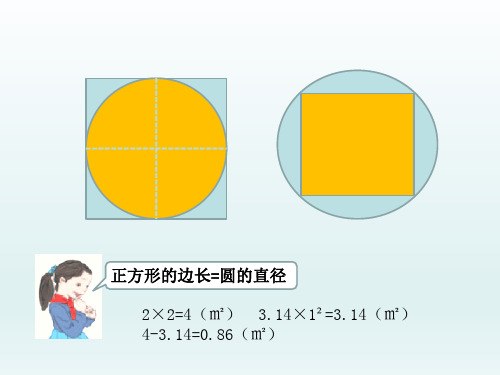
正方形的边长=圆的直径 2×2=4(㎡) 3.14×1²=3.14(㎡) 4-3.14=0.86(㎡)
▪不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年3月28日星期一2022/3/282022/3/282022/3/28 ▪书籍是屹立在时间的汪洋大海中的灯塔。2022年3月2022/3/282022/3/282022/3/283/28/2022 ▪正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/3/282022/3/28March 28, 2022 ▪书籍是屹立在时间的汪洋大海中的灯塔。
第五单元:圆
圆面积的综合应用
一、创设情景,谈话引入
古时候,由于人 们的活动范围狭小, 往往凭自己的直觉认 识世界,看到眼前的 地面是平的,以为整 个大家是平的,并且 把天空看作是倒扣着 的一口巨大的锅。我 国古代有“天圆如张 盖,地方如棋局”的 说法。
一、创设情景,谈话引入
一、创设情景,谈话引入
可以怎样验证 结果是否正确?
四、课堂练习,强化认识
3.在每个正方形中分别作一个最大的圆,并完成下表。
正 方 形 的 面 积 a2
圆的面积πa22
《圆面积的综合应用》教案-2021-2022学年数学六年级上册人教版

1.理论介绍:首先,我们要了解圆面积的基本概念。圆面积是指圆形区域的大小,它的计算公式是S=πr²。这个公式不仅可以帮助我们计算圆形物体的表面积,还广泛应用于工程、设计等领域。
2.案例分析:接下来,我们来看一个具体的案例。假设我们要计算一个半径为4米的圆形花坛的面积,我们可以运用圆面积公式S=πr²,得出面积为16π平方米。这个案例展示了圆面积在实际中的应用,以及它如何帮助我们解决问题。
(3)不规则图形中圆面积的计算:对于不规则图形,学生可能不知道如何将图形分解,并运用圆面积知识进行计算。
突破方法:通过示例和练习,指导学生学会将不规则图形分解为已知的基本图形,再进行面积计算。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《圆面积的综合应用》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要计算圆形物体面积的情况?”比如,我们要给一个圆形桌面铺上玻璃,就需要知道桌面的面积。这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索圆面积的奥秘。
今天的学习,我们了解了圆面积的基本概念、重要性和应用。通过实践活动和小组讨论,我们加深了对圆面积的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
五、教学反思
在《圆面积的综合应用》这节课的教学过程中,我注意到了几个值得反思的方面。首先,学生对圆面积公式的掌握程度参差不齐。有的学生能够熟练运用公式进行计算,但还有一部分学生对此不够熟悉,导致在实际问题中无法准确应用。这提醒我,在今后的教学中,需要加强对基础知识的巩固,确保每个学生都能熟练掌握公式。
六年级数学上册 第5单元圆第6课时圆面积的综合运用课件2_1-5
右图:3.14r2 Nhomakorabea−
1 2
2r
r
2
=
1.14r
2
答:左图中正方形与圆之间的面积是0.86 ㎡,右图中圆
与正方形之间的面积是1.14 ㎡。
1、判断题
(1)直径是2厘米的圆,它的面积是12.56平方厘米。 ( × )
(2)周长相等的两个圆,面积也一定相等。 (3)圆的半径越大,圆的面积就越大。
(√) (√)
(4)圆的半径扩大到原来的4倍,它的面积就扩大到原来的8倍。
( ×)
2、右图是一面我国唐代外圆内方 的铜镜。铜镜的直径是24 cm。外 面的圆与内部的正方形之间的面 积是多少?
3.14×(24÷2)²-24÷2×24÷2×2 =452.16-288 =164.16 (cm²)
答:外面的圆与内部的正方形之间的面积约是 164.16 cm² 。
吊装带
正方形的边长=圆的直径
2×2=4(㎡) 3.14×1²=3.14(㎡) 4-3.14=0.86(㎡)
右图中正方形 的边长是多少?
可以把正方形看 成两个三角形。
1 21 2 = (2 ㎡) 3.14-2=1.14(㎡)
2
回顾反思,比较异同:
如果两个圆的半径都
是r,结果又是怎样的?
左图:(2r)2 − 3.14 r2 = 4r2 − 3.14r2 = 0.86r2
圆的面积的综合运用

四、课堂练习,强化认识
1.有一块长20米,宽15米的长方形草坪,在 它的中间安装了一个射程为5米的自动旋转喷灌装 置,它不能喷灌到的草坪面积是多少?
求不能喷灌到的草坪面积,就是求什么?
2.请计算出你刚才所画“外圆内方”组合图形 中正方形、圆形的面积以及他们之间的面积。
五、课外延伸,提升理解
3.在每个正方形中分别作一个最大的圆,并完成下表。
正方形的面积 a2
π 2 a 圆的面积 π a 4 2
π 2 4 面积之比 a : a 4 π
2
2
如果在圆内作一个最 大的正方形,又会有 怎样的关系呢?
五、全课总结,畅谈收获
谁来说一说:这节课 你有什么收获?
第五单元:圆
圆面积的综合应用
黄山区乌石中心学校
章善明
一、创设情景,谈话引入
古时候,由于人们 的活动范围狭小,往 往凭自己的直觉认识 世界,看到眼前的地 面是平的,以为整个 大家是平的,并且把 天空看作是倒扣着的 一口巨大的锅。我国 古代有“天圆如张盖, 地方如棋局”的说法。
二、探究新知,解决问题
二、探究新知,解决问题
右图中正方形 的边长是多少?
1 2 1 2 2 (㎡) 2
可以把正方形看 成两个三角形。 3.14-2=1.14(㎡)
三、回顾反思,理解算法
如果两个圆的半径都 是r,结果又是怎样的?
左图: (2r )2 3.14 r 2 4r 2 3.14r 2 0.86r 2 1 2 右图: 3.14 r 2r r 2 1.14r 2 2 答:左图中正方形与圆之间的面积是0.86 ㎡,右图中圆 与正方形之间的面积是1.14 ㎡。
5.5《圆面积的综合应用》(教案)2023-2024学年数学六年级上册人教版

5.5《圆面积的综合应用》(教案)20232024学年数学六年级上册人教版作为一名经验丰富的教师,我深刻理解教学内容的重要性,因此,我精心准备了本节课的教学内容。
一、教学内容:本节课的教学内容来自于人教版数学六年级上册第5.5章《圆面积的综合应用》。
在这一章节中,学生将学习圆面积的计算方法,以及如何应用圆面积的知识解决实际问题。
具体内容包括:圆面积的计算公式,圆面积在生活中的应用,以及如何利用圆面积解决实际问题。
二、教学目标:本节课的教学目标是让学生掌握圆面积的计算方法,并能够运用圆面积的知识解决实际问题。
三、教学难点与重点:本节课的教学难点是圆面积公式的理解与应用,教学重点是让学生能够运用圆面积的知识解决实际问题。
四、教具与学具准备:五、教学过程:1. 情景引入:我通过向学生展示一些生活中的圆形物体,如圆桌、圆碗等,引导学生思考这些物体的面积如何计算。
2. 知识讲解:我利用多媒体课件,详细讲解圆面积的计算公式,以及如何应用圆面积的知识解决实际问题。
3. 例题讲解:我选取了一道具有代表性的例题,引导学生一起解答,巩固他们对圆面积公式的理解。
4. 随堂练习:我给出了几道练习题,让学生独立完成,检验他们是否掌握了圆面积的计算方法。
六、板书设计:我将板书设计得简洁明了,主要包括圆面积的计算公式,以及一些关键的解题步骤。
七、作业设计:(1)半径为5厘米的圆;(2)直径为10厘米的圆;(3)半径为7厘米的圆。
答案:(1)面积为78.5平方厘米;(2)面积为78.5平方厘米;(3)面积为153.平方厘米。
2. 应用题:一个圆形花园的直径为20米,求这个花园的面积。
答案:面积为314平方米。
八、课后反思及拓展延伸:本节课结束后,我进行了课后反思。
我认为学生在课堂上积极参与,但对圆面积公式的理解还有待提高。
在今后的教学中,我将继续加强对圆面积公式的讲解,并通过更多的生活实例让学生加深对圆面积知识的理解和应用。
同时,我还鼓励学生在课后观察生活中的圆形物体,尝试计算它们的面积,并将所学知识与实际生活相结合,提高学生的实践能力。
六年级上数学课堂课件-第五单元:3-2.圆的面积应用课件最新版

第5单元
3-2 圆的面积应用
2π= 6.28 8π= 25.12
4π=12.56 9π= 28.26
六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT) 六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
1.教学时,可充分借助文本让学生建 立对童 话体裁 的感性 认识, 由此引 起他们 阅读童 话的兴 趣,鼓 励他们 大量阅 读,继 而由读 到写, 进一步 激发想 象力和 创作热 情。 2.阅读这篇童话,我们既要从现实的 角度理 解这是 一个不 幸的故 事,也 从文化 的角度 理解这 是一个 幸福的 故事, 能够在 小女孩 “幸福 ”的想 象中, 懂得如 何面对 苦难, 汲取怎 样活着 的勇气 和力量 。
4.求图中阴影部分的面积。(单位:cm)
52×3.14=78.5(cm2) (5+2)2×3.14=153.86(cm2) 153.86-78.5=75.36(cm2) 答:阴影部分的面积是75.36cm2。
六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
7.一个儿童游乐场是圆形的,它的周长是62.8 m,现将这个游乐场进行扩建,扩建后游乐场的半 径增加4 m,这个游乐场的面积增加了多少平方 米6?2.8÷3.14÷2=10(m)
7.借助课后提供的例子和资料,了解“预测”和 怎样进 行预测 ,能照 样子说 说旁批 的其他 预测是 怎样得 出来的 。
圆的综合运用

四、课堂练习,强化认识
• 求下图阴影部分的面积
• ① ② ③求半圆的周长和面积。
外圆半径4米, 内圆半径3米
8厘米
直径6分米
四、课堂练习,强化认识
1.有一块长20米,宽15米的长方形草坪,在 它的中间安装了一个射程为5米的自动旋转喷灌装 置,它不能喷灌到的草坪面积是多少?
求不能喷灌到的草坪面积,就是来说一说:这节课 你有什么收获?
圆面积的综合应用
一、创设情景,谈话引入
古时候,由于人 们的活动范围狭小, 往往凭自己的直觉认 识世界,看到眼前的 地面是平的,以为整 个大地是平的,并且 把天空看作是倒扣着 的一口巨大的锅。我 国古代有“天圆如张 盖,地方如棋局”的 说法。
一、创设情景,谈话引入
一、创设情景,谈话引入
一、创设情景,谈话引入
二、探究新知,解决问题
右图中正方形 的边长是多少?
1 2 2 1 2 (㎡) 2
可以把正方形看 成两个三角形。 3.14-2=1.14(㎡)
三、回顾反思,理解算法
如果两个圆的半径都 是r,结果是怎样的? 左图: (2r )2 3.14 r 2 4r 2 3.14r 2 0.86r 2 1 2 右图: 3.14 r 2r r 2 1.14r 2 2 答:左图中正方形与圆之间的面积是0.86 ㎡,右图中圆 与正方形之间的面积是1.14 ㎡。
2.把一个圆形纸片分成若干等份,拼成以半径 为宽的近似长方形,已知长方形的周长为24.84cm。 圆形纸片的面积是多少?
可以怎样验证 结果是否正确?
四、课堂练习,强化认识
3.把一张长6dm,宽4dm的红纸剪成一个最大的圆, 剪掉部分的面积是多少?
六年级上册数学PPT教材-第五单元:3-2.圆的面积应用部编版版

六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
3.看一看,选一选。
(1)半径是2 cm的圆的周长和面积( B )。
A.相等 B.无法比较 C.面积比周长大
8.一个射击靶子,最内环(靶心)的半径是2 cm,各
环宽相等,都等于最内环的半径,你能求出最外环
的面积是多少平方厘米吗?(靶子共有10环)
(10×2)2×3.14=1256(cm2)
(9×2)2×3.14=1017.36(cm2)
1256-1017.36=238.64(cm2) 答:最外环的面积是238.64 cm2。
六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
5.求下面图形中阴影部分的面积。
(1)(2×2)2-3.14×22=16-12.56=3.44(cm2) 1
(2)3.14×62-( 2 ×2×6×6)×2=41.04(cm2)
六年级上册数学课件-第五单元:3-2. 圆的面 积应用 人教版 (2014 秋)( 共13张P PT)
1.本文是中年级学生接触的简单的文 言文, 它犹如 在孩子 面前打 开了一 扇窗户 ,铺开 了一条 通道, 让他们 穿越时 空隧道 ,走近 历史先 贤。 2.在阅读与思考中汲取古代优秀文化 的精髓 ,这将 为培养 学生学 习古文 的兴趣 ,对于 掌握学 习古文 的方法 ,为打 好学习 古文的 基础具 有重要 的地位 和作用 。
4.求图中阴影部分的面积。(单位:cm)
52×3.14=78.5(cm2) (5+2)2×3.14=153.86(cm2) 153.86-78.5=75.36(cm2) 答:阴影部分的面积是75.36cm2。
圆的面积综合知识应用

圆的面积综合知识应用专题分析:圆面积的计算公式是:S=πr2,其中S代表面积,r代表半径。
扇形面积的计算公式是S=nπr2/360,其中其中S代表面积,n代表圆心角的度数,r代表半径。
在有关圆的周长和面积的计算中,组合图形的面积是学习的重点,也是难点。
对于求一些比较复杂的组合图形的面积时,有时直接进行分割求解有一定的困难,那么可以通过把其中的部分图形进行平移、翻折或旋转进行割补,利用重叠思想化难为易,或者利用两个规则图形的差来求。
例题1:图中的三角形是等腰直角三角形,那么阴影部分的面积是多少?(π取近似值3.14)练习1:(1)根据图中所给的数据求阴影部分面积。
(2)如下图,△ABC是等腰直角三角形,直角边AB=2厘米,求阴影部分的面积。
例题2:如下图,直角三角形ABC 中,AB 是圆的直径,且AB=20厘米,如果阴影(1)的面积比阴影(2)的面积大80平方厘米,求BC 长。
(π取3): 练习2:(1)图中有一个矩形和两个半径分别为5和2的直角扇形.两个阴影部分的面积之差是多少?(π近似取3)(2)图中甲区域比乙区域的面积大57,且半圆的半径是10.其中直角三角形竖直的直角边的 长度是多少?(π取近似值3.14)例题3:如图,一只小狗被拴在建筑物的一角,四周都是空地.建筑物是一个边长为4米的等边三 角形,绳长是6米,那么小狗的活动范围是多少平方米? (建筑外墙不可逾越,小狗身长忽略不计,π取3)(2)(1)C(1)如图所示,一只小狗被拴在建筑物的一角,四周都是空地.建筑物是个边长为10米的正方形,绳长是20米,那么小狗的活动范围能有多少平方米?(建筑外墙不可逾越,小狗身长忽略不计,π取3)(2)如图,一只小狗被拴在一个边长为4米的正五边形的建筑物的一个顶点处,四周都是空地,绳长刚好够小狗走到建筑物外墙边的任一位置,小狗的活动范围是多少平方米?(建筑外墙不可逾越,小狗身长忽略不计,π取3)例题4:如图所示,一个半径为1的圆绕着边长为4的正方形滚动一周又回到原来的位置,扫过的面积是多少?(π取3.14)(1)如图所示,一个半径为1的圆绕着边长为4的等边三角形滚动一周又回到原来的位置,扫过的面积是多少?(π取3.14)(2)如图所示,一个半径为1的圆绕着边长为4的正六边形滚动一周又回到原来的位置,扫过的面积是多少?(π取3.14)趣味数学:面上有7个大小相同的圆,位置如图所示.如果每个圆的面积都是10,那么阴影部分的面积是多少?(π取3.14)。
圆面积的综合应用

3、右图中正方形的边长是10m, 中间圆的半径是2m,求出计算 阴影部分的面积。
第五单元:圆
圆面积的综合应用
尹庄镇中心小学
张虹
二、探究新知,解决问题
外 和“外圆内方”中正 方形与圆之间部分的面积,并发现其中的一般 规律。 2、学会解决生活实际中的有关问题。
二、探究新知,解决问题
条件:
r=1m
r=1m
问题:求出正方形和圆之间部分的面积吗?
两个圆的半径都是1m
如果两个圆的半径都是 r呢? 二、探究新知,解决问题
外方内圆 方减圆 0.86r2
外圆内方 圆减方 1.14r2
当堂训练
1、右图是一面我国唐代外圆内方的铜镜。铜 镜的直径是6 cm。外面的圆与内部的正方形之 间的面积是多少?
2、右图中圆的( )与正方形的边长相等, 正方形的周长是16cm,则圆的半径是( )。 求出正方形与圆之间的面积。
六年级上册数学课件-圆面积的综合应用 ppt人教新课标

如果两个圆的半径都 是r,结果又是怎样的? 左 图 : ( 2 r ) 2 3 . 1 4 r 2 4 r 2 3 . 1 4 r 2 0 . 8 6 r 2 右 图 : 3.14r2 1 22rr 21.14r2 答:左图中正方形与圆之间的面积是0.86 ㎡,右图中圆 与正方形之间的面积是1.14 ㎡。
六年级上册数学课件-圆面积的综合应 用 ppt人教新课标
六年级上册数学课件-圆面积的综合应 用 ppt人教新课标
四、课堂练习,强化认识
1.有一块长20米,宽15米的长方形草坪,在 它的中间安装了一个射程为5米的自动旋转喷灌装 置,它不能喷灌到的草坪面积是多少?
求不能喷灌到的草坪面积,就是求什么?
2.一件古代铜钱的模型(如图),已知外圆的 直径是20 cm,中间正方形的边长为6 cm。这个模 型的面积是多少?
二、探究新知,解决问题
说说这两种设计有什么联系和区别?
二、探究新知,解决问题
外
外
方
圆
内
内
圆
方
你能利用学具组合出这两个图形吗?
二、探究新知,解决问题
两个圆的半 径都是1 m。
怎样计算正方形和圆 之间部分的面积?
二、探究新知,解决问题
正方形的边长=圆的直径 2×2=4(㎡) 3.14×1²=3.14(㎡) 4-3.14=0.86(㎡)
六年级上册数学课件-圆面积的综合应 用 ppt人教新课标
二、探究新知,解决问题
右图中正方形 的边长是多少?
可以把正方形看 成两个三角形。
1212( 2 ㎡) 3.14-2=1.14(㎡)
2
六年级上册数学课件-圆面积的综合应 用 ppt人教新课标
圆面积公式的应用

圆面积公式的应用1.圆的面积计算:最常见的应用是计算给定半径的圆的面积。
通过将给定的半径值代入公式A=πr²,可以直接计算出圆的面积。
这在工程、建筑、地理等领域中经常用到,例如计算圆形田地的面积、圆形池塘的面积等。
2.圆的面积比较:圆面积公式也用于比较不同圆的面积大小。
通过将不同圆的半径代入公式可以计算出它们的面积,从而比较它们的大小。
这在图形设计、艺术等领域中经常用到,例如选择不同大小的圆作为设计元素,或者确定哪个圆更适合用于特定的设计。
3.圆的镶嵌:圆面积公式在雕刻、装饰等领域中也有应用。
例如,当要将许多小圆形雕刻或装饰镶嵌在一个大圆形表面上时,需要计算每个小圆的面积以确定它们的位置和布局。
这可以使用圆面积公式来计算每个小圆的面积,并根据需要进行调整和布置。
4.圆的扇形和部分面积:圆面积公式还可以用于计算圆的不完整部分的面积。
例如,当需要计算一个扇形区域或一个圆弧的面积时,可以使用圆面积公式的一部分进行计算。
具体做法是根据所给的角度计算出扇形或圆弧的半径,然后将该值代入圆面积公式中进行计算。
5.轮胎和切割:圆面积公式还可以用于特殊形状的圆或圆环的计算。
例如,当需要计算轮胎的面积时,可以将轮胎看作是一个较大圆和较小圆之间的圆环,然后使用圆面积公式计算出圆环的面积。
同样,当需要计算一个圆形物体被切割后的面积时,可以将它分解为几个部分,然后使用圆面积公式计算每个部分的面积并相加。
在实际应用中,圆面积公式可以通过计算机和数学软件进行快速计算。
这样可以节省时间和减少人为计算错误的可能性。
同时,圆面积公式也是其他相关公式的基础,例如圆周长公式和球体积公式等。
因此,掌握和理解圆面积公式对于数学和科学领域的学习和应用非常重要。
圆的面积公式的应用共16页

谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
圆的面积公式的应用
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
