Matlab实现混沌系统的控制
Matlab软件在时滞混沌系统仿真实验中的应用

Matlab软件在时滞混沌系统仿真实验中的应用Matlab软件在时滞混沌系统仿真实验中的应用时滞混沌系统是一类在现实世界中经常出现的系统,其具有非线性、非平稳、时滞等复杂特性。
这种系统能够产生混沌行为,其行为表现具有高度敏感性和长时间关联性。
对时滞混沌系统进行建模和仿真研究对于理解和预测其行为行为具有重要意义。
Matlab软件作为一种强大的数值计算和仿真工具,在时滞混沌系统的建模和仿真实验中发挥着重要的作用。
Matlab提供了丰富的函数库和工具箱,使得建模和仿真时滞混沌系统变得相对简单。
它提供了数值计算、二维和三维绘图、数据分析等功能,可以对时滞混沌系统的动力学行为进行精确的模拟和分析。
通过Matlab,我们可以编写程序来实现时滞混沌系统的数学模型,并进行仿真实验以观察系统的行为。
在时滞混沌系统的建模过程中,Matlab提供了丰富的数学函数和数值计算工具,可以帮助我们描述系统的动力学行为。
例如,对于时滞的处理,Matlab提供了delay differential equation (DDE) solver函数,可以用来求解带有时滞的微分方程模型。
此外,Matlab还提供了一系列的随机数生成函数,可以模拟系统中的噪声和扰动。
这些功能使得我们能够更准确地建立时滞混沌系统的数学模型,并进行系统行为的仿真实验。
通过Matlab中的绘图功能,我们能够直观地观察和分析时滞混沌系统的行为。
Matlab提供了强大的绘图函数,可以在二维和三维空间中绘制系统状态的变化轨迹。
我们可以通过调整系统参数,观察其对系统行为的影响。
同时,Matlab还提供了频谱分析和正态图等统计工具,帮助我们进一步分析和理解时滞混沌系统的特性。
除了建模和仿真,Matlab还可以用于时滞混沌系统的控制和优化。
通过编写控制算法,我们可以在仿真实验中实现对系统行为的调节和控制。
此外,Matlab还提供了优化算法和工具箱,可以用于对时滞混沌系统进行优化设计。
利用Matlab仿真模拟Rossler混沌系统及混沌控制

第3期郭怡冰等:利用Matlab仿真模拟Rossler混沌系统及混沌控制·19·及XZ平面的轨迹.首先,选择三个积分模块,从上到下排列并分别对应茁,,,,彳的信号输出,这样做的好处是使得模型更加直观,可以直接与系统方程相对应.再根据方程(2),将Y,:的信号输入求和模块,调整符号为减号,并将此求和模块的输出信号作为对应戈的积分模块的输入信号,由此Rossler系统模型中对应茗方程的部分就完成了.同样,将y输入增益模块,乘以增益因子口,其输出口y和茗再输入求和模块,此时的输出就是对应Y的积分模块的输入信号.最后将信号:,茗与Z输人乘法模块、;输入增益模块,其输出茗z与凹加上常数模块输出的常数b,三个同时输入求和模块中,再经过积分模块就是信号厶此外,为了得到直观的模拟结果,将石,Y与髫,z分别输入二维信号显示模块,用于观察输出信号的图像关系.最终得到的Rossler系统模型如图1所示.设定系统模型中各参数值,令o=6=0.2,C:5.7,运行此系统模型,观察XY和XZ的平面轨迹图像.得到图2、图3,分别为仿真时间1000s时系统在XY、XZ平面的混沌轨迹.图1Bossier系统模型同时作为基础的混沌模型,在制作混沌控制模型时,可直接在此混沌模型上加入各种控制器模型,使得建立混沌控制模型的工作更加简便.图3Rossler系统在XZ平面的混沌轨迹1.2混沌控制的仿真模拟延迟反馈控制是于1992年由Pyragas提出的.这种控制器的优点在于:首先,它是基于系统状态的自相似性,用时滞反馈信号近似不稳定周期轨道,从而避免了OGY等方法中目标轨道的确定问题;其次,它采用连续时间激励作为控制信号,而不是OGY法中的间歇脉冲式的微小参数扰动,所以在一定程度上避免了控制对象因系统的涨落和环境噪声而偏离期望轨道;最后,它不需要事先知道系统的任何解析知识,也无需像OGY法那样大量计算机在线分析系统状态,仅使用简单的模拟装置就能实现,所以非常易于工程实现.以Rossler系统为例,施加延迟反馈控制后,原系统变为:皤x+叠ay+KM…h㈤,,(3)同样地,为了便于建设系统模型,将方程(3)由微分形式转变为积分形式,变形后的方程如下:菇=』(一y—z)df,,,=Jr(髫+。
Chen混沌系统控制和同步仿真实验

222021年2月总第355期ISSN1672-1438CN11-4994/T Chen 混沌系统控制和同步仿真实验赵海滨 颜世玉东北大学机械工程与自动化学院 辽宁沈阳 110819摘 要:对于Chen 混沌系统,只采用一个控制器进行系统的镇定控制。
通过Chen 混沌系统的状态方程,建立同步误差系统,只采用一个控制器进行Chen 混沌的同步控制。
采用MatLab 语言编写程序,进行数值仿真实验。
数值仿真结果表明,设计的控制器能够进行Chen 混沌系统的镇定控制和同步控制,控制器比较简单,容易实现。
关键词:Chen 混沌系统;数值仿真;MatLab ;仿真实验作者简介:赵海滨,工学博士,讲师;颜世玉,工学博士,讲师。
混沌系统具有丰富且复杂的非线性动力学行为,对初始值非常敏感。
混沌理论可以用于信号处理、保密通信、图像加密和混沌电路等多个领域[1-2]。
混沌控制与同步始终是非线性科学领域的一个热点问题。
1999年,陈关荣等[3]在Lorenz 系统的基础上,利用工程反馈控制的方法构造了三维自治混沌系统,即Chen 混沌系统。
Chen 混沌系统能够采用硬件电路实现[4]。
张国山等[5]在Chen 混沌系统的第一个方程中加入乘积项,构造了一个新的三维自治混沌系统;胡春华等[6]基于Chen 混沌设计了自动切换混沌系统;李德奎等[7]提出单参数Chen 混沌系统,并采用硬件电路实现。
Chen 混沌系统具有复杂的动力学行为,能够采用硬件电路实现,可用于保密通信。
本文根据Chen 混沌系统的状态方程,设计控制器进行Chen 混沌系统的镇定控制和同步控制。
采用MatLab 语言编写脚本程序进行数值仿真。
在脚本程序中,采用四阶-五阶龙格库塔方法(ode45函数)求解常微分方程。
数值仿真结果表明,设计的控制器能够实现Chen 混沌系统的镇定控制和同步控制,控制器比较简单,容易实现。
1 Chen 混沌系统1963年,气象学家Lorenz 发现第一个混沌吸引子,即Lorenz 吸引子。
基于MATLAB的各类混沌系统的计算机模拟(教学版)

z
20 0 20
50 40 30
z
20 10 0 -20 -10 x 0 10
z
20 10 0 -20 -10 0 y 10 20
4.初值敏感性: 保持初值 x0 和 y0 不变,即 x0=y0=1,改变 z0 为 1.001,千分之一的变化会引起系统 行为的显著改变,如下图所示:
y
Rossler 方 程 X-Z平 面 相 图 (较 短 时 间 后 ) 50 40 30
6. 吸引子: 指相空间的这样的一个点集 s (或一个子空间) , 对 s 邻域的几乎任意一 点, 当 t 时所有轨迹线均趋于 s, 吸引子是稳定的不动点。 7. 奇异吸引子: 又称混沌吸引子, 指相空间中具有分数维的吸引子的集合。 该吸引集 由永不重复自身的一系列点组成, 并且无论如何也不表现出任何周期性。 混沌轨道就运行在 其吸引子集中。 8. 分叉和分叉点: 又称分岔或分支。 指在某个或者某组参数发生变化时, 长时间动力 学运动的类型也发生变化。 这个参数值(或这组参数值)称为分叉点, 在分叉点处参数的微小 变化会产生不同性质的动力学特性, 故系统在分叉点处是结构不稳定的。 9. 周期解: 对于系统 xn 1 f ( xn ) , 当 n 时,若存在 xn i xn , 则称该系 统有周期 i 解 。不动点可以看作是周期为 1 的解, 因为它满足 xn 1 xn 。 10. 初值敏感性: 对初始条件的敏感依赖是混沌的基本特征, 也有人用它来定义混沌: 混沌系统是其终极状态极端敏感地依赖于系统的初始状态的系统。 敏感依赖性的一个严重后 果就在于,使得系统的长期行为变得不可预见。
引言. 混沌探秘
混沌是非线性系统所独有且广泛存在的一种非周期运动形式, 其覆盖面涉及到自然科 学和社会科学的几乎每一个分支。1972 年 12 月 29 日,美国麻省理工学院教授、混沌学开 创人之一 E.N.洛伦兹在美国科学发展学会第 139 次会议上发表了题为《蝴蝶效应》的论文, 提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷 风,并由此提出了天气的不可准确预报性。为什么会出现这种情况呢?这是混沌在作怪! “混沌”译自英语中“chaos”一词,原意是混乱、无序,在现代非线性理论中,混沌 则是泛指在确定体系中出现的貌似无规则的、类随机的运动。 混沌现象是普遍的,就在我们身边,是与我们关系最密切的现象,我们就生活在混沌的 海洋中。一支燃着的香烟,在平稳的气流中缓缓升起一缕青烟,突然卷成一团团剧烈搅动的 烟雾,向四方飘散;打开水龙头,先是平稳的层流,然后水花四溅,流动变的不规则,这就 是湍流;一个风和日丽的夏天,突然风起云涌,来了一场暴风雨。一面旗帜在风中飘扬, 一 片秋叶从树上落下,它们都在做混沌运动。可见混沌始终围绕在我们的周围,一直与人类为 伴。
Matlab实现混沌系统的控制

基于MATLAB 的各类混沌系统的计算机模拟混沌是非线性系统所独有且广泛存在的一种非周期运动形式, 其覆盖面涉及到自然科学和社会科学的几乎每一个分支。
1972年12月29日,美国麻省理工学院教授、混沌学开创人之一E.N.洛伦兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可准确预报性。
为什么会出现这种情况呢?这是混沌在作怪!“混沌”译自英语中“chaos”一词,原意是混乱、无序,在现代非线性理论中,混沌则是泛指在确定体系中出现的貌似无规则的、类随机的运动。
混沌现象是普遍的,就在我们身边,是与我们关系最密切的现象,我们就生活在混沌的海洋中。
一支燃着的香烟,在平稳的气流中缓缓升起一缕青烟,突然卷成一团团剧烈搅动的烟雾,向四方飘散;打开水龙头,先是平稳的层流,然后水花四溅,流动变的不规则,这就是湍流;一个风和日丽的夏天,突然风起云涌,来了一场暴风雨。
一面旗帜在风中飘扬,一片秋叶从树上落下,它们都在做混沌运动。
可见混沌始终围绕在我们的周围,一直与人类为伴。
1.混沌的基本概念1. 混沌: 目前尚无通用的严格的定义, 一般认为,将不是由随机性外因引起的, 而是由确定性方程(内因)直接得到的具有随机性的运动状态称为混沌。
2. 相空间: 在连续动力系统中, 用一组一阶微分方程描述运动, 以状态变量(或状态向量)为坐标轴的空间构成系统的相空间。
系统的一个状态用相空间的一个点表示, 通过该点有唯一的一条积分曲线。
3. 混沌运动: 是确定性系统中局限于有限相空间的高度不稳定的运动。
所谓轨道高度不稳定, 是指近邻的轨道随时间的发展会指数地分离。
由于这种不稳定性, 系统的长时间行为会显示出某种混乱性。
4. 分形和分维: 分形是 n 维空间一个点集的一种几何性质, 该点集具有无限精细的结构, 在任何尺度下都有自相似部分和整体相似性质, 具有小于所在空间维数 n 的非整数维数。
基于Matlab的混沌特性分析

基于Matlab的混沌特性分析1. 引言1.1 研究背景混沌理论起源于1960年代,是一种描述复杂系统行为的新理论,揭示了非线性系统中存在的一种无序、不可预测的动态行为。
混沌系统具有高度敏感性和非周期性,表现出随机性和确定性的结合,对于许多领域的研究具有重要的理论和实际意义。
在现代科学和工程领域,混沌系统的分析和控制已经成为一个热门的研究方向。
随着计算机技术的发展,基于Matlab的混沌特性分析方法成为研究混沌系统的有力工具。
Matlab提供了丰富的算法和库函数,可以方便地进行混沌系统建模、仿真和分析。
利用Matlab进行混沌特性分析,可以更深入地理解混沌系统的动力学行为,为系统的控制与优化提供理论支持。
1.2 研究目的研究目的的主要目标是通过基于Matlab的混沌特性分析,探讨混沌系统的特征和建模方法,并利用Matlab提供的分析工具对混沌系统进行详细分析。
通过深入研究混沌系统的特性和行为,可以更好地理解和预测混沌系统的运动规律和特点,为相关领域的研究和应用提供理论支持和参考依据。
本研究旨在探讨基于Matlab的混沌特性分析方法的有效性和可行性,为混沌系统的研究和应用提供一种新的分析途径和工具。
通过对混沌系统的特性进行深入分析和实验研究,可以揭示混沌系统背后的规律和内在机制,为相关领域的发展和应用提供新的思路和方法。
本研究的目的在于通过基于Matlab的混沌特性分析,深入探讨混沌系统的特性和行为,为相关领域的研究和应用提供新的视角和研究方法。
1.3 研究意义混沌系统在现代科学和工程中具有广泛的应用,例如在通信、控制、密码学等领域都有重要的作用。
对混沌系统进行特性分析,能够帮助我们更好地理解和掌握系统的行为规律,为系统的设计和优化提供重要的参考。
混沌系统的特性分析不仅可以帮助我们更好地理解系统的动态行为,还可以为混沌系统的控制和应用提供理论基础。
通过本文基于Matlab的混沌特性分析,我们可以更深入地探索混沌系统的特性和规律,为未来混沌系统的应用和发展提供重要参考。
各类混沌的matlab程序实现

混沌同步模型驱动系统和响应系统都是Lorenz System,只不过初值不同。
驱动系统: dx/dt=a*(y-x)dy/dt=r*x-y-xzdz/dt=x*y-b*z初值(0.1,0.1,0.1)输出信号令S(t)=x(t)响应系统:将S(t)代替x(t)作为激励信号dx/dt=a*(y-x)dy/dt=r*x-y-xzdz/dt=x*y-b*z初值(0.1,0.1,1)最后求响应系统的输出x(t),y(t),z(t)程序:function [Y1] = Lorenz_response(tspan);%%计算处于响应地位的Lorenz系统的数值解,并由此画出其相图yinit = [0.1,0.1,1];% 初始化输入y(1:3) = yinit;tstart = 0; % 时间初始值tstep = 1e-1; % 时间步长wholetimes = 1e2; % 总的循环次数steps = 1; % 每次演化的步数iteratetimes = wholetimes/steps; % 演化的次数S=output;for i=1:iteratetimes;tspan = tstart:tstep:(tstart + tstep*steps);[T,Y1] = ode45(@Lorenz_driven, tspan, y);y = Y1(size(Y1,1),:);y(1)=S(i,1);% 重新定义起始时刻tstart = tstart + tstep*steps;endfigure(1)plot3(Y1(:,1),Y1(:,2),Y1(:,3))function s=output;tstart = 0; % 时间初始值tstep = 1e-1; % 时间步长wholetimes = 1e2; % 总的循环次数% options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);tspan=tstart:tstep:wholetimes*tstep[T,Y] = ode45(@Lorenz_driven,tspan,[0.1 0.1 0.1]);s=Yfigure(3)plot3(Y(:,1),Y(:,2),Y(:,3))function dY=Lorenz_driven(t,Y);a=10;b=8/3;r=60;dY=zeros(3,1);dY=[a*(Y(2)-Y(1));-Y(1)*Y(3)+r*Y(1)-Y(2);Y(1)*Y(2)-b*Y(3)]MatLab常微分方程及常微分方程组的求解(2011-07-08 23:01:48)转载▼分类:编程之Matlab标签:杂谈最近参加了数学建模,对于老师说的Euler算法的不同步长的精度不一样,编写了一个M 函数文件来实现这个精度的比较,把函数附上:function [x,y]= Euler(varargin)%这里使用可变输出输入函数的%varargin{1}为求解常微分方程的表达式%varargin{2}为求解常微分方程的定解条件%需要给出的变量有常微分方程的范围a,b(varargin{3},varargin{4})%n为对这个区间的分割(varargin{5})%xlt写于7月8日%取得算法需要的变量,并附上容易理解的含义变量a = varargin{3};b = varargin{4};%自变量的范围n = varargin{5};%区间的分割次数h = (b - a)/n;%步长Dy = varargin{1}; %常微分方程的表达式y0 = varargin{2}; %常微分方程的定解条件表达式%首先求出所给常微分方程问题的精确解x1 = zeros(n+1,1);y1 = zeros(n+1,1);syms f1; syms x;f1 = dsolve(Dy,y0,'x');x1(1) = a;y1(1) = subs(f1,{x},{x1(1)});for i = 2:(n+1)x1(i) = x1(i-1) + h;y1(i) = double(subs(f1,{x},{x1(i)}));end%利用Euler方法求解近似数值微分解x2 = zeros(n+1,1);y2 = zeros(n+1,1);syms y;x2(1) = a;y2(1) = subs(f1,{x},{a});%获得原方程的初解for i = 2:(n+1)x2(i) = x2(i-1) + h;y2(i) = y2(i-1) + h .* double(subs(Dy(5:end),{x,y},{x2(i-1),y2(i-1)}));%特别记录Matlab中的字符串操作,提取子字符串即A(3:6)...end%返回经过Euler算法算出x与y的值x = x2;y = y2;%画图进行误差比较plot(x1,y1,'r');hold on;plot(x2,y2,'b');特此记录,以后写了新的算法再分享文 - 汉语汉字编辑词条文,wen,从玄从爻。
利用Matlab模拟混沌系统

第21卷第6期2003年11月泉州师范学院学报(自然科学)Journal of Quanzhou Normal University(Natural Science)Vol.21 No.6Nov.2003利用Matlab模拟混沌系统苏大生,夏小建(泉州师范学院物理系,福建泉州 362000)摘 要:以R ossler方程、Du ffing方程和Van der pol方程为例,应用Matlab仿真工具进行模拟,并对仿真结果作了简要说明和讨论,其中的示例对混沌研究和教学有一定的意义.①关键词:混沌;M AT LAB;仿真中图分类号:TP273 文献标识码:A 文章编号:1009-8224(2003)06-0029-03混沌是非线性科学研究的一个重要概念,近年来由于混沌在控制和保密通讯等方面的应用,使混沌研究成为学术界的热门课题之一.混沌系统的状态通常可用非线性微分方程来描述,这些方程的解一般难于用解析式表达,更多的情况只能采用数值解法.随着计算机技术的发展,数值解法[1]在混沌系统中将起着更重要的作用.本文应用M AT LAB对混沌系统进行数法模拟,该方法也是一种数值解法,具有操作简单、直观、灵活等优点.1 Matlab语言及其动态仿真———SimulinkMatlab是由Math W ork公司推出的一种面向科学与工程计算的高级语言,它集科学计算、自动控制信号处理、神经网络、图象处理等于一体,具有极高的编程效率.Matlab提供的Simulink[2,3]是一个基于Windows环境下的以图形进行编程的软件,可用来对动态系统建模、仿真和分析,编程时只需选择需要的模块,用鼠标将它们联结起来,并设定每一方块的参数,在用Simulink模拟混沌系统时,可根据非线性微分方程建立方块图,并设置参数进行模拟,即可得到对应的数值解.该方法具有直观、方便、灵活等优点,下面以R ossler方程、Van der pol方程和Du ffing方程为例进行模拟.2 混沌系统的模拟2.1 R ossler方程的模拟R ossler方程是由R ossler在1976年建立的一个简单的三维系统,其方程为d xd t=-y-z,d yd t=x+0.2y,d zd t=0.2-5.7z+xz.①收稿日期:2003-04-25作者简介:苏大生(1974- ),男,福建安溪人,助理实验师,主要从事应用软件及实验教学研究.应用Matlab 建模,得到图1的模型,其中,Sum (Sum1、Sum2和Sum3)是求和模块,Integrator (图1中Inte )是积分模块,用于实现求和.Product 是求积模块,实现输入变量的乘积.G ain 是增益模块,实现输入变量的增益,C onst 是常数模块,用于获得一个常数.XY 为显示模块,可显示XY 平面的轨迹.图2、3为在X (0)=Y (0)=1、Z (0)=2、仿真时间200秒的初始条件下,得到的在XY 、X Z 平面的混沌轨迹.03 泉州师范学院学报(自然科学)2003年11月 该方程可以用一阶微分方程组来描述 y ′=ky (1-x 2)-x ,y =x ′.图6是Van der pol 方程的模块连接框图,取式(2)中的参数k =1,并设初始条件x (0)=y (0)=0.1,仿真时间为500秒,Van der pol 方程的混沌轨迹,见图7.3 结论Matlab 的Simulink 工具采用的是数值计算方法,不可避免地会产生数值误差.一个连续的动态系统一般为d x d t =f (x ,t ),(3)其中,x 是n 维状态矢量,函数f 表示一个特定的系统.若给定初始条件x (0),时间步长为h ,则通过对方程(3)差分的方法,可获得x (t )的变化轨迹为x n (nh )=x n -1((n -1)h )+hf (x (n -1),(n -1)h ),当h 足够小时,即可获得x 随时间的变化轨迹.h 取值应适当,实际选用时,h 太小,计算量太大;h 太大,达不到计算精度.在Matlab 中一般选用四阶的龙格库塔方法,它对步长自动选取,既减少计算量又适应精度要求.尽管采用四阶龙格库塔方法,但误差还是不可避免.实际上,除非步长非常小,否则截断误差通常是较严重的误差来源.对于大多数系统而言,随积分步数的增加其误差将逐步减小.但是混沌系统的一个显著特征就是对初始条件的极端敏感性,扰动将明显地改变x (t )的轨迹,使得附近的轨迹呈指数分离.绝大多数工程上感兴趣的系统都是结构稳定的,即在f 中一个小扰动将导致在其吸引子中也产生一个相应的小扰动.而数值误差可看作是一种扰动,因此,对混沌吸引子的模拟在细节上可能和实际情况不完全相同,但它保持了吸引子的宏观形状.文章采用的方法可用于模拟由状态方程描述的时不变系统.该方法实用、简便,对混沌研究和教学有一定的实际意义.参考文献:[1] 李建芬,李农,张祥娥.利用SPICE 模拟混沌系统[J ].电路与系统学报,1997,2(1):68-71.[2] 施阳.M AT LAB 语言精要及动态仿真工具SIM U LINK[M].西安:西北工业大学出版社,1997.[3] 陈怀琛.M AT LAB 及其在理工课程中的应用指南[M].西安:西安电子科技大学出版社,2000.(下转第70页)13 第6期苏大生等:利用Matlab 模拟混沌系统 07 泉州师范学院学报(自然科学)2003年11月 3.3.5 发展农村小型会展业 通过综合或专业的会展提高“闽货”知名度,为农民解决“卖难”问题,同时也通过会展带动农民消费.会展业是投资回报高,又是促进消费,推动经济增长的一种有效的产业.2001年,泉州“会展经济”已初露端倪,仅1-11月,全市举办的大型商展活动67场,有9150多家企业参加,现场销售产品2008.7万多元,签订投资项目1007个,合同金额482.63亿元.参考文献:[1] 福建统计局.福建统计年鉴2003[M].北京:中国统计出版社,2003.[2] 熊宁,曾尊固.试论调整农业结构与构造区域特色农业[J].经济地理,2001,21(5):564-568.[3] 吴海峰.我国农村消费市场启而不动的原因及对策[J].西北农林科技大学学报,2002,2(3):51-53.An Analysis of the Impetus to Expand the Marketin Country of FujianLI Z i2rong(Department of G eography,Quanzhou N ormal University,Fujian362000,China)Abstract:It appears that the development of markets in the country is slow and even static in aspects of consum ption and supply.According to the analysis of its further causes,the author thinks that the im pe2 tus to expand the market lies in raising the peasantry’s incomes,quickening the construction of central country,advancing the urbanization,and cultivating new hotspots on consum ption in country.The article em phasizes that forming characteristic agriculture in Fujian,taking the way to industrialization of farming ,perfecting the service system of farming,and strengthening the cooperation of agriculture between Fujian and T aiwan are im portant approaches to raise the peasantry’s incomes efficiently.Meanwhile,the author suggests that g overnment should cultivate new hotspots such as service industry,in formation industry,ed2 ucation system,small exhibition center and s o on.K ey w ords:Fujian;consum ption marketing in country;cause;im petus(上接第31页)Simulating Chaotic System with MatlabS U Da2sheng,XI A X iao2jian(Department of Physics,Quanzhou N ormal University,Fujian362000,China)Abstract:This article presents a method to simulink R ossler equation,Du ffing equation and Van der pol equation with Matlab.Then presents the brief dem onstration and discussion of result.The exam ples ben2 efit to the research and teaching of chaos.K ey w ords:chaos;Matlab;simulink。
基于MATLAB的各类混沌系统的计算机模拟(教学版)

基于MATLAB的各类混沌系统的计算机模拟―――《混沌实验教学平台的设计与实现》初期报告物电05级1A班张丹伟20050003101摘要:本文利用数学软件MATLAB对Lorenz系统等六个重要的混沌模型进行数值计算,同时模拟出各类混沌系统的独特性质,如混沌吸引子,倍周期,初值敏感性,相图,分岔图等。
通过观察和分析上述特性,加深了我们对混沌现象的理解。
关键词:混沌;微分方程;MA TLAB;引言.混沌探秘混沌是非线性系统所独有且广泛存在的一种非周期运动形式, 其覆盖面涉及到自然科学和社会科学的几乎每一个分支。
1972年12月29日,美国麻省理工学院教授、混沌学开创人之一E.N.洛伦兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可准确预报性。
为什么会出现这种情况呢?这是混沌在作怪!“混沌”译自英语中“chaos”一词,原意是混乱、无序,在现代非线性理论中,混沌则是泛指在确定体系中出现的貌似无规则的、类随机的运动。
混沌现象是普遍的,就在我们身边,是与我们关系最密切的现象,我们就生活在混沌的海洋中。
一支燃着的香烟,在平稳的气流中缓缓升起一缕青烟,突然卷成一团团剧烈搅动的烟雾,向四方飘散;打开水龙头,先是平稳的层流,然后水花四溅,流动变的不规则,这就是湍流;一个风和日丽的夏天,突然风起云涌,来了一场暴风雨。
一面旗帜在风中飘扬,一片秋叶从树上落下,它们都在做混沌运动。
可见混沌始终围绕在我们的周围,一直与人类为伴。
一.混沌的基本概念1. 混沌: 目前尚无通用的严格的定义, 一般认为,将不是由随机性外因引起的, 而是由确定性方程(内因)直接得到的具有随机性的运动状态称为混沌。
2. 相空间: 在连续动力系统中, 用一组一阶微分方程描述运动, 以状态变量(或状态向量)为坐标轴的空间构成系统的相空间。
MATLAB中的混沌系统建模与分析指南

MATLAB中的混沌系统建模与分析指南引言混沌系统是一类表现出复杂、不可预测、非周期性行为的动力学系统。
由于其具有高度敏感性和非线性特性,混沌系统一直备受研究者的关注。
在科学研究和工程领域中,混沌系统的建模与分析对于了解和预测系统的行为非常重要。
而MATLAB作为一种强大的数值计算和数据可视化工具,可以帮助我们进行混沌系统的建模与分析。
本文将介绍MATLAB中的混沌系统建模与分析指南。
第一部分:混沌系统建模混沌系统的建模是研究混沌现象的起点。
在MATLAB中,我们可以通过定义差分方程或微分方程的方式来建立混沌系统的数学模型。
1.1 确定方程形式在建模之前,我们首先需要确定混沌系统的方程形式。
常见的混沌方程包括Logistic映射方程、Lorenz方程等。
以Logistic映射方程为例,其表达式可以表示为:x(n+1) = r * x(n) * (1 - x(n))其中,x是系统状态的变量,n表示时间步长,r是控制参数。
在MATLAB中,我们可以通过定义一个差分方程来表示这个方程,并使用循环语句进行迭代计算。
1.2 设置初始条件在建模过程中,我们还需要设置混沌系统的初始条件。
在Logistic映射方程中,初始条件通常在[0,1]之间选择一个值。
在MATLAB中,我们可以使用rand函数生成一个在指定区间内的随机数作为初始条件。
1.3 模拟系统行为建立混沌系统的数学模型后,我们可以使用MATLAB进行系统行为的模拟。
通过迭代计算,我们可以获得混沌系统的时间序列。
在MATLAB中,我们可以定义一个循环,根据差分方程进行迭代计算,将每一步的结果保存到一个向量中。
通过设定迭代次数和控制参数的不同取值,我们可以观察到不同的动力学行为,例如周期性、混沌和收敛等。
第二部分:混沌系统分析混沌系统的分析对于理解和预测系统的行为非常重要。
MATLAB提供了许多工具和函数,可以帮助我们对混沌系统进行各种分析。
2.1 相图分析相图是了解混沌系统行为的重要工具。
MATLAB、Simulink混沌理论仿真

毕业设计(论文)原创性声明本人郑重声明:所提交的毕业设计(论文),是本人在导师指导下,独立进行研究工作所取得的成果。
除文中已注明引用的内容外,本毕业设计(论文)不包含任何其他个人或集体已经发表或撰写过的作品成果。
对本研究做出过重要贡献的个人和集体,均已在文中以明确方式标明并表示了谢意。
论文作者签名:日期:年月日摘要混沌在现代科学与工程学领域的应用十分广泛,混沌现象存在于自然界各个领域,包括通讯领域、气象学领域、生物学领域、医学诊断疾病等方面。
学习混沌理论在未来的发展过程对我们是很有帮助的。
在非线性的世界里,通过混沌理论洞察所有的非线性运动,对其进行控制和掌握。
通过非线性电路对混沌系统进行分析和理解,进而构造出符合二阶混沌系统的非线性电路和函数模型。
Duffing 方程就是典型的二阶非线性方程。
运用MATLAB/Simulink对其混沌系统进行仿真实现,验证混沌系统的基本特性。
关键词:混沌;非线性;Duffing方程; MATLAB/SimulinkABSTRACTChaos widely used in modern science and engineering and chaos phenomenon exists in various fields of nature, including the communications field, the field of meteorology, biology, medical diagnosis of diseases. Learning Chaos Theory is very helpful to us in the development of this course in the future. In a nonlinear world, insight into the chaos theory, We can control and master non-linear movement. We analyze and understand the chaotic system via nonlinear circuit, and then construct a second-order chaotic systems of nonlinear circuits and function model. Duffing equation is a typical second-order nonlinear equation. Using MATLAB/Simulink, we complete the chaotic system simulation and test the basic characteristics of chaotic systems.Key words:Chaos;nonlinear;Duffing equation;MATLAB/Simulink目录第一章绪论 (1)1.1混沌理论 (1)1.2混沌的应用 (2)第二章二阶混沌系统的仿真实现 (5)2.1混沌系统 (5)2.1.1混沌产生的数学模型 (5)2.1.2 奇异吸引子与分形 (6)2.1.3 混沌系统的特征 (7)2.1.4 研究混沌的主要方法 (8)2.2 二阶混沌系统的实现 (9)第三章二阶非线性电路仿真实现 (15)3.1 Simulink仿真 (17)3.2 MATLAB语句命令演示模拟 (19)第四章结论 (22)致谢 (25)参考文献 (26)附录A (27)第一章绪论1.1混沌理论什么是混沌?现代科学意义上是很难得出确切的定义,之所以这样是因为:到目前为止,还没有足够和统一数学定理可以将混沌理论完全表达出来,在数学理论的基础上通过混沌系统所表现出的普遍现象总结归纳出混沌的本质。
Matlab动态仿真在混沌控制与同步中的应用研究

Journal of Ch angsh a U niversity of Science and T echnology(N atural Science) 收稿日期:2004-05-19作者简介:孙 琳(1980-),女,湖南沅江人,长沙理工大学助教,主要从事电子信息技术的研究. 文章编号:1672-9331(2004)02-0056-05M atlab 动态仿真在混沌控制与同步中的应用研究孙 琳1,姜德平2(1.长沙理工大学物理与电子科学系,湖南长沙 410076;2.广西师范大学物理与信息工程学院,广西桂林 541004)摘 要:针对在分析非线性系统混沌行为时较为复杂这一问题,采用一般的数值计算方法,提出了利用Mat 2lab 对混沌系统进行建模和动态仿真的方法.以蔡电路和洛伦兹系统为例,分析了其动态仿真在混沌控制与同步中的应用.结果表明:Matlab 动态仿真能真实、有效地模拟了控制与同步的全过程,同时这一方法也拓宽了分析和研究非线性问题的途径.关键词:Matlab ;混沌;同步;可视化;动态仿真中图分类号:TP391.9文献标识码:A随着系统设计问题的进一步复杂化及其研究的深入,特别是更具“人性化”的高版本Matlab 问世,建立在Simulink 平台上的动态仿真具有更加广泛的应用.其可视化仿真效果不仅极大地提高了工作效率,增加了对系统模型分析、构建和设计的可控性,而且其交互式仿真形式可以使设计者根据特定的要求对整个仿真过程的模块、参数和输出结果进行实时调整和监控.本研究主要探讨Matlab 动态仿真在非线性系统混沌控制与同步中的应用研究.1 混沌控制中的Matlab 动态仿真随着20世纪90年代国际上混沌控制与同步研究取得突破性进展,全世界掀起了一股研究混沌的热潮,相继提出了多种控制混沌的方法[1~4].但是,由于其所具有的一些基本属性,如不稳定性、不可预见性、内随机性和类噪声性,使得其不易于过程控制和结果分析,这就增加了混沌问题研究的难度.而Matlab 的可视化动态仿真就可以很好地解决这一问题,减轻设计和分析的复杂性,可以对仿真结果实施跟踪控制.以蔡电路[5]为例,对其混沌过程进行动态仿真控制,以使其趋于稳定的周期态.蔡电路的无量纲形式为:x 1=α[x 2-x 1-f (x 1)],x 2=x 1-x 2+x 3,x 3=-βx 2.(1)式中:f (x 1)=bx 1+0.5(a -b )(|x 1+1|-|x 1-1|).(2)第1卷第2期长沙理工大学学报(自然科学版)V ol.1N o.22004年9月 Sep.2004方程(1)中,状态变量x 1,x 2,x 3分别对应蔡电路中的电容C 1,C 2上的电压v c 1,v c 2和电感L 中的电流i L .当系统参数为α=9.78,β=14.97,a =-1.31,b =-0.75时,蔡电路处于混沌运动状态[6].蔡电路模型如图1所示,其变量x 1在混沌时的波形如图2所示.图1 蔡电路模型根据文献[6]的控制方法,得到控制后的系统如下:图2混沌状态时x 1波形x 1=(αk -α)x 1-αf (x 1)+(α-αk )x 2+αkx 3,x 2=x 1-x 2+x 3,x 3=-βx 2.(3)系统发生H opf 分岔时,k 的临界值为k 0=-0.13792732,当再继续增大k (k >k 0),电路系统发生一系列闭轨分岔(倍周期分岔是一种特殊闭轨分岔),并可以得到1P ,2P ,3P ,4P ,6P 等不同的稳定周期轨道,作出控制系统模型如图3所示.控制到1P 时,k 取值为-0.12,控制后的结果如图4~6所示.图3 蔡电路控制模型75第1卷第2期孙 琳,等:Matlab 动态仿真在混沌控制与同步中的应用研究图4控制到1P 时x 1波形 图5控制到1P 时x 1与x 2的相图 图6控制到1P 时x 1与x 3的相图2 混沌同步中的Matlab 动态仿真以洛伦兹系统为例,验证Matlab 动态仿真在混沌同步中的应用.用洛伦兹系统作为驱动系统,其形式如下:x 1=α(x 2-x 1),x 2=βx 1-x 2+x 1x 3,x 3=x 1x 2-λx 3.(4)用x 1与x 2对式(4)进行驱动,得到响应系统为:y 1=α(x 2-y 1),y 2=βx 1-y 2+x 1y 3,y 3=x 1x 2-λy 3.(5)其中:α=10,β=28,λ=8/3.设e 1=x 1-y 1,e 2=x 2-y 2,e 3=x 3-y 3,e 4=x 4-y 4,则由式(4)、式(5)可得:e 1=α(y 1-x 1)=-αe 1,e 2=y 2-x 2-x 1(y 3-x 3)=-e 2+x 1e 3,e 3=λ(y 3-x 3)=-λe 3.(6)因为α,λ均大于零,由式(6)中第1个方程和第3个方程得:lim t →+∞e 1=0,lim t →+∞e 3=0.当时间趋于无穷大时,将上述结果代入式(6)中的第2个方程可得: e 2=-e 2,则lim t →+∞e 2=0.由Lyapunov 稳定性定理[8,9]可知,式(6)零解稳定,即Y →X.因此,在上述参数条件下,驱动系统(4)和响应系统(5)可以实现混沌同步.构建的驱动、响应系统的动态仿真模型如图7所示,从驱动系统中可以观察到图8中著名的“蝴蝶效应”[10].同步结果如图9所示,由图9可知:两系统可以实现精确同步.在实际的动态仿真中,可以从示波器上看到两个系统达到同步后,其二者之间的轨道误差为1条y →0的直线,且随着时间的推移而不断向前延伸.3 结 论Matlab 不仅广泛应用于设计单位和科研院所,而且也是理论和实验教学的有力工具.其可视化的动态仿真,拓宽了非线性问题研究分析的视野,降低了系统设计和仿真分析的难度,提高了研究设计工作的85长沙理工大学学报(自然科学版)2004年9月效率,具有重要的推广和应用价值.随着其版本的不断更新,Matlab 软件的动态仿真将会呈现出越来越大的应用前景.〔参考文献〕[1] Ott E ,G rebogi C ,Y orke J A.C ontrolling Chaos[J ].Phys Rev Lett ,1990,64(11):119621199.[2] Py fragas K.C ontinuous C ontrol of Chaos by Self 2controlling Feedback[J ].Phys Lett A ,1992,(170):4212428.[3] G uemez J ,Matuas M A.C ontrolling of Chaos Unidimensional[J ].Phys Lett A ,1993,(181):29.[4] 罗晓曙,陈关荣,汪秉宏.Hybrid C ontrol of Period 2doubling Bifurcation and Chaos in Discrete N onlinear Dynamical Systems[J ].95第1卷第2期孙 琳,等:Matlab 动态仿真在混沌控制与同步中的应用研究06长沙理工大学学报(自然科学版)2004年9月Chaos,S olitions and Fractal,2003,(18):775.[5] Chua L O,Itoh M,K ocarev L,et al.Chaos Synchronization in Chua’s Circuits[J].J of Circuits,Systems and C omputers,1993,3(1):932108.[6] 邹艳丽,罗晓曙,梁宗经,等.一种控制蔡电路的分岔和混沌的方法[J].广西师范大学学报(自然科学版),2003,21(3):21224.[7] 许淞庆.常微分方程稳定性理论[M].上海:上海科学技术出版社,1961.[8] Jordan D W,Smith P.N onlinear Ordinary Differential Equations[M].New Y ork:Ox ford University Press,1987.[9] Lorenz E.Deterministic N on2periodic Flows[J].J Atm ospheres Science,1963,(20):1302141.Application of Dynamic Simulation of Matlab inChaos Control and SynchronizationS UN Lin1,J I ANG De2ping2(1.Department of Physics and E lectronic Science,Changsha University of Science and T echnology,Changsha410076,China;2.C ollege of Physics and In formation Engineering,G uangxi N ormal University,G uilin541004,China)Abstract:Aiming to the com plexity in analyzing chaos of nonlinear system using numerical calculation,the method for m odel design and dynamic simulation based on Matlab s oftware was studied in this paper.T aking Chua circuit and Lorenz system as an exam ple,the application of dynamic simulation in chaos control and synchronization was anal2 ysed.The results show that dynamic simulation can display the whole process of chaos control and synchronization tru2 ly and effectively,at the same time,the s olution to nonlinear problem was extended through this method.K ey w ords:Matlab;chaos;synchronization;visiblization;dynamic simulation。
连续时间混沌系统MATLAB程序和SIMULINK模型

第6章连续时间混沌系统本章讨论连续时间混沌系统的基本特点与分析方法,主要包括混沌数值仿真和硬件实验方法简介、混沌系数平衡点的计算、平衡点的分类与性质、相空间中的轨道、几类典型连续混沌系统的介绍、混沌机理的分析方法、用特征向量空间法寻找异宿轨道、Lorenz系统及混沌机理定性分析、Lorenz映射、Poincare截面、Chua系统及其混沌机理定性分析、时间序列与相空间重构等内容。
6.1 混沌数值仿真和硬件实验方法简介混沌的数值仿真主要包括MA TLAB编程、SIMULINK模块构建、EWB仿真以及其他一些相关的软件仿真或数值计算等方法,从而获取混沌吸引子的相图、时域波形图、李氏指数、分叉图和功率谱等。
混沌的硬件实验主要包括模拟/数字电路设计与硬件实验、现场可编程门阵列器件(FPGA)、数字信号处理器(DSP)等硬件实现方法来产生混沌信号。
本节仅对各种数值仿真方法作简单介绍。
1)混沌系统的MA TLAB数值仿真该方法主要根据混沌系统的状态方程来编写MA TLAB程序。
现举二例来说明这种编程方法。
(1)已知Lorenz系统的状态方程为dx/dt=-a(x-y)dy/dt=bx-xz-ydz/dt=-cz+xy式中a=10,b=30,c=8/3。
MA TLAB仿真程序如下:>> %**************************************************Function dxdt=lorenz(t,x)%除符号dxdt外,还可用其他编程者习惯的有意义的符号A=10;B=30;C=8/3;dxdt=zeros(3,1);dxdt(1)=-A*(x(1)-x(2));dxdt(2)=B*x(1)-x(1).*x(3)-x(2);dxdt(3)=x(1)*x(2)-C*x(3);%*************************************************options=odeset('RelTol',1e-6,'AbsTol',[ 1e-6 1e-6 1e-6]);t0=[0 200];x0=[0.02,0.01,0.03];[t,x]=ode45('lorenz',t0,x0,options);%**************************************************n=length(t)n1=round(n/2)%n1=1;%**************************************************figure(1);plot(t(n1:n,1),x(n1:n,1));xlabel('t','fontsize',20,'fontname','times new roman','FontAngle','italic');ylabel('x','fontsize',20,'fontname','times new roman','FontAngle','italic');figure(2);plot(x(n1:n,1),x(n1:n,3));xlabel('x','fontsize',20,'fontname','times new roman','FontAngle','italic');ylabel('z','fontsize',20,'fontname','times new roman','FontAngle','italic');%*******************************************************************根据上述MA TLAB程序,得Lorenz系统的时域波形图和混沌吸引子相图的数值仿真结果如图6-1所示。
混沌系统matlab代码

混沌系统通常指的是非线性、动力学复杂的系统,其行为难以预测。
在MATLAB中,您可以模拟混沌系统的行为。
以下是一个简单的混沌系统(例如,Logistic映射)的MATLAB 代码示例:
```matlab
% 定义参数和初始条件
r = 3.9; % 控制参数
x0 = 0.4; % 初始条件
n = 100; % 迭代次数
% 初始化数组来存储混沌序列
x = zeros(1, n);
x(1) = x0;
% 迭代计算混沌序列
for i = 2:n
x(i) = r * x(i-1) * (1 - x(i-1));
end
% 绘制混沌序列
plot(1:n, x);
title('混沌序列');
xlabel('迭代次数');
ylabel('值');
```
上述代码演示了一个简单的Logistic映射的混沌系统,其中`r` 是控制参数,`x0` 是初始条件,`n` 是迭代次数。
代码使用一个循环来迭代计算混沌序列,并通过`plot`函数绘制结果。
请注意,混沌系统有许多不同的方程和变种,具体的模拟方法和参数设置会根据您选择的系统而异。
您可以根据特定的混沌系统方程和参数来调整MATLAB代码以模拟不同的混沌行为。
此外,MATLAB还提供了一些混沌工具箱,可用于更复杂的混沌系统模拟和分析。
利用Matlab模拟混沌控制与同步

{ e , c c-e 4 ; e 一 主 +p
驱 动 系 统
响应 系统
图 7 L u系 统 驱 动 一响 应 同 步 模 型 i
( 下转 第 3 3页)
维普资讯
第 6卷 第 1 2期 20 年 1 月 0 7 2
南阳师 范 学院 学报
J u na fNa y n r lUn v r i o r lo n a g No ma i e st y
Vo . .1 1 6 No 2 De . 2 0 c 0 7
图 4 受控 Lu系 统 模 型 i
图 1中 的“ 蝴蝶 效应 ” 同步 结果 如 图 8 图 9所 示 , . 、
设 e= 一 e , =Y 一Y e 。一 贝 由式 ( ) , = , 0 1 和 () 3 可得 误差 系统 为
两系 统可 以实 现 精 确 同步. 实 际 的 动 态仿 真 中 , 在
利 用 Malb模 拟 混 沌 控 制 与 同 步 t a
任 春 明, 文法 , 苑 江 辉
( 安 建 筑科 技 大 学 理 学院 , 西 西 安 70 5 ) 西 陕 10 5
摘 要 : 新 型 混 沌 系统— — Lu系统 为例 , 用 Ma a 以 i 运 t b对 混 沌 系统 进 行 建 模 和 动 态仿 真 , 析 了其 动 态 仿 真 在 混 沌控 l 分 制 与 同步 中的 应 用 , 并对 仿 真 结 果作 了简要 的说 明 和 讨 论 .
{ b — x一 = x k z
。
() 2
l 一+ c z :
一个超混沌系统在MATLAB环境下的仿真实现

毕业设计(论文)题目一个超混沌系统在MATLAB环境下的仿真实现系(院)物理与电子科学系专业物理学班级2005级1班学生姓名XXX学号2005080119指导教师XXX职称二〇一一年六月十八日独创声明本人郑重声明:所呈交的毕业设计(论文),是本人在指导老师的指导下,独立进行研究工作所取得的成果,成果不存在知识产权争议。
尽我所知,除文中已经注明引用的内容外,本设计(论文)不含任何其他个人或集体已经发表或撰写过的作品成果。
对本文的研究做出重要贡献的个人和集体均已在文中以明确方式标明。
本声明的法律后果由本人承担。
作者签名:二〇一〇年六月一十八日毕业设计(论文)使用授权声明本人完全了解滨州学院关于收集、保存、使用毕业设计(论文)的规定。
本人愿意按照学校要求提交学位论文的印刷本和电子版,同意学校保存学位论文的印刷本和电子版,或采用影印、数字化或其它复制手段保存设计(论文);同意学校在不以营利为目的的前提下,建立目录检索与阅览服务系统,公布设计(论文)的部分或全部内容,允许他人依法合理使用。
(保密论文在解密后遵守此规定)作者签名:二〇一〇年六月一十八日一个超混沌系统在MATLAB环境下的仿真实现摘要在混沌、超混沌理论研究成果的基础上,利用外加驱动信号方法改进一个四阶超混沌系统,通过对外界驱动信号频率的控制,实现系统的动力学特性。
对新构建的超混沌系统的特性进行了详细分析,包括验证其超混沌性质,相空间轨迹分析,Lyapunov指数谱分析等,仿真结果关键词:超混沌;lyapunov指数;EWB;超混沌电路;MATLABIA hyperchaos circuit was simulated in MATLABsimulationAbstractBased on chaotic and the hyperchaotic theory research, by using plussing a drive signal to the fourth-order hyperchaos system to improve the fourth-order hyperchaos system, through to control the external drive signal frequency, realizeing the system’ dynamic characteristics. The construction of the new characteristics of hyperchaos system are analyzed in detail, including its hyperchaos nature, path analysis, phase space Lyapunov index and bifurcation diagram analysis and simulation results show that the system characteristics. Is abundant. Using the signal frequency control and drive can completely accurate control of the entire system dynamics characteristic. Finally,design a simulated circuit, and simulat in EWB environment, through the comparison of simulation results between MATLAB and EWB, Further verify the consistency between experiment results and numerical simulation.Keyword:hyperchaos;Lyapunov exponents;bifurcation;hyperchaotic CircuitII目录引言 (1)第一章动力系统形态及其分析 (2)1.1动力系统 (2)1.1.1动力学系统的基本概念 (2)1.1.2几种常见的平衡态 (4)1.1.3吸引子和结构稳定性 (6)1.2 分岔 (7)1.2.1分岔的基本概念 (7)1.2.2非线性映射及其分岔 (8)第二章混沌系统判别方法讨论 (10)2.1混沌的特性及其判别方法 (10)2.1.1混沌的定义 (10)2.1.2混沌运动的基本特征 (11)2.2超混沌特性及其判别方法 (11)2.3混沌电路研究方法 (12)第三章一个新的超混沌系统设计及其性能分析 (12)3.1超混沌系统 (12)3.1.1一个四阶的超混沌系统 (12)3.1.2平衡点及稳定性分析 (13)3.1.3系统相空间轨迹分析 (13)3.2一个新的超混沌系统 (15)3.2.1一个新的超混沌系统的设计 (15)3.2.2系统相空间轨迹分析 (16)3.2.3李雅普诺夫指数分析 (17)3.2.4系统的电路设计和实验结果 (17)结论 (23)参考文献 (24)i谢辞 (25)ii引言混沌科学是一门新兴的学科,混沌(Chaos)是一种貌似无规则的运动,指在确定性非线性系统中,不需要附加任何随机因素亦可出现的行为(内在随机性)。
MATLAB中的混沌理论和应用

MATLAB中的混沌理论和应用引言:混沌理论是一门重要且广泛应用于科学和工程领域的学科,它研究的是那些看似无法预测的、无序的、非线性的系统行为。
混沌现象的研究不仅对于了解自然界的规律有着重要意义,也有助于我们在信息处理、密码破解、通信领域等方面的应用。
而在MATLAB这样强大的数值计算和数据可视化工具的支持下,我们能更加便捷地研究和应用混沌理论。
一、混沌理论基础:混沌理论源于20世纪60年代的洛伦兹发现的一个关于天气预报的数学模型。
首先,我们需要理解混沌系统的几个基本概念:敏感依赖于初始条件、奇异吸引子和分岔。
敏感依赖于初始条件意味着一个微小的变化可能会引起系统行为的巨大变化。
奇异吸引子是指系统的轨迹将在有限的空间内游荡,并展现出无限的复杂性。
而分岔则是指系统参数的微小变动可能会引起系统行为的剧烈变化。
二、混沌系统的建模与仿真:在MATLAB中,我们可以使用数值方法对混沌系统进行建模和仿真。
通过定义差分方程或微分方程来描述系统的演化过程,并利用数值计算的方式来求解这些方程。
例如,洛伦兹方程是描述流体力学中对流运动的基本方程之一,也是混沌系统的经典模型之一。
通过编写MATLAB脚本,我们可以模拟并可视化洛伦兹系统的行为,如吸引子的轨迹、相空间的分布等。
三、混沌系统的控制与同步:混沌系统的控制与同步是混沌理论中一个重要的研究方向。
控制混沌系统意味着通过某种方法来驱动混沌系统的状态,使其趋于稳定或者遵循我们期望的行为。
而同步则是指多个混沌系统之间的状态在某种条件下保持一致。
在MATLAB中,我们可以使用各种控制方法和同步方案来实现对混沌系统的控制与同步。
例如,可以通过调整系统参数或设计合适的反馈控制来实现对混沌系统的控制。
同时,利用适当的耦合方式和同步算法,我们可以实现多个混沌系统之间的状态同步。
四、混沌系统在信息安全中的应用:混沌系统在信息安全领域有着广泛的应用。
混沌序列的高度复杂性和不可预测性使得它成为一种理想的加密手段。
Matlab混沌仿真实现
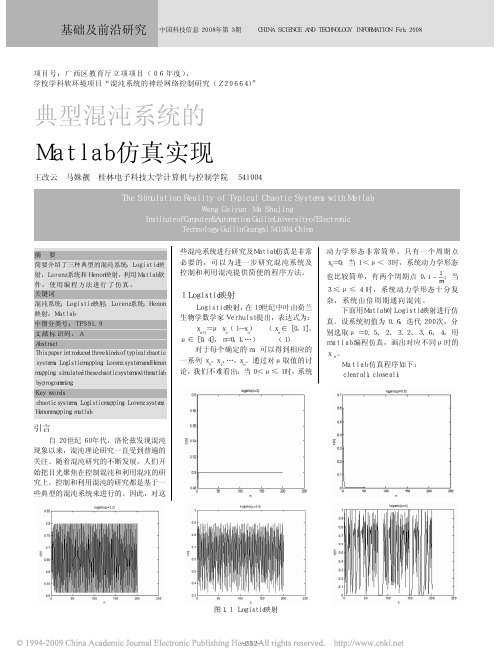
些混沌系统进行研究及Matlab仿真是非常必要的,可以为进一步研究混沌系统及控制和利用混沌提供简便的程序方法。
1 Logistic映射Logistic映射,在19世纪中叶由荷兰生物学数学家Verhulst提出,表达式为:xn+1=μxn(1-xn) (xn∈[0,1],μ∈[0,4],n=0,1,…) (1)对于每个确定的m,可以得到相应的一系列x0,x1,…,xn。
通过对μ取值的讨论,我们不难看出:当0<μ≤1时,系统项目号:广西区教育厅立项项目(06年度),学校学科软环境项目“混沌系统的神经网络控制研究(Z20664)”典型混沌系统的Matlab仿真实现王改云 马姝靓 桂林电子科技大学计算机与控制学院 541004引言自20世纪60年代,洛伦兹发现混沌现象以来,混沌理论研究一直受到普遍的关注。
随着混沌研究的不断发展,人们开始把目光聚焦在控制混沌和利用混沌的研究上。
控制和利用混沌的研究都是基于一些典型的混沌系统来进行的。
因此,对这动力学形态非常简单,只有一个周期点x0=0;当1<μ<3时,系统动力学形态也比较简单,有两个周期点0,;当3≤μ≤4时,系统动力学形态十分复杂,系统由倍周期通向混沌。
下面用Matlab对Logistic映射进行仿真。
设系统初值为0.6,迭代200次,分别选取μ=0.5、2、3.2、3.6、4,用matlab编程仿真,画出对应不同μ时的xn。
Matlab仿真程序如下:clear all;close all;图1.1 Logistic映射mu=0.5;x=0.6*ones(1,200);for n=1:200 x(n+1)=mu*x(n)*(1-x(n));endplot(x(1,:),'k','markersize',10);xlabel('n');ylabel('x(n)');title('logistic(\mu=0.5)');得到的仿真结果:(图1.1)进一步研究m的不断变化对系统的影响。
利用Matlab模拟混沌控制与同步

利用Matlab模拟混沌控制与同步
任春明;苑文法;江辉
【期刊名称】《南阳师范学院学报》
【年(卷),期】2007(6)12
【摘要】以新型混沌系统--Liu系统为例,运用Matlab对混沌系统进行建模和动态仿真,分析了其动态仿真在混沌控制与同步中的应用,并对仿真结果作了简要的说明和讨论.
【总页数】3页(P26-27,33)
【作者】任春明;苑文法;江辉
【作者单位】西安建筑科技大学,理学院,陕西,西安,710055;西安建筑科技大学,理学院,陕西,西安,710055;西安建筑科技大学,理学院,陕西,西安,710055
【正文语种】中文
【中图分类】TP391.9
【相关文献】
1.利用Matlab仿真模拟Rossler混沌系统及混沌控制 [J], 郭怡冰;苑文法
2.利用Matlab模拟混沌系统 [J], 苏大生;夏小建
3.利用反馈控制实现不同混沌(超混沌)系统之间的同步 [J], 薛志远;杨春德
4.Matlab动态仿真在混沌控制与同步中的应用研究 [J], 孙琳;姜德平
5.基于Matlab/Simulink的混沌同步控制实验 [J], 赵海滨;于清文;刘冲;陆志国;颜世玉
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB 的各类混沌系统的计算机模拟
混沌是非线性系统所独有且广泛存在的一种非周期运动形式, 其覆盖面涉及到自然科学和社会科学的几乎每一个分支。
1972年12月29日,美国麻省理工学院教授、混沌学开创人之一E.N.洛伦兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可准确预报性。
为什么会出现这种情况呢?这是混沌在作怪!
“混沌”译自英语中“chaos”一词,原意是混乱、无序,在现代非线性理论中,混沌则是泛指在确定体系中出现的貌似无规则的、类随机的运动。
混沌现象是普遍的,就在我们身边,是与我们关系最密切的现象,我们就生活在混沌的海洋中。
一支燃着的香烟,在平稳的气流中缓缓升起一缕青烟,突然卷成一团团剧烈搅动的烟雾,向四方飘散;打开水龙头,先是平稳的层流,然后水花四溅,流动变的不规则,这就是湍流;一个风和日丽的夏天,突然风起云涌,来了一场暴风雨。
一面旗帜在风中飘扬,一片秋叶从树上落下,它们都在做混沌运动。
可见混沌始终围绕在我们的周围,一直与人类为伴。
1.混沌的基本概念
1. 混沌: 目前尚无通用的严格的定义, 一般认为,将不是由随机性外因引起的, 而是由确定性方程(内因)直接得到的具有随机性的运动状态称为混沌。
2. 相空间: 在连续动力系统中, 用一组一阶微分方程描述运动, 以状态变量(或状态向量)为坐标轴的空间构成系统的相空间。
系统的一个状态用相空间的一个点表示, 通过该点有唯一的一条积分曲线。
3. 混沌运动: 是确定性系统中局限于有限相空间的高度不稳定的运动。
所谓轨道高度不稳定, 是指近邻的轨道随时间的发展会指数地分离。
由于这种不稳定性, 系统的长时间行为会显示出某种混乱性。
4. 分形和分维: 分形是 n 维空间一个点集的一种几何性质, 该点集具有无限精细的结构, 在任何尺度下都有自相似部分和整体相似性质, 具有小于所在空间维数 n 的非整数维数。
分维就是用非整数维——分数维来定量地描述分形的基本性质。
5. 不动点: 又称平衡点、定态。
不动点是系统状态变量所取的一组值, 对于这些值系统不随时间变化。
在连续动力学系统中, 相空间中有一个点0x , 若满足当 t →∞时, 轨迹0()x t x →, 则称0x 为不动点。
6. 吸引子: 指相空间的这样的一个点集 s (或一个子空间) , 对s 邻域的几乎任意一点, 当t →∞时所有轨迹线均趋于s, 吸引子是稳定的不动点。
7. 奇异吸引子: 又称混沌吸引子, 指相空间中具有分数维的吸引子的集合。
该吸引集由永不重复自身的一系列点组成, 并且无论如何也不表现出任何周期性。
混沌轨道就运行在其吸引子集中。
8. 分叉和分叉点: 又称分岔或分支。
指在某个或者某组参数发生变化时, 长时间动力学运动的类型也发生变化。
这个参数值(或这组参数值)称为分叉点, 在分叉点处参数的微小变化会产生不同性质的动力学特性, 故系统在分叉点处是结构不稳定的。
9. 周期解: 对于系统1()n n x f x += , 当n →∞时,若存在n i n x x ξ+== , 则称该系统有周期i 解ξ 。
不动点可以看作是周期为1的解, 因为它满足1n n x x +=。
10. 初值敏感性:对初始条件的敏感依赖是混沌的基本特征,也有人用它来定义混沌:混沌系统是其终极状态极端敏感地依赖于系统的初始状态的系统。
敏感依赖性的一个严重后果就在于,使得系统的长期行为变得不可预见。
2.MATLAB 中的龙格—库塔(Runge-Kutta )实现
MATLAB (Matrix Laboratory )是MathWorks 公司开发的,目前国际上最流行应用最广的科学与工程计算机软件之一。
MA TLAB 软件以矩阵运算为基础,把计算,可视化,程序设计等有机的融合在一起,具有出色的数值计算能力和强大的图形处理功能。
基于Runge —Kutta 法,MA TLAB 提供了求解微分方程数值解的函数,一般调用格式是:
[,]23(@,,0)[,]45(@,,0)
t y ode fname tspan y t y ode fname tspan y ==
其中fname 是定义的函数文件名,该函数文件必须返回一个列向量。
Tspan 形式是[t0,tf],表示求解区间,y0是初始状态向量。
这两个函数分别采用“二阶,三阶Runge —Kutta 法”和“四阶,五阶Runge —Kutta 法”,并采用自适应的求解方法,即当解的变化较慢时采用较大的步长,从而使计算速度很快,当解的变化较快时步长会自动变小长,从而使计算精度很高。
在MA TLAB 中,一般选取四阶的龙格库塔方法。
3.Lorenz 混沌系统
美国气象学家洛伦兹(E.N.Lorenz )于1963年在大气科学杂志上提出第一个表现奇异吸引子的动力学系统。
该混沌系统模型可以用下列微分方程组描述:
)()(z xy b dt
dz
xz y ax dt dy
y x c dt dx
-=--=--= 利用MA TLAB 数学软件对上面微分方程求解,进行数值模拟。
首先建立M -文件 Lorenz.m 定义脚本函数,然后编程调用,其中x (1)表示x ,x (2)表示y ,x (3)表示z ,程序如下:
function r=lorenz(t,x) global a; global b; global c;
r=[-c*(x(1)-x(2));a*x(1)-x(2)-x(1)*x(3);b*(x(1)*x(2)-x(3))]; clear; global a; global b; global c; b=8/3;c=10;
t0=[0,100];f0=[1,1,1]; for a=10:30
[t,x]=ode45(@lorenz,t0,f0); a
subplot(3,1,1);
plot(t,x(:,1),'r',t,x(:,2),'g',t,x(:,3),'b');
title('Lorenz 模型变量时域响应');legend('x','y','z'); xlabel('t');
subplot(3,1,2);
plot3(x(:,1),x(:,2),x(:,3));
title('Lorenz模型相图');xlabel('x');ylabel('y');zlabel('z');
grid on;
subplot(3,1,3);
plot(x(:,1),x(:,3));
title('Lorenz模型X—Z平面相图'); xlabel('x');ylabel('z');
grid on;
pause;
end
1. 固定参数b和c,设置初始值f0 和计算时间t0,通过改变参数a 可以发现系统逐步进入混沌状态的过程。
2. Lorenz 吸引子
当a=28时,系统已经完全进入混沌状态,此时出现双涡旋吸引子,如下所示:
3. 倍周期:
通过系数的调试可以得到Lorenz混沌的一个单倍周期和两个多倍周期,如下:
4.初值敏感性:
保持初值x0和y0不变,即x0=y0=1,改变z0为1.001,千分之一的变化会引起系统行为的显著改变,如下图所示:
4.Rossler 混沌系统
Rossler 系统是化学反应系统的简化模型,是非线性动力学中非常著名的方程,该混沌系统模型可以用下列微分方程组描述
)(a x z c dt
dz
x by dt dy
z y dt dx
-+=-=-= 同样地,利用MATLAB 编程求解(程序见附录),可以对该模型进行分析。
1. 逐步改变参数,观察其进入混沌状态。
2.Rossler吸引子:
3.倍周期:
通过调整参数和初始值,可以得到单倍周期和2倍周期,如下图:
初值敏感性:。
