计算方法实验11

合集下载

数值计算方法LU分解法实验

数值计算方法LU分解法实验LU分解法是一种常见的数值计算方法，用于解线性方程组或求解矩阵的逆。

该方法的核心思想是将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。

在本篇文章中，我们将进行关于LU分解法的实验，并探讨其性能和应用。

首先，我们需要明确LU分解法的数学原理。

假设我们有一个n阶方阵A，LU分解法的目标是找到两个矩阵L和U，使得A=LU。

其中L是一个下三角矩阵，U是一个上三角矩阵。

然后，我们可以将原始的线性方程组Ax=b转化为两个新的方程组Ly=b和Ux=y。

通过求解这两个方程组，我们可以得到原始方程组的解。

接下来，我们将通过一个具体的例子来说明LU分解法的步骤和计算过程。

假设我们有以下方程组：2x+y+z=8-3x-y+2z=-11-2x+y+2z=-3首先，我们将系数矩阵A进行LU分解。

在这个例子中，我们可以得到下三角矩阵L和上三角矩阵U：L=100-1.510-1-11U=21101.52.5001然后，我们将方程组转化为Ly=b和Ux=y的形式。

解这两个方程组，可以得到y和x的值。

最终，我们可以得到方程组的解为x=2，y=3，z=-1通过以上的实例，我们可以看到LU分解法的步骤较为繁琐，但是它的结果是准确的。

那么，接下来我们将进行一系列实验，来评估LU分解法的性能和应用。

首先，我们将进行LU分解法的准确性测试。

我们将随机生成一组方程组，并使用LU分解法求解出它们的解。

然后，我们将使用该解验证原方程组，并计算出其误差。

我们重复这个过程多次，并计算平均误差。

通过这次实验，我们可以判断LU分解法的准确性。

其次，我们将评估LU分解法的计算效率。

我们将随机生成不同规模的方程组，并使用LU分解法求解它们。

然后，我们记录下求解所需的时间，并绘制出问题规模和求解时间的关系图。

通过这个实验，我们可以了解LU分解法在不同规模问题上的计算效率，从而评估其可行性和应用范围。

此外，我们还可以将LU分解法与其他数值计算方法进行比较。

实验11乙酸乙酯皂化反应速率常数的测定

其中反应速率常数与温度的关系式为：
1780 lg K 0.00754 T 4.54 T
乙酸乙酯皂化反应的活化能: Ea=27.3KJ/mol
实验结果与讨论
⑴结果：实测值为Ｅa= ⑵计算实验偏差： ⑶分析产生偏差的原因： ⑷有何建议与想法？
注意事项：
1.电导率仪要进行温度补偿及常数校正； 2.反应液在恒温时都要用橡胶塞子盖好； 3.混合过程既要快速，又要小心谨慎，不要把溶液挤出反应管； 4.严格控制恒温的温度，因为反应过程温度对反应速率常数影响很大； 5.严格配制溶液的浓度，保证氢氧化钠与乙酸乙酯的浓度相等，否则反应速率常数计算公式将发生变化。
积分得：
1 1 Kt c0 x c0
dx K (C0 x) 2 dt
-------------（1）
本实验采用电导法测量皂化反应中电导L随时间t的变化。设L0、Lt、L∞分别代表时间为0、t、∞时溶液的电导。在稀溶液下，乙酸乙醋皂化反应，在不同反应时刻，其电导率与浓度的满足以下关系：
实验原理
乙酸乙酯皂化反应是个典型的二级反应。设反应物起始浓度均为C0，经时间t 后产物的浓度为x。
CH3COOC2 H5 NaOH CH3COONa C2 H5OH t=0 C0 C0 0 0 t=t C0-x C0 -x x x t=∞ 0 0 C0 C0
该反应的速率方程为：

0.924541.168103 t 1.95106 t 2
式中：密度ρ的单位为g/ml; 温度t的单位为℃。
用移液管量取20ml0.02mol/LNaOH溶液和 20ml蒸馏水放于100ml烧杯中，混均后倒入大试管中（盖上橡皮塞）。在反应管的小管中加入20ml0.02mol/L乙酸乙醋溶液，大管中加入20ml0.02mol/L NaOH溶液（均盖上橡皮塞）。把它们同时放入恒温槽中，恒温15分钟。

计算方法-插值方法实验

实验一插值方法一. 实验目的（1）熟悉数值插值方法的基本思想，解决某些实际插值问题，加深对数值插值方法的理解。

（2）熟悉Matlab 编程环境，利用Matlab 实现具体的插值算法，并进行可视化显示。

二. 实验要求用Matlab 软件实现Lagrange 插值、分段线性插值、三次Hermite 插值、Aitken 逐步插值算法，并用实例在计算机上计算和作图。

三. 实验内容1. 实验题目（1）已知概率积分dxe y xx ⎰-=22π的数据表构造适合该数据表的一次、二次和三次Lagrange 插值公式，输出公式及其图形，并计算x =0.472时的积分值。

答：①一次插值公式：输入下面内容就可以得到一次插值结果 >> X=[0.47,0.48];Y=[0.4937452,0.5027498]; >> x=0.472;>> (x-X(2))/(X(1)-X(2))*Y(1)+(x-X(1))/(X(2)-X(1))*Y(2)ans =0.495546120000000>>②两次插值公式为：输入下面内容就可以得到两次插值结果>> X=[0.46,0.47,0.48];Y=[0.4846555,0.4937452,0.5027498]; >> x=0.472;>>(x-X(2))*(x-X(3))/((X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(1))*(x-X(3))/((X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(2))*(x-X(1))/((X(3)-X(2))*(X(3)-X(1)))*Y(3)i 0123x 0.46 047 0.48 0.49 y0.4846555 0.4937452 0.5027498 0.5116683ans =0.495552928000000>>③三次插值公式为：输入下面内容就可以得到三次插值结果>> X=[0.46,0.47,0.48,0.49];Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x=0.472;>>(x-X(2))*(x-X(3))*(x-X(4))/((X(1)-X(4))*(X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(4))*( x-X(1))*(x-X(3))/((X(2)-X(4))*(X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(4))*(x-X(2))*( x-X(1))/((X(3)-X(4))*(X(3)-X(2))*(X(3)-X(1)))*Y(3)+(x-X(3))*(x-X(2))*(x-X(1))/(( X(4)-X(1))*(X(4)-X(2))*(X(4)-X(3)))*Y(4)ans =0.495552960000000输入下面内容，绘出三点插值的图：>> X=[0.46,0.47,0.48,0.49];Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x=linspace(0.46,0.49);>>y=(x-X(2)).*(x-X(3)).*(x-X(4))/((X(1)-X(4))*(X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(4) ).*(x-X(1)).*(x-X(3))/((X(2)-X(4))*(X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(4)).*(x-X(2) ).*(x-X(1))/((X(3)-X(4))*(X(3)-X(2))*(X(3)-X(1)))*Y(3)+(x-X(3)).*(x-X(2)).*(x-X(1) )/((X(4)-X(1))*(X(4)-X(2))*(X(4)-X(3)))*Y(4);>>plot(x,y)（注意上面的“.*”不能用“*”替代）；（2）将区间[-5,5]分为10等份，求作211)(x x f +=的分段线性插值函数，输出函数表达式及其图形，并计算x =3.3152时的函数值。

实验十一蔗糖转化速率常数的测定

如能在一定的时间间隔t 内测得一系列数据，因为t 为定值，所以 ln(c - c ¢) 对 t 作图，即可由直线的斜率求出 k 值。这个方法的困难是必须使t 为一定值，而这通常不易直接求得，需要从 c ~ t 图上求得，因而又多一步计算手续。
六、旋光仪的使用
1．旋光仪的构造及原理光是电磁波，自然光在传播方向垂直的各个方向上都有振动，称为普通光。当光在某个方向的振动占优势时，这种光称为偏振光。某些有机化合物和晶体，因为他们的分子结构和晶体结构的特殊性，当有偏振光通过时，可使偏振光的振动平面向左或向右偏转一定角度。这种使偏振光的振动面发生偏转的化合物称为旋光物质或光学活性物质，这是因为分子内部有手性中心或晶体的各向异性造成的。旋光物质所具有的这种使偏振面偏转的能力称为旋光性。一定温度下，偏转的角度和方向与所测物质的本性、溶液的浓度、液层的厚度及偏振光的波长等因素有关。利用旋光性，可对旋光物质进行定性和
1
2
3
4
5
6
图 11-2 旋光仪的光学系统 1.光源 2.起偏棱镜 3.石英片 4.样品管 5. 检偏镜 6.目镜 Figure11-2 Oource 2. polarizer 3. quartz piece 4.sample compartment 5.analyzer 6.detector
四、实验内容
1．将恒温槽与旋光管保温套相接，将超级恒温水浴的温度调节为 25℃，开通超级恒温水浴的循环水。用受皿天平称取约 10 g 蔗糖于碘量瓶内，并加蒸馏水 50 mL 使蔗糖完全溶解。若溶液浑浊，则需过滤。用移液管移取蔗糖溶液 25.00 mL 放入一个清洁干燥的碘量瓶中，在另一个清洁干燥的碘量瓶内移入 25.00 mL 0.5 mol/L 的 HCl 溶液。将这两只碘量瓶一起放入恒温槽中恒温 5 min ~10 min。 2．将恒温槽中 25mL HCl 溶液迅速倾入 25mL 蔗糖溶液中，立即按下秒表，作为反应起点 t0。再将溶液倒回盛 HCl 溶液的碘量瓶中，如此反复三次，摇匀。迅速取少许混合溶液荡洗旋光管 3 ~ 4 次，然后将此混合溶液装入旋光管，盛满，盖好管盖（勿使管内有气泡），擦净，立刻放进旋光仪内。测量各时间 t 时溶液的旋光度 t，测定时要迅速、准确。剩余混合反应液连同碘量瓶一起放入 65℃ 左右的高温水浴内加速反应至水解完全。 3．测量时间间隔大致如下：从 t0 开始每隔 5、5、10、10、20、20、30 min 各测一次。 4．t 测定完毕后，取出高温水浴内的反应液冷却至实验温度，装入旋光管，测其旋光度的值。 6．实验结束后，必须洗净旋光管和碘量瓶，并将碘量瓶放入烘箱烘干。

实验11 SGPT测定 2010

各管摇匀，37℃水浴箱预热10分钟各管摇匀，37℃水浴箱预热10分钟各管摇匀， ℃水浴箱加热20分钟各管摇匀，37℃水浴箱加热分钟充分摇匀，分钟内，充分摇匀，在10分钟内，520nm处比色分钟内处比色 0.0 0 0.1 100 0.2 200 0.3 300 0.4 400 0.5 500
【实验方法】实验方法】
（一）制作标准曲线
（A）方法一
管号试剂 0.1M磷酸盐缓冲液（ml）磷酸盐缓冲液（）磷酸盐缓冲液 SGPT底物溶液（ml）底物溶液（）底物溶液 2µmol/ml丙酮酸标准液（ml）丙酮酸标准（）丙酮酸标准液 2, 4－二硝基苯肼溶液－ 0.4M NaOH (ml) 相当于丙酮酸含量（相当于丙酮酸含量（µmol））相当于酶活力单位/100ml血清血清相当于酶活力单位 A520 A测定管—A空白管 0.10 0.50 0.00 0.5 5.0 0.10 0.45 0.05 0.5 5.0 0.10 0.40 0.10 0.5 5.0 0.10 0.35 0.15 0.5 5.0 0.10 0.30 0.20 0.5 5.0 0.10 0.25 0.25 0.5 5.0 0 1 2 3 4 5
【思考题】思考题】
1. 什么叫转氨基作用? 在蛋白质代谢中有何重要作什么叫转氨基作用用? 2. 为什么制作标准曲线时,需要加入一定量SGPT底为什么制作标准曲线时,需要加入一定量SGPT底需要加入一定量物溶液? 物溶液 3. 为什么测定酶活力时需要有对照为什么测定酶活力时需要有对照? 4. 两种标准曲线测定方法在设计上有什么优缺点? 两种标准曲线测定方法在设计上有什么优缺点哪一种更为合理?为什么哪一种更为合理为什么? 为什么

FTM11-残余粘着率试验计算方法

FTM11 残余粘着率试验计算方法
残余粘着率强度通常由百分比表示，是将测试样品的剥离力比上控制带的剥离力，再取平均值。

若两个比值不相近，可能的话，需要尽快安排重复实验。

若无法重新实验，需将两个比值同时记录在报告中。

残余粘着率％＝测试胶带的剥离力/控制带的剥离力X100
若测试结果超过100%，简单的将结果记录为≥100%覆盖性较差的涂硅和一些渗透性的基材也会对数值有一定的影响，那样的话，结果之间的比较应该限制在相同的基材之间（思泰仪器）。

实验11 粘度法测定高聚物的摩尔质量

实验十三粘度法测定高聚物的摩尔质量【目的要求】1．了解粘度法测定高聚物摩尔质量的基本原理和方法；2．掌握用乌氏(Ubbelohde)粘度计测定高聚物溶液粘度的原理和方法；3．测定右旋糖苷的摩尔质量。

【实验原理】高聚物是由单体分子经加聚或缩聚过程得到的。

在高聚物中，由于聚合度的不同，每个高聚物分子的大小并非都相同，致使高聚物的分子质量大小不一，参差不齐，且没有一个确定的值。

因此，高聚物的摩尔质量是一个统计平均值。

高聚物摩尔质量不仅反映了高聚物分子的大小，而且直接关系到它的物理性能，是一个重要的基本参数。

测定高聚物摩尔质量的方法很多，例如渗透压、光散射及超离心沉降平衡等方法。

但是不同方法所得平均摩尔质量也有所不同，比较起来，粘度法设备简单，操作方便，并有很好的实验精度，是常用的方法之一。

用此法求得的摩尔质量称为粘均摩尔质量。

粘度是液体流动时内摩擦力大小的反映。

高聚物溶液的特点是粘度特别大，原因在于其分子链长度远大于溶剂分子，加上溶剂化作用，使其在流动时受到较大的内摩擦力，粘性液体在流动过程中所受阻力的大小可用粘度系数（简称粘度）来表示。

纯溶剂粘度反映了溶剂分子间的内摩擦力，高聚物溶液的粘度则是高聚物分子间的内摩擦力、高聚物分子与溶剂分子间的内摩擦力及溶剂分子间内摩擦力三者之和。

在相同温度下，通常高聚物溶液的粘度大于纯溶剂粘度，即：﹥。

为了比较这两种粘度，引入增比粘度的概念，以表示（13.1）式中，称为相对粘度，定义为溶液粘度与纯溶剂粘度的比值，即（13.2）反映的也是粘度行为，而则表示已扣除了溶剂分子间的内摩擦效应。

高聚物的增比粘度往往随质量浓度的增加而增加。

为了便于比较，将单位浓度所显示的增比粘度称为比浓粘度，而称为比浓对数粘度。

当溶液无限稀释时，高聚物分子彼此相隔甚远，它们之间的相互作用可以忽略，此时有关系式图II-13-1 和图1 ；212（13.3）式中，称为特性粘度，它反映的是高分子与溶剂分子之间的内摩擦，其数值取决于溶剂的性质以及高聚物分子的大小和形态。

实验十一配位化合物的组成和稳定常数的测定

实验十一
配位化合物的组成和稳定常数的测定
随着科学技术的发展，配合物在科学研究和生产实践中显示出越来越重要的意义，配合物不仅在化学领域里得到广泛的应用，并且对生命现象也具有重要的意义。人体内各种酶（生物催化剂）的分子几乎都含有以配合状态存在的金属元素。配位化学与有机、分析等化学领域以及生物化学、药物化学、化学工业都有着密切的关系，应用非常广泛。配位化学的研究有一整套的物理实验方法，如测定稳定常数可以采用 pH 法、电位法、极谱法、分光光度法、溶剂萃取法、离子交换法等，这些方法对于配合物的组成、结构和构象的研究是十分有效的。我国化学家陈荣悌还报道了利用高效液相色谱法来测定配位化合物稳定常数的新方法。从上世纪 40 年代起，人们开始涉足于生物配合物的研究，陆续报道了各种生命金属与各种 α-氨基酸、生物配体、羧肽酶和碳酸酐酶配合物的稳定常数。从这些研究中得到了许多有关生物配体的新信息。到了 60 年代，配合物的研究方法又有了新的发展。一方面出现了全新的物理方法，如 M?ssbauer(穆斯堡尔)谱；另一方面对原有的方法作了改进，研究范围进一步扩大，如 Raman(拉曼)光谱采用了激光源，提高了光谱强度，使有色配合物的研究成为可能；核磁共振谱因位移试剂的应用，提高了分辨率。这些方法被应用于生物体内酶的结构和催化反应的研究以及化学模拟的研究。
3．测定吸光度在 500nm 波长下分别测定上述溶液的吸光度，将所得数据记录于表 11-1。以吸光度对磺基水杨酸的摩尔分数作图。从所得的等摩尔系列图中找出最大吸收处的的配位体摩尔分数（XL）和金属离子摩尔分数（1-XL），由公式（1）计算得配合物的组成；由公式（2）计算得配合物的解离度；据公式（3）计算得配合物的表观稳定常数。
' K稳

实验11多孔材料的制备及气体吸附性能测试

实验11 多孔材料的制备及气体吸附性能测试实验目的1.了解掌握多孔聚合物材料的实验制备方法。

2.理解气体分子单层或多层物理吸附理论及BET公式，掌握BET法测定多孔材料比表面积的原理和方法。

3.理解掌握多孔材料的气体吸附性能的评价方法。

实验原理根据孔半径的大小，固体表面的细孔可以分成三类：微孔，孔径小于2nm，活性炭、沸石、分子筛会有此类孔；中孔，孔径2~50nm，多数超细粉体属这一范围；大孔，孔径大于50nm，Fe3O4、硅藻土等含此类孔。

多孔材料的制备和比表面积，孔隙分布测试已逐步引起人们的普遍重视。

各种多孔材料已经广泛应用于药品、陶瓷、活性炭、碳黑、油漆和涂料、医学植入体、推进燃料、航天隔绝材料、燃料电池、储氢，储甲烷材料以及CO2、SO2等温室气体或有害气体的捕捉和分离的研究。

气体与清洁固体表面接触时，在固体表面上气体浓度高于气相，这种现象称为吸附。

吸附气体的固体称为吸附剂；被吸附的气体称为吸附质。

测定吸附量的一般原则是在一定的温度下将一定量的吸附剂至于吸附质气体中，达到吸附平衡后根据吸附前后气体体积和压力的变化或直接称量的结果计算吸附量。

根据吸附剂表面与吸附质分子间作用力的性质不同，吸附可以分为物理吸附和化学吸附。

物理吸附是指被吸附分子与固体表面分子间的作用力为分子间吸引力，即范德华力，是一种可逆吸附过程。

物理吸附的特征是固体表面和吸附质分子不发生任何化学反应，吸附过程进行的较快。

工业上常利用物理吸附的可逆性，通过改变操作条件，使吸附的物质脱附，使吸附剂再生，从而达到分离的目的。

此外，物理吸附也用于测定固体材料的比表面积、孔容和孔径分布。

图1. 多孔材料的气体吸附示意图一种优良吸附剂通常具有大的比表面积。

因为对于特定的吸附剂与吸附质来说，吸附量随比表面积（单位质量的物质具有的所有表面积）的增大而增大。

所以吸附剂多是多孔或者分散的很细的物质。

基本设想是测出在吸附剂表面上某种吸附质分子铺满一层所需的分子数（如图1），再乘以该吸附质每个分子所占的面积，即为该材料的比表面积。

数模实验报告—实验11

数模实验报告—实验11一、实验目的本次数模实验11 的主要目的是通过建立数学模型来解决实际问题，培养我们运用数学知识和方法分析、解决复杂问题的能力，并提高我们的逻辑思维和创新能力。

二、实验内容本次实验围绕一个具体的实际问题展开，即研究某城市的交通流量分布情况。

我们需要收集相关数据，如道路网络结构、不同时间段的车流量、路口的通行能力等，并运用数学建模的方法对这些数据进行分析和处理。

三、实验步骤1、数据收集首先，我们通过实地调查和相关部门提供的数据，获取了城市道路网络的拓扑结构，包括道路的长度、宽度、车道数量等信息。

同时，还收集了不同时间段（如早高峰、晚高峰、平峰期）各个路口的车流量数据，以及路口的信号灯设置和通行能力等数据。

2、模型选择在对数据进行初步分析后，我们决定采用宏观交通流模型中的流体动力学模型来描述交通流量的变化。

该模型将交通流类比为流体，通过建立连续性方程和动量方程来描述车辆的流动情况。

3、模型建立根据所选的模型，我们定义了相关的变量和参数，如交通流量、密度、速度等，并建立了相应的数学表达式。

同时，考虑到实际情况中的各种因素，如道路拥堵、交通事故等，对模型进行了适当的修正和完善。

4、模型求解利用数值计算方法，如有限差分法或有限元法，对建立的数学模型进行求解。

通过编程实现计算过程，并对不同参数条件下的结果进行分析和比较。

5、结果分析对求解得到的结果进行分析，绘制出交通流量随时间和空间的变化曲线，以及密度分布等图像。

通过分析这些结果，评估模型的准确性和可靠性，并找出交通拥堵的关键路段和时间段。

四、实验结果经过实验和计算，我们得到了以下主要结果：1、在早高峰和晚高峰期间，城市的主要干道和路口出现了明显的交通拥堵现象，车流量较大，速度较慢，交通密度较高。

2、一些次干道和支路的交通流量相对较小，但在与主干道的连接处容易出现交通瓶颈，影响整个交通网络的通行效率。

3、通过对不同信号灯设置方案的模拟分析，发现优化信号灯的配时可以在一定程度上缓解交通拥堵，但效果有限。

实验力学盖秉政第11章平面光弹应力计算

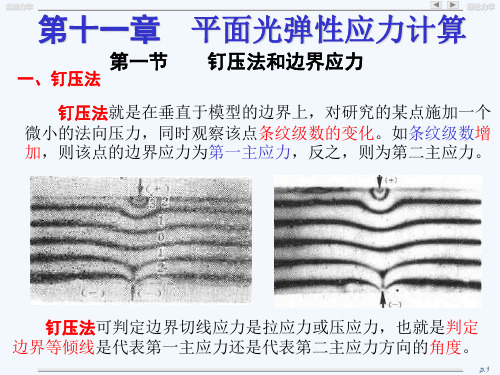
xy,i
A
x,i
xy,j-1
y,j-1 单元体应力状态
至于切应力的指向 (代表正、负符号)以观察主应力的方位确定。如图所示。由切应力作用面的法线N开始，按首先与第一主应力相遇的原则转向，则切应力的指问应与此转向相遇。这个指向着与取平衡条件时单元体A上切应力指向一致时、则为正；反之，为负。切应力正负指向如图所示。
实验力学
第十一章
第一节
一、钉压法
理论力学
平面光弹性应力计算
钉压法和边界应力
钉压法就是在垂直于模型的边界上，对研究的某点施加一个
微小的法向压力，同时观察该点条纹级数的变化。如条纹级数增加，则该点的边界应力为第一主应力，反之，则为第二主应力。
钉压法可判定边界切线应力是拉应力或压应力，也就是判定边界等倾线是代表第一主应力还是代表第二主应力方向的角度。
x、
y、
xy沿直线的分
9、校核
F内＝h
F
0 y dx h
p.17
实验力学
理论力学
第三节
光弹性材料条纹值
利用对径受压的圆盘来求材料条纹值的方法：取一块和模
型同样的材料，制成一圆盘。圆盘直径为D，厚度为h，载荷为 F。由弹性力学知，在圆盘中心处应力为：
1
2F
Dh
6F 2 Dh
1
2
8F
Dh
根据式（9－3）
-0.6639 0.6157 -0.552
-0.6639 0.7501 -0.797
-0.4690 0.8829 -0.801
-0.2249 0.9703 -0.524
0
1
0
xy
-0.049 -0.083 -0.256 -0.416 -0.219

实验十一罗拉法棉纤维长度测试

实验十一罗拉法棉纤维长度测试一、实验目的与要求学习用罗拉式长度分析仪测定棉纤维的长度，了解罗拉式长度分析仪的结构，熟悉罗拉式长度分析的试验方法，掌握棉纤维长度各指标的计算方法。

二、实验仪器与用具Y111型罗半式长度分析仪，两台扭力天平(称重为50mg,分度值为0.05mg),黑绒析,限制器绒板,一号、二号夹子，垫木，压板，梳子，镊子，小钢尺。

三、试样已制作好的试验棉条。

四、实验方法与程序Y111型罗拉式纤维长度分析仪结构如图11—1所示。

1.从试验棉条中取出试验试样，把它整理成小棉束，在50mg扭力天平上称重，细绒棉称30±1mg, 长绒棉称35±1mg。

当重量一旦称定后，在整个试验中必须注意，不得丢弃任何一根纤维。

2.用手扯法先将纤维整理成一端平齐、伸直的小棉束。

3.用手捏住纤维整齐一端，一号夹子搁在限制器绒板的前挡片上,并使夹口紧抵两个前挡片,夹取棉束中伸出的最长纤维(从长至短),分层平铺在限制器绒板上, 铺成宽32mm,且厚薄均匀,露出挡片一端整齐,一号夹子夹住纤维不超过1mm。

如此反复3次，制成一端整齐、平直光滑、层次清晰的棉层。

在整理过程中，不允许丢弃任何一根纤维。

图11—1 Y111型罗拉式纤维长度分析仪1—盖子2—弹簧3—压板4—撑脚5—目罗拉6—偏心杠杆7—下罗拉8—蜗轮9—蜗杆10—手柄11—溜板12—偏心盘4.揭开罗拉式长度分析器的盖子，摇转手柄，使蜗轮上的第9刻度与指针重合。

5.翻下限制器绒板上的前挡片，用一号夹子从绒板上将棉层夹起，移置仪器中。

移置时，一号夹子的挡片紧靠溜板，用水平垫木垫住一号夹子，使棉层处于水平状态。

放下盖子，松去夹子，用弹簧加压7000g握住纤维。

6.扳倒溜板，转动手柄一周，使蜗轮上刻度10与指针重合，此时罗拉将纤维送出1mm（罗拉半径为9.5mm）.这时，凡10.5mm及以下的纤维都没有被夹持住，用二号夹子分三次夹取这些未被握持的纤维，置于黑绒板上，搓成小环，这是最短一组纤维［二号夹子的弹簧压力应为1.96N(200gf) ］。

实验11 流量计标定实验

四、操作步骤
1.熟悉：按事先（实验预习时）分工，熟悉流程，搞清各仪表设备的作用。 2.检查：水箱内罐满清水，检查泵调节阀是否关闭。 3.开车：启动离心泵（检查三相电及泵是否正常转动）。开启仪表电源。 4.排气：缓缓打开调节阀V1到较大值，打开两个差压传感器上的平衡阀，排除管路内气体。当看到引压管路无气泡，可关闭差压传感器上的平衡阀，再关闭管路调节阀V1。
二、基本原理
1.流体在管内Re的测定
Re d u 1/ 4d du 4q 1/ 4d d
式中：ρ、μ— 流体在测量温度下的密度和粘度 [kg/m3]、[Pa·S] d—管内径 d=50mm；q—管内体积流量 [m3/S]
2.孔板流量计
孔板流量计是利用动能和静压能相互转换的原理设计的，它是以消耗大量机械能为代价的。孔板的开孔越小、通过孔口的平均流速u0越大，孔前后的压差 ΔP也越大，阻力损失也随之增大。其具体工作原理及结构图如图1。
七、问题与思考
1.孔板流量计和文丘里流量计的操作原理和特性是什么？流量计的一般标定方法有哪些？ 2.孔板流量计的流量系数C0和文丘里流量计的流量系数Cv与管内Re的关系怎样？ 3.通过C0和Cv与管内Re的关系，比较两种流量计在不同流量下的使用范围？
பைடு நூலகம்
q—流量[m3 / s] C0 —孔流系数（需由实验标定） A0 —孔截面积[m2 ]，孔径d0 31.62[mm]，A0 7.8527*10-4[m2 ] p—压差[Pa] —管内流体密度[kg / m3]
孔板流量计在使用前，必须知道其孔流系数C0（一般由厂家给出，教课书中只是原理性质，只作参考），一般是由实验标定得到的。C0 的大小主要与管道内流体的Re及管道与孔板小孔的截面积比m=A0/A 有关，其中取压方式、孔口形状、加工光洁度、孔板厚度、安装等也

实验11-聚合物熔体流动速率及流动活化能的测定

实验11-聚合物熔体流动速率及流动活化能的测定实验十一聚合物熔体流动速率及流动活化能的测定在塑料加工中，熔体流动速率是用来衡量塑料熔体流动性的一个重要指标。

通过测定塑料的流动速率，可以研究聚合物的结构因素。

此法简单易行，对材料的选择和成型工艺条件的确定有其重要的实用价值，工业生产中采用十分广泛。

但该方法也有局限性，不同品种的高聚物之间不能用其熔融指数值比较其测定结果，不能直接用于实际加工过程中的高切变速率下的计算，只能作为参考数据。

此种仪器测得的流动性能指标，是在低剪切速率下测得的，不存在广泛的应力应变速率关系，因而不能用来研究塑料熔体粘度和温度，粘度与剪切速率的依赖关系，仅能比较相同结构聚合物分子量或熔体粘度的相对数值。

一、实验目的：1．了解热塑性塑料在粘流态时粘性流动的规律。

2．熔体速率仪的使用方法。

二、实验原理：所谓熔体流动速率（MFR）是指热塑性塑料熔体在一定的温、压力下，在10分钟内通过标准毛细管的质量，单位：g/10min。

对于同种高聚物，可用熔体流动速率来比较其分子量的大小，并可作为生产指标。

一般来讲，同一类的高聚物（化学结构相同）若熔体流动速率变小，则其分子量增大，机械强度较高；但其流动性变差，加工性能低；熔体流动速率变大，则分子量减小，强度有所下降，但流动性变好。

研究流动曲线的特性表明，在很低的剪切速率下，聚合物熔体的流动行为是服从牛顿定律的，其粘度不依赖于剪切速率，通常把这种粘度称为最大牛顿粘度或0剪切粘度η0，它是利用η＝f （S ）关系，从很小的剪切应力（S ）外推到零求得的。

根据布契理论，线形聚合物的零剪切粘度与大于临界分子量的重均分子量(w M )的关系式为 3.40w KM η=，式中K 是依赖于聚合物类型及测定温度的常数。

许多研究表明，对于分子量分布较窄或分级的高密度聚乙烯，是遵守3.4次方规则的。

但在分子量分布宽时，M 的指数有所增大。

如果使指数保持为 3.4，则需用某种平均分子量（tM ）代替重均分子量，其关系式为：3.40t KM η= ---------------------------------------- （l ）式中，w t Z M<M <M 。

实验11-种群密度的调查方法-张丽霞版

5. 经过一段时间后，重复步骤2进行重捕，计数重捕虫数及其中标志个体数。 6. 计算种群总数和种群总数95%的置信区间。
（二）模拟实验
1. 将木盒内100个小方格编号：00~99。
2. 取适量黑豆，随机散布在木盒内。
3. 利用随机数字表，确定抽取样方号（大约10~20 个）。 4. 计数并移去已确定抽取样方中的个体，加入等数量的黄豆，做好记录。 5. 将黄豆和黑豆混合，重复步骤2~4。
扎龙自然保护区
假设全部丹顶鹤为10000 只，捕捉1000只进行标记，重新放回。一段时间后，再捕捉1000只，带标记的丹顶鹤理论上是多少只？
答案：100只
二、实验原理
对被调查种群，捕获一部分个体，进行标记后，放回原来环境，经一段时间后进行重捕，根据重捕中标志个体占总捕获数的比例，来估计该种群的数量。
6. 计算种群总数和种群总数95%的置信区间。
五、实验报告
1. 掌握标志重捕法的原理，根据实验步骤进行实验。
2. 根据实验结果，计算模拟种群的数量估计值及95%置信区间。
标志重捕法知识补充：
1. 林可指数法（Lincoln index method）：一次标志一次重捕法。 2. 施夸贝尔法（Schnabel method）：多次标志一次重捕法。 3. 乔利-西贝尔法（Jolly-Seber method）：多次标志多次重捕法。若一次标志重捕可获得足够的个体数，则采用林可指数法；若一次标志重捕不能获得足够的个体数，利用林可指数法，种群数量的估计值往往不够准确，则可采用施夸贝尔法或乔利-西贝尔法。
2. 实验生物：
黄豆（或黑豆、花生等）
四、实验步骤
（一）室内实验
1. 将2000g面粉放在玻璃容器中，加入约500头赤拟谷盗培养一段时间，使其在面粉中分布均匀；

实验11植物组织中丙二醛含量的测定

六、思考题
1.说明膜脂过氧化丙二醛含量有什么变化，分析其原因。
五、结果计算

以测得的OD532减去OD600的非特异吸收值，分别计算衰老和正常组的值。 MDA浓度(μmol/L)=6.45(D532-D600)-0.56D450 MDA含量(μmol/g FW)＝
MDA 浓度（ mol / μ L ）提取液体积 ml ）植物组织鲜重（ g ）
D450、D532、D600分别代表450nm、532nm和600nm波长下的光密度值。
＞10%三氯乙酸（TCA）
0.6%硫代巴比妥酸（先加少量1mol/L氢氧化钠溶解，再用10%三氯乙酸定容）
＞＞石英砂
四、实验步骤
1 MDA的提取：称1g叶片，加入2ml 10% TCA及少量石英砂，研磨至匀浆，再加8ml 10%TCA进一步研磨，定容至10ml,匀浆以4000r/min 离心10min，其上清液即为MDA提取液。 2 MDA的测定:取2ml MDA提取液（对照加2ml蒸馏水），加2ml 0.6％TBA,混和液在沸水浴中保温15min后，立即置于冰浴中冷却，然后离心10min，于波长 532nm、450nm和600nm下测定OD值。
注意事项

MDA-TBA显色反应的加热时间，最好控制沸水浴10-15min 之间。时间太短或太长均会引起532nm下的光吸收值下降；如待测液浑浊，可适当增加离心力及时间，最好使用低温离心机离心。可溶性糖与TBA显色反应的产物在532 nm也有吸收（最大吸收在450 nm），当植物处于干旱、高温、低温等逆境时可溶性糖含量会增高，必要时要排除可溶性糖的干扰。
?可溶性糖与tba显色反应的产物在532nm也有吸收最大吸收在450nm当植物处于干旱高温低温等逆境时可溶性糖含量会增高必要时要排除可溶性糖的干扰