东北大学2013-2014 第一学期 大学物理(下)作业
2013-2014第一学期期末大学物理试卷A

2013/2014学年第一学期期末考试试卷(A卷)科目:《大学物理》考试班级:燃气121-2,热能121,勘查121-2、信工121、信科121、电气121-2、智能121-2、自动化121、建环121-2、给排水121-2、环科121、测绘121-2、软件121、计算机121、网络121、地信121、机械121 考试方式: 闭卷命题人签字:教研室主任签字:教学院长签字:()cos sin r t a ti b tj ω=+,求质点从沿一直线运动,则它对该直线上任一点的角动量为、一质点同时参与三个简谐振动,它们的振动方程分别为:的质点,沿x 轴作直线运动,受到的作用力为00v =。
求质点在任意时刻的速度和位置。
四、一根放在水平光滑桌面上的匀质棒,可绕通过其一端的竖直固定光滑 = 1.5 kg ,长度为一水平运动的子弹垂直地射入棒的另一端,并留在棒中,如图所示.子弹(1) 棒开始和子弹一起转动时角速度ω有多大?(2) 若棒转动时受到大小为M r = 4.0 N·m 的恒定阻力矩作用,棒能转过多大的角度。
五、五题图中(a )表示t=0时刻的波形图,(b )表示原点(x =0)处质元的振动曲线,试求:(1)原点处质元的初位相,振动方程(2)该波的波动方程。
六、0.32kg 的氧气作图中所示循环ABCDA ,设212V V =,1300T K =,2200T K =. 求循环过程中(1)内能的改变E ∆,(2)所做的净功A ,(3)吸收的热量1Q 。
(4)循环效率η(已知氧气的定体摩尔热容的实验值11,21.1V m C J mol k --=⋅⋅)七、两均匀带电无限长直共轴圆筒,内筒半径为a ,沿轴线单位长度电量为λ+,外筒半径为b ,沿轴线单位长度电量为λ-,外筒接地,试求:(1)离轴线为r 处的电势;(2)两筒的电势差八、如题图所示,长直电流1I 附近有一等腰直角三角形线框,通以电流2I ,两者共面。
东北大学的大学的物理附加地的题目标准详解第4,14,5章作业标准详解.doc

实用标准文案第 4章刚体的转动作业一、教材:选择填空题 1~4;计算题: 13, 27,31二、附加题(一)、选择题1、有两个半径相同,质量相等的细圆环 A 和 B . A 环的质量分布均匀, B 环的质量分布不均匀.它们对通过环心并与环面垂直的轴的转动惯量分别为J A和J B,则J A和J B的关系为[C]A、J A J BB、J A J BC、J A J BD、无法确定2、假设卫星环绕地球中心作圆周运动,则在运动过程中,卫星对地球中心的[ A ]A、角动量守恒,动能也守恒; B 、角动量守恒,动能不守恒C、角动量不守恒,动能守恒; D 、角动量不守恒,动量也不守恒E、角动量守恒,动量也守恒3、花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为 J0,角速度为0 .然后她将两臂收回,使转动惯量减少为 1 J 0 .此时她转动的角速度变为[ D ]3A、1B 、1C、3 0 D、3 03 0 3 04、如图所示,一静止的均匀细棒,长为L 、质量为 M ,可绕通过棒的端点且垂直于棒长的光滑固定轴 O 在水平面内转动,转动惯量为 1 ML2.一质量为 m 、速率为3 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为1v, O2 俯视图则此时棒的角速度为[ B ]A、mvB 、 3mv C、5mv D、7mvML 2ML 3ML 4ML(二)、计算题1、质量分别为 m和 2m,半径分别为 r 和 2r 的两个均质圆盘,同轴地粘在一起,可绕通过盘心且垂直于盘面的水平1v 2v实用标准文案光滑轴转动,在大小盘边缘都绕有细绳,绳下端都挂一质量为 m 的重物,盘绳无相对滑动,如图所示,求: 1) 圆盘对水平光滑轴的转动惯量;2) 圆盘的角加速度。
解:( 1) J 1 mr 2 1 2m 2r 29mr22 22(2)T 2 mg ma 2mg T 1 ma 1T 2 2r T 2 r Ja 1 a 2 2g2rr19r2、一根长为 l ,质量为 M 的均质细杆,其一端挂在一个光滑的水平轴上,静止在竖直位置。
13年秋大物期末考题及答案

哈工大2013 年秋季学期大学物理Ⅱ期末试题第1页(共12页)一、填空(共40分)1. (本题3分)在容积为10-2m3的容器中,装有质量200 g 的气体,若气体分子的方均根速率为200 m•s-1,则气体的压强为________________.2.(本题3分)理想气体分子的平均平动动能与热力学温度T的关系式是____________,此式所揭示的气体温度的统计意义是____________________________________________________________.3.(本题4分)氮气在标准状态下的分子平均碰撞频率为5.42×108 s-1,分子平均自由程为6×10-6 cm,若温度不变,气压降为0.2 atm ,则分子的平均碰撞频率变为_______________;平均自由程变为_______________.4.(本题3分)如图所示,一平面简谐波沿Ox轴负方向传播,波长为λ,若P处质点的振动方程是)212cos(π+π=tAyPν,则该波的表达式是_______________________________;P处质点____________________________时刻的振动状态与O处质点t1时刻的振动状态相同.第2页(共12页)5.(本题4分)要使一热力学系统的内能增加,可以通过______________或______________两种方式,或者两种方式兼用来完成.热力学系统的状态发生变化时,其内能的改变量只决定_________________,而与_______________________无关.6.(本题4分)用方解石晶体(负晶体)切成一个截面为正三角形的棱镜,光轴方向如图.若自然光以入射角i 入射并产生双折射.试定性地分别画出o 光和e 光的光路及振动方向.7.(本题4分)氢原子的运动速率等于它在300 K 时的方均根速率时,它的德布罗意波长是 ____________.质量为m =1 g ,以速度=v 1 cm ·s -1运动的小球的德布罗意波长 是______________. (普朗克常量为h =6.63×10-34 J ·s ,玻尔兹曼常量k =1.38×10-23 J ·K -1,氢原子质量m H =1.67×10-27 kg)8.(本题3分)如果电子被限制在边界x 与x +∆x 之间,∆x =0.5 Å,则电子动量x 分量的不 确定量近似地为________________kg ·m /s . (不确定关系式∆x ·∆p ≥h ,普朗克常量h =6.63×10-34 J ·s)9.(本题3分)粒子在一维无限深方势阱中运动(势阱宽度为a ),其波函数为 axa x π=3s i n 2)(ψ ( 0 < x < a ), 粒子出现的概率最大的各个位置是x = ___________________。
东北大学物理期末复习资料

东北大学物理期末复习资料第9章振动作业一、教材:选择1~5道填空题;计算题:13、14、18二。
其他问题(一)、选择题一.沿x轴进行简谐振动的弹簧振子的振幅为A,周期为T。
振动方程用余弦函数表示,4如果该振子的初相为?,则t=0时,质点的位置在:3(a)比x?(c)超过x??11a,向负方向移动;(b)超过x?A、朝着积极的方向前进;2211a,向负方向移动;(d)超过x??A、朝着积极的方向前进。
222.对物体进行简谐振动,振动方程为:x=ACOS(?T+?/4)在t=t/4(t为周期)时刻,物体的加速度为:(a) ??2a?22.(b)2a?22.(c)?3a?22.(d)3a?22(二)、计算题一.物体沿x轴的简谐运动,振幅A=0.12M,周期T=2S。
当t=0时,物体的位移x0=0.06m,并向前移动至x轴。
发现:(1)简谐运动的运动方程;(2)t=t/4时物体的位置、速度和加速度;2.物体沿x轴以简谐运动移动,振幅a=10.0cm,周期T=2.0S。
当t=0时,物体的位移x0=-5cm,并沿x轴的负方向移动。
发现:(1)简谐运动方程;(2)t=0.5s时,物体的位移;(3)物体第一次移动到x=5厘米是什么时候?(4)再经过多少时间物体第二次运动到x=5cm处?3.如果简谐振动方程为x?0.1cos[20?T?/4]m,找到:(1)振幅、频率、角频率、周期和初相;(2)t=2s时的位移、速度和加速度.题图44.简谐振动的振动曲线如图所示。
找出振动方程5、一物体沿x轴作简谐振动,振幅为0.06m,周期为2.0s,当t=0时位移为0.03m,且向轴正方向运动,求:(1) t=0.5s时物体的位移、速度和加速度;(2)物体从x?-0.03m处向x轴负方向运动开始,到达平衡位置,至少需要多少时间?一第10章波动作业一、教材:选择1~5道填空题;计算题:12,13,14,21,30。
其他问题(一)、选择题一.平面简谐波的波动方程为y=0.1cos(3?T-?X+?)(si)。
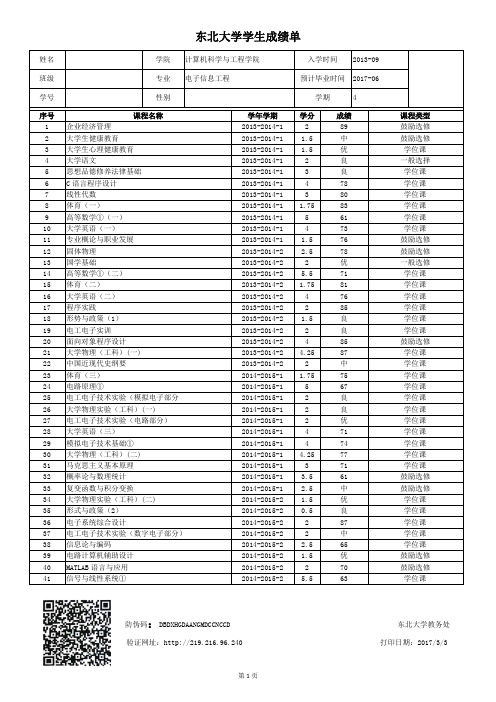
东北大学学生成绩单 成绩表模板
良
学位课
27
电工电子技术实验(电路部分)
2014-2015-1
2
优
学位课
28
大学英语(三)
2014-2015-1
4
71
学位课
29
模拟电子技术基础①
2014-2015-1
4
74
学位课
30
大学物理(工科)(二)
2014-2015-1
4.25
77
学位课
31
马克思主义基本原理
2014-2015-1
3
71
学位课
2013-2014-2
4.25
87
学位课
22
中国近现代史纲要
2013-2014-2
2
中
学位课
23
体育(三)
2014-2015-1
1.75
75
学位课
24
电路原理①
2014-2015-1
5
67
学位课
25
电工电子技术实验(模拟电子部分
2014-2015-1
2
良
学位课
26
大学物理实验(工科)(一)
2014-2015-1
61
学位课
10
大学英语(一)
2013-2014-1
4
73
学位课
11
专业概论与职业发展
2013-2014-1
1.5
76
鼓励选修
12
固体物理
2013-2014-2
2.5
78
鼓励选修
13
国学基础
2013-2014-2
2
优
一般选修
14
2013-2014大学物理A(下)答案

拟题学院(系): 数理学院适用专业: 2013级理工科各专业 2013-2014 学年 1 学期 大学物理A (下) 试题标准答案考试时间:2014-01-14 (答案要注明各个要点的评分标准)一、选择题(共36分、每小题3分)1. ( B )2. ( C )3. ( D )4. ( C )5. ( D )6. ( B )7. ( B )8. ( A )9. ( B) 10. ( A ) 11. ( C ) 12. ( B )二、填空题(共16分、每小题4分)13. 20(2ln31)I aμπ- [ 或 201.2I a μπ 或 200.38I a μ ] 4分; 14. 3 : 2 4分; 15.21arctg2n n π- 4分; 16. 9 : 5 4分.三、计算题 (本题12分)解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定律可得:)(220R r rRIB ≤π=μ 3分 因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r RIRd 2020⎰π=μπ=40I μ 2分在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为)(20R r rIB >π=μ 3分 因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r I R Rd 220⎰π=μ2ln 20π=Iμ 2分 穿过整个矩形平面的磁通量为21ΦΦΦ+=π=40I μ2ln 20π+Iμ 2分拟 题 人:书写标准答案人:IS 2R1 m四、计算题 (本题12分)解: 建立坐标(如图)则21B B B+=xI B π=201μ, )(202a x I B -π=μ 2分xIa x I B π--π=2)(200μμ, B 方向⊙ 2分0v 11d vd ()d 2I B x x x a xμε==-π- 3分202av 11d ()d 2a bI x x a x μεε+==-π-⎰⎰b a b a I ++π=2)(2ln20v μ 3分 感应电动势方向为C →D ,D 端电势较高. 2分五、计算题 (本题12分)解:设平面简谐波的波长为λ,坐标原点处质点振动初相为φ,则该列平面简谐波的表达式可写成 )/27cos(1.0φλ+π-π=x t y (SI) 1分 t = 1 s 时 0])/1.0(27cos[1.0=+π-π=φλy 1分此时a 质点向y 轴负方向运动,故 π=+π-π21)/1.0(27φλ ① 2分而此时,b 质点正通过y = 0.05 m 处向y 轴正方向运动,应有05.0])/2.0(27cos[1.0=+π-π=φλy 1分且 π-=+π-π31)/2.0(27φλ ② 2分由①、②两式联立得 λ = 0.24 m 1分 3/17π-=φ 2分∴ 该平面简谐波的表达式为 ]31712.07cos[1.0π-π-π=x t y (SI) 2分或 ]3112.07cos[1.0π+π-π=x t y (SI)六、计算题 (本题12分)解:(1) 除中央明纹外,由单缝衍射明纹公式可知()111113sin 2122a k ϕλλ=+= (取k 1=1 ) 1分 ()222213sin 2122a k ϕλλ=+= (取k 2=1 ) 1分由于衍射角极小,则 11sin tg ϕϕ≈ , 22sin tg ϕϕ≈ 1分且由几何关系 11tg /x f ϕ= , 22tg /x f ϕ= 1分则两个第一级明纹之间距为 213/2x x x f a λ∆=-=∆=0.27 cm 3分 (2) 由光栅衍射明纹公式 1111sin 1d k ϕλλ==,2222sin 1d k ϕλλ== 1分且有 sin tg /x f ϕϕ≈= 1分 所以 d f x x x /12λ∆=-=∆=1.8 cm 3分2a x +d x 2a +b I I C D v x Ox。
大学物理20132014(2)期末A卷

2013-2014学年第二学期《大学物理》期末试卷专业班级姓名学号开课系室基础物理系考试日期2014年6月15日9:00—11:00注意事项:1.请在试卷正面答题,反面及附页可作草稿纸;2.答题时请注意书写清楚,保持卷面整洁;3.本试卷共四道大题,满分100分;试卷本请勿撕开,否则作废;4. 本试卷正文共8页。
一、选择题(共6小题,每小题2分,共12分) 1.(本题2分)对于一个物体系来说,在下列条件中系统的机械能守恒的是 [ ] (A )合外力为零; (B )合外力不做功;(C )外力和非保守内力都不做功; (D )外力和保守内力都不做功。
2.(本题2分)麦克斯韦速率分布曲线如图所示,图中A 、B 两部分面积相等,则该图表示 [ ] (A) v 0为最概然速率。
(B) v 0为平均速率。
(C) v 0为方均根速率。
(D) 速率大于和小于v 0 的分子数各占一半。
3.(本题2分)如图所示,有两根无限长直载流导线平行放置,电流分别为I 1 和I 2 ,L 是空间一闭合曲线,I 1 在L 内,I 2 在L 外,P 是L 上的一点。
今将 I 2 向 I 1 移近但始终保持在L 外,则有:[ ](A) l B d ⋅⎰L 与BP 同时改变。
(B)l B d ⋅⎰L 与BP 都不改变。
(C) l B d ⋅⎰L不变,BP 改变。
(D)l B d ⋅⎰L改变,BP 不变。
4.(本题2分)若尺寸相同的铁环与铜环包围面积中穿过相同变化率的磁通量,则在两环中 [ ] (A) 感应电动势不同,感应电流相同。
(B) 感应电动势相同,感应电流也相同。
(C) 感应电动势不同,感应电流也不同。
(D) 感应电动势相同,感应电流不同。
5.(本题2分)用两种方法使某一弹簧振子做简谐振动:方法一,使其从平衡位置压缩△l ,由静止开始释放;方法二,使其从平衡位置压缩2△l ,由静止开始释放。
则两次振动的周期T 1,T 2和总能量E 1,E 2满足下面哪个关系? [ ](A) T 1=T 2,E 1=E 2。
东北大学大学物理附加题答案第4,14,5章作业答案-推荐下载

在水平面内转动。今有一质量为 1 m 、速率为 v 的子弹在水平面内沿棒的垂直方 2
向射向棒的中点,子弹穿出时速率减为 1 v ,当棒转动后,设棒上单位长度受到 2
的阻力正比于该点的速率(比例系数为 k)试求:(1)子弹穿出时,棒的角速
度0 为多少?(2)当棒以 转动时,受到的阻力矩 M f 为多大?(3)棒从
以速度v0从杆的中点穿过,穿出速度为v, 求:1)杆开始转动时的角速度;
2)杆的最大摆角。
解:(1)碰撞前后角动量守恒
mv0
l 2
3m v0 v
2Ml
1 3
Ml 2
(2)碰撞后机械能守恒
1 J2 Mg l 1 cos
2
arccos 1
2
mv
3m2 v0 v2
匀速直线运动的乙测得时间间隔为 5 s,则乙相对于甲的运动速度是( c 表示真空
0
变为
1 2
0
时,经历的时间为多少?
解:(1)以子弹和棒组成的系统为研究对象。取子弹和棒碰撞中间的任一状态分析受力,
子弹与棒之间的碰撞力 f 、 f ' 是内力。一对相互作用力对同一转轴来说,其力矩之和为
零。因此,可以认为棒和子弹组成的系统对转轴的合外力矩为零,则系统对转轴的角动量
守恒。
mv 2
J 1 mL2 3
L 2
解上述两式得: 0
m 2
v 2
L 2
J0
3v 8L
(2)设在离转轴距离为 l 得取一微元 dl ,则该微元所受的阻力为: df kvdl kldl
该微元所受的阻力对转轴的力矩为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、教材:选择填空题 1~5;计算题:13,14,18 二、附加题(一)、选择题1、一沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,振动方程用余弦函数表示,如果该振子的初相为π34,则t =0时,质点的位置在:(A )过A x 21=处,向负方向运动; (B) 过A x 21=处,向正方向运动; (C) 过A x 21-=处,向负方向运动; (D) 过A x 21-=处,向正方向运动。
2、一物体作简谐振动,振动方程为:x =A cos(ωt +π/4 )在t=T/4(T 为周期)时刻,物体的加速度为:(A) 222ωA -. (B) 222ωA . (C) 232ωA -. (D) 232ωA .(二)、计算题1、一物体沿x 轴做简谐运动,振幅A = 0.12m ,周期T = 2s .当t = 0时, 物体的位移x 0= 0.06m ,且向x 轴正向运动.求: (1)此简谐运动的运动方程;(2)t = T /4时物体的位置、速度和加速度;2、一物体沿x 轴做简谐运动,振幅A = 10.0cm ,周期T = 2.0s .当t = 0时, 物体的位移x 0= -5cm ,且向x 轴负方向运动.求: (1)简谐运动方程;(2)t = 0.5s 时,物体的位移;(3)何时物体第一次运动到x = 5cm 处?(4)再经过多少时间物体第二次运动到x = 5cm 处?3、若简谐振动方程为m ]4/20cos[1.0ππ+=t x ,求:(1)振幅、频率、角频率、周期和初相; (2)t =2s 时的位移、速度和加速度.4、一简谐振动的振动曲线如图所示,求振动方程.5、一物体沿x 轴作简谐振动,振幅为0.06m ,周期为2.0s ,当t =0时位移为0.03m ,且向轴正方向运动,求:(1)t =0.5s 时,物体的位移、速度和加速度;(2)物体从m 03.0-x =处向x 轴负方向运动开始,到达平衡位置,至少需要多少时间?题图4一、教材:选择填空题 1~5;计算题:12,13,14, 21,30 二、附加题(一)、选择题1、一平面简谐波的波动方程为y = 0.1cos(3πt -πx+π) (SI). t = 0时的波形曲线如图所示,则: (A) O 点的振幅为-0.1m . (B) 波长为3m . (C) a 、b 两点间相位差为π/2 . (D) 波速为9m/s .2、某平面简谐波在t = 0.25s 时波形如图所示,则该波的波函数为:(A) y = 0.5cos[4π (t -x /8)-π/2] (cm) . (B) y = 0.5cos[4π (t + x /8) + π/2] (cm) . (C) y = 0.5cos[4π (t + x /8)-π/2] (cm) .(D) y = 0.5cos[4π (t -x /8) + π/2] (cm) .3、一平面简谐波在0=t 时刻的波形曲线如图所示 ,则O 点的振动初位相为:πππ23)(;)(;21)(;0)(D C B A4、一平面简谐波 ,其振幅为A ,频率为v ,波沿x 轴正方向传播 ,设t t =0时刻波形如图所示 ,则x=0处质点振动方程为:;])(2cos[)(;]2)(2cos[)(];2)(2cos[)(;]2)(2cos[)(0000ππππππππ+-=--=+-=++=t t v A y D t t v A y C t t v A y B t t v A y A5、关于产生驻波的条件,以下说法正确的是: (A) 任何两列波叠加都会产生驻波; (B) 任何两列相干波叠加都能产生驻波; (C) 两列振幅相同的相干波叠加能产生驻波;(D) 两列振幅相同,在同一直线上沿相反方向传播的相干波叠加才能产生驻波.)3(选择题)4(选择题(二) 计算题1、如图所示 ,一平面简谐波沿Ox 轴传播 ,波动方程为])(2cos[ϕλπ+-=xvt A y ,求:1)P 处质点的振动方程;2)该质点的速度表达式与加速度表达式 。
2、一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示. 求:(1)P 点的振动表达式;(2)波动方程;3、 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为0.03cos(4)2A y t ππ=-(m).求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程.4、一平面简谐波沿x 轴正向传播,波的振幅10A cm =,波的角频率7/rad s ωπ=,当1.0t s =时,10x cm =处的a 质点正通过其平衡位置向y 轴负方向运动,而20x cm =处的b 质点正通过5.0y cm =点向y 轴正方向运动.设该波波长10cm λ>,求该平面波的波方程. 王少杰 6-6)5、如图,一平面波在介质中以波速20/u m s =沿x 轴负方向传播,已知A 点的振动方程为)(4cos 1032SI t y π-⨯=.(1)以A 点为坐标原点写出波方程;(2)以距A 点5m 处的B 点为坐标原点,写出波方程.6、6-30火车以u 30m/s =的速度行驶,汽笛的频率为Hz 6500=ν.在铁路近旁的公路上坐在汽车里的人在下列情况听到火车鸣笛的声音频率分别是多少? (1)汽车静止;(2)汽车以h km v /45=的速度与火车同向行驶.(设空气中声速为v 340m/s =)第11章 光学 作 业一、教材:选择填空题 1~6;计算题:12,14,21,22,25(问题(1)、(2)),26,32,二、附加题(一)、选择题u题图5、 一束波长为λ的单色光由空气入射到折射率为n 的透明薄膜上, 要使透射光得到加强, 则薄膜的最小厚度应为(A) λ/2; (B) λ/2n ; (C) λ/4; (D) λ/4n .2、波长λ = 500nm 的单色光垂直照射到宽度b = 0.25 mm 的单缝上,单缝后面放置一凸透镜,在凸透镜的焦面上放置一屏幕,用以观测衍射条纹,今测得屏幕上中央条纹一侧第三个暗条纹和另一侧第三个暗条纹之间的距离为d = 12 mm , 则凸透镜的焦距为(A) 2m. (B) 1m. (C) 0.5m. (D) 0.2m. (E) 0.1m.3、一束由自然光和线偏光组成的复合光通过一偏振片,当偏振片转动时,最强的透射光是最弱的透射光光强的16倍,则在入射光中,自然光的强度I 1和偏振光的强度I 2之比I 1:I 2为(A) 2:15. (B) 15:2. (C) 1:15. (D) 15:1.(二)、计算题1、在双缝干涉实验中,单色光源S 到两缝S 1、S 2的距离分别为l 1、l 2, 并且λλ,321=-l l 为入射光的波长,双缝之间的 距离为d ,双缝到屏幕的距离为D ,如图,求:(1) 零级明纹到屏幕中央O 点的距离; (2) 相邻明条纹间的距离。
2、 两偏振片组装成起偏和检偏器,当两偏振片的偏振化方向夹角成30º时,观察一普通光源,夹角成60º时观察另一普通光源,两次观察所得的光强相等,求两光源光强之比.3、在杨氏双缝实验中,设两缝之间的距离为0.2mm .在距双缝1m 远的屏上观察干涉条纹,若入射光是波长为400nm 至760nm 的白光,问屏上离零级明纹20mm 处,哪些波长的光最大限度地加强?(1nm =10-9m)4、波长为λ的单色光垂直照射到折射率为n 2的劈形膜上,如图所示,图中n 1<n 2<n 3,观察反射光形成的干涉条纹.(1) e 5是多少?(2) 相邻的二明纹所对应的薄膜厚度之差是多少?5、用波长为λ1的单色光垂直照射牛顿环装置时,测得中央暗斑外第1和第4暗环半径之差为l 1,而用未知单色光垂直照射时,测得第1和第4暗环半径之差为l 2,求未知单色光的波长λ2.6、某种单色平行光垂直入射在单缝上,单缝宽b=0.15mm.缝后放一个焦距f = 400 mm的凸透镜,在透镜的焦平面上,测得中央明条纹两侧第三级暗条纹之间的距离为8.0mm,求入射光的波长.7、一束平行光垂直入射到某个光栅上,该光束有两种波长的光,λ1=440 nm,λ2=660 nm(1nm=10-9m).实验发现,两种波长的谱线(不计中央明纹)第二次重合于衍射角 =60°的方向上.求此光栅的光栅常数d.第12章气体动理论作业一、教材:选择填空题1,2,4 计算题:14,16,20,21二、附加题(一)、选择题1、某种理想气体,体积为V,压强为p,绝对温度为T,每个分子的质量为m,R为普通气体常数,N0为阿伏伽德罗常数,则该气体的分子数密度n为(A) pN0/(RT). (B) pN0/(RTV). (C) pmN0/(RT). (D)mN0/(RTV).2、若理想气体的体积为V,压强为p,温度为T,一个分子的质量为m,k为玻耳兹曼常量,R 为摩尔气体常量,则该理想气体的分子数为:(A)pV/m. (B) pV/ (kT) . (C) pV /(RT) . (D) pV/(mT) .3、两瓶质量密度相等的氮气和氧气(氮气和氧气视为理想气体),若它们的方均根速率也相等,则有:(A) 它们的压强p和温度T都相等.(B) 它们的压强p和温度T都都不等.(C) 压强p相等,氧气的温度比氮气的高.(D) 温度T相等, 氧气的压强比氮气的高.(二)、计算题1、将1 mol 温度为T的水蒸气分解为同温度的氢气和氧气,求氢气和氧气的内能之和比水蒸气的内能增加了多少?(所有气体分子均视为刚性分子)2、一瓶氢气和一瓶氧气温度相同.若氢气分子的平均平动动能为6.21×10-21J,求:(1) 氧气分子的平均平动动能和方均根速率;(2) 氧气的温度3、设一理想气体系统由N个同种气体分子组成,其速率分布函数为:⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤<-≤<=)(0)2(2)0()(0000002v v v v v vv v v v v v a a a f 式中0v 为已知速率值,a 为待求常数求:(1)用已知值表示常数 a ;(2)分子的最概然速率;(3)N 个分子的平均速率; (4)速率在0到20v 之间的分子数;(5)速率在20v到0v 之间分子的平均速率。
4、在相同温度下,2摩尔氢气和1摩尔氦气分别放在两个容积相同的容器中。
试求两气体(1)分子平均平动动能之比;(2)分子平均总动能之比;(3)内能之比;(4)方均根速率之比;(5)压强之比;(6)密度之比.5、已知()f v 是气体速率分布函数。
