第四章 串答案52450
概率论第四章习题解答

1第四章随机变量的数字特征I 教学基本要求1、理解随机变量的数学期望与方差的概念,掌握它们的性质与计算,会求随机变量函数的数学期望;2、掌握两点分布、二项分布、泊松分布、均匀分布、指数分布、正态分布的数学期望与方差;3、了解切比雪夫不等式及应用;4、掌握协方差、相关系数的概念与性质,了解矩和协方差矩阵的概念;5、了解伯努利大数定理、切比雪夫大数定律、辛钦大数定理;6、了解林德伯格-列维中心极限定理、棣莫弗―拉普拉斯中心极限定理,掌握它们在实际问题中的应用.II 习题解答A 组1、离散型随机变量X 的概率分布为X -2 0 2 p0.400.300.30求()E X 、(35)E X +、2()E X ?解:()(2)0.4000.3020.300.2E X =-⨯+⨯+⨯=-;(35)3()5 4.4E X E X +=+=;2222()(2)0.4000.3020.30 1.8E X =-⨯+⨯+⨯=.2、某产品表面瑕疵点数服从参数0.8λ=的泊松分布,规定若瑕疵点数不超过1个为一等品,每个价值10元,多于4个为废品,不值钱,其它情况为二等品,每个价值8元求产品的平均价值?解:设X 为产品价格,则0X =、8、10.通过查泊松分布表可知其相应概率分布为X 0 8 10 p0.00140.80880.1898则()80.1898100.80889.61E X =⨯+⨯≈(元).3、设随机变量X 的分布函数为00()/40414x F x x x x ≤⎧⎪=<≤⎨⎪>⎩.求()E X ?解:由分布函数知X 的密度函数为1/404()0x f x <≤⎧=⎨⎩其它则4()()24x E X xf x dx dx +∞-∞===⎰⎰.4、设随机变量X 服从几何分布,即1()(1)k p X k p p -==-(1,2,)k = ,其中01p <<是常数.求()E X ?解:1111()(1)(1)k k k k E X kp p pk p +∞+∞--===-=-∑∑由级数2121123(1)k x x kx x -=+++++- (||1)x <,知 211()[1(1)]E X p p p =⨯=--.5、若随机变量X 服从参数为λ的泊松分布,即的泊松分布,即()!kp X k e k λλ-== (0,1,2,)k =求()E X 、2()E X ?解:1()!(1)!kk k k E X k ee ee k k λλλλλλλλλ-+∞+∞---======-∑∑;12201(1)()[]!(1)!!kk kk k k k k E X keee k k k λλλλλλλλ-+∞+∞+∞---===+===-∑∑∑1210[]()(1)!!k kk k e e e e k k λλλλλλλλλλλλ-+∞+∞--===+=+=+-∑∑. 6、某工程队完成某项工程的时间X (单位:月)服从下述分布X 10 11 12 13 p0.40.30.20.1(1) 求该工程队完成此项工程的平均时间;(2) 设该工程队获利50(13)Y X =-(万元).求平均利润? 解:(1)()100.4110.3120.2130.111E X =⨯+⨯+⨯+⨯=(月);(2) ()[50(13)]65050()100E Y E X E X =-=-⨯=(万元). 7、若随机变量X 服从区间[,]a b 上的均匀分布,即1()a x b f x b a ⎧≤≤⎪=-⎨⎪⎩其它求()E X 、2()E X ?解:()()2bax a b E X xf x dx dx b a +∞-∞+===-⎰⎰;22222()()3baxa ab b E X x f x dx dx b a +∞-∞++===-⎰⎰. 8、若随机变量X 服从参数为λ的指数分布,即的指数分布,即0()0x ex f x x λλ-⎧>=⎨≤⎩0求()E X 、2()E X ?解:0()()xxE X xf x dx x edxxdeλλλ+∞+∞+∞---∞===-⎰⎰⎰1xxxeedxλλλ+∞+∞--=-+=⎰;2222202()()2xxxE X x f x dxx edxx exedxλλλλλ+∞+∞+∞+∞----∞-∞===-+=⎰⎰⎰.9、离散型随机变量X 的概率分布为X 0 2 6 p3/12 4/12 5/12求()E X 、[ln(2)]E X +?解:34519()0261212126E X =⨯+⨯+⨯=;34513[ln(2)]ln(02)ln(22)ln(62)ln 21212126E X +=+⨯++⨯++⨯=.10、设2~(,)X N μσ,求(||)E X μ-?解:22()21(||)||2x E X x e dx μσμμπσ--+∞-∞-=-⎰令x t μσ-=,由偶函数性质有222022(||)()2t t E X e d μσσππ+∞--==⎰.11、设某商品需求量(10,30)X U ,销售商进货量n 在(10,30)之间,是一个整数.每销售一件商品获利500(元),若供小于求,每件产品亏损100(元).若供大于求,则从外地调运,每件商品可获利300(元).为使利润期望值不少于9280(元),进货量最少应为多少?解:按题意利润Y 与X 、n 的关系为500300()1030500100()1030n X n n X Y X n X X n +-≤<≤⎧=⎨--≤<≤⎩则利润平均值为10101()[[500100()][500300()]20n n E Y X n X dx n X n dx =--++-⎰⎰ 27.53505250n n =-++由题意知27.535052509280n n -++≥解得62263n ≤≤,则最少进货量为21.12、某保险公司规定,如果一年内顾客投保事件A 发生,则赔偿顾客a 元.以往资料表明事件A 发生的概率为p .为使公司收益期望值为0.1a ,则应向顾客收取都少保费?解:设应向顾客收取x 元保费,公司的收益为Y 元则Yx x a - p1p -p按题意()(1)()0.1E Y x p x a p a =-+-= 解得0.1x ap a =+.13、设随机变量X 的密度函数为1cos0()220x x f x π⎧≤≤⎪=⎨⎪⎩其它.对X 进行独立重复观测4次,Y 表示观测值大于/3π的次数,求2Y 的数学期望?解:显然~(4,)Y b p ,其中p 是(/3)X π>的概率,故31()cos 0.5322xp p Xdx πππ=>==⎰所以44()0.50.5kkkp Y k C -==⨯ (0,1,2,3,4)k =则有42244()0.50.55k kkk E Y k C -==⨯=∑.14、设随机变量X 、Y 相互独立,且都服从标准正态分布求22Z X Y =+的数学期望?解:由题意知X 、Y 的联合密度函数为2221(,)2x y f x y eπ+-=于是22222221()(,)2x y E Z x y f x y dxdy x y edxdy π++∞+∞+∞+∞--∞-∞-∞-∞=+=+⎰⎰⎰⎰令cos x r θ=、sin y r θ=得222222201()22r r E Z r e drd r e drππθπ+∞+∞--===⎰⎰⎰.15、已知(,)X Y 的分布如下,令max{,}Z X Y =,求()E Z ?YX0 5 10 15 0 0.02 0.06 0.02 0.10 5 0.04 0.15 0.20 0.10 100.010.150.140.01解:由题设可得Z 的分布为Z 0 510 15 p 0.020.25 0.52 0.21()00.0250.25100.52150.219.6E Z =⨯+⨯+⨯+⨯=.16、设(,)X Y 的联合密度函数为21201(,)0yy x f x y ⎧≤≤≤=⎨⎩其它求()E X 、()E Y 、()E XY 、22()E X Y +?解:12004()(,)125xE X xf x y dxdydx xy dy+∞+∞-∞-∞-∞===⎰⎰⎰⎰; 1303()(,)125x E Y yf x y dxdy dx y dy +∞+∞-∞-∞===⎰⎰⎰⎰;;131()(,)122xE XY xyf x y dxdy dx xy dy +∞+∞-∞-∞-∞===⎰⎰⎰⎰; 122222220016()()(,)()15xE XY xy f x y dxdydx xy y dy+∞+∞-∞-∞-∞+=+=+=⎰⎰⎰⎰. 17、设随机变量(,)X Y 的密度函数为1()02,02(,)8x y x y f x y ⎧+≤≤≤≤⎪=⎨⎪⎩其它求()E X ?解:22007()(,)()88xE X xf x y dxdyxy dxdy+∞+∞-∞-∞==+=⎰⎰⎰⎰. 18、甲乙二人相约在12:00~13:00之间会面,设X 、Y 分别表示甲乙到达时间,且相互独立已知X 、Y 的密度函数为2301()0x x f x ⎧<<=⎨⎩其它、201()0y y f y <<⎧=⎨⎩其它求先到达者需要等待时间的数学期望?解:等待时间可以表示为||X Y -,由于X 、Y 的联合密度函数为2601,01(,)0x y x y f x y ⎧<<<<=⎨⎩其它11200(||)||6E X Y x y x ydxdy ⇒-=-⎰⎰112200001()6()|64xyx y x ydydx y xx ydxdy =-+-=⎰⎰⎰⎰.19、设二维随机变量(,)X Y 在曲线2y x =、2y x =+所围区域G 内服从均匀分布,内服从均匀分布,求求数学期望()E X 、()E Y ?解:设(,)X Y 的联合密度函数为(,)(,)0(,)c x y G f x y x y G∈⎧=⎨∉⎩,由密度函数性质解出9/2c =下面分别求出边沿密度函数当12x -≤≤时,有22222()(2)99x X xf x dy x x +==+-⎰,故此 22(2)12()90X x x x f x ⎧+--≤≤⎪=⎨⎪⎩其它 当01y ≤≤时,有24()99y Y y f y dx y--==⎰当14y <≤时,有222()(2)99y Y y f y dx y y --==+-⎰,所以 40192()(2)1490Y y y f y y y y ⎧≤≤⎪⎪⎪=+-<≤⎨⎪⎪⎪⎩其它从而22121()()(2)92XE X xfx dx x x x dx +∞-∞--==+-=⎰⎰; 1401428()()(2)995Y E Y yf y dy y yd y y y dy +∞-∞-∞==++-=⎰⎰⎰. 20、离散型随机变量X 的概率分布为X -2 0 2 p0.40 0.30 0.30求()D X ?解:由题意易知()0.2E X =-、2() 1.8E X =,所以22()()[()] 1.80.04 1.76D X E X E X =-=-=.21、设随机变量X 的分布函数为00()/40414x F x x x x ≤⎧⎪=<≤⎨⎪>⎩.求()D X解:由题意易知X 的密度函数为1/404()0x f x <≤⎧=⎨⎩其它,且()2E X=,则242(2)4()(())()43x D X x E X f x dx dx +∞-∞-=-==⎰⎰. 22、若随机变量X 服从参数为λ的泊松分布,求()D X ? 解:由题意易知()E X λ=、22()E X λλ=+,故22()()[()]D X E X E X λ=-=.23、设随机变量(,)X Y 的密度函数为1()02,02(,)80x y x y f x y ⎧+≤≤≤≤⎪=⎨⎪⎩其它求()D X ?解:由题意易知7()8E X =,故2222001711()[()](,)()()8636D X x E X f x y dxdy x x y dxdy +∞+∞-∞-∞-∞=-=-+=⎰⎰⎰⎰. 24、设二维随机变量(,)X Y 在曲线2y x =、2y x =+所围区域G 内服从均匀分布,内服从均匀分布,求求方差()D X 、()D Y ?解:由题意易知22(2)12()90X x x x f x ⎧+--≤≤⎪=⎨⎪⎩其它、40192()(2)1490Y yy f y y y y ⎧≤≤⎪⎪=+-<≤⎨⎪⎪⎪⎩其它1()2E X =、8()5E Y =22222127()()(2)910X E X x f x dx x x x dx+∞-∞--==+-=⎰⎰14222214247()()(2)9914Y E Yy f y dyy ydyy y dy +∞-∞-∞==++-=⎰⎰⎰229()()[()]20D X E X E X =-=;22279()()[()]350D YE Y E Y =-=.25、设10只同种元件中由2只是坏的,装配仪器时,从中任取1只,如果是不合格品,则扔掉后重取1只,求取出合格品前取出次品数的方差?只,求取出合格品前取出次品数的方差?解:设X 表示取出合格品前已取出次品的数目,则X0 1 2 p8/10 16/90 2/90故2()9E X =、24()15E X =所以2288()()[()]405D XE X E X =-=.26、设随机变量X 的密度函数为||1()2x f x e -=.求()E X 、()D X ?解:||1()()02x E X xf x dx x e dx+∞+∞--∞-∞===⎰⎰; 222||2011()(())()222x xD XE X E X x f x dx x e dx x e dx +∞+∞+∞---∞-∞=-====⎰⎰⎰.27、设X 为随机变量,证明:对任意常数C ,有2()()D X E X C ≤-,当()C E X =时等号成立.证明:22222()(2)()2()E X C E X CX C E X CE X C -=-+=-+22222()[()]{[()]2())}()[()]E X E X E X CE X C D X E X C =-+-+=+-由于2[()]E X C -非负,从而有2()()D X E X C ≤-,且当()C E X =时2()()D X E X C =-.28、设U 服从(-2,2)上的均匀分布,定义X 、Y 如下1111U X U -<-⎧=⎨>-⎩、1111U Y U -<⎧=⎨>⎩求()D X Y +?解:先求X Y +的分布(2)(1,1)(1,1)(1)1/4p X Y p X Y p U U p U +=-==-=-=<-<=<-= (2)(1,1)(1,1)(1)1/4p X Y p X Y p U U p U +=====≥-≥=≥= (0)1(2)(2)1/2p X Y p X Y p X Y +==-+=-+=-=所以()0E X Y +=,从而2()()2D X Y E X Y +=+=.29、已知()750E X =、2()15D X =.请估计概率(700800)p X <<? 解:由切比雪夫不等式有2215(700800)(|750|50)10.9150p X p X <<=-<≥-≈.30、设()2E X =-、()1D X =、()2E Y =、()4D Y =、0.5XY ρ=-,利用由切比雪夫不等式估计概率(||6)p X Y +≥的上限?解:因为()0E X Y +=、()()()2(,)3D X Y D X D Y Cov X Y +=++=,所以,所以2()1(||6)(|()()|6)612D X Y p X Y p X YE X Y ++≥=+-+≥≤=. 31、设()4D X =、()9D Y =、0.5XY ρ=,求(23)D X Y -? 解:(,)()()3XY Cov X Y D X D Y ρ==(23)4()9()2(2,3)16813661D X Y D X D Y Cov X Y -=++-=+-=.32、设(,)X Y 的联合密度函数为21201(,)0yy x f x y ⎧≤≤≤=⎨⎩其它求(,)Cov X Y ?解:由题意易知4()5E X =、3()5E Y =、1()2E XY =,故 1431(,)()()()25550Cov X Y E XY E X E Y ⨯=-=-=⨯. 33、设二维随机变量(,)X Y 在曲线2y x =、2y x =+所围区域G 内服从均匀分布,内服从均匀分布,求求协方差(,)Cov X Y 与相关系数XY ρ?解:由题意易知1()2E X =、8()5E Y =、9()20D X =、279()350D Y =2221225()994x x G E XY xy dxdy xdx ydy +-===⎰⎰⎰⎰所以9(,)()()()20Cov X Y E XY E X E Y =-=; (,)0.751()()XYCov X Y D X D Y ρ=≈.34、设二维随机变量(,)X Y 的联合分布为YX-1 0 1 00.07 0.18 0.15 100.080.320.20求22(,)Cov X Y解:先求2X 、2Y 、22X Y 的分布2(0)0.4p X ==、2(1)0.6p X == 2(0)0.5p Y ==、2(1)0.5p Y == 22(0)0.72p X Y ==、22(1)0.28p X Y ==所以2()0.6E X =、2()0.5E Y =、22()0.28E X Y =,由此得222222(,)()()()0.02Cov X Y E X Y E X E Y =-=-.35、随机变量(,)X Y 的密度函数为201,11(,)0x x y f x y ≤≤-≤≤⎧=⎨⎩其它求()D X Y +?解:当01x <<时,有11()22X x f x d y x -==⎰;当01y <<时,有11()22Y y f y d x y -==⎰,故2()()3E X E Y ==、1()()18D X D Y == 由于(,)()()X Y f x y f x f y ≠,即X 与Y 不独立.所以11015()212xE XY xydxdy -==⎰⎰541(,)()()()12936Cov X Y E XY E X E Y =-=-=- 1()()()2ov(,)18D X Y D X D Y C X Y +=++=.36、将1枚硬币抛n 次,以X 、Y 分别表示正面向上与反面向上的次数,求(,)Cov X Y 、XY ρ解:由于X Y n+=,即Y n X=-,于是1XYρ=-;又因~(,0.5)X b n 、~(,,0.5)Y b n ,所以()()/4D X D Y n ==,故(,)(,)(,)()/4Cov X Y Cov X n X Cov X X D X n =-=-==.37、设X 与Y 独立,且都服从参数为λ的泊松分布,令2U X Y =+、2V X Y =-求U 与V 的相关系数?解:由于()(2)4()()5D U D X Y D X D Y λ=+=+= ()(2)4()()5D V D X Y D X D Y λ=-=+=所以(,)(2,2)Cov U V Cov X Y X Y =+-4()(,2)(2,)()3D X Cov Y X Cov X Y D Y λ=+--=由此得(,)35(),()XYCov X Y D X D Y ρ==. 38、设二维随机变量(,)X Y 的联合密度函数为1||0,01(,)0y x f x y <<<⎧=⎨⎩其它判断X 与Y 之间的相关性与独立性.解:由于12()3x xE X xdydx -==⎰⎰、、10()0x xE Y ydydx -==⎰⎰、10()0xxE XY xydydx -==⎰⎰,则(,)()()()0Cov X Y E X E Y E XY =-=故X 与Y 之间不相关;又因当01x <<时,有()2xXxf x dy x-==⎰,即201()0X x x f x <<⎧=⎨⎩其它同理可以求出110()1010X y y f x y y +-<<⎧⎪=-<<⎨⎪⎩其它由于(,)()()X Y f x y f x f y ≠,故X 与Y 之间不独立.39、设a 为区间(0,1)上一定点,随机变量(0,1)X U ,Y 是X 到a 的距离.问a 为何值时X 与Y 是不相关?解:由题设知()0.5E X =、||Y X a =-,所以11201()||()()2aaE Y x a dx a x dx x a dx a a =-=-+-=-+⎰⎰⎰3101()()()323a a a a E XY x a x dx x x a dx =-+-=-+⎰⎰31(,)3212a aCov X Y =-+令31(,)03212a a Cov X Y =-+=,可得方程2(21)(221)0a a a ---=在(0,1)内解得0.5a =,即0.5a =时,X 与Y 不相关. 40、设计算器进行加法计算时,所有舍入误差相互独立且在(0.5,0.5)-上服从均匀分布.(1) 将1500个数相加,问误差总和的绝对值超过15的概率是多少;(2) 最多可以有几个数相加,其误差总和的绝对值小于10的概率不小于0.90? 解:设第i 个数的舍入误差为i X (1,,)i n = ,故()0i E X =、()1/12i D X = (1,,)i n =记1ni i X X ==∑(1) 由林德伯格-列维中心极限定理有15001150001515000(||15)(||)15001/1215001/12i i x p X p =-⨯-⨯>=>∑151[2()1]0.180215001/12≈-Φ-=;(2) 由林德伯格-列维中心极限定理有1100100.90(||10)(||)2()11/121/121/12ni i x n n p X p n n n =-⨯-⨯≤<=≤≈Φ-∑即10()0.951/12n Φ≥,由于(1.645)0.95Φ=,则101.6451/12n ≥因此443.45n £,再由n 为整数得满足题意的个数为443.41、一批木材中有80%的长度不小于3m ,从中任取100根,求其中至少有30根长度短于3m 的概率?解:以X 表示100根木材中长度短于3m 的数目,则~(100,0.2)X b ,于是()20E X =,()16D X =.由于100n =较大,则由中心极限定理,近似有2~(20,4)X N ,由此有20302010(30)1(30)1()1()0.0062444X p X p X p --≥=-<=-<≈-Φ-=. 42、某商店出售价格分别为1(元)、1.2(元)、1.5(元)的3种蛋糕,种蛋糕,每种蛋糕被购买的概每种蛋糕被购买的概率分别为0.3、0.2、0.5.若某天售出300只蛋糕,(1) 求这天收入为400(元)的概率;(2) 求这天售出价格为1.2(元)蛋糕多于60只的概率?解:(1) 设第i 只蛋糕价格为iX (1,,300)i = .则i X的分布为i X1 1.2 1.5 p0.30.20.5于是可得() 1.29i E X =、2() 1.713iE X =、()0.0489i D X =令3001i i X X ==∑表示总收入,则由林德伯格-列维中心极限定理有300 1.29400300 1.29(400)()1(3.39)0.00033000.04893000.0489X p X p -⨯-⨯≥=>≈-Φ=⨯⨯;(2) 记Y 为300只蛋糕中售价为1.2(元)的蛋糕数目,则~(300,0.2)Y b ,于是()60E Y =、()48D Y =,由中心极限定理,近似有~(60,48)X N ,由此有606060(60)1()1(0)0.54848Y p Y p --≥=-<≈-Φ=.43、进行独立重复试验,每次试验中事件A 发生的概率为0.25.问能以95%的把握保证1000次试验中事件A 发生的频率与概率相差多少?此时A 发生的次数在什么范围内?解:设X 为1000次试验中事件A 发生的次数,则~(1000,0.25)X b ,由二项分布的性质知()250E X =、()187.5D X =,而事件A 发生的频率为/1000X .根据题意,可得如下不等式(|0.25|)0.951000X p ε-≤≥即(|250|1000)0.95p X ε-≤≥,由棣莫弗―拉普拉斯定理有25010001000(||)2()10.95187.5187.5187.5X p εε-≤≈Φ-≥即1000()0.975(1.96)187.5εΦ≥=Φ解得0.026ε³,这表明1000次试验中事件A 发生的频率与概率相差不超过0.026,相应的有1000次试验中事件A 发生的次数在224到276之间.44、某车间有同型号车床150台,在1小时内每台车床约有60%的时间在工作.假定各车床工作相互独立,工作时每台车床要消耗电能15kw.问至少要多少电能,才可以有99.5%的可能性保证此车间正常工作?解:以X 表示同时工作的车床数,则~(150,0.6)X b ,于是()90E X =、()36D X =,由题意知x 应使得下式成立(0)0.995p X x ≤≤≥由中心极限定理,近似有~(90,36)X N ,故有090909090(0)()()(15)0.9956666X x x p X x p ----≤≤=<<≈Φ-Φ-≥ 查标准正态分布表得90 2.586x -≥,即105.28x ≥,取整得106x =.故要保证车间有99.5%的可能性正常工作,需供电能151061590⨯=()kw .B 组1、将n 只球(1n 号)随机的装入n 只盒子(1n 号),一只盒子装一只球.若一只球装入的盒子与球同号,称为一个配对.记X 为配对数,求()D X ?解:引入随机变量i X (1,)i n = ,1i X =表示第i 号配对,0i X =表示第i 号不配对,则1n X X X =++ ,且1(1)i p X n ==(1,)i n = 即1()i E X n = (1,)i n =于是1()()1n E X E X X =++=因为i X 之间不独立,所以11111()()2(,)nn ni i i i j ii ij D X D X Cov X X -=====+∑∑∑∑下面考虑i j X X 的分布,由于i j X X 的取值只能是0、1,且1(1)(1,1)(1)i j i j p X X p X X n n =====- 所以1()(1)i j E X X n n =-,因此 21()()()()(1)i j i j i j Cov X X E X X E X E X n n =-=- 2211()21(1)nn D X Cnn n -⇒=+=-.2、设随机变量X 的分布函数为()F x ,其数学期望存在,证明()[1()]()E X F x dx F x dx +∞-∞=--⎰⎰.证明:00()()()()E X xf x dxxf x dxxf x dx +∞+∞-∞-∞==-⎰⎰⎰由于00()()()xxf x dxxdy f x dx +∞-∞=-⎰⎰⎰改变积分次序有00()(())()yxf x dxf x dx dyF y dy +∞-∞-∞-∞=-=-⎰⎰⎰⎰同理有()[1()]xf x dx F y dy +∞+∞=-⎰⎰ 0()[1()]()E X F x dxF x dx +∞-∞⇒=--⎰⎰.3、设随机变量X 的分布函数为0111()arcsin 11211x F x x x x π⎧<-⎪⎪=+-≤<⎨≥⎪⎩求()E X ?解:由上一题结论有()[1()]()E X F x dxF x dx +∞-∞=--⎰⎰111111[1arcsin ](arcsin )022x dx x dx ππ--=---+=⎰⎰.4、设连续随机变量X 的密度函数为()f x 若对任意常数c 有()()f c x f c x +=- (0)x >且()E X 存在.证明()E X c =.证明:令x t c =-则有()()()()()()E X xf x dxc t f c t dtcf c t dttf c t dt +∞+∞+∞+∞-∞-∞-∞-∞==++=+++⎰⎰⎰⎰由密度函数性质有()()cf c t dt cf c t dt c +∞+∞-∞-∞+=+=⎰⎰令u t =-,有()()()()tf c t dttf c t dtuf c u duuf c u du +∞+∞-∞-∞+=-=+=-+⎰⎰⎰⎰故()0tf c t dt +∞-∞+=⎰所以()E X c =.5、证明事件A 在一次试验中发生次数的方差不超过0.25.证明:设X 表示事件A 在一次试验中发生的次数,则(1,)X b p ,其中p 是事件A 发生的概率,则()(1)0D X p p =-≥由均值不等式得,当0.5p =时,()D X 有最大值0.25. 6、设随机变量X 服从几何分布,即1()(1)k p X k p p -==-(1,2,)k = ,其中01p <<是常数.求()D X解:1111()(1)(1)k k k k E X kp p p k p +∞+∞--===-=-∑∑由级数2121123(1)k x x kx x -=+++++- (||1)x <,知211()[1(1)]E X p p p =⨯=--又111[(1)](1)()(1)(1)k k k E X Xk k p Xk pk k p +∞+∞-==+=+==+-∑∑将21(1)x -的展开式两端求导得 1321223(1)(1)k x k kx x -=⋅+⋅++-+- 3222[(1)][1(1)]E X X pp p ⇒+==--222()()[()][(1)][()]D X E X E X E X X X E X ⇒=-=+-- 221[(1)]()[()]p E X X E X E X p-=+--=. 7、一只昆虫所生虫卵X 服从参数为λ的泊松分布,而每个虫卵发育成幼虫的概率为p ,且每个虫卵是否发育成幼虫相互独立,求一只昆虫所生幼虫数Y 的期望与方差?解:由题意知()!np X n en λλ-==(0,1,2,)λ= ,而n 个虫卵发育成k ()k n ≤个幼虫的概率为(|)(1)k kn knp Y k X n C p p -===- (0,1,,)k n =由全概率公式,对任意0,1,,k n = 有()()(|)(1)!nkkn kn n k n k p Y k p X n p Y k X n e C p p n λλ+∞+∞--========-∑∑(1)()[(1)]()()!()!!!k n kk kp pn k p p p p e e e e k n k k k λλλλλλλλ-+∞----=-===-∑即Y服从参数为pλ的泊松分布所以()()E Y D Y p λ==.8、设随机变量X 的密度函数()f x 是偶函数,且2(||)E X <+∞,证明X 与2X 不相关,但不独立.证明:因()f x 是偶函数,所以()xf x 、3()x f x 是奇函数,故此3()()0E X E X ==222(,)()()()0Cov X X E X X E X E X ⇒=⋅-=因而,X 与2X 不相关;选取0a >使得()1p X a ≤<,考察如下特定事件概率22(,)()()()p X a X a p a X a p X a p a X a ≤≤=-≤≤>≤-≤≤ 22()()p X a p X a =≤≤即2222(,)()()p X a X a p X a p X a ≤≤≠≤≤ 故X 与2X 不独立.9、设1X 、…、n X 中任意两个的相关系数都是ρ,试证:11n ρ≥--. 证明:因为111110()()2(,)nnni iiiji i i j D X D X Cov X X-====≤=+∑∑∑∑1111()2()()nni i i j i ij D X D X D X ρ-====+∑∑∑11111()[()()]()[1(1)]n ni ni i j i i i j i D X D X D X D X n ρρ-====≤++=+-∑∑∑∑11n ρ⇒≥--.。
组合数学第四章习题解答

4.19 试说明S5群的不同格式及其个数, • 9.解:5的拆分共有:00005,00014,00023, 00113,00122,01112,11111共七种,根据讲义4.4 节定理1可得S5中: (1)5共轭类有5!/5!=1个置换; (1)1(4)1共轭类有5!/4=30个置换; (2)1(3)1共轭类有5!/(2· 3)=20个置换; (1)2(3)1共轭类有5!/(2!3)=20个置换; (1)1(2)2共轭类有5!/(2!2 )=15个置换; (1)3(2)1共轭类有5!/(3!2)=10个置换; (5)1共轭类有5!/5=24个置换; ∴共有不同格式7种,如上所示。
旋转 12345
12345 13524 14253 15432
5
2
翻转
12534 21345 32415 51423 41235
4
3
c ( a1 ) c(a2 ) 1 c ( ag ) l [m m ... m ] G
4.23 凸多面体中与一个顶点相关的各角之和与2 的差称为该顶点的欠角,证明凸多面体各顶点欠 角之和为4
证:设V,S,E分别为顶点集,面集,边(棱)集。 由欧拉定理 |V|+|S|-|E|=2. 设aij为与顶点vi, 面Sj为相关的面角,ej为Sj的的边数, 给定Sj则∑aij=(ej-2)π 欠角和为∑(2π-∑aij)=∑2π-∑ ∑aij =2|V|π-∑ ∑aij=2|V|π-∑(ej-2)π =2|V|π-∑ejπ+2|S|π =2|V|π+2|S|π-2|E|π=4π
用4.2和4.8的结论
4.10 若x和y在群G作用下属于同一等价类,则x所 属的等价类Ex,y所属的等价类Ey有|Ex|=|Ey|。 显然
离散数学课后习题答案第四章

离散数学课后习题答案第四章离散数学课后习题答案第四章第⼗章部分课后习题参考答案4.判断下列集合对所给的⼆元运算是否封闭:(1)整数集合Z 和普通的减法运算。
封闭,不满⾜交换律和结合律,⽆零元和单位元(2)⾮零整数集合普通的除法运算。
不封闭(3)全体n n ?实矩阵集合(R )和矩阵加法及乘法运算,其中n2。
封闭均满⾜交换律,结合律,乘法对加法满⾜分配律;加法单位元是零矩阵,⽆零元;乘法单位元是单位矩阵,零元是零矩阵;(4)全体n n ?实可逆矩阵集合关于矩阵加法及乘法运算,其中n 2。
不封闭(5)正实数集合和运算,其中运算定义为:不封闭因为 +?-=--?=R 1111111ο(6)n关于普通的加法和乘法运算。
封闭,均满⾜交换律,结合律,乘法对加法满⾜分配律加法单位元是0,⽆零元;乘法⽆单位元(1>n ),零元是0;1=n 单位元是1 (7)A = {},,,21n a a a Λ n运算定义如下:封闭不满⾜交换律,满⾜结合律,(8)S =关于普通的加法和乘法运算。
封闭均满⾜交换律,结合律,乘法对加法满⾜分配律(9)S = {0,1},S 是关于普通的加法和乘法运算。
加法不封闭,乘法封闭;乘法满⾜交换律,结合律(10)S = ,S 关于普通的加法和乘法运算。
加法不封闭,乘法封闭,乘法满⾜交换律,结合律10.令S={a ,b},S 上有四个运算:*,分别有表10.8确定。
(a) (b) (c) (d)(1)这4个运算中哪些运算满⾜交换律,结合律,幂等律?(a) 交换律,结合律,幂等律都满⾜,零元为a,没有单位元; (b)满⾜交换律和结合律,不满⾜幂等律,单位元为a,没有零元b b a a ==--11,(c)满⾜交换律,不满⾜幂等律,不满⾜结合律 a b a b b a b a a b b a ====οοοοοο)(,)(b b a b b a οοοο)()(≠ 没有单位元, 没有零元(d) 不满⾜交换律,满⾜结合律和幂等律没有单位元, 没有零元 (1) 求每个运算的单位元,零元以及每⼀个可逆元素的逆元。
高等代数第四章及其习题答案
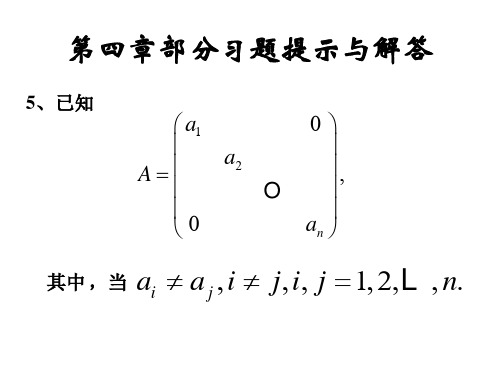
α b11
A1 0
= B1 0
β a11b11 a11β + α B1
A1 B1
,
为上三角形矩阵, 由归纳法假设知 A1 B1 为上三角形矩阵,故 AB 为上三 角形矩阵。 角形矩阵。
2)设 A = ( aij ) 为一可逆的上三角形矩阵,则 ) 为一可逆的上三角形矩阵, nn
= ε iT A j L 0 L L L 0 L a jn i 行 . L 0 L L L 0
0 M 0 a1i AEij = ( B1 , L , Bn ) ε j = Bi ε j = M ( 0, L , 0,1, 0, L , 0 ) a 0 ni M 0 0 0 = L 0 L L L 0 0 0 a1i a2 i L ani 0 L L 0 . L L L 0 L 0 0 L
T
y1 n T T 2 ( Ax) Ax = y y = ( y1 ,L, yn ) M = ∑ yi = 0, y i =1 n
从而 yi = 0, i = 1, L, n , 即 y = Ax = 0 ,由
x 的任意性知 Aε j = 0, j = 1,L , n ,其中
为数量矩阵. 为数量矩阵 级矩阵可交换, 注:因 A 与所有 n 级矩阵可交换,故 A 一定与 可交换, E i j ( i , j = 1, L , n ) 可交换,于是 AEij = Eij A.
10、已知 A为实对称矩阵 且 A2 = 0 , 不妨设 A = aij 、 为实对称矩阵, 阶矩阵, 为 n 阶矩阵, = x
T
( )
nn
湘教版解读-第4章习题答案

1 32-的平方根是士 - ; 2.56的平方根是士 4 221的算数平方根是3习题(P97)36的平方根是士 - ; 1.44的平方根是士 1.2.49 7方法规律:正数有两个平方根,它们互为相反数.2. 49的算术平方根是 7;144的算术平方根是93. (1) x 2= 16;解:x=士 (3) x 2= 15; 解:x=士苗5. (4) 4x 2 = 81第4章实数练习(P95)0.81的平方根是士0.9 .方法规律:正数有两个平方根, 它们互为相反数; 0的平方根是 0;负数没有平方根.练习(P97) 1 . 0.01的算数平方根是 0.1 ;25的算数平方根是160的算数平方根是 0 ; 10的算数平方根是 尿解:x=± 4.(2) x 2= 2549解:81的平方根是士 9; 289的平方根是士 17; 0的平方根是 0;1.6 ;点拨: 注意算数平方根与平方根的区别与联系.2.解: •••△ A B C 是直角三角形, B C = 4, A ' C = 5, ••• A'B'2= B'C 2 + A'C 2 = 42 + 52 = 41 .方法规律:勾股定理是联系直角三角形三边长度的重要纽带, 已知其中任意两边,可以求得第三边长度,即 二求一 ”.3 .解:(1) 4; ( 2) 3 ; ( 3)寸;(4) 2.方法规律:(1) V a = a;(a 0) (a 0)1 . 169的平方根是士 13; 225的平方根是士 15; 1 1-的平方根是士 - ; 11的平方根是士4 2T ii ; 0.16的平方根是士 0.4 ;4; 10的算术平方根是 尿;- 3 2的算术平方根是-3解:X 2 = 814X=± 94 •解:•••/ C= 90 ° ••• AB 2= AC 2 + BC 2.(1) v AC = 5 , BC= 12, ••• AB 2= 52+ 122= 169, ••• AB = ± 13,(舍去负值) ••• AB = 13; (2) v AC = 2,BC= 3, ••• AB 2= 22+ 32= 13, ••• AB = ± 丽,(舍去负值 ••• AB =與;(3) v AB = 25,BC= 24, ••• 252= AC 2 + 242, • AC 2= 49, ••• AC = ± 7,(舍去负值) ••• AB = 7. 点拨:根据勾股定理求解即可,注意区分直角边和斜边. 5. (1)v 直角三角形的两条直角边的长分别为•••斜边 2 = 32 + 52 = 34, •••斜边=±阿,(舍去负值) •••斜边=734 .(2)①若3和5都是直角三角形的直角边,由( 1) ②若3是直角边,5是斜边, 则有:第三边2 = 52- 32 = 16, 第三边=± 4,(舍去负值) •••第三边为4 . 综上,第三边为或4.点拨:根据勾股定理求解即可,注意区分直角边和斜边. 6•解:(1 )依题意知 h= 1.5327km ,•- d^2hR =72 1.5327 6400 ~ 14(km .■/ 140km v 230km ,方法规律:求等式中的X, 实际上就是解方程.一般地, 解这类题,先将方程化为 X 2 = a 的形式,再把方程两边同时开平方,得到 X 的值. 问题的结果有 3种情况: (1 )当a > 0时,X 可以得到两个实数解; (2)当X = 0时,X 可以得到一个实数解;当av 0时,X 没有实数解.5,知,斜边=734 ;说法(1)错误.(2)依题意知 h= 0.125km ,••• =72 0.125 6400 ~4(km .■/ 40km > 35km , •••说法(2)正确. 点拨:准确理解题意是解本题的关键.练习(P100) 127的立方根是—3;**的立方根是0.2 ; 丄3仁25的立方根是¥25 ;—1的立方根是—1; **的立方根是0.4 ;4的立方根是血方法规律:任何实数都有立方根.正数的立方根是一个正数;负数的立方根是一个负数; 2. (1)— 8; ( 2) 2 ; ( 3)— 3; ( 4)— 3 .3_ _方法规律:(1)寻a = a; ( 2) V a 3= a.3•解:设体积为 5120m 3的球半径为R 1,体积为80m 3的球半径为R 2, V 球=-nR 3,3••• 5120 = = 4nR 13, 80 = = 4nV,33•- 4 nR 13 : 4nR 23 = R 13: R 23 = (R 1 : R 2)3= 5120 : 80 = 64,3 3••• R 1 : R 2= 4 .方法规律:根据球体的体积比得到它们的半径之比是解题关键•从本题可以看岀,两个球体体积之比等于它们 的半径之比的立方;两个球体半径之比等于它们的体积之比的立方根. 习题(P100) 1 .— 0.001的立方根是—0.1 ; —27的立方根是一 —64 4 **的立方根是 0.3 ;1的立方根是1;1331的立方根是 11 .方法规律:任何实数都有立方根•正数的立方根是一个正数;负数的立方根是一个负数; 2 •解:(皿)3= 1.2 ;4 . 2立方根0的立方根是 0.0的立方根是 0.肃〒=—6; (吋―53. (1) X 3=— 0.125 ; 解:X=— 0.5 . (2) 8x 3 = 27; 解: X 3= 27,83 X= 一2(3) X 3+ 3 = 2; 解:X 3 = — 1, X=— 1 .(4)(X — 1)3 = 8. 解:X — 1 = 2, x= 3.4无,即,它的棱长扩大到原来的4倍.••• - nR 3= 36 n ,3即,R 3= 27,R = 3.点拨:将相关数据代入公式计算即可. 4. 3实数练习(P103)解:(1)有理数:{4 2,0. 6(.),J 025,「25,—,…};3 ¥49方法规律:(1) 甫=a ; ( 2) V a 3= a.方法规律:求等式中的 X,实际上就是解方程.一般地,解这类题,先将方程化为 X 3 = a 的形式,再把方程两边同时开立方,进而得到 X 的值.4•解:方法1:设正方体原来的棱长为 a,则原来的体积为 a 3,扩大后的体积为64a 3,所以扩大后的棱长为 疯3咏0产=4a ,即,它的棱长扩大到原来的 4 倍.方法2 :设正方体原来的体积为V ,则原来的棱长为迥,扩大后的体积为 64V ,所以扩大后的棱长为 M 64V =方法规律:如果一个正方体的体积扩大到原来的 a 倍,那么它的棱长扩大到原来的V a 倍.5.解:•••球的体积公式:V 球=4T J R 3, R 为球的半径,3答:这个球形容器的半径为 3m.{—筋,727,—, 0.XX001 …,…};3••• 府 =8,.・.屈是有理数;(2)V 旷64 =— 4,.・.旷64是有理数;(3)V 0.030303…是无 0.030303…是有理数;(4 )••• H = 6,•再 是有理数.判断T a 或y a 是有理数还是无理 数,不能只注意根号,还要看这个数的化简结果. 易错提示:对于 術,容易忽视根指数 3,误认为 逅=3,错误地把它划分为有理数范围.无理数: (3) 正实数:{42,0. 6(.,西5,炉,3,0.XX001 …,…};(4) 负实数:{-縛,心,-鸥,…}.易错提示:(i )T 7025 = 7025是有理数;(2)••• 厂25 =— 5,.・. 厂25是有理数;限不循环小数,••• —是无理数;(4)・.・0.XX001…是无限不循环小数,••• 0.XX001…是无理数.3练习(P104) (2) 3A 20 〜1. ( 1)懈~82. (1)V 萌勺.5874,品 «1.7321, ••• V 4 < (2)v1血勺.4142,«0.7071,72•••血〉17004 = 0.2,5,7004•••700? < J3. (1) 3x 72— 2 n — 2.0405 ; (2) — 2X 岳 + 5X 72~ 1.8274 (3) " — ( V 5 + V 2) j 1.5557 . 习题(P105) 1 .解:方法规律:(1) 限循环小数,•••1 2•解:(1) “ + - 一 n4 0.25; 4(3) n —(逅 + n )41.44 .方法规律:精确到百分位,就是精确到 0.01.3.解:实数 相反数 绝对值 倒数725-V 25 7251—nnn—1—质1 #0.9a(a> 0)—aa1 aa(av 0)—a —a1 a点拨:根据相反数、绝对值和倒数的定义逐个判断即可.4•如图4— 1所示,设原点为 A, 3表示的点为B •过点B 作数轴的垂线,在垂线上取一点C,使BC = 1,根据勾股定理得 AC 2= AB 2 + BC 2 = 32 + 12 = 10,所以AC =710 •以点A 为圆心,AC 长为半径画弧,交数轴于点 P,则点P 所表示的数即为710 .2 •解:(1) 40kg ; ( 2) 44kg ; ( 3) 44.0kg .3•解:由图形可知,△ ABC 是直角三角形,且/ ACB = 90 ° 又••• AC = 2.55m , BC = 3m, ••• AB = J AC 2+ BC 2= J 2.552+3243.9m .答:拉索AB 的长为3.9m . 习题(P109)CJ A ―B P-0 1 23 ----- ----- 3方法规律:(1)构造两条直角边分别为 1 和3的直角三角形,是解决本题的关键; (2)根据勾股定理可以计算斜边的长度.4 . 4近似数练习(P108) 1•解:只有(1)是准确数,(2)、(3)、 (4)均为近似数.**的立方根是 0.5 ;丄—64的立方根是—14—5的立方根是—亦;33的立方根是2 4•解:(^/25)2= 2.5,1 .解:(1) 3.3 XO 22; (2) 3.6 X108. 2. (1) 1.7 ; ( 2) 1.71 ; ( 3) 1.710 ; (4) 1.7100 .3•解: (1)精确到 0.01 ; (2)精确到 100; ( 3)精确到 0.1 ; (4)精确到 0.000 000 001 . 4.解:157 22 355 =3.14 ; — = 3.142 857 142 857 142 …; ±^«3.141 592 9 .5071135•解: •••△ ABC 是直角三角形, ••• AB 2 + BC 2 = AC 2,•/ BA = 1.36km , AC = 2.95km , ••• 1.362 + BC 2= 2.952, 解得:BC «2.62,• AB + AC — BC= 1.36 + 2.95 — 2.62 = 1.69 勺.7, 答:走隧道比绕道 BA 和AC 减少1.7km 的行程.方法规律:运用转化与化归思想,将实际问题转化为求 AB+ AC — BC 的长度问题,是解决本题的关键. 复习题(P111)1. T 、4、师是无理数.易错提示:1.732是73的近似值,是有理数;3 —的值是 -,是有理数; 尿 的值是4,是有理数;耳丽 工0.2 ,V 273且开立方开不尽,是无理数. 2.解:—的平方根是士36**的平方根是士 2.5 ;10的平方根是土'^ ;1 1 丄的平方根是士 - 144 12 1 5 6-的平方根是士 - 4 23.— 1 000的立方根是― 10;V 10 =— 10,—7 5 =— 5,5. (1) 5x 2= 10; 解:x 2 = 2, ••• x=± 农; (2) X 3— 2 = 6; 解:x 3 = 8,(3)(X — 1)2 = 0.25 ;解:X — 1 =± 0.5 •- X 1 = 1.5, X 2= 0.5; (4) (x+ 4)3 = — 64. 解:X+ 4 = — 46 .解: 旷2的相反数是 返,绝对值是 返; —2逅的相反数是7.解:Y743 , “018 勺.009, "°.°43627209,习^108P.476, £ 7170 .8.解:(1) 2X ^/3 — 3x 72 +75 勺.46 ;355+ 2n — 72 «2.59 .113屈 «6.8, 転 «2.1 , V G Q P.9.方法规律:比较两个负数大小,可以先比较这两个负数的相反数,相反数较大的负数反而小. 易错提示:I 廖—751是含有绝对值的式子,且计算结果为岳—73,所以 “ —75|=J 5 -灵.11.解:如图4— 2,设甲、乙、丙三地为点 A 、B 、C,过点A 作AD 丄BC 于点D .J 5 — n 的相反数是 n ", 绝对值是 n — 厉; 2—亞的相反数是廳—2,绝对值是2-廳;** —的相反数是一 1.4,绝对值是—1.4 .9.拆8«4.2, 10. (1 )<; (2)<; ( 3)=; ( 4 )>.丙北A甲依题意知/ BAD = 90° —45° = 45° AB = 80km,BC = 100km .•••AD 丄BC ,•••/ ABD = 90° —45°=45°,••• DA =DB ,在Rt△ ABD 中,DA2 + DB2= AB2,••• 2DA2= 2DB2 = 802,DA = DB = 40 72 弋6.6,• CD = BC — BD = 100 — 56.6 =43.4 ,在Rt△ ACD 中,AC= J AD2+ CD2= J56.62+ 4342- 71答:这时轮船离甲地 71km.方法规律:(1)运用概括与抽象的思想,将实际问题转化为几何问题,是解本题的前提; (2)过点A作BC的垂线,构造直角三角形,是解本题的关键; (3)运用方程思想,根据勾股定理构造方程求相关线段的长,是解这类题的常见基本解题思想.12 .解析:求梯子的底端向外滑动的距离,就是求BB '的长,因此,只需分别求岀CB、CB的长,再计算二者长度差BB'即可.解:在Rt△ ABC 中,AC = 8,AB= 10,由勾股定理得:BC = —A C^ J102826 ;•••梯子顶端下降了1m,• A'C= 8— 1 =7.在Rt△ A 'B C 中,A C = 7,A B =10,由勾股定理得: B C = J A'B'2A'C2710272751 -7.14.• BB = BC — BC = 7.141 —6^1.1 .答:梯子的底端向外滑动的距离是 1.1m .13 •解:如图4 — 3,分别取D、E、F三个点,构成长方形 CDEF,则点A、B分别在DE、EF 上.依题意知,AE = 1, EB = 3, BF = 1, FC = 2, CD = 4 , DA = 1 ,(1)在Rt△ AEB、Rt △ BFC 和Rt △ CDA 中,AB = &232V ic ; BC= M22亦;CA = J 242妬•••△ ABC 的周长=AB + BC+ CA =乐+ «9.5.1 1 1(2) $△ ABC = S 四边形 CDEF — $△ AEB — $△ BFC — $△ CDA = 2X4 - — 13 — 12 —2 2 214 .解:如图4 - 4所示,尿、而和J 20的线段,这可以根据勾股定理,构造直角三角形 来解决.15 •解:(1)如图4-5所示将图形剪开,其中, 1移至2处,3移至4处,5移至6处,7移至8处即可. (2)至少需剪2刀•如图4- 6所示将图形剪开,其中,a 移至b 处,c 移至d 处,e 移至f 处.方法规律:画正方形,关键是要确定边长, 根据要画的正方形面积可以求得其边长分别为7T0、7T7 和 725,因此问题就转化为:在图中作岀长度分别为。
组合数学+卢开澄版++答案第四章

4.1证明所有的循环群是ABEL 群 证明:n n ,,**×x ,x ?**m n m n a b G G a b b a x x a b b a ++∈==∴=m m m 循环群也是群,所以群的定义不用再证,只需证明对于任意是循环群,有成立,因为循环群中的元素可写成a=x 形式所以等式左边x 等式右边x =,,即所有的循环群都是ABEL 群。
4.2若x 是群G 的一个元素,存在一最小的正整数m ,使x m =e ,则称m 为x的阶,试证:C={e,x,x 2, …,x m-1} 证:x 是G 的元素,G 满足封闭性所以,xk 是G 中的元素 C ∈G再证C 是群:1、x i , x j ∈C , x i ·x j = x i+j 若i+j<=m-1,则x i+j ∈C若i+j>m,那么x i+j =x m+k =x m ·x k =x k ∈C 所以C 满足封闭性。
2、存在单位元e.3、显然满足结合性。
4、存在逆元, 设x a ·x b =e=x m x b =x m-ax a ∈C, (x a )-1= x b =x m-a4.3设G 是阶为n 的有限群,则G 的所有元素的阶都不超过n.证明:设G 是阶为n 的有限群,a 是G 中的任意元素,a 的阶素为k , 则此题要证n k ≤首先考察下列n+1个元素aa a a a n 1432,....,,,+由群的运算的封闭性可知,这n+1个元素都属于G ,,而G 中仅有n 个元素,所以由鸽巢原理可知,这n+1个元素中至少有两个元素是相同的,不妨设为aaji i+=(n j ≤≤1)aa a jii*=由群的性质3可知,a j是单位元,即a j=e ,又由元素的阶数的定义可知,当a 为k 阶元素时a k=e ,且k 是满足上诉等式的最小正整数,由此可证n j k ≤≤4.4 若G 是阶为n 的循环群,求群G 的母元素的数目,即G 的元素可表示a 的幂:a,a2……..an解:设n=p 1a1…….p k ak ,共n 个素数的乘积,所以群G 中每个元素都以用这k 个素数来表示,而这些素数,根据欧拉定理,一共有 Φ(n)=n(1-1/p 1)………(1-1/p k )所以群G 中母元素的数目为n(1-1/p 1)………(1-1/p k )个. 4.5证明循环群的子群也是循环群证明:设H 是G=<a>的子群,若H=<e>,显然H 是循环群,否则取H 中最小的正方幂元m a ,下面证明m a 是H 的生成元,易见m a ⊆H ,只要证明H 中的任何元素都可以表成m a 的整数次方,由除法可知存在q 和r,使得l=qm+r,其中0≤r ≤m-1,因此有r a =qm l a -,因为m a 是H 中最小的正方幂元,必有r=0,这就证明出l a =mq a }{m a ∈证明完毕。
概率论与数理统计》课后习题答案第四章

习题4.11.设10个零件中有3个不合格. 现任取一个使用,若取到不合格品,则丢弃重新抽取一个,试求取到合格品之前取出的不合格品数X 的数学期望.解 可得X 的概率分布为0123~77711030120120X ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为7771()012310301201204531208E X =⨯+⨯+⨯+⨯==2..某人有n 把外形相似的钥匙,其中只有1把能打开房门,但他不知道是哪一把,只好逐把试开.求此人直至将门打开所需的试开次数X 的数学期望.解 可得X 的概率分布为12~111n X nn n ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为111()121(1)122E X n n n nn n n n =⨯+⨯++⨯++==3.设5次重复独立试验中每次试验的成功率为0.9,若记失败次数为X ,求X 的数学期望。
解 由题意~(5,0.1)X B ,则X 的数学期望为()50.10.5E X =⨯=4.设某地每年因交通事故死亡的人数服从泊松分布.据统计,在一年中因交通事故死亡一人的概率是死亡两人的概率的21,求该地每年因交通事故死亡的平均人数。
解 设该地每年因交通事故死亡的人数为X ,由题意X 服从泊松分布() (0)P λλ>.因1{1}{2}2P X P X === 即121 41!22!ee λλλλλ--=⇒= 于是X 的数学期望为()4E X λ==所以地每年因交通事故死亡的平均人数为4人。
5.设随机变量X 在区间(1,7)上服从均匀分布,求2{()}P X E X <. 解 因X 在区间(1,7)上服从均匀分布,故X 的数学期望为17()42E X +== 于是22{()}{4}1 {22}6P X E X P X P X <=<=<-<<=6.设连续型随机变量X 的概率密度为01() (,0)0 b ax x p x a b ⎧<<=>⎨⎩其它又知()0.75E X =,求,a b 的值解 由密度函数的性质可得()1p x dx +∞-∞=⎰即1111b aax dx b =⇒=+⎰又由()0.75E X =,可得1()0.75b xp x dx x ax dx +∞-∞=⋅=⎰⎰即0.752ab =+ 求解110.752a b a b ⎧=⎪⎪+⎨⎪=⎪+⎩ 可得 3,2a b ==.7.设随机变量X 的概率密度为0<1()2 120 x x p x x x <⎧⎪=-≤<⎨⎪⎩其它求数学期望()E X解12013312201()() (2) ()133E X xp x dxx xdx x x dx x x x +∞-∞==⋅+⋅-=+-=⎰⎰⎰8.设随机变量X 的概率分布为 X -2 -1 0 1 P 0.2 0.3 0.1 0.4 求(1)(21)E X -;(2)2()E X .解 (1) (21)2()1E X E X -=- 其中()20.210.3010.40.3E X =-⨯-⨯++⨯=-则(21)2()12(0.3)1 1.6E X E X -=-=⨯--=-(2)22222()0.2(2)0.3(1)0.100.41 1.5E X =⨯-+⨯-+⨯+⨯=9.假设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作。
工程数学-线性代数第五版答案第四章

第四章 向量组的线性相关性1. 已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示. 证明 由⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫ ⎝⎛------531400251552000751610421301 ~r ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----000000531400751610421301 ~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示.由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 2. 已知向量组A : a 1=(0, 1, 1)T , a 2=(1, 1, 0)T ;B : b 1=(-1, 0, 1)T , b 2=(1, 2, 1)T , b 3=(3, 2, -1)T , 证明A 组与B 组等价. 证明 由⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=000001122010311112201122010311011111122010311) ,(~~r r A B ,知R (B )=R (B , A )=2. 显然在A 中有二阶非零子式, 故R (A )≥2, 又R (A )≤R (B , A )=2, 所以R (A )=2, 从而R (A )=R (B )=R (A , B ). 因此A 组与B 组等价. 3. 已知R (a 1, a 2, a 3)=2, R (a 2, a 3, a 4)=3, 证明 (1) a 1能由a 2, a 3线性表示; (2) a 4不能由a 1, a 2, a 3线性表示.证明 (1)由R (a 2, a 3, a 4)=3知a 2, a 3, a 4线性无关, 故a 2, a 3也线性无关. 又由R (a 1, a 2, a 3)=2知a 1, a 2, a 3线性相关, 故a 1能由a 2, a 3线性表示.(2)假如a 4能由a 1, a 2, a 3线性表示, 则因为a 1能由a 2, a 3线性表示, 故a 4能由a 2, a 3线性表示, 从而a 2, a 3, a 4线性相关, 矛盾. 因此a 4不能由a 1, a 2, a 3线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关. 5. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由211||11(2)(1)011aA a a a a=-=-+=-知, 当a =-1、2时, R (A )<3, 此时向量组线性相关.6. 设a 1, a 2线性无关, a 1+b , a 2+b 线性相关, 求向量b 用a 1, a 2线性表示的表示式. 解 因为a 1+b , a 2+b 线性相关, 故存在不全为零的数λ1, λ2使 λ1(a 1+b )+λ2(a 2+b )=0, 则121122()b a a λλλλ+=--因a 1, a 2线性无关,故120λλ+≠,不然,由上式得1122120,0a a λλλλ+=⇒==。
统计学 贾俊平第四版第四章课后答案(目前最全)

第四章统计数据的概括性描述4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:(1)(2)(3)(4)说明汽车销售分部的特征答:10名销售人员的在5月份销售的汽车数量较为集中。
4.2 随机抽取25个网络用户,得到他们的年龄数据如下:单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:1、排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄从频数看出,众数Mo有两个:19、23;从累计频数看,中位数Me=23。
(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
为分组情况下的直方图:为分组情况下的概率密度曲线:分组:1、确定组数:()l g 25l g ()1.3981115.64l g (2)l g 20.30103n K =+=+=+=,取k=62、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:4.3 某银行为缩短顾客到银行办理业务等待的时间。
线性代数第四章习题答案

0 a+1 1 −1
1 − a2 = (a + 1)2 (a − 2). a
a −1 a
0 a + 1 −1 − a
1 −1
所以, a = −1 或 a = 2 时向量组线性相关. 更常规的思路是: 向量组 a1 , a2 , a3 线性相关, 则存在不全为零的数 k1 , k2 , k3 使得
k1 a1 + k2 a2 + k3 a3 = 0.
50
第四章 向量组的线性相关性 解: (1) 因为
A= −1 2 3 1 1 0 1 −1 0 0 2 7 2 1 7 2 −1 0 0 2 1 0 1 1 , 0
r2 + 3r1 4 r3 + r1 1
可见 R(A) = 2, 所以该向量组是线性相关的. 或者: 由 −1 2 1 3 + 1 = 4 1 0 1 知线性相关. (2) 因为
1 a3 = −1 1
4
.
解: 由 3(a1 − a) + 2(a2 + a) = 5(a3 + a) 得 2 10 1 1 5 + 1 1 a = (3a1 + 2a2 − 5a3 ) = 6 2 1 3 5 3= 3 0 1
2
;
4 −2 1 , b3 = B : b1 = , b2 = 1 1 1 3 1 2
2
0
4
.
即线性方程组
离散数学(第五版)清华大学出版社第4章习题解答

离散数学(第五版)清华大学出版社第4章习题解答离散数学清华大学出版社第4章习题解答4.1 A:⑤;B:③;C:①;D:⑧;E:⑩4.2 A:②;B:③;C:⑤;D:⑩;E:⑦4.3 A:②;B:⑦;C:⑤;D:⑧;E:④分析题都涉及到关系的表示。
先根据题意将关系表示成集合表达式,然后再进行相应的计算或解答,例如,题中的Is ={,}, Es ={,,,} Is ={,,}; 而题中的R={,,,,}. 为得到题中的R须求解方程x+3y=12,最终得到R={,,}. 求RoR有三种方法,即集合表达式、关系矩阵和关系图的主法。
下面题的关系分别加以说明。
1°集合表达式法将domR,domRUran,ranR的元素列出来,如图所示。
然后检查R的每个有序对,若∈R,则从domR中的x到ranR中的y画一个箭头。
若danR中的x经过2步有向路径到达ranR中的y,则∈RoR。
图可知RoR={,,,,,}. 如果求FoG,则将对应于G中的有序对的箭头画在左边,而将对应于F中的有序对的箭头画在右边。
对应的三个集合分别为domG,ranUdomF,ranF,然后,同样地寻找domG到ranF的2步长的有向路径即可。
2°矩阵方法若M是R的关系矩阵,则RoR的关系矩阵就是M·M,也可记作M,在计算2 48 乘积时的相加不是普通加法,而是逻辑加,即0+0=0,0+1=1+0=1+1=1,根据已知条件得?1 0 0 1? ?1 0 0 1? ?1 0 0 1? ?1 0 0 0? ?1 0 0 0? ?1 0 0 1? 2 ?? ?? ?? M =?????=?? ?0 0 0 1? ?0 0 0 1? ?1 0 0 0? ?1 0 0 0? ?1 0 0 0? ?1 0 0 1? M2中含有7个1,说明RoR中含有7个有序对。
图图3°关系图方法n’’ 设G是R的关系图。
为求R 的关系图G ,无将G 的结点复制到G 中,然后依次检查G的每个结点。
概率论第四章习题解答
X9
EX 9
9
9
8 9
20
2024年8月31日7时4分
P104 练习4.2 题1 SD 1
1,1
f XY
x,
y
1 0
0 x 1, x y x 其它
yx
DZ D2X 1 4DX
EX xf x, ydxdy
0D
y x 1
1 0
x x
xdy
dx
1 2x2dx 2
P113 习题四 一 填空题 7 X与Y相互独立
f
X
x
2x
0
0
x 其它
1,fY
y
x y t
FT t PT t P X Y t fXY x, y dxdy
x yt
1当t 0时:FT t 0dxdy 0
0
x yt
2 当0 t时:FT
t
t
dx
tx 25e5x5 ydy
0
0
1 e5t 5te5t
t,0
x
FT
t
1
e5t
0
5te5t
t0 t0
33
2 EX 2
xi2 pij
i1 j1
20.1 30.3 30.1 2
33
3 EY 2
yi2 pij
12 0.212 0.112 0.1 22 0.1
22 0.132 0.332 0.1 4.8
i1 j1
12 0.2 12 0.1 12 0.1
12 0.1 12 0.1 0.6
2024年8月31日7时4分
P100 练习4.1 题12
2
f XY
x,
y
x
概率论与数理统计(茆诗松)第二版课后第四章习题参考答案

h h ,存在 M2 > 0,使得 P{| Y | ≥ M 2 } < , 4 8
h , 8 h , 4
因| Yn | = | (Yn − Y ) + Y | ≤ | Yn − Y | + | Y |,有 P{| Yn | ≥ M 2 + 1} ≤ P{| Yn − Y | ≥ 1} + {| Y | ≥ M 2 } <
n → +∞
则 {D (x + n)} 的极限函数是常量函数 f (x) = 1,有 f (−∞) = 1 ≠ 0, 故 {D (x + n)} 的极限函数不是分布函数; (2)若 x ≥ 0,有 x +
1 1⎞ 1⎞ ⎛ ⎛ > 0 , D⎜ x + ⎟ = 1 ,即 lim D⎜ x + ⎟ = 1 , n → +∞ n n⎠ n⎠ ⎝ ⎝ 1 1 1⎞ 1⎞ ⎛ ⎛ 时,有 x + < 0 , D⎜ x + ⎟ = 0 ,即 lim D⎜ x + ⎟ = 0 , n → +∞ n x n⎠ n ⎠ ⎝ ⎝
⎞ ⎟→0; |⎟ ⎠ ⎞ ⎟→0, |⎟ ⎠
⎛ | Xn − X | 充分性:设 n → +∞ 时,有 E ⎜ ⎜ 1+ | X − X n ⎝
因 P{| X n − X | ≥ ε } =
| y| ≥
∫ εp( y)dy =
1+ ε
ε
| y| ≥
∫ε 1+ ε
ε
p ( y )dy ≤
1+ ε
ε
| y| ≥
ε2 , 1+ ε
⎛ | Xn − X | 则 E⎜ ⎜ 1+ | X − X n ⎝
概率论第4章习题参考解答

概率论第4章习题参考解答 1. 若每次射击中靶的概率为0.7, 求射击10炮, 命中3炮的概率, 至少命中3炮的概率, 最可能命中几炮. 解: 设ξ为射击10炮命中的炮数, 则ξ~B (10,0.7), 命中3炮的概率为 =⨯⨯==733103.07.0}3{C P ξ0.0090至少命中3炮的概率, 为1减去命中不到3炮的概率, 为=⨯⨯-=<-=≥∑=-2010103.07.01}3{1}3{i i i i C P P ξξ0.9984因np +p =10×0.7+0.7=7.7不是整数, 因此最可能命中[7.7]=7炮. 2. 在一定条件下生产某种产品的废品率为0.01, 求生产10件产品中废品数不超过2个的概率. 解: 设ξ为10件产品中的废品数, 则ξ~B (10,0.01), 则废品数不超过2个的概率为=⨯⨯=≤∑=-20101099.001.0}2{i i i iC P ξ0.99993. 某车间有20部同型号机床, 每部机床开动的概率为0.8, 若假定各机床是否开动彼此独立, 每部机床开动时所消耗的电能为15个单位, 求这个车间消耗电能不少于270个单位的概率. 解: 设每时刻机床开动的数目为ξ, 则ξ~B (20,0.8), 假设这个车间消耗的电能为η个单位, 则η=15ξ, 因此2061.02.08.0}18{}15270{}27015{}270{20182020=⨯⨯==≥=≥=≥=≥∑=-i i i iC P P P P ξξξη4. 从一批废品率为0.1的产品中, 重复抽取20个进行检查, 求这20个产品中废品率不大于0.15的概率. 解: 设这20个产品中的废品数为ξ, 则ξ~B (20,0.1), 假设这20个产品中的废品率为η, 则η=ξ/20. 因此∑=-⨯⨯=≤=≤=≤320209.01.0}3{}15.020{}15.0{i i i iC P P P ξξη=0.8675. 生产某种产品的废品率为0.1, 抽取20件产品, 初步检查已发现有2件废品, 问这20件中, 废品不少于3件的概率. 解: 设ξ为这20件产品中的废品数, 则ξ~B (20,0.1), 又通过检查已经知道ξ定不少于2件的条件, 则要求的是条件概率}2{}23{}2|3{≥≥⋂≥=≥≥ξξξξξP P P因事件}3{}2{≥⊃≥ξξ, 因此2}23{≥=≥⋂≥ξξξ因此5312.06083.02852.019.01.0209.019.01.01}{1}2{1}{}2{1}{}2{}{}{}{}2{}3{}2|3{192018222010202202202202203=-=⨯⨯--⨯⨯-==-=-===-===-=====≥≥=≥≥∑∑∑∑∑∑======C i P P i P P i P P i P i P i P P P P i i i i i i ξξξξξξξξξξξξξ6. 抛掷4颗骰子, ξ为出现1点的骰子数目, 求ξ的概率分布, 分布函数, 以及出现1点的骰子数目的最可能值. 解: 因掷一次骰子出现一点的概率为1/6, 则ξ~B (4,1/6), 因此有⎪⎪⎩⎪⎪⎨⎧≥<≤⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛<==⎪⎭⎫ ⎝⎛⨯⨯==∑≤--4140656100)(),4,3,2,1,0(6561}{4444x x C x x F k C k P x k kk k kk kξ或者算出具体的值如下所示:ξ0 1 2 3 4 P0.48230.38580.11570.01540.0008⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥<≤<≤<≤<≤<=41439992.0329838.0218681.0104823.000)(x x x x x x x F从分布表可以看出最可能值为0, 或者np +p =(4/6)+1/6=5/6小于1且不为整数, 因此最可能值为[5/6]=0. 7. 事件A 在每次试验中出现的概率为0.3, 进行19次独立试验, 求(1)出现次数的平均值和标准差; (2)最可能出现的次数. 解: 设19次试验中事件A 出现次数为ξ, 则ξ~B (19,0.3), 因此 (1)ξ的数学期望为E ξ=np =19×0.3=5.7 方差为Dξ=np (1-p )=19×0.3×0.7=3.99标准差为997.199.3===ξσξD(2)因np +p =5.7+0.3=6为整数, 因此最可能值为5和6. 8. 已知随机变量ξ服从二项分布, E ξ=12, D ξ=8, 求p 和n . 解: 由E ξ=np =12 (1) 和D ξ=np (1-p )=8 (2) 由(1)得n =12/p , 代入到(2)得 12(1-p )=8, 解出p =(12-8)/12=1/3=0.3333 代回到(1)式得n =12/p =12×3=36 9. 某柜台上有4个售货员, 并预备了两个台秤, 若每个售货员在一小时内平均有15分钟时间使用台秤, 求一天10小时内, 平均有多少时间台秤不够用. 解: 每个时刻构成一n =4的贝努里试验, 且p =15/60=0.25, 因此, 设ξ为每个时刻要用秤的售货员数, 则ξ~B (4, 0.25), 当ξ>2时, 台秤不够用. 因此每时刻台秤不够用的概率为=+⨯⨯=>433425.075.025.0)2(C P ξ0.0508因此10个小时内平均有0.0508×10=0.508个小时台秤不够用. 10. 已知试验的成功率为p , 进行4重贝努里试验, 计算在没有全部失败的情况下, 试验成功不止一次的概率. 解: 设ξ为4次试验中的成功数, 则ξ~B (4,p ), 事件"没有全部失败"即事件{ξ>0}, 而事件"试验成功不止一次"即事件{ξ>1}, 因此要求的是条件概率P {ξ>1|ξ>0}, 又因事件{ξ>1}被事件{ξ>0}包含, 因此这两个事件的交仍然是{ξ>1}, 因此434141}0{1}1{}0{1}0{}1{}0|1{q pq q P P P P P P ---===-=-=-=>>=>>ξξξξξξξ其中q =1-p 11. ξ服从参数为2,p 的二项分布, 已知P (ξ≥1)=5/9, 那么成功率为p 的4重贝努里试验中至少有一次成功的概率是多少?解: 因ξ~B (2,p ), 则必有9/5)1(1)0(1)1(2=--==-=≥p P P ξξ, 解得3/13/213/219/49/51)1(2=-==-=-=-p p p 则假设η为成功率为1/3的4重贝努里试验的成功次数, η~B (4,1/3), 则802.081161321)1(1)0(1)1(44=-=⎪⎭⎫⎝⎛-=--==-=≥p P P ηη12. 一批产品20个中有5个废品, 任意抽取4个, 求废品数不多于2个的概率解: 设ξ为抽取4个中的废品数, 则ξ服从超几何分布, 且有==≤∑=-204204155}2{i i i C C C P ξ0.968 13. 如果产品是大批的, 从中抽取的数目不大时, 则废品数的分布可以近似用二项分布公式计算. 试将下例用两个公式计算, 并比较其结果. 产品的废品率为0.1, 从1000个产品中任意抽取3个, 求废品数为1的概率. 解: 设任抽3个中的废品数为ξ, 则ξ服从超几何分布, 废品数为0.1×1000=100 ===3100029001100}1{C C C P ξ0.2435 而如果用二项分布近似计算, n =3, p =0.1, ξ~B (3,0.1)=⨯⨯≈=2139.01.0}1{C P ξ0.2430近似误差为0.0005, 是非常准确的.14. 从一副朴克牌(52张)中发出5张, 求其中黑桃张数的概率分布. 解: 设ξ为发出的5张中黑桃的张数, 则ξ服从超几何分布, 则)5,4,3,2,1,0(}{5525135213===--i C C C i P i i ξ则按上式计算出概率分布如下表所示:ξ0 1 2 3 4 5 P0.22150.41140.27430.08150.01070.000515. 从大批发芽率为0.8的种子中, 任取10粒, 求发芽粒数不小于8粒的概率. 解: 设ξ为10粒种子中发芽的粒数, 则ξ服从超几何分布, 但可以用二项分布近似, 其中p =0.8, n =10, 则∑=-⨯⨯=≥10810102.08.0}8{i i i iC P ξ=0.677816. 一批产品的废品率为0.001, 用普哇松分布公式求800件产品中废品为2件的概率, 以及不超过2件的概率. 解: 设ξ为800件产品中的废品数, 则ξ服从超几何分布, 可以用二项分布近似, 则ξ~B (800, 0.001), 而因为试验次数很大废品率则很小, 可以用普阿松分布近似, 参数为 λ=np =800×0.001=0.89526.0!8.0}2{1438.028.0}2{28.08.02=≈≤=≈=∑=--i i e i P e P ξξ 17. 某种产品表面上的疵点数服从普哇松分布, 平均一件上有0.8个疵点, 若规定疵点数不超过1个为一等品, 价值10元, 疵点数大于1不多于4为二等品, 价值8元, 4个以上为废品, 求产品为废品的概率以及产品的平均价值. 解: 设ξ为产品表面上的疵点数, 则ξ服从普哇松分布, λ=0.8, 设η为产品的价值, 是ξ的函数. 则产品为废品的概率为0014.0!8.01}4{1}4{48.0=-=≤-=>∑=-i i e i P P ξξ==≤==∑=-18.0!8.0}1{}10{i i e i P P ξη0.8088==≤<==∑=-428.0!8.0}41{}8{i i e i P P ξη0.1898则产品的平均价值为Eη = 10×P {η=10}+8×P {η=8}=10×0.8088+8×0.1898=9.6064(元) 18. 一个合订本共100页, 平均每页上有两个印刷错误, 假定每页上印刷错误的数目服从普哇松分布, 计算该合订本中各页的印刷错误都不超过4个的概率. 解: 设ξ为每页上的印刷错误数目, 则ξ服从普哇松分布, λ=2, 则1页印刷错误都不超过4个的概率为 ==≤∑=-402!2}4{i i e i P ξ0.9473而100页上的印刷错误都不超过4个的概率为[]=≤100}4{ξP 0.00445419. 某型号电子管的“寿命”ξ服从指数分布, 如果它的平均寿命E ξ=1000小时, 写出ξ的概率密度, 并计算P (1000<ξ≤1200). 解: 因Eξ=1000=1/λ, 其概率密度为⎪⎩⎪⎨⎧≤>=-0010001)(1000x x ex xϕ0667.0)12001000(2.111000120010001000=-=-=≤<----e e ee P ξ20. ξ~N (0,1), Φ0(x )是它的分布函数, φ0(x )是它的概率密度, Φ0(0), φ0(0), P (ξ=0)各是什么值? 解: 因有 20221)(x ex -=πϕ, ⎰∞--=Φxt dt ex 20221)(π, 因此φ0(x )为偶函数, 由对称性可知Φ0(0)=0.5, 并有πϕ21)0(0=,因ξ为连续型随机变量, 取任何值的概率都为0, 即P (ξ=0)=0.21. 求出19题中的电子管在使用500小时没坏的条件下, 还可以继续使用100小时而不坏的概率?解: 要求的概率为P (ξ>600|ξ>500), 因此905.0}500{}600{}500|600{1.010005001000600===>>=>>---e e eP P P ξξξξ22. 若ξ服从具有n 个自由度的χ2-分布, 证明ξ的概率密度为⎪⎪⎩⎪⎪⎨⎧<≥⎪⎭⎫ ⎝⎛Γ=---022)(21212x x e n x x x nn ϕ称此分为为具有n 个自由度的χ-分布 证: 设ξη=, 则因ξ的概率密度函数为⎪⎪⎩⎪⎪⎨⎧≤>⎪⎭⎫ ⎝⎛Γ=--0221)(2122x x e x n x xn nξϕη的分布函数为)0()()()()()(22>=≤=≤=≤=x x F x P x P x P x F ξηξξη对两边求导得)0(22222)(2)(2121222222>⎪⎭⎫ ⎝⎛Γ=⎪⎭⎫ ⎝⎛Γ==-----x en x en x xx x x x n n x n n ξηϕϕ23. ξ~N (0,1), 求P {ξ≥0}, P {|ξ|<3}, P {0<ξ≤5}, P {ξ>3}, P {-1<ξ<3} 解: 根据ξ的对称性质及查表得: P {ξ≥0}=1-Φ0(0)=0.5 P {|ξ|<3}=2Φ0(3)-1=2×0.99865-1=0.9973 P {0<ξ≤5}=Φ0(5)-0.5=0.5P {ξ>3}=1-Φ0(3)=1-0.99865=0.00135P {-1<ξ<3}=Φ0(3)-Φ0(-1)=Φ0(3)+Φ0(1)-1=0.99865+0.8413-1=0.83995 24. ξ~N (μ,σ2), 为什么说事件"|ξ-μ|<2σ"在一次试验中几乎必然出现?解: 因为)1,0(~N σμξ- 19545.0197725.021)2(2}2{}2|{|0≈=-⨯=-Φ=<-=<-σμξσμξP P因此在一次试验中几乎必然出现.25. ξ~N (10,22), 求P (10<ξ<13), P (ξ>13), P (|ξ-10|<2). 解: 因为)1,0(~210N -ξ6826.018413.021)1(2}1210{}2|10{|0.0668193319.01)5.1(1}5.1210{}13{43319.05.093319.0)0()5.1(}5.12100{}1310{0000=-⨯=-Φ=<-=<-=-=Φ-=>-=>=-=Φ-Φ=<-<=<<ξξξξξξP P P P P P26. 若上题中已知P {|ξ-10|<c }=0.95, P {ξ<d }=0.0668, 分别求c 和d .解: 因为)1,0(~210N -ξ, 则有95.01)2(2}2210{}|10{|0=-Φ=<-=<-cc P c P ξξ 解得975.0295.01)2(0=+=Φc, 查表得,96.12=c得c =3.92 再由5.00668.0)210(}210210{}{0<=-Φ=-<-=<d d P d P ξξ知,0210<-d 因此0668.0)210(1)210(00=-Φ-=-Φd d即9332.00668.01)210(0=-=-Φd ,查表得5.1210=-d , 解得7310=-=d27. 若ξ~N (μ,σ2), 对于P {μ-kσ<ξ<μ+kσ}=0.90, 或0.95, 或0.99, 分别查表找出相应的k值.解: 先求P {μ-kσ<ξ<μ+kσ}=0.90对应的k 值. 因)1,0(~N σμξ-, 因此 90.01)(2}{}{0=-Φ=<-=+<<-k k P k k P σμξσμξσμ 即95.0290.01)(0=+=Φk , 查表得k =1.64 同理, 由975.0295.01)(0=+=Φk , 查表得k =1.96 由995.0299.01)(0=+=Φk , 查表得k =2.57 28. 某批产品长度按N (50, 0.252)分布, 求产品长度在49.5cm 和50.5cm 之间的概率, 长度小于49.2cm 的概率.解: 设ξ为产品长度, 则ξ~N (50, 0.252), 且有)1,0(~25.050N -ξ, 则9545.0197725.021)2(2}225.050{}225.0502{}5.505.49{0=-⨯=-Φ=<-=<-<-=<<ξξξP P P0006871.09993129.01)2.3(1)2.3(}25.0502.4925.050{}2.49{00=-=Φ-=-Φ=-<-=<ξξP P29. ξi ~N (0,1)(i =1,2,3), 并且ξ1,ξ2,ξ3相互独立, ∑==3131i i ξξ,∑=-=312)(i i ξξη, 求),cov(,),,cov(1ηξηξξE解: 此题要用到, 两个独立的服从正态分布的随机变量相加后得到的随机变量仍然服从正态分布. 因此, 因为3131,031=⎪⎭⎫ ⎝⎛==∑=i i D D E ξξξ, 则)31,0(~N ξ313131)()cov(2131111==⎪⎭⎫ ⎝⎛==∑=ξξξξξξξE E E i i32313121)cov(2)2()(22222=+⨯-=+-=+-=-ξξξξξξξξξξE E E E i i i i i因此2323)()(312312=⨯=-=⎪⎭⎫ ⎝⎛-=∑∑==i i i i E E E ξξξξη ξξ-i 也服从正态分布, 且有03131)]([),cov(2=-=-=-=-ξξξξξξξξξE E E i i i即ξ与ξξ-i 不相关, 而因为它们服从正态分布, 因此也就是ξ与ξξ-i 相互独立,则ξ与2)(ξξ-i 也相互独立, 则ξ与η中的加和中的每一项相互独立, 当然也与η相互独立, 因此有0),cov(=ηξ, 因为相互独立的随机变量一定不相关.30. (ξ,η)有联合概率密度22)(21,2122ηξζπ+=+-y x e , 求ζ的概率密度.解: 由联合概率密度看出, ξ与η相互独立服从标准正态分布, 则有 ξ2与η2也相互独立且服从自由度为1的χ2-分布, 即ξ2~χ2(1), η2~χ2(1), 因此ζ=ξ2+η2~χ2(2), 即它的概率密度为⎪⎩⎪⎨⎧<>=-00212x x exζϕ即ζ服从λ=1/2的指数分布.。
概率论第四章课后习题解答

概率论第四章习题解答1(1)在下列句子中随机地取一个单词,以X 表示取到的单词所饮食的字母个数,写出X 的分布律并求数学期望()E X 。
“THE GIRL PUT ON HER BEAUTIFUL RED HAT ” (2)在上述句子的30个字母中随机地取一个字母,以Y 表示取到的字母所在单词所包含的字母数,写出Y 的分布律并求()E Y(3)一人掷骰子,如得6点则掷第二次,此时得分为6加第二次得到的点数;否则得分为第一次得到的点数,且不能再掷,求得分X 的分布律。
解 (1)在所给的句子中任取一个单词,则其所包含的字母数,即随机变量X 的取值为:2,3,4,9,其分布律为所以 151115()234988884E X =⨯+⨯+⨯+⨯=。
(2)因为Y 的取值为2,3,4,9当2Y =时,包含的字母为“O ”,“N ”,故121{2}3015C P Y ===; 当3Y =时,包含的3个字母的单词共有5个,故135151{3}30302C P Y ==== 当4Y =时,包含的4个字母的单词只有1个,故1442{4}303015C P Y ==== 当9Y =时,包含的9个字母的单词只有1个,故 993{9}303010P Y ====112314673()234915215103015E Y =⨯+⨯+⨯+⨯==。
(3)若第一次得到6点,则可以掷第二次,那么他的得分为:X =7,8,9,10,11,12;若第一次得到的不是6点,则他的得分为1,2,3,4,5。
由此得X 的取值为: 1,2,3,4,5,7,8,9,10,11,12。
1(1)(2)(3)(4)(5)6P X P X P X P X P X ==========(7)(8)(9)(10)P X P X P X P X =======(11)(12)P X P X ==== 111=⨯= 6121711215759()63663612i i E X i i ===+=+=∑∑2 某产品的次品率为0.1,检验员每天检验4次,每次随机地取10件产品进行检验,如果发现其中的次品多于1,就去调整设备。
离散数学答案-第四章习题解答.doc

习题四1.用归结法证明:(1)\= p^q^r(2)p T r , q — r# pvqir(3)p W 匕(p T q)v(p f r)(4)p /\q r |= (/? ^ r) v(t? r)(5)p v v r , p t r A q v『⑹(〃T q) T O T 厂)f= p T (q T r)解(1)首先将p I q , p I f , 7p T q八门化为合取范式。
p T q o —\p 7 q , p T r o —yp v r ,—>(# T q /\ 厂)u> -1(-1/? v(q A /*)) u> /? /\ (—v -i厂)给出子句集\rpy q’rpy l ”,p,->^rv—»r}的反驳如下。
①rpy q②~yp v r③p④-it?v—«r⑤q由①和③⑥r由②和③⑦由④和⑤⑧口由⑥和⑦因此,p — q , p T r b p I q z⑵将p T r, q T厂7p v q —厂)化为合取范式。
/? T 厂O -1〃\/儿q t ro-yq 7 丫、-i( p v q r) <=> (p v q) /\—^r 给111子句集{ v r, v r, p v ty, -.r}的反驳如下:—p v r②->q v r③p y q④—if⑤q 7 T rti①和③⑥r由②和⑤⑦□由④和⑥因此,p—> r, q T r 匕p v q T r。
⑶首先将p t qy r, -•((/?^^)v(p^r))化为合取范式。
p T q \z 厂 o -yp v <7 v r ,T q) \/ (p —> r)) o -i((-ip v^) v (-i/? v r))<=> p A —yq A -ir给出子句集\rp7 q\/ F ,p, -yq , 的反驳如下。
—7 q7 丫 Prq—>rq7 丫由①和② r由③和⑤ □由④和⑥①②③④⑤⑥⑦因此,p T qvr \= (j?->(7)v(/?^r)(4)首先将 p /\qf r, -i((pr) v ((? -> r))化为合取范式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章串注:子串的定义是:串中任意个连续的字符组成的子序列,并规定空串是任意串的子串,任意串是其自身的子串。
若字符串长度为n(n>0),长为n的子串有1个,长为n-1的子串有2个,长为n-2的子串有3个,……,长为1的子串有n个。
由于空串是任何串的子串,所以本题的答案为:8*(8+1)/2+1=37。
故选B。
但某些教科书上认为“空串是任意串的子串”无意义,所以认为选C。
为避免考试中的二意性,编者认为第9题出得好。
二、判断题三.填空题1.(1) 由空格字符(ASCII值32)所组成的字符串 (2)空格个数2.字符3.任意个连续的字符组成的子序列4.5 5.O(m+n)6.01122312 7.01010421 8.(1)模式匹配 (2)模式串9.(1)其数据元素都是字符(2)顺序存储(3)和链式存储(4)串的长度相等且两串中对应位置的字符也相等10.两串的长度相等且两串中对应位置的字符也相等。
11.’xyxyxywwy’ 12.*s++=*t++ 或(*s++=*t++)!=‘\0’13.(1)char s[ ] (2) j++ (3) i >= j14.[题目分析]本题算法采用顺序存储结构求串s和串t的最大公共子串。
串s用i指针(1<=i<=s.len)。
t串用j指针(1<=j<=t.len)。
算法思想是对每个i(1<=i<=s.len,即程序中第一个WHILE循环),来求从i开始的连续字符串与从j(1<=j<=t.len,即程序中第二个WHILE循环)开始的连续字符串的最大匹配。
程序中第三个(即最内层)的WHILE循环,是当s中某字符(s[i])与t中某字符(t[j])相等时,求出局部公共子串。
若该子串长度大于已求出的最长公共子串(初始为0),则最长公共子串的长度要修改。
程序(a):(1)(i+k<=s.len)AND(j+k<=t.len) AND(s[i+k]=t[j+k])//如果在s和t的长度内,对应字符相等,则指针k 后移(加1)。
(2)con:=false //s和t对应字符不等时置标记退出(3)j:=j+k //在t串中,从第j+k字符再与s[i]比较(4)j:=j+1 //t串取下一字符(5)i:=i+1 //s串指针i后移(加1)。
程序(b):(1) i+k<=s.len && j+k<=t.len && s[i+k]==t[j+k] //所有注释同上(a)(2) con=0 (3) j+=k (4) j++ (5) i++ 15.(1)0 (2)next[k]16.(1)i:=i+1 (2)j:=j+1 (3)i:=i-j+2 (4)j:=1; (5)i-mt(或i:=i-j+1) (6)017.程序中递归调用(1)ch1<>midch //当读入不是分隔符&和输入结束符$时,继续读入字符(2)ch1=ch2 //读入分隔符&后,判ch1是否等于ch2,得出真假结论。
(3)answer:=true(4)answer:=false(5)read(ch)(6)ch=endch18.(1)initstack(s) //栈s初始化为空栈。
(2) setnull (exp) //串exp初始化为空串。
(3) ch in opset //判取出字符是否是操作符。
(4) push (s,ch) //如ch是运算符,则入运算符栈s。
(5) sempty (s) //判栈s是否为空。
(6) succ := false //若读出ch是操作数且栈为空,则按出错处理。
(7) exp (8)ch //若ch是操作数且栈非空,则形成部分中缀表达式。
(9) exp (10) gettop(s) //取栈顶操作符。
(11) pop(s) //操作符取出后,退栈。
(12) sempty(s) //将pre的最后一个字符(操作数)加入到中缀式exp的最后。
四.应用题1.串是零个至多个字符组成的有限序列。
从数据结构角度讲,串属于线性结构。
与线性表的特殊性在于串的元素是字符。
2.空格是一个字符,其ASCII 码值是32。
空格串是由空格组成的串,其长度等于空格的个数。
空串是不含任何字符的串,即空串的长度是零。
3.最优的T(m,n)是O (n )。
串S2是串S1的子串,且在S1中的位置是1。
开始求出最大公共子串的长度恰是串S2的长度,一般情况下,T(m,n) =O(m*n)。
4.朴素的模式匹配(Brute -Force )时间复杂度是O(m *n ),KMP 算法有一定改进,时间复杂度达到O(m +n )。
本题也可采用从后面匹配的方法,即从右向左扫描,比较6次成功。
另一种匹配方式是从左往右扫描,但是先比较模式串的最后一个字符,若不等,则模式串后移;若相等,再比较模式串的第一个字符,若第一个字符也相等,则从模式串的第二个字符开始,向右比较,直至相等或失败。
若失败,模式串后移,再重复以上过程。
按这种方法,本题比较18次成功。
5.KMP 算法主要优点是主串指针不回溯。
当主串很大不能一次读入内存且经常发生部分匹配时,KMP 算法的优点更为突出.6.模式串的next 函数定义如下:next [j ]=⎪⎩⎪⎨⎧=<<=-+--其它情况当此集合不空时‘且时当1}'...''... j k 1 |k max{101111j k j k p p p p j7.解法同上题6,其next 和nextval 值分别为0112123422和010*******。
8.解法同题6,t 串的next 和nextval 函数值分别为0111232和0110132。
9.解法同题6,其next 和nextval 值分别为011123121231和011013020131。
10.p1的next 和nextval 值分别为:0112234和0102102;p2的next 和nextval 值分别为:0121123和0021002。
11.next 数组值为011234567 改进后的next 数组信息值为010101017。
12.011122312。
13.next 定义见题上面6和下面题20。
串p 的next 函数值为:01212345634。
14.(1)S 的next 与nextval 值分别为012123456789和002002002009,p 的next 与nextval 值分别为012123和002003。
(2)利用BF算法的匹配过程:利用KMP算法的匹配过程:第一趟匹配: aabaabaabaac 第一趟匹配:aabaabaabaacaabaac(i=6,j=6)aabaac(i=6,j=6)第二趟匹配:aabaabaabaac 第二趟匹配:aabaabaabaacaa(i=3,j=2) (aa)baac 第三趟匹配:aabaabaabaac 第三趟匹配:aabaabaabaaca(i=3,j=1) (成功) (aa)baac第四趟匹配: aabaabaabaacaabaac(i=9,j=6)第五趟匹配: aabaabaabaacaa(i=6,j=2)第六趟匹配: aabaabaabaaca(i=6,j=1)第七趟匹配: aabaabaabaac(成功) aabaac(i=13,j=7)15.(1)p的nextval函数值为0110132。
(p的next函数值为0111232)。
(2)利用KMP(改进的nextval)算法,每趟匹配过程如下:第一趟匹配: abcaabbabcabaacbacbaabcab(i=5,j=5)第二趟匹配: abcaabbabcabaacbacbaabc(i=7,j=3)第三趟匹配: abcaabbabcabaacbacbaa(i=7,j=1)第四趟匹配: abcaabbabcabaac bacba(成功) abcabaa(i=15,j=8)16.KMP算法的时间复杂性是O(m+n)。
p的next和nextval值分别为01112212321和01102201320。
17.(1)p的nextval函数值为01010。
(next函数值为01123)(2)利用所得nextval数值,手工模拟对s的匹配过程,与上面16题类似,为节省篇幅,故略去。
18.模式串T的next和nextval值分别为0121123和0021002。
19.第4行的p[J]=p[K]语句是测试模式串的第J个字符是否等于第K个字符,如是,则指针J和K均增加1,继续比较。
第6行的p[J]=p[K]语句的意义是,当第J个字符在模式匹配中失配时,若第K个字符和第J个字符不等,则下个与主串匹配的字符是第K个字符;否则,若第K个字符和第J个字符相等,则下个与主串匹配的字符是第K个字符失配时的下一个(即NEXTVAL[K])。
该算法在最坏情况下的时间复杂度O(m2)。
20.(1)当模式串中第一个字符与主串中某字符比较不等(失配)时,next[1]=0表示模式串中已没有字符可与主串中当前字符s[i]比较,主串当前指针应后移至下一字符,再和模式串中第一字符进行比较。
(2)当主串第i个字符与模式串中第j个字符失配时,若主串i不回溯,则假定模式串第k个字符与主串第i个字符比较,k值应满足条件1<k<j 并且‘p1…p k-1’=‘p j-k+1…p j-1’,即k为模式串向后移动的距离,k值有多个,为了不使向右移动丢失可能的匹配,k要取大,由于max{k}表示移动的最大距离,所以取max{k},k的最大值为j-1。
(3)在上面两种情况外,发生失配时,主串指针i不回溯,在最坏情况下,模式串从第1个字符开始与主串第i个字符比较,以便不致丢失可能的匹配。
21.这里失败函数f,即是通常讲的模式串的next函数,其定义见本章应用题的第6题。
进行模式匹配时,若主串第i个字符与模式串第j个字符发生失配,主串指针i不回溯,和主串第i个字符进行比较的是模式串的第next[j]个字符。
模式串的next函数值,只依赖于模式串,和主串无关,可以预先求出。
该算法的技术特点是主串指针i不回溯。
在经常发生“部分匹配”和主串很大不能一次调入内存时,优点特别突出。
22.失败函数(即next)的值只取决于模式串自身,若第j个字符与主串第i个字符失配时,假定主串不回溯,模式串用第k(即next[j])个字符与第i个相比,有‘ p1…p k-1’=‘p j-k+1…p j-1’,为了不因模式串右移与主串第i个字符比较而丢失可能的匹配,对于上式中存在的多个k值,应取其中最大的一个。
