断裂力学总结
材料的断裂力学分析

材料的断裂力学分析在材料科学和工程领域中,断裂力学是一门研究材料在外力作用下如何发生破坏的学科。
通过断裂力学的分析,我们可以了解材料在正常使用条件下的破坏原因,以及如何提高材料的断裂韧性和强度。
本文将对材料的断裂力学进行详细分析。
1. 断裂力学的基本概念在了解材料的断裂力学之前,我们需要了解几个基本概念。
1.1 断裂断裂是指材料在外部应力作用下发生破坏、分离的过程。
断裂可以分为韧性断裂和脆性断裂两种类型。
韧性断裂是指材料在破坏之前会出现塑性变形,具有一定的延展性;而脆性断裂是指材料在外力作用下迅速发生破坏而不发生明显的塑性变形。
1.2 断裂韧性断裂韧性是指材料抵抗断裂破坏的能力。
一个具有高断裂韧性的材料可以在外力作用下发生一定程度的塑性变形,从而使其拉伸长度增加。
1.3 断裂强度断裂强度是指材料在破坏前能够承受的最大应力。
断裂强度可以通过拉伸实验等方式进行测定。
2. 断裂力学的分析方法断裂力学的分析方法主要有线弹性断裂力学和非线弹性断裂力学两种。
2.1 线弹性断裂力学线弹性断裂力学假设材料在破坏前的行为是线弹性的,并且材料的破坏是由于应力达到了一定的临界值所引起的。
在线弹性断裂力学中,断裂过程可以通过应力强度因子和断裂韧性来描述。
2.2 非线弹性断裂力学非线弹性断裂力学考虑了材料在破坏前的非线性行为,如塑性变形、蠕变等。
非线弹性断裂力学可以更准确地预测材料的破坏行为,但其计算复杂度较高。
3. 断裂力学的应用断裂力学在材料科学和工程中具有广泛的应用。
3.1 破坏分析通过断裂力学的分析,我们可以确定材料在受力状态下的破坏原因,从而改进材料的设计和制备工艺。
例如,在航空航天领域,对材料的断裂力学进行精确分析可以提高飞行器的安全性和可靠性。
3.2 材料评估通过断裂力学的测试和分析,我们可以评估材料的断裂韧性和强度,为材料的选择和应用提供依据。
这对于许多行业来说是至关重要的,如汽车制造、建筑工程等。
3.3 研发新材料断裂力学的理论和实验研究对于开发新的高性能材料具有重要意义。
第十讲--断裂力学

纹长 可计算线性解BC部
分,称为等效裂纹长度。
等效模型法:以等效裂纹长度代替裂纹原长对应力强度因子进行修正。
等效裂纹长度和应力强度因子
令按等效裂纹长度计算的应力场在r = R-ry(B点)的应力等于σys,则
:应力松驰后的应力强度因子
σys:y方向屈服应力,σys =σs(平面应力),(平面应变)
长度Δa,扩展部分各点的位移
则释放的能量为
II型和III型裂纹
,
μ:剪切弹性模量
平面应力,平面应变
6.脆性断裂的K准则
KI= KIC
临界应力:(剩余强度)
临界裂纹长度:
KC:平面应力断裂韧度
KIC:平面应变断裂韧度
板厚增加到一定值后,断裂韧度由KC(平面应力断裂韧度)降低至一稳定值KIC(平面应变断裂韧度)。
裂纹尖端应力强度子
平面应变
k =
平面应力
2)滑开型(II型)裂纹尖端应力和位移场
3)撕开型(III型)裂纹尖端应力和位移场
4.应力和位移场的一般形式
,
1)r ( 0,σij ( ((应力奇异性)
2)应力强度因子是代表应力场强度的物理量
σ:名义应力;Y:形状系数
5.应力强度因子和能量释放率的关系
设图示I型裂纹扩展一微小
在平面应力条件下,裂纹尖端有较大范围的塑性变形,线弹性断裂力学K准则不适用(塑性区较小时,经修正后仍可用K准则)。
7.裂纹尖端塑性区的形状和尺寸
a.平面应力情况
主应力
应用Von Mises屈服条件
得出裂纹尖端塑性区的形状
b.平面应变情况
裂纹尖端塑性区的形状
,
考虑塑性区内塑性变形引起的应力松驰后的塑性区修正为
断裂力学
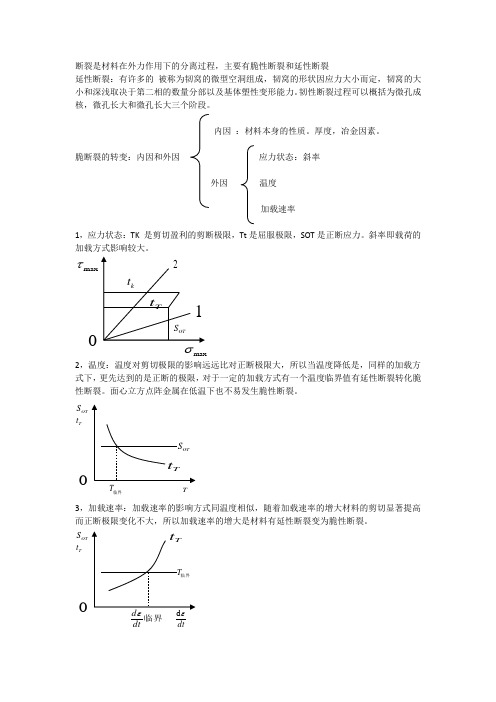
断裂是材料在外力作用下的分离过程,主要有脆性断裂和延性断裂延性断裂:有许多的 被称为韧窝的微型空洞组成,韧窝的形状因应力大小而定,韧窝的大小和深浅取决于第二相的数量分部以及基体塑性变形能力。
韧性断裂过程可以概括为微孔成核,微孔长大和微孔长大三个阶段。
内因 :材料本身的性质。
厚度,冶金因素。
脆断裂的转变:内因和外因 应力状态:斜率 外因 温度加载速率1,应力状态:TK 是剪切盈利的剪断极限,Tt 是屈服极限,SOT 是正断应力。
斜率即载荷的加载方式影响较大。
2,温度:温度对剪切极限的影响远远比对正断极限大,所以当温度降低是,同样的加载方式下,更先达到的是正断的极限,对于一定的加载方式有一个温度临界值有延性断裂转化脆性断裂。
面心立方点阵金属在低温下也不易发生脆性断裂。
3,加载速率:加载速率的影响方式同温度相似,随着加载速率的增大材料的剪切显著提高而正断极限变化不大,所以加载速率的增大是材料有延性断裂变为脆性断裂。
O T TS t d dtεd d t临界O T TS t TT 临界maxτm axσ0断裂机制:第一类是由材料屈服为主的塑性破坏,第二类是一裂纹失稳扩展的断裂破坏。
缺陷对两类破坏都有重要影响,但是机制不同。
塑性破坏而言缺陷主要影响了结构的有效承载面积,破坏的临界条件主要有塑性极限载荷控制。
裂纹失稳扩展的断裂而言缺陷引起的局部应力应变场对结构强度起主导作用。
高强材料:断裂时,裂纹端部发生很小的的屈服:线弹性断裂力学理论。
含有裂纹的材料 延性材料:断裂时裂纹端部发生很大的屈服:弹塑性断裂力学理论。
完全塑性材料:断裂时构件整体发生均匀屈服:塑性材料断裂力学。
剩余强度:含有裂纹的结构在使用过程中任意时刻所具有的承载能力就被称为剩余强度。
所有的断裂理论的落脚点都是比较剩余强度和设计强度的大小。
能量分析:英国物理学家Griffith,在1921年首次提出了裂纹扩展时能量释放的概念。
找他的理论解释,裂纹的上下表面形成导致了应变能的释放。
材料力学断裂力学知识点总结

材料力学断裂力学知识点总结材料力学是研究材料的力学性质和变形行为的学科,而断裂力学则是其中的重要分支。
断裂力学主要研究材料在外界作用下的破坏过程和断裂特性,对于了解材料的强度、可靠性和耐久性具有重要意义。
本文将对材料力学断裂力学的主要知识点进行总结。
1. 断裂力学基础概念1.1 断裂断裂是材料由于内外力作用下发生破裂的现象。
断裂过程包括初期损伤、裂纹扩展和断裂破坏三个阶段。
1.2 断裂韧性断裂韧性是材料在断裂过程中所吸收的能量的量度。
韧性高的材料能够在断裂前吸收大量能量,具有较好的抗断裂能力。
1.3 断裂强度断裂强度是材料在断裂破坏前所能承受的最大拉应力,是衡量材料抗断裂性能的重要指标。
2. 断裂模式2.1 纯拉伸断裂纯拉伸断裂是指材料在纯拉伸作用下破裂的模式。
在该模式下,裂纹往往呈现沿拉伸方向延伸的条状。
2.2 剪切断裂剪切断裂是指材料在剪切载荷作用下破裂的模式。
在该模式下,裂纹往往呈现锯齿状。
2.3 压缩断裂压缩断裂是指材料在压缩载荷作用下破裂的模式。
在该模式下,裂纹多呈现垂直于压缩方向的半环形状。
3. 断裂韧性的评价方法3.1 线性弹性断裂力学线性弹性断裂力学是最早用于断裂韧性评价的方法,其基本假设为材料在破裂前仍满足线性弹性行为。
3.2 弹塑性断裂力学弹塑性断裂力学是考虑了材料的塑性行为。
该方法应用广泛,能较好地描述材料的耐久性和断裂韧性。
3.3 细观断裂力学细观断裂力学是以材料微观层面的裂纹损伤为基础的断裂力学模型,通过对材料中裂纹数量和尺寸的分析,预测材料的断裂韧性。
4. 断裂的影响因素4.1 材料性质材料的力学性质直接影响了其断裂行为,例如强度、韧性、硬度等。
4.2 外界加载条件外界加载条件如载荷类型、载荷大小和加载速率等都会对材料的断裂行为产生重要影响。
4.3 温度和湿度温度和湿度的变化能够引起材料的热膨胀和水分吸附,进而影响材料的断裂性能。
5. 断裂力学应用5.1 材料设计通过对材料的断裂性能研究,可以为材料设计提供依据,提高材料在特定工况下的抗断裂能力。
材料力学中的断裂力学

材料力学中的断裂力学材料力学是研究物质在外力作用下变形、损伤和破坏行为的一门学科。
断裂力学是材料力学中的一个重要分支,研究的是材料在受到外力作用时出现破坏的现象及其规律。
断裂力学对于理解和预测材料破坏行为,具有重要的理论和实践意义,本文将就此展开讨论。
一、破坏的基本形式材料的破坏可分为两种基本形式:拉伸断裂和压缩断裂。
拉伸断裂是指在材料受到拉伸作用时,断口发生的破坏行为;压缩断裂是指在材料受到压缩作用时,断口发生的破坏行为。
除此之外,还有剪切断裂、扭转断裂、弯曲断裂等不同的破坏形式。
二、断裂力学的基本概念1.断裂应力材料在破坏前,能够承受的最大应力称为断裂应力。
断裂应力的大小与材料的强度、形状、尺寸、载荷方向等因素有关。
2.断裂韧性材料在破坏前能够吸收的最大能量称为断裂韧性。
断裂韧性的大小与材料的抗裂性能有关。
3.断裂强度材料在破坏前实际承受的最大应力称为断裂强度。
断裂强度与断裂应力的概念相似,但断裂强度是在材料实际破坏后测定得出的。
4.断裂韧度材料在破坏前能够吸收的最大能量密度称为断裂韧度。
断裂韧度与断裂韧性的概念类似。
三、断裂表征参数1.伸长率材料在破坏前拉伸变形的程度,也称为材料的变形量。
伸长率是指材料在拉伸断裂前的额定延长量比上原长度所得的比值。
2.缩颈率在材料拉伸断裂时,当材料的横截面积开始缩小,称为缩颈。
缩颈率是指材料在拉断时的截面积缩小量比上原截面积所得的比值。
3.断口形貌材料断口的形态与破坏机理有密切关系,通过观察断口形貌,可以较为直观地判断破坏机制。
四、断裂损伤机理材料的断裂破坏是一个复杂和多层次的过程,其损伤机理可以分为微观和宏观两个层次。
1.微观层次在微观层次上,材料的破坏主要是由裂纹的扩展和材料局部的塑性变形共同作用导致的。
材料的破坏前,裂纹的长度会随着载荷的增加而逐渐增加,当裂纹的长度达到一定程度时,就会出现快速扩展和破坏。
2.宏观层次在宏观层次上,材料的破坏主要是由断面剪切和拉伸引起的。
断裂力学

(3.4)
G
1 U B a
(3.5)
3.4 中心裂纹的能量释放率
G 1 U 2 B a
(3.6)
3.5 能量释放率的另一表达形式
1 U1 B a G 1 U1 2 B a
(3.7)
4 应力强度因子
断裂发生时在裂纹端点要释放出多余的能量,因此,裂端区的应力场和应变场必然与此裂端的能量释放 率有关。若裂端应力应变场的强度(intensity)足够大,断裂即可发生,反之则不发生。因此,得到裂端区 应力应变场的解析解是个关键。 近代断裂力学是用弹性力学的解析方法来完成这一工作的,而这些解析法需要用高深的数学工具,这对 于初次接触断裂力学的读者来说,是比较困难的。因此,本章只给出一些主要的概念和结果,并介绍一些 工程近似方法。
x
(4.5)
r 2u K II 2 r 2 v K II 2
III 型裂纹的应力场和位移场 :
1/ 2
2 ( 1) 2cos sin 2 2 2 ( 1) 2sin 2 cos 2
1 断裂力学的形成
1957 年,美国科学家 G.R.Irwin 提出应力强度因子的概念, 线弹性断裂理论的重大突破,应力强度因子 理论作为断裂力学的最初分支——线弹性断裂力学建立起来。
2 断裂力学的发展
现代断裂理论大约是在 1948—1957 年间形成,它是在当时生产实践问题的强烈推动下,在经典 Griffith 理论的基础上发展起来的,上世纪 60 年代是其大发展时期。 我国断裂力学工作起步至少比国外晚了 20 年,直到上世纪 70 年代,断裂 力学才广泛引入我国, 一些单位和科技工作者逐步开展了断裂力学的研究和 应用工作。 断裂力学是起源于 20 世纪初期,发展于 20 世纪后期,并且仍在不断发展 和完善的一门科学。因此,它是具有前沿性和挑战性的研究成果 研究含裂纹物体的强度和裂纹扩展规律的科学。固体力学的一个分支。又 称裂纹力学。它萌芽于 20 世纪 20 年代 A.A.格里菲斯对玻璃低应力脆断的 研究。其后,国际上发生了一系列重大的低应力脆断灾难性事故,促进这方 面的研究,并于 50 年代开始形成断裂力学。根据所研究的裂纹尖端附近材 料塑性区的大小,可分为线弹性断裂力学和弹塑性断裂力学;根据所研究的引起材料断裂的载荷性质,可 分为断裂(静)力学和断裂动力学。断裂力学的任务是:求得各类材料的断裂韧度;确定物体在给定外力 作用下是否发生断裂,即建立断裂准则;研究载荷作用过程中裂纹扩展规律;研究在腐蚀环境和应力同时 作用下物体的断裂(即应力腐蚀)问题。断裂力学已在航空、航天、交通运输、化工、机械、材料、能源 等工程领域得到广泛应用。 线弹性断裂力学应用线弹性理论研究物体裂纹扩展规律和断裂准则。1921 年格里菲斯通过分析材料的低 应力脆断,提出裂纹失稳扩展准则格里菲斯准则。1957 年 G.R.欧文通过分析裂纹尖端附近的应力场,提出
断裂力学总结
平面应变状态下的裂纹扩展阻力(R)曲线的
GⅠ GⅠC
GⅠ 裂纹扩展的动力
GⅠC 平面应变情况下裂纹扩展的阻力率
R GⅠ
1
2
GⅠC
A
C
GⅠ
1 2
E
KⅠ2
KⅠ a
GⅠ
1 2 E
2a
若 一定,则G与a的关系
1、若给定外载荷,则可求得相应情况下的临界裂纹尺寸 2、若给定裂纹尺寸,则可判断在一定载荷作用下,结构
G Ua 1 Ua A A B a
Ua
1 2
P
cP
C为弹性体的柔度 c ca
d 0 d pdc cdP 0
dU a
1 2
Pd
1 dP 2
1 cPdP 2
1 2
p 2 dc
G Ua 1 p2 c A A 2B a
2a
P
2、恒载荷情况
dU a
A cos C cos 0
A
(
1)sin B sin
C D
( 1)sin sin 0
0
B ( 1) cos D ( 1) cos 0
线性齐次方程组有非零解,系数行列式为零,解之,得:
sin 2 0
这种方法的得到的结果为级数形式,敛散性没法确定,且远端的边 界条件不好代入。课本上的方法克服以上缺点但应力函数在未知的 条件下比较难找。
2a
裂纹平板的总能量为
U
U0
Ua
Ur
U0
2a2 E
4a e
dU 0 且
da
dU0 0 da
d da
2a2 E
4a e
0
2 E
2a
4
断裂力学读书感想

断裂力学是一门相对较新的学科,就其研究方法、现状及存在的问题发表自己的读书感想。
(字数1000左右)任何一门科学都是应一定的需要而产生的,断裂力学也是如此。
一提到断裂,人们自然而然地就会联想到各种工程断裂事故。
在断裂力学产生之前,人们根据材料力学强度条件来设计构件,其基本思想就是保证构件的工作应力不超过材料的许用应力,即σ≤[σ]~安全设计安全设计对确保构件安全工作也确实起到了重大的作用,至今也仍然是必不可少的。
这种传统的强度计算方法表达式简洁明了,使用方便,已经有一百多年的历史,它在过去的工程设计中发挥了重要的作用。
但是人们在长期的生产实践中,逐步认识到,在某些情况下,根据强度条件设计出的构件并不安全,断裂事故仍然不断发生,特别是高强度材料构件,焊接结构,处在低温或腐蚀环境中的结构等,断裂事故就更加频繁。
工程中一系列“低应力脆断”事故的发生,动摇了这种传统设计思想的安全感。
1950年美国北极星导弹发动机壳体试验时的爆炸破坏就是一例。
1938-1943年期间,像这样破坏的焊接桥梁有40座之多。
人们经过长期的观察研究发现,这些破坏事故具有共同的特点:一是破坏时工作应力水平大大低于材料的屈服应力;二是破坏均起源于构建内部的微小裂纹。
科学的进步总是为了解决关乎人类自身利益和幸福生活的问题。
在此基础之上,断裂力学应运而生。
目的是研究带裂纹体的强度以及裂纹扩展规律。
断裂力学这一固体力学的新分支就是二十世纪六十年代发展起来的一门边缘学科。
它不仅是材料力学的发展与充实,而且它还涉及金属物理学、冶金学、材料科学、计算数学等等学科内容。
断裂力学的创立对航天航空、军工等现代科学技术部门都产生了重大影响。
随着科学技术的发展,断裂力学这门新的学科在生产实践中得到越来越广泛的应用。
以此同时,断裂力学这门年轻的学科也得到不断地发展和充实。
经过八周的学习,我只是对断裂力学有了感性的认识和了解,如若想深究,往后还得下很大的功夫。
断裂力学知识点概要

7、 为保证线弹性断裂力学的精确性和有效性,裂纹尖部的区域应限制在如下的范围之内: Ry≤r≤a/10. 通常把应力水平(σ/σs)≤0.3~0.5 作为线弹性断裂力学的适用范围。 (σ/σs)≤0.53. 8、 裂纹失稳扩展的条件是裂纹体在裂纹扩展过程中所释放的应变能大于等于裂纹扩展时 形成新的裂纹表面所需要的表面能。这就是能量平衡理论建立的断裂判据,习惯上称为 能量判据。 9、 三大理论:最大周向应力理论、应变能密度因子理论、最大应变能释放率理论。 10、 压力容器中裂纹的应力强度银子 KI 的计算:KI=MK/I M——膨胀效应系数(下述中 C2 为 C2, ) C2 1/2 对球星容器中的穿透裂纹膨胀效应系数计算式:M=(1+1.93* ) Rt C2 1/2 对圆筒形容器中的轴向裂纹,膨胀效应系数计算式:M=(1+1.61* ) Rt C2 1/2 对圆筒形容器中的环向裂纹,膨胀效应系数计算式:M=(1+0.32* ) Rt C——穿透裂纹或当量穿透裂纹的半长 R——容器的半径 T——容器的壁厚 11、一圆筒形压力容器,设计压力 P=2.0MPa,内径 D=7500mm,壁厚 t=40mm,焊接系数 Ψ=1,材料为 16MnR, σs=350MPa,KIC=3250N/mm1.5,在筒体的膜应力区有两条穿透裂纹,
σө≈ σψ≈
pD 2*7500 = =187.5(MPa) 2t 2*40
pD 2*7500 = =93.75(MPa) 4t 4*40
轴向裂纹的鼓胀效应系数为:M=(1+1.61* 环向裂纹的鼓胀效应系数为:M=(1+0.321/2=1.0002 Rt C2 1/2 10*10 ) (1+0.32* )1/2=1.0001 Rt 3600*40
工程断裂力学小结

工程断裂力学小结工程断裂力学课程报告工程断裂力学是一门广泛应用于宇航、航空、海洋、兵器、机械、化工和地质等领域方面的学科。
主要致力于研究以下五个方面的问题:1、多少的裂纹和缺陷是允许存在的,2、用什么判据来判断断裂发生的时机,3、机械结构的寿命如何估算,如何进行裂纹扩展率的测试及研究影响裂纹扩展率的因素。
4、如何在既安全又能避免不必要的停产损失的情况下安排探伤检测周期。
5、如检查时发现了裂纹又如何处理,这些问题的解决将可以从设计、制造、安装和使用等的角度建立评定带缺陷或裂纹运行的机械结构安全性的标准,从而有效防止断裂事故的发生,在为保障人民生命财产安全方面和经济建设方面发挥极大的作用。
工程断裂力学的发展迄今为止大致经历过以下阶段,首先1920年--1949年间主要以能量方法求解,其中最有影响的是英国科学家Griffith提出的能量断裂理论以及据此建立的断裂判据。
而后从1957年开始是线弹性断裂理论阶段,提出了应力强度因子概念及相应的判断依据。
到1961年--1968年间是弹塑性理论阶段,其中以1961年的裂纹尖端位移断裂判据和1968年Rice提出的J积分最为著名。
而1978年又出现了损伤力学。
下面我们对本学期学科的基本概念和几种断裂判断依据加以总结。
在能量断裂理论当中以研究Griffith裂纹问题和矩形平板的单边裂纹问题为代表。
以G表示形成单位长度裂纹时平板每单位面积所释放出的能量,以表示每,s 形成单位裂纹面积所需的能量。
Griffith断裂判据即为G=2,表明当G.>2裂纹,,ss会扩大;G=2处于临界状态;G<2裂纹不扩大。
其中G代表驱动力而2代表阻,,,sss力。
这个判据中含有两个需要解决的问题。
(1) G如何计算 (2 )2如何测定。
而根,s1,U据能量守恒定律与能量释放率的定义,可以测得单边裂纹时,对称中心G,Ba,1,U裂纹为 ,其中U代表的弹性体储存的总应变能。
这一断裂判据仅适用于G,2Ba,脆性材料,因此发生断裂的应力水平远小于屈服应力。
ABAQUS中的断裂力学及裂纹分析总结

也许要暂别simwe一段时间了,在论坛获益良多,作为回报把自己这段时间在ABAQUS断裂方面的一些断断续续的心得整理如下,希望对打算研究断裂的新手有一点帮助,大牛请直接跳过。
本贴所有内容均为原创,转贴请注明,谢谢。
引言:我们知道从1914年Ingless和1921年Griffith提出断裂力学开始,一直到60年代都停留在线弹性断裂力学(LEFM)的层次。
后来由於发现在裂纹尖端进入塑性区后用LEF仍然无法解决stress singularity的问题。
1960年由Barenblatt 和Dugdale率先提出了nonlinear/plastic fracture mechnics的概念,在裂纹前端引入了plastic zone,这也就是我们现在用的cohesive fracture mechnics的前身。
当时这个概念还没引起学术界的轰动。
直到1966年Rice发现J-integral及随后发现在LEFM中J-integral是等于energy release rate的关系。
随后在工程中发现了越来越多的LEFM无法解释的问题。
cohesive fracture mechnics开始引起更多的关注。
在研究以混凝土为代表的quassi-brittle material时,cohesive fracture mechnics提供了非常好的结果,所以在70年代到90年代,cohesive fracture mechnics被大量应用于混凝土研究中。
目前比较常用的方法主要是fictitious crack approach和effective-elastic crack approach或是称为equivalent-elastic crack approach. 其中fictitious crack approach只考虑了Dugdale-Barenblatt energymechanism而effective-elastic crack approach只考虑了基於LEFM的Griffith-Irwinenergy dissipation mechanism,但作了一些修正。
材料力学中的断裂力学分析方法研究

材料力学中的断裂力学分析方法研究引言:断裂力学是材料力学中的一个重要分支,研究材料在受力作用下的破裂行为和断裂过程。
在工程实践和科学研究中,了解材料的断裂行为对于设计和改进工程结构具有重要意义。
本文将介绍材料力学中的断裂力学分析方法,包括线弹性断裂力学、弹塑性断裂力学和断裂力学的数值模拟方法。
一、线弹性断裂力学线弹性断裂力学是材料力学中最基本的断裂理论,适用于强度高、韧性差的材料。
线弹性断裂力学的基本原理是根据材料的线弹性性质,通过应力和应变的关系,计算出材料在受力作用下的应力强度因子。
应力强度因子是描述断裂过程中应力场的一种参数,可用于预测材料的断裂行为。
线弹性断裂力学的主要分析方法包括拉伸试验、根据裂纹尖端应力场求解应力强度因子、确定裂纹扩展方向的K-R曲线等。
二、弹塑性断裂力学当材料的强度和韧性较高时,线弹性断裂力学不能很好地描述材料的断裂行为。
此时,需要采用弹塑性断裂力学进行分析。
弹塑性断裂力学将材料的弹性和塑性行为结合起来,考虑材料在加载过程中的变形和断裂。
在弹塑性断裂力学中,应力强度因子的计算需要考虑材料的塑性缺口效应。
常见的弹塑性断裂力学分析方法包括J-积分法、能量法和应力强度因子法等。
三、断裂力学的数值模拟方法随着计算机技术的发展,断裂力学的数值模拟方法得到了广泛应用。
数值模拟方法能够更准确地描述材料的断裂行为,包括裂纹的扩展路径、失效载荷和断裂过程等。
常用的数值模拟方法有有限元法和离散元法。
有限元法以其广泛的适用性和高精度的计算结果而受到广泛关注。
在有限元法中,利用离散化的网格模型和连续介质力学理论,对材料的断裂过程进行模拟和分析。
离散元法则更适用于颗粒状材料或颗粒之间存在断裂的材料。
四、断裂力学在工程中的应用断裂力学在工程中有着广泛的应用。
通过对材料的断裂行为进行准确的分析和预测,可以为工程结构的设计和改进提供重要的依据。
例如,在航空航天工程中,断裂力学能够用于预测飞机机体的疲劳破坏和碰撞破坏情况;在汽车工程中,断裂力学可以帮助改进车辆的安全性能和减少事故发生的风险;在材料工程中,断裂力学可以用于评估材料的强度和韧性,优化材料生产工艺。
断裂力学雪心心得

在以往我们所学的力学知识中,通常的设计思想是把材料视为无缺陷的均匀连续体,而现今工程实际中的构件或材料都不可避免地存在着缺陷和裂纹,因而实际构件或材料的强度大大低于理想模型的强度。
比如我们在课堂上所看的关于美国哥伦比亚号航天飞机的失事事件,就是由于材料出现缺陷酿成的后果,在传统设计思想中这是容易忽略的一条。
断裂力学则是从构件或材料内部存在缺陷或裂纹这一基础事实出发,恰恰弥补了传统设计思想这一严重的不足。
断裂力学是以变形体为基础,研究含缺陷或裂纹材料和结构的抗断裂性能,以及在各种工作环境下裂纹的平衡、扩展、失稳以及止裂规律的一门学科。
断裂力学在许多领域中解决了大量的生产实际问题,特别是解决了抗断设计、合理选材、适当的热处理制度和加工工艺、预测构件的疲劳寿命、制定合理的质量检测制度和验收标准以及防止断裂事故等方面的问题。
可谓是十分重要的一门学科。
弹性力学的任务是:研究裂纹体的引应力场、应变场与位移场,寻找控制材料开裂的物理参量。
研究材料抵抗裂纹扩展的能力——韧性指标的变化规律,确定其数值与测定方法。
建立裂纹扩展的临界条件——断裂准则。
含裂纹的各种几何构件在不同载荷作用下,控制材料开裂的物理参量的计算。
弹性力学的研究方法是:假设裂纹已经存在,从弹性力学或弹塑性力学的基本方程出发,把裂纹当做边界条件,考察裂纹顶端的应力场、应变场和位移场,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
根据裂纹受力情况,可分为三种基本类型:张开型、划开型、撕开型。
影响断裂力学的因素主要有两个:载荷大小和裂纹长度。
在考虑一条宏观裂纹的构件时,随着使用时间和次数的增加,裂纹会愈来愈长。
在工作载荷较高时,比较短的裂纹就有可能发生断裂,在工作载荷较低时,比较长的裂纹才会带来危险。
这表明表征裂端区应力变场强度的参量与载荷大小和裂纹长短有关,甚至可能与构建的几何形状有关。
线弹性断裂力学研究的对象是线弹性裂纹固体,认为裂纹体内各点的应力和应变的关系都是线性的。
工程断裂力学小结

工程断裂力学小结工程断裂力学课程报告工程断裂力学是一门广泛应用于宇航、航空、海洋、兵器、机械、化工和地质等领域方面的学科。
主要致力于研究以下五个方面的问题:1 、多少的裂纹和缺陷是允许存在的,2 、用什么判据来判断断裂发生的时机,3 、机械结构的寿命如何估算,如何进行裂纹扩展率的测试及研究影响裂纹扩展率的因素。
4、如何在既安全又能避免不必要的停产损失的情况下安排探伤检测周期。
5、如检查时发现了裂纹又如何处理, 这些问题的解决将可以从设计、制造、安装和使用等的角度建立评定带缺陷或裂纹运行的机械结构安全性的标准,从而有效防止断裂事故的发生,在为保障人民生命财产安全方面和经济建设方面发挥极大的作用。
工程断裂力学的发展迄今为止大致经历过以下阶段,首先1 920年--1 949 年间主要以能量方法求解,其中最有影响的是英国科学家Griffith 提出的能量断裂理论以及据此建立的断裂判据。
而后从1957 年开始是线弹性断裂理论阶段,提出了应力强度因子概念及相应的判断依据。
到1961 年--1968 年间是弹塑性理论阶段,其中以1961年的裂纹尖端位移断裂判据和1968年Rice提出的J积分最为著名。
而1978 年又出现了损伤力学。
下面我们对本学期学科的基本概念和几种断裂判断依据加以总结。
在能量断裂理论当中以研究Griffith 裂纹问题和矩形平板的单边裂纹问题为代表。
以G表示形成单位长度裂纹时平板每单位面积所释放出的能量,以表示每,s形成单位裂纹面积所需的能量。
Griffith 断裂判据即为G=2表明当G>2裂纹,,ss会扩大;G=2处于临界状态;G<2裂纹不扩大。
其中G代表驱动力而2代表阻,,,sss力。
这个判据中含有两个需要解决的问题。
(1) G如何计算(2 )2如何测定。
而根,s1,U据能量守恒定律与能量释放率的定义,可以测得单边裂纹时,对称中心G,Ba,1,U裂纹为,其中U代表的弹性体储存的总应变能。
断裂力学要点

金属的断裂
(1)金属断裂的分类 韧性断裂—剪切断裂和微孔聚集断裂(韧窝断裂) 脆性断裂—沿晶断裂和解理断裂、准解理断裂 (2)断裂的机制 解理断裂—zener&stroh模型(位错塞积导致的应力集中不能 被塑性变形所松弛)、cottrell位错反应模型(可动位错反 应生成固定位错在晶界、挛晶界形成裂纹) 沿晶断裂—晶界上连续或者不连续的脆性第二相、夹杂物或 者杂质元素在晶界的偏聚引起 剪切断裂—金属在切应力下沿滑移面分离 微孔聚集断裂—第二相粒子或者夹杂物与位错的交互作用导 致微孔的形成、长大、连接聚合
断裂的力学条件
(1)从能量守恒的角度,可得出裂纹失稳扩展的临界条件 1 平面应力条件下: 2E ( s p ) ) 2E( s p 2 ac c 2 a 1 2E( s p ) 2E ( s p ) 2 ac c 平面应变条件下: 2 2 2 ( ( 1 ) 1 - )a (2)用LEFM计算脆性材料裂尖的应力,可知一点的应力大 小由应力强度因子所K决定。因此可用应力强度因子K值作 为裂纹失稳扩展的力学判据,进而提出断裂韧度Kic或Kc的 概念,并用来表征材料抵抗裂纹失稳扩展的能力。
小裂纹的萌生和扩展
裂纹核的生成,之后逐渐形成微裂纹、小裂纹、大裂纹, 因此疲劳断裂可分为四个阶段。 (1)裂纹成核阶段 裂纹成核,必然存在裂纹源。 裂纹源包括a、金属挤入和挤出形成的滑移带、挛晶界和晶界 b、夹杂物和第二相 (2)微观裂纹扩展阶段 (3)宏观裂纹扩展阶段 (4)最后断裂阶段
小裂纹的扩展特性
s
E
ln(sec
2s
)
c
c
c
断裂力学总结

断裂力学总结(共8页) --本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--断裂力学学习报告姓名:zx 学号:xxxxxxxx一、绪论(1)传统强度理论是在假定材料无缺陷、无裂纹的情况下建立起来的,认为只要满足r []σσ≤,材料将处于安全状态。
其中:[]σ——用安全系数除失效应力得到的许用应力;r σ——为相当应力,它是三个主力学按照一定顺序组合而成的,按照从第一强度理论到第四强度强度理论的顺序,相应的应力分别为1121233134()r r r r σσσσμσσσσσσ==-+=-=但是许多事实表明,材料受应力远小于设计应力,材料仍然被破坏。
使许多力学工作者迷惑不解,于是投入对其研究,最终发现所有材料并不是理想的,材料中含有大大小小、种类各异的裂纹,于是产生了对裂纹地研究。
断裂力学从客观存在裂纹出发,把构件看成连续和和间断的统一体,从而形成了这门新兴的强度学科。
(2)断裂力学的任务是: 1.研究裂纹体的应力场、应变场与位移场,,寻找控制材料开裂的物理参量; 2.研究材料抵抗裂纹扩展的能力——韧性指标的变化规律,确定其数值与及测定方法; 3.建立裂纹扩展的临界条件——断裂准则; 4. 含裂纹的各种几何构件在不同荷载作用下,控制材料开裂的物理参量的计算。
(3)断裂力学的研究方法是:假设裂纹已经存在,从弹性力学或弹塑性力学的基本方程出发,把裂纹当作边界条件,考察裂纹顶端的应力场、应变场和位移场,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
(4)断裂力学的几个基本概念:根据裂纹受力情况,裂纹可以分为三种基本类型:1. 张开型(I 型)裂纹受垂直于裂纹面的拉应力作用,裂纹上下两表面相对张开,如上图a 所示;2. 滑开型(II 型),又称平面内剪切型裂纹受平行于裂纹面而垂直于裂纹前缘OO ’的剪应力作用,裂纹上下两表面沿x 轴相对滑开,如上图b 所示;3. 撕开型(III 型),又称出平面剪切型或反平面剪切型裂纹受既平行于裂纹面又平行于裂纹前缘的剪应力作用,裂纹上下两表面沿z 轴相对错开,如上图c 所示.上述三种裂纹中I 型最为危险.而我们主要也是研究I 型裂纹,因为只要确定了I 型裂纹是安全的,则其它两种裂纹也是安全的。
断裂力学报告

目录一、断裂力学的基本概念 (2)Griffith断裂判据 (2)能量平衡理论 (3)应力强度因子··········错误!未定义书签。
裂纹问题的三种基本类型··········错误!未定义书签。
利用应力强度因子提出的断裂判据 (4)J积分 (5)J积分简介 (5)J积分断裂判据 (5)J积分的物理意义 (6)二、冻土断裂力学在挡墙基础稳定性分析中的应用 (6)冻土断裂力学判据 (6)挡墙基础强度和稳定性分析 (6)三、个人小结 (8)参考文献: (8)断裂力学G、K、J断裂判据及其应用通过对断裂力学的学习,我们知道断裂力学作为一门新兴的学科,由于生产实践、工程设计等方面的需要,已成为固体力学的一个重要组成部分。
目前断裂力学已广泛应用于宇航与航空工程、化学工程、机械工程、核能工程、造船等各个部门。
近年来,对岩石这类地质材料的破坏过程与机理的研究也应用了断裂力学的方法和理论,可见断裂力学的发生与发展也是以生产与工程实践的需要为动力的。
在本文总共分两部分,一部分为断裂力学的基本概念,一部分为一断裂力学的实例。
一、 断裂力学的基本概念1.1 Griffith 断裂判据我们知道研究断裂的目的主要是防止构件断裂,这个任务长期以来人们已经积累了丰富的经验,建立了许多强度理论条件:⎪⎪⎪⎩⎪⎪⎪⎨⎧→→→=≤在交变应力作用下对塑形材料对脆性材料nn n r ss bb σσσσσ][ 式中:→σ根据外载计算的工作应力;→][σ许用应力;b σ、s σ、→r σ由实验得到的不同材料的极限强度、屈服极限、持久极限; b n 、s n 、→r n 对应于b σ、s σ、r σ的安全系数;但是对于有裂纹的物体上述强度理论已经不再适用,为此本世纪二十年代英国著名的科学家Griffith ,提出了能量释放(energy release)的观点,以及根据这个观点而建立的断裂判据。
断裂力学小结报告

断裂力学小结报告一 前语断裂力学是一门应用线弹性和弹塑性力学,研究带裂纹的结构或部件在外部及内部因素作用下,裂纹再萌生、扩展直至断裂的条件和规律,并研究部件材料抗裂纹扩展、抗断裂能力,做出部件安全性和寿命估算的学科。
它在航空、航天、交通运输、化工、机械、材料、能源等工程领域有着广泛应用。
断裂力学的任务是:求得各类材料的断裂韧度;确定物体在给定外力作用下是否发生断裂,即建立断裂准则;研究载荷作用过程中裂纹扩展规律;研究在腐蚀环境和应力同时作用下物体的断裂(即应力腐蚀)问题等。
二 断裂力学的研究内容及核心概念⑴ 断裂力学研究的内容:① 按工程的需要可以概括为1、裂纹的起裂条件。
2、裂纹在外部载荷和(或)其他因素作用下的扩展过程。
3、裂纹扩展到什么程度物体会发生断裂。
4、含裂纹结构在什么条件下破坏。
5、临界裂纹长度。
② 按材料的应力过程分为1、线弹性断裂力学。
2、弹塑性断裂力学。
3、断裂动力学。
⑵ 断裂力学的核心概念:① 材料的脆性、韧性。
在材料力学中通常以光滑试样的拉伸试验的结果把固体材料分为脆性和韧性,脆性材料是指材料直到拉断前,不发生塑性变形或仅有微小的塑性变形,如玻璃,陶瓷等;而韧性材料在拉断前要发生可观的塑性变形,如多数金属。
正是由于材料的脆性与韧性的区别,才导致了线弹性断裂力学和弹塑性断裂力学的分类。
② 线弹性断裂力学。
对于完全脆性的材料和和裂纹尖端的塑性区尺寸小于裂纹的长度(小范围屈服)的多数金属材料,采用线弹性理论或修正后的理论能很好很快的描述,并且与实际和相符,所以发展迅速,比较成熟。
③ 能量平衡理论。
对于脆性材料,裂纹尖端的能量释放率G ∶能量释放率是指裂纹由某一端点向前扩展一个单位长度时,平板每单位厚度所释放出来的能量,若试样厚度为B ,裂纹长度用a 表示,则裂纹扩展面积为A=Ba ,则a u B A u G I ∂∂-=∂∂-=1。
表面自由能γs :材料每形成单位裂纹面积所需的能量,其量纲与能量释放率相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
失稳扩展
可以止裂
若材料的表面自由能是常数,则有:
失稳扩展
可以止裂
第二章应力பைடு நூலகம்度因子
2.1裂纹的几种基本型
断裂发生时在裂纹端点要释放出多余的能量,因此,裂端区的应力场和应变场必然与此裂端的能量释放率有关。若裂端应力应变场的强度足够大,断裂即可发生,反之则不发生。
图4-2
等于 时,则 ,当 时, 趋近于 值,得 ;当 时, 得: ,最后得到 。
4.2裂纹张开位移CTOD及J积分
裂纹张开位移是指一个理想裂纹受载荷时,其裂纹表面间的距离。对I型裂纹来说,线弹性断裂力学给出 。若用Irwin塑性区修正,真正裂纹长度被有效裂纹长度所取代,此时原点移动到有效裂纹的端点,以 代替 , 代替 ,可得小范围屈服修正时 ,利用能量释放率 与 的关系有:
考虑带有裂纹的弹性体,在拉伸载荷作用下,若裂纹仍然维持静止,则此弹性体所储存的总应变能 要比在没有裂纹时所储存的总应变能 大,两者之差用 表示。由于没裂纹时的总应变能 与裂纹长度无关,故有:
1.2能量平衡理论的应用
按照热力学的能量守恒定律,在单位时间内,外界对于系统所做功的改变量,应等于系统储存应变能的该变量,加上动能的改变量,再加上不可恢复消耗能地改变量。假设 为外界对系统所做的功, 为系统储存的应变能, 为裂纹总面积, 为表面能,则断裂发生的临界条件为: 此式为带裂纹物体的断裂判据。按照线性弹性力学的原理,在外力拉伸下,因裂纹扩展而引起的功的变化量 ,将等于两倍的总应变能的变量 ,因此能量释放率在给定外力拉伸的情形下,有:
现以I型单边裂纹为例,来说明柔度法的原理。一块很长的矩形板,如图3-3,
图3-3
板厚为B,板下边固定,上边某点有拉力P,载荷点位移 (a),当裂纹增至 时,位移也增至 ( ),这里当 很小时,有 。因为位移和拉力有如下关系: ,式中C是柔度。恒载荷时, ,得 。
对于一单独型的裂纹,利用应力强度因子和能量释放率的关系,可有断裂判据 。I型裂纹是最常见的裂纹型,其失稳断裂开始的临界点 ,通常与试件的厚薄、大小有关。当试件厚到某一程度和大到某一程度,脆性材料的 值达到极小值,以后尺寸厚度再增加, 仍维持此极小值,此极小值用符号表示即为 ,其相应的 值为平面应变的断裂韧度。因此,I型裂纹保守的判据为: 。
则有: ,在此情况下,设裂纹可以延长 长度,则裂端前方撑开成长度为 ,如图3-2。
图3-1图3-2
新裂纹上表面位移 。由于作用力对裂纹上表面所做得功为 。因此,按照I型裂纹能量释放率 的定义,可有: 经积分得: 。
对于平面问题,若取有效弹性模量 和有效泊松比 ,而
又因为 ,则 。
3.2柔度法
柔度法是通过柔度随裂纹长度而改变这个性质,用测量的方法来得能量释放率G,然后利用G和K的关系式来得到K值。设A为裂纹一个表面的面积,即为裂纹长度和板厚之积,则有: 。若系统边界某范围是给定载荷,则做功的大小由此范围的载荷来决定。当保持此载荷不变时,裂纹长度若有增加,则加载点的位移 也会增加,即 时, 。应变能的改变可由下式得: 。功的改变为 则 ,下标P表示恒载荷。
假设裂纹是I型,如图4-1所示,裂端前 和 处 方向的拉伸应力刚好达到
图4-1
平面应力
平面应变
屈服应力 ,则 就是塑性区的尺寸,则有: 所以,塑性区的尺寸为 Irwin建议取 或
第二步估计可以假设裂纹的有效长度为 ,而 , ,用此 来计算力应强度因子 和应力场。如图4-2,I型裂纹,当有效裂纹端点前 处的
材料本身是具有抵抗裂纹扩展的能力的,因此只有当抗伸应力足够大时,裂纹才有可能扩展。此抵抗裂纹扩展的能力可以用表面自由能来度量。根据能量守恒定律,不考虑脆性断裂,裂纹发生扩展的必要条件是裂纹区要释放的能量等于形成裂纹面积所需要的能量。设每个裂端的裂纹扩展量为 ,则有:
————表面自由能
化简得: 这就是著名的Griffith断裂判据。若 ,发生断裂;若 ,则不发生断裂。
一般将裂纹问题分为三种基本型。第一种称为张开型或拉伸型,简称I型。其裂纹面的位移方向是在使裂纹张开的裂纹面法线方向,它通常发生在载荷和几何形状对称于裂纹平面的情形。第二种裂纹型称为同平面剪切型或者滑移型,简称II型,裂纹上下表面的位移方向刚好相反。第三种裂纹型称为反平面剪切型,简称III型。除了这三种基本型外,尚有复合型裂纹。
第一章能量守恒于断裂判据
1.1能量释放率的由来
断裂力学的一大特点是,假定物体已经带有裂纹。现代断裂力学就能对此带裂纹物体的裂纹端点区进行应力应变分析,从而得到表征裂端区应力应变场强度的参量。
如图1-1,1-2的Griffith裂纹问题(即无限大平板带有穿透板厚的中心裂纹,且受到无穷远处的单向均匀拉伸的裂纹问题),以及图1-2的矩形平板带有单边裂纹的问题。
第三章线弹性断裂力学的基本概要
3.1应力强度因子与能量释放观点的统一
假设不考虑塑性变形能、热能和动能等其他能量的损耗,则能量转换表现为所有能量在裂端释放以形成新的裂纹面积。下面以带有穿透板厚的I型裂纹的平板为例,来建立应力强度因子和能量释放率间的关系。
如图3-1所示,裂纹长度为a的裂纹端点正前方有使裂纹面撑开得拉伸应力,
2.2裂端的应力场和位移场
我们考虑二维的I型裂纹问题。如图2-1,给出一个裂纹端点为原点的坐标系,x方向是裂纹正前方,y方向是裂纹面的法线方向,z方向则是离开纸面的方向。
图2-1
考虑一个离裂端很近,位置在极坐标( )的单元,其应力状态可以用 、 和 三个应力分量来表示,得裂端的应力恒为:
可见,裂端区应力场的形式恒定,其强度完全由 值的大小来决定,因此 就称为I型裂纹的应力强度因子。由弹性规律,裂端区的应变场可以由弹性力学公式求得为: = i,j=x,y
摘要:由高强度合金所制成的机械结构发生断裂时的应力水平,往往远低于屈服应力。因此,当机械结构带有裂纹时,判断机械结构发生断裂的时机,不能用屈服判据,而应该寻求新的断裂判据。现代断裂力学就是在这种背景下诞生的,从五十年代中期以来,断裂力学发展很快,目前理论部分已相当成熟,在工程方面,已广泛应用于宇航、航空、海洋、兵器、机械、化工和地质等许多领域。
裂端应力应变场的综合强度可用J积分值来表示。同时,证明J积分值与裂端弹塑性能量的释放关系,正好和Griffith能量释放率与裂端弹性能量释放的关系相似。在小范围屈服时,J等于G,存在 , 表示裂端前的屈服应力。延性断裂通常带有启裂、稳定扩展和失稳扩展三个阶段,而裂纹扩展时裂纹尾迹免不了要发生局部卸载,因此,J积分判据用作启裂判据是完全正确的,但用来预测失稳扩展则尚须加一些限制。对I型裂纹,J积分的启裂判据为 , 是I型裂纹在启裂时平面应变断裂韧度。
通过应变——位移关系,经过比较复杂的计算,可得到裂端区的位移场为:
和 分别为x和y方向的位移分量, 是剪切模量, 与泊松比 的关系为:
应力是看不见的,它是个抽象的概念,然而位移的过程却有可能看到。物体
个别点具有无限大的应力并不会使该点的位移趋于无限。因此,裂端具有无限大应力式允许的。三种基本裂纹型端区某点的应力值、应变值、位移值和应变能密度值都由应力强度因子及其位置来决定。因此,只要知道应力强度因子,裂端区的应力、应变、位移和应变能密度就都能求得。由于有这一特点,应力强度因子可以作为表征裂端应力应变场强度的参量。
图1-1 图1-2
设两采板的厚度均为B,Griffith裂纹长度是2a,单边裂纹长度为a。由于对称关系,现在只考虑图1-1中右边的裂纹端点。在拉伸应力的作用下,此裂纹端点是向正前方扩展的。根据Griffith能量释放观点,在裂纹扩展的过程中,能量在裂端区释放出来,此释放出来的能量将用来形成新的裂纹面积。因此,能量释放率是指裂纹由某一端点向前扩展一个单位长度时,平板每单位厚度所释放出来的能量。
第四章弹性断裂力学的基本概念
4.1Irwin对裂端塑性区的估计
在真正的材料里,不论是强度何等高的材料,无限大的应力是不可能存在的。尤其是断裂力学主要应用于金属材料,金属材料总是有一定的塑性,这种无限大应力的结果并不适合。当含裂纹的弹塑性体受到外载荷作用时,裂纹端点附近有个塑性区,塑性区内的应力是有界的,其大小与外载荷、裂纹长短和材料的屈服强度等都有关。若是塑性区已大到超过裂纹长度或物体的尺寸,则此时线弹性力学的理论已不再适用,必须用弹塑性力学的计算和寻找表征裂端应力应变场强度的新力学参量。
