18热力学第一定律
热力学第一定律
21
例1: 一定量的理想气体从体积V1 膨胀到体积V2 ,经历 以下几个过程: AB等压过程; AC等温过程; AD绝热 过程。问:从P-V图上,(1) 哪一个过程做功较多?哪 一个过程做功较少?(2) 经历哪一个过程内能增加?经 历哪一个过程内能减少?(3) 经历哪一个过程吸热最多? P 解: (1) 等压过程做功最多 A A A P A B p T Q 绝热过程做功最少 P C
例2:图示两卡诺循环,S1 = S2 P (1) 吸热和放热差值是否相同? (2) 对外所做净功是否相同? (3) 效率是否相同? 答案:(1)相同;(2)相同;(3)不相同
讨论
T2 1 )卡诺热机效率C 1 T1
只与T1和T2有关
与物质种类、膨胀的体积无关
2 ) 理论指导作用
T1 提高 c T2
提高高温热源的温度现实些
31
3)理论说明低温热源温度T2 0
说明热机效率 且只能 进一步说明 •热机循环不向低温热源放热是不可能的
T
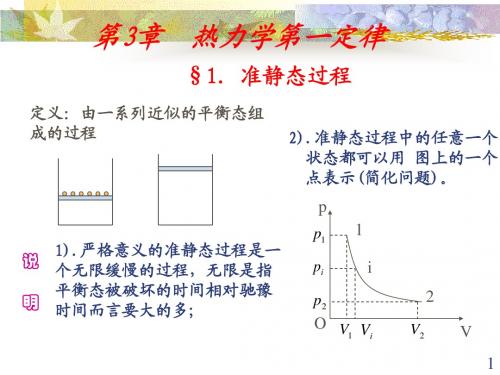
(2) 等压膨胀:系统吸热 O V1 V2 V 系统内能增加,且对外做功; 等温膨胀:系统吸热,全部用来对外做功,内能不变; 绝热膨胀:系统不吸收热量,靠减少系统的内能对外做功
PQ
D
等压:内能增加;等温:内能不变;绝热:内能减少。
(3) 等压膨胀过程吸热最多。(4)绝热线比等温线陡 22
例2: 一mol单原子理想气体在汽缸中,设汽缸与活塞无 摩擦,开始时,P1=1.013*105Pa, V1=1.0*10 –2m3 ,将 此气体在等压下加热,使其体积增大一倍,然后在等体 下加热至压强增大一倍,最后绝热 膨胀为起始温度。 (1)画P-V图(2)求内能的增量(3)过程中的功 解: (1)图示 (2)0 (3) P2
热力学第一定律

23
本章学习要求
• 掌握能量、热力系统储存能、热力学能、热量和功量 的概念,理解热量和功量是过程量而非状态参数。 • 理解热力学第一定律的实质能量守恒定律。 • 掌握稳定流动能量方程,能熟练运用稳定流动能量方 程对简单的工程问题进行能量交换的分析和计算。 • 掌握膨胀功、轴功、流动功和技术功的概念、计算及 它们之间的关系。 • 理解焓的定义式及其物理意义。 • 了解常用热工设备主要交换的能量及稳定流动能量方 程的简化形式。
2. 宏观位能: Ep ,单位为 J 或 kJ
Ep mgz
5
热力系总储存能:E ,单位为 J 或 kJ
E U Ek Ep
比储存能:e ,单位为 J/kg 或 kJ /kg
1 2 e u ek ep u cf gz 2
6
内动能-温度 热力学能 (内能U、u) 外储存能 内位能-比体积
∴流动功是一种特殊的功,其数值取决于
控制体进、出口界面上工质的热力状态。
14
根据热力学第一定律, 有 :
1 2 1 2 u1 cf 1 gz1 p1v1 q u2 cf 2 gz2 p2v2 ws 0 2 2
令 upv h,由于u、p、v都是状态参数,所以h也是 状态参数,称为比焓。
对一切热力系统和热力过程,有:
进入系统的能量-离开系统的能量 = 系统储存能量的变化
8
二、闭口热力系的能量方程
如图: Q=△U+W 对微元过程: Q QdUW 或 qduw 即: 热力系获得热量= 增加的热力学能+膨胀做功 对于可逆过程 : qdupdv 或
ΔU
W
qu pdv
第十八章 热力学第一定律讲解

ln
V1 V3
RT1
ln
V1 8V1
2.08 RT1
Q3 A3 2.08RT1
(2)循环效率 1 Q3
Q1
1 2.08 RT1 3RT1
30.7%
例题5: 内燃机的循环之一——奥托循环.内燃机利用液体或气体 燃料,直接在气缸中燃烧,产生巨大的压强而作功.内燃机的种类很 多,试说明四冲程汽油内燃机循环的效率.
P P2
P1 1
2
解:
QA对吸(外(吸A热代之数和和)) 1
Q2 Q1
3
A
1 2
(V2
V1 )( P2
P1 )
分析哪段吸热:
0 V1 V2 V
T2 T3 T1 只有12吸热
Q吸
A12
(E2
E1)
1 2
(P1
P2
)(V2
V1 )
i 2
R(T2
T1)
A
...
p
1 2
P0
V0
V0
V0
V0
V0
V0
V0
V0
节流过程
多孔塞
p1 大压强 空间
p2 小压强
空间
1)对理想气体经历节流过程:
A E 0
T2 T1
说明理想气体经历节流过程后温度不变。
2)对真实气体,节流膨胀后温度要发生变化。因为分子间存 在相互作用的势能。
正焦耳--汤姆逊效应:节流膨胀后温度降低; 负焦耳--汤姆逊效应:节流膨胀后温度升高
和已知常量表示)
第18章 热力学第一定律

22
结果为正,表示气体从外界吸了热。得 气体内能增加了1.90×105J。 对于a→2的等压过程
∆E)1a =νCV ,m (Ta −T ) = Q a =1.90×105 ( J ) ( 1 1
Aa2 = ∫ pdV = p2 (V2 −V ) = −0.81×105 ( J ) 1
V2 V 1
等温过程中气体对外做功 等温过程 V2 V2 ν RT V2 dV =ν RT ln A = ∫ pdV = ∫ V V 1 1 V V 1 说明等温膨胀过程(V2>V1)时,气体对外界做正 功;等温压缩(V2<V1)时, 外界对气体做功。 12
理想气体的内能公式 i E = ν RT 2 等温过程中,由于温度T不变,∆E=0,根据热力 学第一定律可得气体从外界吸收的热量为 V2 Q = ∆E + A = A =ν RT ln V 1 此结果说明,气体膨胀时,Q>0,气体从外界 吸热;气体等温压缩时,Q<0,气体对外界放热。
负号表示气体内能减少了0.13×105J.
5 5
Q =∆E + A =−0.13×10 −0.51×10 =−0.64×10 ( J )
5
是气体向外界放了热。
26
18.4 绝热过程
如果系统在整个过程中始终不和外界交换热 则这种过程称为绝热过程。 量,则这种过程称为绝热过程。
1. 准静态绝热过程
特征: 特征:dQ=0,Q=0 , 过程方程:由 过程方程 由 pV=νRT 全微分 pdV+Vdp=νRdT (1) ) 由热一律 dQ=νCVdT+pdV=0 (2) ) 消去dT (1)(2)联立 得 消去 ) )
等温线 绝热线
p
热力学第一定律和第二定律

热力学第一定律和第二定律热力学第一定律1. 内容:一般情况下,如果物体跟外界同时发生做功和热传递的过程,那么外界对物体做的功W,与物体从外界吸收的热量Q之和,等于物体的内能的增加量2. 数学表达式:W+Q=ΔU(1)Q取决于温度变化:温度升高,Q>0;温度降低,Q<0.(2)W取决于体积变化:V增大时,气体对外做功,W<0;V减小时,外界对气体做功,W>0.(3)特例:如果气体向真空扩散,那么W=0.(4)绝热过程Q=0,关键词是“绝热材料”或“变化迅速”。
3. 热力学第1定律的理解(1)做功改变物体的内能:外界对物体做功,物体内能增加;物体对外做功,物体内能减少。
在绝热过程,物体做多少功,改变多少内能。
(2)热传递改变物体的内能:外界向物体传递热量,即物体吸热,物体的内能增加;物体向外界传递热量,即物体放热,物体的内能减少。
传递多少热量,内能就改变多少。
(3)做功和热传递的实质,做功改变内能是能量的变化,用功的数值来度量;热传递改变内能是能量的转移,用热量来度量。
热力学第二定律1.热传导的方向性:热传导的过程可以自发地由高温物体向低温物体进行,但相反方向却不能自发地进行,即热传导具有方向性,是一个不可逆过程。
2.补充说明:(1)“自发地”过程就是不受外界干扰的条件下进行的自然过程;(2)热量可以自发地从高温物体向低温物体传递,却不能自发的从低温物体传向高温物体;(2)热力学第二定律的能量守恒表达式:ds≥δQ/T(3)热量可以从低温物体传向高温物体,必须有“外界的影响或帮助”,就是要由外界对其做功才能完成。
3.热力学第二定律的两种表述(1)克劳修斯表述:热量不能自发地从低温物体传向高温物体。
(2)开尔文表述:不可能从单一热源吸收热量,使之完全变为有用功,而不引起其他变化。
热力学第一定律

= PdV
A=
∫
V2
V1
pdV
7
A =
∫ dA = ∫
V2
V1
pdV
dV > 0, dA > 0, 系统对外作正功;
dV < 0,dA < 0, 系统对外作负功;
dV = 0,dA = 0, 系统不作功。
A = ∫ pdV
V1
V2
由积分意义可知,功的大小等于p—V 图上过程 曲线p(V)下的面积。功的数值不仅与初态和末 态有关,而且还依赖于所经历的中间状态,功 8 与过程的路径有关.
QT 热源 Q V
等容过程
热源 QP
等压过程
T 恒温大 V
6
三、功 热量 内能 dx 1功 如图示的热力学系统: P S 若过程为无摩擦的准静 态过程 活塞迎着气体一侧的面积为S气体膨胀推动活塞对 外作功:
dA =
当系统体积从 V1→ V2,系统对外界作功:
F Fdx = S Sdx
在等温过程中,理想气体吸热全部用于对外作 功,或外界对气体作功全转换为气体放出的热。 22
四、绝热过程
系统在状态变化过程中始终与外界没有热交换。
绝热膨胀过程中,系统对外作的功,是靠内能减少实 现的,故温度降低;绝热压缩过程中,外界对气体作 功全部用于增加气体内能,故温度上升。 绝热过程方程: 气体绝热自由膨胀 Q=0, A=0,△E=0
14
Q=∫
V2
V1
i pdV + νR(T2 − T1 ) 2
Q = ( E 2 − E 1) + A = ∆ E + A
热力学第一定律,是包含热量在内的能量守恒定律。
Q>0 Q<0
热力学第一定律

1.热力学第一定律热力学第一定律的主要内容,就是能量守恒原理。
能量可以在一物体与其他物体之间传递,可以从一种形式转化成另一种形式,但是不能无中生有,也不能自行消失。
而不同形式的能量在相互转化时永远是数量相当的。
这一原理,在现在看来似乎是顺理成章的,但他的建立却经历了许多失败和教训。
一百多年前西方工业革命,发明了蒸汽机,人们对改进蒸汽机产生了浓厚的兴趣。
总想造成不供能量或者少供能量而多做功的机器,曾兴起过制造“第一类永动机”的热潮。
所谓第一类永动机就是不需供给热量,不需消耗燃料而能不断循环做工的机器。
设计方案之多,但是成千上万份的设计中,没有一个能实现的。
人们从这类经验中逐渐认识到,能量是不能无中生有的,自生自灭的。
第一类永动机是不可能制成的,这就是能量守恒原理。
到了1840年,由焦耳和迈尔作了大量试验,测量了热和功转换过程中,消耗多少功会得到多少热,证明了热和机械功的转换具有严格的不变的当量关系。
想得到1J的机械功,一定要消耗0.239卡热,得到1卡热,一定要消耗4.184J的功,这就是著名的热功当量。
1cal = 4.1840J热功当量的测定试验,给能量守恒原理提供了科学依据,使这一原理得到了更为普遍的承认,牢牢的确立起来。
至今,无论是微观世界中物质的运动,还是宏观世界中的物质变化都无一例外的符合能量守恒原理。
把这一原理运用到宏观的热力学体系,就形成了热力学第一定律。
2.热力学第二定律能量守恒和转化定律就是热力学第一定律,或者说热力学第一定律是能量守恒和转化定律在热力学上的表现。
它指明热是物质运动的一种形式,物质系统从外界吸收的热量等于这个能的增加量和它对外所作的功的总和。
也就是说想制造一种不消耗任何能量就能永远作功的机器,即“第一种永动机”,是不可能的。
人们继续研究热机效率问题,试图从单一热源吸取能量去制作会永远作功的机器,这种机器并不违背能量守恒定律,只需将热源降温而利用其能量推动机器不断运转。
大学物理第十八单元 热力学第一定律

第十八单元 热力学第一定律[课本内容] 马文蔚,第四版,上册 [6]-[40] [典型例题]例18-1.一定量的某种理想气体,开始时处于压强、体积、温度分别为P 0=1.2×106Pa, V 0=8.31×10-3m 3,, T 0=300K 的初态,后经过一等容过程,温度升高到T 1=450K ,再经过一等温过程,压强降到P=P O 末态,已知该理想气体的等压摩尔热容与等容摩与热容之比C P /C V =5/3。
求:(1)理想气体的等压摩尔热容C P 和等容摩尔热容C V 。
(2)气体从始态变到末态的全过程中从外界吸收的热量。
提示:(1)52,,3322P V P V C i i C R C R i C +===⇒=Q 、(2)1101()ln V opQ E A C T T RT p νν=∆+=-+4110103()ln 1.35102p R T T RT Jp νν=-+=⨯例18-2.一定量的刚性双原子分子理想气体,开始时处于压强为p 0=1.0×106Pa,体积为V 0=4×10-3m 3温度为T 0=300K 的初态,后经等压膨胀过程温度上升到T 1=450K ,再经绝热过程温度回到T 2=300K ,求气体在整过程中对外界作的功。
提示:)(700)300450(300104100.127)(27)(25)()(25)(3601000010112010J T T T V p T T R T T R T T R V V p A =-⨯⨯⨯⋅=-⋅=-+-=---=-ννν练习十八一、选择题:18-1.有两个相同的容器,容积固定不变,一个盛有氨气,另一个盛有氢气(看成刚性分子的理想气体),它们的压强和温度都相等,现将5J 的热量传给氢气,使氢气温度升高,如果使氨气也升高同样的温度,则应向氨气传递热量是: [ ](A) 6 J. (B) 5 J. (C) 3 J. (D) 2 J.652i M iQ E A R T Q i A μ===∆+=∆⇒∝1提示:由V 不变,知功A=0;氨气i ,氢气;,所以选18-2.一定量的理想气体分别由初态a 经①过程ab 和由初态a ′经②过程a ′cb 到达相同的终态b ,如p -T 图所示,则两个过程中气体从外界吸收的热量 Q 1,Q 2的关系为: [ ] (A) Q 1<0,Q 1> Q 2. (B) Q 1>0,Q 1> Q 2. (C) Q 1<0,Q 1< Q 2. (D) Q 1>0,Q 1< Q 2.10cb cb E E A Q A V ∆>=∆+=-→↑↓2提示:过程①,等体过程,Q=过程②,等体再等温,Q (c b ;p ,)所以选B18-3.对于室温下的双原子分子理想气体,在等压膨胀的情况下,系统对外所作的功与从外界吸收的热量之比W / Q 等于 [ ] (A) 2/3. (B) 1/2. (C) 2/5. (D) 2/7.pOTab a ′c① ②2227p p W R Q C i βνν⇒===+21p 21p 21提示:双原子i=5,W=(V -V )=C (T -T )① Q=C (T -T )②①得②所以选D18-4.1 mol 理想气体从p -V 图上初态a 分别经历如图所示的(1) 或(2)过程到达末态b .已知T a <T b ,则这两过程中气体吸收的热量Q 1和Q 2的关系是 [ ](A) Q 1> Q 2>0. (B) Q 2> Q 1>0. (C) Q 2< Q 1<0. (D) Q 1< Q 2<0.(E) Q 1= Q 2>0.1212000E E A A E A ∆=∆>>>=∆+>>12提示:由过程①②,,,由Q ,得Q Q 所以选A18-5.氦气、氮气、水蒸汽(均视为刚性分子理想气体),它们的摩尔数相同,初始状态相同,若使它们在体积不变情况下吸收相等的热量,则 [ ] (A) 它们的温度升高相同,压强增加相同. (B) 它们的温度升高相同,压强增加不相同. (C) 它们的温度升高不相同,压强增加不相同.(D) 它们的温度升高不相同,压强增加相同.22v i iE C T R T P Cννν∆=∆=∆=∆提示:Q=所以选18-6.一定量的理想气体,经历某过程后,温度升高了.则根据热力学定律可以断定: (1) 该理想气体系统在此过程中吸了热. (2) 在此过程中外界对该理想气体系统作了正功. (3) 该理想气体系统的内能增加了. (4) 在此过程中理想气体系统既从外界吸了热,又对外作了正功.以上正确的断言是: [ ] (A) (1)、(3). (B) (2)、(3).(C) (3). (D) (3)、(4). 提示:选C二、填空题18-7.一气缸内贮有10 mol 的单原子分子理想气体,在压缩过程中外界作功209J ,气体升温 1 K ,此过程中气体内能增量为 ____ ,外界传给气体的热量为____ __________.3 2.091125284i A J E iR T JQ E A J ν==-∆=∆==∆-=-提示:,,18-8.一定量的某种理想气体在等压过程中对外作功为 200 J .若此种气体为单原子分子气体,则该过程中需吸热___________ J ;若为双原子分子气体,则需吸热____________ J.22i =+W 提示:参看18-3题,,所以答案为:500J ;700JQ18-9.2 mol 单原子分子理想气体,从平衡态1经一等体过程后达到平衡态2,温度从 200 K 上升到 500 K ,若该过程为平衡过程,气体吸收的热量为____________;若为不平衡过程,气体吸收的热量为______________.221328.3130074722i E iR T Jν=+∆=∆=⨯⨯⨯=W 提示:参看18-3题,,所以答案为:500J ;700JQ 提示:功W=0,Q=所以答案为:747J ;大于747J18-10.一定量理想气体,从A 状态 (2p 1,V 1)经历如图所示的直线过程变到B 状态(p 1,2V 1),则AB 过程中系统作功W =_________;内能改变∆E =_________.11302PV E =∆=面积提示:由图,W=S ;18-11.常温常压下,一定量的某种理想气体(其分子可视为刚性分子,自由度为i ,在等压过程中吸热为Q ,对外作功为W ,内能增加为E ∆,则W /Q =_____________. =∆Q E / _____________.222v i E iE C T i νν=+∆∆=∆∆=+p W 提示:参看18-3,;Q 由;Q=C T 得Q18-12.压强、体积和温度都相同的氢气和氦气(均视为刚性分子的理想气体),它们的质量之比为m 1∶m 2=__________,它们的内能之比为E 1∶E 2=__________,如果它们分别在等压过程中吸收了相同的热量,则它们对外作功之比为W 1∶W 2=__________. (各量下角标1表示氢气,2表示氦气)121212152232527v E M i C T iRT PV i E W i W νμ===∝===+12M 提示:由状态方程的,M 因为E=,所以;W 由知Q18-13.同一种理想气体的定压摩尔热容C p 大于定体摩尔热容C V ,其原因是 ________________________________________.提示:等容过程,A=0,等压过程,A>0三、计算题18-14. 0.02 kg 的氦气(视为理想气体),温度由17℃升为27℃.若在升温过程中, (1) 体积保持不变; (2) 压强保持不变; (3) 不与外界交换热量;试分别求出气体内能的改变、吸收的热量、外界对气体所作的功.3310.0238.3110623241026230.026238.3110416410623623M E iR T J Q E JME J W P V R T J E J A E J μμ--∆=∆=⨯⨯⨯=⨯=∆=∆==∆=∆=⨯⨯=⨯∆==-∆=- 提示:(1)功W=0,所以(2)由,,所以外界对气体做功为-416J(3)Q=0,,,所以外界对气体做功623J18-15. 1 mol 双原子分子理想气体从状态A (p 1,V 1)沿p -V 图所示直线变化到状态B (p 2,V 2),试求:(1) 气体的内能增量.(2) 气体对外界所作的功. (3) 气体吸收的热量.(4) 此过程的摩尔热容.(摩尔热容C =ΔQ/ΔT ,其中ΔQ 表示1 mol 物质在过程中升高温度T ∆时所吸收的热量.)2122112211221122112121215:(1)()()221(2)()2(3)3()3()3()(4)3i E R T T PV PV A S S PV PV Q E A PV PV PV PV R T T Q C RT T T T T ∆=-=-=-=-=∆+=---====∆--大小提示18-16. 一定量的理想气体,由状态a 经b 到达c .(如图,abc为一直线)求此过程中(1) 气体对外作的功; (2) 气体内能的增量;(3)气体吸收的热量.(1 atm =1.013×105 Pa)53(13) 1.0310:(1)2104052(2),;0(3)405a b W S J PV vRT T T E Q W J+⨯⨯==⨯⨯===∆===面积提示由知18-17.一定量的理想气体在标准状态下体积为 1.0×10-2 m 3,求下列过程中气体吸收的热量(设气体的C V = 5R / 2.): (1) 等温膨胀到体积为 2.0×10-2 m 3; (2) 先等体冷却,再等压膨胀到 (1) 中所到达的终态.BAOp p 2 p V 1 21 2 3 1 2 3 a bc V (L) p (atm)2011ln ln2702ababacbacb acb ac cbE E WVW vRT PV JVEQ E W W W P∆=∆+===→→∆==∆+=+=02121提示:如图:由等温过程,且Q=(1)(2)整个过程a b c,P(V-V)=(V-V)=507J2。
热力学第一定律的内容及公式

热力学第一定律的内容及公式
热力学第一定律是热力学很重要的定律,简称为第一定律。
热力学第一定律是物理和化学中最基本也是最重要的定律,概括地说,它指出了总热量是不可消失的,即能量守恒定律。
它是由德国物理学家莱布尼兹在1850年发现的。
热力学第一定律指出,内能系统内所有物质之间的总热量交换是不可消失的,即总热量守恒定律,在反应过程中能量不会消失,它只能以动能形式存在,也就是说,能量可以有很多形式存在,但是总量是不变的。
它可以用如下的公式来表示:
E=q+w
其中,E表示热力学第一定律定义的能量总量;q表示热量;w
表示功能。
热力学第一定律可以用来解释诸如内能的变化、热动力学中的功能过程、经典热力学定律的发展,以及熵的概念。
它的应用还可以普遍用于热力学和热工程的其他领域。
所有的能量转换都可以用热力学第一定律进行表述,即能量在某种形式变换到另一种形式的守恒定律。
比如,当将动能转化为功能,则q+w=E,即动能变为功能的过程中,能量总量E是不变的。
当功能转化为动能,则q-w=E,即功能变为动能的过程中,能量总量E也是不变的。
总之,热力学第一定律是一个重要的定律,它表明能量总量在任何过程中都是守恒的,它是对物理和化学中反应过程能量变化的最基
本的定律。
热力学第一定律解释了热力学和热工程中诸如内能的变化、热动力学中的功能过程、熵的性质及其变化的原理,在热力学和热工程的理论和应用方面有着重要的意义。
热力学第一定律的表达式

热力学第一定律的表达式热力学第一定律的表达式:ΔE=W+Q。
在热力学中,热力学第一定律通常表述为:热能和机械能在转化时,总能量保持不变。
其数学表达式为ΔE=W+Q,其中ΔE表示系统内能的改变,W表示系统对外所做的功,Q表示系统从外界吸收的热量。
这个定律表明,能量的转化和守恒定律是自然界的基本定律之一,它适用于任何与外界没有能量交换的孤立系统。
换句话说,在一个封闭系统中,能量的总量是恒定的,改变的只是能量的形式。
因此,热力学第一定律是能量守恒定律在热现象领域中的应用。
另外,对于一个封闭系统,如果系统内部没有发生化学反应或相变等过程,那么系统对外做的功等于系统从外界吸收的热量。
这是因为系统内能的改变量等于系统对外做的功和系统从外界吸收的热量之和。
值得注意的是,热力学第一定律也适用于非平衡态系统。
即使系统处于非平衡态,热力学第一定律仍然适用。
因此,它不仅是热力学的基石之一,也是整个物理学的基石之一。
为了更好地理解热力学第一定律,我们可以考虑一些具体的应用场景。
例如,在汽车发动机中,汽油燃烧产生的热能转化为汽车的动能和废气中的内能。
在这个过程中,系统内能的改变量等于系统对外做的功和系统从外界吸收的热量之和。
因此,根据热力学第一定律,我们可以计算出汽车发动机的效率,从而评估其能源利用效果。
此外,热力学第一定律还可以应用于电学、化学等领域。
例如,在电学中,当电流通过电阻时会产生热量,根据热力学第一定律可以计算出电阻产生的热量。
在化学中,反应热的计算也可以根据热力学第一定律来进行。
以下是一些具体例子,说明热力学第一定律的应用:1. 热电站:在热电站中,燃料燃烧产生的热能转化为蒸汽的机械能,再转化为电能。
根据热力学第一定律,热能被转化为机械能和电能,而总能量保持不变。
通过计算输入和输出的能量,我们可以评估热电站的效率。
2. 制冷机:制冷机是一种将热量从低温处转移到高温处的设备。
在制冷过程中,制冷剂在蒸发器中吸收热量并转化为气态,然后通过压缩机和冷凝器将热量释放到高温处。
第一章热力学第一定律章总结

第一章热力学第一定律本章主要公式及其使用条件一、热力学第一定律W Q U +∆= W Q dU δδ+=热力学中规定体系吸热为正值,体系放热为负值;体系对环境作功为负值,环境对体系作功为正值。
功分为体积功和非体积功。
二、体积功的计算体积功:在一定的环境压力下,体系的体积发生改变而与环境交换的能量。
体积功公式⎰⋅-=dV p W 外 1 气体向真空膨胀:W =0 2气体在恒压过程:)(12 21V V p dV p W V V --=-=⎰外外3理想气体等温可逆过程:2112ln lnp p nRT V V nRT W -=-= 4理想气体绝热可逆过程:)(12,T T nC W U m V -=∆=理想气体绝热可逆过程中的p ,V ,T 可利用下面两式计算求解1212,ln ln V V R T T C m V -=21,12,ln lnV V C p p C m p m V =三、热的计算热:体系与环境之间由于存在温度差而引起的能量传递形式。
1. 定容热与定压热及两者关系定容热:只做体积功的封闭体系发生定容变化时, U Q V ∆= 定压热:只做体积功的封闭体系定压下发生变化, Q p = ΔH定容反应热Q V 与定压反应热Q p 的关系:V p Q Q V p ∆+= nRT U H ∆+∆=∆n ∆为产物与反应物中气体物质的量之差。
或者∑+=RT g Q Q m V m p )(,,ν ∑+∆=∆RT g U Hm m)(ν式中∑)(g ν为进行1mol 反应进度时,化学反应式中气态物质计量系数的代数和。
2.热容 1.热容的定义式dTQ C δ=dT Q C VV δ=dT Q C pp δ=n CC VmV =,n C C p m p =, C V ,C p 是广度性质的状态函数,C V ,m ,C p,m 是强度性质的状态函数。
2.理想气体的热容对于理想气体 C p ,m - C V ,m =R 单原子理想气体 C V ,m = 23R ;C p ,m = 25R 双原子理想气体 C V ,m =25R ;C p ,m = 27R 多原子理想气体: C V ,m = 3R ;C p ,m = 4R通常温度下,理想气体的C V ,m 和C p,m 均可视为常数。
热力第一定律

热力学第一定律热力学第一定律是能量守恒原理的一种表达方式。
此定律曰:在一个热力学系统内,能量可转换,即可从一种形式转变成另一种形式,但不能自行产生,也不能毁灭。
一般公式化为:一个系统内能的改变等于供给系统的热量减去系统对外环境所作的功。
热力学第一定律是生物,物理化学等学科的重要定律。
20本词条无基本信息模块, 正文缺少最新信息, 欢迎各位编辑词条,额外获取20个积分。
基本信息∙中文名称热力学第一定律∙外文名称the first law of thermodynamics∙应用学科物理∙提出时间19世纪50年代∙提出者迈耳 J.R.Mayer、焦耳 T.P.Joule∙表达式△U=Q+W目录1 基本介绍1.1 简单解释1.2 定义1.3 基本内容2 发展历史2.1 发展历史2.2 表述展开1 基本介绍1.1 简单解释1.2 定义1.3 基本内容2 发展历史2.1 发展历史2.2 表述+1QQ空间新浪微博腾讯微博百度贴吧人人豆瓣基本介绍编辑本段热力学第一定律:△U=Q+W。
系统在过程中能量的变化关系英文翻译:the first law of thermodynamics简单解释在热力学中,系统发生变化时,设与环境之间交换的热为Q,与环境交换的功为W,可得热力学能(亦称内能)的变化为ΔU = Q+ W或ΔU=Q-W(目前通用这两种说法,以前一种用的多),为了避免混淆,物理中普遍使用第一种,而化学中通常是说系统对外做功,故会用后一种。
定义自然界一切物体都具有能量,能量有各种不同形式,它能从一种形式转化为另一种形式,从一个物体传递给另一个物体,在转化和传递过程中能量的总和不变。
英文翻译:The first explicit statement of the first law of thermodynamics, by Rudolf Clausius in 1850, referred to cyclic thermodynamic processes"In all cases in which work is produced by the agency of heat, a quantity of heat is consumed which is proportional to the work done; and conversely, by the expenditure of an equal quantity of work an equal quantity of heat is produced."基本内容热可以转变为功,功也可以转变为热;消耗一定的功必产生一定的热,一定的热消失时,也必产生一定的功。
热力学第一定律完整

热力学第一定律摘要:热力学第一定律亦即能量转换与守恒定律,广泛地应用于各个学科领域。
本文回顾了其建立的背景及经过,它的准确的文字表述和数学表达式,及它在理想气体、热机等方面的应用。
关键词:热力学第一定律能量转换理想气体1.热力学第一定律的产生1.1历史渊源与科学背景人类使用热能为自己服务有着悠久的历史,火的发明和利用是人类支配自然力的伟大开端,是人类文明进步的里程碑。
中国古代就对火热的本性进行了探讨,殷商时期形成的“五行说”——金、木、水、火、土,就把火热看成是构成宇宙万物的五种元素之一。
北宋时刘昼更明确指出“金性苞水,木性藏火,故炼金则水出,钻木而生火。
”古希腊米利都学派的那拉克西曼德(Anaximander,约公元前611—547) 把火看成是与土、水、气并列的一种原素,它们都是由某种原始物质形成的世界四大主要元素。
恩培多克勒(Empedocles,约公元前500—430)更明确提出四元素学说,认为万物都是水、火、土、气四元素在不同数量上不同比例的配合,与我国的五行说十分相似。
但是人类对热的本质的认识却是很晚的事情。
18世纪中期,苏格兰科学家布莱克等人提出了热质说。
这种理论认为,热是由一种特殊的没有重量的流体物质,即热质(热素)所组成,并用以较圆满地解释了诸如由热传导从而导致热平衡、相变潜热和量热学等热现象,因而这种学说为当时一些著名科学家所接受,成为十八世纪热力学占统治地位的理论。
十九世纪以来热之唯动说渐渐地为更多的人们所注意。
特别是英国化学家和物理学家克鲁克斯(M.Crookes,1832—1919),所做的风车叶轮旋转实验,证明了热的本质就是分子无规则动的结论。
热动说较好地解释了热质说无法解释的现象,如摩擦生热等。
使人们对热的本质的认识大大地进了一步。
戴维以冰块摩擦生热融化为例而写成的名为《论热、光及光的复合》的论文,为热功相当提供了有相当说服力的实例,激励着更多的人去探讨这一问题。
1.2热力学第一定律的建立过程在18世纪末19世纪初,随着蒸汽机在生产中的广泛应用,人们越来越关注热和功的转化问题。
热力学第一定律

c,z是力学参数,处于同一热力学状态的 物体可以有不同的c,z.因此c,z是独立 于热力系统内部状态的外部参数, 系统的宏 观动能和重力位能又称为外储存能.
三,系统总储存能 系统的总储存能E为外储存能和内储存能之 和.
E = U + Ek + Ep
或
1 2 E = U + mc + mgz 2
对于1kg质量物体的总储存能为
对于可逆过程,有
δw = pdv ,或 w = ∫ pdv
1
2
代入闭口系统的守恒关系式,有
q = u + ∫ pdv ,或 δq = du + pdv
1
2
以上两式适用可逆过程.
分析热力学问题需建立(选择)热力学模 分析热力学问题需建立(选择) 型 1,确定热力系,即系统,边界和外界. 2,分析系统内部变化,各种作用量(外部), 各种作用量与系统内部变化的内在联系. 3,必须注意作用量的独立性,针对性和相互 性. (1)独立性 独立性是指热量,功量和质量交换这 独立性 三种不同作用量是相互独立的,每种
从微观角度看: 从微观角度看: 功——所起的作用是物体的有规律运动 所起的作用是物体的有规律运动 所起的作用是物体的 与系统内分子无规热运动 无规热运动之间的 与系统内分子无规热运动之间的 转换. 转换. 问题:热量与功的相同点和不同点 问题:热量与功的相同点和不同点?
相同点:功和热量都是过程量.只有在系 相同点 统和外界通过边界传递能量时才有意义, 一旦它们越过界面,便转化为系统或外界 的能量. 不能说在某状态下,系统或外界有多少功 或热.
对于理想气体,因忽略了分子间的作用力, 没有位能,故其内能仅包括分子内动能, 所以理想气体的内能只是温度的单值函数 理想气体的内能只是温度的单值函数, 理想气体的内能只是温度的单值函数 即
热力学第一定律

P2V2
ln
V2 V1
7
又 ∵ 等温过程有
V2 P1 V1 P2
有
AT
P1V1 M
ln P1 P2 RT
ln
P2V2 P1
ln
P1 P2
M mol
P2
(3)强调QT=AT
即在等温过程中,系统的热交换不能直接计算,但可用等 温过程中的功值AT来间接计算。
8
※三种过程中气体做的功
等体过程
(1)特征:dT=0, ∴dE=0 热一律为 QT=AT
在等温过程中,理想气体所吸收 的热量全部转化为对外界做功,系 统内能保持不变。
(2)等温过程的功
PI
P1
P2
o
V1
II
V2 V
∵T=C(常数),
P RT 1
V
dAT PdV
AT
V2 RTdV RT ln V2
V V1
V1
P1V1
ln
V2 V1
T1)
M M mol R(T2 T1)
5
C p
C V
R i2R 2
──此即迈耶公式
(3)比热容比:
定义
Cp
Cv
i 2
RR iR
i2 i
2
对理想气体刚性分子有:
单原子分子:
双原子分子:
5 3 7 5
1.67 1.4
*: 经典理论的缺陷
多原子分子:
8 6
1.33
6
3、等温过程
1
符号规定
Q
吸热为正, 放热为负.
系统对外做功为正, A 外界对系统做功为负.
各物理量的单位统一用国际单位制。
热力学第一定律

第1章热力学第一定律
1.1重要概念
这是两类完全不同的物理量。状态函数是系统的性质,如温度(T),压力(p),体积(V),
内能(U),焓(H)和定压热容(CV)等,而过程量是指功(W)和热(Q),它们是过程的属性。状态
函数与过程量主要区别如下:
(1)状态函数决定于系统的状态,而过程量取决于过程。所以状态函数用来描述系统状
(3)若在系统的初末态之间存在多个等温过程,则其中的等温可逆过程的功值最大,即
WT,r>WT,ir
5.绝热过程(绝热膨胀或绝热压缩)
(1)由于系统与环境不交换热量,所以在绝热过程中系统内能的增加与它从环境中所得
到的功等值,即
∆U=- W
(2)一般说来,在绝热过程中系统的pVT同时变化。
(3)从同一状态出发,不同的绝热过程具有不同的末态。即在相同的初末态之间不会有
多种绝热途径。
(4)一个实际的绝热过程发生之后,系统不可能循任何绝热途径恢复到原来状态。
(5)从同一初态出发,经多种绝热过程后,系统到达同一压力(或同一体积),则其中绝热
可逆过程的功值最大。即
Wr,Q=0>WirQ=0
(6)与等温可逆过程相比,绝热可逆过程的压力对体积的变化更敏感。所以在—V图上,
绝热线比等温线要陡,即
(2)关于理想气体的重要结论:
①理想气体的U,H,CV和CP只是温度的函数,即⎛源自∂p⎛ ∂H
⎜⎞
程,即
Tl=T2=T环=常数
所谓等温过程,是指上式中三个等号同时成立的过程。有人认为等温过程是系统
温度始终不变的过程,这是一种误解。诚然,在某一过程中如果系统温度始终不
变,则过程必是等温过程,因为该过程服从上式。但这并非等温过程的全部,只
热力学第一定律

q du w
q d h pv pdv
q dh - pdv - vdp pdv dh - vdp
三、稳定流动能量方程式的分析
总结
热力学第一定律的解析式在形式上虽有不同, 但由热功转换的实质是一致的,都是能量守恒定律 在热力学和热力工程上的体现。 从热功互换角度来看,第一解析式反映出热 力过程中热能向机械能的转化,是各种热动力设备 实现动力输出的理论核心,是最基本的能量方程。
1
2
1
vdp
(2-4a)
g
2 v
根据上式可在 p-v 图上表示可 逆过程的技术功,如右图中的曲边 梯形面积 f-1-2-g-f 所示。
图2-2 可逆过程的技术功
稳定流动能量方程可进一步表达为
1 2 q u c f g z wi pv 2
微元 过程
q h wt h2 h1 wt
即过程中气体自外界吸热112 000 J。
(2)气体对外界作的功有两部分功用,一是用于排斥 活塞背面的大气(Wr),另一部分(Wu)转变成活塞的动 能增量。
例题索引
摩擦功
Wu W Wr W1
可逆过程输出有用功
Wr p0V p0 (V2 V1 ) 50,000J 第二部分Wu为:
移项
Q U W
2.第一定律的第一解析式的微元形式是:
对于1kg工质,则有:
Q dU W
q u w , q d u w
3.式中热量Q,热力学能变量Δ U 和功W都是代数值,可正可
负。
4.第一定律的第一解析式的微元形式具有普适性(可逆与不 可逆过程,理想气体与实际气体甚至液体)
热力学第一定律及其表达式

热力学第一定律及其表达式
热力学第一定律是能量守恒定律在热系统中的应用,它表明在任何一个封闭系统中,能量的增量等于系统所做的功加上系统所吸收的热量。
这一定律的表达式为ΔU=Q-W,其中ΔU表示系统内能量的增量,Q表示系统吸收的热量,W表示系统所做的功。
热力学第一定律的实质是能量不能自行消失,只能从一种形式转变为另一种形式。
这一定律对于热力学的研究具有重要的意义,它为热力学第二定律提供了理论基础,并为工程技术的发展提供了指导。
热力学第一定律的表达式ΔU=Q-W可以用于热力学系统的能量平衡分析。
例如,在化学反应中,反应物和产物的内能差可以通过测量反应热来确定,从而可以计算反应所做的功或吸收的热量。
在热机和制冷机中,热力学第一定律的表达式也被广泛应用。
总之,热力学第一定律是热力学研究的基础,它为热力学的发展和应用提供了重要的理论支持。
- 1 -。
热力学第一定律的表达式为

热力学第一定律的表达式为热力学第一定律,也叫热力学总体定律,是热力学中最基本的定律之一,也是热力学中最重要的定律。
它概括地说明热力学系统的能量是保守的,也就是说,热力学系统的总能量是不变的。
这条定律最早是由德国数学家、物理学家卡尔弗里德里希热平克(Karl Freidrich Zeipel)在1850年提出的,他将热力学第一定律定义为“一个系统里,只有当机械作用之后,系统的总能量才会改变,而在没有机械作用的情况下,总能量不变”。
热力学第一定律的表达式热力学第一定律的表达式有多种,最常用的表达式是:U = Q - W,其中U为能量变化,Q 为热量, W 为功。
根据热力学定律,任何热力学的过程中,所有的热力学性质和能量都是不变的,热力学系统的能量变化只与工作量有关。
因此,热力学第一定律可以用其表达式来描述:U=Q-W 。
事实上,在物理学中,热力学第一定律可以用其他表达式来表示,比如:dU=dQ+dW 。
这两个表达式是等价的,可以互相转化,只是在不同情况下有不同的用法。
热力学第一定律的应用热力学第一定律是物质研究的基础,它提供了一种物质能量守恒的规律。
它既可以解释室温和低温的物理过程,也可以用于解释电能和热能的转化过程。
热力学第一定律可以用来研究物理学热学中的各种热力学过程,比如对热源的熔点和温度的变化,熔融过程的变换,物质在冷却、冷热相变和熔点转变时的行为等等,都可以用热力学第一定律来研究。
此外,热力学第一定律还可以用来解释和研究热电转换和涡轮机等储能机械的运行原理,以及热能学、物质动力学和材料的散热机理。
热力学第一定律是一个重要的物理学原理,它在很多物理学领域有重要的应用,比如能源技术、物质动力学、热力学、材料科学等等,都离不开它的应用。
所以,热力学第一定律是极具重要意义的物理学原理。
结论热力学第一定律是物理学中最基本的定律之一,它表明热力学系统的总能量是不变的,这也是物质能量守恒的基本原理。
它既可以用来研究室温和低温的物理过程,也可以用来研究热电转换的原理,热力学第一定律在很多物理学领域有重要的应用,它具有极具重要意义的物理学原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
功
系统在某过程作的功与过程有关,其大小等于其p– V曲线下的面积。当过程中热力学系统的体积是减 少的,系统对外作负功 ;当系统体积增加,作正功。
等压过程:A V pdV p(V2 V1 ) p V ( p1 ,V1 ) 等温过程: A pdV
1
V2
例: m过程:dV>0, 系统对外作正功
§18.4 绝热过程
1、理想气体准静态绝热过程
由热力学第一定律:
说明:(1)理想气体准静态绝热过程既满足理想气
dQ=0
dA dE
体状态方程也满足理想气体绝热方程 pV c (2)绝热曲线 P A 等温 绝热 O V 过同一点的绝热线和等温线比较: 绝热线的斜率大 于等温线的斜率
dP dP dV 绝热 dV 等温
16
§18.3 热容
定义: 系统温度升高 1K 所吸收的热量称系统的热容量
热容
1、 等容摩尔热容 Cv 2、 等压摩尔热容 Cp
CV i R 2
C
dQ dT
1 摩尔系统的热容量称摩尔热容,记做 C 1克物质系统的热容量称比热,记做c C'、 C、c 的数值与系统及系统经历的过程有关 1、 等容摩尔热容Cv
o
4 103
因此,有
Aacb Qacb 200J
Q A Aacb Abd Ada 200 0 1200 1000J
13 14
1200J
例3
1mol 理想气体在 P~V 图上经历的过程方程为 P P0 V
P0和 为常数,求:此过程经历的最高温度 RT 解: 将理想气体状态方程 PV P RT P V 代入过程方程中,得到:
A
2V1
pV 2 p1V12
1 p1V12 dV p1V1 2 V2
dQ dE dA
dA pdV
dE dQV CV dT
V1
pdV
2V1
V1
dQ (CV R )dT
TV const
19 F. Y. Meng
或
pV 2 const
20 F. Y. Meng
Q0:系统从外界吸热; Q0:系统向外界放热 设: 系统从外界吸收热量 Q 外界对系统作功 A′ 由能量守恒:Q + A′= E 其微分形式: dQ dA dE 准静态无摩擦过程
内能是状态量,是状态参量T 的单值函数。
使系统的内能改变:
传热和作功。 热源 实际气体内能:
A’
系统对外界作功 A
p1V1 RT1
Ada 1200J
A 1200J
由热一律得:
B 1000J
C 700J
P (pa )
D 1000J
解:气体经历 acbda过程 E 0
4 10
5
a
c
d
Aacb ?
Qacb 200J Eacb
i R(Tb Ta ) 2 i ( PbVb PaVa ) 0 2
dP P dV V
dA pdV i RdT pdV CV dT i 2 dE RdT pdV Vdp RdT 2 pdV Vdp R ( R CV ) pdV CVVdp pdV CV
C p pdV CVVdp lnV ln p C
Q E A
A 209J
0
Q 1 2 4 .7 2 0 9 8 4 .3 J
பைடு நூலகம்12
i pdV R(T2 T1 ) 2
2
2016/1/28
例2、一定量的理想气体经历acb过程时吸热200J,则经 历acbda过程时,吸热为:
例 2解
P (pa )
Abd 0
11
解: 单原子分子 i 3
10
T 1K
p C1 0 T p(V2 V1 ) V C2 RT T V pV C 3 RT ln 2 V1
Q
V2 V1
3 i E R T 10 8.31 1 124.7 J 2 2
A A
dQ dE dA
dQ dE dA
Q
所有分子热运动的动能和分子间势能的总和。
热力学第 系统从外界吸收的热量等于系统对 一定律: 外界做的功和系统内能的增量之和 其积分形式: Q dA dE A E
7 8
热力学第一定律
dQ dE dA
CV
i R 2
理想气体热容比:
2 i i (1 ) 1 2 2 i
17
F. Y. Meng
18
F. Y. Meng
3
2016/1/28
例4、 1摩尔刚性双原子分子理想气体经历某一过程的摩尔热容量
例4、 1摩尔刚性双原子分子理想气体经历某一过程的摩尔热容量
C CV R , 其中 CV为定容摩尔热容量,R 为气体普适常数, 求:1)此过程的过程方程;2)设初始状态为 ( P1 ,V1 )
dQ=dA =pdV
QT AT V
过程 等容 等压 等温
V2
1
RT
V
dV
p V pdV RT ln 2 RT ln 1 V1 p2
过程方程
A
E
i RT 2 i RT 2
Q
i RT 2 i (1 ) RT 2 V RT ln 2 V1
作业
《大学物理习题集》 268,269, 270, 271, 282(功、 热量、准静态过程、热一律)
V
P0V V 2 R dT 0 求极值, dV T
O 最高温度: Tmax
《课本》P69/ 18.2, 18.5
P 求得极值点: V V0 0
15 F. Y. Meng
2
P02 4R
i i dE RdT dQV dE RdT 2 2 i QV E RT 2 B)理想气体等压过程:dp 0
2
Q
V2 V1
i p d V R (T 2 T1 ) 2
说 明 1)热力学第一定律适用于任何热力学系统和过程 2)系统内能变化量只与系统始末状态有关,与过程无关 3)系统对外做的功、系统从外界吸收的热量与过程有关 9
pV c1
21
TV 1 c2
p 1T c3
PV const
P V 1dV V dP 0
dP P dV V
理想气体绝热过程方程
F. Y. Meng 22
PV const PdV VdP 0
四种准静态过程
过程 等容 等压 等温 绝热 特点 过程方程
沿此过程膨胀到 2V1对外所做的功
C CV R , 其中 CV为定容摩尔热容量,R 为气体普适常数, 求:1)此过程的过程方程;2)设初始状态为 ( P1 ,V1 ) 沿此过程膨胀到 2V1对外所做的功
解:
解:
摩尔热容定义: dQ C CV R dT
热一律:
pV 2 const
1
1) dQ=0 特点: 2)自由过程不是准静态过程,中间过程不满足状态方程 3)过程仍满足热力学第一定律 dA+dE=dQ=0 4)系统自由膨胀,对外不作功 dA=0 5)系统始末态仍是平衡态,满足理想气体状态方程
24
F. Y. Meng
p1V1 p2V 2 1
0
23
4
2016/1/28
理想气体等压过程: i dQ p dQ p (1 ) RdT C p dT Cp 2 dT
i C p (1 ) R 2
C p CV R
迈耶公式
CV
dQV dT
定义:
Cp CV
为系统的热容比
CV
R
1
理想气体等容过程:
dQV dE
i RdT CV dT 2
2、绝热自由膨胀
A
0
p(V2 V1 ) RT
Q
CV (T2 T1 )
C p (T2 T1 )
dV 0
dp 0
dT 0
dQ 0
p C1 T V C2 T
开始 . .. .. ... . . . . . .. . .. . . .. . . . . . . . .
pdV pV Vd p RT RdT
dQ p dAp dE (1 i ) RdT
dAp pdV RdT dE 2 RdT
i
2 i Q p (1 ) RT 2
10
C)理想气体等温过程: dT=0
∴dE=0
例1 一汽缸内储有10 mol 单原子分子理想气体,在压 缩过程中外界作功209J,气体升温1K,此过程中气 体内能增量是多少?外界传给气体的热量是多少?
绝热自由膨胀
设: 系统初态体积 V1 膨胀后体积 V2
末
dQ 0,dA 0 dE 0 E dE 0 初
T 0
T1 T2
例 5、一绝热容器,若中间以隔板隔开,左半部分充满理想 气体,其压强为P0,容积为V0,右半部分是真空,容积为V0, (1) 当抽开隔板达到平衡后,求终态压强P1 (2) 隔板换成活塞,让它非常缓慢地向右移动至终态容积为 2V0时,求终态压强P2 (1) 绝热自由膨胀:
dl S P
若过程为准静态过程
(c)
恒温大热源
