热力学第一定律
热力学第一定律总结

298 K时,H2(g)的∆cHmө = -285.83 kJ·mol-1, H2S(g)和 SO2(g)的∆fHmө分别为-20.63 kJ·mol-1和-296.83 kJ·mol-1。 求下列反应在498 K时的∆rUmө。已知水在373 K时的摩 尔蒸发焓∆vapHm (H2O, 373 K) = 40.668 kJ·mol-1. 2H2S (g) + 3O2 (g) = 2SO2 (g) + 2H2O(g)
其中,T2的值由理想气体绝热方程式(pVγ=C)求得。
3、Q的计算 、 的计算
• Q = ∆U – W • 如恒容,Q = ∆U • 如恒压,Q = ∆H
1. 绝热密闭体系里,以下过程的ΔU不等于零的是: A) 非理想气体混合 B) 白磷自燃 C) 乙醚挥发 D) 以上均为0 2.“爆竹声中一岁除,春风送暖入屠苏”。我国 春节有放鞭炮的习俗。在爆竹爆炸的过程中,以 下热力学量的符号表示正确的是(忽略点火时火柴 传递给引线的少量热量) ( ) A) Q<0,W<0,ΔU<0 B) Q<0,W=0,ΔU<0 C) Q=0,W<0,ΔU<0 D) Q=0,W=0,ΔU=0
nN2CV, m(N2)(T-T1) + nCuCV,误二: ∆U =∆UN2 + ∆UCu = 0
nN2CV, m(N2)*(T-T1) + nCuCV, m(Cu)*(T-T2) = 0
正确解法:
∆U =∆UN2 + ∆UCu = ∆UN2 + ∆HCu = 0 nN2CV, m(N2)*(T-T1) + nCuCp, m(Cu)*(T-T2) = 0
• 求火焰最高温度: Qp = 0, ΔH = 0 求火焰最高温度: • 求爆炸最高温度、最高压力:QV = 0, W = 0 求爆炸最高温度、最高压力: =0
热力学第一定律

举例2:门窗紧闭房间用空调降温
以房间为系统 闭口系能量方程
Q U W Q0 W 0 U Q W
if Q W
T
闭口系
Air-
conditioner
Q
空 调
§ 2-4 开口系能量方程
mout
out
•
•
u pv c2 / 2 gz min W net
in
开口系能量方程微分式(续)
当有多条进出口:
•
•
Q dEcv / W net
•
u pv c2 / 2 gz mout out
•
u pv c2 / 2 gz min in
流动时,总一起存在
焓Enthalpy的引入
1、焓是状态量 state property
2、H为广延参数 H=U+pV= m(u+pv)= mh h为比参数
3、对流动工质,焓代表能量(内能+推进功) 对静止工质,焓不代表能量
4、物理意义:开口系中随工质流动而携带的、 取决于热力状态的能量。
§2-5 稳定流动能量方程
Energy balance for steady-flow systems
可理解为:由于工质的进出,外界与系统
之间所传递的一种机械功,表现为流动工质 进出系统使所携带或所传递的一种能量。
开口系能量方程的推导
uin pvin
min
1 2
ci2n
gzin
Wnet
Q
Q + min(u + c2/2 + gz)in
热力学第一定律总结

热一定律总结一、 通用公式ΔU = Q + W绝热: Q = 0,ΔU = W 恒容(W ’=0):W = 0,ΔU = Q V恒压(W ’=0):W =-p ΔV =-Δ(pV ),ΔU = Q -Δ(pV ) ΔH = Q p 恒容+绝热(W ’=0) :ΔU = 0 恒压+绝热(W ’=0) :ΔH = 0焓的定义式:H = U + pV ΔH = ΔU + Δ(pV )典型例题:思考题第3题,第4题。
二、 理想气体的单纯pVT 变化恒温:ΔU = ΔH = 0变温: 或或如恒容,ΔU = Q ,否则不一定相等。
如恒压,ΔH = Q ,否则不一定相等。
C p , m – C V , m = R双原子理想气体:C p , m = 7R /2, C V , m = 5R /2 单原子理想气体:C p , m = 5R /2, C V , m = 3R /2典型例题:思考题第2,3,4题书、三、 凝聚态物质的ΔU 和ΔH 只和温度有关或ΔU = n C V,T 2 T 1∫ΔH = nC p, T 2 T 1∫ΔU = nC V, ΔH = nC p, ΔU ≈ ΔH = n C p, m d T T 2 T1∫ ΔU ≈ ΔH = nC p,典型例题:书四、可逆相变(一定温度T 和对应的p 下的相变,是恒压过程)ΔU ≈ ΔH –ΔnRT(Δn :气体摩尔数的变化量。
如凝聚态物质之间相变,如熔化、凝固、转晶等,则Δn = 0,ΔU ≈ ΔH 。
kPa 及其对应温度下的相变可以查表。
其它温度下的相变要设计状态函数不管是理想气体或凝聚态物质,ΔH 1和ΔH 3均仅为温度的函数,可以直接用C p,m 计算。
或典型例题:作业题第3题 五、化学反应焓的计算H 1 +Δ H m (βα αβΔ αβ可逆相变K:ΔH = Q p = n Δ α βΔH = nC p,ΔH = nC p, T 2 T1∫其他温度:状态函数法ΔU 和ΔH 的关系:ΔU = ΔH –ΔnRT (Δn :气体摩尔数的变化量。
热力学第一定律

23
本章学习要求
• 掌握能量、热力系统储存能、热力学能、热量和功量 的概念,理解热量和功量是过程量而非状态参数。 • 理解热力学第一定律的实质能量守恒定律。 • 掌握稳定流动能量方程,能熟练运用稳定流动能量方 程对简单的工程问题进行能量交换的分析和计算。 • 掌握膨胀功、轴功、流动功和技术功的概念、计算及 它们之间的关系。 • 理解焓的定义式及其物理意义。 • 了解常用热工设备主要交换的能量及稳定流动能量方 程的简化形式。
2. 宏观位能: Ep ,单位为 J 或 kJ
Ep mgz
5
热力系总储存能:E ,单位为 J 或 kJ
E U Ek Ep
比储存能:e ,单位为 J/kg 或 kJ /kg
1 2 e u ek ep u cf gz 2
6
内动能-温度 热力学能 (内能U、u) 外储存能 内位能-比体积
∴流动功是一种特殊的功,其数值取决于
控制体进、出口界面上工质的热力状态。
14
根据热力学第一定律, 有 :
1 2 1 2 u1 cf 1 gz1 p1v1 q u2 cf 2 gz2 p2v2 ws 0 2 2
令 upv h,由于u、p、v都是状态参数,所以h也是 状态参数,称为比焓。
对一切热力系统和热力过程,有:
进入系统的能量-离开系统的能量 = 系统储存能量的变化
8
二、闭口热力系的能量方程
如图: Q=△U+W 对微元过程: Q QdUW 或 qduw 即: 热力系获得热量= 增加的热力学能+膨胀做功 对于可逆过程 : qdupdv 或
ΔU
W
qu pdv
热力学第一定律

R=8.314 J/mol.K.
• 由理想气体的模型, 无论分子间的距离大或小,其分 子间均无作用势能,故理想气体的内能与体系的体积 无关,因而与体系的压力也无关.
• 对于理想气体体系,其内能不含分子间作用势能这一 项,所以, 内能与体系的体积无关, 只与体系的温度有 关. 在体系的物质的量已确定的条件下,理想气体体 系的内能只是温度的函数,即:
第四节
可逆过程和不可逆过程
• 热力学函数中的过程量(Q,W)的数值与体系经 历的途径密切相关。 • 体系从一始态到一末态,理论上可以通过无 数条途径,所有这些途径,按其性质可分为 两大类:
•
可逆过程和不可逆过程
• 当体系的状态发生变化时,环境的状态也多少有所 变化,若将体系的状态还原为始态,环境的状态可 能还原,也可能未还原,正是根据环境是否能完全 还原,将过程分为可逆过程和不可逆过程。
CV,m=5/2R
• 多原子分子理想气体: 分子具有3个平动自由度和3个 转动自由度, 每个分子对内能的贡献为3kT, 多原子分 子理想气体的摩尔等容热容为(不考虑振动): •
CV,m=3R
• 2. 理想气体等压热容与等容热容之差 Cp,m﹣CV,m=(H/T)p﹣ (U/T)V =((U+pV)/T)p﹣ (U/T)V
A
•
E=U
B
因为宇宙的总能量是不变的,故体系能量的变化必 来自于周围环境。
若体系的能量增加,则环境的能量减少; 若体系的能量减少;则环境的能量增加。
体系与环境之间的能量交换形式只有热与功两种,故有:
U =Q+W
其物理意义是:
(体系对外做功为负)
上式即为热力学第一定律的数学表达式。
自然界的能量是恒定的,若体系的内能 发生了变化 (U),其值必定等于体系与环 境之间能量交换量(Q、W)的总和。
热力学第一定律

1.热力学第一定律热力学第一定律的主要内容,就是能量守恒原理。
能量可以在一物体与其他物体之间传递,可以从一种形式转化成另一种形式,但是不能无中生有,也不能自行消失。
而不同形式的能量在相互转化时永远是数量相当的。
这一原理,在现在看来似乎是顺理成章的,但他的建立却经历了许多失败和教训。
一百多年前西方工业革命,发明了蒸汽机,人们对改进蒸汽机产生了浓厚的兴趣。
总想造成不供能量或者少供能量而多做功的机器,曾兴起过制造“第一类永动机”的热潮。
所谓第一类永动机就是不需供给热量,不需消耗燃料而能不断循环做工的机器。
设计方案之多,但是成千上万份的设计中,没有一个能实现的。
人们从这类经验中逐渐认识到,能量是不能无中生有的,自生自灭的。
第一类永动机是不可能制成的,这就是能量守恒原理。
到了1840年,由焦耳和迈尔作了大量试验,测量了热和功转换过程中,消耗多少功会得到多少热,证明了热和机械功的转换具有严格的不变的当量关系。
想得到1J的机械功,一定要消耗0.239卡热,得到1卡热,一定要消耗4.184J的功,这就是著名的热功当量。
1cal = 4.1840J热功当量的测定试验,给能量守恒原理提供了科学依据,使这一原理得到了更为普遍的承认,牢牢的确立起来。
至今,无论是微观世界中物质的运动,还是宏观世界中的物质变化都无一例外的符合能量守恒原理。
把这一原理运用到宏观的热力学体系,就形成了热力学第一定律。
2.热力学第二定律能量守恒和转化定律就是热力学第一定律,或者说热力学第一定律是能量守恒和转化定律在热力学上的表现。
它指明热是物质运动的一种形式,物质系统从外界吸收的热量等于这个能的增加量和它对外所作的功的总和。
也就是说想制造一种不消耗任何能量就能永远作功的机器,即“第一种永动机”,是不可能的。
人们继续研究热机效率问题,试图从单一热源吸取能量去制作会永远作功的机器,这种机器并不违背能量守恒定律,只需将热源降温而利用其能量推动机器不断运转。
热力学第一定律

热力学第一定律科技名词定义中文名称:热力学第一定律英文名称:first law of thermodynamics其他名称:能量守恒和转换定律定义:热力系内物质的能量可以传递,其形式可以转换,在转换和传递过程中各种形式能源的总量保持不变。
概述热力学第一定律热力学第一定律:△U=Q+W。
系统在过程中能量的变化关系英文翻译:the first law of thermodynamics简单解释在热力学中,系统发生变化时,设与环境之间交换的热为Q(吸热为正,放热为负),与环境交换的功为W(对外做功为负,外界对物体做功为正),可得热力学能(亦称内能)的变化为ΔU = Q+ W或ΔU=Q-W物理中普遍使用第一种,而化学中通常是说系统对外做功,故会用后一种。
定义自然界一切物体都具有能量,能量有各种不同形式,它能从一种形式转化为另一种形式,从一个物体传递给另一个物体,在转化和传递过程中能量的总和不变。
英文翻译:The first explicit statement of the first law of thermodynamics, byRudolf Clausiusin 1850, referred to cyclic thermodynamic processes "In all cases in which work is produced by the agency of heat, a quantity of heat is consumed which is proportional to the work done; and conversely, by the expenditure of an equal quantity of work an equal quantity of heat is produced."基本内容能量是永恒的,不会被制造出来,也不会被消灭。
热力学第一定律

热力学第一定律1 焦耳热功当量能量守恒与转化定律及对热本质的认识是在焦耳热功当量实验的基础上突破的。
从1840年起,焦耳先后用了20年的时间,做了四类实验,测定了可以转化为一定数量的热的各种形式能量。
(1) 将水放在一绝热容器,通过重物下落带动铜浆叶轮,叶轮搅动水,使水温升高。
(2) 以机械压缩气缸中的气体,气缸浸入水中,水温升高。
(3) 以机械功转动电机,电机产生电流通过水中的线圈,水温升高。
(4) 以机械功使两块在水中的铁片互相摩擦,水温升高。
实验结果就是著名的焦耳热功当量:1ca l= 4.157 J。
之后更精确的测量结果是:1cal = 4.1840 J。
热功当量的意义在于:为能量守恒与转化定律奠定了可靠的实验基础,肯定了热是能量的一种形式,可以与机械能电能等相互转化,转化是等当量的。
从此,人类对于热的认识才有了突破性的进展。
2 能量守恒与转化定律到1850年,科学界已公认能量守恒是自然界的一个普遍规律。
这条定律指出:自然界的一切物质都具有能量,能量有各种不同的形式,能够从一种形式转化为另一种形式,在转化过程,能量的总量不变。
换而言之:在隔离体系中,能量的形式可以转化,但能量总值不变。
通常体系的总能量由三个部分组成:动能、势能和内能。
一般的化学热力学体系是宏观静止、无整体运动的,而且没有特殊的外场作用(如电磁场,离心力场), 因此,关注的主要是内能。
内能包括:分子运动的平动能,转动能,振动能,电子及原子核的能量,以及分子间的相互作用能。
3 热力学第一定律热力学第一定律是能量守恒与转化原理在热力学体系的应用。
对于不同类型的体系,定律的形式将有所不同。
对于封闭体系,热力学第一定律可以表述为:任何一个不作整体运动的封闭体系,在平衡态都存在一个单值的状态函数,称之为内能U,它是一个广度量。
当体系从平衡态 A经任一过程变到平衡态 B,体系内能的增量U=U(B)-U(A)就等于该过程体系从环境吸收的热量Q与环境对体系所做功W之和。
热力学第一定律
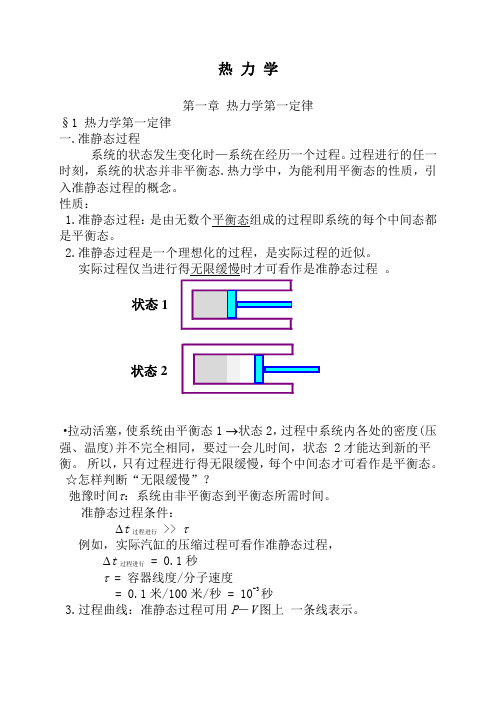
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。
过程进行的任一时刻,系统的状态并非平衡态.热力学中,为能利用平衡态的性质,引入准静态过程的概念。
性质:1.准静态过程:是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。
2.准静态过程是一个理想化的过程,是实际过程的近似。
实际过程仅当进行得无限缓慢时才可看作是准静态过程 。
·拉动活塞,使系统由平衡态1 →状态2,过程中系统内各处的密度(压强、温度)并不完全相同,要过一会儿时间,状态 2才能达到新的平衡。
所以,只有过程进行得无限缓慢,每个中间态才可看作是平衡态。
☆怎样判断“无限缓慢”?弛豫时间τ:系统由非平衡态到平衡态所需时间。
准静态过程条件: ∆t 过程进行 >> τ例如,实际汽缸的压缩过程可看作准静态过程, ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线:准静态过程可用P -V 图上 一条线表示。
状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。
·机械功(摩擦功、体积功)2.内能·内能包含系统内:(1)分子热运动的能量;(2)分子间势能和分子内的势能;(3)分子内部、原子内部运动的能量; (4)电场能、磁场能等。
·内能是状态的函数*对于一定质量的某种气体,内能一般是T 、V 或P 的函数; *对于理想气体,内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i :自由度; ν :摩尔数 ·通过作功改变系统内能的实质是:分子的有规则运动能量和分子的无规则运动能量的转化和传递。
3.热量·传热也可改变系统的状态,其条件是系统和外界的温度不同。
·传热的微观本质:是分子的无规则运动能量从高温物体向低温物体传递。
热力学第一定律

热力学第一定律热力学第一定律是热力学中最基本的定律之一,也被称为能量守恒定律。
它描述了能量在物质系统中的转化和守恒关系。
在本文中,我们将深入探讨热力学第一定律的原理和应用。
1. 热力学第一定律的原理热力学第一定律表明,一个系统的内能的增量等于吸热与做功之和。
简单来说,即能量的增加等于热量输入和功输入之和。
在一个封闭系统中,内能变化可以表示为ΔU = Q + W,其中ΔU表示内能变化量,Q表示吸热,W表示做功。
根据能量的守恒原理,一个系统的能量不会凭空消失或增加,而是转化成其他形式。
2. 热力学第一定律的应用热力学第一定律在各个领域都有广泛的应用。
以下是其中一些常见的应用场景:2.1. 理想气体的过程分析在理想气体的过程分析中,热力学第一定律被广泛应用于计算气体的工作、吸热和内能变化等参数。
根据热力学第一定律的原理,我们可以通过测量系统吸热和做功的量来计算内能的变化。
2.2. 热机效率的计算热力学第一定律也可用于计算热机的效率。
根据热力学第一定律原理,热机的效率可以表示为η = 1 - Q2/Q1,其中Q1表示热机输入的热量,Q2表示热机输出的热量。
通过计算输入和输出的热量可以确定热机的效率。
2.3. 化学反应的能量变化热力学第一定律也可用于描述化学反应的能量变化。
在化学反应中,热力学第一定律可以帮助我们计算反应的吸热或放热量,从而确定反应是否放热或吸热以及能量变化的大小。
3. 热力学第一定律在能源利用中的应用能源利用是热力学第一定律的一个重要应用领域。
通过研究能源的转化过程和能量损失,我们可以更有效地利用能源资源。
3.1. 热力学循环热力学循环是将热能转化为功的过程,如蒸汽轮机和内燃机。
通过分析热力学循环中各个环节的能量转化和损失,可以优化循环系统的效率,提高能源利用率。
3.2. 可再生能源利用热力学第一定律也可以应用于可再生能源的利用。
通过分析可再生能源的收集、转化和储存过程中的能量转化和守恒关系,可以优化利用这些能源的方式,减少能量的损失和浪费。
热力学第一定律的表达式

热力学第一定律的表达式热力学第一定律的表达式:ΔE=W+Q。
在热力学中,热力学第一定律通常表述为:热能和机械能在转化时,总能量保持不变。
其数学表达式为ΔE=W+Q,其中ΔE表示系统内能的改变,W表示系统对外所做的功,Q表示系统从外界吸收的热量。
这个定律表明,能量的转化和守恒定律是自然界的基本定律之一,它适用于任何与外界没有能量交换的孤立系统。
换句话说,在一个封闭系统中,能量的总量是恒定的,改变的只是能量的形式。
因此,热力学第一定律是能量守恒定律在热现象领域中的应用。
另外,对于一个封闭系统,如果系统内部没有发生化学反应或相变等过程,那么系统对外做的功等于系统从外界吸收的热量。
这是因为系统内能的改变量等于系统对外做的功和系统从外界吸收的热量之和。
值得注意的是,热力学第一定律也适用于非平衡态系统。
即使系统处于非平衡态,热力学第一定律仍然适用。
因此,它不仅是热力学的基石之一,也是整个物理学的基石之一。
为了更好地理解热力学第一定律,我们可以考虑一些具体的应用场景。
例如,在汽车发动机中,汽油燃烧产生的热能转化为汽车的动能和废气中的内能。
在这个过程中,系统内能的改变量等于系统对外做的功和系统从外界吸收的热量之和。
因此,根据热力学第一定律,我们可以计算出汽车发动机的效率,从而评估其能源利用效果。
此外,热力学第一定律还可以应用于电学、化学等领域。
例如,在电学中,当电流通过电阻时会产生热量,根据热力学第一定律可以计算出电阻产生的热量。
在化学中,反应热的计算也可以根据热力学第一定律来进行。
以下是一些具体例子,说明热力学第一定律的应用:1. 热电站:在热电站中,燃料燃烧产生的热能转化为蒸汽的机械能,再转化为电能。
根据热力学第一定律,热能被转化为机械能和电能,而总能量保持不变。
通过计算输入和输出的能量,我们可以评估热电站的效率。
2. 制冷机:制冷机是一种将热量从低温处转移到高温处的设备。
在制冷过程中,制冷剂在蒸发器中吸收热量并转化为气态,然后通过压缩机和冷凝器将热量释放到高温处。
热力学第一定律

二、推动功(或流动功) 除了体积功这类与系统的界面移动有关的功外,还有因工质在开口系统中流动而传递的功,称之为推动功或流动功。对开口系统进行功的计算时需要考虑这种功。
第六章 热力学第一定律
图6-2 工质流动过程中所传递的推动功
解:因为是可逆定压过程,
第六章 热力学第一定律
*
*
3.但由于碳和氧的电负性不同,所以碳氧双键是极性键,π电子向氧偏移;结果氧带部分负电荷(δ-),碳带部分正电荷(δ+);这一点与碳碳双键不同。 碳氧双键中的π键易受到亲核试剂进攻,发生亲核加成反应。
*
4、受羰基的影响,α碳上的氢原子较为活泼,易发生取代反应;还可发生缩合反应。
O
C
C
H
*
5. 羰基也可发生氧化还原反应等。 要注意醛酮的相似性质和不同之处。 要注意结构特别是空间结构对化学性质的影响。
*
3. 加醇
醇作为含氧的亲核试剂,可以与醛发生加成反应,但需要干燥HCl催化。生成的产物称为半缩醛: 半缩醛
*
本章学习要点:
1.掌握醛酮的结构和命名。 2.掌握醛酮的相同化学性质: ⑴亲核加成反应 ⑵α-活泼氢的反应 3.熟悉醛的特殊反应 3.了解醌的结构和性质。
*
醛、酮、醌都是含氧化合物,都含有共同的官能团—羰基(carbonyl group),是重要的有机合成原料。在自然界中广泛存在,例如黄酮类化合物和挥发油、人体内的某些激素、碳水化合物等,都有重要的生物功能。
第六章 热力学第一定律
变质量热力系统开口边界处流入工质与流出工质的质量流量不相同,流动工质做出机械功率或与外界交换的热流量不一定是常数,这时热力系统的总能量往往是时间的函数,但任意时刻系统内的状态仍可做为均匀态处理。 【本章小结】 一、热力学第一定律 热力学第一定律实质上是能量守恒定律在工程热力学领域的应用,具体表现为热能和机械能之间的相互转化和守恒。第一定律说明了热能和机械转化时所遵循的数量平衡规律。 二、功与热量 系统体积变化时所做的功称为体积功(包括膨胀功和压缩功),体积功不是状态参数,而是一个过程量。
热力学第一定律

c,z是力学参数,处于同一热力学状态的 物体可以有不同的c,z.因此c,z是独立 于热力系统内部状态的外部参数, 系统的宏 观动能和重力位能又称为外储存能.
三,系统总储存能 系统的总储存能E为外储存能和内储存能之 和.
E = U + Ek + Ep
或
1 2 E = U + mc + mgz 2
对于1kg质量物体的总储存能为
对于可逆过程,有
δw = pdv ,或 w = ∫ pdv
1
2
代入闭口系统的守恒关系式,有
q = u + ∫ pdv ,或 δq = du + pdv
1
2
以上两式适用可逆过程.
分析热力学问题需建立(选择)热力学模 分析热力学问题需建立(选择) 型 1,确定热力系,即系统,边界和外界. 2,分析系统内部变化,各种作用量(外部), 各种作用量与系统内部变化的内在联系. 3,必须注意作用量的独立性,针对性和相互 性. (1)独立性 独立性是指热量,功量和质量交换这 独立性 三种不同作用量是相互独立的,每种
从微观角度看: 从微观角度看: 功——所起的作用是物体的有规律运动 所起的作用是物体的有规律运动 所起的作用是物体的 与系统内分子无规热运动 无规热运动之间的 与系统内分子无规热运动之间的 转换. 转换. 问题:热量与功的相同点和不同点 问题:热量与功的相同点和不同点?
相同点:功和热量都是过程量.只有在系 相同点 统和外界通过边界传递能量时才有意义, 一旦它们越过界面,便转化为系统或外界 的能量. 不能说在某状态下,系统或外界有多少功 或热.
对于理想气体,因忽略了分子间的作用力, 没有位能,故其内能仅包括分子内动能, 所以理想气体的内能只是温度的单值函数 理想气体的内能只是温度的单值函数, 理想气体的内能只是温度的单值函数 即
热力学第一定律

1.2 热 力 学 第 一 定 律1.2.1 热功当量热力学第一定律的数学表达式设有任一个物系做一个任意循环(如图),吸热为Q ',做功为W ,我们发现0=+'W Q J(1)由于Q '的单位为卡,功的单位为焦耳,二者 不能直接相加,Q '前必须乘以热功转换系数或称热功当量J (焦耳/卡)。
Joule (焦耳)和 Mayer (迈耶尔)自1840年起,历经20多年,用各种实验求证热和功的转换关系,得到的结果是一致的。
即: 1 cal = 4.1840 J这就是著名的热功当量,为能量守恒原理提供了科学的实验证明。
1.2.2 能量守恒定律自然界的一切物质都具有能量,能量有各种不同形式,能够从一种形式转化为另一种形式,但在转化过程中,能量的总值不变。
到1850年,科学界公认能量守恒定律是自然界的普遍规律之一。
1.2.3 热力学能(Internal energy)系统总能量通常有三部分组成: 1)系统整体运动的动能 2)系统在外力场中的位能 3)热力学能,也称为内能 1.2.3.1 定义热力学能是指系统内部能量的总和,包括分子运动的平动能、分子内的转动能、振动能、电子能、核能以及各种粒子之间的相互作用位能等。
p V热力学中一般只考虑静止的系统,无整体运动,不考虑外力场的作用,所以只注意热力学能1.2.3.2 热力学能的特点1) 内能是体系内部能量的总和 U ,单位J ,kJ ,包括:• 对于组成一定的均匀体系,只要体系的量确定, U 由体系的两个性质确定。
2)3)4) 5) 6) 热力学能是状态函数。
∆U=U 2-U 1,, 微小变化d U 。
1.2.4 热力学第一定律的数学表达式W Q dU δδ+=或 W Q U +=∆这就是热力学第一定律的数学表达式。
对于非循环过程,状态函数的变化值只与初末态有关,与具体的历程无关:w ad =U f -U i =△Uh =A f -A i =△A △U = Q + W (宏观过程)—the First Law of thermodynamics无穷小过程)process( mal infinitesi -+=W Q dU δδ热力学第一定律是能量转化和守恒定律的特殊形式。
热力学第一定律

P2V2
ln
V2 V1
7
又 ∵ 等温过程有
V2 P1 V1 P2
有
AT
P1V1 M
ln P1 P2 RT
ln
P2V2 P1
ln
P1 P2
M mol
P2
(3)强调QT=AT
即在等温过程中,系统的热交换不能直接计算,但可用等 温过程中的功值AT来间接计算。
8
※三种过程中气体做的功
等体过程
(1)特征:dT=0, ∴dE=0 热一律为 QT=AT
在等温过程中,理想气体所吸收 的热量全部转化为对外界做功,系 统内能保持不变。
(2)等温过程的功
PI
P1
P2
o
V1
II
V2 V
∵T=C(常数),
P RT 1
V
dAT PdV
AT
V2 RTdV RT ln V2
V V1
V1
P1V1
ln
V2 V1
T1)
M M mol R(T2 T1)
5
C p
C V
R i2R 2
──此即迈耶公式
(3)比热容比:
定义
Cp
Cv
i 2
RR iR
i2 i
2
对理想气体刚性分子有:
单原子分子:
双原子分子:
5 3 7 5
1.67 1.4
*: 经典理论的缺陷
多原子分子:
8 6
1.33
6
3、等温过程
1
符号规定
Q
吸热为正, 放热为负.
系统对外做功为正, A 外界对系统做功为负.
各物理量的单位统一用国际单位制。
热力学第一定律

工质的容 积变化功
膨胀功
工质机械 能的变化
维持工质流 动的流动功
工质对机 器作的功
热能转变成的机械能(由于膨胀而导致1的7 )
技术功:技术上可资利用的功,符号为
联立(2-18)与
,则
(2-19) (2-20)
18
对于可逆过程,
图中的阴影面积,即 对于微元过程,
图中的面积5-1-2-6-5
说明: (1)若dp为负(过程中工质压力降低),技 术功为正,工质对机器作功。如燃气轮机; (2)若dp为正,机器对工质作功,如活塞式 压气机和叶轮式压气机。
对于闭口系统:进入和离开系统的能量只包括热量和作功两项; 对于开口系统:进入和离开系统的能量除热量和作功外,
还有随同物质带进、带出系统的能量(因为有物 质进出分界面)
2
闭口系统的基本能量方程式
取气缸活塞系统中的工质为研究系统,考察其在状态变化过程 中和外界(热源和机器设备)的能量交换。由于过程中没有工 质越过边界,所以这是一个闭口系统。
的平均值为该截面的流速;
8
一、开口系统能量方程
开口系统内既有质量变化,又有能量变化,控 制体内应同时满足质量守恒与能量守恒关系。 考察以下开口系统(dτ)
9
➢ 从1-1’界面进入控制体流体的质量为 m1 ➢ 从2-2’界面进入控制体流体的质量为 m2
➢ 系统从外界吸热 Q ,对机器设备作功 Wi
加入系统的能量总和-热力系统输出的能量总和=热力系总储存能的增量
则有:
整理得:
11
考虑到
和
,且
,则上式可以写成
(2-13)
假设流进流出控制容积的工质各有若干股,则上式可写成
(2-14)
热力学第一定律

i
i 为分子的自由度.
单原子气体: i = 3 氦、氖等 双原子气体: i = 5 氢、氧、氮等 多原子气体: i = 6 水蒸汽、甲烷等
➢ 准静态过程中的内能变化
内能: 热力学系统的能量, 它包括了分子热运动的平动 、 转动和振动动能、化学能、原子能、核能... 以及分子 间相 互作用的势能. (不包括系统整体运动的机械能)
F S
p,V dV
p
(p1,V1,T1)
dl dW pS d l p d V
(p2,V2,T2)
W V2 pdV V1
O V1
dV
V2 V
结论: 系统所做的功在数值上等于p-V 图上过程曲线以 下的面积.
➢ 准静态过程中的热量 热容量 热量是系统之间由于热相互作用而传递的能量.
热容量: 物体温度升高一度所需要吸收的热量.
T1 )
等体过程中, 热力学第一定律为 (dQ )V,m dE
等体摩尔热容可表示为 同理可得等压摩尔热容为
C V,m
dQ dT
V,mol
dE dT
C p,m
dQ dT
p,mol
dE dT
p dV dT
1 mol 理想气体的状态方程
为 C p,m CV,m R
pV RT pdV RdT 称为迈耶公式
➢ 热力学第一定律 包括热现象在内的能量守恒和转换定律. Q = (E 2 - E 1 ) +W
其中: Q 表示系统吸收的热量; W 表示系统对外所做的功; E (=E2-E1) 表示系统内能的增量.
热力学第一定律微分形式: dQ = dE + dW
热量和功是过程量. 内能是状态量.
➢ 准静态过程中的功
热力学第一定律

热力学第一定律热力学第一定律,也被称为能量守恒定律,是热力学基本定律之一。
它阐述了能量在物理系统中的守恒原理,即能量不会被创造或消灭,只会在不同形式之间转换或传递。
该定律在许多领域都有广泛的应用,包括工程、物理、化学等。
1. 定律的表述热力学第一定律可从不同的角度进行表述,以下是几种常见的表述方式:1.1 内能变化根据热力学第一定律,一个封闭系统内能的变化等于系统所吸收的热量与系统所做的功的代数和。
数学表达式如下:ΔU = Q + W其中,ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统所做的功。
1.2 能量守恒根据能量守恒定律,能量既不能被创造也不能被摧毁,只会在不同形式之间传递或转换。
能量的总量在一个封闭系统中保持不变。
2. 系统内能的变化系统内能的变化是热力学第一定律的核心内容之一。
系统内能的变化是由系统吸收或释放的热量以及系统所做的功决定的。
2.1 系统吸收的热量系统吸收的热量指的是系统从外界获得的热能。
当一个热源与系统接触时,能量会以热量的形式从热源传递到系统中。
系统吸收的热量可以引起系统内能的增加。
2.2 系统所做的功系统所做的功指的是系统对外界做的能量转移。
当系统对外界施加力并移动时,能量会以功的形式从系统传递到外界。
系统所做的功可以引起系统内能的减少。
3. 热力学第一定律的应用3.1 工程应用热力学第一定律在工程领域有着广泛的应用。
例如,在能源系统的设计与优化中,需要根据系统的能量转换过程,计算系统的内能变化和热功效率等参数,以提高能源利用效率。
3.2 物理学应用在物理学研究中,热力学第一定律通常用于分析热力学过程中的能量转化。
例如,在热力学循环中,通过计算各个环节的能量转换情况,可以确定工作物质的热效率,从而评估系统的性能。
3.3 化学反应在化学反应中,热力学第一定律对于研究反应的能量变化和平衡状态具有重要意义。
通过计算反应过程中释放或吸收的热量,可以确定反应的放热性或吸热性,并预测反应的发生与否。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热力学第一定律功:δW =δW e +δW f(1)膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T )p (2)等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11-γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =H p T ⎪⎪⎭⎫⎝⎛∂∂=-()pT C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫ ⎝⎛∂∂+dp p H T⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2)Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=V T p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂ (3)热容与T 、S 、p 、V 的关系:C V =T VT S ⎪⎭⎫⎝⎛∂∂ C p =T p T S ⎪⎭⎫ ⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
(2)Clausius -Clapeyron 方程式(两相平衡中一相为气相):dT dlnp=2m vap RTH ∆ (3)外压对蒸汽压的影响:()()**g e m gg p p RTl V p p ln-=p g 是在惰性气体存在总压为p e 时的饱和蒸汽压。
吉不斯-杜亥姆公式:SdT -Vdp +∑BB B d n μ=0dU =TdS -pdV +∑BB B d n μ dH =TdS +Vdp +∑BB B d n μdF =-SdT -pdV +∑BB B d n μ dG =-SdT +Vdp +∑BB B d n μ在等温过程中,一个封闭体系所能做的最大功等于其Helmbolz 自由能的减少。
等温等压下,一个封闭体系所能做的最大非膨胀功等于其Gibbs 自由能的减少。
统计热力学波兹曼公式:S =kln Ω一种分布的微观状态数:定位体系:t i =N !∏i i N i N g i ! 非定位体系:t i =∏i i N i N g i!波兹曼分布:N N i =∑∈∈ikTi kTi i i eg e g -- 在A 、B 两个能级上粒子数之比:B A N N =kT /B kT/A B A e g e g ∈∈--波色-爱因斯坦统计:N i =1eg ii ---∈βα 费米-狄拉克统计:N i =1eg ii +--∈βα分子配分函数定义:q =∑∈i/i i e g kT - -∈i 为能级能量q =∑∈i/i e kT - -∈i 为量子态能量分子配分函数的分离:q =q n q e q t q r q v能级能量公式:平动:εt =⎪⎪⎭⎫ ⎝⎛22Z 22Y 22X 2c n b n a n m 8h ++ 转动:εr =()I 8h 1J J 22π+ 振动:εv =γh 21v ⎪⎭⎫ ⎝⎛+分子配分函数表达式:平动:当所有的平动能级几乎都可被分子到达时一维:q t=L h mkT 2212⎪⎭⎫ ⎝⎛π 二维:q t =2h mkT 2πA 三维:q t=V h mkT 2232⎪⎭⎫ ⎝⎛π 转动:线性q r=22h IkT 8σπ=r T Θσ rΘ=kI 8h 22π r Θ为转动特征温度 非线性q r=()()21Z Y X 3232I I I h kT 28σππ振动:双原子分子q V =kT 2/h kT 2/h e 1e γγ---=T 2/T 2/V Ve1e ΘΘ--- vΘ=k h γ 为振动特征温度 多原子线性:q V=∏5n 31i /2/1-=---kT h kT h i i e e γγ 多原子非线性:q V=∏6n 31i /2/1-=---kTh kT h i i e e γγ 电子运动:q e=(2j +1)kT/e 0e∈- 原子核运动:q n=(2S n +1)kT/n0e∈-热力学函数表达式:F =-kTlnq N(定位) F =-kTln !N q N(非定位)S =klnq N+NkT N V T lnq ,⎪⎭⎫ ⎝⎛∂∂(定位) S =kln !N q N +NkT NV T lnq ,⎪⎭⎫⎝⎛∂∂(非定位) G =-kTlnq N +NkTV NT V lnq ,⎪⎭⎫⎝⎛∂∂(定位) G =-kTln !N q N +NkTV NT V lnq ,⎪⎭⎫⎝⎛∂∂(非定位) U =NkT 2N V T lnq ,⎪⎭⎫ ⎝⎛∂∂ H =NkT 2N V T lnq ,⎪⎭⎫ ⎝⎛∂∂+NkTV NT V lnq ,⎪⎭⎫⎝⎛∂∂ P =NkT N T V lnq ,⎪⎭⎫ ⎝⎛∂∂ C V =V N V 2T lnq NkT T ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∂∂,溶液-多组分体系体系热力学在溶液中的应用溶液组成的表示法:(1)物质的量分数:B B n x n =(2)质量摩尔浓度:B B Anm W =(3)物质的量浓度:BB n c V=(4)质量浓度B ω 拉乌尔定律 A A Ap p x *= 亨利定律:x m B c B p k x k m k c === 化学势的各种表示式和某些符号的物理意义: 气体:(1)纯理想气体的化学势()()T,p T RTln p p μμΦΦ=+ 标准态:任意温度,p=p φ=101325Pa 。
μφ(T )为标准态时的化学势(2)纯实际气体的化学势()()T,p T RTlnf p μμΦΦ=+ 标准态:任意温度,f=p φ且复合理想气体行为的假想态(即p =p φ,γ=1),μφ(T )为标准态时的化学势。
(3)混合理想气体中组分B 的化学势()()B B B T,p T,RTln x μμ*=p + 因为()()B B T,p T RTln p p μμ*ΦΦ=+ 所以()B T,p μ*不是标准态时的化学势,是纯B气体在指定T 、p 时的化学势。
溶液: (1) 理想溶液组分的化学势()()B BB T,p T,RTln x μμ*=p + ()()pB B B ,m pT ,p TV dp μμΦ*Φ⎰=+ 所以()B T,p μ*不是标准态时的化学势而是温度为T 、溶液上方总压为p 时,纯液体B 的化学势。
(2) 稀溶液中各组分的化学势溶剂:()()A A A T,p T,RTln x μμ*=p + ()A T,μ*p 不是标准态时的化学势而是温度为T 、溶液上方总压为p 时,纯溶剂A 的化学势。
溶质:()()B B B T,p T,RTln x μμ*=p + ()()()B B x T ,p T R T l n k p μμ*ΦΦ=+ ()()B B B T,p T,RTlnm m μμΦ=p + ()()()B B m T ,p TR T l n k m p μμΦΦΦ⋅ =+ ()()B B B T ,p T,R T l n c c μμ∆Φ=p + ()()()B B cT ,p T R T l n k c pμμ∆ΦΦΦ⋅=+ ()B T,μ*p ,()B T,μ p ,()B T,μ∆p 均不是标准态时的化学势,均是T ,p 的函数,它们分别为:当x B =1,m B =1molkg -1,c B =1moldm -3时且服从亨利定律的那个假想态的化学势。
(4)非理想溶液中各组分的化学势溶剂:()()A A A,x T,p T,RTlna μμ*=p + ()A T,μ*p 不是标准态的化学势,而是a A,x=1即x A =1,γA =1的纯组分A 的化学势。
溶质:()()B B B,x T,p T,RTlna μμ*=p + B ,x B ,xa x γ=()()B B B,m T,p T,RTlna μμ=p + B ,m mBa m mγΦ= ()()B B B ,C T ,p T,R T l n a μμ∆=p + B ,c cBa c cγΦ= ()B T,μ*p ,()B T,μ p ,()B T,μ∆p 均不是标准态时的化学势,均是T ,p 的函数,它们分别为:当a B,x =1,a B,m =1,a B,c =1时且服从亨利定律的那个假想态的化学势。
(4)活度a 的求算公式:✓ 蒸汽压法:溶剂a A =γA x A =p A /p A * 溶质:a B =γB x B =p A /k c✓ 凝固点下降法:溶剂()fus m A f fH A 11ln a R T T *∆⎛⎫⎪⎝⎭=- ✓ Gibbs -Duhem 公式从溶质(剂)的活度求溶剂(质)的活度。
