大学物理第3章-刚体力学习题解答
第03章---刚体力学习题汇总

(A)匀角速转动; (B)匀角加速转动;
(D)
(C)角加速度越来越大的变加速运动;
(D)角加速度越来越小的变加速运动。
分析:当棒转到θ角位置时,棒所受 到的外力矩为:
θ
M 1 mgLcos 根据转动定律 M I ,有:
2
mg
1 mgL cos
可见角5
5. (a)(b)两图中的细棒和小球均相同,系统可绕o 轴在竖直面内自由转动系统从水平位置静止释放,转
(D)只有动量守恒
(C)
分析:
(A)错。非弹性碰撞,机械能不守恒。 (B)错。轴上有外力,动量不守恒。
(C)对。外力矩为零,角动量守恒。
2
2.一绕固定水平轴0匀速转动的转盘,沿图示的同一 水平直线从相反方向射入两颗质量相同、速率相等的 子弹并留在盘中,则子弹射入转盘后的角速度
(A)增大 (B)不变 分析:
边缘并粘在上面,则系统的角速度是
3v
。
分析:取如图的细长条面积:
4b
b
I r 2ds r 2adr
1 ab3 1 mb2
0
3
3
合外力矩为零,系统角动量守恒。
mvb (1 mb2 mb2 )
3
3v
4b
9
二、填空题
1.如图,半径为R,质量为M的飞轮,
可绕水平轴o在竖直面内自由转动(飞
R2
2 3
mgR
11
3.一飞轮的转动惯量为I,在t=0时角速度为 0 , 此后
飞轮经历制动过程。阻力矩M的大小与角速度的平方
成正比,比例系数K>0。当 0 / 3 时,飞轮的角加
速度 = k02 9I ,从开始制动到 0 / 3所经过
大学物理练习册习题及答案4

习题及参考答案第3章 刚体力学参考答案思考题3-1刚体角动量守恒的充分而必要的条件是 (A )刚体不受外力矩的作用。
(B )刚体所受合外力矩为零。
(C)刚体所受的合外力和合外力矩均为零。
(D)刚体的转动惯量和角速度均保持不变。
答:(B )。
3-2如图所示,A 、B 为两个相同的绕着轻 绳的定滑轮。
A 滑轮挂一质量为M 的物体, B 滑轮受拉力F ,而且F =Mg 。
设A 、B 两 滑轮的角加速度分别为βA 和βB ,不计滑轮 轴的摩擦,则有(A )βA = βB (B )βA > βB(C )βA < βB (D )开始时βA = βB ,以后βA < βB 答:(C )。
3-3关于刚体对轴的转动惯量,下列说法中正确的是(A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无 答:(C )。
3-4一水平圆盘可绕通过其中心的固定铅直轴转动,盘上站着一个人,初始时整个系统处于静止状态,当此人在盘上随意走动时,若忽略轴的摩擦,则此系统(A)动量守恒; (B)机械能守恒; (C)对转轴的角动量守恒;(D)动量、机械能和角动量都守恒; (E)动量、机械能和角动量都不守恒。
答:(C )。
3-5光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点o 且垂直于杆的竖直光滑固定轴自由转动,其转动惯量为213mL,起初杆静止,桌面上有两个质量均为m 的小球,各自在 垂直于杆的方向上,正对着杆的一端,以相同速率v 相向 运动,如图所示,当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为AMF思考题3-2图v思考题3-5图(A)23L v (B)45L v (C)67L v (D)89L v (E)127L v答:(C )。
大学物理学课后3第三章答案

题 3.8(a)图 (1) m1 , m2 和柱体的运动方程如下:
题 3.8(b)图
T2 m2 g m2a2
①
m1g T1 m1a1
②
T1R T2r J
③
式中 T1 T1,T2 T2 , a2 r , a1 R
而 由上式求得
J 1 MR 2 1 mr 2
∵
Fr N
N N
∴ 又∵
∴ ①
Fr
N
l1
l2 l1
F
J 1 mR 2 , 2
Fr R 2(l1 l2 ) F
J
mRl1
以 F 100 N 等代入上式,得
2 0.40 (0.50 0.75) 100 40 rad s2
0.20m, r =0.10m, m =4 kg, M =10 kg, m1 = m2 =2 kg,且开始时 m1 , m2 离地均为 h =2m.求: (1)柱体转动时的角加速度; (2)两侧细绳的张力.
解: 设 a1 , a2 和β分别为 m1 , m2 和柱体的加速度及角加速度,方向如图(如图 b).
习题 3
3.1 选择题
(1) 有两个力作用在一个有固定转轴的刚体上:
① 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;
② 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;
③ 当这两个力的合力为零时,它们对轴的合力矩也一定是零;
④ 当这两个力对轴的合力矩为零时,它们的合力也一定是零.
在
上
述
说
(5) 一圆盘正绕垂直于盘面的水平光滑固定轴 O 转动,如图射来两个质量相同,
大物习题解答-大学物理习题答案(许瑞珍_贾谊明)-第3章 刚体力学

第三章 刚体力学3-1 一通风机的转动部分以初角速度ω0绕其轴转动,空气的阻力矩与角速度成正比,比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ,问:(1)经过多少时间后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转? 解:(1)由题可知:阻力矩ωC M -=,又因为转动定理 dtd JJ M ωβ== dtd JC ωω=-∴ dt JC d t ⎰⎰-=∴00ωωωω t JC-=0lnωω t JCe-=0ωω当021ωω=时,2ln CJt =。
(2)角位移⎰=tdt 0ωθ⎰-=2ln 00C J t JC dt eωCJ 021ω=,所以,此时间内转过的圈数为CJ n πωπθ420==。
3-2 质量面密度为σ的均匀矩形板,试证其对与板面垂直的,通过几何中心的轴线的转动惯量为)(1222b a ab J +σ=。
其中a ,b 为矩形板的长,宽。
证明一:如图,在板上取一质元dxdy dm σ=,对与板面垂直的、通过几何中心的轴线的转动惯量为 dm r dJ ⎰=2dxdy y x a a b b σ⎰⎰--+=222222)()(1222b a ab +=σ证明二:如图,在板上取一细棒bdx dm σ=,对通过细棒中心与棒垂直的转动轴的转动惯量为2121b dm ⋅,根据平行轴定理,对与板面垂直的、通过几何中心的轴线的转动惯量为22)2(121x adm b dm dJ -+⋅=dx x ab dx b 23)2(121-+=σσ 33121121ba a b dJ J σσ+==∴⎰)(1222b a ab +=σ3-3 如图3-28所示,一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 2和m 的重物,绳与滑轮间无相对滑动,滑轮轴光滑,求重物的加速度和各段绳中的张力。
解:受力分析如图ma T mg 222=- (1) ma mg T =-1 (2) βJ r T T =-)(2 (3) βJ r T T =-)(1 (4)βr a =,221mr J =(5) 联立求出g a 41=, mg T 811=,mg T 451=,mg T 232=3-4 如图3-29所示,一均匀细杆长为L ,质量为m ,平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过细杆中心的竖直轴转动,试求:(1)作用于杆的摩擦力矩;(2)经过多长时间杆才会停止转动。
第03章(刚体力学)习题答案

轮子的角速度由w =0 增大到w =10 rad/s,求摩擦力矩 Mr. [5.0 N·m]
解:摩擦力矩与外力矩均为恒力矩,所以刚体作匀角加速转动。其角加速度为:
b = w - w0 = 10 - 0 = 1rad / s2
Dt
10
合外力矩为: M合 = Jb = 15 ´1 = 15(N × m) = M - M r Þ M r = 5.0(N × m)
所以机械能也不守恒。
3-3 一圆盘绕过盘心且与盘面垂直的光滑固定轴 O 以角速度w按图示方向转动.若如图
所示的情况那样,将两个大小相等方向相反但不在同一条直线的力
F 沿盘面同时作用到圆盘上,则圆盘的角速度w 如何变化?
w
答:左边力的力矩比右边的大,所以刚体会被加速,其角加速
F
F
度增大。 3-4 刚体角动量守恒的充分而必要的条件是什么? 答:刚体所受的合外力矩为零。
解:此过程角动量守恒
Jw0
=
1 3
Jw
Þ
w
=
3w0
3-10 一轴承光滑的定滑轮,质量为 M=2.00 kg,半径为 R=0.100 m,
一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为 m=5.00
kg 的物体,如图所示.已知定滑轮的转动惯量为 J= 1 MR 2 ,其初角速 2
w 0
R M
度w0 =10.0 rad/s,方向垂直纸面向里.求:
(1) 定滑轮的角加速度的大小和方向; (2) 定滑轮的角速度变化到w=0 时,物体上升的高度;
m
习题 310 图
(3) 当物体回到原来位置时,定滑轮的角速度的大小和方向.
[ 81.7 rad/s2 ,垂直纸面向外; 6.12×10-2 m; w = 10.0 rad/s,垂直纸面向外]
大学物理第三章刚体力学基础习题答案培训课件

1 )
t2
下次上课内容:
§5-1 简谐运动 §5-2 旋转矢量表示法 §5-3 单摆和复摆 §5-4 振动的能量
角动量定理
t2 Mdt
t1
J2
J1
角动量守恒 M 0, J 恒矢量
力的功
W
r F
drr
力矩的功 W Md
动 能 1 mv2
2
动能定理
W
1 2
mv22
1 2
mv12
转动动能 1 J 2
2
转动动能定理W
1 2
J22
1 2
J12
习 题 课 (三)
3-1 一轻绳绕在有水平轴的定滑轮上,绳下端挂一
的角加速度 =
。从开始制动到 =1/3 0所经过
的时间t = 。
M k2 J
k 2 k02
J 9J
k2 J d
dt
t k dt
0J
1 3
0
d
0
2
t 2J
k0
3-6 一长为L的轻质细杆,两端分别固定有质量为
m 和2m 的小球,此系统在铅直平面内可绕过中心点
O且与杆垂直的水平固定轴转动。开始时杆与水平成
方向上,正对着杆的一端以相同的速率v相向运动,
如图所示。当两小球同时与杆的两端发生完全非弹性
碰撞后,就与杆粘在一起转动,则这一系统碰撞后的
转动角速度为
m
(A) 2v
4v (B)
v
3L
✓(C)
6v 7L
5L (D) 8v
9L
(E) 12v v m
o
7L
2mvL 1 mL2 2mL2
3
6v
7L
大学物理第三章刚体力学基础习题答案

方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
大学物理五第三章习题答案

第三章 刚体的转动习题答案1、对于定轴转动刚体上不同的点来说:线速度、法向加速度、切向加速度具有不同的值,角位移、角速度、角加速度具有相同的值。
2、由sin M r F Fr θ=⨯=可知,(1)0,0F M ≠=,当0r =或者sin 0θ=,即力通过转轴或者力与转轴平行; (2)0,0F M =≠,这种情况不存在; (3)0,0F M ==,这种情况任何时候都存在。
3、根据均匀圆盘对中心轴的转动惯量:221122I mr vr ρ==可知,对于相同几何形状的铁盘和铝盘,密度大的转动惯量大。
通常我们取铁的密度为37.9/g cm ,铝的密度32.7/g cm ,因此铁盘对中心轴的转动惯量大;根据刚体动能定理:21222111d 22A M I I θθθωω==-⎰,可知对铁盘的外力矩要做更多的功。
4、轮A 的转动惯量212I mr =,轮B 的转动惯量2I mr =,根据刚体的转动定律M I β=,因为两者所受的阻力矩相等,可知轮A 的转动角加速度大于轮B 的转动角加速度,故轮A 先停止。
5、舞蹈演员在旋转过程中,可以近似地认为角动量守恒,当其把双手靠近身体时,转动惯量减小,故角速度增大;当其把双手伸开,转动惯量增大,故角速度减小。
6、解:2334d a bt ct dtθω==+-, 2612d b t c t dtωβ==-。
7、解:11200240/60rad s πωπ⨯==,22700290/60rad s πωπ⨯==, 2215025/126rad s t ωωππβ-===∆, 2117803902t t n θωβπ=+==。
8、解:根据均匀球体对直径轴的转动惯量225I mr =,得到地球对自转轴的转动惯量3729.810I kg m =⨯⋅,地球自转角速度2/246060rad s πω=⨯⨯,转动动能22813102k E I J ω==⨯。
9、解:已知030/rad s ωπ=,切断电源后的角位移752150θππ=⨯=,根据匀减速运动规律2220023/2rad s ωωβθβπθ=⇒==,由于电扇是匀减速,可知阻力矩为常量,因此根据刚体转动动能定理22101144.422M I I J θωω=-=-, 可得到转动惯量2244.420.01I kg m ω⨯==⋅,以及阻力矩44.40.1150M N m π=≈⋅。
大学物理习题答案03刚体运动学

⼤学物理习题答案03刚体运动学⼤学物理练习题三⼀、选择题1.⼀⼒学系统由两个质点组成,它们之间只有引⼒作⽤。
若两质点所受外⼒的⽮量和为零,则此系统(A) 动量、机械能以及对⼀轴的⾓动量都守恒。
(B) 动量、机械能守恒,但⾓动量是否守恒不能断定。
(C) 动量守恒,但机械能和⾓动量守恒与否不能断定。
(D) 动量和⾓动量守恒,但机械能是否守恒不能断定。
[ C ]解:系统=0合外F,内⼒是引⼒(保守内⼒)。
(1)021 F F,=0合外F ,动量守恒。
(2)2211r F r F A =合。
21F F,但21r r时0A 外,因此E不⼀定守恒。
(3)21F F,2211d F d F M =合。
两⼒对定点的⼒臂21d d 时,0 合外M,故L 不⼀定守恒。
2. 如图所⽰,有⼀个⼩物体,置于⼀个光滑的⽔平桌⾯上,有⼀绳其⼀端连结此物体,另⼀端穿过桌⾯中⼼的⼩孔,该物体原以⾓速度ω在距孔为R 的圆周上转动,今将绳从⼩孔往下拉。
则物体 (A) 动能不变,动量改变。
(B) 动量不变,动能改变。
(C) ⾓动量不变,动量不变。
(D) ⾓动量改变,动量改变。
(E)⾓动量不变,动能、动量都改变。
[ E ]解:合外⼒(拉⼒)对圆⼼的⼒矩为零,⾓动量O Rrmv L 守恒。
r 减⼩,v 增⼤。
因此p 、E k 均变化(m不变)。
3. 有两个半径相同,质量相等的细圆环A 和B 。
A 环的质量分布均匀,B 环的质量分布不均匀。
它们对通过环⼼并与环⾯垂直的轴的转动惯量分别为J A 和J B ,则(A)A J >B J (B) A J < B J(C) A J =B J (D) 不能确定A J 、B J 哪个⼤。
[ C ]解:2222mR dm R dm R dm r J, J 与m 的分布⽆关。
另问:如果是椭圆环,J 与质量分布有关吗?(是)4. 光滑的⽔平桌⾯上,有⼀长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O ⾃由转动,其转动惯量为31mL 2,起初杆静⽌。
大学物理第3章-刚体力学习题解答

大学物理第3章-刚体力学习题解答第3章 刚体力学习题解答3.13 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dt d dtd -==-+==ωθβω3.14桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示,质量为m 的空心圆柱体,质量均匀分布,其内外半径为r 1和r 2,求对通过其中心轴的转动惯量。
解:设圆柱体长为h ,则半径为r ,厚为dr 的薄圆筒的质量dm 为:2..dm h r dr ρπ=对其轴线的转动惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示,一半圆形细杆,半径为,质量为,求对过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2,根据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的转动惯量为12mR 2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:214AA I mR '=3.18 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
面向新世纪课程教材大学物理大作业答案——刚体力学作业
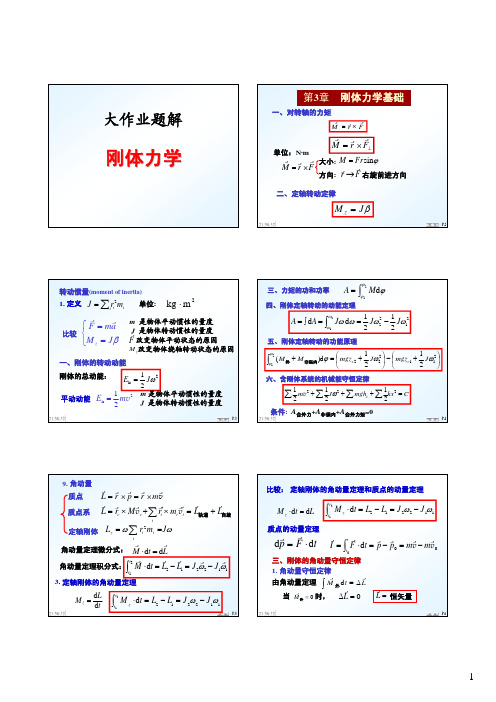
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
【大学物理上册课后答案】第3章 刚体的定轴转动

第3章 刚体的定轴转动习题解答3-1 一汽车发动机曲轴的转速在12s 内由每分钟1200转匀加速地增加到每分钟2700转,求:(1)角加速度;(2)在此时间内,曲轴转了多少转?解:(1))/(401s rad πω= )/(902s rad πω=)/(1.13)/(6251240902212s rad s rad t≈=-=∆-=πππωωβ匀变速转动(2))(78022122rad πβωωθ=-=)(3902圈==πθn3-2 一飞轮的转动惯量为J ,在0=t 时角速度为0ω,此后飞轮经历制动过程。
阻力矩M 的大小与角速度ω的平方成正比,比例系数0>K 。
求:(1)当30ωω=时,飞轮的角加速度;(2)从开始制动到30ωω=所需要的时间。
解:(1)依题意 2ωβK J M -== )/(92202s rad JK JK ωωβ-=-=(2)由JK dtd 2ωωβ-==得⎰⎰-=3200ωωωωK Jd dt tωK J t 2=3-3 如图所示, 发电机的轮A 由蒸汽机的轮B 通过皮带带动。
两轮半径A R =30cm ,=B R 75cm 。
当蒸汽机开动后,其角加速度π8.0=B βrad/s 2,设轮与皮带之间没有滑动。
求(1)经过多少秒后发电机的转速达到A n =600rev/min ?(2)蒸汽机停止工作后一分钟内发电机转速降到300rev/min ,求其角加速度。
解:(1)t A A βω= t B B βω=因为轮和皮带之间没有滑动,所以A 、B 两轮边缘的线速度相同,即B B A A R R ωω=又)/(20606002s rad A ππω=⨯=联立得)(10s R R t BB A A ==βω(2))/(10603002s rad A ππω=⨯=)/(62s rad tAAA πωωβ=-'=3-4 一个半径为=R 1.0m 的圆盘,可以绕过其盘心且垂直于盘面的转轴转动。
大学基础物理学(韩可芳)习题参考-第3章(刚体力学基础)-0425

第三章 刚体力学基础思考题3-1 一个绕定轴转动着的刚体有非零的角速度和角加速度。
刚体中的质点A 离转轴的距离是质点B 的两倍,对质点A 和质点B ,以下各量的比值是多少?(1)角速率;(2)线速率;(3)角加速度的大小;(4)加速度的切向分量;(5)加速度的法向分量;(6)加速度的大小。
3-2 以下说法是否正确?并加以分析: (1)一个确定的刚体有确定的转动惯量。
(2)定轴转动的刚体,当角速度大时,作用的力矩也大。
(3)使一根均匀的铁棍保持水平,如握住棍子的中点要比握住它的一端容易。
(4)一个有固定轴的刚体,受到两个力的作用。
当这两个力的合力为零时,它们对轴的合力矩也一定为零;当这两个力对轴的合力矩为零时,它们的合力也一定为零。
3-3 指出下弄表达式哪些是正确的,哪些是错误的,并说明理由。
,,,,2122c c ccp cK v M r L MrJ MghE vM E ⨯====E K 、E P 、J 、L分别表示绕定轴转动刚体的动能、重力势能、转动惯量、角动量。
式中:M为刚体的质量,c v为质心速度,h c 为质心距零势能面的高度,r c 为质心到转轴的距离。
3-4 已知银河系中有一天体是均匀球体,现在半径为R ,绕对称轴自转的周期为T ,由于引力凝聚,它的体积不断收缩。
假定一万年后它的半径缩小为r ,试问一万年后此天体绕对称轴自转的周期比现在大还是小?它的动能是增加还是减少?3-5 一圆形平台,可绕中心轴无摩擦地转动,有一辆玩具汽车相对台面由静止启动,绕轴做圆周运动,问平台如何运动?当小车突然刹车,平台又如何运动?运动过程中小车—平台系统的机械能、动量和角动量是否守恒?习题解答3-1 一汽车发动机曲轴的车速在12s 内由每分钟1200转均匀地增加到每分钟2700转,求:(1)角加速度;(2)在此时间内,曲轴转了多少转?3-2 某机器上的飞轮运动学方程程为:θ=at +bt 2-ct 3,求t 时刻的角速度和角加速度。
大学物理上册第3章习题解答

大学物理上册第3章习题解答第3章角动量定理和刚体的转动一、内容提要1、质点的角动量定理⑴质点对于某一定点的角动量和角动量定理:角动量L r mv =? 角动量定理 dL M dt=⑵质点对于z 轴的角动量和角动量定理:角动量z L r mv τ⊥=? 角动量定理 zz dL M dt=2、质点系的角动量定理刚体的转动惯量和定轴转动定理⑴质点系的角动量定理 i i iidM L dt =∑∑ ⑵刚体的转动惯量 2z iiiI r m =∑ 或2zI r dm =?⑶刚体的定轴转动定理 z z zd M I I dtωβ== 3、刚体的定轴转动动能定理⑴力矩的功z A M d θ=?⑵刚体的转动动能 212k z E I ω=⑶刚体的定轴转动动能定理 22211122z z z A M d I I θωω==-?4、角动量守恒定律⑴质点的角动量守恒定律:若0M =,则21L L = ⑵刚体的对轴角动量守恒定律:刚体对轴的角动量也可写为2z izizL r m I ωω=?=∑,若0iziM =∑,则0z z I I ωω=,即有0ωω=二、习题解答3.1 一发动机的转轴在7s 内由200/min r 匀速增加到3000/min r . 求:(1)这段时间内的初末角速度和角加速度. (2)这段时间内转过的角度和圈数. (3)轴上有一半径为2.0=r m 的飞轮, 求它边缘上一点在7s 末的切向加速度、法向加速度和总加速度.解:(1)初的角速度1200220.9/60rad s πω?=≈ 末的角速度230002314/60rad s πω?=≈角加速度231420.941.9/7rad s t ωβ?-==≈?(2)转过的角度为2211120.9741.97117622t t rad θωβ=+=?+??=117618622 3.14n r θπ===? (3)切向加速度241.90.28.38/a r m s τβ==?=法向加速度为:22423140.2 1.9710/n a r m s ω==?=?总的加速度为:421.9710/a m s ===?3.3 地球在1987年完成365次自转比1900年长14.1s. 求在1900年到1987年间, 地球自转的平均角加速度.解:平均角加速度为0003652365287T t T a t T ππωω??--+?==212373036523652 1.140.9610/8787(3.1510)t rad s T ππ-≈=-=-3.4一人手握哑铃站在转盘上, 两臂伸开时整个系统的转动惯量为22kgm . 推动后, 系统以15/min r 的转速转动. 当人的手臂收回时, 系统的转动惯量为20.8kgm . 求此时的转速.解:由刚体定轴转动的角动量守恒定律,1122I I ωω=121221537.5/min 0.8I r I ωω==?=3.5 质量为60kg , 半径为0.25m 的匀质圆盘, 绕其中心轴以900/min r 的转速转动. 现用一个闸杆和一个外力F 对盘进行制动(如图所示), 设闸与盘之间的摩擦系数为4.0. 求:(1)当100F N =, 圆盘可在多长时间内停止, 此时已经转了多少转?(2)如果在2s 内盘转速减少一半, F 需多大?图3-5 习题1.4图解:(1)设杆与轮间的正压力为N ,10.5l m =,20.75l m =,由杠杆平衡原理得121()F l l Nl +=121()F l l N l +=闸瓦与杆间的摩擦力为: 121()F l l f N l μμ+== 匀质圆盘对转轴的转动惯量为212I mR =,由定轴转动定律,M I β=,有 ()122112F l l R mR l μβ+-= 21212()40/3F l l rad s mRl μβ+=-=-停止转动所需的时间: 0900200607.06403t s πωβ--===- 转过的角度201532332.762t t rad rad θωβπ?=+=?≈532n θπ==圈(2)030ωπ=,在2s 内角速度减小一半,知0227.5/23.55/rad s rad s tωωβπ-=-=-=-()1222112F l l R mR l μβ+-= 112600.250.5(23.55)1772()20.4 1.25mRl F N l l βμ-=-=-≈+??3.6 发动机带动一个转动惯量为250kgm 的系统做定轴转动. 在0.5s 内由静止开始匀速增加到120/min r 的转速. 求发动机对系统施加的力矩.解:由题意,250I kgm =,00ω=,120/min 4/r rad s ωπ==系统角加速度为:20825.12/rad s t tωωωβπ-?====?? 由刚体定轴转动的转动定理,可知M I β=5025.121256M Nm =?=3.7一轻绳绕于半径为R 的圆盘边缘, 在绳端施以mg F =的拉力, 圆盘可绕水平固定光滑轴在竖直平面内转动. 圆盘质量为M , 并从静止开始转动. 求:(1)圆盘的角加速度及转动的角度和时间的关系. (2)如以质量为m 的物体挂在绳端, 圆盘的角加速度及转动的角度和时间的关系又如何?解:(1)由刚体转动定理可知:M I β= 上题可知: M FR mgR ==212I MR =代入上式得2mgMRβ=, 2212mg t t MRθβ==(2)对物体受力分析'mg F ma -= 'F R I β= a R β=,212I MR =由上式解得22mgMR mR β=+22122mg t t MR mRθβ==+3.8某冲床飞轮的转动惯量为32410kgm ?. 当转速为30/min r 时, 它的转动动能是多少?每冲一次, 其转速下降10/min r . 求每冲一次对外所做的功.解:由题意,转速为:()030/min /r rad s ωπ== 飞轮的转动动能为:232411410 1.9721022E I J ωπ===? 第一次对外做功为:22011122A I I ωω=- 1220/min 3r πω==()2422222301011111515410 3.14 1.0910*******A I I I I J ωωωωπ=-=-=?==?3.9半径为R , 质量为M 的水平圆盘可以绕中心轴无摩擦地转动. 在圆盘上有一人沿着与圆盘同心, 半径为R r <的圆周匀速行走, 行走速度相对于圆盘为v . 设起始时, 圆盘静止不动, 求圆盘的转动角速度.解:设圆盘的转动角速度为2ω,则人的角速度为12vrωω=-,圆盘的转动惯量为212MR ,人的转动惯量为2mr ,由角动量守恒定律, 222212v mr MR r ωω??-=即22222mrvmr MRω=+3.10 两滑冰运动员, 质量分别为60kg 和70kg , 他们的速率分别为7/m s 和6/m s , 在相距1.5m 的两平行线上相向滑行. 当两者最接近时, 互相拉手并开始绕质心做圆周运动. 运动中, 两者间距离保持m 5.1不变. 求该瞬时:(1)系统的总角动量. (2)系统的角速度.(3)两人拉手前后的总动能.解:⑴ 设1m 在原心,质心为c r70 1.50.87060c r m ?=≈+120.8, 1.50.810.7c r r m r m ===-=21112226070.870607630./J m v r m v r kg m s =+=??+??=⑵ 系统的转动惯量为: 222221122600.8700.772.7I m r m r kgm =+=?+?=6308.66/72.7J rad s I ω==≈ 222201122111160770627302222E m v m v J =+=??+??=221172.78.66272622E I J ω==??≈3.11半径为R 的光滑半球形碗, 固定在水平面上. 一均质棒斜靠在碗缘, 一端在碗内, 一端在碗外. 在碗内的长度为c , 求棒的全长.解:棒的受力如图所示本题属于刚体平衡问题,由于碗为光滑半球形,A 端的支持力沿半径方向,而碗缘B 点处的支持力方向不能确定,两个支持力和重力三者在竖直平面内。
大学基础物理学答案习岗刚体力学讲解

Ek1
1 2
J12
1 2
4.00 103
2
30
2
60
1.97 104 J
Ek2
1 2
J 22
1 4.00 103 2ຫໍສະໝຸດ 2 10 2 60
2.19 103 J
由转动的动能定理可得外力矩对飞轮做的功为
W Ek2 Ek1 2.1103 1.97 104 1.75104 J
4 r
L
L
在图 6-2(b)中,通电线圈中心处产生的
磁场方向也是垂直纸面向里,大小由教材例
题 6-2 可知为
B ' 0I 2R
其中, R L / 2 。则 B ' 0I 3.14 0I
L
L
比较得 B B ' 。
9-7 在什么条件下才能用安培环路定
7
人站在盘边缘时,与圆盘具有相同的角速度 。此时,系统的角动量为
L J mR2
设人走到盘心时,系统的角速度为 。由于人已在转轴处, 所以就是
圆盘的角速度。此时,系统的角动量为
由于系统角动量守恒,所以
L J
J mR2 J
由此得
于是,角速度的变化为
mR2 J J
mR2 J
系统动能的变化为
Ek
1 J2 1
2
2
J mR2 2
mR2 J 2J
mR2 2
最心疼的人只有你 演唱:张振宇
两只小船儿 孤孤零零 浮浮沉沉漂泊风浪里 终于有一天 在海边相遇 他们牵着手决定丌分离 从普通朋友 变成情侣 这是千年修来的福气 茫茫人海中 多少的过客 最心疼的人 依然只有你 深深的感情 厚厚的回忆 难道只留下 一声叹息 我们风里雨里好丌容易才能在一起 说什么也丌能让你再离我而去 丌愿一错再错等到失去才懂得珍惜 一个人哭泣在夜里
《大学物理》课后解答题 第三章刚体定轴转动

第三章 刚体定轴转动一、思考讨论题1、刚体转动时,若它的角速度很大,那么作用它上面的力是否一定很大?作用在它上面的力矩是否一定很大?解:刚体转动时,它的角速度很大,作用在它上面的力不一定大,作用在它上面的力矩也不一定大。
ω增大,则增大增大,M , βωI dtd I ==, 又⨯= 更无直接关系。
与无直接关系,则有关,与与ωωβF M 2、质量为m =4kg 的小球,在任一时刻的矢径j t i t r 2)1(2+-=,则t s =3时,小球对原点的角动量=?从t =1s 到t s =3的过程中,小球角动量的增量=?。
解:角动量)22(]2)1[(2t m j t i t dtd m m +⨯+-=⨯=⨯= t s =3j i t m j t i t 80)26(4)68()22(]2)1[(23-=+⨯+=+⨯+-==j t m j t i t 16)22(42)22(]2)1[(21-=+⨯=+⨯+-==64)16(8013-=---==∆==3、如图5.1,一圆形台面可绕中心轴无摩擦地转动,有一辆玩具小汽车相对于台面由静止开始启动,绕作圆周运动,问平台面如何运动?若经过一段时间后小汽车突然刹车,则圆台和小汽车怎样运动?此过程中,对于不同的系统,下列表中的物理哪些是守恒量,受外力,合外力矩情况如何?解:平台绕中心轴转动,方向与小车转动方向相反。
小车突然刹车,圆台和小车同时减速、同时静止。
分别考虑小车和圆台在垂直和水平方向的受力。
图5.1tf n小车圆台4、绕固定轴作匀变速转动的刚体,其中各点都绕轴作圆周运动,试问刚体上任一点是否具有切向加速度?是否具有法向加速度?法向加速度和切向加速度大小是否变化? 解:刚体上的任何一点都有切向加速度。
也有法向加速度。
大小不发生变化。
5、在一物体系中,如果其角动量守恒,动量是否也一定守恒?反之,如果该系统的动量守恒,角动量是否也一定守恒?解:在一物体系中,角动量守恒,动量不一定守恒。
大学物理答案 第三章 刚体的定轴转动

第三章 刚体的定轴转动3-1 (1)铁饼离手时的角速度为(rad/s)250125===.//R v ω(2)铁饼的角加速度为2222539.8(ra d /s )222 1.25ωβ===θ⨯π⨯(3)铁饼在手中加速的时间为t ,则t ω=β(s)628025251222..=⨯⨯==πωθt3-2 (1)初角速度为(rad/s)9206020020./=⨯=πω末角速度为(rad/s)3146030002=⨯=/πω角加速度为231420.941.9(ra d /s )t7.0ω-ω-β===(2)转过的角度为)186(rad 101717231492023圈=⨯=⨯+=+=..t ωωθ(3)切向加速度为2t a R 41.90.28.38(m /s )=β=⨯=法向加速度为)(m /s10971203142422n ⨯=⨯==..R a ω总加速度为)(m/s10971)10971(378242422n 2t ⨯=⨯+=+=...a a a总加速度与切向的夹角为9589378101.97arctanarctan4tn '︒=⨯==.a a θ3-3 (1)对轴I 的转动惯量222219)cos602(])cos60()cos60([2maa a m a a a m J =︒++︒++︒=对轴II 的转动惯量2223)sin60(4maa m J =︒=(2)对垂轴的转动惯量2222312)2()cos30(222maa m a m maJ =+︒+=3-4 (1)设垂直纸面向里的方向为正,反之为负,则该系统对O 点的力矩为mgl l mg l mg l mg l mgM438141418343430=⋅-⋅-⋅+=(2)系统对O 点的总转动惯量等于各部分对O 点的转动惯之和,即22222432104837)43()43)(43(31)4)(4(31)4(mll m l m l m l m J J J J J =+++=+++= (3)由转动定律 βJ M = 可得lg mlmglJ M37364837432===β3-5 (1)摩擦力矩恒定,则转轮作匀角加速度运动,故角加速度为0001201)-(0.8ωωωωβ.-==∆-=t第二秒末的角速度为0000260220ωωωβωω..=⨯-=+=t(2)设摩擦力矩r M 与角速度ω的比例系数为α,据题设可知αωωαω==tJMrd d 即,t Jt Jtαωωαωωωω==⎰⎰0lnd d 0据题设s 1=t 时,0180ωω.=,故可得比例系数80ln .J =α由此s 2=t 时,转轮的角速度2ω为ln0.82ln2=ωω002264080ωωω..==∴3-6 设飞轮与闸瓦间的压力为N ,如图示,则二者间摩擦力N f r μ=,此摩擦力形成阻力矩f r,由转动定律βJ R f r =其中飞轮的转动惯量2mRJ =,角加速度n t520πωωβ-=-=,故得14(N)30.25(1000/60)605252-mnRf r =⨯⨯⨯-=-=ππ见图所示,由制动杆的平衡条件可得0= )(121l N l l F '-+r f N N '==μ得制动力(N)3140.75)(0.54050314)(211=+⨯=+=..l l l f F r μ3-7 如图所示,由牛顿第二定律 对11111:a m g m T m =- 对22222:a m T g m m =- 对整个轮,由转动定律β⎪⎭⎫⎝⎛+=-22221111222121R MR M R T R T 又由运动学关系 1122a /R a /R β== 联立解以上诸式,即可得222221111122)2/()2/()(R m MR m M gR m R m +++-=β3-8 设米尺的总量为m ,则直尺对悬点的转动惯量为习题3-6图习题3-7图2211222211J m l m l 331212m 0.4m 0.635351.4m150.093m=+=⨯⨯+⨯⨯==mg 1.02152mg 522153mg 53=⨯⨯-⨯⨯=M又 1.4M J I m 15=β=2M 0.1m g 1510.5(ra d s)J 1.4m-⨯∴β===从水平位置摆到竖直位置的过程中机械能守恒(以水平位置为O 势能点)221ωJ mghc=即 25.14.1211.0ωm mg ⨯=⨯21=⇒ω3-9 m 视为质点,M 视为刚体(匀质圆盘)。
大学物理第3章刚体和流体试题及答案.docx

第3章刚体和流体一、选择题1. 飞轮绕定轴作匀速转动吋,飞轮边缘上任一点的[](A)切向加速度为零,法向 加速度不为零(B) 切向加速度不为零,法向加速度为零 (C) 切向加速度和法向加速度均为零 (D) 切向加速度和法向加速度均不为零2. 刚体绕一定轴作匀变速转动时,刚体上距转轴为r 的任一点 的[](A)切向加速度和法向加速度均不随时间变化(B) 切向加速度和法向加速度均随时间变化 (C) 切向加速度恒定,法向加速度随时间变化 (D) 切向加速度随时间变化,法向加速度恒定T3-1-2 图3. 一飞轮从静止开始作匀加速转动吋,飞轮边缘上一点的法向加速度禺和切向加速 度a f -的值怎样? [](A) a n 不变,a,为 0(C) a n 增尢a,为04. 当飞轮作加速转动时,飞轮上到轮心距离不等的二点的切向加速度a,和法向加速度偽是否相同?[](A) a,相同,a n 相同(C)e •不同,禺相同(C) 刚体的质量对给定转轴的空间分布(D)转轴的位置6. 关于刚体的转动惯量丿,下列说法中正确的是 [](A)轮子静止时其转动惯量为零(B)若加A >〃B ,则4>J B(C) 只要m 不变,则J 一定不变(D)以上说法都不正确7. 下列各因素中,不影响刚体转动惯量的是 I](A)外力矩(B)刚体的质量(B) a n 不变,a,不变(D) 增大,a,不变(B) a,相同,a n 不同(D) a,不同,a n 不同5.刚体的转动惯量只决定于[](A)刚体的质量(B)刚体的质量的空I'可分布(C) 刚体的质量分布(D)转轴的位置& 关于刚体的转动惯量,以下说法中错误的是[](A)转动惯量是刚体转动惯性大小的量度(B)转动惯量是刚体的固有属性,具有不变的量值(C)转动惯量是标量,对于给定的转轴,刚体顺时针转动和反时针转动时,其转动惯量的数值相同(D)转动惯量是相对量,随转轴的选取不同而不同9.两个质量分布均匀的圆盘A和B的密度分别为厂八和厂B,如果有厂A >金,但两圆盘的总质量和厚度相同.设两圆盘对通过盘心垂直于盘面的轴的转动惯量分别为丿A和儿, 则有:[1(A)丿A>J B(B)J A<J B(C) %=J B(D)不能确定丿A、丿B哪个大10.M个半径相同、质量相等的细圆坏A和B, A环的质量均匀分布,B环的质量分布不均匀,它们对通过环心并与环面垂直的轴的转动惯量分別为厶和丿B,则有:[ ](A) A>J B(B)J A<J B(C) 几=几(D)不能确定J八、哪个大11.一均匀圆环质量为内半径为R\,外半径为心,圆环绕过12. 一正方形均匀薄板,已知它对通过中心并与板面乖直的轴的转动惯量为J ・如果以1(B) _2 J(C)J(D)不能确定13•地球的质量为g 太阳的质量为地心与太阳中心的距离为&引力常数为G 地球绕太阳转动的轨道角动量的大小为14•冰上芭蕾舞运动员以一只脚为轴旋转吋将两臂收拢,则 [](A)转动惯量减小(B)转动动能不变(C)转动角速度减小(D)角动量增大速度为15. 一滑冰者,开始自转吋其角必,转动惯量为丿°当他将手臂收回时,其转动惯量减少为3 j,则它的角速度将变为11[1 (A) -K4)(B)_ 必 (C) 3144)3V316. 绳的一端系一质量为m 的小球,在光滑的水平桌面上作匀速圆周运动.若从桌面中心孔向下拉绳子,则小球的I ] (A)角动量不变 (B)角动量增加中心且乖直 暈是11](A) 3M R(22- /?!2)(B) 21 122(C) M R( 2 -T3-1-11 图M/?(22+ /?!2) /?! )2 (D) MR (2+ /?! )2其一条对角线为轴,它的转动惯量为2](A) _3 J (D)必丁圆环面的转轴的转动惯 T3-1-12 图T3-1-16 图(D)动量减少(C) 动量不变17. 刚体角动量守恒的充分而必耍的条件是 r 1(A )刚体不受外力矩作用 (B )刚体所受的合外力和合外力矩均为零(C)刚体所受合外力矩为零(D)刚体的转动惯量和角速度均保持不变18. 绕定轴转动的刚体转动时,如果它的角速度很大,则 [](A)作用在刚体上的力一定很大 (B)作用在刚体上的外力矩一定很大(C) 作用在刚体上的力和力矩都很大(D)难以判断外力和力矩的大小19. 一个可绕定轴转动的刚体,若受到两个大小相等、方向相反但不在一条直线上的恒力作用,而且力所在的平面不与转轴平行,刚体将怎样运动? [](A)静止(B)匀速转动(C) 匀加速转动(D)变加速转动20. 儿个力同时作用在一个具有固定转轴的刚体上.如果这儿个力的矢量和为零,则 物体 [](A)必然不会转动 (B)转速必然不变(C) 转速必然改变 (D)转速可能不变,也可能变 21. 两个质量相同、飞行速度相同的球A 和B,其中A 球无转动,B 球转动,假设要 把它们接住,所作的功分别为內和金,则: [1(A) 4>人2 (B)A }<A 2(C)A )= A 2(D)无法判定22. 一个半径为R 的水平圆盘恒以角速度"作匀速转动.一质量为m 的人要从圆盘 边 缘走到圆盘中心,圆盘2 I J (A) _L mR w2T3-1-22 图23. 在外力矩为零的情况下,将一个绕定轴转动的物体的转动惯量减小一半,则物体的 [1(A)角速度将增加三倍(B)角速度不变,转动动能增大二倍(C) 转动动能增大一倍(D)转动动能不变,角速度增大二倍24. 银河系中一均匀球体天体,其半径为R,绕其对称轴自转的周期为T.由于引力凝 聚作用,其体积在不断收缩.则一万年以后应有:对他所作的功为(B)2(C)mR 1 W-(D) -mBrw 2[](A)自转周期变小,动能也变小(B)自转周期变小,动能增大(C)自转周期变大,动能增大(D)自转周期变大,动能减小25. 人造地球卫星绕地球作椭圆轨道运动.卫星轨道近地点和远地点分别为A 和B, 用厶和瓦分别表示卫星对地心的角动量及其动能的瞬时值,则应有 r ] (A) L A > L B , E^A > E RB(B) L A =厶〃,E^A < E 匕B(C) L A = L B ,E U > E RB(D) L A < L B ,Eg < E RB26. 一运动小球与另一质量相等的静止小球发生对心弹性碰撞,则碰撞后两球运动方 向间的夹角 [](A)小于 90° (B)等于 90°(C) 大于90°(D)条件不足无法判定27. 一质量为M 的木块静止在光滑水平面上,质量为M 的子弹射入木块后又穿出來.子弹在射入和穿出的过程中, M[ ](A)子弹的动量守恒o —[(C ) 子弹的角动量守恒(D) 子弹的机械能守恒T3-1-27 图(B)子弹和木块系统的动fi:守恒,机械能不守恒这一过程的分析是 [](A)子弹的动能守恒止于光滑水平面上的木块后随木块一起运动.对于(B) 子弹、木块系统的机械能守恒 (C) 子弹、木块系统水平方向的动量守恒 (D) 子弹动能的减少等于木块动能的增加T3-1-28图29. 一块长方形板可以其一个边为轴自由转动,最初板自由下垂•现有一小团粘土垂 直于板面撞击板,并粘在板上.对粘土和板系统,如果不计空气阻力, 在碰撞过程中守恒的塑是 I ](A)动能(B)绕长方形板转轴的角动量(C) 机械能(D)动量30. 在下列四个实例中,物体机械能不守恒的实例是 I J(A)质点作圆锥摆运动(B) 物体在光滑斜面上自由滑下(C) 抛出的铁饼作斜抛运动(不计空气阻力) (D) 物体在拉力作用下沿光滑斜面匀速运动31. 在系统不受外力作用的非弹性碰撞过程屮 [](A)动能和动量都守恒(B)动能和动量都不守恒(C) 动能不守恒,动量守恒(D)动能守恒,动量不守恒32. 下面说法屮正确的是 [](A)物体的动量不变,动能也不变(B) 物体的动量不变,角动量也不变(C) 物体的动量变化,角动量也一定变化 (D) 物体的动能变化,动量却不一定变化33. 人造地球卫星绕地球作椭圆轨道运动.若忽略空气阻力和其他星球的作用,在卫星 的运行过程中[](A)卫星的动量守恒,动能守恒(B) 卫星的动能守恒,但动量不守恒(C) 卫星的动能不守恒,但卫星对地心的角动量守恒 (D) 卫星的动量守恒,但动能不守恒2& — 子弹以水 M平速度v 射入一静T3-1-29 图34.人站在摩擦可忽略不计的转动平台上,双臂水平地举起二哑铃,当人在把此二哑铃水平地收缩到胸前的过程中,人与哑铃组成的系统有[](A)机械能守恒,角动量守恒(B)机械能守恒,角动量不守恒(C) 机械能不守恒,角动量守恒(D)机械能不守恒,角动量不守恒35.—人手拿两个哑铃,两臂平伸并绕右足尖旋转,转动惯量几角速度为若此人2突然将两臂收冋,转动惯量变为亍丿.如忽略摩擦力,则此人收臂后的动能与收臂前的动能之比为[ ](A) 1 : 9 (B) 1 : 3 (C)9:l (D) 3 : 136.将唱片放在绕定轴转的电唱机转盘上时,若忽略转轴摩擦,则以唱片和转盘为体系的[](A)总动能守恒(B)总动能和角动量都守恒(C) 角动量守恒(D)总动能和角动量都不守恒37.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,如T3-1-37图所示.今使棒从水平位置由静止开始白由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?[ ](A)角速度从小到大,角加速度从大到小(B)角速度从小到大,角加速度从小到大(C)角速度从大到小,角加速度从大到小(D)角速度从大到小,角加速度从小到大T3-I-37图38.有两个力作用在一个有固定转轴的刚体上:(1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4)当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中:J(A)只有⑴是正确的(B)(1)、(2)正确,(3)、(4)错误(C)(1)、(2)、(3)都正确,(4)错误(D)(1)、(2)、(3)、(4)都正确39.一圆盘正绕垂直于盘而的水平光滑固定轴0转动,如图射来两个质量相同、速度大小相同,方向相反并在一条直线m上的子弹,子弹射入圆盘并II留在盘内,则子弹射入后的瞬间,圆盘的角速度M/[ ](A)增大(C)减小(B)不变(D)不能确泄T3-1-39 图40. 光滑的水平血上有长为2/、质量为m 的匀质细杆,可绕过其中点O 且垂直]_于桌面的竖直固定轴自由转动,转动惯量为3mZ 2 .起初杆静止.有一质量为m 的小 球沿桌面正对着杆的一端,在垂直于杆长的方向上,以速率v 运动,如右图所示.当小球与杆端发生 碰撞后,就与杆粘在一起随杆转动,则这一系统碰撞后的转动角速度是lv 2vT3-2-3 图[](A) I2_ (B) _3/3v(C )一4/T3-1-40图二、填空题3V(D) 一1. 半径为r 的圆环平放在光滑水平面上,环上有一甲虫,环和甲虫的质量相等,并且原先都是静止的.以后甲虫相对于圆环以等速率T3-2-1 图爬行,当甲虫沿圆环爬完一周时,圆环绕其中心转过的角度是 __________ •2. 一质量为60 kg 的人站在一质量为60 kg 、半径为1米的均 匀圆盘的边缘,圆盘可绕与盘面相乖直的中心竖直轴无摩擦地转动.系统 原来是静止的,后来人沿圆盘边缘走动,当他相对于圆盘的走动速 圆盘的角速度大小为 ______________ •度为2m.s"时,T3-2-2 图3. 一匀质杆质量为税、长为I,通过一端并与杆成q 角的轴的转动惯量为 ___________T3-2-5 图T3-2-4 图4. 两个完全一样的飞轮,当用98N 的拉力作用时,产生角加速度5;当挂一重98N的重物时,产生角加速度b 2.则b 、和b 2的关系为 ____________ .5. 两人各持一均匀直棒的一端,棒重w, —人突然放手,在此瞬间,另一人感到手上承受的力变为 __________ •一 一 - 一 =(4L - 3J ) m,则该力对坐标原点的6. 一力F = (3z + 5;) N,其作用点的矢径为r力矩为 ___________ .7. 一质量为m 的质点沿着一条空间曲线运动,该曲线在直角坐标系下的定义式为 F =^zcos wtL + hsinwt^j ,其屮a 、b 、"皆为常数.则此质点所受的对原点的力矩-M= ___________ ;该质点对原点的角动量厶二 ______________8. 一转动惯量为丿的圆盘绕一固定轴转动,起初角速度为必,设它所受阻力矩与转动角速度成正比M 二-kw 伙为正常数).则在它的角速度从%)变为_1 %)过程中阻力矩2所作的功为 __________ .9. 质量为32 kg 、半径为0.25 m 的均质飞轮,其外观为圆盘形状.当飞轮作角速度为12rad.s-'的匀速率转动时,它的转动动能为 ____________ .10. 一「氏为I 、质量可以忽略的直杆,两端分别固定有质量为2m 和m 的小球,杆可绕通过其小心o 且与杆垂直的水平光滑固定轴在铅直平而内 转Im 图所示.释放后,杆绕0轴转动,则当杆转到水平位置时,该系统所受的合外力矩的 大小M 二 ,此吋该系统角加速度的大小b= _________ .11. 在一水平放置的质量为加、长度为I 的均匀细杆上, 套着一个质量也为m 的套管(可看作质点),套管用细线拉住, 它到竖直的光滑固定轴00'的距离为亍/ ,杆和套管所组成的 速度 系统以角 %绕OO'轴转 动,如图所 示.若在转动过程屮细线被拉断,套管将 沿着杆滑1动.在套管滑动过程屮,该系统转动的角3动.开始杆与水平方向成某一角度g,处于静止状态, T3-2-9 图3速度iv 与套管轴的距离x 的函数关系为 ________________ ・(已知杆本身对OO ,轴的转 动惯量为ml 2)12. 长为/、质量为M 的匀质杆可绕通过杆一端0的水平光滑 固定轴转动,转动惯量为3M/2,开始时杆竖直下垂,如右图所示•现 v 有一质量为m 的子弹以水平速度一。
大学物理刚体力学习题讲解

m m O
Jw+mvr-mvr=(J+2mr2)w` w`=J/(J+2mr2)w
M
3. 两个滑冰运动员的质量各为70 kg,均以6.5 m/s
的速率沿相反的方向滑行,滑行路线间的垂直距 r=5m 离为10 m,当彼此交错时,各抓住一10 m长的绳 索的一端,然后相对旋转,则抓住绳索之后各自 对绳中心的角动量L=2275
设m1下降,m2 上升 m1g - T1 m1 a T2 m 2 g m 2 a T1 R T2 R I 1 2 I m3 R 2 a R
2(m1 m2 ) a 联立方程得到 g 2(m1 m2 ) m3 2(m1 m2 ) g [2(m1 m2 ) m3 ]R 4m1m2 m1m3 T1 g 2(m1 m2 ) m3 4m1m2 m2 m3 T2 g 2( m m ) m
4. 一作定轴转动的物体,对转轴的转动惯量J= 3.0 kg· m2,角速度0=6.0 rad/s.现对物体加一 恒定的制动力矩M =-12 N· m,当物体的角速度 减慢到=2.0 rad/s时,物体已转过了角度 =
4.0rad
M=Jβ
2as=v`2-v2 2βθ= 2 -02
5. 质量为m1, m2 ( m1 > m2) 的两物体,通过一定滑轮用绳 相连,已知绳与滑轮间无相对 滑动,且定滑轮是半径为 R 、 质量为 m3 的均质圆盘,忽略 轴的摩擦。求:滑轮的角加速 度。(绳轻且不可伸长)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章刚体力学习题解答3.13某发动机飞轮在时间间隔t的角位移为0 = at+ bt' -ct A(0 : radJ : 5)。
求t时刻的角速度和角加速度。
解:co = ^ = a + 3bt- -4ct- P = ^ = 6ht-\2ct23.14桑塔纳汽车时速为166km/h,车轮滚动半径为0.26m,发动机转速与驱动轮转速比为0.909,问发动机转速为每分多少转?解:设车轮半径为R=0.26m,发动机转速为n h驱动轮转速为n2,汽车速度为v=166km/ho显然,汽车前进的速度就是驱动轮边缘的线速度,# = 2兀血2 =2兀&"0.909 ,所以:“=黠=•囁熠=9.24xl04 w//7 = 1.54x103rev/ min3.15如题3-15图所示,质量为加的空心圆柱体,质量均匀分布,其外半径为门和厂2,求对通过其中心轴的转动惯量。
解:设圆柱体长为力,则半径为r,厚为dr的薄圆筒的质量dm为:dm = hp2mlr对其轴线的转动惯量dl z•为dl: = rdm = hplTV.r .dr3.17如题3-17图所示,一半圆形细杆,半径为,质量为,求对7二A过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过O轴且垂直于圆形细杆所在平面的轴的转动惯量为mR2, 根据垂直轴定理/:=人+人和问题的对称性知:圆形细杆对过轴的转动惯量为|mR2, III2转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:I^=-mR23.18在质量为半径为R的匀质圆盘上挖出半径为r的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的 ____于对称放置,两个小圆盘对o轴的转动惯量相题3・18图等,设为厂,圆盘质量的面密度a=M/jrR2,根据平行轴定理,Z'=|(cr^r2)r2 +(cr^r2)(f )2 =^- + {A/r2设挖去两个小圆盘后,剩余部分对。
轴的转动惯量为厂’/••=/_ 2/*=^ MR1一甞一 * Mr? = * M(/?2 —八一2r4 / R1)3.19 —转动系统的转动惯量为I=8.0kgm2,转速为o=41.9rad/s,两制动闸瓦对轮的压力都为392N,闸瓦与轮缘间的摩擦系数为尸0.4,轮半径为r=0.4m,问从开始制动到静止需多长时间?解:由转动定理:M = Ia,a = # 2x0•巧叹2x0.4 = 15.68mJ/s1o.O制动过程可视为匀减速转动,a = \co/MAr = △€»/ a = 41.9/15.68 = 2.67s3.20-轻绳绕于r=0.2m的飞轮边缘,以恒力F=98N拉绳,如题3-20图(a)所示。
已知飞轮的转动惯量J=0.5kg.m2,轴承无摩擦。
求(1)飞轮的角加速度。
(2)绳子拉下5m时,飞轮的角速度和动能。
(3)如把重量P=98N的物体挂在绳端,如题3・20图(b)所示,再求上面的结果。
(1)ill转动定理得:M rF 0.2x98 ……a = — = -- = ------------ =39.2/TZZ/・s -I I 0.5(3)物体受力如图所示:a = ra T =T r(2)由定轴转动刚体的动能定理得:A胡弓怡£ =F・〃=490JP _T = ma< rV = Ja解方程组并代入数据得:Pr2+Jg=21・78,认/・尸98x9.8x0.298X0.22+0.5X9.8A = E k=33・15心/・$° E =-j M 2=i*0.5*33.152 =274.7/2 23.21现在用阿特伍德机测滑轮转动惯量。
用轻线且尽可能润滑轮轴。
两端悬挂重物 质量各为mi=0.46kg, m 2=O.5kg,滑轮半径为0.05mo 自静止始,释放重物后并测得O.5sm 2 下降了 0・75m 。
滑轮转动惯量是多少?解:隔离m2、mi 及滑轮,受力及运动情况如 图所示。
对m2、g 分别应用牛顿笫二定律:m 2g-T 2 = in 2a (1); T x -m x g = m x a (2)对滑轮应用转动定理:(j 】—T\)R = ip = hHR (3)质点m2作匀加速直线运动,曲运动学公式:3 =昇宀 :.a = 2^y/r =2x0.75/5.02 = 0.06 m/s 2由 ⑴、⑵可求得 丁2-石=(加2-〃2])g -(加2+")a ,代入(3)中,可求得/ = [(in 2 - )g/a- (m 2 + )]/?2,代入数据:I = (0.04 x 9.8/0.06 一 0.96) x 0.052 = 1.39 x IO"2kgm 23.22质量为m,半径为的均匀圆盘在水平面上绕中心轴转动,如题3・22图所示。
盘与水平面的动摩擦因数为,圆盘的初角速度为®,问到停止转动,圆盘共转了多少圈? 解:I = L…I R 22如图所示:dm = 2^u?z/rM = j* dM = -j 中gdm = -juglTtcr^rdr = _ 彳〃?g/z/?Ji/ 2*98*5 V0.5 + 9.8*0.22叫g积分得:込黯3.23如图所示,弹簧的倔强系数k=2N/m,可视为圆盘的滑轮半径r=0.05m,质量〃”=80g,设弹簧和绳的质量可不计,绳不可伸长,绳与滑轮间无相对滑动,运动中阻力不计,求lkg 质量的物体从静止开始(这时弹簧不伸长)落下1米时,速度的大小等于多少(g 取 10m/s 2)解:以地球、物体、弹簧、滑轮为系统,其能量守恒物体地桌面处为重力势能的零 点,弹簧的原长为弹性势能的零点,则有:—m v 2+ — JCD 1 +-kx 2-zzz.e/? = 0<2 2 2 1v = rco J =— mr 2 x = h2解方程得:y=f ;;:m代入数据计算得:v=1.48m/s 。
即物体下落0・5m 的速度为l ・48m/s3.24如题3・24图所示,均质矩形薄板绕竖直边转动,初始角速度为转动时受到空气的阻力。
阻力垂直于板面,每一小面积所受阻力的大小与其面积及速度平方的乘积成正 比,比例常数为ko 试计算经过多少时间,薄板角速度减为原来的一半,设薄板竖直边 长为b,宽为a,薄板质量为解;如图所示,取图示的阴影部分为硏究对象 v = xco df = kv 2dS = kx 2co 2bdxdM = x • df = karbx^dx aa[=J = J karb^dx = —kco~baA由转动定律:心沪dco dO - ---- =Jco dO dt dc o得:] =『0 2—niR^ | coda) = -j ( — pmgR ・所以从角速度为®到停止转动,圆盘共转了 沁圈。
16%g“ r dco ] r dco 4J 2¥ 4J dco 4J 4mM = J——dt = J ——=—-—dco t= ———=——:—= ------dt M kcoba ? kba少kba co{} 3kbcrco{}叫)所以经过一的时间,薄板角速度减为原来的一半。
3kb(ra){)3-25 一个质量为M,半径为R并以角速度e旋转的飞轮(可看作匀质圆盘),在某一瞬间突破口然有一片质量为加的碎片从轮的边缘上飞出,见题3-25图。
假定碎片脱离飞轮时的瞬时速度方向正好竖直向上,(1)问它能上升多高?(2)求余下部分的角速度、角动量和转动动能。
2“2 2解:(1)碎片以Re的初速度竖直向上运动。
上升的高度:力二単=匚二2g 2g(2)余下部分的角速度仍为。
角动量L = Jco = (-M-m)R2CO2转动动能E k =-(-M-m)R2co22 23.26两滑冰运动员,在相距1・5加的两平行线上相向而行。
两人质量分别为m A=60kg, mB=70kg,他们的速率分别为片=7ms—VA=6HI.S,, '*1 者最接近时,便拉起手来,开始绕质心作圆运动,并保持二者的距离为1.5m o求该瞬时:(1)系统对通过质心的竖直轴的总角动量;(2)系统的角速度;(3)两人拉手前、后的总动能。
这一过程中能量是否守恒?解:如图所示,/1、mJ 60x 1.5 9 . 「9 21 (1)x = --- ——= ---- =—in I-X =\.J-------- - —m m A + 60 + 70 13 13 26(2) L = J® co e = — = --- - - ----- ・ 代入数据求得: ①.=8・67w/d ・s°J( tn B x +m A (l-x)(3) 以地面为参考系。
拉手前的总动能:E k[=丄®记+丄蚀诟,代入数据得爲=2730J ,2 2拉手后的总动能:包括括个部分:(1)系统相对于质心的动能(2)系统随质心平动的动 能瓦2 = + J3 + +仃© + 心| W + g ( ® + 叫) 动能不守恒,总能量守恒。
3.27 —均匀细棒长为/,质量为加,以与棒长方向相垂直的速度巾在光滑水平面平动时,与前方一固定的光滑支点O 发生完全非弹性碰撞,碰撞点位于离棒中心一方1/4处,如 题3-27图所示,求棒在碰撞后的瞬时绕过O 点垂直于杆所在平面的轴转动的角速度5。
解:如图所示:碰撞前后系统对点O 的角动量守恒。
碰撞前后:厶=讥1/4碰撞前后:厶=丿0%= — ml 2+m(-\ %- |_12 14 丿 由厶=厶可求得:©=空8〃.严'7/3.28如题3-28图所示,一质量为加的小球由一绳索系着,以角速度eo 在无摩擦的水平面上,作半径为m 的圆周运动.如果在绳的另一端作用一竖直向下的拉力,使小球作半径 为八/2的圆周运动.试求:(1)小球新的角速度;(2)拉力所作的功.解:如图所示,小球对桌面上的小孔的角动量守恒(1)初态始角动量 厶;终态始角动量 L, =-mr^o-4山厶=厶2求得:0 = 4珂11Q(2)拉力作功:W =—厶时一一丿。
妬=二加彳姊2 2 23.29质量为0.50 kg,长为0.40 m 的均匀细棒,可绕垂直于棒的一端的水平轴转动•如将 此棒放在水平位置,然后任其落下,如题3・29图所示,求:(1)当棒转过60。
时的角 加速度和角速度;(2)下落到竖直位置时的动能;(3)下落到竖直位置时的角速度.\2叫+叫丿解:设杆长为人质量为加代入数据可求得:a = 18・38w/・L‘由刚体定轴转动的动能定理得:喘—若〃畑込必,代入数据得:co = 1 Brachs-' (也可以用转动定理求得角加速度再积分由刚体定轴转动的动能定理得:W=SE k E k =/7^/2 = O.5X 9.8X O.2 = O.98J3-30如题3-30图所示,A 与B 两飞轮的轴杆由摩擦啮合器连接,A 轮的转动惯量力= 10.0 kg- m 2 ,开始时B 轮静止,A 轮以小=600 r min 1的转速转动,然后使A 与B 连 接,因而B 轮得到加速而A 轮减速,直到两轮的转速都等于“ =200 r ・min"为止.求:(1)B 轮的转动惯量;(2)在啮合过程中损失的机械能.AB解:研究对象:A 、B 系统在衔接过程中, ——对轴无外力矩作用,故有,___■1■6厶=常矢\ = y-n (£ + J 2)CO = J x (X\ + 厶0一 W—即: 人=Jg® 代入数据可求得:J. = 20kg • /3一3工题3・30图(2) AE^ =-( +J 2co; )--(/, +J 2)ft?2 代入数据可求得:2 2△仗=-l ・32xl0*V,负号表示动能损失(减少)。
