二叉平衡树

合集下载

平衡二叉树用途

平衡二叉树用途平衡二叉树是一种常用的数据结构，具有广泛的应用。

它的设计和实现使得它成为一种高效的数据结构，可以用于快速插入、搜索和删除数据，并且在各种场景下提供了良好的性能。

平衡二叉树在搜索引擎中起到了重要的作用。

在搜索引擎中，需要快速地找到相关的搜索结果，并按照相关性进行排序。

平衡二叉树的特性使得它可以高效地实现这一功能。

通过使用平衡二叉树，搜索引擎可以快速地定位到相关的数据，并返回给用户相关的搜索结果。

平衡二叉树在数据库中也得到了广泛的应用。

数据库需要高效地存储和检索大量的数据。

平衡二叉树的特性使得它可以快速地插入、搜索和删除数据。

在数据库中，平衡二叉树通常被用作索引结构，以加快数据的检索速度。

通过使用平衡二叉树，数据库可以快速地找到需要的数据，提高了数据库的性能。

平衡二叉树还可以用于实现高效的排序算法。

在排序算法中，需要对一组数据进行排序，以便后续的处理。

平衡二叉树可以用来实现一些高效的排序算法，例如二叉排序树和红黑树。

通过使用平衡二叉树，可以快速地对数据进行排序，提高排序算法的效率。

平衡二叉树还可以用于实现高效的缓存淘汰算法。

在缓存淘汰算法中，需要根据一定的策略来选择要从缓存中淘汰的数据。

平衡二叉树可以用来实现一些高效的缓存淘汰算法，例如LRU（Least Recently Used）算法。

通过使用平衡二叉树，可以快速地选择要淘汰的数据，提高缓存淘汰算法的效率。

平衡二叉树还可以用于实现高效的路由算法。

在路由算法中，需要根据一定的规则来选择数据包应该传输的路径。

平衡二叉树可以用来实现一些高效的路由算法，例如最短路径算法。

通过使用平衡二叉树，可以快速地选择最短路径，提高路由算法的效率。

平衡二叉树是一种非常有用的数据结构，可以在各种场景下提供高效的性能。

它在搜索引擎、数据库、排序算法、缓存淘汰算法和路由算法等方面都得到了广泛的应用。

通过合理地设计和实现平衡二叉树，可以提高各种应用的效率，提升用户的体验。

平衡二叉树用途

平衡二叉树用途
平衡二叉树是一种常用的数据结构，在计算机科学中有广泛的应用。

以下是平衡二叉树的几个主要用途：
1. 查找和排序：
平衡二叉树可以用于快速查找和排序数据。

由于平衡二叉树的特殊结构，它可以在O(log n)的时间内完成查找和排序操作。

这使得它成为一种比线性搜索更有效的方法。

2. 实现字典：
平衡二叉树可以用来实现字典，其中键是树中的节点，值是与该键相关联的数据。

在这种情况下，平衡二叉树的节点将按照键的顺序排列，因此查找特定键的值是非常快速的。

3. 数据库：
平衡二叉树可以用于实现数据库中的索引。

索引可以帮助加速数据库的查询操作。

平衡二叉树可以在不需要扫描整个数据库的情况下快速定位特定的记录。

4. 线性数据结构的实现：
平衡二叉树可以用于实现一些常见的线性数据结构，如栈、队列和优先队列。

这是通过在树的一侧添加新节点并在另一侧移除节点来实现的，从而保持平衡性。

5. 模拟：
平衡二叉树可以用于模拟一些实际情况下的问题。

例如，可以使用平衡二叉树来模拟航班预定系统中的座位分配。

总之，平衡二叉树是一种非常有用的数据结构，它可以在许多应用中提供高效的解决方案。

平衡二叉树构造过程

平衡二叉树构造过程
平衡二叉树的构造过程主要分为以下几个步骤：
1.定义平衡二叉树的结构：平衡二叉树的结构类似于普通二叉树，每
个节点的左子树和右子树的深度差不超过1。

2.插入节点：当往平衡二叉树中插入一个节点时，需要先通过二叉搜
索树的方式找到新节点的插入位置。

然后，通过旋转操作将树重新平衡。

旋转分为左旋和右旋两种操作。

3.左旋：当一个节点的右子树深度大于左子树深度时，需要进行左旋
操作。

左旋操作是将该节点的右子树进行旋转，使其成为该节点的父节点，该节点成为该节点的右子树的左子树。

4.右旋：当一个节点的左子树深度大于右子树深度时，需要进行右旋
操作。

右旋操作是将该节点的左子树进行旋转，使其成为该节点的父节点，该节点成为该节点的左子树的右子树。

5.删除节点：当从平衡二叉树中删除一个节点时，需要通过旋转操作
将树重新平衡，避免树退化成非平衡二叉树，导致性能下降。

6.重新计算节点深度：平衡二叉树的关键是保证每个节点的左子树和
右子树深度差不超过1，因此在进行节点插入和删除操作后，需要重新计
算每个节点的深度，并检查是否满足平衡二叉树的结构。

通过以上步骤，可以构造一个平衡二叉树。

在应用中，平衡二叉树常
用于高效的查找和排序操作。

平衡二叉树10.3.2

11
28
96 98
25
(1) LL型调整型调整 p A 1 2
调整方法: 调整方法: 单向右旋平衡,即将的左孩子单向右旋平衡,即将A的左孩子 B 向右上旋转代替成为根结点, 向右上旋转代替A成为根结点成为根结点, 结点向右下旋转成为B的右将A结点向右下旋转成为的右结点向右下旋转成为子树的根结点, 子树的根结点,而B的原右子树的原右子树则作为A结点的左子树结点的左子树. 则作为结点的左子树. h d e B
1 38 -1 24 88
0 -1 -2
0
11
28 1
96
0
-1 0
25
0
98
1,平衡二叉树插入结点的调整方法
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 首先从根结点到该新插入结点的路径之逆向根结点方向找第一个失去平衡的结点, 衡的结点,然后以该失衡结点和它相邻的刚查找过的两个结点构成调整子树(最小不平衡子树即调整子树是指以离插入结点最近,且平衡因子最小不平衡子树), 子树最小不平衡子树 ,即调整子树是指以离插入结点最近且平衡因子绝对值大于1的结点为根结点的子树使之成为新的平衡子树. 的结点为根结点的子树,使之成为新的平衡子树绝对值大于的结点为根结点的子树使之成为新的平衡子树. 38 24 88 -2
(2)RR型调整型调整 p A -1 -2
调整方法: 调整方法: 单向左旋平衡:即将的右孩子的右孩子B向单向左旋平衡:即将A的右孩子向左上旋转代替A成为根结点成为根结点, 左上旋转代替成为根结点,将A结结点向左下旋转成为B的左子树的根点向左下旋转成为的左子树的根结点, 的原左子树则作为A结点结点,而B的原左子树则作为结点的原左子树则作为的右子树. 的右子树. B

平衡二叉树高度计算公式

平衡二叉树高度计算公式
平衡二叉树的高度可以使用以下公式计算：
H = log2(N+1) - 1
其中，N为平衡二叉树中节点的个数，H为平衡二叉树的高度。

公式的基本思想是，对于一棵高度为H的平衡二叉树，它的节点数N最小值是2^H - 1，最大值是2^(H+1) - 1。

因此，根据节点数N 可以推导得到平衡二叉树的高度H。

需要注意的是，此公式适用于普通的平衡二叉树，例如AVL树、红黑树等，但对于某些特殊的平衡二叉树，可能无法直接使用此公式计算高度。

例如，B树、B+树等平衡树的高度计算方法是不同的。

此外，需要注意在实际编写代码时，为了避免精度问题，可以将公式转化为H = ceil(log(N+1)/log(2)) - 1，其中ceil函数表示向上取整。

平衡二叉树

1 1 0 0 0 1 0 0 (a) 平衡二叉树 -1 -1 1
2 -1 0 0 0
-1
-2 0 0 1
0 0
1
(b) 不平衡二叉树图9.6 平衡与不平衡二叉树及结点的平衡因子
平衡二叉树是二叉排序树的另一种形式. 平衡二叉树我们希望由任何初始序列构成的二叉排序树都是平衡二叉树平衡二叉树.因为平衡二叉树平衡二叉树上任平衡二叉树平衡二叉树 1 何结点的左右子树的深度之差都不超过1, 则可以证明它的深度和logN是同数量级的 (其中N是结点的个数).由此,它的平均查找长度也和logN同数量级.
typedef structBSTNode { ElemType data; int bf; //结点的平衡因子结点的平衡因子 struct BSTNode *lchild, *rchild; //左,右孩子指针左 } BSTNode, * BSTree;
算法9.7如下: 算法如下: 如下 void R_Rotate (BSTree &p) { //对以为根的二叉排序树作右旋处理,处理之后p指向新的树根结点, 对以*p为根的二叉排序树作右旋处理,处理之后指向新的树根结点, 对以为根的二叉排序树作右旋处理指向新的树根结点 //即旋转处理之前的左子树的根结点即旋转处理之前的左子树的根结点 lc = p->lchild; //lc指向的的左子树根结点指向的*p的左子树根结点 - 指向的 p->lchild = lc->rchild; //lc的右子树挂接为的左子树的右子树挂接为*p的左子树 - - 的右子树挂接为 lc->rchild = p; - p = lc; //p指向新的根结点指向新的根结点 } // R_Rotate

平衡二叉树

2算法
编辑
红黑树
红黑树是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的，他称之为"对称二叉B树"，它现代的名字是在 Leo J. Guibas 和 Robert Sedgewick 于1978年写的一篇论文中获得的。它是复杂的，但它的操作有着良好的最坏情况运行时间，并且在实践中是高效的: 它可以在O(log n)时间内做查找，插入和删除，这里的n是树中元素的数目。
伸展树
伸展树（Splay Tree）是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。它的优势在于不需要记录用于平衡树的冗余信息。在伸展树上的一般操作都基于伸展操作。
SBT
Size Balanced Tree（简称SBT）是一自平衡二叉查找树，是在计算机科学中用到的一种数据结构。它是由中国广东中山纪念中学的陈启峰发明的。陈启峰于2006年底完成论文《Size Balanced Tree》，并在2007年的全国青少年信息学奥林匹克竞赛冬令营中发表。由于SBT的拼写很容易找到中文谐音，它常被中国的信息学竞赛选手和ACM/ICPC选手们戏称为“傻B树”、“Super BT”等。相比红黑树、AVL树等自平衡二叉查找树，SBT更易于实现。据陈启峰在论文中称，SBT是“目前为止速度最快的高级二叉搜索树”。SBT能在O(log n)的时间内完成所有二叉搜索树（BST）的相关操作，而与普通二叉搜索树相比，SBT仅仅加入了简洁的核心操作Maintain。由于SBT赖以保持平衡的是size域而不是其他“无用”的域，它可以很方便地实现动态顺序统计中的select和rank操作。

平衡二叉树

#define EH 0 //等高
#define RH -1 //右高
//平衡二叉树的类型
struct AVLNode
{
int data;
int bf; //bf结点的平衡因子,只能够取0，-1，1，为左子树的深度减去右子树的深度
struct AVLNode *lchild,*rchild; //左、右孩子指针
{
AVLNode *rc,*rd;
rc=T->rchild;
switch(rc->bf)
{
case RH:
T->bf=rc->bf=EH;
L_Rotate(T);
break;
case LH:
rd=rc->lchild;
switch(rd->bf)
{
case RH:
T->bf=LH;
rc->bf=EH;
};
2.右旋操作：
void R_Rotate(AVLNode *&p)//LL型算法
{
AVLNode *lc=p->lchild; // lc指向p的左子树根结点
p->lchild=lc->rchild; // lc的右子树挂接为p（之前跟节点）的左子树
lc->rchild=p;
p=lc; // p指向新的根结点
插入和删除：
插入删除是互为镜像的操作。我们可以采用前面对二叉排序树的删除操作来进行。然后，在删除掉结点后，再对平衡树进行平衡化处理。删除之所以删除操作需要的平衡化可能比插入时次数多，就是因为平衡化不会增加子树的高度，但是可能会减少子树的高度，在有有可能使树增高的插入操作中，一次平衡化能抵消掉增高；在有可能使树减低的删除操作中，平衡化可能会带来祖先节点的不平衡。AVL树体现了一种平衡的美感，两种旋转是互为镜像的，插入删除是互为镜像的操作，没理由会有那么大的差别。实际上，平衡化可以统一的这样来操作：

平衡二叉树

构造二叉平衡（查找）树的方法是：
在插入过程中，采用平衡旋转技术。
例如:依次插入的关键字为5, 4, 2, 8, 6, 9
5 4 2
向右旋转一次
4 2 5 8 2
4 6 5
先向右旋转再向左旋转
8
6
向左旋转一次
4 2 5 6 8 9 4 6 8 5 9
继续插入关键字 9
2
④平衡调整假设由于在二叉排序树上插入结点而失去平衡的最小子树根结点的指针为a（即a是离插入结点最近，且平衡因子绝对值超过1的祖先结点)，则失去平衡后进行调整的规律可归纳为下列4种情况： 1．单向右旋平衡处理：由于在*a的左子树根结点的左子树上插入结点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行一次向右的顺时针旋转操作。如图9.6(a)所示。
0 C
RL
0 A AL CL CR
-1 B BR
插入结点
⑤插入算法算法思想：在平衡二叉排序树BBST上插入一个新的数据元素e的递归算法可描述如下： 1．若BBST为空树，则插入一个数据元素为e的新结点作为 BBST的根结点，树的深度增1； 2．若e的关键字和BBST的根结点的关键字相等，则不进行插入； 3．若e的关键字小于BBST的根结点的关键字，而且在BBST的左子树中不存在和e有相同关键字的结点，则将e插入在BBST的左子树上，并且当插入之后的左子树深度增加（＋1）时，分别就下列不同情况处理之：
p
lc
算法9.10如下：
#define #define #define
LH EH RH
+1 0 -1
//左高 //等高 //右高
Status InsertAVL (BSTree &T, ElemType e, Boolean &taller) { //若在平衡的二叉排序树T中不存在和e有相同关键字的结点，则插入 //一个数据元素为e的新结点，并返回1，否则返回0。若因插入而使二 //叉排序树失去平衡，则作平衡旋转处理，布尔变量taller反映T长高 //与否。

平衡二叉树旋转例题

平衡二叉树旋转例题【实用版】目录I.平衡二叉树的定义及特点II.平衡二叉树旋转的实例III.平衡二叉树旋转的规则IV.平衡二叉树旋转的作用V.结论正文I.平衡二叉树的定义及特点平衡二叉树，又称为 AVL 树，是一种特殊的二叉树。

其特点是：它是一棵空树，或者它的左右两个子树的高度差的绝对值不能超过 1，并且左右两个子树都是一棵平衡二叉树。

平衡二叉树的构建要求在插入节点时，要保持左右子树的高度差不超过 1，以确保树的平衡。

II.平衡二叉树旋转的实例假设我们有一个平衡二叉树，根节点为 A，左子树节点为 B，右子树节点为 C。

现在，我们在 C 节点插入一个新节点 D，使得 C 成为 D 的左子树。

此时，C 的右子树 E 的深度增加了 1，而 B 的右子树 F 的深度没有变化。

因此，左右子树的高度差为 1，违反了平衡二叉树的定义。

为了解决这个问题，我们需要进行旋转操作。

III.平衡二叉树旋转的规则平衡二叉树的旋转操作分为左旋和右旋。

左旋指的是将当前节点的右子树变为左子树，原左子树变为右子树；右旋则相反，将当前节点的左子树变为右子树，原右子树变为左子树。

在本例中，我们需要先进行右旋操作。

将 C 的左子树 E 变为 C 的右子树，将 C 的右子树 F 变为 C 的左子树。

此时，C 的左右子树高度差为 0，满足平衡二叉树的定义。

接下来，我们需要进行左旋操作。

将 A 的左子树 B 变为 A 的右子树，原右子树 C 变为 A 的左子树。

此时，A 的左右子树高度差为 0，满足平衡二叉树的定义。

IV.平衡二叉树旋转的作用平衡二叉树旋转操作的主要目的是维护树的平衡。

在插入新节点的过程中，可能会破坏原有的平衡关系。

通过旋转操作，可以将破坏的平衡关系重新恢复，确保树的高度差不超过 1。

此外，旋转操作还可以将不平衡的子树调整为平衡状态，提高树的搜索效率。

V.结论平衡二叉树旋转是一种重要的操作，它可以维护树的平衡，确保树的搜索效率。

平衡二叉树实现代码

平衡二叉树实现代码平衡二叉树（Balanced Binary Tree），也叫 AVL 树，是一种特殊的二叉树，它的每个节点的左子树和右子树的高度差不超过1、当插入或删除一个节点后，如果导致树的不平衡，就通过旋转操作来恢复平衡。

下面是平衡二叉树的实现代码：```python#定义平衡二叉树的节点类class AVLNode:def __init__(self, key):self.key = keyself.left = Noneself.right = Noneself.height = 1#定义平衡二叉树类class AVLTree:def __init__(self):self.root = None#获取节点的高度def get_height(self, node):if node is None:return 0return node.height#计算平衡因子def get_balance(self, node):if node is None:return 0return self.get_height(node.left) -self.get_height(node.right)#左旋操作def left_rotate(self, z):y = z.rightT2 = y.lefty.left = zz.right = T2z.height = 1 + max(self.get_height(z.left), self.get_height(z.right))y.height = 1 + max(self.get_height(y.left), self.get_height(y.right))return y#右旋操作def right_rotate(self, z):y = z.leftT3 = y.righty.right = zz.left = T3z.height = 1 + max(self.get_height(z.left), self.get_height(z.right))y.height = 1 + max(self.get_height(y.left), self.get_height(y.right))return y#插入节点def insert(self, key):def insert_node(node, key):if node is None:return AVLNode(key)elif key < node.key:node.left = insert_node(node.left, key)else:node.right = insert_node(node.right, key)node.height = 1 + max(self.get_height(node.left), self.get_height(node.right))balance = self.get_balance(node)#如果节点不平衡，进行旋转操作来恢复平衡if balance > 1:if key < node.left.key:return self.right_rotate(node)else:node.left = self.left_rotate(node.left)return self.right_rotate(node)if balance < -1:if key > node.right.key:return self.left_rotate(node)else:node.right = self.right_rotate(node.right)return self.left_rotate(node)return nodeself.root = insert_node(self.root, key)#删除节点def delete(self, key):def delete_node(node, key):if node is None:return nodeelif key < node.key:node.left = delete_node(node.left, key) elif key > node.key:node.right = delete_node(node.right, key) else:if node.left is None:temp = node.rightnode = Nonereturn tempelif node.right is None:temp = node.leftnode = Nonereturn temptemp = self.get_min_value_node(node.right)node.key = temp.keynode.right = delete_node(node.right, temp.key)if node is None:return nodenode.height = 1 + max(self.get_height(node.left), self.get_height(node.right))balance = self.get_balance(node)#如果节点不平衡，进行旋转操作来恢复平衡if balance > 1:if self.get_balance(node.left) >= 0:return self.right_rotate(node)else:node.left = self.left_rotate(node.left)return self.right_rotate(node)if balance < -1:if self.get_balance(node.right) <= 0:return self.left_rotate(node)else:node.right = self.right_rotate(node.right)return self.left_rotate(node)return nodeself.root = delete_node(self.root, key) #获取以一些节点为根的子树中的最小值节点def get_min_value_node(self, node):if node is None or node.left is None: return nodereturn self.get_min_value_node(node.left) #中序遍历树def inorder_traversal(self):def inorder(node):if node is None:returninorder(node.left)print(node.key, end=" ")inorder(node.right)inorder(self.root)#测试代码if __name__ == '__main__':tree = AVLTreenodes = [50, 30, 70, 20, 40, 60, 80, 25, 10, 55]for node in nodes:tree.insert(node)print("平衡二叉树中序遍历结果：")tree.inorder_traversalprint("\n删除节点 40 后的平衡二叉树中序遍历结果：")tree.delete(40)tree.inorder_traversal```以上就是平衡二叉树的实现代码，代码中包含了平衡二叉树节点类的定义，以及插入节点、删除节点、左旋和右旋操作等方法的实现。

高度平衡的二叉树

高度平衡的二叉搜索树
AVL( Addison-Velski and Landis )树伸展树红黑树

二叉搜索树性能分析

对于有 n 个关键码的集合，其关键码有 n! 种不同排列，可构成不同二叉搜索树有 1 n C 2 n (棵)
n 1
{2, 1, 3} {1, 2, 3} {1, 3, 2} {2, 3, 1} {3, 1, 2} {3, 2, 1}
B
BRAຫໍສະໝຸດ AR中序序列：BL
B
BR
A
AR
注意：改组后
B
A
平衡度为 0
2）RR平衡旋转：若在A的右子树的右子树上插入结点，使A的平衡
因子从-1增加至-2，需要进行一次逆时针旋转。
(以B为旋转轴）
A B A C
左单旋转 (RotateLeft )
+1
A
0
+2
A
+1
C C A
0
0
B h D h
(a)
C E
Double Rotations
Fig. 28-5 (a) Adding 70 to the tree in Fig. 28-2c destroys its balance; to restore the balance, perform both (b) a right rotation and (c) a left rotation.
h
B
E
h D h
(b)
E
h + 1
B
h
D h + h 1
(c)
如果在子树E中插入一个新结点，该子树高度增1导致结点A的平衡因子变成+2，出现不平衡。沿插入路径检查三个结点A、C和E。它们处于一条方向为“\”的直线上，需要做左单旋转。以结点C为旋转轴，让结点A反时针旋转。

自平衡二叉树概念

自平衡二叉树概念
自平衡二叉树是一种二叉搜索树，它通过旋转操作来保持树的平衡。

在二叉搜索树中，每个节点的左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。

这种结构使得在树中查找、插入和删除操作的时间复杂度为O(log n)。

然而，如果二叉搜索树的结构不平衡，例如出现了一条链，那么查找、插入和删除操作的时间复杂度将退化为O(n)，这显然是不可接受的。

因此，需要一种方法来保持树的平衡。

自平衡二叉树通过在插入和删除节点时进行旋转操作来保持树的平衡。

旋转操作可以分为左旋和右旋两种。

左旋是将一个节点的右子树作为新的子树，而右旋是将一个节点的左子树作为新的子树。

这些旋转操作可以使树重新平衡，从而保证树的查找、插入和删除操作的时间复杂度为O(log n)。

自平衡二叉树有许多种实现方法，包括红黑树、AVL树、B树等。

其中，红黑树是应用最广泛的一种自平衡二叉树，它不仅能够保持树的平衡，还能够在插入和删除节点时保持树的颜色平衡，从而保证树的高度不会超过2log(n+1)。

简述二叉树的五种形态

简述二叉树的五种形态二叉树是一种常用的数据结构，它由节点组成，每个节点最多有两个子节点。

根据节点的分布情况，二叉树可以分为五种形态，分别是满二叉树、完全二叉树、平衡二叉树、搜索二叉树和线索二叉树。

一、满二叉树满二叉树是指除了叶子节点外，每个节点都有两个子节点的二叉树。

也就是说，满二叉树的所有层都是满的，并且最后一层的叶子节点都靠左排列。

满二叉树的节点数可以通过公式计算得到，假设树的高度为h，则节点数为2^h - 1。

满二叉树的特点是结构简单，查找速度快。

在满二叉树中，任意两个节点的路径长度都相同。

二、完全二叉树完全二叉树是指除了最后一层之外，其他层都是满的，并且最后一层的叶子节点都靠左排列的二叉树。

完全二叉树的特点是节点数较少，结构相对简单。

完全二叉树通常用数组来表示，因为它的节点之间的关系可以通过数组的下标来表示。

在完全二叉树中，任意一个节点的左子节点的下标为2i，右子节点的下标为2i+1。

三、平衡二叉树平衡二叉树是指左右子树的高度差不超过1的二叉树。

平衡二叉树的特点是查找、插入和删除的时间复杂度都为O(logn)，其中n是节点的数量。

平衡二叉树的高度可以通过节点的平衡因子来计算，平衡因子定义为左子树的高度减去右子树的高度。

平衡因子的取值范围为-1、0和1，当平衡因子的绝对值大于1时，需要通过旋转操作来调整树的平衡性。

四、搜索二叉树搜索二叉树，也称为二叉搜索树或排序二叉树，是一种特殊的二叉树。

它的特点是对于树中的任意一个节点，其左子树中的所有节点都小于它，右子树中的所有节点都大于它。

搜索二叉树的中序遍历结果是一个递增的有序序列。

搜索二叉树的特点是可以快速地查找某个节点，时间复杂度为O(logn)，其中n是节点的数量。

但是，如果搜索二叉树不平衡，即左子树或右子树过深，则会导致查找的时间复杂度退化为O(n)。

五、线索二叉树线索二叉树是对二叉树进行了优化的数据结构，它通过添加指向前驱和后继节点的线索，使得遍历操作更加高效。

平衡二叉树-构造方法(绝妙)

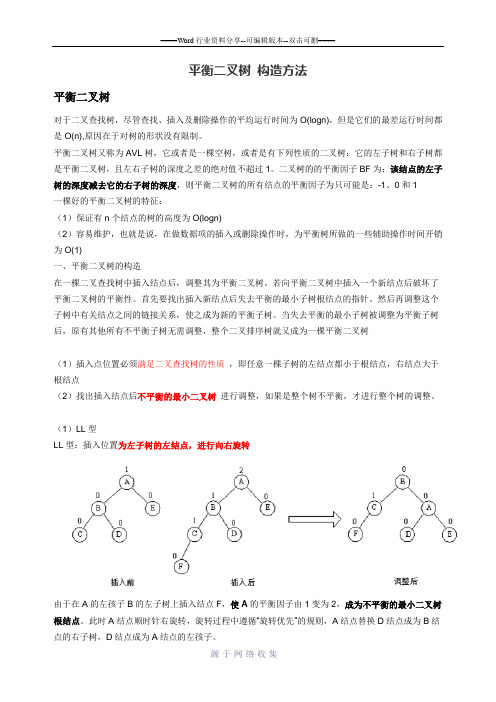
平衡二叉树构造方法平衡二叉树对于二叉查找树，尽管查找、插入及删除操作的平均运行时间为O(logn)，但是它们的最差运行时间都是O(n),原因在于对树的形状没有限制。

平衡二叉树又称为AVL树，它或者是一棵空树，或者是有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左右子树的深度之差的绝对值不超过1。

二叉树的的平衡因子BF为：该结点的左子树的深度减去它的右子树的深度，则平衡二叉树的所有结点的平衡因子为只可能是：-1、0和1一棵好的平衡二叉树的特征：（1）保证有n个结点的树的高度为O(logn)（2）容易维护，也就是说，在做数据项的插入或删除操作时，为平衡树所做的一些辅助操作时间开销为O(1)一、平衡二叉树的构造在一棵二叉查找树中插入结点后，调整其为平衡二叉树。

若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。

首先要找出插入新结点后失去平衡的最小子树根结点的指针。

然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。

当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树（1）插入点位置必须满足二叉查找树的性质，即任意一棵子树的左结点都小于根结点，右结点大于根结点（2）找出插入结点后不平衡的最小二叉树进行调整，如果是整个树不平衡，才进行整个树的调整。

（1）LL型LL型：插入位置为左子树的左结点，进行向右旋转由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1变为2，成为不平衡的最小二叉树根结点。

此时A结点顺时针右旋转，旋转过程中遵循“旋转优先”的规则，A结点替换D结点成为B结点的右子树，D结点成为A结点的左孩子。

（2）RR型RR型：插入位置为右子树的右孩子，进行向左旋转由于在A的右子树C的右子树插入了结点F，A的平衡因子由-1变为-2，成为不平衡的最小二叉树根结点。

此时，A结点逆时针左旋转，遵循“旋转优先”的规则，A结点替换D结点成为C的左子树，D结点成为A的右子树。

平衡二叉树的最大深度计算公式

平衡二叉树的最大深度计算公式
平衡二叉树是一种特殊的二叉树，它的左子树和右子树的高度差不超过1。

这种特殊的性质使得平衡二叉树的查找效率非常高，因为它的高度比普通二叉树低很多。

计算平衡二叉树的最大深度是很重要的一个问题，因为它直接关系到平衡二叉树的性能。

平衡二叉树的最大深度可以使用递归算法来计算。

对于一个平衡二叉树，它的最大深度等于它左子树的最大深度和右子树的最大深度中较大的一个加一。

因此，可以用下面的公式来计算平衡二叉树的最大深度：
maxDepth(root) = max(maxDepth(root.left),
maxDepth(root.right)) + 1
其中，root是平衡二叉树的根节点。

这个公式的意思是，如果一个节点有左子树和右子树，那么它的深度就是它左子树的深度和右子树的深度中较大的一个加一。

如果一个节点没有左子树或右子树，那么它的深度就是1。

使用这个公式可以很方便地计算平衡二叉树的最大深度。

需要注意的是，这个公式的时间复杂度是O(n)，其中n是平衡二叉树的节点数。

因此，在计算平衡二叉树的最大深度时，需要注意平衡二叉树的节点数不能太大，否则时间复杂度会很高。

- 1 -。

平衡二叉树例题

平衡二叉树例题平衡二叉树是一种特殊的二叉树，其中每个节点的左子树和右子树的高度差不超过1。

以下是一个平衡二叉树的例题：给定一棵平衡二叉树的节点值分别为 [3,9,20,15,7] ，构建这棵平衡二叉树并对其进行中序遍历。

首先，我们可以根据给定的节点值构建平衡二叉树。

根据题目要求，我们可以使用递归的方式构建平衡二叉树。

以下是构建平衡二叉树的Python代码：pythonclass TreeNode:def __init__(self, val):self.val = valself.left = Noneself.right = Nonedef buildTree(arr):if not arr:return Nonearr.sort() # 先对数组进行排序root = TreeNode(arr[0]) # 创建根节点i = 0while i < len(arr) - 1: # 找到下一个未被使用的元素的下标if arr[i + 1] > root.val:breaki += 1root.left = buildTree(arr[1:i + 1]) # 递归构建左子树root.right = buildTree(arr[i + 1:]) # 递归构建右子树return rootarr = [3,9,20,15,7]root = buildTree(arr) # 构建平衡二叉树接下来，我们可以使用递归的方式对平衡二叉树进行中序遍历。

以下是中序遍历的Python代码：pythondef inorderTraversal(root):if not root:return []res = []res += inorderTraversal(root.left) # 递归遍历左子树res.append(root.val) # 访问根节点res += inorderTraversal(root.right) # 递归遍历右子树return resinorder = inorderTraversal(root) # 对平衡二叉树进行中序遍历print(inorder) # 输出结果：[9, 3, 15, 20, 7]。

平衡二叉树的最大深度公式

平衡二叉树的最大深度公式
平衡二叉树的最大深度公式是指确定平衡二叉树的最大深度所使用的公式。

一棵平衡二叉树是一棵二叉搜索树，其中每个节点的左右子树深度差不超过1。

因此，平衡二叉树的最大深度公式为
h=log_2(n+1)，其中n表示平衡二叉树中节点的数量，h表示平衡二叉树的最大深度。

换句话说，平衡二叉树的最大深度与节点数量之间的关系是对数关系。

这个公式可以用来估算平衡二叉树的深度，从而帮助我们设计更高效的算法或优化数据结构。

- 1 -。

平衡二叉树最大深度公式

平衡二叉树最大深度公式在计算机科学中，平衡二叉树是一种特殊的二叉树，它的左右子树的高度差不超过1。

平衡二叉树的一个重要性质是，它的搜索、插入、删除操作的时间复杂度都是O(log n)。

因此，平衡二叉树在计算机科学中有着广泛的应用。

平衡二叉树的最大深度是指树中从根节点到最远叶子节点的最长路径上的节点数。

计算平衡二叉树的最大深度是很重要的，因为它可以帮助我们评估平衡二叉树的性能。

如果平衡二叉树的最大深度太大，那么搜索、插入、删除操作的时间复杂度就会变得很高，这会影响平衡二叉树的性能。

在本文中，我们将介绍平衡二叉树的最大深度公式，并通过一个例子来说明如何计算平衡二叉树的最大深度。

平衡二叉树的最大深度公式平衡二叉树的最大深度可以通过以下公式计算：maxDepth(root) = 1 + max(maxDepth(root.left),maxDepth(root.right))其中，root是平衡二叉树的根节点。

maxDepth(root.left)表示左子树的最大深度，maxDepth(root.right)表示右子树的最大深度。

max函数返回两个参数中的最大值。

因此，maxDepth(root)表示根节点到最远叶子节点的最长路径上的节点数。

通过递归的方式，我们可以计算平衡二叉树的最大深度。

具体而言，我们首先计算左子树的最大深度，然后计算右子树的最大深度，最后返回左右子树中的最大值加1。

这样，我们就可以得到平衡二叉树的最大深度。

计算平衡二叉树的最大深度为了说明如何计算平衡二叉树的最大深度，我们考虑以下平衡二叉树：1/2 3/4 5我们可以使用上述公式来计算这棵平衡二叉树的最大深度。

首先，根节点的值为1，因此我们需要计算左右子树的最大深度。

左子树的最大深度为2，因为左子树的根节点为2，左子树的左子树为空，左子树的右子树的最大深度为1（因为右子树只有一个叶子节点5）。

因此，我们可以得到maxDepth(root.left) = 2。

平衡二叉树和二叉排序树（二叉搜索树）区别

平衡⼆叉树和⼆叉排序树（⼆叉搜索树）区别
平衡⼆叉树是⼀种⼆叉搜索树。

其可以保证在log2(n)的时间内找到节点，⽽普通的⼆叉搜索树在最坏情况下性能近似与链
表，所⽤时间为log(n)。

常⽤的平衡⼆叉树有AVL树和红⿊树其算法的难点在于插⼊删除节点后树的旋转
平衡⼆叉树 ----> O(log2(n))
普通⼆叉搜索树 ----> O(n)
在⼆叉搜索树的插⼊和删除运算中，采⽤平衡树的优点是：使树的结构较好，从⽽提⾼查找运算的速度。

缺点是：是插⼊和删除运算变得复杂化，从⽽降低了他们的运算速度。

对⼆叉搜索树删除节点⽽引起的不平衡性进⾏的操作⽐插⼊节点的情况要复杂，在此就不再论述了。

操作系统的设计也有⽤到哦
很多数据库的实现是基于更复杂的平衡⼆叉树
可以⾃⼰实现⼀个集合或者map,统计单词出现的次数
stl的map/set都在⽤
普通⼆叉搜索树最坏情况是只有左边⼀个分⽀，如1-2-3-4-5（5在最上⾯，1在左下⾓），但是平衡⼆叉树可以调整。

为1-2-3-4-5（3在最上⾯，1在左下⾓，5在右下⾓）。

平衡⼆叉树 ----> O(log2(n))
普通⼆叉搜索树 ----> O(n)
所以平衡⼆叉树的搜索性能⽐⼆叉搜索树（⼆叉排序树）好。