平衡二叉树10.3.2

合集下载

二叉树总结（四）平衡二叉树

⼆叉树总结（四）平衡⼆叉树平衡⼆叉树概念AVL树是根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的。

它是最先发明的⾃平衡⼆叉查找树，也被称为⾼度平衡树。

相⽐于"⼆叉查找树"，它的特点是：AVL树中任何节点的两个⼦树的⾼度最⼤差别为1。

AVL树的查找、插⼊和删除在平均和最坏情况下都是O(logn)。

如果在AVL树中插⼊或删除节点后，使得⾼度之差⼤于1。

此时，AVL树的平衡状态就被破坏，它就不再是⼀棵⼆叉树；为了让它重新维持在⼀个平衡状态，就需要对其进⾏旋转处理。

平衡⼆叉树结构：typedef int Type;typedef struct AVLTreeNode{Type key;int height; //当前节点的⾼度struct AVLTreeNode *left; // 左孩⼦struct AVLTreeNode *right; // 右孩⼦}Node, *AVLTree;平衡⼆叉树修复⽅法当插⼊⼀个元素使平衡⼆叉树不平衡时，可能出现以下的四种情况：1. LL：称为"左左"。

插⼊或删除⼀个节点后，根节点的左⼦树的左⼦树还有⾮空⼦节点，导致"根的左⼦树的⾼度"⽐"根的右⼦树的⾼度"⼤2，导致AVL树失去了平衡。

例如，在上⾯LL情况中，由于"根节点(8)的左⼦树(4)的左⼦树(2)还有⾮空⼦节点"，⽽"根节点(8)的右⼦树(12)没有⼦节点"；导致"根节点(8)的左⼦树(4)⾼度"⽐"根节点(8)的右⼦树(12)"⾼2。

1. LR：称为"左右"。

插⼊或删除⼀个节点后，根节点的左⼦树的右⼦树还有⾮空⼦节点，导致"根的左⼦树的⾼度"⽐"根的右⼦树的⾼度"⼤2，导致AVL树失去了平衡。

平衡二叉排序树

A
不平衡二叉排序树的调整——LR型
80 B
20 40 C 60 85 30 50 45 70 A 60 C 40 B 95 10 20 30 45 50 70 85 80 A 90 95
90
10
A->lchild=c->rchild B->rchild=c->lchild c->rchild=A c->lchild=B
插入之后仍应保持平衡分类二叉树的性质不变。
-1
危机结点
14
+1 -1
-1
9
0 0 +1
28
-1
14
+2 +1 -1
9
原平衡度为 0 +1 +1 0 0 +1
28
-1
5
0 0
12
0
18
0
50 30
0
5
0 0
12
0
18
0
50 30
0
3
7
17
60
0
3 2
7
17
60
0
53
平衡树
63
53
63
如何用最简单、最有效的办法保持平衡分类二叉树的性质不变？
不平衡二叉排序树的调整——RR型
最低层失衡结点为A，在结点A的右子树的右子树上插入新结点S后，导致失衡，由A和B的平衡因子可知，BL、BR和AL深度相同，为恢复平衡并保持二叉排序树的特性，可将A改为B的左子，B原来的左子BL改为A的右子，这相当于以B为轴，对A做了一次逆时针旋转。
A AR BL B BR A AL BL B
F F F F F F

平衡二叉树的实现及分析

平衡二叉树的实现及分析平衡二叉树（Balanced Binary Tree），也称为AVL树，是一种二叉树的特殊类型。

它的特点是树的所有节点的左子树和右子树的高度差不超过1，即任意节点的子树高度差的绝对值不超过1、通过保持树的平衡性，可以有效地提高树的查询效率。

```pythonclass Node:def __init__(self, val):self.val = valself.left = Noneself.right = Noneself.height = 1```接下来是平衡二叉树的实现：```pythonclass AVLTree:def __init__(self):self.root = None#获取节点高度def get_height(self, node):if not node:return 0return node.height#获取节点的平衡因子def get_balance_factor(self, node):if not node:return 0return self.get_height(node.left) -self.get_height(node.right)#左旋转def left_rotate(self, node):new_root = node.rightnode.right = new_root.leftnew_root.left = nodenode.height = 1 + max(self.get_height(node.left),self.get_height(node.right))new_root.height = 1 + max(self.get_height(new_root.left), self.get_height(new_root.right))return new_root#右旋转def right_rotate(self, node):new_root = node.leftnode.left = new_root.rightnew_root.right = nodenode.height = 1 + max(self.get_height(node.left),self.get_height(node.right))new_root.height = 1 + max(self.get_height(new_root.left), self.get_height(new_root.right))return new_root#插入节点def insert_node(self, root, val):if not root:return Node(val)elif val < root.val:root.left = self.insert_node(root.left, val)else:root.right = self.insert_node(root.right, val)root.height = 1 + max(self.get_height(root.left),self.get_height(root.right))balance_factor = self.get_balance_factor(root) if balance_factor > 1:if val < root.left.val:return self.right_rotate(root)else:root.left = self.left_rotate(root.left)return self.right_rotate(root)if balance_factor < -1:if val > root.right.val:return self.left_rotate(root)else:root.right = self.right_rotate(root.right) return self.left_rotate(root)return root#中序遍历def inorder_traversal(self, root):if root:self.inorder_traversal(root.left)print(root.val)self.inorder_traversal(root.right)```在上述代码中，`get_height`函数用于获取节点的高度，`get_balance_factor`函数用于计算节点的平衡因子，`left_rotate`函数实现了左旋转操作，`right_rotate`函数实现了右旋转操作。

平衡二叉树详解

平衡⼆叉树详解平衡⼆叉树详解简介平衡⼆叉树（Balanced Binary Tree）具有以下性质：它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1，并且左右两个⼦树都是⼀棵平衡⼆叉树。

平衡⼆叉树的常⽤实现⽅法有红⿊树、AVL、替罪⽺树、Treap、伸展树等。

其中最为经典当属AVL树，我们总计⽽⾔就是：平衡⼆叉树是⼀种⼆叉排序树，其中每⼀个结点的左⼦树和右⼦树的⾼度差⾄多等于1。

性值AVL树具有下列性质的⼆叉树（注意，空树也属于⼀种平衡⼆叉树）：l 它必须是⼀颗⼆叉查找树l 它的左⼦树和右⼦树都是平衡⼆叉树，且左⼦树和右⼦树的深度之差的绝对值不超过1。

l 若将⼆叉树节点的平衡因⼦BF定义为该节点的左⼦树的深度减去它的右⼦树的深度，则平衡⼆叉树上所有节点的平衡因⼦只可能为-1,0,1.l 只要⼆叉树上有⼀个节点的平衡因⼦的绝对值⼤于1，那么这颗平衡⼆叉树就失去了平衡。

实现平衡⼆叉树不平衡的情形：把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个⼉⼦，因此⾼度不平衡时，α结点的两颗⼦树的⾼度相差2.容易看出，这种不平衡可能出现在下⾯4中情况中：1.对α的左⼉⼦的左⼦树进⾏⼀次插⼊2.对α的左⼉⼦的右⼦树进⾏⼀次插⼊3.对α的右⼉⼦的左⼦树进⾏⼀次插⼊4.对α的右⼉⼦的右⼦树进⾏⼀次插⼊（1）LR型（2）LL型（3）RR型（4）RL型完整代码#include<stdio.h>#include<stdlib.h>//结点设计typedef struct Node {int key;struct Node *left;struct Node *right;int height;} BTNode;int height(struct Node *N) {if (N == NULL)return0;return N->height;}int max(int a, int b) {return (a > b) ? a : b;}BTNode* newNode(int key) {struct Node* node = (BTNode*)malloc(sizeof(struct Node));node->key = key;node->left = NULL;node->right = NULL;node->height = 1;return(node);}//ll型调整BTNode* ll_rotate(BTNode* y) {BTNode *x = y->left;y->left = x->right;x->right = y;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;}//rr型调整BTNode* rr_rotate(BTNode* y) {BTNode *x = y->right;y->right = x->left;x->left = y;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;}//判断平衡int getBalance(BTNode* N) {if (N == NULL)return0;return height(N->left) - height(N->right);}//插⼊结点&数据BTNode* insert(BTNode* node, int key) {if (node == NULL)return newNode(key);if (key < node->key)node->left = insert(node->left, key);else if (key > node->key)node->right = insert(node->right, key);elsereturn node;node->height = 1 + max(height(node->left), height(node->right)); int balance = getBalance(node);if (balance > 1 && key < node->left->key) //LL型return ll_rotate(node);if (balance < -1 && key > node->right->key) //RR型return rr_rotate(node);if (balance > 1 && key > node->left->key) { //LR型node->left = rr_rotate(node->left);return ll_rotate(node);}if (balance < -1 && key < node->right->key) { //RL型node->right = ll_rotate(node->right);return rr_rotate(node);return node;}//遍历void preOrder(struct Node *root) { if (root != NULL) {printf("%d ", root->key);preOrder(root->left);preOrder(root->right);}}int main() {BTNode *root = NULL;root = insert(root, 2);root = insert(root, 1);root = insert(root, 0);root = insert(root, 3);root = insert(root, 4);root = insert(root, 4);root = insert(root, 5);root = insert(root, 6);root = insert(root, 9);root = insert(root, 8);root = insert(root, 7);printf("前序遍历：");preOrder(root);return0;}。

名词解释平衡二叉树

平衡二叉树介绍平衡二叉树（Balanced Binary Tree），简称AVL树，是一种特殊的二叉搜索树。

在平衡二叉树中，任意节点的左子树和右子树的高度之差不超过1。

这种平衡性的特点使得平衡二叉树的查找、插入和删除操作的时间复杂度保持在O(log n)级别，极大地提高了数据结构的效率。

定义和性质平衡二叉树是一种特殊的二叉搜索树，满足以下性质： 1. 空树或者任意节点的左右子树高度之差的绝对值不超过1。

2. 左子树和右子树都是平衡二叉树。

对于平衡二叉树，我们还可以得出一些重要的结论： 1. 平衡二叉树的任意节点的左子树和右子树的高度差不超过1。

也就是说，平衡二叉树的高度是一个较小的常数倍数。

2. 平衡二叉树的最小高度是log n，最大高度是2log n。

实现方法为了保持二叉树的平衡，我们需要对插入和删除操作进行适当的调整。

下面介绍两种常见的平衡二叉树实现方法。

AVL树AVL树是最早提出的平衡二叉树之一。

在AVL树中，每个节点都会存储一个额外的信息，即平衡因子（balance factor）。

平衡因子的定义是左子树的高度减去右子树的高度。

如果平衡因子的绝对值大于1，就需要进行平衡调整。

AVL树的平衡调整分为四种情况：左-左旋转(LL)，右-右旋转(RR)，左-右旋转(LR)，和右-左旋转(RL)。

通过这四种旋转操作，可以使得树重新达到平衡状态。

红黑树红黑树是另一种常见的平衡二叉树。

红黑树的平衡调整是通过变换节点的颜色和旋转节点来完成的。

红黑树的规则如下： 1. 每个节点要么是红色，要么是黑色。

2. 根节点是黑色。

3. 所有叶子节点（NIL节点）都是黑色。

4. 如果一个节点是红色的，则它的两个子节点都是黑色的。

5. 任意节点到其每个叶子节点的路径上包含相同数目的黑色节点。

通过对节点进行颜色变换和旋转操作，红黑树可以在插入和删除节点的过程中保持平衡。

平衡二叉树的应用平衡二叉树在计算机科学中有广泛的应用。

算法（平衡二叉树）

算法（平衡⼆叉树）科普⼆叉树⼆叉树⼆叉数是每个节点最多有两个⼦树,或者是空树(n=0),或者是由⼀个根节点及两个互不相交的,分别称为左⼦树和右⼦树的⼆叉树组成满⼆叉树有两个⾮空⼦树(⼆叉树中的每个结点恰好有两个孩⼦结点切所有叶⼦结点都在同⼀层)也就是⼀个结点要么是叶结点，要么是有两个⼦结点的中间结点。

深度为k且含有2^k-1个结点的⼆叉树完全⼆叉树从左到右依次填充从根结点开始，依次从左到右填充树结点。

除最后⼀层外，每⼀层上的所有节点都有两个⼦节点，最后⼀层都是叶⼦节点。

平衡⼆叉树AVL树[3,1,2,5,9,7]⾸先科普下⼆叉排序树⼜称⼆叉查找树,议程⼆叉搜索树⼆叉排序树的规则⽐本⾝⼤放右边,⽐本⾝⼩放左边平衡⼆叉数⾸先是⼀个⼆叉排序树左右两个⼦树的⾼度差不⼤于1下⾯图中是平衡的情况下⾯是不平衡的情况引⼊公式(LL)右旋function toateRight(AvlNode){let node=AvlNode.left;//保存左节点 AvlNode.left=node.right;node.right=AvlNode;}(RR)左旋function roateLeft(AvlNode){let node=AvlNode.right;//保存右⼦节点AvlNode.right=node.left;node.left=AvlNode;return node;}左右旋⼤图判断⼆叉树是不是平衡树⼆叉树任意结点的左右⼦树的深度不超过1深度计算定义⼀个初始化的⼆叉树var nodes = {node: 6,left: {node: 5,left: {node: 4},right: {node: 3}},right: {node: 2,right: {node: 1}}}//计算⾼度const treeDepth = (root) => {if (root == null) {return 0;}let left = treeDepth(root.left)let right = treeDepth(root.right)return 1+(left>right?left:right)}//判断深度const isTree=(root)=>{if (root == null) {return true;}let left=treeDepth(root.left)let right=treeDepth(root.right)let diff=left-right;if (diff > 1 || diff < -1) {return false}return isTree(root.left)&&isTree(root.right) }console.log(isTree(nodes))判断⼆叉数是不是搜索⼆叉树//第⼀种 //中序遍历let last=-Infinity;const isValidBST=(root)=>{if (root == null) {return true;}//先从左节点开始if (isValidBST(root.left)) {if (last < root.node) {last=root.node;return isValidBST(root.right)}}return false}console.log(isValidBST(nodes))//第⼆种const isValidBST = root => {if (root == null) {return true}return dfs(root, -Infinity, Infinity)}const dfs = (root, min, max) => {if (root == null) {return true}if (root.node <= min || root.node >= max) {return false}return dfs(root.left, min, root.node) && dfs(root.right, root.node, max)}console.log(isValidBST(nodes))实现⼀个⼆叉树实现了⼆叉树的添加,删除,查找,排序//⼆叉树结点class TreeNode {constructor(n, left, right){this.n = n;this.left = left;this.right = right;}}//⼆叉树class BinaryTree {constructor(){this.length = 0;this.root = null;this.arr = [];}//添加对外⼊⼝，⾸个参数是数组，要求数组⾥都是数字，如果有不是数字则试图转成数字，如果有任何⼀个⽆法强制转成数字，则本操作⽆效 addNode(){let arr = arguments[0];if(arr.length == 0) return false;return this.judgeData('_addNode', arr)}//删除结点deleteNode(){let arr = arguments[0];if(arr.length == 0) return false;return this.judgeData('_deleteNode', arr)}//传值判断，如果全部正确，则全部加⼊叉树judgeData(func, arr){let flag = false;//任何⼀个⽆法转成数字，都会失败if(arr.every(n => !Number.isNaN(n))){let _this = this;arr.map(n => _this[func](n));flag = true;}return flag;}//添加的真实实现_addNode(n){n = Number(n);let current = this.root;let treeNode = new TreeNode(n, null, null);if(this.root === null){this.root = treeNode;}else {current = this.root;while(current){let parent = current;if(n < current.n){current = current.left;if(current === null){parent.left = treeNode;}}else {current = current.right;if(current === null){parent.right = treeNode;}}}}this.length++;return treeNode;}//删除节点的真实实现_deleteNode(n){n = Number(n);if(this.root === null){return;}//查找该节点，删除节点操作⽐较复杂，为排除找不到被删除的节点的情况，简化代码，先保证该节点是存在的，虽然这样做其实重复了⼀次查询了，但⼆叉树的查找效率很⾼，这是可接受的let deleteNode = this.findNode(n);if(!deleteNode){return;}//如果删除的是根节点if(deleteNode === this.root){if(this.root.left === null && this.root.right === null){this.root = null;}else if(this.root.left === null){this.root = this.root.right;}else if(this.root.right === null){this.root = this.root.left;}else {let [replaceNode, replacePNode, rp] = this.findLeftTreeMax(deleteNode);replacePNode[rp] = null;replaceNode.left = this.root.left;replaceNode.right = this.root.right;this.root = replaceNode;}}else {//被删除的⽗节点，⼦节点在⽗节点的位置p，有left,right两种可能let [deleteParent, p] = this.findParentNode(deleteNode);if(deleteNode.left === null && deleteNode.right === null){deleteParent[p] = null;}else if(deleteNode.left === null){deleteParent[p] = deleteNode.right;}else if(deleteNode.right === null){deleteParent[p] = deleteNode.left;}else {//⽤来替换被删除的节点，⽗节点，节点在⽗节点的位置let [replaceNode, replacePNode, rp] = this.findLeftTreeMax(deleteNode);if(replacePNode === deleteNode){deleteParent[p] = replaceNode;}else {deleteParent[p] = replaceNode;replacePNode.right = null;}replacePNode[rp] = null;replaceNode.left = deleteNode.left;replaceNode.right = deleteNode.right;}}this.length--;}//查找findNode(n){let result = null;let current = this.root;while(current){if(n === current.n){result = current;break;}else if(n < current.n){current = current.left;}else {current = current.right;}}return result;}//查找⽗节点findParentNode(node){let [parent, child, p] = [null, null, null];if(this.root !== node){parent = this.root;if(node.n < parent.n){child = parent.left;p = 'left';}else {child = parent.right;p = 'right';}while(child){if(node.n === child.n){break;}else if(node.n < child.n){parent = child;child = parent.left;p = 'left';}else {parent = child;child = parent.right;p = 'right';}}}return [parent, p];}//查找当前有左⼦树的节点的最⼤值的节点M，如有A个节点被删除，M是最接近A点之⼀（还有⼀个是右⼦树节点的最⼩值） findLeftTreeMax(topNode){let [node, parent, p] = [null, null, null];if(this.root === null || topNode.left === null){return [node, parent, p];}parent = topNode;node = topNode.left;p = 'left';while(node.right){parent = node;node = node.right;p = 'right';}return [node, parent, p];}//查找最⼤值maxValue(){if(this.root !== null){return this._findLimit('right');}}//查找最⼩值minValue(){if(this.root !== null){return this._findLimit('left');}}//实现查找特殊值_findLimit(pro){let n = this.root.n;let current = this.root;while(current[pro]){current = current[pro];n = current.n;}return n;}//中序排序,并⽤数组的形式显⽰sortMiddleToArr(){this._sortMiddleToArr(this.root);return this.arr;}//中序⽅法_sortMiddleToArr(node){if(node !== null){this._sortMiddleToArr(node.left);this.arr.push(node.n);this._sortMiddleToArr(node.right);}}//打印⼆叉树对象printNode(){console.log(JSON.parse(JSON.stringify(this.root)));}}//测试var binaryTree = new BinaryTree();binaryTree.addNode([50, 24, 18, 65, 4, 80, 75, 20, 37, 40, 60]);binaryTree.printNode();//{n: 50, left: {…}, right: {…}}console.log(binaryTree.maxValue());//80console.log(binaryTree.minValue());//4console.log(binaryTree.sortMiddleToArr());// [4, 18, 20, 24, 37, 40, 50, 60, 65, 75, 80] binaryTree.deleteNode([50]);binaryTree.printNode();//{n: 40, left: {…}, right: {…}}排序复习function ArrayList() {this.array = [];}ArrayList.prototype = {constructor: ArrayList,insert: function(item) {this.array.push(item);},toString: function() {return this.array.join();},swap: function(index1, index2) {var aux = this.array[index2];this.array[index2] = this.array[index1];this.array[index1] = aux;},//冒泡排序bubbleSort: function() {var length = this.array.length;for (var i = 0; i < length; i++) {for (var j = 0; j < length - 1 - i; j++) {if (this.array[j] > this.array[j + 1]) {this.swap(j, j + 1);}}}},//选择排序selectionSort: function() {var length = this.array.length;var indexMin;for (var i = 0; i < length - 1; i++) {indexMin = i;for (var j = i; j < length; j++) {if (this.array[indexMin] > this.array[j]) {indexMin = j;}}if (indexMin !== i) {this.swap(indexMin, i);}}},//插⼊排序insertionSort: function() {var length = this.array.length;var j;var temp;for (var i = 1; i < length; i++) {temp = this.array[i];j = i;while (j > 0 && this.array[j - 1] > temp) {this.array[j] = this.array[j - 1];j--;}this.array[j] = temp;}},//归并排序mergeSort: function() {function mergeSortRec(array) {var length = array.length;if (length === 1) {return array;}var mid = Math.floor(length / 2);var left = array.slice(0, mid);var right = array.slice(mid, length);return merge(mergeSortRec(left), mergeSortRec(right)); }function merge(left, right) {var result = [];var il = 0;var ir = 0;while (il < left.length && ir < right.length) {if (left[il] < right[ir]) {result.push(left[il++]);} else {result.push(right[ir++]);}}while (il < left.length) {result.push(left[il++]);}while (ir < right.length) {result.push(right[ir++]);}return result;}this.array = mergeSortRec(this.array);},//快速排序quickSort:function(){function sort(array){if (array.length <= 1) {return array;}var pivotIndex = Math.floor(array.length/2);var pivot = array.splice(pivotIndex,1)[0];var left = [];var right = [];for(var i = 0; i < array.length; i++){if (array[i] < pivot) {left.push(array[i]);}else{right.push(array[i]);}}return sort(left).concat([pivot],sort(right));}this.array = sort(this.array);}};...................................................................................................................############################################################################ ###################################################################################。

平衡二叉树数字万能法

平衡二叉树数字万能法
平衡二叉树：
背景：平衡二叉树首先是二叉排序树。

基于二叉排序树，外国的两个大爷发现树越矮查找效率越高，进而发明了二叉平衡树。

定义：
平衡因子（BF，Balance factor）：BF（T）=hL-hR，其中hL和hR分别为T的左、右子树的高度。

平衡二叉树（Balanced Binary Tree）（AVL树）：空树或者任一结点左、右子树高度差的绝对值不超过1，即|BF（T）<=1|。

最小不平衡子树：距离插入点最近的，且平衡因子的绝对值大于1的结点为根的子树，我们称为最小不平衡子树。

性质：
它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

若将二叉树节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有节点的平衡因子只可能为-1，0，1。

只要二叉树上有一个节点的平衡因子的绝对值大于1，那么这颗平衡二叉树就失去了平衡。

平衡二叉树（AVL树）

平衡⼆叉树（AVL树）平衡⼆叉树(AVL树)平衡⼆叉树简介：平衡树(Balance Tree，BT) 指的是，任意节点的⼦树的⾼度差都⼩于等于1。

常见的符合平衡树的有，B树（多路平衡搜索树）、AVL树（⼆叉平衡搜索树）等。

具有以下特点:它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1, 并且左右两个⼦树都是-棵平衡⼆叉树。

平衡⼆叉树的常⽤实现⽅法有红⿊树、AVL、替罪⽺树、Treap、伸展树等。

可以保证查询效率⾼。

举例看下下⾯AVL树的特点吧：左右两个⼦树的⾼度差的绝对值不超过1第三棵树的左⼦树⾼度是3，右⼦树⾼度是1,3-1=2,所以第三个不是AVL树AVL树左旋AVL树左旋图解要求: 给你⼀个数列，创建出对应的平衡⼆叉树.数列 {4,3,6,5,7,8}AVL树左旋步骤：1. 创建⼀个新的节点，值为当前节点的值2. 把新节点的的左⼦树设置为原节点的左⼦树：4-->指向33. 把新节点的右⼦树设置为当前节点的右⼦树的左⼦树4. 把当前节点的值：4 换成当前右⼦节点的值：65. 把当前节点的右⼦树设为右⼦树的右⼦树6. 把当前节点的左⼦树设为新的节点：6-->指向4AVL树的⾼度计算核⼼：⾸先要把⼀棵树的⾼度以及左⼦树和右⼦树的⾼度计算出来Node类中添加这三个⽅法：1/**2 * 返回以当前节点为根节点的树的⾼度3 *4 * @return返回树的⾼度5*/6public int heightTree() {7// ⽐较左⼦树跟右⼦树的⾼度，返回最⼤的。

+1是因为树本⾝还要站⼀层8return Math.max(left == null ? 0 : left.heightTree(), right == null ? 0 : right.heightTree()) + 1;9 }1011/**12 * 返回左⼦树的⾼度13 *14 * @return左⼦树⾼度15*/16public int leftHeight() {17if (left == null) {18return 0;19 }20return left.heightTree();21 }2223/**24 * 返回右⼦树的⾼度25 *26 * @return右⼦树⾼度27*/28public int rightHeight() {29if (right == null) {30return 0;31 }32return right.heightTree();33 }View CodeAVLTree类：直接⽤上个⼆叉排序树的树代码即可！1class AVLTree {2private Node root;34public Node getRoot() {5return root;6 }78/**9 * 查找要删除的节点10 *11 * @param value12 * @return13*/14public Node delSearch(int value) {15if (root == null) {16return null;17 } else {18return root.delSearch(value);19 }20 }2122/**23 * 查找到要删除节点的⽗节点24 *25 * @param value26 * @return27*/28public Node delSearchParent(int value) {29if (root == null) {30return null;31 } else {32return root.delSearchParent(value);33 }34 }3536/**38 *39 * @param node40 * @return返回删除节点的值41*/42public int delRightTreeMin(Node node) {43// 作⼀个辅助节点44 Node target = node;45// 循环往左⼦树进⾏查找，就会找到最⼩值46while (target.left != null) {47 target = target.left;48 }49// 删除最⼩值50 delNode(target.value);51// 返回最⼩值52return target.value;53 }5455/**56 * 删除节点57 *58 * @param value59*/60public void delNode(int value) {61if (root == null) {62return;63 } else {64// 1、找到要删除的节点65 Node targetNode = delSearch(value);66// 没有找到67if (targetNode == null) {68return;69 }70// 表⽰这颗⼆叉排序树只有⼀个节点(⽗节点)71if (root.left == null && root.right == null) {72 root = null;73return;74 }7576// 2、找到要删除节点的⽗节点77 Node parentNode = delSearchParent(value);78// 表⽰要删除的节点是⼀个叶⼦节点79if (targetNode.left == null && targetNode.right == null) {80// 继续判断这个叶⼦节点是⽗节点的左⼦节点还是右⼦节点81if (parentNode.left != null && parentNode.left.value == value) {82// 将这个叶⼦节点置为空83 parentNode.left = null;84 } else if (parentNode.right != null && parentNode.right.value == value) {85 parentNode.right = null;86 }87 } else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗⼦树的节点 88// 找到最⼩值89int minVal = delRightTreeMin(targetNode.right);90// 重置91 targetNode.value = minVal;92 } else {// 删除只有⼀颗⼦树的节点93if (targetNode.left != null) {// 如果要删除的节点有左⼦节点94if (parentNode != null) {95// 待删除节点是⽗节点的左⼦节点96if (parentNode.left.value == value) {97 parentNode.left = targetNode.left;98 } else {// 待删除节点是⽗节点的右⼦节点99 parentNode.right = targetNode.left;100 }101 } else {102 root = targetNode.left;103 }104 } else {// 如果要删除的节点有右⼦节点105if (parentNode != null) {106// 待删除节点是⽗节点的左⼦节点107if (parentNode.left.value == value) {108 parentNode.left = targetNode.right;109 } else {// 待删除节点是⽗节点的右⼦节点110 parentNode.right = targetNode.right;111 }112 } else {113 root = targetNode.right;114 }115 }116 }117 }118 }119120/**121 * 添加节点的⽅法122 *123 * @param node124*/125public void addNode(Node node) {126// root节点为空，就让root成为根节点127if (root == null) {128 root = node;129 } else {// root节点不为空,就继续向树中添加节点130 root.addNode(node);131 }132 }133134/**135 * 进⾏中序遍历136*/137public void infixOrder() {138if (root != null) {139 root.infixOrder();140 } else {141 System.out.println("⼆叉树为空，⽆法进⾏排序！");142 }143 }144 }View Code测试树的⾼度：public static void main(String[] args) {int[] arr = {4, 3, 6, 5, 7, 8};// 创建AVL树对象AVLTree avlTree = new AVLTree();for (int i = 0; i < arr.length; i++) {// 添加节点avlTree.addNode(new Node(arr[i]));}// 中序遍历System.out.println("======================中序遍历======================");System.out.println("======================没有平衡处理前======================");System.out.println("没有平衡处理前树的⾼度：" + avlTree.getRoot().heightTree());System.out.println("没有平衡处理前树的左⼦树⾼度：" + avlTree.getRoot().leftHeight());System.out.println("没有平衡处理前树的右⼦树⾼度：" + avlTree.getRoot().rightHeight());}附上总体代码实现：1package Demo11_平衡⼆叉树_AVL树;23/**4 * @author zhangzhixi5 * @date 2021/3/12 22:586*/7public class AVLTreeDemo {8public static void main(String[] args) {9int[] arr = {4, 3, 6, 5, 7, 8};1011// 创建AVL树对象12 AVLTree avlTree = new AVLTree();1314for (int i = 0; i < arr.length; i++) {15// 添加节点16 avlTree.addNode(new Node(arr[i]));17 }1819// 中序遍历20 System.out.println("======================中序遍历======================");21 avlTree.infixOrder();22 System.out.println("======================没有平衡处理前======================");23 System.out.println("没有平衡处理前树的⾼度：" + avlTree.getRoot().heightTree());24 System.out.println("没有平衡处理前树的左⼦树⾼度：" + avlTree.getRoot().leftHeight());25 System.out.println("没有平衡处理前树的右⼦树⾼度：" + avlTree.getRoot().rightHeight());26 }27 }2829class AVLTree {30private Node root;3132public Node getRoot() {33return root;34 }3536/**37 * 查找要删除的节点38 *39 * @param value40 * @return41*/42public Node delSearch(int value) {43if (root == null) {44return null;45 } else {46return root.delSearch(value);47 }48 }4950/**51 * 查找到要删除节点的⽗节点52 *53 * @param value54 * @return55*/56public Node delSearchParent(int value) {57if (root == null) {58return null;59 } else {60return root.delSearchParent(value);61 }62 }6364/**65 * 找到最⼩值并删除66 *67 * @param node68 * @return返回删除节点的值69*/70public int delRightTreeMin(Node node) {71// 作⼀个辅助节点72 Node target = node;73// 循环往左⼦树进⾏查找，就会找到最⼩值74while (target.left != null) {75 target = target.left;76 }77// 删除最⼩值78 delNode(target.value);79// 返回最⼩值80return target.value;81 }8283/**84 * 删除节点85 *86 * @param value87*/88public void delNode(int value) {89if (root == null) {90return;91 } else {92// 1、找到要删除的节点93 Node targetNode = delSearch(value);94// 没有找到95if (targetNode == null) {96return;97 }98// 表⽰这颗⼆叉排序树只有⼀个节点(⽗节点)99if (root.left == null && root.right == null) {100 root = null;101return;102 }103104// 2、找到要删除节点的⽗节点105 Node parentNode = delSearchParent(value);106// 表⽰要删除的节点是⼀个叶⼦节点107if (targetNode.left == null && targetNode.right == null) {108// 继续判断这个叶⼦节点是⽗节点的左⼦节点还是右⼦节点109if (parentNode.left != null && parentNode.left.value == value) {110// 将这个叶⼦节点置为空111 parentNode.left = null;112 } else if (parentNode.right != null && parentNode.right.value == value) {113 parentNode.right = null;114 }115 } else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗⼦树的节点116// 找到最⼩值117int minVal = delRightTreeMin(targetNode.right);118// 重置119 targetNode.value = minVal;120 } else {// 删除只有⼀颗⼦树的节点121if (targetNode.left != null) {// 如果要删除的节点有左⼦节点122if (parentNode != null) {123// 待删除节点是⽗节点的左⼦节点124if (parentNode.left.value == value) {125 parentNode.left = targetNode.left;126 } else {// 待删除节点是⽗节点的右⼦节点127 parentNode.right = targetNode.left;128 }129 } else {130 root = targetNode.left;131 }132 } else {// 如果要删除的节点有右⼦节点133if (parentNode != null) {134// 待删除节点是⽗节点的左⼦节点135if (parentNode.left.value == value) {136 parentNode.left = targetNode.right;137 } else {// 待删除节点是⽗节点的右⼦节点138 parentNode.right = targetNode.right;139 }140 } else {141 root = targetNode.right;142 }143 }144 }145 }146 }147148/**149 * 添加节点的⽅法150 *151 * @param node152*/153public void addNode(Node node) {154// root节点为空，就让root成为根节点155if (root == null) {156 root = node;157 } else {// root节点不为空,就继续向树中添加节点158 root.addNode(node);159 }160 }161162/**163 * 进⾏中序遍历164*/165public void infixOrder() {166if (root != null) {167 root.infixOrder();168 } else {169 System.out.println("⼆叉树为空，⽆法进⾏排序！");170 }171 }172 }173174class Node {175int value;176 Node left;177 Node right;178179public Node(int value) {180this.value = value;181 }182183 @Override184public String toString() {185return "Node{" +186 "value=" + value +187 '}';188 }189190/**191 * 返回以当前节点为根节点的树的⾼度192 *193 * @return返回树的⾼度194*/195public int heightTree() {196// ⽐较左⼦树跟右⼦树的⾼度，返回最⼤的。

(转载)查找之平衡二叉树

(2) RR型调整
RR型调整：因为在A结点的右孩子（设为B结点）的右子树上插入结点，使得结点A的平衡因子变为-2而引起不平衡。调整的方法是：单向左旋转调整至平衡，即将A结点的右孩子B向左上旋转代替结点A（成为根结点），将结点A向左下旋转，成为结点B 的左子树的根结点（即成为结点B的左子树），而将B结点的原有的左子树作为结点A的右子树。
所以，含有n个结点的平衡二叉树的平均查找长度为O14 (l)插入 14 0 26
(n)LR 调整
在平衡二叉树上进行查找的过程和在二叉排序树上进行查找的过程完全相同，因此，在平衡二叉树上进行查找关键字的比较次数不会超过平衡二叉树的深度。在最坏的情况下，普通二叉排序树的查找长度为 O(n)。那么，平衡二叉树的情况又是怎样的呢？下面分析平衡二叉树的高度h和结点个数n之间的关系。
LL型调整：因为在A结点的左孩子（设为B结点）的左子树上插入结点，使得结点A的平衡因子变为2而引起不平衡。调整的方法是：单向右旋转调整平衡，即将A结点的左孩子B向右上旋转代替结点A（成为根结点），将结点A向右下旋转，成为结点B的右子树的根结点（即成为结点B的右子树），而将B结点的原有的右子树作为结点A的左子树。
首先，构造一系列的平衡二叉树 T1 ， T2 ， T3，…，其中，Th（h=1，2，3，…）是高度为h且结点数尽可能少的平衡二叉树，如图10.12中所示的 T1，T2，T3和T4。为了构造Th，先分别构造Th-1和 Th-2，使Th以Th-1和Th-2作为其根结点的左、右子树。对于每一个Th，只要从中删去一个结点，就会失去平衡或高度不再是h（显然，这样构造的平衡二叉树在结点个数相同的平衡二叉树中具有最大高度）。 T T T T T

平衡二叉树详解

动态查找树之平衡二叉树（Balanced Binary Tree，AVL树一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的，所以又称为AVL树。

定义：平衡二叉树或为空树,或为如下性质的二叉排序树:（1）左右子树深度之差的绝对值不超过1;（2）左右子树仍然为平衡二叉树.平衡因子BF=左子树深度－右子树深度.平衡二叉树每个结点的平衡因子只能是1，0，-1。

若其绝对值超过1，则该二叉排序树就是不平衡的。

如图所示为平衡树和非平衡树示意图：二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。

首先要找出插入新结点后失去平衡的最小子树根结点的指针。

然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。

当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。

失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。

假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。

（1）LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。

故需进行一次顺时针旋转操作。

即将A的左孩子B向右上旋转代替A 作为根结点，A向右下旋转成为B的右子树的根结点。

而原来B的右子树则变成A的左子树。

（2）RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。

故需进行一次逆时针旋转操作。

即将A的右孩子C向左上旋转代替A 作为根结点，A向左下旋转成为C的左子树的根结点。

而原来C的左子树则变成A的右子树。

（3）LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。

平衡二叉树的定义及基本操作（查找、插入、删除）及代码实现

平衡⼆叉树的定义及基本操作（查找、插⼊、删除）及代码实现⽂章⽬录平衡⼆叉树的定义为了避免树的⾼度增长过快，降低⼆叉排序树的性能，我们规定在插⼊和删除⼆叉树结点时，要保证在任意结点的左、右⼦树⾼度差的绝对值不超过1，将这样的树称为平衡⼆叉树（Balanced Binary Tree），简称平衡树（AVL）。

此外，AVL树⼜称为⾼度平衡的⼆叉查找树。

定义结点左⼦树与右⼦树的⾼度差为该结点的平衡因⼦，则平衡⼆叉树结点的平衡因⼦的值只可能是-1，0或1 。

平衡⼆叉树可定义为：或者是⼀棵空树，或者是具有下列性质的⼆叉树：它的左⼦树和右⼦树都是平衡⼆叉树，且左⼦树和右⼦树的⾼度差的绝对值不超过1。

平衡⼆叉树的结点类型描述：typedef struct AVLNode{int data;//数据域int bf;//平衡因⼦struct AVLNode *lchild,*rchild;//指针域}AVLNode,*AVLTree;平衡⼆叉树的查找平衡⼆叉树上进⾏查找的过程与⼆叉排序树相同，详细完整代码请参照。

因此，在查找过程中，与给定值进⾏⽐较的关键字个数不超过树的深度。

可以证明，含有n个结点的平衡⼆叉树的最⼤深度为O(log n)，因此平衡⼆叉树的平均查找长度为O(log n)。

22平衡⼆叉树的平衡旋转⼆叉排序树保证平衡的基本思想如下：每当在⼆叉排序树中插⼊（或删除）⼀个结点时，⾸先检查其插⼊路径上的结点是否因为此次操作导致了不平衡。

若导致了不平衡，则先找到插⼊路径上离插⼊结点最近的平衡因⼦的绝对值⼤于1的结点A，再对以A为根的⼦树，在保持⼆叉排序树特性的前提下，调整各结点的位置关系，使之重新达到平衡。

⼀般可将失去平衡后进⾏调整的规律归纳为下列四种情况：LL平衡旋转，RR平衡旋转，LR平衡旋转，RL平衡旋转。

LL平衡旋转（右单旋转）由于在结点A的左孩⼦（L）的左⼦树（L）上插⼊了新结点，A的平衡因⼦由1增⾄2，导致了以A为根的⼦树失去平衡。

二叉查找树（BST）、平衡二叉树（AVL树）

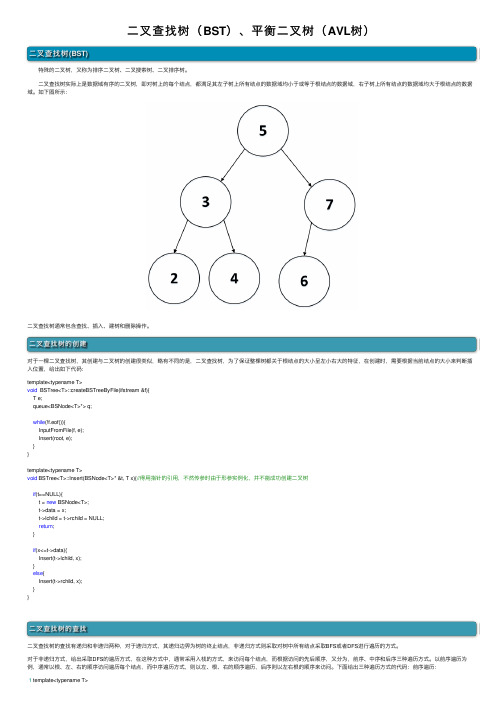
⼆叉查找树（BST）、平衡⼆叉树（AVL树）⼆叉查找树(BST) 特殊的⼆叉树，⼜称为排序⼆叉树、⼆叉搜索树、⼆叉排序树。

⼆叉查找树实际上是数据域有序的⼆叉树，即对树上的每个结点，都满⾜其左⼦树上所有结点的数据域均⼩于或等于根结点的数据域，右⼦树上所有结点的数据域均⼤于根结点的数据域。

如下图所⽰：⼆叉查找树通常包含查找、插⼊、建树和删除操作。

⼆叉查找树的创建对于⼀棵⼆叉查找树，其创建与⼆叉树的创建很类似，略有不同的是，⼆叉查找树，为了保证整棵树都关于根结点的⼤⼩呈左⼩右⼤的特征，在创建时，需要根据当前结点的⼤⼩来判断插⼊位置，给出如下代码：template<typename T>void BSTree<T>::createBSTreeByFile(ifstream &f){T e;queue<BSNode<T>*> q;while(!f.eof()){InputFromFile(f, e);Insert(root, e);}}template<typename T>void BSTree<T>::Insert(BSNode<T>* &t, T x){//得⽤指针的引⽤，不然传参时由于形参实例化，并不能成功创建⼆叉树if(t==NULL){t = new BSNode<T>;t->data = x;t->lchild = t->rchild = NULL;return;}if(x<=t->data){Insert(t->lchild, x);}else{Insert(t->rchild, x);}}⼆叉查找树的查找⼆叉查找树的查找有递归和⾮递归两种，对于递归⽅式，其递归边界为树的终⽌结点，⾮递归⽅式则采取对树中所有结点采取BFS或者DFS进⾏遍历的⽅式。

平衡二叉树10.3.2

p2->bf=0;
p=p2; }
平衡二叉树
#include <stdio.h> #include <malloc.h> typedef int KeyType; typedef char InfoType; typedef struct node { KeyType key; int bf; InfoType data; struct node *lchild,*rchild; } BSTNode;
0 -1
A
c
a
b h c
b
lc=p->rchild; p->rchild=lc->lchild; lc->lchild=p; p=lc;
/*lc指向B*/ /*把B结点的左子树挂接为A的右子树*/ /*A结点成为B的左孩子*/ /*p指向新的根结点*/
(3)LR型调整
p
2 1 b 0 －1 B 0 1 c m h i A
1 38 －1 24 88
0 －1 -2
0
11
28 1
96
0
-1 0
25
0
98
1、平衡二叉树插入结点的调整方法
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性，首先从根结点到该新插入结点的路径之逆向根结点方向找第一个失去平衡的结点，然后以该失衡结点和它相邻的刚查找过的两个结点构成调整子树(最小不平衡子树)，即调整子树是指以离插入结点最近,且平衡因子绝对值大于1的结点为根结点的子树,使之成为新的平衡子树。
0
LL调整后
-2 7
属于”\”型,应该进行RR调整 11 单向左旋平衡 RR调整后
-1
-2

平衡二叉树的生成过程

平衡二叉树的生成过程1. 平衡因子（Balance Factor）：平衡因子是指左子树的高度减去右子树的高度，即平衡因子 = 左子树的高度 - 右子树的高度。

平衡因子的取值范围为-1、0和1，如果平衡因子的绝对值超过1，则称该树为不平衡树。

2.AVL树：AVL树是一种平衡二叉树，它的平衡因子在任何时刻都是在合法范围内的，即平衡因子的绝对值不超过1接下来，我们将详细介绍平衡二叉树的生成过程。

1.插入新节点：首先，我们从根节点开始，将新节点插入到合适的位置。

如果新节点的值小于当前节点的值，则将其插入到当前节点的左子树中；如果新节点的值大于当前节点的值，则将其插入到当前节点的右子树中。

如果当前节点为空，则将新节点作为当前节点，并返回。

2.调整树结构：在插入新节点之后，需要检查树的平衡性。

如果插入新节点导致树的不平衡，则需要进行相应的调整。

（1）LL旋转：当新节点插入到当前节点的左子树的左子树中时，需要进行LL旋转。

LL旋转是指，将当前节点的左子树向右旋转，使当前节点变成其左子树的右子树，其左子树的右子树变成当前节点的左子树。

LL旋转的具体步骤如下：-将当前节点的左子树的右子树变成新节点的左子树；-将当前节点的左子树变成新节点的右子树；-将新节点变成当前节点的左子树。

（2）RR旋转：当新节点插入到当前节点的右子树的右子树中时，需要进行RR旋转。

RR旋转是指，将当前节点的右子树向左旋转，使当前节点变成其右子树的左子树，其右子树的左子树变成当前节点的右子树。

RR旋转的具体步骤如下：-将当前节点的右子树的左子树变成新节点的右子树；-将当前节点的右子树变成新节点的左子树；-将新节点变成当前节点的右子树。

（3）LR旋转：当新节点插入到当前节点的左子树的右子树中时，需要进行LR旋转。

LR旋转是指，先对当前节点的左子树进行RR旋转，然后对当前节点进行LL旋转。

即先右旋再左旋。

LR旋转的具体步骤如下：-对当前节点的左子树进行RR旋转；-对当前节点进行LL旋转。

数据结构平衡二叉树的操作演示

数据结构平衡二叉树的操作演示平衡二叉树（AVL树）是一种自平衡的二叉树，可以在O(log n)的时间内完成插入、删除和操作。

AVL树的平衡性是通过对树节点进行左旋和右旋操作来实现的。

下面将详细介绍AVL树的操作演示。

AVL树的定义和二叉树相似，每个节点包含一个键值和指向左右子树的指针。

任意节点的左子树和右子树的高度最多相差1，这个特性使得AVL树始终保持平衡。

1.插入操作插入操作是AVL树中最复杂的操作之一，因为插入后可能会破坏树的平衡性。

下面通过一个示例来演示AVL树的插入操作。

假设我们要向一棵空树插入节点5，插入过程如下：1.创建一个新节点，值为52.将新节点插入根节点。

3.检查树的平衡性。

根据AVL树的定义，左子树和右子树的高度差最多为1、在这个例子中，树是平衡的。

4.更新每个节点的高度值。

如果我们插入节点6，插入过程如下：1.创建一个新节点，值为62.将新节点插入到节点5的右子树。

3.检查树的平衡性。

在这个例子中，树不再是平衡的，因为节点5的左子树和右子树的高度差为24.执行旋转操作来恢复树的平衡性。

在这个例子中，我们需要对节点5进行左旋操作。

5.更新每个节点的高度值。

2.删除操作删除操作是AVL树中另一个可能破坏树的平衡性的操作。

下面通过一个示例来演示AVL树的删除操作。

假设我们要删除节点5，删除过程如下：1.在树中找到要删除的节点，即节点52.如果要删除的节点是叶子节点或只有一个子节点，直接删除。

在这个例子中，节点5是一个叶子节点，可以直接删除。

3.如果要删除的节点有两个子节点，找到其后继节点（即右子树中的最小节点）或前驱节点（即左子树中的最大节点）来取代它。

在这个例子中，我们找到节点6来取代节点54.如果取代节点是叶子节点或只有一个子节点，直接用它取代要删除的节点。

在这个例子中，我们用节点6取代了节点55.检查树的平衡性。

在这个例子中，树是平衡的。

6.更新每个节点的高度值。

3.左旋操作左旋操作用于恢复树的平衡性。

python平衡二叉树方法-概述说明以及解释

python平衡二叉树方法-概述说明以及解释1.引言1.1 概述在计算机科学中，树是一种常用的数据结构，它由节点和边组成。

平衡二叉树是一种特殊的二叉树，它的左子树和右子树的高度之差不超过1。

这种特性使得平衡二叉树在进行插入、删除和搜索等操作时能够保持较好的性能。

Python作为一种强大且易于入门的编程语言，提供了丰富的库和工具，方便我们处理各种问题。

在编写程序时，我们经常需要使用到树这种数据结构来解决实际的问题。

因此，掌握平衡二叉树的方法对于Python 程序员来说是非常重要的。

本文将全面介绍平衡二叉树的概念、性质以及实现方法。

首先，我们将详细解释平衡二叉树的定义，包括它的基本特征和约束条件。

然后，我们将讨论平衡二叉树的性质，如平衡因子和AVL树的平衡性质。

最后，我们将总结平衡二叉树的方法，并与其他二叉树方法进行对比，以突出平衡二叉树在某些场景下的优势。

通过本文的学习，读者将能够全面了解平衡二叉树的概念和原理，并能够使用Python语言来实现和应用平衡二叉树，从而提高程序的效率和性能。

1.2 文章结构:本文将按照以下结构进行讲述平衡二叉树的方法。

首先，将介绍概述，即对平衡二叉树方法的总体概述。

我们将讨论平衡二叉树的定义和性质，并说明为什么它们在数据结构中起着重要的作用。

其次，将详细介绍平衡二叉树的定义。

我们将解释什么是平衡二叉树，它与普通二叉树的区别是什么，以及平衡二叉树的基本特征和要求。

接下来，我们将探讨平衡二叉树的性质。

我们将介绍这些性质在实际应用中的重要性，以及它们如何帮助我们在处理大量数据时提高效率和性能。

在结论部分，我们将总结平衡二叉树的方法。

我们将强调这些方法的优点，包括高效的插入和删除操作以及平衡性的维护。

最后，我们将对比其他二叉树方法的优势。

我们将讨论与平衡二叉树相比，其他常见的二叉树方法在性能和效率方面的差异。

通过这些比较，我们可以更好地理解为什么平衡二叉树在某些场景下是更好的选择。

平衡二叉树操作演示

数据结构实习报告题目：平衡二叉树的操作演示班级：信息管理与信息系统11-1姓名：崔佳学号：3完成日期：2013.06.25一、需求分析1. 初始，平衡二叉树为空树，操作界面给出两棵平衡二叉树的显示、查找、插入、删除、销毁、合并两棵树，几种选择。

其中查找、插入和删除操作均要提示用户输入关键字。

每次插入或删除一个节点后都会更新平衡二叉树的显示。

2. 平衡二叉树的显示采用凹入表形式。

3.每次操作完毕后都会给出相应的操作结果，并进入下一次操作，知道用户选择退出二、概要设计1.平衡二叉树的抽象数据类型定义：ADT BalancedBinaryTree{数据对象D：D是具有相同特性的数据元素的集合。

各个数据元素均含有类型相同，可唯一标志的数据元素的关键字。

数据关系R：数据元素同属一个集合。

基本操作P：InitAVL(BSTree& T)操作结果：构造一个空的平衡二叉树TDestroyAVL(BSTree& T)初始条件：平衡二叉树T存在操作结果：销毁平衡二叉树TSearchAVL(BSTree T,int key)初始条件：平衡二叉树T存在，key为和关键字相同类型的给定值操作结果：若T中存在关键字和key相等的数据元素，则返回指向该元素的指针，否则为空InsertAVL(BSTree& T,int key,Status& taller)初始条件：平衡二叉树T存在，key和关键字的类型相同操作结果：若T中存在关键字等于key的数据元素则返回，若不存在则插入一个关键字为key的元素DeleteAVL(BSTree& T,int &key,Status& lower)初始条件：平衡二叉树T存在，key和关键字的类型相同操作结果：若T中存在关键字和key相同的数据元素则删除它}ADT BalancedBinaryTree2.本程序包含二个模块1）主程序模块：void main（）{接收命令；While(“命令”！＝“退出”){处理命令；清屏并得新打印提示信息；接收下一条命令；}}2）平衡二叉树基本操作实现平衡二叉树的抽象数据类型的各函数原型。