平衡二叉树高度计算公式

平衡二叉树10.3.2

11
28
96 98
25
(1) LL型调整型调整 p A 1 2
调整方法: 调整方法: 单向右旋平衡,即将的左孩子单向右旋平衡,即将A的左孩子 B 向右上旋转代替成为根结点, 向右上旋转代替A成为根结点成为根结点, 结点向右下旋转成为B的右将A结点向右下旋转成为的右结点向右下旋转成为子树的根结点, 子树的根结点,而B的原右子树的原右子树则作为A结点的左子树结点的左子树. 则作为结点的左子树. h d e B
1 38 -1 24 88
0 -1 -2
0
11
28 1
96
0
-1 0
25
0
98
1,平衡二叉树插入结点的调整方法
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 首先从根结点到该新插入结点的路径之逆向根结点方向找第一个失去平衡的结点, 衡的结点,然后以该失衡结点和它相邻的刚查找过的两个结点构成调整子树(最小不平衡子树即调整子树是指以离插入结点最近,且平衡因子最小不平衡子树), 子树最小不平衡子树 ,即调整子树是指以离插入结点最近且平衡因子绝对值大于1的结点为根结点的子树使之成为新的平衡子树. 的结点为根结点的子树,使之成为新的平衡子树绝对值大于的结点为根结点的子树使之成为新的平衡子树. 38 24 88 -2
(2)RR型调整型调整 p A -1 -2
调整方法: 调整方法: 单向左旋平衡:即将的右孩子的右孩子B向单向左旋平衡:即将A的右孩子向左上旋转代替A成为根结点成为根结点, 左上旋转代替成为根结点,将A结结点向左下旋转成为B的左子树的根点向左下旋转成为的左子树的根结点, 的原左子树则作为A结点结点,而B的原左子树则作为结点的原左子树则作为的右子树. 的右子树. B

二叉树结点计算公式

二叉树结点计算公式二叉树结点的计算公式及解释1. 二叉树的节点个数•公式：N = 2^h - 1，其中 N 表示二叉树的节点个数，h 表示二叉树的高度。

•解释：二叉树的高度 h 可以通过树的层数来确定，根节点所在的层数为 1，依次往下递增。

每个节点都可以有两个子节点，所以二叉树的节点个数 N 可以通过计算 2 的 h 次方再减去 1 来得出。

例如：A/ \B C/ \ / \D E F G根据上面的二叉树来计算节点个数：h = 3，2^3 - 1 = 8 - 1 = 7所以，该二叉树的节点个数为 7。

2. 二叉树的叶子节点个数•公式：L = (N + 1) / 2，其中 L 表示二叉树的叶子节点个数，N 表示二叉树的节点个数。

•解释：在二叉树中，叶子节点是指没有子节点的节点。

根据二叉树的性质，每个节点最多有两个子节点，所以二叉树的叶子节点个数可以通过节点个数加 1 再除以 2 来计算。

例如：A/ \B C/ \ / \D E F G根据上面的二叉树来计算叶子节点个数：N = 7，(7 + 1) / 2 = 8 / 2 = 4所以，该二叉树的叶子节点个数为 4。

3. 二叉树的高度•公式：h = log2(N + 1)，其中 h 表示二叉树的高度，N 表示二叉树的节点个数。

•解释：由于二叉树中每个节点都可以有两个子节点，所以可以通过节点个数 N 加 1 后取对数以 2 为底的对数来计算二叉树的高度。

例如：A/ \B C/ \ / \D E F G根据上面的二叉树来计算高度：N = 7，log2(7 + 1) ≈ log2(8) ≈ 3所以，该二叉树的高度为 3。

以上就是关于二叉树结点的计算公式及解释。

通过这些公式，我们可以更方便地计算二叉树的相关属性，进而优化算法或者进行更深入的研究。

平衡二叉树

#define EH 0 //等高
#define RH -1 //右高
//平衡二叉树的类型
struct AVLNode
{
int data;
int bf; //bf结点的平衡因子,只能够取0，-1，1，为左子树的深度减去右子树的深度
struct AVLNode *lchild,*rchild; //左、右孩子指针
{
AVLNode *rc,*rd;
rc=T->rchild;
switch(rc->bf)
{
case RH:
T->bf=rc->bf=EH;
L_Rotate(T);
break;
case LH:
rd=rc->lchild;
switch(rd->bf)
{
case RH:
T->bf=LH;
rc->bf=EH;
};
2.右旋操作：
void R_Rotate(AVLNode *&p)//LL型算法
{
AVLNode *lc=p->lchild; // lc指向p的左子树根结点
p->lchild=lc->rchild; // lc的右子树挂接为p（之前跟节点）的左子树
lc->rchild=p;
p=lc; // p指向新的根结点
插入和删除：
插入删除是互为镜像的操作。我们可以采用前面对二叉排序树的删除操作来进行。然后，在删除掉结点后，再对平衡树进行平衡化处理。删除之所以删除操作需要的平衡化可能比插入时次数多，就是因为平衡化不会增加子树的高度，但是可能会减少子树的高度，在有有可能使树增高的插入操作中，一次平衡化能抵消掉增高；在有可能使树减低的删除操作中，平衡化可能会带来祖先节点的不平衡。AVL树体现了一种平衡的美感，两种旋转是互为镜像的，插入删除是互为镜像的操作，没理由会有那么大的差别。实际上，平衡化可以统一的这样来操作：

平衡二叉树特点

平衡二叉树特点
平衡二叉树是一种特殊的二叉查找树，具有以下特点：
1. 左右子树的高度差不超过1：平衡二叉树要求树中任意节点的左子树和右子树的高度差不超过1。

这样可以保证树的整体结构比较平衡。

2. 每个节点的左子树和右子树都是平衡二叉树：除了要求整棵树是平衡的，平衡二叉树还要求每个节点的左子树和右子树都是平衡二叉树。

这个特点可以通过递归来实现。

3. 平衡二叉树的高度大致为logN：由于平衡二叉树的高度差不超过1，因此在最坏情况下，一棵有N个节点的平衡二叉树的高度约为logN，这大大优于普通的二叉查找树。

4. 查找、插入和删除的时间复杂度都是O(logN)：由于平衡二叉树的高度较低，对于含有N个节点的平衡二叉树，可以在O(logN)的时间复杂度内进行查找、插入和删除操作。

需要额外注意的是，平衡二叉树并不是绝对平衡的，只是相比于普通的二叉查找树，它更趋于平衡，通过旋转操作来维持平衡。

完全二叉树深度公式

完全二叉树深度公式
完全二叉树深度公式：在完全二叉树中，具有n个结点的完全二叉树深度为(log2n)+1，其中(log2n)+1是向下取整。

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。

对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

完全二叉树是由满二叉树而引出来的。

对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

(1)所有的叶结点都出现在第k层或k-l层（层次最大的两层）
(2)对任一结点，如果其右子树的最大层次为L，则其左子树的最大层次为L或L+l。

1。

二叉树公式

二叉树公式一、引言二叉树是计算机科学中常见的数据结构之一，它由一个根节点和最多两个子节点组成。

在二叉树中，每个节点最多有两个子节点，左子节点和右子节点。

二叉树在算法和程序设计中具有广泛的应用，因为它能够高效地表示和处理各种数据关系。

本文将介绍二叉树的基本概念和公式。

二、二叉树的定义二叉树是一种特殊的树结构，它的每个节点最多有两个子节点。

二叉树可以为空，当二叉树不为空时，它满足以下几个条件：1. 每个节点最多有两个子节点，分别称为左子节点和右子节点。

2. 左子节点和右子节点可以为空。

3. 二叉树中不存在重复的节点。

三、二叉树的性质1. 二叉树的最大深度等于根节点到最远叶子节点的路径长度。

2. 二叉树的最小深度等于根节点到最近叶子节点的路径长度。

3. 二叉树的节点个数等于根节点加上左子树和右子树的节点个数之和。

4. 二叉树的高度等于根节点到叶子节点的最长路径长度。

四、二叉树的遍历二叉树的遍历是指按照某种顺序访问二叉树中的所有节点。

常见的遍历方式有三种：前序遍历、中序遍历和后序遍历。

1. 前序遍历：先访问根节点，然后递归地遍历左子树和右子树。

2. 中序遍历：先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。

3. 后序遍历：先递归地遍历左子树和右子树，最后访问根节点。

五、二叉树的平衡性在二叉树中，平衡性是指左子树和右子树的高度差不超过1。

平衡二叉树是一种特殊的二叉树，它的左子树和右子树的高度差不超过1，并且左子树和右子树也都是平衡二叉树。

平衡二叉树的插入和删除操作时间复杂度都是O(logn)，因此在某些应用场景中，平衡二叉树比普通二叉树更加高效。

六、二叉树的应用1. 二叉搜索树：二叉搜索树是一种特殊的二叉树，它的每个节点的值都大于其左子树的所有节点的值，小于其右子树的所有节点的值。

二叉搜索树可以高效地支持插入、删除和查找操作。

2. 堆：堆是一种特殊的二叉树，它满足堆序性质。

在最小堆中，每个节点的值都小于或等于其子节点的值；在最大堆中，每个节点的值都大于或等于其子节点的值。

13个结点的平衡二叉树的最大高度

提前警告：本篇文章将深入探讨13个结点的平衡二叉树的最大高度这一主题，以让你更全面地了解和掌握相关知识。

目录1.什么是平衡二叉树2.13个结点的平衡二叉树构建3.平衡二叉树的最大高度究竟有多高4.与平衡二叉树相关的应用场景5.总结与展望1. 什么是平衡二叉树让我们来了解一下什么是平衡二叉树。

平衡二叉树是一种特殊的二叉树，它要求对于树中的每一个节点，它的左子树和右子树的高度差不能超过1。

这个定义保证了平衡二叉树的查询效率始终保持在一个较高水平。

2. 13个结点的平衡二叉树构建接下来，我们来看看怎样构建一个包含13个结点的平衡二叉树。

在构建平衡二叉树时，一般会选择中间结点作为根结点，然后将剩下的结点平分成左右两部分，分别作为左子树和右子树。

这样构建出来的平衡二叉树，可以确保树的高度尽可能地小，从而提高了查询效率。

3. 平衡二叉树的最大高度究竟有多高既然我们已经了解了如何构建平衡二叉树，接下来就是了解13个结点的平衡二叉树的最大高度究竟有多高了。

对于包含13个结点的平衡二叉树，它的最大高度应该是4。

这是由平衡二叉树的特性决定的，即每个结点的左右子树高度差不超过1。

通过数学计算可以得出，当结点数为13时，平衡二叉树的最大高度为4。

4. 与平衡二叉树相关的应用场景平衡二叉树作为一种高效的数据结构，被广泛地应用在各个领域。

其中，最常见的应用场景包括数据库索引、缓存淘汰算法、负载均衡等。

特别是在现代大数据处理和分布式系统中，平衡二叉树的应用更是不可或缺。

通过合理地构建平衡二叉树，可以大大提高系统的性能和稳定性。

5. 总结与展望我们在本文中深入探讨了13个结点的平衡二叉树的最大高度这一主题。

从平衡二叉树的定义、构建、最大高度以及应用场景等多个方面展开讨论，希望能够让你对这一主题有更深入的理解。

在未来的学习和工作中，希望你能够灵活运用平衡二叉树，发挥其高效查询的优势，为自己的发展增添动力。

个人观点：平衡二叉树作为一种重要的数据结构，在计算机领域有着广泛的应用前景。

完全二叉树的总结点数公式

完全二叉树的总结点数公式完全二叉树是一种特殊的二叉树结构，它的每个节点都有两个子节点，除了最后一层的叶子节点外，其他层的节点都是满的。

在完全二叉树中，叶子节点只会出现在最后一层或者倒数第二层，并且最后一层的叶子节点都靠左排列。

在这篇文章中，我们将探讨完全二叉树的总结点数公式以及相关的性质。

完全二叉树的总结点数公式是一个重要的数学公式，它可以帮助我们计算完全二叉树中节点的数量。

这个公式的表达式如下：总结点数 = 2的h次方 - 1其中，h代表完全二叉树的高度。

这个公式的推导过程是基于完全二叉树的性质而得出的。

在完全二叉树中，每一层的节点数都是满的，除了最后一层。

因此，在计算总结点数时，我们只需要计算除了最后一层外的节点数量，然后再加上最后一层的节点数即可。

我们来看完全二叉树的第一层。

由于完全二叉树的定义，第一层只有一个节点，即根节点。

因此，第一层的节点数为1。

接下来，我们来看完全二叉树的第二层。

根据完全二叉树的定义，第二层的节点数等于第一层节点数的两倍，即2。

继续往下，我们可以得到第三层的节点数为4，第四层的节点数为8，以此类推。

可以观察到，每一层的节点数都是2的次方。

因此，我们可以用2的h次方来表示每一层的节点数。

接下来，我们需要计算除了最后一层之外的节点数。

在完全二叉树中，除了最后一层的节点数是满的，其他层的节点数都是满的。

如果完全二叉树的高度为h，那么除了最后一层之外的节点数可以用以下公式表示：除最后一层之外的节点数 = 2的(h-1)次方 - 1接下来，我们需要计算最后一层的节点数。

根据完全二叉树的定义，最后一层的节点数是小于或等于前面各层节点数的两倍。

因此，最后一层的节点数可以用以下公式表示：最后一层的节点数 = 2的(h-1)次方或者 2的h次方 - 2的(h-1)次方我们将除了最后一层之外的节点数和最后一层的节点数相加，即可得到完全二叉树的总结点数。

将上述公式代入，我们可以得到完全二叉树的总结点数公式：总结点数 = 2的(h-1)次方 - 1 + 2的h次方 - 2的(h-1)次方简化上述公式，我们可以得到：总结点数 = 2的h次方 - 1这就是完全二叉树的总结点数公式。

平衡二叉树详解

平衡⼆叉树详解平衡⼆叉树详解简介平衡⼆叉树（Balanced Binary Tree）具有以下性质：它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1，并且左右两个⼦树都是⼀棵平衡⼆叉树。

平衡⼆叉树的常⽤实现⽅法有红⿊树、AVL、替罪⽺树、Treap、伸展树等。

其中最为经典当属AVL树，我们总计⽽⾔就是：平衡⼆叉树是⼀种⼆叉排序树，其中每⼀个结点的左⼦树和右⼦树的⾼度差⾄多等于1。

性值AVL树具有下列性质的⼆叉树（注意，空树也属于⼀种平衡⼆叉树）：l 它必须是⼀颗⼆叉查找树l 它的左⼦树和右⼦树都是平衡⼆叉树，且左⼦树和右⼦树的深度之差的绝对值不超过1。

l 若将⼆叉树节点的平衡因⼦BF定义为该节点的左⼦树的深度减去它的右⼦树的深度，则平衡⼆叉树上所有节点的平衡因⼦只可能为-1,0,1.l 只要⼆叉树上有⼀个节点的平衡因⼦的绝对值⼤于1，那么这颗平衡⼆叉树就失去了平衡。

实现平衡⼆叉树不平衡的情形：把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个⼉⼦，因此⾼度不平衡时，α结点的两颗⼦树的⾼度相差2.容易看出，这种不平衡可能出现在下⾯4中情况中：1.对α的左⼉⼦的左⼦树进⾏⼀次插⼊2.对α的左⼉⼦的右⼦树进⾏⼀次插⼊3.对α的右⼉⼦的左⼦树进⾏⼀次插⼊4.对α的右⼉⼦的右⼦树进⾏⼀次插⼊（1）LR型（2）LL型（3）RR型（4）RL型完整代码#include<stdio.h>#include<stdlib.h>//结点设计typedef struct Node {int key;struct Node *left;struct Node *right;int height;} BTNode;int height(struct Node *N) {if (N == NULL)return0;return N->height;}int max(int a, int b) {return (a > b) ? a : b;}BTNode* newNode(int key) {struct Node* node = (BTNode*)malloc(sizeof(struct Node));node->key = key;node->left = NULL;node->right = NULL;node->height = 1;return(node);}//ll型调整BTNode* ll_rotate(BTNode* y) {BTNode *x = y->left;y->left = x->right;x->right = y;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;}//rr型调整BTNode* rr_rotate(BTNode* y) {BTNode *x = y->right;y->right = x->left;x->left = y;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;}//判断平衡int getBalance(BTNode* N) {if (N == NULL)return0;return height(N->left) - height(N->right);}//插⼊结点&数据BTNode* insert(BTNode* node, int key) {if (node == NULL)return newNode(key);if (key < node->key)node->left = insert(node->left, key);else if (key > node->key)node->right = insert(node->right, key);elsereturn node;node->height = 1 + max(height(node->left), height(node->right)); int balance = getBalance(node);if (balance > 1 && key < node->left->key) //LL型return ll_rotate(node);if (balance < -1 && key > node->right->key) //RR型return rr_rotate(node);if (balance > 1 && key > node->left->key) { //LR型node->left = rr_rotate(node->left);return ll_rotate(node);}if (balance < -1 && key < node->right->key) { //RL型node->right = ll_rotate(node->right);return rr_rotate(node);return node;}//遍历void preOrder(struct Node *root) { if (root != NULL) {printf("%d ", root->key);preOrder(root->left);preOrder(root->right);}}int main() {BTNode *root = NULL;root = insert(root, 2);root = insert(root, 1);root = insert(root, 0);root = insert(root, 3);root = insert(root, 4);root = insert(root, 4);root = insert(root, 5);root = insert(root, 6);root = insert(root, 9);root = insert(root, 8);root = insert(root, 7);printf("前序遍历：");preOrder(root);return0;}。

高度平衡的二叉树

高度平衡的二叉搜索树
AVL( Addison-Velski and Landis )树伸展树红黑树

二叉搜索树性能分析

对于有 n 个关键码的集合，其关键码有 n! 种不同排列，可构成不同二叉搜索树有 1 n C 2 n (棵)
n 1
{2, 1, 3} {1, 2, 3} {1, 3, 2} {2, 3, 1} {3, 1, 2} {3, 2, 1}
B
BRAຫໍສະໝຸດ AR中序序列：BL
B
BR
A
AR
注意：改组后
B
A
平衡度为 0
2）RR平衡旋转：若在A的右子树的右子树上插入结点，使A的平衡
因子从-1增加至-2，需要进行一次逆时针旋转。
(以B为旋转轴）
A B A C
左单旋转 (RotateLeft )
+1
A
0
+2
A
+1
C C A
0
0
B h D h
(a)
C E
Double Rotations
Fig. 28-5 (a) Adding 70 to the tree in Fig. 28-2c destroys its balance; to restore the balance, perform both (b) a right rotation and (c) a left rotation.
h
B
E
h D h
(b)
E
h + 1
B
h
D h + h 1
(c)
如果在子树E中插入一个新结点，该子树高度增1导致结点A的平衡因子变成+2，出现不平衡。沿插入路径检查三个结点A、C和E。它们处于一条方向为“\”的直线上，需要做左单旋转。以结点C为旋转轴，让结点A反时针旋转。

算法（平衡二叉树）

算法（平衡⼆叉树）科普⼆叉树⼆叉树⼆叉数是每个节点最多有两个⼦树,或者是空树(n=0),或者是由⼀个根节点及两个互不相交的,分别称为左⼦树和右⼦树的⼆叉树组成满⼆叉树有两个⾮空⼦树(⼆叉树中的每个结点恰好有两个孩⼦结点切所有叶⼦结点都在同⼀层)也就是⼀个结点要么是叶结点，要么是有两个⼦结点的中间结点。

深度为k且含有2^k-1个结点的⼆叉树完全⼆叉树从左到右依次填充从根结点开始，依次从左到右填充树结点。

除最后⼀层外，每⼀层上的所有节点都有两个⼦节点，最后⼀层都是叶⼦节点。

平衡⼆叉树AVL树[3,1,2,5,9,7]⾸先科普下⼆叉排序树⼜称⼆叉查找树,议程⼆叉搜索树⼆叉排序树的规则⽐本⾝⼤放右边,⽐本⾝⼩放左边平衡⼆叉数⾸先是⼀个⼆叉排序树左右两个⼦树的⾼度差不⼤于1下⾯图中是平衡的情况下⾯是不平衡的情况引⼊公式(LL)右旋function toateRight(AvlNode){let node=AvlNode.left;//保存左节点 AvlNode.left=node.right;node.right=AvlNode;}(RR)左旋function roateLeft(AvlNode){let node=AvlNode.right;//保存右⼦节点AvlNode.right=node.left;node.left=AvlNode;return node;}左右旋⼤图判断⼆叉树是不是平衡树⼆叉树任意结点的左右⼦树的深度不超过1深度计算定义⼀个初始化的⼆叉树var nodes = {node: 6,left: {node: 5,left: {node: 4},right: {node: 3}},right: {node: 2,right: {node: 1}}}//计算⾼度const treeDepth = (root) => {if (root == null) {return 0;}let left = treeDepth(root.left)let right = treeDepth(root.right)return 1+(left>right?left:right)}//判断深度const isTree=(root)=>{if (root == null) {return true;}let left=treeDepth(root.left)let right=treeDepth(root.right)let diff=left-right;if (diff > 1 || diff < -1) {return false}return isTree(root.left)&&isTree(root.right) }console.log(isTree(nodes))判断⼆叉数是不是搜索⼆叉树//第⼀种 //中序遍历let last=-Infinity;const isValidBST=(root)=>{if (root == null) {return true;}//先从左节点开始if (isValidBST(root.left)) {if (last < root.node) {last=root.node;return isValidBST(root.right)}}return false}console.log(isValidBST(nodes))//第⼆种const isValidBST = root => {if (root == null) {return true}return dfs(root, -Infinity, Infinity)}const dfs = (root, min, max) => {if (root == null) {return true}if (root.node <= min || root.node >= max) {return false}return dfs(root.left, min, root.node) && dfs(root.right, root.node, max)}console.log(isValidBST(nodes))实现⼀个⼆叉树实现了⼆叉树的添加,删除,查找,排序//⼆叉树结点class TreeNode {constructor(n, left, right){this.n = n;this.left = left;this.right = right;}}//⼆叉树class BinaryTree {constructor(){this.length = 0;this.root = null;this.arr = [];}//添加对外⼊⼝，⾸个参数是数组，要求数组⾥都是数字，如果有不是数字则试图转成数字，如果有任何⼀个⽆法强制转成数字，则本操作⽆效 addNode(){let arr = arguments[0];if(arr.length == 0) return false;return this.judgeData('_addNode', arr)}//删除结点deleteNode(){let arr = arguments[0];if(arr.length == 0) return false;return this.judgeData('_deleteNode', arr)}//传值判断，如果全部正确，则全部加⼊叉树judgeData(func, arr){let flag = false;//任何⼀个⽆法转成数字，都会失败if(arr.every(n => !Number.isNaN(n))){let _this = this;arr.map(n => _this[func](n));flag = true;}return flag;}//添加的真实实现_addNode(n){n = Number(n);let current = this.root;let treeNode = new TreeNode(n, null, null);if(this.root === null){this.root = treeNode;}else {current = this.root;while(current){let parent = current;if(n < current.n){current = current.left;if(current === null){parent.left = treeNode;}}else {current = current.right;if(current === null){parent.right = treeNode;}}}}this.length++;return treeNode;}//删除节点的真实实现_deleteNode(n){n = Number(n);if(this.root === null){return;}//查找该节点，删除节点操作⽐较复杂，为排除找不到被删除的节点的情况，简化代码，先保证该节点是存在的，虽然这样做其实重复了⼀次查询了，但⼆叉树的查找效率很⾼，这是可接受的let deleteNode = this.findNode(n);if(!deleteNode){return;}//如果删除的是根节点if(deleteNode === this.root){if(this.root.left === null && this.root.right === null){this.root = null;}else if(this.root.left === null){this.root = this.root.right;}else if(this.root.right === null){this.root = this.root.left;}else {let [replaceNode, replacePNode, rp] = this.findLeftTreeMax(deleteNode);replacePNode[rp] = null;replaceNode.left = this.root.left;replaceNode.right = this.root.right;this.root = replaceNode;}}else {//被删除的⽗节点，⼦节点在⽗节点的位置p，有left,right两种可能let [deleteParent, p] = this.findParentNode(deleteNode);if(deleteNode.left === null && deleteNode.right === null){deleteParent[p] = null;}else if(deleteNode.left === null){deleteParent[p] = deleteNode.right;}else if(deleteNode.right === null){deleteParent[p] = deleteNode.left;}else {//⽤来替换被删除的节点，⽗节点，节点在⽗节点的位置let [replaceNode, replacePNode, rp] = this.findLeftTreeMax(deleteNode);if(replacePNode === deleteNode){deleteParent[p] = replaceNode;}else {deleteParent[p] = replaceNode;replacePNode.right = null;}replacePNode[rp] = null;replaceNode.left = deleteNode.left;replaceNode.right = deleteNode.right;}}this.length--;}//查找findNode(n){let result = null;let current = this.root;while(current){if(n === current.n){result = current;break;}else if(n < current.n){current = current.left;}else {current = current.right;}}return result;}//查找⽗节点findParentNode(node){let [parent, child, p] = [null, null, null];if(this.root !== node){parent = this.root;if(node.n < parent.n){child = parent.left;p = 'left';}else {child = parent.right;p = 'right';}while(child){if(node.n === child.n){break;}else if(node.n < child.n){parent = child;child = parent.left;p = 'left';}else {parent = child;child = parent.right;p = 'right';}}}return [parent, p];}//查找当前有左⼦树的节点的最⼤值的节点M，如有A个节点被删除，M是最接近A点之⼀（还有⼀个是右⼦树节点的最⼩值） findLeftTreeMax(topNode){let [node, parent, p] = [null, null, null];if(this.root === null || topNode.left === null){return [node, parent, p];}parent = topNode;node = topNode.left;p = 'left';while(node.right){parent = node;node = node.right;p = 'right';}return [node, parent, p];}//查找最⼤值maxValue(){if(this.root !== null){return this._findLimit('right');}}//查找最⼩值minValue(){if(this.root !== null){return this._findLimit('left');}}//实现查找特殊值_findLimit(pro){let n = this.root.n;let current = this.root;while(current[pro]){current = current[pro];n = current.n;}return n;}//中序排序,并⽤数组的形式显⽰sortMiddleToArr(){this._sortMiddleToArr(this.root);return this.arr;}//中序⽅法_sortMiddleToArr(node){if(node !== null){this._sortMiddleToArr(node.left);this.arr.push(node.n);this._sortMiddleToArr(node.right);}}//打印⼆叉树对象printNode(){console.log(JSON.parse(JSON.stringify(this.root)));}}//测试var binaryTree = new BinaryTree();binaryTree.addNode([50, 24, 18, 65, 4, 80, 75, 20, 37, 40, 60]);binaryTree.printNode();//{n: 50, left: {…}, right: {…}}console.log(binaryTree.maxValue());//80console.log(binaryTree.minValue());//4console.log(binaryTree.sortMiddleToArr());// [4, 18, 20, 24, 37, 40, 50, 60, 65, 75, 80] binaryTree.deleteNode([50]);binaryTree.printNode();//{n: 40, left: {…}, right: {…}}排序复习function ArrayList() {this.array = [];}ArrayList.prototype = {constructor: ArrayList,insert: function(item) {this.array.push(item);},toString: function() {return this.array.join();},swap: function(index1, index2) {var aux = this.array[index2];this.array[index2] = this.array[index1];this.array[index1] = aux;},//冒泡排序bubbleSort: function() {var length = this.array.length;for (var i = 0; i < length; i++) {for (var j = 0; j < length - 1 - i; j++) {if (this.array[j] > this.array[j + 1]) {this.swap(j, j + 1);}}}},//选择排序selectionSort: function() {var length = this.array.length;var indexMin;for (var i = 0; i < length - 1; i++) {indexMin = i;for (var j = i; j < length; j++) {if (this.array[indexMin] > this.array[j]) {indexMin = j;}}if (indexMin !== i) {this.swap(indexMin, i);}}},//插⼊排序insertionSort: function() {var length = this.array.length;var j;var temp;for (var i = 1; i < length; i++) {temp = this.array[i];j = i;while (j > 0 && this.array[j - 1] > temp) {this.array[j] = this.array[j - 1];j--;}this.array[j] = temp;}},//归并排序mergeSort: function() {function mergeSortRec(array) {var length = array.length;if (length === 1) {return array;}var mid = Math.floor(length / 2);var left = array.slice(0, mid);var right = array.slice(mid, length);return merge(mergeSortRec(left), mergeSortRec(right)); }function merge(left, right) {var result = [];var il = 0;var ir = 0;while (il < left.length && ir < right.length) {if (left[il] < right[ir]) {result.push(left[il++]);} else {result.push(right[ir++]);}}while (il < left.length) {result.push(left[il++]);}while (ir < right.length) {result.push(right[ir++]);}return result;}this.array = mergeSortRec(this.array);},//快速排序quickSort:function(){function sort(array){if (array.length <= 1) {return array;}var pivotIndex = Math.floor(array.length/2);var pivot = array.splice(pivotIndex,1)[0];var left = [];var right = [];for(var i = 0; i < array.length; i++){if (array[i] < pivot) {left.push(array[i]);}else{right.push(array[i]);}}return sort(left).concat([pivot],sort(right));}this.array = sort(this.array);}};...................................................................................................................############################################################################ ###################################################################################。

平衡二叉树-构造方法(绝妙)

平衡二叉树构造方法平衡二叉树对于二叉查找树，尽管查找、插入及删除操作的平均运行时间为O(logn)，但是它们的最差运行时间都是O(n),原因在于对树的形状没有限制。

平衡二叉树又称为AVL树，它或者是一棵空树，或者是有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左右子树的深度之差的绝对值不超过1。

二叉树的的平衡因子BF为：该结点的左子树的深度减去它的右子树的深度，则平衡二叉树的所有结点的平衡因子为只可能是：-1、0和1一棵好的平衡二叉树的特征：（1）保证有n个结点的树的高度为O(logn)（2）容易维护，也就是说，在做数据项的插入或删除操作时，为平衡树所做的一些辅助操作时间开销为O(1)一、平衡二叉树的构造在一棵二叉查找树中插入结点后，调整其为平衡二叉树。

若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。

首先要找出插入新结点后失去平衡的最小子树根结点的指针。

然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。

当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树（1）插入点位置必须满足二叉查找树的性质，即任意一棵子树的左结点都小于根结点，右结点大于根结点（2）找出插入结点后不平衡的最小二叉树进行调整，如果是整个树不平衡，才进行整个树的调整。

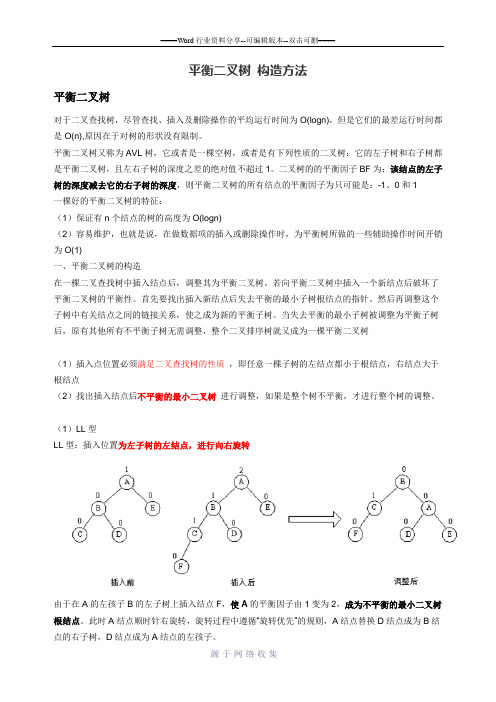
（1）LL型LL型：插入位置为左子树的左结点，进行向右旋转由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1变为2，成为不平衡的最小二叉树根结点。

此时A结点顺时针右旋转，旋转过程中遵循“旋转优先”的规则，A结点替换D结点成为B结点的右子树，D结点成为A结点的左孩子。

（2）RR型RR型：插入位置为右子树的右孩子，进行向左旋转由于在A的右子树C的右子树插入了结点F，A的平衡因子由-1变为-2，成为不平衡的最小二叉树根结点。

此时，A结点逆时针左旋转，遵循“旋转优先”的规则，A结点替换D结点成为C的左子树，D结点成为A的右子树。

计算机二级二叉树知识点

计算机二级二叉树知识点1.二叉树的定义：二叉树是一种常见的树形结构，其中每个节点最多有两个子节点，分别称为左子节点和右子节点。

二叉树的节点结构通常包括一个数据元素和指向左右子节点的指针。

2.二叉树的性质：(1)二叉树的第i层最多有2^(i-1)个节点。

(2)高度为h的二叉树最多有2^h-1个节点。

(3)对于任意一棵二叉树，如果其叶子节点数为n0，度为2的节点数为n2，则n0=n2+1(4)一棵深度为k且节点总数为n的二叉树，当且仅当其满足2^(k-1)<=n<=2^k-1时，才称为完全二叉树。

3.二叉树的分类：(1)满二叉树：除了叶子节点之外，每个节点都有两个子节点，且所有叶子节点在同一层次上。

(2)完全二叉树：最后一层之前的层都是满的，并且最后一层的节点都靠左排列。

(3)平衡二叉树：左右子树的高度差不超过1的二叉树。

(4)线索二叉树：对于每个节点，除了指向其左右子节点的指针外，还包含指向其在其中一种序列下的前驱节点和后继节点的指针。

4.二叉树的遍历方法：(1)前序遍历：先访问根节点，然后递归地遍历左子树，最后递归地遍历右子树。

(2)中序遍历：先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。

(3)后序遍历：先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。

(4)层次遍历：按照从上到下、从左到右的顺序逐层访问每个节点。

5.二叉树：二叉树（Binary Search Tree，BST）是一种特殊的二叉树，它的每个节点的值都大于其左子树中的所有节点值，小于其右子树中的所有节点值。

因此，对于一个二叉树，可以采用中序遍历的方法得到一个有序序列。

二叉树的插入操作：按照二叉树的定义，从根节点开始，将要插入的值与当前节点的值比较，如果小于当前节点的值，则向左子树递归插入，如果大于当前节点的值，则向右子树递归插入，直至找到一个空节点，然后插入新节点。

二叉树的删除操作：删除一个节点需要考虑三种情况：删除节点没有子节点、只有一个子节点、有两个子节点。

平衡二叉树平衡因子

平衡二叉树平衡因子平衡二叉树平衡因子指的是左子树高度和右子树高度之差，它是保持平衡二叉树平衡的重要因素。

在平衡二叉树中，每个节点的平衡因子为-1、0或1。

平衡二叉树（AVL树）是一种高效的数据结构，它的时间复杂度为O(logn)，可以在非常快的时间内完成数据的查找、插入和删除操作。

但是，如果平衡二叉树的平衡因子不合适，就会导致树的高度增加，使得查找、插入和删除操作的效率变低。

因此，平衡二叉树的平衡因子非常重要。

下面，我们来分步骤阐述平衡二叉树的平衡因子：第一步：计算节点的高度平衡二叉树的高度是指从根节点到叶子节点的最长路径的长度。

因此，计算节点的高度需要从底部开始向上递归计算。

节点的高度等于其子节点中高度最大的节点的高度加一，如果节点没有子节点，那么它的高度为零。

第二步：计算节点的平衡因子计算节点的平衡因子需要知道其左子树和右子树的高度。

节点的平衡因子等于左子树的高度减去右子树的高度。

如果平衡因子为-1、0或1，则节点是平衡的，否则节点需要被调整。

第三步：调整平衡如果平衡因子不为-1、0或1，那么需要对节点进行调整，使其重新保持平衡。

调整平衡的方法有四种：左旋、右旋、左右旋、右左旋。

左旋和右旋是最基本的调整方法，左右旋和右左旋是组合方法。

左旋：如果节点的平衡因子为2，那么需要进行左旋操作。

左旋是指将节点向左旋转，使其右子树的高度减一，左子树的高度加一。

右旋：如果节点的平衡因子为-2，那么需要进行右旋操作。

右旋是指将节点向右旋转，使其左子树的高度减一，右子树的高度加一。

左右旋：如果节点的平衡因子为2且其右子树的平衡因子为-1，那么需要进行左右旋操作。

左右旋是指将节点先进行右旋，再进行左旋。

右左旋：如果节点的平衡因子为-2且其左子树的平衡因子为1，那么需要进行右左旋操作。

右左旋是指将节点先进行左旋，再进行右旋。

总结：平衡二叉树的平衡因子是保持树平衡的重要因素。

计算节点高度和平衡因子，及时进行平衡调整，是平衡二叉树实现高效的关键。

数据结构树与二叉树常用计算公式

数据结构树与⼆叉树常⽤计算公式在⼆叉树的理论推导以及⼀些⾼频类型题中，我们经常需要计算⼆叉树的总结点数，某⼀层的结点数以及已知结点数反推树的⾼度，本⽂围绕这⼏个⾼频知识点，归纳总结以下公式。

公式（1）⾮空⼆叉树叶⼦结点数 = 度为2的结点数 + 1 即，N0=N2+1（2）⾮空⼆叉树上第K层⾄多有2k−1个结点（K≥1）（3）⾼度为H的⼆叉树⾄多有2H−1 个结点（H≥1）（4）具有N个（N>0）结点的完全⼆叉树的⾼度为⌈log2(N+1)⌉或⌊log2N⌋+1（5）对完全⼆叉树按从上到下、从左到右的顺序依次编号1,2，...，N，则有以下关系：①当i>1 时，结点i的双亲结点编号为⌊i/2⌋，即当i为偶数时，其双亲结点的编号为i/2 ，它是双亲结点的左孩⼦；当i为奇数时，其双亲结点的编号为 (i−1)/2 ，它是双亲结点的右孩⼦。

②当 2i≤N时，结点i的左孩⼦编号为 2i，否则⽆左孩⼦。

③当 2i+1≤N时，结点i的右孩⼦编号为 2i+1 ，否则⽆右孩⼦。

④结点i所在层次（深度）为⌊log2i⌋+1 。

（设根结点为第1层）经典例题**408考研-2011-4** 若⼀棵完全⼆叉树有768个结点，则⼆叉树中叶结点的个数是_____。

A.257B.258C.384D.385解法1根据完全⼆叉树的性质，最后⼀个分⽀结点的序号为⌊n/2⌋=⌊768/2⌋=384 ，故叶⼦结点的个数为 768−384=384解法2由⼆叉树的性质N=N0+N1+N2和N0=N2+1 可知N=2N0−1+N1，2N0−1+N1=768显然，N1=1，2N0=768，则N0=384解法3完全⼆叉树的叶⼦结点只可能出现在最下两层，由题可计算完全⼆叉树的⾼度为10。

第10层的叶⼦结点数为 768−(29−1)=257第10层的叶⼦结点在第9层共有⌈257/2⌉=129 个⽗节点第9层的叶⼦结点数为 (29−1)−129=127则叶⼦结点总数为 257+127=384Processing math: 100%。

课题_一步一步写平衡二叉树(AVL树)

一步一步写平衡二叉树（AVL树）平衡二叉树（Balanced Binary Tree）是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。

1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。

平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。

这个方案很好的解决了二叉查找树退化成链表的问题，把插入、查找、删除的时间复杂度最好情况和最坏情况都维持在O(logN)。

但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

平衡二叉树实现的大部分过程和二叉查找树是一样的（学平衡二叉树之前一定要会二叉查找树），区别就在于插入和删除之后要写一个旋转算法去维持平衡，维持平衡需要借助一个节点高度的属性。

我参考了机械工业出版社的《数据结构与算法分析- C语言描述》写了一个C++版的代码。

这本书的AVLTree讲的很好，不过没有很完整的去描述。

我会一步一步的讲解如何写平衡二叉树，重点是平衡二叉树的核心部分，也就是旋转算法。

第一步：节点信息相对于二叉查找树的节点来说，我们需要用一个属性表示二叉树的高度，目的是维护插入和删除过程中的旋转算法。

代码如下：//AVL树节点信息template<class T>class TreeNode{public:TreeNode():lson(NULL),rson(NULL),freq(1),hgt(0){}T data;//值int hgt;//以此节点为根的树的高度unsigned int freq;//频率TreeNode* lson;//指向左儿子的地址TreeNode* rson;//指向右儿子的地址};第二步：平衡二叉树（AVL）类的声明声明中的旋转函数将在后边的步骤中详解。

某二叉树的先序序列和后序序列正好相反

某二叉树的先序序列和后序序列正好相反答案是高度等于其节点数的二叉树；
分析如下：
先序遍历顺序是：M-L-R，后序遍历顺序是：L-R-M，可以看到，只有
中间的结点（M）顺序变化了，左右结点相对位置是不变的；
那可以推断出，要满足题意的话“二叉树的先序序列与后序序列正好
相反”，说明整个二叉树左子树或者右子树有一个没有（遍历就成了，先：M-L；后：L-M或者
先：M-R；后：R-M）也就是必然是一条链。

因此该二叉树的高度一定
等于其节点数。

扩展资料：
二叉树的其他类型介绍：
1、完全二叉树：
若设二叉树的高度为h，除第h层外，其它各层(1～h-1)的结点数都
达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树；
2、满二叉树：
除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二
叉树；
3、平衡二叉树：
平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

树和二叉树的计算公式

树和二叉树的计算公式
树和二叉树是计算机科学中常见的数据结构，它们可以用于存储、搜索、排序等操作。

在进行算法分析时，我们需要知道树和二叉树的一些基本计算公式，例如节点数、深度、叶节点数等。

对于一棵普通的树，我们可以用以下公式计算节点数和深度：
节点数 = 1 + 所有子树的节点数之和
深度 = 1 + 所有子树的深度的最大值
对于一棵二叉树，我们可以用以下公式计算节点数、深度和叶节点数：
节点数 = 2^(深度+1) - 1
深度 = log2(节点数+1) - 1
叶节点数 = (节点数+1)/2
其中，log2表示以2为底的对数。

这些公式可以帮助我们在算
法分析中更准确地估计时间和空间复杂度，从而更好地设计和优化算法。

- 1 -。

平衡二叉树的算法

(2) 链地址法

设有MAXSIZE＝5，H(K)＝K mod 5，关键字值序例 5，21，17，9，15，36，41，24，按外链地址法所建立的哈希表如图10.12所示：
外链地址的存储结构

IZE = 100; // 哈希表的最大长度,数组的容量 typedef int KeyType; // 关键字的类型 struct ElemNode //每个记录结点的结构 { KeyType key ; //其他属性……; ElemNode *next; }; class SqHash { private: ElemType *ht; // ht将作为动态分配的数组 //其它代码……; };
GOSUB
IF

………
哈稀（散列）查找的关键问题
一、选择什么样的
哈稀函数？
二、用什么方法
解决地址冲突？
8.4.2

构造哈希函数的常用方法
构造哈希函数的方法很多，杂凑。这里只介绍一些常用的计算简便的方法。

(1) 平方取中法 (2) 除留余数法 (3) 数字分析法
(1) 平方取中法

(2) 链地址法解决冲突的主要方法与存储结构相关。

哈稀（散列）查找的关键问题
一、选择什么样的

哈稀函数？
除留余数等
二、用什么方法

解决地址冲突？
相关与存储结构
(1) 开放地址法

typedef int KeyType; // 关键字的类型 const int MAXSIZE=100; // 数组的容量 struct ElemType { KeyType key ; //其他属性 ……; }; class SqHash { private: ElemType *ht; //ht将作为动态分配的一维数组 //其他代码……; };