次谐波相位匹配及其实现方法
shg的相位匹配条件

shg的相位匹配条件1.引言1.1 概述相位匹配是在光学中非常重要的概念。
在激光技术、光通信、光谱分析等领域中,相位匹配条件的实现对于光的传播和调控具有关键性的影响。
相位匹配条件是指在非线性光学效应中,通过调整光的波矢或折射率,使得不同频率的光在介质中传播时,相位速度保持一致的条件。
在这种匹配条件下,不同频率的光能够进行相互作用,从而实现一系列重要的光学过程。
对于二阶非线性光学过程,如二次谐波产生(SHG),相位匹配条件是其有效实现的关键。
在SHG过程中,通过将两个频率相互关联的入射光束输入到非线性晶体中,可以实现光频率的加倍。
然而,由于不同频率的光在晶体中的传播速度不同,如果不满足相位匹配条件,那么SHG的效率将会大大降低。
在实际应用中,为了满足相位匹配条件,可以通过选择合适的晶体材料、调整入射光束的入射角度或改变晶体的温度等方法来实现。
这些调控手段可以有效地使得不同频率的光在晶体中传播时,其相位速度保持一致,从而最大限度地提高二次谐波产生的效率。
相位匹配条件的实现对于光学器件的性能和效率有着重要的影响。
因此,在光学领域中,对相位匹配条件的研究是一个非常热门和重要的课题。
通过深入理解相位匹配条件的原理和调控方法,可以为光学器件的设计和应用提供有力的理论指导和技术支持。
本文将重点探讨SHG的相位匹配条件及其在光学领域中的应用。
接下来的章节将分别介绍相位匹配条件的基本原理、相位匹配条件的调控方法,以及未来相位匹配技术的发展趋势。
通过对这些内容的深入研究,我们可以更加全面地认识和理解相位匹配条件在光学中的重要作用,为光学器件的设计和优化提供有益的启示。
1.2文章结构文章结构部分的内容可以这样编写:1.2 文章结构本文分为引言、正文和结论三个部分。
在引言部分,将概述相关背景信息,介绍shg的相位匹配条件的重要性,并明确文章的目的。
接下来,在正文部分,将分别讨论第一个要点和第二个要点。
在第一个要点中,将详细介绍shg的相位匹配条件的基本原理、公式和模型,并给出实际应用中的示例。
相位匹配及实现方法
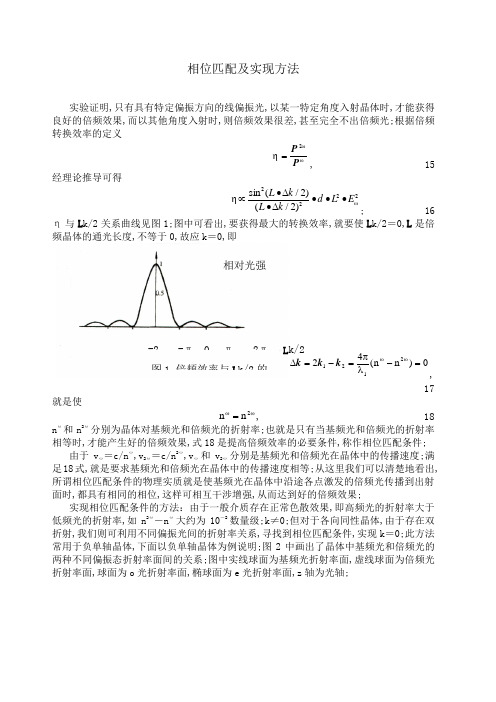
相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光;根据倍频转换效率的定义ωω2ηP P =, 15经理论推导可得2ω222)2/()2/(sin ηE L d k L k L •••∆•∆•∝; 16 η与L k/2关系曲线见图1;图中可看出,要获得最大的转换效率,就要使L k/2=0,L 是倍频晶体的通光长度,不等于0,故应k =0,即0)n n (422121=-λπ=-=∆ωωk k k ,17就是使ωω=2n n , 18n ω和n 2ω分别为晶体对基频光和倍频光的折射率;也就是只有当基频光和倍频光的折射率相等时,才能产生好的倍频效果,式18是提高倍频效率的必要条件,称作相位匹配条件;由于v ω=c/n ω,v 2ω=c/n 2ω,v ω和v 2ω分别是基频光和倍频光在晶体中的传播速度;满足18式,就是要求基频光和倍频光在晶体中的传播速度相等;从这里我们可以清楚地看出,所谓相位匹配条件的物理实质就是使基频光在晶体中沿途各点激发的倍频光传播到出射面时,都具有相同的相位,这样可相互干涉增强,从而达到好的倍频效果;实现相位匹配条件的方法:由于一般介质存在正常色散效果,即高频光的折射率大于低频光的折射率,如n 2ω―n ω大约为10-2数量级;k ≠0;但对于各向同性晶体,由于存在双折射,我们则可利用不同偏振光间的折射率关系,寻找到相位匹配条件,实现k =0;此方法常用于负单轴晶体,下面以负单轴晶体为例说明;图2中画出了晶体中基频光和倍频光的两种不同偏振态折射率面间的关系;图中实线球面为基频光折射率面,虚线球面为倍频光折射率面,球面为o 光折射率面,椭球面为e 光折射率面,z 轴为光轴;图1 倍频效率与L k/2的相对光强-22π π -π L k/2折射率面的定义:从球心引出的每一条矢径到达面上某点的长度,表示晶体以此矢径为波法线方向的光波的折射率大小;实现相位匹配条件的方法之一是寻找实面和虚面交点位置,从而得到通过此交点的矢径与光轴的夹角;图中看到,基频光中o 光的折射率可以和倍频光中e 光的折射率相等,所以当光波沿着与光轴成θm 角方向传播时,即可实现相位匹配,θm 叫做相位匹配角,θm 可从下式中计算得出22o 22e 22o 2o m 2)n ()n ()n ()n (sin -ω-ω-ω-ω--=θ,19式中ωωω2e 2o o n ,n ,n 都可以查表得到,表1列出几种常用的数值;法线的夹角;为了减少反射损失和便于调节,实验中一般总希望让基频光正入射晶体表面;所以加工倍频晶体时,须按一定方向切割晶体,以使晶体法线方向和光轴方向成θm ,见图3;以上所述,是入射光以一定角度入射晶体,通过晶体的双折射,由折射率的变化来补偿正常色散而实现相位匹配的,这称为角度相位匹配;角度相位匹配又可分为两类;第一类是入射同一种线偏振光,负单轴晶体将两个e 光光子转变为一个倍频的o 光光子;第二类是入射光中同时含有o 光和e 光两种线偏振光,负单轴晶体将两个不同的光子变为倍频的e 光光子,正单轴晶体变为一个倍频的o 光光子;见表2图 2 负单轴晶体折射图3 非线性晶体的切晶体图5 基频光与倍频光的脉宽及相对线I ω I 2ω t 1t 2t 1t t 1′′ t 2′ t 2t ν1 ν1′ ν2′ ν2 νν 偏振性质 相位匹配条件 偏振性质相位匹配条件正单轴 负单轴本实验用的是负单轴铌酸锂晶体第一类相位匹配;相位匹配的方法除了前述的角度匹配外,还有温度匹配,这里不作细述;在影响倍频效率的诸因素中,除前述的比较重要的三方面外,还需考虑到晶体的有效长度L s 和模式状况;图4为晶体中基频光和倍频光振幅随距离的变化;如果晶体过长,例L>L s 时,会造成倍频效率饱和;晶体过短;例L<L s ,则转换效率比较低;L s 的大小基本给出了倍频技术中应该使用的晶体长度;模式的不同也影响转换效率,如高阶横模,方向性差,偏离光传播方向的光会偏离相位匹配角;所以在不降低入射光功率的情况下,以选用基横模或低阶横模为宜;1.5. 倍频光的脉冲宽度和线宽通过对倍频光脉冲宽度t 和相对线宽v 的观测,还可看到两种线宽都比基频光变窄的现象;这是由于倍频光强与入射基频光强的平方成比例的缘故;图5中,假设在t =t 0时;基频和倍频光具有相同的极大值;基频光在t 1和t 1'时,功率为峰值的1/2,脉冲宽度t 1=t 1'―t 1,而在相同的时间间隔内,倍频光的功率却为峰值的1/4,倍频光的半值宽度t 2 '―t 2< t 1'―t 1,即t 2<t 1,脉冲宽度变窄;同样道理可得到倍频后的谱线宽度也会变窄; 1064→532:I 类匹配为theta=90 phi=25C II 类为theta= phi=9025 CLBO 匹配分两种,一种为非临界相位匹配,一种为临界相位匹配即角度匹配.后一种都是在常温下使用的,也可以根据不同的工作温度进行角度的调整;L s L2L s图 4 晶体中基频光和倍频光。
相位匹配及实现方法

相位匹配及实现方法相位匹配(Phase Matching)是光学领域中一个重要的概念,指的是将不同波长或频率的光束进行匹配,使其在特定的光学介质中具有相同的相位速度,并能够有效地进行光学交互或干涉。
在光学器件或系统中,相位匹配是实现各种光学效应和应用的关键步骤,如广义的非线性光学过程(如和二次谐波,差频,和和频,以及光学参量放大等),光学波导中的耦合效应,以及光学分子束松弛和谐变等。
相位匹配是基于光波的相位速度相等原理,即在特定的介质中,不同波长的光束的相位速度差等于零。
光波的相位速度是指波前通过其中一点的速度,一般用vg表示。
相位速度等于光速c除以折射率n,即vg = c/ n。
在普通的介质中,折射率随波长而变化,从而导致不同波长的光束具有不同的相位速度。
为了实现相位匹配,需要通过选择合适的光学材料、设计合理的结构或施加特殊的相位调制手段,来调节不同波长光束的相位速度,使其相等。
相位匹配的实现方法有多种,下面列举几种常用的方法:1.正常相位匹配:正常相位匹配是最简单的相位匹配方式,即通过选择合适的光学材料,使得光束在该材料中的折射率随波长的变化足够小,从而实现相位匹配。
这种方法适用于波长较长(红外或中红外)的光束。
2.利用非线性光学晶体:非线性光学晶体具有特殊的频率响应特性,可以实现泵浦光和信号光在特定波长下的相位匹配。
这种方法常用于二次谐波,和差频等非线性光学过程。
3.使用光学波导:光学波导是一种能够限制光的传播方向和有效控制光传输的器件。
通过选择合适的波导材料和结构,可以实现不同波长光束在波导中的相位匹配,从而实现光的耦合和传输。
4.利用光栅或光子晶体:通过在特定的光学材料中制作周期性的光栅结构或光子晶体结构,可以实现不同波长光束的衍射,使其相位速度相等化。
这种方法常用于光学滤波器和光学分光仪等光学设备。
5.使用光学段通用接口(OBCI)技术:OBCI技术是一种基于宏观时间相位匹配思想的光传输接口。
激光器二次谐波产生机理与波长可调技术研究

激光器二次谐波产生机理与波长可调技术研究随着现代科学技术的飞速发展,激光技术在人类生产生活中有着广泛的应用。
而在激光技术的应用过程中,激光器的性能和稳定性显然具有重要的作用。
其中,激光器的二次谐波的发生机理及其波长可调技术的研究,对于激光器在生产和应用中的发挥有着至关重要的作用。
一、激光器二次谐波的发生机理所谓二次谐波,是指在光的能量传导过程中,其频率加倍。
而激光器二次谐波的产生是由于激光器中产生的高频率的光波作为输入,通过非线性晶体使光能量逐渐过渡到二次谐波波段的过程。
对于激光器的二次谐波的发生机理,主要包括两个方面,即非线性光学机理和相位匹配问题。
1.非线性光学机理非线性光学是指在光的传输过程中出现强烈的相互作用,使光产生非线性效应的系统。
而在非线性光学中,常见的效应包括非线性折射率、非线性吸收、非线性发光和非线性光学等。
而对于激光器的二次谐波的产生过程而言,主要是依托着非线性光学的效应来实现。
在激光器二次谐波产生过程中,光在非线性晶体中进行传输,而晶体中的物理性质是随着光的强度而发生变化的。
同时,由于非线性晶体的透明度随着光的强度增加而降低,因此使得光进一步加强,最后能够产生二次谐波。
这种非线性效应的产生,具有极高的非线性响应速度和力足够强度的能力,并长能够直接影响到第二谐波的低阶极向。
2.相位匹配问题相位匹配问题是指在激光器二次谐波产生过程中,相位的匹配非常重要,因为非线性晶体对光的双折射作用将对它的相位发生改变。
此时,如果谐波光和基波光的相位不匹配,则将会导致无法产生谐波。
解决这个问题的有效方法就是通过控制相位的方法生成二次谐波。
在实际应用中,主要采用以下几种方式实现:(1)直接相位匹配:直接将基波光和谐波光的相位匹配到倍频器中即可。
(2)间接相位匹配:通过调节折射率和非线性效应参数,即可实现相位匹配。
(3)积成相位匹配:通过将两种相位匹配的方法结合起来,即可实现相位匹配。
二、波长可调技术研究随着对激光器性能的不断要求,波长可调技术成为实现功能多样化的重要手段。
090323 相位匹配

2ω
ω
0.000 -0.002 -0.004 -0.006 -0.008 -0.010 -0.012 250 300 350 400 450 500
Temperature /K
z
ne
e光 偏振方向
光轴
Refractive
2.5
T=358K
0.532µm
2.4 2.3 2.2 2.1 0.2
no ne
1 cos 2 θ sin 2 θ = 2 + 2 2 ne (θ m , 0.532 ) no ( 0.532 ) ne ( 0.532 )
1 cos 2 θ sin 2 θ = 2 + ne2 (θ m ,1.064 ) no ( 1.064 ) ne2 ( 1.064 )
n = A + B / ( λ − C ) + Dλ
0
Wavelength /µm
KDP晶体的倍频(1.064µm→0.532µm)双折射相位匹配 晶体的倍频( 晶体的倍频 µ µ 双折射相位匹配
ne (θ ,2ω ) no (2 ω )
z 光轴 k
s
θ
α
x,y
no ( ω ) n e (θ , ω )
折射率椭球
L ω α
d 2ω
Lα
离散效应
离散角
在相位匹配 ∆k = 0 条件下, 条件下, 二次谐波产生过程效率最高; 二次谐波产生过程效率最高; 条件下, 而相位失配 条件下, ∆k ≠ 0 二次谐波产生过程效率大大 降低
I 2ω
∆kL sin 2 ∝ 2 ∆kL 2
2
1.0 0.8
I2ω(a.u.)
ε xx ≠ ε yy ≠ ε zz
次谐波产生湍流相位方法的原理

次谐波产生湍流相位方法的原理次谐波产生湍流相位方法是一种在流体力学领域中的重要技术,用于研究湍流现象及其特性。
本文将详细阐述这一方法的原理,帮助读者更好地理解其在湍流研究中的应用。
湍流现象广泛存在于自然界和工程领域,如何准确地描述和预测湍流特性一直是流体力学研究的热点。
次谐波产生湍流相位方法为这一领域提供了一种新的研究手段。
下面我们将深入探讨其原理。
一、次谐波产生原理次谐波产生(Subharmonic Generation)是一种非线性现象,当非线性系统受到周期性激励时,会产生频率为激励频率整数倍的响应。
在湍流研究中,次谐波产生原理可以用于揭示湍流结构的动态特性。
1.非线性相互作用:在湍流中,流体微团之间存在非线性相互作用,这种相互作用使得流体微团的运动轨迹变得复杂。
当外部施加一定频率的激励时,这些非线性相互作用会导致次谐波的产生。
2.湍流相位:湍流相位是指流体微团在空间和时间上的相对位置关系。
在次谐波产生过程中,湍流相位的变化会影响次谐波的强度和相位。
二、湍流相位方法湍流相位方法是一种基于次谐波产生原理的实验技术,通过测量次谐波信号的相位信息,可以揭示湍流结构的动态特性。
1.实验装置:湍流相位实验通常采用热线风速仪、激光多普勒测速仪等设备,对流体速度场进行测量。
同时,通过施加外部激励,如振动、声波等,以产生次谐波信号。
2.相位测量:在实验过程中,通过测量次谐波信号的相位差,可以得到流体微团之间的相对运动信息。
这些信息有助于揭示湍流结构的时空演化规律。
3.数据处理:对测量得到的相位数据进行处理,可以得到湍流结构的动态特性,如涡旋的生成、发展和消亡过程。
三、应用与意义次谐波产生湍流相位方法在湍流研究中具有广泛的应用前景,以下列举几个方面的应用:1.湍流结构识别:通过分析次谐波相位信息,可以识别湍流中的涡旋结构,为研究涡旋动力学提供重要依据。
2.湍流模型验证:该方法可以为湍流模型的验证提供实验数据,有助于改进和完善湍流模型。
第4讲 二次谐波产生、相位匹配考虑

dE2 z dz
i
w1
n2c
deff E
2 1
z e
ikz
(2) ( 1) eff 2deff
有效非线性光学系数
辐射基频波的极化强度: 2 2 * P w1 , z 1 0 w1;w2 , w1 2 z E 1 z 产生基频波的耦合波方程: d E1 z w1 2 ikz i P w1 , z e dz 2 0 n2c dE1 z w1 (2) * i eff E2 z E1 z e ikz dz 2n1c
等于零。 晶体长度为L;边界条 件:在入射端,基频光 电场强度幅度为E1(0), 二次谐波的电场强度幅 度E2(0)=0,。
二次谐波的耦合波方程组为:
k k2 2k1
小信号近似:指的是基频波不发生损耗,因此方程(1)右边
L
w2
w1
E 1 (0) E 2 (0)=0
产生二次谐波的示意图和边界条件
二次谐波产 生过程的 曼利-罗关系
* * * E E E E E E 1 1 2 1 1 2 * * * E E E E E E 1 1 2 1 1 2
能量守恒(产生二次谐波的曼利——罗关系):
I1 z I2 z cons
E1 z E2 z E1 0
第4讲 二次谐波产生和相位匹配考虑
(Second-Harmonic Generation
& Phase-Matching Consideration)
通过求解产生二次谐波的耦合方程,得到小信号和大信号二次谐波光强 表达式,讨论获得强相干信号的相位条件,分析在双折射晶体材料中实 现完全相位匹配条件的角度和温度相位匹配两种技术途径,讨论准相位匹 配技术。
超短脉冲强激光场产生高次谐波相位匹配技术的最新研究进展

a
(1) (1) [ V ( q X) - V ( X) ], 式中 q 为谐波
级次, N a 为气体密度, V(1) 为气体极化率。 自 由电子导致的相位失谐量可表示为 $ k f r = ( q 2 - 1) re K 其中 re = 2. 82×10- 13 cm 为 1N e。
q
3 强场高次谐波相位匹配理论
3
体与激光脉冲相互作用时的压强能够保持恒 定。 毛细管波导的引入克服了激光脉冲在传 输中出现的自散焦效应[ 20 ] , 使基波与谐波能 在波导的中心轴上共线传播, 此时通过简单 地调整气体压强就可以使谐波实现相位匹 配。 另外, 毛细管波导的使用让人们在实验中 有了许多可调整参数, 如毛细管半径, 光波传 播模式等, 可以用来精确地控制高次谐波相 位匹配的条件。 法国的 H. R. L ange 小组则 是利用自生波导超短激光脉冲与惰性气体相 互 作 用, 在 三 次 谐 波 中 实 现 了 准 相 位 匹 配[ 14 ] , 实验装置如图 4 所示。从原理上看, 超 短激光脉冲的自生波导效应起到了与毛细管 波导相似的作用, 即消除了自散焦效应, 使基 波与谐波能以近似于平面波的方式传播, 从 而有利于相位匹配。 日本的 T am ak i 小组对 上述两种方式的相位匹配都进行了实验研 究, 并取得了较好的结果。他们用 80 fs 激光 脉冲在 3 cm 长的充氩毛细管波导实现了 25 次谐波的相位匹配[ 15 ] , 用 100 fs 的自生波导 激光脉冲在氖气中实现了高次谐波的相位匹 配[ 16 ]。
波导或自生波导等手段来实现基波与谐波的 相位匹配[ 13~ 16 ] , 以及利用固体或团簇介质与 超短脉冲激光相互作用[ 17 ] 等。其中相位匹配 技术在实验中进展较大。 本文以超短激光场 中 ( 气体) 高次谐波相位匹配技术为主题, 回 顾了近年来在利用相位匹配技术提高强场谐 波转换效率方面的理论及实验的进展, 并对 今后强场高次谐波的研究提出了一些看法。
二次谐波相位匹配及其实现方法

二次谐波的应用二次谐波成像是近年发展起来的一种三维光学成像技术,具有非线性光学成像所特有的高空间分辨率和高成像深度,可避免双光子荧光成像中的荧光漂白效应。
此外二次谐波信号对组织的结构对称性变化高度敏感,因此二次谐波成像对于某些疾病的早期诊断或术后治疗监测具有很好的生物医学应用前景.二次谐波英文名称:second harmonic component定义:将非正弦周期信号按傅里叶级数展开,频率为原信号频率两倍的正弦分量。
SHG的一个必要条件是需要没要反演对称的介质其次是必须满足相位匹配,传播中的倍频光波和不断昌盛的倍频极化波保持了相位的一致性.谐波产生的根本原因是由于非线性负载所致。
当电流流经负载时,与所加的电压不呈线性关系,就形成非正弦电流,从而产生谐波。
SHG实验装置SHG实验装置按二次谐波信号收集方式可分为前向和后向,图2为前向和后向二次谐波产生的实验装置示意图.以图2(a)为例:由激光器产生的角频率为的入射基频光,经过物镜聚焦到样品上,产生频率为2的二次谐波,由另一个高数值孔径的物镜收集,滤光片(一般为窄带滤光片)滤掉激发光和可能产生的荧光和其他背景光,再用探测器件(如PMT)和计算机系统进行信号的采集、存储、分析和显示.要实现二次谐波微成像需要对以下因素进行最优化考虑:超短脉冲激光、高数值孑L径的显微物镜、高灵敏度的非解扫面探测器、准相位匹配和具有高二阶非线性的样品J.激光器:掺Ti蓝宝石飞秒激光器因具有高重复频率(80MHz)和高峰值功率,单脉冲能量低且町在整个近红外区(700~1000nm)内连续调谐,所以是二次谐波显微成像的理想光源.激光的重复频率对SHG也有影响,如果提高激发光的重复频率,激发光的平均功率可相应提高,二次谐波信号也得到增强.物镜:一般情况下,二次谐波主要非轴向发射,即信号收集时必须有一个足够大的数值孑L径来有效接收整个二次谐波信号.滤光片:为保证所收集的信号为二次谐波信号,必须使用滤光片.一般采用一长波滤光片和窄带滤光片(带宽10nm)组合以过滤任何干扰信号.信号收集系统:为尽晕减少二次谐波信号在系统中的损失,提高系统的探测灵敏度,最好采用非解扫(non.descanned)的信号.信号收集系统中的主要部件是PMT探测器.首先,为收集整个二次谐波信号,需要探测器的接收面足够宽.其次,对于由可调谐Ti:蓝宝石飞秒激光器,要接收的二次谐波信号处于350~500nm波段,故可采用双碱阴极光电倍增管.由于激发光波长离探测器的响应区很远,故可有效探N--次谐波信号.除了使用不同的滤光片外,二次谐波显微成像和双光子激发荧光显微成像在系统结构上是完全兼容的.已有人成功地将激光扫描共聚焦显微镜改造成双光子系统9,同样,也可以方便的用改造后的系统进行两者的复合成像二次谐波显微成像技术的发展及其在生物医学中的应用.细胞膜电压的测量对理解细胞信号传递过程有重要作用. 使用合适的膜染剂进行标记, 通过对染剂分子的二次谐波显微成像, 信号强度变化便能反映膜电压的大小.近年来, 二次谐波显微成像的一个主要领域, 就是发展具有高时空分辨率及高灵敏度的活细胞中横跨膜电压的光学测量方法.SHG成像用于膜电压测量细胞膜电压的测量对理解细胞信号传递过程有重要作用.使用合适的膜染剂进行标记,通过对染剂分子的二次谐波显微成像,信号强度变化便能反映膜电压的大小.近年来,二次谐波显微成像的一个主要领域,就是发展具有高时空分辨率及高灵敏度的活细胞中横跨膜电压的光学测量方法.1993年,OBouevitch等人¨证明,所加电场可强烈地调制SHG强度.1999年,PJCampagno!a等人则证明了SHG信号随膜电压变化.实验结果表明,激发波长为850nm时,SHG对膜电压的灵敏度为18/100mV,而TPEF只有10/100mV_J.2004年,Andrew等人进一步研究了苯乙烯基染剂产生的二次谐波信号对膜电压的敏感性.实验表明,使用850~910nm的激发波长,膜染剂di-4.ANEPPS和di4.ANEPMPOH使SHG对膜电压的敏感度高达20/100mV,且由于共振增强,使用950—970nm的激发波长时,敏感度达到40/100mV.这些研究结果进一步巩固了SHG在活细胞中膜电压的功能成像中的重要性.最近,Cornell大学的科学家,通过使用一种低毒性的有机染剂DHPESBP,对海参神经细胞进行二次谐波微成像(如图5),并成功实现了脑组织巾的电脉冲成像¨,这对于解渎大脑工作过程,解释大脑退化疾病如Alzheimer’s症等,具有巨大度、高空间分辨率和对生物的低杀伤性特点,为活体测量提供了一种新方法,有望成为组织形态学和 生理学研究的・个强大工具.目的,SHG在神经科 学、药理学及疾病早期 断方面的应用研究已取得 一些进展.但二次谐波成像还是一¨不很成熟的技 术,随着研究的逐步深入,对它的应用仍然有待进 一步的开发.随着微光纤技术的发展,二次谐波成 像技术还可与光纤光学结合进行人体内窥镜检查, 实现活体生物体内深处的组织在分子水平的成像. 随着信号检测技术和计算机技术等的发展,还可运 用二次谐波成像实时观察生物细胞活动.由于二次 谐波显微应用于肌纤维长度的精确度已达到20 nm_¨ ,活体未标记心脏和肌肉组织的纳米药理学 研究也将发挥很大的作用.本实验室正着手研究将 ■次谐波成像、共聚焦显微成像以及双光子激发荧 光成像结合,根据视网膜的分层结构和特点,采用 不 方法成像,进而揭示视网膜的正常生理结构及 病变部位,为视网膜疾病的早期诊断提供一种新型 的具有三维高空间分辨牢的手段相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光。
相位匹配及实现方法
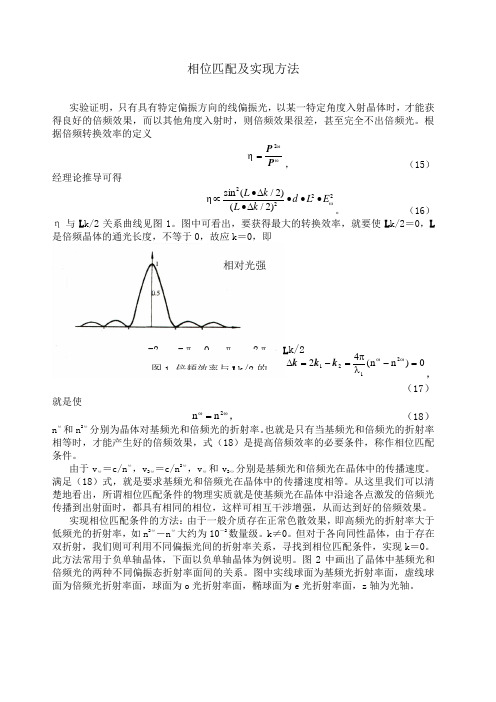
相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光。
根据倍频转换效率的定义ωω2ηP P =, (15)经理论推导可得2ω222)2/()2/(sin ηE L d k L k L •••∆•∆•∝。
(16) η与L k/2关系曲线见图1。
图中可看出,要获得最大的转换效率,就要使L k/2=0,L是倍频晶体的通光长度,不等于0,故应k =0,即0)n n (422121=-λπ=-=∆ωωk k k ,(17)就是使ωω=2n n , (18)n ω和n 2ω分别为晶体对基频光和倍频光的折射率。
也就是只有当基频光和倍频光的折射率相等时,才能产生好的倍频效果,式(18)是提高倍频效率的必要条件,称作相位匹配条件。
由于v ω=c/n ω,v 2ω=c/n 2ω,v ω和v 2ω分别是基频光和倍频光在晶体中的传播速度。
满足(18)式,就是要求基频光和倍频光在晶体中的传播速度相等。
从这里我们可以清楚地看出,所谓相位匹配条件的物理实质就是使基频光在晶体中沿途各点激发的倍频光传播到出射面时,都具有相同的相位,这样可相互干涉增强,从而达到好的倍频效果。
实现相位匹配条件的方法:由于一般介质存在正常色散效果,即高频光的折射率大于低频光的折射率,如n 2ω―n ω大约为10-2数量级。
k ≠0。
但对于各向同性晶体,由于存在双折射,我们则可利用不同偏振光间的折射率关系,寻找到相位匹配条件,实现k =0。
此方法常用于负单轴晶体,下面以负单轴晶体为例说明。
图2中画出了晶体中基频光和倍频光的两种不同偏振态折射率面间的关系。
图中实线球面为基频光折射率面,虚线球面为倍频光折射率面,球面为o 光折射率面,椭球面为e 光折射率面,z 轴为光轴。
图1 倍频效率与L k/2的相对光强-22π π -π L k/2折射率面的定义:从球心引出的每一条矢径到达面上某点的长度,表示晶体以此矢径为波法线方向的光波的折射率大小。
bbo晶体相位匹配

BBO晶体相位匹配1. 介绍BBO(β-BaB2O4)晶体是一种非线性光学晶体,具有广泛的应用领域,包括激光技术、光通信、光学成像等。
在这些应用中,相位匹配是一个重要的概念,它可以帮助优化光学器件的性能。
本文将深入探讨BBO晶体的相位匹配原理、方法和应用。
2. 相位匹配原理在非线性光学中,相位匹配是指将入射光波的相位与晶体中的非线性极化相位进行匹配,以实现最大的非线性效应。
BBO晶体具有正交非线性极化,因此需要满足相位匹配条件才能实现最大的非线性转换效率。
相位匹配条件可以通过相位匹配角度和相位匹配温度来实现。
相位匹配角度是指入射光波矢量与晶体中的非线性极化矢量之间的夹角,而相位匹配温度是指晶体的温度,使得晶体的折射率与入射光波的折射率相匹配。
3. 相位匹配方法相位匹配方法主要包括类型-I相位匹配和类型-II相位匹配。
在类型-I相位匹配中,入射光波和非线性极化矢量具有相同的偏振态,而在类型-II相位匹配中,入射光波和非线性极化矢量具有正交的偏振态。
对于BBO晶体,类型-I相位匹配是最常用的方法。
在类型-I相位匹配中,需要选择适当的入射光波波长、角度和温度,以实现最佳的相位匹配效果。
可以使用光学参数计算软件或实验方法来确定最佳的相位匹配条件。
4. 相位匹配应用BBO晶体的相位匹配技术在许多光学应用中发挥着重要作用。
以下是一些常见的应用示例:4.1 高效二次谐波产生通过相位匹配技术,可以在BBO晶体中实现高效的二次谐波产生。
二次谐波产生是一种将入射光波频率加倍的方法,利用BBO晶体的非线性效应可以将红外激光转换为可见光激光。
相位匹配条件的选择可以实现最大的转换效率。
4.2 光学参量放大器BBO晶体可以用作光学参量放大器的非线性介质。
通过相位匹配技术,可以实现在特定波长范围内的高增益放大效果。
这在激光技术和光通信中具有重要的应用,可以实现高效的信号放大和传输。
4.3 光学波长转换相位匹配技术可以实现光学波长转换,将输入光波的频率转换为不同的频率。
如何在晶体中实现相位匹配
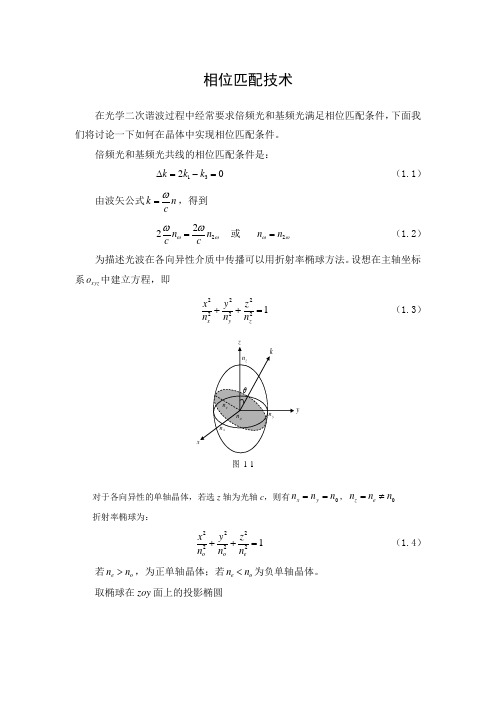
相位匹配技术在光学二次谐波过程中经常要求倍频光和基频光满足相位匹配条件,下面我们将讨论一下如何在晶体中实现相位匹配条件。
倍频光和基频光共线的相位匹配条件是:0231=-=∆k k k(1.1) 由波矢公式nck ω=,得到ωωωω222n c n c=或 ωω2n n = (1.2)为描述光波在各向异性介质中传播可以用折射率椭球方法。
设想在主轴坐标系xyz o 中建立方程,即1222222=++zyxn zn yn x(1.3)y图 1-1对于各向异性的单轴晶体,若选z 轴为光轴c ,则有0n n n y x ==,0n n n e z ≠= 折射率椭球为:1222222=++eoonz ny nx (1.4)若o e n n >,为正单轴晶体;若o e n n <为负单轴晶体。
取椭球在zoy 面上的投影椭圆y图 1-2椭圆方程为:12222=+eonz ny (1.5)如图(1-2)[][]1sin )(cos )(2222=+-ee oe nn nn θθθθ (1.6)22222cos sin )(1oee n n n θθθ+=(1.7)令θπβ-=2/则方程(1.7)可化为:[][]1sin )(cos )(2222=+oe ee nn nn βθβθ(1.8) 以β为极角,)(θe n 为极径建立极坐标系,则图形仍为椭圆。
图1-3对负单轴晶体,即e o n n >,其o 光折射率与e 光折射率椭圆如图1-4所示图1-4很显然,图中ω2的e 椭圆与ω的o 椭圆的交点处满足相位匹配条件 由方程组[]22222222)(cos )(sin )(1ωωωθθθo m e m en n n +=(1.9)[]22222)()2/(cos )()2/(sin )2/(1ωωωπππo e en n n+=(1.10)得 222222222)()()()()(sin ωωωωωωθe o o o oem n n n n n n --= (1.11)这称为第一类相位匹配,表示为e o o →+图1-5如图1-5,可以通过调节光轴C 和和入射波矢之间的夹角θ,使之满足式(1.11),实现角度相位匹配。
二次谐波的相位匹配条件

二次谐波的相位匹配条件
二次谐波的相位匹配条件是指在非线性光学过程中,产生的二次谐波与基波之间的相位关系满足一定条件。
具体来说,相位匹配条件要求二次谐波的波矢k2等于两倍基波的波矢k1,即k2 = 2k1。
在非线性光学中,当光在非线性介质中传播时,会发生各种频率转换过程,其中之一就是二次谐波产生。
在这个过程中,基波的频率ω1将会被加倍,产生一个频率为2ω1的二次谐波。
为了实现高效的二次谐波产生,相位匹配条件需要被满足。
这是因为在非线性光学过程中,相位匹配条件的满足可以有效地增强二次谐波的产生效率。
如果相位不匹配,即波矢k2与2k1不相等,那么二次谐波的产生效率将显著降低。
为了满足相位匹配条件,可以采取一些措施,例如选择适当的非线性光学材料,调整入射光的角度和波长,或者使用相位匹配技术,如温度调谐相位匹配等。
这样可以最大程度地提高二次谐波的产生效率和输出功率。
总之,二次谐波的相位匹配条件要求二次谐波的波矢k2等于两倍基波的波矢k1,只有满足相位匹配条件,才能实现高效的二次谐波产生。
光纤通信波段KN晶体二次谐波相位匹配角的计算

摘 要:在光纤通信系统 中,超短光脉冲的检测一直是一个重要的问题。二次谐波强度 自 相关法是被广泛使用 的超短光脉冲波形测量的方法。由于光纤通信 系统中光功率很低 , 使得满足晶体的相位匹配变得更加重要。K 作为 N 双轴晶体相位 匹配问 比较复杂, 题 本文从双轴晶体主平面上的相位 匹配出发, 讨论 K 的相位 匹配问题, N 得到其在光 纤通信波段 15p 处的最佳相位匹配参量。 .5r o 关键词:光纤通信;超短光脉冲;K 晶体;相位 匹配 N 中图分类号:T 28 N 4. 4 文献标识码 :A
Z A G Q a , H N i -u n ,I N ay , A GB - n H N i Z A G X a g a gJA GD -aY N o u n o j
(h c olf c neB in iesyo ota dT l o ] e h oo i c, eig vri P s n ee mmu i t n , yL b rtr f t a r S Se j Un t f s c nci s Ke a oaoy i l ao o Op c
Co mmu ia o n ihwa e eh o ge ns f d ct n B in 0 8 6 Chn ) nc t na dL g t v c n l is i T o Mii r o u a o , e ig10 7 , ia t y E i j
Ab ta t I i e r be t ee th l ah r p l pia c mmu iains se . dtes c n -amo i sr c : tsak yp o lm d tc eut s o t us i o t l o o t r en c nc t y tm An e o dh r nc o h itn i uoc rea o to d l sdt aueteut s ot us v . dd et elw pia o ro ne s ya t—orlt nme di wieyu e me s r l ah r p l wa e An u t t i h s o h r e o h o o t l we f c p h p i l mmu iains se ,tsmoei otn ac ecy tl h e . N rsa, sa ido ba i r s li teo t a o c c n c t y tm ii r o mp r tom tht r s a s K c tla n f ixa c t ,s a t h aps y k l y a
如何在晶体中实现相位匹配

如何在晶体中实现相位匹配相位匹配技术在光学⼆次谐波过程中经常要求倍频光和基频光满⾜相位匹配条件,下⾯我们将讨论⼀下如何在晶体中实现相位匹配条件。
倍频光和基频光共线的相位匹配条件是:0231=-=?k k k(1.1)由波⽮公式nck ω=,得到ωωωω222n c n c=或ωω2n n = (1.2)为描述光波在各向异性介质中传播可以⽤折射率椭球⽅法。
设想在主轴坐标系xyz o 中建⽴⽅程,即1222222=++zyxn zn yn x(1.3)对于各向异性的单轴晶体,若选z 轴为光轴c ,则有0n n n y x ==,0n n n e z ≠= 折射率椭球为:1222222=++eoonz ny nx (1.4)若o e n n >,为正单轴晶体;若o e n n <为负单轴晶体。
取椭球在zoy ⾯上的投影椭圆y图 1-2椭圆⽅程为:12222=+eonz ny (1.5)如图(1-2)[][]1sin )(cos )(2222=+-en nn θθθθ(1.6)22222cos sin )(1oee n n n θθθ+=(1.7)令θπβ-=2/则⽅程(1.7)可化为:[][]1sin )(cos )(2222=+oe ee nn nn βθβθ(1.8)以β为极⾓,)(θe n 为极径建⽴极坐标系,则图形仍为椭圆。
图1-3对负单轴晶体,即e o n n >,其o 光折射率与e 光折射率椭圆如图1-4所⽰图1-4很显然,图中ω2的e 椭圆与ω的o 椭圆的交点处满⾜相位匹配条件由⽅程组[]22222222)(cos )(sin )(1ωωωθθθo m e m en n n +=(1.9)[]22222)()2/(cos )()2/(sin )2/(1ωωπππo e en n n+=(1.10)得 222222222)()()()()(sin ωωωωωωθe o o o oem n n n n n n --= (1.11)这称为第⼀类相位匹配,表⽰为e o o →+图1-5如图1-5,可以通过调节光轴C 和和⼊射波⽮之间的夹⾓θ,使之满⾜式(1.11),实现⾓度相位匹配。
整流装置交流谐波电流的相位

整流装置交流侧谐波电流的相位⒈ 确定谐波电流相位的要点⑴ 不同次数(频率)谐波电流相互间无向量关系,不能进行向量计算。
① 不同次数谐波的周期用时间来表示是不相等的:不同次数谐波的频率1f n f n ⋅=,不同次数谐波的周期用时间表示则为: 111f n f T n n ⋅== 基波频率Z H f 501= 基波的周期s f T 02.0111==。
5次谐波的周期s f T 004.0155==; 7次谐波的周期s f T 003.0177≈=。
② 不同次数谐波的周期用角度来表示是相同的:ππϑ22=⋅⋅=n n n T f⑵ 在等效p 相整流系统中,1+=pK n 次谐波电流的相序为正序;1-=pK n 次谐波电流的相序为负序。
对于正序,顺时针方向为滞后;对于负序,顺时针方向为超前。
当整流变压器网侧绕组△联结时,正序及负序谐波的线电流均较相应同次谐波的相电流滞后30°,这30°的相位移对于不同次谐波所代表的时间是不相等的。
另外,虽然正序及负序谐波的线电流均滞后相应同次谐波的相电流滞后30°,但是它们向量图的画法却不相同。
()BL n i ()CA n i ()CL n i()AL n i()CL n i ()BL n i B ()AL n 图1 网侧绕组△联结时正序谐波线、相电流相位关系()CL n i ()CA n i ()BL n i()AL n i) ()BL n i ()CL n i C ()AL n 图2 网侧绕组△联结时负序谐波的线、相电流相位关系⑶ 整流装置阀侧交流电压对于网侧交流电压相位上是有所移动的,若确定装置网侧交流电流的相位关系时,应注意以下两点:① 整流变压器阀侧电流基波相位在不控整流时与阀侧电压相位是一致的。
因此网侧交流电流与阀侧交流电流相位差等于阀侧电压与网侧电压的相位差。
在绘制不同次谐波的向量图时,该相位差均为同一数值,不因谐波次数而异,也与移相方式无关。
非线性光学中有关相位匹配的几个问题

1 9 6 2年 , Ar ms t o n g等人提 出一 种新 方法 l 2 ] , 在 二 阶非 线性 介质 中用 周期性 极化 方 向反 转 的光栅 作 为附加 波矢 , 补偿 基波 与谐 波之 间 的相 位失 配 , 即
9竹
得到 满足 . 因此 , 人们 一 直在 探索 和寻 求各 种可 能 的 方 法来 补偿 由于色散 所 引起 的相 位失 配.
同 的方 向. 例 如, 负单 轴 晶体 ( < 。 )中 , 基波 ( o
1 引 言
光 )的 折 射 率 n 。 n
谐 波 的产生是 非 线性光 学 效应 的重要 技术 应用 之一 . 以二 次 谐 波 的 产 生 ( 即倍 频 效应 )为 例 , 它 可 以广泛地 应 用于产 生 可 见 到 近 紫外 波段 的光 波 . 而
现在将 以非线性 光 学 中相位 匹配方 法 的发展 过
Байду номын сангаас
Ak — k 2 一 2 忌 一 k
k一
l
其 中 以 为附加 光栅 的光 栅 周期 , 这种 方 法 被称 作 准
相 位 匹配 ( QP M) . 值得注意的是, 这种 技 术 只 适 用
程 中的难题 为 线索 , 对 目前 比较 常 用 且 发展 成 熟 的 几种 相位 匹配 方法 进行 讨论 .
波 的产 生高 度地依 赖 于 相 位 匹 配条 件 的满 足 , 即 基 频 波与 倍频 波波 矢之 差 A k 一0 . 由于
△忌 一
然而, 这 种 方 法
[ 翌 ) _ 二
C
]
要 求参 与作 用 的光 波 必 须具 有 不 同 的偏 振 方 向 , 因
相位匹配及实现方法
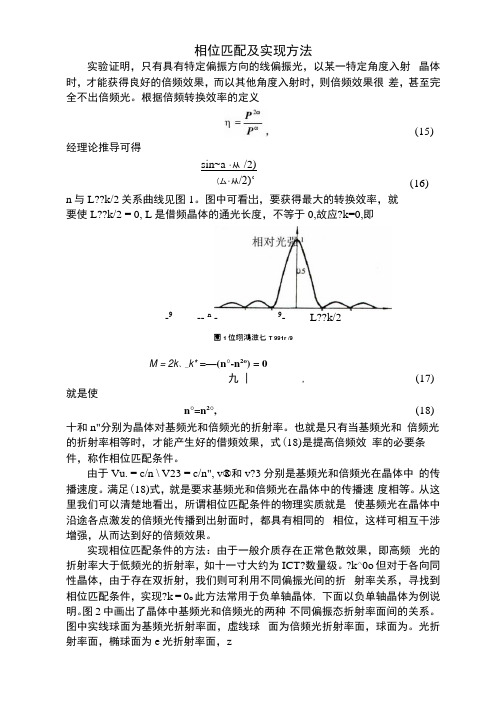
相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光。
根据倍频转换效率的定义(15) 经理论推导可得sin~a •从/2)(厶•从/2)‘n与L??k/2关系曲线见图1。
图中可看岀,要获得最大的转换效率,就要使L??k/2 = 0, L是借频晶体的通光长度,不等于0,故应?k=0,即-9-- n - 9- L??k/2園1位翊鴻滋匕T 991r /9M = 2k、_k* =—(n°-n2o) = 0九 | , (17)就是使n°=n2°, (18) 十和n"分别为晶体对基频光和倍频光的折射率。
也就是只有当基频光和倍频光的折射率相等时,才能产生好的借频效果,式(18)是提高倍频效率的必要条件,称作相位匹配条件。
由于Vu. = c/n \ V23 = c/n", v®和v?3分别是基频光和倍频光在晶体中的传播速度。
满足(18)式,就是要求基频光和倍频光在晶体中的传播速度相等。
从这里我们可以清楚地看出,所谓相位匹配条件的物理实质就是使基频光在晶体中沿途各点激发的倍频光传播到出射面时,都具有相同的相位,这样可相互干涉增强,从而达到好的倍频效果。
实现相位匹配条件的方法:由于一般介质存在正常色散效果,即高频光的折射率大于低频光的折射率,如十一寸大约为ICT?数量级。
?k^0o 但对于各向同性晶体,由于存在双折射,我们则可利用不同偏振光间的折射率关系,寻找到相位匹配条件,实现?k = 0o此方法常用于负单轴晶体, 下面以负单轴晶体为例说明。
图2中画出了晶体中基频光和倍频光的两种不同偏振态折射率面间的关系。
图中实线球面为基频光折射率面,虚线球面为倍频光折射率面,球面为。
光折射率面,椭球面为e光折射率面,z(16)轴为光轴。
折射率面的定义:从球心引出的 每一条矢径到达面上某点的长度, 表示晶体以此矢径为波法线方向的 光波的折射率大小。
第n次谐波电流滞后电压的相角

第n次谐波电流滞后电压的相角本文将探讨第n次谐波电流滞后电压的相角问题。
在交流电路中,电流和电压之间存在一定的相位差,也就是所谓的相角。
在正弦波电路中,电流和电压的相位差是固定的,而在非正弦波电路中,相位差则会随着谐波次数的增加而发生变化。
首先,我们需要了解什么是谐波。
谐波是指频率是基波频率的整数倍的波形,它们在交流电路中是非常常见的。
在交流电路中,电流和电压可以表示为:I = I1sin(ωt + φ1)U = U1sin(ωt + φ2)其中,I和U分别表示电流和电压,I1和U1分别表示它们的最大值,ω表示角频率,t表示时间,φ1和φ2分别表示它们的相位角。
在正弦波电路中,φ1和φ2的值是固定的,而在非正弦波电路中,则会随着谐波次数的增加而发生变化。
假设我们要求第n次谐波电流滞后电压的相角,我们可以先求出第n次谐波的频率和相位角。
在一个周期内,第n次谐波的周期为Tn = T/ n,其中T为基波周期,n为谐波次数。
第n次谐波的频率为fn = 1/Tn = n/T。
第n次谐波的相位角可以表示为:φn = nφ1 - mφ2其中,m为谐波次数与基波频率之比。
在理想情况下,m应该是整数,但在实际情况下,它可能是一个分数或小数。
因此,在实际计算中,我们需要将m取整到最接近的整数。
当我们求出第n次谐波的频率和相位角后,就可以求出第n次谐波电流滞后电压的相角了。
根据欧姆定律,电阻元件中的电流和电压是同相的,而电容元件中的电流则领先于电压90度,电感元件中的电流则滞后于电压90度。
因此,在求解第n次谐波电流滞后电压的相角时,需要根据具体的电路元件进行计算。
总之,第n次谐波电流滞后电压的相角是一个比较复杂的问题,需要根据具体的电路元件进行计算。
在实际应用中,我们需要根据具体情况进行分析和计算,以保证电路的正常工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次谐波的应用二次谐波成像是近年发展起来的一种三维光学成像技术,具有非线性光学成像所特有的高空间分辨率和高成像深度,可避免双光子荧光成像中的荧光漂白效应。
此外二次谐波信号对组织的结构对称性变化高度敏感,因此二次谐波成像对于某些疾病的早期诊断或术后治疗监测具有很好的生物医学应用前景.二次谐波英文名称:second harmonic component定义:将非正弦周期信号按傅里叶级数展开,频率为原信号频率两倍的正弦分量。
SHG的一个必要条件是需要没要反演对称的介质其次是必须满足相位匹配,传播中的倍频光波和不断昌盛的倍频极化波保持了相位的一致性.谐波产生的根本原因是由于非线性负载所致。
当电流流经负载时,与所加的电压不呈线性关系,就形成非正弦电流,从而产生谐波。
SHG实验装置SHG实验装置按二次谐波信号收集方式可分为前向和后向,图2为前向和后向二次谐波产生的实验装置示意图.以图2(a)为例:由激光器产生的角频率为的入射基频光,经过物镜聚焦到样品上,产生频率为2的二次谐波,由另一个高数值孔径的物镜收集,滤光片(一般为窄带滤光片)滤掉激发光和可能产生的荧光和其他背景光,再用探测器件(如PMT)和计算机系统进行信号的采集、存储、分析和显示.要实现二次谐波微成像需要对以下因素进行最优化考虑:超短脉冲激光、高数值孑L径的显微物镜、高灵敏度的非解扫面探测器、准相位匹配和具有高二阶非线性的样品J.激光器:掺Ti蓝宝石飞秒激光器因具有高重复频率(80MHz)和高峰值功率,单脉冲能量低且町在整个近红外区(700~1000nm)内连续调谐,所以是二次谐波显微成像的理想光源.激光的重复频率对SHG也有影响,如果提高激发光的重复频率,激发光的平均功率可相应提高,二次谐波信号也得到增强.物镜:一般情况下,二次谐波主要非轴向发射,即信号收集时必须有一个足够大的数值孑L径来有效接收整个二次谐波信号.滤光片:为保证所收集的信号为二次谐波信号,必须使用滤光片.一般采用一长波滤光片和窄带滤光片(带宽10nm)组合以过滤任何干扰信号.信号收集系统:为尽晕减少二次谐波信号在系统中的损失,提高系统的探测灵敏度,最好采用非解扫(non.descanned)的信号.信号收集系统中的主要部件是PMT探测器.首先,为收集整个二次谐波信号,需要探测器的接收面足够宽.其次,对于由可调谐Ti:蓝宝石飞秒激光器,要接收的二次谐波信号处于350~500nm波段,故可采用双碱阴极光电倍增管.由于激发光波长离探测器的响应区很远,故可有效探N--次谐波信号.除了使用不同的滤光片外,二次谐波显微成像和双光子激发荧光显微成像在系统结构上是完全兼容的.已有人成功地将激光扫描共聚焦显微镜改造成双光子系统9,同样,也可以方便的用改造后的系统进行两者的复合成像二次谐波显微成像技术的发展及其在生物医学中的应用.细胞膜电压的测量对理解细胞信号传递过程有重要作用. 使用合适的膜染剂进行标记, 通过对染剂分子的二次谐波显微成像, 信号强度变化便能反映膜电压的大小.近年来, 二次谐波显微成像的一个主要领域, 就是发展具有高时空分辨率及高灵敏度的活细胞中横跨膜电压的光学测量方法.SHG成像用于膜电压测量细胞膜电压的测量对理解细胞信号传递过程有重要作用.使用合适的膜染剂进行标记,通过对染剂分子的二次谐波显微成像,信号强度变化便能反映膜电压的大小.近年来,二次谐波显微成像的一个主要领域,就是发展具有高时空分辨率及高灵敏度的活细胞中横跨膜电压的光学测量方法.1993年,OBouevitch等人¨证明,所加电场可强烈地调制SHG强度.1999年,PJCampagno!a等人则证明了SHG信号随膜电压变化.实验结果表明,激发波长为850 nm时,SHG对膜电压的灵敏度为 18/100 mV,而TPEF只有10/100 mV_J .2004年, Andrew等人进一步研究了苯乙烯基染剂产生的二次 谐波信号对膜电压的敏感性.实验表明,使用850 ~9 10 nm的激发波长,膜染剂di-4.ANEPPS和di4. ANEPMPOH使SHG对膜电压的敏感度高达20/100 mV,且由于共振增强,使用950—970 nm的激发 波长时,敏感度达到40/100 mV .这些研究结果 进一步巩固了SHG在活细胞中膜电压的功能成像 中的重要性. 最近,Cornell大学的科学家,通过使用一种低 毒性的有机染剂DHPESBP,对海参神经细胞进行 二次谐波 微成像(如图5),并成功实现了脑组 织巾的电脉冲成像¨ ,这对于解渎大脑工作过程, 解释大脑退化疾病如Alzheimer’s症等,具有巨大度、高空间分辨率和对生物的低杀伤性特点,为活 体测量提供了一种新方法,有望成为组织形态学和 生理学研究的・个强大工具.目的,SHG在神经科 学、药理学及疾病早期 断方面的应用研究已取得 一些进展.但二次谐波成像还是一¨不很成熟的技 术,随着研究的逐步深入,对它的应用仍然有待进 一步的开发.随着微光纤技术的发展,二次谐波成 像技术还可与光纤光学结合进行人体内窥镜检查, 实现活体生物体内深处的组织在分子水平的成像. 随着信号检测技术和计算机技术等的发展,还可运 用二次谐波成像实时观察生物细胞活动.由于二次 谐波显微应用于肌纤维长度的精确度已达到20 nm_¨ ,活体未标记心脏和肌肉组织的纳米药理学 研究也将发挥很大的作用.本实验室正着手研究将 ■次谐波成像、共聚焦显微成像以及双光子激发荧 光成像结合,根据视网膜的分层结构和特点,采用 不 方法成像,进而揭示视网膜的正常生理结构及 病变部位,为视网膜疾病的早期诊断提供一种新型 的具有三维高空间分辨牢的手段相位匹配及实现方法实验证明,只有具有特定偏振方向的线偏振光,以某一特定角度入射晶体时,才能获得良好的倍频效果,而以其他角度入射时,则倍频效果很差,甚至完全不出倍频光。
根据倍频转换效率的定义, (15)经理论推导可得。
(16)η与L ∙∆k/2关系曲线见图1。
图中可看出,要获得最大的转换效率,就要使L ∙∆k/2=0,L 是倍频晶体的通光长度,不等于0,故应∆k =0,即, (17)就是使 , (18)n ω和n 2ω分别为晶体对基频光和倍频光的折射率。
也就是只有当基频光和倍频光的折射率相等时,才能产生好的倍频效果,式(18)是提高倍频效率的必要条件,称作相位匹配条件。
由于v ω=c/n ω,v 2ω=c/n 2ω,v ω和v 2ω分别是基频光和倍频光在晶体中的传播速度。
满足(18)式,就是要求基频光和倍频光在晶体中的传播速度相等。
从这里我们可以清楚地看出,所谓相位匹配条件的物理实质就是使基频光在晶体中沿途各点激发的倍频光传播到出射面时,都具有相同的相位,这样可相互干涉增强,从而达到好的倍频效果。
实现相位匹配条件的方法:由于一般介质存在正常色散效果,即高频光的折射率大于低频光的折射率,如n 2ω―n ω大约为10-2数量级。
∆k ≠0。
但对于各向同性晶体,由于存在双折射,我们则可利用不同偏振光间的折射率关系,寻找到图1 倍频效率与L ∙∆k/2的关相对光强-2π 2π π -π L ∙∆k/2 0相位匹配条件,实现∆k =0。
此方法常用于负单轴晶体,下面以负单轴晶体为例说明。
图2中画出了晶体中基频光和倍频光的两种不同偏振态折射率面间的关系。
图中实线球面为基频光折射率面,虚线球面为倍频光折射率面,球面为o 光折射率面,椭球面为e 光折射率面,z 轴为光轴。
折射率面的定义:从球心引出的每一条矢径到达面上某点的长度,表示晶体以此矢径为波法线方向的光波的折射率大小。
实现相位匹配条件的方法之一是寻找实面和虚面交点位置,从而得到通过此交点的矢径与光轴的夹角。
图中看到,基频光中o 光的折射率可以和倍频光中e 光的折射率相等,所以当光波沿着与光轴成θm 角方向传播时,即可实现相位匹配,θm 叫做相位匹配角,θm 可从下式中计算得出, (19)式中都可以查表得到,表1列出几种常用的数值。
是与入射面法线的夹角。
为了减少反射损失和便于调节,实验中一般总希望让基频光正入射晶体表面。
所以加工倍频晶体时,须按一定方向切割晶体,以使晶体法线方向和光轴方向成θm ,见图3。
以上所述,是入射光以一定角度入射晶体,通过晶体的双折射,由折射率的变化来补偿正常色散而实现相位匹配的,这称为角度相位匹配。
角度相位匹配又可分为两类。
第一类是入射同一种线偏振光,负单轴晶体将两个e 光光子转变为一个倍频的o 光光子。
第二类是入射光中同时含有o 光和e 光两种线偏振光,负单轴晶体将两个不同的光子变为倍频的e 光光子,正单轴晶体变为一个倍频的o 光光子。
见表2图2 负单轴晶体折射率球面 图3 非线性晶体的切割晶体图5 基频光与倍频光的脉宽及相对线宽的比较 I ω I 2ω t 1 t 2 t 1 t t 1t 2 t 2 t ν1 ν1ν2ν2 ν ν相位匹配的方法除了前述的角度匹配外,还有温度匹配,这里不作细述。
在影响倍频效率的诸因素中,除前述的比较重要的三方面外,还需考虑到晶体的有效长度L s 和模式状况。
图4为晶体中基频光和倍频光振幅随距离的变化。
如果晶体过长,例L>L s 时,会造成倍频效率饱和;晶体过短。
例L<L s ,则转换效率比较低。
L s 的大小基本给出了倍频技术中应该使用的晶体长度。
模式的不同也影响转换效率,如高阶横模,方向性差,偏离光传播方向的光会偏离相位匹配角。
所以在不降低入射光功率的情况下,以选用基横模或低阶横模为宜。
1.5. 倍频光的脉冲宽度和线宽 通过对倍频光脉冲宽度t 和相对线宽v 的观测,还可看到两种线宽都比基频光变窄的现象。
这是由于倍频光强与入射基频光强的平方成比例的缘故。
图5中,假设在t =t 0时。
基频和倍频光具有相同的极大值。
基频光在t 1和t 1'时,功率为峰值的1/2,脉冲宽度∆t 1=t 1'―t 1,而在相同的时间间隔内,倍频光的功率却为峰值的1/4,倍频光的半值宽度t 2 '―t 2< t 1'―t 1,即∆t 2<∆t 1,脉冲宽度变窄。
同样道理可得到倍频后的谱线宽度也会变窄。
1064→532:I 类匹配为theta=90 phi=@25CII 类为theta= phi=90@25 CLBO 匹配分两种,一种为非临界相位匹配,一种为临界相位匹配即角度匹配.后一种都是在常温下使用的,也可以根据不同的工作温度进行角度的调整。
二次谐波的应用二次谐波成像是近年发展起来的一种三维光学成像技术,具有非线性光学成像所特有的高空间分辨率和高成像深度,可避免双光子荧光成像中的荧光漂白效应。
