高中数学新课程精品限时训练(17)
2021_2022学年新教材高中数学课时分层作业17均值不等式的应用(含解析)新人教B版必修第一册

课时分层作业(十七) 均值不等式的应用(建议用时:60分钟)[合格根底练]一、选择题1.假设a >1,那么a +1a -1的最小值是( ) A .2 B .a C.2a a -1D .3 D [∵a >1,∴a -1>0,∴a +1a -1=a -1+1a -1+1≥2 (a -1)·1a -1+1=3.] 2.x <0,那么y =x +1x-2有( ) A .最大值为0B .最小值为0C .最大值为-4D .最小值为-4 C [∵x <0,∴y =-⎣⎢⎡⎦⎥⎤(-x )+1(-x )-2≤-2-2=-4,当且仅当-x =1-x,即x =-1时取等号.] 3.设x >0,那么y =3-3x -1x的最大值是( ) A .3 B .-3 2 C .3-2 3D .-1 C [∵x >0,∴y =3-⎝ ⎛⎭⎪⎫3x +1x ≤3-23x ·1x =3-2 3.当且仅当3x =1x,且x >0,即x =33时,等号成立.] 4.假设x >0,y >0,且1x +4y=1,那么x +y 的最小值是( ) A .3 B .6 C .9 D .12C [x +y =(x +y )·⎝ ⎛⎭⎪⎫1x +4y =1+y x +4x y +4 =5+y x +4x y≥5+2y x ·4x y =5+4=9. 当且仅当⎩⎪⎨⎪⎧ 1x +4y =1,y x =4x y ,即⎩⎪⎨⎪⎧ x =3,y =6时等号成立,故x +y 的最小值为9.]5.x >0,y >0,且x +y =8,那么(1+x )(1+y )的最大值为( )A .16B .25C .9D .36 B [(1+x )(1+y )≤⎣⎢⎡⎦⎥⎤(1+x )+(1+y )22 =⎣⎢⎡⎦⎥⎤2+(x +y )22=⎝ ⎛⎭⎪⎫2+822=25, 当且仅当1+x =1+y ,即x =y =4时,(1+x )(1+y )取最大值25,应选B.]二、填空题6.函数y =x +1x +1(x ≥0)的最小值为________. [答案] 17.如图,有一张单栏的竖向张贴的海报,它的印刷面积为72 dm 2(图中阴影局部),上下空白各宽2 dm ,左右空白各宽1 dm ,那么四周空白局部面积的最小值是________dm 2. 56 [设阴影局部的高为x dm ,那么宽为72xdm ,四周空白局部的面积是y dm 2. 由题意,得y =(x +4)⎝ ⎛⎭⎪⎫72x +2-72 =8+2⎝ ⎛⎭⎪⎫x +144x ≥8+2×2x ·144x =56(dm 2). 当且仅当x =144x ,即x =12 dm 时等号成立.]8.假设a ,b ∈(0,+∞),满足a +b +3=ab ,那么a +b 的取值范围是________.[6,+∞) [∵a +b +3=ab ≤⎝⎛⎭⎪⎫a +b 22, ∴(a +b )2-4(a +b )-12≥0,解得a +b ≥6,当且仅当a =b =3时取等号.]三、解答题9.当x <32时,求函数y =x +82x -3的最大值. [解] y =12(2x -3)+82x -3+32=-⎝ ⎛⎭⎪⎫3-2x 2+83-2x +32, ∵当x <32时,3-2x >0, ∴3-2x 2+83-2x ≥23-2x 2 ·83-2x =4,当且仅当3-2x 2=83-2x ,即x =-12时取等号.于是y ≤-4+32=-52,故函数有最大值-52. 10.为了改善居民的居住条件,某城建公司承包了棚户区改造工程,按合同规定在4个月内完成.假设提前完成,那么每提前一天可获2 000元奖金,但要追加投入费用;假设延期完成,那么每延期一天将被罚款5 000元.追加投入的费用按以下关系计算:6x +784x +3-118(千元),其中x 表示提前完工的天数,试问提前多少天,才能使公司获得最大附加效益?(附加效益=所获奖金-追加费用)[解] 设城建公司获得的附加效益为y 千元,由题意得y =2x -⎝ ⎛⎭⎪⎫6x +784x +3-118=118-⎝ ⎛⎭⎪⎫4x +784x +3 =118-⎣⎢⎡⎦⎥⎤4(x +3)+784x +3-12 =130-⎣⎢⎡⎦⎥⎤4(x +3)+784x +3 ≤130-24(x +3)·784x +3=130-112=18(千元), 当且仅当4(x +3)=784x +3,即x =11时取等号. 所以提前11天,能使公司获得最大附加效益.[等级过关练]1.假设-4<x <1,那么y =x 2-2x +22x -2( ) A .有最小值1B .有最大值1C .有最小值-1D .有最大值-1D [y =x 2-2x +22x -2=12⎣⎢⎡⎦⎥⎤(x -1)+1x -1, 又∵-4<x <1,∴x -1<0.∴-(x -1)>0.故y =-12⎣⎢⎡⎦⎥⎤-(x -1)+1-(x -1)≤-1. 当且仅当x -1=1x -1,即x =0时等号成立.] 2.x >0,y >0,且2x +1y=1,假设x +2y >m 2恒成立,那么实数m 的取值范围是( ) A .m ≤-22或m ≥2 2B .m ≤-4或m ≥2C .-2<m <4D .-22<m <2 2 D [∵x >0,y >0且2x +1y=1, ∴x +2y =(x +2y )⎝ ⎛⎭⎪⎫2x +1y =4+4y x +x y≥4+24y x ·x y =8,当且仅当4y x =x y, 即x =4,y =2时取等号,∴(x +2y )min =8,要使x +2y >m 2恒成立,只需(x +2y )min >m 2恒成立,即8>m 2,解得-22<m <2 2.]3.假设x >0,y >0,且x +4y =1,那么xy 的最大值为________.116[1=x +4y ≥24xy =4xy , ∴xy ≤116,当且仅当x =4y =12时等号成立.] 4.假设实数x ,y 满足x 2+y 2+xy =1,那么x +y 的最大值是________.233 [x 2+y 2+xy =(x +y )2-xy =1,∴(x +y )2=xy +1≤⎝ ⎛⎭⎪⎫x +y 22+1.∴34(x +y )2≤1. ∴-233≤x +y ≤233,当且仅当x =y =33时等号成立.] 5.在下面等号右侧两个分数的分母方块处,各填上一个正整数,并且使这两个正整数的和最小,1=1□+9□,试求这两个数. [解] 设1a +9b=1,a ,b ∈N *, ∴a +b =(a +b )·1=(a +b )⎝ ⎛⎭⎪⎫1a +9b =1+9+b a +9a b≥10+2b a ·9a b=10+2×3=16, 当且仅当b a =9a b,即b =3a 时等号成立. 又1a +9b =1,∴1a +93a=1,∴a =4,b =12. 这两个数分别是4,12.。
高中数学新课程精品限时训练(27)

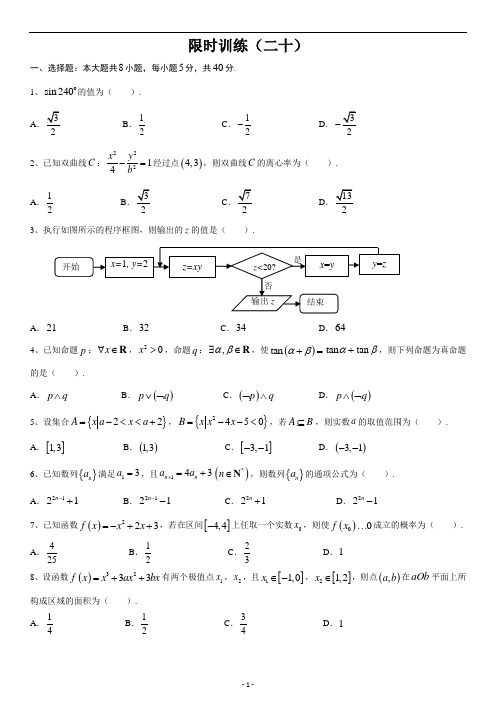
a=结束是输出ai 开始限时训练(二十七)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}0,1,2,4A =,集合{}04B x x =∈<R …,集合C A B =I ,则集合C 表示为 ( ) . A.{}0,1,2,4B.{}1,2,3,4C.{}1,2,4D.{}04x x ∈<R …2.复数z 满足()1i 1z -=(其中i 为虚数单位),则z = ( ) . A .11i22- B.11i 22+ C .11i 22-+ D.11i 22-- 3.下列函数中,为奇函数的是 ( ) . A .122x xy += B .{},0,1y x x =∈C .sin y x x ⋅=D .1,00,01,0x y x x ⎧⎪⎨⎪⎩<->==4.“1ω=”是“函数()cos f x x ω=在区间[]0,π上单调递减”的 ( ) . A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 5.执行如图所示的程序框图,则输出的a 的值为 ( ) .A .2B .13C .12- D .3-6.已知直线1:4360l x y -+=和直线2:1l x =-,抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值为( ) . A.2 B.3 C.115 D. 37167. 如图所示,1F ,2F 是双曲线1:C 2213y x -=与椭圆2C 的公共焦点,点A 是1C ,2C 在第一象限的公共点.若121F F F A =,则2C 的离心率是( ) .A .13B .23 C.2235或 D .25(第7题图)8.在平面直角坐标系中,定义两点()11,P x y 与()22,Q x y 之间的“直角距离”为()1212,d P Q x x y y =-+-.给出下列命题:(1)若()1,2P ,()()sin ,2cos Q ααα∈R ,则(),d P Q的最大值为3(2)若,P Q 是圆221x y +=上的任意两点,则(),d P Q的最大值为(3)若()1,3P ,点Q 为直线2y x =上的动点,则(),d P Q 的最小值为12. 其中为真命题的是( ) .A .(1)(2)(3)B .(1)(2)C .(1)(3)D .(2)(3)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中的横线上. 9.设α为锐角,若π4cos 65α⎛⎫+= ⎪⎝⎭,则πsin 23α⎛⎫+= ⎪⎝⎭ .10.已知向量()2,1x =-m ,()1,x =n ,若⊥m n ,则实数x 的值为 . 11.函数()x f 的定义域为 .12.某几何体的三视图如图所示,其正视图是边长为2的正方形,侧视图和俯视图都是等腰直角三角形,则此几何体的体积是 .13.以抛物线24y x =的焦点为圆心且与双曲线222214x y a a-=的渐近线相切的圆的方程是 .14.已知奇函数()f x 是定义在R 上的增函数,数列{}n x 是一个公差为2的等差数列,且满足()()()()8910110f x f x f x f x +++=,则2014_______x =.限时训练(二十七)答案部分一、选择题二、填空题 9.242510. 1 11. [)2,+∞ 12.83 13.()22415x y -+= 14. 4009 解析部分1. 解析 因为{}{}0,1,2,4,04A B x x ==<…,所以{}1,2,4C A B ==I .故选C. 2. 解析 由题可得()()11i 1i1i 1i 1i 2z ++===--+.故选B. 3. 解析 A 选项中令()122xx f x =+,则()()112222x xx xf x f x ---=+=+=,所以()f x 为偶函数, 故选项A 中的函数不是奇函数;B 选项中的函数的定义域为{}0,1,不关于原点对称,所以B 中函数不是奇函数;C 选项中令()sin f x x x =,则()()()()sin sin f x x x x x f x -=--==,所以()f x 为偶函数,故C 中函数不是奇函数;D 选项中的函数的定义域及图像都是关于原点对称的,所以D 中函数是奇函数.故选D.4. 解析 当1ω=时,()cos f x x =,它在区间[]0,π上是单调递减的;若()cos f x x ω=在区间[]0,π上是单调递减的,则12ππ2ω⋅…,即01ω<…,所以()1cos f x x ωω=⇒=在[]0,π上单调递减,()cos f x x ω=在区间[]0,π上单调递减1ω⇒=/,所以1ω=是()cos f x x ω=在区间[]0,π上单调递减的充分不必要条件.故选A. 5. 解析 该程序框图的模拟分析如下表.根据上表得输出的a 的值为3-.故选D.6. 解析 如图所示,设点P 到直线1l 的距离为1d ,到直线2l 的距离为2d ,点F 为抛物线的焦点.因为抛物线方程为24y x =,所以直线2l 为抛物线的准线,所以2d PF =,即距离之和等于1d PF +.过点F 作1FH l ⊥与点H ,FH 与抛物线交于点0P ,则点P 位于点0P 的位置时,1d PF +最小,此时()1min d PF FH +==4130625⨯-⨯+=.故选A.7. 解析 设焦半径为c ,椭圆的长半轴长为a .由双曲线方程2213yx -=可得2c =,所以11224AF F F c ===.由双曲线的定义及点A 在第一象限可得122AF AF -=,所以212422AF AF =-=-=.由椭圆定义知,12422AF AF a +=+=,则3a =,所以椭圆2C 的离心率23c e a ==.故选B. 8. 解析(1)由“直角距离”的定义知(),1sin 22cos 1sin 22cos d P Q αααα=-+-=-+-=()()3sin 2cos 3αααϕ-+=+(其中tan 2α=).又因为sin()1,αϕ+-…所以()33αϕ+…,即(),3d P Q …(),d P Q 的最大值为3,故(1)正确.(2)过点P 作x 轴的垂线,过点Q 作y 轴的垂线,两垂线交于点R,如图所示,设,QR a PR b ==,根据“直角距离”的定义有()1212,d P Q x x y y ab =-+-=+.因为2224a b PQ +=…,所以2a b +a b +…(),d P Q …,(),d P Q的最大值为,故(2)正确.(3)因为点Q 在直线2y x =上运动,所以可设点Q 的坐标为(),2x x .由“直角距离”的定义得()43,13,1322,12334,2x x d P Q x x x x x x ⎧⎪-<⎪⎪=-+-=-<⎨⎪⎪-⎪⎩……,画出这个函数的图像如图所示.当32x =时函数有最小值为313422⨯-=,即(),d P Q 的最小值为12,故(3)正确.综上可知(1),(2),(3)均为真命题.故选A. 9. 解析 因为π0,2α⎛⎫∈ ⎪⎝⎭,所以ππ2π,663α⎛⎫+∈ ⎪⎝⎭.又由已知π4cos ,65α⎛⎫+= ⎪⎝⎭得πππ,662α⎛⎫+∈ ⎪⎝⎭, 所以π3sin ,65α⎛⎫+= ⎪⎝⎭故πππ3424sin 22sin cos 23665525ααα⎛⎫⎛⎫⎛⎫+=++=⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 10. 解析 因为⊥m n ,所以20x x ⋅-+=m n =,可得1x =. 11. 解析 若使函数()f x =240x -…,所以2x …,即()f x 的定义域为[)2,+∞. 12. 解析 符合条件中的三视图的几何体如图所示,图中ABCD 为正方形,边长为2,BE ⊥平面ABCD ,且2BE =,所以11824333E ABCD ABCD V BE S -=⋅=⨯⨯=.13. 解析 抛物线24y x =的焦点为()1,0F ,双曲线222214x y a a-=的渐近线为2y x =±.设点F 到其中一条渐近线2y x =的距离为d ,因为以点F 为圆心的圆与2y x =相切,所以r d ===, 所以所求圆的方程为()22415x y -+=. 14. 解析 因为数列{}n x 为等差数列,所以811910x x x x +=+.若8119100x x x x +=+>,则()()8110f x f x +>,()()9100f x f x +>,所以()()()()8910110f x f x f x f x +++>与已知矛盾;若8119100x x x x +=+<,则()()()()8119100,0f x f x f x f x +<+<,所以()()89f x f x ++()()10110f x f x +<也与已知矛盾,故8119100x x x x +=+=.又因为数列{}n x 的公差为2,即1092x x -=,由91010902x x x x +=⎧⎨-=⎩,得101x =, 所以2014102004=1+20042=4009x x d =+⨯.E222DCBA。
(新课标)_学年高中数学双基限时练17新人教A版必修3【含答案】

双基限时练 (十七 ) 1.以下说法正确的选项是( ) PAA.某事件发生的频次为 ()= 1.1 B.不行能事件的概率为0,必定事件的概率为 1 C.小概率事件就是不行能发生的事件,大体率事件就是必定要发生的事件D.某事件发生的概率是跟着试验次数的变化而变化的 PA 分析∵事件发生的概率0≤() ≤1,∴A项错;小概率事件是指这个事件发生的可能性很小,几乎不发生.大体率事件发生的可能性较大,但其实不是必定发生,∴ C 项错;某事件发生的概率为一个常数,不随试验的次数变化而变化,∴ D 项错; B 项正确.答案 B 2.每道选择题有 4 个选择支,此中只有 1 个选择支是正确的.某次考试共有12 道选择 1 题,某人说:“每个选择支正确的概率是,我每题都选择第一选择支,则必定有 3 道题选 4 择结果正确”这句话 ( ) A.正确B.错误C.不必定D .没法解说分析这句话是错误的.12道题中都选第一选择支其结果可能选对 0 道, 1 道, 2 道,, 12 道都有可能.答案 B 3.先后投掷两枚均匀的一分、贰分的硬币,察看落地后硬币的正反面状况,则以下哪个事件的概率最大( )A.起码一枚硬币正面向上 B.只有一枚硬币正面向上 C.两枚硬币都是正面向上 D.两枚硬币一枚正面向上,另一枚反面向上分析投掷两枚梗币,其结果有“正正”,“正反”,“反正”,“反反”四种状况.起码有一枚硬币正面向上包含三种状况,其概率最大.答案 A 4.从一同意备出厂的电视机中随机抽取10 台进行质量检查,此中有一台是次品,若用AA 表示抽到次品这一事件,则对的说法正确的选项是( ) 1A .概率为101B.频次为10 11C.概率靠近10D.每抽 10 台电视机必有一台是次品答案 B 5.经过市场抽检,质检部门得悉市场上食用油合格率为80%,经检查,某市市场上的食用油大概有80 个品牌,则不合格的食用油品牌大概有 ( ) A. 64 个 B.640 个 C.16 个 D. 160 个解析 80×(1- 80%)= 16. 答案 C 6.掷一颗骰子 100 次,“向上的点数是 2”的状况出现了19 次,则在一次试验中,向上的点数是 2 的频次是 ________.事件发生的次数19 分析事件发生的频次== . 试验的次数 100 答案 0.19 7.设某厂产品的次品率为2%,估量该厂8000 件产品中合格品的件数可能为________.分析依题意得8000×(1-2%)=7840. 答案7840 8.公元 1053 年,大元帅狄青奉旨,率兵征讨侬智高,出征前狄青取出100 枚“宋元天宝”铜币,向众将士许愿:“假如钱币扔在地上,有字的一面会全面向上,那么此次发兵必定能够战胜仇敌!”在千军万马的注视之下,狄青使劲将铜币向空中抛去,奇观发生了:100 枚铜币,枚枚有字的一面向上.立时,三军喝彩雀跃,将士个个以为是神灵保佑,战争必胜无疑.事实上铜币有可能是________.①铜币两面均有字;②铜币质量不均匀;③神灵保佑;④ 铜币质量均匀.把你以为正确的填在横线上.答案①② 9.解说以下概率的含义. (1)某厂生产的产品合格的概率为;(2)一次抽奖活动中,中奖的概率为 0.2. 解 (1)说明该厂产品合格的可能性为90%,也就是说, 100 件该厂的产品中大概有90 件是合格品.(2)说明参加抽奖的人,每抽一张,有20%的时机中奖,也就是说,抽100 张,可能有20 张中奖.10.对某电视机厂生产的电视机进行抽样检测的数据以下表所示. 2抽取台数优等品数计算表中优等品的各个频次;(2)预计该厂生产的电视机优等品的概率是多少?mfA 解(1)联合公式() =及题意计算出优等品的频次挨次为n,0.954.(2)由 (1)知,计算出优等品的频次固然各不同样,但却在常数0.95 左右摇动,且跟着n 的增添,摇动的幅度越来越小,所以,预计该厂生产的电视机优等品的概率为0.95. ABA11.如图所示,有两个能够自由转动的均匀转盘、.转盘被均匀分红 3 等份,分别B 标上1,2,3 三个数字;转盘被均匀分红 4 等份,分别标上3,4,5,6 四个数字.有人为甲、 AB 乙两人设计了一个游戏规则:自由转动转盘与,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,假如和是那么甲获胜,不然乙获胜.你以为这样的游戏规则公正吗?假如公正,6,请说明原因;假如不公正,如何改正规则才能使游戏对两方公正?两个转盘指针数字之和共有12 种状况: 4,5,6,7,5,6,7,8,6,7,8,9. 当和为解6 时甲获胜,不然乙获胜,这类游戏规则不公正,应改为当两数字之和为偶数时,甲获胜,不然乙获胜.这类规则可使甲、乙获胜的时机均等.12.元旦就要到了,某校将举行庆贺活动,每班派 1 人主持节目.高一 (2)班的小明、小华和小利实力相当,又都争着要去,班主任决定用抽签的方式决定,灵巧的小强给小华出想法,要小华先抽,说先抽的时机大,你是如何以为的?谈谈看.解我们取三张卡片,上边标有1,2,3,抽到 1 表示中签,谁抽到 1 就去主持节目,假定抽签的序次为甲、乙、丙,则把全部抽签的结果状况填入下表:人名一二三四五六状况甲112233 乙231312 丙323121 3从上表能够看出:甲、乙、丙挨次抽签,一共有六种状况,第一、二种状况甲中签;第三、五种状况乙中签;第四、六种情况丙中签.由此可知,甲、乙、丙中签的可能性都是同样的,即甲、乙、丙中签的时机是同样的,先抽后抽签的时机是均等的. 4。
高中数学新课程精品限时训练(38)

限时训练(三十八)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知集合413A x x ⎧⎫=-⎨⎬-⎩⎭…,(){}2log 21B x x =-<,则A B =I ( ).(A )()1,4- (B )()1,3- (C ) ()2,3 (D )()3,4(2)复数z 满足()12i 3i z +=+,则复数z =( ).(A )1i + (B )1i - (C )1i -+ (D )1i -- (3)已知函数()22f x x mx =+-,在区间[]2,4-上随机取一个实数x ,若事件“()0f x '<”发生的概率为23,则m 的值为( ). (A )2(B )2-(C )4(D )4-(4)在ABC △中,三个内角A ,B ,C 所对的边为a ,b ,c ,若cos cos 2cos a B b A c C +=,6a b +=且ABC S =△,则c =( ). (A) (B) (C )3 (D)(5)数列{}n a 满足11=a ,且11n n a a n +=++,对任意的*n ∈N 恒成立,则122017111a a a +++=L ( ). (A )20151008 (B )20171009 (C )40342017 (D )20152018(6)下列命题正确的个数是( ). ①“1x ≠”是“0232≠+-x x”的充分不必要条件② 若()()sin 2f x x θ=+,则“()f x 的图像关于π3x =对称”是“π6θ=-”的必要不充分条件 ③()0,0x ∃∈-∞,使0034xx <成立④命题“角α的终边在第一象限,则α是锐角”的逆否命题为真命题 (A )4 (B )3 (C )2 (D )1(7)过双曲线()222210,0x y a b a b -=>>的右焦点F 作直线by x a=-的垂线,垂足为A 交双曲线左支于B 点,若12OAF OBF S S =△△,则该双曲线的离心率为( ). (A(B )2 (C )(D(8)已知Rt AOB △的面积为1,O 为直角顶点.设向量OAOA=uu r uu r a ,OB OB=uuruur b ,2OP =+uura b ,则PA PB -uu r uu r 的最小值为( ). (A )1(B )2(C)(D )4(9)某三棱锥的三视图如图所示,该三棱锥的外接球半径是( ). (A(B(C(D(10)阅读如图所示的程序框图,运行相应的程序,输出的结果S =( ).(A )20172018 (B )20162017 (C )40332018 (D )40332017俯视图(11)已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示,则π6y f x ⎛⎫=- ⎪⎝⎭图的单调递增区间为( ).(A )πππ,π,44k k k ⎡⎤-+∈⎢⎥⎣⎦Z (B )ππ2π,2π,44k k k ⎡⎤-+∈⎢⎥⎣⎦Z (C )πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (D ) ππ2π,2π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (12)设函数()e xxf x =,关于的方程()()210f x mf x +-=⎡⎤⎣⎦有三个不同的实数解,则实数m 的取值范围是( ).(A )1,e e ⎛⎫-∞- ⎪⎝⎭ (B )1e ,e⎛⎫-+∞ ⎪⎝⎭(C )()0,e (D )()1,e 二、填空题:本题共4小题,每小题5分.(13)若变量x ,y 满足约束条件200220x y x y x y +⎧⎪-⎨⎪-+⎩…„…,则2z x y =-的取值范围是________.(14)已知cos 212sin 2αα+=,()tan 2αβ+=,则tan =β .(15)设定义在R 的偶函数()y f x =,满足对任意x R ∈都有()()2f t f t +=-,且(]0,1x ∈时,()1xf x x =+.若20153a f ⎛⎫= ⎪⎝⎭,20165b f ⎛⎫= ⎪⎝⎭,20177c f ⎛⎫= ⎪⎝⎭,则 .(16)过抛物线22y x =的焦点F 的直线分别交抛物线于,A B 两点,交直线12x =-于点P ,若PA mAF =u u u r u u u r ,(),PB nBF m n =∈R u u u r u u u r,则m n +=____________.限时训练(三十八)答案部分一、选择题二、填空题13. []1,2- 14.3415. c b a << 16. 0 解析部分(1)解析 因为{}13A x x =-<„,()()2log 21022242,4x x x B -<⇒<-<⇒<<⇒=, 所以()2,3A B =I.故选C .(2)解析 根据题意可知()()3i 12i 3i 55i1i12i 55z +-+-====-+,所以1i z =+.故选A. (3)解析()20f x x m '=+<,2m x <-,22m -=,4m =-.故选D.(4)解析 由正弦定理得sin cos sin cos 2sin cos A B B A C C +=,()sin 2sin cos A B C C +=⋅,sin 2sin cos C C C =⋅, 因为sin 0C ≠,所以1cos 2C =. ()0,πC ∈,π3C =,又ABC S =△,则1sin 2ab C = 所以8ab =,又因为6a b +=,所以()()2222222cos 2363812c a b ab C a b ab ab a b ab =+-=+--=+-=-⨯=. 所以c =.故选B.(5)解析 因为11n n a a n +=++,所以1n n a a n -=+,即1nn a a n --=,121n n a a n ---=-,…,()2122a a n -=….以上1n -个等式分别相加得()()()11222n n n a a n -+-=….所以()()212122nn n n na -++=+=,所以2121121n a n n n n ⎛⎫==- ⎪++⎝⎭. 所以12201711111111201721223201720181009a a a ⎛⎫+++=-+-++-= ⎪⎝⎭L L .故选B.(6)解析 对于①1x ≠推不出2320x x -+≠,因为22320x x x =⇒-+=,但2320x x -+≠,可得1x ≠且2x ≠,故为必要不充分条件,①为假命题.对于②充分性明显不成立,对于π6θ=-时, ()sin 26f x x π⎛⎫=- ⎪⎝⎭,又sin 21336f πππ⎛⎫⎛⎫=⨯-= ⎪ ⎪⎝⎭⎝⎭,故π3x =是()f x 的对称轴,必要性成立,故②为真命题.对于③()003,0,14x x ⎛⎫∀∈-∞> ⎪⎝⎭,故③为假命题.对于④第一象限角不一定是锐角,原名题为假命题,则其逆否命题为假命题,故选D.(7)解析 设(),0F c ,则直线AB 的方程为()a y x c b =-代入双曲线渐近线方程by x a =-得2,a ab M cc ⎛⎫- ⎪⎝⎭,由2FB FA =u u u r u u u r ,可得2222,33c a ab B c c ⎛⎫+-- ⎪⎝⎭,把B 点坐标代入双曲线方程22221x y a b -=,即()222222224199c a a c a c +-=,整理可得c =即离心率ce a==.故选C. (8)解析 以O 为原点,直线OA 为x 轴建立直角坐标系.由已知2OA OB ⋅=,设()0OA t t =>,则点(),0A t ,20,B t ⎛⎫⎪⎝⎭,()1,0=a ,()0,1=b ,()1,2OP =u u u r . 从而()1,2PA t =--u u u r ,21,2PB t ⎛⎫=-- ⎪⎝⎭u u u r .2,PA PB t t ⎛⎫-=- ⎪⎝⎭u uu r u u u r所以PA PB -u u u r u u u r =2t =时取等号;所以PA PB ⋅u u u r u u u r的最小值为故选A . (9)解析 根据题意,可得出如图所示的三棱锥A BCD -,底面Rt BCD △中,BC CD ⊥,且5BC =,4CD =,侧面ABC △中,高AE BC ⊥于E ,且4AE =,2BE =,3CE =,侧面ACD △中,5AC =.因为平面ABC ⊥平面BCD ,平面ABC I 平面BCD BC =,AE BC ⊥,所以AE ⊥平面BCD ,结合CD ⊆平面BCD ,得AE CD ⊥,因为BC CD ⊥,AE BC E =I , 所以CD ⊥平面ABC ,结合AC ⊆平面ABC ,得AC CD ⊥,所以在ADB △中,AB ==BD ==AD ==设ABC △外心为O ,如图设G 为AB 中点, H 为BC 中点.过1O 的垂线与过CD 中点F 且平行1C C 的直线相交于O ,则O 为外接球球心.则1Rt RtCHO AEB△△:,故1O C HCAB AE=,故14O C=.所以R==.故选D.(10)解析由程序框图知,S可看成一个数列{}n a的前2017项和,其中()()*1,12017nannnn∈=+N„,所以1111111112017112122017201822320172018201820118 S⎛⎫⎛⎫++⋯+++⋯+-⎪ ⎪⎝⎛⎫==---==⎭⎪⎝⎭⎭⨯⨯⨯⎝.故输出的是20172018.故选A.(11)解析由图可知2A=,ππ4π312T⎛⎫=-=⎪⎝⎭,所以2π2πω==.因为由图可得点π,212⎛⎫⎪⎝⎭在函数图像上,可得:π2sin2212ϕ⎛⎫⨯+=⎪⎝⎭,解得ππ22π,122k kϕ⨯+=+∈Z,所以由π2ϕ<,可得π3ϕ=.所以()π2sin23f x x⎛⎫=+⎪⎝⎭.因为若将()y f x=的图像向右平移π6个单位后,得到的函数解析式为()ππ2sin22sin263g x x x⎡⎤⎛⎫=-+=⎪⎢⎥⎝⎭⎣⎦.所以由ππ2π22π,22k x k k-+∈Z剟,可得ππππ,44k x k k-+∈Z剟,所以函数()g x的单调增区间为πππ,π,44k k k⎡⎤-+∈⎢⎥⎣⎦Z.故选A.(12)解析11()()01e ex xx xf x f x x--'=⇒==⇒=,因此当1x„时,()1ef x„;当1x>时()1ef x<<,因此2()10g t t mt=+-=有两个根,其中110,et⎛⎫∈ ⎪⎝⎭,(]21,0et⎧⎫∈-∞⎨⎬⎩⎭U,因为()01g=-,所以110ee eg m⎛⎫>⇒>-⎪⎝⎭.故选B.(13)解析如图所示,2y x z=-,当2y x z=-过()0,1A时,z-取得最大值,此时z取得最小值;当2y x z=-过点()2,2B时,z-取得最小值,此时z取得最大值.故min max1,2z z=-=,故z的范围是[]1,2-.=0评注 2z x y =-的范围呢?这是基本类型,希望同学们滚瓜烂熟!(14)解析 依题意22cos 22sin cos ααα=,故1tan 2α=,故()()()tan tan 3tan tan 1tan tan 4αβαβαβααβα+-=+-==⎡⎤⎣⎦++.(15)解析 ()()()2f t f t f t +=-=,故()y f x =是周期为2的偶函数.()y f x =在(]0,1上为增函数,20151116723333a f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,201644140515555b f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,201711288777c f f f ⎛⎫⎛⎫⎛⎫==+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因为111753<<,所以c b a <<. 评注 在研究函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时,要注意用好条件的相互关系,结合特征进行等价转化研究.如奇偶性可实现自变量正负转化,周期可实现自变量大小转化,单调性可实现去“f ”,把函数值的大小转化自变量大小关系.(16)解析 直线1x =-是抛物线的准线,如图设,A B 在直线上的射影分别是,M N ,AM AF =,BN BF =,PA PA AF AM =,PB PB BF BN=,因为//AM BN ,所以PA PBAF BF =,m n =, 又0,0m n <>,所以0m n +=.评注 抛物线问题中抛物线的定义在解题中常常用到.抛物线上点到焦点距离与点到准线的距离常用定义相互转化.利用定义还可得出与焦点弦有关的一些常用结论:(以下图为依据)(1)212y y p =-,1224x x p =;(2)1222sin AB x x p pθ=++=(θ为AB 的倾斜角); (3)11AF BF +为定值2p; (4)以AB 为直径的圆与准线相切; (5)以AF 或BF 为直径的圆与y 轴相切.。
[精品]2019学年高中数学课时达标训练十七北师大版必修
![[精品]2019学年高中数学课时达标训练十七北师大版必修](https://img.taocdn.com/s3/m/d16be3d8d4d8d15abe234ec4.png)
课时达标训练(十七)一、选择题1.(重庆高考)函数y =x +x -1的定义域是( )A .(-1,+∞)B .[-1,+∞)C .(-1,1)∪(1,+∞)D .[-1,1)∪(1,+∞)2.函数y =log 2|x |的图像大致是( )3.已知函数y =log 2x ,其反函数y =g (x ),则g (x -1)的图像是( )4.设f (x )是奇函数,当x >0时,f (x )=log 2x ,则当x <0时,f (x )等于( ) A .-log 2x B .log 2(-x ) C .log x 2 D .-log 2(-x ) 二、填空题5.集合A ={y |y =log 2x ,x >1},B =yy =⎝ ⎛⎭⎪⎫12x,x >1,则(∁R A )∩B =________.6.若函数y =f (x )是函数y =a x(a >0,且a ≠1)的反函数,其图像经过点(a ,a ),则f (x )=________. 7.若log 2a <log 2b <0,则a ,b,1的大小关系是________. 18.函数f (x )=log 2x 在区间[a,2a ](a >0)上的最大值与最小值之差为________. 三、解答题9.求下列函数的定义域. (1)y =lg(x +1)+2x 2-x;(2)y =log (x -2)(5-x ).10.已知函数f (x )=log 2(x +1),g (x )=log 2(1-x ). (1)若函数f (x )的定义域为[3,63],求函数f (x )的最值; (2)求使f (x )-g (x )>0的x 的取值范围; (3)判断函数F (x )=f (x )+g (x )的奇偶性.答案1.解析:选C 由题意得⎩⎪⎨⎪⎧x +1>0,x -1≠0,∴⎩⎪⎨⎪⎧x >-1,x ≠1,故选C.2.解析:选A y =log 2|x |=⎩⎪⎨⎪⎧log 2x x ,log 2-xx,分别作图知A 正确.3.解析:选C 由已知g (x )=2x,∴g (x -1)=2x -1,故选C.4.解析:选D ∵x <0,∴-x >0,∴f (-x )=log 2(-x ). 又∵f (x )是奇函数,∴f (-x )=-f (x ), ∴f (x )=-log 2(-x ).5.解析:∵x >1,∴log 2x >log 21=0,∴A ={y |y >0}.而当x >1时,0<⎝ ⎛⎭⎪⎫12x <⎝ ⎛⎭⎪⎫121,∴B =y 0<y <12.∴(∁R A )∩B ={y |y ≤0}∩⎩⎨⎧⎭⎬⎫y 0<y <12=∅.答案:∅6.解析:∵y =f (x )的图像过点(a ,a ), ∴其反函数y =a x的图像过点(a ,a ), ∴a a=a =,∴a =12,∴f (x )=.答案:7.解析:log 2a <log 2b <0⇔log 2a <log 2b <log 21, ∵y =log 2x 在(0,+∞)上是增函数,∴a <b <1. 答案:a <b <18.解析:∵f (x )=log 2x 在区间[a,2a ]上是增函数, ∴f (x )max -f (x )min =f (2a )-f (a )=log 22a -log 2a =log 22=1. 答案:19.解:(1)要使函数有意义,需⎩⎪⎨⎪⎧x +1>0,2-x >0,即⎩⎪⎨⎪⎧x >-1,x <2,∴函数的定义域为(-1,2). (2)要使函数有意义.需⎩⎪⎨⎪⎧ 5-x >0,x -2>0,x -2≠1,即⎩⎪⎨⎪⎧x <5,x >2,x ≠3.∴定义域为(2,3)∪(3,5).10.解:(1)由题意知,3≤x ≤63,∴4≤x +1≤64, ∵函数y =log 2x 是增函数,∴log 24≤log 2(x +1)≤log 264,∴2≤f (x )≤6, ∴f (x )的最大值为6,最小值为2. (2)f (x )-g (x )>0⇔f (x )>g (x ), 即log 2(x +1)>log 2(1-x ),则⎩⎪⎨⎪⎧x +1>0,1-x >0,x +1>1-x ,得:0<x <1,∴x 的取值范围为(0,1).(3)要使函数F (x )=f (x )+g (x )有意义,需⎩⎪⎨⎪⎧1+x >0,1-x >0,即-1<x <1,∴定义域为(-1,1) 又F (-x )=f (-x )+g (-x ) =log 2(1-x )+log 2(1+x )=log 2(1-x 2)=f (x )+g (x )=F (x ), ∴F (x )为偶函数.。
人教版高中数学全套试题双基限时练17(2)

双基限时练(十七)1.设a >b >c ,且a +b +c =0,则下列不等式恒成立的是( )A .ab >bcB .ac >bcC .ab >acD .a |b |>c |b |解析 由题设,知a >0,c <0,且b >c ,∴ab >ac .答案 C2.已知a +b >0,b <0,那么a ,b ,-a ,-b 的大小关系是() A .a >b >-b >-a B .a >-b >-a >bC .a >-b >b >-aD .a >b >-a >-b解析 借助数轴:∴a >-b >b >-a .答案 C3.已知a <b <|a |,则以下不等式中恒成立的是( )A .|b |<-aB .ab >0C .ab <0D .|a |<|b |解析 由条件a <b <|a |,知a <0.∴|a |=-a ,∴a <b <-a .∴|b |<|a |=-a .故A 正确.答案 A4.若α,β满足-π2<α≤β≤π2,则α-β的取值范围是( )A .-π≤α-β<0B .-π<α-β≤0C .-π<α-β<πD .-π≤α-β≤π解析 ∵-π2<α≤β≤π2,∴-π2<α≤π2,-π2≤-β<π2.∴-π<α-β<π,又α-β≤0,∴-π<α-β≤0.答案 B5.已知a ,b ,c ,d ∈R 且ab >0,-c a <-d b ,则( )A .bc <adB .bc >ad C.a c >b d D.a c <b d解析 ∵ab >0,-c a <-d b ,∴-bc <-ad ,∴bc >ad .答案 B6.给出下列命题:①a >b ⇒ac 2>bc 2;②a >|b |⇒a 2>b 2;③a >b ⇒a 3>b 3;④|a |>b ⇒a 2>b 2.其中正确的命题是________.解析 当c =0时,①错;∵a >|b |≥0⇒a 2>b 2,∴②正确;∵a >b ⇒a 3>b 3,∴③正确;当b <0时,④错.答案 ②③7.给出四个条件:①b >0>a ;②0>a >b ;③a >0>b ;④a >b >0.能推得1a <1b 成立的是________.解析 ①b >0>a ⇒1a <1b ;②0>a >b ,则ab >0,∴1b >1a ;④a >b >0,则ab >0,∴1b >1a .答案 ①②④8.如图所示的程序框图是将一系列指令和问题用框图的形式排列而成,箭头将告诉你下一步到哪一个框图,阅读下边的程序框图,并回答下面的问题:(1)若a >b >c ,则输出的是__________;(2)若a =⎝ ⎛⎭⎪⎫1213,b =23,c =log 32,则输出的数是__________. 解析 该程序框图的功能是输出a ,b ,c 中的最大者.∵a 3=12,b 3=827<12,∴a >b ,又3b =2, 而3c =3log 32=log 38<2,∴b >c ,∴a >b 且a >c ,∴输出a .答案 (1)a (2)a9.已知α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫π2,π,求α-2β的范围. 解 ∵π2<β<π,∴-2π<-2β<-π.又0<α<π2,∴-2π<α-2β<-π2.10.已知f (x )=ax 2-c ,且-4≤f (1)≤-1,-1≤f (2)≤5,求f (3)的取值范围.解 由⎩⎪⎨⎪⎧f (1)=a -c ,f (2)=4a -c ,令f (3)=9a -c =mf (1)+nf (2), 知m =-53,n =83.∴f (3)=83f (2)-53f (1).∵-1≤f (2)≤5,∴-83≤83f (2)≤403.又-4≤f (1)≤-1,∴53≤-53f (1)≤203.∴-1≤83f (2)-53f (1)≤20.即-1≤f (3)≤20.11.已知1<a <2,3<b <4,求下列各式的取值范围.(1)2a +b ;(2)a -b ;(3)a b .解 (1)∵1<a <2,∴2<2a <4.又3<b <4,∴5<2a +b <8.(2)∵3<b <4,∴-4<-b <-3.又1<a <2,∴-3<a -b <-1.(3)∵3<b <4,∴14<1b <13.又1<a <2,∴14<a b <23.12.已知三个不等式①ab >0,②c a >d b ,③bc >ad .以其中两个作条件,余下的一个作结论,能否组成正确的命题?若能,能组成几个?写出所有正确的命题;若不能,说明理由.解 ∵②c a >d b ⇔bc -ad ab >0,③bc >ad ⇔bc -ad >0.根据实数的符法则有:①②⇒③,①③⇒②,②③⇒①.故能组成三个正确命题,它们分别是:⎭⎬⎫ab >0c a >d b ⇒bc >ad , ⎭⎬⎫ab >0bc >ad ⇒c a >d b, ⎭⎬⎫c a >d b bc >ad ⇒ab >0.。
人教B版高中数学必修二双基限时练17.docx

高中数学学习材料马鸣风萧萧*整理制作双基限时练(十七)基础强化1.经过点(-2,2),倾斜角是30°的直线的方程是()A.y+2=33(x-2) B.y+2=3(x-2)C.y-2=33(x+2) D.y-2=3(x+2)解析由题意直线的斜率k=tan30°=33,又因直线经过点(-2,2),所以直线方程为y-2=33(x+2).答案 C2.已知直线方程y+2=-x-1,则() A.直线经过定点(2,-1),斜率为-1 B.直线经过定点(-2,-1),斜率为1 C.直线经过定点(1,-2),斜率为-1 D.直线经过定点(-1,-2),斜率为-1 解析∵y-(-2)=-[x-(-1)],∴该直线过(-1,-2),斜率为-1.答案 D3.下列四个命题中的真命题是()A.经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示B.经过任意两个不同的点P1(x1,y1)、P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示C.不经过原点的直线都可以用方程xa+yb=1表示D.经过定点A(0,b)的直线都可以用方程y=kx+b表示解析直线的点斜式方程与斜截式方程不能表示斜率不存在的直线方程;直线的两点式方程与截距式方程不能表示斜率为0与斜率不存在的直线,另外截距式方程还不能表示过原点的直线.故选B.答案 B4.直线2x-3y+6=0的截距式方程为()A.x3+y2=1 B.x-3+y2=1C.x3+y-2=1 D.x-3+y-2=1解析直线2x-3y+6=0的横、纵截距分别为x=-3和y=2,∴它的截距式方程为x-3+y2=1.答案 B5.直线l经过(-2,2)且与直线y=x+6在y轴上的截距相等,则直线l的方程为()A.x+2y+6=0 B.x-2y-6=0C.2x-y+6=0 D.2x-y-6=0解析设所求直线方程为y=kx+6.∵过(-2,2),∴-2k+6=2,∴k=2,故l:2x-y+6=0.答案 C6.直线y =ax +b 和y =bx +a 在同一坐标系中的图形可能是( )答案 D7.过点(3,-4)且平行于x 轴的直线方程为__________. 答案 y =-48.若点M (a,12)在过点A (1,3),B (5,7)的直线上,则a =________. 解析 过A 、B 的直线方程为x -y +2=0, ∵M (a,12)在直线AB 上, ∴a -12+2=0,∴a =10. 答案 10能 力 提 升9.经过点(4,9),且在y 轴上的截距为-3的直线方程为________. 解析 k =9-(-3)4-0=3,∴y -9=3(x -4),即3x -y -3=0. 答案 3x -y -3=010.直线l 过(-3,2),(9,-1)两点,求直线l 的方程. 解 y -2-1-2=x +39+3,∴4y -8=-x -3,∴x +4y -5=0.∴直线l 的方程为x +4y -5=0.11.直线l 过A (-2,3),且与x 轴、y 轴分别交于M 、N 两点,若点A 恰好为MN 中点,求直线l 的方程.解 设M (m,0),N (0,n ),∵A 为MN 中点,∴⎩⎨⎧m +02=-2,0+n2=3,∴⎩⎪⎨⎪⎧m =-4,n =6,∴M (-4,0),N (0,6). ∴l 的方程为x -4+y6=1,即3x -2y +12=0.12.过点(-5,-4)作一直线l ,使它与两坐标轴相交且与两坐标轴所围成的三角形面积为5.解 方法一:设直线l 的方程为y +4=k (x +5),分别令y =0,x =0,得l 在x 轴、y 轴上的截距为:a =-5k +4k ,b =5k -4.由条件得ab =±10,∴-5k +4k ·(5k -4)=±10,得25k 2-30k +16=0无实数解;或25k 2-50k +16=0,解得k 1=85,k 2=25.故所求的直线方程为8x -5y +20=0或2x -5y -10=0.方法二:设l 的方程为x a +yb =1,因为l 经过点(-5,-4),则有-5a +-4b =1.① 又∵ab =±10,②联立①、②,得方程组⎩⎨⎧-5a+-4b =1,ab =±10.解得⎩⎨⎧a =-52,b =4,或⎩⎪⎨⎪⎧a =5,b =-2.因此,所求直线方程为8x -5y +20=0或2x -5y -10=0.品 味 高 考13.过点A (1,4)且在x 轴、y 轴上的截距的绝对值相等的直线条数为( )A .1B .2C .3D .4解析 当直线经过原点时,横截距、纵截距都为0,符合题意.当直线不经过原点时,设直线方程为x a +y b =1,由题意得⎩⎨⎧1a +4b =1,|a |=|b |,解得⎩⎪⎨⎪⎧ a =-3,b =3,或⎩⎪⎨⎪⎧a =5,b =5.综上可知,符合题意的直线共有3条. 答案 C。
高中数学人教B版课时作业:第三章 不等式17 Word版含答案

答案:C
5.小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则()
A.a<v< B.v=
C. <v< D.v=
解析:v= = < = .
因为 -a= = > =0,所以 >a,即v>a.故选A.
答案:A
6.已知函数y=x-4+ (x>-1),当x=a时,y取得最小值b,则a+b=()
所以 + = (2a+3b)=4+9+ + ≥13+2 =25,当且仅当 = ,即a=b= 时取等号,所以 + 的最小值为25,选B.
答案:B
4.设常数a>0,若9x+ ≥a+1对一切正实数x成立,则a的取值范围为________.
解析:∵x>0,a>0,∴9x+ ≥6a,当且仅当9x= ,即x= 时取等号.
A.-3 B.2
C.3 D.8
解析:y=x-4+ =x+1+ -5,
因数x>-1,所以x+1>0, >0.
所以由均值不等式得y=x+1+ -5≥2 -5=1,
当且仅当x+1= ,即(x+1)2=9,所以x+1=3,x=2时取等号,所以a=2,b=1,a+b=3,选C.
答案:C
7.已知x>0,则 的最大值为________.
答案:2
9.建造一个容积为8 m3,深为2 m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低总造价为________元.
解析:设池底的长和宽分别为a,b,则2ab=8,ab=4,总造价y=(2a+2b)×2×80+120ab=320(a+b)+480≥320×2 +480=1 760(当且仅当a=b=2 m时取等号).
北师大版高中数学必修一双基限时练17

双基限时练(十七) 指数函数的概念 指数函数y =2x和y =⎝⎛12⎭⎪⎫x的图像和性质 基础强化1.下列函数是指数函数的是( ) A.y =-3 B.y =3x +1 C.y =(3-1)xD.y =1x解析 ∵y =(3-1)x=⎝ ⎛⎭⎪⎫13x符合指数函数的定义,∴选C. 答案 C2.要得到y =2x +1+2的图像,只需将y =2x 的图像( ) A.向左平移1个单位,再沿y 轴向上平移2个单位 B.向右平移1个单位,再沿y 轴向上平移2个单位 C.向左平移1个单位,再沿y 轴向下平移2个单位 D.向右平移1个单位,再沿y 轴向下平移2个单位答案 A3.在同一直角坐标系中,y=2x与y=2-x的图像关于( ) A.x轴对称 B.y轴对称C.关于原点对称D.直线y=x对称解析由y=2x与y=2-x的图像可知答案为B.答案 B4.已知f(2x)=3x,则f(8)的值为( )A.3B.9C.27D.1解析由2x=8,得x=3,∴f(8)=f(23)=3×3=9.答案 B5.函数f(x)=2|x|的值域是( )A.(0,1] B.(0,1)C.[1,+∞) D.R解析∵|x|≥0,∴2|x|≥20=1,故值域为[1,+∞).答案 C6.函数y=|2x-2|的图像是( )解析 y =|2x -2|的图像是把y =2x -2的图像落在x 轴下方的部分沿x 轴翻折上去得到,考查四个选择支,只有B 符合.答案 B7.已知函数f (x )=a x -1的图像过点⎝⎛⎭⎪⎫2,12,其中a >0且a ≠1,则f (4)=________.解析 由f (x )=ax -1过点⎝⎛⎭⎪⎫2,12知,a 1=12,得a =12,∴f (4)=⎝ ⎛⎭⎪⎫123=18.答案 18能力提升8.将f (x )的图像向左平移2个单位,再向上平移一个单位,就得到y =2x 的图像,则f (x )=________.答案 2x -2-19.若函数y =2x +m 的图像在一、三、四象限,则m 的取值范围是________.解析 由题意得当x =0时,函数值1+m <0,得m <-1. 答案 (-∞,-1)10.判断下列函数是否是一个指数函数?y =x 2,y =8x ,y =2·4x ,y =(2a -1)x(a >12,a ≠1),y =(-4)x ,y =πx ,y =6x 3+2.解 由指数函数的定义知y =x 2,y =2·4x ,y =(-4)x ,y =6x 3+2都不符合y =a x 的形式,∴y =8x ,y =(2a -1)x (a >12,a ≠1),y =πx 是指数函数;y =x 2,y =2·4x ,y =(-4)x ,y =6x 3+2不是指数函数.11.设f (x )=3x,g (x )=⎝ ⎛⎭⎪⎫13x.(1)在同一坐标系中作出f (x )、g (x )的图像;(2)计算f (1)与g (-1),f (π)与g (-π),f (m )与g (-m )的值,从中你能得到什么结论?解 (1)函数f (x )与g (x )的图像如图所示:(2)f (1)=31=3,g (-1)=⎝ ⎛⎭⎪⎫13-1=3;f (π)=3π,g (-π)=⎝ ⎛⎭⎪⎫13-π=3π;f (m )=3m,g (-m )=⎝ ⎛⎭⎪⎫13-m=3m .从以上计算的结果看,两个函数当自变量取值互为相反数时,其函数值相等,即当指数函数的底数互为倒数时,它们的图像关于y 轴对称.12.已知一个指数函数y =f (x )过点(2,4), (1)求f (x )的解析式;(2)若函数g (x )=bf (x )+b -1f (x )+1为奇函数,求b 的值.解 (1)∵f (x )为指数函数, 故设f (x )=a x (a >0,且a ≠1), ∵f (x )过点(2,4),∴a 2=4,得a =2,∴f (x )=2x .(2)由(1)知g (x )=b ·2x+b -12x +1.∵g (x )为奇函数, ∴g (-x )=-g (x ), 即b ·2-x +b -12-x +1=-b ·2x +b -12x +1,b +(b -1)·2x 2x +1=-b ·2x +(1-b )2x +1,得1-b =b ,得b =12.考题速递13.函数y =⎩⎪⎨⎪⎧2x(x ≥0),2-x(x <0))的图像为( )答案 B。
高中数学新课程精品限时训练(17)

高考数学选择题、填空题限时训练文科(十七)一、 选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有 一项是符合题目要求的. 1. 已知命题p :两个共轭复数的和一定为实数;命题q :两个共轭复数的差一定为纯虚数,则下列命题中真命题的是( ). A .p q ∧B .()p q ⌝∧C .()p q ⌝∨D .()()p q ⌝⌝∨2. 设集合2{|20}A x x x =+->,集合2{|log [14]}B y y x x ==∈,,,则()A B =R( ).A .[01],B .(01],C .[12],D .(12],3.函数ln(1)y x =+的定义域为( ).A .[11]-,B .(11]-,C .[10)(01]-,,D .(10)(01]-,,4. 已知,a b均为单位向量,且(2)(2)2+⋅-=a b a b ,则向量,a b 的夹角为( ). A .6π B .3π C .32π D .65π 5. 设()f x 是定义在R 上的奇函数,且对任意的x ∈R 都有(2)(2)f x f x -=+,当(02)x ∈,时,()2x f x =,则(2015)f =( ).A .2-B .12-C .12D .26. 已知实数x y ,满足约束条件020y x y x x -⎧⎪+⎨⎪⎩≥≤≥,向量(2)x m =-,a 与(1)y =,b 平行,其中m ∈R ,则目标函数12mz ⎛⎫= ⎪⎝⎭的最大值为( ).A .14B .1C .2D .167. 一个四面体的三视图如图所示,则该四面体的体积是( ). A .16 B .13 C .23 D .438. 已知抛物线22(0)y px p =>上一点(1)(0)M m m >,到其焦点的距离为5,双曲线2221(0)x y a a-=>的左顶点为A ,若双曲线一条渐近线与直线AM 平行,则实数a 的值为( ). A .19B .14C .13D .12二、 填空题(本大题共6小题,每小题5分,共30分) 9.执行如图所示的程序框图,输出的S 值为 .10.已知直线20x y +-=被圆2220x y y a +-+=截得的弦长为2,则实数a 的值是 . 11.等比数列{}n a 中,42a =,75a =,则数列{}lg n a 的前10项和等于 .12. 某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了200分到450 分之间的2000名学生的成绩,并根据这2000名学生的成绩画出样本的频率分布直方图,如图所示.则成绩在[250350],内的学生共有 人.俯视图1主视图 左视图13. 已知直线2y x =+与曲线ln()y x a =+相切,则a 的值为 .14.设()f x 与()g x 是定义在同一区间[],a b 上的两个函数,若函数()()()=-h x f x g x 在[],a b 上有两个不同的零点,则称()f x 与()g x 在[],a b 上是“关联函数”.若()=f x 234-+x x 与()2=+g x x m 在[03],上是“关联函数”,则实数m 的取值范围是 .限时训练(十七)文科参考答案一、选择题二、填空题9. 133 10. 12-11. 5 12. 1000 13. 3 14. 31023⎡⎫⎪⎢⎣⎭,解析部分1. 解析 对于命题p ,“0a =且0b ≠”是“复数i a b +为纯虚数”的充分必要条件,而“0a =”是“复数i a b +为纯虚数”的必要不充分条件,故命题p 为假;对于命题q ,ii ia b +=-+,所以()()i i i 1i a b b +=+-=-,所以1a =,1b =-,即复数i a b +的虚部为1-,故命题q 为真.所以p ⌝为真,q ⌝为假, 则p q ∧为假,()p q ⌝∧为真,()p q ⌝∨为假,()()p q ⌝⌝∧为假. 故选B .2. 解析 易得{|21}A xx x =<->或,{|02}B y y=,则{|21}A x x =-R,所以()[01]A B =R ,. 故选A .3. 解析 由题意得2101011x x x ⎧-⎪+>⎨⎪+≠⎩,解得1110x x x -⎧⎪>-⎨⎪≠⎩,由此可得函数ln(1)y x =+的定义域为(10)(01]-,,. 故选D . 4. 解析 因为,a b 均为单位向量,所以(2)(2)+-=a b a b 222323--=-a a b b a b =2,所以32-a b =,所以3cos 2〈〉==-,a b a b |a ||b |.又[0]〈〉∈π,,a b ,所以56π〈〉=,a b . 故选D . 5. 解析 由()()22f x f x -=+可知,函数()f x 是以4为周期的周期函数, 所以()()()2015504411f f f =⨯-=-.又()f x 是定义在R 上的奇函数,所以()()112f f -=-=-. 故选A .6. 解析 因为向量(2)x m =-,a 与(1)y =,b 平行,所以()120x m y -⨯-=, 即2m x y =-,作出不等式组所表示的平面区域如图所示.由12mz ⎛⎫= ⎪⎝⎭,结合指数函数的单调性,知当m 最小时,z 最大.平移直线2m x y =-,由图可知,当其过点(02)B ,时,m 最小, 此时4max1162z -⎛⎫== ⎪⎝⎭. 故选D .7. 解析 将该几何体放入棱长为1的正方体中,如图所示.由三视图可知该四面体为11C ABA -,以面1ABA 为底,点11C B 为高,所以体积11111326V ⨯=⨯⨯=.故选A .8. 解析 由题意可知,(1)(0)M m m >,到抛物线22(0)y px p =>的准线2px =-的距离为5,A 1即42p-=-,得8p =,则点(14)M ,.可知0)A ,所以直线AM .由题=,解得19a =.故选A .9. 解析 根据框图,依次运行.第一次:0S =,1n =,120(2)1140S =+-+=-; 第二次:1S =-,2n =,221(2)2740S =-+-+=;第三次:7S =,3n =,327(2)3840S =+-+=;第四次:8S =,4n =,428(2)440S =+-+;第五次:40S =,5n =,5240(2)53340S =+-+=;第六次:33S =,6n =,6233(2)613340S =+-+=>,此时程序结束. 故输出的S 值为133.10. 解析 圆2220x y y a +-+=,即22(1)1x y a +-=-.从而圆心(01),,半径r =圆心到直线20x y +-=的距离2d ==弦长2l ==,所以221r d -=, 即1112a --=,解得12a =-. 11. 解析 数列的前10项和()1012101210lg lg lg lg S a a a a a a =+++=,在等比数列{}n a 中,()5512104710a a a a a ==.所以510lg105S ==.12. 解析 根据题意,可知(0.0020.00420.002)501a +++⨯=,解得0.006a =,则成绩在[250350],内的频率为(0.0040.006)500.5+⨯=, 则成绩在[250350],内的学生共有20000.51000⨯=(人).13. 解析 由题意可知切点为(),eaa a ,切线y b =的斜率为0,而e xy x =的导数为()1e xy x '=+,所以()e 1e 0a aa b a ⎧=⎪⎨+=⎪⎩.又e 0a>,所以11e a b =-⎧⎪⎨=-⎪⎩.因为0m >,所以112e e a m bm m m -⎛⎫+=-+- ⎪⎝⎭(当且仅当1emm =,即m =,所以m 14. 解析 设()()()()321120332h x f x g x x x x m x=-=--+,则()22h x x x '=--,容易求得函数()h x 在[]02,上单调递减,在[]23,上单调递增,因此只要m同时满足()()()200030h h h <⎧⎪⎨⎪⎩≥≥即可,解得31023m <≤,所以m 的取值范围是31023⎡⎫⎪⎢⎣⎭,.。
江苏省新课标数学限时训练17(必修2)

第17练 班级 姓名
1.在△ABC 中,已知030,35,5===A c b ,则面积S 为 .
2.已知点),2,5(),2,2(-N M 且点A 在x 轴上,,90 =∠MAN 则点A 的坐标为 .
3.在等差数列{n a }中, 已知3a +4a +5a +6a +7a =450,则=9S .
4.能表示图中阴影部分的不等式组为 .
5.已知圆()2
222210x y ax y a +--+-=(0<a <1),则原点O 与圆的位置关系为 .
6. 如图,矩形''''C B A O 是水平放置的一个平面图形的直观图''C O =2,则
原图形的面积为 .
7.已知2s i n (3)c πθπθ+=
+,则222sin 3sin cos cos θθθθ+-的值为 .
8.直线l :3x -y +m =0与圆C :x 2+y 2-2x -2=0相切,则直线l 在x 轴上的截距是 .
9.正四棱台上,下底面边长为a ,b ,侧棱长为c ,求它的高和斜高.
x '
y '
10.已知曲线22:2(410)10200C x y kx k y k ++++++=,其中1k ≠-;
(1)求证:曲线C 都是圆,并且圆心在同一条直线上;
(2)证明:曲线C 过定点;(3)若曲线C 与x 轴相切,求k 的值;。
2024高中数学计算限时训练(解析版)

2024高中数学计算限时训练(解析版)计算预备知识1.关于平方112=121122=144132=169142=196152=225162=256172=289182=324 192=361202=4002.关于平方根2≈1.4143≈1.7325≈2.2366≈2.4507≈2.64610≈3.1623.关于立方根32≈1.26033≈1.44234≈1.58735≈1.71036≈1.81737≈1.91339≈2.080310≈2.1544.关于ππ≈3.14π2≈1.57π3≈1.05π4≈0.79π5≈0.63π6≈0.52πe≈22.465.关于ee≈2.718e2≈7.389e3≈20.086e≈1.6491e≈0.3681≈0.135eπ≈23.14e26.关于lnln2≈0.693ln3≈1.099ln5≈1.609ln7≈1.946ln10≈2.3037.关于三角函数sinπ5≈0.588sinπ8≈0.383cosπ5≈0.809cosπ8≈0.924tanπ5≈0.727tanπ8≈0.4148.关于loglg2≈0.301lg3≈0.477lg7≈0.8459.关于阶乘4!=245!=1206!=7207!=504010.关于双重根号3±22=2±14±23=3±17±43=2±38±27=7±1 11.关于三角度数sin15°=cos75°=6-24sin75°=cos15°=6+24tan15°=2-3tan75°=2+3初中内容(简单回顾初中的相关计算)训练1(建议用时:10分钟)1.当x>2时, |x-2|=2.若|m-n|=n-m, 且|m|=4,|n|=3, 则m+n=3.用科学记数法表示248000004.若x,y为有理数, 且|x+2|+(y-2)2=0, 则x+y=5.若|a+2|+(b-3)2=0, 则a b=6.用科学记数法表示0.000000217.若有理数x,y的乘积xy为正, 则|x|x+|y|y+|xy|xy的值为8.已知|x|=3,|y|=5, 且|y-x|=x-y, 则2x+y=9.已知代数式x-3y2的值是5 , 则代数式x-3y22-2x+6y2的值是10.关于x,y的单项式2m3x2y的次数是11.已知代数式a2+2a-2b-a2+3a+mb的值与b无关, 则m的值是12.若a,b互为倒数, m,n互为相反数, 则(m+n)2+2ab=13.-2πx3y5的系数是14.已知a-3b-4=0, 则代数式4+2a-6b的值为15.已知代数式x2+x+1的值是3 , 那么代数式5x2+5x+8的值是16.若a,b互为相反数, m,n互为倒数, 则a+b+2mn-3=17.单项式4πx2y49的系数为 , 次数为训练2(建议用时:10分钟)1.已知3a2x-3b与-12a5b4y+5是同类项,则|x+5y|等于2.多项式-2ab2+4a5b-1的项分别是,次数是3.已知多项式x2-3kxy-y2+6xy-8不含xy项, 则k的值是4.单项式πx2y37的系数是 , 次数是;多项式5x2y-3y2的次数是5.已知(a+1)2+|b-2|=0, 则a b+1的值等于6.当x=时,式子2x+56与x+114+x的值互为相反数.7.已知代数式5x-2的值与110互为倒数, 则x=8.某件商品, 按成本提高40%后标价, 又以8折优惠卖出, 结果仍可获利15元, 则这件商品的成本价为9.当x=时, 32x+1与x-3的值相等10.当代数式1-(3m-5)2有最大值时, 关于x的方程3m-4=3x+2的解为11.若方程4x-1=5与2-a-x3=0的解相同, 则a的值为=b, 则当b=1时方程的解为12.已知13x-213.已知关于x的一元一次方程x+2m=-1的解是x=m, 则m的值是14.已知x=1是方程3x-m=x+2n的一个解, 则整式m+2n+2020的值为15.当x=时,式子3-2x与2+x互为相反数16.若-4a m b3与3a2-m b n-1可以合并成一项,则m n的值是17.已知x=3是方程11-2x=ax-1的解,则a=18.已知一元一次方程(m-4)x+m2=16的解是x=0, 则m=19.要使关于x,y的多项式my3+3nx2y+2y3-x2y+y不含三次项, 则2m+3n的值为训练3(建议用时:10分钟)1.已知a m=3,a n=9, 则a3m-n=2.当a时, (a-2)0=13.已知2x+5y-5=0, 则4x⋅32y的值是4.已知2a=3,2b=5, 则22a+2a+b=5.若3x=10,3y=5, 则32x-y=6.已知3x÷9y=27, 则2020+2y-x的值为7.已知x+4y=1, 则2x⋅16y=8.计算:(-3)2021×13 2020=9.已知2x=3,2y=5, 则22x-y=2020×(1.5)2021=10.-2311.若2x+y=3, 则4x⋅2y=12.若5x=18,5y=3, 则5x-y==0, 则y x=13.若(x-2)2+y+1314.计算:(-1)0+13 -1=15.计算:a2⋅a4+-3a32-10a6=16.已知6m=2,6n=3, 则6m+n2=17.已知2x+3-2x=112, 则x的值为18.已知x-y=5,xy=2, 则x2+y2=19分解因式:-xy2+4x=20.已知m-n=3, 则m2-n2-6n=21.已知25x2+kxy+4y2是一个完全平方式, 则k的值是=22.若m+1m=3, 则m2+1m223.若x2-(m-3)x+4是一个完全平方式, 则m的值是训练4(建议用时:10分钟)1.已知关于x的二次三项式x2+2kx+16是一个完全平方式, 则实数k的值为2.分解因式:4x2-4y2=3.分解因式:3xy3-27x3y=4.分解因式:4(a+b)2-(a-b)2=5.若x2-ax+1(x-1)的展开式是关于x的三次二项式, 则常数a=6.已知x+1x=3, 且0<x<1, 则x-1x=7.若a2+6a+b2-4b+13=0, 则a b=8.若y2+py+q=(y+3)(y-2), 则-pq=9.(-2a)3⋅1-2a+a2=10.已知a+b=2,ab=-2, 则(a-2)(b-2)=11.已知方程组x+2y=k,2x+y=2的解满足x+y=2, 则k的平方根为12.已知2x+5y=3, 用含y的式子表示x, 则x=13.若单项式-3a2m+1b8与4a3m b5m+n是同类项, 则这两个单项式的和为14.若方程组x+y=4,2x-y=-1的解也是2x-ay=14的解, 则a=15.已知二元一次方程组2x+y=7,x+2y=8,则x-y=x+y=16.不等式2x-12-3≤0的非负整数解共有个17.已知不等式12x-3≥2x与不等式3x-a≤0的解集相同, 则a=18.解不等式2+3x≤3-5x, 则x19.不等式组-13x>2,5-x>3的解集为20.不等式组2x-3<1,1-x≤3的解集为训练5(建议用时:10分钟)1.已知直角三角形的两边长分别为3,5 , 且第三边是整数, 则第三边的长度为2.若三角形的三边长分别为a,b,c, 且|a-b|+a2+b2-c2=0, 则△ABC的形状为3.已知直角三角形两直角边a,b满足a+b=17,ab=60, 则此直角三角形斜边上的高为4.在直角坐标系中, 点A(2,-2)与点B(-2,1)之间的距离AB=5.在直角三角形中,其中两边的长度分别为3,4 , 则第三边的长度是6.在直角三角形ABC中, ∠C=90°,BC=12,CA=5,AB=7.若a、b为实数, 且(a+3)2+b-2=0, 则a b的值为8.11的整数部分是小数部分是9.已知实数x,y满足3x+4+y2-6y+9=0, 则-xy的算术平方根的平方根的相反数等于10.计算:|-5|+(2-1)0=11.计算:20+|1-2|=12.3-7的相反数是 , 绝对值等于3的数是13.116的平方根是14.-8的立方根是,16的平方根是15.19-35的整数部分为a, 小数部分为b, 则2a-b=16.若x-4+(y+3)2=0, 则x+y=17.已知a是64的立方根, 2b-3是a的平方根,则114a-4b的算术平方根为训练6(建议用时:10分钟)1.在第三象限内到x轴的距离为2 , 到y轴的距离为3的点的坐标为2.在平面直角坐标系中, 点A(-2,1)关于y轴的对称点A 的坐标是3.点P(-1,1)先向左平移2个单位长度, 再向上平移3个单位长度得点P1, 则点P1的坐标是4.在平面直角坐标系中, 点M(a,b)与点N(5,-3)关于x轴对称, 则ab的值是5.如果点P(m,1-2m)在第四象限,那么m的取值范围是6.点A(3,-2)关于x轴对称的点的坐标为 , 关于y轴对称的点的坐标为7.在平面直角坐标系中, 过点P(6,8)作PA⊥x轴, 垂足为A, 则PA的长为8.点P(-2,6)到x轴的距离是9.若点A(m+2,-3)与点B(-4,n+5)在二、四像限的角平分线上, 则m+n=10.已知点A(m,3)与点B(2,n)关于x轴对称, 则(m+n)2020的值为11.已知点P(2m,m-1), 当m=时, 点P在二、四象限的角平分线上12.点A(-7,9)关于y轴的对称点是13.如果(3a-3b+1)(3a-3b-1)=80, 且a>b, 那么a-b的值为14.已知1<x<5, 化简(x-1)2+|x-5|=15.已知a-1+|b-5|=0,则(a-b)2的值是16.若|x+1|+y-2=0, 则x2+y2的值为17.a,b是自然数,规定a∇b=3×a-b3, 则2∇17的值是训练7(建议用时:15分钟)1.若一组数据1,2,x,4的平均数是2 , 则这组数据的方差为2.有40个数据, 其中最大值为35 , 最小值为14 , 若取组距为4 , 则分成的组数是3.小明抛掷一枚质地均匀的硬币, 抛掷100次硬币,结果有55次正面朝上,那么朝上的频率为4.当m=时, 解分式方程x-5x-3=m3-x会出现增根5.若(x-y-2)2+|xy+3|=0, 则3xx-y+2x y-x÷1y的值是6.分式方程3x2-x +1=xx-1的解为7.若关于x的方程axx-2=4x-2+1无解,则a的值是8.化简:1x-1-1x2-x=9.计算2aa2-16-1a-4的结果是10.若m+n=3,mn=2, 则1m+1n=11.若关于x的分式方程2x-ax-2=12的解为非负数, 则a的取值范围是12.若一次函数y=(a-1)x+a-8的图象经过第一、三、四象限, 且关于y的分式方程y-5 1-y+3=ay-1有整数解, 则满足条件的整数a的值之和为13.若整数a使关于x的不等式组x-12<1+x3,5x-2≥x+a有且只有四个整数解, 且使关于y的方程y+ay-1+2a1-y=2的解为非负数, 则符合条件的所有整数a的和为14.若关于x的分式方程2x-ax-2=13的解为非负数, 则实数a的取值范围是15.已知关于x的分式方程2a+1x+1=a有解,则a的取值范围是16.若分式方程2xx-1-m-1x-1=1有增根,则m的值是训练8(建议用时:15分钟)1.已知5x+1(x-1)(x+2)=Ax-1+Bx+2, 则实数A+B=2.当分式21-3m的值为整数时, 整数m的值为3.解方程:3-2xx-1=-1x-1.4.若x=3-1, 则代数式x2+2x-3的值是5.已知等式|a-2021|+a-2022=a成立, 则a-20212的值为6.若m=20202021-1, 则m3-m2-2022m+2020=7.计算(5-2)2021(5+2)2022的结果是8.已知xy=2,x+y=4, 则x y+yx=9.若M=1ab-a b⋅ab, 其中a=3,b=2, 则M的值为10.如果y=x-2+4-2x-5,那么y的值是11.已知16-n是整数, 则自然数n所有可能的值为12.已知20n是整数,则满足条件的最小正整数n为13.若3+5的小数部分是a,3-5的小数部分是b, 则a+b=14.已知整数x,y满足x+3y=72, 则x+y的值是15.已知x=5-12,y=5+12, 则x2+y2+xy的值是16.已知4a+3b与b+12a-b+6都是最简二次根式且可以合并, 则a+b的值为17.已知m,n是正整数, 若2m+5n是整数, 则满足条件的有序数对(m,n)为18.已知4a+1是最简二次根式, 且它与54是同类二次根式, 则a=训练9(建议用时:15分钟)1.设x1,x2是方程5x2-3x-2=0的两个实数根, 则1x1+1x2的值为2.方程(x-1)(x+5)=3转化为一元二次方程的一般形式是3.已知关于x的方程x2+2kx-1=0有两个不相等的实数根, 则k的取值范围是4.如果α,β(α≠β)是一元二次方程x2+2x-1=0的两个根, 则α2+α-β的值是5.写出一个以-1为一个根的一元二次方程6.已知一元二次方程(a-1)x2+7ax+a2+3a-4=0有一个根为零, 则a的值为7.设m,n是一元二次方程x2+3x-7=0的两个根, 则m2+4m+n=8.已知一元二次方程x2+3x-4=0的两个根为x1,x2, 则x21+x1x2+x22=9.已知关于x的方程x2-6x+p=0的两个根是α,β, 且2α+3β=20, 则p=10.已知一个正六边形的边心距是3, 则它的面积为11.同一个圆的内接正方形和正三角形的内切圆半径比为12.以半径为1的⊙O的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是13.用一个圆心角为120°, 半径为9cm的扇形围成一个圆雉侧面, 则圆雉的高是cm.14.有一组数据:-1,a,-2,3,4,2, 它们的中位数是1 , 则这组数据的平均数是15.已知一组数据3,4,6,8,x的平均数是6 , 则这组数据的中位数是16.五个整数从小到大排列后, 其中位数是4 , 如果这组数据的唯一众数是6 , 那么这组数据可能的最大的和是17.小明用s2=110x1-32+x2-32+⋯+x10-32计算一组数据的方差,那么x1+x2+x3+⋯+x10=训练10(建议用时:15分钟)1.一个不透明的布袋里放有5个红球、3个黄球和2个黑球, 它们除颜色外其余都相同,则任意摸出一个球是黑球的概率是2.二次函数y=-x2-2x+3的图象上有两点A-7,y1,B-8,y2, 则y1y2. (填">"∗"或"=")3.若关于x的函数y=ax2+(a+2)x+(a+1)的图象与x轴只有一个公共点, 则实数a的值为4.把抛物线y=x2+1先向右平移3个单位长度, 再向下平移2个单位长度, 得到的抛物线为5.若抛物线y=ax2+bx+c经过点(-1,10), 则a-b+c=6.若二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1), 则代数式1-a-b的值为7.若把二次函数y=x2-2x+3化为y=(x-m)2+k的形式, 其中m,k为常数, 则m+k=8.若抛物线y=-(x-m)(x-2-n)+m-2与抛物线y=x2-4x+5关于原点对称, 则m+n =9.已知△ABC∼△DEF, 且相似比为3:4,S△ABC=2cm2, 则S△DEF=cm210.在△ABC中, 点D,E分别在AB,AC上, 且DE⎳BC. 如果ADAB=35,DE=6, 那么BC=11.在△ABC中, 如果∠A,∠B满足|tan A-1|+cos B-122=0, 那么∠C=12.计算:sin230°+cos260°-tan245°=13.已知等腰三角形的两边长分别为5和8 , 则底角的余弦值为14.已知在△ABC中, ∠B=30°,∠C=45°,AB=4, 则BC的长为15.一个不透明的袋中放有4个红球和x个黄球,从中任意摸出一个恰为黄球的概率为34, 则x 的值为高中内容计算专题加强训练训练11对数运算(建议用时:5分钟)1.log312.log232 33.lg1004.lg0.0015.lg1100006.log1101007.ln e8.log31279.log12410.lg0.1211.lg310012.ln1e13.log214 214.log13915.写出高中阶段学过的对数运算公式.训练12指数运算(建议用时:13分钟)1.化简:56a 13b -2⋅-3a -12b -1 ÷4a 23⋅b -3 12(a >0,b >0).2.化简:a 3b 23ab 2a 14b 12 4a -13b 13(a >0,b >0).3.已知x 12+x -12=3, 求x 32+x -32+2x 2+x -2+3的值.4.已知a 2x=2+1, 求a 3x +a -3x a x +a -x 的值.5.x -1x 23+x 13+1+x +1x 13+1-x -x 13x 13-1.6.a 3+a -3 a 3-a -3a 4+a -4+1 a -a -1 +a 21+a -4 -2a -a -1.训练13指对运算(建议用时:5分钟)这个训练考查对数的相关计算, 要记住什么是指对互换、对数恒等变形、换底公式、对数运算公式,还有就是幂的运算.1.823-log 2510 -1+4log 23+4lg 22-4lg2+1.2.20222023 0+80.25⋅42+(32⋅3)6--23 23⋅49 -13-1.3.4(3-π)4+(0.008)-13-(0.25)12×12 -4.4.12lg 3249-43lg 8+lg 245+21+log 23.训练14错位相减(建议用时:20分钟)1.求b n =(2n -1)2n 的前n 项和.2.求b n=n22n-1的前n项和.3.求c n=(2n-1)4n-1的前n项和.4.求b n=(2n-1)13 n-1的前n项和.+2n的前n项和.5.求b n=n+14n训练15求值域(建议用时:20分钟)下列题目涉及了高中阶段不少求值域的方法, 要学会看到什么式子大概清楚使用什么方法或者说哪些方法来求解, 比如看到y=x-3+5-x就知道可以使用平方法来求解.1.y=5x-14x+2,x∈[-3,-1]..2.y=x2+2x2+13.y=2x+1-2x.4.y=x+4+9-x2..5.y=2x2+4x-7x2+2x+36.y=log3x+log x3-1.7.y=(x+3)2+16+(x-5)2+4.8.y=sin x+2cos x-2.9.y=ln x-x.训练16含参一元二次不等式(建议用时:20分钟)1.解不等式ax2>1.2.解不等式2ax2-(a+2)x+1>0(a≠0,a≠2).3.解不等式ax2+(a+2)x+1>0(a≠0).4.解不等式x2+ax+1<0.训练17解三角形周长(建议用时:20分钟)1.若A=π3,a=3, 求△ABC周长的取值范围.建议使用两种方法来解决:法一:余弦定理+不等式+三角形三边关系.法二:正弦定理+辅助角公式.2.若A=π3,a=3, 求锐角△ABC周长的取值范围.3.在△ABC中, B=π3, 若a+c=1, 求b的取值范围.训练18解三角形面积(建议用时:20分钟)1.若A=π3,a=3, 求S△ABC的最大值.建议使用两种方法来解决:法一:余弦定理+不等式.法二:正弦定理+辅助角公式十三角形面积公式.2.若A=π3,a=2, 求锐角△ABC面积的取值范围.3.在平面四边形ABCD中, AD=2,CD=4,△ABC为等边三角形, 求三角形BCD面积的最大值.训练19数列存在性(建议用时:20分钟)在新高考的模式下, 原本的数列压轴题被调整到了解答题的前两题,但是得分率并不乐观, 接下来的几篇训练着重练习数列中的存在性、奇偶项、绝对值、不等式(放缩)等问题.1.已知等差数列a n=2n-1, 求m,k m,k∈N∗的值, 使得a m+a m+1+a m+2+⋯+a m+k=65.2.已知等差数列a n=2n-7, 试求所有的正整数m, 使得a m a m+1a m+2为数列a n中的项.3.已知数列a n=1n(n+1), 问:是否存在正整数m,k, 使1akS k=1a m+19成立?若存在, 求出m,k的值;若不存在, 请说明理由.4.已知数列a n=3n,b n=2n-1, 数列b n的前n项和为T n, 问:是否存在正整数m,n,r, 使得T n=a m+r⋅b n成立?如果存在, 请求出m,n,r的关系式;如果不存在, 请说明理由.训练20数列奇偶项(建议用时:20分钟)常见的奇偶项问题(1)a n+a n+1=f(n)或a n⋅a n+1=f(n)类型;(2)(-1)n类型;(3)a2n,a2n-1类型.1已知数列a n满足a n+1+a n=11-n+(-1)n, 且0<a6<1. 记数列a n的前n项和为S n, 求当S n取最大值时n的值.2.已知数列a n满足a1=1,a n+1=12a n+n-1,n为奇数a n-2n,n为偶数记bn-a2n,求数列a n的通项公式.3.设S n为数列a n的前n项和, S n=(-1)n a n-12n,n∈N∗, 求数列a n的通项公式.4.已知等差数列a n=2n-1, 令b n=(-1)n-14na n a n+1, 求数列b n的前n项和T n.训练21数列绝对值(建议用时:20分钟)求数列绝对值的前n项和T n的一般步骤为:(1)求出数列的通项公式;(2)令a n≥0或a n≤0, 求出n的临界值m;(3)若等差数列的项先负后正, 则:T n=-S n,n≤m, -2S m+S n,n>m(4)若等差数列的项先正后负,则:T n=S n,n≤m, 2S m-S n,n>m.1.已知数列a n=53-3n, 求数列a n的前n项和T n.2.已知数列a n=2n-4n, 求数列a n的前n项和S n.3.已知数列a n=sin nπ6-34, 记数列a n 的前n项和为S n, 求S2021.训练22数列不等式(建议用时:20分钟)在学习裂项时我们遇到了数列不等式, 后来随着难度的加大, 各式各样的不等式出现, 比如:12+13+14+⋯+1n=ni=21i<ln n(n≥2)同时这类不等式还会和放缩联系在一起,即:1 n2=44n2<44n2-1=212n-1-12n+1,1n+2<n+2-n类似于这样的还有很多,在此就不一一列举了.1.已知数列a n=12 n-1,数列a n 的前n项和为T n,令b1=a1,b n=T n-1n+ 1+12+13+⋯+1n ⋅a n(n≥2), 求证:数列b n 的前n项和S n满足S n<2+2ln n.2.已知数列a n=2n-1的前n项和为S n, 设b n=1a n S n , 数列b n的前n项和为T n, 求证:T n<323.已知数列a n=3n-1,b n=2n-1, 求证:对任意的n∈N∗且n≥2, 有1a2-b2+1a3-b3+⋯+1a n-b n<32训练23导数单调性(建议用时:20分钟)1.讨论函数f (x )=ln x +ax x +1的单调性.2.已知函数f (x )=(ax +1)e x , 其中a ∈R 且a 为常数, 讨论函数f (x )的单调性.3.函数f (x )=xe x -ax 2-2ax +2a 2-a , 其中a ∈R , 讨论f (x )的单调性.训练24圆锥计算化简求值(建议用时:11分钟)这个训练主要考查学生在圆锥曲线上面的计算能力,一方面考查能否化简到底,另一方面考查能否对最后的式子进行求最值计算.1.已知1212-k 2k +22k 2+2k +4+1+12-k 2+2k +4-4-1 =0, 求k 的值.2.求24k 1+2k 2+-16k -44k 2-61+2k 224k 1+2k 2+-48k +124k 2-61+2k 2.3.求1+k 2⋅-12k 21+3k 2 2-4×12k 2-61+3k 2.4.已知12⋅21+k 21+k 2 64k 21+2k 22-241+2k 2 =225, 求k 的值.训练25联立后的韦达与判别式(建议用时:15分钟)1.写出Δ以及韦达式子:y2=8x,y=kx+b.2.写出Δ以及韦达式子:y=kx+2, x28+y22=1.3.写出Δ以及韦达式子:y=kx+m, x26+y2=1.4.写出Δ以及韦达式子:y=k(x-1)+2, x23+y2=1.(建议用时:20分钟)1.已知y=32(x-1),x24+y23=1,求y1-y2的值.2.已知x24+y2=1,x=my+3,m≠0, 两交点分别为M,N, 原点到直线的距离为d, 求当|MN|⋅d取得最大值时直线的方程.3.已知x=my-1,x24+y23=1,若y1-y2=1227, 求m的值.4.已知y=x+b,y2=4x,若y1x1+2+y2x2+2=0, 则求其直线方程.(建议用时:20分钟)1.化简(x+1)2+(y+4)2(x-a)2+(y-2a+2)2=λ(λ>0,λ≠1)之后为(x-2)2+(y-2)2=10, 求a,λ.2.已知直线x=ky+m与圆x2+y2=1联立得1+k2y2+2kmy+m2-1=0, 且k2+m=0, 若x1x2+y1y2=0, 求m,k.3.已知R=t2+16-2, 求y=t+R3-t-R31+t+R3⋅t-R3的最大值.4.已知直线y=kx+1与圆(x-2)2+(y-3)2=1相交, 若x1x2+y1y2=12, 求k.(建议用时:20分钟)1.当λ≠1时, 把(x+1)2+y2(x-1)2+y2=λ化简成圆的标准方程的形式.2.当k>0,k≠1时, 把x2+y2(x-a)2+y2=k化简成圆的标准方程的形式.3.已知0<m2<13, 求41-3m21+m2⋅6m2+11-3m2的取值范围.4.使用两种方式求S△ABC=121+k23+4k24+3k2的最小值.(建议用时:20分钟)1.已知x22+y2=1,x=my+1,且t≠1, 若要使y1x1-ty2x2-t是定值, 求t的值.2.已知x24-y25=1,x=my+3,若k1=y1x1+2,k2=y2x2-2, 求k1k2的值.3.已知x=ty+p2,y2=2px,求k1+k2=y1-px1+p2+y2-px2+p2的值.4.已知y=kx+m,x2+2y2=2,若x1x2+y1-1y2-1=0, 求m的值.1.已知圆(x +1)2+(y -2)2=20与过点B (-2,0)的动直线l 相交于M ,N 两点, 当|MN |=219时,求直线l 的方程.2.已知圆C :x 2+y 2-8y +12=0, 直线l :ax +y +2a =0, 当直线l 与圆C 相交于A ,B 两点,且|AB |=22时,求直线l 的方程.3.已知圆C :x 2+(y +1)2=4, 过点P (0,2)的直线l 与圆相交于不同的两点A ,B .(1)若OA ⋅OB =1, 求直线l 的方程.(2)判断PA ⋅PB 是否为定值. 若是, 求出这个定值;若不是, 请说明理由.4.已知圆C :(x +3)2+(y -3)2=4, 一动直线l 过点P (-4,0)且与圆C 相交于A ,B 两点, Q 是AB 的中点, 直线l 与直线m :x +3y +6=0相交于点E .(1)当|AB |=23时,求直线l 的方程.(2)判断PQ ⋅PE 的值是否与直线l 的倾斜角有关. 若无关, 请求出其值;若有关, 请说明理由.1.已知两点A (0,3),B (-4,0), 若P 是圆x 2+y 2-2y =0上的动点,求△ABP 面积的最大值.2.已知P (m ,n )是函数y =-x 2-2x 图象上的动点,求|4m +3n -21|的最小值.3.已知圆C :(x -1)2+(y -2)2=2, 点P (2,-1), 过P 点作圆C 的切线PA ,PB ,A ,B 为切点.求:(1)PA ,PB 所在直线的方程;(2)切线长|PA |.4.已知圆C 经过坐标原点, 且与直线x -y +2=0相切, 切点为A (2,4).(1)求圆C 的方程;(2)若斜率为-1的直线l 与圆C 相交于不同的两点M ,N , 求AM ⋅AN 的取值范围.1.已知直线l:x+3y-4=0, 圆C的圆心在x轴的负半轴上,半径为3, 且圆心C到直线l的距离为310 5.(1)求圆C的方程;(2)由直线l上一点Q作圆C的两条切线, 切点分别为M,N, 若∠MQN=120°, 求点Q的坐标.2.已知圆C:(x-3)2+(y-4)2=4, 直线l1过定点A(1,0).(1)若l1与圆相切, 求l1的方程;(2)若l1与圆相交于P,Q两点, 线段PQ的中点为M,l1与l2:x+2y+2=0的交点为N, 求证:|AM|⋅|AN|为定值.3.已知圆C的圆心在x轴上, 且与直线4x-3y-2=0相切于点-25,-65.(1)求圆C的方程;(2)经过点P(1,0)作斜率不为0的直线l与圆C相交于A,B两点, 若直线OA,OB的斜率之和等于8 , 求直线l的方程.4.已知P是直线3x+4y+8=0上的动点, PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线, A,B是切点.(1)求四边形PACB面积的最小值.(2)直线上是否存在点P, 使∠BPA=60°?若存在, 求出点P的坐标;若不存在, 说明理由.训练33解析解答(4)(建议用时:25分钟)1.已知直线l:y=2x+m和椭圆C:x24+y2=1,m为何值时, 直线l被椭圆C所截的弦长为20172.已知椭圆x23+y22=1(a>b>0), 过左焦点F1的斜率为1的直线与椭圆分别交于A,B两点,求|AB|.3.已知点A(0,-1)在椭圆C:x23+y2=1上, 设直线l:y=k(x-1)(其中k≠1 与椭圆C交于E,F两点, 直线AE,AF分别交直线x=3于点M,N. 当△AMN的面积为33时, 求k 的值.4.已知F是抛物线x2=4y的焦点,过点F的直线与曲线C交于A,B两点, Q(-2,-1), 记直线QA,QB的斜率分别为k1,k2, 求证:1k1+1k2为定值.训练34解析解答(建议用时:25分钟)1.已知椭圆C:x24+y2=1, 直线l:y=x+m与椭圆C交于A,B两点, P为椭圆的上顶点, 且|PA|=|PB|, 求m的值.2.已知椭圆E:x24+y22=1, 设直线y=kx-2被椭圆C截得的弦长为83, 求k的值.3.已知F 为椭圆x 22+y 2=1的左焦点, 设直线l 同时与椭圆和抛物线y 2=4x 各恰有一个公共交点,求直线l 的方程.4.已知抛物线x 2=4y 的焦点为F , 过点F 的直线l 交抛物线于P ,Q 两点, 交直线y =-1于点R , 求RP ⋅RQ 的最小值.训练35解析解答(6)(建议用时:25分钟)1.已知椭圆C :x 24+y 22=1, 点A (0,1), 若点B 在椭圆C 上, 求线段AB 长度的最大值.2.已知椭圆C :x 26+y 23=1, 直线y =x +1与椭圆交于A ,B 两点, 求AB 中点的坐标和AB 的长度.3.已知椭圆M :x 23+y 2=1, 直线l 与椭圆M 有两个不同的交点A ,B , 设直线l 的方程为y =x +m , 先用m 表示|AB |, 再求其最大值.4.已知抛物线y2=6x的弦AB经过点P(4,2), 且OA⊥OB(O为坐标原点), 求弦AB的长.训练36复合求导(1)(建议用时:3分钟)本训练考查复合函数求导, 这在一些导数压轴题中可能会出现..1.求x-1e x.2.求-34ln x+1+x23.求y=ln2x+1-1的导数.4.求y=cos(-2x)+32x+1的导数.训练37复合求导(2)(建议用时:6分钟)求下列函数的导数.1.y=ln x+1+x22.y=e x+1e x-13.y=2x sin(2x+5)4.y=3x e x-2x+e5.y=ln xx2+16.y=x2(2x+1)37.y=e-x sin2x训练38二面角求解(建议用时:10分钟)1.两平面的法向量为n1=(0,1,-2),n2=(-1,1,-2), 设二面角的平面角为α, 且为锐角, 则求二面角的大小.2.两平面的法向量为n1=(1,0,1),n2=(1,1,1), 求两平面所成锐二面角α的余弦值.3.一个平面的法向量n1=(x,y,z)满足方程组2x+y-z=0,x+2y-z=0,另一个平面的法向量n2=(0,2,0), 求两平面所成锐二面角α的余弦值.4.一个平面的法向量n1=x1,y1,z1满足方程组-x1+12z1=0,-y1+12z1=0,另一个平面的法向量n2=x2,y2,z2满足方程组2x2+2y2-2z2=0,2y2-2z2=0,求两平面所成锐二面角α的大小.训练39卡方计算(1)(建议用时:6分钟)本训练主要考查独立性检验的计算,附表: (1)独立性检验统计量K2值的计算公式:K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),n=a+b+c+d(2)独立性检验临界值表:PK2≥k00.150.100.050.0250.010.0050.001k0 2.072 2.706 3.841 5.024 6.6357.87910.828 1.列联表如下,计算K2:成绩优良人数成绩非优良人数总计男生92130女生11920总计203050数学成绩优秀数学成绩不优秀合计物理成绩优秀527物理成绩不优秀11213合计614204.列联表如下,计算K2:[0,150](150,475] [0,75]6416(75,115]1010训练40卡方计算(2)(建议用时:10分钟)1.列联表如下, 计算K2:甲有机肥料乙有机肥料合计质量优等603090质量非优等4070110合计100100200选择物理不选择物理合计男451560女202040合计65351003.列联表如下, 计算K2:视力正常视力不正常总计男生6040100女生401050总计100501504.列联表如下, 计算K2:女性男性合计直播电商用户8040120非直播电商用户404080合计12080200满意不满意合计工薪族403070非工薪族401050合计8040120训练41线性回归计算(1)(建议用时13分钟)本训练考查的是线性回归方程的相关计算, 参考公式:b=ni=1x i-xy i-yni=1x i-x2=ni=1x i y i-nx yni=1x2i-nx 2,a=y -bx ,y=bx+ar=ni=1x i-xy i-yni=1x i-x2ni=1y i-y2=ni=1x i y i-xxyni=1x2i-nx 2ni=1y2i-ny 21,某餐厅查阅了最近5次食品交易会参会人数x(万人)与餐厅所用原材料数量y(袋), 得到如下统计表:第一次第二次第三次第四次第五次参会人数x/万人13981012原材料y/袋3223182428根据所给5组数据,求出y关于x的线性回归方程.2.某连锁经营公司旗下的5个零售店某月的销售额和利润额如下表:商店名称A B C D E销售额x/千35679万元利润额y/百23345万元用最小二乘法计算利润额y关于销售额x的线性回归方程.3.某企业坚持以市场需求为导向, 合理配置生产资源, 不断改革、探索销售模式. 下表是该企业每月生产的一种核心产品的产量x(件)与相应的生产总成本y(万元)的五组对照数据:产量x/件12345生产总成本y3781012 /万元试求y与x的相关系数r, 并利用相关系数r说明y与x是否具有较强的线性相关关系(若|r|>0.75, 则线性相关程度很高, 可用线性回归模型拟合).训练42线性回归计算(2)(建议用时13分钟)1某专营店统计了近五年来该店的创收利润y(单位:万元)与时间t i(单位:年)的相关数据,列表如下:t i12345y i 2.4 2.7 4.1 6.47.9依据表中给出的数据, 是否可用线性回归模型拟合y与t的关系?请计算相关系数r并加以说明(计算结果精确到0.01, 若|r|>0. 8 , 则认为y与t高度相关, 可用线性回归模型拟合y 与t的关系).2某部门统计了某网红景点在2022年3月至7月的旅游收人y(单位:万元), 得到以下数据:月份x34567旅游收人y1012111220根据表中所给数据, 用相关系数r加以判断, 是否可用线性回归模型拟合y与x的关系?若可以,求出y关于x的线性回归方程;若不可以,请说明理由.3某汽车4S店关于某品牌汽车的使用年限x(年)和所支出的维修费用y(千元)有如下的统计资料:x23456y 2.0 3.5 6.0 6.57.0试求y关于x的线性回归方程.训练43期望求解(1)(建议用时:12分钟) 1.求期望值.P(X=0)=C02C23C25=P(X=1)=C12C13C25=P(X=2)=C22C03C25=2.求期望值.P(X=0)=C36C310=P(X=1)=C26C14C310=P(X=2)=C16C24C310=P(X=3)=C34C310=3.求分布列Y的期望值, 已知Y=5X,X的可能取值为0,1,2,3,4, 且X∼B4,34.(1)P(X=0)=C0434 014 4=(2)P(X=1)=C1434 114 3=(3)P(X=2)=C2434 214 2=(4)P(X=3)=C3434 314 1=(5)P(X=4)=C4434 414 0=训练44期望求解(2)(建议用时:12分钟)1随机变量ξ的可能取值为0,1,2,3,4.P (ξ=0)=1-34 21-232=P (ξ=1)=C 1234 1-34 1-23 2+C 1223 1-23 1-34 2=P (ξ=2)=34 21-23 2+1-34 223 2+C 12231-23 C 1234 1-34 =P (ξ=3)=34 2C 1223 1-23 +C 1234 1-34 23 2=P (ξ=4)=34223 2=求随机变量ξ的期望值.2随机变量X 的可能取值为2,3,4,5.P (X =2)=C 12C 22+C 22C 12C 310=P (X =3)=C 12C 24+C 22C 14C 310=P (X =4)=C 12C 26+C 22C 16C 310=P (X =5)=C 12C 28+C 22C 18C 310=求随机变量X 的期望值.(建议用时:20分钟)1.C r 12⋅212-r ≥C r -112⋅213-r ,C r 12⋅212-r ≥C r +112⋅211-r ,为整数, 则r =2.(-2)r C r 8≥(-2)r +2C r +28,(-2)r C r 8≥(-2)-2C r -28,为偶数, 则r =3.设m ,n ∈N ∗,m ≤n , 求证:C m +1n +1=n +1m +1C mn.4.用二项式定理证明:3n >2n 2+1n ≥3,n ∈N ∗ .(建议用时:20分钟)1.求r的取值范围:C r7⋅2r≥C r-17⋅2r-1,C r7⋅2r≥C r+17⋅2r+1 .2.求r的取值范围:C r8⋅2r≥C r+18⋅2r+1, C r8⋅2r≥C r-18⋅2r-1.3.求k的取值范围:C k1012 k≥C k-11012 k-1, C k1012 k≥C k+11012 k+1.4.展开:x-12x6=。
高中数学新课程精品限时训练(7)

1
3
C. 2
B.
1
2
或
6
6
).
2
D.
3
,则 A (
2
2
1
正视图
2
俯视图
2
侧视图
).
7.函数 f x x
A. 1,
1
在 , 1 上单调递增,则实数 a 的取值范围是(
ax
).
B. ,0 0,1
C. 0,1
A.
2
2
17
3
B.
).
C. 5
D.
3 5
5
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.把答案填在题中的横线上.
13. 若 cos
3
,且角 的终边经过点 P x, 2 ,则 P 点的横坐标 x 是
2
14. 等差数列 an 中, a5 a6 4 ,则 log 2 2 2 2 2
A.
1
5
B.
4.下列说法正确的是(
2
5
C.
).
3
5
D.
).
4
5
).
A.若 p q 为真命题,则 p q 为真命题
B.命题“若 cos x cos y ,则 x y ”的否命题是“若 cos x cos y ,则 x y ”
C. “ x 0 ”是“ x 2 x 0 ”的充分不必要条件
限时训练(七)
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分.在每个小题给出的四个选项中,只有一项是
符合 x x 2 x 0 , B x x„ 1或x… 1 ,则 A
2021年高二下学期限时训练17含答案

2021年高二下学期限时训练17含答案班级姓名学号成绩1.已知集合A = { 2, 1,0,1,2 },集合B = { x | x2 < 1 },订正反则AB = .2.若关于x的函数在区间(1,∞)上是单调增函数,则实数a的取值范围是.3.曲线在处的切线方程为.4.“a = 2”是“直线和直线平行”的条件.5.函数的值域为.6.已知为锐角,,则.7.已知函数的图象与正半轴交点的横坐标由小到大构成一个公差为的等差数列,将该函数的图像向左平移个单位后,所得图像关于原点对称,则的最小值为.8.已知函数,对于上的任意,有如下条件:①;②;③;④.其中能使恒成立的条件是▲ .(写出所有序号)9.(本小题满分16分)某企业生产一种产品,日产量基本保持在万件到0万件之间,由于受技术水平等因素的影响,会产生一些次品,根据统计分析,其次品率()与日产量(万件)之间基本满足关系:目前,每生产万件合格的产品可以盈利万元,但每生产万件次品将亏损万元.(1)试将生产这种产品每天的盈利额(万元)表示为日产量(万件)的函数;(2)问当生产这种产品的日产量约为多少时(精确到万件),企业可获得最大利润?订正反18.(1)()(1)1040(1050)T x x P x P x P =⋅-⨯-⋅⨯=-…………… 2分 ()()21105015,501111050510250255x x x x x x x ⎧⎛⎫-⨯ ⎪⎪⎝⎭⎪=⎨⎡⎤⎛⎫⎪--+< ⎪⎢⎥⎪⎝⎭⎣⎦⎩≤≤≤…………… 6分(2)当时,; …………… 8分当时,∵,令,得(舍去).…………… 12分 ∵在(5,10]上图象不间断,∴在(5,10]上最大值. …………… 13分∵,在上最大值在时取得. …………… 15分答:当生产这种产品的日产量为万件时,企业可获得最大利润.……… 16分37392 9210 鈐35691 8B6B 譫'33736 83C8 菈D32843 804B 聋35244 89AC 覬33012 80F4 胴33820 841C 萜24444 5F7C 彼cN39709 9B1D 鬝36946 9052 遒31672 7BB8 箸。
「精品」高中数学课时达标训练十七北师大版必修1

课时达标训练(十七)一、选择题1.(重庆高考)函数y =x +x -1的定义域是( )A .(-1,+∞)B .[-1,+∞)C .(-1,1)∪(1,+∞)D .[-1,1)∪(1,+∞)2.函数y =log 2|x |的图像大致是( )3.已知函数y =log 2x ,其反函数y =g (x ),则g (x -1)的图像是( )4.设f (x )是奇函数,当x >0时,f (x )=log 2x ,则当x <0时,f (x )等于( ) A .-log 2x B .log 2(-x ) C .log x 2 D .-log 2(-x ) 二、填空题5.集合A ={y |y =log 2x ,x >1},B =yy =⎝ ⎛⎭⎪⎫12x,x >1,则(∁R A )∩B =________.6.若函数y =f (x )是函数y =a x(a >0,且a ≠1)的反函数,其图像经过点(a ,a ),则f (x )=________.7.若log 2a <log 2b <0,则a ,b,1的大小关系是________. 18.函数f (x )=log 2x 在区间[a,2a ](a >0)上的最大值与最小值之差为________. 三、解答题9.求下列函数的定义域. (1)y =lg(x +1)+2x 2-x;(2)y =log (x -2)(5-x ).10.已知函数f (x )=log 2(x +1),g (x )=log 2(1-x ). (1)若函数f (x )的定义域为[3,63],求函数f (x )的最值;(2)求使f (x )-g (x )>0的x 的取值范围; (3)判断函数F (x )=f (x )+g (x )的奇偶性.答案1.解析:选C 由题意得⎩⎪⎨⎪⎧x +1>0,x -1≠0,∴⎩⎪⎨⎪⎧x >-1,x ≠1,故选C.2.解析:选A y =log 2|x |=⎩⎪⎨⎪⎧log 2x x ,log 2-x x,分别作图知A 正确.3.解析:选C 由已知g (x )=2x,∴g (x -1)=2x -1,故选C.4.解析:选D ∵x <0,∴-x >0,∴f (-x )=log 2(-x ). 又∵f (x )是奇函数,∴f (-x )=-f (x ), ∴f (x )=-log 2(-x ).5.解析:∵x >1,∴log 2x >log 21=0,∴A ={y |y >0}.而当x >1时,0<⎝ ⎛⎭⎪⎫12x <⎝ ⎛⎭⎪⎫121,∴B =y 0<y <12.∴(∁R A )∩B ={y |y ≤0}∩⎩⎨⎧⎭⎬⎫y 0<y <12=∅.答案:∅6.解析:∵y =f (x )的图像过点(a ,a ), ∴其反函数y =a x的图像过点(a ,a ), ∴a a=a =,∴a =12,∴f (x )=.答案:7.解析:log 2a <log 2b <0⇔log 2a <log 2b <log 21, ∵y =log 2x 在(0,+∞)上是增函数,∴a <b <1. 答案:a <b <18.解析:∵f (x )=log 2x 在区间[a,2a ]上是增函数, ∴f (x )max -f (x )min =f (2a )-f (a )=log 22a -log 2a =log 22=1. 答案:19.解:(1)要使函数有意义,需⎩⎪⎨⎪⎧x +1>0,2-x >0,即⎩⎪⎨⎪⎧x >-1,x <2,∴函数的定义域为(-1,2). (2)要使函数有意义.需⎩⎪⎨⎪⎧ 5-x >0,x -2>0,x -2≠1,即⎩⎪⎨⎪⎧x <5,x >2,x ≠3.∴定义域为(2,3)∪(3,5).10.解:(1)由题意知,3≤x ≤63,∴4≤x +1≤64, ∵函数y =log 2x 是增函数,∴log 24≤log 2(x +1)≤log 264,∴2≤f (x )≤6, ∴f (x )的最大值为6,最小值为2. (2)f (x )-g (x )>0⇔f (x )>g (x ), 即log 2(x +1)>log 2(1-x ),则⎩⎪⎨⎪⎧x +1>0,1-x >0,x +1>1-x ,得:0<x <1,∴x 的取值范围为(0,1).(3)要使函数F (x )=f (x )+g (x )有意义,需⎩⎪⎨⎪⎧1+x >0,1-x >0,即-1<x <1,∴定义域为(-1,1) 又F (-x )=f (-x )+g (-x ) =log 2(1-x )+log 2(1+x )=log 2(1-x 2)=f (x )+g (x )=F (x ), ∴F (x )为偶函数.。
2021年高中数学课时达标训练十七北师大版必修

2021年高中数学课时达标训练十七北师大版必修一、选择题1.(重庆高考)函数y =lg x +1x -1的定义域是( )A .(-1,+∞)B .[-1,+∞)C .(-1,1)∪(1,+∞)D .[-1,1)∪(1,+∞)2.函数y =log 2|x |的图像大致是( )3.已知函数y =log 2x ,其反函数y =g (x ),则g (x -1)的图像是( )4.设f (x )是奇函数,当x >0时,f (x )=log 2x ,则当x <0时,f (x )等于( ) A .-log 2x B .log 2(-x ) C .log x 2 D .-log 2(-x ) 二、填空题5.集合A ={y |y =log 2x ,x >1},B =yy =⎝ ⎛⎭⎪⎫12x,x >1,则(∁R A )∩B =________.6.若函数y =f (x )是函数y =a x(a >0,且a ≠1)的反函数,其图像经过点(a ,a ),则f (x )=________.7.若log 2a <log 2b <0,则a ,b,1的大小关系是________. 18.函数f (x )=log 2x 在区间[a,2a ](a >0)上的最大值与最小值之差为________. 三、解答题9.求下列函数的定义域. (1)y =lg(x +1)+2x 2-x;(2)y =log (x -2)(5-x ).10.已知函数f (x )=log 2(x +1),g (x )=log 2(1-x ). (1)若函数f (x )的定义域为[3,63],求函数f (x )的最值; (2)求使f (x )-g (x )>0的x 的取值范围; (3)判断函数F (x )=f (x )+g (x )的奇偶性.答案1.解析:选C 由题意得⎩⎪⎨⎪⎧x +1>0,x -1≠0,∴⎩⎪⎨⎪⎧x >-1,x ≠1,故选C.2.解析:选A y =log 2|x |=⎩⎪⎨⎪⎧log 2x x >0,log 2-x x <0,分别作图知A 正确.3.解析:选C 由已知g (x )=2x,∴g (x -1)=2x -1,故选C.4.解析:选D ∵x <0,∴-x >0,∴f (-x )=log 2(-x ). 又∵f (x )是奇函数,∴f (-x )=-f (x ), ∴f (x )=-log 2(-x ).5.解析:∵x >1,∴log 2x >log 21=0,∴A ={y |y >0}.而当x >1时,0<⎝ ⎛⎭⎪⎫12x <⎝ ⎛⎭⎪⎫121,∴B =y 0<y <12.∴(∁R A )∩B ={y |y ≤0}∩⎩⎨⎧⎭⎬⎫y 0<y <12=∅.答案:∅6.解析:∵y =f (x )的图像过点(a ,a ), ∴其反函数y =a x的图像过点(a ,a ), ∴a a=a =,∴a =12,∴f (x )=. 答案:7.解析:log 2a <log 2b <0⇔log 2a <log 2b <log 21, ∵y =log 2x 在(0,+∞)上是增函数,∴a <b <1. 答案:a <b <18.解析:∵f (x )=log 2x 在区间[a,2a ]上是增函数, ∴f (x )max -f (x )min =f (2a )-f (a )=log 22a -log 2a =log 22=1. 答案:19.解:(1)要使函数有意义,需⎩⎪⎨⎪⎧x +1>0,2-x >0,即⎩⎪⎨⎪⎧x >-1,x <2,∴函数的定义域为(-1,2). (2)要使函数有意义.需⎩⎪⎨⎪⎧ 5-x >0,x -2>0,x -2≠1,即⎩⎪⎨⎪⎧x <5,x >2,x ≠3.∴定义域为(2,3)∪(3,5).10.解:(1)由题意知,3≤x ≤63,∴4≤x +1≤64, ∵函数y =log 2x 是增函数,∴log 24≤log 2(x +1)≤log 264,∴2≤f (x )≤6, ∴f (x )的最大值为6,最小值为2. (2)f (x )-g (x )>0⇔f (x )>g (x ), 即log 2(x +1)>log 2(1-x ),则⎩⎪⎨⎪⎧x +1>0,1-x >0,x +1>1-x ,得:0<x <1,∴x 的取值范围为(0,1).(3)要使函数F (x )=f (x )+g (x )有意义,需⎩⎪⎨⎪⎧1+x >0,1-x >0,即-1<x <1,∴定义域为(-1,1) 又F (-x )=f (-x )+g (-x ) =log 2(1-x )+log 2(1+x )=log 2(1-x 2)=f (x )+g (x )=F (x ), ∴F (x )为偶函数.。
高中数学新课程精品限时训练(20)
限时训练(二十)一、选择题:本大题共8小题,每小题5分,共40分. 1、sin 240o的值为( ).A.2 B .12 C .12- D.2- 2、已知双曲线C :22214x y b-=经过点()4,3,则双曲线C 的离心率为( ). A .12BCD3、执行如图所示的程序框图,则输出的z 的值是( ).A .21B .32C .34D .644、已知命题p :x ∀∈R ,20x >,命题q :,αβ∃∈R ,使()tan αβ+=tan α+tan β,则下列命题为真命题的是( ).A .p q ∧B .()p q ∨⌝C .()p q ⌝∧D .()p q ∧⌝5、设集合{}22A x a x a =-<<+,{}2450B x x x =--<,若A B ⊆,则实数a 的取值范围为( ). A .[]1,3 B .()1,3 C .[]3,1-- D .()3,1--6、已知数列{}n a 满足13a =,且143n n a a +=+()*n ∈N ,则数列{}n a 的通项公式为( ).A .2121n -+ B .2121n -- C .221n +D .221n-7、已知函数()223f x x x =-++,若在区间[]4,4-上任取一个实数0x ,则使()00f x …成立的概率为( ). A .425B .12C .23D .18、设函数()3233f x x ax bx =++有两个极值点1x ,2x ,且[]11,0x ∈-,[]21,2x ∈,则点(),a b 在aOb 平面上所构成区域的面积为( ). A .14 B .12 C .34D .1二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中的横线上. 9、已知i 为虚数单位,复数1iiz -=,则z = . 10、已知向量(),1x =a ,()2,y =b ,若()1,1+=-a b ,则x y += .11、某种型号的汽车紧急刹车后滑行的距离y km 与刹车时的速度x km/h 的关系可以用2y ax =来描述,已知这 种型号的汽车在速度为60km/h 时,紧急刹车后滑行的距离为b km .一辆这种型号的汽车紧急刹车后滑行的距离12、若x ,y 满足11010y x y x y ⎧⎪--⎨⎪+-⎩………,则z x =+的最小值为 .13、一个几何体的三视图如图所示,图中直角三角形的直角边长均为1,则该几何体体积为 .14、设点()0,1M x ,若在圆O :221x y +=上存在点N ,使得45OMN ∠=o,则0x 的取值范围是 .限时训练(二十)答案部分一、选择题二、填空题9. 10. 3-11. 12. 113. 1614. []1,1-。
2021_2022学年新教材高中数学课时练十七第二单元等式与不等式2.2.4第2课时均值不等式的应用

十七 均值不等式的应用基础全面练(15分钟·35分)1.已知正数x ,y 满足x +2y -xy =0,则x +2y 的最小值为( ) A .8 B .4 C .2 D .0【解析】选A.由x +2y -xy =0,得2x +1y=1,且x>0,y>0.所以x +2y =(x +2y)×⎝⎛⎭⎫2x +1y =4y x +x y+4≥4+4=8,当且仅当x =2y 时等号成立.2.(2021·某某高一检测)若实数x ,y 满足xy +6x =4⎝⎛⎭⎫0<x<23 ,则4x +1y 的最小值为( ) A .4 B .8 C .16 D .32【解析】选B.因为xy +6x =4,故4x +1y =xy +6x x +1y =y +6+1y,因为0<x<23 ,故y =4-6x x =4x -6>0,故y +6+1y ≥8,当且仅当y =1,x =47 时等号成立,故4x +1y的最小值为8. 3.对于直角三角形的研究,中国早在商朝时期商高就提出了“勾三股四玄五”勾股定理的特例,而西方直到公元前6世纪,古希腊的毕达哥拉斯才提出并证明了勾股定理.如果一个直角三角形的斜边长等于5,那么这个直角三角形面积的最大值等于( ) A .254 B .252C .25D .5【解析】选A.设直角三角形的斜边为c ,直角边分别为a ,b ,由题意知c =5,则a 2+b 2=25, 则三角形的面积S =12ab ,因为25=a 2+b 2≥2ab ,所以ab≤252,则三角形的面积S =12 ab≤12 ×252 =254 ,当且仅当a =b =522 时取等号,即这个直角三角形面积的最大值等于254.4.已知正实数a ,b 满足a +1b =2,则2a +2b 的最小值为________.【解析】由题意,正实数a ,b 满足a +1b=2,则2a +2b =12 ×⎝⎛⎭⎫2a +2b ⎝⎛⎭⎫a +1b =12 ×⎝⎛⎭⎫4+2ab +2ab ≥12 ×⎝⎛⎭⎫4+22ab ·2ab =4,当且仅当2ab=2ab ,即ab =1时,取得最小值,其最小值为4. 答案:45.某公司购买抗击新冠肺炎疫情物资200 t 用于支援抗疫一线,平均分成若干次进行购买,每次购买的运费为2万元,一年的总存储费用数值(单位:万元)恰好为每次的购买吨数数值,要使一年的总运费与总存储费用之和最小,则每次购买该种货物的吨数是________. 【解析】设每次购买抗疫物资x t ,则需要购买200x 次,则一年的总运费为200x ×2=400x ,一年的总存储费用为x 万元,所以一年的总运费与总存储费用为400x +x≥2400x ·x =40,当且仅当400x=x , 即x =20时等号成立,故要使一年的总运费与总存储费用之和最小,每次应购买该种货物20 t. 答案:206.(2021·高一检测)围建一个面积为40 m 2的矩形场地,要求矩形场地的一面利用旧墙(旧墙足够长),利用的旧墙需维修,其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m 的进出口,如图所示,已知旧墙的维修费用为5元/米,新墙的造价为20元/米,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)(1)将y 表示为x 的函数;【解析】设矩形的另一边长为a m ,则y =5x +20()x -2 +20·2a =25x +40a -40, 由已知ax =40,得a =40x ,所以y =25x +1 600x-40()x>2 .(2)试确定x ,使修建此矩形场地围墙的总费用最小,并求出最小总费用. 【解析】 因为x>2, 所以25x +1 600x≥225x·1 600x=400,所以y =25x +1 600x-40≥360,当且仅当25x =1 600x,即x =8时,等号成立.即当x =8 m 时,修建围墙的总费用最小,最小总费用是360元.【补偿训练】国内某知名企业为适应发展的需要,计划加大对研发的投入,据了解,该企业原有100名技术人员,年人均投入m 万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员x 名(x ∈N *且x ∈[45,60]),调整后研发人员的年人均投入增加2x%,技术人员的年人均投入调整为m ⎝⎛⎭⎫a -3x50 万元. (1)要使这100-x 名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数.【思路引导】根据题意列式,并求解即可;【解析】由题,可列方程为(100-x)m(1+2x%)=100m ,则x =50,故调整后的技术人员的人数为50.(2)是否存在这样的实数a ,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出a 的X 围,若不存在,说明理由. 【思路引导】需满足两个不等关系:①技术人员的年人均投入不减少,②研发人员的年总投入始终不低于技术人员的年总投入,列出不等式求解即可.【解析】存在,a 的X 围为⎣⎡⎦⎤235,5 .由题意得(100-x)m(1+2x%)≥mx ⎝⎛⎭⎫a -3x50 , 则a≤100x +x 25 +1,在x ∈N *且x ∈[45,60]上恒成立,因为100x +x25 +1≥1+2100x ·x25=1+4=5,当且仅当100x =x25即x =50时取等号,所以a≤5.又因为m ⎝⎛⎭⎫a -3x 50 ≥m 即a≥1+3x 50 ,设t =1+3x50 ,则t 在x ∈N *且x ∈[45,60]上为增函数,当x =60时,t 取得最大值为235 ,所以a≥235,综上,a 的X 围为⎣⎡⎦⎤235,5 .综合突破练 (30分钟·60分) 一、单选题(每小题5分,共20分)1.(2021·某某高一检测)若a>0,b>0且2a +b =4,则1ab 的最小值为( )A .2B .12C .4D .14【解析】选B.因为a>0,b>0,所以2a +b≥22ab ,当且仅当2a =b 时等号成立,又2a +b =4,所以22a·b ≤4即0<ab≤2,当且仅当a =1,b =2时等号成立,所以1ab ≥12 ,所以1ab 的最小值为12.2.若a>0,b>0,a +b =ab ,则a +b 的最小值为( ) A .2 B .4 C .6 D .8【解析】选B.因为a>0,b >0,a +b =ab≤(a +b )24 ,所以a +b≥4,当a =b =2时取等号,则a +b 的最小值为4.3.若对任意x>0,xx 2+3x +1 ≤a 恒成立,则a 的取值X 围是( )A .⎩⎨⎧⎭⎬⎫a ⎪⎪a ≥15B .⎩⎨⎧⎭⎬⎫a ⎪⎪a >15 C .⎩⎨⎧⎭⎬⎫a ⎪⎪a <15 D .⎩⎨⎧⎭⎬⎫a ⎪⎪a ≤15 【解析】选A.因为对任意x>0,xx 2+3x +1≤a 恒成立,所以对x ∈(0,+∞),a≥⎝ ⎛⎭⎪⎫x x 2+3x +1max , 又因为x ∈(0,+∞), 所以x x 2+3x +1 =1x +1x+3 ≤12x·1x +3 =15 ,当且仅当x =1时等号成立,所以a≥15 .【补偿训练】已知正实数x ,y 满足x +4y -xy =0,若x +y≥m 恒成立,则实数m 的取值X 围为________. 【解析】由于x +4y -xy =0,即x +4y =xy ,等式两边同时除以xy 得,4x +1y =1,由均值不等式可得x +y =(x +y)⎝⎛⎭⎫4x +1y =4y x +xy+5≥24y x ·x y +5=9,当且仅当4y x =xy,即当x =2y =6时,等号成立,所以,x +y 的最小值为9.因此,实数m 的取值X 围为m≤9.答案:m≤94.已知正实数m ,n 满足m +n =1,且使1m +16n 取得最小值.若y =5m ,x =4n 是方程y =x α的解,则α =( )A .-1B .12 C .2 D .3【解析】选C.1m +16n =⎝⎛⎭⎫1m +16n (m +n) =1+16m n +n m +16=17+16m n +nm≥17+216m n ·nm=25. 当且仅当16m n =nm 又m +n =1,即m =15 ,n =45时,上式取等号,即1m +16n 取得最小值时, m =15 ,n =45 , 所以y =25,x =5, 25=5α. 得α=2.【误区警示】本题易错之处在于不能灵活的利用均值不等式得到m 与n 的解,从而无法代入方程的所求结果.二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分) 5.下列不等式一定成立的是( ) A .x 2+14 >x ()x>0 B .x +1x ≥2()x>0C .x 2+1≥2|x|()x ∈RD .1x 2+1>1()x ∈R【解析】选BC.对于选项A ,当x =12 时,x 2+14 =x ,所以A 不一定成立;对于选项B ,当x>0时,不等式x +1x≥2成立,所以B 一定成立;对于选项C ,不等式x 2+1-2|x|=(|x|-1)2≥0,即x 2+1≥2|x|恒成立,所以C 一定成立; 对于选项D ,因为 x 2+1≥1,所以 0<1x 2+1 ≤1,所以D 不成立. 6.设a +b =2(a>0,b>0),则12a +ab取最小值时下列结论正确的是( )A .a =23B .ab =1C .12a +a b =54D .12a +a b =14【解析】选AC.因为a +b =2,所以12a +a b =24a +a b =a +b 4a +a b =a 4a +b 4a +a b ≥a 4a +2b 4a ×a b =a 4a +1=54. 当且仅当b 4a =ab,即b 2=4a 2时等号成立.又因为a>0,b>0,a +b =2,所以解得a =23 ,b =43 ,所以12a +a b 的最小值为54 .三、填空题(每小题5分,共10分)7.已知一次函数y =-12 x +1的图像分别与x 轴、y 轴相交于A ,B 两点,若动点P(a ,b)在线段AB 上,则ab 的最大值是________,取得最值时a 的值为________. 【解析】因为A(2,0),B(0,1),所以0≤b≤1,由题意得a =2-2b ,ab =(2-2b)b =2(1-b)·b≤2·⎝ ⎛⎭⎪⎫1-b +b 2 2 =12 .当且仅当1-b =b ,即b =12 时等号成立,此时a =1,因此当b =12 ,a =1时,ab 的最大值为12 .答案:1218.如图有一X 单栏的竖向X 贴的海报,它的印刷面积为72 dm 2(图中阴影部分),上下空白各宽2 dm ,左右空白各宽1 dm ,则四周空白部分面积的最小值是________dm 2.【解析】设阴影部分的高为x dm ,则宽为72x dm ,四周空白部分的面积是y dm 2.由题意,得y =(x +4)⎝⎛⎭⎫72x +2 -72=8+2⎝⎛⎭⎫x +144x ≥8+2×2x·144x=56(dm 2). 当且仅当x =144x ,即x =12 dm 时等号成立.答案:56四、解答题(每小题10分,共20分) 9.已知a>0,b>0,a +b =1,求证: (1)1a +1b +1ab≥8. 【证明】因为a +b =1,a>0,b>0, 所以1a +1b +1ab=2⎝⎛⎭⎫1a +1b . 所以1a +1b =a +b a +a +b b =2+a b +b a ≥2+2=4,所以1a +1b +1ab ≥8(当且仅当a =b =12 时等号成立).(2)⎝⎛⎭⎫1+1a ⎝⎛⎭⎫1+1b ≥9. 【证明】方法一:因为a>0,b>0,a +b =1, 所以1+1a =1+a +b a =2+b a ,同理1+1b =2+a b ,所以⎝⎛⎭⎫1+1a ⎝⎛⎭⎫1+1b =⎝⎛⎭⎫2+b a ⎝⎛⎭⎫2+a b =5+2⎝⎛⎭⎫b a +a b ≥5+4=9.所以⎝⎛⎭⎫1+1a ⎝⎛⎭⎫1+1b ≥9(当且仅当a =b =12 时等号成立). 方法二:⎝⎛⎭⎫1+1a ⎝⎛⎭⎫1+1b =1+1a +1b +1ab , 由(1)知,1a +1b +1ab≥8,故⎝⎛⎭⎫1+1a ⎝⎛⎭⎫1+1b =1+1a +1b +1ab ≥9. 当且仅当a =b =12时取等号.10.经观测,某公路段在某时段内的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间有函数关系:y =900vv 2+5v +1 000(v>0).(1)在该时段内,当汽车的平均速度v 为多少时车流量y 最大? 【解析】y =900vv 2+5v +1 000 =900v +1 000v+5,因为v +1 000v ≥2v·1 000v=2010 ,所以y =900v +1 000v +5 ≤9002010+5 =180410+1.当且仅当v =1 000v,即v =1010 时等号成立.所以当汽车的平均速度v =1010 千米/小时时车流量y 最大.(2)为保证在该时段内车流量至少为12千辆/小时,则汽车的平均速度应控制在什么X 围内? 【解析】令900vv 2+5v +1 000≥12,则可化为v 2-70v +1 000≤0,即(v -20)(v -50)≤0,解得20≤v≤50.所以汽车的平均速度应控制在20千米/小时到50千米/小时X 围内. 应用创新练1.某种商品原来每件售价为25元,年销售量为8万件.(1)据市场调查,若价格每提高1元,销售量将相应减少2 000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元? 【解析】设每件定价为x 元,依题意得⎝ ⎛⎭⎪⎫8-x -251×0.2 x≥25×8,整理得x 2-65x +1 000≤0,解得25≤x≤40.所以要使销售的总收入不低于原收入,每件定价最多为40元.(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x 元.公司拟投入16 (x 2-600)万元作为技改费用,投入50万元作为固定宣传费用,投入15 x 万元作为浮动宣传费用.试问:当该商品明年的销售量a 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.【解析】依题意不等式ax≥25×8+50+16 (x 2-600)+15 x 有解,等价于x >25时a≥150x +16 x+15 有解,因为150x +16x≥2150x ·16x =10(当且仅当x =30时,等号成立),所以a≥10.2. 所以当该商品明年的销售量a 至少应达到10.2万件时,才可能使明年的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元.2.我们学习了二元均值不等式:设a>0,b>0,a +b2 ≥ab ,当且仅当a =b 时,等号成立.利用均值不等式可以证明不等式,也可以利用“和定积最大,积定和最小”求最值. (1)对于三元均值不等式请猜想:设a>0,b>0,c>0,a +b +c3≥________,当且仅当a =b =c 时,等号成立(把横线补全).【解析】设a>0,b>0,c>0,a +b +c 3 ≥3abc , 当且仅当a =b =c 时,等号成立.答案:3abc(2)利用(1)猜想的三元均值不等式证明:设a>0,b>0,c>0,a +b +c =1,求证:(a 2+b 2+c 2)(a +b +c)≥9abc.【解析】设a>0,b>0,c>0,因为a +b +c≥33abc >0,a 2+b 2+c 2≥33a 2b 2c 2 >0, 所以(a 2+b 2+c 2)(a +b +c)≥93a 3b 3c 3 =9abc , 即(a 2+b 2+c 2)(a +b +c)≥9abc.(3)利用(1)猜想的三元均值不等式求最值:设a>0,b>0,c>0,a +b +c =1,求(1-a)(1-b)(1-c)的最大值. 【解析】设a>0,b>0,c>0,a +b +c 3≥3abc ,所以abc≤⎝ ⎛⎭⎪⎫a +b +c 3 3,又因为a +b +c =1,0<1-a<1,0<1-b<1,0<1-c<1,所以(1-a)(1-b)(1-c)≤⎝ ⎛⎭⎪⎫1-a +1-b +1-c 3 3=827 ,当且仅当a =b =c =13 时,等号成立.所以(1-a)(1-b)(1-c)的最大值为827.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.一个四面体的三视图如图所示,则该四面体的四个面中最大的面积是( ).
A. B. C. D.
8.已知方程 恰有三个不相等的实数根,则实数 的取值范围是( ).
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,共30分)
9.执行如图所示的程序框图,输出的 值为.
10.已知△ 的面积为 , ,则 的值为.
.因为 ,所以 为奇函数,则 ,即 ,由 知 的最小值为 .故选D.
7.解析将该几何体放入棱长为1的正方体中,如图所示,由三视图可知该四面体为 ,由直观图可知,最大的面为面 ,在等边三角形 中, ,所以面积 .故选A.
8.解析令函数 , ,方程 恰有三个不相等的实数根等价于函数 和 的图像恰有三个不同的交点,在同一坐标系内作出其图像如图所示,当直线 介于直线 和 之间时符合题意,故实数 的取值范围是 .故选B.
高考数学选择题、填空题限时训练理科(十七)
一、选择题:本大题共 小题,每小题 分,共 分. 在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设 是虚数单位,复数 满足 ,则在复平面内, 的共轭复数 所对应的点的坐标为( ).
A. B. C. D.
2.设集合 ,集合 ,则 ( ).
A. B. C. D.
3. 函数 的定义域为( ).
A. B.
C. D.
4.在平面直角坐标系 中,已知定点 区域 : 的面积为 ,且动点 ,则 的最小值为( ).
A. B. C. D.
5.将 件不同奖品全部奖给 个学生,每人至少一件奖品,则不同的获奖情况种数是( ).
A. B. C. D.
6.已知函数 ,若将其图像先向右平移 个单位,再向下平移 个单位后得到函数 的图像,且 ,则 的最小值为( ).
双曲线 的一条渐近线的距离为 ,则该双曲线的离心率为.
14.设 与 是定义在同一区间 上的两个函数,若函数 在
上有两个不同的零点,则称 与 在 上是“关联函数”.若
与 在 上是“关联函数”,则实数 的取值范围
是.
限时训练(十七)理科参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
答案
B
A
C
D
A
D
A
B
二、填空题
则成绩在 内的学生共有 (人).
12.解析由题意, .可以解得直线 与曲线 的交点坐标为 和 ,所以封闭图形的面积 ,
解得 .故答案为 .
13.解析因为 , ,所以 ,解得 ,所以 .双曲线 的渐近线方程为 .即 .因为点 到其中一条渐进线的距离为 ,则 ,解得 ,所以 ,故 .
14.解析设 ,
则 ,容易求得函数 在 上单调递减,在 上单调递增,因此只要 同时满足 即可,解得 ,所以 的取值范围是 .
9.解析根据框图,依次运行.
第一次: , , ;
第二次: , , ;
第三次: , , ;
第四次: , , ;
第五次: , , ;
第六次: , , ,所以 ,而△ 的面积
,所以 ,
所以 .
11.解析根据题意,可知 ,解得 ,
则成绩在 内的频率为 ,
11.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了 分到 分之间的 名学生的成绩,并根据这 名学生的成绩画出样本的频率分布直方图(如图),则成绩在 内的学生共有人.
12.若直线 与曲线 在第二象限内围成的封闭图形的面积为 ,则实数 的值是.
13.已知抛物线 上一点 到其焦点 的距离为 ,点 到
,解得 ,设点 ,则 ,
平移直线 ,由图知,当其过点 时 最小,此时 .故选D.
5.解析由题意,需要将 件奖品分成 组,有“ ”和“ ”两类分法.若按“ ”分组,有 种分法;若按“ ”分组,有 种分法.所以不同的获奖情况共有 种.故选A.
6.解析由题意, ,将其图像先向右平移 个单位,再向下平移 个单位后的解析式为
9. 10. 11. 12.
13. 14.
解析部分
1.解析由 , ,得 .
所以 的共轭复数 ,则在复平面内, 对应的点的坐标为 .故选B.
2.解析易得 , ,
则 ,所以 .故选A.
3.解析由题意,得 ,解得 ,由此可得函数 的
定义域为 .故选C.
4.解析作出不等式所表示的平面区域 的示意图,可求得 , , ,由题意知 ,此时区域 的面积即△ABC的面积,所以
