2013年全国名校中考模拟试卷分类汇编4因式分解
(全国120套)2013年中考数学试卷分类汇编(打包53套)-22.doc

列方程解应用题(一元一次方程不等式)1、(2013•资阳)在芦山地震抢险时,太平镇部分村庄需8组战士步行运送物资,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人;若按每组人11,2、(2013•宜昌)地球正面临第六次生物大灭绝,据科学家预测,到2050年,目前的四分之一到一半的物种将会灭绝或濒临灭绝,2012年底,长江江豚数量仅剩约1000头,其数量年平均下降的百分率在13%﹣15%范围内,由此预测,2013年底剩下江豚的数量可能为()头.3、(2013•呼和浩特)某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少要答对多少道题?,4、(2013•黔西南州)义洁中学计划从荣威公司购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元.(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?(2)根据义洁中学实际情况,需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的.请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?,5、(2013•莱芜)某学校将周三“阳光体育”项目定为跳绳活动,为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的两倍多4元,且购买2条长跳绳与购买5条短跳绳的费用相同.(1)两种跳绳的单价各是多少元?(2)若学校准备用不超过2000元的现金购买200条长、短跳绳,且短跳绳的条数不超过长跳绳的6倍,问学校有几种购买方案可供选择?由题意得:.所以长跳绳单价是由题意得:6、(2013年临沂)为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B 两种型号的学习用品共1000件,已知A 型学习用品的单价为20元,B 型学习用品的单价为30元.(1)若购买这批学习用品用了26000元,则购买A,B 两种学习用品各多少件?(2)若购买这批学习用品的钱不超过28000元,则最多购买B 型学习用品多少件? 解析:(1)设购买A 型学习用品x 件,则B 型学习用品为(1000)x -. ……(1分)根据题意,得2030(1000)26000x x +-=………………(2分)解方程,得x =400.则10001000400600x -=-=.答:购买A 型学习用品400件,购买B 型学习用品600件. ………………………(4分)(2)设最多购买B 型学习用品x 件,则购买A 型学习用品为(1000)x -件. 根据题意,得20(1000)+3028000x x -≤……………………(6分)解不等式,得800x ≤.答:最多购买B 型学习用品800件. ……………………(7分)7、(2013•绥化)为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙(1)求m 的值;(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a (50<a <70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?)依题意得,=,8、(2013•恩施州)某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.(1)求这两种商品的进价.(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?y,.29≤m≤329、(2013•黄冈)为支援四川雅安地震灾区,某市民政局组织募捐了240吨救灾物资,现准如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.10、(2013•益阳)“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.(2)利用“‘益安’车队需要一次运输沙石165吨以上”得出不等式求出购买方案即可.解答:解:(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,根据题意得:,解之得:.∴“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆;11、(2013•德州)设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值改变第4列改变第2行(2)∵每一列所有数之和分别为2,0,﹣2,0,每一行所有数之和分别为﹣1,1,解得:≤a,12、(2013•温州)一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.(1)求从袋中摸出一个球是黄球的概率;(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于,问至少取出了多少个黑球?=;由题意,得≥,解得:x≥=13、(2013•泸州)某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.(1)符合题意的组建方案有几种?请你帮学校设计出来;(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?由题意,得,当x=18时,30﹣x=12;当x=19时,30﹣x=11;当x=20时,30﹣x=10.故有三种组建方案:方案一,中型图书角18个,小型图书角12个;方案二,中型图书角19个,小型图书角11个;方案三,中型图书角20个,小型图书角10个.(2)方案一的费用是:860×18+570×12=22320(元);方案二的费用是:860×19+570×11=22610(元);方案三的费用是:860×20+570×10=22900(元).14、(2013•眉山)2013年4月20日,雅安发生7.0级地震,某地需550顶帐蓬解决受灾群众临时住宿问题,现由甲、乙两个工厂来加工生产.已知甲工厂每天的加工生产能力是乙工厂每天加工生产能力的1.5倍,并且加工生产240顶帐蓬甲工厂比乙工厂少用4天.①求甲、乙两个工厂每天分别可加工生产多少顶帐蓬?②若甲工厂每天的加工生产成本为3万元,乙工厂每天的加工生产成本为2.4万元,要使这批救灾帐蓬的加工生产总成本不高于60万元,至少应安排甲工厂加工生产多少天?﹣3y+2.4×15、(2013•攀枝花)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.(1)求购进甲,乙两种钢笔每支各需多少元?(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?,16、(2013•自贡)某校住校生宿舍有大小两种寝室若干间,据统计该校高一年级男生740人,使用了55间大寝室和50间小寝室,正好住满;女生730人,使用了大寝室50间和小寝室55间,也正好住满.(1)求该校的大小寝室每间各住多少人?(2)预测该校今年招收的高一新生中有不少于630名女生将入住寝室80间,问该校有多少种安排住宿的方案?,17、(2013•遵义)2013年4月20日,四川雅安发生7.0级地震,给雅安人民的生命财产带来巨大损失.某市民政部门将租用甲、乙两种货车共16辆,把粮食266吨、副食品169吨全部运到灾区.已知一辆甲种货车同时可装粮食18吨、副食品10吨;一辆乙种货车同时可装粮食16吨、副食11吨.(1)若将这批货物一次性运到灾区,有哪几种租车方案?(2)若甲种货车每辆需付燃油费1500元;乙种货车每辆需付燃油费1200元,应选(1)中的哪种方案,才能使所付的费用最少?最少费用是多少元?食和副食品数不少于所需要运送的吨数列出一元一次不等式组,求解后再根据x是正整数设计租车方案;(2)方法一:根据所付的费用等于两种车辆的燃油费之和列式整理,再根据一次函数的增减性求出费用的最小值;方法二:分别求出三种方案的燃油费用,比较即可得解.解答:解:(1)设租用甲种货车x辆,租用乙种货车为(16﹣x)辆,根据题意得,,18、(2013•牡丹江)某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过105700元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A 型每台售价3000元,B型每台售价3200元,预计销售额不低于123200元.设A型电脑购进x台、商场的总利润为y(元).(1)请你设计出进货方案;(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?(3)商场准备拿出(2)中的最大利润的一部分再次购进A型和B型电脑至少各两台,另一部分为地震灾区购买单价为500元的帐篷若干顶.在钱用尽三样都购买的前提下请直接写出购买A型电脑、B型电脑和帐篷的方案..19、(2013年南京) 某商场促销方案规定:商场内所有商品案标价的80%出售,同时,当顾消费金额(元) 300~400 400~500 500~600 600~700 700~900 …返还金额(元) 30 60 100 130 150 …注:300~400表示消费金额大于300元且小于或等于400元,其他类同。
(全国120套)2013年中考数学试卷分类汇编(打包53套)

代数综合2、(2013•攀枝花)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).(1)求抛物线的解析式;(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.,解得PN•OA=×3(﹣x2﹣3x)=﹣(x+)2+,∴当x=﹣时,S有最大值,此时点P的坐标为(﹣,﹣);(3)在y轴上是否存在点M,能够使得△ADE是直角三角形.理由如下:∵y=x2+2x﹣3=y=(x+1)2﹣4,t+4 t=)﹣,﹣,﹣3、(2013达州压轴题)如图,在直角体系中,直线AB 交x 轴于点A (5,0),交y 轴于点B ,AO 是⊙M 的直径,其半圆交AB 于点C ,且AC=3。
取BO 的中点D ,连接CD 、MD 和OC 。
(1)求证:CD 是⊙M 的切线;(2)二次函数的图象经过点D 、M 、A ,其对称轴上有一动点P ,连接PD 、PM ,求△PDM 的周长最小时点P 的坐标; (3)在(2)的条件下,当△PDM 的周长最小时,抛物线上是否存在点Q ,使16QAMPDMSS=?若存在,求出点Q 的坐标;若不存在,请说明理由。
解析:(1)证明:连结CM. ∵OA 为⊙M 直径, ∴∠OCA=90°. ∴∠OCB=90°. ∵D 为OB 中点, ∴DC=DO.∴∠DCO=∠DOC.………………………(1分) ∵MO=MC,∴∠MCO=∠MOC.………………………(2分)∴∠DCM=∠DCO+∠MCO=∠DOC+∠MOC=∠DOM=90°.………………………(3分) 又∵点C 在⊙M 上,∴DC 是⊙M 的切线.………………………(4分) (2)解:在Rt △ACO 中,有OC=22AC OA -.又∵A 点坐标(5,0), AC=3, ∴OC=2235-=4. ∴tan ∠OAC=OAOB ACOC =.∴534OB =.解得 OB=320. 又∵D 为OB 中点,∴OD=310.D 点坐标为(0,310).………………………(5分)连接AD ,设直线AD 的解析式为y=kx+b,则有 ⎪⎩⎪⎨⎧=+=.05,310b k b j 解得⎪⎪⎩⎪⎪⎨⎧-==.32,310k b ∴直线AD 为y=-32x+310. ∵二次函数的图象过M (25,0)、A(5,0),∴抛物线对称轴x=415.………………………(6分)∵点M 、A 关于直线x=415对称,设直线AD 与直线x=415交于点P,∴PD+PM 为最小. 又∵DM 为定长,∴满足条件的点P 为直线AD 与直线x=415的交点.………………………(7分)当x=415时,y=-32⨯415+310=65.故P 点的坐标为(415,65).………………………(8分)(3)解:存在. ∵S △PDM =S △DAM -S △PAM =21AM ·y D -21AM ·y P =21AM(y D -y p ). S △QAM =21AM ·Q y ,由(2)知D (0,310),P(415,65),∴61×(310-65)=y Q 解得y Q =±125………………………(9分) ∵二次函数的图像过M(0,25)、A(5,0),∴设二次函数解析式为y=a(x-25)(x-5).又∵该图象过点D (0,310),a ×(-25)×(-5)=310,a=154.∴y=154(x-25)(x-5).………………………(10分) 又∵C 点在抛物线上,且y Q =±125,∴154(x-25)(x-5)=±125.解之,得x 1=42515+,x 2=42515-,x 3=415.∴点Q 的坐标为(42515+,125),或(42515-,125),或(415,-125).…………(12分)4、(2013•天津压轴题)已知抛物线y 1=ax 2+bx+c (a≠0)的对称轴是直线l ,顶点为点M .若自变量x 和函数值y 1的部分对应值如下表所示: (Ⅰ)求y 1与x 之间的函数关系式;(Ⅱ)若经过点T (0,t )作垂直于y 轴的直线l′,A 为直线l′上的动点,线段AM 的垂直平分线交直线l 于点B ,点B 关于直线AM 的对称点为P ,记P (x ,y 2). (1)求y 2与x 之间的函数关系式;12t 的取值范围.0 )得出,)>,><也符合题意.).+bx++bx+上,∴,解得,∴y1与x之间的函数关系式为:y1=﹣x2+x+;(II)∵y1=﹣x2+x+,∴y1=﹣(x﹣1)2+3,(+ x x+,x﹣x+,,y1﹣y2=﹣(x﹣1)+3﹣[(x﹣1)+]=(x﹣1)2+,若3t﹣11≠0,要使y1<y2恒成立,只要抛物线y=(x﹣1)2+开口方向向下,且顶点(1,)在轴下方,∵3﹣t<0,只要3t﹣11>0,解得t>,符合题意;<t=t≥5、(2013年江西省压轴题)已知抛物线抛物线y n=-(x-a n)2+a n(n为正整数,且0<a1<a2<…<a n)与x轴的交点为A n-1(b n-1,0)和A n(b n,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.(1)求a1,b1的值及抛物线y2的解析式;(2)抛物线y3的顶点坐标为(,);依此类推第n条抛物线y n的顶点坐标为(,);所有抛物线的顶点坐标满足的函数关系是;(3)探究下列结论:①若用A n-1A n表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出A n-1A n;②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.【答案】解:(1)∵y1=―(x―a1)2+a1与x轴交于点A0(0,0),∴―a12+ a1=0,∴a1=0或1.由已知可知a1>0,∴a1=1.即y1=―(x―1)2+1方法一:令y1=0代入得:―(x―1)2+1=0,∴x1=0,x2=2,∴y1与x轴交于A0(0,0),A1(2,0)∴b1=2,方法二:∵y1=―(x―a1)2+a1与x轴交于点A0(0,0),∴―(b1―1)2+1=0,b1=2或0,b1=0(舍去).∴b1=2.又∵抛物线y2=―(x―a2)2+a2与x轴交于点A1(2,0),∴―(2―a2)2+ a2=0,∴a2=1或4,∵a2> a1,∴a2=1(舍去).∴取a2=4,抛物线y2=―(x―4)2+4.(2)(9,9);(n2,n2)y=x.详解如下:∵抛物线y2=―(x―4)2+4令y2=0代入得:―(x―4)2+4=0,∴x1=2,x2=6.∴y2与x轴交于点A1(2,0),A2(6,0).又∵抛物线y3=―(x―a3)2+a3与x轴交于A2(6,0),∴―(6―a3)2+a3=0∴a3=4或9,∵a3> a3,∴a3=4(舍去),即a3=9,∴抛物线y3的顶点坐标为(9,9).由抛物线y1的顶点坐标为(1,1),y2的顶点坐标为(4,4),y3的顶点坐标为(9,9),依次类推抛物线y n的顶点坐标为(n2,n2).∵所有抛物线的顶点的横坐标等于纵坐标,∴顶点坐标满足的函数关系式是:y= x;③∵A0(0,0),A1(2,0),∴A0A1=2.又∵y n=―(x―n2)2+n2,令y n =0,∴―(x ―n 2)2+n 2=0,即x 1=n 2+n ,x 2=n 2-n ,∴A n -1(n 2-n ,0),A n (n 2+n ,0),即A n -1 A n =( n 2+n )-( n 2-n )=2 n . ②存在.是平行于直线y =x 且过A 1(2,0)的直线,其表达式为y =x -2.【考点解剖】 本题考查了二次函数的一般知识,求字母系数、解析式、顶点坐标;字母表示数(符号意识),数形结合思想,规律探究,合情推理,解题方法的灵活性等等,更重要的是一种胆识和魄力,敢不敢动手,会不会从简单,从特殊值入手去探究一般规律,画一画图帮助思考,所有这些都是做学问所必需的品质和素养,也是新课程改革所倡导的精神和最高境界.【解题思路】 (1)将A 0坐标代入y 1的解析式可求得a 1的值;a 1的值知道了y 1的解析式也就确定了,已知抛物线就可求出b 1的值,又把(b 1,0)代入y 2,可求出a 2 ,即得y 2的解析式;(2)用同样的方法可求得a 3 、a 4 、a 5 ……由此得到规律2n a n =,所以顶点坐标满足的函数关系式是:y = x ;(3)由(2)可知0112232,4,6A A A A A A ===得12n n A A n -=; 最后一问我们会猜测这是与直线y =x 平行且过A (2,0)的一条直线,用特殊值法取2(4)4,2y x y x ⎧=--+⎨=-⎩得112,0x y =⎧⎨=⎩和225,3x y =⎧⎨=⎩,得所截得的线段长度为试试,求出的值也为222(),2y x n n y x ⎧=--+⎨=-⎩得21211,1x n y n ⎧=+⎪⎨=-⎪⎩和22222,4x n y n ⎧=-⎪⎨=-⎪⎩,求得所截得的线段长度也为. 【解答过程】 略.【方法规律】 掌握基础(知识),灵活运用(方法),敢于动手,不畏艰难.【关键词】二次函数 抛物线 规律探究6、(2013年武汉压轴题)如图,点P 是直线l :22--=x y 上的点,过点P 的另一条直线m 交抛物线2x y =于A 、B 两点. (1)若直线m 的解析式为2321+-=x y ,求A 、B 两点的坐标;(2)①若点P 的坐标为(-2,t ),当PA =AB 时,请直接写出点A 的坐标;②试证明:对于直线l 上任意给定的一点P ,在抛物线上都能找到点A ,使得PA =AB成立.(3)设直线l 交y 轴于点C ,若△AOB 的外心在边AB 上,且∠BPC =∠OCP ,求点P 的坐标.(1)依题意,得⎪⎩⎪⎨⎧=+-=.,23212x y x y 解得⎪⎪⎩⎪⎪⎨⎧=-=492311y x ,⎩⎨⎧==1122y x ∴A (23-,49),B (1,1).(2)①A 1(-1,1),A 2(-3,9).②过点P 、B 分别作过点A 且平行于x 轴的直线的垂线,垂足分别为G 、H.设P (a ,22--a ),A (m ,2m ),∵PA =PB ,∴△PAG ≌△BAH , ∴AG =AH ,PG =BH ,∴B (a m -2,2222++a m ),将点B 坐标代入抛物线2x y =,得0224222=--+-a a am m , ∵△=()()081816168228162222>++=++=---a a a a a a∴无论a 为何值时,关于m 的方程总有两个不等的实数解,即对于任意给定的 点P ,抛物线上总能找到两个满足条件的点A .(3)设直线m :()0≠+=k b kx y 交y 轴于D ,设A (m ,2m ),B (n ,2n ).过A 、B 两点分别作AG 、BH 垂直x 轴于G 、H . ∵△AOB 的外心在AB 上,∴∠AOB =90°, 由△AGO ∽△OHB ,得BHOH OGAG =,∴1-=mn .联立⎩⎨⎧=+=2xy b kx y 得02=--b kx x ,依题意,得m 、n 是方程02=--b kx x 的两根,∴b mn -=,∴1-=b ,即D (0,1). ∵∠BPC =∠OCP ,∴DP =DC =3.P设P (a ,22--a ),过点P 作PQ ⊥y 轴于Q ,在Rt △PDQ 中,222PD DQ PQ =+,∴()2223122=---+a a .∴01=a (舍去),5122-=a ,∴P (512-,514).∵PN 平分∠MNQ ,∴PT =NT ,∴()t tt -=+-22212,7、(2013•内江压轴题)已知二次函数y=ax 2+bx+c (a >0)的图象与x 轴交于A (x 1,0)、B(x 2,0)(x 1<x 2)两点,与y 轴交于点C ,x 1,x 2是方程x 2+4x ﹣5=0的两根. (1)若抛物线的顶点为D ,求S △ABC :S △ACD 的值; (2)若∠ADC=90°,求二次函数的解析式.线的解析式.解答:解:(1)解方程x2+4x﹣5=0,得x=﹣5或x=1,由于x1<x2,则有x1=﹣5,x2=1,∴A(﹣5,0),B(1,0).抛物线的解析式为:y=a(x+5)(x﹣1)(a>0),∴对称轴为直线x=2,顶点D的坐标为(﹣2,﹣9a),令x=0,得y=﹣5a,∴C点的坐标为(0,﹣5a).依题意画出图形,如右图所示,则OA=5,OB=1,AB=6,OC=5a,过点D作DE⊥y轴于点E,则DE=2,OE=9a,CE=OE﹣OC=4a.,(=﹣﹣),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).(1)求抛物线的解析式;(2)在该抛物线的对称轴上,是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;(3)如果点P是该抛物线上x轴上方的一个动点,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)),﹣∵y=﹣x﹣x=﹣(x+1)+,∴抛物线的对称轴为x=﹣1.∵点C在对称轴x=﹣1上,△BOC的周长=OB+BC+CO;∵OB=2,要使△BOC的周长最小,必须BC+CO最小,∵点O与点A关于直线x=﹣1对称,有CO=CA,△BOC的周长=OB+BC+CO=OB+BC+CA,∴当A、C、B三点共线,即点C为直线AB与抛物线对称轴的交点时,BC+CA最小,此时△BOC的周长最小.设直线AB的解析式为y=kx+t,则有:,解得:﹣,﹣)﹣+y(x+(﹣x+x x+(﹣×+,的坐标为(﹣,)9、(2013聊城压轴题)已知△ABC中,边BC的长与BC边上的高的和为20.(1)写出△ABC的面积y与BC的长x之间的函数关系式,并求出面积为48时BC的长;(2)当BC多长时,△ABC的面积最大?最大面积是多少?(3)当△ABC面积最大时,是否存在其周长最小的情形?如果存在,请说出理由,并求出其最小周长;如果不存在,请给予说明.考点:二次函数综合题.分析:(1)先表示出BC边上的高,再根据三角形的面积公式就可以表示出表示y与x之间的函数关系式,当y=48时代入解析式就可以求出其值;(2)将(1)的解析式转化为顶点式就可以求出最大值.(3)由(2)可知△ABC的面积最大时,BC=10,BC边上的高也为10过点A作直线L平行于BC,作点B关于直线L的对称点B′,连接B′C 交直线L于点A′,再连接A′B,AB′,根据轴对称的性质及三角形的周长公式就可以求出周长的最小值.解答:解:(1)由题意,得y==﹣x2+10x,当y=48时,﹣ x2+10x=48,解得:x1=12,x2=8,∴面积为48时BC的长为12或8;(2)∵y=﹣x2+10x,∴y=﹣(x﹣10)2+50,∴当x=10时,y最大=50;(3)△ABC面积最大时,△ABC的周长存在最小的情形.理由如下:由(2)可知△ABC的面积最大时,BC=10,BC边上的高也为10过点A作直线L平行于BC,作点B关于直线L的对称点B′,连接B′C 交直线L于点A′,再连接A′B,AB′则由对称性得:A′B′=A′B,AB′=AB,∴A′B+A′C=A′B′+A′C=B′C,当点A不在线段B′C上时,则由三角形三边关系可得:△ABC的周长=AB+AC+BC=AB′+AC+BC >B′C+BC,当点A在线段B′C上时,即点A与A′重合,这时△ABC的周长=AB+AC+BC=A′B′+A′C+BC=B′C+BC,因此当点A与A′重合时,△ABC的周长最小;这时由作法可知:BB′=20,∴B′C==10,∴△ABC的周长=10+10,因此当△ABC面积最大时,存在其周长最小的情形,最小周长为10+10.点评:本题是一道二次函数的综合试题,考查了二次函数的解析式的运用,一元二次方程的解法和顶点式的运用,轴对称的性质的运用,在解答第三问时灵活运用轴对称的性质是关键.10、(2013•苏州压轴题)如图,已知抛物线y=x2+bx+c(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(﹣1,0).(1)b= +c ,点B的横坐标为﹣2c (上述结果均用含c的代数式表示);(2)连接BC,过点A作直线AE∥BC,与抛物线y=x2+bx+c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;(3)在(2)条件下,点P是x轴下方的抛物线上的一个动点,连接PB,PC,设所得△PB C 的面积为S.①求S的取值范围;②若△PBC的面积S为整数,则这样的△PBC共有11 个.b=,即xx+c y=y=x+;解方程组x+cy=﹣,﹣x﹣2),则点F坐标为(x,x﹣2),PF=PG﹣GF=﹣x2+2x,S=PF•OB=﹣x2+4x=﹣(x﹣2)2+4,根据二次函数的性质求出S最大值=4,即0<S≤4.则0<S<5;②由0<S<5,S为整数,得出S=1,2,3,4.分两种情况进行讨论:(Ⅰ)当﹣1<<0时,根据△PBC中BC边上的高h小于△ABC中BC边上的高AC=,得出满足条件的△PBC共有4个;(Ⅱ)当0<x<4时,由于S=﹣x2+4x,根据一元二次方程根的判别式,得出满足条件的△PBC共有7个;则满足条件的△PBC共有4+7=11个.解答:解:(1)∵抛物线y=x2+bx+c过点A(﹣1,0),×(﹣+cxx=y=,x+cx+m×(﹣,y=x+由,解得,,∴点E坐标为(1﹣2c,1﹣c).∵点C坐标为(0,c),点D坐标为(2,0),∴直线CD的解析式为y=﹣x+c.∵C,D,E三点在同一直线上,∴1﹣c=﹣×(1﹣2c)+c,(与+c=﹣x x,﹣y=x=,﹣(﹣x x=PF•OB=(﹣x∴AC2+BC2=AB2,∠ACB=90°,BC边上的高AC=.∵S=BC•h,∴h===S.如果S=1,那么h=×1=<,此时P点有1个,△PBC有1个;如果S=2,那么h=×2=<,此时P点有1个,△PBC有1个;如果S=3,那么h=×3=<,此时P点有1个,△PBC有1个;h=×4=,此时故答案为11、(2013•宜昌压轴题)如图1,平面之间坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)(1)填空:用含t的代数式表示点A的坐标及k的值:A (t,4),k= (k>0);(2)随着三角板的滑动,当a=时:①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y=的图象上;②当三角板滑至点E为AB的中点时,求t的值;(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.横坐标是+4t+4=,其顶点坐标为(,﹣)y=×=,y=②如图1,过点E作EK⊥x轴于点K.∵AC⊥x轴,∴AC∥EK.∵点E是线段AB的中点,∴K为BC的中点,∴EK是△ACB的中位线,∴EK=AC=2,CK=BC=2,∴E(t+2,2).∵点E在抛物线y=x(x﹣t)上,,则x=的横坐标是+t+t12、(2013•黄冈压轴题)如图,在平面直角坐标系中,四边形ABCD是梯形,其中A(6,0),B(3,),C(1,),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).(1)求经过A,B,C三点的抛物线的解析式;(2)当点Q在CO边上运动时,求△OPQ的面积S与时间t的函数关系式;(3)以O,P,Q顶点的三角形能构成直角三角形吗?若能,请求出t的值;若不能,请说明理由;(4)经过A,B,C三点的抛物线的对称轴、直线OB和PQ能够交于一点吗?若能,请求出此时t的值(或范围),若不能,请说明理由).的解析式,得出,),,x+∴△OPQ的高为:OQ×sin60°=(4﹣t)×,又∵OP=2t,∴S=×2t×(4﹣t)×=﹣(t2﹣4t)(2≤t≤3);(3)根据题意得出:0≤t≤3,当0≤t≤2时,Q在BC边上运动,此时OP=2t,OQ=,x﹣x,,y=﹣,(1﹣t)×=3﹣t﹣2t,恒成立,即0≤t≤2时,P,M,Q总在一条直线上,即M在直线PQ上;当2<t≤3时,OQ=4﹣t,∠QOP=60°,∴Q(,),代入上式得:×(1﹣t)=﹣2t,(均不合题意,舍去)(2013•荆门压轴题)已知关于x的二次函数y=x2﹣2mx+m2+m的图象与关于x的函数y=kx+1 13、的图象交于两点A(x1,y1)、B(x2,y2);(x1<x2)(1)当k=1,m=0,1时,求AB的长;(2)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.(3)当m=0,无论k为何值时,猜想△AOB的形状.证明你的猜想.(平面内两点间的距离公式).,角形,根据勾股定理得出AB=AC,根据两点间距离公式及完全平方公式求出AB=;同理,当k=1,m=1时,AB=;(2)当k=1,m为任何值时,联立,得x2﹣(2m+1)x+m2+m﹣1=0根据一元二次方程根与系数的关系得到x1+x2=2m+1,x1•x2=m2+m﹣1,同(1)可求出AB=;(3)当m=0,k为任意常数时,分三种情况讨论:①当k=0时,由,得A(﹣时,联立1,则为任意实数时,联立AC=|x;AB=AB=AC=|x;由,得A(﹣1,1),B(1,1),显然△AOB为直角三角形;②当k=1时,则一次函数为直线y=x+1,由,得x2﹣x﹣1=0,∴x1+x2=1,x1•x2=﹣1,AC=|x,+2k14、(2013•黔东南州压轴题)已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.(1)求抛物线的解析式;(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P 在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.15、(13年北京7分23)在平面直角坐标系x O y 中,抛物线222--=mx mx y (0≠m )与y 轴交于点A ,其对称轴与x 轴交于点B 。
【中考宝典】2013年中考数学真题分类汇编(Word版,含答案)

第一单元数与式一、实数1、绝对值、相反数、倒数2、科学记数法3、实数的概念及其运算二、整式1.幂的运算、整式的乘除2.因式分解三、分式四、二次根式第二单元方程(组)与不等式组一、一次方程(方程组)二、一元一次不等式与一元一次不等式组三、一元二次方程四、分式方程第三单元函数及其图像一、函数及其图像二、一次函数三、反比例函数四、二次函数五、函数的应用第四单元图形的认识与三角形一、角、相交线与平行线二、三角形与全等三角形三、等腰三角形与直角三角形第五单元四边形一、多边形与平行四边形二、矩形、菱形、正方形三、梯形第六单元圆一、圆的有关概念及性质二、点、直线、圆和圆的位置关系三、和圆有关的计算第七单元图形与变换一、尺规作图、视图与投影二、图形的对称、平移与旋转三、图形的相似与位似四.锐角三角函数和解直角三角形第八单元概率与统计一、统计二、概率第二单元 方程(组)与不等式组一、一次方程(方程组) 1、(2013黄石)四川雅安地震期间,为了紧急安置60名地震灾民,需要搭建可容纳6人或4人的帐篷,若所搭建的帐篷恰好(既不多也不少)能容纳这60名灾民,则不同的搭建方案有( )A .1种B .11种C .6种D .9种解析:设6人的帐篷有x 顶,4人的帐篷有y 顶,依题意,有:6x+4y=60,整理得y=15-1.5x ,因为x 、y 均为非负整数,所以15-1.5x≥0,解得:0≤x≤10,从2到10的偶数共有5个,所以x 的取值共有6种可能,即共有6种搭建方案. 答案:C2.(2013广安)如果y x b a 321与12+-x y b a 使同类项,则( )A. ⎩⎨⎧=-=32y xB.⎩⎨⎧==3-2y xC.⎩⎨⎧=-=3-2y xD.⎩⎨⎧==32y x解析:y x b a 321 与12+-x y b a 是同类项,∴⎩⎨⎧+==123x y y x ,解得:⎩⎨⎧==32y x 。
答案:D3、(2013凉山州)已知方程组⎩⎨⎧=+=+5242y x y x ,则y x +的值为 ( )A .-1B .0C .2D .3 解析:利用两式相加得:9)(3=+y x ,3=+y x .答案:D4、(2013济宁)服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多 ( )A .60元B .80元C .120元D .180元 解析:设衣服的进价为x 元,依题意得300×80%-x=60,解得x=180.因此这款服装每件的标价比进价多300-180=120(元).答案:C5、(2013淄博)楠溪江某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1225元,设其中有x 张成人票,y 张儿童票,根据题意,下列方程组正确的是 ( )+=20.35+70=1225x y A x y ⎧⎨⎩ +y=20.70+35=1225x B x y ⎧⎨⎩ +=1225.70+35=20x y C x y ⎧⎨⎩ +=1225.35+70=20x y D x y ⎧⎨⎩ 解析:确定等量关系:总票数=承认票数+儿童票数,总票钱数=成人票钱数+儿童票钱数.依据等量关系列出方程组即可.答案:B6、(2013•永州)已知(x-y+3)2+y x +2=0,则x+y 的值为( ) A .0 B .-1 C .1 D .5解析:∵ 02)3(2=+++-y x y x ,∴⎩⎨⎧=+=+-0203y x y x ,解得⎩⎨⎧=-=21y x∴121=+-=+y x 答案:C7、(2013南宁)陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )A .19B .18C .16D .15解析:设笑脸形的气球x 元一个,爱心形的气球y 元一个,由题意,得,解得:2x+2y=16.答案:C答案:B8、(2013毕节)二元一次方程组⎩⎨⎧=-=+112312y x y x 的解是_。
(全国120套)2013年中考数学试卷分类汇编(打包53套)-4.doc

命题1、(绵阳市2013年)下列说法正确的是( D )A.对角线相等且互相垂直的四边形是菱形B.对角线互相垂直的梯形是等腰梯形C.对角线互相垂直的四边形是平行四边形D.对角线相等且互相平分的四边形是矩形[解析]由矩形的性质可知,只有D正确。
平行四边形的对角线是互相平行,菱形的对角线互相平分且垂直,故A、C错,等腰梯形的对角线相等B也错。
2、(2013杭州)在一个圆中,给出下列命题,其中正确的是()A.若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直B.若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有4个公共点C.若两条弦所在直线不平行,则这两条弦可能在圆内有公共点D.若两条弦平行,则这两条弦之间的距离一定小于圆的半径考点:直线与圆的位置关系;命题与定理.分析:根据直线与圆的位置关系进行判断即可.解答:解:A.圆心到两条直线的距离都等于圆的半径时,两条直线可能垂直,故本选项错误;B.当两圆经过两条直线的交点时,圆与两条直线有三个交点;C.两条平行弦所在直线没有交点,故本选项正确;D.两条平行弦之间的距离一定小于直径,但不一定小于半径,故本选项错误,故选C.点评:本题考查了直线与圆的位置关系、命题与定理,解题的关键是熟悉直线与圆的位置关系.3、(2013凉山州)下列说法中:①邻补角是互补的角;②数据7、1、3、5、6、3的中位数是3,众数是4;③|﹣5|的算术平方根是5;④点P(1,﹣2)在第四象限,其中正确的个数是()A.0 B.1 C.2 D.3考点:算术平方根;点的坐标;对顶角、邻补角;中位数;众数.分析:根据邻补角、算术平方根、中位数及众数的定义、点的坐标的知识,分别进行各项的判断即可.解答:解:①邻补角是互补的角,说法正确;②数据7、1、3、5、6、3的中位数是5,众数是3,原说法错误;③|﹣5|的算术平方根是,原说法错误;④点P(1,﹣2)在第四象限,说法正确;综上可得①④正确,共2个.故选C.点评:本题考查了邻补角、中位数、众数及算术平方根的知识,掌握基础知识是解答此类题目的关键.的平方根是±y=的自变量8、(2013聊城)下列命题中的真命题是()A.三个角相等的四边形是矩形B.对角线互相垂直且相等的四边形是正方形C.顺次连接矩形四边中点得到的四边形是菱形D.正五边形既是轴对称图形又是中心对称图形考点:命题与定理.分析:根据矩形、菱形、正方形的判定以及正五边形的性质得出答案即可.解答:解:A.根据四个角相等的四边形是矩形,故此命题是假命题,故此选项错误;B.根据对角线互相垂直、互相平分且相等的四边形是正方形,故此命题是假命题,故此选项错误;C.顺次连接矩形四边中点得到的四边形是菱形,故此命题是真命题,故此选项正确;D.正五边形是轴对称图形不是中心对称图形,故此命题是假命题,故此选项错误.故选:C.点评:此题主要考查了矩形、菱形、正方形的判定以及正五边形的性质等知识,熟练掌握相关定理是解题关键.10、(2013•包头)已知下列命题:①若a>b,则c﹣a<c﹣b;②若a>0,则=a;③对角线互相平行且相等的四边形是菱形;④如果两条弧相等,那么它们所对的圆心角相等.=a;逆命题:若15、(2013•鄂州)下列命题正确的个数是()①若代数式有意义,则x的取值范围为x≤1且x≠0.②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.③若反比例函数(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中有意义,则(17、(2013年深圳市)下列命题是真命题的有()①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等;④有三个角是直角的四边形是矩形;⑤平分弦的直径垂直于弦,并且平分弦所对的弧。
全国各地2013年中考数学试题最新分类汇编 因式分解

因式分解(2013•某某)已知a+b=2,ab=1,则a2b+ab2的值为 2 .考点:因式分解的应用.专题:计算题.分析:所求式子提取公因式化为积的形式,将各自的值代入计算即可求出值.解答:解:∵a+b=2,ab=1,∴a2b+ab2=ab(a+b)=2.故答案为:2点评:此题考查了因式分解的应用,将所求式子进行适当的变形是解本题的关键.(2013•株洲)多项式x2+mx+5因式分解得(x+5)(x+n),则m= 6 ,n= 1 .考点:因式分解的意义.专题:计算题.分析:将(x+5)(x+n)展开,得到,使得x2+(n+5)x+5n与x2+mx+5的系数对应相等即可.解答:解:∵(x+5)(x+n)=x2+(n+5)x+5n,∴x2+mx+5=x2+(n+5)x+5n∴,∴,故答案为6,1.点评:本题考查了因式分解的意义,使得系数对应相等即可. 分解因式:2a 2﹣8= 2(a+2)(a ﹣2) .考点:提公因式法与公式法的综合运用. 专题:因式分解. 分析:先提取公因式2,再对余下的多项式利用平方差公式继续分解. 解答: 解:2a 2﹣8=2(a 2﹣4),=2(a+2)(a ﹣2).故答案为:2(a+2)(a ﹣2).点评: 本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.(2013•达州)分解因式:39x x =_ _.答案:x (x +3)(x -3)解析:原式=x (x 2-9)=x (x +3)(x -3)(2013•某某)把多项式分解因式:ax 2-ay 2=(2013凉山州)已知(2x ﹣21)(3x ﹣7)﹣(3x ﹣7)(x ﹣13)可分解因式为(3x+a )(x+b ),其中a 、b 均为整数,则a+3b=.考点:因式分解-提公因式法.分析:首先提取公因式3x ﹣7,再合并同类项即可得到a 、b 的值,进而可算出a+3b 的值. 解答:解:(2x ﹣21)(3x ﹣7)﹣(3x ﹣7)(x ﹣13),=(3x ﹣7)(2x ﹣21﹣x+13),=(3x ﹣7)(x ﹣8),则a=﹣7,b=﹣8,a+3b=﹣7﹣24=﹣31,故答案为:﹣31.点评:此题主要考查了提公因式法分解因式,关键是找准公因式.(2013•某某)分解因式:24x y y -= .(2013•某某)因式分解:2442x y x y -=。
2013年中考数学模拟试卷四及答案(含答题卡)A3

A
D
(2)已知 1 + 1 = 5 (a≠b),求 a b 的值.
O
ab
b(a b) a(a b)
17. (9 分)如图,四边形 ABCD 是矩形,对角线 AC,BD 相交于点
B
C
O,BE∥AC 交 DC 的延长线于点 E.
(1)求证:BD=BE;
(2)若DBC=30,BO=4,求四边形 ABED 的面积.
8. 已知二次函数 yax2bxc 的图象如图所示,它与 x 轴的两个
y
交点分别为(1,0),(3,0).对于下列命题:
①b2a0;②abc<0;③a2b4c<0;④8ac>0.其中正确的 有【 】
1 O
3x
A.3 个
B.2 个
C.1 个
D.0 个
二、填空题(每小题 3 分,共 21 分)
E
18. (9 分)某市把中学生学习情绪的自我控制能力分为四个等级,即 A 级:自我控制能力
很强;B 级:自我控制能力较好;C 级:自我控制能力一般;D 级:自我控制能力较
差.通过对该市的初中学生学习情绪的自我控制能力的随机抽样调查,得到下面两幅
不完整的统计图,请根据图中的信息解决下面的问题.
(1)在这次随机抽样调查中,共抽查了多少名学生?
14. 如图,∠MON=30°,点 A1,A2,A3,…在射线 ON 上,点 B1,B2,B3,…在射线 OM
上,△ A1B1A2 ,△ A2B2 A3 ,△ A3B3 A4 …均为等边三角形.若 OA1 1 ,则△ AnBn An1 的边
长为_____________.
1
15. 如图,已知 Rt△ABC≌Rt△DEF,∠C=∠F=90°,AC=DF=3,BC=EF=4,△DEF 绕着
(全国120套)2013年中考数学试卷分类汇编(打包53套)-38.doc
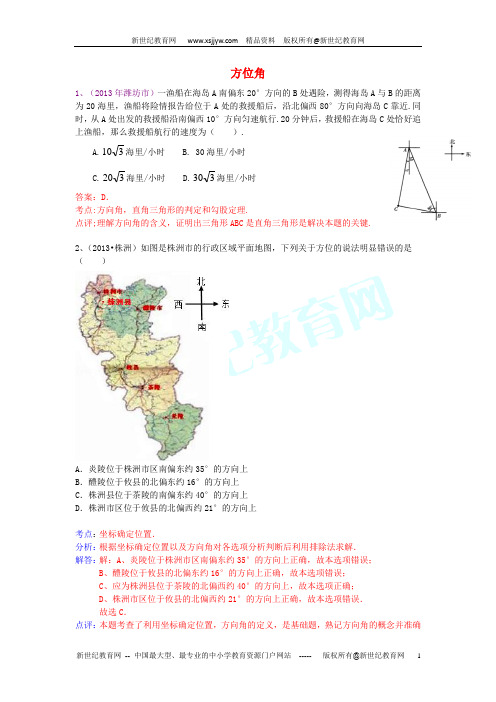
方位角1、(2013年潍坊市)一渔船在海岛A 南偏东20°方向的B 处遇险,测得海岛A 与B 的距离为20海里,渔船将险情报告给位于A 处的救援船后,沿北偏西80°方向向海岛C 靠近.同时,从A 处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C 处恰好追上渔船,那么救援船航行的速度为( ).A.310海里/小时B. 30海里/小时C.320海里/小时D.330海里/小时答案:D .考点:方向角,直角三角形的判定和勾股定理.点评;理解方向角的含义,证明出三角形ABC 是直角三角形是解决本题的关键.2、(2013•株洲)如图是株洲市的行政区域平面地图,下列关于方位的说法明显错误的是( )3、(2013年河北)如图1,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为A.40海里B.60海里C.70海里D.80海里答案:D解析:依题意,知MN=40×2=80,又∠M=70°,∠N=40°,所以,∠MPN=70°,从而NP=NM=80,选D4、(2013•荆门)A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.=5、(2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B 处,发现此时钓鱼岛C与该船距离最短.(1)请在图中作出该船在点B处的位置;(2)求钓鱼岛C到B处距离(结果保留根号)=56、(2013年广州市)如图10,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.(1)求船P到海岸线MN的距离(精确到0.1海里);(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.分析:(1)过点P作PE⊥AB于点E,在Rt△APE中解出PE即可;(2)在Rt△BPF中,求出BP,分别计算出两艘船需要的时间,即可作出判断解:(1)过点P作PE⊥AB于点E,由题意得,∠PAE=32°,AP=30海里,在Rt△APE中,PE=APsin∠PAE=APsin32°≈15.9海里;(2)在Rt△PBE中,PE=15.9海里,∠PBE=55°,则BP=≈19.4,A船需要的时间为:=1.5小时,B船需要的时间为:=1.3小时,故B船先到达.点评:本题考查了解直角三角形的应用,解答本题的关键是理解方位角的定义,能利用三角函数值计算有关线段,难度一般.7、(2013年广东湛江)如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30ο的方向上,随后渔政船以80海里小时的速度向北偏东30ο的方向航行,半小时后到达B 处,此时又测得钓鱼岛A 在渔政船的北偏西60ο的方向上,求此时渔政船距钓鱼岛A 的距离AB .1.732≈)解:延长EB 至F ,则030CBF ∠=,00000180180603090ABC EBF CBF ∴∠=-∠-∠=--=,在Rt △ABC 中,060ACB ∠=,180402BC =⨯=,tan ,AB ACB BC=∠tan 44 1.732 6.9AB BC ACB ∴=∠=≈⨯≈答:此时渔政船距钓鱼岛A 的距离AB 约为:6.9海里8、(2013•荆门)A 、B 两市相距150千米,分别从A 、B 处测得国家级风景区中心C 处的方位角如图所示,风景区区域是以C 为圆心,45千米为半径的圆,tan α=1.627,tan β=1.373.为了开发旅游,有关部门设计修建连接AB 两市的高速公路.问连接AB 高速公路是否穿过风景区,请说明理由.=9、(2013•苏州)如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(1)求点P到海岸线l的距离;(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)BF=BF=kmPD=xkmx=2AB=1kmBF=km之间的距离为10、(2013•莱芜)如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A、B上的观测点进行观测,从A岛测得渔船在南偏东37°方向C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时28.8海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?(参考数据:cos37°≈0.8,sin37°≈0.6,sin66°≈0.9,cos66°≈0.4)(小时)(小时)11、(2013泰安)如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C 处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为(取,结果精确到0.1海里).考点:解直角三角形的应用-方向角问题.专题:应用题.分析:过点D作DE⊥AB于点E,设DE=x,在Rt△CDE中表示出CE,在Rt△BDE中表示出BE,再由CB=25海里,可得出关于x的方程,解出后即可计算AB的长度.解答:解:∵∠DBA=∠DAB=45°,∴△DAB是等腰直角三角形,过点D作DE⊥AB于点E,则DE=AB,设DE=x,则AB=2x,在Rt△CDE中,∠DCE=30°,则CE=DE=x,在Rt△BDE中,∠DAE=45°,则DE=BE=x,由题意得,CB=CE﹣BE=x﹣x=25,解得:x=,故AB=25(+1)=67.5海里.故答案为:67.5.点评:本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度,难度一般.12、(2013•烟台)如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据:≈1.41,≈1.73,≈2.45,结果精确到0.1),CD==6﹣≈6.2(海里)13、(2013•遂宁)钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)中,BD=AB•sin∠BAD=20×=10BC==(海里)海里.14、(2013•资阳)钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.(1)当日本渔船受到严重警告信号后,必须沿北偏东转向多少度航行,才能恰好避免进入钓鱼岛12海里禁区?(2)当日本渔船不听严重警告信号,仍按原速度,原方向继续前进,那么海监船必须尽快到达距岛12海里,且位于线段AC上的F处强制拦截渔船,问海监船能否比日本渔船先到达F处?(注:①中国海监船的最大航速为18节,1节=1海里/小时;②参考数据:sin26.3°≈0.44,sin20.5°≈0.35,sin18.1°≈0.31,≈1.4,≈1.7)=≈0.35,∴∠AEN=20.5°,∴∠NEM=69.5°,即必须沿北偏东至少转向69.5°航行,才能恰好避免进入钓鱼岛12海里禁区.(2)过点D作DH⊥AB于点H,由题意得,BD=2×12=24海里,在Rt△DBH中,DH=BD=12海里,BH=12海里,∵AF=12海里,的时间为:===2.415、(2013•自贡)在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M 的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A 相距km的C处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.km==16∵1小时20分钟=80分钟,1小时=60分钟,∴×60=12(千米/小时).(2)作线段BR⊥x轴于R,作线段CS⊥x轴于S,延长BC交l于T.∵∠2=60°,∴∠4=90°﹣60°=30°.∵AC=8(km),∴CS=8sin30°=4(km).cos30°=8×∴BR=40•sin60°=20=20=,16、(2013年黄石)高考英语听力测试期间,需要杜绝考点周围的噪音。
(全国120套)2013年中考数学试卷分类汇编(打包53套)-50.doc
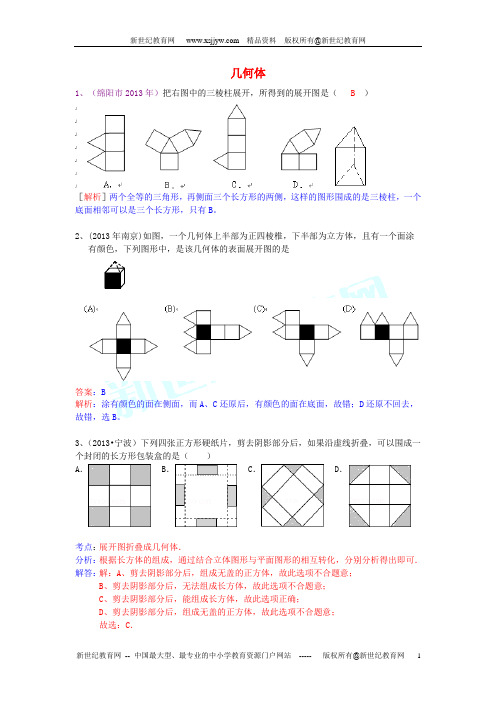
几何体1、(绵阳市2013年)把右图中的三棱柱展开,所得到的展开图是( B )[解析]两个全等的三角形,再侧面三个长方形的两侧,这样的图形围成的是三棱柱,一个底面相邻可以是三个长方形,只有B。
2、(2013年南京)如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是答案:B解析:涂有颜色的面在侧面,而A、C还原后,有颜色的面在底面,故错;D还原不回去,故错,选B。
3、(2013•宁波)下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一4、(2013河南省)如图是正方形的一种张开图,其中每个面上都标有一个数字。
那么在原正方形中,与数字“2”相对的面上的数字是【】(A)1 (B)4 (C)5 (D)6【解析】将正方形重新还原后可知:“2”与“4”对应,“3”与“5”对应,“1”与“6”对应。
【答案】B5、(2013•自贡)如图,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为(),高为=6、(2013山西,3,2分)如图是一个长方体包装盒,则它的平面展开图是()【答案】A【解析】长方体的四个侧面中,有两个对对面的小长方形,另两个是相对面的大长方形,B、C中两个小的与两个大的相邻,错,D中底面不符合,只有A符合。
7、(2013•温州)下列各图中,经过折叠能围成一个立方体的是()8、(2013•巴中)如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是()9、(2013菏泽)下列图形中,能通过折叠围成一个三棱柱的是( )A .B .C .D .考点:展开图折叠成几何体.分析:根据三棱柱及其表面展开图的特点对各选项分析判断即可得解.解答:解:A .另一底面的三角形是直角三角形,两底面的三角形不全等,故本选项错误;B.折叠后两侧面重叠,不能围成三棱柱,故本选项错误;C.折叠后能围成三棱柱,故本选项正确;D.折叠后两侧面重叠,不能围成三棱柱,故本选项错误.故选C.点评:本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,不能有两个侧面在两三角形的同一侧.10、(2013•黄冈)已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为()B C...13、(2013•南宁)如图所示,将平面图形绕轴旋转一周,得到的几何体是()14、(2013台湾、25)附图的长方体与下列选项中的立体图形均是由边长为1公分的小正方体紧密堆砌而成.若下列有一立体图形的表面积与附图的表面积相同,则此图形为何?( )A .B .C .D .考点:几何体的表面积.分析:根据立体图形的面积求法,分别得出几何体的表面积即可. 解答:解:∵立体图形均是由边长为1公分的小正方体紧密堆砌而成,∴附图的表面积为:6×2+3×2+2×2=22,只有选项B的表面积为:5×2+3+4+5=22.故选:B.点评:此题主要考查了几何体的表面积求法,根据已知图形求出表面积是解题关键.15、(2013杭州)四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1,S2,则|S1﹣S2|= (平方单位)考点:圆锥的计算;点、线、面、体;圆柱的计算.分析:梯形ABCD分别绕直线AB,CD旋转一周所得的几何体的表面积的差就是AB和CD旋转一周形成的圆柱的侧面的差.解答:解:AB旋转一周形成的圆柱的侧面的面积是:2π×2×3=12π;AC旋转一周形成的圆柱的侧面的面积是:2π×2×2=8π,则|S1﹣S2|=4π.故答案是:4π.点评:本题考查了图形的旋转,理解梯形ABCD分别绕直线AB,CD旋转一周所得的几何体的表面积的差就是AB和CD旋转一周形成的圆柱的侧面的差是关键.16、(2013•咸宁)如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是泉.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因式分解
一、选择题
1、(2013山西中考模拟六)因式分解()2
19x --的结果是( )
A. ()()24x x +-
B. ()()81x x ++
C. ()()24x x -+
D. ()()108x x -+ 答案:A 二、填空题
1、(2013山东省德州一模)因式分解:224a a -= .
答案:2a(a-2)
2、 (2013·吉林中考模拟)把多项式a 3—2a 2+a 分解因式的结果是 .
答案:a (a -1)2
3、(2013·温州市中考模拟)因式分解:x 3-x =____________.
答案:x(x+1)(x -1)
4、(2013·湖州市中考模拟试卷1)分解因式:x 3-4x = _.
答案:x (x+2)(x -2)
5、(2013·湖州市中考模拟试卷3)因式分解:22
a x a y -=_ .
答案:()()a x y x y -+
6、(2013·湖州市中考模拟试卷8)因式分解22x x -= . 答案:x(x -2)
7、(2013·湖州市中考模拟试卷10)因式分解m m 43- = .
答案:)2)(2(-+m m m
8、 (2013年深圳育才二中一摸)分解因式:=+-a a a 232▲
答案:2
)1(-a a
9、(2013年广西南丹中学一摸)分解因式:2x 2-8= .
答案:2(x +2)(x -2)
10、(2013年河北省一摸)|把a 3-ab 2分解因式的结果为 . 答案:13.))((b a b a a -+;
11、(2013年河北二摸)分解因式am an bm bn +++= . 答案:(a +b )(m +n )
12、(2013年温州一摸)因式分解:x 3-x =____________.
答案:X(x+1)(x-1)
13、分解因式:22944x y y ---= ▲ . 答案:(32)(32)x y x y ++--。
