平新乔《微观经济学十八讲》答案
平新乔《微观经济学十八讲》课后习题详解(策略性博弈与纳什均衡)

第10讲 策略性博弈与纳什均衡1.假设厂商A 与厂商B 的平均成本与边际成本都是常数,10A MC =,8B MC =,对厂商产出的需求函数是50020D Q p =-(1)如果厂商进行Bertrand 竞争,在纳什均衡下的市场价格是多少? (2)每个厂商的利润分别为多少? (3)这个均衡是帕累托有效吗?解:(1)如果厂商进行Bertrand 竞争,纳什均衡下的市场价格是10B p ε=-,10A p =,其中ε是一个极小的正数。
理由如下:假设均衡时厂商A 和B 对产品的定价分别为A p 和B p ,那么必有10A p ≥,8B p ≥,即厂商的价格一定要高于产品的平均成本。
其次,达到均衡时,A p 和B p 都不会严格大于10。
否则,价格高的厂商只需要把自己的价格降得比对手略低,它就可以获得整个市场,从而提高自己的利润。
所以均衡价格一定满足10A p ≤,10B p ≤。
但是由于A p 的下限也是10,所以均衡时10A p =。
给定10A p =,厂商B 的最优选择是令10B p ε=-,这里ε是一个介于0到2之间的正数,这时厂商B 可以获得整个市场的消费者。
综上可知,均衡时的价格为10A p =,10B p ε=-。
(2)由于厂商A 的价格严格高于厂商B 的价格,所以厂商A 的销售量为零,从而利润也是零。
下面来确定厂商B 的销售量,此时厂商B 是市场上的垄断者,它的利润最大化问题为:max pq cq ε>- ①其中10p ε=-,()5002010q ε=-⨯-,把这两个式子代入①式中,得到:()()0max 1085002010εεε>----⎡⎤⎣⎦解得0ε=,由于ε必须严格大于零,这就意味着ε可以取一个任意小的正数,所以厂商B 的利润为:()()500201010εε-⨯--⎡⎤⎣⎦。
(3)这个结果不是帕累托有效的。
因为厂商B 的产品的价格高于它的边际成本,所以如果厂商B 和消费者可以为额外1单位的产品协商一个介于8到10ε-之间的价格,那么厂商B 的利润和消费者的剩余就都可以得到提高,同时又不损害厂商A 的剩余(因为A 的利润还是零)。
平新乔《微观经济学十八讲》课后习题详解(一般均衡与福利经济学的两个基本定理)

第16讲 一般均衡与福利经济学的两个基本定理1.考虑一种两个消费者、两种物品的交易经济,消费者的效用函数与禀赋如下()()211212,u x x x x = ()118,4e = ()()()21212,ln 2ln u x x x x =+ ()23,6e =(1)描绘出帕累托有效集的特征(写出该集的特征函数式); (2)发现瓦尔拉斯均衡。
解:(1)由消费者1的效用函数()()211212,u x x x x =,可得121122MU x x =,122122MU x x =,故消费者1的边际替代率为1211112212121212122MU x x x MRS MU x x x ===。
同理可得消费者2的边际替代率为22212212x MRS x =。
在帕累托有效集上的任一点,每个消费者消费两种物品的边际替代率都相同,即:121212MRS MRS = 从而有:122212112x x x x = ① 又因为212210x x =-,211121x x =-,把这两个式子代入①式中,就得到了帕累托有效集的特征函数:1122111110422x x x x -=- ② (2)由于瓦尔拉斯均衡点必然位于契约曲线上,所以在均衡点②式一定成立。
此外在均衡点处,预算线和无差异曲线相切(如图16-1所示),这就意味着边际替代率等于预算线的斜率,即:1112121211211418x p x MRS p x x -===- ③联立②、③两式,解得:1158/4x =,1258/11x =。
进而有21112126/4x x =-=,21221052/11x x =-=。
图16-1 均衡时边际替代率等于预算线的斜率2.证明:一个有n 种商品的经济,如果(1n -)个商品市场上已经实现了均衡,则第n 个市场必定出清。
证明:假设第k 种商品的价格为k p ,{}1,2,,k n ∈。
系统内存在I (I 为正整数)个消费者,第i 个消费者拥有第k 种物品的初始禀赋为ik e ,而第i 个消费者对第k 种商品的消费量为k i x ,根据瓦尔拉斯定律可知系统中的超额的市场价值为零,即:()10ni ik k k k i Ii Ip x e =∈∈-=∑∑∑当前1n -个商品市场已经实现均衡,即前1n -个商品市场的超额需求为零,这时有:()()()11n i i i ik k k n k k k i Ii Ii Ii Ii i nkki Ii Ii i k ki Ii Ip x e p x e p x e x e -=∈∈∈∈∈∈∈∈-+-=∑∑∑∑∑-=∑∑=∑∑由此就可以得出第n 个市场的超额需求也为零,即第n 个商品市场也实现了均衡。
06平新乔微观经济学十八讲

解:因为对 t > 0 ,都有 f (tx, ty ) = 2tx + ty + 3t ( xy ) 2 = t f ( x, y ) ,所以它是一
1 1
次齐次函数,规模报酬不变. 2.3
f ( x, y, w) = x 4 5 yw 3
(
)
1 2 2 3
解:因为对 t > 0 ,都有 f (tx, ty , tw) = t f ( x, y, w) ,因此,它是齐次函数.当
恒成立的条件是, r ∈ R ,使得
8 2r = 4 2r = 0
即
8=4
因此对 r ∈ R ,f (2 x,2 y ) = 2 f ( x, y ) 在 R 上都不成立, 而 8 = 4 是不可能的.
r
2
这就证明了前面的结论. 2.2
f ( x, y ) = 2 x + y + 3( xy ) 2
x = h(q1 , q 2 )
范围经济生产有效率,必然有联合经营所需要素投入低于分别经营要素投入量总 和.即,如果 (αq1 , (1 α )q 2 , h(αq1 , (1 α )q 2 )) 是有效率的生产,必有:
h(αq1 ,0 ) + h(0, (1 α )q 2 ) ≥ h(αq1 , (1 α )q 2 )
如果生产可能性边界是外凸的,必然有 h(q1 ,0 ) + h(0, q 2 ) ≥ h(q1 , q 2 ) ,这样在生 产可能性边界上必然存在一个最高效率的生产线. 但是,考虑下面的图, 绿线是等要素投入线,橙线表示两种产出的(消费者)边际替代率. 尽管 A 点是有效率的,但是,它所在的生产可能性边界不是外凸的.它是一个凹
如果多增加一个单位的投入总产量的增量高于平均产量那么平均产量在增加该单位的投入后将上升但是也可能出现总产量增量在为正的同时低于平均产量的情况因为平均产量严格大于零那么平均产量在增加该单位的投入将上升
微观经济学十八讲答案

微观经济学十八讲答案【篇一:平新乔《微观经济学十八讲》课后习题详解(第13讲委托—代理理论初步)】t>经济学考研交流群点击加入平新乔《微观经济学十八讲》第13讲委托—代理理论初步跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.一家厂商的短期收益由r?10e?e2x给出,其中e为一个典型工人(所有工人都假设为是完全一样的)的努力水平。
工人选择他减去努力以后的净工资w?e(努力的边际成本假设为1)最大化的努力水平。
根据下列每种工资安排,确定努力水平和利润水平(收入减去支付的工资)。
解释为什么这些不同的委托—代理关系产生不同的结果。
(1)对于e?1,w?2;否则w?0。
(2)w?r/2。
(3)w?r?12.5。
解:(1)对于e?1,w?2;否则w?0,此时工人的净工资为:?2?ee?1w?e???ee?1?所以e*?1时,工人的净工资最大。
雇主利润为:?*?r?w?10e?e2x?2?10?x?2?8?x工人的净工资线如图13-1所示。
图13-1 代理人的净工资最大化(2)当w?r/2时,工人的净工资函数为:11w?e?5e?e2x?e??e2x?4e22净工资最大化的一阶条件为:d?w?e?de??ex?4?0解得:e??4。
x?2111?4?4??12雇主利润??r?r?r??10?????x??。
222?x?x????xborn to win经济学考研交流群点击加入(3)当w?r?12.5时,工人的净工资函数为:w?e?10e?e2x?12.5?e??e2x?9e?12.5净工资最大化的一阶条件为:d?w?e?de??2ex?9?0解得:e??4.5。
平新乔十八讲答案第三讲

7.1求反需求函数
解: .
7.2计算需求的价格弹性
解: .
7.3 的值为多少时,称需求是无弹性的?
答:当 时,称需求是无弹性的.
7.4证明边际收入函数对反需求函数的比, ,独立于产出 .
证明: ,因此
;
,与 无关.
8判断下述论断是否正确,并给出理由:
8.1如果需求曲线是一条直线,则直线上各点的需求价格弹性是一样的.
3.3请算出价格变化的收入效应.
解由3.1与3.2得,收入效应为 .
4某个消费者的效用函数为 .令 , 与 分别表示商品1的价格、商品2的价格和收入.
4.1如果 , , ,现在 上升为2,求此消费者关于商品1的斯拉茨基替代效应和收入效应.
解:令 为商品1价格变化前的消费量, 为变化后的消费量.有:
, .
判断:并不是所有直线上的弹性都是一样的.
理由:一类线性需求曲线可以由 , , 来表示,它的弹性
即,弹性 是价格 的函数,也就是说,这样的直线上需求价格弹性是随价格变化,不是一样的.
但考虑与 轴垂直的需求曲线 ,它的弹性就是不变的.
最后考虑与 轴水平的需求曲线,它们的弹性均为无穷大,无法比较.
[注]无穷大“之间”无法比较.
答:符合.如果要符合显示性偏好弱公理,因为
所以必然应当预测到
而后一个等式确实是成立的( ),符合预测.因此他的行为符合显示性偏好的弱公理.
15设消费者的反需求函数为 ,这里 , .假定政府开征消费税(从价税),因此消费者支付的价格会从 上升到 (这里, 为税率).证明:消费者剩余的损失总是超过政府通过征税而获得的收入.
令 为调整收入以保持购买力条件下,对商品1的消费量. 为为保持购买力对收入进行调整后得到的收入.有:
平新乔微观经济学十八讲02

5
代 5 入 4 式,得 x 2 的需求函数:
x2 =
y 3 p2
2
6
代 5,6 两式入效用函数中,得到当效用最大化时有间接效用函数:
2y y v( p, y ) = u ( x1 , x 2 ) = x x 2 = 3p 3p 2 1
2 1
2
第二讲 间接效用……
又消费者效用最大化意味着
(x1 , x2 ) ∈ R+2 . 已 知 北 京 的 物 价 为 ( p1a , p 2a ) , 上 海 的 物 价 为 ( p1b , p 2b ) , 并 且
a b p1a p 2 = p1b p 2 , 但 a b p1a ≠ p1b , p 2 ≠ p 2
. 又 知 广 州 的 物 价 为
u = x1 x2 u′ ln u u ′ = ln u 2 p1 p2 e = 2 p1 p2 e = 2 p1 p2u u ′ = ln x1 + ln x2 e′( p1 , p 2 , u ′) = e( p1 , p 2 , u )
根据 5.1 与 5.2 的结果,得到
6
设某消费者的间接效用函数为 v( p1 , p2 , m ) =
y = e( p, v( p, y ))
即可得到支出函数:
e( p, u ) = e( p, v( p, y )) = y = 108 p12 p 2 u
3 考虑下列间接效用函数
(
)
1 3
=
3 2 p12 p 2 u 2
(
)
1 3
v( p1 , p 2 , m ) =
这里 m 表示收入,问:
m p1 + p 2
由 1 式,2 式,得 e( p1 , p2 , u )
平新乔 微观十八讲习题答案
第八讲 完全竞争与垄断
5
Max
π = pQ C
π = (100 qa )qa + (120 2qb )qb 8 20(qa + qb )
一阶条件:
π = 100 2qa 20 = 0 qa π = 120 4qb 20 = 0 qb
q a , qb
s.t.
构造拉氏方程: 一阶条件:
Q = qa + qb
L(q, λ ) = Ca (qa ) + Cb (qb ) + λ (Q qb qa )
L = 8qa λ = 0 qa L = 4qb λ = 0 q2 L = Q qa qb = 0 λ
(1)
(2)
(3)
8-19-5 12/20/2005 11:00:15 PM
一阶条件:
π = 100 4qa 4qb 8qa = 0 qa π = 100 4qa 4qb 4qa = 0 qa
(1)
(2)
qa = 5 ; qb = 10 ; Q = qa + qb = 15 ; p = 70 ; π = 735
另一种解法,先求出成本函数:
min Ca (qa ) + Cb (qb )
Il =
3(1)由霍特林引理 S ( p ) =
1 dp Q 15 9 = = 3 = ∈ dQ p 175 35
π p, k π p, k 1 可得厂商的供给函数: S p, k = = kp p 8 p
( )
( )
( )
(2)由长期均衡可知,企业的长期利润为零, π ( p ) =
p2 1 = 0 ;得 p = 4 16
平新乔十八讲课后习题答案

1-6-1
第一讲 偏好、效用与消费者的基本问题
让我们首先来看一个例子,而在例子结束时,也就是我们回答此问题结束之际;
假设生产 a 单位的产出要固定用用上 a1 单位的 x1 与 a2 单位的 x2 ,那么此技术的生产函
越靠上的曲线所代表的效用水平就越高。
(3)
Y
y =−2 x3
Y
y = 2x
X
对于李楠而言汽水 x 与冰棍 y 是完全替代 的;三杯汽水 x 与两根冰棍 y 所带来的效用水
平是一样的,她的效用曲线拥有负的斜率;对
于一定量的汽水 x 而言,越多的冰棍 y 越好,
所以越靠上的曲线所代表的效用水平就越高;
她效用函数可用 u(x, y) = 3x + 2 y 表示。
ψ (x,λ) = x1 + λ(m − p1x1 − p2x2 )
∂ψ ∂x1
= 1 − λp1
=0
∂ψ ∂x2
= −λp2
=0
∂ψ ∂λ
=m−
p1x1 −
p2 x2
=0
由上式可得马歇尔需求函数: x1
=
m p1
; x2
=0
10
max = u(x)
x
s.t. m = p1x1 + p2x2
构造拉氏方程: ψ (x, λ) = Ax1α x12−α + λ(m − p1x1 − p2x2 )
∂ψ ∂x1
= 20(x1 +
x2 ) − λp1
=0
∂ψ ∂x2
=
20( x1
平新乔《微观经济学十八讲》课后习题详解(第14讲 信息不对称、逆向选择与信号博弈)

平新乔《微观经济学十八讲》第14讲 信息不对称、逆向选择与信号博弈1.假定二手车的质量q 是服从于下列均匀分布的[](),0q u t z t >~证明:如果卖主和买主的效用函数分别为1u M qn =+和232u M qn =+,预算约束分别为1y M p n =+⋅和2y M p n =+⋅,那么:(1)当市场价格为p 时,平均质量必为:()1122t p p t μ⎛⎫+ ⎪⎝⎭≥= (2)市场不会彻底萎缩。
(3)与信息完全相对照,关于q 的信息不对称使交易缩小了多少?使买卖双方的利益损失了多少?证明:(1)卖主的效用函数为1u M qn =+,其中q 对于卖主来说是确定的,因此,将卖主的预算约束代入效用函数之中可得:()11u y q p n =+- 当且仅当q p >时卖主才不会将车卖出,因此,一定有q p ≤,此时0n =,即出售二手车。
因此有:()2t Eq p p t μ+=≥= (2)把卖主的预算约束1y M p n =+⋅代入他的效用函数中,就有: ()11u y q p n =+-当且仅当出售汽车可以带给他更高的效用时,卖主选择出售汽车,即:()11y q p n y +-≤从而解得p q ≥,即市场价格不低于汽车质量时,卖主会出售汽车,这就意味着,当对于给定的市场价格p ,只有质量低于p 的汽车会出售。
把买主的预算约束2y M p n =+⋅代入他的效用函数中,就有2232u y q p n ⎛⎫=+- ⎪⎝⎭,由于买主不清楚市场上每辆汽车的具体质量,所以他只能最大化自己的期望效用,即:2232Eu y p n μ⎛⎫=+- ⎪⎝⎭这里()E q μ=。
当且仅当买车可以带给他更高的效用时,买主购买汽车,即:2232y p n y μ⎛⎫+-≥ ⎪⎝⎭其中()E q μ=。
从而得到32p μ≤,这就意味着买主的保留价格不会高于市场上汽车平均质量的1.5倍。
下面来求解市场均衡,分两种情况讨论:①3z t ≥时,假设均衡时市场上汽车的质量服从[],U t x ,那么市场上汽车的平均质量为2t x +,此时买主的保留价格为()33=224t x t x +⨯+,均衡时,买主的保留价格必然等于市场上最好的汽车的质量,即:()34x t x =+ 解得3x t =。
平新乔课后习题详解(第3讲--价格变化对消费者的配置效应与福利效应习)

平新乔《微观经济学十八讲》第3讲价格变化对消费者的配置效应与福利效应1 •证明:如果一个消费者只消费两种商品,假设是为与X2,那么它们不可能都是劣等品。
证明:劣等品是指随着消费者收入的增加,其需求量减少的商品。
如果假设第i种商品的马歇尔需求函数,那么商品i是劣等品就意味着 % p,m::. 0。
dm对于消费两种商品的消费者,如下的预算约束恒成立:px i Pigm P2X2 P,P2,m①式两边关于收入m求导,得到:% p i, p2,m X P i, P2,mp P2 1tm dm对于消费两种商品的消费者,等式②恒成立。
假设商品1和2都是劣等品,那么就有* P,m:::0,i =1或2,从而②式左边恒小于dm零,等式②不成立,这与假设矛盾!所以如果一个消费者只消费两种商品,那么它们不可能者E是劣等品。
2•如果偏好是凹的,替代效应仍然为负吗?答:如果偏好是凹的,替代效应不一定为负,但肯定是非正的。
分析如下:一种商品的替代效应是指价格变化引起商品需求量的总变化当中,仅仅因为该商品和其他商品之间的相对价格变化而引起的需求量的变化。
替代效应包括希克斯替代效应和斯拉茨基替代效应。
希克斯替代效应是指保持消费者的效用不变的情况下,价格变化引起的需求量的变化(如图3-1所示);斯拉茨基替代效应是指保持消费者的购买能力不变的情况下,价格变化引起的需求量的变化(如图3-2所示)。
X( P,m )是①图3-1 希克斯替代图3-2 斯拉茨基替代当消费者的偏好为凹的时候,替代效应非正,即替代效应或者为零,或者为负,见图3-3 (这里只考虑希克斯替代效应,斯拉茨基替代效应的分析也是类似的):图3-3 凹偏好的替代效应①替代效应为零的情况当商品1的价格上升引起预算线从AB转动到AC时,消费者对商品1的需求由B减少到C,如果保持消费者的效用不变,仅仅考虑相对价格的变化对商品1的需求的影响,那么由图中虚线BH的位置可以看出,商品1的需求不变,即价格变动的替代效应为零。
平新乔《微观经济学十八讲》课后习题和强化习题详解(1-3讲)【圣才出品】

lim
→0
1
x1 ln x1 1 x1
+ +
2 2
x2 x2
ln
x2
= exp
1 ln x1 +
2 ln x2
=
x1 1
x2 2
1 + 2 = 1
1
( ) (3)当 → − 时,对效用函数 u( x1, x2 ) = 1x1 + 2 x2 两边变换求极限有:
( ) ( ) lim u
3 / 62
4.设
u
(
x1,
x2
)
=
1 2
ln
x1
+
1 2
ln
x2
,这里
x1,x2
R+
。
(1)证明: x1 与 x2 的边际效用都递减。
(2)请给出一个效用函数形式,但该形式不具备边际效用递减的性质。
答:(1)将 u
关于
x1
和
x2
分别求二阶偏导数得
2u x12
=
−
1 2x12
y)
=
min
x,
y 2
,如图
1-3
所示。
图 1-3 喝一杯汽水就要吃两根冰棍 (4)如图 1-4 所示,其中 x 为中性品。
图 1-4 对于有无汽水喝毫不在意
2.作图:如果一个人的效用函数为 u ( x1, x2 ) = maxx1, x2
2 / 62
(1)请画出三条无差异曲线。 (2)如果 p1 = 1 , p2 = 2 , y = 10 。请在图 1-5 上找出该消费者的最优消费组合。 答:(1)由效用函数画出的三条无差异曲线如图 1-5 所示。
平新乔微观经济学十八讲04

7
支 赌 局 1 2 3 4 0.10 0.20 0.02 0.01 0.90 0.60 0.06 0.09 0.00 0.20 0.92 0.90 付 10000 元 1000 元 0元
上表内,矩阵中的数字代表每一种结果的发生概率(比如,在赌局 1 中,发生 10000 元的概率为 0.1) .如果有人告诉你,他在赌局"1"与"2"之间严格偏好于"1" ,在赌 局"3"与"4"之间严格偏好于"3" .请问他的选择一致吗?请做出说明. 说明:他的选择是一致的.设该赌徒的效用函数为 u ( w) ,设它原来的财富为零(初始 财富量不影响分析结果,后面会看到. ) 那么
A
B
C
D .试验显示,他认为 B = 0.4 A + 0.6 D C = 0.2 B + 0.8 D (这里的等号表示"无差异" )
请对 A,B,C,D 四种结局构筑出一组 VNM 效用值. (由连续性公理)有 解:令 u A = 1 , u B = 0 ,
u B = 0.4u A + 0.6u D = 0.4
bw bw
+ c ,则他的绝对风险规避系数
ab e ′′ Ra ( w) = u ( w) ′ = u ( w) abe bw
2
=b
cw
2
证明:若一个人的绝对风险规避系数为常数 c ,则其效用函数形式必为 u ( w) = e 这里 w 代表财产水平. (这个结论是有问题的,见证明结果) 证明:由已知得
u ( w) = e w
5 证明:在下列效用函数中,哪些显示出递减的风险规避行为: 5.1
平新乔十八讲答案第五讲

解:记 为初始财富,显然效用函数 二阶可微,被罚款的效用可以写成
, .
记被抓到的可能性按比例增加为 ,罚金按比例增加为 ;记 分别为被抓到的可能性增加的倍数和罚金增加的倍数.有
,
,其中 ;
根据条件, ,我们得到结果 .罚金按比例增加在防止非法停车上更有效.
解:他的财富现值为 ,最大化问题是
得, , .
因为 ,因此,他该借贷.
[注]当第零期消费的价格是1的时候,第一期的价格是 ,于是可以用前面的最大化框架来方便理解和处理类似跨期问题.
6.2如果 ,他该储蓄还是借贷?
解:最大化问题是
得, ,
因为 ,因此,他还是该借贷.
7一个人拥有固定财富 ,并把它分配在两时期的消费中,个人的效用函数由 给出,预算约束为 ,这里 是单期利率.
5.3如果所有的资产收益都要按比例交收入税,你对5.2的回答会怎样变化?
4题和5题的答案在文件“第五讲第四、五题”.
6某消费者的效用函数为 .这里 表示其在时期0的消费开支, 表示其在时期1的消费开支.银行存贷利率相等且为 ,该消费者在 期的收入为 ,在 的收入 .问
6.1如果 ,他该储蓄还是借贷?
解:种小麦和谷子的期望效用分别记为 和 ,有
,同理可得 ;
有 ,因此他会选择种谷子.
1.2假定农民在他的土地上可以每种作物都播种一半的话,他还会选择这样做吗?请解释你的结论.
解:农民这样播种的效用记为 ,有
;
因为 ,因此他会选择这样做.
1.3怎样组合小麦和谷子才可以给这个农民带来最大的效用?
解:最大化问题是
4在固定收益率为 的资产上投资 美元,可以在两种状态时获得 ;而在风险资产上的投资在好日子收益为 ,在坏日子为 ,其中 .通过上述假定,风险资产上的投资就可以在状态偏好的框架中被加以研究.
平新乔课后习题详解(第8讲--完全竞争与垄断)

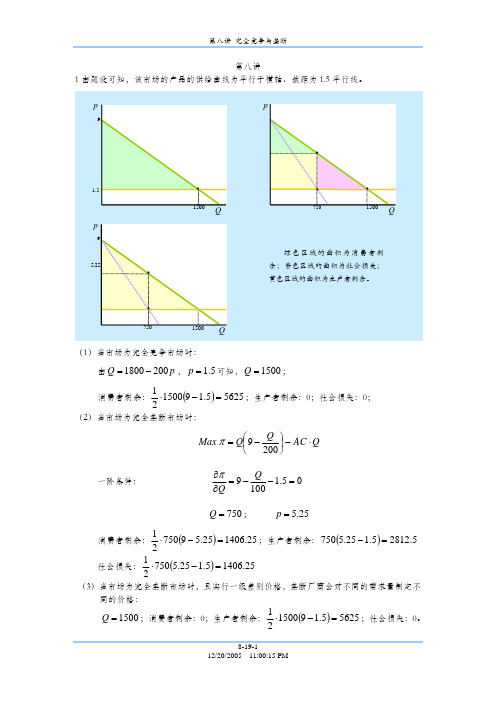
平新乔《微观经济学十八讲》第8讲 完全竞争与垄断1.某产品的市场需求曲线为:1800200Q p =-。
无论什么市场结构,该产品的平均成本始终是1.5。
(1)当该产品的市场是完全竞争市场时,市场价格和销量多大?消费者剩余、生产者剩余和社会的无谓损失是多大?(2)当该产品的市场是完全垄断市场时,只能实行单一价格,市场价格和销量多大?消费者剩余、生产者剩余和社会的无谓损失是多大?(3)当该产品的市场是完全垄断市场,同时生产者可以实行一级差别价格,市场销量多大?消费者剩余、生产者剩余和社会的无谓损失是多大?解:(1)在完全竞争的市场上,厂商的利润最大化问题为:()max qpq c q -从中解得利润最大化的必要条件为()p MC q =,即市场价格等于厂商的边际成本,事实上,这也给出了完全竞争厂商的供给曲线,即对于给定的价格,厂商总是愿意供给使边际成本等于市场价格的数量的产品。
根据本题的成本函数() 1.5c q q =,可知市场供给曲线为 1.5p =。
再利用需求曲线1800200Q p =-可以解得均衡的市场价格为 1.5p =,均衡产量为1500Q =。
消费者剩余1500019d 1.515005625200CS Q Q ⎛⎫=--⨯=⎰⎪⎝⎭,生产者剩余为零,社会的无谓损失也是零,如图8-1所示。
图8-1 消费者剩余和生产者剩余(2)在完全竞争的市场上,实行单一价格的垄断厂商的利润最大化问题为:()()max qp q q c q -其中()p q 是市场反需求函数。
把本题的市场反需求函数19200p q =-和成本函数() 1.5c q q =代入上式中整理得到:21max 7.5200q q q -解得利润最大化的产量为750q =,价格 5.25p =,厂商利润(生产者剩余)为:217.57507502812.5200π=⨯-⨯=消费者剩余为:750019d 5.257501406.25200CS Q Q ⎛⎫=--⨯=⎰ ⎪⎝⎭社会损失等于完全竞争市场的总剩余(消费者剩余和生产者剩余之和)减去垄断市场的总剩余,为56252812.51406.251406.25--=,如图8-2所示。
平新乔-微观十八讲答案

第七讲18%9.一个富有进取心的企业家购买了两个工厂以生产装饰品.每个工厂生产相同的产品且每个工厂的生产函数都是q=(K i L i) 1/2(i=1,2),但是K1=25,K2=100,K 与L的租金价格由w=r=1元给出。
(1)如果该企业家试图最小化短期生产总成本,产出应如何分配。
(5%)min{STC}= min{125+L1 +L2}S.T 5 L11/2+10L21/2≥QL(L1 ,L2)=125+ L1 +L2+λ[ Q-(5 L11/2+10L21/2 )]F.O.C(一阶条件) :1=5/2*λ* L1-1/21=10/2*λ* L2-1/2将两式相除得L2=4 L1再代入5 L11/2+10L21/2=Q得q1=5* L11/2=1/5Q ,q2=10* L21/2=4/5Q(2)给定最优分配,计算短期总成本、平均成本、边际成本曲线。
产量为100、125、200时的边际成本是多少?(5%)STC(Q)=125+5* L1=125+Q2/125SAC(Q)=125/Q+Q/125SMC(Q)=2/125*Q SMC(Q=100)=1.6, SMC(Q=125)=2, SMC(Q=200)=3.2(3)长期应如何分配?计算长期总成本、平均成本、边际成本。
(5%)min{LTC}= min{ K1+ K2+L1 +L2}S.T (K1 L1) 1/2 +(K2 L2) 1/2≥QL(L1 ,L2,K1,K2)= K1+ K2+ L1 +L2+λ[ Q-(K1 L1) 1/2 -(K2 L2) 1/2 )]F.O.C 1=1/2*λ*(K1/ L1 ) 1/21=1/2*λ*(K2/ L2 ) 1/21=1/2*λ*(L1/ K1 ) 1/21=1/2*λ*(L2/ K2 ) 1/2从而有K1/ L1 =K2/ L2,K1=L1,K2= L2所以L1+L2=Q,分配比例任意LC(Q)=2(L1+L2)=2Q LAC=2 LMC=2(4)如果两个厂商呈现规模报酬递减,则第三问会有什么变化?(3%)如果两个厂商呈现规模报酬递减则长期总成本、平均成本、边际成本均是产量的增函数。
平新乔微观经济学十八讲》答案

p1c + p2 s = M
(**)
s = 2M
c= M
综合*与**式,可以得到, p1 + 2 p2 , p1 + 2 p 2
6
第一讲 偏好、效用……
s′ = 2M
c′ = M
如果价格变成
p1′
和
p
′
2
,同样可以得到
p1′ + 2 p2′ ,
p1′ + 2 p2′ .咖啡和糖的
消费比例不会发生变化.
2 x12
因此 x1 的边际效用是递减的.同理, x2 的边际效用也是递减的.i
4.2. 请给出一个效用函数形式,使该形式不具备边际效用递减的性质.
答:可能的一个效用函数是 u(x1, x2 ) = x1 + x2 .
5. 常见的常替代弹性效用函数形式为
请证明:
( )1
u(x1 , x2 ) = α1 x1ρ + α 2 x2 ρ ρ
lim
ρ →−∞
t
(
x1
,
x2 )
=
x2
5
第一讲 偏好、效用……
当 x1 = x2 时,有 t(x1, x2 ) ≡ x1 = x2 综上所述,当 ρ → −∞ 时,原效用函数描述的偏好关系趋近于
u(x1, x2 ) = min{x1, x2} 所描述的偏好关系.
如果α1 与α 2 满足α1 + α 2 = 1 ,那么当 ρ → −∞ 时,同时有效用函数
为 p1′ 和 p2′ ,对她关于咖啡和糖的消费会发生什么影响?
解:咖啡和糖对茜茜而言是完全互补品(perfect complements),即她的效用函数可以表 示为(假设她的偏好满足单调性):
平新乔十八讲答案第三讲

10以需求函数 为例,试分析为什么在需求曲线缺乏弹性的部分经营不可能产生最大利润.
分析:该需求的弹性表达式为
,
需求曲线缺乏弹性时,有
.
经营的总收益为 ,
考虑企业的成本函数 ,其中 , ,
企业的利润函数为 .
最大利润产生在利润对价格一阶导等于零的地方:
.
9判断对错并简要说明理由:
和 是一个消费者消费的两种物品,我们说 是 的替代品,如果 , 为 的价格.如果 是 的替代品,则 也是 的替代品.
答:按照替代品的定义,第一句正确.第二句错误.
用斯勒兹基恒等式来分析,记 为 对 的替代效应, 为收入,有
,
和 符号均为负,但每个式子中的收入效应是不确定的.因此 ,并不意味着 一定成立.
证明:征税前消费者的消费者剩余为
,
费者剩余为
.
政府征税所获收入为
.
因此, .和
即消费者剩余的损失总是超过政府通过征税而获得的收入.
16设一个消费者只消费两类商品,他在 元, 元时购买了 , .现在, 下降至8元, 上升至6元.问该消费者的生活水平在价格变动后提高了还是降低了?为什么?
令 为调整收入以保持购买力条件下,对商品1的消费量. 为为保持购买力对收入进行调整后得到的收入.有:
,
.
其中,斯拉茨基替代效应 为
,
收入效应 为
.
4.2请根据计算,验证恩格尔加总规则.
解:由4.1知
, , , .
因此
,
恩格尔加总规则成立.
5(单项选择)当价格是(3,1)时,某个消费者选择的消费束是 .在新的价格 下,他选择的消费束是 ,若此消费者的行为满足显示偏好的弱公里,那么必定有:
平新乔《微观经济学十八讲》课后习题和强化习题详解(企业的性质、边界与产权)

第18讲企业的性质、边界与产权18.1 课后习题详解1.有三种类型的契约被用来区分一块农地的租佃者向地主支付租金的方式:(1)以货币(或固定数量的农产品);(2)以收成的固定比率;(3)以“劳动租”,即同意在地主的另一块土地上工作的形式来付租金。
这些各自不同的契约规范会对佃农的生产决策产生什么影响?在实施每种契约时会发生何种交易费用?在不同的地方或在不同的历史阶段中,哪些经济因素会影响已确定的契约类型?答:(1)对于货币租来说,这种形式的租金是将市场的风险在地主与佃农之间进行分担,这使得佃农在做生产决策时不仅要考虑生产上可能出现的风险,比如天气状况变化对生产的影响等等,还必须考虑到市场上农产品价格变化对佃农利益的影响。
如果佃农是风险回避的,则这种加大佃农风险的承租方式会导致农民不愿意租土地进行经营。
这样会使土地的出租率下降,从而导致土地的租金下降,最终影响到地主的利益。
交易费用主要是地主为鼓励农民使用这种形式的契约而不得不放弃部分地租。
对于这种形式的契约,一般是在市场经济有了很大的发展以后才会发生,因此,必然出现在资本主义萌芽以后的社会。
在资本主义社会里,由于货币的普遍使用,因此使得土地的租金更多地采用了货币的形式,这对于农民来说意味着更大的风险,因此租金比以前的租金形式有所下调,并且出现了各种各样的金融工具来帮助农民来分散风险,例如金融衍生工具中的期货便具有这种功能。
(2)对于分成地租,更多是在劳动地租逐渐消亡以后才出现的,它是为了调动农民积极性而采取的一种租金形式。
在征收分成地租的情况下,农民要承担一定的生产风险,即如果收成不好,则农民的收入就会减少。
通常情况下,分成地租是通过将每年收成的一个固定的百分比给予地主,而将收入的剩余部分留给农民。
这种形式的契约有利于调动农民的积极性,当然同时也给农民带来了一定的风险。
在历史上,还出现过另外的一种固定地租的形式,即地主规定农民必须在每年上缴一定的收成,剩余的归农民,这种形式的租金是将全部的风险都留给了农民,其前提假设是农民是风险中性的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平新乔《微观经济学十八讲》答案目录第一讲偏好、效用与消费者的基本问题 (2)第二讲间接效用函数与支出函数 (9)第三讲价格变化对消费者配置效应与福利效应 (18)第四讲 VNM效用函数与风险升水 (25)第五讲风险规避、风险投资和跨期决策 (32)第六讲生产函数与规模报酬 (45)第七讲要素需求函数、成本函数、利润函数与供给函数 (57)第八讲完全竞争与垄断 (68)第九讲 Cournot均衡、Bertrand均衡与不完全竞争 (80)第十讲策略性博弈与纳什均衡 (93)第十一讲广延型博弈与反向归纳策略 (100)第十二讲子博弈与完美性 (105)第十三讲委托–代理理论初步 (110)第十四讲信息不对称、逆向选择与信号博弈 (118)第十五讲工资、寻找工作与劳动市场中的匹配 (125)第十六讲一般均衡与福利经济学的两个基本定理 (134)第十七讲外在性、科斯定理与公共品理论 (140)12221221111p ap p p ap ap p ayv p v q =⎟⎟⎠⎞⎜⎜⎝⎛−−=∂∂∂∂−=22222121221p ap y p p yp a ap p ayv p vq −=−−=∂∂∂∂−=与从直接效用函数中推得的结果一致.2. 某个消费者的效用函数是22121),(x x x x u =,商品1和2的价格分别是1p 和2p ,此消费者的收入为m ,求马歇尔效用函数和支出函数.解:解线性规划:y x p x p t s x x x x =+2211221,..max 21 其拉格朗日函数为:)(),;(221122121x p x p y x x x x L −−+=λλ使)(⋅L 最大化要求λ,,21x x 满足一阶条件021211=−=∂∂p x x x Lλ 102212=−=∂∂p x x Lλ 202211=−−=∂∂x p x p y Lλ 31式除以2式,得:2112211222p x p x p px x =⇒= 4 代4入3式,得1x 的需求函数:111132023p yx x p y =⇒=−5代5入4式,得2x 的需求函数:223p yx =6代5、6两式入效用函数中,得到当效用最大化时有间接效用函数:22122121332),(),(p yp y x x x x u y p v ⎟⎟⎠⎞⎜⎜⎝⎛===又消费者效用最大化意味着()()y p v p e y ,,=即可得到支出函数:()()()3122131221223108)),(,(,u p p up p y y p v p e u p e ====3. 考虑下列间接效用函数()2121,,p p mm p p v +=这里m 表示收入,问:什么是该效用函数所对应的马歇尔需求函数),,(21*1m p p x 与),,(21*2m p p x 解iii :根据罗尔恒等式,可以得到这个效用函数所对应的马歇尔需求函数:()2121221111p p m p p p p myv p vx +=++−−=∂∂∂∂−=()2121221121p p m p p p p myv p vx +=++−−=∂∂∂∂−=4. 考虑一退休老人,他有一份固定收入,想在北京、上海与广州三成事中选择居住地.假定他的选择决策只根据其效用函数,设该效用函数的形式为21x x u =,这里()221,+∈R x x .已知北京的物价为()a a p p 21,,上海的物价为()b b p p 21,,并且b b a a p p p p 2121=,但ba b a p p p p 2211,≠≠.又知广州的物价为()()()⎟⎠⎞⎜⎝⎛++=b a b a c c p p p pp p 22112121,21,.若该退休老人是理智的,他会选择哪个城市去生活?iv解:设老人在北京、上海、广州的效用分别为c b a u u u ,,,设老人的收入为m .有⎦⎤⎢⎣⎡−+=−+=−+c c b b a a c c b b a a cba p p p p p p m p p m p p m p p m u u u 2121212212212212211842442因为bbaap p p p 2121=,所以⎦⎤⎢⎣⎡−=−+c c a a c b a p p p p m u u u 212121142(*)又ba b a p p p p 2211,≠≠,有()()a a bb a a ba b a c c p p p p p p p p p p p p 2121212211211282=<++=(**)由*与**,得02<−+c ba u u u又bau u =,所以有0<−c a u u ,0<−cb u u即老人将选择在广州生活.1 5.5.1. 设21x x u =,这里()221,+∈R x x ,求与该效用函数想对应的支出函数()u p p e ,,21.解:解线性规划:u x x t s x p x p x x =+212211,..min 21其拉格朗日函数为:())(.,;21221121x x u x p x p x x L −++=λλ使)(⋅L 最大化要求λ,,21x x 满足一阶条件0211=−=∂∂x p x Lλ 10122=−=∂∂x p x Lλ 2021=−=∂∂x x u Lλ 31该题解答的修正得益于网友caidb 在中心论坛上的帖子.关于caidb 的个人信息在/forum/user_info.asp?id=121264上由1式、2式,得()u p p e ,,21λ12p x =,λ21p x =4代4入3,得u p p p p u 212210=⇒=−λλ 5代5入4,得212p p u x =,121p p u x =于是可以得到对应的支出函数()u p p x p x p u p p e 212211212,,=+=5.2. 又设21ln ln x x u +=′,同样()221,+∈R x x ,求与该效用函数想对应的支出函数()u p p e ′′,,21解:解法与5.1完全相同,得到()u e p p u p p e ′=′′21212,,5.3. 证明:()()u p p e u p p e ,,,,2121=′′证明:up p e p p e p p u u x x u x x u uu 21ln 21212121222ln ln ln ==⇒=′⇒⎭⎬⎫+=′=′根据5.1与5.2的结果,得到()()u p p e u p p e ,,,,2121=′′6. 设某消费者的间接效用函数为()αα−=12121,,p p m m p p v ,这里10<<α.什么是该消费者对物品1的希克斯需求函数?解:若消费束x 是消费者的最优选择,那么根据引理一,间接效用函数与支出函数存在以下关系()()m p v p e m ,,= 1由该消费者的间接效用函数,得到αα−=121p p u m ,其中),,(21m p p v u = 2由1式和2式,得到()()αα−=121,,p p u m p v p e因此,由Shepard 引理,得到12111−⎟⎟⎠⎞⎜⎜⎝⎛=∂∂=αp p u p ex h ,α⎟⎟⎠⎞⎜⎜⎝⎛=∂∂=2122p p u p ex h7. 考虑含n 种商品的Cobb-Douglass 效用函数∏==ni i ix A x u 1)(α这里,0>A ,∑==ni i11α7.1. 求马歇尔需求函数解:解线性规划:ypx t s x A ni i xi=∏=..max 1α其拉格朗日函数为:()()px y x A x L ni i i −+=∏=λλα1;使)(⋅L 最大化要求λ,,21x x 满足一阶条件01=−=−=∂∂∏≠−j j j j j i i j j j p x u p x A x x L i j λαλααα,n j ,...,3,2,1= 10=−=∂∂px y Lλ 2由1式,得j jj p u x λα=,n j ,...,3,2,1= 3代3入2,得y uuy u y p u p y ni ni iii i =⇒=−=−=−∑∑==λλλαλα110 4代4入3,得希克斯需求函数j j j p yx α=,n j ,...,3,2,1=7.2. 求间接效用函数解:根据7.1的结果()iini iini iin i ii ni i i p Ay p Ay p y A x u y p v ααααααα∏∏∏===⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛∑=⎟⎟⎠⎞⎜⎜⎝⎛===1111)(,其中x 为消费者的需求量.7.3. 计算支出函数(同第6题的解法.不过这样的写法可能会好些☺) 解:令ini i i p Ay y p v u αα∏=⎟⎟⎠⎞⎜⎜⎝⎛==1),(得到in i iip A u y αα−=−∏⎟⎟⎠⎞⎜⎜⎝⎛=11又由()),,(y p v p e y =,得到()ini ii p A u u p e αα∏=−⎟⎟⎠⎞⎜⎜⎝⎛=11,7.4. 计算希克斯需求函数解:根据Shepard 引理和7.3的结果,得到希克斯需求函数∏≠−−⎟⎟⎠⎞⎜⎜⎝⎛=∂∂=j i ii j j h j ij p p A u p e x ααα11,n j ,...,3,2,1=8. 以Cobb-Douglass 效用函数为例说明求解效用最大化问题和求解支出最小化问题可以得到同一需求函数.解:令效用函数形式为∏==ni i ix A x u 1)(α,预算约束为y px =************************************************************* 求解效用最大化问题得到的需求函数为(见7.1题)jj j p yx α=,n j ,...,3,2,1=************************************************************* 求解支出最小化问题的拉格朗日函数为()⎟⎟⎠⎞⎜⎜⎝⎛−′+=′∏=ni iix A u px x L 1;αλλ使)(⋅L 最大化要求λ′,x 满足一阶条件jjj p u x αλ′=1代入1=−∏=ni i i x A u α,得∏∏=−=⎟⎟⎠⎞⎜⎜⎝⎛=′⇒=⎟⎟⎠⎞⎜⎜⎝⎛′−ni iini i iiip A p u A u 1110αααλαλ 2代2入1得到希克斯需求函数:j j ni iijjh j pu p A p u x iαααλα∏=−⎟⎟⎠⎞⎜⎜⎝⎛=′=11,n j ,...,3,2,1= 3代∏==ni i ix A x u 1)(α入3得到∏=⎟⎟⎠⎞⎜⎜⎝⎛=ni j j i i i hj px p x i1ααα,n j ,...,3,2,1= 4代4入预算约束y px =得⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛=∏∑∏∑∏=====ii i n i i i in j j n i i i i nj j j n i i i i j x p x p p x p p y αααααααα11111 5代5入4得∏==⎟⎟⎠⎞⎜⎜⎝⎛=ni j jj j i i i h jpy p x p x i1αααα,n j ,...,3,2,1= 6由3式与6式知,求解支出最小化与效用最大化得到的需求函数是一样的. 9. 下列说法对吗?为什么?函数21)(),(u p u p x x x hj+=可以作为某种商品的希克斯需求函数. 答:不对.由于该需求函数仅与该商品的价格相关,因此可以令所有其它商品的消费量为零.根据Shepard 引理,支出函数是该希克斯需求函数的一个原函数. 又()()C u p dp u p x x x ++=+∫232132其中,无论C 取什么值,()Cu p x ++2332都不是x p 的一次齐次函数,因此该函数不可以作为某种商品的希克斯需求函数.10. 下列函数能成为一个马歇尔需求函数吗?为什么?()222,,y x x y x p p I p y p p x +=这里,x 与y 是两种商品,I 为收入. 答:假设该函数是一个马歇尔需求函数.由>∂∂Ix可知,x 是正常商品,它的需求量在任何情况下随收入上升而上升.又当x yp p >时,0>∂∂xp x,因此在x y p p >时,x 的需求量随价格上升而上升.综上所述,当x y p p >时,该商品的替代效应为正.而任何商品价格变化对该商品需求量所起的替代效应为非正.因此,该函数不是一个马歇尔需求函数.第五讲,第4题第一问,第二问基本上的图就是这样,A 点为将财富全部投入到风险投资时的状态,B 点为全部投入到安全资产时的状态,以这两点为端点的线段表示的就是投资者所有可能的资产组合. 第三问见第5题的解答.第五讲,第5题设投资者的效用函数为)(w u . 设g w 为投资者在好的状态下的财富,b w 为坏状态下的财富.设投资者认为有P 的概率出现好的状态.设]1,0[∈λ为风险资产在投资组合中所占比例. 由题意知,投资者决定λ是以u 的最大化为标准.即:),(max arg *]1,0[λλλw u ∈∈7因此,λ必须满足0)·(=λd du *又7事实上,很明显这个集合里面至多只有一个元素.[][]*****)1)(1()1()1()1)(1()1()()1((),(w r w r u P w r w r Pu w u P w Pu w u g g b g +−++−++−++=−+=λλλλλ代入(*)得,krr r r P P dw w du dw w du g b b g =−−−−=·1)()( **现在证明dw w du dww du b g )()(是λ的单调函数.若0)(>′w u ,0)(<′′w u ***那么,如果有ijλλ>则有)]([)]([ig j g w u w u λλ>,)]([)]([i b j b w u w u λλ< 由假设(***)知,必然有dw w du dww du dww du dw w du i b i g j b j g )]([)]([)]([)]([λλλλ>(即为λ的单调递增函数)也就是说,等式(**)决定了唯一一个最优风险资本比例λ.如果k 值并不在dw w du dww du b g )()(的值域内,事实上就说明,投资者将选择纯风险投资,即1=λ,如果1=k ,那么,投资者将选择1=λ(这解答了第4题的第三问) 第一问设对财富按比例征税的税率为w t ,那么dw w du dw w du dww du t dw w du t dww du dw w du b g b w g w t b t g w w )()()()1()()1()()(,,=−−=,而仍然对应原有的风险资产比例λ,风险资产的比例不变. 第二问设对安全资产的收益按比例征税的税率为s t 那么krr r r P P rt t r r rt t r r P P dw w du dw w du g b s s g s s b t b t g s s =−−−−>++−++−−−=·1·1)()(,,所以,如果考虑对安全资产的征税,风险资产比例λ应该增加.这对只投资无风险资产的投资者的影响最大. 第三问设对安全资产的收益按比例征税的税率为s t ,对风险资产收益按比例征税的税率为r t .那么ss r g r g ss r g r b t t b t t g rt t t r t r r rt t t r t r r P P dw w du dw w du r s r s ++−−−++−−−−−=·1)()(,,,, 结果是,如果0>++−−s s r g r rt t t r t ,那么最优风险资产比例λ应该上升,如果0<++−−s s r g r rt t t r t ,那么最优λ应当下降,0=++−−s s r g r rt t t r t 时,最优λ应当保持不变.请以横轴表示布的数量,纵轴表示以粮食数量所代表的布的价格,作出该村布的供给曲线.两张图的连线都是假设的,它们可以有其他的(比如说平滑的)形状.对下面的生产函数。
